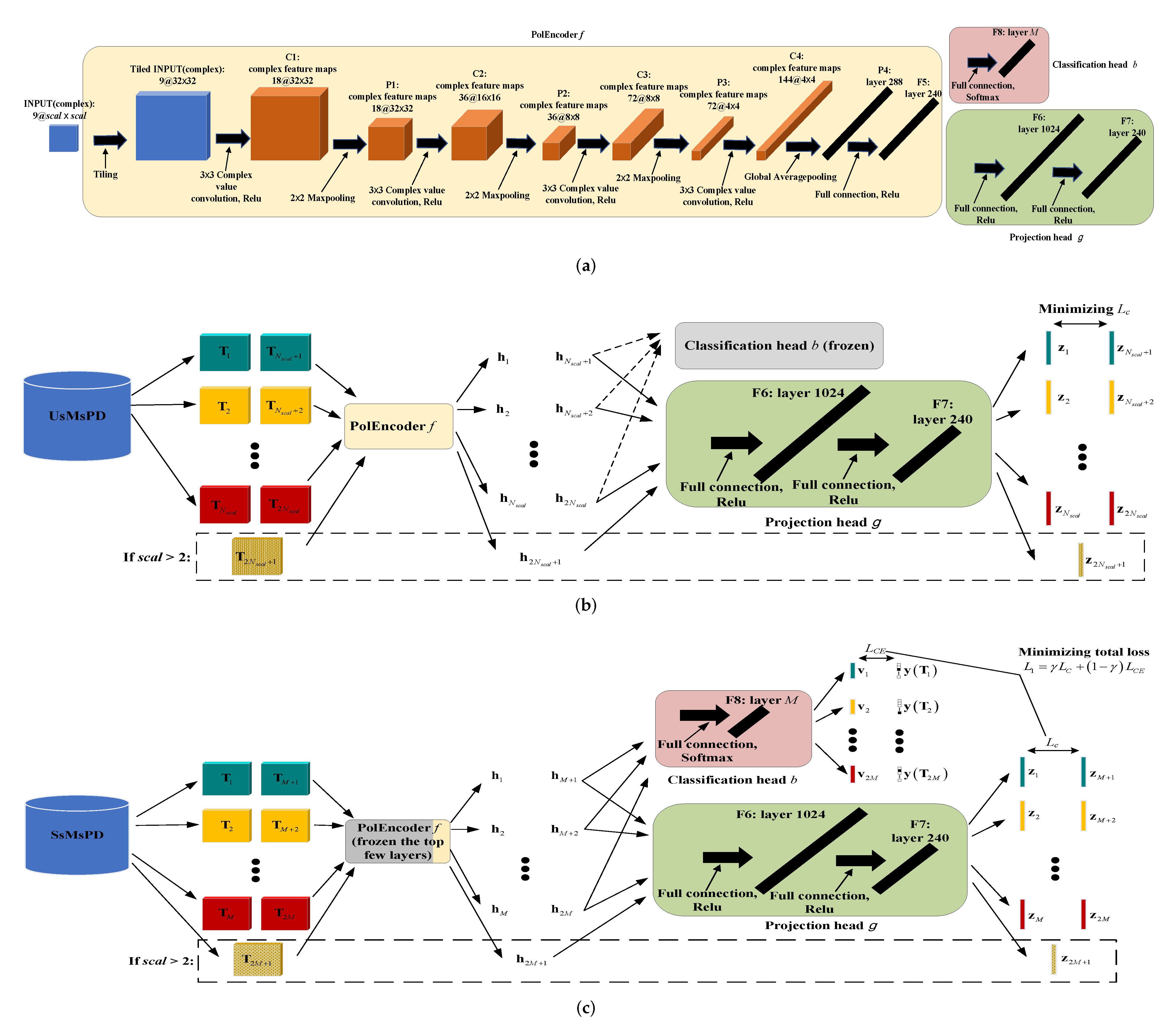
3.1.1. Unsupervised Multi-Scaled Patch-Level Dataset
For the first contrastive learning stage of the TCNet, basing on multi-PolSAR images, we construct the dataset UsMsPD, consisting of patch samples of multi-scales, in an unsupervised manner.
Figure 3a overviews how to establish the UsMsPD. Given a scale, firstly, patch samples are selected and clustered without supervision, conditioned on different PolSAR images. Secondly, clusters of all the PolSAR images are fused, so that each sample cluster contains multi-PolSAR images’ patches. Thirdly, we execute data cleaning for attaining more consistent clusters. Fourthly, the corresponding positive samples are picked from the multi-PolSAR images. Lastly, all these positive samples and their original samples are stored together to constitute the UsMsPD.
(1) Unsupervised sampling and clustering:
Figure 3b displays how to receive and organize the qualified patch samples containing as few land cover categories as possible in an unsupervised manner. Simple linear iterative clustering (SLIC) [
31] is a classical superpixel algorithm, which is fast, memory efficient and exhibits nice boundary adherence. So we resort to SLIC to segment a PolSAR image into individual superpixels. The Pauli scatter vector
is used to represent every pixel in conducting SLIC, where
means the scattering matrix element with the
polarization of a receiving-transmitting wave (
h and
v are the notations of the horizon and vertical linear polarizations, respectively). After running SLIC in the PolSAR image
, we look at all the superpixels, and get the set
of path samples with the specific scale
, as follows:
where
refers to the PolSAR image segmented by SLIC;
means the scale of the selected patches;
is the sampled complex-valued patch contained in the superpixel
where every pixel is a coherency matrix, i.e.,
;
is to calculate the number of pixels of a superpixel or a patch, so the second condition of (
1) stipulates a superpixel must have above 4 times more pixels than the sampled patch it contains. As an unsupervised image segmentation algorithm, SLIC may produce a few under-segmented superpixels, where most heterogeneous pixels are far from central positions. To reduce the impact of under-segmented superpixels on the purity of the sampled patches, each patch is located in the center of whose corresponding superpixel which should possess more pixels than the sampled patch. The pixel multiple of a superpixel to its corresponding patch sample is consistent with the selection range (4 fold neighborhood) of a positive sample, so that both patches of a positive sample pair are covered by one superpixel as much as possible.
As mentioned before, it is not that arbitrary two patches can be negative samples of each other. Therefore, the popular Spetral Cluster [
32] is leveraged to divide all the patches of the same size from the same PolSAR image into several clusters, where any two patches belonging to different clusters are regarded as negative samples of each other. Spectral Clustering uses a similarity matrix of all samples as the input. At first, we compute the Wishart distribution based distance [
14]
for each two patch samples
i and
j, where
and
are the mean coherency matrixes of patch
i and
j, respectively. And then, the reciprocal of
is utilized to form the similarity matrix
A, as follows:
It can be found from (
2) that
, so the matrix
is asymmetric. In order to botain a symmetric similarity matrix and avoid the measurement inaccuracy caused by the asymmetry of
, we carry out a simple and efficient average operation of
and its transpose. Finally, using
, spectral clustering segments
into
clusters. Performing the above operations on all the PolSAR images to be classified, several groups of sample clusters
are achieved, where
is the patch set of cluster
n for PolSAR image
.
(2) Cluster fusing: After the previous operations, all the
I PolSAR images to be classified are processed into
patch clusters separately. It is necessary to fuse these clusters into
larger clusters, each composed of clusters stemming from different PolSAR images, to use these samples in training the same model. It is clearly a stable matching problem, which can be solved by the Gale–Shapley algorithm [
33], as follows:
where,
is the set of vector representations of PolSAR image
at scale
, whose every element is the mean of all averaged coherency matrixes
for cluster
n;
is the final fused result, which is worked out by recursively executing Gale–Shapley algorithm
according to (
4). In (
4), the matching score of two clusters is computed through
to generate the “ranking matrix” according to [
33] and get the matching result.
Figure 3c is the diagram of cluster fusing. In the execution of cluster fusing, the ordering of patch clusters also matters. We should first fuse the clusters of images containing more samples. In the first few steps of fusion, the size of one cluster has a great influence on its representation. Clusters with fewer samples may be more easily affected by some bad samples, leading to inconsistent matching of clusters, and finally result in an unreasonable fusion, and even hinder the network from learning the intrinsic representation of PolSAR images. At the later stage of fusion, the fusion will be more robust to the small clusters because larger clusters have been generated.
(3) Data cleaning: To keep the patch samples of the same cluster consistent, the “outlier samples” that differ greatly from the others should be removed through data cleaning.
Figure 3d demonstrates the procedure of data cleaning for one fused cluster. Firstly, we build a fully connected graph with all patch samples as the nodes by (
3). Next, the connectivity of each node is acquired by summing all the connection weights between it and the other nodes. Then, we find the node of the highest connectivity, and compute the ratio of each node’s connectivity to the highest value. Finally, by removing the nodes with a connectivity ratio below the predefined threshold, the ultimate “fairly clean” clusters are acquired.
(4) Positive sampling: In order not to destroy the polarization characteristics of the sampled PolSAR patches, we do not construct positive sample pairs by data augmentation. It is also unreasonable to directly view a cluster’s image patches as positive samples of one another because they still possibly belong to different land cover types. Our scheme is to collect positive samples near the original ones. The two patches that make up a positive sample pair should near to each other in polarization space and include as few duplicate pixels. To this end, we put forward a mixed distance, as follows:
where the first term is the Wishart distribution based distance as (
2), the second term represents the spatial distance,
(or
) and
(or
) are the vertical and horizontal coordinates for the center of patch sample
i (or
j), respectively, and
(we set
in this article) is the hyper-parameter to control the contribution of spatial distance to the mixed distance. For any patch
sampled before, in its four times area neighbourhood, a certain number of new image patches
are sampled as the set of its candidate positive samples, in which the candidate sample has minimum mixed distance to
is chosen as the positive sample
, as follows:
Figure 3e shows three relationships between an original sample and its candidate samples. The left two patches are too close in spatial space and have lots of the same pixels. The middle two patches are too far away in polarization characteristics and may belong to different land covers. The right two patches are neither too close in spatial space nor far away in polarization characteristics and have the minimum mixed distance, which can be positive samples of each other. Besides, four times neighbourhood restricts every pair of positive samples to one superpixel, reducing the risk that the two samples containing different land covers due to the extremely large spatial distance.
The previous operations are under a single value of . For the UsMsPD, . As stated at the beginning of this section, for learning the purity of a patch sample, the context inside a patch can be modeled by extracting the dependence in the sub-patches of this patch (the specific procedure will be described later). Although a patch can continue to be evenly split into four smaller sub-patch, i.e., four pixels, their dependence is not enough to reflect the purity of the patch. Because individual pixels are susceptible to noise. Therefore, we define as the smallest sample scale, that is, the minimum of is 2.
Using all the optional , we get the entire unsupervised multi-scaled patch-level dataset, UsMsPD.
3.1.2. Semi-Supervised Multi-Scale Patch-Level Dataset
It is essential to establish the dataset SsMsPD, including category labels, to make the network gain discrimination capability for concrete land cover categories, which cannot be learned from the UsMsPD. In realistic application, an entire PolSAR image cannot be classified satisfactorily with only one scale of patches, so the dataset should contain multi-scaled patches. In addition, when predicting, it cannot be ensured that all patches contain only one land cover. The annotated patch-level dataset SsMsPD should include two kinds of patch samples: the patches only contain one type of land cover, i.e., pure patches; the patches contain two or more land cover categories, i.e., impure patches. As is shown in
Figure 4a, in the SsMsPD, the pure patches are collected by hand, while the impure patches are automatically generated. Thus, the SsMsPD is obtained in a semi-supervised way.
Figure 4b is the specific sampling and generating process from one PolSAR image in
Figure 4a. Firstly, some big PolSAR blocks are selected manually, each corresponding to a land cover category. And then, multi-scaled pure patches
are randomly sampled from these blocks. All the pure patches from the same big block share the same land cover category, thus their labels
are given. Here,
and
are defined before. Next, impure patches
are generated based on smaller pure patches
and impures patches
, as follows:
where
represents stitching four patches into a larger impure patch; the first condition suggests that impure patches have only four scales to choose from, i.e.,
; the second condition means the smaller patch-level samples used in
contain pure patches and impure patches; the third condition avoids that an impure patch is stitched by four pure patches that have the same land cover category. In the actual implementation, smaller impure patches must be generated earlier in order that they can be used in generating larger impure patches. Thus, see
Figure 4c, the larger an impure patch is, the more complex its land cover is.