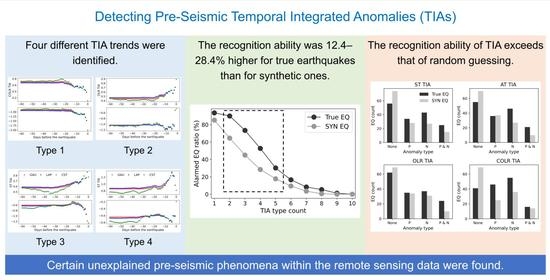
Pre-Seismic Temporal Integrated Anomalies from Multiparametric Remote Sensing Data

Abstract

Pre-seismic anomalies have the potential to indicate imminent strong earthquakes in the short to medium terms. However, an improved understanding of the statistical significance between anomalies and earthquakes is required to develop operational forecasting systems. We developed a temporal integrated anomaly (TIA) method to obtain the temporal trends of multiparametric anomalies derived from the Atmospheric Infrared Sounder (AIRS) product before earthquakes. A total of 169 global earthquakes that occurred from 2006 to 2020 and had magnitudes of ≥7.0 and focal depths of ≤70 km were used to test this new method in a retrospective manner. In addition, 169 synthetic earthquakes were randomly generated to demonstrate the suppression capacity of the TIA method for false alarms. We identified four different TIA trends according to the temporal characteristics of positive and negative TIAs. Long-term correlation analyses show that the recognition ability was 12.4–28.4% higher for true earthquakes than for synthetic earthquakes (i.e., higher than that of a random guess). Incorporating 2–5 kinds of TIAs offered the best chance of recognizing imminent shocks, highlighting the importance of multiparameter anomalies. Although the TIA trend characteristics before the earthquakes were not unique, we identified certain unexplained pre-seismic phenomena within the remote sensing data. The results provide new insight into the relationships between pre-seismic anomalies and earthquakes; moreover, the recognition ability of the proposed approach exceeds that of random guessing.

1. Introduction

Earthquakes and their associated disasters are major hazards around the world. Accurately predicting earthquakes would give communities more time to prepare [1,2]; however, despite decades of research, earthquake prediction remains an open question [2,3,4,5,6,7]. Utilizing pre-seismic anomalies in remote sensing data has become a research focus owing to the continuous development of space-based remote sensing technologies that provide various geophysical parameters from the top of the atmosphere (TOA) to the Earth’s surface [8,9]. However, current anomaly detection methods fail to meet the requirements of operational earthquake forecasting systems [10,11]. In particular, improved pre-seismic anomaly recognition is fundamental to advancing short-to-medium term earthquake forecasting based on remote sensing data.

Precursory signals are most significant in epicentral areas and close by, and their possible correlation with earthquake preparation phases is the basis of earthquake forecasts. By monitoring tectonic activity using remote sensing technologies in seismically active areas, we can further our scientific understanding of pre-seismic diagnostic variation [12,13]. An earthquake is a dynamic process that involves the transition of mechanical energy, electromagnetic radiation, and thermal effects [14]. Thus, many physical pre-seismic parameters have been used to analyze the anomalous signals of earthquake events during preparation phases [2,15,16,17,18,19]. Remote sensing data offer a variety of geophysical and geochemical parameters, and thereby provide abundant data for pre-seismic anomaly detection [8,20]. Moreover, remotely sensed data derived from satellite platforms are of high spatial and temporal resolution, take global measurements, generate rigorously validated data products, are easily accessed, and have broad community applications. Therefore, observable parameters have the potential to indicate the spatial extent, time window, and magnitude of an imminent event at different time scales with various degrees of probability. As such, remote sensing is the principal means of gathering and discerning pre-seismic anomalous information to prepare for potentially destructive earthquakes.

The earthquake preparation phase involves complex nucleation and non-linear faulting processes, and a variety of geophysical parameters have been considered for pre-seismic anomaly analysis [15,21]. Promising correlations between pre-seismic anomalies and strong earthquakes have been reported [4,8,9,15,20,22,23]. Surface temperature is a widely used parameter to detect earthquake-related thermal effects, with anomalous changes of $\pm 10 \mathrm{K}$ being reported before earthquakes [24,25,26]. Near-surface air temperature is strongly related to surface temperature, and significant anomalies of air temperature have been observed prior to large earthquakes because of degassing and air ionization along the fault system [27,28]. Column water vapor, which can be accurately estimated from remote sensing data, shows anomalous changes in epicentral areas, possibly related to ascending fluids and surface latent heat flux [29,30]. Outgoing longwave radiation (OLR) at the TOA is another candidate precursor for predicting earthquakes [31]. OLR anomalies represent the overall thermal effects from the clouds, atmosphere, and Earth’s surface, all of which are impacted by seismogenic activity; large variations of >10 W/m² have been reported prior to earthquakes [32,33]. Finally, multi-parametric analyses have been carried out with the aim of improving correlations between pre-seismic anomalies and imminent shocks [30,33,34].

However, despite some promising advances, in practice, earthquake forecasting results indicate the low statistical significance of these precursors. As a result, forecasts suffer from a high rate of false alarms when using remotely sensed land surface temperatures [11], while the false alarm rate can be effectively suppressed using seismic catalog data based on the natural time analysis approach [23]. Surface and atmospheric anomalies can have different effects. The impacts of short-term meteorological disturbances and anthropogenic interferences are difficult to eliminate. As such, anomaly detection methods require improved knowledge of pre-seismic anomalous characteristics in both the spatial and temporal domains to improve the forecasting ability.

Pre-seismic anomalies are influenced by topography, land cover, meteorology, and deep tectonic features. Observable information that is drawn from deep strata only accounts for a small proportion of most dominant features. Therefore, it is difficult to eliminate the influence of non-tectonic factors on thermal infrared radiation and to extract weak signals (i.e., pre-seismic anomalies) from strong noise backgrounds that reflect both natural processes and anthropogenic activities. Meanwhile, the pre-seismic phase before a significant earthquake is important for identifying anomalous signals. Therefore, we developed a pre-earthquake temporal integrated anomaly (TIA) method to describe the overall anomalous variation in a specified period (from days to months). The foreshocks before strong earthquakes are accompanied by a significant nucleation process [35] and exhibit intensive enhancement with a power law [36,37,38]. This will affect the occurrence and evolution of pre-seismic anomalies to a certain extent. By using the TIA, the influence of the weakness, transience, and discontinuity of the anomaly was reduced to highlight the overall change over a specific period. Then, the cumulative temporal trend of the TIA was used to identify the intensive enhancement of seismic-related anomalies in different time periods. Moreover, multiparametric TIAs were analyzed to inspect their feasibility for improving earthquake forecasting ability.

2. Data

2.1. Atmospheric Infrared Sounder (AIRS) Product

Hyperspectral infrared data make it possible to retrieve surface and atmospheric properties into various geophysical parameters [39]. Since 2002, the AIRS on the Aqua satellite has measured thermal infrared radiation emitted from the Earth’s surface and atmosphere in a three-dimensional structure on a global scale twice a day. In this study, we used the Aqua/AIRS L3 Daily Standard Physical Retrieval (AIRS-only) V7.0 (AIRS3STD) product with 1-degree spatial resolution from descending (nighttime) orbits to estimate pre-seismic anomalies, including skin temperature (ST; K), near-surface air temperature (AT; K), total integrated column water vapor burden (CWV; kg/m²), OLR (W/m²), and clear-sky OLR (COLR; W/m²). These parameters measure information at different vertical levels from the surface to the TOA and reflect the process of thermal radiative energy, which can be affected by seismic-related anomalous interference. Using nighttime remote sensing data minimizes the effect of solar radiation and improves the reliability of pre-seismic anomalies [40,41]. The AIRS data from 2002 to 2020 were used for pre-seismic anomalies.

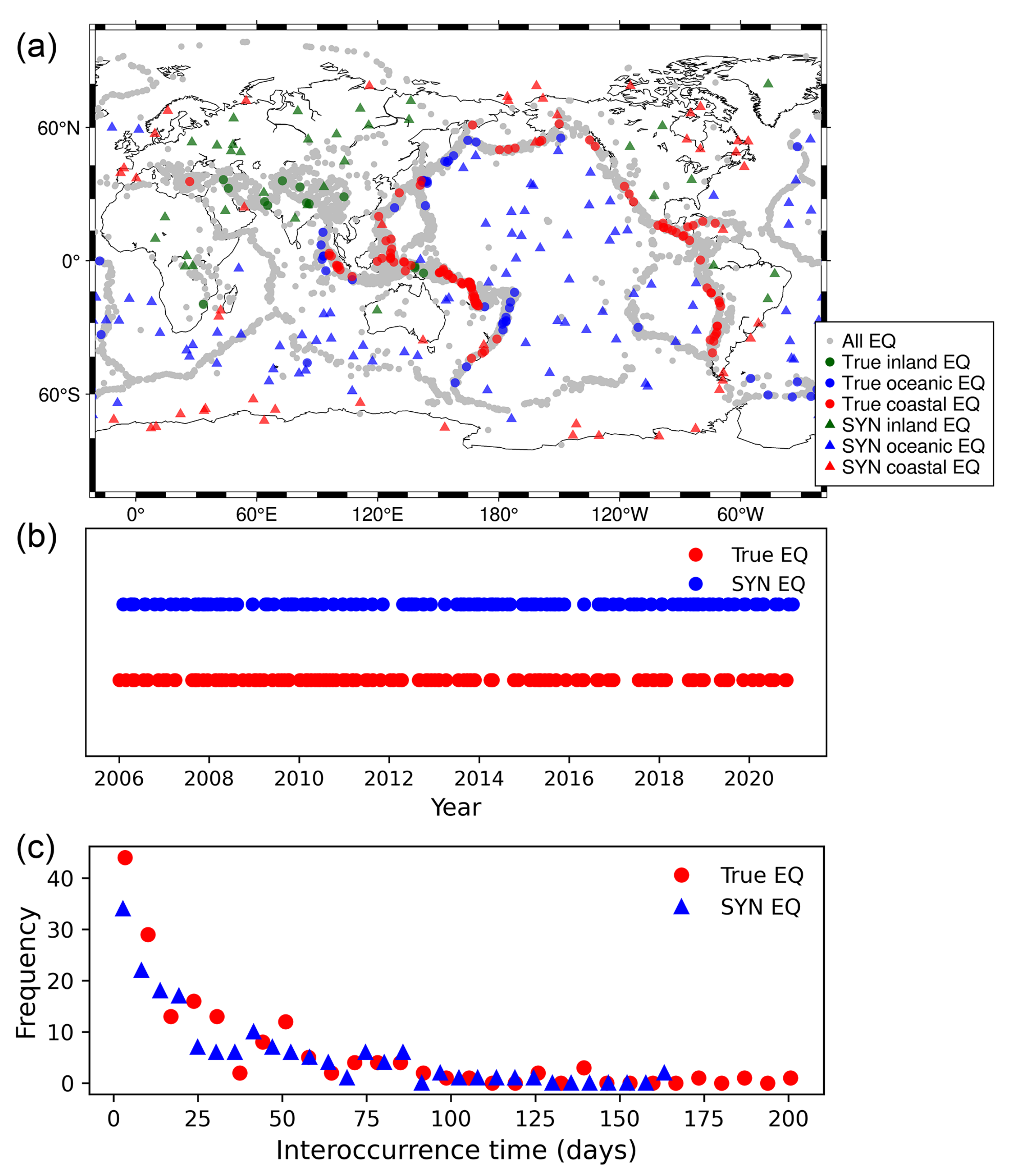
2.2. Global Earthquake Events

A total of 169 earthquakes representing the most significant seismic events of recent years were collected from the USGS Earthquake Hazards Program (Figure 1). The earthquakes were divided into inland, oceanic, and coastal for comparison, wherein most earthquakes belonged to the coastal class. In addition, to validate the forecasting effectiveness of TIA, 169 synthetic earthquakes were randomly generated based on three criteria: (1) within $\pm 75°$ latitudes; (2) occurring between 2006 and 2020; and (3) for day t and position p, we built a spatiotemporal cube of 11 × 11 pixels around p as the spatial dimension, within which a day ranged between t − 60 and t + 90 as the time dimension, and if no $\mathrm{M}\ge 5.5$ earthquakes occurred within this cube, it was reserved. Randomly generated earthquakes were iteratively produced to check these restrictions, and we collected the first 169 valid events. The synthetic events were more widely dispersed compared with the true earthquakes in earthquake-prone regions (Figure 1a, light gray areas). This was due to the random generation mechanism; compared with the true earthquakes, a higher proportion of the synthetic earthquakes were in the ocean and inland classes; therefore, the number of synthetic coastal earthquakes was very small compared with that of the true earthquakes. As shown in Figure 1b, the temporal distribution of synthetic earthquakes was similar to that of true earthquakes, and their interoccurrence time presented similar statistical characteristics in Figure 1c, which indicates the rationality of the randomly generated synthetic earthquakes.

3. Methods

3.1. Pre-Seismic Anomaly Detection

A simple and yet widely used anomaly detection method was used to calculate the initial anomalous values from five surface and atmospheric parameters. The Z-Score (ZS) method is defined as the multiple of standard deviation (STD) between measured and mean values [42], and its mathematical formula is:

$$\mathrm{ZS}\left(x,y,t\right)=\frac{v\left(x,y,t\right)-\mu \left(x,y\right)}{\delta \left(x,y\right)},$$

(1)

where $v\left(x,y,t\right)$ is the pixel value at position $\left(x,y\right)$ and at time t, $\mu \left(x,y\right)$ is the average of the reference field for the same or similar period in multiple years, and $\delta \left(x,y\right)$ is the standard deviation of the reference field.

The daily reference field for each geophysical parameter is essential for calculating anomalies on a robust basis. A time series-based reference field synthesis method was developed to filter outliers in order to improve stability. A dataset of one parameter (e.g., ST) at the same location on the same day during historical years was collected from AIRS3STD data. Negative outliers were removed by retaining only samples with a negative deviation from the mean value of the dataset less than n times STD, where n is a scaling coefficient of 3. Next, samples with a deviation from the mean value greater than n times STD were regarded as positive outliers and were excluded from the dataset. These two steps were executed for each pixel within the study area, and finally, a daily reference field image was created to represent the long-term average status on that specific day. The 11-day moving window approach was applied to generate daily reference field according to aforementioned method. For example, the reference field for 6 January 2010 was calculated using AIRS data from 1 January to 11 January for each year from 2002 to 2010, representing a 9-year average.

Anomalies calculated by any anomaly detection methods are based on mathematical formula and observation data. A correlation between anomalies and seismogenic conditions is not guaranteed. Moreover, real pre-seismic anomalous signals triggered by earthquakes remain unclear. Therefore, recognition criteria were proposed based on empirical evidence in order to refine anomalies and make them as close as possible to the true situation in terms of spatial and temporal correlations [43]. In a 5° × 5° spatial window surrounding a central pixel (a total of 25 pixels), if pixels had absolute anomaly values of ≥2 (i.e., valid pixels), and the average absolute anomaly value from these valid pixels was ≥2.5, the anomaly value at the central pixel was considered valid and was retained for subsequent analyses.

3.2. Definition of TIA

The TIA of a pixel is a weighted average calculated from daily anomaly values within a specific time interval (from several days to months). Two types of TIAs were calculated using positive and negative anomalies (e.g., warming and cooling anomalies for temperature) derived from the ZS method for each selected parameter. Daily anomalies were weighted by a given integration function with a temporal distance from the time of earthquake occurrence used as the input. The integration function significantly affects the value of temporally integrated anomalies. Thus, three functions were used to analyze their differences and feasibility in detecting multiparametric anomalies prior to an earthquake. The constant (CST) weighted integration function is an arithmetic mean method using all selected daily anomaly values. Its formula is as follows:

$${\overline{\mathrm{TIA}}}_{\mathrm{CST}}=\frac{{{\displaystyle \sum }}_{t=1}^n\Theta A_t}{{{\displaystyle \sum }}_{t=1}^n\frac{\Theta }{n}},$$

(2)

where t is the temporal distance relative to the day of an earthquake, which is set to zero; n is the number of days used in the calculation; $\Theta$ is a flag with 1 for valid $A_t$ and 0 for invalid $A_t$; and $A_t$ is the valid anomaly value at day t, which was first calculated by Equation (1), and then filtered according to the recognition criteria in Section 3.1.

Generally, anomaly magnitudes measured closer to the time of an earthquake are more significant. Nevertheless, a TIA with constant weighted integration cannot denote this temporal characteristic. Hence, using two additional methods, we assigned different weights to anomaly points for each day of the integration interval. The Gaussian distribution is widely used to describe a normal distribution in statistics and to define the Gaussian filter in signal processing. The distribution of a Gaussian function is suitable for situations where anomalies occurring closer to the occurrence day have a higher weight. The Gaussian (GAU) weighted integration function was calculated as follows:

$${\overline{\mathrm{TIA}}}_{\mathrm{GAU}}=\frac{{{\displaystyle \sum }}_{t=0}^n\Theta \frac{1}{\sigma \sqrt{2\pi }}{e}^{\frac{-{\left(t-\mu \right)}^2}{2{\sigma }^2}}·A_t}{{{\displaystyle \sum }}_{t=0}^n\Theta \frac{1}{\sigma \sqrt{2\pi }}{e}^{\frac{-{\left(t-\mu \right)}^2}{2{\sigma }^2}}},$$

(3)

where $\mu$ is set to 0, and $\sigma$ is the STD that controls the width of the shape of the Gaussian function. The other integration function was the Laplace (LAP) distribution, which has a steeper distribution, causing the weight assigned to anomaly values to vary more significantly. LAP is calculated as follows:

$${\overline{\mathrm{TIA}}}_{\mathrm{LAP}}=\frac{{{\displaystyle \sum }}_{t=0}^n\frac{\Theta }{2\sigma }{e}^{\frac{-\left|t-\mu \right|}{\sigma }}·A_t}{{{\displaystyle \sum }}_{t=0}^n\frac{\Theta }{2\sigma }{e}^{\frac{-\left|t-\mu \right|}{\sigma }}},$$

(4)

where $\mu$ is set to 0, t is a positive value of zero to n, and $\sigma$ is the STD of the distribution.

In general, the closer the timing of an anomaly to the time of an earthquake, the greater the weight value for the GAU and LAP, but not for the CST (Figure 2). Among them, the largest weight is from the LAP function in the first few days. If the anomalies for some days are invalid, the corresponding weights of the integration functions are set to zero and the change of the sum of weights reallocates the relative weights, causing different relative weights among different functions. The TIA was calculated using $5\times 5$ window data around the epicenter pixel, where valid positive/negative anomalies were used to calculate positive/negative TIAs (PTIA and NTIA, respectively). The temporal range for predicting impending earthquakes was from 60 days before until the day of the earthquake itself. Note that a longer anomaly window could capture more anomaly counts for anomalies with short durations; however, it would also record more irrelevant anomalies, resulting in higher uncertainties.

4. Results

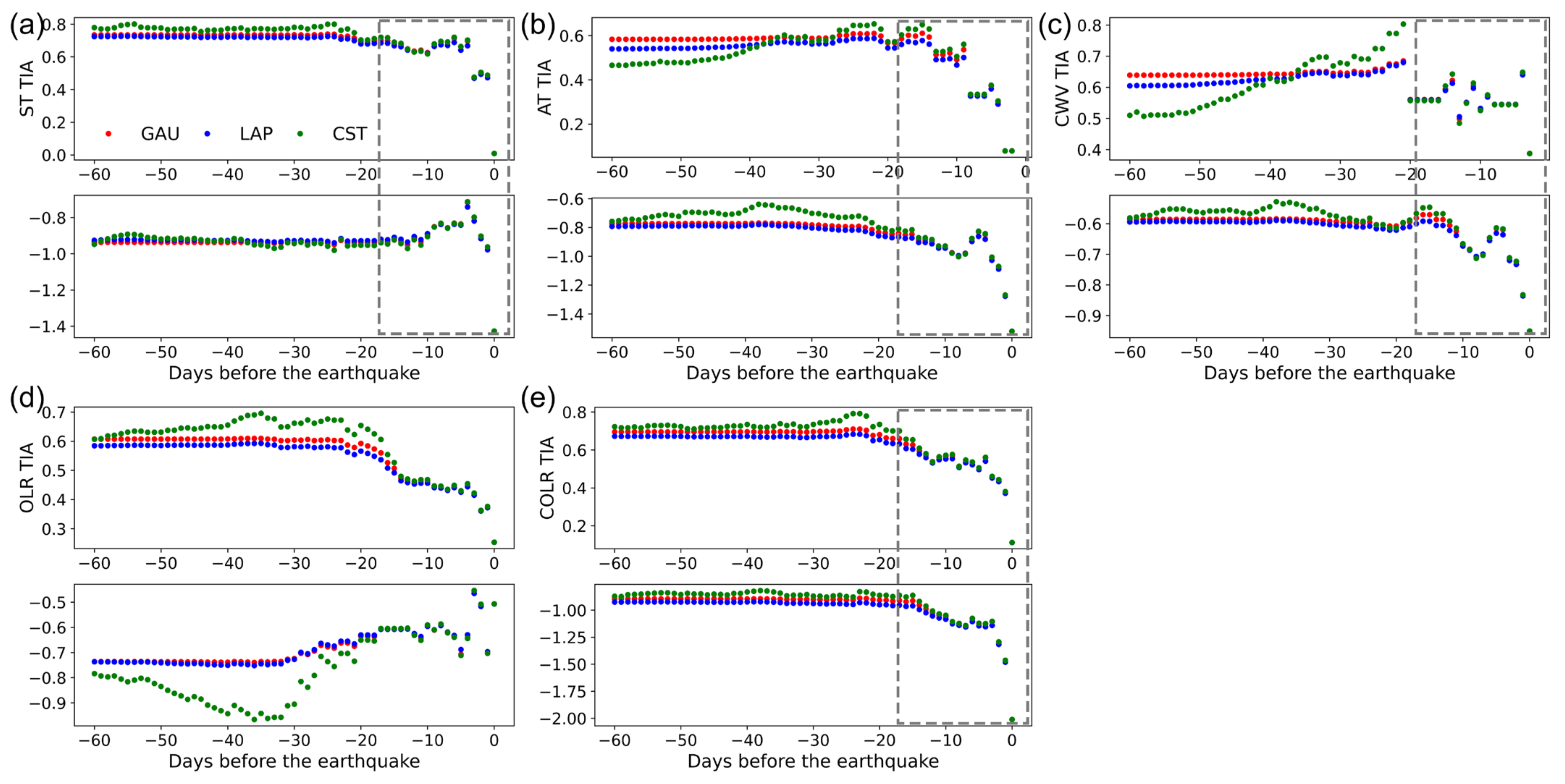
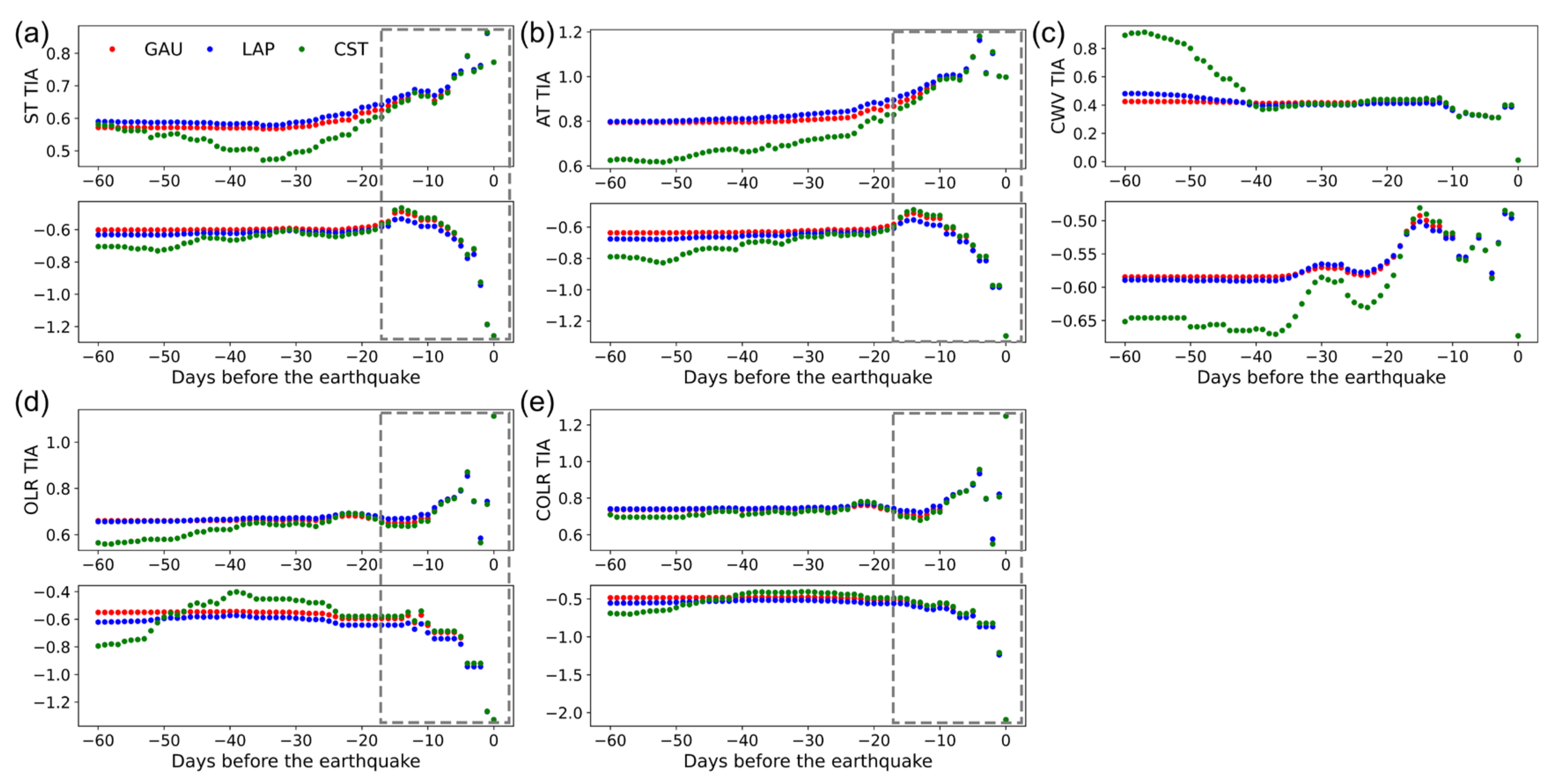
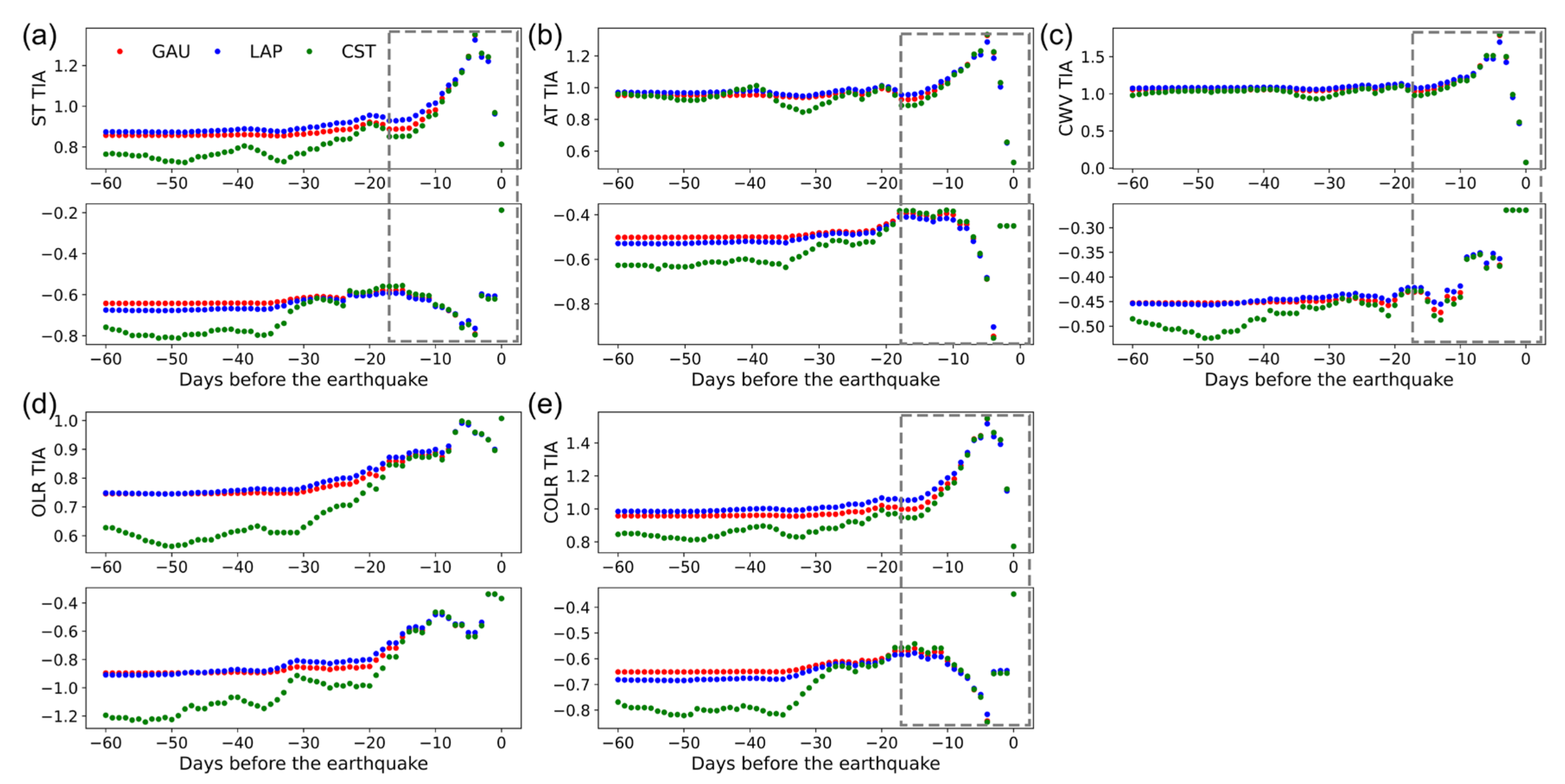
4.1. Trend Characteristics of Multiparametric TIA

The time series of pre-seismic anomalies of different geophysical parameters used in this study was first obtained within 60 days prior to a true or synthetic earthquake. The TIA for each parameter was calculated with different time intervals according to the method described in Section 3.2, and then the calculated TIA values were plotted in a cumulative manner (Figure 3a). For example, the ST TIA value for the 10th day was calculated using data from 0 to 10 days before the earthquake. Thus, the time series indicates the temporal evolution characteristics of pre-seismic anomalies. When anomalies were observed in multiple parameters, a pre-seismic anomaly was identified, and an alarm warned that an M ≥ 7 earthquake would likely take place within the 5° × 5° grid within the next few days (

Table 1. Fundamental forecasting parameters of pre-seismic anomalies in retrospective analyses according to the trend characteristics of multiparametric TIA.

Parameters	Values
Time range	<10 days
Spatial extent	5° × 5° around the epicenter (equivalent of a circle with the radius of ~275 km)
Magnitude	≥7

). We identified four different TIA trends, especially for the first ~30 days prior to the events. For one earthquake, five parameters could present different TIA trends, even when some parameters had no anomalous variation.

Type 1: PTIA and NTIA decrease rapidly before the earthquake with negative anomalies dominating the area near the epicenter (e.g., significant temperature reduction effects) (see ST, AT, CWV, and COLR TIAs in Figure 3). Prior to the 2011 M9.1 Great Tohoku Earthquake, significant crust uplift was detected along with the full southward alignment of Global Positioning System (GPS) azimuths [19], which may have led to cold water upwelling from the seafloor. Meanwhile, in a well 155 km northwest of the epicenter, anomalous decreases in groundwater level and temperature were observed starting 3 months before the earthquake due to possible pre-seismic crustal deformation [44]. These observations could explain negative anomaly phenomena. Similar phenomena can also be observed for inland earthquakes. Significant cooling phenomena along the Himalayas prior to the 2015 Mw 7.9 Nepal earthquake have been reported, and stress relaxation is suggested as a possible explanation [24].

Type 2: PTIA and NTIA increase rapidly before the earthquake with positive anomalies dominating the area near the epicenter (e.g., significant warming effects) (see AT, CWV, OLR, and COLR TIAs in Figure 4). This phenomenon has been reported by many studies; that is, anomalous increases in diverse parameters prior to earthquakes [15].

Type 3: PTIA increases and NTIA decreases rapidly before the earthquake, with both positive and negative anomalies apparent in the area near the epicenter before the earthquake (see ST, AT, OLR, and COLR TIAs in Figure 5). This bidirectional trend indicates strongly anomalous perturbation around the epicenter [45].

Type 4: Similar to Type 3, with either PTIA or NTIA reaching a peak and then rapidly disappearing within several days following the strong earthquakes (Figure 6). This delayed phenomenon was observed for only a small percentage of the tested earthquakes.

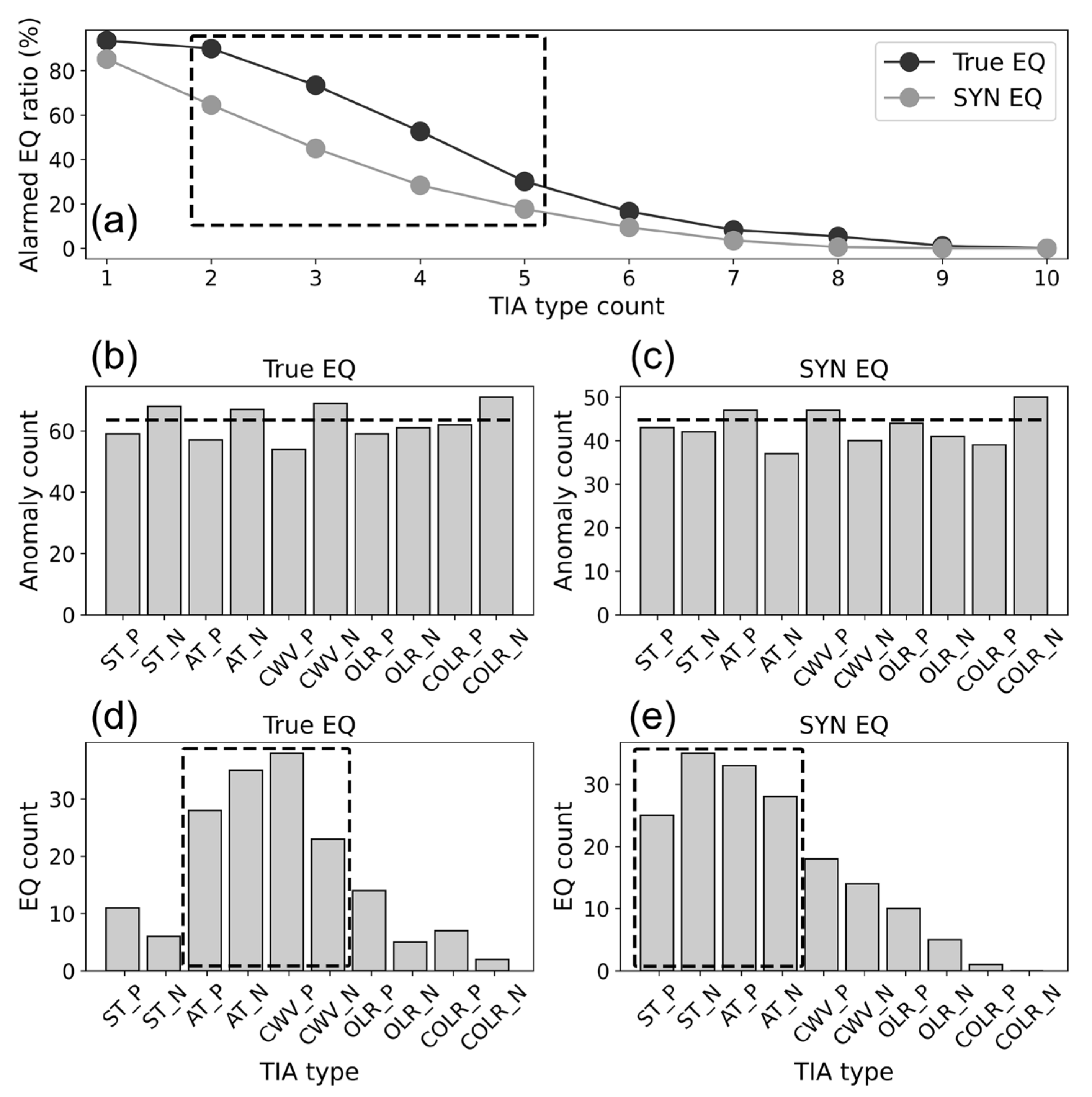
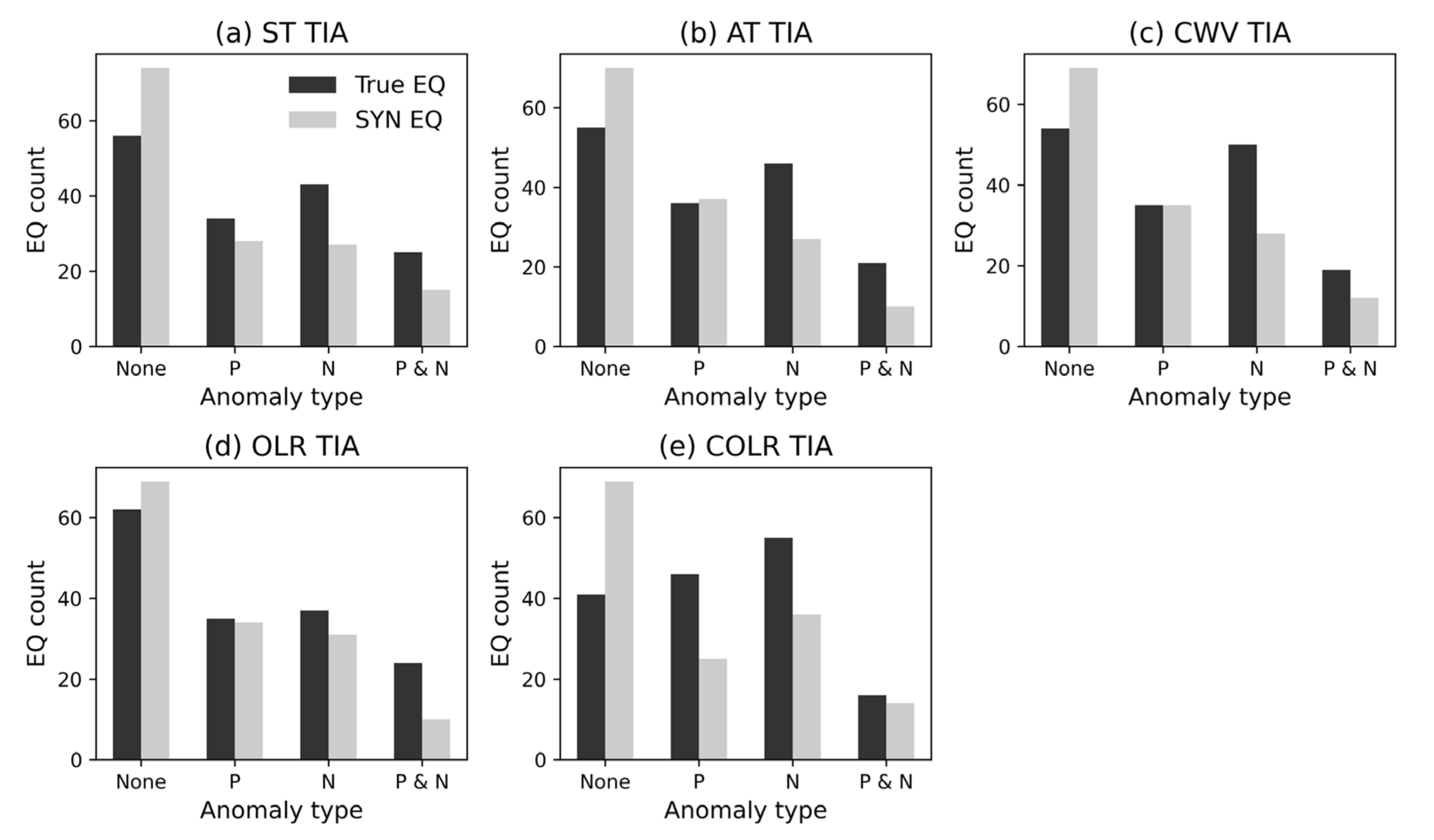
4.2. Comparison between True and Synthetic Earthquake TIAs

A higher rate of earthquake alarms was triggered for true earthquakes compared with synthetic earthquakes, and the rates decreased from 93.5% to 0% and from 85.2% to 0% as the number of TIA parameters increased for true and synthetic earthquakes, respectively (Figure 7a). The optimal number of parameters was found to be 2–5, for which the recognition ability for true earthquakes was 12.4–28.4% higher than that for synthetic earthquakes; when >6 TIA parameters were used, the rate of earthquake recognition dropped significantly for both true and synthetic events. In total, we identified 627 TIA for true earthquakes and 430 TIA for synthetic earthquakes. The different TIA types were similar between the true and synthetic earthquakes (Figure 7b,c). For true earthquakes, the NTIAs of ST, AT, CWV, and COLR had slightly more counts; for the synthetic earthquakes, the PTIAs of AT and CWV, and NTIA of COLR had slightly more counts. This suggests that NTIAs tend to correlate with true earthquakes, while PTIAs correlate with synthetic earthquakes. This is consistent with the results of past studies in which significant negative anomalies were confirmed around epicenters [24,45]. For true earthquakes, positive and negative TIAs of AT and CWV had the highest recognition counts (>15); for synthetic earthquakes, positive and negative TIAs of ST and AT had the highest recognition counts (>20) (Figure 7d,e). The TIA trend characteristics before earthquake occurrence were not unique; however, the data revealed certain unexplained anomalous phenomena.

Positive/negative anomalies could have one of four combinations: (1) neither positive nor negative TIA, (2) only positive TIA, (3) only negative TIA, and (4) both positive and negative TIAs. For each geophysical parameter, the likelihood of identifying pre-seismic anomalies was higher for true earthquakes than for synthetic earthquakes (Figure 8). More specifically, synthetic earthquakes had more no-TIA situations, and the counts of the other three combinations were less than those of the true earthquakes. While we identified a small number of exceptions for the AT and CWV TIAs, these results confirm that TIAs for all parameters can identify pre-seismic anomalous signals to some extent (Figure 7). As such, the proposed approach has good potential for predicting future earthquakes. Remote sensing observations from space-borne platforms contain seismogenic information that is subtle and transient compared with the strong background signals from natural processes and anthropogenic activities. As a result, most precursory parameters also had high missed detection and false alarm rates. Moreover, when the false alarm rate was suppressed, the accuracy rate also decreased [45]. The TIA provides the potential to improve forecast accuracy.

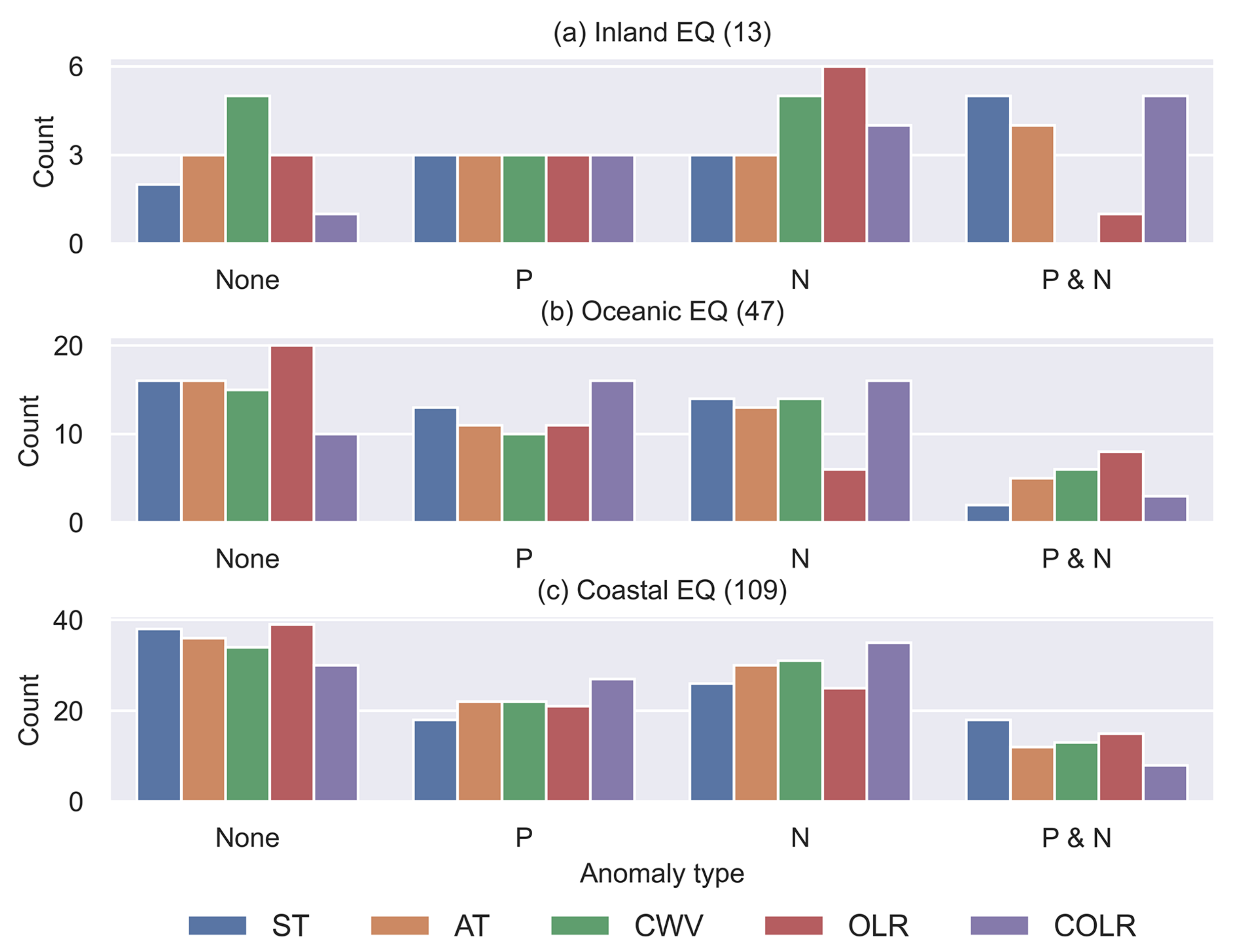
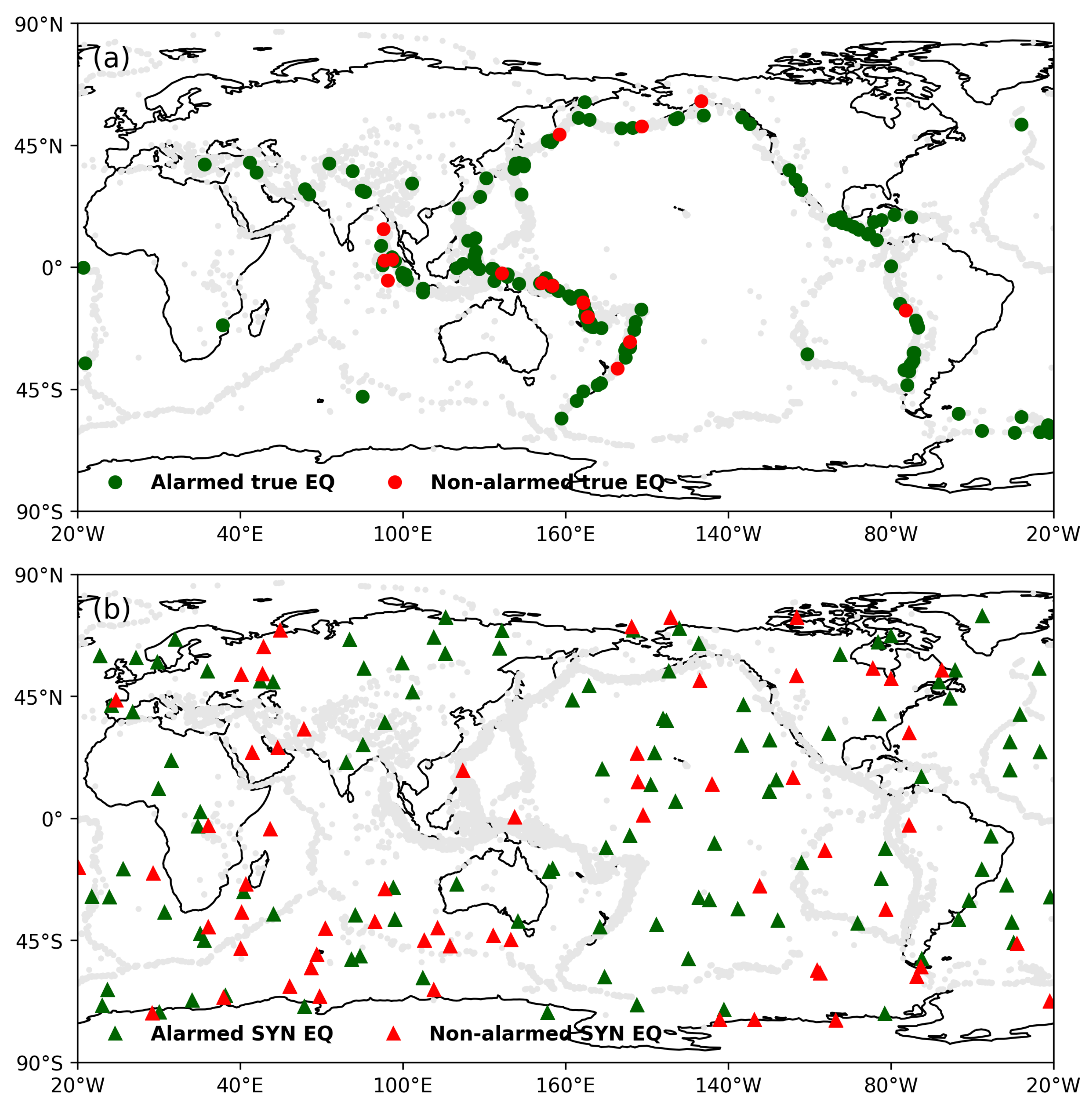
4.3. Statistical Analysis Based on Earthquake Locations

Earthquake location influences anomaly characteristics owing to different underlying surfaces and medium properties. For true earthquakes, coastal earthquakes were the most common (109), and inland earthquakes were the least common (13; Figure 9). OLR and CWV NTIAs recognized more inland earthquakes but with higher missed earthquakes (Figure 9a). COLR TIA had a strong ability to recognize oceanic earthquakes with both positive and negative anomalies. Similar patterns were observed for coastal and oceanic earthquakes (Figure 9c). The synchronous positive and negative TIAs always had poor recognition ability for oceanic and coastal earthquakes. Land cover affects the spatial distributions of diverse parameters, leading to high spatial heterogeneity, while seawater has high thermal inertia, which changes thermal radiative transfer from the seabed to the sea surface [8]. For instance, CWV increased after the 2001 Gujarat earthquake, for which the epicenter was beneath the sea [29]. Significantly reduced sea surface temperatures have been observed prior to some earthquakes and may be related to the upwelling of cold water from the ocean floor [46].

Figure 10 shows the spatial distributions of recognition and non-recognition earthquakes. The recognized rates were higher near earthquake-prone regions (light gray areas). Therefore, the proposed method provides insight into the apparent statistical significance between anomaly phenomena and earthquakes and has a forecasting ability that exceeds that of random guessing. Our results clearly demonstrate that seismically active regions are the most appropriate for testing methods to forecast earthquakes (e.g., in Japan; [32,43]).

4.4. Statistical Analysis Based on Earthquake Focal Mechanisms

Focal mechanisms were obtained from the GEOFON data center of the GFZ German Research Centre [47]. Focal mechanism solutions, which were only available for 94 of the 169 earthquakes (mostly those after 2011), were classified into strike-slip, normal, and thrust. If more than one type existed for a given earthquake, the major component was chosen. For normal earthquakes in Figure 11a, ST PTIA and OLR/COLR NTIAs showed the best recognition ability. Thrust earthquakes were the most numerous (49 events) and were most commonly associated with NTIAs (Figure 11b). For strike-slip earthquakes, synchronous positive and negative TIAs (particularly OLR/COLR TIAs) had better recognition ability than they did for the other earthquake types. Overall, negative anomalies were the most prevalent phenomena for all earthquake types (Figure 9; [45]).

5. Discussion

5.1. Implications for Earthquake Forecasts

The prediction of earthquakes has been recognized as a global problem [10]. Earthquakes are rapid energy release processes that must produce various anomalous phenomena with respect to normal reference signals [4,19]. The basic assumptions are: (1) the bigger the earthquake, the more obvious the anomalous signals; and (2) the shorter the interval until the earthquake, the clearer the anomalous signals. TIA trend characteristics were observed for both true and synthetic earthquakes; as such, earthquake alarms based on the proposed method come with significant uncertainties. This is a prevalent issue that impedes operational earthquake forecasting. Anomaly detection methods have good performance for retrospective correlation analysis (i.e., high accuracy and low missed detection rates); however, earthquake forecasting based on prospective statistics in seismically active regions has low forecasting capacity [45].

Despite the optimism of some researchers, routine and accurate earthquake forecasting remains a challenge [48]. Therefore, new approaches (e.g., artificial intelligence) need to be developed and verified [21]. The extension of natural time analysis to remote sensing data is also an important aspect, based on the success of this approach, in the detection of precursory phenomena of seismicity, surface displacements, Earth’s magnetic field, and seismic electric signals prior to the strong earthquakes [7,19]. Combining multiple data sources offers the potential to refine the detection of anomalous phenomena [4,15], as confirmed by our results. Therefore, short-term earthquake forecasting models that combine multiple data streams are deemed to be the most promising approach [43]. Moreover, a robust and quantitative evaluation of anomaly detection methods is needed to gain new insights into the feasibility of earthquake forecasts. By constructing a uniform baseline using historical observation data and earthquake catalogs in retrospective and prospective ways [45], we will be better able to compare various approaches and parameters, offering the potential to develop models for integrating precursors and anomaly detection methods for operational earthquake forecasting.

5.2. Underlying Geophysical Mechanisms of Pre-Seismic Anomalies

The findings derived from rock experiments offer an experimental basis for relating temperature anomalies to variations in crustal stress fields and tectonic activities from remote sensing observations [49,50,51,52]. Elastic energy continuously accumulates in the rock mass during earthquake preparation. Both theoretical calculations and laboratory measurements indicate that temperature variations are related to the quantity of volume strain measured under elastic stress conditions for solid materials. The thermal elastic coefficient of roughly 1 mK/MPa is proportional to the principal stress [50,53]. When the volume strain increases due to compression, the temperature also rises, while it will decline in the tensile state. Accompanying thermal effects caused by the change in the strain levels of the deformation field are likely associated with surface temperature, which can be retrieved from thermal infrared (TIR) measurements [54]. TIR radiation field (e.g., ST, AT, and OLR) derived from satellite observations serves as a feasible physical parameter related to regional overall stress fields to some extent in this research field [55].

Fault deformation is always local and mostly deep below the ground surface. However, multiparametric anomalies are widespread and regional at the seismogenic zones. The geophysical mechanism of how the heating derived from fault deformation transfers to the ground surface or the atmosphere is a key point. The thermal conductivity, thermal inertia, and time constant of the thermal diffusion of rocks are the controlling factors for transmitting the Joule temperature to the TIR radiation field. The low heat conductivity of rocks delays the transfer of increased temperatures caused by fault deformation at the scales of months to years, even decades. This is inconsistent with the satellite observation. In p-hole theory [56,57,58,59,60], however, mechanical stresses between rocks lead to the activation of peroxy defects deep in the Earth’s crust. These peroxy defects release electronic charge carriers, electrons e’ and holes h^•. The h^• have the remarkable ability to flow out into and through the surrounding rocks that are less stressed or unstressed and to propagate rapidly to the distant regions. When the h^• arrive on the Earth’s surface, they lead to a series of follow-up reactions. The exothermal recombination of h^• on the Earth’s surface leads to a stimulated TIR emission, another source of thermal radiation other than Joule temperature, which could be received by satellite sensors.

This work illustrates the extensive TIR measurements that can be derived from a satellite platform. It is worth noting that multiparametric anomalies may reflect the fault activities of tectonically active regions that do not always correspond to an impending earthquake, as the anomaly is not a sufficient condition. Various non-seismic factors affect TIR radiation changes and anomalous features [8], and the triggering of an earthquake is also influenced by intricate geologic conditions, tectonic movements, and dynamic processes.

6. Conclusions

The short-term (days or weeks) pre-seismic period is a critical phase during which stress accumulation becomes stronger and corresponding precursory responses (e.g., ST) likely increase in amplitude. We developed a TIA method to obtain the temporal trend of multiparametric anomalies derived from AIRS products before earthquakes; four types of TIA trends were identified. A total of 169 global earthquakes with magnitudes of ≥7.0 were used to test this new method in a retrospective manner. In addition, we generated 169 synthetic earthquakes to test the suppression capacity of anomaly detection in tectonically non-active areas. A time series-based anomaly removal method was developed to generate the reference fields of ZS methods. Long-term correlation analyses showed that recognition ability was 12.4–28.4% higher for true earthquakes than for synthetic earthquakes (i.e., higher than that of a random guess). TIA incorporating 2–5 parameters was optimal for recognizing the earthquakes, indicating that multiparametric anomalies can provide complementary information to improve statistical significance. Our results confirm the appearance of TIA in spatiotemporal correspondence with forthcoming earthquakes, and some unexplained anomalous signals around epicentral areas were observed. A greater understanding of geophysical mechanisms and the development of new anomaly detection methods would strengthen the uniqueness of pre-seismic anomalous phenomena.