Antarctic Basal Water Storage Variation Inferred from Multi-Source Satellite Observation and Relevant Models
Abstract
:1. Introduction
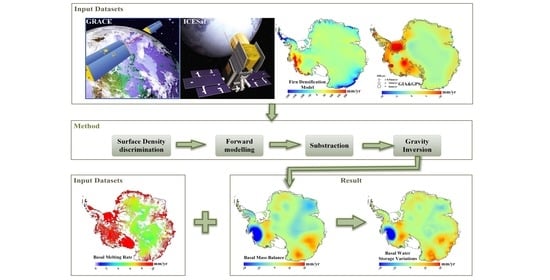
2. Materials and Methods
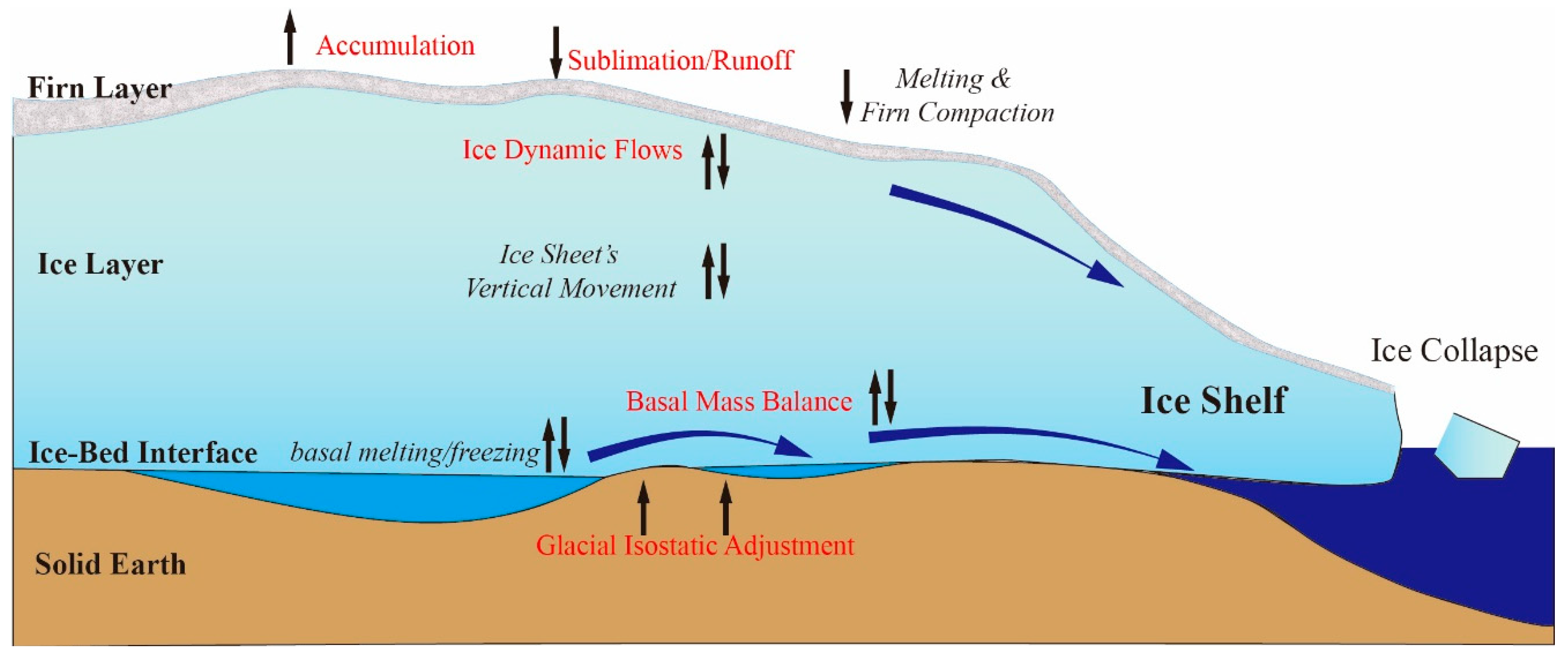
2.1. Overview of Mass Redistributions of AIS
2.2. Estimation of BMB and BWSV
2.2.1. Initialization of the Iteration Procedure
2.2.2. Estimating BMB and BWSV through Iteration Method
2.3. Uncertainty Estimation
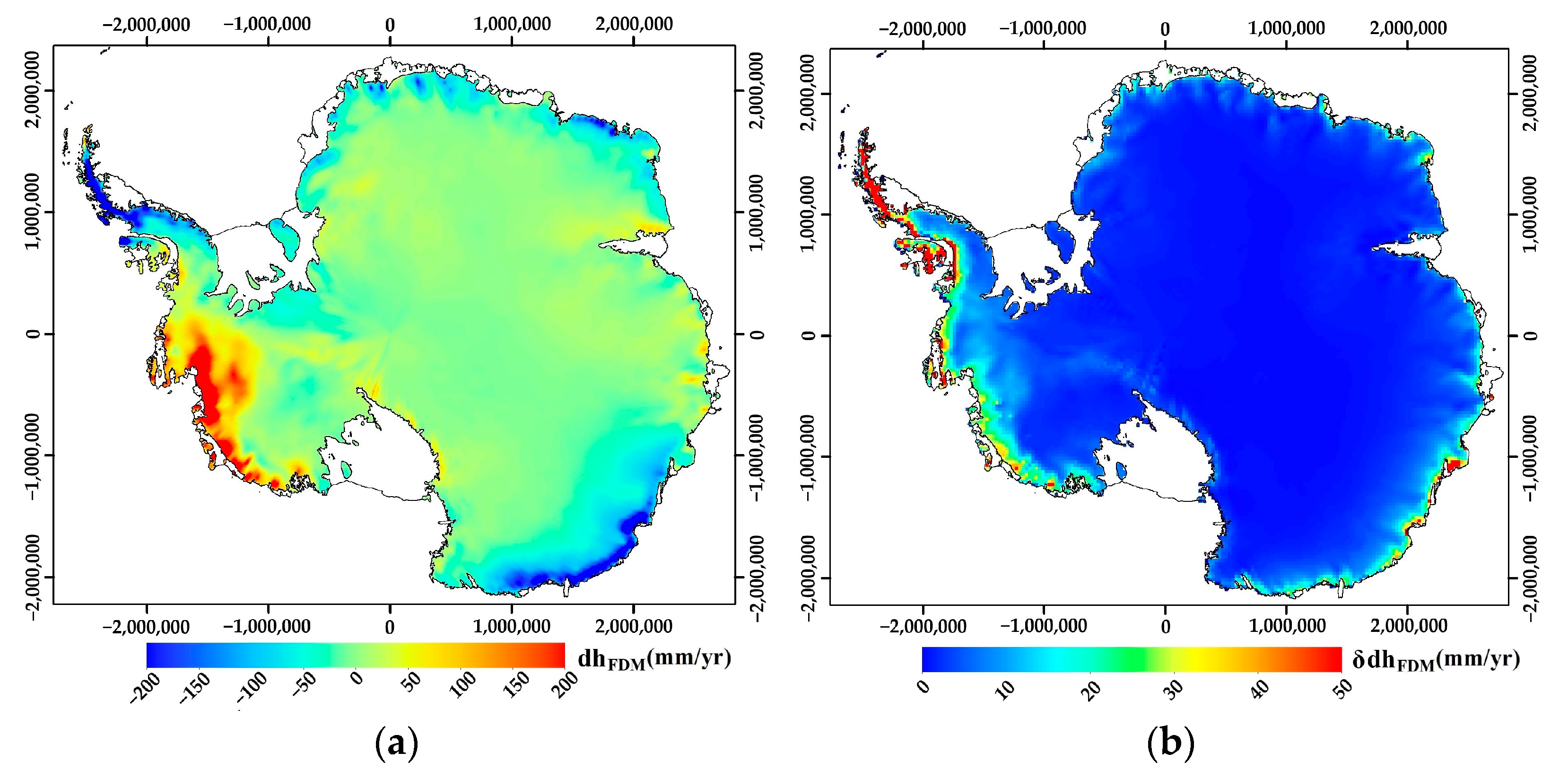
2.4. Input Data Processing
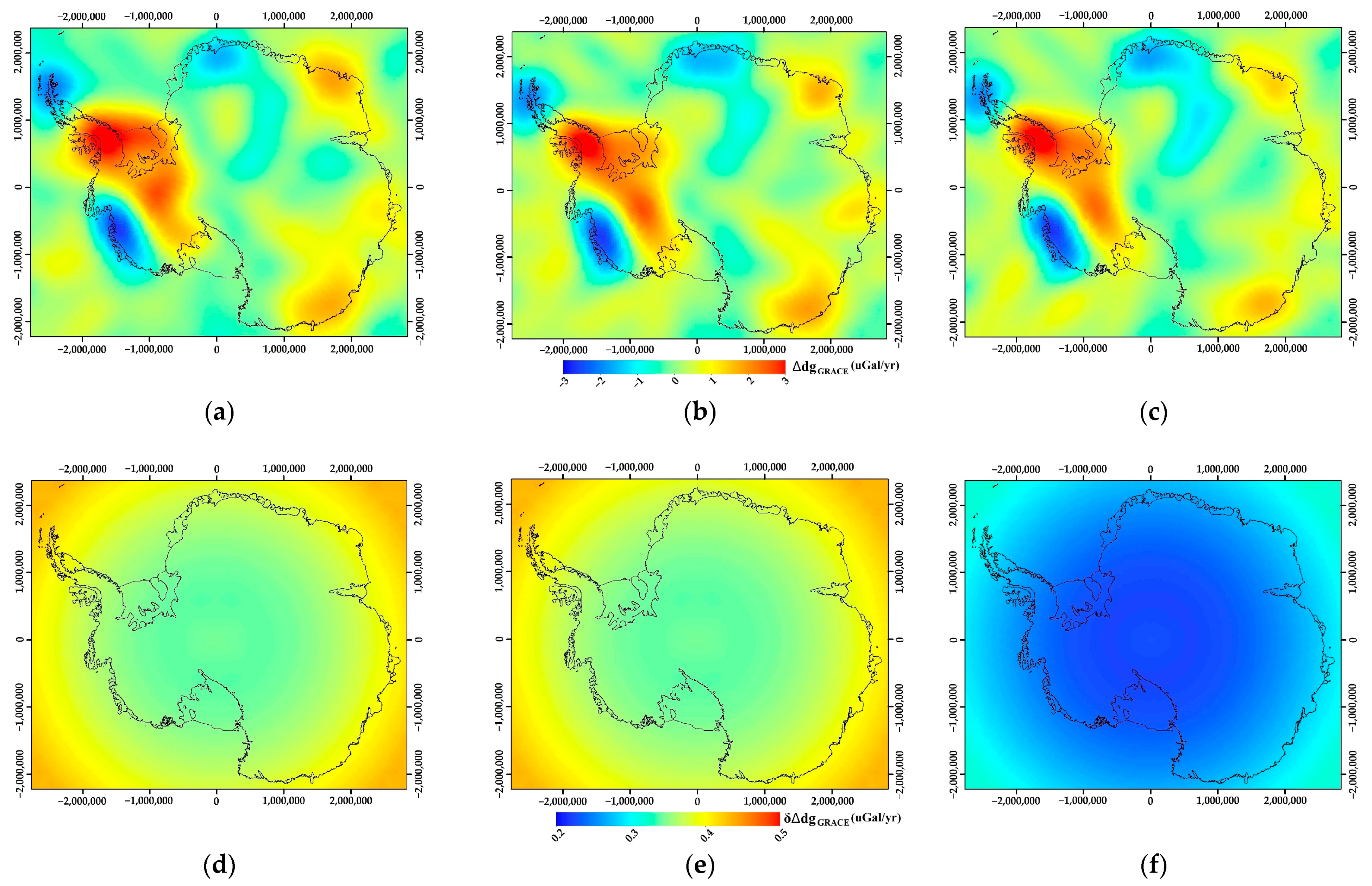
2.4.1. Gravimetry
2.4.2. Altimetry
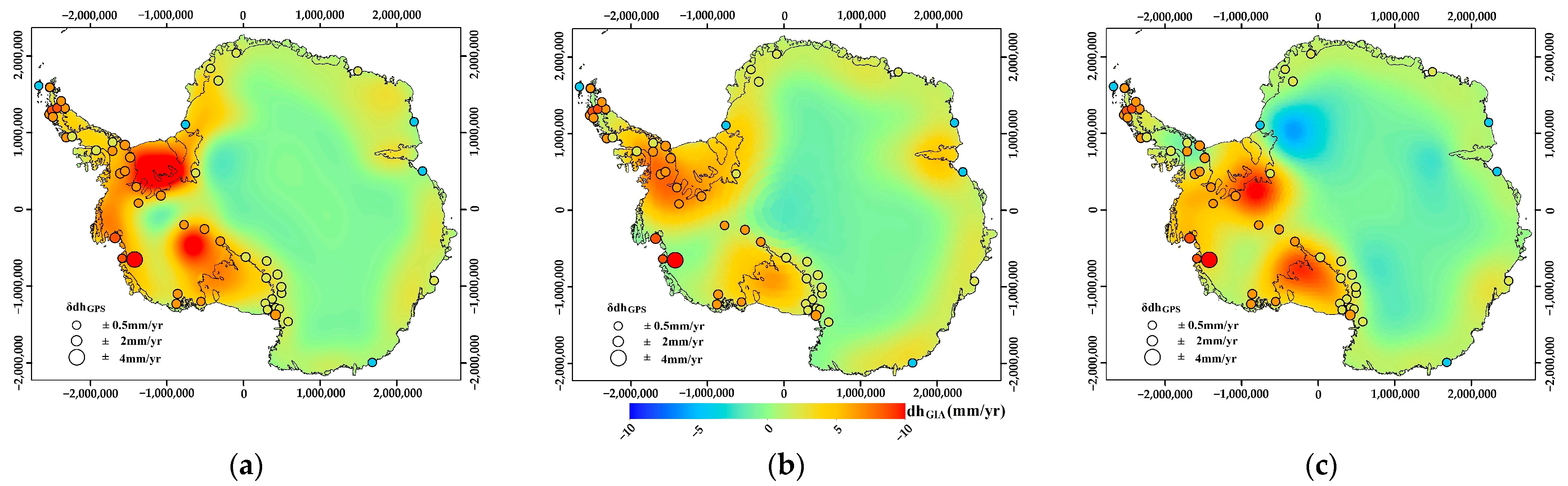
2.4.3. GIA Models and GPS Data
2.4.4. Additional Datasets
3. Results and Discussion
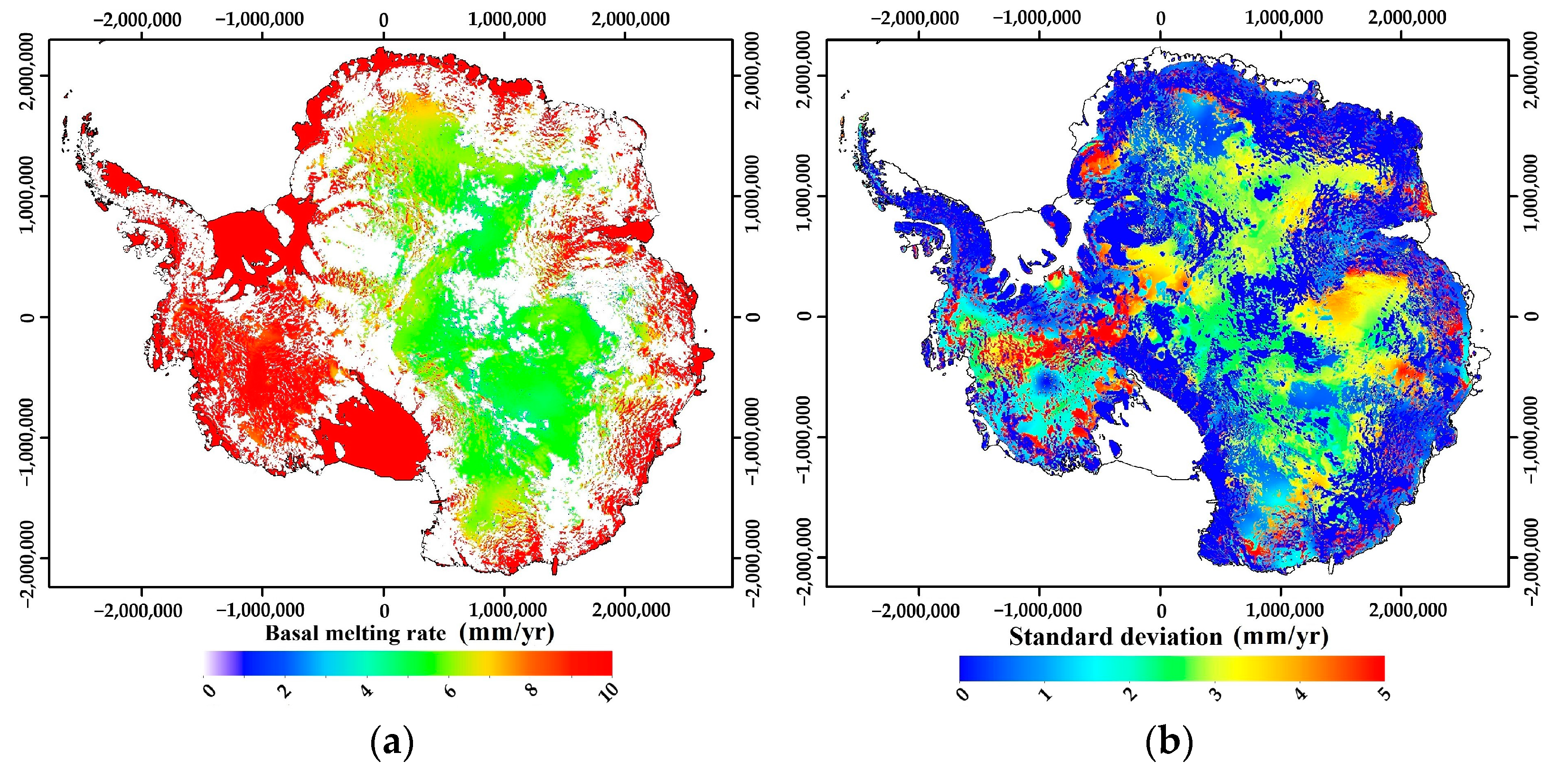
3.1. Basal Mass Balance Beneath Antarctic Ice Sheet
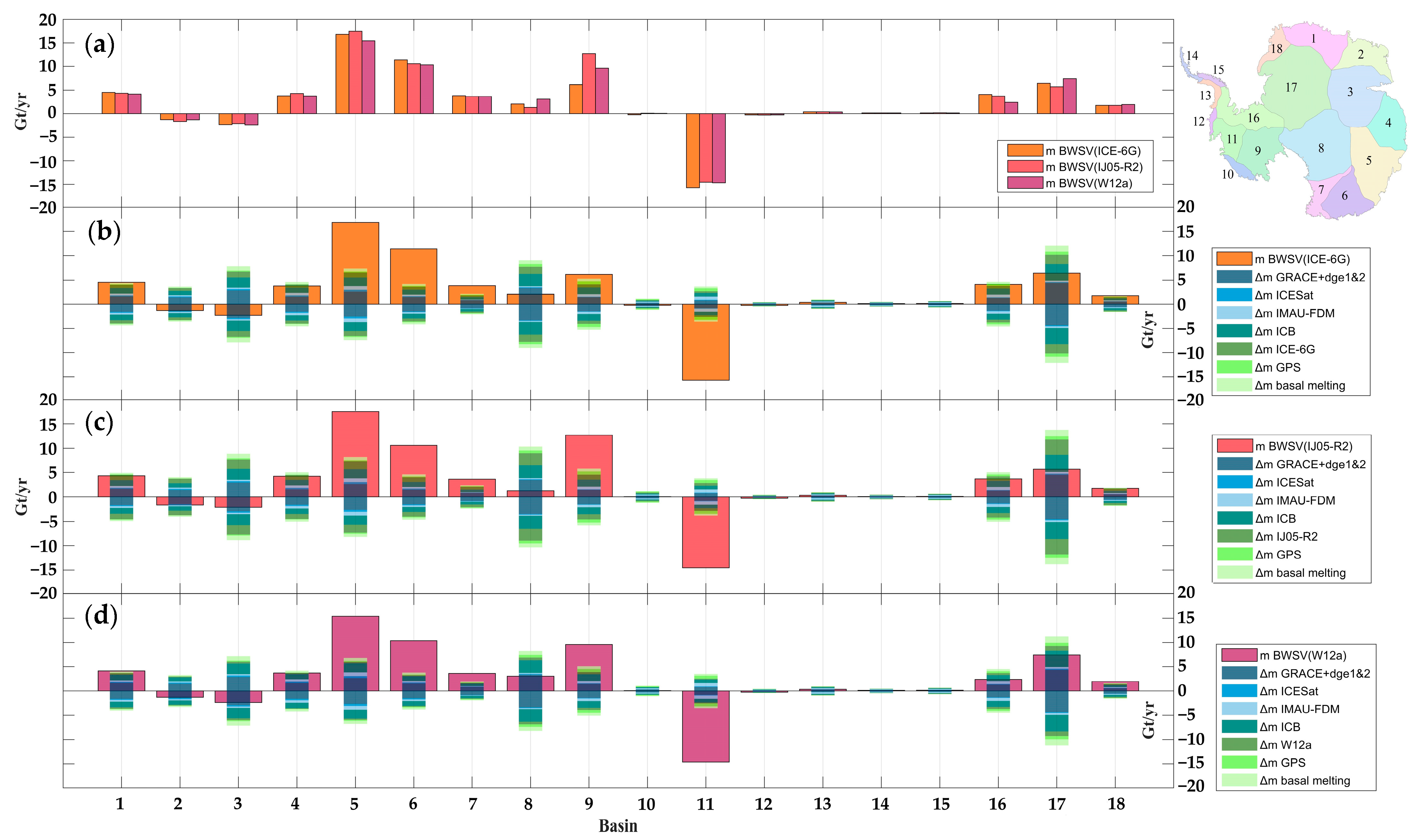
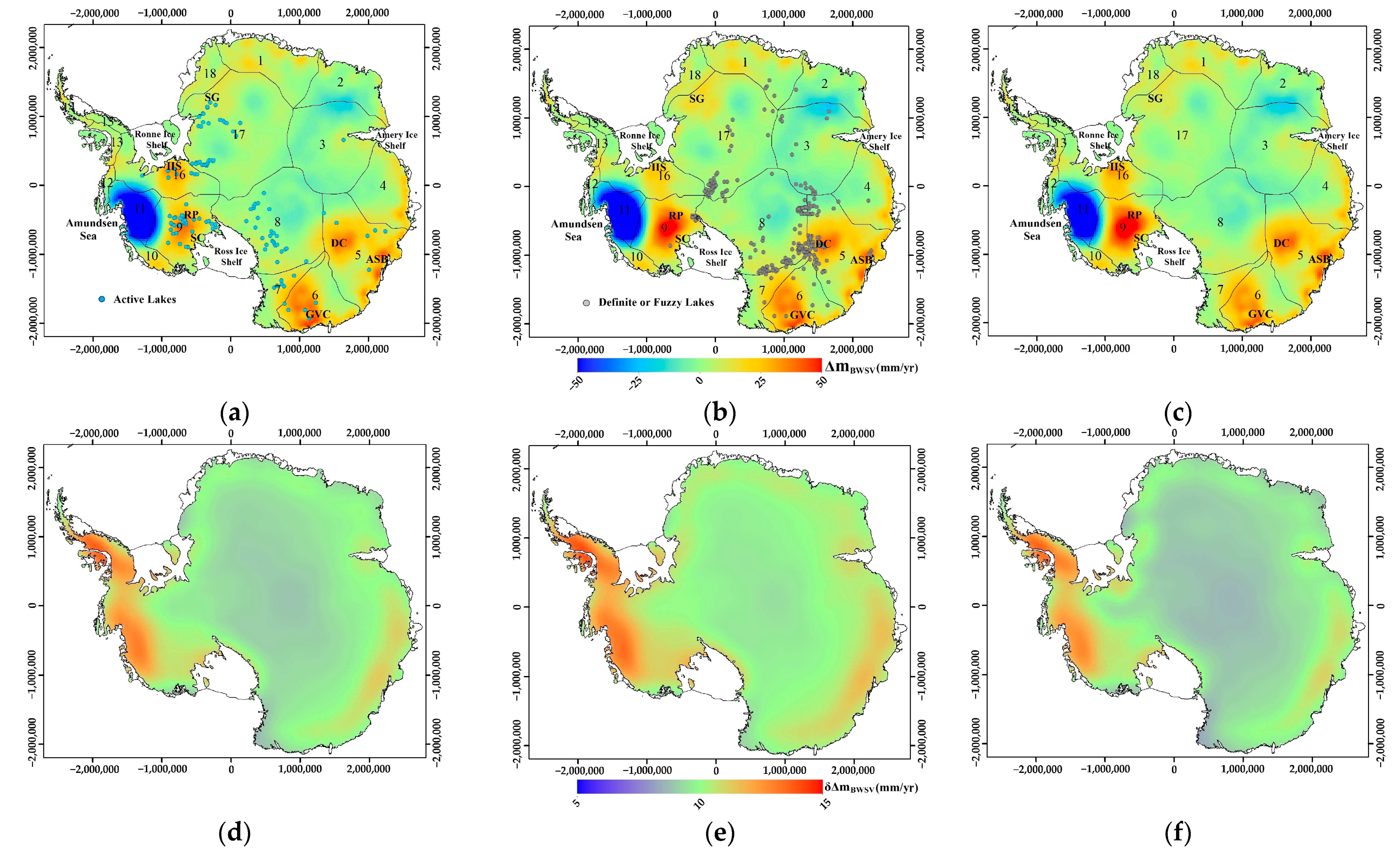
3.2. Basal Water Storage Variations Beneath Antarctic Ice Sheet
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Joughin, I.R.; Tulaczyk, S.; Engelhardt, H.E. Basal melt beneath whillans ice stream and ice streams A and C, west Antarctica. In Annals of Glaciology; Annals of Glaciology-Series; Raymond, C.F., Ed.; Cambridge University Press: Cambridge, UK, 2003; Volume 36, pp. 257–262. [Google Scholar]
- Fricker, H.A.; Siegfried, M.R.; Carter, S.P.; Scambos, T.A. A decade of progress in observing and modelling Antarctic subglacial water systems. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20140294. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wingham, D.J.; Siegert, M.J.; Shepherd, A.; Muir, A.S. Rapid discharge connects Antarctic subglacial lakes. Nature 2006, 440, 1033–1036. [Google Scholar] [CrossRef] [PubMed]
- Carter, S.P.; Fricker, H.; Siegfried, M. Active lakes in Antarctica survive on a sedimentary substrate–Part 1: Theory. Cryosphere Discuss. 2015, 9, 2053–2099. [Google Scholar]
- Bell; Robin, E. The role of subglacial water in ice-sheet mass balance. Nat. Geosci. 2008, 1, 297–304. [Google Scholar] [CrossRef]
- Fricker, H.A.; Scambos, T.; Bindschadler, R.; Padman, L. An active subglacial water system in West Antarctica mapped from space. Science 2007, 315, 1544–1548. [Google Scholar] [CrossRef] [Green Version]
- Alley, R.B. Flow-law hypotheses for ice-sheet modeling. J. Glaciol. 1992, 38, 245–256. [Google Scholar] [CrossRef] [Green Version]
- Jordan, T.A.; Martin, C.; Ferraccioli, F.; Matsuoka, K.; Corr, H.; Forsberg, R.; Olesen, A.; Siegert, M. Anomalously high geothermal flux near the South Pole. Sci. Rep. 2018, 8, 16785. [Google Scholar] [CrossRef] [Green Version]
- Wilch, E.; Hughes, T.J. Calculating basal thermal zones beneath the Antarctic ice sheet. J. Glaciol. 2000, 46, 297–310. [Google Scholar] [CrossRef] [Green Version]
- Verbitsky, M.; Saltzman, B. Modeling the Antarctic ice sheet. In Proceedings of the International Symposium on Representation of the Cryosphere in Climate and Hydrological Models, Victoria, BC, Canada, 12–15 August 1996; pp. 259–268. [Google Scholar]
- Pattyn, F. Antarctic subglacial conditions inferred from a hybrid ice sheet/ice stream model. Earth Planet. Sci. Lett. 2010, 295, 451–461. [Google Scholar] [CrossRef]
- Liefferinge, B.V.; Pattyn, F.; Cavitte, M.G.P.; Karlsson, N.B.; Eisen, O. Promising oldest ice sites in east Antarctica based on thermodynamical modelling. Cryosphere Discuss. 2018, 12, 2773–2787. [Google Scholar] [CrossRef] [Green Version]
- Rignot, E.; Jacobs, S.S. Rapid bottom melting widespread near Antarctic ice sheet grounding lines. Science 2002, 296, 2020–2023. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fisher, A.T.; Mankoff, K.D.; Tulaczyk, S.M.; Tyler, S.W.; Foley, N. High geothermal heat flux measured below the west Antarctic ice sheet. Sci. Adv. 2015, 1, e1500093. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Martos, Y.M.; Catalán, M.; Jordan, T.A.; Golynsky, A.; Golynsky, D.; Eagles, G.; Vaughan, D.G. Heat flux distribution of Antarctica unveiled. Geophys. Res. Lett. 2017, 44, 11–417. [Google Scholar] [CrossRef] [Green Version]
- Cui, X.; Wang, T.; Sun, B.; Tang, X.; Guo, J. Chinese radioglaciological studies on the Antarctic ice sheet: Progress and prospects. Adv. Polar Sci. 2017, 28, 14–23. [Google Scholar]
- Wolovick, M.J.; Bell, R.E.; Creyts, T.T.; Frearson, N. Identification and control of subglacial water networks under Dome A, Antarctica. J. Geophys. Res. Earth Surf. 2013, 118, 140–154. [Google Scholar] [CrossRef]
- Evatt, G.W.; Fowler, A.C.; Clark, C.D.; Hulton, N.R.J. Subglacial floods beneath ice sheets. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2006, 364, 1769–1794. [Google Scholar] [CrossRef]
- Livingstone, S.J.; Li, Y.; Rutishauser, A.; Sanderson, R.J.; Winter, K.; Mikucki, J.A.; Bjornsson, H.; Bowling, J.S.; Chu, W.N.; Dow, C.F.; et al. Subglacial lakes and their changing role in a warming climate. Nat. Rev. Earth Environ. 2022, 3, 106–124. [Google Scholar] [CrossRef]
- Null, K.A.; Corbett, D.R.; Crenshaw, J.; Peterson, R.N.; Peterson, L.E.; Lyons, W.B. Groundwater discharge to the western Antarctic coastal ocean. Polar Res. 2019, 38. [Google Scholar] [CrossRef]
- Gooch, B.T.; Young, D.A.; Blankenship, D.D. Potential groundwater and heterogeneous heat source contributions to ice sheet dynamics in critical submarine basins of East Antarctica. Geochem. Geophys. Geosystems 2016, 17, 395–409. [Google Scholar] [CrossRef] [Green Version]
- Flament, T.; Berthier, E.; Rémy, F. Cascading water underneath wilkes land, east Antarctic ice sheet, observed using altimetry and digital elevation models. Cryosphere 2014, 8, 673–687. [Google Scholar] [CrossRef] [Green Version]
- Young, D.A.; Schroeder, D.; Blankenship, D.D.; Kempf, S.D.; Quartini, E. The distribution of basal water between Antarctic subglacial lakes from radar sounding. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20140297. [Google Scholar] [CrossRef] [PubMed]
- Göeller, S.; Thoma, M.; Grosfeld, K.; Miller, H. A balanced water layer concept for subglacial hydrology in large-scale ice sheet models. Cryosphere 2013, 7, 1095–1106. [Google Scholar] [CrossRef] [Green Version]
- Gunter, B.; Didova, O.; Riva, R.; Ligtenberg, S.; Lenaerts, J.; King, M.; Van den Broeke, M.; Urban, T. Empirical estimation of present-day Antarctic glacial isostatic adjustment and ice mass change. Cryosphere 2014, 8, 743–760. [Google Scholar] [CrossRef] [Green Version]
- Martin-Espanol, A.; Zammit-Mangion, A.; Clarke, P.J.; Flament, T.; Helm, V.; King, M.A.; Luthcke, S.B.; Petrie, E.; Remy, F.; Schon, N.; et al. Spatial and temporal Antarctic ice sheet mass trends, glacio-isostatic adjustment, and surface processes from a joint inversion of satellite altimeter, gravity, and GPS data. J. Geophys. Res. Earth Surf. 2016, 121, 182–200. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sasgen, I.; Martín-Espanol, A.; Horvath, A.; Klemann, V.; Petrie, E.J.; Wouters, B.; Horwath, M.; Pail, R.; Bamber, J.L.; Clarke, P.J. Joint inversion estimate of regional glacial isostatic adjustment in Antarctica considering a lateral varying Earth structure (ESA STSE Project REGINA). Geophys. J. Int. 2017, 211, 1534–1553. [Google Scholar] [CrossRef]
- Gao, C.C.; Lu, Y.; Zhang, Z.Z.; Shi, H.L. A joint inversion estimate of Antarctic ice sheet mass balance using multi-geodetic data sets. Remote Sens. 2019, 11, 653. [Google Scholar] [CrossRef] [Green Version]
- Zwally, H.J.; Robbins, J.W.; Luthcke, S.B.; Loomis, B.D.; Remy, F. Mass balance of the Antarctic ice sheet 1992–2016: Reconciling results from GRACE gravimetry with ICESat, ERS1/2 and Envisat altimetry. J. Glaciol. 2021, 67, 533–559. [Google Scholar] [CrossRef]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Watkins, M.M.; Wiese, D.N.; Yuan, D.N.; Boening, C.; Landerer, F.W. Improved methods for observing Earth’s time variable mass distribution with GRACE using spherical cap mascons. J. Geophys. Res. Solid Earth 2015, 120, 2648–2671. [Google Scholar] [CrossRef]
- Heiskanen, W.A.; Moritz, H. Physical geodesy. Bull. Gæodésique 1967, 86, 491–492. [Google Scholar] [CrossRef]
- Aster, R.C.; Borchers, B.; Thurber, C.H. Parameter estimation and inverse problems. In Parameter Estimation and Inverse Problems, 2nd ed.; Aster, R.C., Borchers, B., Thurber, C.H., Eds.; Academic Press: Boston, MA, USA, 2013; pp. 141–168. [Google Scholar]
- Ligtenberg, S.; Helsen, M.; Van den Broeke, M. An improved semi-empirical model for the densification of Antarctic firn. Cryosphere 2011, 5, 809–819. [Google Scholar] [CrossRef] [Green Version]
- Wahr, J.; Swenson, S.; Velicogna, I. The accuracy of GRACE mass estimates. Geophys. Res. Lett. 2006, 33, 6. [Google Scholar] [CrossRef] [Green Version]
- Swenson, S.; Chambers, D.; Wahr, J. Estimating geocenter variations from a combination of GRACE and ocean model output. J. Geophys. Res. Solid Earth 2008, 113, B8. [Google Scholar] [CrossRef] [Green Version]
- Cheng, M.K.; Tapley, B.D.; Ries, J.C. Deceleration in the Earth’s oblateness. J. Geophys. Res. Solid Earth 2013, 118, 740–747. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D.; Grand, S. GRACE detects coseismic and postseismic deformation from the Sumatra-Andaman earthquake. Geophys. Res. Lett. 2007, 34, 13. [Google Scholar] [CrossRef] [Green Version]
- Gao, C.C.; Lu, Y.; Zhang, Z.Z.; Shi, H.L.; Zhu, C.D. Ice sheet mass balance in Antarctica measured by GRACE and its uncertainty. Chin. J. Geophys. Chin. Ed. 2015, 58, 780–792. [Google Scholar]
- Hofmann-Wellenhof, B.; Moritz, H. Physical Geodesy; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Zwally, H.J.; Schutz, B.; Abdalati, W.; Abshire, J.; Bentley, C.; Brenner, A.; Bufton, J.; Dezio, J.; Hancock, D.; Harding, D.; et al. ICESat’s laser measurements of polar ice, atmosphere, ocean, and land. J. Geodyn. 2002, 34, 405–445. [Google Scholar] [CrossRef] [Green Version]
- Brenner, A.C.; DiMarzio, J.R.; Zwally, H.J. Precision and accuracy of satellite radar and laser altimeter data over the continental ice sheets. IEEE Trans. Geosci. Remote Sens. 2007, 45, 321–331. [Google Scholar] [CrossRef]
- Gunter, B.; Urban, T.; Riva, R.; Helsen, M.; Harpold, R.; Poole, S.; Nagel, P.; Schutz, B.; Tapley, B. A comparison of coincident GRACE and ICESat data over Antarctica. J. Geod. 2009, 83, 1051–1060. [Google Scholar] [CrossRef] [Green Version]
- Shi, H.L.; Lu, Y.; Du, Z.L.; Jia, L.L.; Zhang, Z.Z.; Zhou, c. Mass change detection in Antarctic ice sheet using ICESat block analysis techniques from 2003–2008. Chin. J. Geophys. 2011, 54, 965. [Google Scholar]
- Smith, B.E.; Bentley, C.R.; Raymond, C.F. Recent elevation changes on the ice streams and ridges of the Ross Embayment from ICESat crossovers. Geophys. Res. Lett. 2005, 32, 21. [Google Scholar] [CrossRef] [Green Version]
- Zwally, H.J.; Li, J.; Robbins, J.W.; Saba, J.L.; Yi, D.H.; Brenner, A.C. Mass gains of the Antarctic ice sheet exceed losses. J. Glaciol. 2015, 61, 1019–1036. [Google Scholar] [CrossRef] [Green Version]
- Richter, A.; Popov, S.V.; Fritsche, M.; Lukin, V.V.; Matveev, A.Y.; Ekaykin, A.A.; Lipenkov, V.Y.; Fedorov, D.V.; Eberlein, L.; Schroder, L.; et al. Height changes over subglacial Lake Vostok, East Antarctica: Insights from GNSS observations. J. Geophys. Res. Earth Surf. 2014, 119, 2460–2480. [Google Scholar] [CrossRef] [Green Version]
- Schroeder, L.; Horwath, M.; Dietrich, R.; Scheinert, M.; Ligtenberg, S.; Van, D. Long Term Elevation Change of the Antarctic Ice Sheet from Multi-Mission Satellite Altimetry. In Proceedings of the AGU Fall Meeting, San Francisco, CA, USA, 12–16 December 2016. [Google Scholar]
- Whitehouse, P.L. Glacial isostatic adjustment modelling: Historical perspectives, recent advances, and future directions. Earth Surf. Dyn. 2018, 6, 401–429. [Google Scholar] [CrossRef] [Green Version]
- Peltier, W.R.; Argus, D.F.; Drummond, R. Space geodesy constrains ice age terminal deglaciation: The global ICE-6G_C (VM5a) model. J. Geophys. Res. Solid Earth JGR 2015, 120, 450–487. [Google Scholar] [CrossRef] [Green Version]
- Argus, D.F.; Peltier, W.R.; Drummond, R.; Moore, A.W. The Antarctica component of postglacial rebound model ICE-6G_C (VM5a) based on GPS positioning, exposure age dating of ice thicknesses, and relative sea level histories. Geophys. J. Int. 2014, 198, 537–563. [Google Scholar] [CrossRef]
- Ivins, E.R.; James, T.S.; Wahr, J.O.; Schrama, E.J.; Landerer, F.W.; Simon, K.M. Antarctic contribution to sea level rise observed by GRACE with improved GIA correction. J. Geophys. Res. Solid Earth 2013, 118, 3126–3141. [Google Scholar] [CrossRef] [Green Version]
- Whitehouse, P.L.; Bentley, M.J.; Milne, G.A.; King, M.A.; Thomas, I.D. A new glacial isostatic adjustment model for Antarctica: Calibrated and tested using observations of relative sea-level change and present-day uplift rates. Geophys. J. Int. 2012, 190, 1464–1482. [Google Scholar] [CrossRef] [Green Version]
- Sasgen, I.; Martin, A.; Horvath, A.; Klemann, V.; Petrie, E.; Wouters, B.; Horwath, M.; Pail, R.; Bamber, J.; Clarke, P.J. Regional glacial-isostatic adjustment in Antarctica inferred from combining spaceborne geodetic observations (ESA-STSE CryoSat+ Project REGINA). In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 23–28 April 2016. [Google Scholar]
- Van Liefferinge, B.; Pattyn, F. Using ice-flow models to evaluate potential sites of million year-old ice in Antarctica. Clim. Past 2013, 9, 2335–2345. [Google Scholar] [CrossRef] [Green Version]
- Rignot, E.; Mouginot, J.; Scheuchl, B.; van den Broeke, M.; van Wessem, M.J.; Morlighem, M. Four decades of Antarctic ice sheet mass balance from 1979–2017. Proc. Natl. Acad. Sci. USA 2019, 116, 1095–1103. [Google Scholar] [CrossRef] [Green Version]
- Shepherd, A.; Ivins, E.; Rignot, E.; Smith, B.; van den Broeke, M.; Velicogna, I.; Whitehouse, P.; Briggs, K.; Joughin, I.; Krinner, G.; et al. Mass balance of the Antarctic ice sheet from 1992 to 2017. Nature 2018, 558, 219–222. [Google Scholar]
- Göeller, S. Antarctic Subglacial Hydrology-Interactions of Subglacial Lakes, Basal Water Flow and Ice Dynamics; State and University Library of Bremen: Bremen, Germany, 2014. [Google Scholar]
- Gray, L.; Joughin, I.; Tulaczyk, S.; Spikes, V.B.; Bindschadler, R.; Jezek, K. Evidence for subglacial water transport in the west Antarctic ice sheet through three-dimensional satellite radar interferometry. Geophys. Res. Lett. 2005, 32, 3. [Google Scholar] [CrossRef] [Green Version]
- Bell, R.E.; Studinger, M.; Shuman, C.A.; Fahnestock, M.A.; Joughin, I. Large subglacial lakes in east Antarctica at the onset of fast-flowing ice streams. Nature 2007, 445, 904–907. [Google Scholar] [CrossRef] [PubMed]
- Creyts, T.T.; Ferraccioli, F.; Bell, R.E.; Wolovick, M.; Corr, H.; Rose, K.C.; Frearson, N.; Damaske, D.; Jordan, T.; Braaten, D. Freezing of ridges and water networks preserves the Gamburtsev Subglacial Mountains for millions of years. Geophys. Res. Lett. 2014, 41, 8114–8122. [Google Scholar] [CrossRef] [Green Version]
- Schroeder, D.M.; Blankenship, D.D.; Young, D.A.; Quartini, E. Evidence for elevated and spatially variable geothermal flux beneath the west Antarctic ice sheet. Proc. Natl. Acad. Sci. USA 2014, 111, 9070–9072. [Google Scholar] [CrossRef] [Green Version]
- Smith, B.E.; Fricker, H.A.; Joughin, I.R.; Tulaczyk, S. An inventory of active subglacial lakes in Antarctica detected by ICESat (2003–2008). J. Glaciol. 2009, 55, 573–595. [Google Scholar] [CrossRef] [Green Version]
- Andrew, W.; Martin, S. A fourth inventory of Antarctic subglacial lakes. Antarct. Ence 2012, 24, 659–664. [Google Scholar]
- Siegfried, M.R.; Fricker, H.A. Thirteen years of subglacial lake activity in Antarctica from multi-mission satellite altimetry. Ann. Glaciol. 2018, 59, 42–55. [Google Scholar] [CrossRef] [Green Version]
- Carter, S.P. Radar-based subglacial lake classification in Antarctica. Geochem. Geophys. Geosystems 2007, 8, 3. [Google Scholar] [CrossRef]
- Fretwell, P.; Pritchard, H.D.; Vaughan, D.G.; Bamber, J.L.; Barrand, N.E.; Bell, R.; Bianchi, C.; Bingham, R.G.; Blankenship, D.D.; Casassa, G. Bedmap2: Improved ice bed, surface and thickness datasets for Antarctica. Cryosphere 2013, 7, 375–393. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.; Zhong, B.; Li, X. Gravimetric terrain corrections by triangular-element method. Geophysics 1990, 55, 232–238. [Google Scholar] [CrossRef]



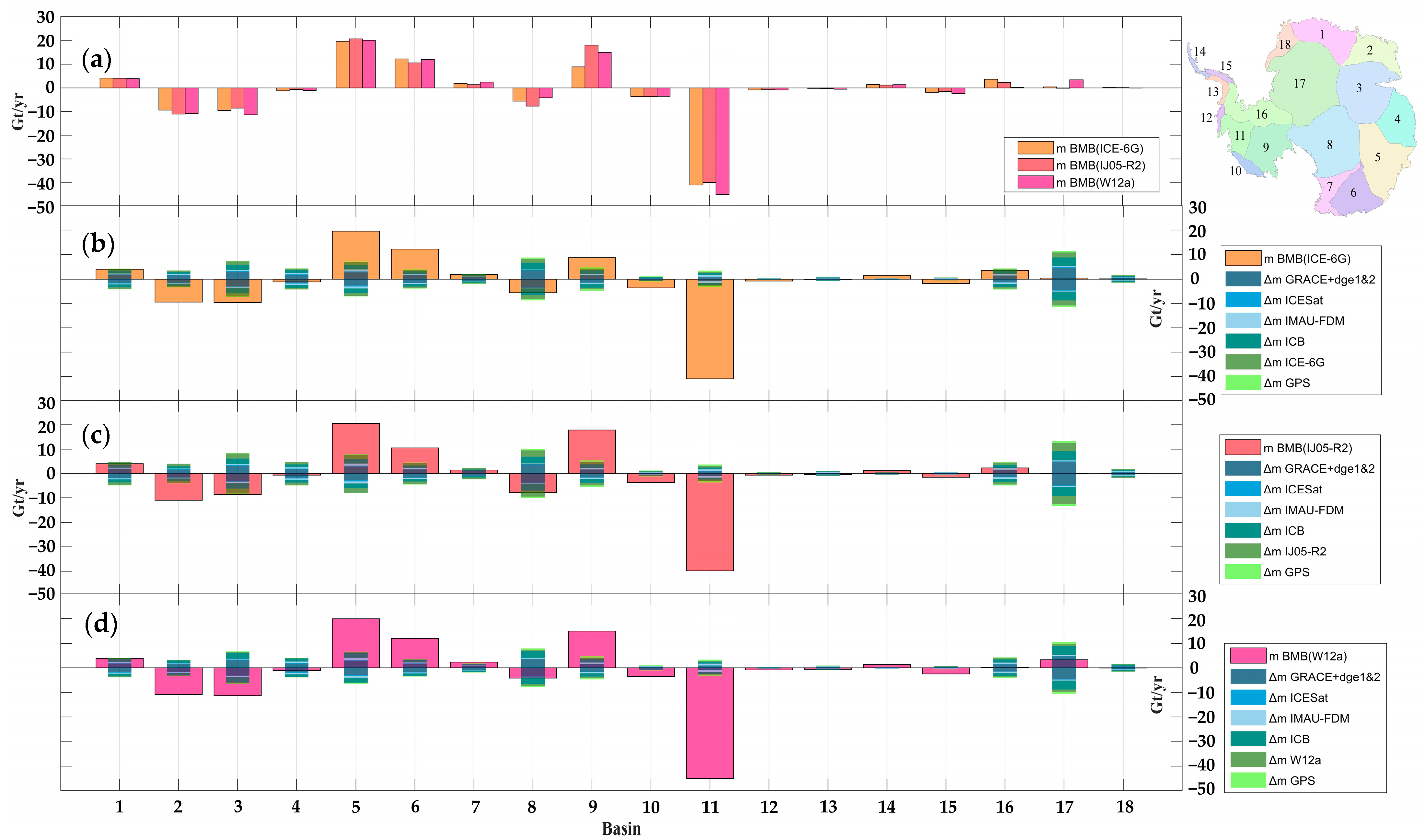

| Basin | BMB (ICE-6G) | BMB (IJ05_R2) | BMB (W12a) | Basin | BMB (ICE-6G) | BMB (IJ05_R2) | BMB (W12a) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rates | Std | Rates | Std | Rates | Std | Rates | Std | Rates | Std | Rates | Std | ||
| B1 | 4 | 4 | 4 | 5 | 4 | 4 | B11 | −41 | 3 | −40 | 4 | −45 | 3 |
| B2 | −10 | 4 | −11 | 4 | −11 | 3 | B12 | −1 | 1 | −1 | 1 | −1 | 1 |
| B3 | −10 | 7 | −9 | 9 | −11 | 7 | B13 | 0 | 1 | 0 | 1 | −1 | 1 |
| B4 | −1 | 4 | −1 | 5 | −1 | 4 | B14 | 1 | 1 | 1 | 1 | 1 | 1 |
| B5 | 20 | 7 | 21 | 8 | 20 | 7 | B15 | −2 | 1 | −2 | 1 | −2 | 1 |
| B6 | 12 | 4 | 11 | 5 | 12 | 4 | B16 | 4 | 4 | 2 | 5 | 0 | 4 |
| B7 | 2 | 2 | 1 | 2 | 2 | 2 | B17 | 0 | 12 | 0 | 13 | 3 | 11 |
| B8 | −6 | 9 | −8 | 10 | −4 | 8 | B18 | 0 | 2 | 0 | 2 | 0 | 2 |
| B9 | 9 | 5 | 18 | 6 | 15 | 5 | |||||||
| B10 | −4 | 1 | −4 | 1 | −4 | 1 | Total | −23 | 21 | −18 | 24 | −22 | 20 |
| Basin | BWSV (ICE-6G) | BWSV (IJ05_R2) | BWSV (W12a) | Basin | BWSV (ICE-6G) | BWSV (IJ05_R2) | BWSV (W12a) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rates | Std | Rates | Std | Rates | Std | Rates | Std | Rates | Std | Rates | Std | ||
| B1 | 5 | 4 | 4 | 5 | 4 | 4 | B11 | −16 | 4 | −15 | 4 | −15 | 4 |
| B2 | −1 | 4 | −2 | 4 | −1 | 3 | B12 | 0 | 1 | 0 | 1 | 0 | 1 |
| B3 | −2 | 8 | −2 | 9 | −2 | 7 | B13 | 0 | 1 | 0 | 1 | 0 | 1 |
| B4 | 4 | 5 | 4 | 5 | 4 | 4 | B14 | 0 | 1 | 0 | 1 | 0 | 1 |
| B5 | 17 | 7 | 18 | 8 | 15 | 7 | B15 | 0 | 1 | 0 | 1 | 0 | 1 |
| B6 | 11 | 4 | 11 | 5 | 10 | 4 | B16 | 0 | 5 | 4 | 5 | 2 | 5 |
| B7 | 4 | 2 | 4 | 2 | 4 | 2 | B17 | 6 | 12 | 6 | 14 | 7 | 11 |
| B8 | 2 | 9 | 1 | 10 | 3 | 8 | B18 | 2 | 2 | 2 | 2 | 2 | 2 |
| B9 | 6 | 5 | 13 | 6 | 10 | 5 | |||||||
| B10 | 0 | 1 | 0 | 1 | 0 | 1 | Total | 38 | 22 | 48 | 25 | 43 | 21 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, J.; Lu, Y.; Li, Y.; Zhang, Z.; Shi, H. Antarctic Basal Water Storage Variation Inferred from Multi-Source Satellite Observation and Relevant Models. Remote Sens. 2022, 14, 2337. https://doi.org/10.3390/rs14102337
Kang J, Lu Y, Li Y, Zhang Z, Shi H. Antarctic Basal Water Storage Variation Inferred from Multi-Source Satellite Observation and Relevant Models. Remote Sensing. 2022; 14(10):2337. https://doi.org/10.3390/rs14102337
Chicago/Turabian StyleKang, Jingyu, Yang Lu, Yan Li, Zizhan Zhang, and Hongling Shi. 2022. "Antarctic Basal Water Storage Variation Inferred from Multi-Source Satellite Observation and Relevant Models" Remote Sensing 14, no. 10: 2337. https://doi.org/10.3390/rs14102337
APA StyleKang, J., Lu, Y., Li, Y., Zhang, Z., & Shi, H. (2022). Antarctic Basal Water Storage Variation Inferred from Multi-Source Satellite Observation and Relevant Models. Remote Sensing, 14(10), 2337. https://doi.org/10.3390/rs14102337