Improvement of VHR Satellite Image Geometry with High Resolution Elevation Models
Abstract
:1. Introduction
- (1)
- Are standard methods (RPC estimation, global transformations) sufficient to remove systematic errors or are more complex methods required for improving the accuracy of VHR satellite-based elevation models?
- (2)
- Which form of reference data is appropriate for removing systematic height errors in VHR satellite-based elevation models: ground control points, or terrain models of high or low resolution?
- (3)
- Can the distortions in image geometry be explained by satellite sensor vibrations?
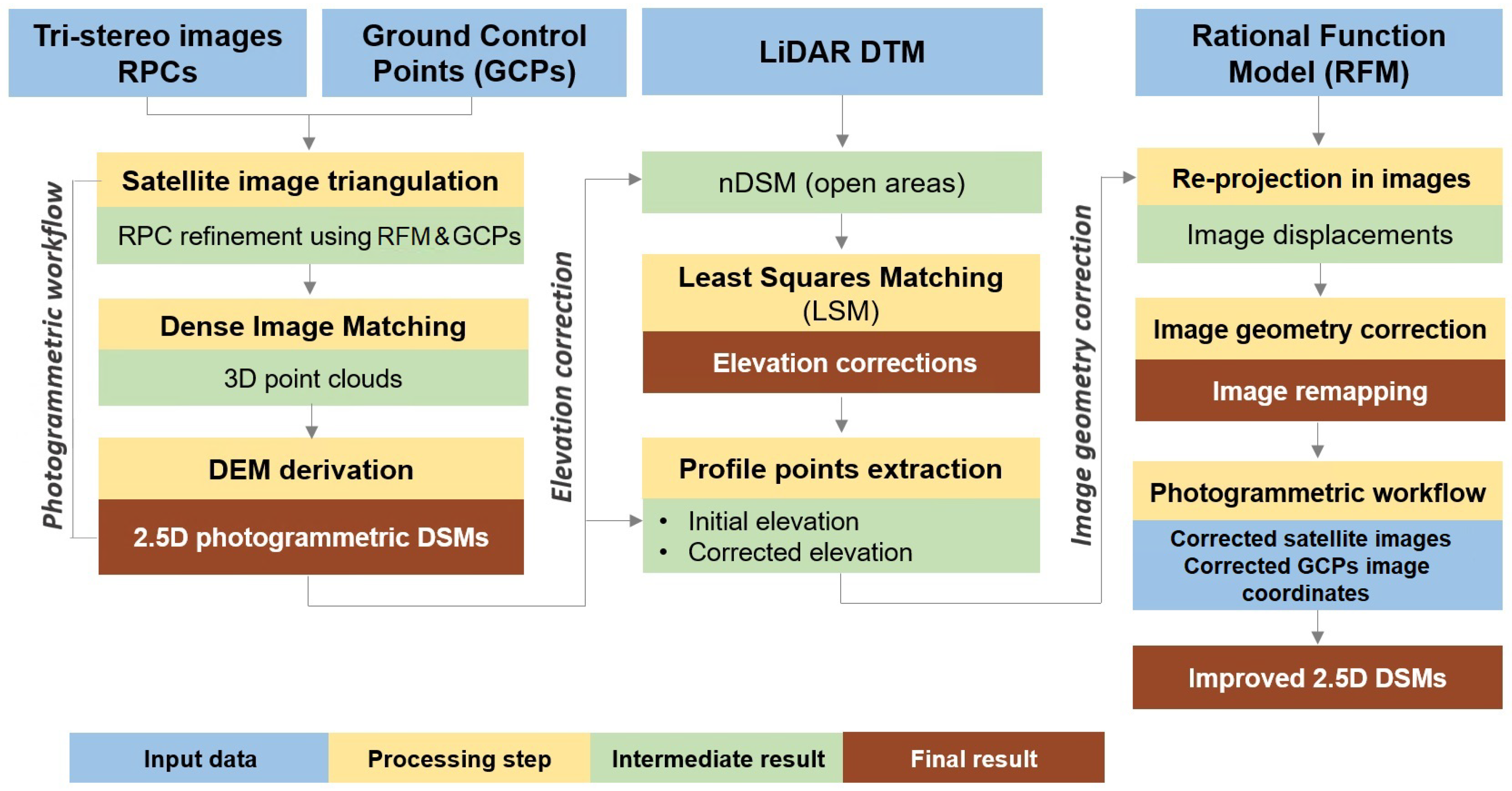
2. Materials and Methods
2.1. Satellite Image Acquisition, Lidar DTM and GCP measurement
2.2. DSM Derivation and Accuracy Assessment
2.3. Satellite DSMs’ Improvement
2.3.1. Least Squares Matching Technique
- Global LSM—for global improvement of the georeferencing of photogrammetrically derived DSMs.
- Continuous LSM—for modelling the periodic systematic elevation errors (waves) in object space (described in Section 2.3.2).
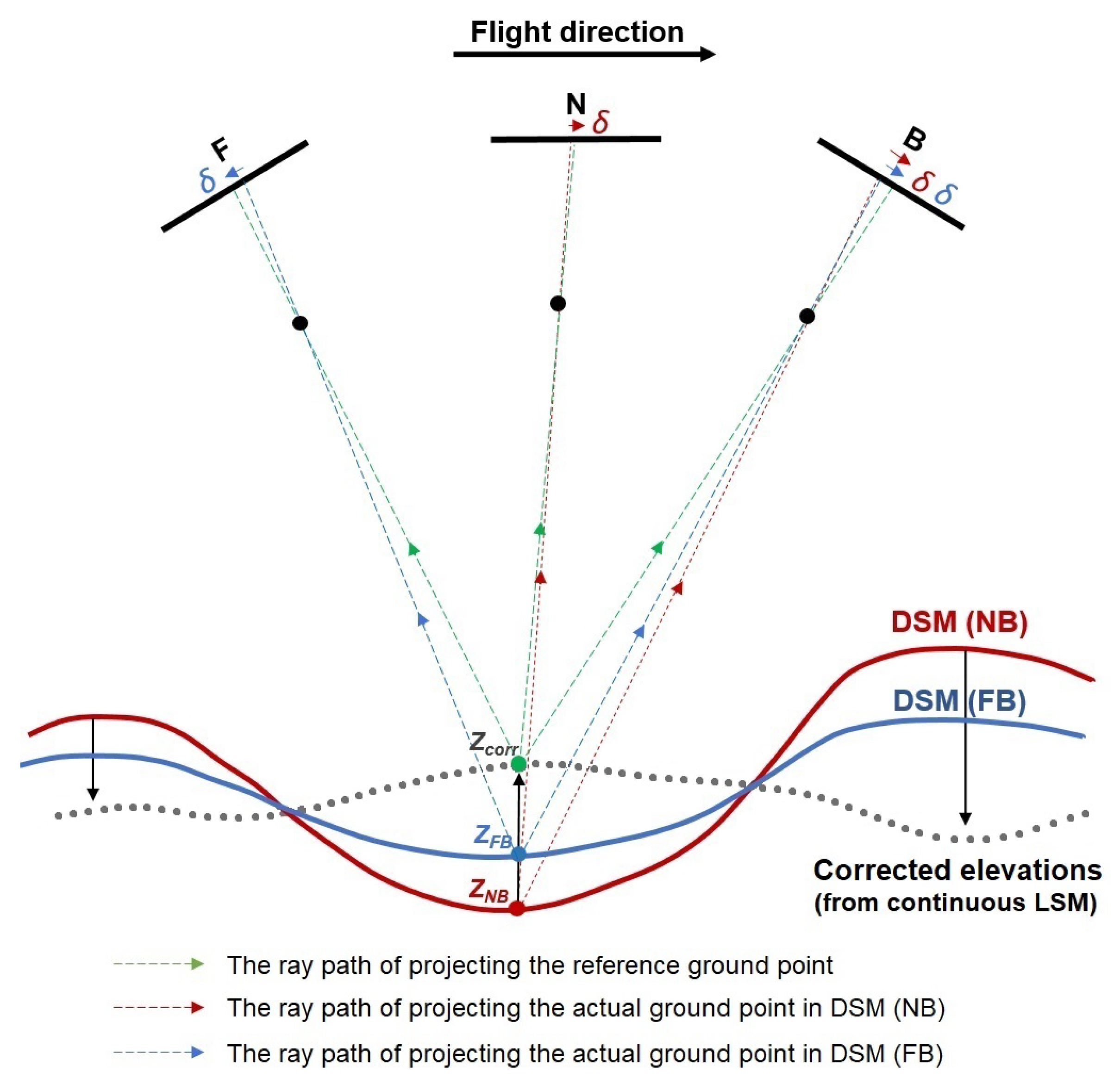
2.3.2. Image Geometry Correction
- Photogrammetric processing;
- Elevation difference computation;
- Image geometry improvement.
- (1)
- Re-projection of 3D points in image space
- (2)
- Corrections in image space
- (3)
- Correction average of profile point lines
- (4)
- Final average correction model for Backward satellite image
3. Results
3.1. Satellite-Based DSM from Image Orientation with Bias-Corrected RPCs Using 43 and 300 GCPs
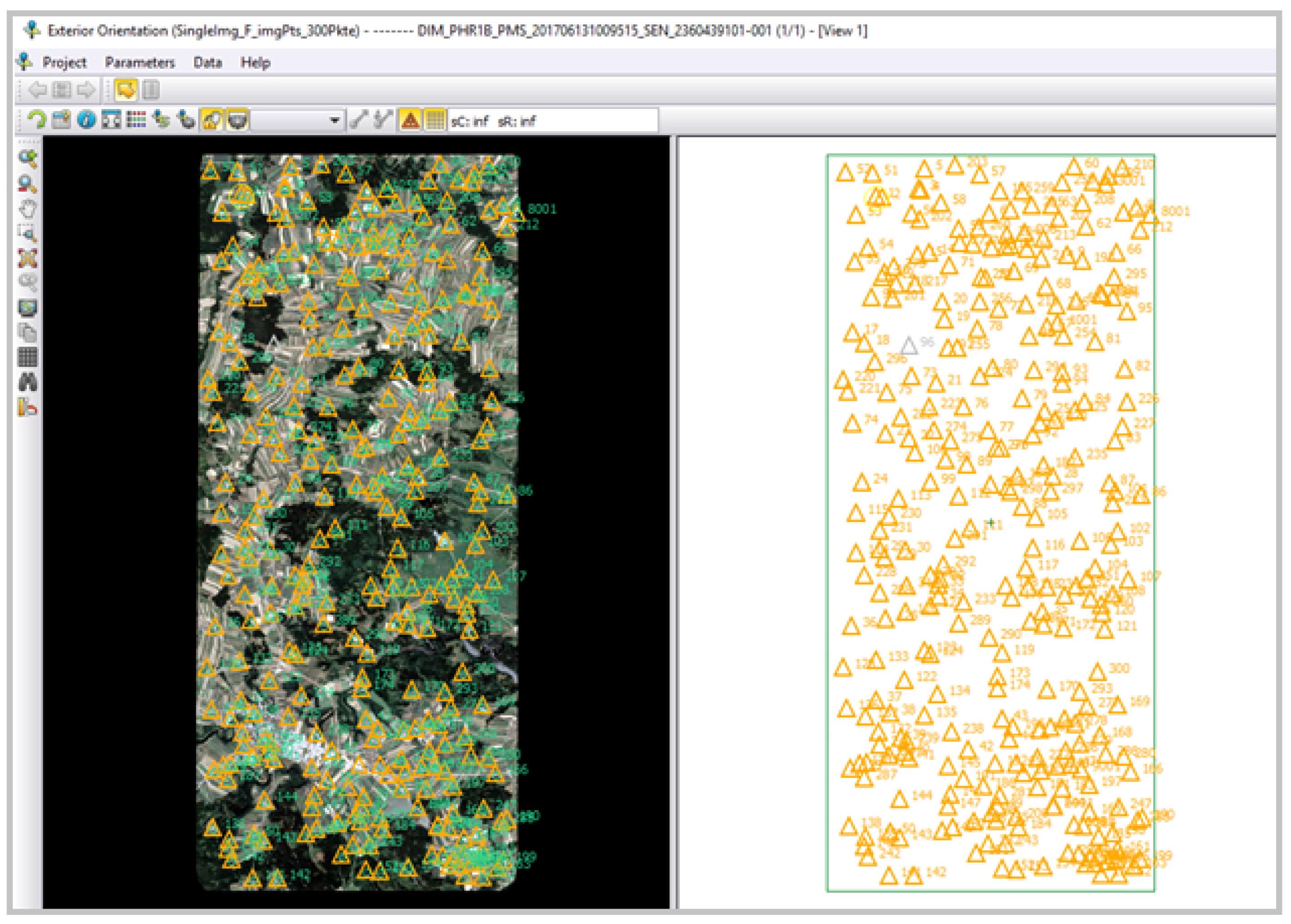
3.1.1. Image Orientation Results
- (1)
- Image georeferencing with bias-corrected RPCs using 43 GCPs and automatically extracted TPs
- (2)
- Image georeferencing with bias-corrected RPCs using 300 GCPs (no TPs are involved).
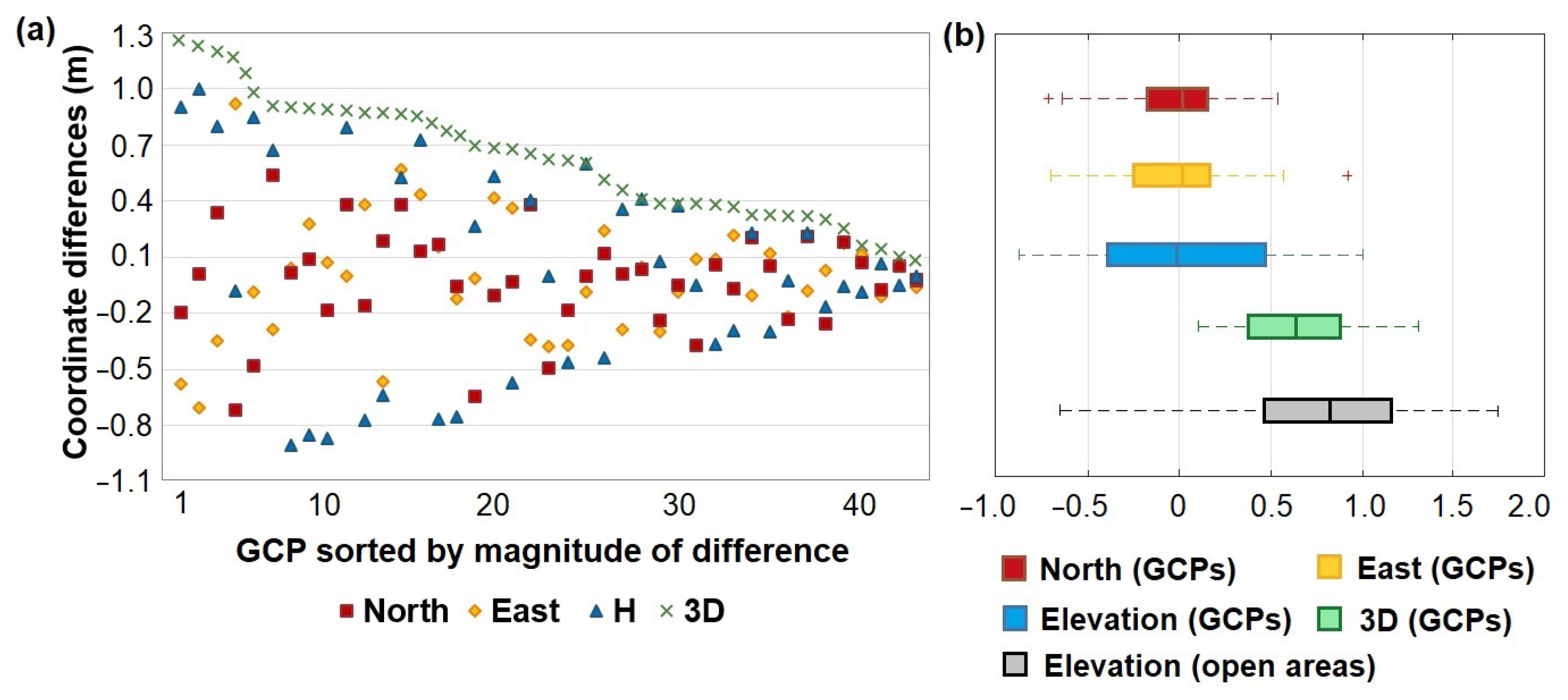
3.1.2. DSM Accuracy Evaluation
3.2. Satellite DSMs Corrected with LSM
3.3. Satellite DSMs Corrected Based on Image Warping
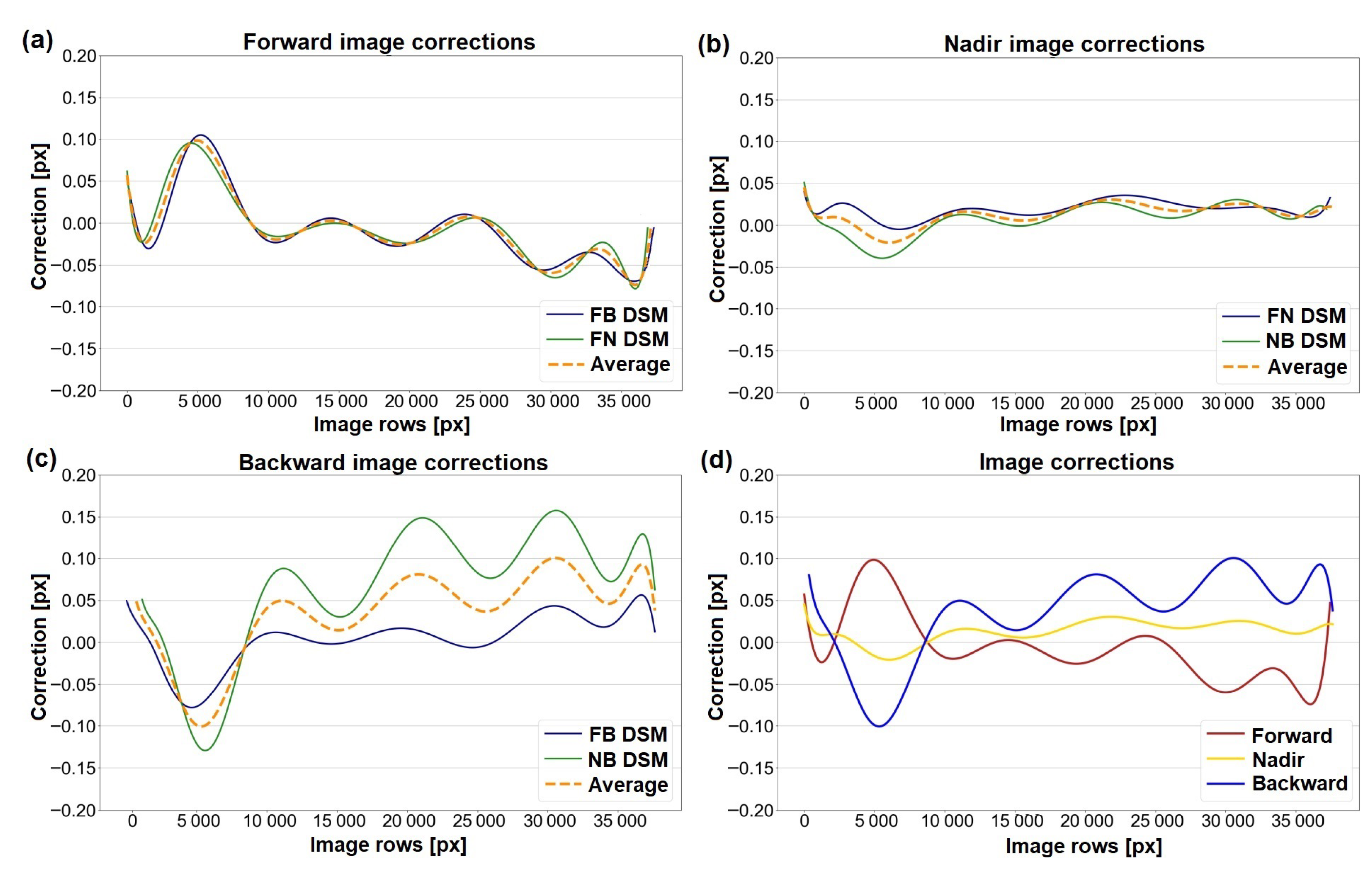
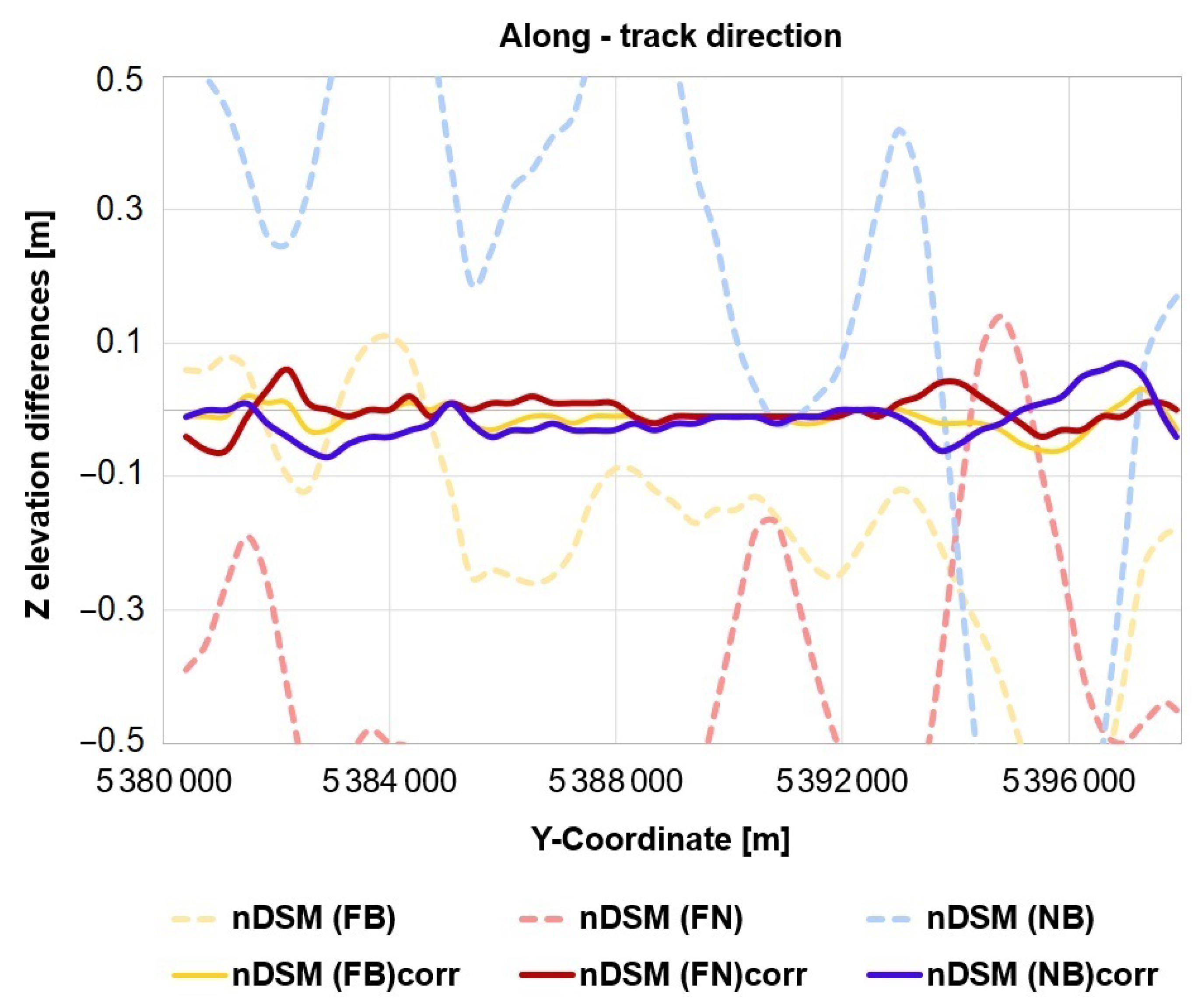
3.3.1. Image Correction Models
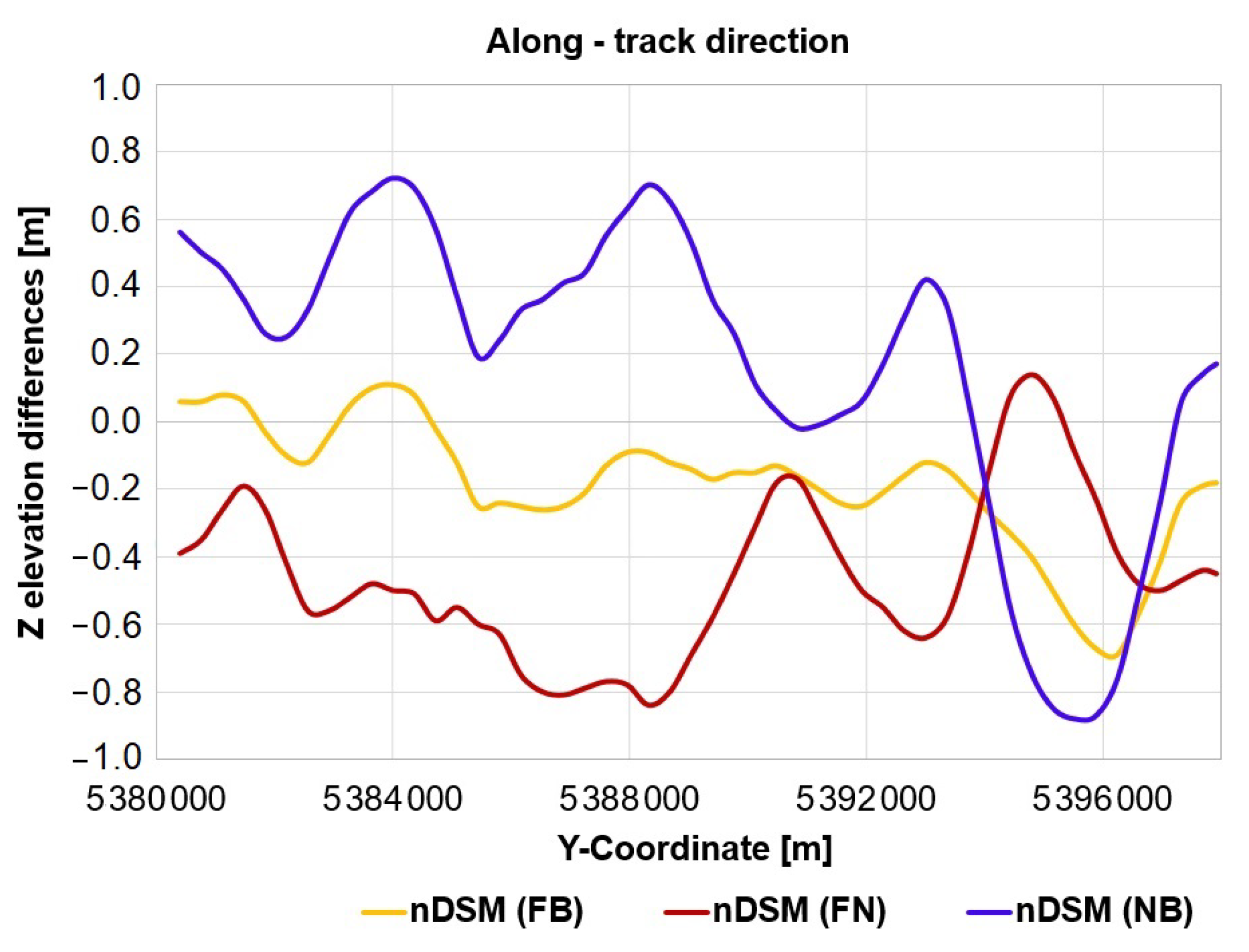
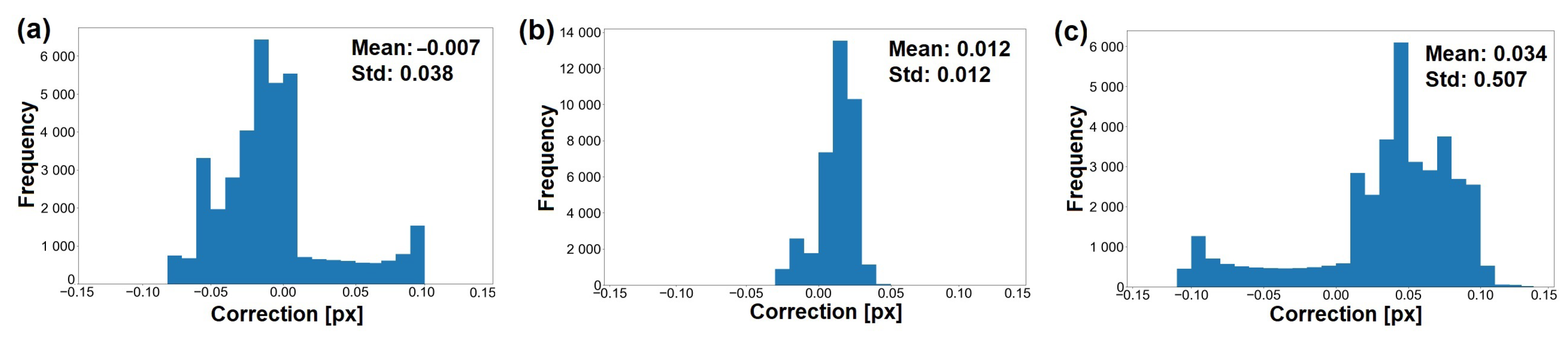
3.3.2. Sensor Oscillations
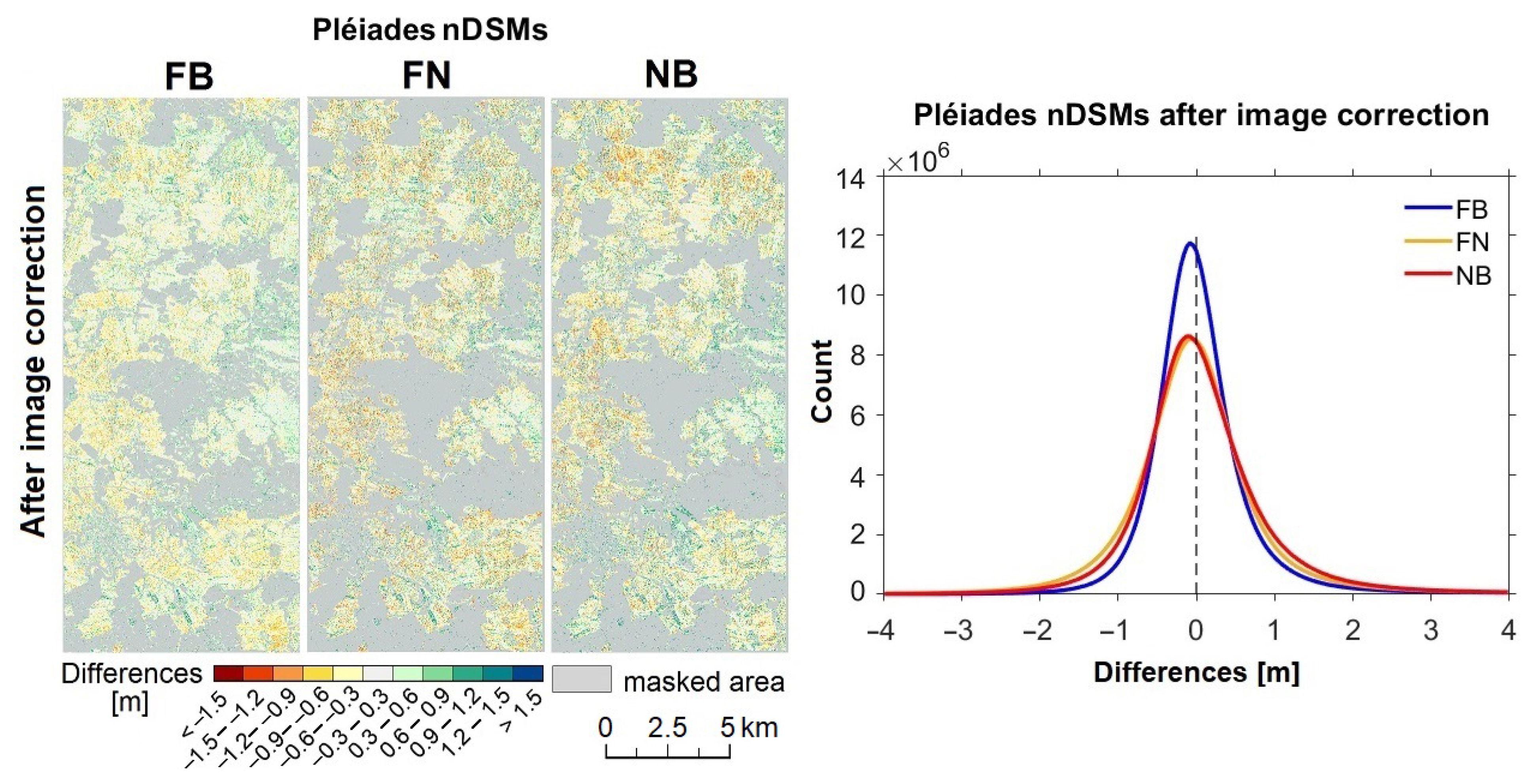
3.3.3. Evaluation of Pléiades DSMs after Image Geometry Correction
4. Discussion
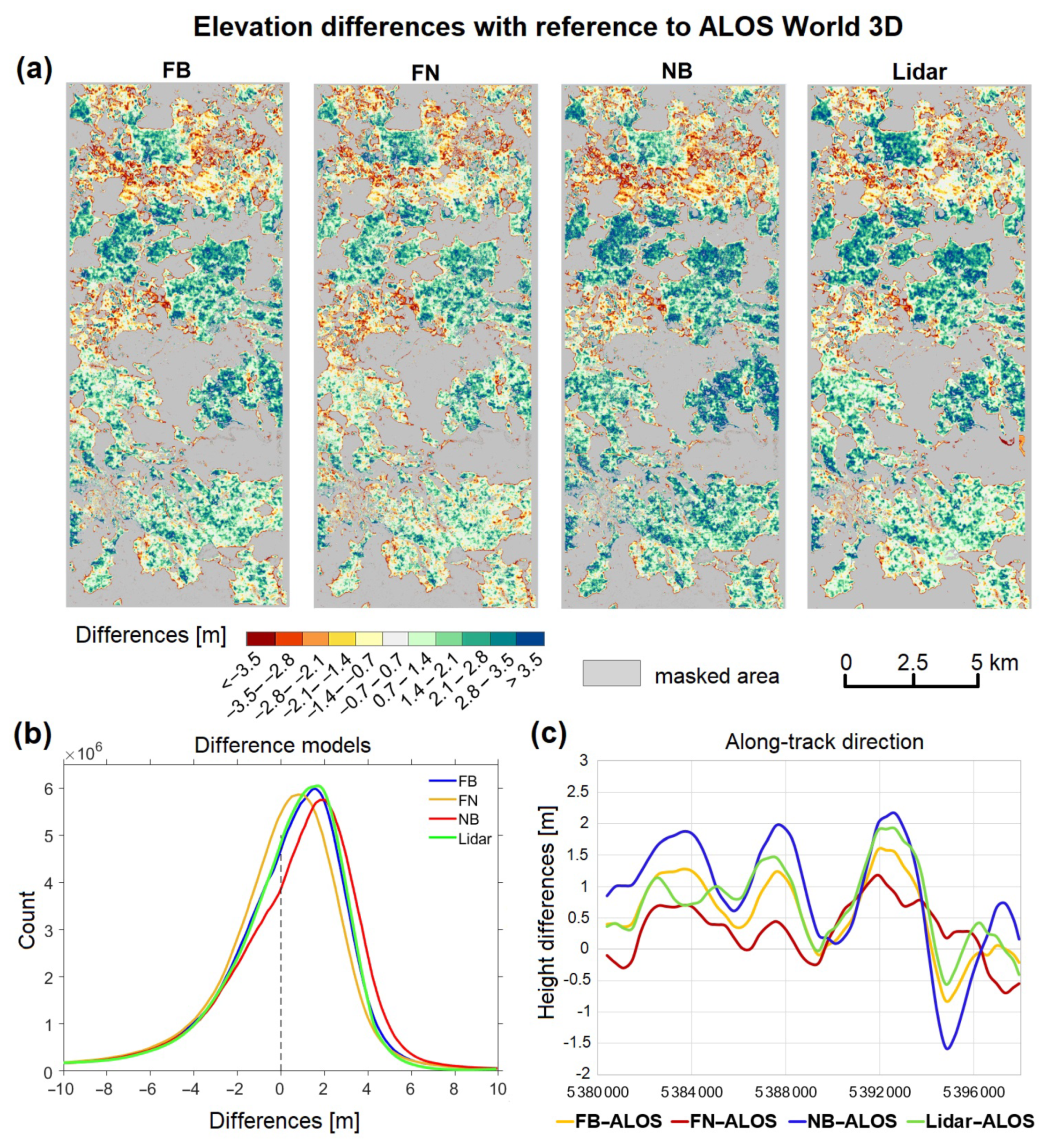
4.1. Suitability of Coarser Resolution DSMs for Satellite Image Geometry Improvement
4.2. Further Remarks
5. Conclusions
- (1)
- In the flying direction, the geometric accuracy of Pléiades images depends on the sensor attitude, which is apparently affected by satellite oscillations.
- (2)
- When compared to a Lidar high resolution elevation model, the computed satellite-based DSMs show periodic systematic height errors as undulations (similar to waves with a maximum amplitude of 1.5 pixels) visible in the along-track direction. This suggests that image orientations are not sufficiently determined by employing a common number of GCPs for RPC bias-correction.
- (3)
- The periodic vertical offsets in the computed DSMs could not be effectively compensated even if the number of GCPs was increased to 300. This strategy brought improvements to the vertical accuracy of the Pléiades DSMs with 20% in the overall RMSE, which implies that the accuracy in height is sensitive to the number and distribution of GCPs. Nevertheless, the systematic elevation offsets are preserved.
- (4)
- Similar to the 300 GCPs strategy, the applied global LSM technique in object space brought significant improvements to the photogrammetrically derived DSMs, since the RMSE were reduced by 26%. However, the systematics in-track direction are still present.
- (5)
- The preservation of systematic height errors in the computed satellite-based elevation models suggests a not sufficient bias-correction model for the RPCs. This is explained by the fact that in the flying direction, satellite image geometry highly depends on the accuracy of the sensor orientation angle. Hence, a quick change in viewing direction leads to sensor vibrations, which cannot be captured by the bias-compensated 3rd-order rational polynomial coefficients.
- (6)
- The proposed approach based on corrections in image space can detect and estimate the periodic image distortions in-track direction. With amplitudes of less than 0.10 pixels, oscillation period (T) of 0.70 s, and frequency of 1.42 Hz, the image corrections describe actually the small vibrations of the Pléiades satellite during image acquisition with a pitch angle of degrees.
- (7)
- The effectiveness of our method is proven by the successfull removal of the systematic elevations discrepancies in the DSM and by the improvement of the overall accuracy with 33% in RMSE.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| VHR | Very High Resolution |
| ALS | Airborne Laser Scanning |
| LiDAR | Light Detection And Ranging |
| DEM | Digital Elevation Model |
| DTM | Digital Terrain Model |
| DSM | Digital Surface Model |
| RFM | Rational Function Model |
| RPC | Rational Polynomial Coefficient |
| GSD | Ground Sampling Distance |
| GCP | Ground Control Point |
| CP | Check Point |
| TP | Tie Point |
| CBM | Cost Based Matching |
| FBM | Feature Based Matching |
| LSM | Least Squares Matching |
| DIM | Dense Image Matching |
| RTK | Real Time Kinematic |
| GNSS | Global Navigation Satellite System |
Appendix A
| Elevation Models | Lidar Reference | LSM ALOS Reference | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| μ | Med | σ | σMAD | RMSE | μ | Med | σ | σMAD | RMSE | |
| LSM ALOS | −0.18 | 0.17 | 2.76 | 2.14 | 2.62 | |||||
| Pléiades comb. | ||||||||||
| FB | −0.10 | −0.16 | 0.64 | 0.53 | 0.65 | −0.27 | 0.04 | 2.70 | 2.21 | 2.71 |
| FN | −0.32 | −0.39 | 0.78 | 0.73 | 0.84 | −0.54 | −0.31 | 2.70 | 2.19 | 2.76 |
| NB | 0.21 | 0.24 | 0.83 | 0.82 | 0.85 | 0.05 | 0.42 | 2.82 | 2.36 | 2.82 |

References
- Holland, D.; Boyd, D.; Marshall, P. Updating topographic mapping in Great Britain using imagery from high-resolution satellite sensors. ISPRS J. Photogramm. Remote Sens. 2006, 60, 212–223. [Google Scholar] [CrossRef]
- Nichol, J.E.; Shaker, A.; Wong, M.S. Application of high-resolution stereo satellite images to detailed landslide hazard assessment. Geomorphology 2006, 76, 68–75. [Google Scholar] [CrossRef]
- Poon, J.; Fraser, C.S.; Chunsun, Z.; Li, Z.; Gruen, A. Quality assessment of digital surface models generated from IKONOS imagery. Photogramm. Rec. 2005, 20, 162–171. [Google Scholar] [CrossRef]
- Toutin, T.; Schmitt, C.; Wang, H. Impact of no GCP on elevation extraction from WorldView stereo data. ISPRS J. Photogramm. Remote Sens. 2012, 72, 73–79. [Google Scholar] [CrossRef]
- Tong, X.; Ye, Z.; Xu, Y.; Tang, X.; Liu, S.; Li, L.; Xie, H.; Wang, F.; Li, T.; Hong, Z. Framework of jitter detection and compensation for high resolution satellites. Remote Sens. 2014, 6, 3944–3964. [Google Scholar] [CrossRef] [Green Version]
- Wang, M.; Zhu, Y.; Pan, J.; Yang, B.; Zhu, Q. Satellite jitter detection and compensation using multispectral imagery. Remote Sens. Lett. 2016, 7, 513–522. [Google Scholar] [CrossRef]
- Fraser, C.S.; Dial, G.; Grodecki, J. Sensor orientation via RPCs. ISPRS J. Photogramm. Remote Sens. 2006, 60, 182–194. [Google Scholar] [CrossRef]
- Zhang, Y.; Zheng, M.; Xiong, X.; Xiong, J. Multistrip bundle block adjustment of ZY-3 satellite imagery by rigorous sensor model without ground control point. IEEE Geosci. Remote Sens. Lett. 2014, 12, 865–869. [Google Scholar] [CrossRef]
- Jiang, Y.H.; Zhang, G.; Tang, X.; Li, D.R.; Wang, T.; Huang, W.C.; Li, L.T. Improvement and assessment of the geometric accuracy of Chinese high-resolution optical satellites. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4841–4852. [Google Scholar] [CrossRef]
- Oh, J.; Lee, C. Automated bias-compensation of rational polynomial coefficients of high resolution satellite imagery based on topographic maps. ISPRS J. Photogramm. Remote Sens. 2015, 100, 14–22. [Google Scholar] [CrossRef]
- Shen, X.; Li, Q.; Wu, G.; Zhu, J. Bias compensation for rational polynomial coefficients of high-resolution satellite imagery by local polynomial modeling. Remote Sens. 2017, 9, 200. [Google Scholar] [CrossRef] [Green Version]
- Dong, Y.; Lei, R.; Fan, D.; Gu, L.; Ji, S. A novel RPC bias model for improving the positioning accuracy of satellite images. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 5, 35–41. [Google Scholar] [CrossRef]
- Hu, Y.; Tao, V.; Croitoru, A. Understanding the rational function model: Methods and applications. Int. Arch. Photogramm. Remote Sens. 2004, 20, 119–124. [Google Scholar]
- Poli, D.; Toutin, T. Review of developments in geometric modelling for high resolution satellite pushbroom sensors. Photogramm. Rec. 2012, 27, 58–73. [Google Scholar] [CrossRef]
- Toutin, T. State-of-the-art of geometric correction of remote sensing data: A data fusion perspective. Int. J. Image Data Fusion 2011, 2, 3–35. [Google Scholar] [CrossRef]
- Tong, X.; Liu, S.; Weng, Q. Bias-corrected rational polynomial coefficients for high accuracy geo-positioning of QuickBird stereo imagery. ISPRS J. Photogramm. Remote Sens. 2010, 65, 218–226. [Google Scholar] [CrossRef]
- Dial, G.; Grodecki, J. Block adjustment with rational polynomial camera models. In Proceedings of the ASPRS 2002 Conference, Washington, DC, USA, 19–26 April 2002; pp. 22–26. [Google Scholar]
- Aguilar, M.A.; Aguilar, F.J.; Mar Saldaña, M.d.; Fernández, I. Geopositioning accuracy assessment of GeoEye-1 panchromatic and multispectral imagery. Photogramm. Eng. Remote Sens. 2012, 78, 247–257. [Google Scholar] [CrossRef]
- Alkan, M.; Buyuksalih, G.; Sefercik, U.G.; Jacobsen, K. Geometric accuracy and information content of WorldView-1 images. Opt. Eng. 2013, 52, 026201. [Google Scholar] [CrossRef]
- Fraser, C.S.; Hanley, H.B. Bias-compensated RPCs for sensor orientation of high-resolution satellite imagery. Photogramm. Eng. Remote Sens. 2005, 71, 909–915. [Google Scholar] [CrossRef]
- Tao, C.V.; Hu, Y.; Jiang, W. Photogrammetric exploitation of IKONOS imagery for mapping applications. Int. J. Remote Sens. 2004, 25, 2833–2853. [Google Scholar] [CrossRef]
- Grodecki, J.; Dial, G. IKONOS geometric accuracy validation. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2002, 34, 50–55. [Google Scholar]
- Fraser, C.S.; Hanley, H.B. Bias compensation in rational functions for IKONOS satellite imagery. Photogramm. Eng. Remote Sens. 2003, 69, 53–57. [Google Scholar] [CrossRef]
- Noguchi, M.; Fraser, C.S.; Nakamura, T.; Shimono, T.; Oki, S. Accuracy assessment of QuickBird stereo imagery. Photogramm. Rec. 2004, 19, 128–137. [Google Scholar] [CrossRef]
- Teo, T.A. Bias compensation in a rigorous sensor model and rational function model for high-resolution satellite images. Photogramm. Eng. Remote Sens. 2011, 77, 1211–1220. [Google Scholar] [CrossRef]
- Shen, X.; Liu, B.; Li, Q.Q. Correcting bias in the rational polynomial coefficients of satellite imagery using thin-plate smoothing splines. ISPRS J. Photogramm. Remote Sens. 2017, 125, 125–131. [Google Scholar] [CrossRef]
- Hong, Z.; Tong, X.; Liu, S.; Chen, P.; Xie, H.; Jin, Y. A comparison of the performance of bias-corrected RSMs and RFMs for the geo-positioning of high-resolution satellite stereo imagery. Remote Sens. 2015, 7, 16815–16830. [Google Scholar] [CrossRef] [Green Version]
- Grodecki, J.; Dial, G. Block adjustment of high-resolution satellite images described by rational polynomials. Photogramm. Eng. Remote Sens. 2003, 69, 59–68. [Google Scholar] [CrossRef]
- Zhang, Y.; Lu, Y.; Wang, L.; Huang, X. A new approach on optimization of the rational function model of high-resolution satellite imagery. IEEE Trans. Geosci. Remote Sens. 2011, 50, 2758–2764. [Google Scholar] [CrossRef]
- Aguilar, M.A.; del Mar Saldana, M.; Aguilar, F.J. Assessing geometric accuracy of the orthorectification process from GeoEye-1 and WorldView-2 panchromatic images. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 427–435. [Google Scholar] [CrossRef]
- Cao, J.; Fu, J.; Yuan, X.; Gong, J. Nonlinear bias compensation of ZiYuan-3 satellite imagery with cubic splines. ISPRS J. Photogramm. Remote Sens. 2017, 133, 174–185. [Google Scholar] [CrossRef]
- Jacobsen, K. Satellite image orientation. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 703–709. [Google Scholar]
- Kornus, W.; Lehner, M.; Schroeder, M. Geometric inflight-calibration by block adjustment using MOMS-2P-imagery of three intersecting stereo-strips. In Proceedings of the ISPRS Workshop on Sensors and Mapping from Space, Hannover, Germany, 27–30 September 1999; pp. 27–30. [Google Scholar]
- Dial, G.; Grodecki, J. Test ranges for metric calibration and validation of high-resolution satellite imaging systems. In Post-Launch Calibration of Satellite Sensors, Proceedings of the International Workshop on Radiometric and Geometric Calibration, Gulfport, MI, USA, 2–5 December 2003; CRC Press: Boca Raton, FL, USA, 2004; Volume 2, p. 171. [Google Scholar]
- Jacobsen, K. Systematic geometric image errors of very high resolution optical satellites. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 42, 233–238. [Google Scholar] [CrossRef] [Green Version]
- Pan, J.; Che, C.; Zhu, Y.; Wang, M. Satellite jitter estimation and validation using parallax images. Sensors 2017, 17, 83. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Teshima, Y.; Iwasaki, A. Correction of attitude fluctuation of Terra spacecraft using ASTER/SWIR imagery with parallax observation. IEEE Trans. Geosci. Remote Sens. 2007, 46, 222–227. [Google Scholar] [CrossRef]
- Amberg, V.; Dechoz, C.; Bernard, L.; Greslou, D.; De Lussy, F.; Lebegue, L. In-flight attitude perturbances estimation: Application to PLEIADES-HR satellites. In Earth Observing Systems XVIII; SPIE: Bellingham, WA, USA, 2013; Volume 8866, pp. 327–335. [Google Scholar]
- Tong, X.; Li, L.; Liu, S.; Xu, Y.; Ye, Z.; Jin, Y.; Wang, F.; Xie, H. Detection and estimation of ZY-3 three-line array image distortions caused by attitude oscillation. ISPRS J. Photogramm. Remote Sens. 2015, 101, 291–309. [Google Scholar] [CrossRef]
- Ayoub, F.; Leprince, S.; Binet, R.; Lewis, K.W.; Aharonson, O.; Avouac, J.P. Influence of camera distortions on satellite image registration and change detection applications. In Proceedings of the IGARSS 2008-2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 8–11 July 2008; Volume 2, p. II-1072. [Google Scholar]
- Mattson, S.; Robinson, M.; McEwen, A.; Bartels, A.; Bowman-Cisneros, E.; Li, R.; Lawver, J.; Tran, T.; Paris, K.; Team, L. Early assessment of spacecraft jitter in LROC-NAC. In Proceedings of the 41st Annual Lunar and Planetary Science Conference, The Woodlands, TX, USA, 1–5 March 2010; Volume 41, p. 1871. [Google Scholar]
- Pan, H.; Zhang, G.; Tang, X.; Li, D.; Zhu, X.; Zhou, P.; Jiang, Y. Basic products of the ZiYuan-3 satellite and accuracy evaluation. Photogramm. Eng. Remote Sens. 2013, 79, 1131–1145. [Google Scholar] [CrossRef]
- Robertson, B.C. Rigorous geometric modeling and correction of QuickBird imagery. In Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium (IEEE Cat. No. 03CH37477), Toulouse, France, 21–25 July 2003; Volume 2, pp. 797–802. [Google Scholar]
- Schwind, P.; Schneider, M.; Palubinskas, G.; Storch, T.; Muller, R.; Richter, R. Processors for ALOS optical data: Deconvolution, DEM generation, orthorectification, and atmospheric correction. IEEE Trans. Geosci. Remote Sens. 2009, 47, 4074–4082. [Google Scholar] [CrossRef]
- Mattson, S.; Boyd, A.; Kirk, R.; Cook, D.; Howington-Kraus, E. HiJACK: Correcting spacecraft jitter in HiRISE images of Mars. Health Manag. Technol 2009, 33, A162. [Google Scholar]
- Iwasaki, A. Detection and estimation satellite attitude jitter using remote sensing imagery. Adv. Spacecr. Technol. 2011, 13, 257–272. [Google Scholar]
- Mumtaz, R.; Palmer, P. Attitude determination by exploiting geometric distortions in stereo images of DMC camera. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 1601–1625. [Google Scholar] [CrossRef]
- Jiang, Y.h.; Zhang, G.; Tang, X.; Li, D.; Huang, W.c. Detection and correction of relative attitude errors for ZY1-02C. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7674–7683. [Google Scholar] [CrossRef]
- Lehner, M.; Müller, R. Quality check of MOMS-2P ortho-images of semi-arid landscapes. In Proceedings of the ISPRS Workshop High Resolution Mapping Space, Hanover, Germany, 6–8 October 2003; pp. 1–5. [Google Scholar]
- Li, R.; Hwangbo, J.; Chen, Y.; Di, K. Rigorous photogrammetric processing of HiRISE stereo imagery for Mars topographic mapping. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2558–2572. [Google Scholar]
- Bostelmann, J.; Heipke, C. Modeling spacecraft oscillations in HRSC images of Mars Express. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2011, 38, 51–56. [Google Scholar] [CrossRef] [Green Version]
- Gwinner, K.; Scholten, F.; Preusker, F.; Elgner, S.; Roatsch, T.; Spiegel, M.; Schmidt, R.; Oberst, J.; Jaumann, R.; Heipke, C. Topography of Mars from global mapping by HRSC high-resolution digital terrain models and orthoimages: Characteristics and performance. Earth Planet. Sci. Lett. 2010, 294, 506–519. [Google Scholar] [CrossRef]
- Astrium. Pléiades Imagery—User Guide v 2.0; Technical report; Astrium GEO-Information Services: Toulouse, France, 2012. [Google Scholar]
- Heipke, C. Automation of interior, relative, and absolute orientation. ISPRS J. Photogramm. Remote Sens. 1997, 52, 1–19. [Google Scholar] [CrossRef]
- Toutin, T. Geometric processing of remote sensing images: Models, algorithms and methods. Int. J. Remote Sens. 2004, 25, 1893–1924. [Google Scholar] [CrossRef]
- Förstner, W. Quality assessment of object location and point transfer using digital image correlation techniques. IBID 1984, 25, 197–219. [Google Scholar]
- Maas, H.G. Least-squares matching with airborne laserscanning data in a TIN structure. Int. Arch. Photogramm. Remote Sens. 2000, 33, 548–555. [Google Scholar]
- Ressl, C.; Kager, H.; Mandlburger, G. Quality checking of ALS projects using statistics of strip differences. Int. Arch. Photogramm. Remote Sens. 2008, 37, 253–260. [Google Scholar]
- Ressl, C.; Pfeifer, N.; Mandlburger, G. Applying 3-D affine transformation and least squares matching for airborne laser scanning strips adjustment without GNSS/IMU trajectory Data. In Proceedings of the ISPRS Workshop Laser Scanning, Calgary, AB, USA, 29–31 August 2011. [Google Scholar]
- Piltz, B.; Bayer, S.; Poznanska, A.M. Volume based DTM generation from very high resolution photogrammetric DSMs. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 83–90. [Google Scholar] [CrossRef] [Green Version]
- Pfeifer, N.; Mandlburger, G.; Otepka, J.; Karel, W. OPALS–A framework for Airborne Laser Scanning data analysis. Comput. Environ. Urban Syst. 2014, 45, 125–136. [Google Scholar] [CrossRef]
- Tadono, T.; Takaku, J.; Tsutsui, K.; Oda, F.; Nagai, H. Status of “ALOS World 3D (AW3D)” global DSM generation. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 3822–3825. [Google Scholar]
- Santillan, J.R.; Makinano-Santillan, M.; Makinano, R.M. Vertical accuracy assessment of ALOS World 3D-30M Digital Elevation Model over northeastern Mindanao, Philippines. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 5374–5377. [Google Scholar]
- Caglar, B.; Becek, K.; Mekik, C.; Ozendi, M. On the vertical accuracy of the ALOS world 3D-30m digital elevation model. Remote Sens. Lett. 2018, 9, 607–615. [Google Scholar] [CrossRef]
- Takaku, J.; Tadono, T.; Tsutsui, K. Generation of High Resolution Global DSM from ALOS PRISM. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 2, 243–248. [Google Scholar] [CrossRef] [Green Version]
- Kraus, K. Photogrammetrie: Geometrische Informationen aus Photographien und Laserscanneraufnahmen; Walter de Gruyter: Berlin, Germany, 2012. [Google Scholar]
- Ressl, C.; Brockmann, H.; Mandlburger, G.; Pfeifer, N. Dense Image Matching vs. Airborne Laser Scanning–Comparison of two methods for deriving terrain models. Photogramm. Fernerkund. Geoinf. 2016, 57–73. [Google Scholar] [CrossRef]
- Takaku, J.; Tadono, T. High resolution dsm generation from alos prism-processing status and influence of attitude fluctuation. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 4228–4231. [Google Scholar]
- Jacobsen, K. Verbesserung der Geometrie von Satellitenbildern durch Höhenmodelle. In Publikationen der Deutschen Gesellschaft für Photogrammetrie; Würzburg, Germany, 2017; p. 13. [Google Scholar]
- Loghin, A.M.; Otepka-Schremmer, J.; Pfeifer, N. Potential of Pléiades and WorldView-3 tri-stereo DSMs to represent heights of small isolated objects. Sensors 2020, 20, 2695. [Google Scholar] [CrossRef]
- Piermattei, L.; Marty, M.; Karel, W.; Ressl, C.; Hollaus, M.; Ginzler, C.; Pfeifer, N. Impact of the acquisition geometry of very high-resolution Pléiades imagery on the accuracy of canopy height models over forested alpine regions. Remote Sens. 2018, 10, 1542. [Google Scholar] [CrossRef] [Green Version]
- Piermattei, L.; Marty, M.; Ginzler, C.; Pöchtrager, M.; Karel, W.; Ressl, C.; Pfeifer, N.; Hollaus, M. Pléiades satellite images for deriving forest metrics in the Alpine region. Int. J. Appl. Earth Obs. Geoinf. 2019, 80, 240–256. [Google Scholar] [CrossRef]
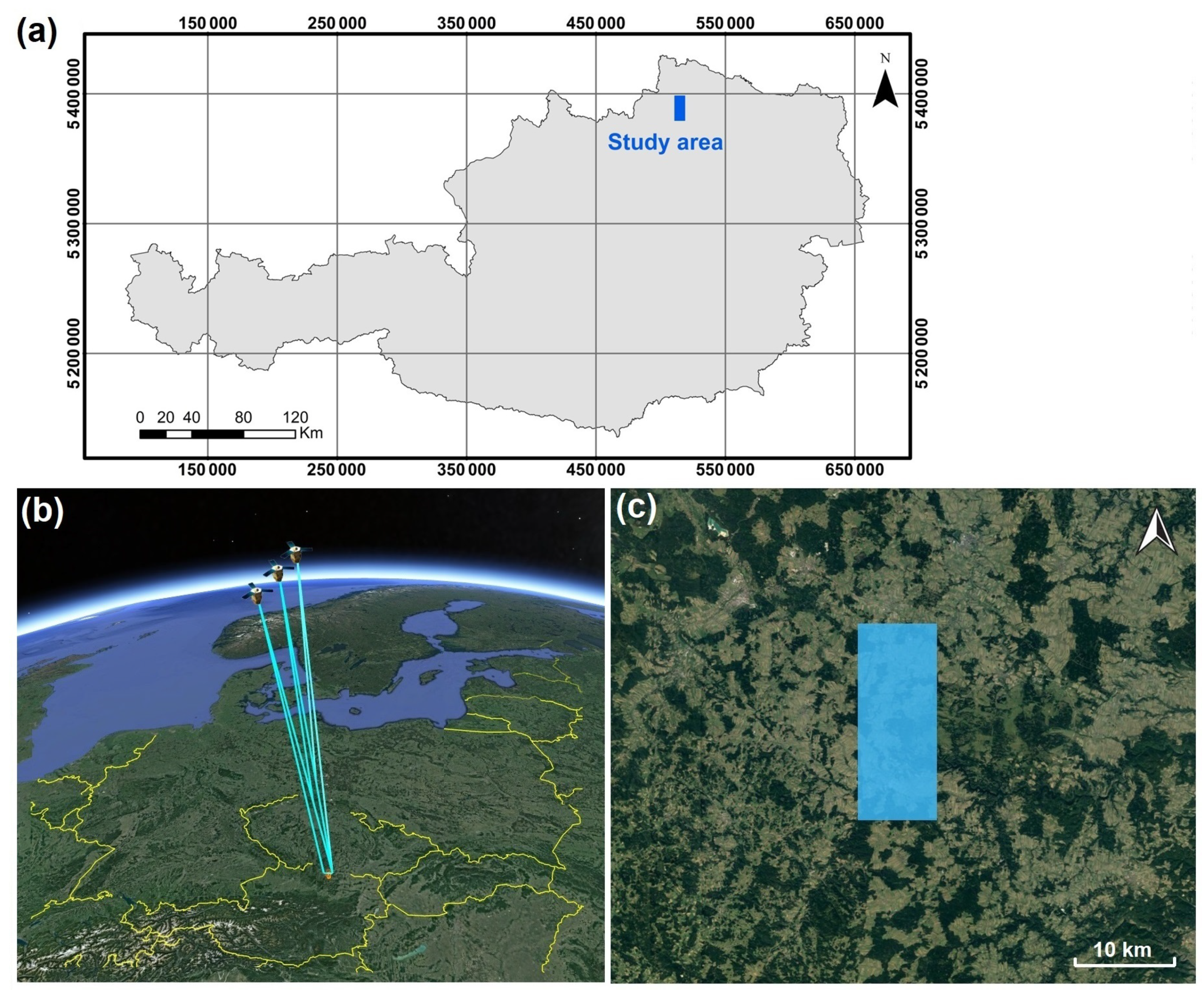







| Acq. Date | Acq. Time (UTC) | Image (View) | GSD [m] | Viewing Angles [°] | B/H Ratio | Convergence Angle (°) | |
|---|---|---|---|---|---|---|---|
| In-Track | Cross-Track | ||||||
| 13 June 2017 | 10:09:51.5 | Forward | 0.71 | 3.15 | −5.66 | 0.13 (FN) | 7.5 (FN) |
| 10:10:03.7 | Nadir | 0.70 | 3.37 | 0.46 | 0.11 (NB) | 6.3 (NB) | |
| 10:10:14.0 | Backward | 0.71 | 3.62 | 5.19 | 0.24 (FB) | 13.8 (FB) | |
| Image | No. GCPs | No. TPs/ Image | Sigma (px) | Image Residual Statistics for GCPs & TP Observations | |||||
|---|---|---|---|---|---|---|---|---|---|
| x-Residual (px) | y-Residual (px) | ||||||||
| μ | σMAD | RMSE | μ | σMAD | RMSE | ||||
| Forward | 373 | 0.00 | 0.26 | 0.26 | 0.00 | 0.13 | 0.13 | ||
| Nadir | 43 | 378 | 0.28 | 0.00 | 0.28 | 0.27 | 0.00 | 0.21 | 0.22 |
| Backward | 375 | 0.00 | 0.26 | 0.26 | 0.00 | 0.12 | 0.12 | ||
| Forward | - | 0.00 | 0.26 | 0.26 | 0.00 | 0.24 | 0.24 | ||
| Nadir | 300 | - | 0.32 | 0.00 | 0.40 | 0.40 | 0.00 | 0.38 | 0.38 |
| Backward | - | 0.00 | 0.32 | 0.31 | 0.00 | 0.32 | 0.31 | ||
| Study Site | Allentsteig | |||
|---|---|---|---|---|
| Mean (m) | Median (m) | σ (m) | RMSE (m) | |
| Easting | −0.01 | 0.02 | 0.29 | 0.32 |
| Northing | −0.02 | 0.01 | 0.22 | 0.27 |
| Elevation | 0.05 | −0.01 | 0.12 | 0.57 |
| 3D | 0.64 | 0.64 | 0.16 | 0.71 |
| * Open areas (Elevation) | 0.80 | 0.79 | 0.53 | 0.89 |
| Scene Comb. | RPC Refinement with 43 GCPs | RPC Refinement with 300 GCPs | ||||||
|---|---|---|---|---|---|---|---|---|
| Mean | Std | σMAD | RMSE | Mean | Std | σMAD | RMSE | |
| FB | 0.77 | 0.53 | 0.51 | 0.93 | −0.10 | 0.64 | 0.53 | 0.65 |
| FN | 0.72 | 0.65 | 0.68 | 0.97 | −0.32 | 0.78 | 0.73 | 0.84 |
| NB | 0.78 | 0.70 | 0.73 | 1.04 | 0.21 | 0.83 | 0.82 | 0.85 |
| Scene Comb. | Before LSM | After LSM | ||||||
|---|---|---|---|---|---|---|---|---|
| Mean | Std | σMAD | RMSE | Mean | Std | σMAD | RMSE | |
| FB | 0.77 | 0.53 | 0.51 | 0.93 | 0.13 | 0.60 | 0.50 | 0.60 |
| FN | 0.72 | 0.65 | 0.68 | 0.97 | 0.13 | 0.75 | 0.72 | 0.76 |
| NB | 0.78 | 0.70 | 0.73 | 1.04 | 0.17 | 0.79 | 0.80 | 0.81 |
| Scene Comb. | Before Image Correction | After Image Correction | ||||||
|---|---|---|---|---|---|---|---|---|
| Mean | Std | σMAD | RMSE | Mean | Std | σMAD | RMSE | |
| FB | −0.10 | 0.64 | 0.53 | 0.65 | −0.00 | 0.44 | 0.45 | 0.44 |
| FN | −0.32 | 0.78 | 0.73 | 0.84 | −0.02 | 0.57 | 0.52 | 0.57 |
| NB | 0.21 | 0.83 | 0.82 | 0.85 | 0.10 | 0.55 | 0.51 | 0.56 |
| Elevation Models | Lidar Reference | ALOS Reference | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| μ | Med | σ | σMAD | RMSE | μ | Med | σ | σMAD | RMSE | |
| ALOS | 0.39 | 0.83 | 2.77 | 2.32 | 2.79 | |||||
| Pléiades comb. | ||||||||||
| FB | −0.10 | −0.16 | 0.64 | 0.53 | 0.65 | 0.28 | 0.70 | 2.85 | 2.38 | 2.86 |
| FN | −0.32 | −0.39 | 0.78 | 0.73 | 0.84 | 0.03 | 0.34 | 2.81 | 2.32 | 2.82 |
| NB | 0.21 | 0.24 | 0.83 | 0.82 | 0.85 | 0.62 | 1.08 | 2.98 | 2.54 | 3.04 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Loghin, A.-M.; Otepka-Schremmer, J.; Ressl, C.; Pfeifer, N. Improvement of VHR Satellite Image Geometry with High Resolution Elevation Models. Remote Sens. 2022, 14, 2303. https://doi.org/10.3390/rs14102303
Loghin A-M, Otepka-Schremmer J, Ressl C, Pfeifer N. Improvement of VHR Satellite Image Geometry with High Resolution Elevation Models. Remote Sensing. 2022; 14(10):2303. https://doi.org/10.3390/rs14102303
Chicago/Turabian StyleLoghin, Ana-Maria, Johannes Otepka-Schremmer, Camillo Ressl, and Norbert Pfeifer. 2022. "Improvement of VHR Satellite Image Geometry with High Resolution Elevation Models" Remote Sensing 14, no. 10: 2303. https://doi.org/10.3390/rs14102303
APA StyleLoghin, A.-M., Otepka-Schremmer, J., Ressl, C., & Pfeifer, N. (2022). Improvement of VHR Satellite Image Geometry with High Resolution Elevation Models. Remote Sensing, 14(10), 2303. https://doi.org/10.3390/rs14102303









