Assimilation of Wheat and Soil States into the APSIM-Wheat Crop Model: A Case Study

Abstract

Optimised farm crop productivity requires careful management in response to the spatial and temporal variability of yield. Accordingly, combination of crop simulation models and remote sensing data provides a pathway for providing the spatially variable information needed on current crop status and the expected yield. An ensemble Kalman filter (EnKF) data assimilation framework was developed to assimilate plant and soil observations into a prediction model to improve crop development and yield forecasting. Specifically, this study explored the performance of assimilating state observations into the APSIM-Wheat model using a dataset collected during the 2018/19 wheat season at a farm near Cora Lynn in Victoria, Australia. The assimilated state variables include (1) ground-based measurements of Leaf Area Index (LAI), soil moisture throughout the profile, biomass, and soil nitrate-nitrogen; and (2) remotely sensed observations of LAI and surface soil moisture. In a baseline scenario, an unconstrained (open-loop) simulation greatly underestimated the wheat grain with a relative difference (RD) of −38.3%, while the assimilation constrained simulations using ground-based LAI, ground-based biomass, and remotely sensed LAI were all found to improve the RD, reducing it to −32.7%, −9.4%, and −7.6%, respectively. Further improvements in yield estimation were found when: (1) wheat states were assimilated in phenological stages 4 and 5 (end of juvenile to flowering), (2) plot-specific remotely sensed LAI was used instead of the field average, and (3) wheat phenology was constrained by ground observations. Even when using parameters that were not accurately calibrated or measured, the assimilation of LAI and biomass still provided improved yield estimation over that from an open-loop simulation.

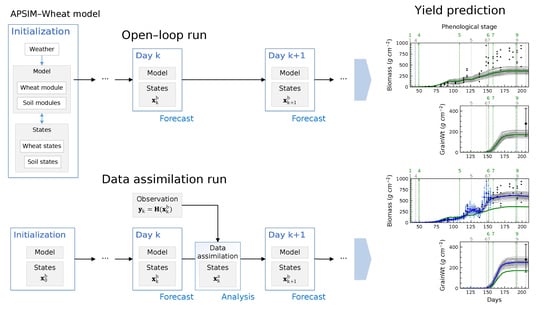
1. Introduction

Understanding spatial and temporal variability in crop yield is essential to site-specific management [1]. Physically based crop models simulate daily crop growth based on energy, water, and nutrient exchange with the atmosphere, soil, climate, and field management [1], with such simulations providing insights into the reasons for yield variability [2]. However, a common issue with crop modelling is that they typically require site specific parameters that can only be calibrated from long-term observations over several growing seasons [1,3] or measured using site-specific soil investigation. Thus, for accurate yield estimation and crop monitoring, key input and parameter data, particularly those with large model sensitivity and spatial heterogeneity (e.g., rainfall and soil characteristics) [4,5,6,7,8], must be collected near the study site to avoid considerable uncertainty in the crop model [9,10,11]. As it is impractical to collect the spatial input and parameter data required due to the high labour and time costs, broad-scale application of these models for yield prediction is difficult [1].

Remote sensing provides vegetation and soil information from space with broad coverage, and a satisfactory resolution and accuracy (root mean squared error) for agricultural purposes at regional scales. Low resolution satellite products such as the Moderate Resolution Imaging Spectroradiometer (MODIS) leaf area index (LAI) has a pixel size of 500 m and a repeat time of 8 days, with global coverage and a reported accuracy of 0.38 m²/m² in grass and cereal crops [12]. The Soil Moisture and Ocean Salinity (SMOS; 35–50 km resolution and 2–3 days repeat) and the Soil Moisture Active Passive (SMAP; 36–9 km resolution and 2–3 days repeat) surface soil moisture products have a reported accuracy of 0.04 m³/m³ from validation field experiments [13,14]. Biomass estimation for winter wheat from Landsat Thematic Mapper (TM) and MODIS images has achieved an accuracy of 664 kg/ha [15]. Moreover, high-resolution satellites data such as Sentinel-2 (10 m, 5 days) and Sentinel-1 (5–40 m, 6 days) have been used to map LAI with an accuracy of 0.35–0.63 m²/m² in wheat fields [16], and surface soil moisture with an accuracy of 0.08–0.12 m³/m³ in a vegetated areas [17]. Based on global remote sensing observations, a broad range of vegetation and water indices have been used to estimate crop status, water status and yield using models ranging from simple linear [18,19,20,21], quadratic [20], and exponential [22,23] regressions to complex machine learning approaches [24,25,26,27].

Fusing remote sensing observations and crop models is expected to take advantage of both the model and remote sensing data to improve estimates of spatial and temporal yield variability [28]. While the model is sensitive to input data accuracy, and the observation accuracy can be affected by the instrument and estimation errors, advanced data assimilation techniques (referred to as data assimilation hereafter) can be used to combine the two sources of information to derive a more accurate estimate of the physical system than any one approach on its own [29]. Accordingly, assimilation methods have been developed to estimate a true system state by carefully estimating and evaluating uncertainties to which model estimates and external observations are subjected [30]. Data assimilation techniques could therefore be used to combine remotely sensed data as observations of the dynamic system with the dynamic model state predictions in order to approach the true states, by reducing the uncertainties from both the model and the external observations.

Data assimilation applications have so far been mainly focused on monitoring food security at regional scale, with the results evaluated using official statistics to support policy-making [31,32,33]. However, application is required at the field or subfield scale using high-resolution remote sensing data in order to support agricultural decision-making. Only a few studies have explored and validated the application of crop model data assimilation at farm scales [33,34,35]. Moreover, only limited plant and soil states (usually LAI and/or surface soil moisture) have been tested in these studies, due to the limitations of current remote sensing techniques. Accordingly, Zhang [28] developed an APSIM-EnKF framework and presented a synthetic study to show the potential improvements from assimilating a range of wheat and soil states. This paper expands on that work at experimental plot scale using a field dataset collected over the 2018/19 wheat season. The data assimilation experiments involved in this study were designed to address the following five research questions:

(1)

Which wheat and soil states improve the APSIM yield estimation at field scale?

(2)

Do the remotely sensed observations of model states have a potential to provide spatial variation at subfield scale when assimilated into the one dimensional APSIM-Wheat model?

(3)

At which phenological stage(s) does the wheat and soil states efficiently improve the model yield estimation?

(4)

Does constraining the phenology reduce uncertainties?

(5)

Do the remotely sensed observations of model states have the potential to provide better yield estimation when applied to an uncalibrated model?

2. Methodology

2.1. Dataset

The study site used is a 75 × 75 m square wheat field, located in the Cora Lynn area of Victoria, Australia. The ground-based dataset was collected in a 2018/19 field experiment described in detail by Zhang [28]. The satellite-based remotely sensed LAI consisted of a series of 3 m daily LAI images produced by the fusion of Sentinel-2 LAI and PlanetScope surface reflectance, with an accuracy of 0.35–0.63 m²/m² when evaluated using 57 wheat fields (including the study site) across Australia and Israel [16]. This study uses the dataset for model input, wheat and soil state observations to be assimilated into the model, and validation.

The model input includes weather and soil properties. The daily weather dataset used in this study consists of daily rainfall, solar radiation, maximum/minimum temperature, pan evaporation, wind speed, and vapour pressure. The weather dataset was created from the average of several nearby weather stations sourced from the Australian Bureau of Meteorology (BoM, http://www.bom.gov.au/ (accessed on 16 July 2019)) and the Weather Underground weather station network (WU, https://www.wunderground.com/ (accessed on 2 March 2019)) to best-match the in situ weather station. The soil property information required for model input was measured in the field during the wheat season at five locations, in six layers throughout the soil profile (0–5, 5–15, 15–25, 25–35, 35–45, 45–55 cm).

The observations of wheat and soil states assimilated into APSIM included ground-measured (ground) and remotely sensed (RS) data. Ground data included: (1) measurements of LAI, biomass (total and separately for leaf and stem), and soil nitrogen in the form of nitrate (NO3N) in 0–5 cm and 5–15 cm soil layers, from laboratory processing of weekly vegetation and soil samples, (2) in situ station-based daily soil moisture throughout the soil profile (0–5, 5–15, 15–25, 25–35, 35–45, 45–55 cm), and (3) phenology from weekly experimental records and an in situ camera estimated according to Zadoks et al. [36]. The remotely sensed data included (1) high spatiotemporal resolution (3 m, daily) LAI images from a fused Sentinel-2 and PlanetScope dataset [16], and (2) surface soil moisture (field scale by treating the whole field as a single pixel, daily) retrieved from tower-based microwave brightness temperature.

The validation data included the above time series of wheat and soil observations, the date of major phenological stages, and wheat grain yield.

2.2. Model Configuration

The APSIM-EnKF data assimilation framework used in this study was the version developed and described by Zhang [28] (source code available on https://github.com/yuxi-research/APSIM-EnKF, published on 6 December 2021). The simulation window was set from 1 July 2018 (Day 0), to 1 March 2019 (Day 243). Winter wheat (variety: RGT Accroc) was sown on 7 August 2018 with a sowing depth of 5 cm. When sowing, fertiliser was applied at the rate of 100 kg/ha using mono-ammonium phosphate (MAP, containing 10% ammonium nitrogen). The row spacing was 0.2 m, and the population was 251 plants/m².

The soil was defined by six layers, with depths of 0–5, 5–15, 15–25, 25–35, 35–45, and 45–55 cm. Key soil parameters controlling the soil moisture dynamics, including the drained upper limit, the lower limit at 15 bars, and the volumetric moisture content of saturated and air-dry soil, were estimated from the maximum and minimum soil moisture during the growing season. Both default and calibrated parameters were used, with the calibrated parameters specified in

Table 1. The calibrated soil parameters in the SoilWat and SoilN modules.

Parameter	Description	Layer	Default Value	Calibrated Value
ConA summer (ConAsummer)	A regression coefficient that specifies the change of cumulative evaporation in the second stage of soil evaporation calculation. Applied to summer days.	-	5	3.8
U summer (Usummer)	Amount of cumulative evaporation before soil supply decreases below the atmospheric demand. Applied to summer days.	-	5	3.8
ConA winter (ConAwinter)	Same as the ConAsummer but for winter days.	-	5	1.5
U winter (Uwinter)	Same as the Usummer but for winter days.	-	5	1.5
SummerDate	Start date for switching to summer parameters for soil water evaporation.	-	1-Nov	19-Nov
DiffusConst	Parameter in the soil water diffusivity calculation. Unit in mm2/day.	-	40	400
SWCON	Fractional amount of water above drain upper limit that can dry under gravity per day. Unit in 1/mm.	1	0.3	0.02
		2	0.3	0.1
		3	0.3	0.1
		4	0.3	0.1
		5	0.3	0.3
		6	0.3	0.3
Fbiom (Fbiom)	The biom pool carbon as a fraction of the hum carbon that is subject to decomposition.	1	0.04	0.1
		2	0.04	0.05
		3	0.02	0.03
		4	0.02	0.02
		5	0.02	0.01
		6	0.02	0.01

. Parameter calibration was performed manually and according to sensitivity: seven parameters in the SoilWat module controlling the rate of infiltration and evapotranspiration were calibrated manually to the station soil moisture data in all six layers, and one parameter in the SoilN module controlling soil nitrogen decomposition was calibrated to the variation of ground-measured soil nitrate in the first two layers. The remaining parameters were set to measured values in the first four layers, with deeper layers assumed to be the same as those in the fourth layer.

An ensemble of 50 was generated by adding Gaussian distributed random noise to the weather forcings, parameters and the assimilated observations. The random noise applied to each quantity has a mean of zero and a standard deviation being the uncertainty value as shown in

Table 2. Uncertainties of weather data, model parameters, and state observations to generate the ensembles.

Data	Description	Unit	Uncertainty
			Type 1	Std.
Weather (daily)
Rainfall	Rainfall	mm	M	0.160
Radiation	Radiation	mm	A	1.254
Max/min temperature	Max/min air temperature		A	0.882
Wind speed	Wind speed	m/s	A	0.679
Parameters
DUL	Drained upper limit	m3/m3	A	0.03
WheatLL	Permanent wilting point	m3/m3	A	0.01
Observations (ground-based measurements)
LAI	Leaf area index	m2/m2	M	0.15
LeafWt	Dry leaf weight	g/m2	M	0.2
StemWt	Dry stem weight	g/m2	M	0.2
Biomass	Aboveground dry biomass	g/m2	M	0.2
SM1	Surface soil moisture (0–5 cm)	m3/m3	A	0.03
SM2,…, SM6	Root-zone soil moisture (5–15, 15–25, 25–35, 35–45, 45–55 cm)	m3/m3	A	0.01
NO3N1, NO3N2	Soil nitrogen in the form of nitrate (0–5, 5–15 cm)	kg/ha	M	0.1
Observations (remotely sensed)
LAI-RS	Leaf area index	m2/m2	M	0.1
SM1-RS	Surface soil moisture	m3/m3	A	0.036

¹ Uncertainty type: M = multiplicative, A = additive.

, with types of either additive, meaning that the standard deviation is a constant over time, or multiplicative, meaning that the standard deviation changes with time with at a proportion of the quantity value.

Filter divergence is a common problem in EnKF data assimilation, with the prior error covariance underestimated due to approximations underlying the algorithm. Accordingly, new observations are given less weight at update steps to impact the analysis result, with the forecast diverging from the observations [37]. This problem is usually addressed by appending a model uncertainty term in the state transfer function or multiplying the forecast error covariance by an inflation factor having a value greater than 1. In this study, a covariance inflation factor was used to inflate the ensemble spread, with a value tuned to avoid filter divergence while keeping the ensemble spread small. Further details on this inflation factor are provided in Section 3.2.1.

2.3. Data Assimilation Experiments

A baseline data assimilation scenario is first presented by assimilating all wheat and soil states at the field scale. In all subsequent scenarios described in the remainder of this section, the configurations remain the same as the baseline scenario unless specifically specified.

The baseline scenario assimilated states at the field scale at three-day intervals (except for the soil moisture that was assimilated daily). In the baseline scenario, all state observations, except for the soil moisture which was assimilated daily, were averaged and interpolated/resampled to 3 days to create a 3-day field-average time series for each state. The assimilation window was from stage 4 to the middle of stage 7, being the period between the end of juvenile and near the end of grain filling, to avoid model failure when perturbed in early stages and direct update of the grain weight in the late grain-filling stage.

Wheat and soil states were assimilated into the model individually and jointly, with observations obtained from field and remote sensing. The wheat and soil states assimilated into APSIM-Wheat included (1) LAI from ground-based measurements and remote sensing, respectively; (2) total aboveground dry biomass (biomass hereafter) and organ weight (LeafWt and StemWt) from ground-based measurements; (3) soil moisture in the depths of 0–5, 5–15, 15–25, 25–35, 35–45, 45–55 cm measured by in situ soil moisture stations, and 0–5 cm retrieved from brightness temperature by the tower-based passive microwave radiometer; and (4) soil nitrogen in the depths of 0–5 and 5–15 cm measured by destructive sampling and laboratory chemical analysis.

In addition to the baseline scenario, several other scenarios were tested:

(1)

A plot-specific scenario to study the assimilation performance on a spatial scale. Here the assimilation focused on four 1 m × 1 m experimental plots distributed in the field rather than the entire field to explore the impact of high-resolution simulation. The wheat grain yield in each plot was measured by harvesting the grain in the four experimental plots and weighing the dry weight after drying in an oven at 60° for more than 72 h, with the field-average yield calculated as the average yield of the four plots. Only remotely sensed LAI extracted from the nearest nine pixels of the four specific plots were assimilated to estimate the yield in each plot. The simulated yield was validated by the yield data collected in each plot, respectively.

(2)

An observation-limited scenario to explore the optimal assimilation stage. The APSIM-Wheat module describes ten wheat phenological phases: 1—sowing, 2—germination, 3—emergence, 4—end of juvenile, 5—floral initiation, 6—flowering (anthesis), 7—start of grain filling, 8—end of grain filling, 9—maturity, and 10—harvest; with phenological stages being the period between two adjacent phases. Here the study focused on the assimilation of state observations for a single phenological stage among stages 4 (end of juvenile to floral initiation), 5 (floral initiation to flowering), and 6–7 (flowering to end of grain filling).

(3)

A phenology-constrained scenario to minimise the uncertainty from phenology estimation. Here the phenology was also constrained with field observations. However, instead of using the EnKF for constraining the phenology, a more primitive data assimilation method known as direct insertion [29,38,39] was applied. The direct insertion method replaced the modelled phenology with the observed date without weighing their uncertainties. Wheat phenology in the Zadoks phenology scale [36] was estimated through weekly field experimental records and an in situ time-lapse camera. APSIM wheat phenology was then obtained by mapping the Zadoks scale to the APSIM wheat scale through an in-built linear equation provided by the APSIM wheat module documentation.

(4)

An uncalibrated scenario to test the performance of assimilation in a field where the in situ data for model calibration are not available. Here uncalibrated models were used with soil module parameters obtained from the APSIM soil library. In this scenario, fourteen generic soil types measured in the same state of the study site were used to replace the calibrated soil parameters in the baseline scenarios. The parameters include those controlling soil water retention, evapotranspiration, and the percentage of active/inactive nitrogen pool.

The outcomes of the data assimilation experiments were evaluated with the root mean square error (RMSE) of the state variables and the relative difference of yield (RDyield; note that the yield refers to the dry grain weight at harvest), expressed as:

$$\mathrm{RMSE}=\frac{1}{\mathrm{L}}{{\displaystyle \sum }}_{\mathrm{k}=1}^{\mathrm{L}}\left(X_{\mathrm{k}}^{\mathrm{est}}-X_{\mathrm{k}}^{\mathrm{obs}}\right),$$

(1)

$${\mathrm{RD}}_{\mathrm{yield}}=\frac{{\mathrm{yield}}_{\mathrm{est}}-{\mathrm{yield}}_{\mathrm{obs}}}{{\mathrm{yield}}_{\mathrm{obs}}},$$

(2)

where L is the total time step. The estimated states $X_{\mathrm{k}}^{\mathrm{est}}$ is the analysis ensemble mean for the assimilation while $X_{\mathrm{k}}^{\mathrm{obs}}$ is the ground observations of the state at time step k. The ${\mathrm{yield}}_{\mathrm{est}}$and ${\mathrm{yield}}_{\mathrm{obs}}$ are the estimated and observed grain weight in kg/ha at the date of harvest, respectively. Therefore, a value of ${\mathrm{RD}}_{\mathrm{yield}}$ closer to zero means that the yield estimation is more accurate. An absolute value of ${\mathrm{RD}}_{\mathrm{yield}}$ from a data assimilation experiment being less than the open-loop indicates that the data assimilation contributed to a better yield estimation than when no data are assimilated. A negative value indicates that the yield estimation error was overcorrected.

3. Results and Discussion

3.1. Model Calibration

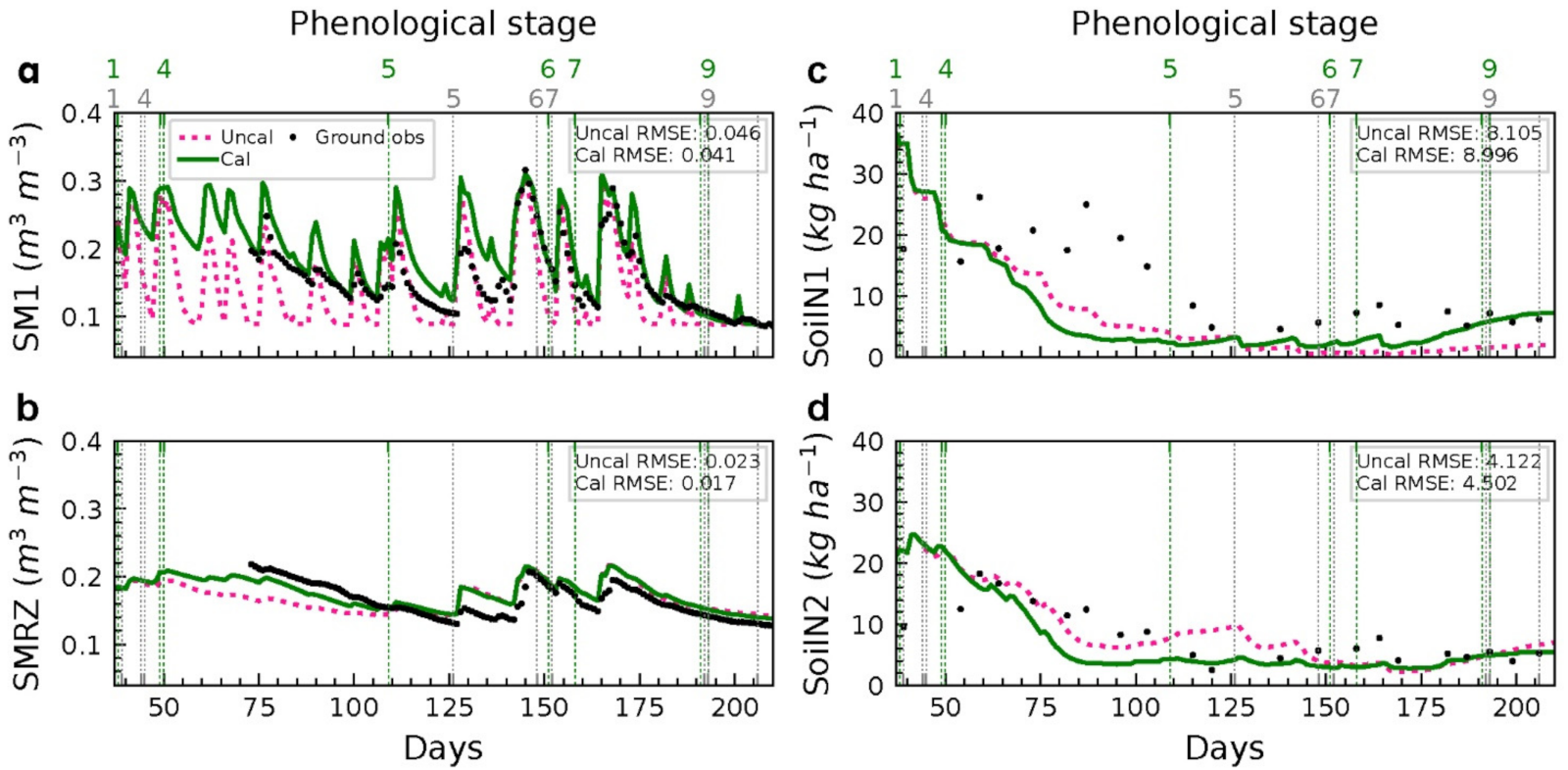
An example of soil module calibration outcomes is shown in Figure 1, as the time series of the estimated soil moisture and ammonium nitrogen before and after the model calibration. After calibration, the soil moisture and nitrogen followed the measured field data with a reduced RMSE of soil moisture in the surface layer (layer 1) and the root zone (layers 2–6). The parameter Fbiom in the SoilN module was adjusted to fit the soil nitrogen (as the sum of nitrogen in the ammonium and nitrate) dynamics. However, the estimation of soil nitrogen only fitted the observations in the late growing season due to a delay of the estimated LAI growing period (further discussed in the results of the soil nitrate assimilation).

3.2. Baseline Scenario

3.2.1. Inflation Factor Selection

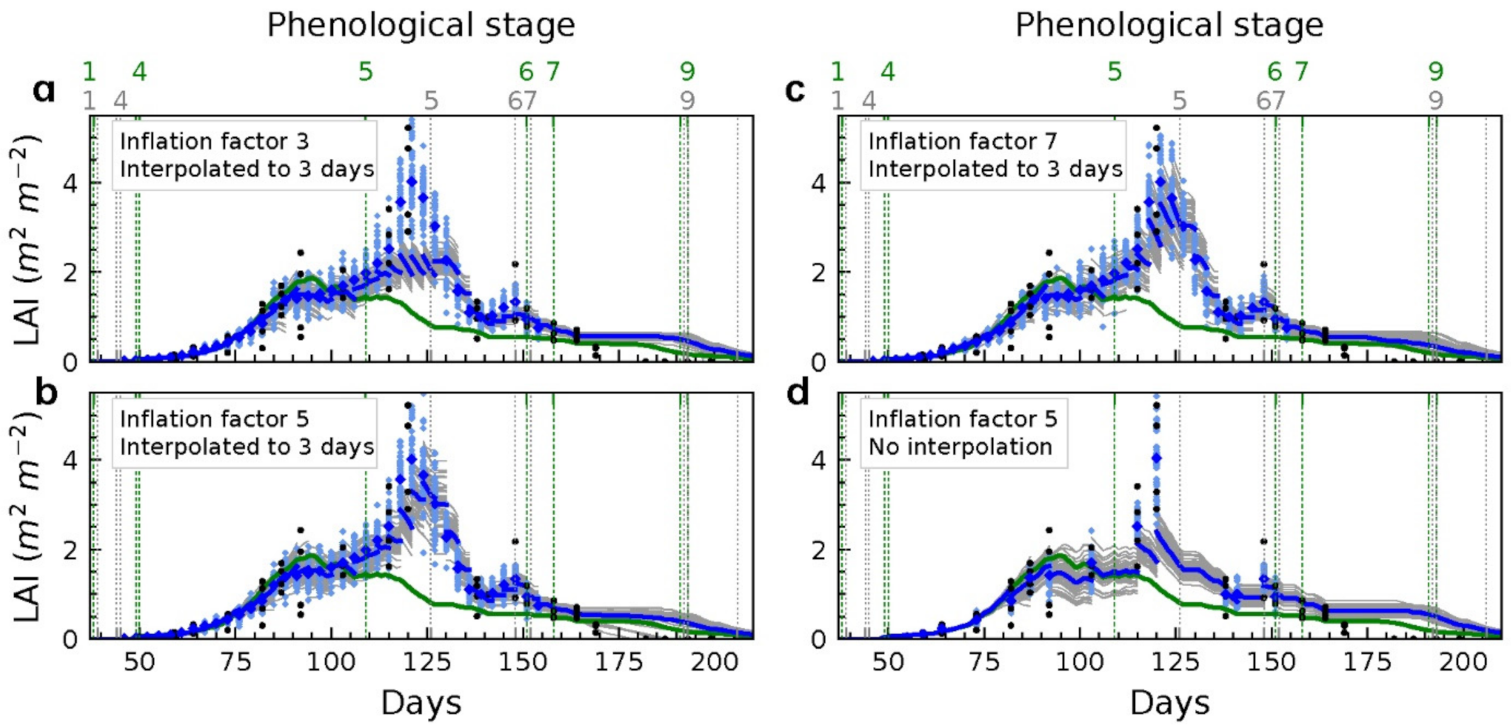
The purpose of the inflation factor is to ensure that the ensemble spread is maintained such that the derived error covariance correctly represents the background uncertainty. An ideal scenario is that the ensemble of model state predictions overlaps with the ensemble of observations, with the ensembles approximating the probability distribution of the state using a finite number of ensemble members. With the model estimates and the external observations each providing a probability distribution of the true state according to their own values and uncertainties, the overlay in the two probability distributions identifies those model ensemble members that best agree with the observations when accounting for the uncertainty of each.

Identification of an appropriate inflation factor was a trial-and-error process. Accordingly, the data assimilation run was performed with an initial inflation factor set slightly greater than 1, then the ensemble spread checked. The ensemble spread is too narrow if the state ensemble does not enclose the observation ensemble, with the inflation factor adjusted to a greater value. The adjustment process repeats until an overlay was found between the state and observation ensemble in most assimilation timesteps over the entire period, while ensuring that the spread was not drastically greater than the spread of the stochastic open-loop run without any inflation.

An inflation factor of 5 was found to be appropriate in the assimilation of wheat states and soil nitrate, except for the biomass assimilation, where a smaller inflation factor of 4 was found. As the inflation factor was only applied when observations were assimilated, a smaller inflation factor of 2 was selected to assimilate soil moisture daily rather than every three days as in the other states.

It should be noted that while the inflation factor of 5 is very large relative to the commonly used inflation factor values that are usually slightly greater than 1 in meteorological data assimilation [40], where the numerical weather prediction models are chaotic, complex, and three-dimensional [41,42,43,44,45,46]. However, the crop models are relatively simple one-dimensional simulations at a daily time step. In this case, the ensemble spread cannot be maintained with a small inflation factor. For example, Figure 2 shows LAI assimilation results using the selected inflation factor compared to smaller and larger inflation factors. A smaller inflation factor resulted in a limited overlap between the observation and the model ensembles, as found in the ensembles of the five successively assimilated LAI observations starting from day 119 (Figure 2a). In comparison, a larger inflation factor introduced unnecessary noise, making the model less trusted by the data assimilation algorithm (Figure 2c). The EnKF works suboptimally with a larger inflation factor because the Kalman gain is derived to minimise the model error without accounting for the inflation factor. An alternative method is to add noise to the model states at each time step, but this approach sometimes causes model failure when errors are added in the growth stage, accidentally driving the wheat states to be near zero, and is also less computational effective.

3.2.2. Assimilation of LAI

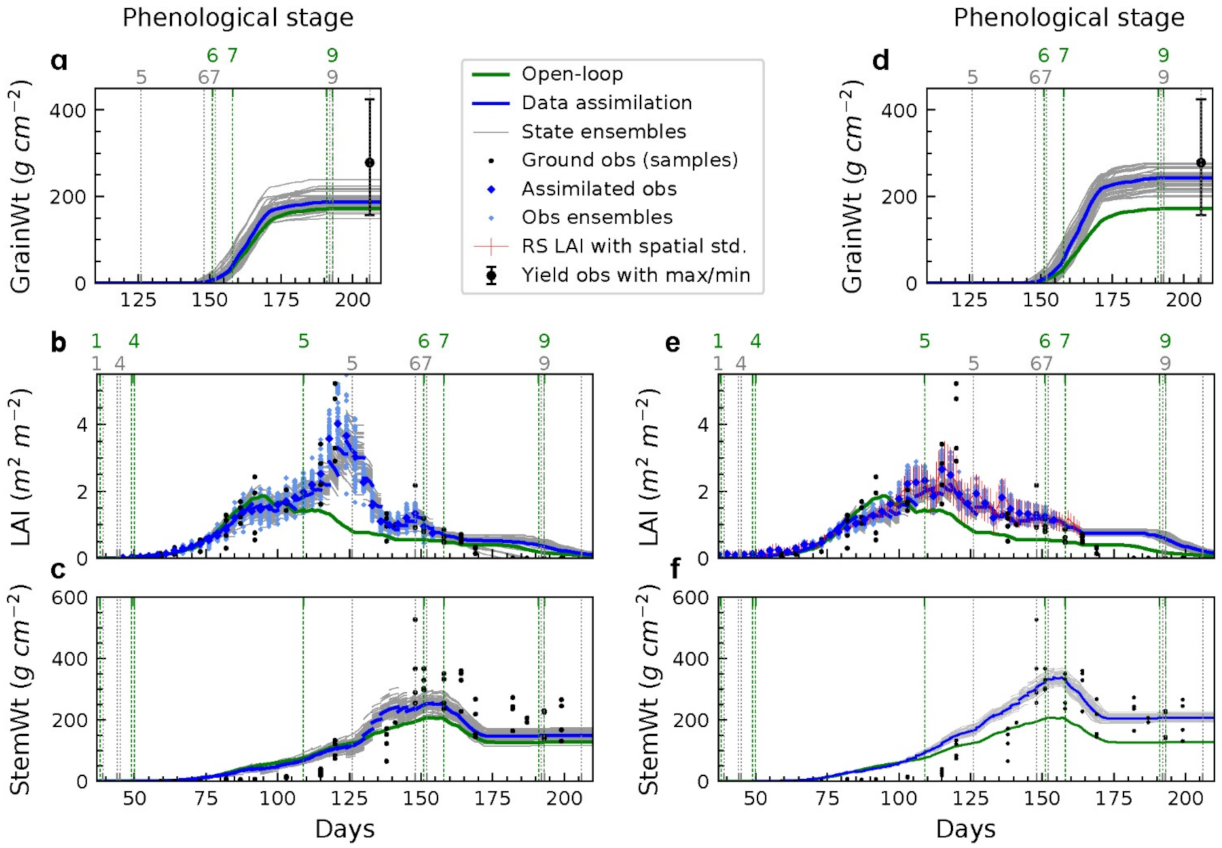
The year of this study was drier than average, resulting in heavy water stress in the vegetative stages (before phase 5, the floral initiation). With the model calibrated to fit the in situ soil moisture time series, the open-loop simulation greatly underestimated the LAI, organ weight, and wheat yield at harvest.

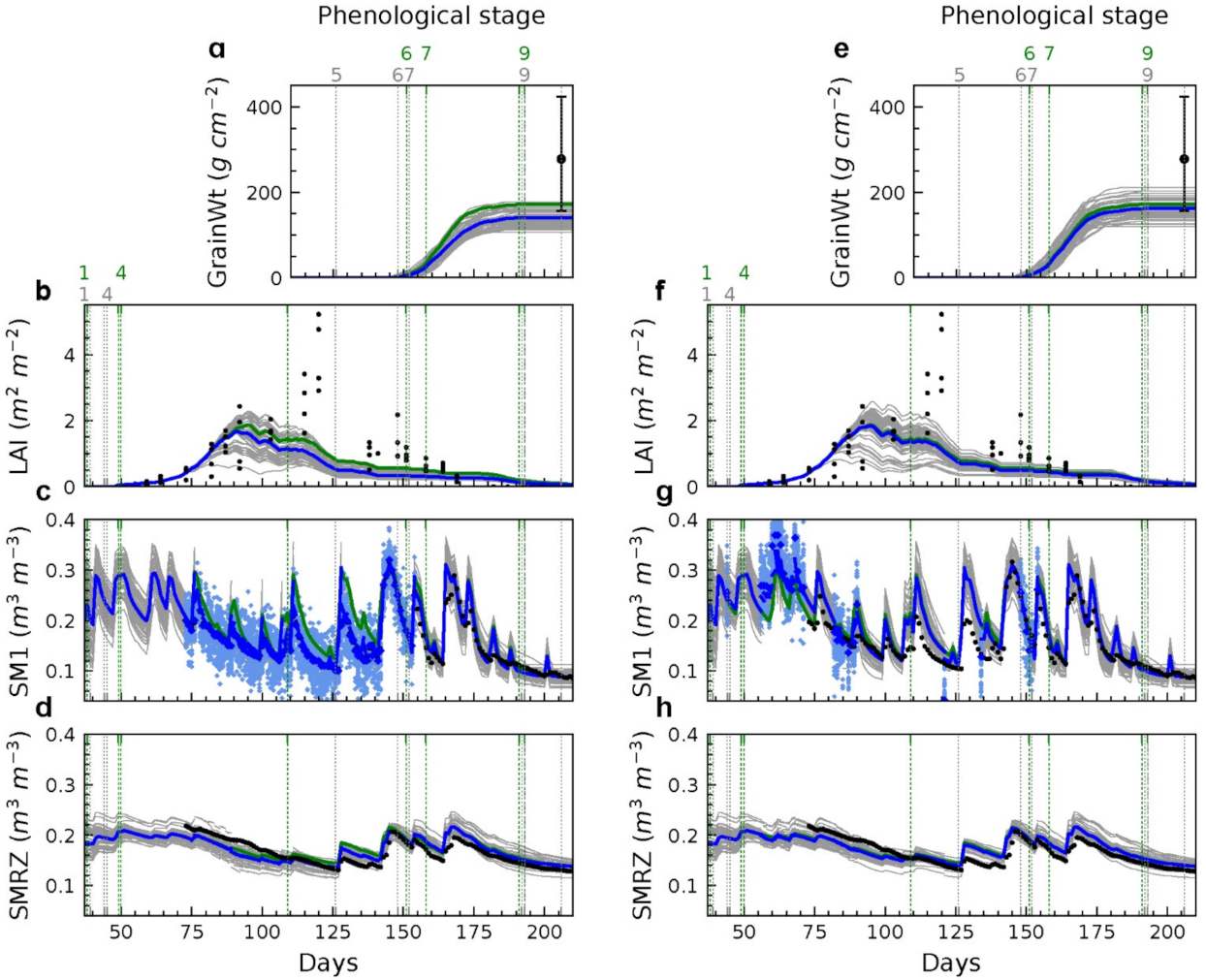
The baseline scenario confirmed the benefit of LAI assimilation into wheat modelling for improved yield estimation. When the ground and RS LAI data were assimilated at intervals of every three days, the estimated LAI time series from both sources was closer to the ground observation than the open-loop (Figure 3). In both assimilation experiments, the development of grain weight in the grain-filling stage (stage 7) became slightly faster with a steeper slope (Figure 3a,d). The measured average yield of the field is 2781.5 kg/ha. The estimated yield was increased from 1716 to 1871 kg/ha (ground LAI) and 2570 kg/ha (RS LAI), reducing the yield RD from −38.3% to −32.7% (ground LAI) and −7.6% (RS LAI). Accordingly, the RMSE of LAI, LeafWt, StemWt, and biomass estimation was reduced (

Table 3. Relative difference (RD) and root mean square error (RMSE) of yield and wheat states from the assimilation of wheat states in the baseline, plot-specific, and phenology-constrained scenarios.

Assimilated State (s)	Scenario	Yield (kg/ha)	RD% of Yield	RMSE
				LAI	LeafWt	StemWt	Biomass
				m2/m2	kg/ha	kg/ha	kg/ha
Open-loop	Baseline	1716	−38.3	0.91	49.5	93.5	150.4
Ground LAI	Baseline	1871	−32.7	0.40	29.2	83.0	114.5
RS LAI	Baseline	2570	−7.6	0.56	34.8	81.7	75.5
Ground biomass	Baseline	2520	−9.4	0.75	44.7	34.1	78.4
Ground LeafWt and StemWt	Baseline	2289	−17.7	0.69	40.5	35.7	98.0
Ground SM1	Baseline	1407	−49.4	1.07	55.9	126.4	186.8
RS SM1	Baseline	1618	−41.8	0.94	50.8	100.7	159.2
Ground SM1-2	Baseline	1451	−47.8	1.08	56.2	126.7	187.0
Ground SM1-6	Baseline	1242	−55.4	1.06	54.8	132.8	195.8
Ground NO3N1	Baseline	1660	−40.3	1.04	54.9	105.4	166.4
Ground NO3N2	Baseline	2016	−27.5	0.95	51.1	87.5	144.0
Ground NO3N1-2	Baseline	2061	−25.9	0.97	52.6	84.8	139.9
RS LAI (Plot A)	Plot-specific	2652	−4.6	0.50	29.3	93.6	76.3
RS LAI (Plot B)	Plot-specific	2685	−3.5	0.56	30.9	105.2	80.2
RS LAI (Plot C)	Plot-specific	2819	1.3	0.57	31.5	111.2	82.3
RS LAI (Plot D)	Plot-specific	2574	−7.5	0.58	35.1	93.3	78.5
Open-loop	Phenology-constrained	1931	−30.6	0.86	47.4	85.1	149.4
Ground LAI	Phenology-constrained	2232	−19.7	0.40	28.6	63.9	108.5
Ground biomass	Phenology-constrained	2779	−0.1	0.82	43.3	38.2	73.4
Ground LeafWt and StemWt	Phenology-constrained	2224	−20.0	0.52	33.0	32.4	108.4

). Noting that LAI was only assimilated before the early stage of grain filling (approximately day 156 in stage 7), the differences of the grain weight development between the data assimilation and open-loop runs before stage 7 were indirectly caused by more accurate estimation in other states (indicated by reduced RMSEs of wheat states in Table 3) rather than direct updates. Therefore, the assimilation of LAI in stages earlier than the grain-filling corrected errors in states that affect grain-filling and thus led to a better yield estimation.

Although both the ground and RS LAI showed improvements in yield estimation, the performance of ground LAI was disappointingly worse than for RS LAI (Figure 3 and Table 3) with the ground measurements expected to be more accurate than from remote sensing. However, the degraded results can be explained by two reasons. First, the result from a later phenological limited scenario showed that the ground LAI assimilated in stages 4 and 5 provided much better performance than assimilating in all stages (further discussed in the results of observation-limited scenario). While wheat leaves at the phenological stage 6–7 are in the middle to late senescence stage, the dried leaves make the ground LAI measurement from destructive sampling difficult and less accurate. Meanwhile, the model is more sensitive to changes of LAI in stage 6–7 than in other stages [28]. Although the assimilation of stage 6–7 showed the best efficiency in a synthetic study [28] where the synthetic LAI observations were assumed more accurate, it also diverged greatly with an inaccurate LAI observation. Second, the time series of the remotely sensed LAI is more smoothly varying than the ground measured LAI. The updates in stage 5, particularly days 120 to 150, persistently drove the StemWt to a greater value that was closer to the observations. In the model physics, the grain-filling rate is proportional to the StemWt value on the day of flowering. Thus, the assimilation of remotely sensed LAI resulted in a greater grain-filling rate in stage 7 than using the ground measured LAI, and consequently, a greater yield that is closer to the observation.

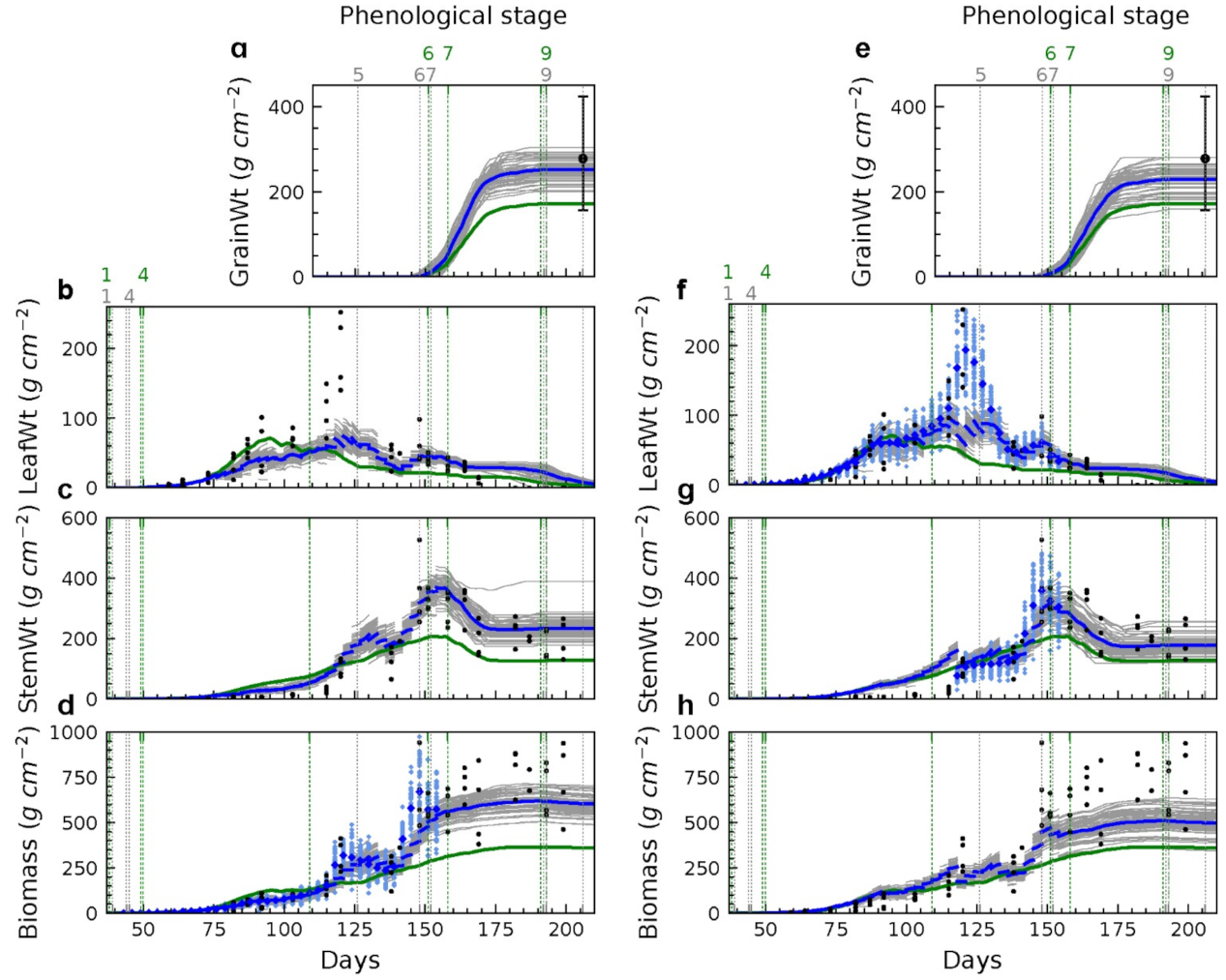
3.2.3. Assimilation of Biomass

Two schemes were applied to the assimilation of field biomass: (1) the assimilation of total biomass as an observation of the sum of aboveground organ weight (Figure 4 left panel); and (2) the joint assimilation of individual organ weight, namely, LeafWt and StemWt (Figure 4, right panel). Both assimilation schemes provided more accurate model estimation for wheat states and yield at harvest compared to the open-loop, according to the reduced RD in the yield and RMSE in the LAI, LeafWt, StemWt, and biomass estimates (Table 3). Moreover, the performance of biomass assimilation in the two schemes both provided reduced absolute RD in the yield and RMSE in the other wheat states than the assimilation of ground-measured LAI (Table 3). The reason that the scheme of assimilating total biomass provided better performance than using organ biomass or LAI (which is highly correlated to the LeafWt) is that it provides more information on the state variables in the system, and it allocates the weight to the observations of these wheat states through the error covariance calculated by the EnKF, meaning it avoided internal inconsistency caused by assimilating multiple state variables.

In practice, the scheme of assimilating total biomass is also more applicable than the organ weight. First, Table 3 shows that the assimilation of total biomass provided more accurate yield estimation than individual organ weight. Second, measuring organ weight requires extra work than total biomass measurements, requiring cutting and partitioning the plant organs manually. In contrast, total biomass is less labour-consuming when measured from destructive sampling, and it can be estimated from remote sensing often with empirical regression techniques [15,47,48,49,50]. Third, solely constraining the biomass of one of the wheat organs may lead the other biomass states to be erroneous (particularly in the grain-filling stage). For example, state updating can increase the stem biomass by increasing the biomass in other organs because the error covariance shows a positive correlation among all the organ weight states. However, in the process of wheat development, the leaf starts to wither when the stem starts to grow quickly, so the increased StemWt should imply a decreased LeafWt in an actual situation, which could be opposite to the state updating result.

3.2.4. Assimilation of Soil Moisture

The assimilation of soil moisture in the first soil layer (SM1) from in situ stations (ground) and remotely sensed microwave radiometer (RS) provided a slightly worse estimation in wheat states and yield than the open-loop (Figure 5). The RMSE of LAI and total biomass (Table 3) increased from 0.91 m²/m² and 150.4 g/cm² (open-loop) to 1.07 m²/m² and 186.8 g/cm² (ground) and 0.94 m²/m² and 159.5 g/cm² (RS), with the absolute value of yield relative difference increased from 38.3% to 49.4% (ground) and 41.8% (RS). The assimilation of in situ soil moisture in soil layers 1–2 (SM1–2) and soil layers 1–6 (SM1–6) provided similar degradation to performance in the estimation of yield and other states than the open-loop (Table 3 and

Table 4. Relative difference (RD) and root mean square error (RMSE) of yield and soil states from the assimilation of soil moisture in layer 1 (SM1), layers 1–2 (SM1–2), and layers 1–6 (SM1–6), and soil nitrate-nitrogen in layer 1 (NO₃N1), layer 2 (NO₃N2), and layers 1–2 (NO₃N1–2), respectively.

Assimilated State (s)	Yield (kg/ha)	RD% of Yield	RMSE
			LAI	SM1	SM1	SM3	SM4	SM5	SM6
			m2/m2	m3/m3	m3/m3	m3/m3	m3/m3	m3/m3	m3/m3
Open-loop	1716	−38.3	0.91	0.041	0.026	0.024	0.026	0.016	0.018
Ground SM1	1407	−49.4	1.07	0.025	0.021	0.028	0.025	0.016	0.017
RS SM1	1618	−41.8	0.94	0.038	0.025	0.026	0.026	0.016	0.018
Ground SM1-2	1451	−47.8	1.08	0.025	0.020	0.028	0.025	0.017	0.018
Ground SM1-6	1242	−55.4	1.06	0.027	0.015	0.010	0.017	0.011	0.012
Ground NO3N1	1660	−40.3	1.04	0.039	0.026	0.036	0.023	0.015	0.018
Ground NO3N2	2016	−27.5	0.95	0.040	0.027	0.028	0.026	0.016	0.019
Ground NO3N1-2	2061	−25.9	0.97	0.041	0.025	0.031	0.031	0.020	0.020
RS LAI	2570	−7.6	0.56	0.044	0.027	0.032	0.029	0.021	0.022

). Thus, the assimilation of soil moisture did not benefit yield or model state estimation.

The result that assimilating SM did not improve yield estimation contradicts a previous synthetic study [28], which showed improvement in wheat states and yield estimation when soil moisture was assimilated. This can be explained by the fact that the synthetic study assumed perfect physics in the water balance model and attributed all uncertainty to the model parameters and initial conditions, which was accounted for by perturbing parameters and initial conditions when generating ensembles. However, in reality, the uncertainty from the model physics, which the algorithm cannot consider, cannot be neglected. Moreover, in this case, the available period of soil moisture observation was not long enough to solve all parameters in the model, particularly in subsurface layers whose soil moisture dynamics are reduced.

The assimilation of SM1 resulted in a lower SM1 level, as the SM1 observations were smaller than the model estimates with a reduced RMSE in SM1. Some correction was made to the SM estimates in the first two layers, but such correction was not found in deeper layers, as shown in the RMSE values of SM in each layer (Table 4).

Although the assimilation of SM1 pushed the estimated SM1 to approach the station observation, this improvement over other simulations only remains until the soil is completely wet or dry again. When the soil moisture becomes very wet (or dry), and the soil moisture is at the upper (or lower) limit of soil moisture determined by the soil moisture characteristics, the soil cannot become wetter (or dryer) with any water flowing into (or out of) the system. Therefore, even if the soil moisture is updated by data assimilation in a timestep, it resets once it reaches the upper or lower limit. The effect of data assimilation is thus cancelled.

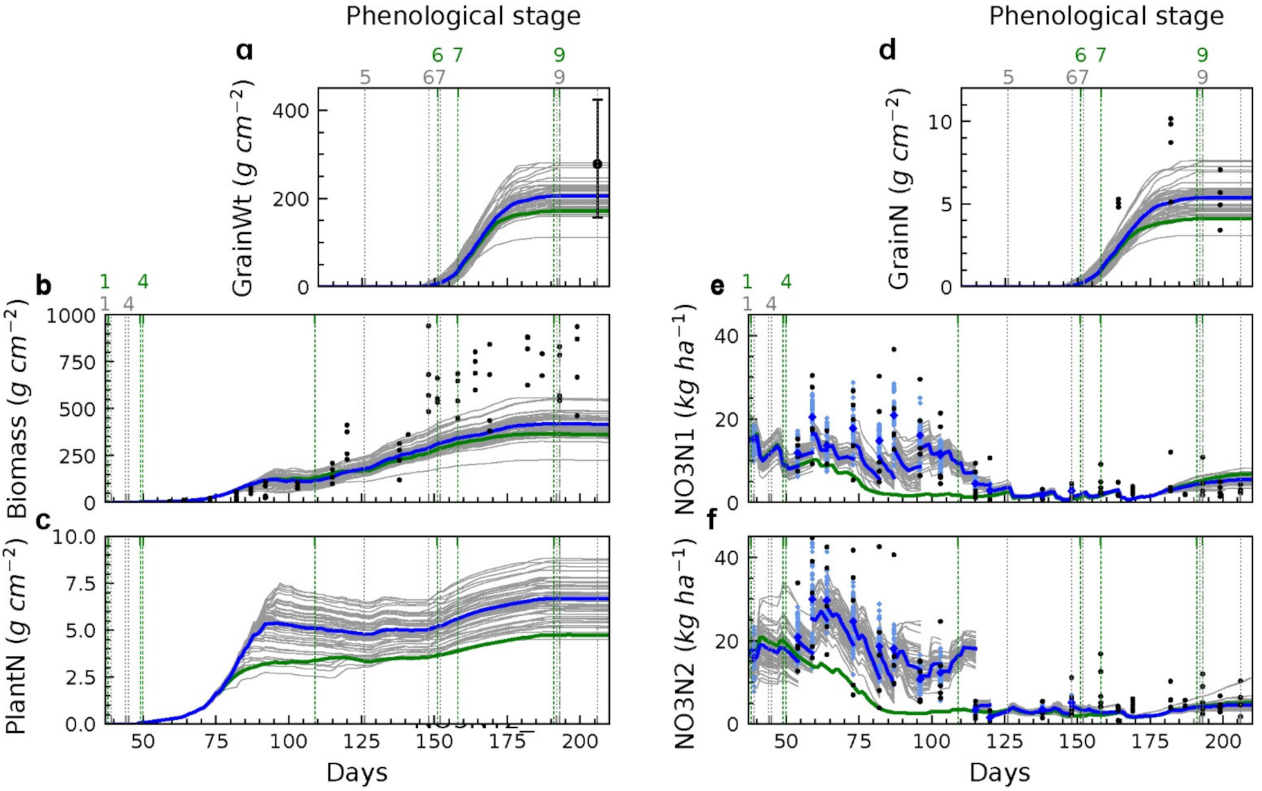
3.2.5. Assimilation of Soil Nitrate

The model provided a poor performance in estimating ammonium-nitrogen; thus the assimilation of soil nitrogen was limited to nitrate-nitrogen (NO₃N). Measurements of soil nitrate in the first two soil layers (NO₃N1, NO₃N2) were assimilated individually and collectively into the model. When assimilated collectively, a higher grain and plant nitrogen (Grain N, PlantN) level was found (Figure 6), as the NO₃N1 and NO₃N2 observations were higher than the model estimates. A higher level of plant organ nitrogen was also found in the individual assimilation of NO₃N in each soil layer. A higher yield estimation was given by the individual assimilation of NO₃N1 and the collective assimilation of NO₃N1 and NO₃N2 (Table 3), but the grain-filling rate remained unchanged from the open-loop. This result indicates that the increased yield in the NO₃N assimilation was not caused by a higher grain-fill rate associated with greater plant biomass, which is only slightly higher than the open-loop, but rather by the relief of nitrogen stress because of a higher plant nitrogen level.

3.3. Plot-Specific Scenario

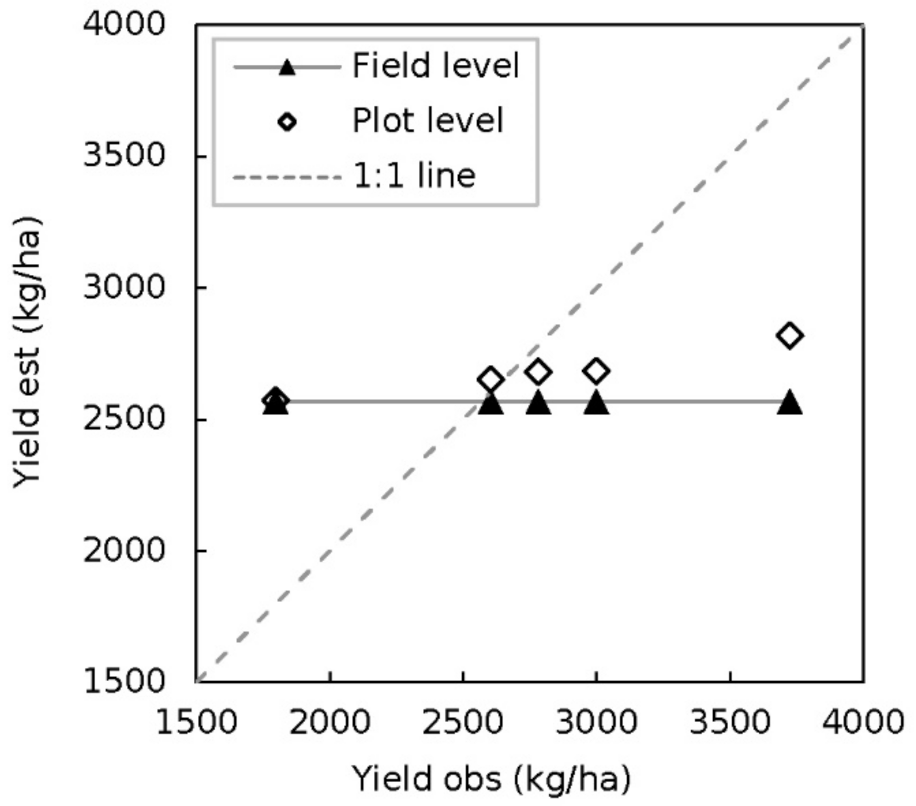
Figure 7 shows data pairs of yield estimated by RS LAI assimilation in the plot-specific scenario and from ground observations in each experimental plot labelled A–D and the field average. The model was initialised and driven by spatially homogeneous initial conditions, parameters, and weather forcings across the field. At the field scale, the mean yield was estimated by assimilating the average LAI of the field (baseline scenario), while at the plot level, it was estimated by assimilating the LAI of the four plots (plot scale). The yield estimates in the plots were evaluated against the yield observations collected in each plot, with mean yield being evaluated by the average yield of the four plots. A huge yield range (1926.4 kg/ha) was presented across the four experimental plots due to poor field management: unevenly sowed seeds, fail to treat weeds, delayed irrigation in the drought, etc. Results show that at the field level (black dots with a grey horizontal line), the estimated yield in each plot was uniform when LAI was assimilated at the field scale and no spatial heterogenetic information was included in the model settings and the assimilated LAI observations. In the plot-specific scenario, different plot-specific LAI data were assimilated into the spatially homogeneous model at the plot-specific scale, resulting in different yield estimation. Moreover, the data pairs in plots B and D more closely approached the 1:1 line, while the remaining data pairs were only slightly further from the line. Therefore, the spatially distributed LAI data brought spatial information into the model and further improved the spatial estimation of yield.

The results from the plot-specific scenario imply that even when the available data only allow spatially homogeneous simulation across the field, high spatial resolution LAI images can provide subfield spatial variation to the model. However, these results are limited to the data collected at only four experimental plots during one growing season, meaning that this result must be further evaluated with more validation experiments.

3.4. Observation-Limited Scenario

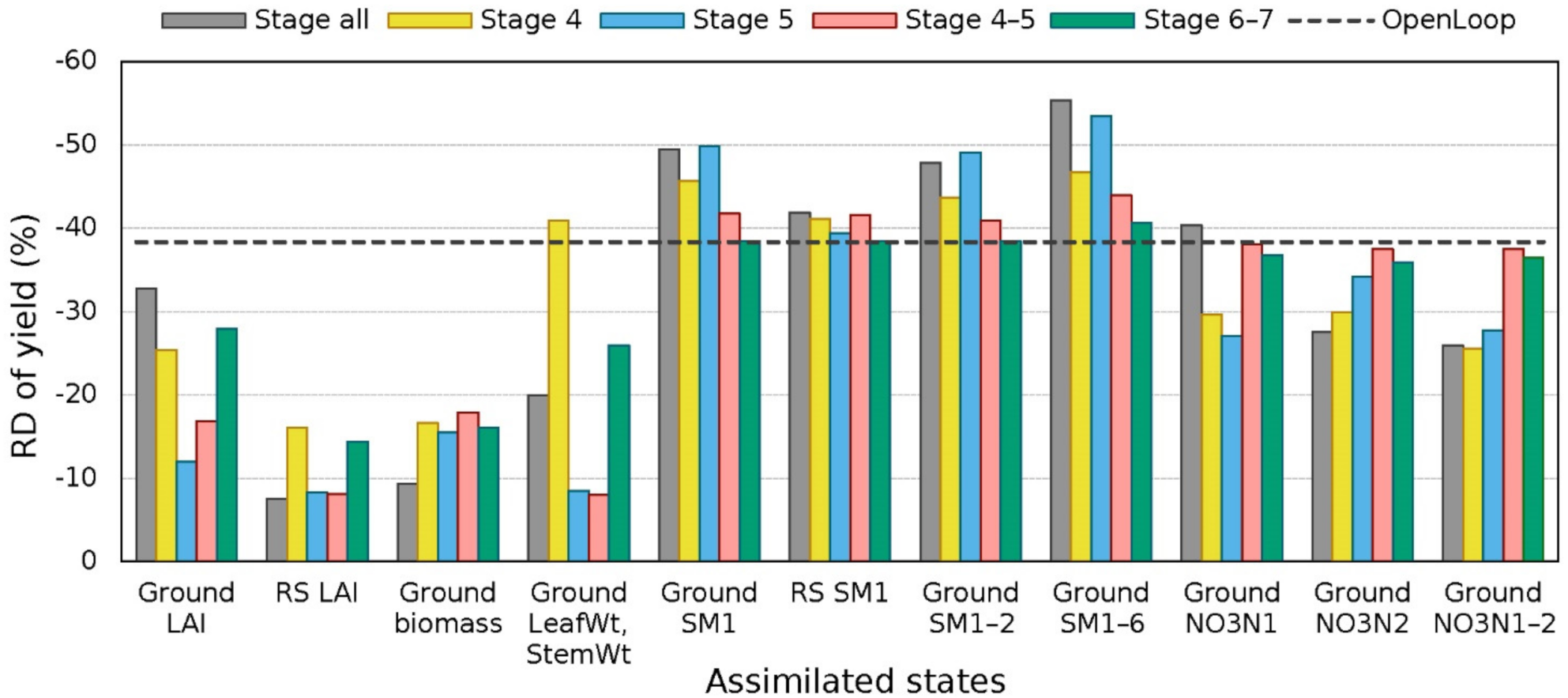
Figure 8 shows the RD of yield from different assimilation experiments in the observation-limited scenario. These experiments included assimilation of ground measurements of LAI, biomass, LeafWt and StemWt, soil moisture in the first soil layer (SM1), first two soil layers (SM1–2), all six soil layers (SM1–6), soil nitrate-nitrogen in the first (NO₃N1), second (NO₃N2) and first two soil layers (NO₃N1–2), and remotely sensed LAI and SM1.

The results show that the assimilation of LAI (ground and RS) and the joint assimilation of LeafWt and StemWt in stages 5 and 4–5 (vegetative stage) provided more accurate yield estimates than in other phenological stages. Biomass observations in every stage improved yield estimation, while the best yield estimation was provided when observations were available over the whole season. Soil nitrate-nitrogen (NO₃N1, NO₃N2, and NO₃N1–2) contributed to better yield estimation in stages 4 and 5. The observations of SM did not benefit yield estimation when assimilated in any stage.

3.5. Phenology-Constrained Scenario

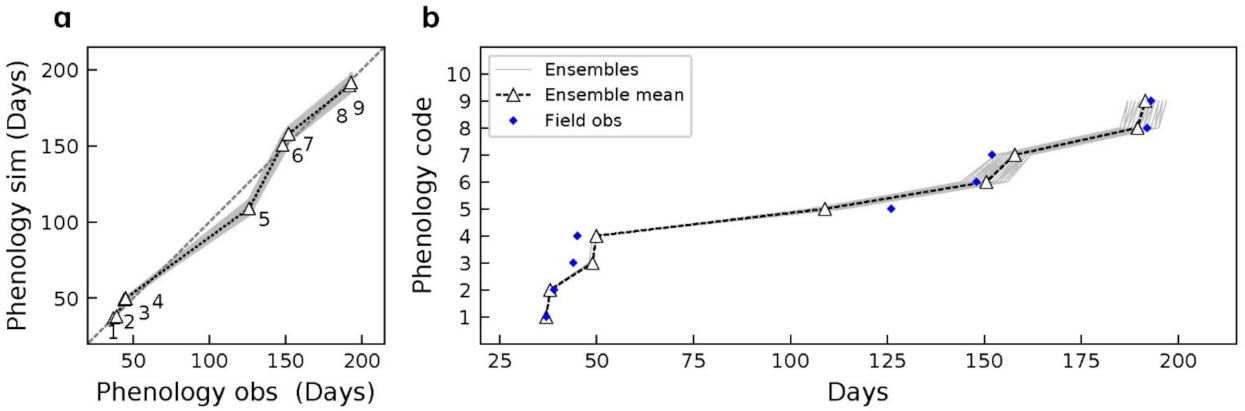
In the open-loop run of the baseline scenario, the model provided phenology estimates within ±5 days from the field observations for all phenological phases except phase 5 (floral initiation), when the estimated timing was 18 days ahead of the observations (Figure 9a). The reason is that the drought in this season caused a delay in phenology development, but the impact of water stress on phenology development is not described in the model physics. Another reason is that the wheat cultivar grown in this study may have a different requirement for the target accumulative thermal time in stages 4 and 5 from the parameters used in the model. Thus, it requires different periods to complete these stages.

By running the open-loop with the phenology constrained by ground observations, the underestimation of yield was reduced (absolute RD of yield reduced from 38.3% to 30.6%) with a slight reduction of RMSE in all estimated wheat states (Table 3). Furthermore, when assimilating wheat states (LAI, biomass or organ weight) with the phenology constrained, the underestimation of yield was further reduced. The yield estimated by the LAI and biomass assimilation (RD of yield, Table 3), and the wheat state estimation (RMSE, Table 3) by the LAI and the organ weight assimilation, showed improved accuracy when the phenology was determined by observation compared to that determined by model simulation.

3.6. Uncalibrated Scenario

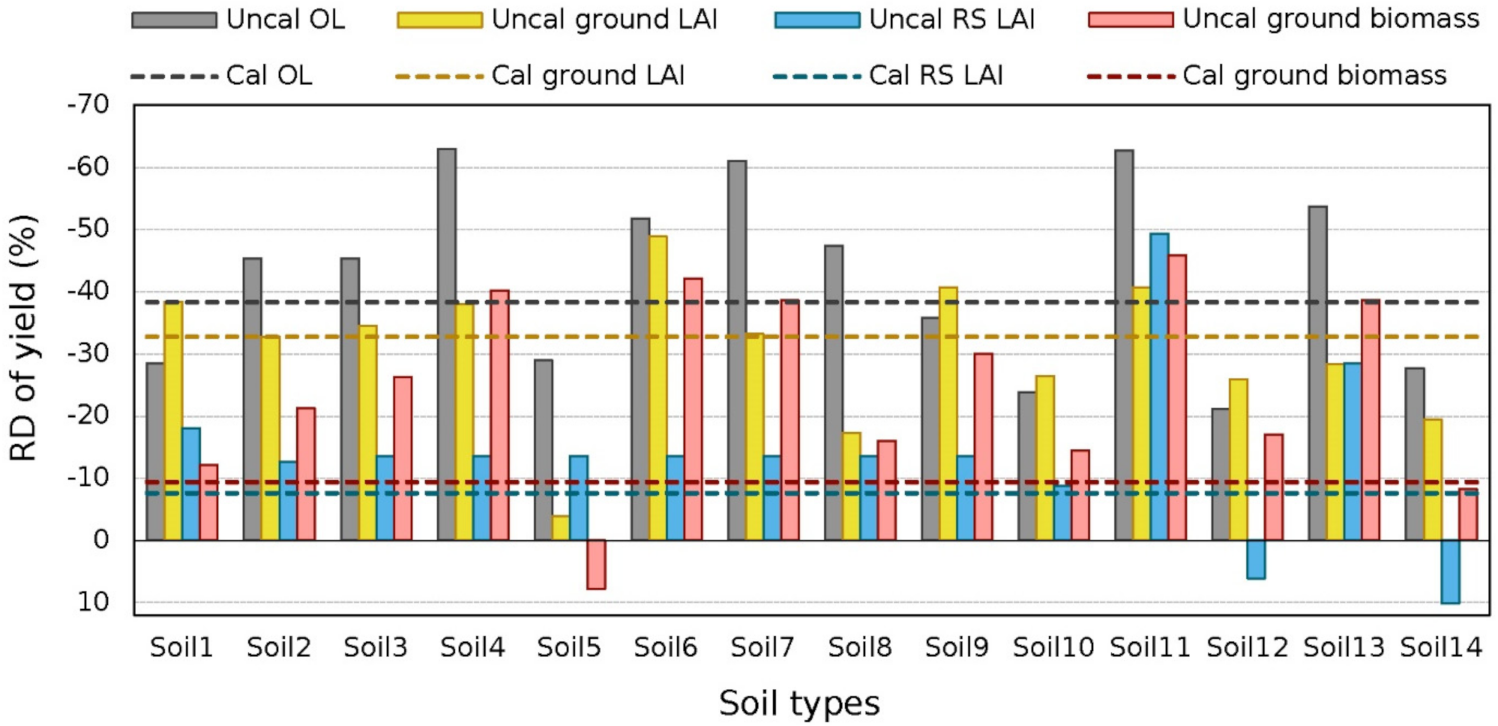
The open-loop simulation from 8 out of the 14 uncalibrated models showed a substantial underestimation of yield (Figure 10, grey bar). When the ground LAI or biomass was assimilated into the uncalibrated models, the underestimation of yield was reduced in 10 and 14 models, respectively. When using RS LAI, the underestimation of yield was reduced in all 14 cases compared to the open-loop and in 11 cases compared to the ground LAI but with two models being overcorrected. When assimilating in situ soil moisture in the top two layers (ground SM1–2), the estimated yield from all 14 models was near zero, representing model failure due to a distinct mismatch in soil moisture between the observations and model estimation.

The result illustrates that the assimilation of wheat states, especially the biomass, reduced uncertainties caused by incorrect model parameters (cultivar-specific parameters, soil properties). Thus, assimilating wheat states is expected to improve APSIM-Wheat yield estimation even in a wheat field where soil properties have not been accurately measured or calibrated. In particular, remotely sensed LAI provided the best improvement in yield estimation.

4. Limitations and Perspectives

The main and fundamental limitation of this study is that it was tested only on one small experimental field over one growing season due to the difficulty of collecting a wide range of data required to drive the model and test different observations for assimilation. Secondly, for best performance, the method needs site-specific calibration and soil measurements (both time-consuming and expensive) and a quantitative description of uncertainties from diverse sources. Finally, although the ground-measured biomass outperformed other states in improving yield estimation, the observations of biomass from remote sensing were not obtained and tested for assimilation due to a lack of a suitable dataset.

The application of the APSIM-EnKF framework is not limited to wheat yield estimation. It is also applicable for near real-time crop monitoring for crop and soil status, including over 20 other crop types (corn, barley, sorghum, cotton, etc.) available in the APSIM system. It can also be adapted to other state-updating algorithms (Kalman filter, particle filter, etc.) with minor modifications to the source code. With more observations becoming available in the future, this work can be expanded to an agricultural monitoring service platform to provide agricultural monitoring and forecasting.

5. Conclusions

This paper presented a data assimilation case study for the Cora Lynn area with the 2018/19 wheat season dataset. In a baseline scenario, the ground-measured and remotely sensed wheat and soil states were assimilated, including LAI, biomass, organ weight of leaf and stem, soil moisture in six soil layers from depth 0 to 55 cm, and soil nitrogen in the top two soil layers from depth 0 to 15 cm. These results were compared to scenarios where the state variables were assimilated into the APSIM-Wheat model under different spatial scales, availability of observations, and model parameters.

In the baseline scenario, the data assimilation showed that biomass and LAI, particularly biomass, provided improved yield estimation. Being observable from remote sensing makes them promising future data assimilation practices. Poor performance was found from assimilating soil moisture and soil nitrate. However, this does not imply that soil moisture and nitrogen data are unimportant for wheat modelling and yield estimation. Rather, that in this case they were already well estimated. Accordingly, they are essential in calibrating parameters related to soil moisture and nitrogen estimation where such parameters are not already well defined. With wheat growth primarily subject to water and nitrogen stress and the model highly sensitive to soil moisture and initial nitrogen, a correct estimation of soil water and nitrogen states is essential. Importantly, although a basic calibration to soil parameters is recommended, uncalibrated scenarios showed that the assimilation of biomass and LAI reduced the errors of yield estimates caused by parameter uncertainties (wheat cultivar type, soil properties) in uncalibrated models. Consequently, the heavy dependence of the APSIM-Wheat model on the soil information that is usually unavailable, particularly in spatial scale, can be relieved.

A plot-specific scenario showed the potential to provide subfield spatial variation in a spatially homogeneous model when high-resolution LAI was assimilated. Moreover, an observation-limited scenario showed that the assimilation of wheat states (LAI, biomass, LeafWt, and StemWt) benefited yield estimation the most when the observations were collected before the anthesis was completed (stages 4 and 5). Furthermore, a phenology-constrained scenario found that the uncertainty from model inputs (e.g., temperature) and parameters (e.g., target thermal time of phenological stages) that control phenology development can be partially reduced by direct insertion, with further improvement on yield estimates.