Abstract
An increased interest in computer-aided heritage reconstruction has emerged in recent years due to the maturity of sophisticated computer vision techniques. Concretely, feature-based matching methods have been conducted to reassemble heritage assets, yielding plausible results for data that contains enough salient points for matching. However, they fail to register ancient artifacts that have been badly deteriorated over the years. In particular, for monochromatic incomplete data, such as 3D sunk relief eroded decorations, damaged drawings, and ancient inscriptions. The main issue lies in the lack of regions of interest and poor quality of the data, which prevent feature-based algorithms from estimating distinctive descriptors. This paper addresses the reassembly of damaged decorations by deploying a Generative Adversarial Network (GAN) to predict the continuing decoration traces of broken heritage fragments. By extending the texture information of broken counterpart fragments, it is demonstrated that registration methods are now able to find mutual characteristics that allow for accurate optimal rigid transformation estimation for fragments alignment. This work steps away from feature-based approaches, hence employing Mutual Information (MI) as a similarity metric to estimate an alignment transformation. Moreover, high-resolution geometry and imagery are combined to cope with the fragility and severe damage of heritage fragments. Therefore, the testing data is composed of a set of ancient Egyptian decorated broken fragments recorded through 3D remote sensing techniques. More specifically, structured light technology for mesh models creation, as well as orthophotos, upon which digital drawings are created. Even though this study is restricted to Egyptian artifacts, the workflow can be applied to reconstruct different types of decoration patterns in the cultural heritage domain.
1. Introduction
The digital reassembly of heritage artifacts captured with remote sensing techniques is an important task that allows the further study of archaeological sites, monuments, and ancient inscriptions. It is a complex problem to solve due to three reasons: the numerous quantity of fragments to puzzle, the loss of heritage documents, and the severe damage of existing assets. Therefore, researchers have focused on developing technologies to aid experts in the task of finding correspondences between fragmented heritage data. In general, these approaches rely on geometry-based local feature descriptors to find matches between broken surfaces. These methods yield reliable solutions as long as the fragmented surface footprint remains intact. However, this is a major constraint on the reconstruction of severely damaged heritage artifacts since many of their broken surfaces are eroded, and matching points between counterpart fragments have disappeared. As a result, highly deteriorated artifacts are still puzzled manually. This manual puzzling approach seldom considers the broken surface to find correspondences. Instead, experts rely on decoration traces to guess where and how to fit the fragments. Only a few computer-assisted approaches have used decoration traces as a matching clue for digital heritage reassembling, which has left room for new research opportunities.
Leveraging decoration traces for puzzling allows experts to find more matching points regardless of the fragment damage. This manual puzzling approach relies on visible matching clues, which help to predict how the drawing traces should continue in the counterpart fragment. Therefore, computer-assisted registration approaches have used line extraction methods to aid experts in distinguishing line-based decoration traces more easily [1]. Furthermore, the extracted lines have been deployed as points of reference to perform alignment algorithms, thus improving the registration accuracy [2]. Although these puzzling approaches have positively contributed to the state of the art, semi-automatic digital reassembling is still a time-consuming task. Alternatively, fully automatic registration approaches have been proposed recently to reassemble incomplete and slightly eroded textured heritage assets, such as paints and murals [3]. These deep learning-based approaches have shown plausible registration results, but they require training images with distinctive textures to learn the unique features. As a result, they are not able to reassemble fragments with monochromatic eroded decoration, such as text inscriptions, ancient hieroglyphs, damaged epigraphic documents, and sunk relief drawings. To tackle this problem, the proposed approach attempts to mimic the process that experts follow to puzzle highly deteriorated decorated fragments. This includes identifying decoration traces of drawings or inscriptions, prediction of their continuing shape, and alignment based on the predicted decoration traces.
The proposed methodology consists of three stages: preliminary reconstruction, decoration completion, and registration. In the first stage, a Convolutional Neural Network (CNN) is used to fill the line-based decoration gaps. This pre-processing step is deployed to enable a classifier to correctly estimate the type of shape that decoration traces should form. Based on these classification results, the goal of the second stage is to complete the decoration shape by means of a Generative Adversarial Network. This is a crucial step since predicted textures allow for registration algorithms to find sufficient corresponding points, which is fundamental to estimate an accurate alignment transformation. Finally, similar to multimodal image registration approaches, counterpart fragments are aligned based on Mutual Information. The registration pipeline is tested on a set of ancient Egyptian damaged fragments, whose decoration corresponds to hieroglyphs drawn on 3D block fragments and 2D drawings. Structured light technology is employed to digitize the input fragments since their decoration traces are highly eroded; therefore, dense mesh models are required to accurately extract them. Furthermore, digital drawings resulting from two epigraphic studies are used to complement the 3D data and obtain more accurate decoration completion results. This novel methodology is an alternative to feature-based geometric approaches when the input data is highly deteriorated and contains few salient points for matching. Moreover, the GAN-based decoration completion module can be deployed independently to aid experts in the interpretation of deteriorated digital heritage in two ways: by highlighting and reconstructing decoration traces and by providing experts with depictions of potential complete decoration drawings.
In short, the main contributions of the presented work are:
- The automatic registration workflow for digital heritage reassembling, which relies on both a generative model and an entropy-based registration approach to find correspondences between broken fragments. This allows for the reassembly of highly deteriorated heritage fragments with monochromatic decoration traces in 3D or 2D space.
- The novel way of training a GAN model for the completion of monochromatic decoration traces, which can be deployed to support different kinds of registration approaches in the digital heritage field. This includes not only the proposed entropy-based methodology, but also feature-based and semi-automatic alignment systems when the input data is incomplete.
- The proof-of-concept experiments, which show that an MI-based registration can be deployed to estimate reliable alignments for input data outside the medical domain.
The remainder of the paper is structured as follows. Section 2 provides an overview of the existing literature on deep learning-based approaches for digital heritage reassembly; it also provides background information on inpainting and generative approaches in the field of digital heritage. Section 3 describes, in detail, the steps that compose the registration pipeline, as well as the dataset of Egyptian fragments used to test the proposed methodology. Section 4 details both the technical and algorithmic aspects of the implementation. Additionally, it describes the experimental framework carried out to evaluate the registration performance of the methodology as a whole. Finally, a discussion of the obtained results and conclusions are presented in Section 5 and Section 6.
2. Related Work
Although the proposed work tackles the issue of reassembling fragmented decoration, the main contributions lie in the completion and alignment modules. Therefore, the literature study focuses on the methodologies that exploit texture for the reassembly of digital heritage, from feature-based to machine learning methods.
The reassembly of digital heritage is mainly addressed by estimating feature correspondences among counterpart fragments. These features are points of interest, computed based on either geometric [4] or texture properties [5], depending on the data space: 3D or 2D, respectively. For example, in [6,7], curvatures are computed to build 3D descriptors of salient points, which are deployed to reassemble broken blocks of sculptures. Similarly, 3D shapes are further studied in [8,9] to automatically extract drawing patterns from mesh models of archaeological objects. The latter works are essential to developing the segmentation and matching methods proposed within the research program of the project “gravitate” [10]. Following the same registration workflow, but in a 2D-space, the broadly used SIFT [11] descriptor is calculated to register various types of heritage artifacts, such as fresco fragments [12], ancient paintings [13], and historical buildings [14]. However, feature-based approaches require sufficient overlap to estimate reliable transformations for data alignment. This is an important limitation when dealing with digital heritage. As such, recent studies have resorted to Artificial Intelligence (AI) methods to solve puzzles of incomplete, damaged data. In [15], Generative Adversarial Networks (GANs) [16] are deployed to puzzle jigsaw fragments based on semantic information rather than on features of the image boundaries. Even though this approach mitigates the lack of overlap, it requires square images as input data, which is a limitation when it comes to reassembling sophisticated archaeological materials, such as pottery drawings or inscriptions. Consequently, Neural Networks are trained in [3,17] to predict the position of pottery shapes and jigsaw puzzles regardless of the gaps between them. Similar methods are deployed to develop a mobile app for the recognition and matching of pottery shards within the context of the ArchAIDE [18] European project. These latter studies are similar to our approach in the sense that they address the issue of incomplete heritage data.
The presented deep learning registration approaches have been proven to cope well with the lack of overlap between input fragments. Nevertheless, they still require sufficient texture information to train the neural network. This is a major issue since highly deteriorated fragments suffer from color degradation, material erosion, incomplete decoration traces, and the lack of assembled artifacts’ documents for training. To solve these data incompleteness constraints, image inpainting and completion approaches [19] have been studied to reconstruct incomplete or deteriorated images. Inpainting and completion are normally solved by image-to-image translation approaches [20,21]. These methods attempt to learn a set of characteristics that transform a group of images A into a dataset B and vice-versa. GAN approaches [22,23] have gained popularity in this field since they only require uncorrelated input datasets A and B, thus easing the task of collecting training data. In the heritage domain, inpainting and completion methodologies have been seldom studied due to the lack of ground truth training samples, as images with intact decoration are hard to compile. However, a few examples are found in the field of ancient mural reconstruction [24,25].
Another limitation of deep learning-based reassembling approaches is that they do not cope with rotation variations. This registration property is key to align any kind of data, either automatically [26] or through a computer-assisted approach [2]. Feature-based registration methods are popular since they are able to cope with rotations. Moreover, they yield accurate translation and rotation transformations as long as sufficient correct matches are computed. However, as mentioned before, the lack of data overlap represents a big challenge for feature-based algorithms when dealing with heritage fragments. In the medicine field, researchers have resorted to feature-free registration alternatives [27] to align images from different sources. This means that the input data do not share exact information in terms of pixel intensities, which is an unfeasible scenario for feature-based approaches. This matching alternative relies on the entropy of counterpart images to determine the similarities between them. Mutual Information (MI) [28,29] is the most commonly used metric to compare image similarities in this field. Therefore, alignments are estimated by MI-based methods when a pair of input images exhibit a high MI value. Even though this is quite a broadly studied approach, to the best of our knowledge, it has not been used to reassemble heritage assets.
The proposed work integrates deep learning inpainting completion approaches and MI into a registration pipeline for the reassembly of incomplete heritage drawings. Given the maturity of GANs, similar to [23], a network is trained to predict the extended decoration of Egyptian inscriptions. Next, inspired by the way in which multimodal images are registered in the medicine field, MI is deployed to find a rigid transformation that aligns two counterpart fragments. Unlike the mentioned deep learning registration approaches, our workflow only takes as input monochromatic images, which represent decoration traces of inscriptions. This way, our methodology is able to cope with non-square input shapes, such as in [3,17]. This also allows the input of 2D projections of sunk relief traces extracted from 3D models. Therefore, the paper tackles two main constraints of the state of the art: the lack of features overlap for registration and data incompleteness.
3. Materials and Methods
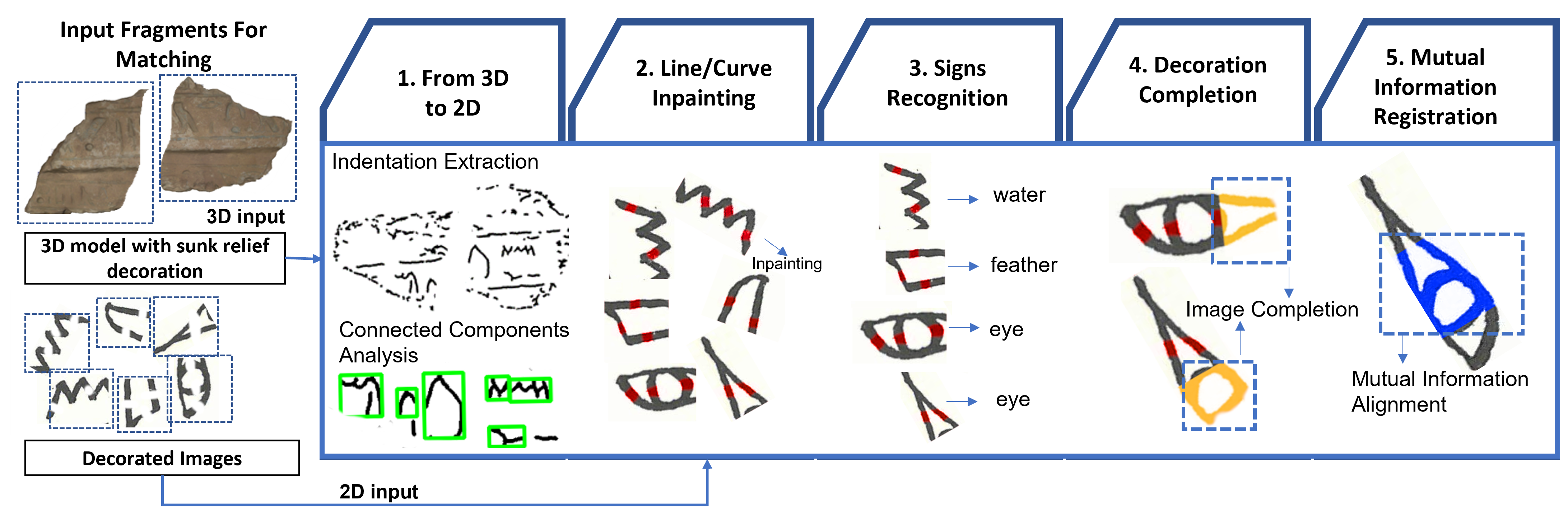
In this section, an overall overview of the proposed registration workflow is presented. Figure 1 depicts the consecutive steps that compose the registration pipeline: valley lines extraction, line/curve inpainting, signs recognition, decoration completion, and MI registration. The system handles broken fragments of ancient inscriptions in the form of either 3D mesh models with sunk relief decoration or monochromatic drawings. If the process receives the former input, the 3D points that shape the fragment indentations are extracted and projected onto a planar surface, thus obtaining an image in which the sunk relief details stand out. Next, a connected component analysis is performed on the resulting image to estimate decoration traces of actual inscriptions. Since these signs are made of incomplete segments, the line/curve inpainting step aims at filling decoration gaps in a way that the curve properties and line thickness are preserved. This preliminary reconstruction helps improve the performance of the sign recognition and completion steps. The sign classifier is paramount to the algorithm because it determines which image completion model will be applied to extend the decoration. According to the classified sign, an image-to-image translation method is then deployed to predict the continuing traces of broken counterpart fragments. Finally, an MI-based registration approach is used to calculate a rigid optimal transformation for fragments alignment.
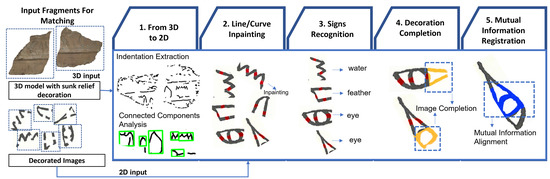
Figure 1.
Overview of the proposed registration pipeline based on decoration completeness. The input can be either a 3D model with sunk relief decoration or a monochromatic image. The first step is conducted only when the input is a mesh model. The second and third steps aim to determine the decorated fragments’ completed sign. Finally, the predicted signs are registered by computing their mutual information.
The remainder of this section first explains the dataset used to develop this research, after which each of the pipeline modules are described in detail.
3.1. Dataset
The data for this study come from heritage documents recorded in Dayr al-Bersha, Egypt. We chose a set of ancient broken fragments that were excavated in the decorated tombs of this region. Their current state is quite deteriorated since they date back to the Middle Kingdom period of ancient Egypt, from 1975 BC to 1640 BC, and have suffered from earthquakes, looting, and vandalism. Since the proposed work handles 3D and 2D input data, the dataset is composed of 3D mesh models of decorated blocks and drawings of two epigraphic studies.The description of the technology employed to digitize the former data type and their recording process can be found in [30]. In terms of data quality and accuracy, the triangles density of the recorded 3D mesh models is 300–1000 k faces, and the average distance among the vertices is 3 mm. Figure 2 depicts some of the selected 3D models containing sunk relief decorations of ancient Egyptian inscriptions. Although 30 decorated fragments are used for this study, only four are shown in this paper so that their sunk relief properties can be distinguished from the picture. As we are only interested in the decorated surface, only the planar region of the fragment is considered as input information. The 2D data come from the epigraphic studies carried out by Newberry in 1894, whose digital results were published in [31]. The second epigraphic study was conducted by egyptologists of KU Leuven, within the framework of the Dayr al-Bersha project [32]. Both studies are depicted in Figure 3. By collecting inscriptions from decorated blocks and different epigraphic studies of the same site, our data contains shape similarities, and it is also differs in terms of drawing style.

Figure 2.
3D models of ancient Egyptian decorated blocks with sunk relief decorations. In total, 30 fragments of this type are used to develop and test the proposed study.

Figure 3.
Samples of epigraphic studies used to develop and test the registration pipeline. Study A was provided by the Dayr al-Bersha project [32]. Study B is published in [31].
3.2. From 3D to 2D Extraction of Sunk Relief
Sunk and high relief decoration traces are commonly found in ancient heritage fragments. For this reason, the proposed workflow is designed in a way that not only permits the input images of texture decoration but also mesh models with sunk/high relief decoration. Since such 3D inputs are textureless, we resort to differential geometry-based approaches [33] to convert them into images. More specifically, the 3D ridge–valley lines approach proposed by Ohtak Y. [34] is deployed to extract fragment indentations. This algorithm is able to extract irregular surfaces and classify them as a ridge or a valley line based on their curvatures. However, not all indentations are decoration traces. Some of them are footprints of damage or shape errors that occurred during the 3D scanning process. Therefore, after extracting the valley lines, a connected component analysis [35] is conducted to remove small indentations that do not form a decoration shape. The remaining lines are projected onto a 2D plane, yielding a segmented image with separated components, in which each segmented component represents a potential trace of decoration.
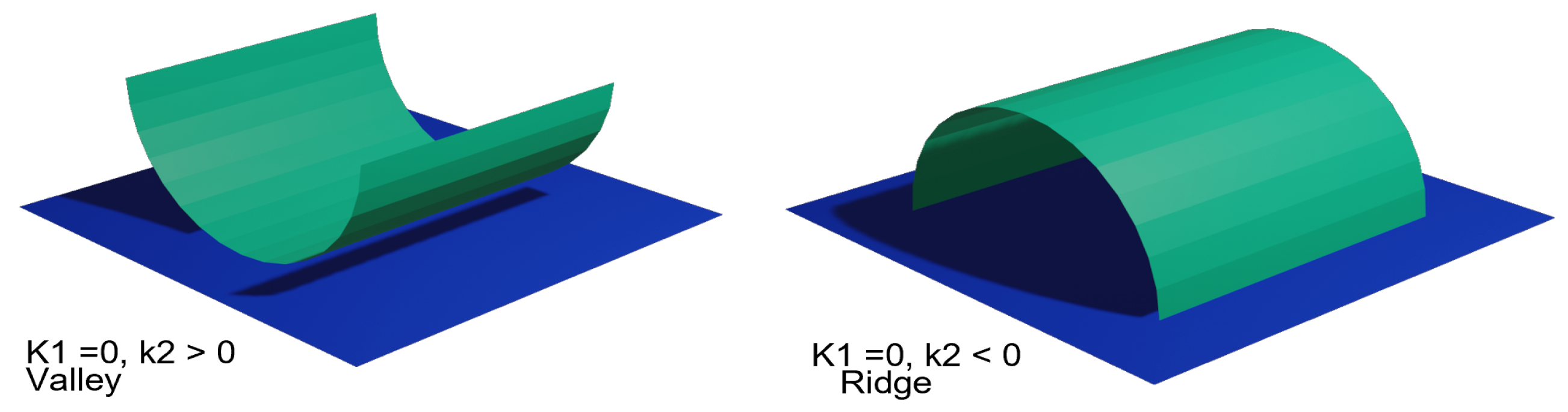
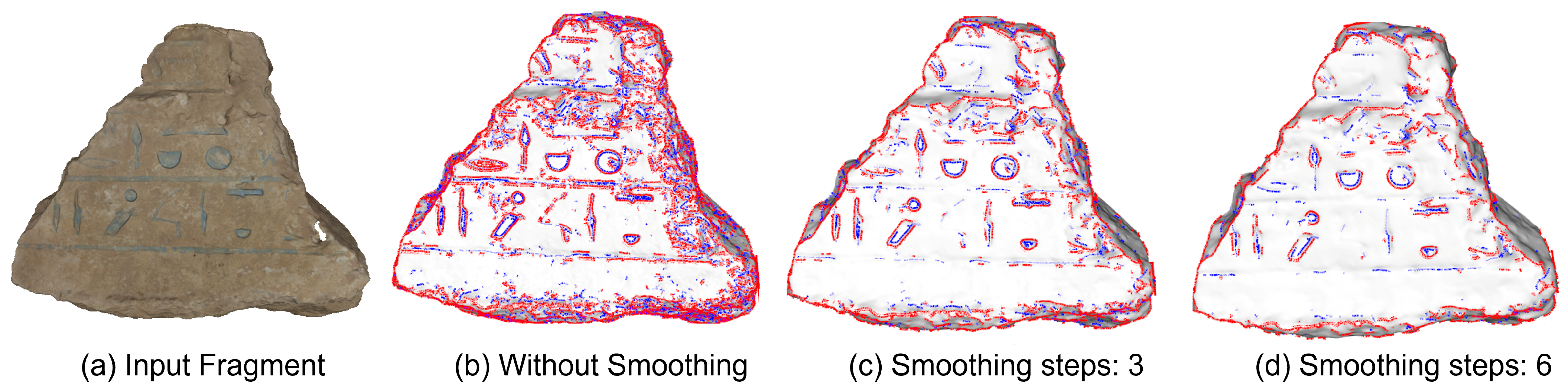
The ridge–valley lines method relies on the relationship between the principal curvatures and of a surface to mathematically describe its local bending. To visually understand this concept, Figure 4 illustrates the principal curvature values for ridge and valley surfaces. Note that ridge shapes are similar to high relief traces while valley shapes resemble sunk relief traces. Considering this observation, the mathematical description of valley surfaces is taken into account to extract decoration traces out of the mesh models. For each vertex p, the neighboring surface S and the principal curvatures are computed. If and , then S is taken as an indentation. This process yields every sunk surface present in the model, which might lead to many unwanted points. This effect is illustrated in Figure 5a. As observed, numerous indentations with shape irregularities are segmented, making it difficult to distinguish decoration from damage. This result was expected since the ancient fragment’s decoration does not lie on a perfect plane-like surface. To mitigate this effect, the input mesh is smoothed by using the Laplacian method proposed by J. Vollmer et al. [36]. The impact of smoothing the input 3D mesh several times is shown in Figure 5c,d. The number of smoothing steps is determined based on the mesh density. For our dataset, three smoothing steps are sufficient to remove a significant amount of undesired traces, while keeping the decoration lines.
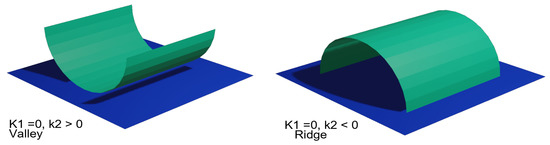
Figure 4.
Principal Curvature values of the valley (left) and ridge (right) surfaces.
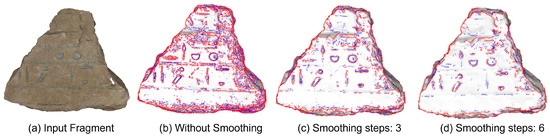
Figure 5.
Ridge–valley lines extraction of a decorated fragment smoothed with 0, 3, and 6 steps. Ridges and valley surfaces are marked in red and blue lines, respectively.
Even though the previous step removed a significant number of damage traces, some small, unconnected and non-uniform lines remain present. These unwanted traces are removed by performing a connected component analysis on the extracted valley lines. Since the goal of this module is to extract decoration in 3D space and convert it into an image, the connected components are computed in 2D space. In order to avoid shape deformations when converting the lines from 3D to 2D, the convex hull [37] of the fragment is calculated to estimate the output image dimensions. This way, we keep the height and width proportions of the 3D model in the image. Next, the 3D valley lines are drawn onto a canvas, producing a binary 2D representation of the decoration traces. Finally, based on custom-defined size thresholds, small connected components are discarded. This process is illustrated in Figure 6. From left to right, the first image depicts the input 3D valley lines marked in blue and the convex hull delineated by a red rectangle. The second image shows the 3D extracted lines projected into 2D space. Finally, the last image depicts the connected components extracted marked in green. Each component represents potential traces of decoration and is the input of the Line/Curve inpainting module.

Figure 6.
Left: Valley lines of a decorated fragment. Center: Lines projected onto an image. Right: Segmented connected components delineated with green rectangles.
3.3. Lines and Curves Inpainting
There exist two main techniques to tackle drawing inpainting: via rudimentary computer vision methods and through data-driven approaches. The former includes morphological operations, contour drawing, and flood fill algorithms. These methods are mainly deployed as a pre-processing step for blob-based solutions. The latter performs unsupervised and supervised learning methods to visually enhance sketches, corrupted documents, and hand-made drawings. Since damaged decoration traces are made of curvy shapes and lines with multiple intersections, the core of the inpainting module relies on a data-driven approach. Concretely, the joint gap detection and inpainting method proposed by Kazuma S. et al. [38] is integrated in our pipeline to complete decoration traces. The authors proved that line segments of basic 2D shapes are sufficient to train a CNN for automatic detection and completion of drawing gaps while preserving line thickness and curvature.
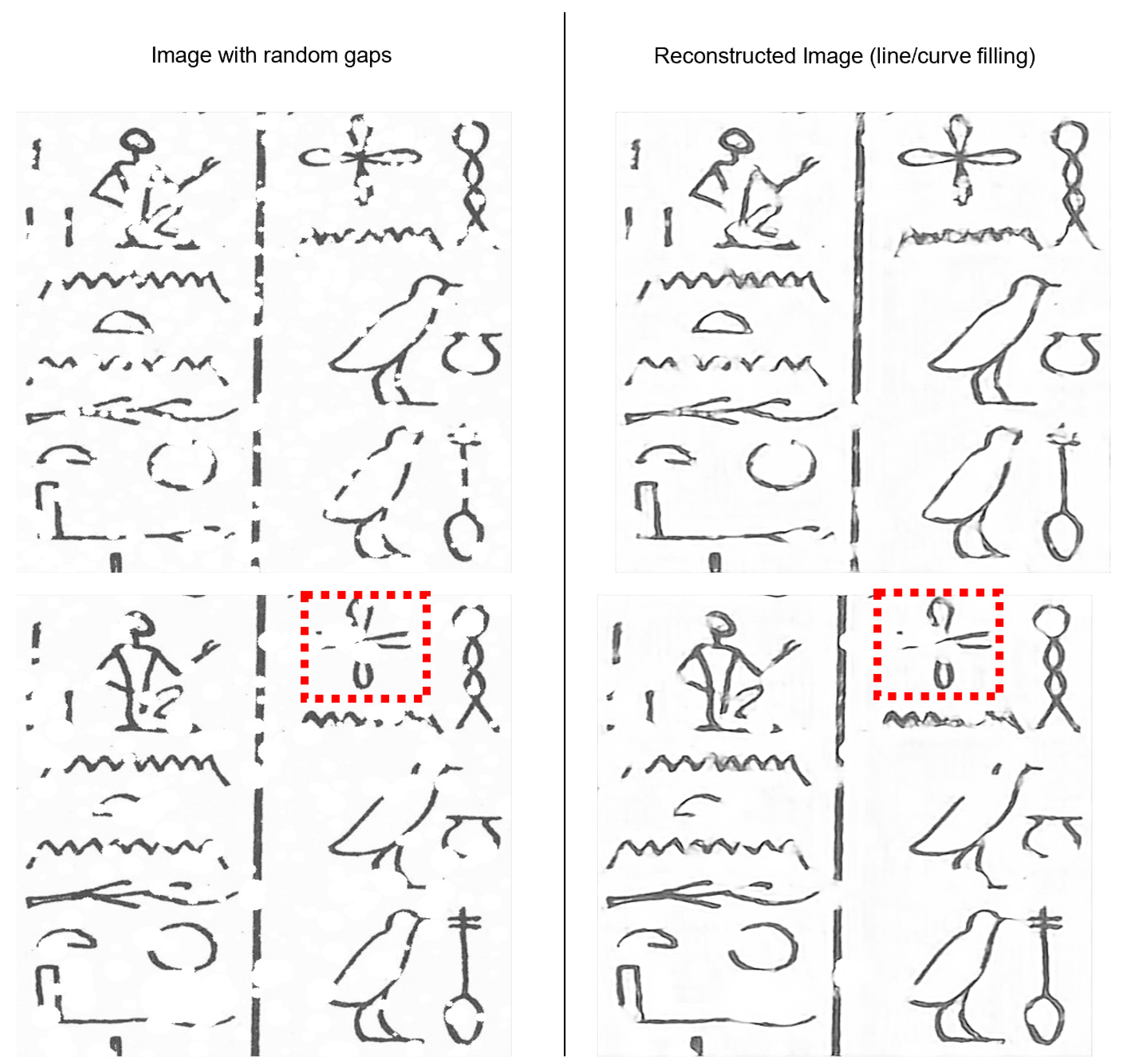
The unsupervised method for gap detection and inpainting presented in [38] is trained with fragmented segments of 2D shapes, such as triangles, circles, and squares. The authors provide a pre-trained model to complete the gaps on drawings of any size since the network is fully convolutional. This model is tested on some images of our dataset of Egyptian drawings, which are made of straight lines and curves. To this end, random gaps of different sizes are deliberately added to the input drawings, and the pre-trained model is applied to fill the created gaps. Figure 7 depicts the obtained results. For most of the small gaps, the network is able to fill the line gaps while maintaining curvature and thickness. However, the method struggles to detect gaps of complex shapes, such as the flower sign marked in red dotted lines, in which the model is not able to predict expected line traces. Nevertheless, this test shows that the inpainting data-driven approach is suitable to complete small decoration traces of heritage signs.
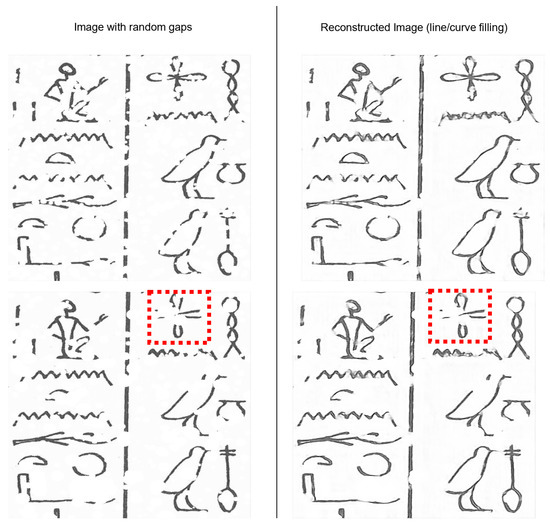
Figure 7.
Joint Gap Detection and inpainting method [38] tested on our dataset of Egyptian Drawings. The left column shows the Egyptian signs with gaps of different sizes. The middle column is the predicted image with gaps completed. The right column is the ground truth image. The red dashed lines highlight the areas in which the inpainting algorithm failed to detect and fill the line gaps.
The line/curve inpainting module serves as a pre-processing step in the registration workflow to complete small decoration gaps caused by erosion over time or valley lines that were not properly detected. As a consequence, the likelihood of recognizing the correct decoration class is increased. The details of the Egyptian signs classifier are presented in the next subsection.
3.4. Signs Recognition
The sign recognition module’s goal is to decide on the type of hieroglyph that is going to be used as a reference to extend the decoration of a broken fragment. Since the Egyptian signs mainly correspond to silhouettes of body parts, objects, and animals, transfer learning can be performed to train the classifier. Similar to sketch recognition network models [39,40], a CNN is designed using Resnet50 as a backbone. This architecture has proved to yield a high classification score for the TU-Berlin sketch dataset [41], whose images are similar to ours. Moreover, Barucci A. et al. [42] have recently shown plausible classification results of Egyptian hieroglyphs by building a CNN, which takes Resnet50 as a basis. In contrast to this work, we are interested in classifying segments of a sign rather than the entire hieroglyph shape. Therefore, our network is trained with random segments of hieroglyphs. To this end, different drawing styles of inscriptions are selected from the Egyptian epigraphic study described in Section 3.1. Additionally, to recognize the decoration traces from the 3D models, the extracted valley lines that delineate the fragments’ hieroglyphs are extracted and included in the training data. As a proof of concept, five Egyptian inscriptions are selected to test the proposed registration workflow. These signs are chosen because they are commonly found in the set of recorded fragments. Moreover, they are made of basic drawing shapes, such as circles, zigzag lines, square corners, semi-circles and combinations of them. Thus, these shapes are not only relevant to drawing Egyptian signs, but also they form the basis of other heritage drawing styles, such as Hieratic and Greek inscriptions [43,44].
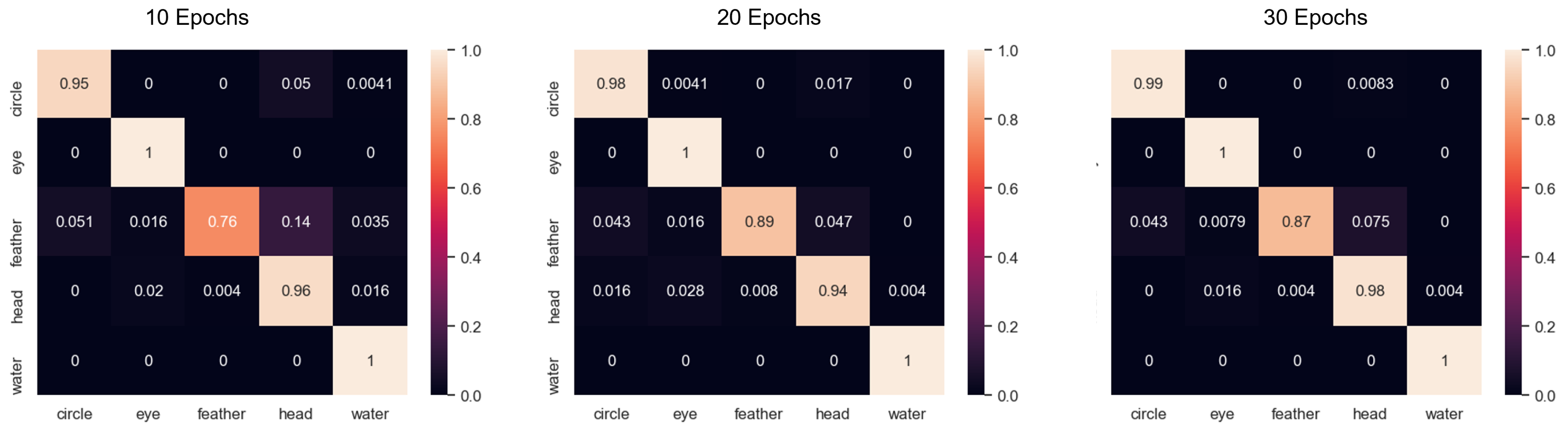
As previously mentioned, the goal is to classify segments of traces rather than the full hieroglyph. With this objective in mind, the training images are created, as shown in Figure 8. Complete signs are used as a reference, from which random segments are extracted to compose the set of training images. In order for the classifier to cope with scale effects, the reference image is resized for different resolutions. The size of the square mask used to delineate the segmented area is more than 25% of the reference image to ensure that the network is able to extract distinctive features. Otherwise, drawings would become too small and might lead to misclassifications due to the similarity between decoration traces. In total, 6500 segments per class are used to train the model, including image augmentations. The confusion matrices of the trained classifier for 10, 20, and 30 epochs are depicted in Figure 9. The classifier yields some false positives for the feather sign because it is made of less distinctive shapes. It is composed of one straight line and a rounded rectangle. However, the overall results prove that the trained network yields reliable classifications. The trained classifier is deployed to determine which completion model should be used as a decoration predictor. This module is explained in the next subsection.

Figure 8.
Left column: Classes and reference images used to create the training data for sign classification. Right Column: Random segments extracted from the reference images, which resemble decoration traces of broken fragments.
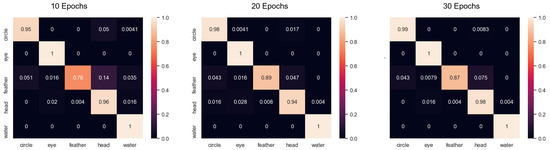
Figure 9.
Confusion matrices of the trained CNN for 10, 20, and 30 epochs, respectively.
3.5. Decoration Completion
The completion module attempts to extend the decoration traces of a classified sign to obtain a more complete image from which we can extract features for image registration. The completion task is performed by training an image-to-image translation model using Cycle-GAN [45]. This unsupervised approach is able to learn special characteristics of one image collection X and translate them into the other target image collection Y. CycleGan is deployed to extend decoration pixels since it relies on learned features rather than on relationships between paired images. This way, the network learns the decoration pattern that needs to be extended based on the characteristics of the incomplete input drawing. In our case, the image collections domains X and Y are composed of incomplete and complete drawings, respectively. The idea is to create two images that resemble both the decoration of a broken fragment and its complete decoration. As the salient image characteristics vary from one Egyptian inscription to another, we train five different models for each of the classified classes: eye, head, feather, water, and circle. The next paragraphs provide a detailed explanation of how the training data is produced as well as an evaluation of the decoration completion results.
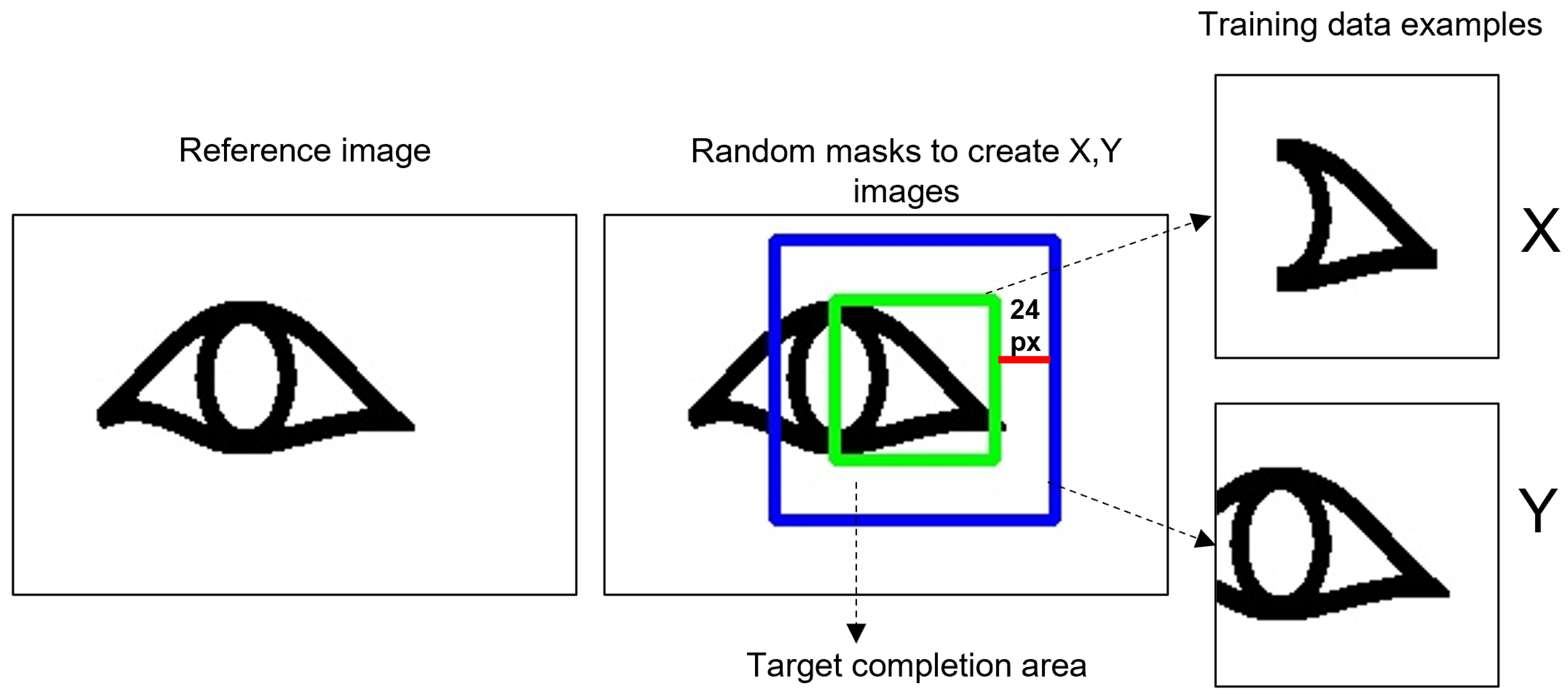
The data is created from the same reference images used to train the sign recognition model (see Figure 8). The process to create an image for X and Y domains is illustrated in Figure 10. Square masks, randomly distributed across the reference sign, are utilized to delineate the target completion area. The masks’ size is determined based on two factors: the recommended input image dimensions for Cycle-GAN and the area length that can be extended by the model without altering the inscription shape. For the former, the input image size needs to be a multiple of for, since CycleGAN entails downsampling/upsampling operations. For the latter, an exhaustive experimentation showed that 24 px is the optimal length that can be extended by the model. Therefore, if we consider a square mask of 64 × 64 px (marked in green), plus the image extensions of 24 px for each side, the total size of the training images is 112 × 112 px (marked in blue). To extend the dataset, random rotations and scale operations are applied to the images. In total, for each reference inscription, 1400 images are created for each domain by varying the masks location, number of rotations, and scale transformations.
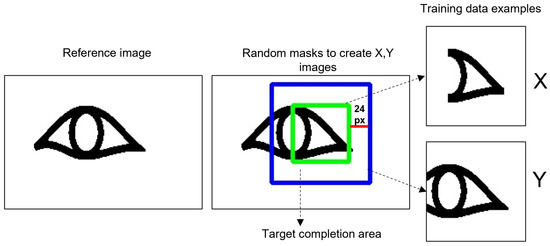
Figure 10.
Example of how the training data for the decoration completion GAN model is produced.
To show the performance of the trained networks, the decoration completion models are tested on a set of incomplete signs with different rotations. Figure 11 depicts some predicted images for the selected classes. Keeping in mind that the goal of this module is to predict the continuing traces of a fragmented drawing, instead of aesthetically reconstructing the input sign, it becomes difficult to select the appropriate evaluation metrics. From a general perspective, the completion problem falls into the inpainting approaches category. As such, for the sake of a quantitative assessment, the image completion results may be evaluated based on image quality metrics [46], such as SSIM and PSNR. However, it is not of our interest to accurately reconstruct a drawing. Instead, we seek to extend the input texture to intuitively find common characteristics between broken counterpart signs. Consequently, aside from SSIM and PSNR, Mutual Information is also computed to estimate whether the predicted image might provide more distinctive points for matching.
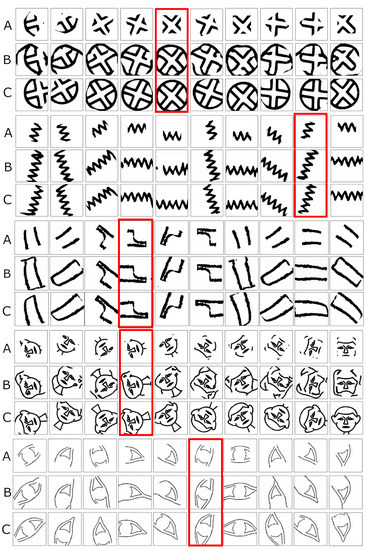
Figure 11.
Examples of decoration completion for the circle, water, feather, head, and eye inscriptions. The rows are labeled as A, B, and C to indicate incomplete signs, predicted completion, and ground truth complete signs, respectively. The red rectangle highlights the best results, which are used to evaluate the generative model.
For the purpose of evaluating the trained models’ performance, the expected complete image is compared not only against the predicted sign but also to the incomplete input hieroglyph. This way, we are able to measure how much the predicted image has improved or distorted the incomplete input drawing. As there are numerous test images, computing the evaluation metrics for all of them might lead to confusion when interpreting the results. Thus, the best-predicted signs, qualitatively wise, are manually selected for evaluation. These signs are highlighted with dashed lines in Figure 11. Moreover, note on the left side of the figures that nomenclatures A, B, and C refer to incomplete signs, predicted signs, and ground truth complete signs, respectively. The image quality results are summarized in Table 1. For the selected signs, C is compared to A and B in terms of the evaluation metrics: SSIM, PSNR, and MI. As shown in the first two columns, the SSIM and PSNR quality results do not provide useful information for evaluation. These obtained metrics are inconsistent; in some cases, the similarity values are higher when comparing B vs. C or vice-versa, which makes it difficult to assess whether the predicted images are providing more salient points for matching or not. This fluctuation of values is expected since SSIM and PSNR metrics measure pixel-to-pixel relationships, and the completion models are not trained to enhance the quality of the input image at the pixel level, such as noise reduction or inpainting methods. For MI results, on the other hand, the estimated values are consistent and allow us to quantitatively assess the predicted decoration. The MI metrics indicate that the predicted images contain more overlap with respect to the ground truth complete sign. Particularly, the MI results for water and eye signs (highlighted in bold) have increased 41 and 24 times, respectively, with respect to the C vs. A comparison. Although the SSIM and PSNR metrics also show an increase, the differences are not as notable as with MI. This quantitative assessment proves that MI is a reliable similarity metric to register the predicted complete inscriptions.

Table 1.
Comparison of image quality and similarity metrics between incomplete signs A, predicted signs B, and ground truth signs C. Their range is from 0 to 1, where 1 means images are more alike. For this evaluation, only the best decoration completion results are considered. These are highlighted with a red rectangle in Figure 11.
3.6. Puzzling Fragments with Mutual Information
As mentioned in Section 2, MI is an entropy-based approach that detects similarities between complex relationships. Instead of exploiting pixel-based properties to estimate correspondences, MI compares density heat maps or 2D histograms of two input sources. This metric is high when input signals share significant information and zero when they are independent. This method has been widely used in the medical field to register data from different sources, for example, computerized tomography (CT) vs. magnetic resonance (MR) images [47]. Motivated by these characteristics, MI is the core of our registration module.
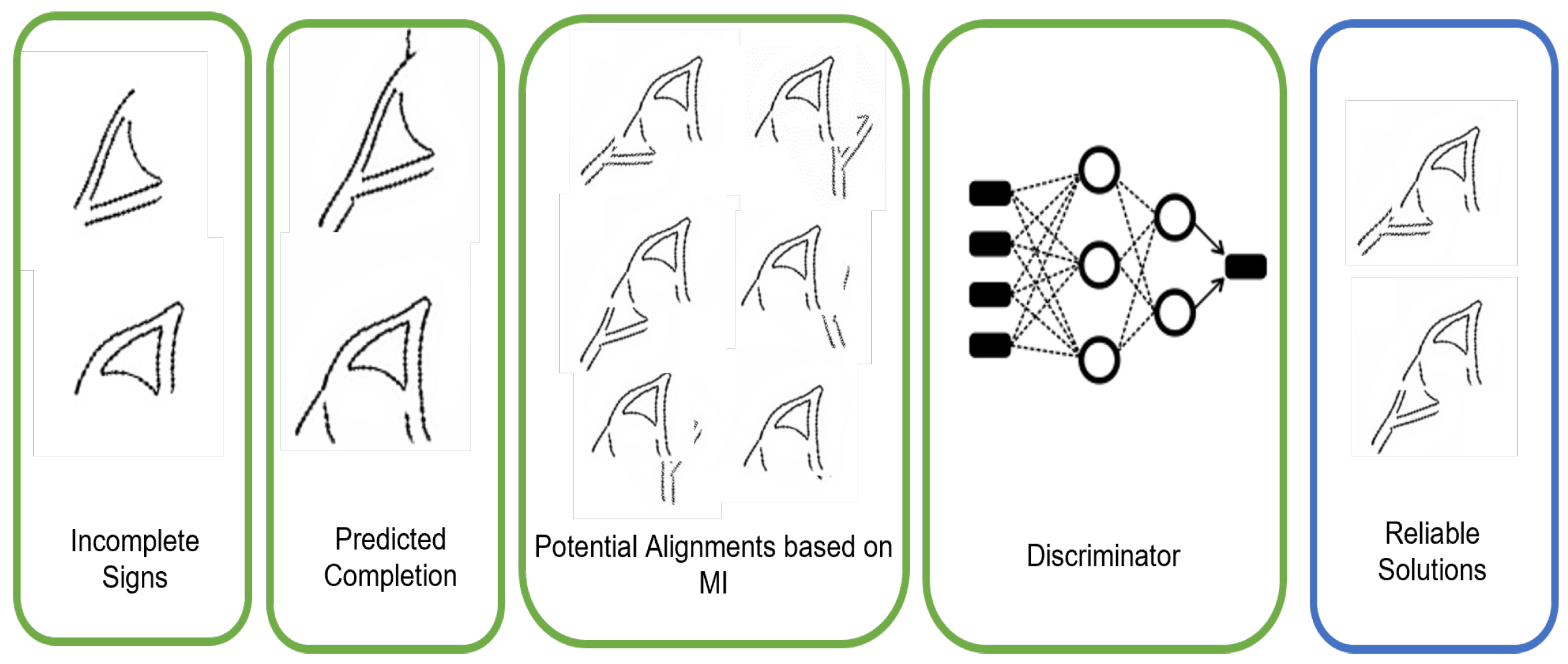
We make use of MI to select possible alignments. Given a pair of counterpart fragments resulting from the completion step, the generated overlap between the predicted images is now leveraged to estimate common regions for matching estimation. The registration process is illustrated in Figure 12. First, we compute MI over all possible alignments, considering rotations and translations. This step yields all possible alignments sorted from highest to lowest MI. In other words, this list represents a set of potential registrations. However, since a pair of broken signs might contain multiple segments with similar shapes that can be matched, the highest alignment in the list does not always correspond to the correct registration. Therefore, a discriminator is implemented to filter out registered images that form a different shape than the expected sign in a way that the final result consists of a set of shape-coherent alignments.
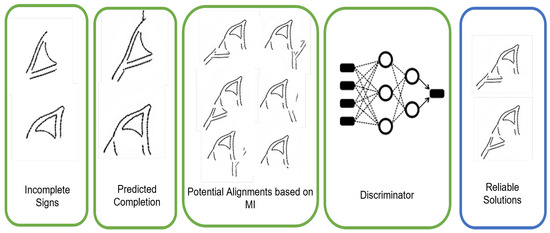
Figure 12.
Step-by-step process to register two incomplete signs using the proposed MI-based approach.
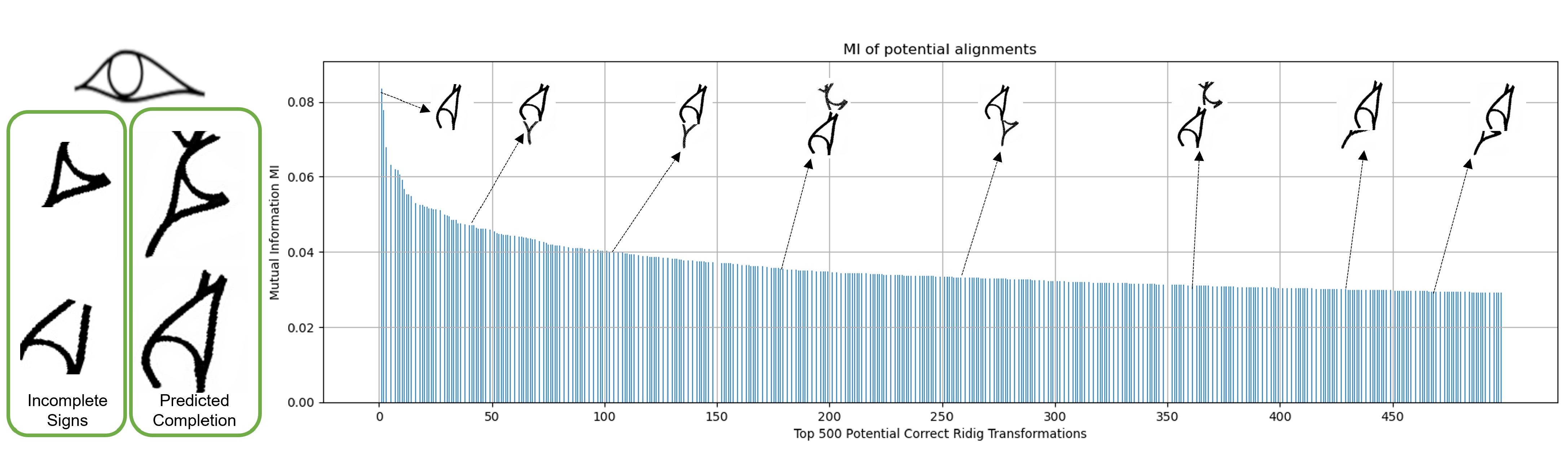
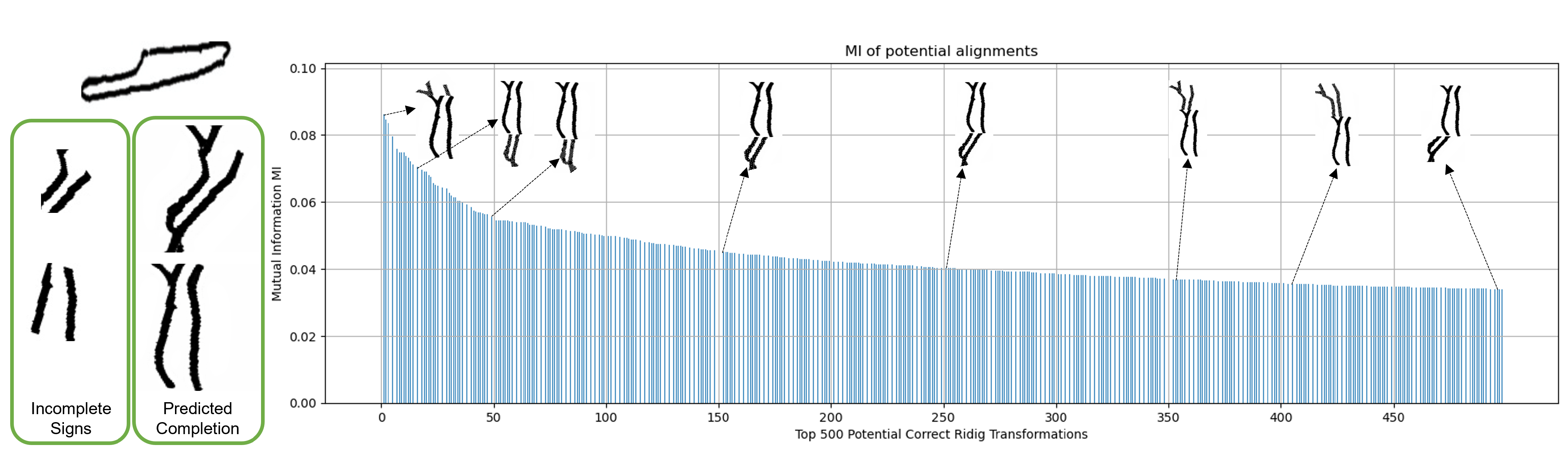
To illustrate why relying only on the highest MI might lead to false registrations (opposite to medical images), Figure 13 and Figure 14 depict the top 500 MI values and shows the resulting alignments of some of the values. For example, the highest MI for the eye sign is 0.083, but the expected registration has a MI of 0.048 (position 40 of top 500). The same goes for the feather inscription, the rough alignments that form the actual sign are found in positions 12 and 49 of Figure 14. We found that the correct potential alignments are always found within the top 100 MI values. As such, a sign discriminator is implemented to select only alignments that form the expected hieroglyph. This module is performed by training a CNN model that classifies misaligned and properly aligned fragments.
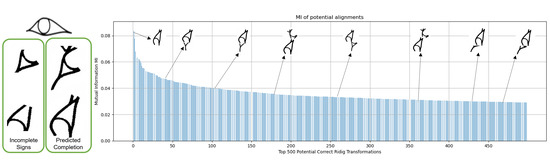
Figure 13.
Example of the top 500 potential signs alignments based on MI for the eye sign. The Y-axis is the MI value, and the X-axis corresponds to the respective alignment index.
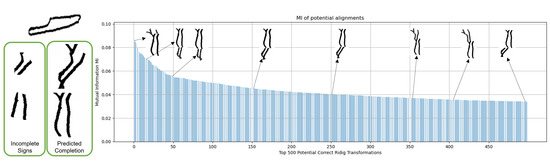
Figure 14.
Example of the top 500 potential signs alignments based on MI for the feather sign. The Y-axis is the MI value, and the X-axis corresponds to the respective alignment index.
The integration of MI with the sign discriminator is described in Algorithm 1. It takes as input the resulting images of the completion module. One of them is set as the target, and the other is used as the query. All possible rotations and translations are applied to the query image in a nested loop so that each step represents a possible alignment. Each iteration of the query and target images are compared by means of MI. Next, the computed metrics are sorted from highest to lowest, saving the top 100 values with the respective alignment. Finally, the CNN discriminator filters out registrations that do not correspond to the expected sign.
| Algorithm 1. Mutual Information registration |
|
4. Results
In this section, the implementation details of the modules that compose the registration pipeline are described. Moreover, a qualitative and quantitative assessment of the puzzling performance of the complete pipeline is presented.
4.1. Implementation
The following libraries and pre-trained models are utilized to implement the registration pipeline. The C++ library for the manipulation of 3D triangles and meshes. Trimesh2 [48] is deployed to implement the extraction of valley lines. Auxiliary computer vision algorithms, such as resizing, convex hull, and connected components analysis, are performed using Opencv [49]. For the line/curve inpainting module, the trained models provided by [38] are used. The CNN network for sign recognition is designed using Tensorflow and Keras [50]. The GAN network for decoration completion is built upon the Cycle-GAN pytorch-based implementation presented in [51]. Finally, the python libraries, Numpy and Scikit-learn [52,53], are deployed to implement the MI registration. The system is tested on a computer with the following specs: processor intel i7, 16GB RAM, GPU Nvidia GeForce GTX 1080.
The integration of all modules is performed following the structure of Algorithm 2. For the sake of clarity, each step of the pipeline is described succinctly by comments in the code. The system requires as input two broken fragments, , that contain decoration traces in the form of 3D sunk relief and monochromatic images. When the system receives the former input, the decoration lines are extracted and converted into an image. Otherwise, the system starts to process from the inpainting stage. Once the line and curve gaps are filled, the partially reconstructed segments are classified to determine the model for decoration completion. After that, the decoration lines are extended according to the classified sign. Finally, the predicted complete signs are aligned by deploying Algorithm 1. The final result is a list of potential alignments that can be evaluated by experts to determine the best registration or can serve as candidates for further matching approaches.
4.2. Evaluation
The proposed pipeline is analyzed as a whole in terms of processing time and qualitative/quantitative metrics for each of its modules. Since the registration depends on a set of consecutive steps, it is important to determine the influence of each step on the final result, thus providing an insight into how the pipeline performs. Concretely, the following modules are evaluated: line/curve inpainting, sign recognition, decoration completion, and MI-based registration.
The processing times are presented in Table 2. The input image dimensions correspond to the size of the training images for the completion model, namely 112 × 112 pixels. The estimated results do not include the time to load the trained model parameters, as this process is performed only once. The table clearly shows that the MI registration process is the bottleneck. This module is time-consuming since its algorithmic complexity is . The algorithm itself is a nested loop that iterates through all possible alignments for each image row and column. The processing time can be reduced by calculating the MI of all possible alignments in parallel. This is not performed in this work as the fragments registration problem does not require a real-time solution.
| Algorithm 2. General Registration Pipeline |
|

Table 2.
Average processing time of each step of the registration pipeline for every fragment expressed in seconds.
For the qualitative and quantitative evaluation of the registration pipeline, random pairwise puzzles are created from the input dataset. This includes segments of inscriptions from the epigraphic studies and 2D traces extracted from the mesh models. Random gaps are added to the generated counterpart signs with the aim of resembling damaged decorated fragments. Aside from the experiments presented in this section, an implementation of the pipeline is provided (https://www.kaggle.com/robdelima/genreassembly, accessed on 17 November 2021) for independent third-party evaluation. This jupyter notebook contains not only the code for each module, but also the pretrained models for sign recognition and completion. It allows the user to generate random puzzles and to process each of the pipeline steps for further results analysis.
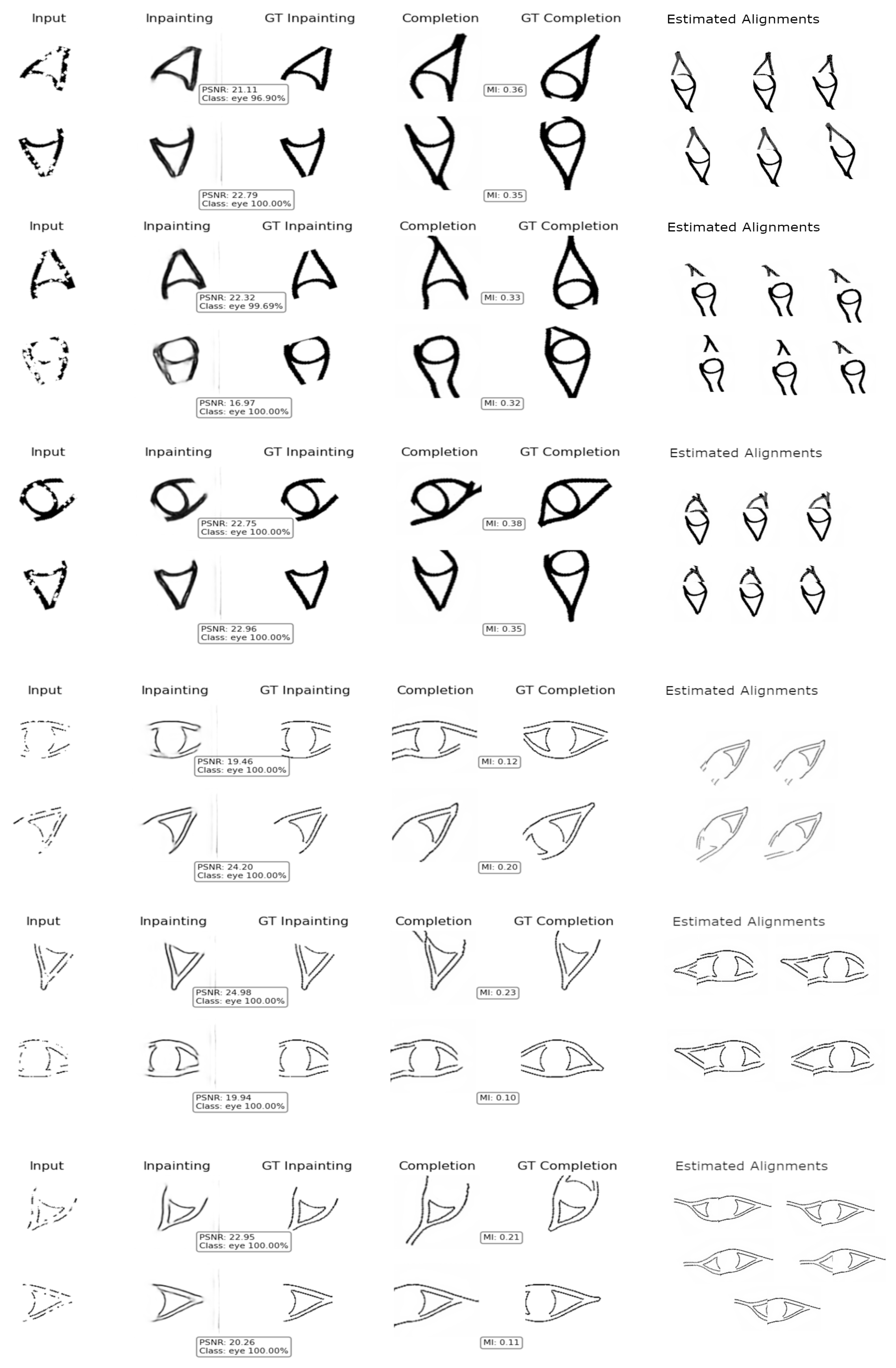
The evaluated pairwise puzzles for each sign are shown in Figure 15, Figure 16, Figure 17, Figure 18 and Figure 19. To qualitatively assess each step, their respective performance metric and expected result are depicted as well. The inpainting module is evaluated via the image quality metric PSNR. Since the sign classifier was already evaluated in Section 3.4, only the classification score is shown. For the completion module evaluation, MI between the predicted image and the ground truth is computed. Finally, on the right side of the figures, the potential estimated alignments are shown.
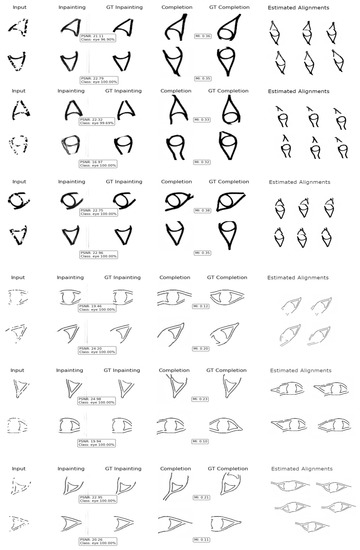
Figure 15.
Examples of obtained results for the eye sign. From inpainting to registration.

Figure 16.
Examples of obtained results for the water sign. From inpainting to registration.

Figure 17.
Examples of obtained results for the feather sign. From inpainting to registration.

Figure 18.
Examples of obtained results for the circle sign. From inpainting to registration.

Figure 19.
Examples of obtained results for the head sign. From inpainting to registration.
Figure 15 depicts the results for the eye sign. For the majority of the cases, the inpainting module yields reliable results, obtaining a PSNR of more than 20, except for the broken sign on row five. This performance positively impacted the classification score, which was 100 % for all input signs. The completion module is not completely accurate when compared to the ground truth data, but the predicted traces help to generate sufficient overlap between images to estimate correct alignments through MI. In general, this sign is challenging to align since counterpart fragments are symmetrical. This characteristic might lead to false positives due to the fact that the maximal MI is estimated when broken signs completely overlap with each other, yielding two ’half eyes’ on top of each other instead of one ’full eye’. This issue is exemplified on row seven, where the best alignment is the full overlap of the input signs. For the other alignments, however, the sign discriminator correctly filtered out false positives, yielding reliable solutions. Since the registration results only represent potential alignments, some of them require further interpretation by experts to determine true positives. For instance, the results on rows 9 and 10 seem correct, but their left segment is flipped. Therefore, in this particular case, the results are false positives and need to be discarded by an expert.
Figure 16 shows the results for the water sign. Unlike the eye inscription, the inpainting result struggles to fill lines of populated gaps. This is depicted on rows 1, 3, 7, 9, and 11. The spaces between zigzag traces are interpreted by the module as line/curve gaps; therefore, it attempts to fill them, resulting in blurry traces. This slight issue does not affect the performance of subsequent steps. For all examples, the inscription classifier yields a score of 100%. The completion module accurately expands the decoration traces, which is translated into a high MI score when compared to the ground truth data. All in all, the registration workflow is capable of registering this type of decoration, as traces were properly extended and matched.
Figure 17 shows the results for the feather sign. Similar to the water inscription, when line gaps are small, the inpainting module fills them with blurry traces. However, the obtained outcome enables subsequent steps to estimate reliable intermediate results. As expected from the confusion matrices presented in Section 3.4, the confidence of the sign classifier is reduced by roughly 20%. As explained, this has to do with the fact that the broken feather segments might look similar to eye segments. Nonetheless, the classification score is more than 60 % for all cases, allowing the completion module to select the correct model. The completion step proves to cope well with a different type of inscription styles for both inputs: 3D traces (rows from 5 to 12) and epigraphic drawings (rows 1 and 2). These accurate completion results are translated into reliable alignments, as obtained results are coherent with the expected shape.
Figure 18 and Figure 19 show the results for the circle and head signs, respectively. They are analyzed together since they exhibit similar registration results. As with previous signs, the inpainting model successfully fills the line and curve gaps. Consequently, the obtained classification score is over 90% for all input drawing segments. The main issue for this sign lies in the decoration completion module. When a straight line is expected to extend a drawing trace, the model attempts to complete it with a circular shape. This problem negatively affects the MI-based registration approach, as incorrectly generated segments are considered correspondences. As a result, the estimated rigid transformation is inaccurate, leading to misalignment, which distorts the input inscription’s form. This registration issue can be clearly seen in Figure 18 rows 9 and 10, where the obtained alignments result in a highly distorted sign. The same effect is shown in Figure 19, rows 4, 11, and 12.
Although the predicted completion leads to incorrect alignments, some of the predicted pixels are actually correct, which might serve as a guide for manual reassembling. This is illustrated in Figure 20, in which correct predicted segments are highlighted in blue and dotted lines. For the head sign, note that the traces that delineate the ’face’ are correctly extended. Similarly, for the circle sign, the straight lines that form a ’cross’ and the curves that join two points (see rows 1 and 2) are predicted properly. These results confirm that the completion module can serve as a matching clue for either manual reassembling or automatic matching when additional information is included, such as geometry.

Figure 20.
Examples of decoration completions for the head and circle inscription. The delineated areas correspond to correct predictions. Although the general inscription is distorted, the correct segments might support semi-automatic registration approaches.
5. Discussion
The integration of an inpainting method, GAN-based model, and an MI-based alignment approach results in a potential approach to not only find correspondences between broken decorated fragments but also to synthetically produce heritage monochromatic drawings. GAN models are normally used to solve inpainting or pixel-to-pixel image translation problems, in which the prediction consists only of filling the gaps between two points based on salient features and pixels’ position. However, our study proves that by deploying the proposed training strategy, GANs also can be used to extend drawings solely based on the texture information of the image perimeter. In order to predict shape-coherent decoration traces, the experimental framework suggests a filling area of 24 px for each side of the image. As illustrated in the experiments, for Egyptian signs made of curves and lines, such as the eye, water, and feather inscription, the proposed pipeline is able to yield reliable registration and completion results. This is a significant finding as this approach can be deployed for reconstructions of other types of heritage data, such as ancient papyrus.
Moreover, the extraction of valley lines proves to be an efficient solution to extract 3D-relief traces and convert them into lines that can be used as input data for sophisticated 2D algorithms or as training data. For example, in this research, the segmented inscriptions extracted from 3D indentations serve as complementary data for training the completion model, thus enabling the registration pipeline to cope not only with images but with mesh models as well. For the feather sign, in particular, these additional images played a fundamental role in the completion module, as the predicted decorations serve to successfully perform the MI-based registration approach. This result is relevant due to the fact that the line segments of such extracted signs are quite irregular but sufficient for GAN models to learn distinct features and improve the decoration completion results. Therefore, combining the extraction of 3D sunk relief lines, GANs, and MI represents a novel solution to reconstruct mesh models of antique decorated stelas, which are commonly found in ancient cultures, such as the Egyptian, Greek, and Roman.
Although the proposed approach yields plausible alignment results for sophisticated decoration shapes, the MI-based registration module struggles to estimate the optimal alignment transformation. As mentioned in the previous section, this problem is caused by incorrectly predicted decoration segments, which distort the inscription and affect the rigid transformation’s accuracy. This means that prominent features have an impact on the decoration completion, such as the circle and head sign that are mainly constructed by a circle. In these kinds of scenarios, the reconstruction and completion modules can be part of a semi-automatic registration approach. As such, they can serve as tools for experts to easily find matching decoration clues from either drawings or 3D-decorated blocks via a puzzling virtual interface. Along the same lines, the deep learning reconstruction and completion approach offers the opportunity to create synthetic training data from highly damaged archaeological assets. Enabling data-driven approaches to tackle unsolved topics in the field of digital heritage, such as segmentation and classification of archaeological monuments [54,55], ancient text deciphering [56], and visualization enhancement [57].
6. Conclusions
This paper presents a registration pipeline for ancient broken fragments with highly damaged decoration traces in 3D and 2D space. Its main modules are: (i) decoration inpainting and completion and (ii) MI-based alignment. The first stage attempts to mitigate the fragments’ lack of texture (caused by erosion and damage over the years) by reconstructing line-curved decoration traces and completing its expected shape. To this purpose, a novel way to train a GAN-based model is proposed for digital heritage decoration completion. We proved that this completion methodology is able to cope with highly deteriorated drawing traces of ancient Egyptian fragments since the predicted decoration completions produce sufficient distinctive salient points for matching. In the second stage, the predicted images are used to find common segments between counterpart fragments on the basis of MI. The results show that the registration pipeline is suited to puzzle fragments with textureless decorations made of zigzag lines, curves, and combinations of straight lines and curves. For such shapes, the proposed approach is able to accurately perform the core modules of the registration workflow: decoration inpainting, completion, and alignment. Therefore, this methodology can be implemented to automatically register fragments of ancient inscriptions or texts made of similar forms, such as some of the presented Egyptian Hieroglyphs. However, for decorations made of more complex shapes, the proposed work can serve as a tool for experts to seamlessly find matching clues by means of a virtual environment or a semi-automatic registration approach. Future work includes the investigation of ways to homogenize the different types of decoration for a particular set of inscriptions. Since this work requires a completion model for each type of inscription, the training process becomes tedious and time-consuming.
Author Contributions
R.d.L.-H. and M.V. contributed equally to the work. All authors have read and agreed to the published version of the manuscript.
Funding
The research presented here features within the Puzzling Tombs project (nr. 3H170337), funded by the KU Leuven Bijzonder Onderzoeksfonds.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
We thank Toon Sykora for providing the epigraphic study used to develop this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lawonn, K.; Trostmann, E.; Preim, B.; Hildebrandt, K. Visualization and extraction of carvings for heritage conservation. IEEE Trans. Vis. Comput. Graph. 2016, 23, 801–810. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Papaioannou, G.; Karabassi, E.A.; Theoharis, T. Reconstruction of three-dimensional objects through matching of their parts. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 114–124. [Google Scholar] [CrossRef]
- Paumard, M.M.; Picard, D.; Tabia, H. Deepzzle: Solving visual jigsaw puzzles with deep learning and shortest path optimization. IEEE Trans. Image Process. 2020, 29, 3569–3581. [Google Scholar] [CrossRef]
- Guo, Y.; Bennamoun, M.; Sohel, F.; Lu, M.; Wan, J.; Kwok, N.M. A comprehensive performance evaluation of 3D local feature descriptors. Int. J. Comput. Vis. 2016, 116, 66–89. [Google Scholar] [CrossRef]
- Ma, J.; Jiang, X.; Fan, A.; Jiang, J.; Yan, J. Image matching from handcrafted to deep features: A survey. Int. J. Comput. Vis. 2021, 129, 23–79. [Google Scholar] [CrossRef]
- Huang, Q.X.; Flöry, S.; Gelfand, N.; Hofer, M.; Pottmann, H. Reassembling fractured objects by geometric matching. In ACM SIGGRAPH 2006 Papers; Association for Computing Machinery: New York, NY, USA, 2006; pp. 569–578. [Google Scholar]
- Hernandez, R.; Vincke, S.; Bassier, M.; Mattheuwsen, L.; Derdeale, J.; Vergauwen, M. Puzzling Engine: A Digital Platform to Aid the Reassembling of Fractured Fragments. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 42, 563–570. [Google Scholar] [CrossRef]
- Torrente, M.L.; Biasotti, S.; Falcidieno, B. Recognition of feature curves on 3D shapes using an algebraic approach to Hough transforms. Pattern Recognit. 2018, 73, 111–130. [Google Scholar] [CrossRef]
- Thompson, E.M.; Biasotti, S. Description and retrieval of geometric patterns on surface meshes using an edge-based LBP approach. Pattern Recognit. 2018, 82, 1–15. [Google Scholar] [CrossRef]
- Gravitate Geometric Reconstruction and NoVel SemantIc ReunificaTion of culturAl heriTage objEcts. Available online: https://cordis.europa.eu/project/id/665155 (accessed on 17 November 2021).
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Barra, P.; Barra, S.; Nappi, M.; Narducci, F. SAFFO: A SIFT based approach for digital anastylosis for fresco recOnstruction. Pattern Recognit. Lett. 2020, 138, 123–129. [Google Scholar] [CrossRef]
- Chen, L.; Chen, J.; Zou, Q.; Huang, K.; Li, Q. Multi-view feature combination for ancient paintings chronological classification. J. Comput. Cult. Herit. (JOCCH) 2017, 10, 1–15. [Google Scholar] [CrossRef]
- Bakirman, T.; Bayram, B.; Akpinar, B.; Karabulut, M.F.; Bayrak, O.C.; Yigitoglu, A.; Seker, D.Z. Implementation of ultra-light UAV systems for cultural heritage documentation. J. Cult. Herit. 2020, 44, 174–184. [Google Scholar] [CrossRef]
- Li, R.; Liu, S.; Wang, G.; Liu, G.; Zeng, B. JigsawGAN: Self-supervised Learning for Solving Jigsaw Puzzles with Generative Adversarial Networks. arXiv 2021, arXiv:2101.07555. [Google Scholar]
- Creswell, A.; White, T.; Dumoulin, V.; Arulkumaran, K.; Sengupta, B.; Bharath, A.A. Generative adversarial networks: An overview. IEEE Signal Process. Mag. 2018, 35, 53–65. [Google Scholar] [CrossRef]
- Ostertag, C.; Beurton-Aimar, M. Matching ostraca fragments using a siamese neural network. Pattern Recognit. Lett. 2020, 131, 336–340. [Google Scholar] [CrossRef]
- Archaide New System for the Automatic Recognition of Archaeological Pottery. Available online: http://www.archaide.eu/ (accessed on 10 December 2021).
- Mehra, S. From Textural Inpainting to Deep Generative Models: An Extensive Survey of Image Inpainting Techniques. Int. J. Trends Comput. Sci. 2020, 16, 35–49. [Google Scholar] [CrossRef][Green Version]
- Harms, J.; Lei, Y.; Wang, T.; Zhang, R.; Zhou, J.; Tang, X.; Curran, W.J.; Liu, T.; Yang, X. Paired cycle-GAN-based image correction for quantitative cone-beam computed tomography. Med. Phys. 2019, 46, 3998–4009. [Google Scholar] [CrossRef]
- Qu, Y.; Chen, Y.; Huang, J.; Xie, Y. Enhanced pix2pix dehazing network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–17 June 2019; pp. 8160–8168. [Google Scholar]
- Cai, W.; Wei, Z. PiiGAN: Generative adversarial networks for pluralistic image inpainting. IEEE Access 2020, 8, 48451–48463. [Google Scholar] [CrossRef]
- Liu, F.; Deng, X.; Lai, Y.K.; Liu, Y.J.; Ma, C.; Wang, H. Sketchgan: Joint sketch completion and recognition with generative adversarial network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–17 June 2019; pp. 5830–5839. [Google Scholar]
- Cao, J.; Zhang, Z.; Zhao, A.; Cui, H.; Zhang, Q. Ancient mural restoration based on a modified generative adversarial network. Herit. Sci. 2020, 8, 1–14. [Google Scholar] [CrossRef]
- Wang, H.; Li, Q.; Jia, S. A global and local feature weighted method for ancient murals inpainting. Int. J. Mach. Learn. Cybern. 2020, 11, 1197–1216. [Google Scholar] [CrossRef]
- Abate, D. FRAGMENTS: A fully automatic photogrammetric fragments recomposition workflow. J. Cult. Herit. 2021, 47, 155–165. [Google Scholar] [CrossRef]
- Melbourne, A.; Ridgway, G.; Hawkes, D.J. Image similarity metrics in image registration. In Medical Imaging 2010: Image Processing; International Society for Optics and Photonics: San Diego, CA, USA, 2010; Volume 7623, p. 762335. [Google Scholar]
- Chen, S.; Li, X.; Zhao, L.; Yang, H. Medium-low resolution multisource remote sensing image registration based on SIFT and robust regional mutual information. Int. J. Remote Sens. 2018, 39, 3215–3242. [Google Scholar] [CrossRef]
- Song, S.; Herrmann, J.M.; Si, B.; Liu, K.; Feng, X. Two-dimensional forward-looking sonar image registration by maximization of peripheral mutual information. Int. J. Adv. Robot. Syst. 2017, 14, 1729881417746270. [Google Scholar] [CrossRef]
- Bassier, M.; Vincke, S.; de Lima Hernandez, R.; Vergauwen, M. An overview of innovative heritage deliverables based on remote sensing techniques. Remote Sens. 2018, 10, 1607. [Google Scholar] [CrossRef]
- Newberry, P.E. El Bersheh: Part I. The Tomb of Tehuti-Hetep; Egypt Exploration Fund: London, UK, 1893. [Google Scholar]
- Dayr Al-Barsha Project an Interdisciplinary Archaeological Research Project in Middle Egypt. Available online: https://www.arts.kuleuven.be/dayr-al-barsha (accessed on 5 October 2021).
- Meyer, M.; Desbrun, M.; Schröder, P.; Barr, A.H. Discrete differential-geometry operators for triangulated 2-manifolds. In Visualization and Mathematics III; Springer: Berlin/Heidelberg, Germany, 2003; pp. 35–57. [Google Scholar]
- Ohtake, Y.; Belyaev, A.; Seidel, H.P. Ridge-valley lines on meshes via implicit surface fitting. In ACM SIGGRAPH 2004 Papers; Association for Computing Machinery: New York, NY, USA, 2004; pp. 609–612. [Google Scholar]
- Wagner, T.; Lipinski, H.G. IJBlob: An ImageJ library for connected component analysis and shape analysis. J. Open Res. Softw. 2013, 1, e6. [Google Scholar]
- Vollmer, J.; Mencl, R.; Mueller, H. Improved laplacian smoothing of noisy surface meshes. In Computer Graphics Forum; Wiley Online Library: New York, NY, USA, 1999; Volume 18, pp. 131–138. [Google Scholar]
- Stein, A.; Geva, E.; El-Sana, J. CudaHull: Fast parallel 3D convex hull on the GPU. Comput. Graph. 2012, 36, 265–271. [Google Scholar] [CrossRef]
- Sasaki, K.; Iizuka, S.; Simo-Serra, E.; Ishikawa, H. Joint Gap Detection and Inpainting of Line Drawings. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Zhang, X.; Huang, Y.; Zou, Q.; Pei, Y.; Zhang, R.; Wang, S. A hybrid convolutional neural network for sketch recognition. Pattern Recognit. Lett. 2020, 130, 73–82. [Google Scholar] [CrossRef]
- Li, L.; Zou, C.; Zheng, Y.; Su, Q.; Fu, H.; Tai, C.L. Sketch-R2CNN: An attentive network for vector sketch recognition. arXiv 2018, arXiv:1811.08170. [Google Scholar]
- Eitz, M.; Hays, J.; Alexa, M. How Do Humans Sketch Objects? ACM Trans. Graph. Proc. SIGGRAPH 2012, 31, 44:1–44:10. [Google Scholar] [CrossRef]
- Barucci, A.; Cucci, C.; Franci, M.; Loschiavo, M.; Argenti, F. A Deep Learning Approach to Ancient Egyptian Hieroglyphs Classification. IEEE Access 2021, 9, 123438–123447. [Google Scholar] [CrossRef]
- Goldwasser, O. Hieratic inscriptions from Tel Sera’in southern Canaan. Tel Aviv 1984, 11, 77–93. [Google Scholar] [CrossRef]
- Cook, B.F. Greek Inscriptions; University of California Press: London, UK, 1987; Volume 5. [Google Scholar]
- Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Hore, A.; Ziou, D. Image quality metrics: PSNR vs. SSIM. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 2366–2369. [Google Scholar]
- Chen, H.M.; Varshney, P.K. Mutual information-based CT-MR brain image registration using generalized partial volume joint histogram estimation. IEEE Trans. Med Imaging 2003, 22, 1111–1119. [Google Scholar] [CrossRef] [PubMed]
- Trimesh2 A C++ Library and Set of Utilities for Input, Output, and Basic Manipulation of 3D Triangle Meshes. Available online: https://gfx.cs.princeton.edu/proj/trimesh2/ (accessed on 5 October 2021).
- OpenCV Computer Vision Library. Available online: https://opencv.org/ (accessed on 5 October 2021).
- TensorFlow an End-to-End Open Source Machine Learning Platform. Available online: https://www.tensorflow.org/ (accessed on 5 October 2021).
- Isola, P.; Zhu, J.Y.; Zhou, T.; Efros, A.A. Image-to-Image Translation with Conditional Adversarial Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Numpy The Fundamental Package for Scientific Computing with Python. Available online: https://numpy.org/ (accessed on 5 October 2021).
- Scikit-Learn Machine Learning in Python. Available online: https://scikit-learn.org/ (accessed on 5 October 2021).
- Grilli, E.; Dininno, D.; Marsicano, L.; Petrucci, G.; Remondino, F. Supervised segmentation of 3D cultural heritage. In Proceedings of the 2018 3rd Digital Heritage International Congress (DigitalHERITAGE) Held Jointly with 2018 24th International Conference on Virtual Systems & Multimedia (VSMM 2018), San Francisco, CA, USA, 26–30 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–8. [Google Scholar]
- Paliokas, I. Serious games classification for digital heritage. Int. J. Comput. Methods Herit. Sci. IJCMHS 2019, 3, 58–72. [Google Scholar] [CrossRef][Green Version]
- Heenkenda, H.; Fernando, T. Approaches Used to Recognise and Decipher Ancient Inscriptions: A Review. Vidyodaya J. Sci. 2020, 23, 42–45. [Google Scholar]
- Pflüger, H.; Thom, D.; Schütz, A.; Bohde, D.; Ertl, T. VeCHArt: Visually enhanced comparison of historic art using an automated line-based synchronization technique. IEEE Trans. Vis. Comput. Graph. 2019, 26, 3063–3076. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).