Evaluation of Network RTK Positioning Performance Based on BDS-3 New Signal System
Abstract
:1. Introduction
2. Network RTK Positioning Algorithm
2.1. Ambiguity Resolution of Reference Stations
2.2. Classification Modeling of Ionospheric and Tropospheric Delay
2.3. Generation of Virtual Observations (VRS)
- The ambiguity of all satellite observations of the VRS is the same as that of the main reference station.
- The clock error between the virtual reference station and the main reference station is the same; that is, the capture time of the observation of the two stations is the same.
- The ionospheric and tropospheric delays of the reference satellite of the VRS are the same as those of the main reference station.
3. Datasets and Processing Strategy
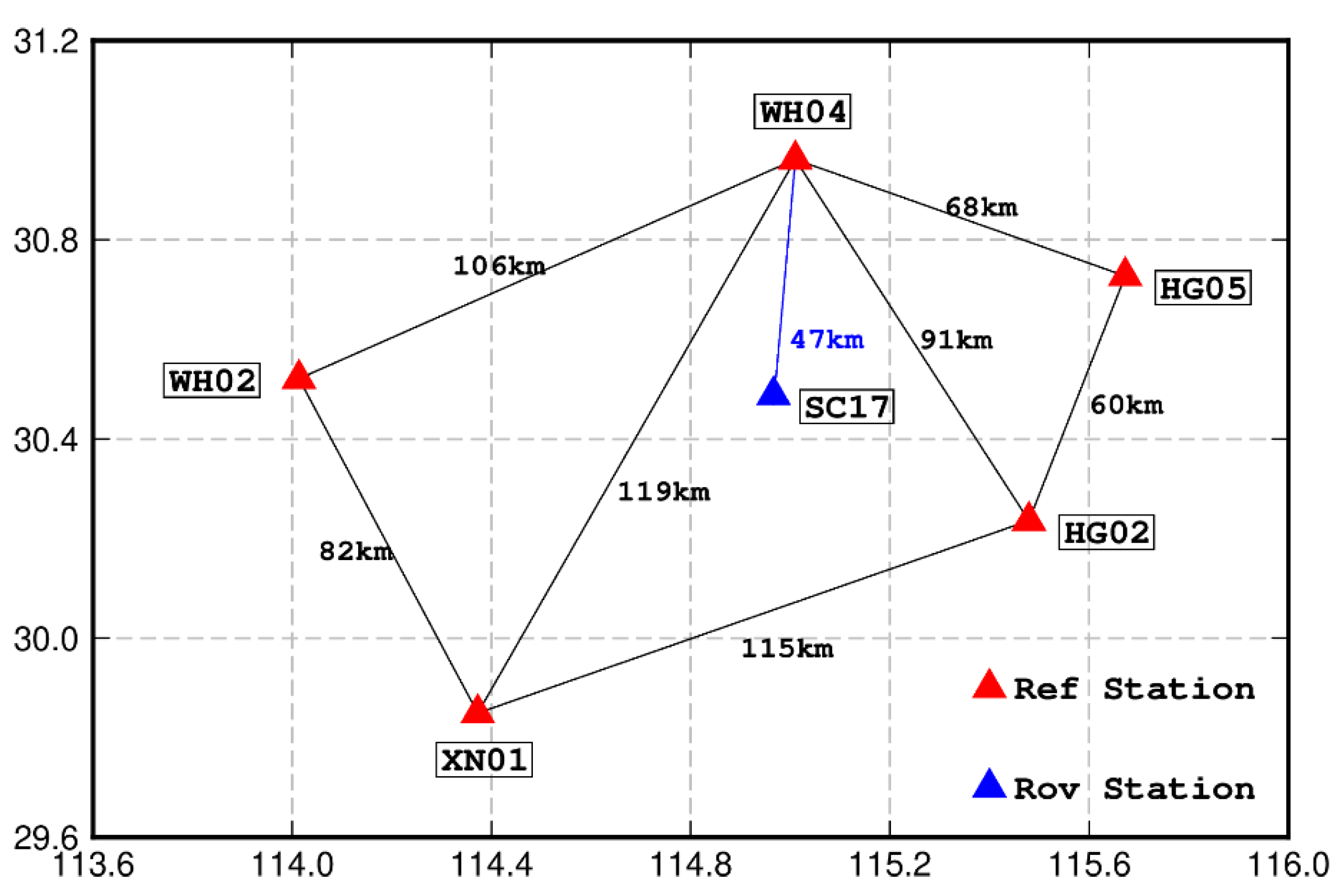
3.1. Datasets
3.2. Processing Strategy
4. Experiment and Analysis
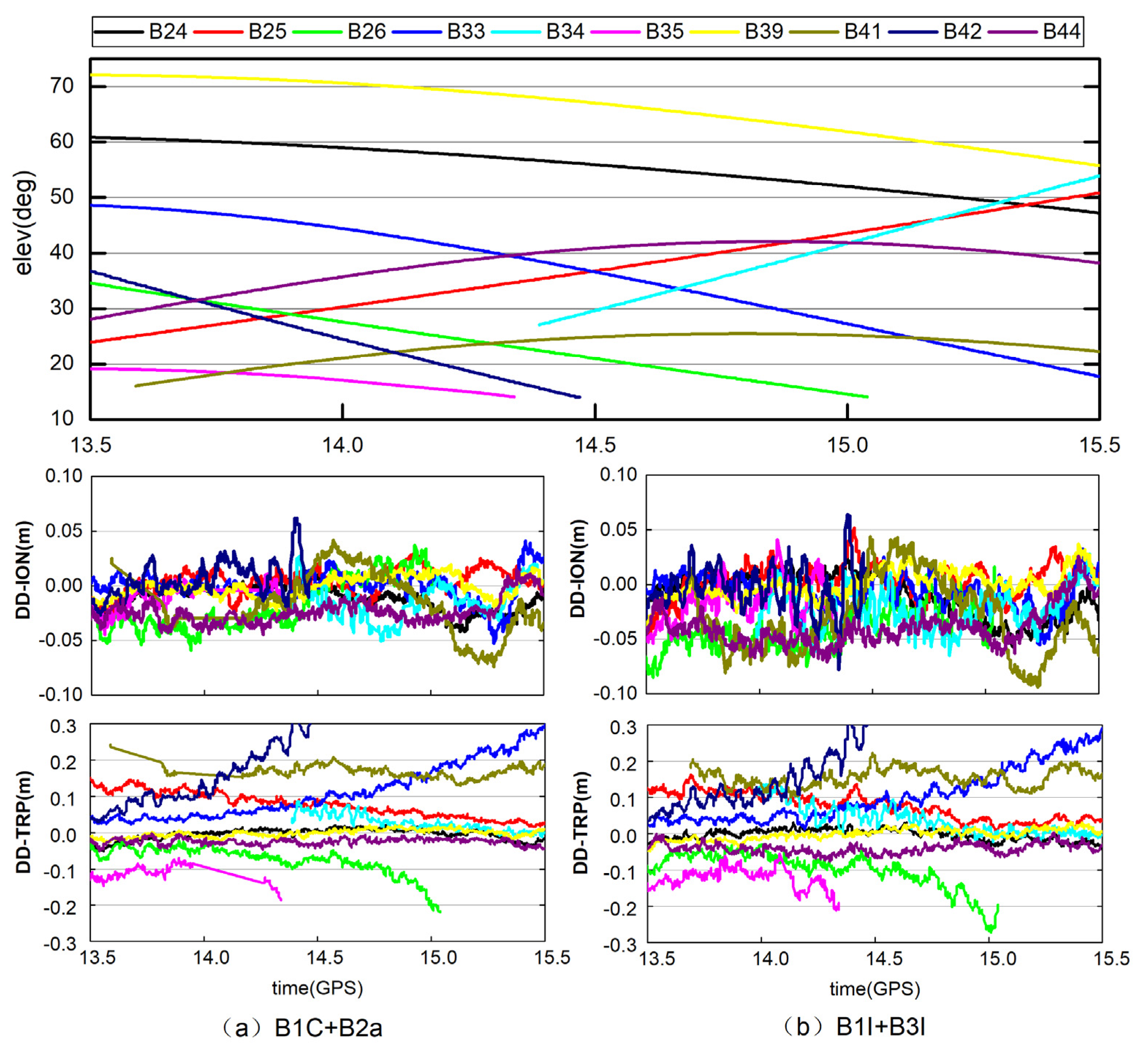
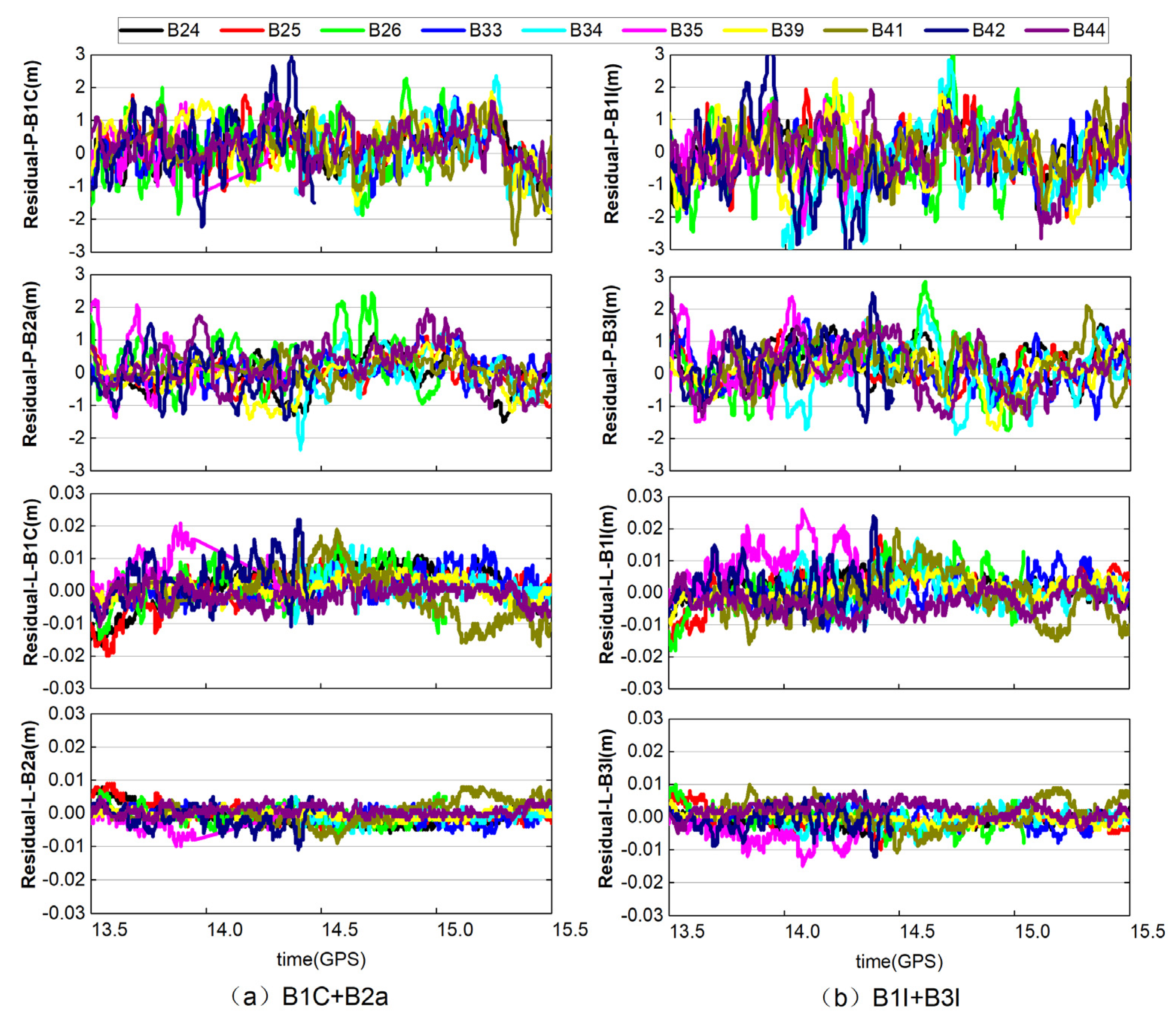
4.1. Analysis of DD Atmospheric Correction at Reference Stations
4.2. Accuracy Analysis of Regional Atmosphere Modeling and Interpolation
4.3. Analysis of Positioning Performance of Network RTK Terminal
5. Discussion
- Firstly, in the long-distance baseline calculation between reference stations, tropospheric wet delay and ionospheric delay were estimated as parameters to assist the fixation of ambiguity. Although random walk was used to estimate parameters and a variance constraint was applied to accelerate the convergence of the baseline, the initial parameter values were set to zero. Theoretically, adding an external correction model to provide relatively accurate initial values would further shorten the baseline convergence time.
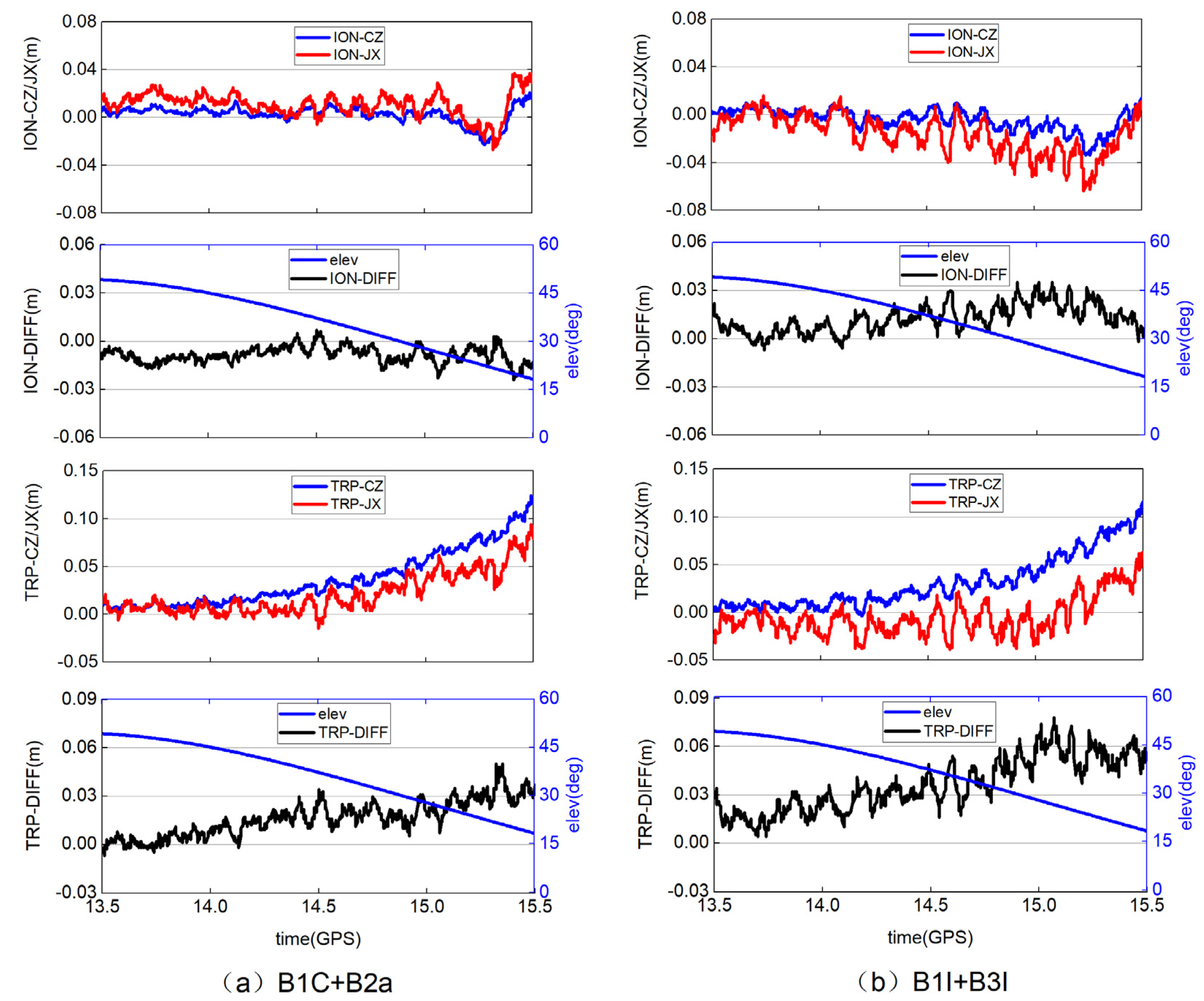
- Secondly, the experimental analysis results in Section 4.1 and Section 4.2 show that the ionospheric and troposphere atmospheric modeling and interpolation accuracy are negatively correlated with the satellite elevation angle. In Section 2.2 of atmospheric modeling strategy, this paper gives a preliminary method of ionospheric weighting based on elevation angle, but a more refined modeling weighting method considering the influence of elevation angle needs to be further studied.
- Finally, Section 4.3 of this paper takes the GPS system as reference and designs five schemes to preliminarily evaluate the positioning performance of network RTK of BDS-3. The horizontal error of each scheme is basically within 3 cm, and the elevation error is within 5 cm, which can meet the requirements of providing network RTK high-precision service independently. In addition, the terminal positioning effect statistics show that the positioning accuracy of BDS-2 is relatively poor, the positioning accuracy of BDS-3 is only slightly better than that of GPS, and the combined processing effect of BDS-2/3 using B1I+B3I transition signal is the best. The reason why the positioning performance of BDS-3 is slightly better than that of GPS may be attributed to the fact that the experimental data in this paper were collected in central China. Compared with GPS, the number of BDS-3 satellites and the distribution of DOP values in the Asia-Pacific region are obviously more advantageous. The number of satellites and the distribution of PDOP values of Station SC17, shown in Figure 9, can also be seen as related laws. Further comparative analysis requires further data collection of more regions for experimental demonstration.
6. Conclusions
- When the combination of B1C+B2a and B1I+B3I of a single BDS-3 constellation provides VRS service, the fixed rate of terminal RTK is above 95%, and the horizontal and elevation accuracy are within 1 cm and 2 cm, respectively. The single BDS-3 system is sufficient to meet the needs of providing network RTK high-precision positioning service in surveying and mapping operations. In addition, the terminal positioning effect statistics show that the positioning accuracy of BDS-2 is relatively poor, GPS is superior to BDS-2, the positioning accuracy of BDS-3 is better than that of GPS and BDS-2, BDS-2/3 combined processing of B1I+B3I transition signal has the best effect, and its accuracy in the E and N directions is better than 0.5 cm, and that in the U direction is better than 1.5 cm.
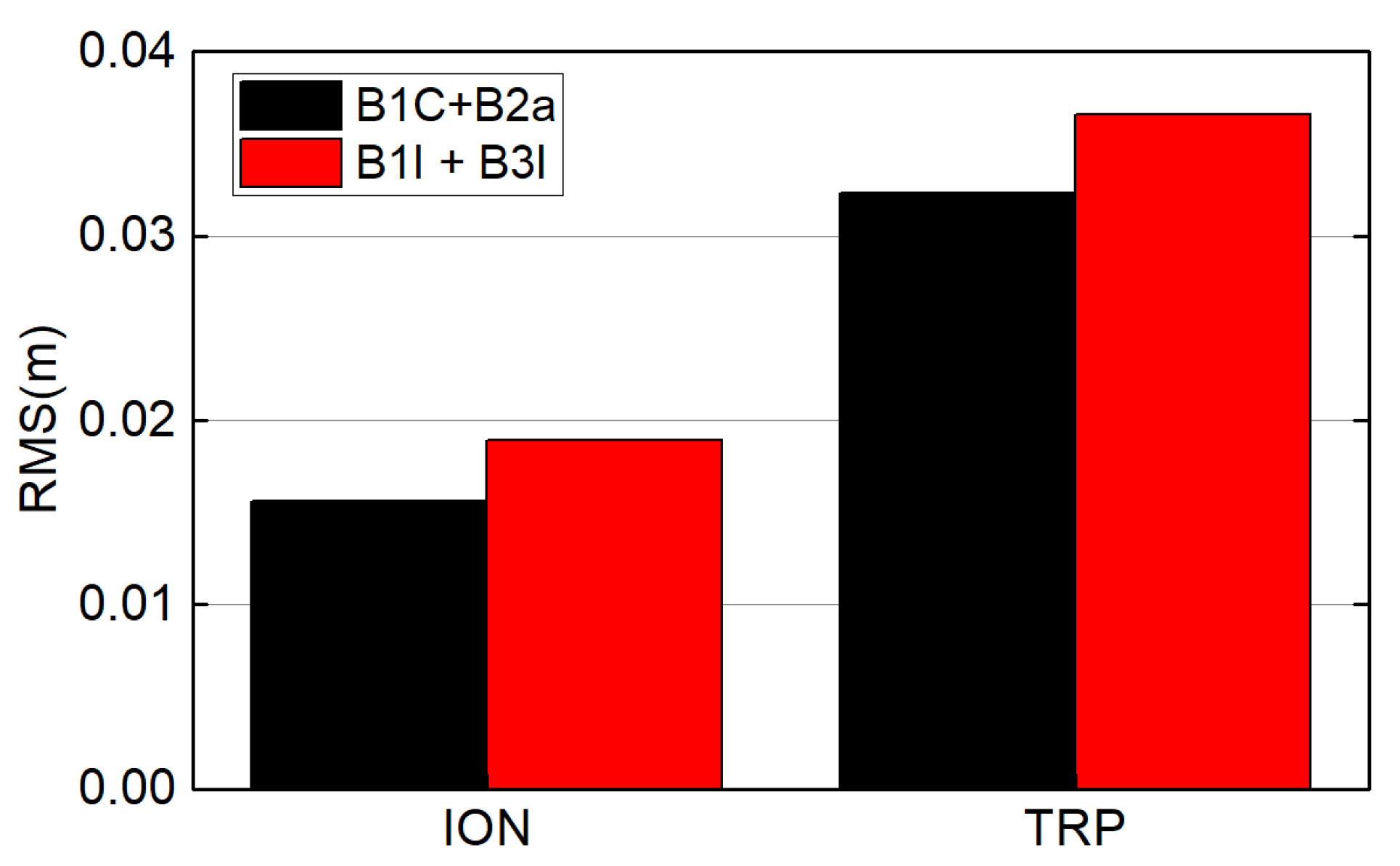
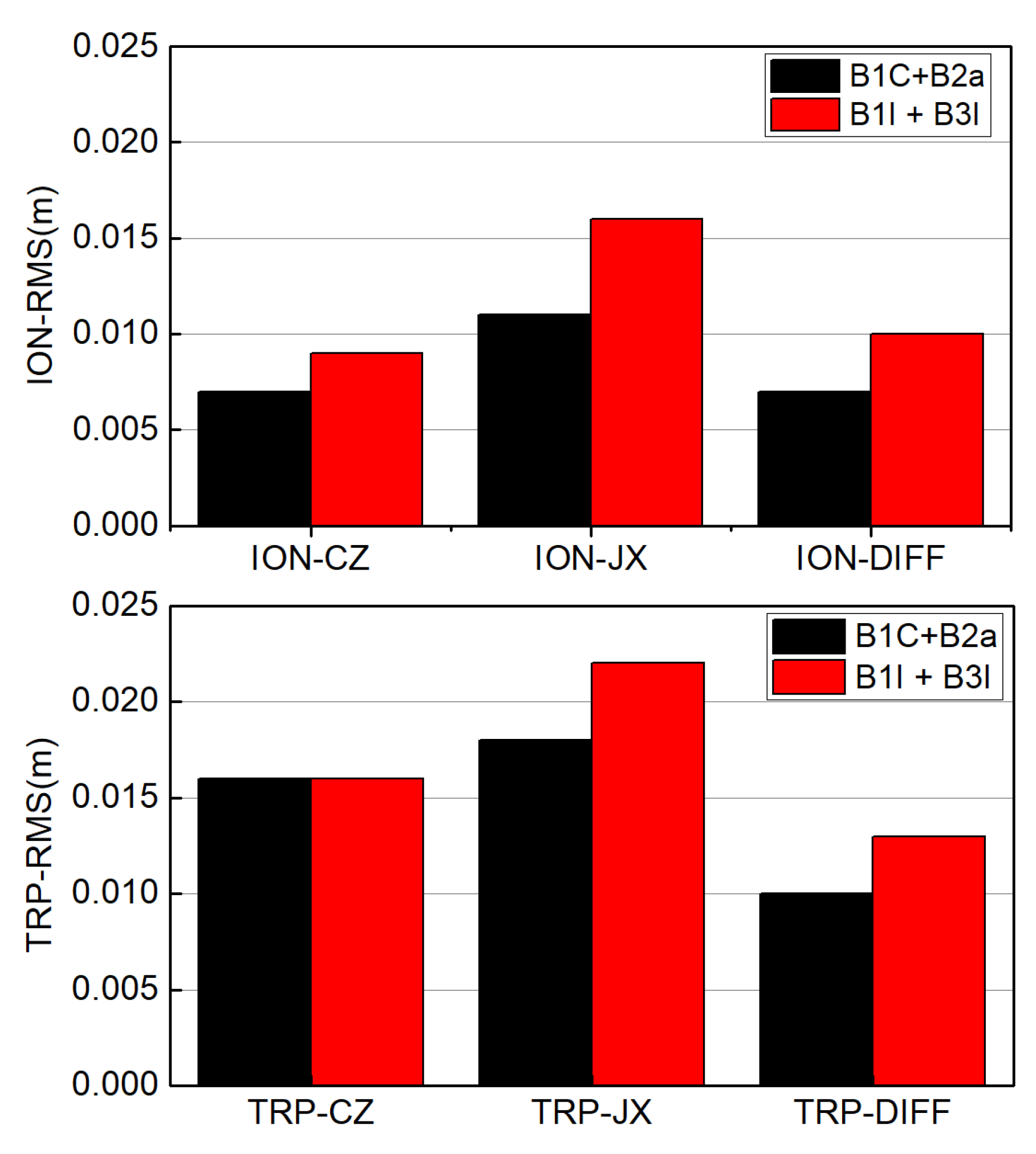
- Based on the analysis of atmospheric correction, regional atmospheric modeling, and network RTK terminal positioning accuracy, it can be seen that the new signal combination (B1C+B2a) of the BDS-3 system is slightly better than the transition signal combination (B1I+B3I). In addition, the double-difference atmospheric correction of the reference station and the accuracy of regional atmospheric modeling both show a positive correlation with elevation angle, so it is necessary to carry out reasonable weighting processing for the satellite according to elevation angle in regional atmospheric modeling.
- According to the above analysis, when a single BDS-3 constellation provides network RTK service, the combination of B1C+B2a is suggested to be adopted as the main frequency signals for calculation. When the BDS-2/3 combined solution provides network RTK service, it is recommended to adopt the B1I+B3I combination as the main frequency signals for the solution.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- CSNO. Development of the BeiDou Navigation Satellite System (Version 4.0); China Satellite Navigation Office Technical Report; China Satellite Navigation Office: Beijing, China, 2019. Available online: http://en.beidou.gov.cn/SYSTEMS/Officialdocument/index_1.html (accessed on 18 August 2021).
- Yang, Y.; Xu, Y.; Li, J.; Yang, C. Progress and performance evaluation of BeiDou global navigation satellite system: Data analysis based on BDS-3 demonstration system. Sci. China Earth Sci. 2018, 61, 614–624. [Google Scholar] [CrossRef]
- Yang, Y.; Gao, W.; Guo, S.; Mao, Y.; Yang, Y. Introduction to BeiDou-3 navigation satellite system. Navig.-J. Inst. Navig. 2019, 66, 7–18. [Google Scholar] [CrossRef] [Green Version]
- Jia, X.; Zeng, T.; Ruan, R.; Mao, Y.; Xiao, G. Atomic Clock Performance Assessment of BeiDou-3 Basic System with the Noise Analysis of Orbit Determination and Time Synchronization. Remote Sens. 2019, 11, 17. [Google Scholar] [CrossRef] [Green Version]
- Zhang, B.; Jia, X.; Sun, F.; Xiao, K.; Dai, H. Performance of BeiDou-3 Satellites: Signal Quality Analysis and Precise Orbit Determination. Adv. Space Res. 2019, 64, 687–695. [Google Scholar] [CrossRef]
- Huang, C.; Song, S.; Chen, Q.; Zhou, W. Preliminary Analysis of BDS-3 Data Based on iGMAS. Chin. Astron. Astrophys. 2019, 43, 390–404. [Google Scholar] [CrossRef]
- Wang, C.; Zhao, Q.; Guo, J.; Liu, J.; Chen, G. The contribution of intersatellite links to BDS-3 orbit determination: Model refinement and comparisons. J. Inst. Navig. 2019, 66, 71–82. [Google Scholar] [CrossRef] [Green Version]
- Xie, X.; Geng, T.; Zhao, Q.; Cai, H.; Zhang, F.; Wang, X.; Meng, Y. Precise orbit determination for BDS-3 satellites using satellite-ground and inter-satellite link observations. GPS Solut. 2019, 23, 12. [Google Scholar] [CrossRef]
- Jiao, G.; Song, S.; Ge, Y.; Su, K.; Liu, Y. Assessment of BeiDou-3 and Multi-GNSS Precise Point Positioning Performance. Sensors 2019, 19, 20. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Hu, J.; Ren, X. New progress of PPP/PPP-RTK and positioning performance comparison of BDS/GNSS PPP. Acta Geod. Et Cartogr. Sin. 2020, 49, 1084–1100. [Google Scholar] [CrossRef]
- Jin, S.; Su, K. PPP models and performances from single- to quad-frequency BDS observations. Satell. Navig. 2020, 1, 16. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, B.; Nie, L.; Wei, C.; Jia, S.; Jiang, S. Initial assessment of BeiDou-3 global navigation satellite system: Signal quality, RTK and PPP. GPS Solut. 2019, 23, 111. [Google Scholar] [CrossRef]
- Hou, P.; Zhang, B.; Yuan, Y.; Zhang, X.; Zha, J. Stochastic modeling of BDS2/3 observations with application to RTD/RTK positioning. Meas. Sci. Technol. 2019, 30, 095002. [Google Scholar] [CrossRef]
- Yuan, Y.; Mi, X.; Zhang, B. Initial assessment of single- and dual-frequency BDS-3 RTK positioning. Satell. Navig. 2020, 1, 31. [Google Scholar] [CrossRef]
- CSNO. BeiDou Navigation Satellite System Open Service Performance Standard (Version 2.0); China Satellite Navigation Office Technical Report; China Satellite Navigation Office: Beijing, China, 2018. Available online: http://en.beidou.gov.cn/SYSTEMS/Officialdocument/index.html (accessed on 18 August 2021).
- Liu, J.; Tu, R.; Han, J.; Zhang, R.; Fan, L.; Zhang, P.; Hong, J.; Lu, X. Initial evaluation and analysis of NRTK positioning performance with new BDS-3 signals. Meas. Sci. Technol. 2020, 32, 014002. [Google Scholar] [CrossRef]
- Li, C. Generation and Distribut Iontechn Ique of Precise Differential Corrections for GPS/VRS Network; Southwest Jiaotong University: Chengdu, China, 2007. [Google Scholar]
- Zhang, M. Research on the Key Technologies of GPS/BDS Long-Range Network RTK; Wuhan University: Wuhan, China, 2016. [Google Scholar]
- Zhu, H.; Lu, Y.; Xu, A.; Li, J. A Network Real-Time Kinematic Method for GPS and BDS Double Systems between Long Range. Geomat. Inf. Sci. Wuhan Univ. 2021, 46, 252–261. [Google Scholar] [CrossRef]
- Yao, Y.; Hu, M.; Xu, C. Positioning Accuracy Analysis of GPS/BDS/GLONASS Network RTK Based on DREAMNET. Acta Geod. Et Cartogr. Sin. 2016, 45, 1009–1018. [Google Scholar] [CrossRef]
- Xu, L.; Liu, H.; Shu, B.; Zheng, F.; Zhang, M.; Qian, C.; Duan, Y. GLONASS real-time wide-lane ambiguity resolution with an enhanced geometry-based model for medium-range baselines. Adv. Space Res. 2018, 62, 2467–2479. [Google Scholar] [CrossRef]
- Odijk, D. Stochastic modelling of the ionosphere for fast GPS ambiguity resolution. In Geodesy Beyond 2000. International Association of Geodesy Symposia; Springer: Berlin/Heidelberg, Germany, 2000; pp. 387–392. [Google Scholar] [CrossRef]
- Li, J.; Yang, Y.; Xu, J.; He, H.; Guo, H. GNSS multi-carrier fast partial ambiguity resolution strategy tested with real BDS/GPS dual- and triple-frequency observations. GPS Solut. 2015, 19, 5–13. [Google Scholar] [CrossRef]
- Yan, Z.; Ding, L.; Hang, E.; Yu, X. A New Method of Ambiguity Resolution in Network RTK between Reference Stations. Geomat. Inf. Sci. Wuhan Univ. 2013, 38, 295–298. [Google Scholar]
- Zhang, J. Algorithm of Generating VRS Data for Compass Navigation System; Chinese Academy of Surveying and Mapping: Beijing, China, 2014. [Google Scholar]
- Zhang, S. The GPS/GLONASS Integrated CORS Network Atmosphere Modeling and RTK Algorithm Implementation; Wuhan University: Wuhan, China, 2010. [Google Scholar]
- Dai, L.; Han, S.; Wang, J.; Rizos, C. Comparison of interpolation algorithms in network-based GPS techniques. Navigation 2003, 50, 277–293. [Google Scholar] [CrossRef]
- Lagler, K.; Schindelegger, M.; Bohm, J.; Krasna, H.; Nilsson, T. GPT2: Empirical slant delay model for radio space geodetic techniques. Geophys. Res. Lett. 2013, 40, 1069–1073. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- RTCM. Differential GNSS (Global Navigation Satellite Systems) Services-Version 3. Available online: https://rtcm.myshopify.com/collections/differential-global-navigation-satellite-dgnss-standards (accessed on 28 April 2020).
- Shu, B. Research on the Key Technologies of GNSSRT-PPP & RTK and Their Integrated Service Method; Wuhan University: Wuhan, China, 2019. [Google Scholar]
- Böhm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global Mapping Function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef] [Green Version]
- Brack, A. Reliable GPS+BDS RTK positioning with partial ambiguity resolution. GPS Solut. 2016, 21, 1083–1092. [Google Scholar] [CrossRef]



| Signals | Frequency (MHz) | Wavelength (cm) | System |
|---|---|---|---|
| B1I | 1561.098 | 19.20 | BDS-2/3 |
| B1C | 1575.420 | 19.03 | BDS-3 |
| B2a | 1176.450 | 25.48 | BDS-3 |
| B2b | 1207.140 | 24.83 | BDS-3 |
| B3I | 1268.520 | 23.63 | BDS-2/3 |
| Schemes | Items | Description |
|---|---|---|
| Observations | Double-difference non-combined model | |
| Sampling interval | 1 s | |
| Elevation mask | 10° | |
| Weighting | Priori precision 0.003 m for phase and 0.3 m for code; Elevation-dependent weight: P/sin(el) | |
| Relativistic effect | IERS Conventions 2010 | |
| Satellite phase center | PCO and PCV for GPS and only PCO corrected for BDS using igs14.atx | |
| Receiver phase center | PCO and PCV corrected for GPS and BDS using igs14.atx | |
| Network RTK | Tropospheric dry delay | Saastamoinen model and GMF mapping function [31] |
| Tropospheric wet delay | Random-walk process: zenith wet delay + GMF mapping functionVariance constraint: initial noise (0.0/m) + process noise (0.001*BL 1 m) | |
| Ionospheric delay | Random-walk process: double-difference ionospheric delay on oblique pathVariance constraint: initial noise (0.0 m) + process noise (0.04*0.1*BL/sin(el) m) | |
| Ambiguities | WL/NL joint estimation + partial ambiguity fixing strategy [32] + LAMBDA | |
| Estimator | Kalman filtering | |
| Observations | Double-difference non-combined model | |
| Sampling interval | 1 s | |
| Elevation mask | 10° | |
| Weighting | Priori precision 0.003 m for phase and 0.3 m for code; Elevation-dependent weight: P/sin(el) | |
| Relativistic effect | IERS Conventions 2010 | |
| Terminal RTK | Satellite phase center | PCO and PCV for GPS and only PCO corrected for BDS using igs14.atx |
| Receiver phase center | PCO and PCV corrected for GPS and BDS using igs14.atx | |
| Tropospheric dry delay | Saastamoinen model and GMF mapping function | |
| Coordinate (x/y/z) | Dynamic estimation + white noise | |
| Ambiguities | Original frequency ambiguity + partial ambiguity fixing strategy + LAMBDA | |
| Estimator | Kalman filtering |
| B1C+B2a | B1I+B3I | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PRN | ION | TRP | P-B1C | P-B2a | L-B1C | L-B2a | ION | TRP | P-B1I | P-B3I | L-B1I | L-B3I |
| B24 | 0.012 | 0.016 | 0.526 | 0.541 | 0.006 | 0.003 | 0.019 | 0.015 | 0.703 | 0.643 | 0.004 | 0.002 |
| B25 | 0.011 | 0.034 | 0.551 | 0.394 | 0.006 | 0.003 | 0.016 | 0.037 | 0.711 | 0.492 | 0.005 | 0.003 |
| B26 | 0.024 | 0.039 | 0.831 | 0.708 | 0.006 | 0.003 | 0.019 | 0.051 | 0.994 | 0.833 | 0.006 | 0.003 |
| B33 | 0.013 | 0.074 | 0.606 | 0.389 | 0.004 | 0.002 | 0.015 | 0.073 | 0.738 | 0.559 | 0.004 | 0.002 |
| B34 | 0.017 | 0.024 | 0.796 | 0.692 | 0.004 | 0.002 | 0.019 | 0.04 | 1.118 | 0.844 | 0.005 | 0.003 |
| B35 | 0.012 | 0.023 | 0.669 | 0.894 | 0.006 | 0.003 | 0.018 | 0.029 | 0.762 | 0.927 | 0.006 | 0.003 |
| B39 | 0.01 | 0.01 | 0.752 | 0.568 | 0.003 | 0.001 | 0.012 | 0.015 | 0.86 | 0.521 | 0.003 | 0.002 |
| B41 | 0.029 | 0.016 | 0.787 | 0.355 | 0.008 | 0.004 | 0.033 | 0.024 | 0.677 | 0.617 | 0.007 | 0.004 |
| B42 | 0.017 | 0.078 | 0.958 | 0.671 | 0.007 | 0.003 | 0.021 | 0.068 | 1.355 | 0.761 | 0.006 | 0.004 |
| B44 | 0.011 | 0.009 | 0.566 | 0.649 | 0.003 | 0.002 | 0.017 | 0.014 | 0.79 | 0.797 | 0.003 | 0.002 |
| AVG | 0.016 | 0.032 | 0.704 | 0.586 | 0.0053 | 0.0026 | 0.019 | 0.037 | 0.871 | 0.699 | 0.0049 | 0.0028 |
| Baseline | B1C+B2a | B1I+B3I |
|---|---|---|
| WH04-HG02 | 99.9% | 99.7% |
| WH04-HG05 | 99.9% | 99.2% |
| WH04-WH02 | 99.6% | 96.3% |
| WH04-XN01 | 98.4% | 97.3% |
| HG02-HG05 | 99.9% | 98.6% |
| HG02-XN01 | 97.9% | 98.2% |
| WH02-XN01 | 99.3% | 98.9% |
| B1C+B2a (ION) | B1C+B2a (TRP) | B1I+B3I (ION) | B1I+B3I (TRP) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PRN | CZ | JX | DIFF | CZ | JX | DIFF | CZ | JX | DIFF | CZ | JX | DIFF |
| B24 | 0.006 | 0.008 | 0.005 | 0.005 | 0.011 | 0.007 | 0.01 | 0.02 | 0.01 | 0.006 | 0.017 | 0.012 |
| B25 | 0.006 | 0.01 | 0.006 | 0.011 | 0.011 | 0.009 | 0.007 | 0.013 | 0.008 | 0.014 | 0.025 | 0.012 |
| B26 | 0.008 | 0.012 | 0.006 | 0.016 | 0.022 | 0.01 | 0.006 | 0.013 | 0.01 | 0.022 | 0.034 | 0.015 |
| B33 | 0.007 | 0.01 | 0.005 | 0.029 | 0.022 | 0.011 | 0.009 | 0.016 | 0.009 | 0.028 | 0.02 | 0.017 |
| B34 | 0.009 | 0.01 | 0.007 | 0.01 | 0.009 | 0.006 | 0.012 | 0.014 | 0.006 | 0.017 | 0.022 | 0.011 |
| B35 | 0.006 | 0.014 | 0.01 | 0.028 | 0.027 | 0.012 | 0.008 | 0.015 | 0.012 | 0.014 | 0.019 | 0.016 |
| B39 | 0.004 | 0.006 | 0.003 | 0.004 | 0.007 | 0.004 | 0.005 | 0.01 | 0.006 | 0.005 | 0.012 | 0.008 |
| B41 | 0.01 | 0.018 | 0.011 | 0.015 | 0.016 | 0.013 | 0.013 | 0.022 | 0.015 | 0.017 | 0.024 | 0.013 |
| B42 | 0.008 | 0.013 | 0.008 | 0.037 | 0.035 | 0.01 | 0.012 | 0.021 | 0.011 | 0.033 | 0.032 | 0.014 |
| B44 | 0.005 | 0.011 | 0.008 | 0.005 | 0.015 | 0.013 | 0.007 | 0.015 | 0.01 | 0.006 | 0.018 | 0.014 |
| AVG | 0.007 | 0.011 | 0.007 | 0.016 | 0.018 | 0.010 | 0.009 | 0.016 | 0.010 | 0.016 | 0.022 | 0.013 |
| Schemes | Fix Rate | E (m) | N (m) | U (m) |
|---|---|---|---|---|
| GPS | 98.6% | 0.0054 | 0.0062 | 0.0173 |
| BDS-2 | 97.5% | 0.0063 | 0.0072 | 0.0202 |
| BDS-3 [1I+3I] | 99.4% | 0.0055 | 0.0057 | 0.0170 |
| BDS-3 [1C+2a] | 99.8% | 0.0049 | 0.0047 | 0.0162 |
| BDS-2/3 | 100% | 0.0047 | 0.0040 | 0.0139 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; Liu, H.; Yang, Z.; Shu, B.; Xu, X.; Nie, G. Evaluation of Network RTK Positioning Performance Based on BDS-3 New Signal System. Remote Sens. 2022, 14, 2. https://doi.org/10.3390/rs14010002
Wang P, Liu H, Yang Z, Shu B, Xu X, Nie G. Evaluation of Network RTK Positioning Performance Based on BDS-3 New Signal System. Remote Sensing. 2022; 14(1):2. https://doi.org/10.3390/rs14010002
Chicago/Turabian StyleWang, Pengxu, Hui Liu, Zhixin Yang, Bao Shu, Xintong Xu, and Guigen Nie. 2022. "Evaluation of Network RTK Positioning Performance Based on BDS-3 New Signal System" Remote Sensing 14, no. 1: 2. https://doi.org/10.3390/rs14010002
APA StyleWang, P., Liu, H., Yang, Z., Shu, B., Xu, X., & Nie, G. (2022). Evaluation of Network RTK Positioning Performance Based on BDS-3 New Signal System. Remote Sensing, 14(1), 2. https://doi.org/10.3390/rs14010002






