Coupling Relationship Analysis of Gold Content Using Gaofen-5 (GF-5) Satellite Hyperspectral Remote Sensing Data: A Potential Method in Chahuazhai Gold Mining Area, Qiubei County, SW China
Abstract
:1. Introduction
2. Materials and Methods
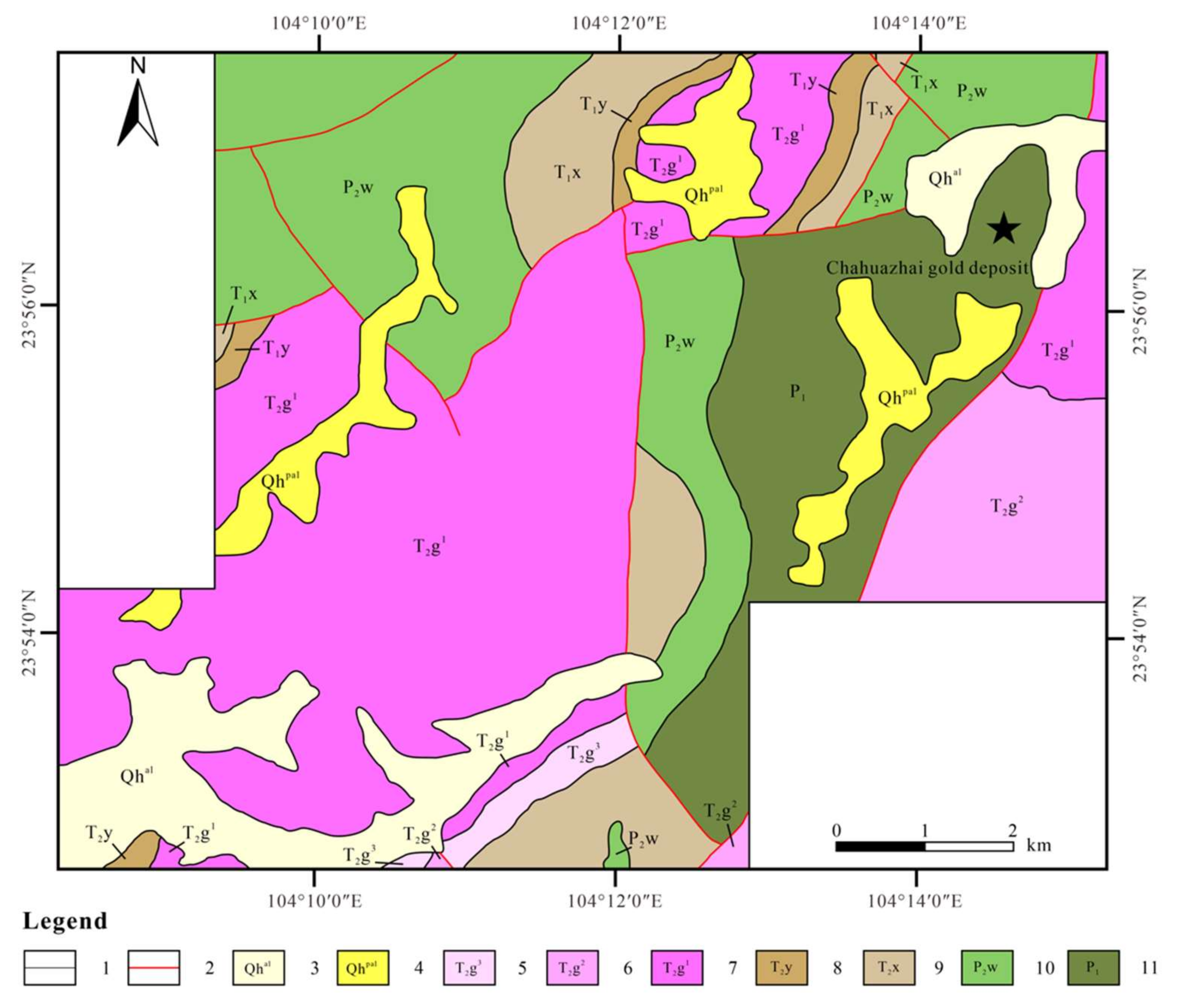
2.1. Study Area
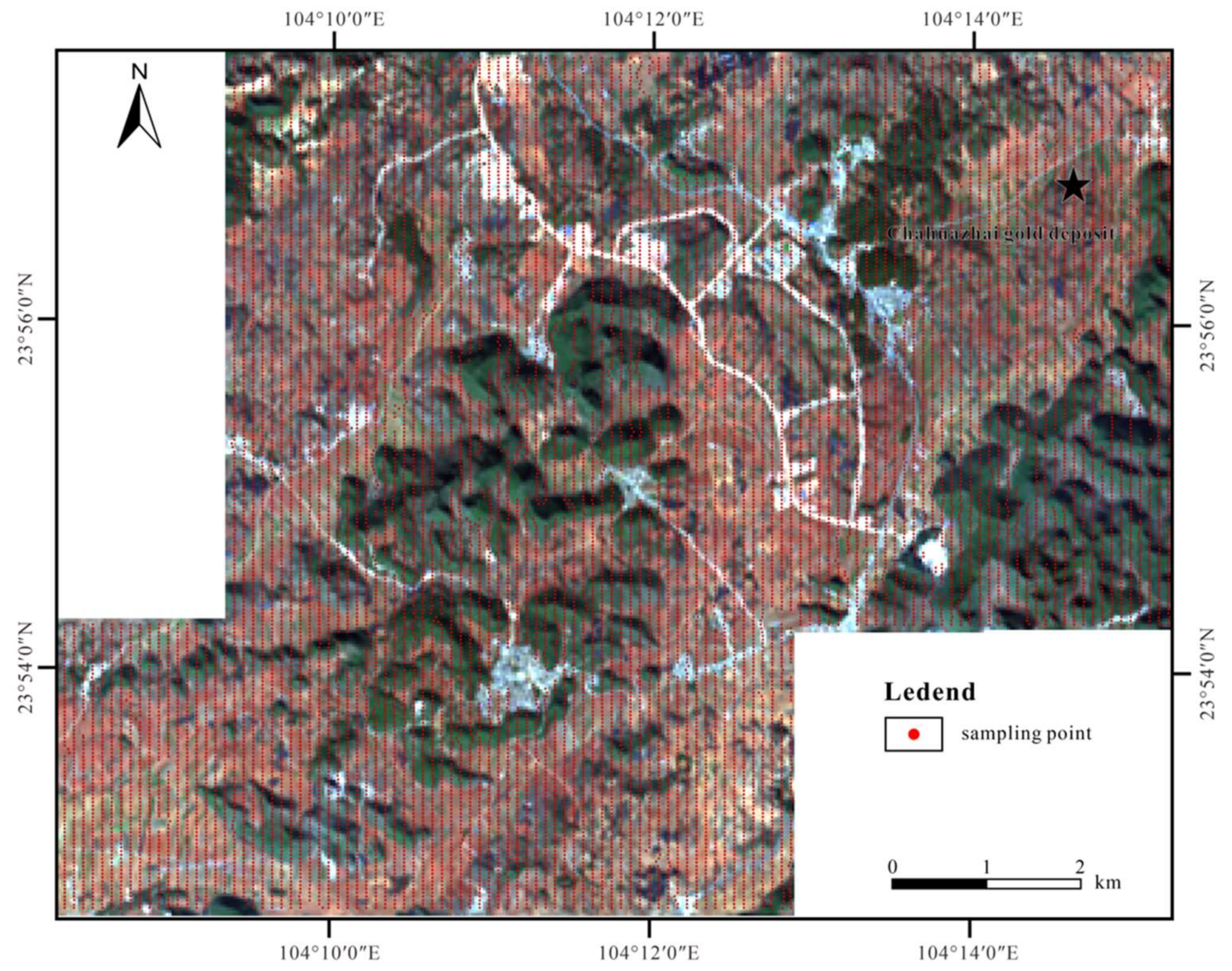
2.2. Data
2.2.1. Hyperion Data
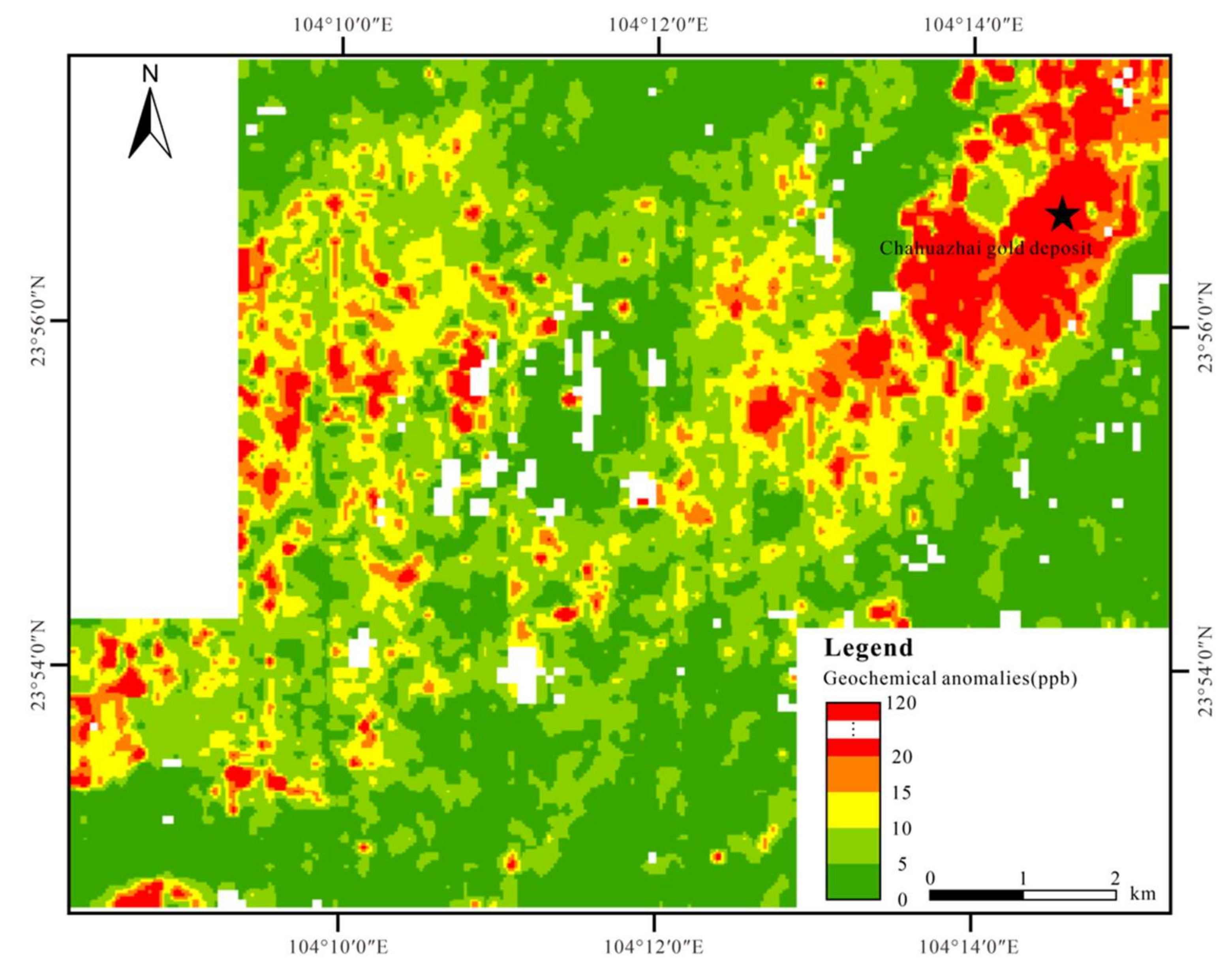
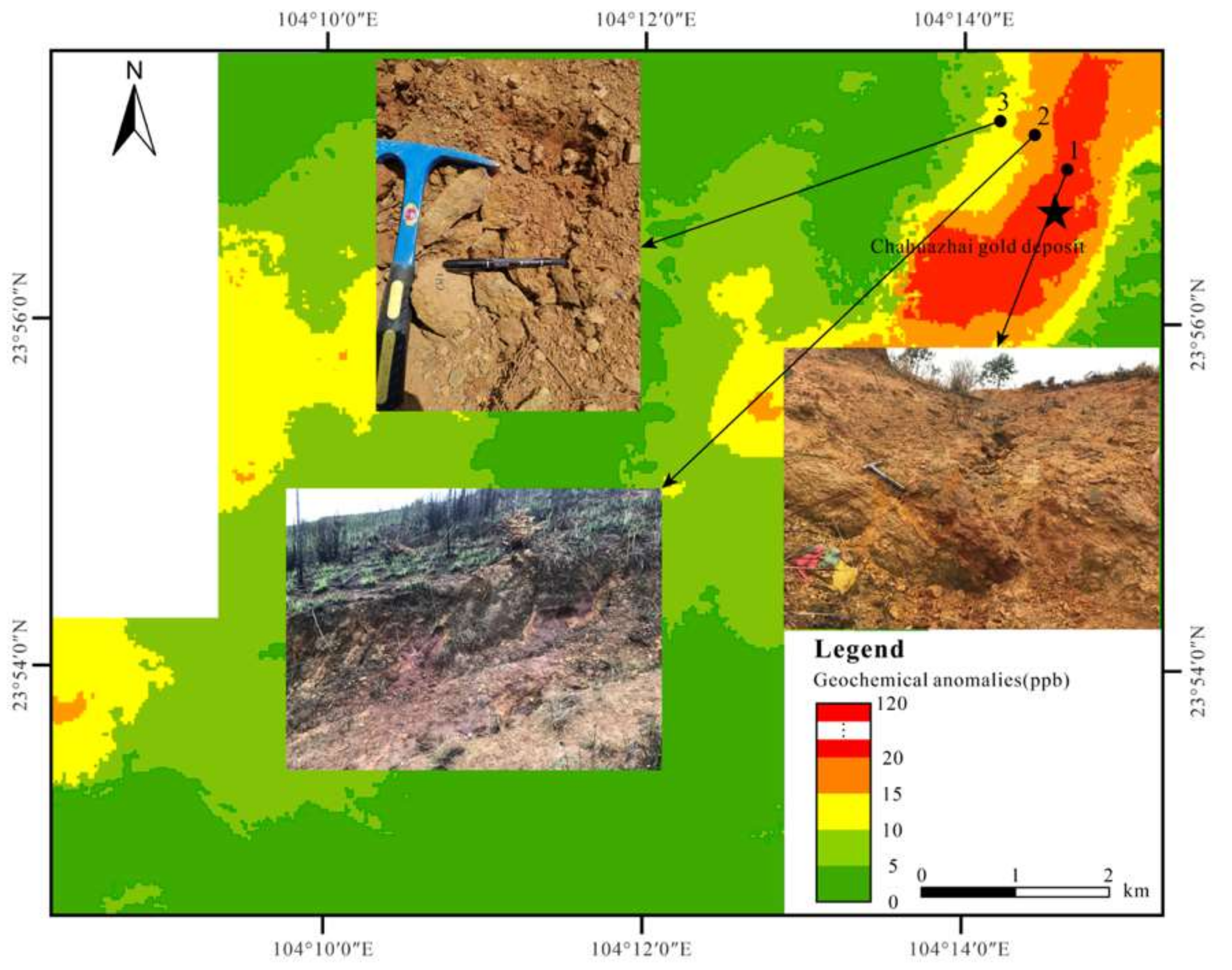
2.2.2. Geochemical Data
2.3. Data Processing
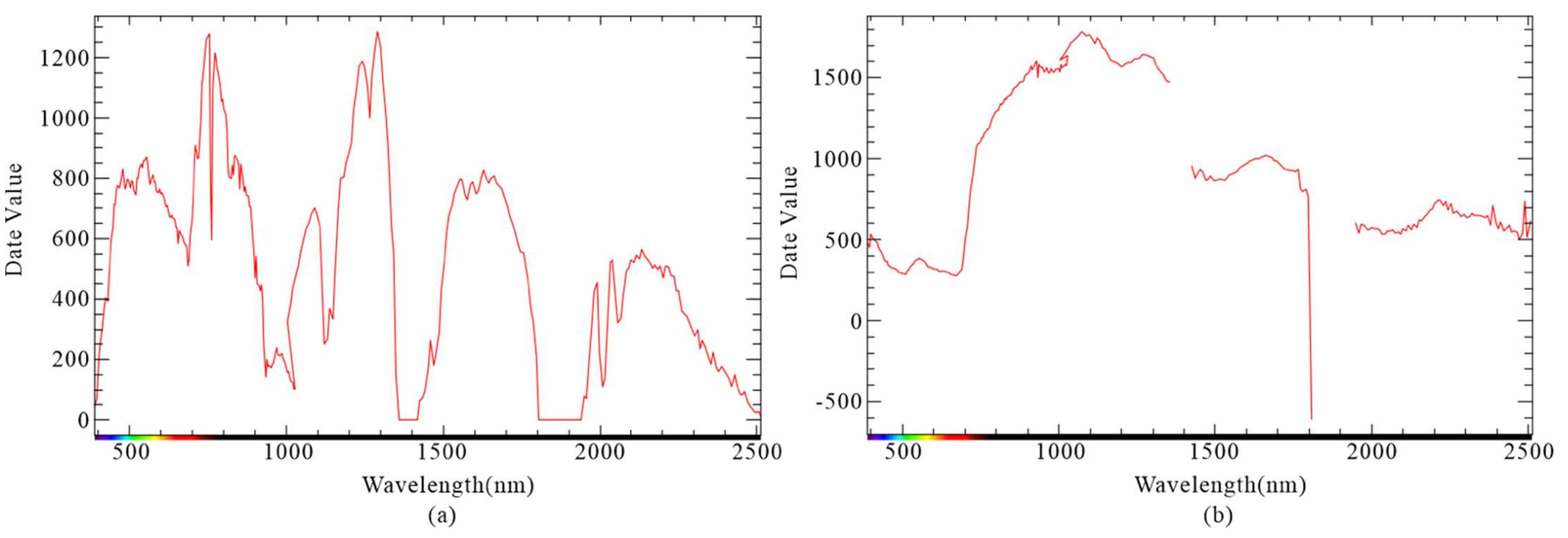
Data Preprocessing
Savitzky–Golay Filter
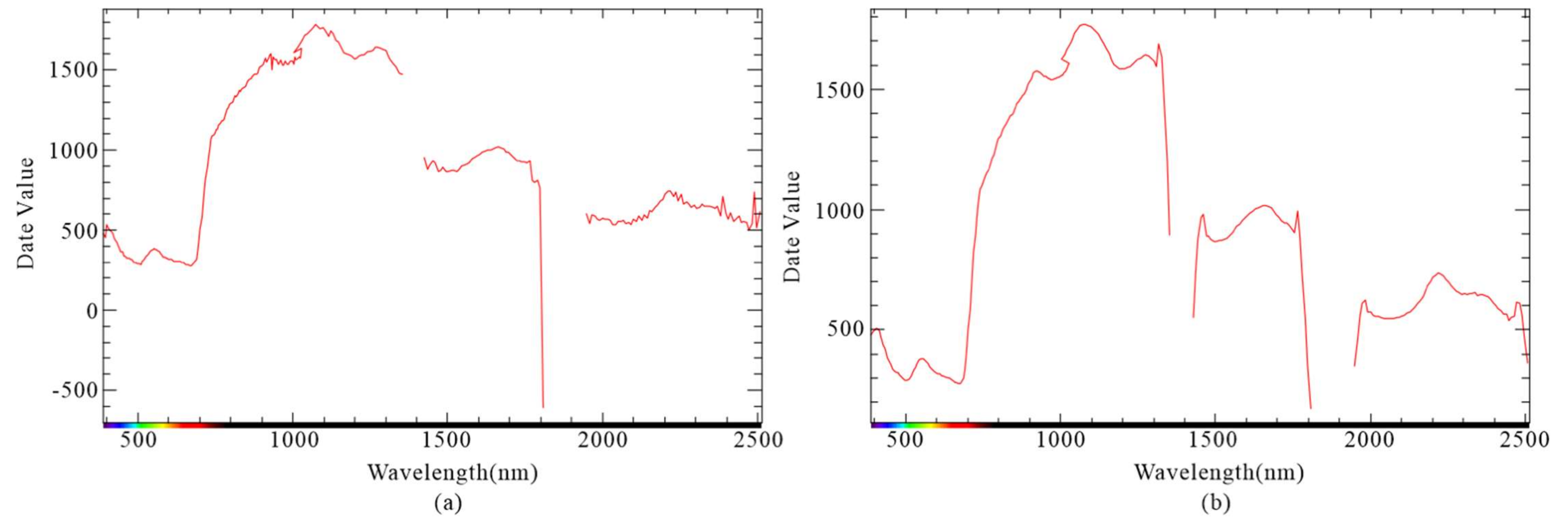
Reciprocal Logarithm
Continuum Removal
First Derivative
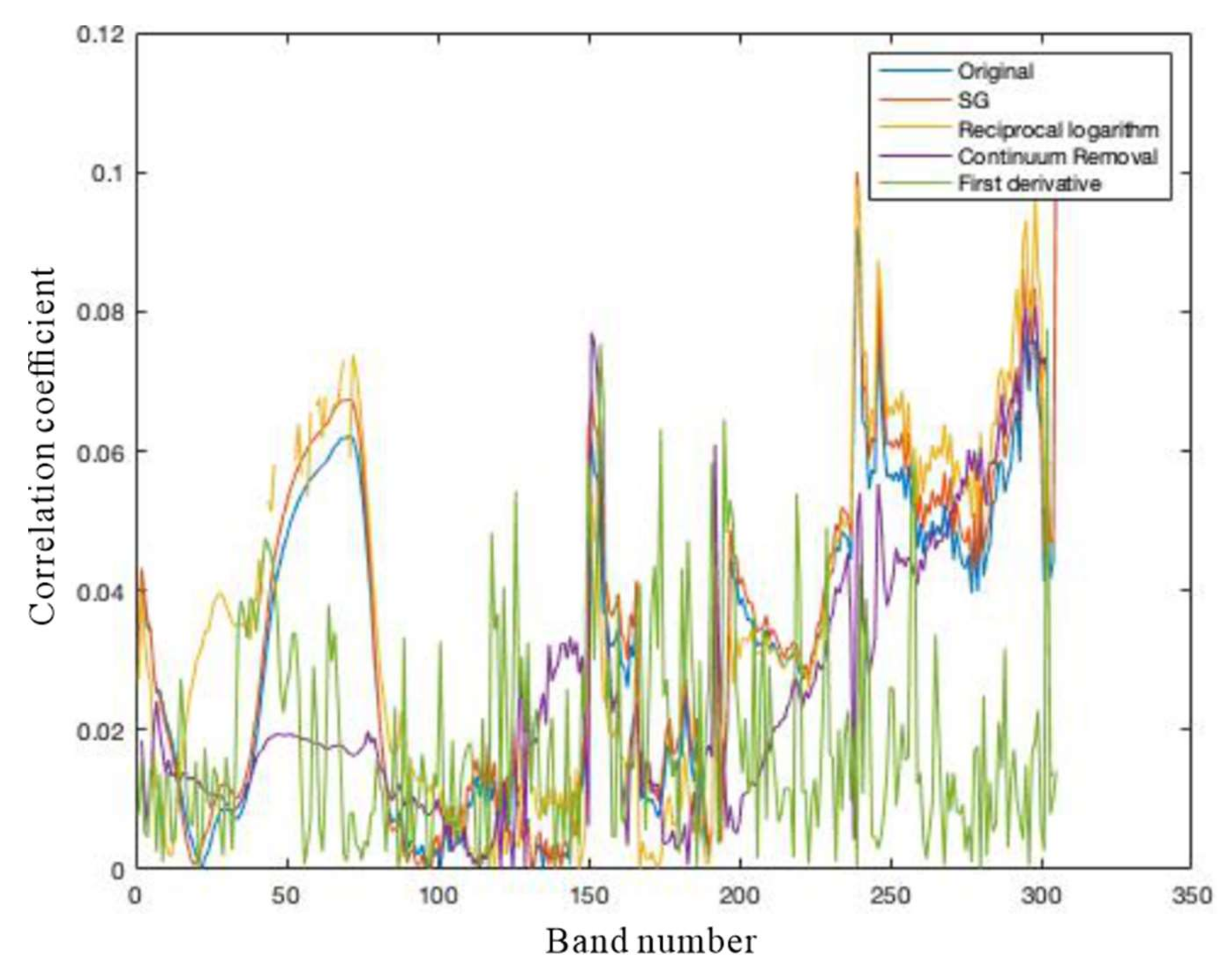
2.4. Characteristic Spectra Selection
2.5. Endmember Choosing
2.5.1. Matched Filtering
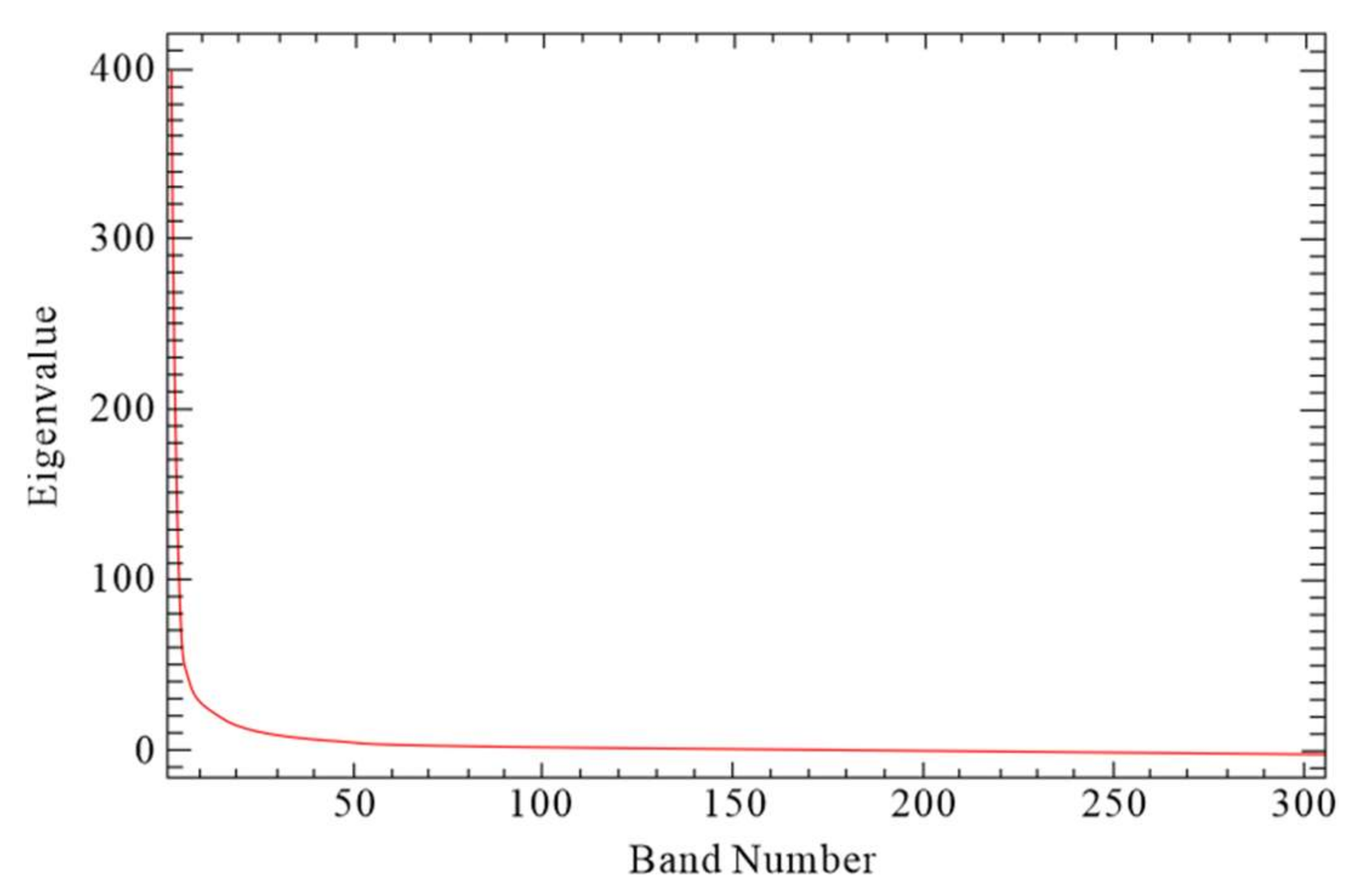
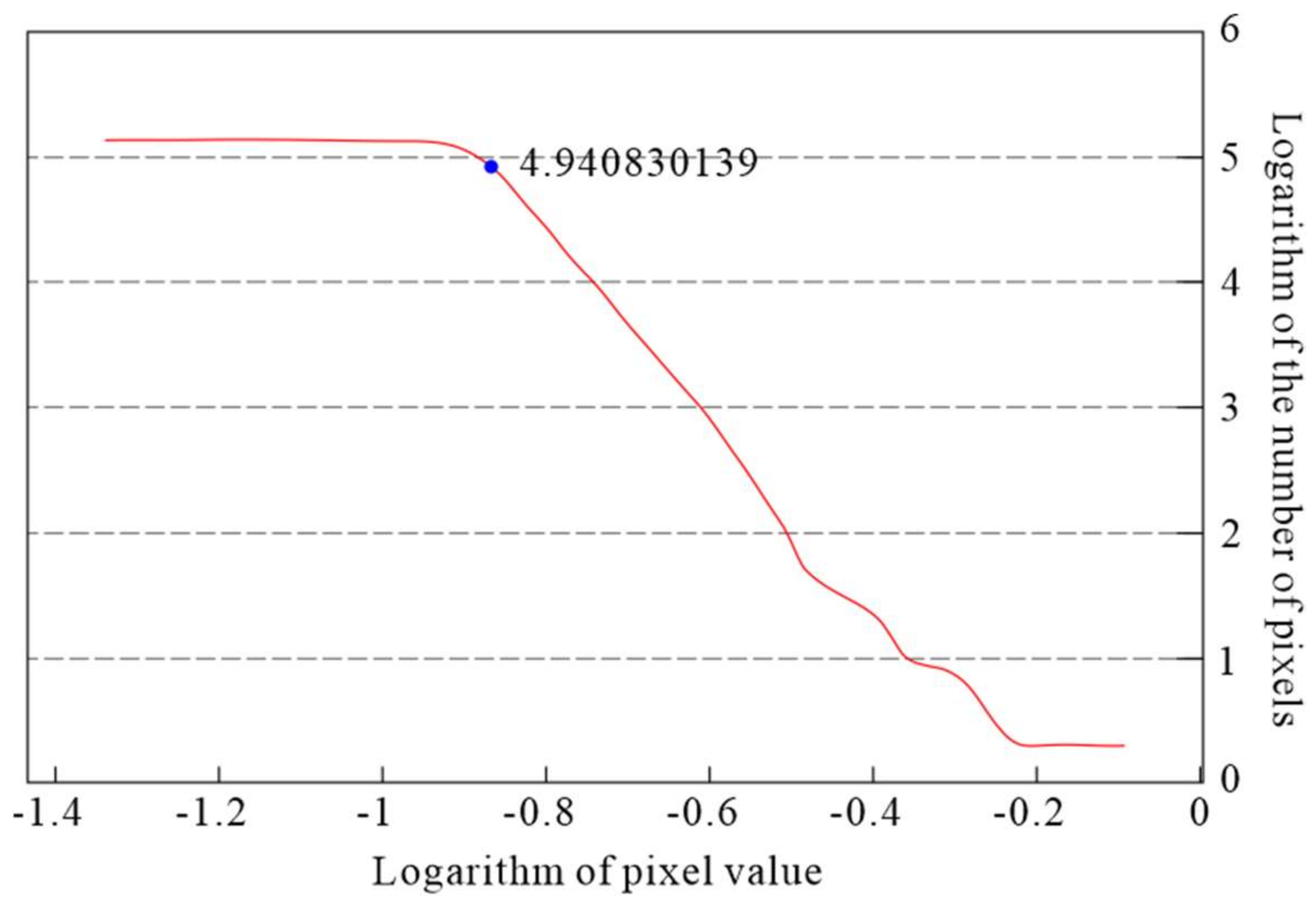
2.5.2. Fast Fourier Transform (FFT) with Spectrum-Area (S-A) Method
2.6. Regression Models
2.6.1. Multiple Linear Regression (MLR)
2.6.2. Partial Least Squares (PLS) Regression
2.6.3. Back Propagation (BP) Neural Network
2.6.4. Geographically Weighted Regression (GWR)
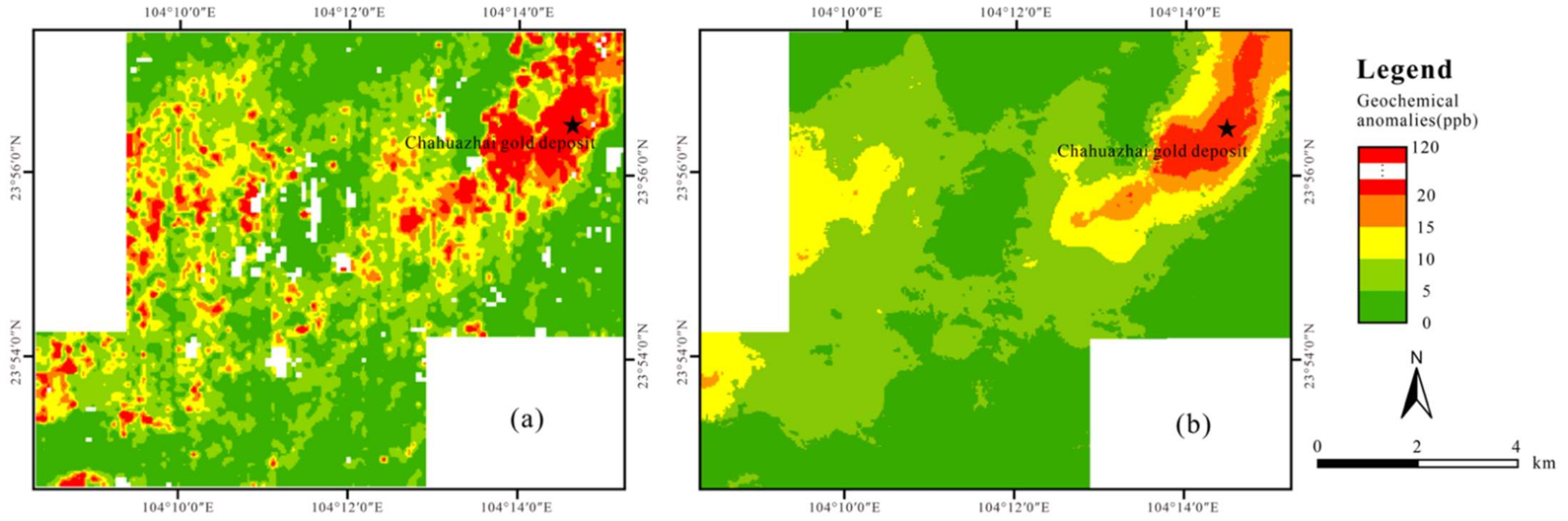
3. Results
4. Discussions
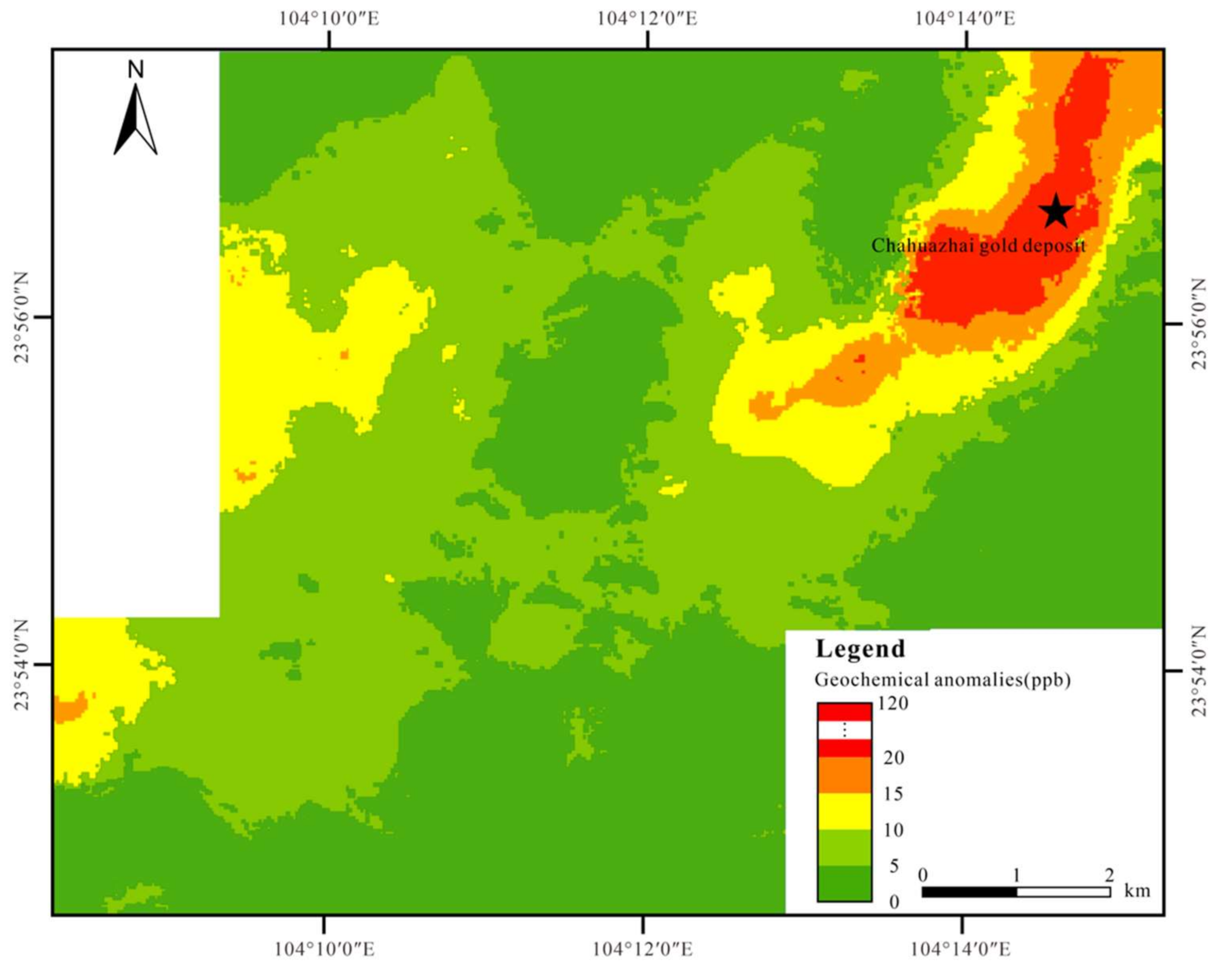
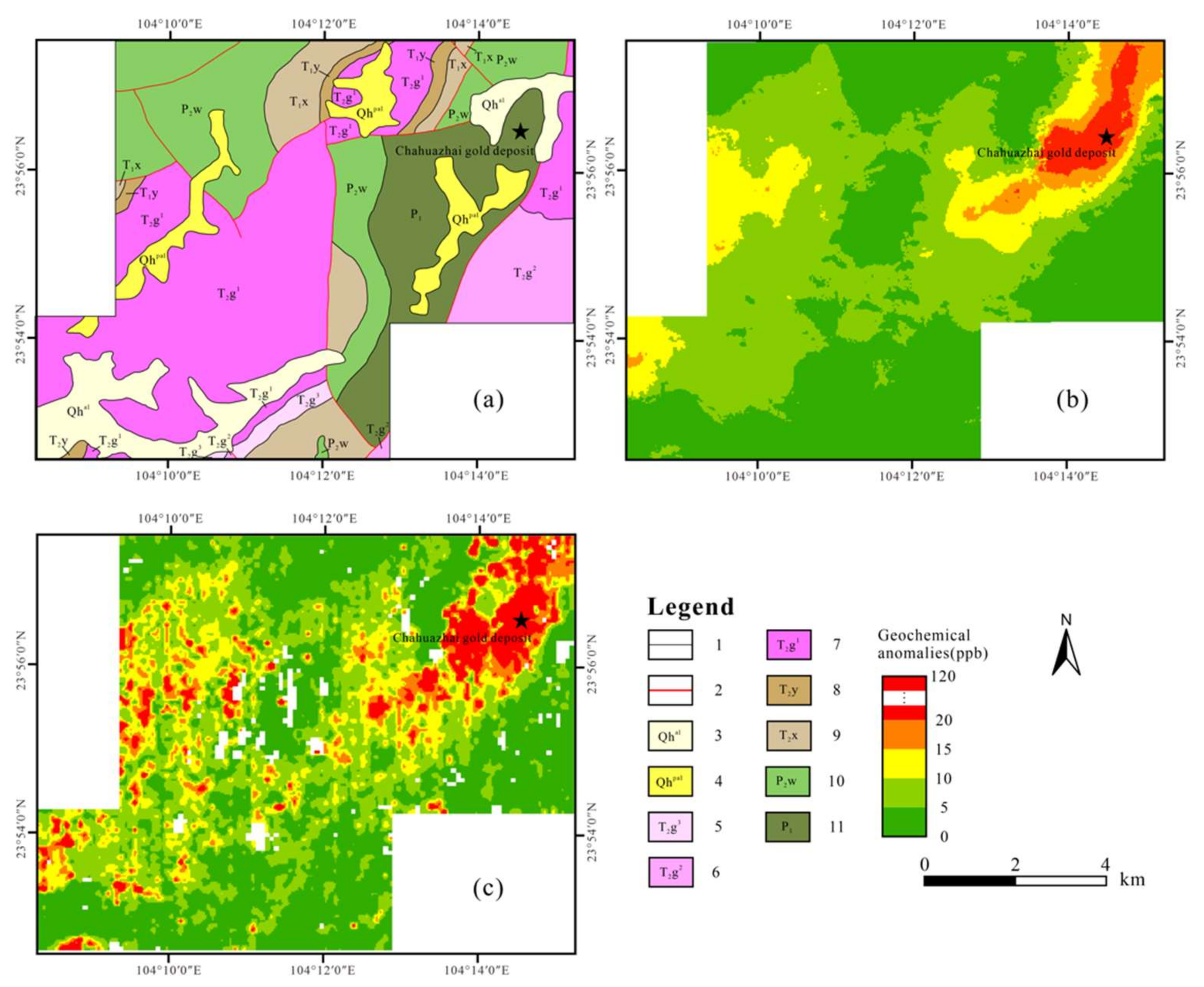
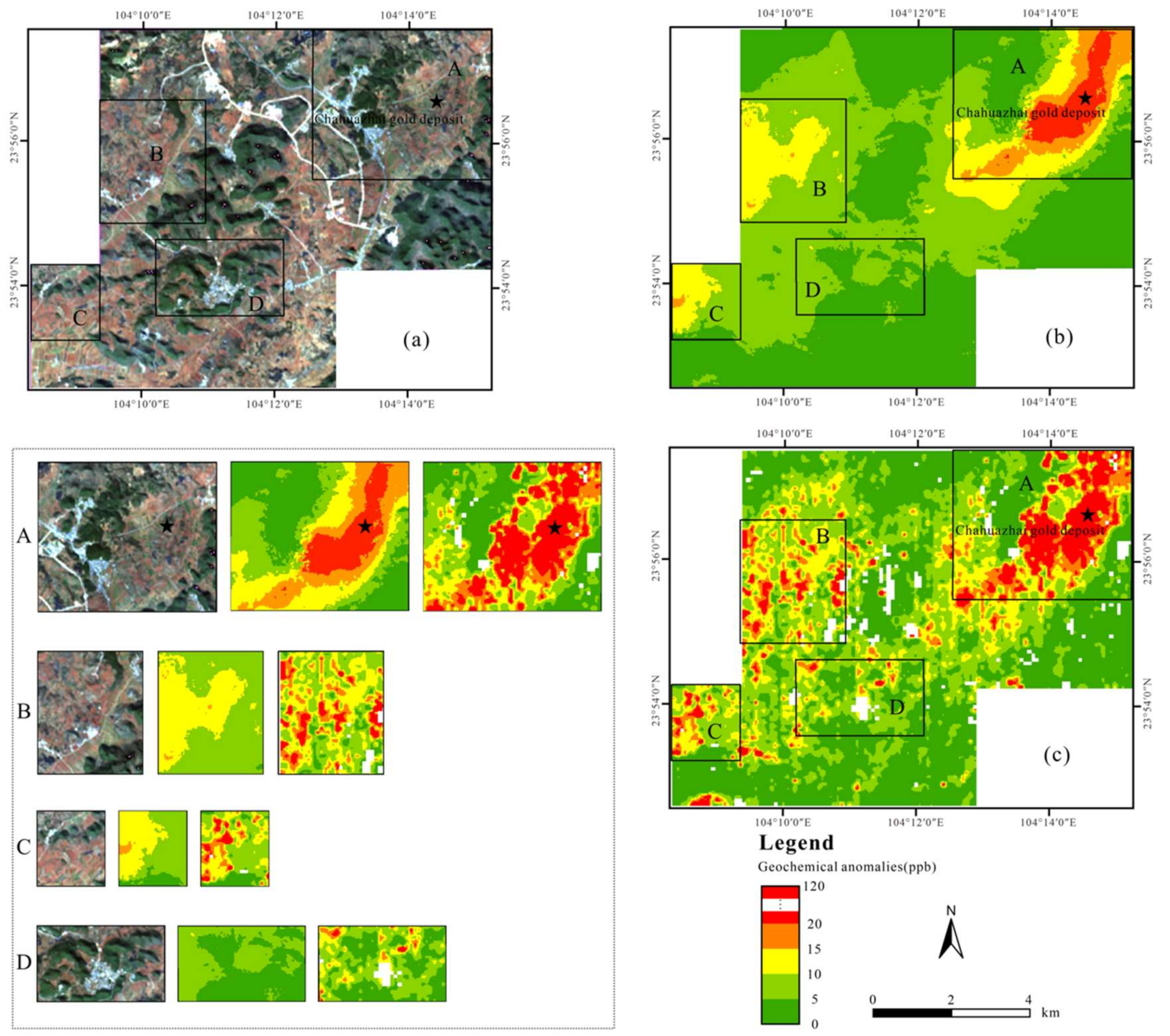
4.1. Prediction Results Spatial Distribution
4.2. Influence Factors of Prediction
4.2.1. Lithology and Tectonic
4.2.2. Vegetation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, S.; Hu, G.; Zhou, Z. Geo-anomaly structure and mineral prediction in the Mianxian–Lueyang–Ningqiang area. Earth Sci. J. China Univ. Geosci. 1999, 24, 472–475. [Google Scholar]
- Yuan, Y.; Li, S.; Peng, J.; Si, J.; Cheng, H.; Sun, J.; Wei, J.; Shao, J. An integrated ore prospecting model for the Nyasirori gold deposit in Tanzania. Geol. China 2019, 2, 407–421. [Google Scholar] [CrossRef]
- Liu, H.; Beaudoin, G. Geochemical signatures in native gold derived from Au-bearing ore deposits. Ore Geol. Rev. 2021. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, S.; Zuo, R. Identifying geochemical anomalies associated with Au–Cu mineralization using multifractal and artificial neural network models in the Ningqiang district, Shaanxi, China. Geochem. Explor. 2016, 164, 54–64. [Google Scholar] [CrossRef]
- Sun, X.; Zheng, Y.; Wang, C.; Zhao, Z.; Gneg, X. Identifying geochemical anomalies associated with Sb–Au–Pb–Zn–Ag mineralization in North Himalaya, southern Tibet. Ore Geol. Rev. 2016, 73, 1–12. [Google Scholar] [CrossRef]
- Simon, G.; Kesler, S.; Chryssoulis, S. Geochemistry and textures of gold-bearing arsenian pyrite, Twin Creeks, Nevada: Implications for deposition of gold in Carlin-type deposits. Econ. Geol. 1999, 94, 405–421. [Google Scholar] [CrossRef]
- Li, Z. Comparative Geology and Geochemistry of Sedimentary Rock-Hosted (Carlin-Type) Gold Deposits in the People’s Republic of China and in Nevada, United States of America; Order No. 1395247; University of Nevada: Reno, NV, USA, 1999. [Google Scholar]
- Hu, Z.; Su, C.; Bi, W.; Tu, Z.; Hofstra, H. Geology and geochemistry of Carlin-type gold deposits in China. Miner. Deposita. 2002, 37, 378–392. [Google Scholar] [CrossRef]
- Zhang, C.; Spiro, B.; Halls, C.; Stanley, J.; Yang, Y. Sediment-hosted disseminated gold deposits in Southwest Guizhou, PRC: Their geological setting and origin in relation to mineralogical, fluid inclusion, and stable-isotope characteristics. Int. Geol. Rev. 2003, 45, 407–470. [Google Scholar] [CrossRef]
- Peters, G.; Huang, J.; Li, Z.; Jing, C. Sedimentary rock-hosted Au deposits of the Dian-Qian-Gui area, Guizhou, and Yunnan Provinces, and Guangxi District, China. Ore Geol. Rev. 2007, 31, 170–204. [Google Scholar] [CrossRef]
- Su, C.; Heinrich, A.; Pettke, T.; Zhang, C.; Hu, Z.; Xia, B. Sediment-hosted gold deposits in Guizhou, China: Products of wall-rock sulfidation by deep crustal fluids. Econ. Geol. 2009, 104, 73–93. [Google Scholar] [CrossRef] [Green Version]
- Hofstra, A.H.; Leventhal, J.S.; Northrop, R.; Landis, G.P.; Rye, R.O.; Birak, D.J.; Dahl, A.R. Genesis of sediment-hosted disseminated-gold deposits by fluid mixing and sulfidization: Chemical-reaction-path modeling of ore-depositional processes documented in the Jerritt Canyon district, Nevada. Geology 1991, 19, 36–40. [Google Scholar] [CrossRef]
- Su, W.; Dong, W.; Zhang, X.; Shen, N.; Hu, R.; Hofstra, A.; Cheng, L.; Xia, Y.; Yang, K. Carlin-Type gold deposits in the Dian-Qian-Gui “Golden Triangle” of Southwest China. Diversity in Carlin-Style Gold Deposits. Rev. Econ. Geol. 2018, 20, 157–185. [Google Scholar]
- Su, W.C.; Hu, R.Z.; Xia, B.; Xia, Y.; Liu, Y.P. Calcite Sm-Nd isochron age of the Shuiyindong Carlin-type gold deposit, Guizhou, China. Chem. Geol. 2009, 258, 269–274. [Google Scholar] [CrossRef]
- Cline, J.S.; Muntean, J.L.; Gu, X.X.; Xia, Y. A comparison of Carlin-type gold deposits: Guizhou Province, Golden Triangle, Southwest China, and Northern Nevada, USA. Earth Sci. Front. 2013, 20, 1–18. [Google Scholar]
- Reich, M.; Kesler, S.E.; Utsunomiya, S.; Palenik, C.S.; Chryssoulis, S.L.; Ewing, R.C. Solubility of gold in arsenian pyrite. Geochim. Et Cosmochim. Acta 2005, 69, 2781–2796. [Google Scholar] [CrossRef]
- Gopon, P.; Douglas, J.O.; Auger, M.A.; Hansen, L.; Wade, J.; Cline, J.S.; Robb, L.J.; Moody, M.P. A Nanoscale Investigation of Carlin-Type Gold Deposits: An Atom-Scale Elemental and Isotopic Perspective. Econ. Geol. 2019, 114, 1123–1133. [Google Scholar] [CrossRef] [Green Version]
- Zuo, R.; Wang, J.; Xiong, Y.; Wang, Z. The processing methods of geochemical exploration data: Past, present, and future. Appl. Geochem. 2021, 132, 105072. [Google Scholar] [CrossRef]
- Cheng, Q.; Agterberg, F.P.; Bonham-Carter, G.F. A spatial analysis method for geochemical anomaly separation. Geochem Explor. 1996, 56, 183–195. [Google Scholar] [CrossRef]
- Cheng, Q. Multifractality and spatial statistics. Comput. Geosci. 1999, 25, 949–961. [Google Scholar] [CrossRef]
- Ayoobi, I.; Tangestani, M.H. Evaluation of subpixel unmixing algorithms in mapping the porphyry copper alterations using EO-1 Hyperion data, a case study from SE Iran. Remote Sens. Appl. Soc. Environ. 2018, 10, 120–127. [Google Scholar] [CrossRef]
- van der Meer, F.; Vazquez-Torres, M.; van Dijk, P.M. Spectral characterization of ophiolite lithologies in the troodos ophiolite complex of Cyprus and its potential in prospecting for massive sulphide deposits. Int. J. Rem. Sens. 1997, 18, 1245–1257. [Google Scholar] [CrossRef]
- Wan, Y.; Fan, Y.; Jin, M. Application of hyperspectral remote sensing for supplementary investigation of polymetallic deposits in Huaniushan ore region, northwestern China. Sci. Rep. 2021, 11, 440. [Google Scholar] [CrossRef] [PubMed]
- Ye, B.; Tian, S.; Cheng, Q.; Ge, Y. Application of lithological mapping based on Advanced Hyperspectral Imager (AHSI) imagery onboard Gaofen-5 (GF-5) satellite. Remote Sens. 2020, 12, 3990. [Google Scholar] [CrossRef]
- Liu, L.; Shang, K. Mineral information extraction based on Gaofen-5’s thermal infrared data. ISPRS. 2018, 42, 1157–1160. [Google Scholar] [CrossRef] [Green Version]
- Cracknell, M.J.; Reading, A.M. Geological mapping using remote sensing data: A comparison of five machine learning algorithms, their response to variations in the spatial distribution of training data and the use of explicit spatial information. Comput. Geosci. 2014, 63, 22–33. [Google Scholar] [CrossRef] [Green Version]
- Othman, A.; Gloaguen, R. Improving lithological mapping by SVM classification of spectral and morphological features: The discovery of a new chromite body in the Mawat ophiolite complex (Kurdistan, NE Iraq). Remote Sens. 2014, 6, 6867–6896. [Google Scholar] [CrossRef] [Green Version]
- Othman, A.A.; Gloaguen, R. Integration of spectral, spatial and morphometric data into lithological mapping: A comparison of different Machine Learning Algorithms in the Kurdistan Region, NE Iraq. J. Asian Earth Sci. 2017, 146, 90–102. [Google Scholar] [CrossRef]
- Lary, D.J.; Alavi, A.H.; Gandomi, A.H.; Walker, A.L. Machine learning in geosciences and remote sensing. Geosci. Front. 2016, 7, 3–10. [Google Scholar] [CrossRef] [Green Version]
- Wei, J.; Liu, X.; Liu, J. Integrating textural and spectral features to classify silicate- bearing rocks using Landsat 8 data. Appl. Sci. 2016, 6, 283. [Google Scholar] [CrossRef] [Green Version]
- Pourmohammadi, P.; Strager, M.P.; Dougherty, M.J.; Adjeroh, D.A. Analysis of land development drivers using Geographically Weighted Ridge Regression. Remote. Sens. 2021, 13, 1307. [Google Scholar] [CrossRef]
- Shabrina, Z.; Buyuklieva, B.; Ng, M.K.M. Short-term rental platform in the urban tourism context: A Geographically Weighted Regression (GWR) and a Multiscale GWR (MGWR) approaches. Geogr. Anal. 2021, 53, 686–707. [Google Scholar] [CrossRef]
- Liu, C.; Wu, X.; Wang, L. Analysis on land ecological security change and affect factors using RS and GWR in the Danjiangkou Reservoir area, China. Appl Geogr. 2019, 105, 1–14. [Google Scholar] [CrossRef]
- Kumar, C.; Chatterjee, S.; Oommen, T.; Guha, A. Automated lithological mapping by integrating spectral enhancement techniques and machine learning algorithms using AVIRIS-NG hyperspectral data in Gold-bearing granite-greenstone rocks in Hutti, India. Int. J. Appl. Earth Obs. 2020, 86, 102006. [Google Scholar] [CrossRef]
- Pour, A.B.; Hashim, M.; van Genderen, J. Detection of hydrothermal alteration zones in a tropical region using satellite remote sensing data: Bau goldfield, Sarawak, Malaysia. Ore Geol. Rev. 2013, 54, 181–196. [Google Scholar] [CrossRef]
- Lypaczewski, P.; Rivard, B.; Gaillard, N.; Perrouty, S.; Lauzière, N.P.; Bérubé, C.L.; Linnen, R.L. Using hyperspectral imaging to vector towards mineralization at the Canadian Malartic gold deposit, Québec, Canada. Ore Geol. Rev. 2019, 111, 102945. [Google Scholar] [CrossRef]
- Ye, X.; Ren, H.; Liu, R.; Qin, Q.; Liu, Y.; Dong, J. Land surface temperature estimate from Chinese Gaofen-5 satellite data using split-window algorithm. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5877–5888. [Google Scholar] [CrossRef]
- Ren, H.; Ye, X.; Liu, R.; Dong, J.; Qin, Q. Improving land surface temperature and emissivity retrieval from the Chinese Gaofen-5 satellite using a hybrid algorithm. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1080–1090. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Boardman, J.W.; Kruse, F.A. Automated spectral analysis: A geological example using AVIRIS data, north Grapevine Mountains, Nevada: In Proceedings, ERIM Tenth Thematic Conference on Geologic Remote Sensing; Environmental Research Institute of Michigan: Ann Arbor, MI, USA, 1994. [Google Scholar]
- Green, A.A.; Berman, M.; Switzer, P.; Craig, M.D. A transformation for ordering multispectral data in terms of image quality with implications for noise removal. IEEE Trans. Geosci. Remote Sens. 1988, 26, 65–74. [Google Scholar] [CrossRef] [Green Version]
- Harsanyi, J.C.; Chang, C.I. Hyperspectral image classification and dimensionality reduction: An orthogonal subspace projection approach. IEEE Trans. Geosci. Remote Sens. 1994, 32, 779–785. [Google Scholar] [CrossRef] [Green Version]
- Boardman, J.W. Leveraging the high dimensionality of AVIRIS data for improved sub-pixel target unmixing and rejection of false positives: Mixture tuned matched filtering. In Summaries of the Seventh Annual JPL Airborne Geoscience Workshop; JPL Publication: Pasadena, CA, USA, 1998; Volume 6. [Google Scholar]
- Tobler, W.R. A Computer movie simulating urban growth in the Detroit Region. Econ. Geogr. 1970, 46, 234. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships; John Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]


| Model Type | Neighborhood Type | Neighborhood Selection Type | Local Weighting Scheme |
|---|---|---|---|
| Gaussian | Number of neighbors | Golden search | Gaussian |
| Multiple Linear Regression | Partial Least Squares Regression | Geographically Weighted Regression | |
|---|---|---|---|
| R2 | 0.004 | 0.4099 | 0.6295 |
| Adjusted R2 | 0.004 | 0.4037 | 0.6133 |
| RMSE | 3.005 | 7.903053 | 0.3038 |
| Accuracy | BP Neural Network |
|---|---|
| Training | 0.23424 |
| Validation | 0.20639 |
| Test | 0.21792 |
| Total | 0.22799 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, Y.; Zhang, X.; Zhao, Z.; Li, Z.; Yang, C.; Huang, Q. Coupling Relationship Analysis of Gold Content Using Gaofen-5 (GF-5) Satellite Hyperspectral Remote Sensing Data: A Potential Method in Chahuazhai Gold Mining Area, Qiubei County, SW China. Remote Sens. 2022, 14, 109. https://doi.org/10.3390/rs14010109
Qin Y, Zhang X, Zhao Z, Li Z, Yang C, Huang Q. Coupling Relationship Analysis of Gold Content Using Gaofen-5 (GF-5) Satellite Hyperspectral Remote Sensing Data: A Potential Method in Chahuazhai Gold Mining Area, Qiubei County, SW China. Remote Sensing. 2022; 14(1):109. https://doi.org/10.3390/rs14010109
Chicago/Turabian StyleQin, Yuehan, Xinle Zhang, Zhifang Zhao, Ziyang Li, Changbi Yang, and Qunying Huang. 2022. "Coupling Relationship Analysis of Gold Content Using Gaofen-5 (GF-5) Satellite Hyperspectral Remote Sensing Data: A Potential Method in Chahuazhai Gold Mining Area, Qiubei County, SW China" Remote Sensing 14, no. 1: 109. https://doi.org/10.3390/rs14010109
APA StyleQin, Y., Zhang, X., Zhao, Z., Li, Z., Yang, C., & Huang, Q. (2022). Coupling Relationship Analysis of Gold Content Using Gaofen-5 (GF-5) Satellite Hyperspectral Remote Sensing Data: A Potential Method in Chahuazhai Gold Mining Area, Qiubei County, SW China. Remote Sensing, 14(1), 109. https://doi.org/10.3390/rs14010109






