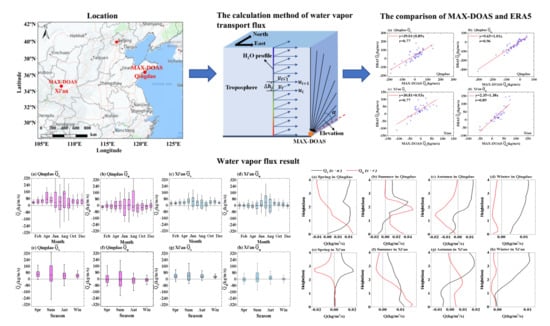
Estimation of the Precipitable Water and Water Vapor Fluxes in the Coastal and Inland Cities of China Using MAX-DOAS
Abstract
1. Introduction
2. Instruments and Methods
2.1. Overview of the Measurement Station
2.2. MAX-DOAS Retrieval
2.3. Precipitable Water
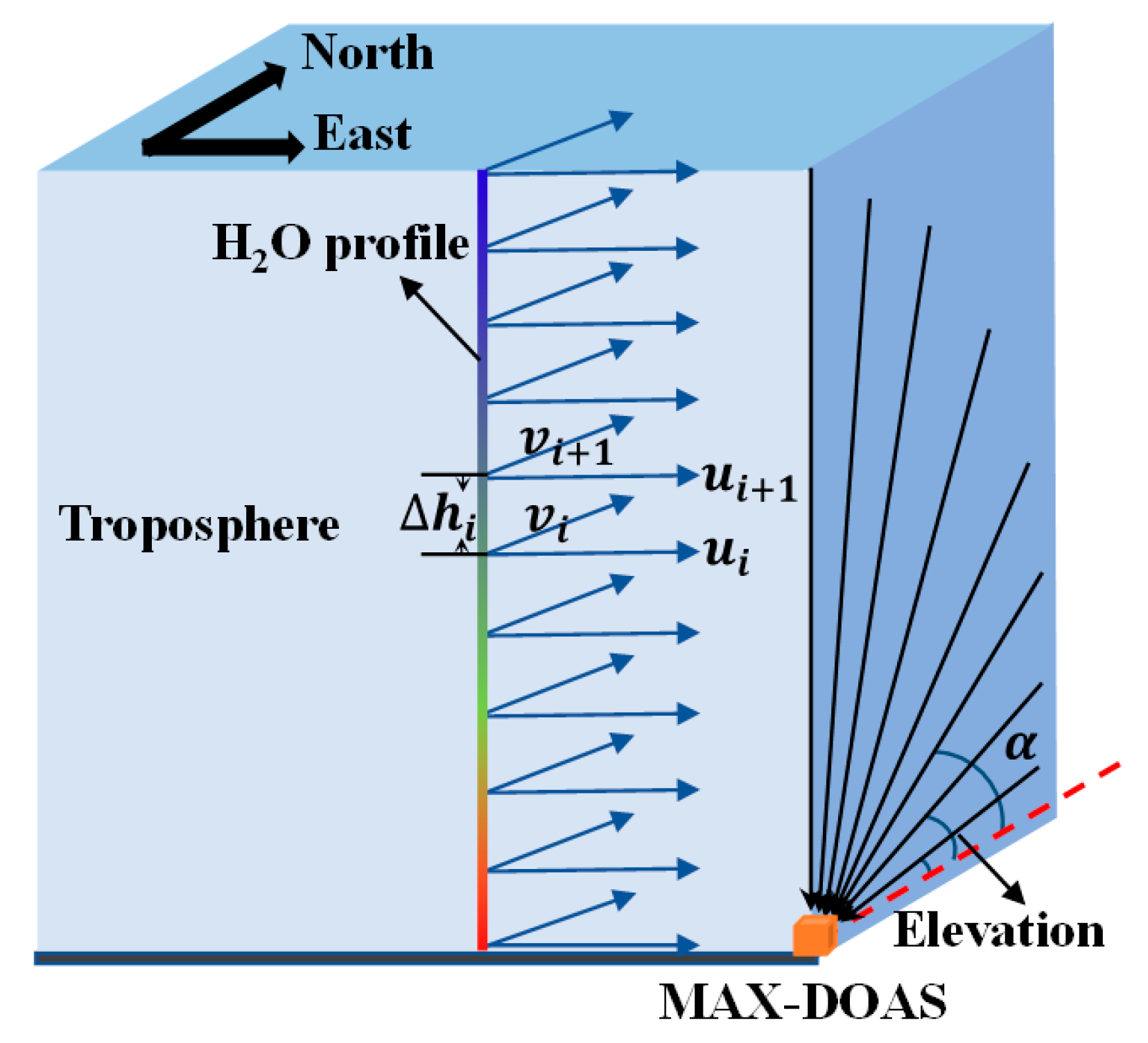
2.4. Water Vapor Flux
2.5. Precipitable Water and Water Vapor Flux Error Sources
2.5.1. Precipitable Water Error Sources
2.5.2. Water Vapor Flux Error Sources
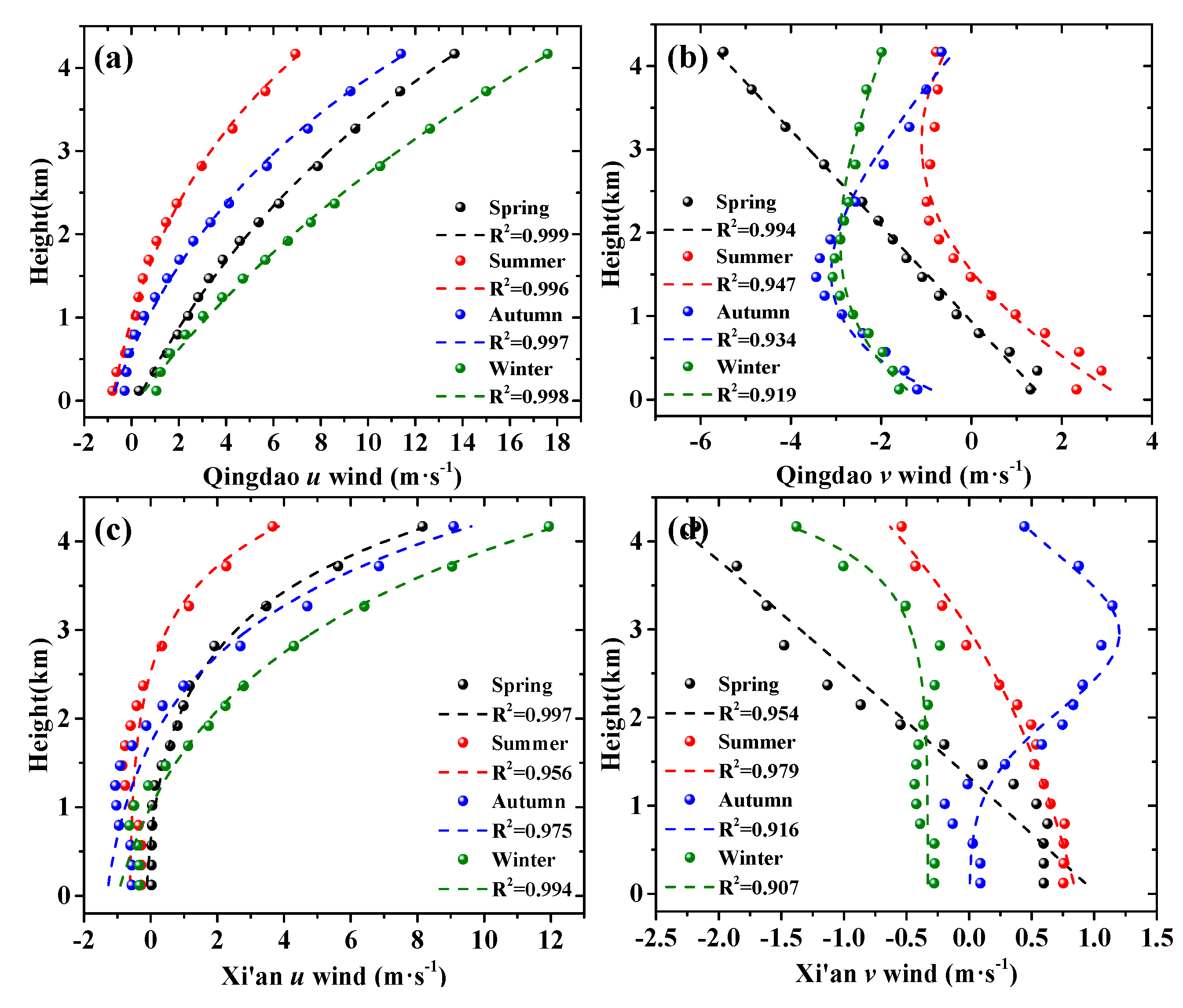
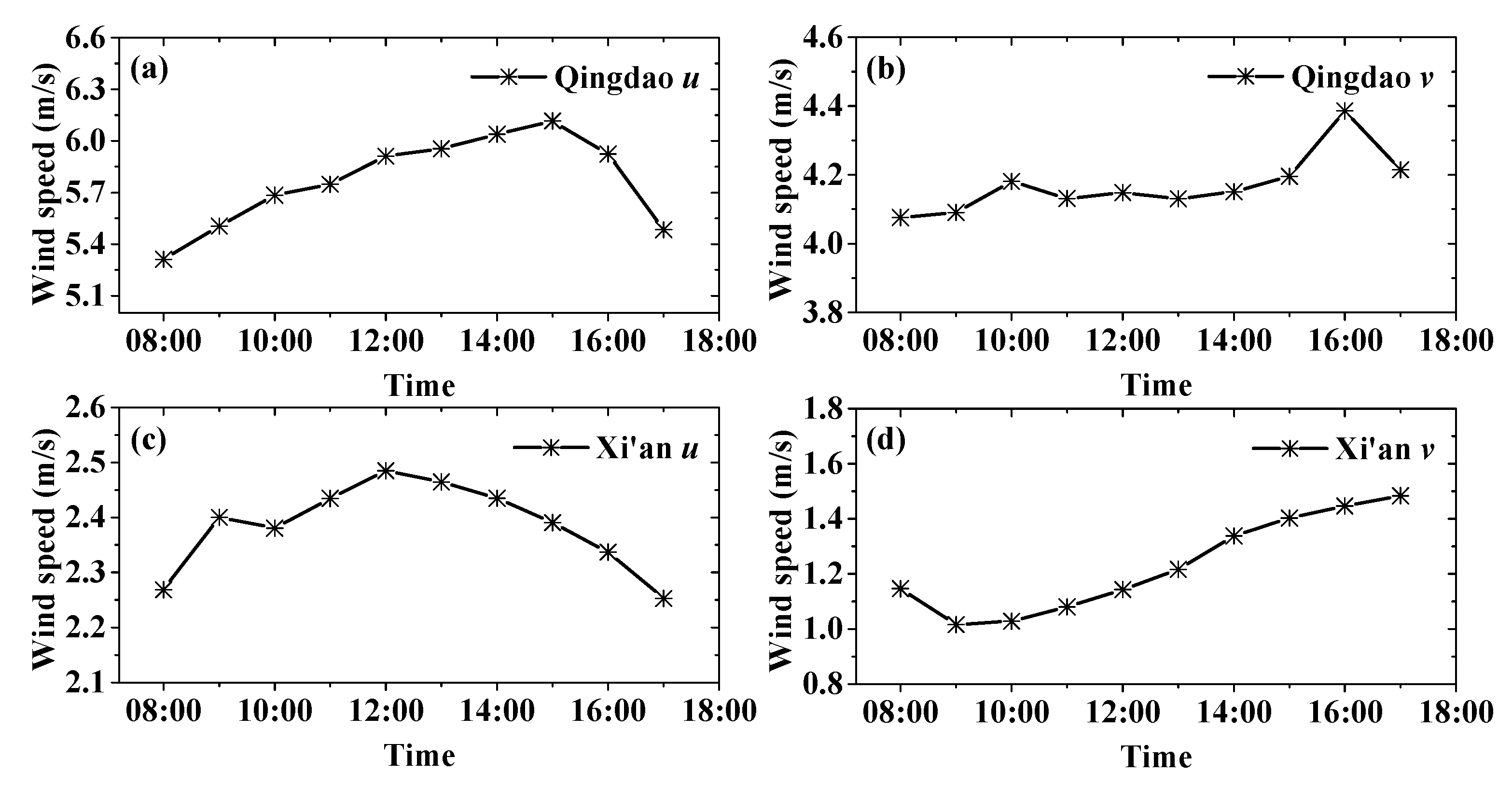
2.6. Selection of the Wind Profile Interpolation Function
3. Results and Discussion
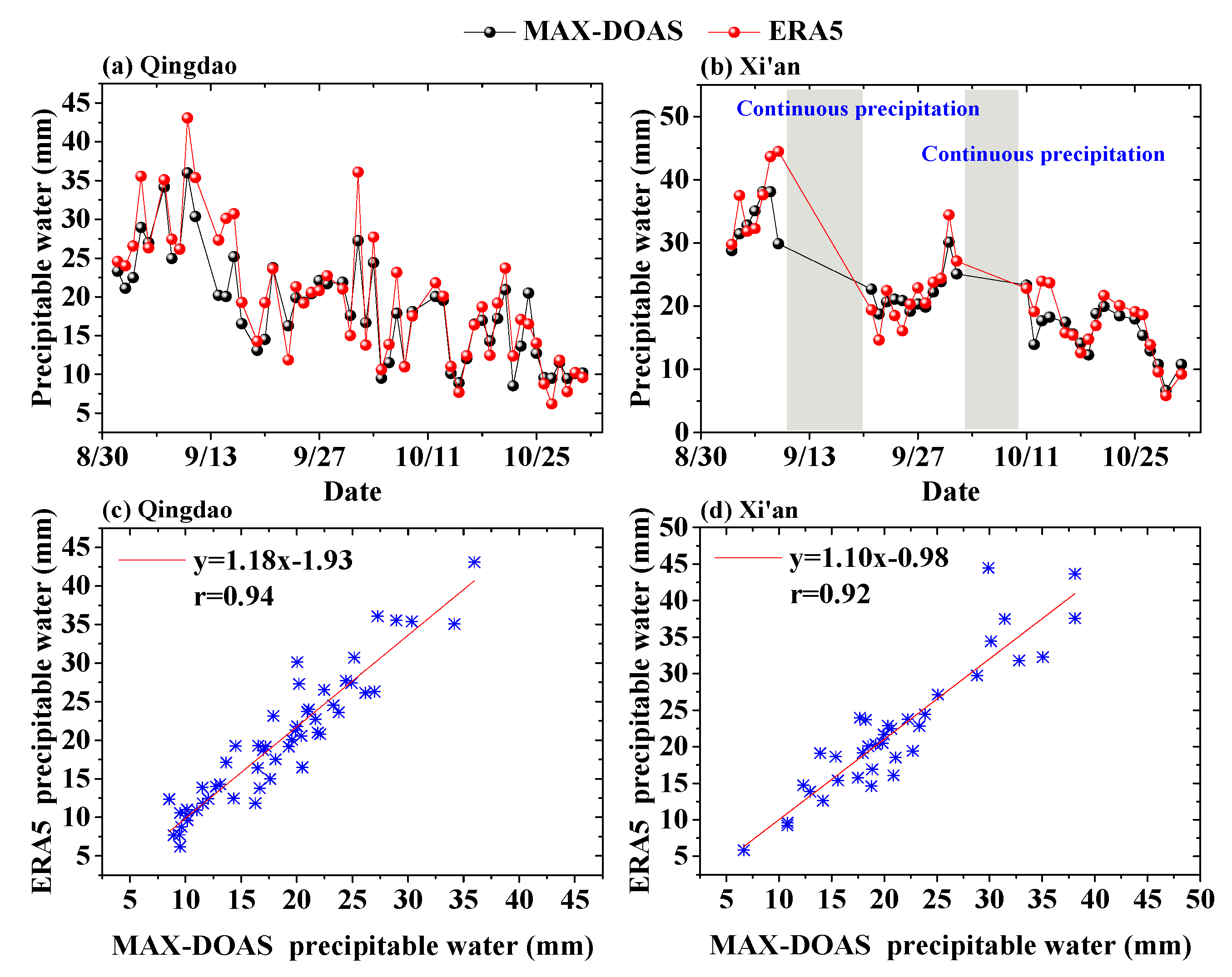
3.1. Comparison of MAX-DOAS and ERA5 Reanalysis Datasets
3.1.1. Precipitable Water Comparison
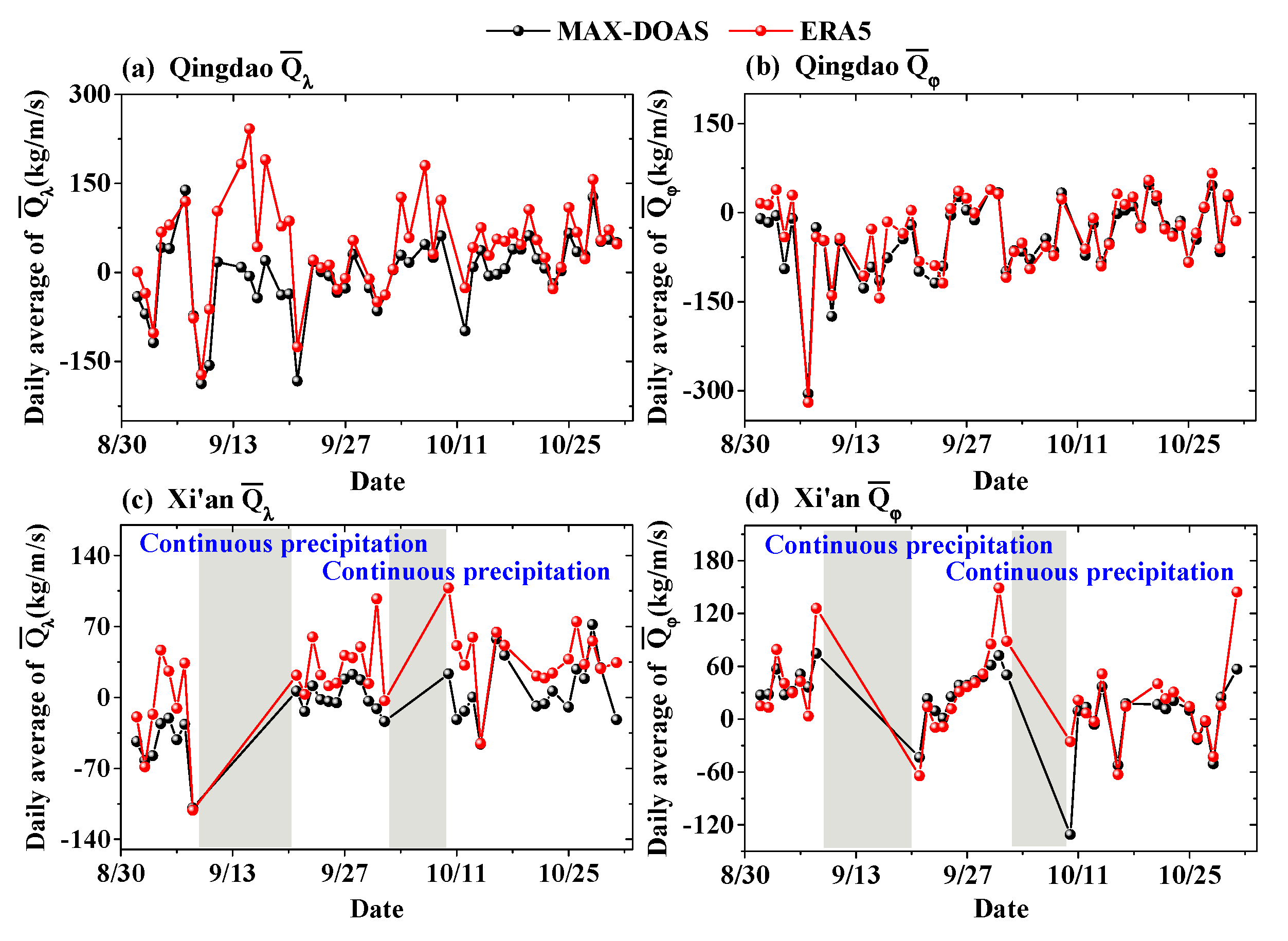
3.1.2. Water Vapor Flux Comparison
3.2. Precipitable Water Variations in Qingdao and Xi’an
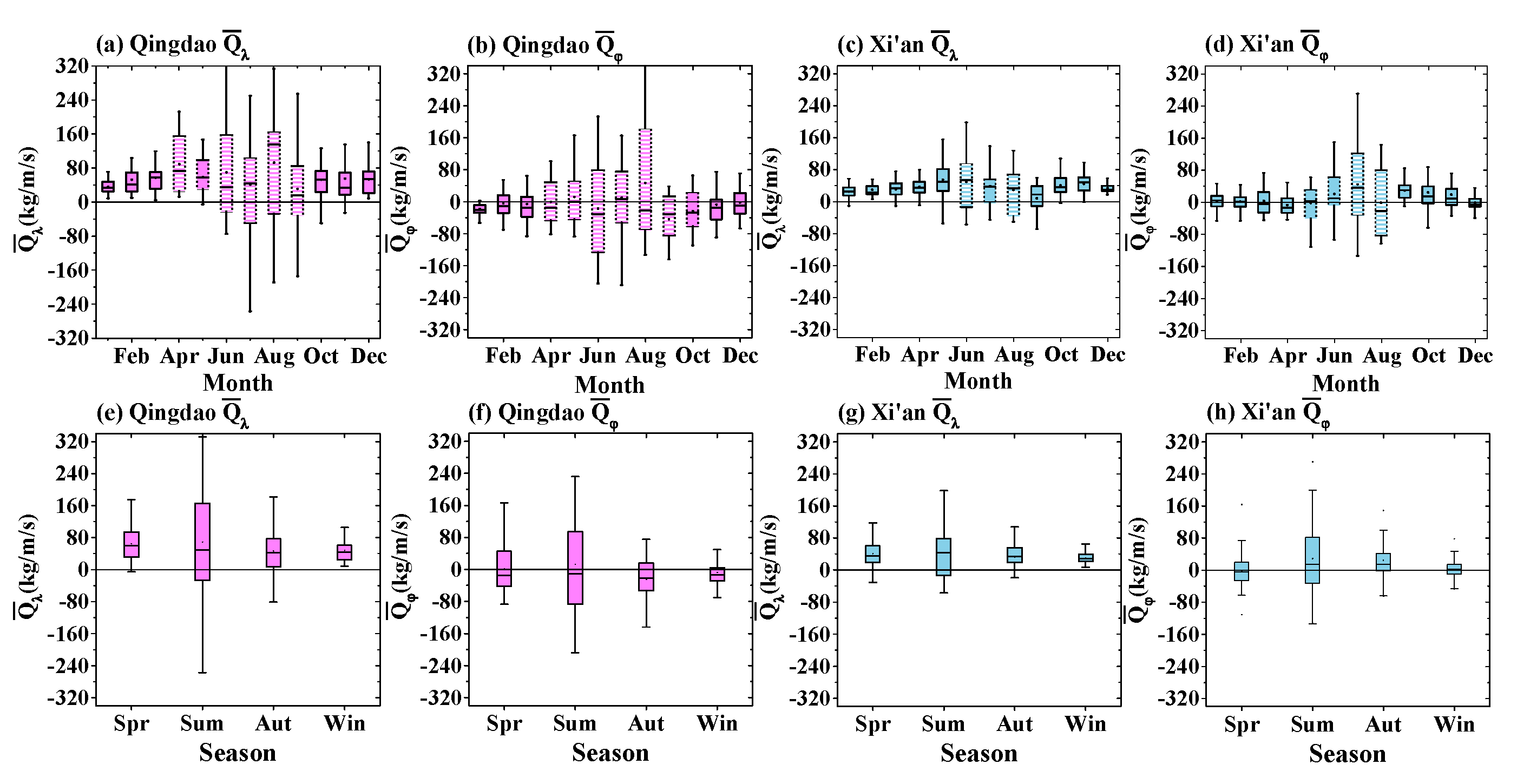
3.3. Water Vapor Flux Variations in Qingdao and Xi’an
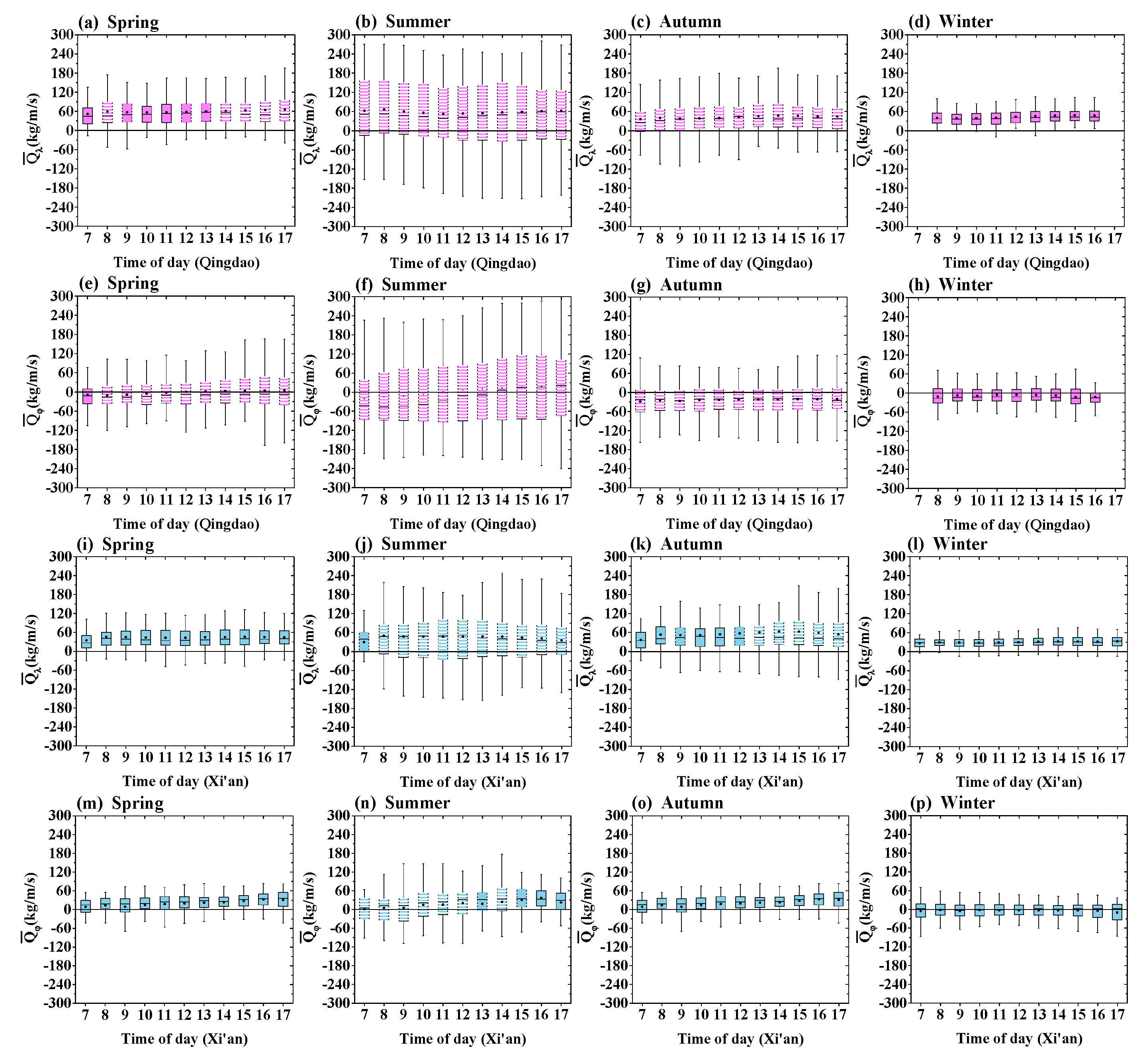
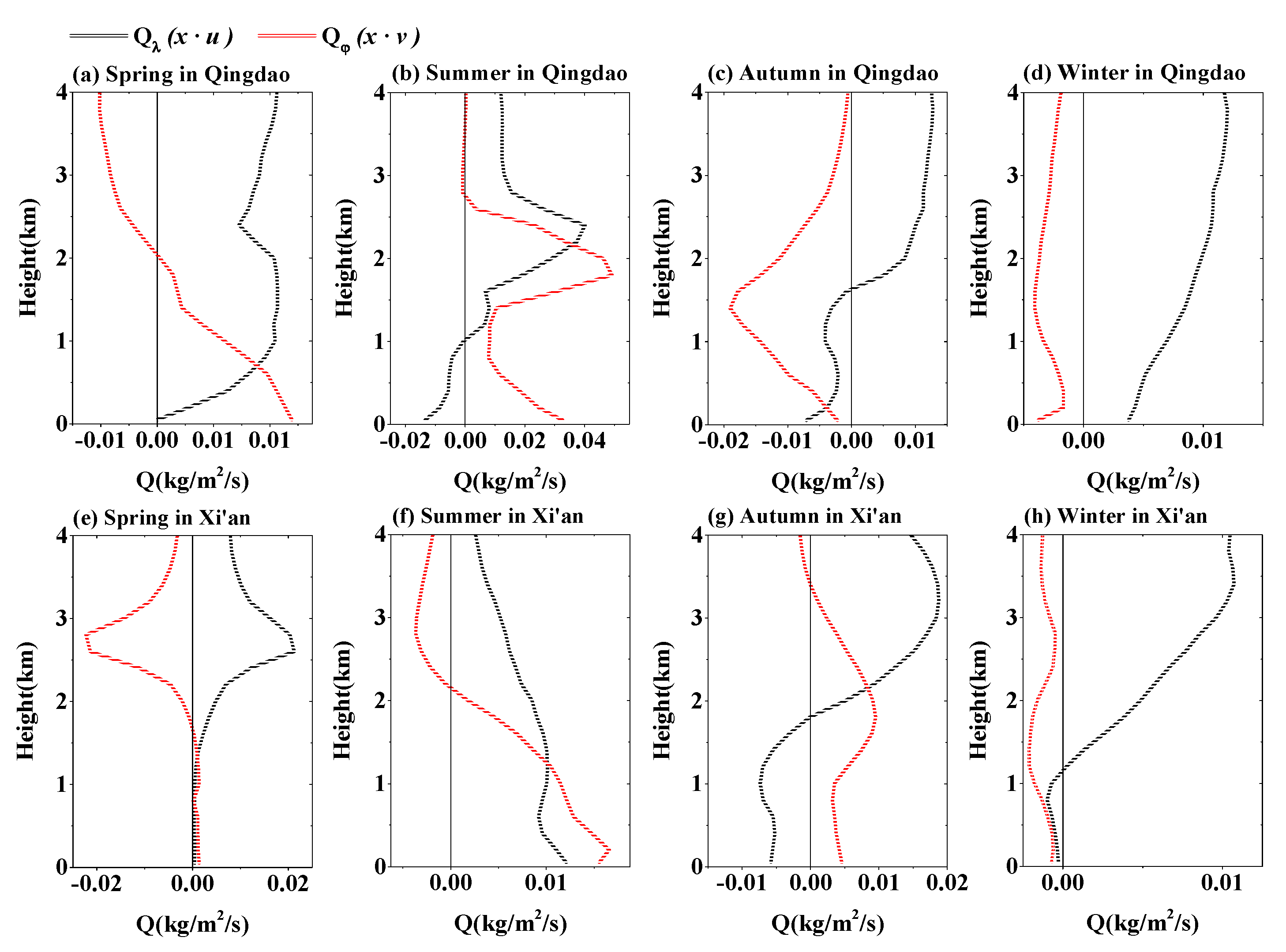
3.4. Water Vapor Flux Profile in Qingdao and Xi’an
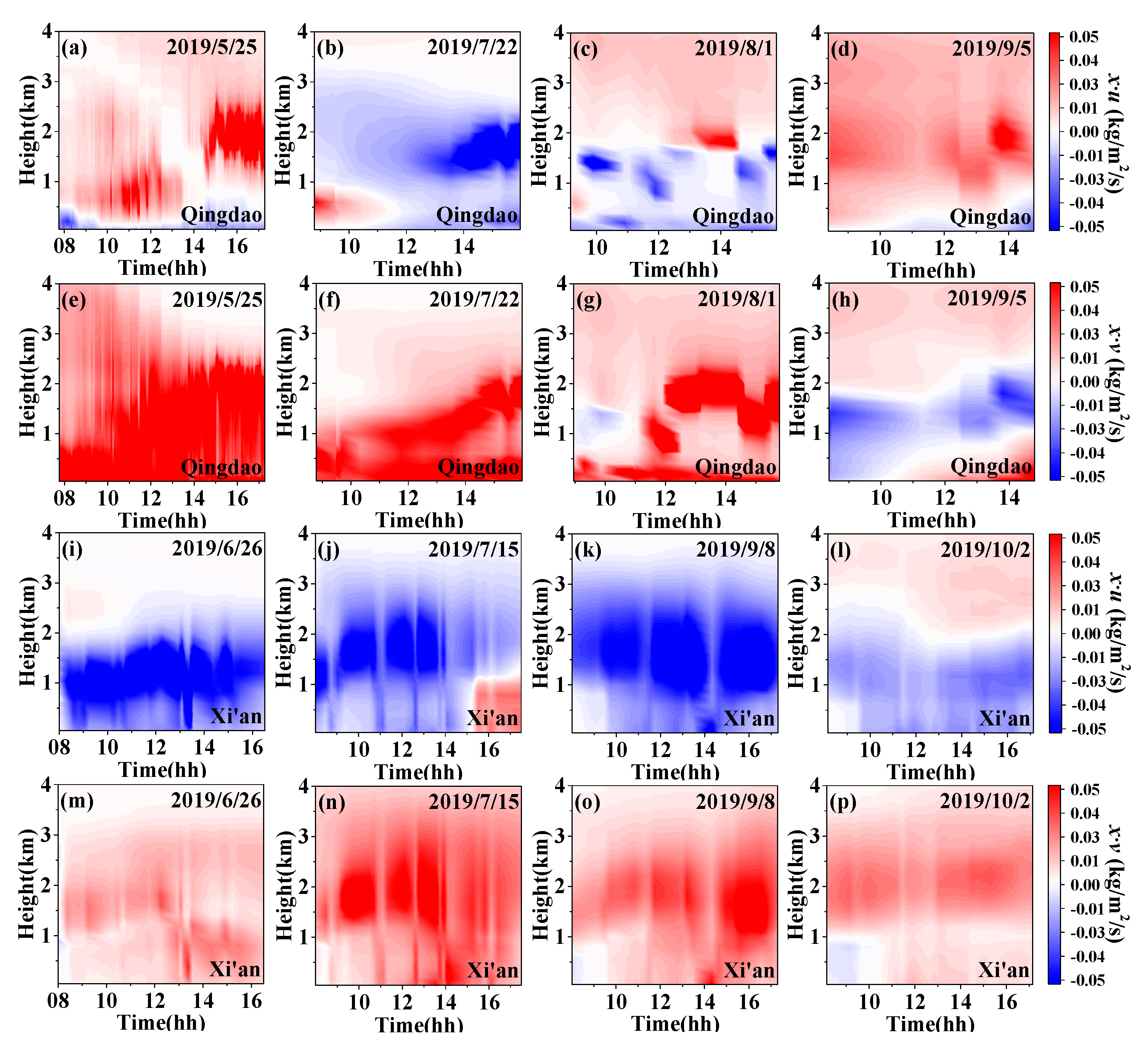
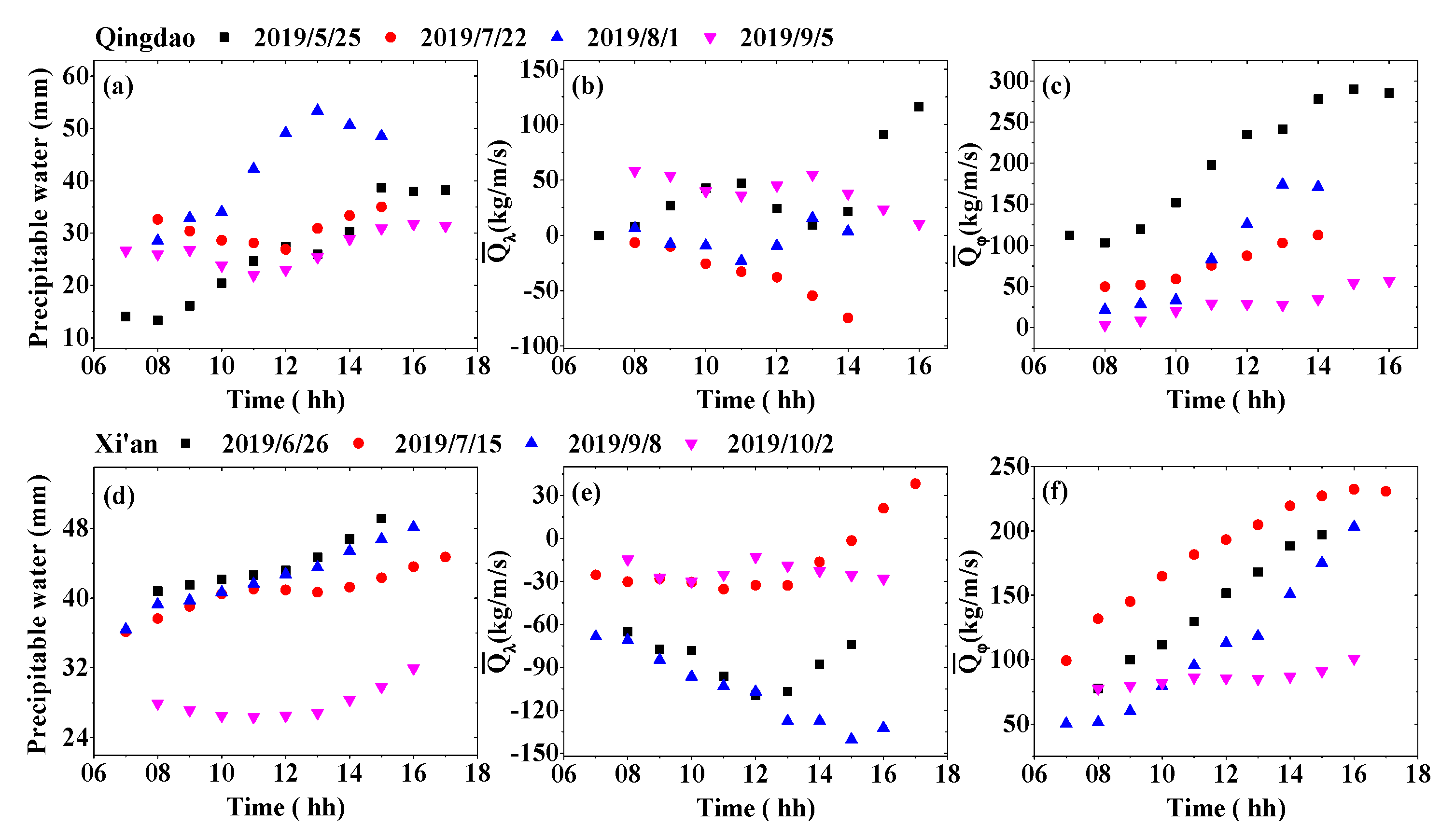
3.5. Water Vapor Transport before Precipitation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ryu, Y.H.; Smith, J.A.; Bou-Zeid, E. On the Climatology of Precipitable Water and Water Vapor Flux in the Mid-Atlantic Region of the United States. J. Hydrometeorol. 2014, 16, 70–87. [Google Scholar] [CrossRef]
- Hanesiak, J.; Melsness, M.; Raddatz, R. Observed and Modeled Growing-Season Diurnal Precipitable Water Vapor in South-Central Canada. J. Appl. Meteorol. Climatol. 2010, 49, 2301–2314. [Google Scholar] [CrossRef]
- Darrag, M.; Aboualy, N.; Mohamed, A.M.S.; Becker, M.; Saleh, M. Evaluation of precipitable water vapor variation for east mediterranean using GNSS. Acta Geod. Geophys. 2020, 55, 257–275. [Google Scholar] [CrossRef]
- Held, I.M.; Soden, B.J. Robust Responses of the Hydrological Cycle to Global Warming. J. Clim. 2006, 19, 5686–5699. [Google Scholar] [CrossRef]
- Back, L.; Russ, K.; Liu, Z.; Inoue, K.; Zhang, J.; Otto-Bliesner, B. Global Hydrological Cycle Response to Rapid and Slow Global Warming. J. Clim. 2013, 26, 8781–8786. [Google Scholar] [CrossRef]
- Xue, D.; Lu, J.; Leung, L.R.; Zhang, Y. Response of the hydrological cycle in Asian monsoon systems to global warming through the lens of water vapor wave activity analysis. Geophys. Res. Lett. 2018, 45, 11904–11912. [Google Scholar] [CrossRef]
- Hill, S.A.; Ming, Y.; Zhao, M. Robust Responses of the Sahelian Hydrological Cycle to Global Warming. J. Clim. 2018, 31, 9793–9814. [Google Scholar] [CrossRef]
- Baldocchi, D.; Valentini, R.; Running, S.; Oechel, W.; Dahlman, R. Strategies for measuring and modelling carbon dioxide and water vapour fluxes over terrestrial ecosystems. Glob. Chang. Biol. 1996, 2, 159–168. [Google Scholar] [CrossRef]
- Shukla, J.; Mintz, Y. Influence of Land-Surface Evapotranspiration on the Earth’s Climate. Science 1982, 215, 1498–1501. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Liu, Y.; Yang, X.; Li, J. Studies on water-vapor flux characteristic and the relationship with environmental factors over a planted coniferous forest in Qianyanzhou Station. Acta Ecol. Sin. 2006, 26, 2249–2456. [Google Scholar] [CrossRef]
- Shu, H.; Jiang, H.; Chen, X.; Sun, W. Variation characteristics of water vapor flux in Anji Phyllostachys edulis forest ecosystem. Chin. J. Ecol. 2016, 35, 1154–1161. [Google Scholar]
- Giez, A.; Ehret, G.; Schwiesow, R.L.; Davis, K.J.; Lenschow, D.H. Water Vapor Flux Measurements from Ground-Based Vertically Pointed Water Vapor Differential Absorption and Doppler Lidars. J. Atmos. Ocean. Technol. 1999, 16, 237–250. [Google Scholar] [CrossRef]
- Di Girolamo, P.; Summa, D.; Stelitano, D.; Cacciani, M.; Scoccione, A.; Schween, J.H. Characterization of water vapor fluxes by the raman lidar system basil and the univeristy of cologne wind lidar in the frame of the HD(CP)2 Observational Prototype Experiment–HOPE. In Proceedings of the 27th International Laser Radar Conference, New York City, NY, USA, 5–10 July 2015; Gross, B., Moshary, F., Arend, M., Eds.; EDP Sciences: Les Ulis, France, 2016; Volume 119. [Google Scholar]
- Platt, U.; Stutz, J. Differential Optical Absorption Spectroscopy; Springer: Heidelberg/Berlin, Germany, 2008. [Google Scholar]
- Irie, H.; Takashima, H.; Kanaya, Y.; Boersma, K.F.; Gast, L.; Wittrock, F.; Brunner, D.; Zhou, Y.; Van Roozendael, M. Eight-component retrievals from ground-based MAX-DOAS observations. Atmos. Meas. Tech. 2011, 4, 1027–1044. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, W.; Li, A.; Xie, P.; Chen, H.; Mou, F.; Xu, J.; Wu, F.; Zeng, Y.; Liu, J. Measuring tropospheric vertical distribution and vertical column density of NO2 by multi-axis differential optical absorption spectroscopy. Acta Phys. Sin. 2013, 62, 138–151. [Google Scholar]
- Wang, Y.; Beirle, S.; Lampel, J.; Koukouli, M.; De Smedt, I.; Theys, N.; Li, A.; Wu, D.; Xie, P.; Liu, C.; et al. Validation of OMI, GOME-2A and GOME-2B tropospheric NO2, SO2 and HCHO products using MAX-DOAS observations from 2011 to 2014 in Wuxi, China: Investigation of the effects of priori profiles and aerosols on the satellite products. Atmos. Chem. Phys. 2017, 17, 5007–5033. [Google Scholar] [CrossRef]
- Wang, Y.; Lampel, J.; Xie, P.; Beirle, S.; Li, A.; Wu, D.; Wagner, T. Ground-based MAX-DOAS observations of tropospheric aerosols, NO2, SO2 and HCHO in Wuxi, China, from 2011 to 2014. Atmos. Chem. Phys. 2017, 17, 2189–2215. [Google Scholar] [CrossRef]
- Wang, Y.; Doerner, S.; Donner, S.; Boehnke, S.; De Smedt, I.; Dickerson, R.R.; Dong, Z.; He, H.; Li, Z.; Li, Z.; et al. Vertical profiles of NO2, SO2, HONO, HCHO, CHOCHO and aerosols derived from MAX-DOAS measurements at a rural site in the central western North China Plain and their relation to emission sources and effects of regional transport. Atmos. Chem.Phys. 2019, 19, 5417–5449. [Google Scholar] [CrossRef]
- Tian, X.; Xie, P.; Xu, J.; Li, A.; Wang, Y.; Qin, M.; Hu, Z. Long-term observations of tropospheric NO2, SO2 and HCHO by MAX-DOAS in Yangtze River Delta area, China. J. Environ. Sci. 2018, 71, 207–221. [Google Scholar] [CrossRef]
- Wagner, T.; Andreae, M.O.; Beirle, S.; Doerner, S.; Mies, K.; Shaiganfar, R. MAX-DOAS observations of the total atmospheric water vapour column and comparison with independent observations. Atmos. Meas. Tech. 2013, 6, 131–149. [Google Scholar] [CrossRef]
- Lampel, J.; Poehler, D.; Tschritter, J.; Friess, U.; Platt, U. On the relative absorption strengths of water vapour in the blue wavelength range. Atmos. Meas. Tech. 2015, 8, 4329–4346. [Google Scholar] [CrossRef]
- Lampel, J.; Poehler, D.; Polyansky, O.L.; Kyuberis, A.A.; Zobov, N.F.; Tennyson, J.; Lodi, L.; Friess, U.; Wang, Y.; Beirle, S.; et al. Detection of water vapour absorption around 363 nm in measured atmospheric absorption spectra and its effect on DOAS evaluations. Atmos. Chem. Phys. 2017, 17, 1271–1295. [Google Scholar] [CrossRef]
- Borger, C.; Beirle, S.; Doerner, S.; Sihler, H.; Wagner, T. Total column water vapour retrieval from S-5P/TROPOMI in the visible blue spectral range. Atmos. Meas. Tech. 2020, 13, 2751–2783. [Google Scholar] [CrossRef]
- Chan, K.L.; Valks, P.; Slijkhuis, S.; Koehler, C.; Loyola, D. Total column water vapor retrieval for Global Ozone Monitoring Experience-2 (GOME-2) visible blue observations. Atmos. Meas. Tech. 2020, 13, 4169–4193. [Google Scholar] [CrossRef]
- Ren, H.-M.; Li, A.; Hu, Z.-K.; Huang, Y.-Y.; Xu, J.; Xie, P.-H.; Zhong, H.-Y.; Li, X.-M. Measurement of atmospheric water vapor vertical column concentration and vertical distribution in Qingdao using multi-axis differential optical absorption spectroscopy. Acta Phys. Sin. 2020, 69, 204204. [Google Scholar]
- Lin, H.; Liu, C.; Xing, C.; Hu, Q.; Hong, Q.; Liu, H.; Li, Q.; Tan, W.; Ji, X.; Wang, Z.; et al. Validation of Water Vapor Vertical Distributions Retrieved from MAX-DOAS over Beijing, China. Remote Sens. 2020, 12, 3193. [Google Scholar] [CrossRef]
- Liu, X.-D.; Fang, J.-G.; Yang, X.-C.; Li, X.-Z. Climatology of dekadly precipitation around the Qinling mountains and characteristics of its atmospheric circulation. Arid Meteorol. 2003, 21, 8–13. [Google Scholar]
- Ma, Y.; Gao, R.-Z.; Miao, S.-G.; Huang, R. Impacts of urbanization on summer-time sea-land breeze circulation in Qingdao. Acta Sci. Circumst. 2013, 33, 1690–1696. [Google Scholar]
- Wang, Y.; Li, A.; Xie, P.H.; Wagner, T.; Chen, H.; Liu, W.Q.; Liu, J.G. A rapid method to derive horizontal distributions of trace gases and aerosols near the surface using multi-axis differential optical absorption spectroscopy. Atmos. Meas. Tech. 2014, 7, 1663–1680. [Google Scholar] [CrossRef]
- Wang, Y.; Beirle, S.; Hendrick, F.; Hilboll, A.; Jin, J.; Kyuberis, A.A.; Lampel, J.; Li, A.; Luo, Y.; Lodi, L.; et al. MAX-DOAS measurements of HONO slant column densities during the MAD-CAT campaign: Inter-comparison, sensitivity studies on spectral analysis settings, and error budget. Atmos. Meas. Tech. 2017, 10, 3719–3742. [Google Scholar] [CrossRef]
- Danckaert, T.; Fayt, C.; Van Roozendael, M.; De Smedt, I.; Letocart, V.; Merlaud, A.; Pinardi, G. QDOAS Software User Manual Version 3.2; Royal Belgian Institute for Space Aeronomy: Brussels, Belgium, 2017. [Google Scholar]
- Perliski, L.M.; Solomon, S. On the evaluation of air mass factors for atmospheric near-ultraviolet and visible absorption spectroscopy. J. Geophys. Res. Atmos. 1993, 98, 10363–10374. [Google Scholar] [CrossRef]
- Frieß, F.; Monks, P.S.; Remedios, J.J.; Rozanov, A.; Sinreich, R.; Wagner, T.; Platt, U. MAX-DOAS O4 measurements: A new technique to derive information on atmospheric aerosols. (II) Modelling studies. Med. Educ. 2006, 12, 222–225. [Google Scholar]
- Richter, A.; Wagner, T. The Use of UV, Visible and Near IR Solar Back Scattered Radiation to Determine Trace Gases. In The Remote Sensing of Tropospheric Composition from Space; Burrows, J.P., Borrell, P., Platt, U., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 67–121. [Google Scholar]
- Ibrahim, O.; Platt, U.; Shaiganfar, R.; Wagner, T. Mobile MAX-DOAS observations of tropospheric trace gases. Atmos. Meas. Tech. 2010, 3, 129–140. [Google Scholar]
- Rozanov, A.; Rozanov, V.; Buchwitz, M.; Kokhanovsky, A.; Burrows, J.P. SCIATRAN 2.0–A new radiative transfer model for geophysical applications in the 175–2400 nm spectral region. Adv. Space Res. 2005, 36, 1015–1019. [Google Scholar] [CrossRef]
- Cui, X.-A.; Gu, H.; Cao, Y. Simplification of Barometric Height Formola in Geopotential Height Calculation and Resulted Errors. Meteorol. Sci. Technol. 2017, 45, 307–312. [Google Scholar]
- Meng, X.; Guo, J.; Han, Y. Preliminarily assessment of ERA5 reanalysis data. J. Mar. Meteorol. 2018, 38, 91–99. [Google Scholar]
- Sun, W.; Yuan, W.; Li, J.; Yu, R. Correlation between peak intensity of extreme afternoon short-duration rainfall and humidity and surface air temperature in southeast coast China. J. Trop. Meteorol. 2015, 21, 276–284. [Google Scholar]
- Zhou, T.J.; Yu, R.C. Atmospheric water vapor transport associated with typical anomalous summer rainfall patterns in China. J. Geophys. Res. Atmos. 2005, 110. [Google Scholar] [CrossRef]
- Arraut, J.M.; Satyamurty, P. Precipitation and Water Vapor Transport in the Southern Hemisphere with Emphasis on the South American Region. J. Appl. Meteorol. Climatol. 2009, 48, 1902–1912. [Google Scholar] [CrossRef]
- Oigawa, M.; Realini, E.; Tsuda, T. Study of Water Vapor Variations Associated with Meso-γ Scale Convection: Comparison between GNSS and Non-Hydrostatic Model Data. SOLA-Sci. Online Lett. Atmos. 2015, 11, 27–30. [Google Scholar] [CrossRef]
- Hendrix, C.S.; Salehyan, I. After the Rain: Rainfall Variability, Hydro-Meteorological Disasters, and Social Conflict in Africa. Soc. Sci. Electron. Publ. 2011, 6, 5152–5160. [Google Scholar] [CrossRef]
- Saito, H.; Matsuyama, H. Catastrophic Landslide Disasters Triggered by Record-Breaking Rainfall in Japan: Their Accurate Detection with Normalized Soil Water Index in the Kii Peninsula for the Year 2011. Sola 2012, 8, 81–84. [Google Scholar] [CrossRef]
- Zheng, Y. A Preliminary Analysis on the Applicability of ERA5 Reanalysis Data in Guangdong Province. Meteorol. Environ. Res. 2020, 11, 37–48. [Google Scholar]
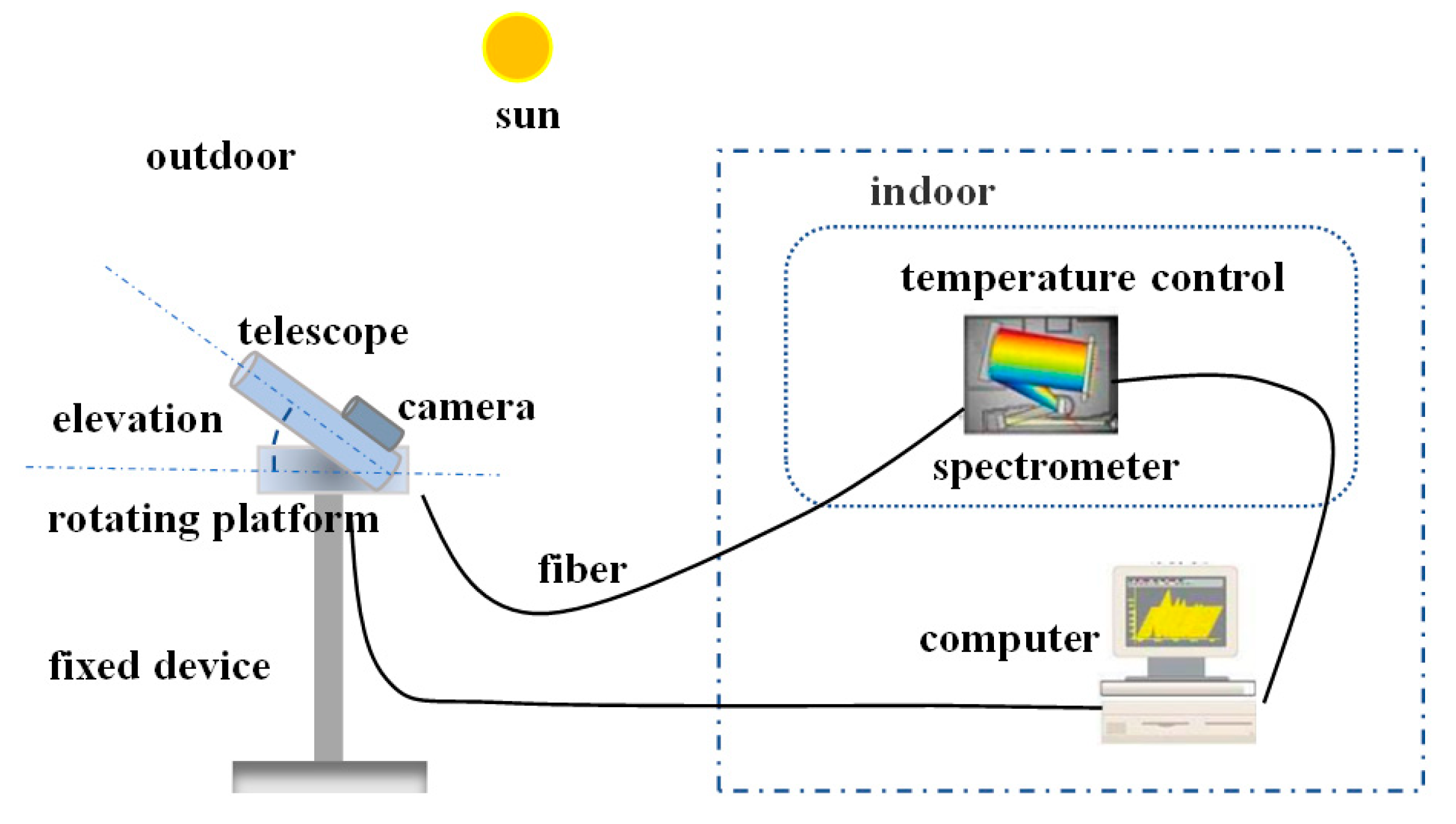





| Spectrometer | Location and Time | Angle Setting | |||
|---|---|---|---|---|---|
| Name | Avantes | Xi’an | 108.05° E | Azimuth | 0° (North) |
| Spectral range of Xi’an | 290–459 nm | 34.53° N | |||
| Spectral range of Qingdao | 285–453 nm | Qingdao | 120.67° E | ||
| FWHM of Xi’an | 0.4 nm | 36.35° N | |||
| FWHM of Qingdao | 0.5 nm | Measuring time | 4:00–22:00 LT | Elevation angle selection [26] | 1°, 2°, 3°, 4°, 5°, 6°, 8°, 10°, 20°, 30°, 90° |
| Temperature control | 25 °C | ||||
| ECMWF ERA5 Pressure Levels (hPa) | MAX-DOAS Levels (km) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1000 | 975 | 950 | 925 | 900 | 875 | 850 | 825 | 0.05 | 0.2 | 0.4 | 0.6 | 0.8 |
| 800 | 775 | 750 | 700 | 650 | 600 | 550 | 500 | 1 | 1.2 | 1.4 | 1.6 | 1.8 |
| 450 | 400 | 350 | 300 | 250 | 225 | 200 | 175 | 2 | 2.2 | 2.4 | 2.6 | 2.8 |
| 150 | 125 | 100 | 70 | 50 | 30 | 20 | 10 | 3 | 3.2 | 3.4 | 3.6 | 3.8 |
| 7 | 5 | 3 | 2 | 1 | 4 | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, H.; Li, A.; Xie, P.; Hu, Z.; Xu, J.; Huang, Y.; Li, X.; Zhong, H.; Tian, X.; Ren, B.; et al. Estimation of the Precipitable Water and Water Vapor Fluxes in the Coastal and Inland Cities of China Using MAX-DOAS. Remote Sens. 2021, 13, 1675. https://doi.org/10.3390/rs13091675
Ren H, Li A, Xie P, Hu Z, Xu J, Huang Y, Li X, Zhong H, Tian X, Ren B, et al. Estimation of the Precipitable Water and Water Vapor Fluxes in the Coastal and Inland Cities of China Using MAX-DOAS. Remote Sensing. 2021; 13(9):1675. https://doi.org/10.3390/rs13091675
Chicago/Turabian StyleRen, Hongmei, Ang Li, Pinhua Xie, Zhaokun Hu, Jin Xu, Yeyuan Huang, Xiaomei Li, Hongyan Zhong, Xin Tian, Bo Ren, and et al. 2021. "Estimation of the Precipitable Water and Water Vapor Fluxes in the Coastal and Inland Cities of China Using MAX-DOAS" Remote Sensing 13, no. 9: 1675. https://doi.org/10.3390/rs13091675
APA StyleRen, H., Li, A., Xie, P., Hu, Z., Xu, J., Huang, Y., Li, X., Zhong, H., Tian, X., Ren, B., & Zhang, H. (2021). Estimation of the Precipitable Water and Water Vapor Fluxes in the Coastal and Inland Cities of China Using MAX-DOAS. Remote Sensing, 13(9), 1675. https://doi.org/10.3390/rs13091675