Data-Driven Approaches for Tornado Damage Estimation with Unpiloted Aerial Systems
Abstract
1. Introduction
2. Materials and Methods
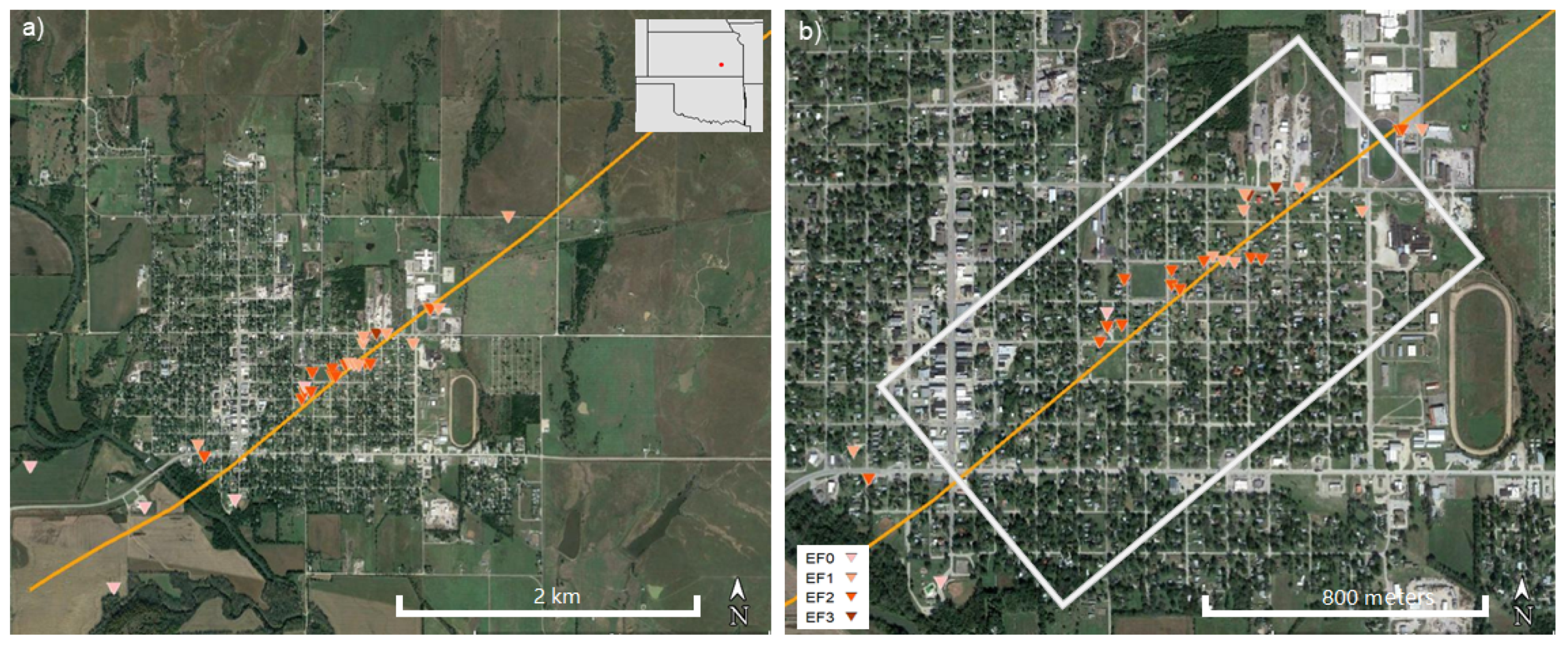
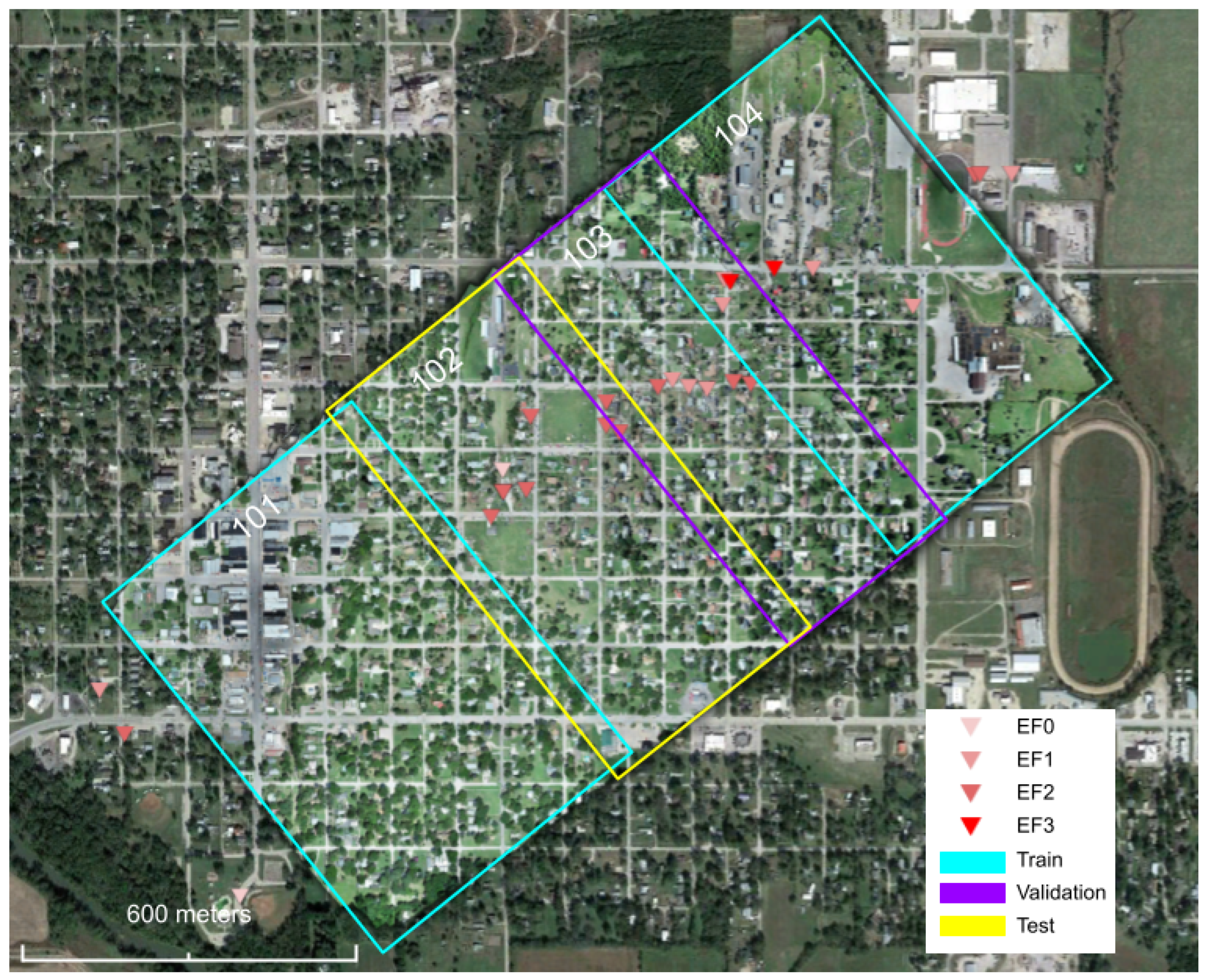
2.1. Study Area
2.2. Data Collection
2.2.1. Uas Survey Data
2.2.2. Ground Survey Data
2.3. Structure from Motion
2.4. Deep Learning
2.4.1. Data Preparation
2.4.2. Neural Network Training
2.4.3. Neural Network Evaluation
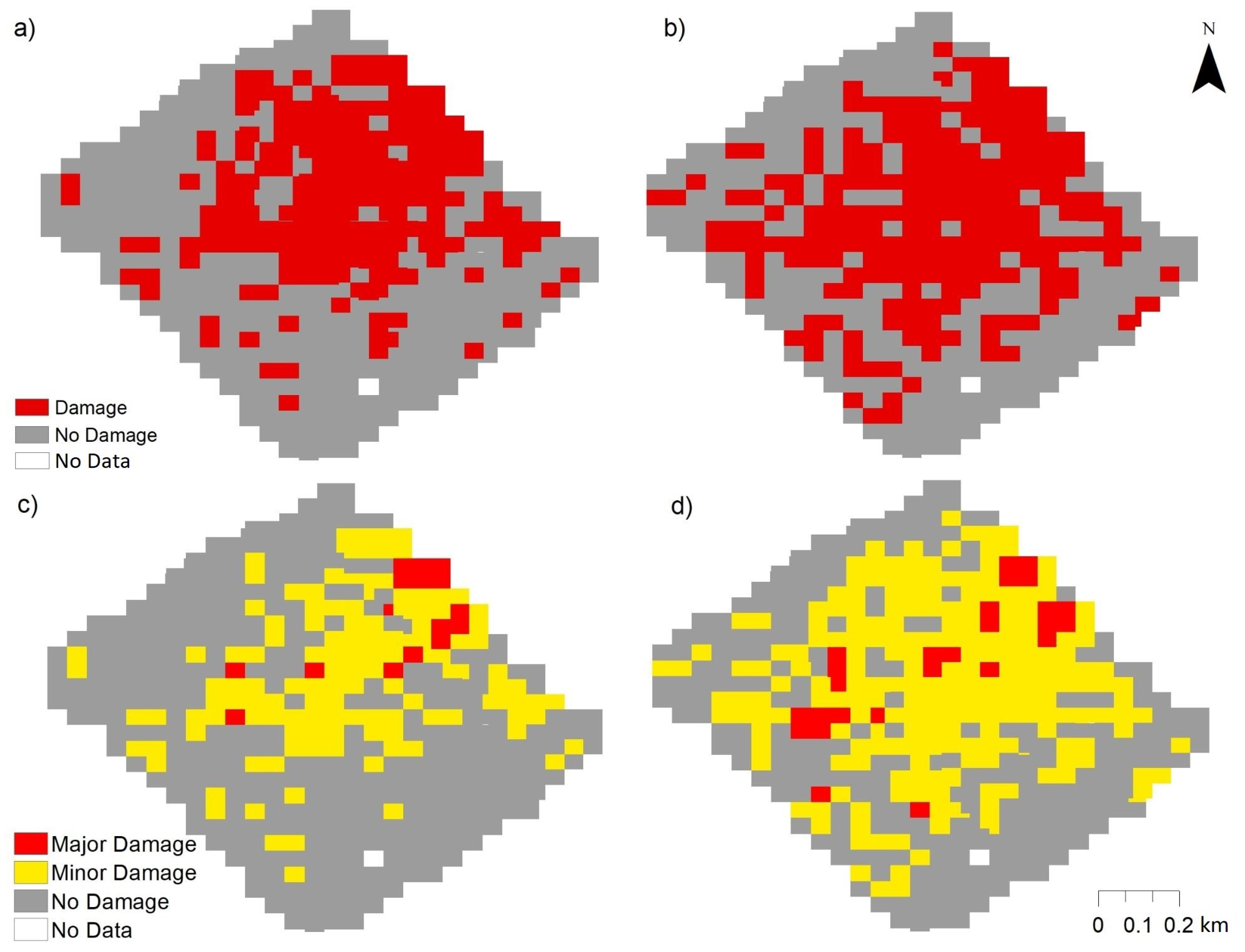
2.4.4. Post-Processing
2.5. Gaussian Process Regression
2.5.1. GP Regression Scheme
2.5.2. Model Efficiency Techniques
2.5.3. Sampling Strategy
2.5.4. Monte Carlo Sampling
2.5.5. Post-Processing
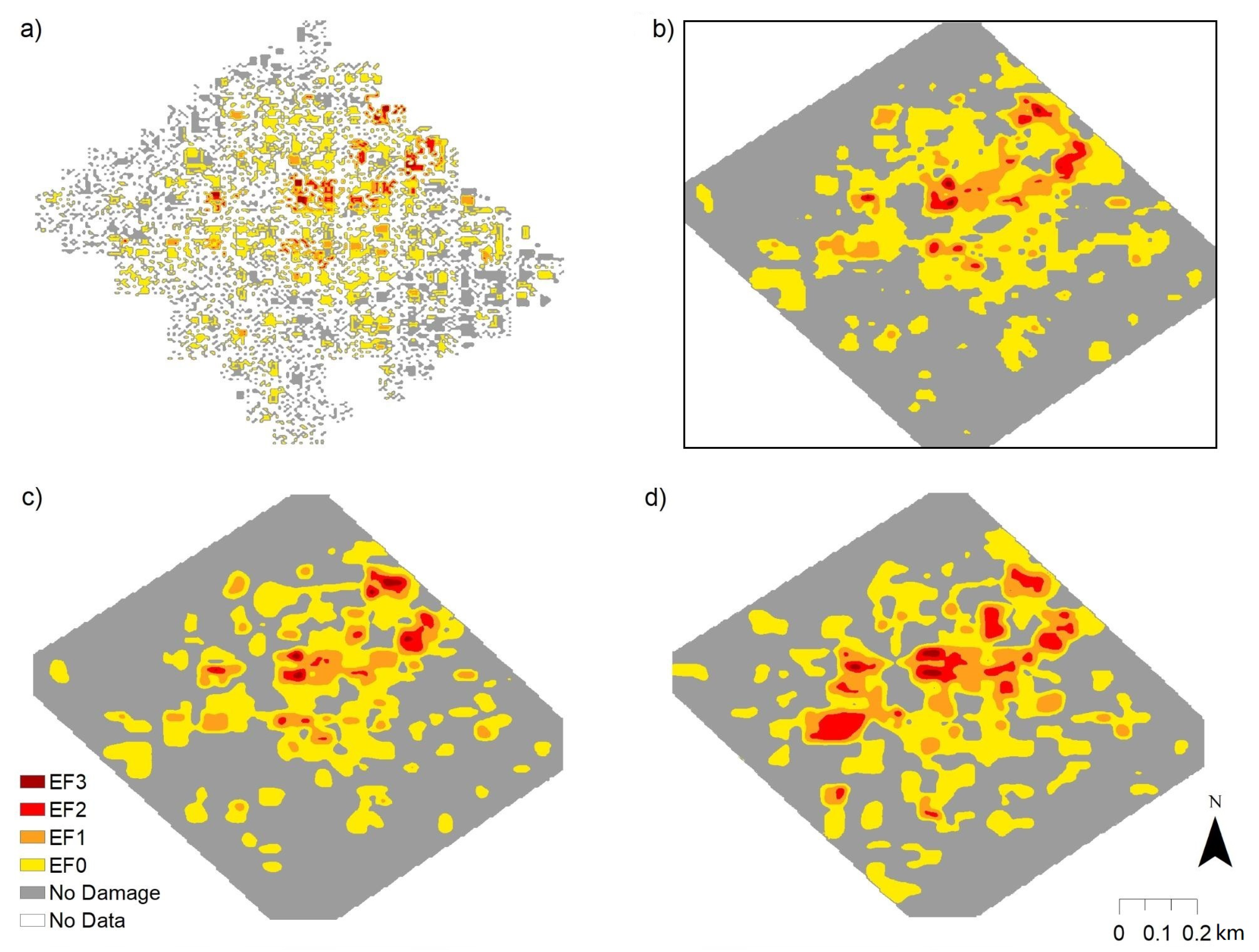
3. Results
3.1. Neural Network Object Detection
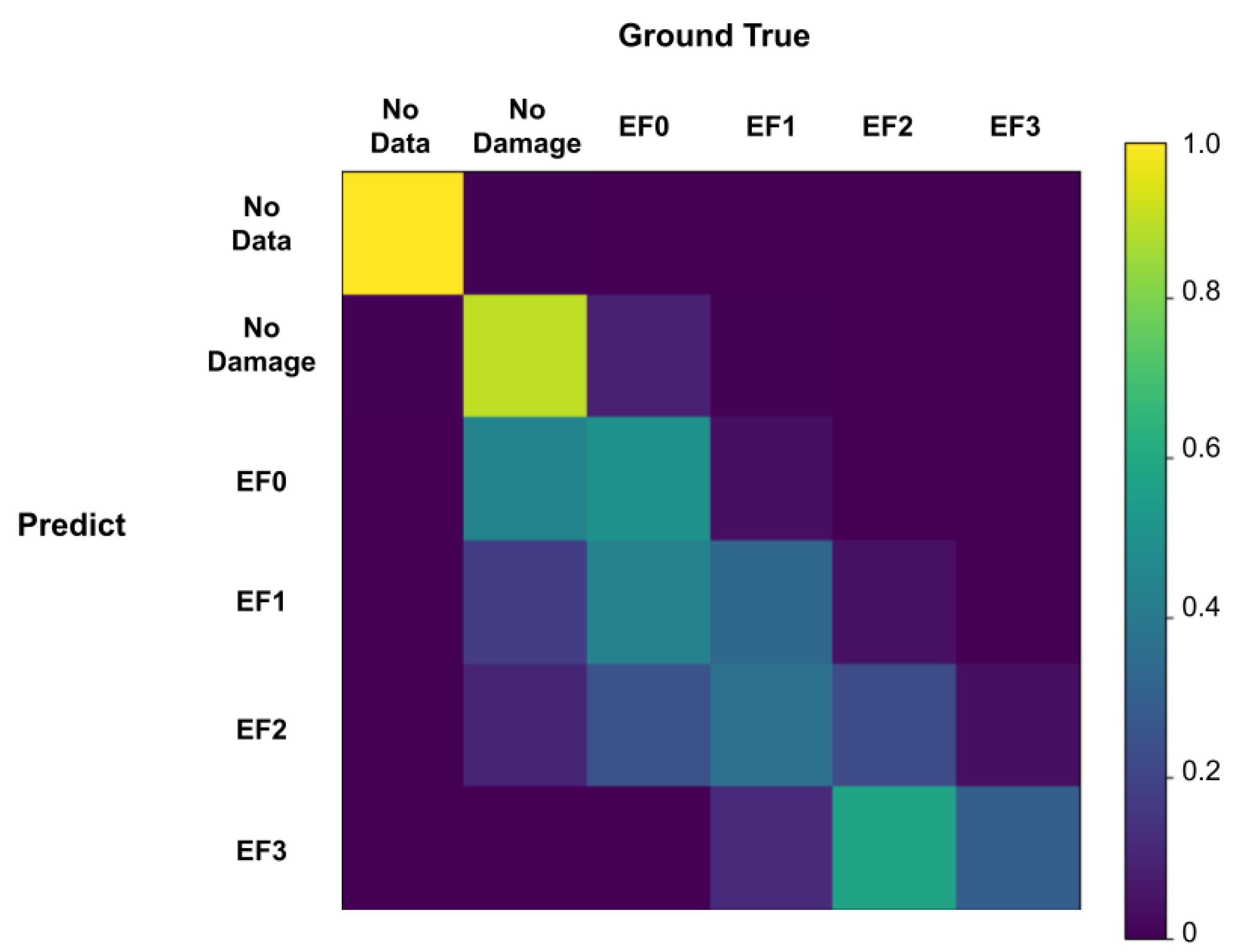
3.2. Neural Network Image Classification
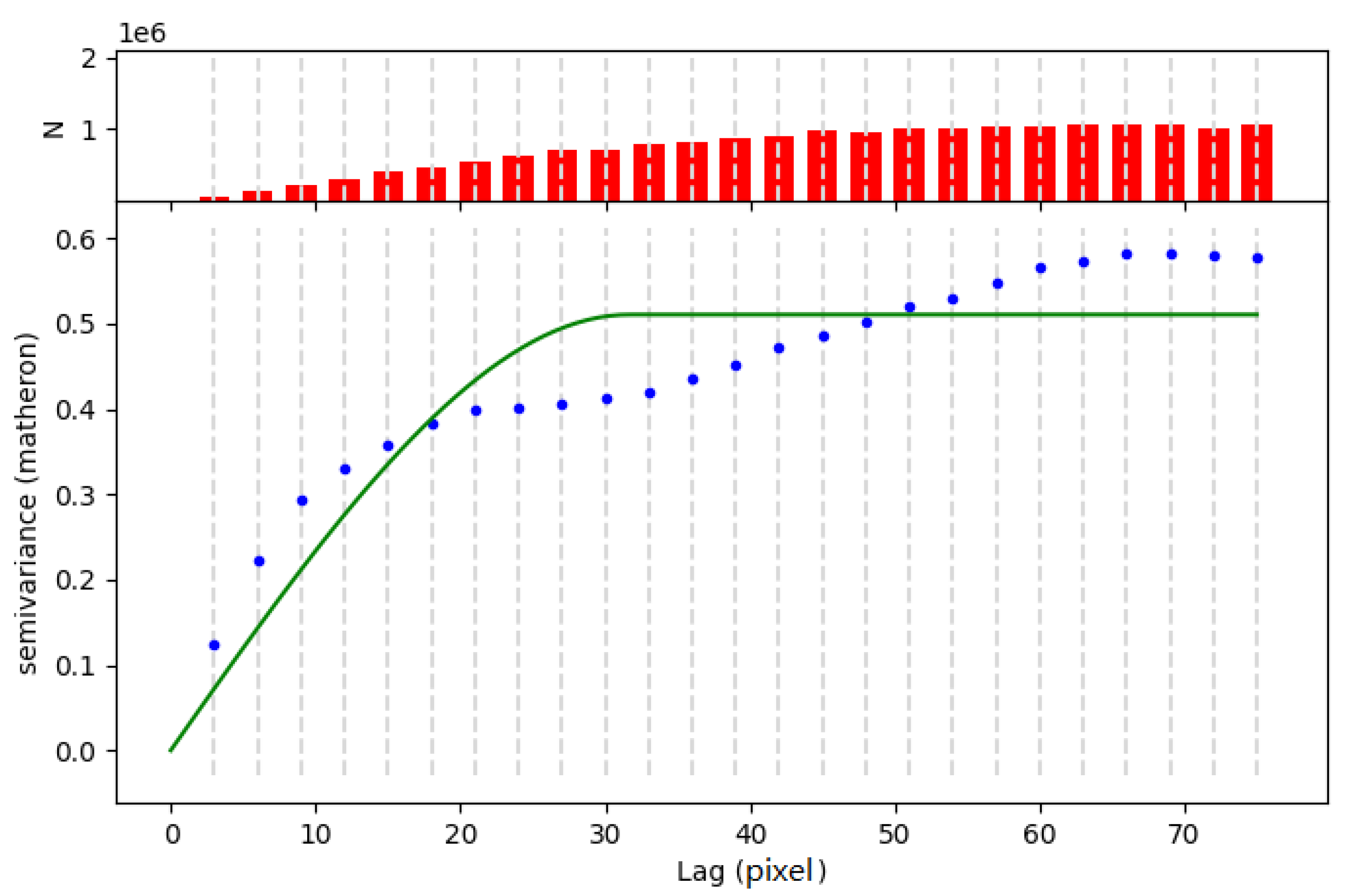
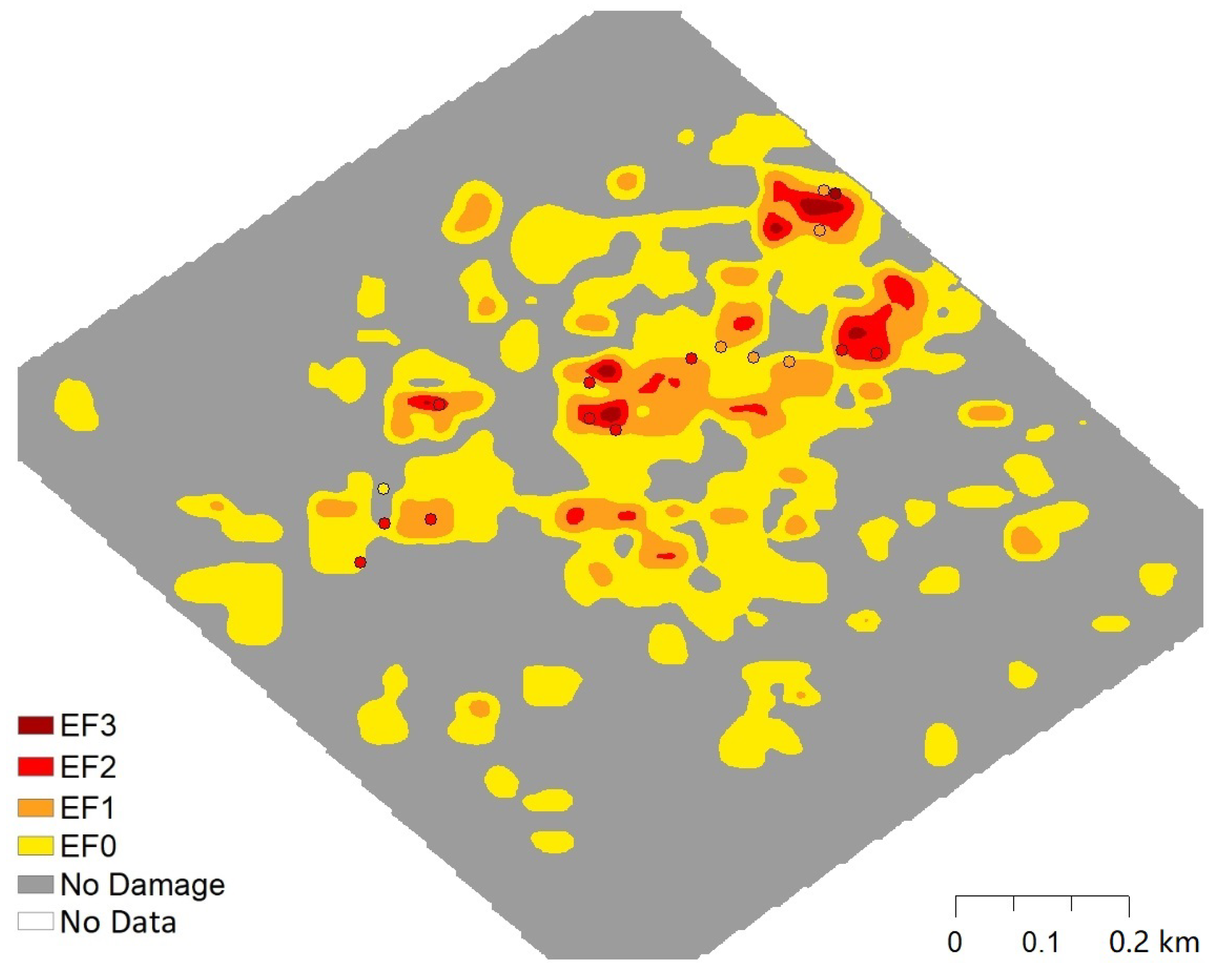
3.3. Gaussian Process Regression
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CNN | Convolutional Neural Network |
| DL | Deep Learning |
| DNN | Deep Neural Network |
| EF | Enhanced Fujita |
| FCN | Fully Convolutional Network |
| GCP | Ground Control Point |
| GNSS | Global Navigation Satellite System |
| GP | Gaussian Process |
| IoU | Intersection over Union |
| MA | Major Damage |
| mAP | mean Average Precision |
| mAR | mean Average Recall |
| MI | Minor Damage |
| ND | No Damage |
| NWS | National Weather Service |
| NWS WFO | National Weather Service Weather Forecast Office |
| PFN | Pyramid Feature Network |
| RMSD | Root-Mean-Square Deviation |
| SfM | Structure from Motion |
| UAS | Unpolited Aerial System |
Appendix A

Appendix B
References
- Edwards, R.; LaDue, J.G.; Ferree, J.T.; Scharfenberg, K.; Maier, C.; Coulbourne, W.L. Tornado intensity estimation: Past, present, and future. Bull. Am. Meteorol. Soc. 2013, 94, 641–653. [Google Scholar] [CrossRef]
- Center for Disaster Philanthropy—Tornadoes. Available online: https://disasterphilanthropy.org/issue-insight/tornadoes/ (accessed on 4 January 2020).
- Changnon, S.A. Tornado losses in the United States. Nat. Hazards Rev. 2009, 10, 145–150. [Google Scholar] [CrossRef]
- Doswell, C.A., III; Brooks, H.E.; Dotzek, N. On the implementation of the enhanced Fujita scale in the USA. Atmos. Res. 2009, 93, 554–563. [Google Scholar] [CrossRef]
- Giordan, D.; Manconi, A.; Remondino, F.; Nex, F. Use of unmanned aerial vehicles in monitoring application and management of natural hazards. Geomat. Natl. Hazards Risk 2017, 8, 1–4. [Google Scholar] [CrossRef]
- Myint, S.W.; Yuan, M.; Cerveny, R.S.; Giri, C.P. Comparison of remote sensing image processing techniques to identify tornado damage areas from Landsat TM data. Sensors 2008, 8, 1128–1156. [Google Scholar] [CrossRef]
- Wang, W.; Qu, J.J.; Hao, X.; Liu, Y.; Stanturf, J.A. Post-hurricane forest damage assessment using satellite remote sensing. Agric. For. Meteorol. 2010, 150, 122–132. [Google Scholar] [CrossRef]
- Wagner, M.; Doe, R.K.; Johnson, A.; Chen, Z.; Das, J.; Cerveny, R.S. Unpiloted aerial systems (UASs) application for tornado damage surveys: Benefits and procedures. Bull. Am. Meteorol. Soc. 2019, 100, 2405–2409. [Google Scholar] [CrossRef]
- Diaz, J.; Joseph, M.B. Predicting property damage from tornadoes with zero-inflated neural networks. Weather Clim. Extrem. 2019, 25, 100216. [Google Scholar] [CrossRef]
- Le, V.; Caracoglia, L. A neural network surrogate model for the performance assessment of a vertical structure subjected to non-stationary, tornadic wind loads. Comput. Struct. 2020, 231, 106208. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical image computing and computer-assisted intervention, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask R-CNN. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Vakalopoulou, M.; Karantzalos, K.; Komodakis, N.; Paragios, N. Building detection in very high resolution multispectral data with deep learning features. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 1873–1876. [Google Scholar]
- Abdollahi, A.; Pradhan, B.; Alamri, A.M. An ensemble architecture of deep convolutional Segnet and Unet networks for building semantic segmentation from high-resolution aerial images. Geocarto Int. 2020, 1–16. [Google Scholar] [CrossRef]
- Sony, S.; Dunphy, K.; Sadhu, A.; Capretz, M. A systematic review of convolutional neural network-based structural condition assessment techniques. Eng. Struct. 2021, 226, 111347. [Google Scholar] [CrossRef]
- Pi, Y.; Nath, N.D.; Behzadan, A.H. Convolutional neural networks for object detection in aerial imagery for disaster response and recovery. Adv. Eng. Informatics 2020, 43, 101009. [Google Scholar] [CrossRef]
- Cao, Q.D.; Choe, Y. Post-Hurricane Damage Assessment Using Satellite Imagery and Geolocation Features. arXiv 2020, arXiv:2012.08624. [Google Scholar]
- Kakareko, G.; Jung, S.; Ozguven, E.E. Estimation of tree failure consequences due to high winds using convolutional neural networks. Int. J. Remote Sens. 2020, 41, 9039–9063. [Google Scholar] [CrossRef]
- Kocatepe, A.; Ulak, M.B.; Kakareko, G.; Ozguven, E.E.; Jung, S.; Arghandeh, R. Measuring the accessibility of critical facilities in the presence of hurricane-related roadway closures and an approach for predicting future roadway disruptions. Nat. Hazards 2019, 95, 615–635. [Google Scholar] [CrossRef]
- Li, Y.; Ye, S.; Bartoli, I. Semisupervised classification of hurricane damage from postevent aerial imagery using deep learning. J. Appl. Remote Sens. 2018, 12, 045008. [Google Scholar] [CrossRef]
- Abdollahi, A.; Pradhan, B.; Gite, S.; Alamri, A. Building footprint extraction from high resolution aerial images using Generative Adversarial Network (GAN) architecture. IEEE Access 2020, 8, 209517–209527. [Google Scholar] [CrossRef]
- Cheng, C.S.; Behzadan, A.H.; Noshadravan, A. Deep learning for post-hurricane aerial damage assessment of buildings. Comput.-Aided Civ. Infrastruct. Eng. 2020. [Google Scholar] [CrossRef]
- Kerle, N.; Nex, F.; Gerke, M.; Duarte, D.; Vetrivel, A. UAV-based structural damage mapping: A review. ISPRS Int. J. Geo-Inf. 2020, 9, 14. [Google Scholar] [CrossRef]
- Duarte, D.; Nex, F.; Kerle, N.; Vosselman, G. Satellite image classification of building damages using airborne and satellite image samples in a deep learning approach. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 4, 89–96. [Google Scholar] [CrossRef]
- Nex, F.; Duarte, D.; Tonolo, F.G.; Kerle, N. Structural building damage detection with deep learning: Assessment of a state-of-the-art CNN in operational conditions. Remote Sens. 2019, 11, 2765. [Google Scholar] [CrossRef]
- Mohammadi, M.E.; Watson, D.P.; Wood, R.L. Deep learning-based damage detection from aerial SfM point clouds. Drones 2019, 3, 68. [Google Scholar] [CrossRef]
- Liao, Y.; Mohammadi, M.E.; Wood, R.L. Deep learning classification of 2D orthomosaic images and 3D point clouds for post-event structural damage assessment. Drones 2020, 4, 24. [Google Scholar] [CrossRef]
- Krawczyk, B. Learning from imbalanced data: Open challenges and future directions. Prog. Artif. Intell. 2016, 5, 221–232. [Google Scholar] [CrossRef]
- National Centers for Environmental Information. Available online: https://www.ncdc.noaa.gov/stormevents/eventdetails.jsp?id=757551 (accessed on 11 November 2018).
- Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. ’Structure-from-Motion’ photogrammetry: A low-cost, effective tool for geoscience applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef]
- NOAA Damage Assessment Toolkit. Available online: https://apps.dat.noaa.gov/StormDamage/DamageViewer/ (accessed on 5 January 2021).
- Agisoft. Available online: https://www.agisoft.com/ (accessed on 8 May 2020).
- Johnson, K.; Nissen, E.; Saripalli, S.; Arrowsmith, J.R.; McGarey, P.; Scharer, K.; Williams, P.; Blisniuk, K. Rapid mapping of ultrafine fault zone topography with structure from motion. Geosphere 2014, 10, 969–986. [Google Scholar] [CrossRef]
- Chen, Z.; Scott, T.R.; Bearman, S.; Anand, H.; Keating, D.; Scott, C.; Arrowsmith, J.R.; Das, J. Geomorphological analysis using unpiloted aircraft systems, structure from motion, and deep learning. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020; pp. 1276–1283. [Google Scholar]
- Labelbox. Available online: https://labelbox.com/ (accessed on 25 May 2020).
- Lin, T.Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2117–2125. [Google Scholar]
- Zagoruyko, S.; Komodakis, N. Wide residual networks. arXiv 2016, arXiv:1605.07146. [Google Scholar]
- Xie, S.; Girshick, R.; Dollár, P.; Tu, Z.; He, K. Aggregated residual transformations for deep neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1492–1500. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Marcel, S.; Rodriguez, Y. Torchvision the machine-vision package of torch. In Proceedings of the 18th ACM International Conference on Multimedia, Firenze, Italy, 25–29 October 2010; pp. 1485–1488. [Google Scholar]
- Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft coco: Common objects in context. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 740–755. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.-J.; Li, K.; Li, F. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes in Machine Learning; MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Gardner, J.R.; Pleiss, G.; Bindel, D.; Weinberger, K.Q.; Wilson, A.G. Gpytorch: Blackbox matrix-matrix gaussian process inference with gpu acceleration. arXiv 2018, arXiv:1809.11165. [Google Scholar]
- Bentley, J.L. Multidimensional binary search trees used for associative searching. Commun. ACM 1975, 18, 509–517. [Google Scholar] [CrossRef]
- Scikit-Learn: Sklearn.metrics.confusion_matrix. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.metrics.confusion_matrix.html (accessed on 15 February 2021).




| Roof Cover Failure | Roof Structure Failure | Debris | Tree | |
|---|---|---|---|---|
| no damage | <2% | no | sparsely scattered and coverage <1% | minor broken branch |
| minor damage | >2% and <50% | no | coverage >1% | major broken branch or broken trunk or visible root |
| major damage | >50% | yes |
| No Data (0) | No Damage (1) | EF0 (2) | EF1 (3) | EF2 (4) | EF3 (5) | |||
|---|---|---|---|---|---|---|---|---|
| No Data (0) | 0 | 1 | 2 | 3 | 4 | 5 | ||
| No Damage (1) | 0 | 1 | 1.5 | 2.5 | 3.5 | 3.5 | ||
| Minor Damage (2) | 0 | 1.5 | 2 | 3 | 3.5 | 4 | ||
| Major Damage (3) | 0 | 1.5 | 2.5 | 3.5 | 4 | 5 | ||
| [0, 1.5) | [1.5, 2) | [2, 2.5) | [2.5, 3) | [3, 4) | [4, 4.5) | [4.5, 5] | |||
|---|---|---|---|---|---|---|---|---|---|
| No Data (0) | 0 | ||||||||
| No Damage (1) | (1+)/2 | 1.5 | |||||||
| Minor Damage (2) | 1.5 | ( | 3.5 | ||||||
| Major Damage (3) | 3.5 | ||||||||
| (−inf, 0.5) | [0.5, 1.5) | [1.5, 2.5) | [2.5, 3.5) | [3.5, 4.5) | [4.5, +inf) | |
|---|---|---|---|---|---|---|
| EF Scale | No Data | No Damage | EF0 | EF1 | EF2 | EF3 |
| Section | Detection | mAP(IoU = [0.5:0.95]) | mAP(IoU = 0.5) | mAP(IoU = 0.75) | mAR(IoU = [0.5:0.95]) |
|---|---|---|---|---|---|
| 103 | Binary | 59.1% | 74.3% | 66.0% | 73.2% |
| Augmented binary | 58.9% | 72.3% | 65.5% | 72.8% | |
| Multi-class | 32.8% | 44.3% | 35.7% | 59.1% | |
| Augmented multi-class | 36.1% | 48.5% | 37.9% | 52.8% | |
| 102 | Binary | 48.2% | 63.0% | 50.7% | 63.3% |
| Augmented multi-class | 35.7% | 42.8% | 39.6% | 45.3% |
| Section | Classification | ResNet-152 | Wide ResnNet-101 | ResNeXt-101 | DenseNet-161 | DenseNet-201 |
|---|---|---|---|---|---|---|
| 103 | Binary | 83.5% | 84.2% | 83.8% | 84.8% | 83.5% |
| Multi-class | 76.2% | 77.9% | 81.5% | 78.9% | 80.9% | |
| 102 | Binary | 84.0% | ||||
| Multi-class | 74.0% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Wagner, M.; Das, J.; Doe, R.K.; Cerveny, R.S. Data-Driven Approaches for Tornado Damage Estimation with Unpiloted Aerial Systems. Remote Sens. 2021, 13, 1669. https://doi.org/10.3390/rs13091669
Chen Z, Wagner M, Das J, Doe RK, Cerveny RS. Data-Driven Approaches for Tornado Damage Estimation with Unpiloted Aerial Systems. Remote Sensing. 2021; 13(9):1669. https://doi.org/10.3390/rs13091669
Chicago/Turabian StyleChen, Zhiang, Melissa Wagner, Jnaneshwar Das, Robert K. Doe, and Randall S. Cerveny. 2021. "Data-Driven Approaches for Tornado Damage Estimation with Unpiloted Aerial Systems" Remote Sensing 13, no. 9: 1669. https://doi.org/10.3390/rs13091669
APA StyleChen, Z., Wagner, M., Das, J., Doe, R. K., & Cerveny, R. S. (2021). Data-Driven Approaches for Tornado Damage Estimation with Unpiloted Aerial Systems. Remote Sensing, 13(9), 1669. https://doi.org/10.3390/rs13091669






