Estimating Agricultural Soil Moisture Content through UAV-Based Hyperspectral Images in the Arid Region
Abstract
1. Introduction
2. Materials and Methods
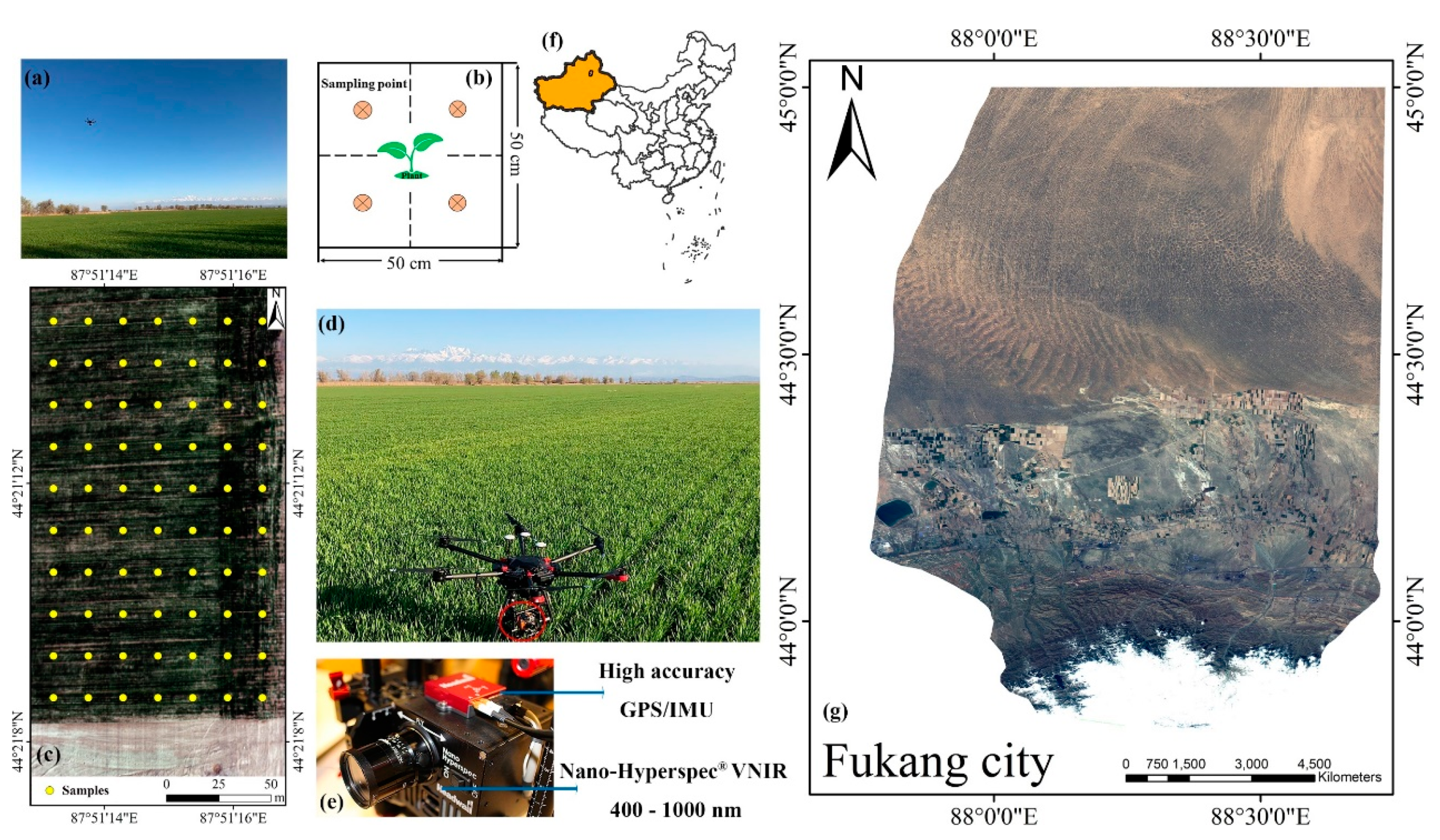
2.1. Study Area and Data Collection
2.1.1. Study Area
2.1.2. Soil Moisture Content Measurement
2.1.3. Hyperspectral Imaging Measurement
2.2. FOD Strategy
2.3. MI Strategy
2.4. XGBoost
2.5. Model Evaluation and Strategies
3. Results
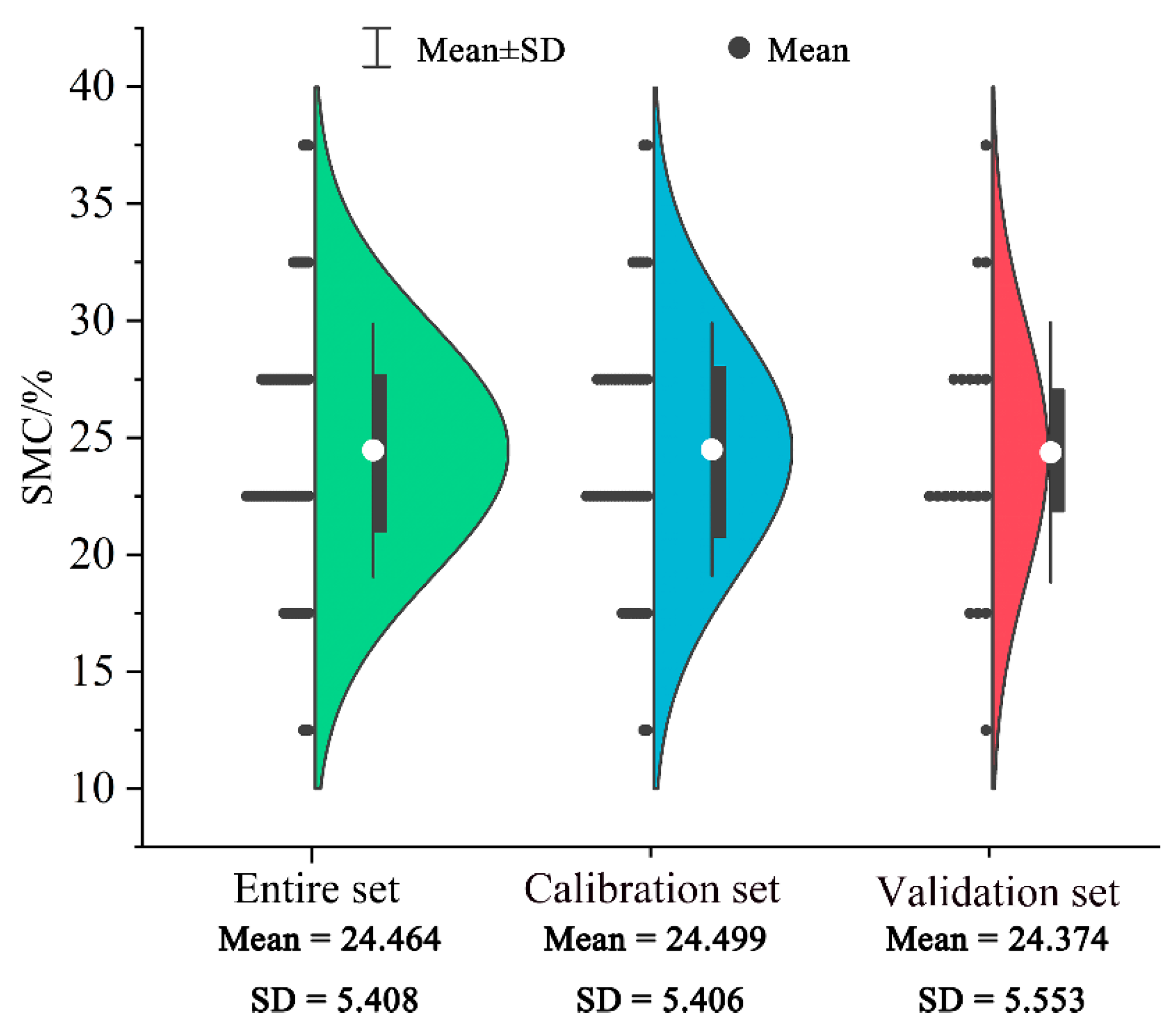
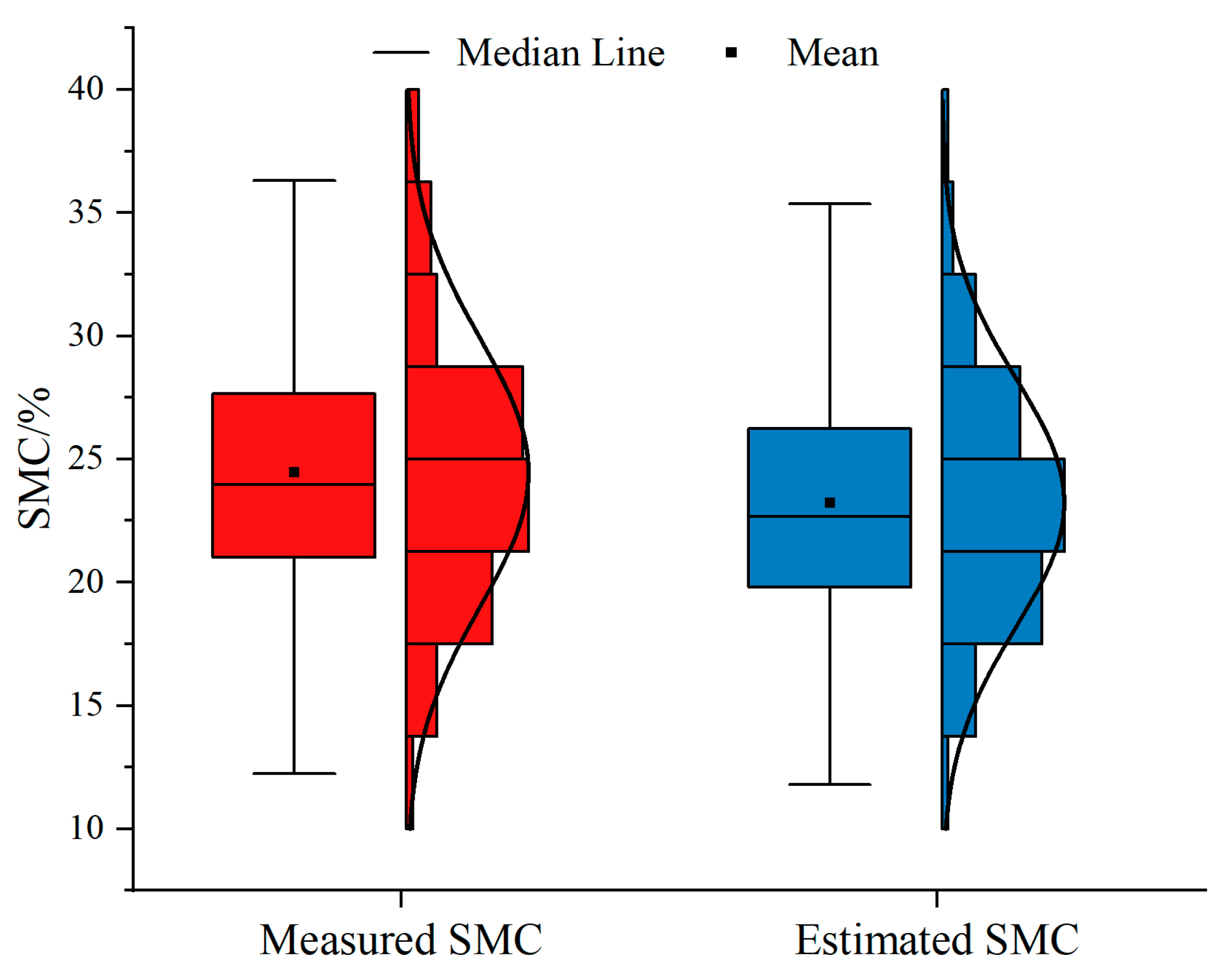
3.1. Descriptive Statistics
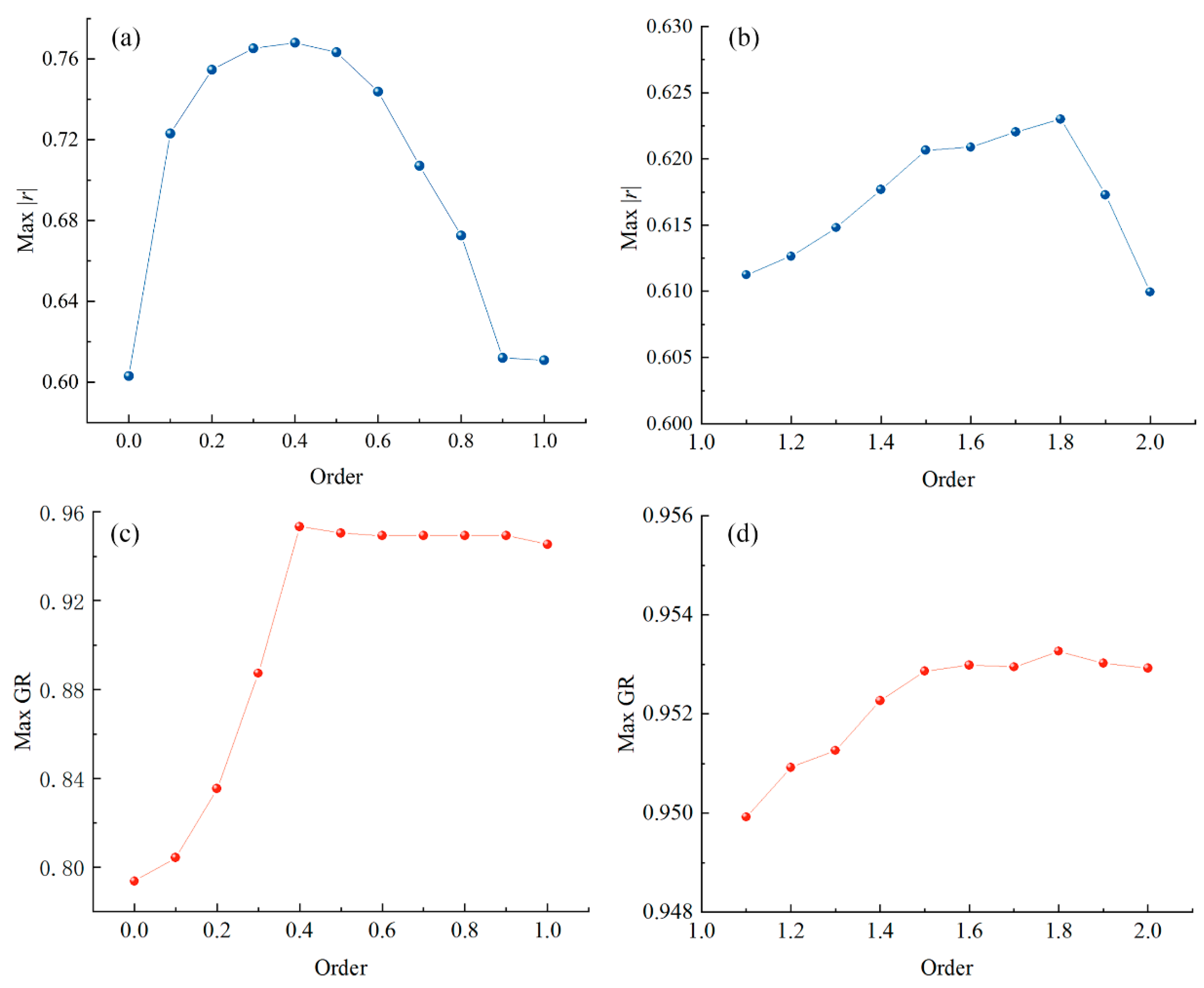
3.2. The Evaluation of the FOD Strategy
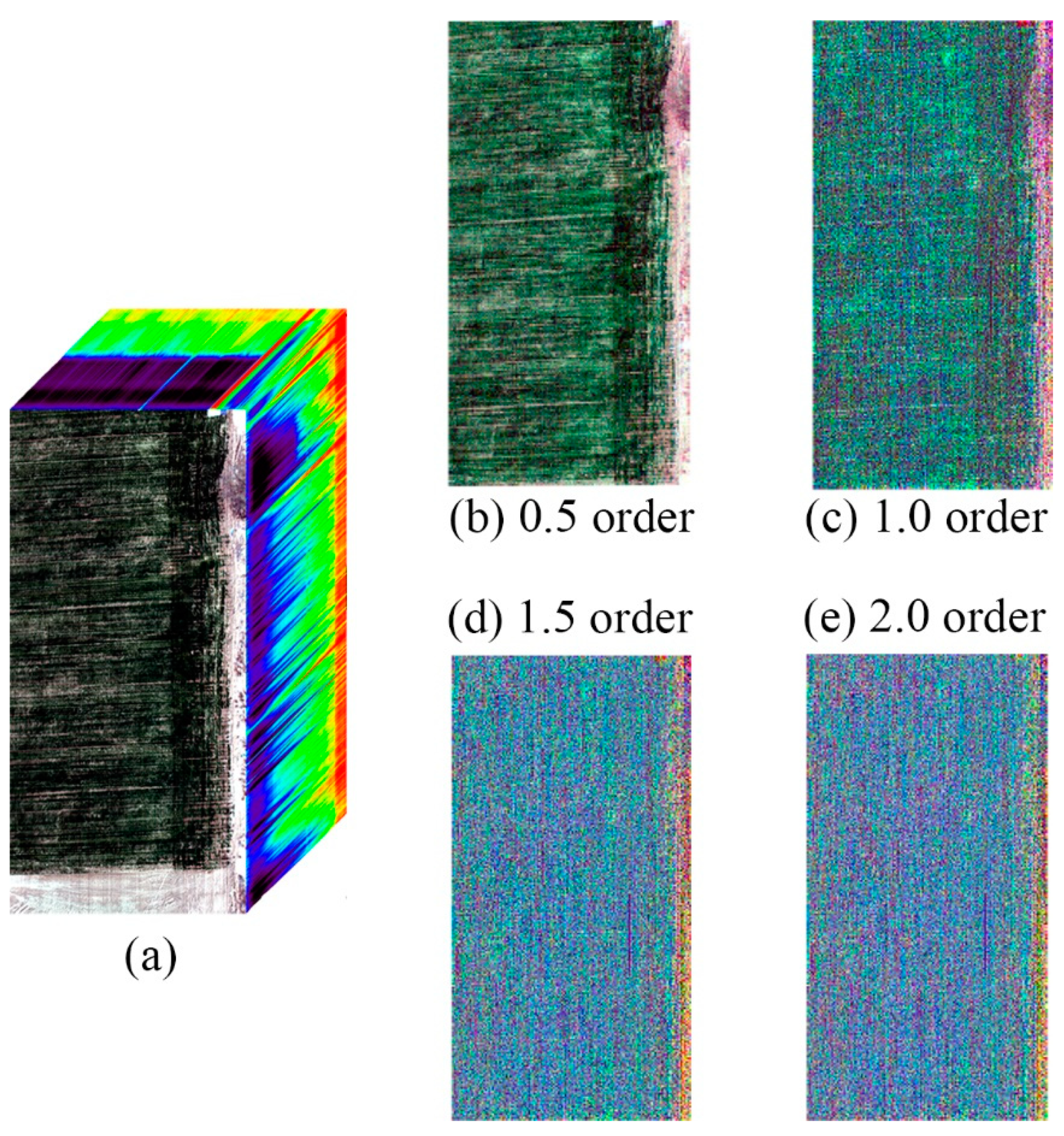
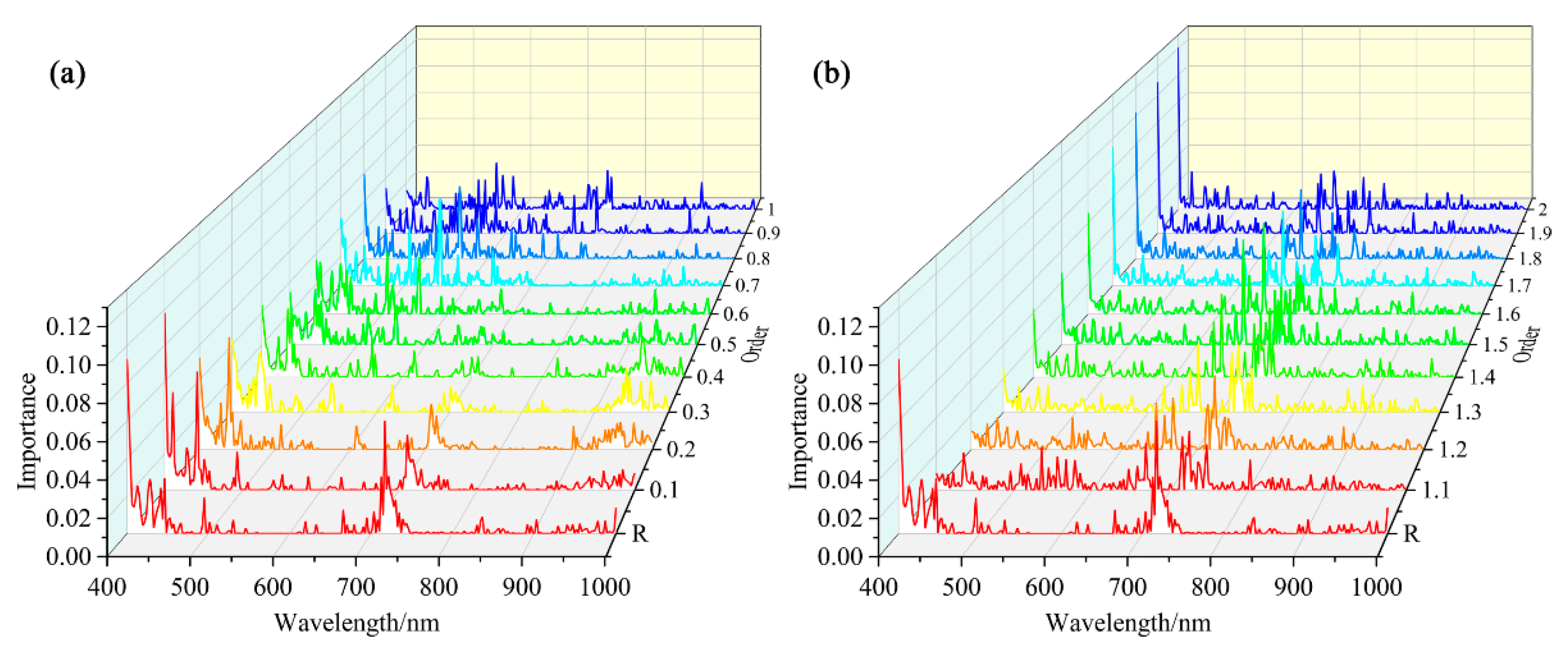
3.2.1. Varying Features of Spectra and Images Based on the FOD
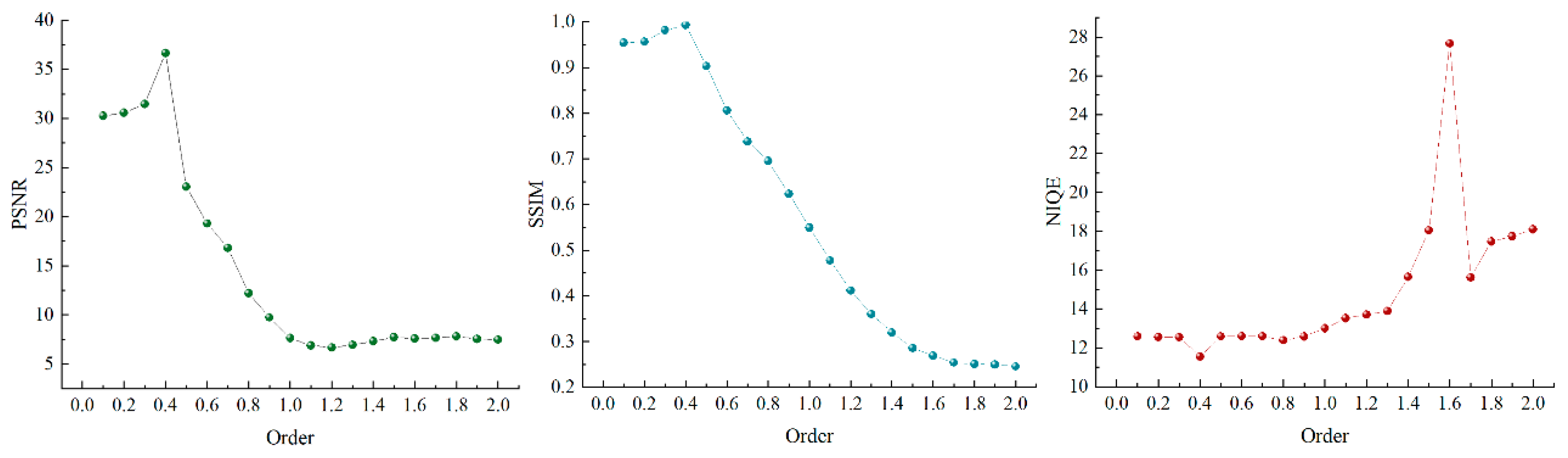
3.2.2. Effects of the Spectra and Images Based on FOD
3.3. MI Strategy
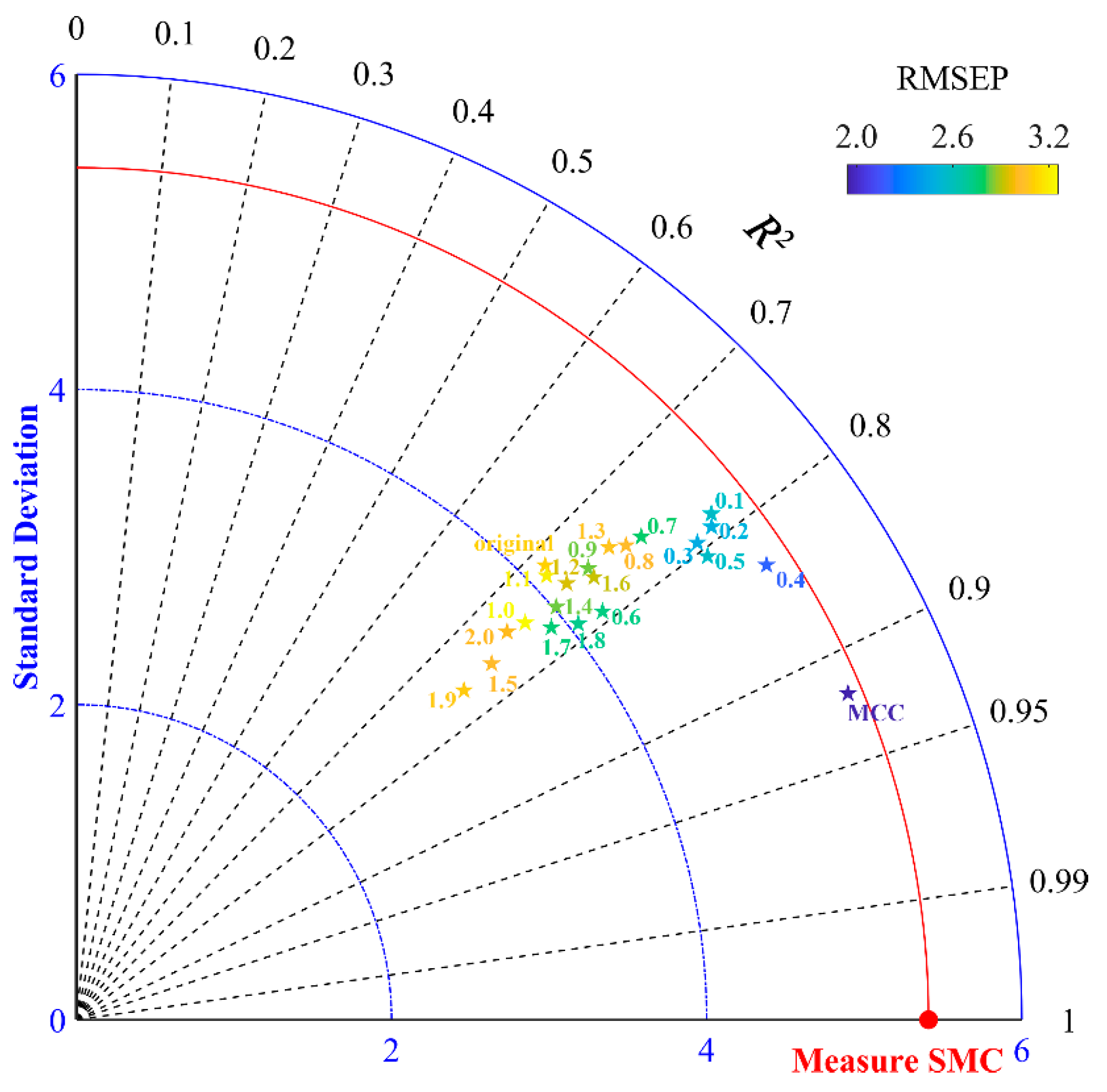
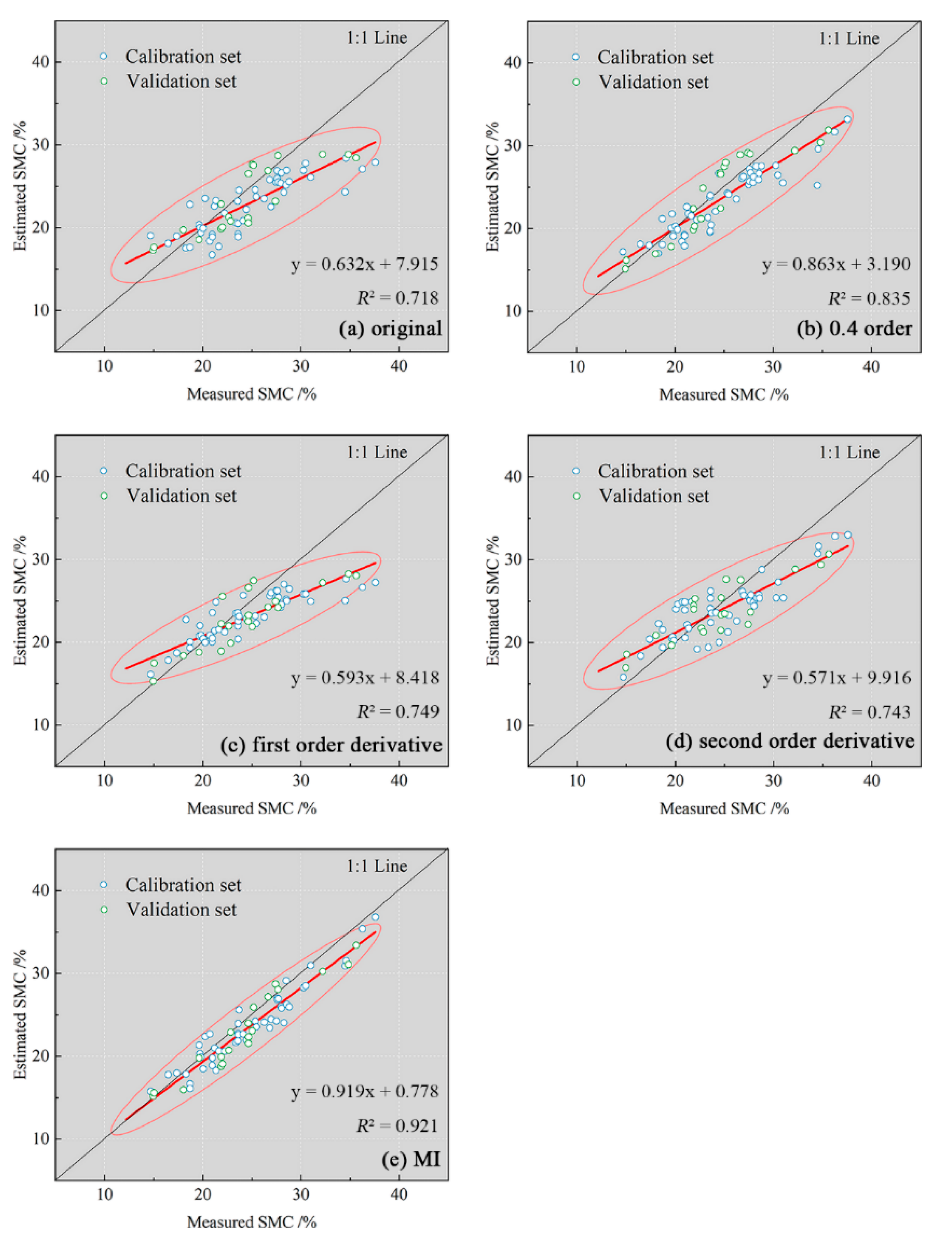
3.4. Construction and Evaluation of the Estimation Model
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| UAV | unmanned aerial vehicle |
| SMC | soil moisture content |
| XGBoost | eXtreme Gradient Boost |
| FOD | fractional-order derivative |
| MI | multiband indices |
| RGB | red–green–blue |
| R2 | the coefficient of determination |
| R2cal | the coefficient of determination about calibration |
| R2val | the coefficient of determination about validation |
| RMSE | the root mean square errors |
| RMSEC | the root mean square errors about the calibration set |
| RMSEP | the root mean square errors about the validation set |
| RPD | the ratio of the performance to the deviation |
| Vis-NIR | visible and near-infrared |
| IODs | integer-order derivatives |
| S-G | second-order polynomial smoothing and five-band smoothing |
| SD | standard deviation |
| G-L | Grünwald–Letnikov |
| PSNR | peak signal-to-noise ratio |
| SSIM | structural similarity index |
| NIQE | naturalness image quality evaluator |
| GRA | gray relational analyses |
| GR | gray relational grade |
| DI | difference index |
| RI | ratio index |
| NDI | normalized difference index |
| SPXY | sample partitioning used a joint x–y distance |
| r | correlation coefficient |
| max | maximum |
| min | minimum |
References
- Humphrey, V.; Berg, A.; Ciais, P.; Gentine, P.; Jung, M.; Reichstein, M.; Seneviratne, S.I.; Frankenberg, C. Soil moisture—Atmosphere feedback dominates land carbon uptake variability. Nature 2021, 592, 65–69. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Gudmundsson, L.; Hauser, M.; Qin, D.; Li, S.; Seneviratne, S.I. Soil moisture dominates dryness stress on ecosystem production globally. Nat. Commun. 2020, 11, 4892. [Google Scholar] [CrossRef] [PubMed]
- Lian, X.; Piao, S.; Chen, A.; Huntingford, C.; Fu, B.; Li, L.Z.X.; Huang, J.; Sheffield, J.; Berg, A.M.; Keenan, T.F.; et al. Multifaceted characteristics of dryland aridity changes in a warming world. Nat. Rev. Earth Environ. 2021. [Google Scholar] [CrossRef]
- Rockström, J.; Falkenmark, M.; Karlberg, L.; Hoff, H.; Rost, S.; Gerten, D. Future water availability for global food production: The potential of green water for increasing resilience to global change. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Iizumi, T.; Sakuma, H.; Yokozawa, M.; Luo, J.-J.; Challinor, A.J.; Brown, M.E.; Sakurai, G.; Yamagata, T. Prediction of seasonal climate-induced variations in global food production. Nat. Clim. Chang. 2013, 3, 904–908. [Google Scholar] [CrossRef]
- Cleverly, J.; Eamus, D.; Restrepo Coupe, N.; Chen, C.; Maes, W.; Li, L.; Faux, R.; Santini, N.S.; Rumman, R.; Yu, Q.; et al. Soil moisture controls on phenology and productivity in a semi-arid critical zone. Sci. Total Environ. 2016, 568, 1227–1237. [Google Scholar] [CrossRef]
- Stagakis, S.; González-Dugo, V.; Cid, P.; Guillén-Climent, M.L.; Zarco-Tejada, P.J. Monitoring water stress and fruit quality in an orange orchard under regulated deficit irrigation using narrow-band structural and physiological remote sensing indices. ISPRS J. Photogramm. Remote Sens. 2012, 71, 47–61. [Google Scholar] [CrossRef]
- Stagakis, S.; Markos, N.; Sykioti, O.; Kyparissis, A. Monitoring canopy biophysical and biochemical parameters in ecosystem scale using satellite hyperspectral imagery: An application on a Phlomis fruticosa Mediterranean ecosystem using multiangular CHRIS/PROBA observations. Remote Sens. Environ. 2010, 114, 977–994. [Google Scholar] [CrossRef]
- Martínez-Fernández, J.; González-Zamora, A.; Sánchez, N.; Gumuzzio, A.; Herrero-Jiménez, C.M. Satellite soil moisture for agricultural drought monitoring: Assessment of the SMOS derived Soil Water Deficit Index. Remote Sens. Environ. 2016, 177, 277–286. [Google Scholar] [CrossRef]
- Xu, S.; Liu, Y.; Wang, X.; Zhang, G. Scale effect on spatial patterns of ecosystem services and associations among them in semi-arid area: A case study in Ningxia Hui Autonomous Region, China. Sci. Total Environ. 2017, 598, 297–306. [Google Scholar] [CrossRef]
- Xue, J.; Guan, H.; Huo, Z.; Wang, F.; Huang, G.; Boll, J. Water saving practices enhance regional efficiency of water consumption and water productivity in an arid agricultural area with shallow groundwater. Agric. Water Manag. 2017, 194, 78–89. [Google Scholar] [CrossRef]
- Maes, W.H.; Steppe, K. Perspectives for Remote Sensing with Unmanned Aerial Vehicles in Precision Agriculture. Trends Plant Sci. 2019, 24, 152–164. [Google Scholar] [CrossRef]
- Jin, X.; Liu, S.; Baret, F.; Hemerlé, M.; Comar, A. Estimates of plant density of wheat crops at emergence from very low altitude UAV imagery. Remote Sens. Environ. 2017, 198, 105–114. [Google Scholar] [CrossRef]
- Brook, A.; De Micco, V.; Battipaglia, G.; Erbaggio, A.; Ludeno, G.; Catapano, I.; Bonfante, A. A smart multiple spatial and temporal resolution system to support precision agriculture from satellite images: Proof of concept on Aglianico vineyard. Remote Sens. Environ. 2020, 240, 111679. [Google Scholar] [CrossRef]
- Camino, C.; González-Dugo, V.; Hernández, P.; Sillero, J.C.; Zarco-Tejada, P.J. Improved nitrogen retrievals with airborne-derived fluorescence and plant traits quantified from VNIR-SWIR hyperspectral imagery in the context of precision agriculture. Int. J. Appl. Earth Obs. Geoinf. 2018, 70, 105–117. [Google Scholar] [CrossRef]
- Bian, J.; Zhang, Z.; Chen, J.; Chen, H.; Cui, C.; Li, X.; Chen, S.; Fu, Q. Simplified Evaluation of Cotton Water Stress Using High Resolution Unmanned Aerial Vehicle Thermal Imagery. Remote Sens. 2019, 11. [Google Scholar] [CrossRef]
- Bhatti, A.U.; Mulla, D.J.; Frazier, B.E. Estimation of soil properties and wheat yields on complex eroded hills using geostatistics and thematic mapper images. Remote Sens. Environ. 1991, 37, 181–191. [Google Scholar] [CrossRef]
- Zhou, Z.; Majeed, Y.; Diverres Naranjo, G.; Gambacorta, E.M.T. Assessment for crop water stress with infrared thermal imagery in precision agriculture: A review and future prospects for deep learning applications. Comput. Electron. Agric. 2021, 182, 106019. [Google Scholar] [CrossRef]
- Mulla, D.J. Twenty five years of remote sensing in precision agriculture: Key advances and remaining knowledge gaps. Biosyst. Eng. 2013, 114, 358–371. [Google Scholar] [CrossRef]
- Pulley, S.; Collins, A.L. Sediment loss in response to scheduled pasture ploughing and reseeding: The importance of soil moisture content in controlling risk. Soil and Tillage Research 2020, 204, 104746. [Google Scholar] [CrossRef]
- Jin, X.; Song, K.; Du, J.; Liu, H.; Wen, Z. Comparison of different satellite bands and vegetation indices for estimation of soil organic matter based on simulated spectral configuration. Agric. For. Meteorol. 2017, 244–245, 57–71. [Google Scholar] [CrossRef]
- Ge, X.; Wang, J.; Ding, J.; Cao, X.; Zhang, Z.; Liu, J.; Li, X. Combining UAV-based hyperspectral imagery and machine learning algorithms for soil moisture content monitoring. PeerJ 2019, 7, e6926. [Google Scholar] [CrossRef]
- Guo, L.; Zhang, H.; Shi, T.; Chen, Y.; Jiang, Q.; Linderman, M. Prediction of soil organic carbon stock by laboratory spectral data and airborne hyperspectral images. Geoderma 2019, 337, 32–41. [Google Scholar] [CrossRef]
- Gago, J.; Douthe, C.; Coopman, R.E.; Gallego, P.P.; Ribas-Carbo, M.; Flexas, J.; Escalona, J.; Medrano, H. UAVs challenge to assess water stress for sustainable agriculture. Agric. Water Manag. 2015, 153, 9–19. [Google Scholar] [CrossRef]
- Maimaitijiang, M.; Sagan, V.; Sidike, P.; Maimaitiyiming, M.; Hartling, S.; Peterson, K.T.; Maw, M.J.W.; Shakoor, N.; Mockler, T.; Fritschi, F.B. Vegetation Index Weighted Canopy Volume Model (CVMVI) for soybean biomass estimation from Unmanned Aerial System-based RGB imagery. ISPRS J. Photogramm. Remote Sens. 2019, 151, 27–41. [Google Scholar] [CrossRef]
- Song, Z.; Zhang, Z.; Yang, S.; Ding, D.; Ning, J. Identifying sunflower lodging based on image fusion and deep semantic segmentation with UAV remote sensing imaging. Comput. Electron. Agric. 2020, 179, 105812. [Google Scholar] [CrossRef]
- Gerhards, M.; Schlerf, M.; Mallick, K.; Udelhoven, T. Challenges and Future Perspectives of Multi-/Hyperspectral Thermal Infrared Remote Sensing for Crop Water-Stress Detection: A Review. Remote Sens. 2019, 11. [Google Scholar] [CrossRef]
- Lei, F.; Crow, W.T.; Kustas, W.P.; Dong, J.; Yang, Y.; Knipper, K.R.; Anderson, M.C.; Gao, F.; Notarnicola, C.; Greifeneder, F.; et al. Data assimilation of high-resolution thermal and radar remote sensing retrievals for soil moisture monitoring in a drip-irrigated vineyard. Remote Sens. Environ. 2020, 239, 111622. [Google Scholar] [CrossRef] [PubMed]
- Khanal, S.; Fulton, J.; Shearer, S. An overview of current and potential applications of thermal remote sensing in precision agriculture. Comput. Electron. Agric. 2017, 139, 22–32. [Google Scholar] [CrossRef]
- Messina, G.; Modica, G. Applications of UAV Thermal Imagery in Precision Agriculture: State of the Art and Future Research Outlook. Remote Sens. 2020, 12. [Google Scholar] [CrossRef]
- Wagner, W.; Lemoine, G.; Rott, H. A Method for Estimating Soil Moisture from ERS Scatterometer and Soil Data. Remote Sens. Environ. 1999, 70, 191–207. [Google Scholar] [CrossRef]
- Walker, J.P.; Willgoose, G.R.; Kalma, J.D. In situ measurement of soil moisture: A comparison of techniques. J. Hydrol. 2004, 293, 85–99. [Google Scholar] [CrossRef]
- Rushton, K.R.; Eilers, V.H.M.; Carter, R.C. Improved soil moisture balance methodology for recharge estimation. J. Hydrol. 2006, 318, 379–399. [Google Scholar] [CrossRef]
- Jones, H.G. Irrigation scheduling: Advantages and pitfalls of plant-based methods. J. Exp. Bot. 2004, 55, 2427–2436. [Google Scholar] [CrossRef]
- Lobell, D.B.; Asner, G.P. Moisture Effects on Soil Reflectance. Soil Sci. Soc. Am. J. 2002, 66, 722–727. [Google Scholar] [CrossRef]
- Huang, S.; Ding, J.; Zou, J.; Liu, B.; Zhang, J.; Chen, W. Soil Moisture Retrival Based on Sentinel-1 Imagery under Sparse Vegetation Coverage. Sensors 2019, 19. [Google Scholar] [CrossRef] [PubMed]
- Ben-Dor, E.; Chabrillat, S.; Demattê, J.A.M.; Taylor, G.R.; Hill, J.; Whiting, M.L.; Sommer, S. Using Imaging Spectroscopy to study soil properties. Remote Sens. Environ. 2009, 113, S38–S55. [Google Scholar] [CrossRef]
- Peñuelas, J.; Gamon, J.A.; Fredeen, A.L.; Merino, J.; Field, C.B. Reflectance indices associated with physiological changes in nitrogen- and water-limited sunflower leaves. Remote Sens. Environ. 1994, 48, 135–146. [Google Scholar] [CrossRef]
- Rapaport, T.; Hochberg, U.; Shoshany, M.; Karnieli, A.; Rachmilevitch, S. Combining leaf physiology, hyperspectral imaging and partial least squares-regression (PLS-R) for grapevine water status assessment. ISPRS J. Photogramm. Remote Sens. 2015, 109, 88–97. [Google Scholar] [CrossRef]
- Dzikiti, S.; Verreynne, J.S.; Stuckens, J.; Strever, A.; Verstraeten, W.W.; Swennen, R.; Coppin, P. Determining the water status of Satsuma mandarin trees [Citrus Unshiu Marcovitch] using spectral indices and by combining hyperspectral and physiological data. Agric. For. Meteorol. 2010, 150, 369–379. [Google Scholar] [CrossRef]
- Ihuoma, S.O.; Madramootoo, C.A. Recent advances in crop water stress detection. Comput. Electron. Agric. 2017, 141, 267–275. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Plaza, A.; Dobigeon, N.; Parente, M.; Du, Q.; Gader, P.; Chanussot, J. Hyperspectral Unmixing Overview: Geometrical, Statistical, and Sparse Regression-Based Approaches. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 354–379. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Y.; Chen, Y.; Zhang, Y.; Shi, T.; Wang, J.; Hong, Y.; Fei, T.; Zhang, Y. The Influence of Spectral Pretreatment on the Selection of Representative Calibration Samples for Soil Organic Matter Estimation Using Vis-NIR Reflectance Spectroscopy. Remote Sens. 2019, 11. [Google Scholar] [CrossRef]
- Nawar, S.; Buddenbaum, H.; Hill, J.; Kozak, J.; Mouazen, A.M. Estimating the soil clay content and organic matter by means of different calibration methods of vis-NIR diffuse reflectance spectroscopy. Soil Tillage Res. 2016, 155, 510–522. [Google Scholar] [CrossRef]
- Shi, T.; Wang, J.; Chen, Y.; Wu, G. Improving the prediction of arsenic contents in agricultural soils by combining the reflectance spectroscopy of soils and rice plants. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 95–103. [Google Scholar] [CrossRef]
- Wang, J.; Ding, J.; Abulimiti, A.; Cai, L. Quantitative estimation of soil salinity by means of different modeling methods and visible-near infrared (VIS–NIR) spectroscopy, Ebinur Lake Wetland, Northwest China. PeerJ 2018, 6, e4703. [Google Scholar] [CrossRef]
- Hong, Y.; Shen, R.; Cheng, H.; Chen, S.; Chen, Y.; Guo, L.; He, J.; Liu, Y.; Yu, L.; Liu, Y. Cadmium concentration estimation in peri-urban agricultural soils: Using reflectance spectroscopy, soil auxiliary information, or a combination of both? Geoderma 2019, 354, 113875. [Google Scholar] [CrossRef]
- Hong, Y.; Chen, S.; Liu, Y.; Zhang, Y.; Yu, L.; Chen, Y.; Liu, Y.; Cheng, H.; Liu, Y. Combination of fractional order derivative and memory-based learning algorithm to improve the estimation accuracy of soil organic matter by visible and near-infrared spectroscopy. CATENA 2019, 174, 104–116. [Google Scholar] [CrossRef]
- Lao, C.; Chen, J.; Zhang, Z.; Chen, Y.; Ma, Y.; Chen, H.; Gu, X.; Ning, J.; Jin, J.; Li, X. Predicting the contents of soil salt and major water-soluble ions with fractional-order derivative spectral indices and variable selection. Comput. Electron. Agric. 2021, 182, 106031. [Google Scholar] [CrossRef]
- Hong, Y.; Guo, L.; Chen, S.; Linderman, M.; Mouazen, A.M.; Yu, L.; Chen, Y.; Liu, Y.; Liu, Y.; Cheng, H.; et al. Exploring the potential of airborne hyperspectral image for estimating topsoil organic carbon: Effects of fractional-order derivative and optimal band combination algorithm. Geoderma 2020, 365, 114228. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, F.; Kung, H.-t.; Johnson, V.C. New methods for improving the remote sensing estimation of soil organic matter content (SOMC) in the Ebinur Lake Wetland National Nature Reserve (ELWNNR) in northwest China. Remote Sens. Environ. 2018, 218, 104–118. [Google Scholar] [CrossRef]
- Yang, P.; van der Tol, C.; Verhoef, W.; Damm, A.; Schickling, A.; Kraska, T.; Muller, O.; Rascher, U. Using reflectance to explain vegetation biochemical and structural effects on sun-induced chlorophyll fluorescence. Remote Sens. Environ. 2019, 231, 110996. [Google Scholar] [CrossRef]
- Holzman, M.E.; Rivas, R.; Piccolo, M.C. Estimating soil moisture and the relationship with crop yield using surface temperature and vegetation index. Int. J. Appl. Earth Obs. Geoinf. 2014, 28, 181–192. [Google Scholar] [CrossRef]
- Sandholt, I.; Rasmussen, K.; Andersen, J. A simple interpretation of the surface temperature/vegetation index space for assessment of surface moisture status. Remote Sens. Environ. 2002, 79, 213–224. [Google Scholar] [CrossRef]
- Santos, W.J.R.; Silva, B.M.; Oliveira, G.C.; Volpato, M.M.L.; Lima, J.M.; Curi, N.; Marques, J.J. Soil moisture in the root zone and its relation to plant vigor assessed by remote sensing at management scale. Geoderma 2014, 221–222, 91–95. [Google Scholar] [CrossRef]
- El-Hendawy, S.E.; Al-Suhaibani, N.A.; Elsayed, S.; Hassan, W.M.; Dewir, Y.H.; Refay, Y.; Abdella, K.A. Potential of the existing and novel spectral reflectance indices for estimating the leaf water status and grain yield of spring wheat exposed to different irrigation rates. Agric. Water Manag. 2019, 217, 356–373. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Estimation of vegetation water content and photosynthetic tissue area from spectral reflectance: A comparison of indices based on liquid water and chlorophyll absorption features. Remote Sens. Environ. 2003, 84, 526–537. [Google Scholar] [CrossRef]
- Van der Meer, F. The effectiveness of spectral similarity measures for the analysis of hyperspectral imagery. Int. J. Appl. Earth Obs. Geoinf. 2006, 8, 3–17. [Google Scholar] [CrossRef]
- Steinberg, A.; Chabrillat, S.; Stevens, A.; Segl, K.; Foerster, S. Prediction of Common Surface Soil Properties Based on Vis-NIR Airborne and Simulated EnMAP Imaging Spectroscopy Data: Prediction Accuracy and Influence of Spatial Resolution. Remote Sens. 2016, 8, 613. [Google Scholar] [CrossRef]
- Metternicht, G.I.; Zinck, J.A. Remote sensing of soil salinity: Potentials and constraints. Remote Sens. Environ. 2003, 85, 1–20. [Google Scholar] [CrossRef]
- Lary, D.J.; Alavi, A.H.; Gandomi, A.H.; Walker, A.L. Machine learning in geosciences and remote sensing. Geosci. Front. 2016, 7, 3–10. [Google Scholar] [CrossRef]
- Nawar, S.; Mouazen, A.M. Predictive performance of mobile vis-near infrared spectroscopy for key soil properties at different geographical scales by using spiking and data mining techniques. CATENA 2017, 151, 118–129. [Google Scholar] [CrossRef]
- Hassan-Esfahani, L.; Torres-Rua, A.; Jensen, A.; McKee, M. Assessment of Surface Soil Moisture Using High-Resolution Multi-Spectral Imagery and Artificial Neural Networks. Remote Sens. 2015, 7. [Google Scholar] [CrossRef]
- Jin, X.; Du, J.; Liu, H.; Wang, Z.; Song, K. Remote estimation of soil organic matter content in the Sanjiang Plain, Northest China: The optimal band algorithm versus the GRA-ANN model. Agric. For. Meteorol. 2016, 218–219, 250–260. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, F.; Ding, J.; Kung, H.-t.; Latif, A.; Johnson, V.C. Estimation of soil salt content (SSC) in the Ebinur Lake Wetland National Nature Reserve (ELWNNR), Northwest China, based on a Bootstrap-BP neural network model and optimal spectral indices. Sci. Total Environ. 2018, 615, 918–930. [Google Scholar] [CrossRef]
- Chen, S.; Liang, Z.; Webster, R.; Zhang, G.; Zhou, Y.; Teng, H.; Hu, B.; Arrouays, D.; Shi, Z. A high-resolution map of soil pH in China made by hybrid modelling of sparse soil data and environmental covariates and its implications for pollution. Sci. Total Environ. 2019, 655, 273–283. [Google Scholar] [CrossRef]
- Nawar, S.; Mouazen, A.M. On-line vis-NIR spectroscopy prediction of soil organic carbon using machine learning. Soil Tillage Res. 2019, 190, 120–127. [Google Scholar] [CrossRef]
- Chen, S.; Martin, M.P.; Saby, N.P.A.; Walter, C.; Angers, D.A.; Arrouays, D. Fine resolution map of top- and subsoil carbon sequestration potential in France. Sci. Total Environ. 2018, 630, 389–400. [Google Scholar] [CrossRef]
- Jia, Y.; Jin, S.; Savi, P.; Gao, Y.; Tang, J.; Chen, Y.; Li, W. GNSS-R Soil Moisture Retrieval Based on a XGboost Machine Learning Aided Method: Performance and Validation. Remote Sens. 2019, 11. [Google Scholar] [CrossRef]
- Loggenberg, K.; Strever, A.; Greyling, B.; Poona, N. Modelling Water Stress in a Shiraz Vineyard Using Hyperspectral Imaging and Machine Learning. Remote Sens. 2018, 10, 202. [Google Scholar] [CrossRef]
- Wu, T.; Luo, J.; Dong, W.; Sun, Y.; Xia, L.; Zhang, X. Geo-Object-Based Soil Organic Matter Mapping Using Machine Learning Algorithms With Multi-Source Geo-Spatial Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1091–1106. [Google Scholar] [CrossRef]
- Tziachris, P.; Aschonitis, V.; Chatzistathis, T.; Papadopoulou, M. Assessment of spatial hybrid methods for predicting soil organic matter using DEM derivatives and soil parameters. CATENA 2019, 174, 206–216. [Google Scholar] [CrossRef]
- Kou, Y.; Li, J.; Wang, Y.; Li, C.; Tu, B.; Yao, M.; Li, X. Scale-dependent key drivers controlling methane oxidation potential in Chinese grassland soils. Soil Biol. Biochem. 2017, 111, 104–114. [Google Scholar] [CrossRef]
- Librán-Embid, F.; Klaus, F.; Tscharntke, T.; Grass, I. Unmanned aerial vehicles for biodiversity-friendly agricultural landscapes—A systematic review. Sci. Total Environ. 2020, 732, 139204. [Google Scholar] [CrossRef]
- Barreto, M.A.P.; Johansen, K.; Angel, Y.; McCabe, M.F. Radiometric Assessment of a UAV-Based Push-Broom Hyperspectral Camera. Sensors 2019, 19. [Google Scholar] [CrossRef]
- Pu, Y.; Zhou, J.; Yuan, X. Fractional Differential Mask: A Fractional Differential-Based Approach for Multiscale Texture Enhancement. IEEE Trans. Image Process. 2010, 19, 491–511. [Google Scholar] [CrossRef] [PubMed]
- He, N.; Wang, J.-B.; Zhang, L.-L.; Lu, K. An improved fractional-order differentiation model for image denoising. Signal Process. 2015, 112, 180–188. [Google Scholar] [CrossRef]
- Pu, Y.; Wang, W.; Zhou, J.; Wang, Y.; Jia, H. Fractional differential approach to detecting textural features of digital image and its fractional differential filter implementation. Sci. China Ser. F Inf. Sci. 2008, 51, 1319–1339. [Google Scholar] [CrossRef]
- Hong, Y.; Liu, Y.; Chen, Y.; Liu, Y.; Yu, L.; Liu, Y.; Cheng, H. Application of fractional-order derivative in the quantitative estimation of soil organic matter content through visible and near-infrared spectroscopy. Geoderma 2019, 337, 758–769. [Google Scholar] [CrossRef]
- Fu, C.; Gan, S.; Yuan, X.; Xiong, H.; Tian, A. Impact of Fractional Calculus on Correlation Coefficient between Available Potassium and Spectrum Data in Ground Hyperspectral and Landsat 8 Image. Mathematics 2019, 7, 488. [Google Scholar] [CrossRef]
- Lin, X.; Su, Y.-C.; Shang, J.; Sha, J.; Li, X.; Sun, Y.-Y.; Ji, J.; Jin, B. Geographically Weighted Regression Effects on Soil Zinc Content Hyperspectral Modeling by Applying the Fractional-Order Differential. Remote Sens. 2019, 11, 636. [Google Scholar] [CrossRef]
- Pande-Chhetri, R.; Abd-Elrahman, A. De-striping hyperspectral imagery using wavelet transform and adaptive frequency domain filtering. ISPRS J. Photogramm. Remote Sens. 2011, 66, 620–636. [Google Scholar] [CrossRef]
- Zhou, W.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Mittal, A.; Soundararajan, R.; Bovik, A.C. Making a “Completely Blind” Image Quality Analyzer. IEEE Signal Process. Lett. 2013, 20, 209–212. [Google Scholar] [CrossRef]
- Yue, J.; Feng, H.; Yang, G.; Li, Z. A Comparison of Regression Techniques for Estimation of Above-Ground Winter Wheat Biomass Using Near-Surface Spectroscopy. Remote Sens. 2018, 10. [Google Scholar] [CrossRef]
- Tian, Y.C.; Yao, X.; Yang, J.; Cao, W.X.; Hannaway, D.B.; Zhu, Y. Assessing newly developed and published vegetation indices for estimating rice leaf nitrogen concentration with ground- and space-based hyperspectral reflectance. Field Crop. Res. 2011, 120, 299–310. [Google Scholar] [CrossRef]
- Wang, J.; Ding, J.; Yu, D.; Ma, X.; Zhang, Z.; Ge, X.; Teng, D.; Li, X.; Liang, J.; Lizaga, I.; et al. Capability of Sentinel-2 MSI data for monitoring and mapping of soil salinity in dry and wet seasons in the Ebinur Lake region, Xinjiang, China. Geoderma 2019, 353, 172–187. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, F.; Qi, Y.; Deng, L.; Wang, X.; Yang, S. New research methods for vegetation information extraction based on visible light remote sensing images from an unmanned aerial vehicle (UAV). Int. J. Appl. Earth Obs. Geoinf. 2019, 78, 215–226. [Google Scholar] [CrossRef]
- Liang, Z.; Chen, S.; Yang, Y.; Zhou, Y.; Shi, Z. High-resolution three-dimensional mapping of soil organic carbon in China: Effects of SoilGrids products on national modeling. Sci. Total Environ. 2019, 685, 480–489. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13 August 2016; pp. 785–794. [Google Scholar]
- Galvão, R.K.H.; Araujo, M.C.U.; José, G.E.; Pontes, M.J.C.; Silva, E.C.; Saldanha, T.C.B. A method for calibration and validation subset partitioning. Talanta 2005, 67, 736–740. [Google Scholar] [CrossRef]
- Nawar, S.; Mouazen, M.A. Comparison between Random Forests, Artificial Neural Networks and Gradient Boosted Machines Methods of On-Line Vis-NIR Spectroscopy Measurements of Soil Total Nitrogen and Total Carbon. Sensors 2017, 17. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.-W.; Laird, D.A.; Mausbach, M.J.; Hurburgh, C.R. Near-Infrared Reflectance Spectroscopy—Principal Components Regression Analyses of Soil Properties. Soil Sci. Soc. Am. J. 2001, 65, 480–490. [Google Scholar] [CrossRef]
- Wetterlind, J.; Stenberg, B. Near-infrared spectroscopy for within-field soil characterization: Small local calibrations compared with national libraries spiked with local samples. Eur. J. Soil Sci. 2010, 61, 823–843. [Google Scholar] [CrossRef]
- Terhoeven-Urselmans, T.; Vagen, T.-G.; Spaargaren, O.; Shepherd, K.D. Prediction of Soil Fertility Properties from a Globally Distributed Soil Mid-Infrared Spectral Library. Soil Sci. Soc. Am. J. 2010, 74, 1792–1799. [Google Scholar] [CrossRef]
- Minasny, B.; Tranter, G.; McBratney, A.B.; Brough, D.M.; Murphy, B.W. Regional transferability of mid-infrared diffuse reflectance spectroscopic prediction for soil chemical properties. Geoderma 2009, 153, 155–162. [Google Scholar] [CrossRef]
- Côté, J.-F.; Fournier, R.A.; Luther, J.E.; van Lier, O.R. Fine-scale three-dimensional modeling of boreal forest plots to improve forest characterization with remote sensing. Remote Sens. Environ. 2018, 219, 99–114. [Google Scholar] [CrossRef]
- Tmušić, G.; Manfreda, S.; Aasen, H.; James, M.R.; Gonçalves, G.; Ben-Dor, E.; Brook, A.; Polinova, M.; Arranz, J.J.; Mészáros, J.; et al. Current Practices in UAS-based Environmental Monitoring. Remote Sens. 2020, 12. [Google Scholar] [CrossRef]
- Jalilvand, E.; Tajrishy, M.; Ghazi Zadeh Hashemi, S.A.; Brocca, L. Quantification of irrigation water using remote sensing of soil moisture in a semi-arid region. Remote Sens. Environ. 2019, 231, 111226. [Google Scholar] [CrossRef]
- Wang, J.; Shi, T.; Yu, D.; Teng, D.; Ge, X.; Zhang, Z.; Yang, X.; Wang, H.; Wu, G. Ensemble machine-learning-based framework for estimating total nitrogen concentration in water using drone-borne hyperspectral imagery of emergent plants: A case study in an arid oasis, NW China. Environ. Pollut. 2020, 266, 115412. [Google Scholar] [CrossRef]
- Zhang, Z.; Ding, J.; Wang, J.; Ge, X. Prediction of soil organic matter in northwestern China using fractional-order derivative spectroscopy and modified normalized difference indices. CATENA 2020, 185, 104257. [Google Scholar] [CrossRef]
- Xiaoping, W.; Fei, Z.; Hsiang-te, K.; Haiyang, Y. Spectral response characteristics and identification of typical plant species in Ebinur lake wetland national nature reserve (ELWNNR) under a water and salinity gradient. Ecol. Indic. 2017, 81, 222–234. [Google Scholar] [CrossRef]
- Maimaitiyiming, M.; Ghulam, A.; Bozzolo, A.; Wilkins, J.L.; Kwasniewski, M.T. Early Detection of Plant Physiological Responses to Different Levels of Water Stress Using Reflectance Spectroscopy. Remote Sens. 2017, 9. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated narrow-band vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Meng, X.; Bao, Y.; Liu, J.; Liu, H.; Zhang, X.; Zhang, Y.; Wang, P.; Tang, H.; Kong, F. Regional soil organic carbon prediction model based on a discrete wavelet analysis of hyperspectral satellite data. Int. J. Appl. Earth Obs. Geoinf. 2020, 89, 102111. [Google Scholar] [CrossRef]
- Zheng, H.; Li, W.; Jiang, J.; Liu, Y.; Cheng, T.; Tian, Y.; Zhu, Y.; Cao, W.; Zhang, Y.; Yao, X. A Comparative Assessment of Different Modeling Algorithms for Estimating Leaf Nitrogen Content in Winter Wheat Using Multispectral Images from an Unmanned Aerial Vehicle. Remote Sens. 2018, 10. [Google Scholar] [CrossRef]
- Gong, P.; Liu, H.; Zhang, M.; Li, C.; Wang, J.; Huang, H.; Clinton, N.; Ji, L.; Li, W.; Bai, Y.; et al. Stable classification with limited sample: Transferring a 30-m resolution sample set collected in 2015 to mapping 10-m resolution global land cover in 2017. Sci. Bull. 2019, 64, 370–373. [Google Scholar] [CrossRef]
- Zhou, B.; Erell, E.; Hough, I.; Shtein, A.; Just, A.C.; Novack, V.; Rosenblatt, J.; Kloog, I. Estimation of Hourly near Surface Air Temperature Across Israel Using an Ensemble Model. Remote Sens. 2020, 12. [Google Scholar] [CrossRef]
- He, M.; Kimball, J.S.; Running, S.; Ballantyne, A.; Guan, K.; Huemmrich, F. Satellite detection of soil moisture related water stress impacts on ecosystem productivity using the MODIS-based photochemical reflectance index. Remote Sens. Environ. 2016, 186, 173–183. [Google Scholar] [CrossRef]
- Jin, X.; Kumar, L.; Li, Z.; Feng, H.; Xu, X.; Yang, G.; Wang, J. A review of data assimilation of remote sensing and crop models. Eur. J. Agron. 2018, 92, 141–152. [Google Scholar] [CrossRef]
- Sagan, V.; Maimaitijiang, M.; Sidike, P.; Eblimit, K.; Peterson, T.K.; Hartling, S.; Esposito, F.; Khanal, K.; Newcomb, M.; Pauli, D.; et al. UAV-Based High Resolution Thermal Imaging for Vegetation Monitoring, and Plant Phenotyping Using ICI 8640 P, FLIR Vue Pro R 640, and thermoMap Cameras. Remote Sens. 2019, 11. [Google Scholar] [CrossRef]
- Deng, L.; Mao, Z.; Li, X.; Hu, Z.; Duan, F.; Yan, Y. UAV-based multispectral remote sensing for precision agriculture: A comparison between different cameras. ISPRS J. Photogramm. Remote Sens. 2018, 146, 124–136. [Google Scholar] [CrossRef]
- Jay, S.; Baret, F.; Dutartre, D.; Malatesta, G.; Héno, S.; Comar, A.; Weiss, M.; Maupas, F. Exploiting the centimeter resolution of UAV multispectral imagery to improve remote-sensing estimates of canopy structure and biochemistry in sugar beet crops. Remote Sens. Environ. 2019, 231, 110898. [Google Scholar] [CrossRef]



| Method | Advantage | Disadvantage | References |
|---|---|---|---|
| Oven drying technique | Regular and accurate measurement of the soil water content | Labor-intensive, destructive and time-consuming | [31] |
| In situ sensors | Real-time monitoring, measuring the soil profile moisture | Needs multiple sensors | [32] |
| Soil–water balance approach | Good indicator of the amount of irrigation water and easy to apply | Inaccurate, vulnerable to meteorological conditions | [33] |
| Plant-based approaches | Indirect estimation of plant statuses to understand the effects of drought stress on vegetation | Labor-intensive, destructive, time consuming, requires complex instrumentation | [34] |
| Near-grounded photoelectric technology | Timely, nondestructive, and high spectral resolution | Independent point data lack a spatial scale | [35] |
| Space-borne photoelectric technology | Large scale, nondestructive | Vulnerable to clouds and rain, contradiction among spatial, temporal and spectral resolutions | [36] |
| UAV-based photoelectric technology | Nondestructive, highly maneuverable, centimeter resolution, and rich photoelectric information | Requisite image analysis is still a challenging task, reduced precision | [22] |
| Thermography | Effectively identified SMC and water stress from plant temperature | Lower image resolution | [18] |
| Spectral Range (nm) | Band | Function |
|---|---|---|
| 400–420 | Violet-Blue | Strong absorption of chlorophyll |
| 420–440 | Blue | Strong absorption of chlorophyll a and carotenoids |
| 440–460 | Strong absorption of chlorophyll | |
| 460–500 | Strong absorption of carotenoids | |
| 520–540 | Green | Strong reflection of chlorophyll and phycoerythrin absorption peak |
| 540–640 | Green and Red | Phycoerythrin absorption peak |
| 640–660 | Red | Strong absorption of chlorophyll and phycoerythrin absorption peak |
| 660–680 | Strong absorption of chlorophyll, absorption trough of most vegetation, red edge | |
| 680–750 | NIR | Red edge region |
| 820–860 | High Reflection of vegetation and the top of red edge region | |
| 880–900 | Reflection peak of vegetation |
| Details | Items | Specifications |
|---|---|---|
| Drone | Version | DJI MATRICE 600 PRO |
| Weight | 10 kg | |
| Dimensions | 1668 mm × 1518 mm × 727 mm with propellers, frame arms and GPS mount unfolded (including landing gear) | |
| Max speed | 65 km/h | |
| Flight control system | A3 Pro | |
| Hyperspectral camera | Camera | Headwall Nano-Hyperspec hyperspectral sensor |
| Dispersion/Pixel | 2.2 nm/pixel | |
| Wavelength range | 400–1000 nm | |
| FWHM Slit Image | 6 nm | |
| Spectral bands | 271 | |
| Spatial bands | 640 | |
| Max Frame Rate | 300 Hz | |
| GIMBAL | Version | DJI RONIN-MX |
| Controlled Rotation Range | Pan axis control: 360° Tilt axis control: +45° to −135° Roll axis control: ±25° | |
| Angular Vibration Range | ±0.02° | |
| Operating environment | −15 °C–50 °C | |
| Remote Control | Operating Frequency | 2.400–2.483 GHz |
| Max Operating Distance | 5 km | |
| Battery | Supported Battery Configurations | TB48S |
| Modeling Strategies | Method |
|---|---|
| Strategy I | The original image (order = 0) |
| Strategy II | The first- and second-order derivatives (order = 1 and 2) |
| Strategy III | The FOD (order = 0.1–0.9 and 1.1–1.9) |
| Strategy IV | The optimal pretreatment scheme combined with the MI scheme |
| MI | Max |r| | Bands of MI | MI | Max |r| | Bands of MI |
|---|---|---|---|---|---|
| MI1 | 0.812 | R644, R648, R513 | MI6 | 0.770 | R710, R753, R524 |
| MI2 | 0.797 | R446, R959, R559 | MI7 | 0.776 | R959, R446, R893 |
| MI3 | 0.799 | R446, R959, R651 | MI8 | 0.818 | R635, R651, R446 |
| MI4 | 0.783 | R710, R753, R524 | MI9 | 0.770 | R651, R648V, R531 |
| MI5 | 0.803 | R959, R651, R446 | MI10 | 0.781 | R651, R448, R446 |
| Model Strategy | R2cal | RMSEC | R2val | RMSEP | RPD |
|---|---|---|---|---|---|
| 0 order | 0.719 | 3.623 | 0.718 | 3.109 | 1.333 |
| 0.1 order | 0.784 | 3.181 | 0.782 | 2.566 | 2.008 |
| 0.2 order | 0.794 | 3.179 | 0.790 | 2.496 | 2.044 |
| 0.3 order | 0.791 | 3.090 | 0.793 | 2.461 | 2.019 |
| 0.4 order | 0.851 | 2.707 | 0.835 | 2.208 | 2.375 |
| 0.5 order | 0.805 | 3.076 | 0.806 | 2.573 | 1.932 |
| 0.6 order | 0.780 | 3.142 | 0.790 | 2.731 | 1.547 |
| 0.7 order | 0.762 | 3.279 | 0.760 | 2.774 | 1.700 |
| 0.8 order | 0.781 | 3.539 | 0.757 | 3.023 | 1.525 |
| 0.9 order | 0.784 | 3.268 | 0.750 | 2.828 | 1.531 |
| 1 order | 0.768 | 3.518 | 0.749 | 3.257 | 1.117 |
| 1.1 order | 0.754 | 3.590 | 0.727 | 3.213 | 1.277 |
| 1.2 order | 0.746 | 3.577 | 0.747 | 2.944 | 1.415 |
| 1.3 order | 0.758 | 3.435 | 0.748 | 3.054 | 1.479 |
| 1.4 order | 0.777 | 3.123 | 0.758 | 2.834 | 1.418 |
| 1.5 order | 0.781 | 2.974 | 0.759 | 3.026 | 1.147 |
| 1.6 order | 0.791 | 3.533 | 0.760 | 2.922 | 1.479 |
| 1.7 order | 0.795 | 2.847 | 0.771 | 2.762 | 1.415 |
| 1.8 order | 0.806 | 2.684 | 0.785 | 2.704 | 1.500 |
| 1.9 order | 0.780 | 3.035 | 0.762 | 3.076 | 1.049 |
| 2 order | 0.751 | 2.910 | 0.743 | 3.000 | 1.226 |
| MI | 0.921 | 1.956 | 0.921 | 1.943 | 2.736 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, X.; Ding, J.; Jin, X.; Wang, J.; Chen, X.; Li, X.; Liu, J.; Xie, B. Estimating Agricultural Soil Moisture Content through UAV-Based Hyperspectral Images in the Arid Region. Remote Sens. 2021, 13, 1562. https://doi.org/10.3390/rs13081562
Ge X, Ding J, Jin X, Wang J, Chen X, Li X, Liu J, Xie B. Estimating Agricultural Soil Moisture Content through UAV-Based Hyperspectral Images in the Arid Region. Remote Sensing. 2021; 13(8):1562. https://doi.org/10.3390/rs13081562
Chicago/Turabian StyleGe, Xiangyu, Jianli Ding, Xiuliang Jin, Jingzhe Wang, Xiangyue Chen, Xiaohang Li, Jie Liu, and Boqiang Xie. 2021. "Estimating Agricultural Soil Moisture Content through UAV-Based Hyperspectral Images in the Arid Region" Remote Sensing 13, no. 8: 1562. https://doi.org/10.3390/rs13081562
APA StyleGe, X., Ding, J., Jin, X., Wang, J., Chen, X., Li, X., Liu, J., & Xie, B. (2021). Estimating Agricultural Soil Moisture Content through UAV-Based Hyperspectral Images in the Arid Region. Remote Sensing, 13(8), 1562. https://doi.org/10.3390/rs13081562










