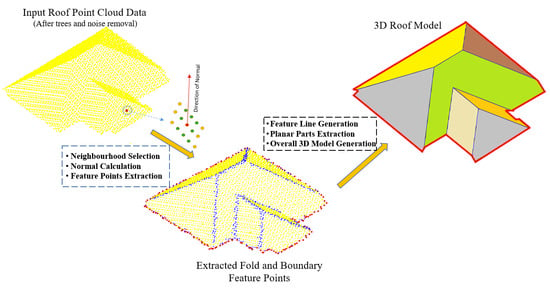
Effective Selection of Variable Point Neighbourhood for Feature Point Extraction from Aerial Building Point Cloud Data
Abstract
1. Introduction
- In the context of calculating an accurate normal, a new robust method is proposed for automatic selection of neighbouring points of each point in a LiDAR point cloud data. This proposed method can select the optimal minimum number of neighbouring points and, thus, can solve the existing problems of accurate normal calculation of individual points.
- Based on the calculated direction of the normal, we propose an effective method for finding the fold feature points. Maximum angle differences of the neighbouring normal vectors are clustered, and an experimentally selected threshold is adopted to decide fold edge points.
- To find the boundaries of individual objects, a new method for boundary point detection is suggested. This method depends on the distance from a point to the calculated mean of its neighbouring points, selected by the proposed technique of automatic neighbouring point selection.
2. Review
2.1. Neighbourhood Selection
2.2. Normal Vector Calculation
2.3. Feature Point Extraction
3. Proposed Method
3.1. Estimating Minimal Neighbourhood
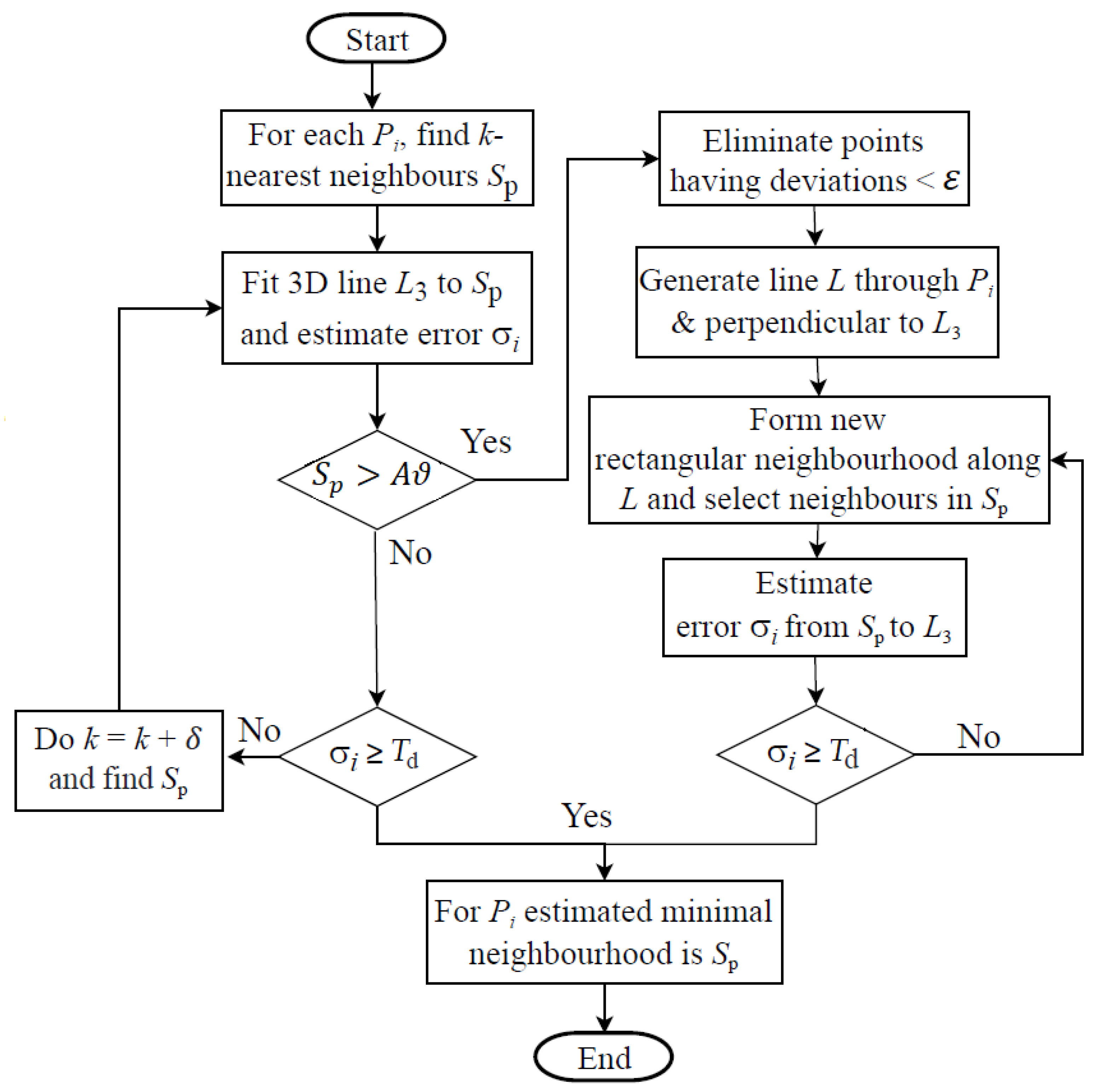
- The proposed method first selects a minimal number of neighbouring points (say, since a minimum of 3 points are necessary to calculate a plane normal) for using the k-NN algorithm. Let the set of neighbouring points be including the point .
- A best fit 3D line is constructed using . The distance from each point of to is calculated.
- The standard deviation of the calculated distances is compared with a selected distance threshold . If , the value of k is increased (say, k = ) and the procedure is repeated with the updated . Ideally, is set to iteratively find a minimal value of k for . However, to avoid a large number of iterations, is selected and, once a minimal k is found, a smaller minimal k is obtained by testing its previous values.is equal to the distance between two neighbouring points in the case of regular distribution of LiDAR points and can be calculated using Equation (3) according to Tarsha-Kurdi et al. [59], where represents the input point density. The mean area occupied by a single LiDAR point is in a square form, and the area of the square is equal to the inverse of the point density in a regular distributed point cloud data. The side length of the square represents the mean distance between two neighbouring points that satisfies Equation (3).
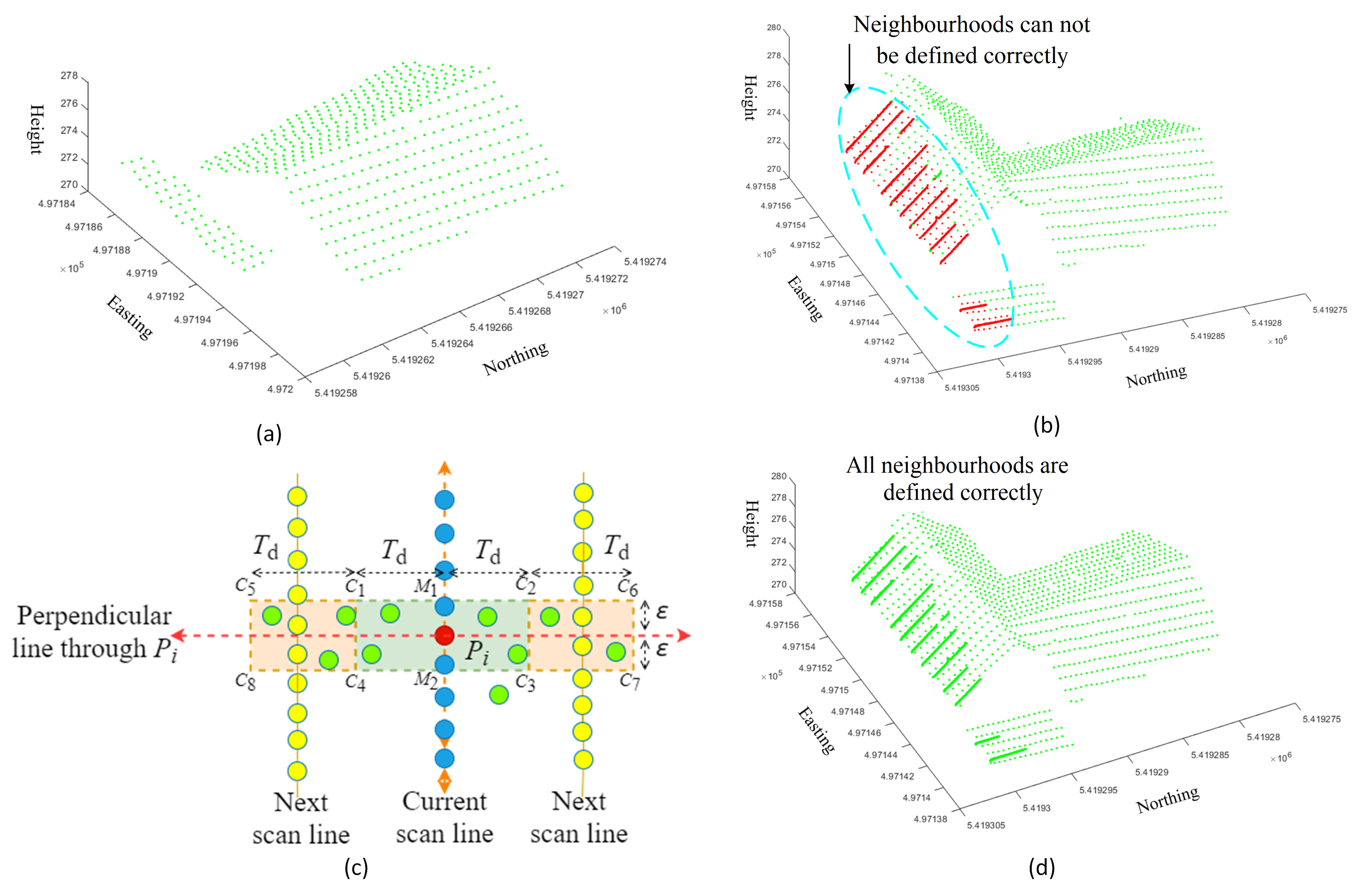
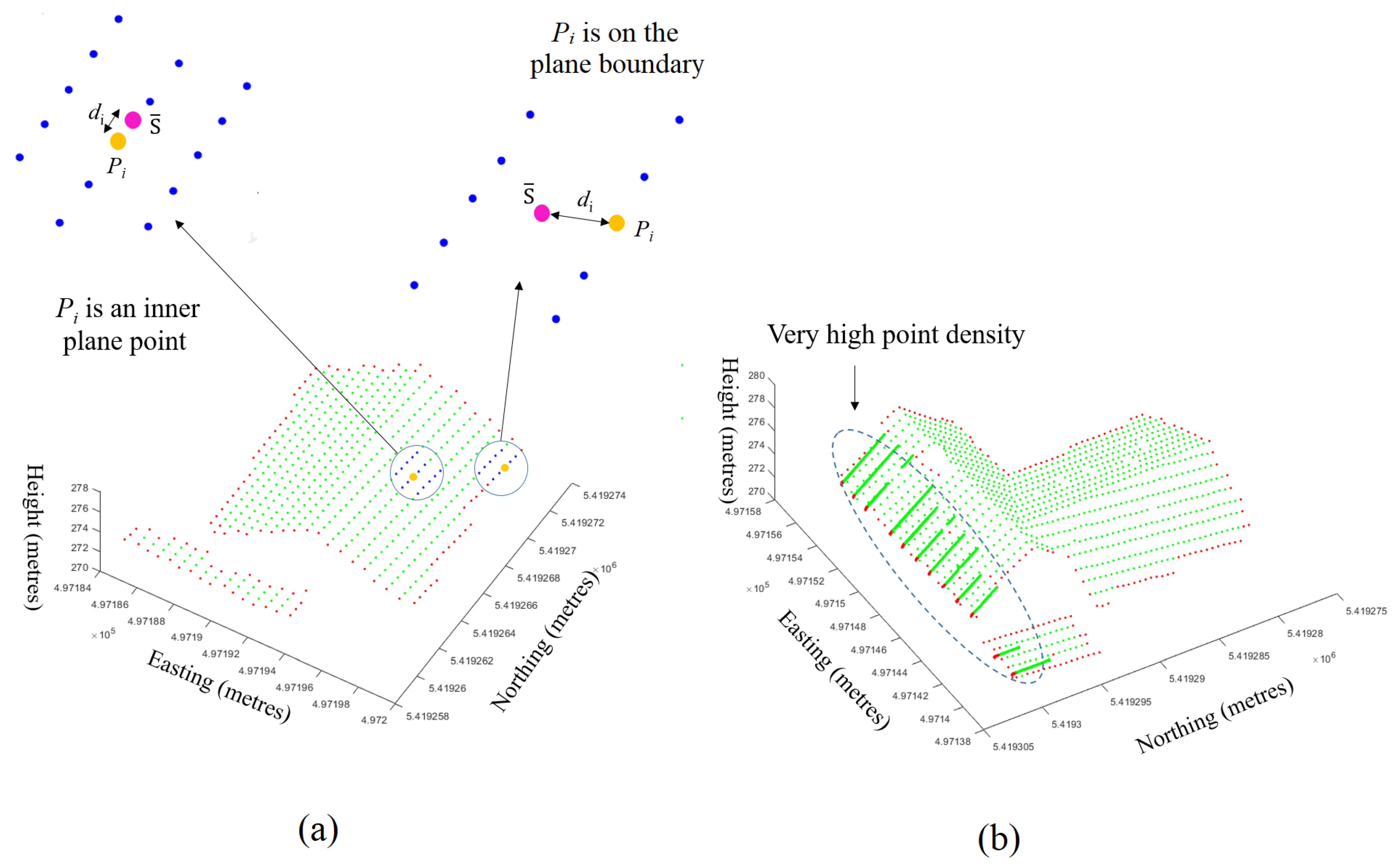
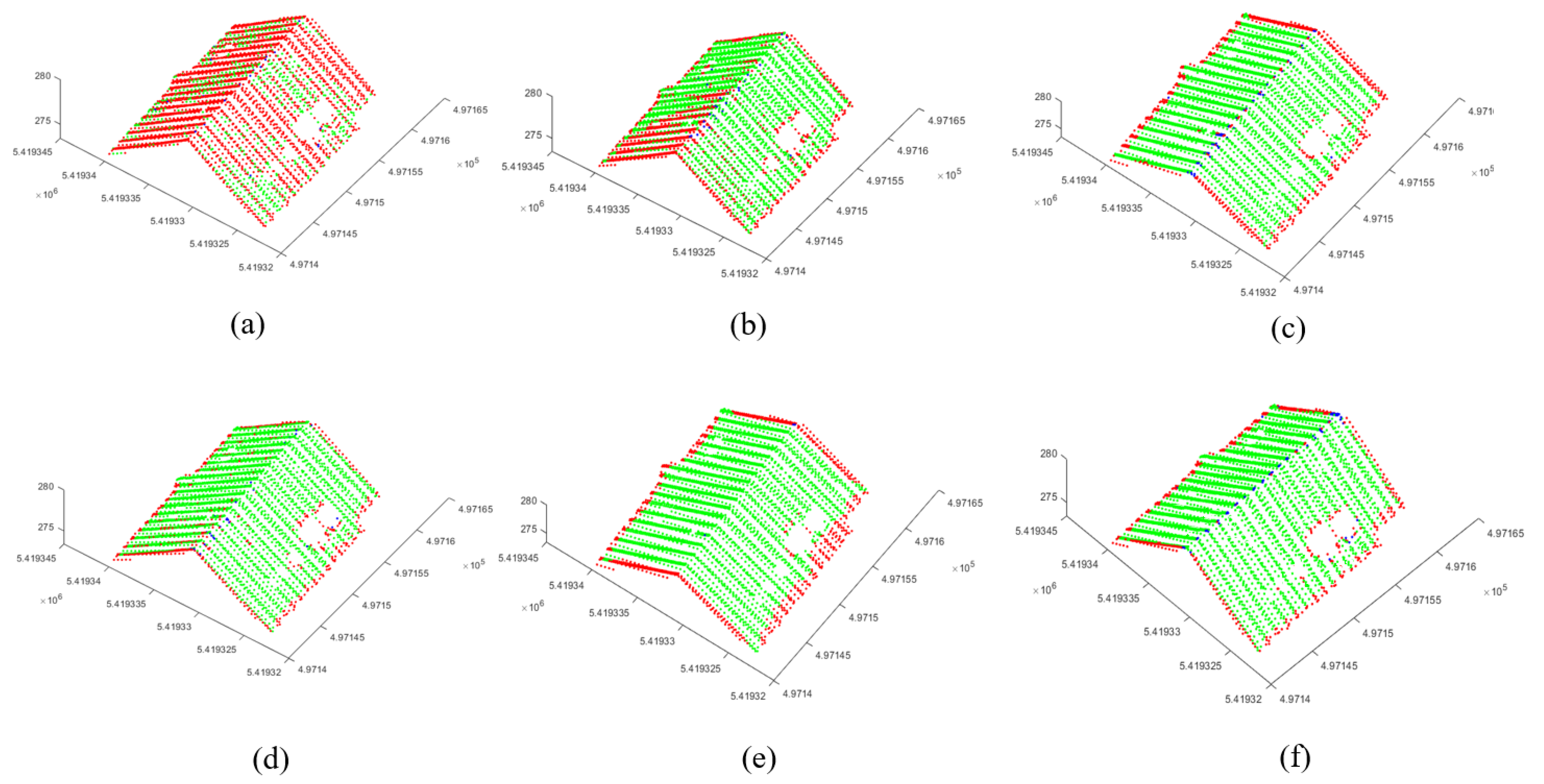
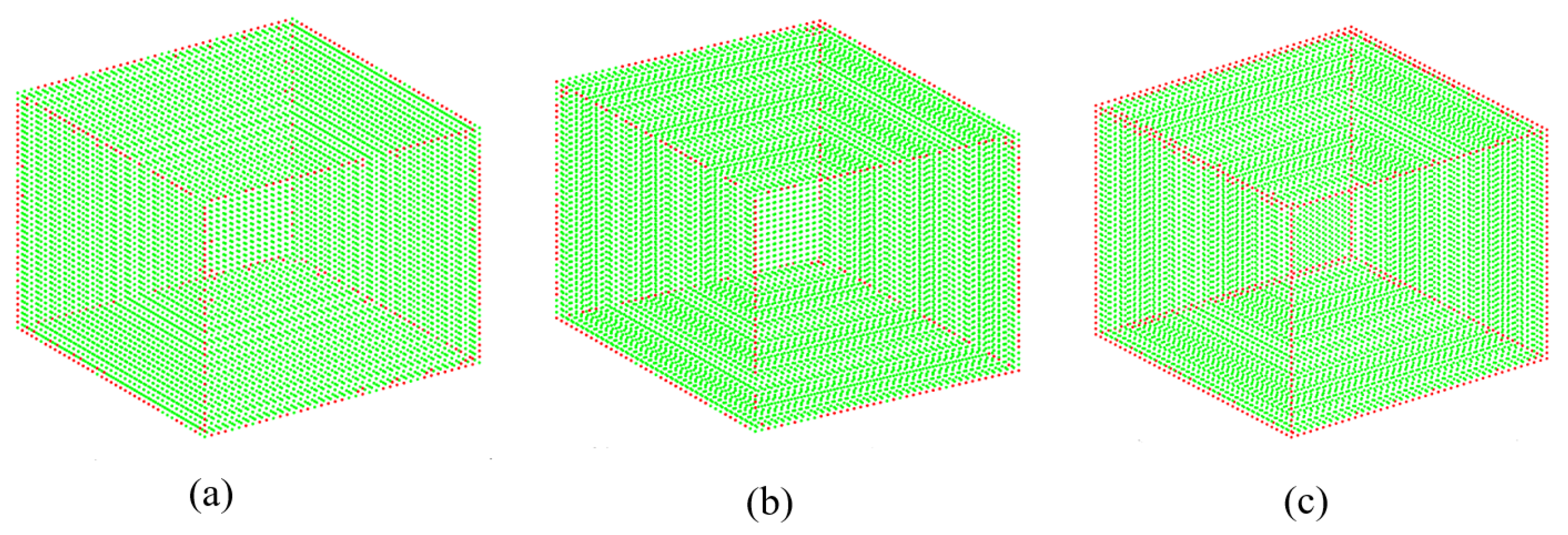
- If , is the estimated minimal neighbourhood for . The green points in Figure 3a show that the above steps successfully define the minimal neighbourhood for all points on a building roof. However, when there are unexpectedly a large number of points residing along a portion of a scanline, then these steps fail to define the neighbourhood, as in this case, all or most of the points in are obtained from the same scanline using the k-NN algorithm (see Figure 3b). Since points are not selected from two or more scanlines, the 3D line is repeatedly formed on the scanline that offers a low value.
- To avoid the above issue, this paper proposes a new neighbourhood search procedure for (see Figure 3c). First, depending on the input point density , when the number of points in is larger than , where A is the area of the smallest detectable plane, points that are very close (e.g., = 0.01 m) to are removed from (blue points remain). Second, a line L passing through and perpendicular to (scanline) is generated. Third, a new rectangular neighbourhood (green shaded in Figure 3c) for is formed. is long along L but short along , and thus, the idea is to reduce the neighbouring points from the current scanline (blue points) and to include more points from outside the scanline (green points) and even from the next scanlines (yellow points). Finally, only six points closest to four corners and two midpoints (, , , , , and ) from within and are assigned to an empty and is again estimated to . If the condition () is still not satisfied, the rectangle is enlarged (orange shaded) along L to include more points from outside , i.e., four more points closest to corners , , , and are added to . It is experimentally observed that, when (mostly in the second iteration) points from the next scanlines are considered in , the condition is satisfied. Figure 3d shows that all points on the roof now have minimal neighbourhoods.
3.2. Finding Fold Points
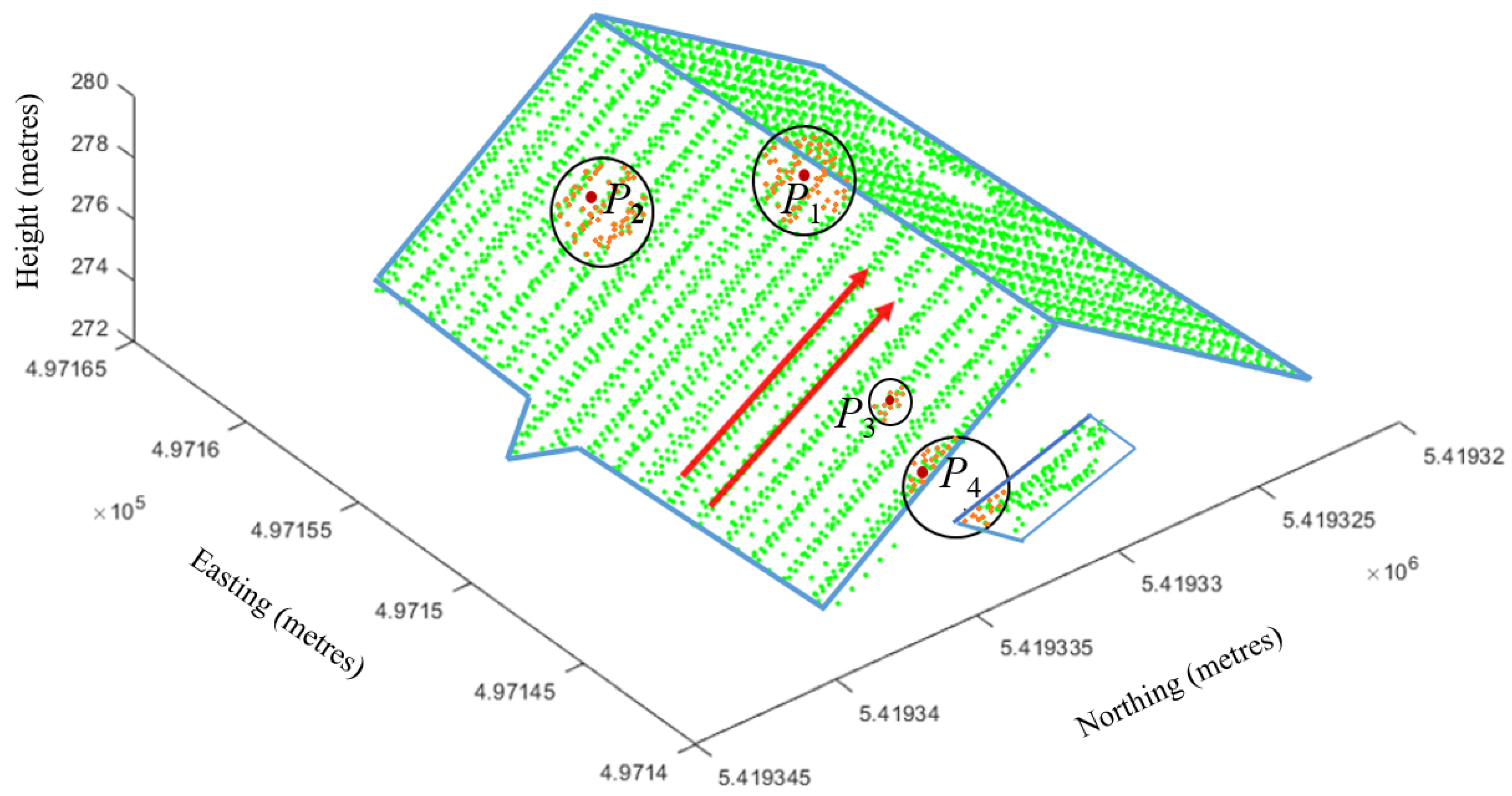
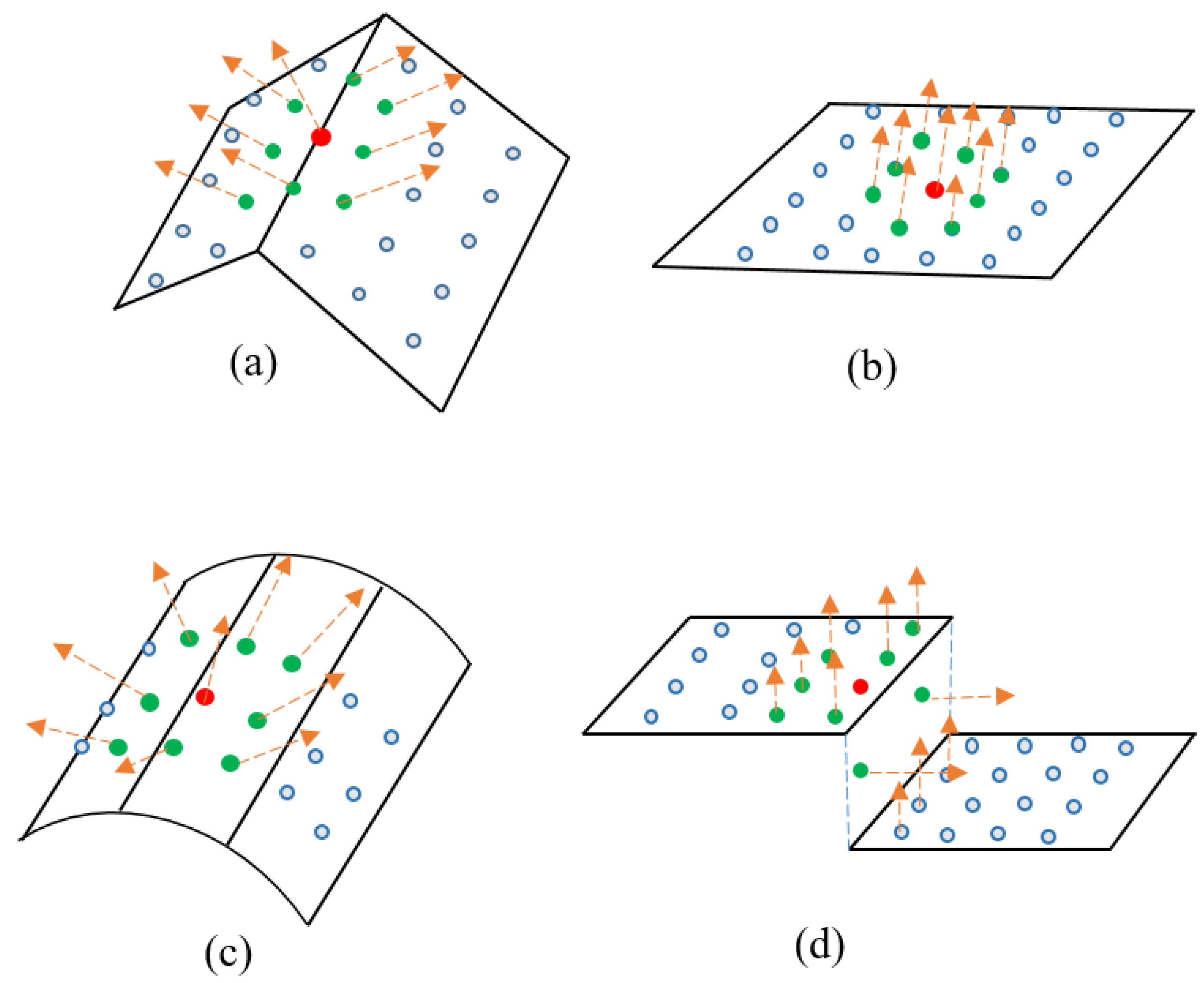
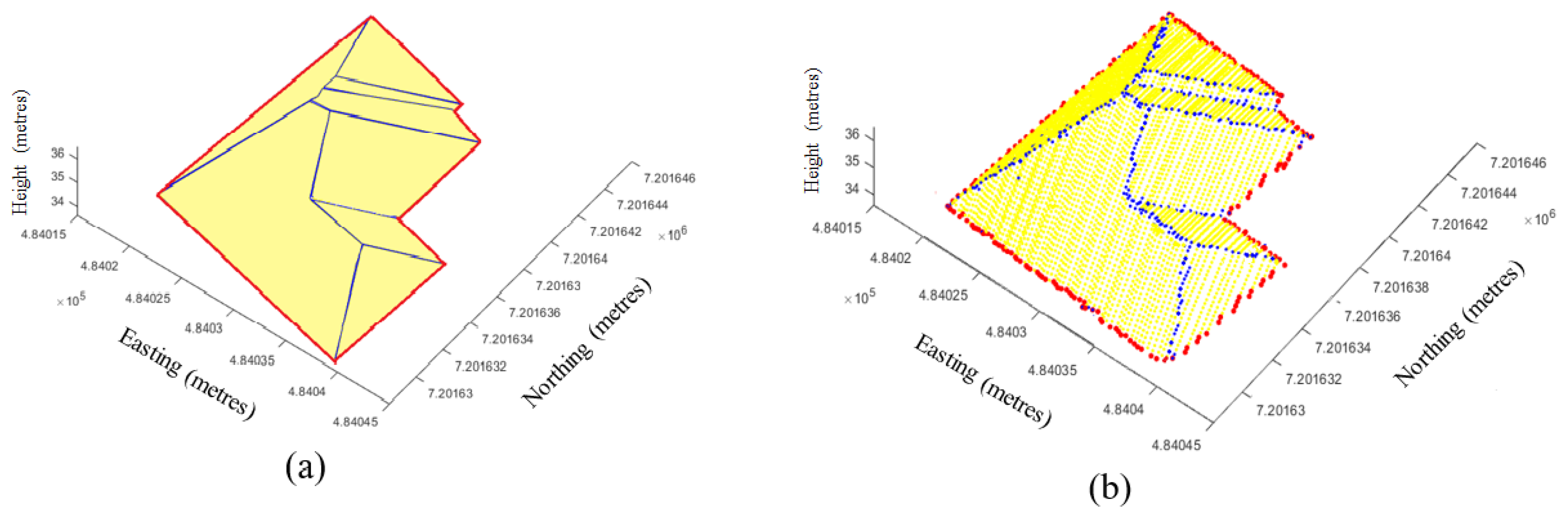
- When two planes physically intersect, as shown in Figure 4a, and if for (red dot) but for its neighbours (green dots) can be clustered into two major groups, where the clusters are not close to each other, is a fold point.
- When is a planar point, as shown in Figure 4b, for and all its neighbours.
- When is on a curved surface, as shown in Figure 4c, for and for its neighbours are very close to .
- When is on a step edge, as shown in Figure 4d, there can be one of two situations. The adjacent vertical plane may have no or a small number of points. When there are no points on the vertical plane, then the fold points may be completely undetermined if the two planes (top and bottom) are parallel. If there is a large slope difference between these two planes, then the case in Figure 4a applies and fold points will be determined. When there are points reflected from the vertical plane, the fold points (between vertical and top planes and between vertical and bottom planes) can also be determined using the case in Figure 4a.
3.3. Determining the Threshold
3.4. Detection of Boundary Points
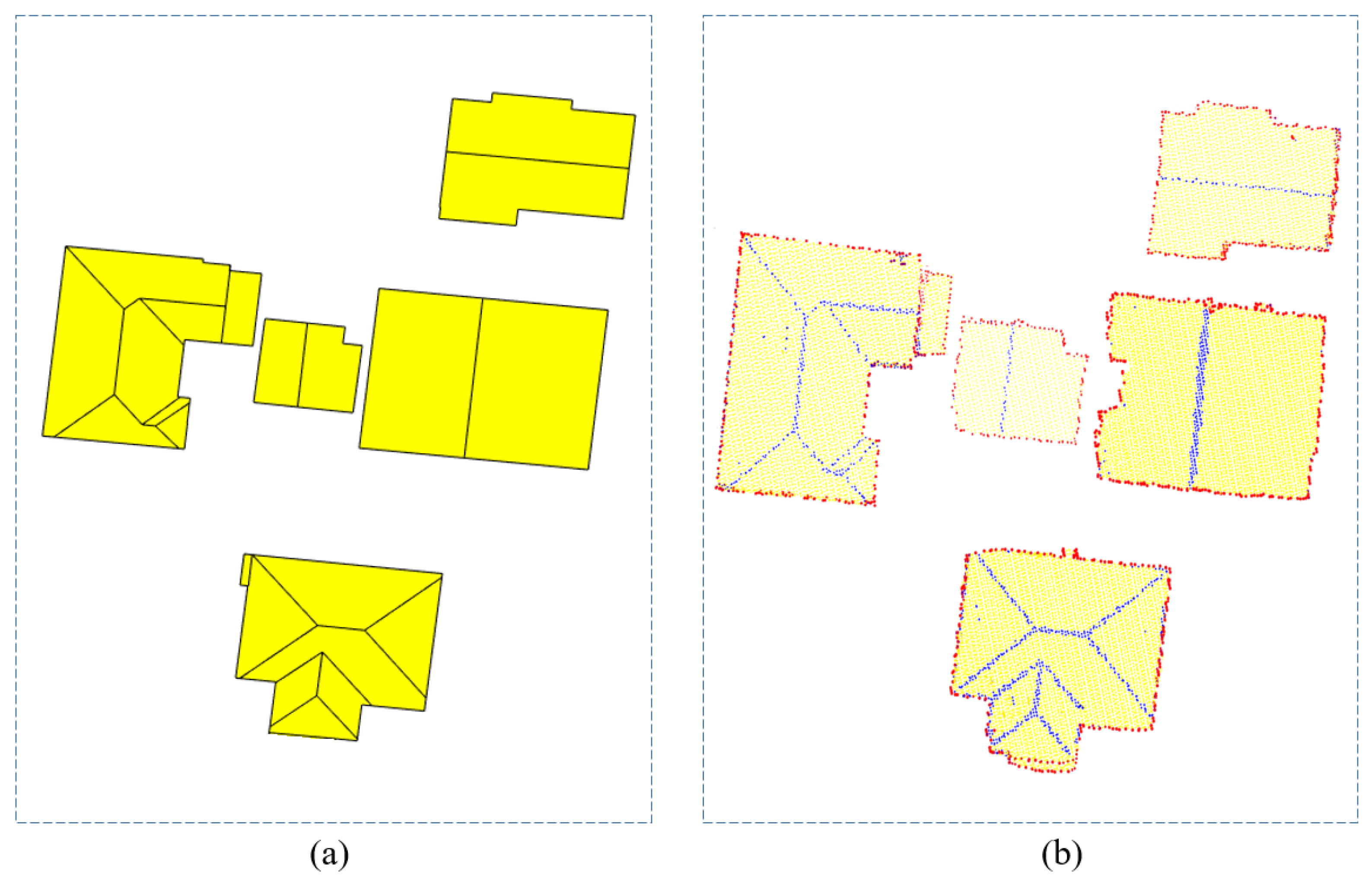
4. Experimental Results
4.1. Datasets
4.2. Comparison
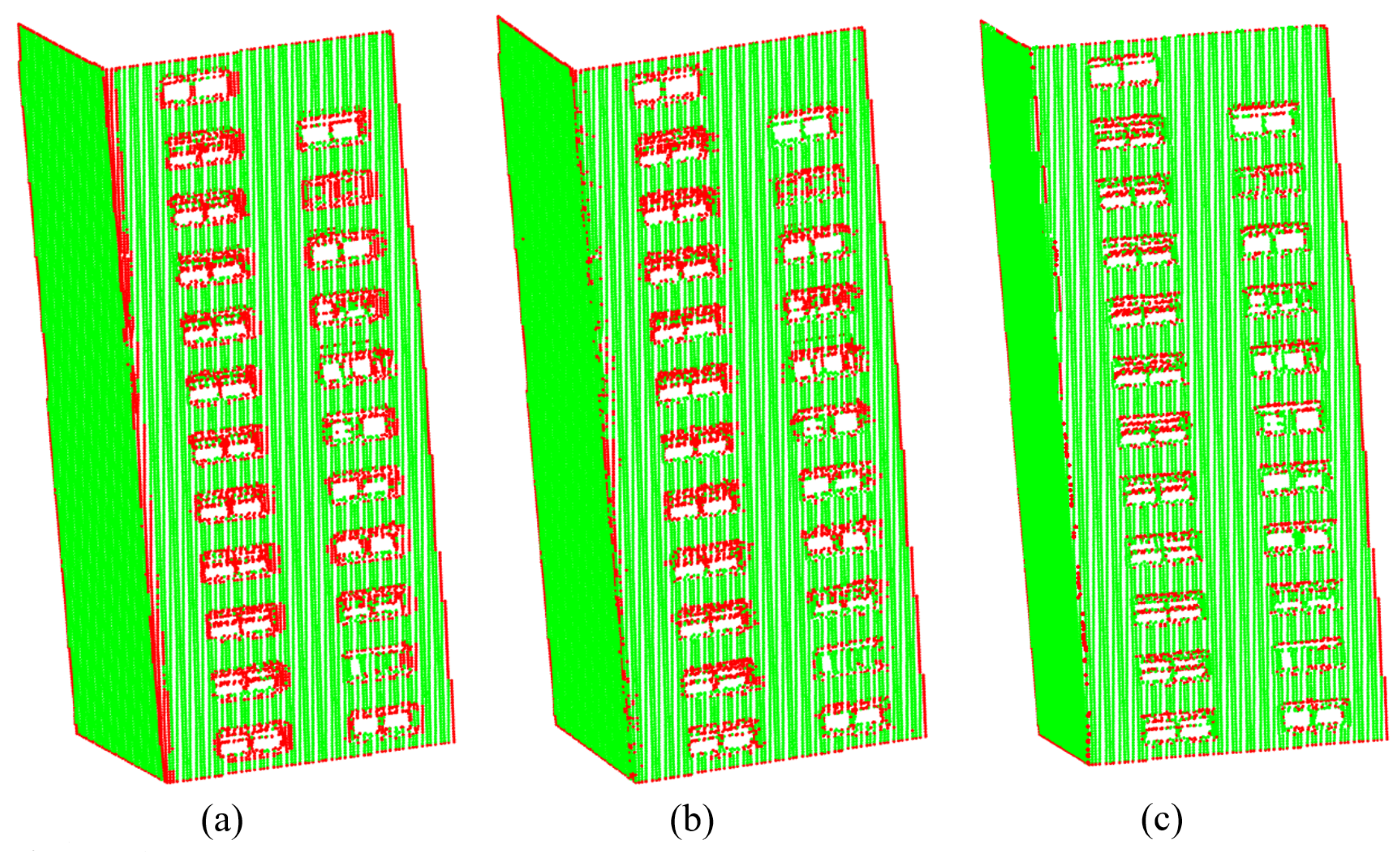
4.2.1. Fold Points
4.2.2. Boundary Points
4.2.3. Eigenvalue-Based Features
4.2.4. Combined Results
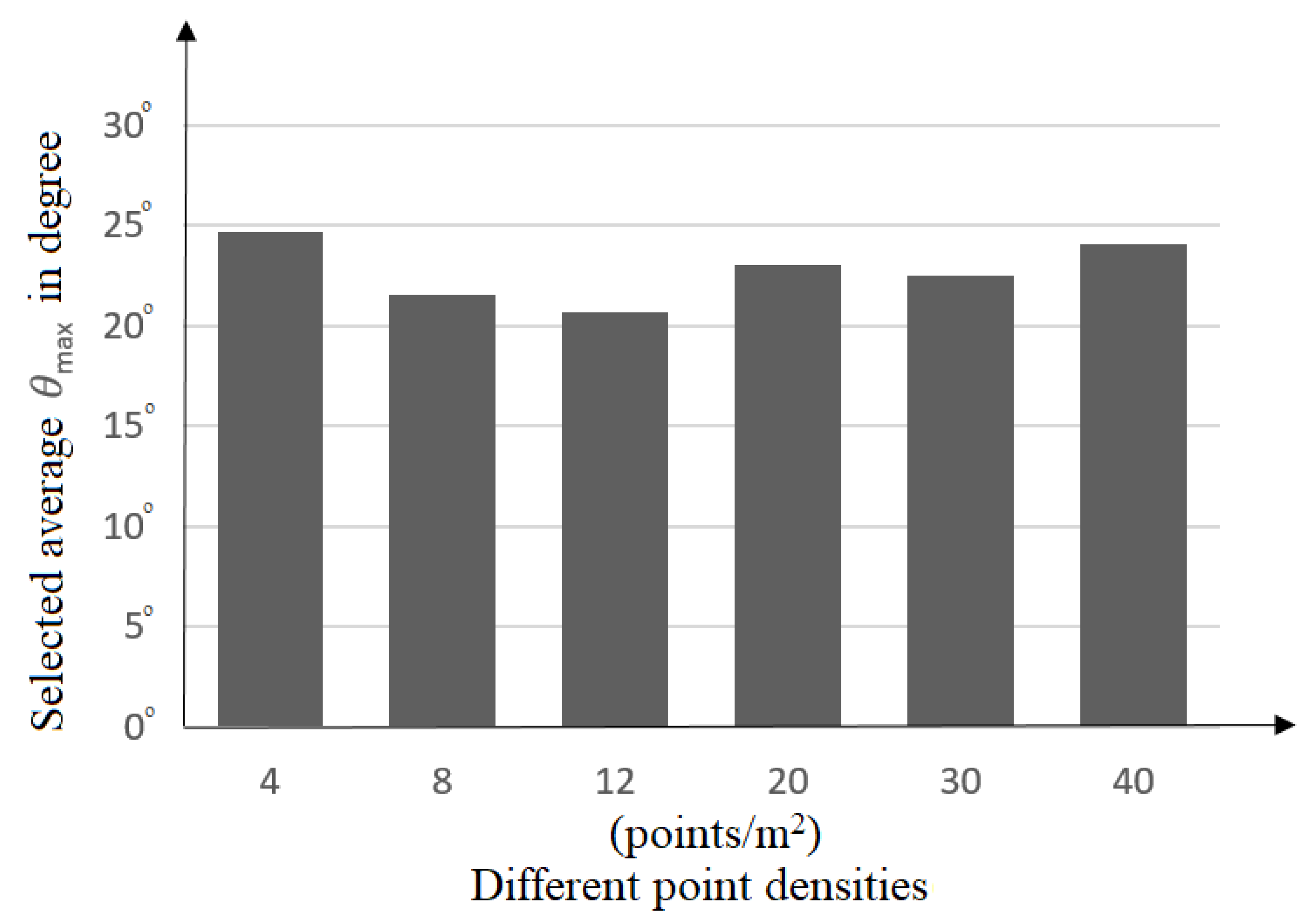
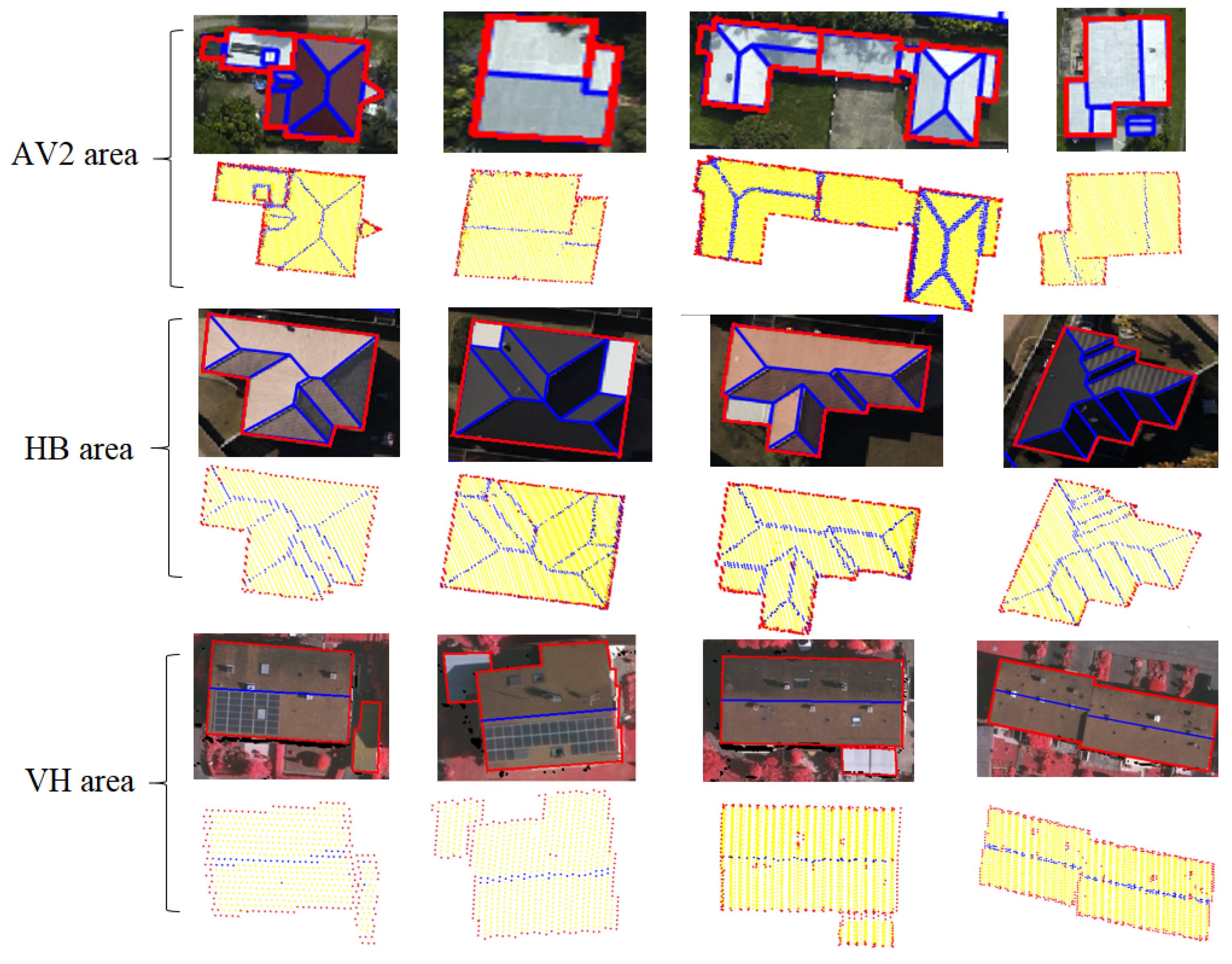
4.3. Applicability in Different Types of Point Clouds
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Koch, T.; Korner, M.; Fraundorfer, F. Automatic alignment of indoor and outdoor building models using 3D line segments. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Las Vegas, NV, USA, 27–30 June 2016; pp. 10–18. [Google Scholar]
- Kang, Z.; Zhong, R.; Wu, A.; Shi, Z.; Luo, Z. An efficient planar feature fitting method using point cloud simplification and threshold-independent BaySAC. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1842–1846. [Google Scholar] [CrossRef]
- Yang, B.; Fang, L.; Li, J. Semi-automated extraction and delineation of 3D roads of street scene from mobile laser scanning point clouds. ISPRS J. Photogramm. Remote Sens. 2013, 79, 80–93. [Google Scholar] [CrossRef]
- Poullis, C. A framework for automatic modeling from point cloud data. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2563–2575. [Google Scholar] [CrossRef] [PubMed]
- Albano, R. Investigation on Roof Segmentation for 3D Building Reconstruction from Aerial LIDAR Point Clouds. Appl. Sci. 2019, 9, 4674. [Google Scholar] [CrossRef]
- Tarsha Kurdi, F.; Awrangjeb, M. Automatic evaluation and improvement of roof segments for modelling missing details using Lidar data. Int. J. Remote Sens. 2020, 41, 4702–4725. [Google Scholar] [CrossRef]
- Dey, E.K.; Awrangjeb, M.; Stantic, B. Outlier detection and robust plane fitting for building roof extraction from LiDAR data. Int. J. Remote. Sens. 2020, 41, 6325–6354. [Google Scholar] [CrossRef]
- Sanchez, J.; Denis, F.; Dupont, F.; Trassoudaine, L.; Checchin, P. Data-driven modeling of building interiors from lidar point clouds. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 2, 395–402. [Google Scholar] [CrossRef]
- Lafarge, F.; Mallet, C. Creating large-scale city models from 3D-point clouds: a robust approach with hybrid representation. Int. J. Comput. Vis. 2012, 99, 69–85. [Google Scholar] [CrossRef]
- Sampath, A.; Shan, J. Segmentation and reconstruction of polyhedral building roofs from aerial lidar point clouds. IEEE Trans. Geosci. Remote Sens. 2009, 48, 1554–1567. [Google Scholar] [CrossRef]
- Ni, H.; Lin, X.; Zhang, J. Applications of 3d-edge detection for ALS point cloud. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42. [Google Scholar] [CrossRef]
- Awrangjeb, M.; Gilani, S.A.N.; Siddiqui, F.U. An effective data-driven method for 3-d building roof reconstruction and robust change detection. Remote Sens. 2018, 10, 1512. [Google Scholar] [CrossRef]
- Balado, J.; Arias, P.; Díaz-Vilariño, L.; González-deSantos, L.M. Automatic CORINE land cover classification from airborne LIDAR data. Procedia Comput. Sci. 2018, 126, 186–194. [Google Scholar] [CrossRef]
- Tarsha-Kurdi, F.; Landes, T.; Grussenmeyer, P. Extended RANSAC algorithm for automatic detection of building roof planes from LiDAR data. Photogramm. J. Finl. 2008, 21, 97–109. [Google Scholar]
- Awrangjeb, M.; Zhang, C.; Fraser, C.S. Automatic extraction of building roofs using LIDAR data and multispectral imagery. ISPRS J. Photogramm. Remote Sens. 2013, 83, 1–18. [Google Scholar] [CrossRef]
- Ni, H.; Lin, X.; Ning, X.; Zhang, J. Edge detection and feature line tracing in 3d-point clouds by analyzing geometric properties of neighborhoods. Remote Sens. 2016, 8, 710. [Google Scholar] [CrossRef]
- Chen, X.; Yu, K. Feature line generation and regularization from point clouds. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9779–9790. [Google Scholar] [CrossRef]
- Zhang, Y.; Geng, G.; Wei, X.; Zhang, S.; Li, S. A statistical approach for extraction of feature lines from point clouds. Comput. Graph. 2016, 56, 31–45. [Google Scholar] [CrossRef]
- Vosselman, G.; Dijkman, S. 3D building model reconstruction from point clouds and ground plans. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2001, 34, 37–44. [Google Scholar]
- Demarsin, K.; Vanderstraeten, D.; Volodine, T.; Roose, D. Detection of closed sharp edges in point clouds using normal estimation and graph theory. Comput. Aided Des. 2007, 39, 276–283. [Google Scholar] [CrossRef]
- Bazazian, D.; Casas, J.R.; Ruiz-Hidalgo, J. Fast and robust edge extraction in unorganized point clouds. In Proceedings of the 2015 International Conference on Digital Image Computing: Techniques and Applications (DICTA), Adelaide, Australia, 23–25 November 2015; pp. 1–8. [Google Scholar]
- Yang, L.; Sheng, Y.; Wang, B. 3D reconstruction of building facade with fused data of terrestrial LiDAR data and optical image. Optik 2016, 127, 2165–2168. [Google Scholar] [CrossRef]
- Wang, Z.; Prisacariu, V.A. Neighbourhood-Insensitive Point Cloud Normal Estimation Network. arXiv 2020, arXiv:2008.09965. [Google Scholar]
- Sanchez, J.; Denis, F.; Coeurjolly, D.; Dupont, F.; Trassoudaine, L.; Checchin, P. Robust normal vector estimation in 3D point clouds through iterative principal component analysis. ISPRS J. Photogramm. Remote Sens. 2020, 163, 18–35. [Google Scholar] [CrossRef]
- Zhu, Q.; Wang, F.; Hu, H.; Ding, Y.; Xie, J.; Wang, W.; Zhong, R. Intact planar abstraction of buildings via global normal refinement from noisy oblique photogrammetric point clouds. ISPRS Int. J. Geo-Inf. 2018, 7, 431. [Google Scholar] [CrossRef]
- Zhao, R.; Pang, M.; Liu, C.; Zhang, Y. Robust normal estimation for 3D LiDAR point clouds in urban environments. Sensors 2019, 19, 1248. [Google Scholar] [CrossRef] [PubMed]
- Leichter, A.; Werner, M.; Sester, M. Feature-extraction from all-scale neighborhoods with applications to semantic segmentation of point clouds. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 43, 263–270. [Google Scholar] [CrossRef]
- Ben-Shabat, Y.; Lindenbaum, M.; Fischer, A. Nesti-net: Normal estimation for unstructured 3d point clouds using convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 10112–10120. [Google Scholar]
- He, E.; Chen, Q.; Wang, H.; Liu, X. A curvature based adaptive neighborhood for individual point cloud classification. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42. [Google Scholar] [CrossRef]
- Weinmann, M.; Jutzi, B.; Hinz, S.; Mallet, C. Semantic point cloud interpretation based on optimal neighborhoods, relevant features and efficient classifiers. ISPRS J. Photogramm. Remote Sens. 2015, 105, 286–304. [Google Scholar] [CrossRef]
- Weinmann, M.; Jutzi, B.; Mallet, C. Semantic 3D scene interpretation: A framework combining optimal neighborhood size selection with relevant features. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 2, 181. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Ben-Shabat, Y.; Lindenbaum, M.; Fischer, A. 3dmfv: Three-dimensional point cloud classification in real-time using convolutional neural networks. IEEE Robot. Autom. Lett. 2018, 3, 3145–3152. [Google Scholar] [CrossRef]
- Weinmann, M.; Jutzi, B.; Mallet, C. Feature relevance assessment for the semantic interpretation of 3D point cloud data. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 5, 1. [Google Scholar] [CrossRef]
- Hughes, G. On the mean accuracy of statistical pattern recognizers. IEEE Trans. Inf. Theory 1968, 14, 55–63. [Google Scholar] [CrossRef]
- Weber, C.; Hahmann, S.; Hagen, H.; Bonneau, G.P. Sharp feature preserving MLS surface reconstruction based on local feature line approximations. Graph. Model. 2012, 74, 335–345. [Google Scholar] [CrossRef]
- Nurunnabi, A.; West, G.; Belton, D. Outlier detection and robust normal-curvature estimation in mobile laser scanning 3D point cloud data. Pattern Recognit. 2015, 48, 1404–1419. [Google Scholar] [CrossRef]
- Dey, T.K.; Li, G.; Sun, J. Normal estimation for point clouds: A comparison study for a Voronoi based method. In Proceedings of the Eurographics/IEEE VGTC Symposium Point-Based Graphics, Brook, NY, USA, 21–22 June 2005; pp. 39–46. [Google Scholar]
- Pauly, M.; Gross, M.; Kobbelt, L.P. Efficient simplification of point-sampled surfaces. In Proceedings of the IEEE Visualization, Boston, MA, USA, 27 October–1 November 2002; pp. 163–170. [Google Scholar]
- Alexa, M.; Behr, J.; Cohen-Or, D.; Fleishman, S.; Levin, D.; Silva, C.T. Computing and rendering point set surfaces. IEEE Trans. Vis. Comput. Graph. 2003, 9, 3–15. [Google Scholar] [CrossRef]
- Hubert, M.; Rousseeuw, P.J.; Vanden Branden, K. ROBPCA: A new approach to robust principal component analysis. Technometrics 2005, 47, 64–79. [Google Scholar] [CrossRef]
- Nurunnabi, A.; Belton, D.; West, G. Diagnostic-robust statistical analysis for local surface fitting in 3D point cloud data. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 269–274. [Google Scholar] [CrossRef]
- Dey, E.K.; Awrangjeb, M.; Stantic, B. An Unsupervised Outlier Detection Method For 3D Point Cloud Data. In Proceedings of the 2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 2495–2498. [Google Scholar]
- Huber, P.J. Robust Statistics. In International Encyclopedia of Statistical Science; Lovric, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 1248–1251. [Google Scholar]
- Kanungo, T.; Mount, D.M.; Netanyahu, N.S.; Piatko, C.D.; Silverman, R.; Wu, A.Y. An efficient k-means clustering algorithm: Analysis and implementation. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 881–892. [Google Scholar] [CrossRef]
- Guennebaud, G.; Gross, M. Algebraic point set surfaces. In ACM Siggraph 2007 Papers; ACM: New York, NY, USA, 2007. [Google Scholar]
- Lu, X.; Liu, Y.; Li, K. Fast 3D line segment detection from unorganized point cloud. arXiv 2019, arXiv:1901.02532. [Google Scholar]
- Xu, S.; Wang, R.; Zheng, H. Road curb extraction from mobile LiDAR point clouds. IEEE Trans. Geosci. Remote Sens. 2016, 55, 996–1009. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, C.; Cheng, J.; Chen, B.; Jia, F.; Chen, Z.; Li, J. Line segment extraction for large scale unorganized point clouds. ISPRS J. Photogramm. Remote Sens. 2015, 102, 172–183. [Google Scholar] [CrossRef]
- Ge, X. Automatic markerless registration of point clouds with semantic-keypoint-based 4-points congruent sets. ISPRS J. Photogramm. Remote Sens. 2017, 130, 344–357. [Google Scholar] [CrossRef]
- Moghadam, P.; Bosse, M.; Zlot, R. Line-based extrinsic calibration of range and image sensors. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 3685–3691. [Google Scholar]
- Xia, S.; Wang, R. A fast edge extraction method for mobile LiDAR point clouds. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1288–1292. [Google Scholar] [CrossRef]
- Dey, E.K.; Awrangjeb, M. A Robust Performance Evaluation Metric for Extracted Building Boundaries From Remote Sensing Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4030–4043. [Google Scholar] [CrossRef]
- Lu, Z.; Baek, S.; Lee, S. Robust 3d line extraction from stereo point clouds. In Proceedings of the 2008 IEEE Conference on Robotics, Automation and Mechatronics, Chengdu, China, 21–24 September 2008; pp. 1–5. [Google Scholar]
- Gumhold, S.; Wang, X.; MacLeod, R.S. Feature Extraction from Point Clouds; Citeseer: State College, PA, USA, 2001; pp. 293–305. [Google Scholar]
- Ioannou, Y.; Taati, B.; Harrap, R.; Greenspan, M. Difference of normals as a multi-scale operator in unorganized point clouds. In Proceedings of the 2012 Second International Conference on 3D Imaging, Modeling, Processing, Visualization & Transmission, Zurich, Switzerland, 13–15 October 2012; pp. 501–508. [Google Scholar]
- Belton, D.; Lichti, D.D. Classification and segmentation of terrestrial laser scanner point clouds using local variance information. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2006, 36, 44–49. [Google Scholar]
- Santos, R.C.d.; Galo, M.; Tachibana, V.M. Classification of LiDAR data over building roofs using k-means and principal component analysis. Boletim de Ciências Geodésicas 2018, 24, 69–84. [Google Scholar] [CrossRef]
- Tarsha-Kurdi, F.; Landes, T.; Grussenmeyer, P.; Smigiel, E. New approach for automatic detection of buildings in airborne laser scanner data using first echo only. In Proceedings of the ISPRS Commission III Symposium, Photogrammetric Computer Vision, Bonn, Germany, 13 September 2006; pp. 25–30. [Google Scholar]
- Cochran, R.N.; Horne, F.H. Statistically weighted principal component analysis of rapid scanning wavelength kinetics experiments. Anal. Chem. 1977, 49, 846–853. [Google Scholar] [CrossRef]
- Awrangjeb, M. Using point cloud data to identify, trace, and regularize the outlines of buildings. Int. J. Remote Sens. 2016, 37, 551–579. [Google Scholar] [CrossRef]
- Awrangjeb, M.; Fraser, C.S. Automatic segmentation of raw LiDAR data for extraction of building roofs. Remote Sens. 2014, 6, 3716–3751. [Google Scholar] [CrossRef]
- Cramer, M. The DGPF test on digital aerial camera evaluation–overview and test design. Photogrammetrie–Fernerkundung–Geoinformation 2, 73–82 (2010). In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1026–1034. [Google Scholar]
- Alexiou, E.; Ebrahimi, T. Benchmarking of objective quality metrics for colorless point clouds. In Proceedings of the 2018 Picture Coding Symposium (PCS), San Francisco, CA, USA, 24–27 June 2018; pp. 51–55. [Google Scholar]




| Number of Neighbouring Points | Proposed Method | |||||
|---|---|---|---|---|---|---|
| 9 | 20 | 30 | 45 | 80 | ||
| 0–2 | 783 | 2602 | 2793 | 2895 | 2851 | 2465 |
| 2–10 | 2378 | 620 | 380 | 285 | 331 | 765 |
| 10–20 | 178 | 109 | 224 | 276 | 371 | 161 |
| 20–30 | 58 | 167 | 152 | 103 | 6 | 135 |
| 30–90 | 162 | 61 | 10 | 0 | 0 | 23 |
| F1-Score | 0.71 | 0.75 | 0.77 | 0.68 | 0.50 | 0.90 |
| Datasets | k-NN (k = 30) | k-NN (k = 45) | k-NN (k = 60) | Proposed |
|---|---|---|---|---|
| VH3 | 0.090 | 0.091 | 0.093 | 3.120 |
| AV1 | 0.058 | 0.058 | 0.060 | 0.232 |
| AGPN [16] | Chen [17] | Proposed | |
|---|---|---|---|
| Neighbourhood | Fixed k-NN | Fixed k-NN | Variable |
| Extraction approach | Plane fitting and angular gap | Minimal number of clusters of neighbouring normal vectors | Maximum angle difference of the calculated normal vectors |
| Normal estimation | RANSAC | Weighted PCA | Weighted PCA |
| Geometric property | The RANSAC and angular gap metric | Direction of k-nearest normal vectors | Maximum angle differences among k-nearest normal |
| Plane fitting | Required | Not required | Not required |
| ISPRS Site (VH3) | Australian Site (AV1) | |||||
|---|---|---|---|---|---|---|
| Precision | Recall | F1 | Precision | Recall | F1 | |
| AGPN [16] | 0.67 | 0.84 | 0.75 | 0.78 | 0.76 | 0.77 |
| Chen [17] | 0.74 | 0.79 | 0.77 | 0.75 | 0.73 | 0.74 |
| Proposed | 0.79 | 0.87 | 0.83 | 0.84 | 0.85 | 0.84 |
| Improved RANSAC [16] | Chen [17] | Proposed | |
|---|---|---|---|
| Neighbourhood | -tree | Fixed k-NN | Variable |
| Decision of boundary point | Substantial angular gap between vectors in a single plane | Distribution of azimuth angle | Euclidian distance from mean point to the point of interest |
| Plane fitting | Required | Required | Not required |
| Effect of outliers | High sensitive | Low sensitive | Low sensitive |
| ISPRS Site (VH3) | Australian Site (AV1) | |||||
|---|---|---|---|---|---|---|
| Precision | Recall | F1 | Precision | Recall | F1 | |
| Improved RANSAC [16] | 0.80 | 0.73 | 0.76 | 0.85 | 0.80 | 0.82 |
| Chen [17] | 0.84 | 0.72 | 0.78 | 0.96 | 0.75 | 0.84 |
| Proposed | 0.82 | 0.82 | 0.83 | 0.94 | 0.87 | 0.90 |
| Values of k | No. of Linear Points ≥ 0.5 | No. of Planar Points ≥ 0.5 | F1 (Linearity) | F1 (Planarity) |
|---|---|---|---|---|
| 9 | 2434 | 1115 | 0.19 | 0.15 |
| 30 | 1739 | 1810 | 0.61 | 0.68 |
| 45 | 571 | 2978 | 0.84 | 0.88 |
| 60 | 705 | 2844 | 0.71 | 0.79 |
| 90 | 843 | 2706 | 0.75 | 0.84 |
| Proposed | 409 | 3140 | 0.91 | 0.94 |
| Total Extracted Points | Precision | Recall | F1 | |
|---|---|---|---|---|
| AGPN [16] | 404 | 0.92 | 0.80 | 0.85 |
| Chen [17] | 331 | 0.96 | 0.67 | 0.78 |
| Proposed | 597 | 0.82 | 1.00 | 0.90 |
| Original Point Cloud | Outline Points | Extraction Rate | |
|---|---|---|---|
| AGPN Method | 29,339 | 5989 | 20.4% |
| Chen’s Method | 29,339 | 5097 | 17.4% |
| Proposed | 29,339 | 4203 | 14.3% |
| Original Point Cloud | Outline Points | Extraction Rate | |
|---|---|---|---|
| AGPN Method | 53,963 | 5146 | 9.50% |
| Chen’s Method | 53,963 | 9150 | 16.95% |
| Proposed | 53,963 | 6061 | 11.23% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dey, E.K.; Tarsha Kurdi, F.; Awrangjeb, M.; Stantic, B. Effective Selection of Variable Point Neighbourhood for Feature Point Extraction from Aerial Building Point Cloud Data. Remote Sens. 2021, 13, 1520. https://doi.org/10.3390/rs13081520
Dey EK, Tarsha Kurdi F, Awrangjeb M, Stantic B. Effective Selection of Variable Point Neighbourhood for Feature Point Extraction from Aerial Building Point Cloud Data. Remote Sensing. 2021; 13(8):1520. https://doi.org/10.3390/rs13081520
Chicago/Turabian StyleDey, Emon Kumar, Fayez Tarsha Kurdi, Mohammad Awrangjeb, and Bela Stantic. 2021. "Effective Selection of Variable Point Neighbourhood for Feature Point Extraction from Aerial Building Point Cloud Data" Remote Sensing 13, no. 8: 1520. https://doi.org/10.3390/rs13081520
APA StyleDey, E. K., Tarsha Kurdi, F., Awrangjeb, M., & Stantic, B. (2021). Effective Selection of Variable Point Neighbourhood for Feature Point Extraction from Aerial Building Point Cloud Data. Remote Sensing, 13(8), 1520. https://doi.org/10.3390/rs13081520