Uncertainty Estimation for Deep Learning-Based Segmentation of Roads in Synthetic Aperture Radar Imagery
Abstract
1. Introduction
1.1. Overview
1.2. Prior Work
2. Materials and Methods
2.1. Dataset
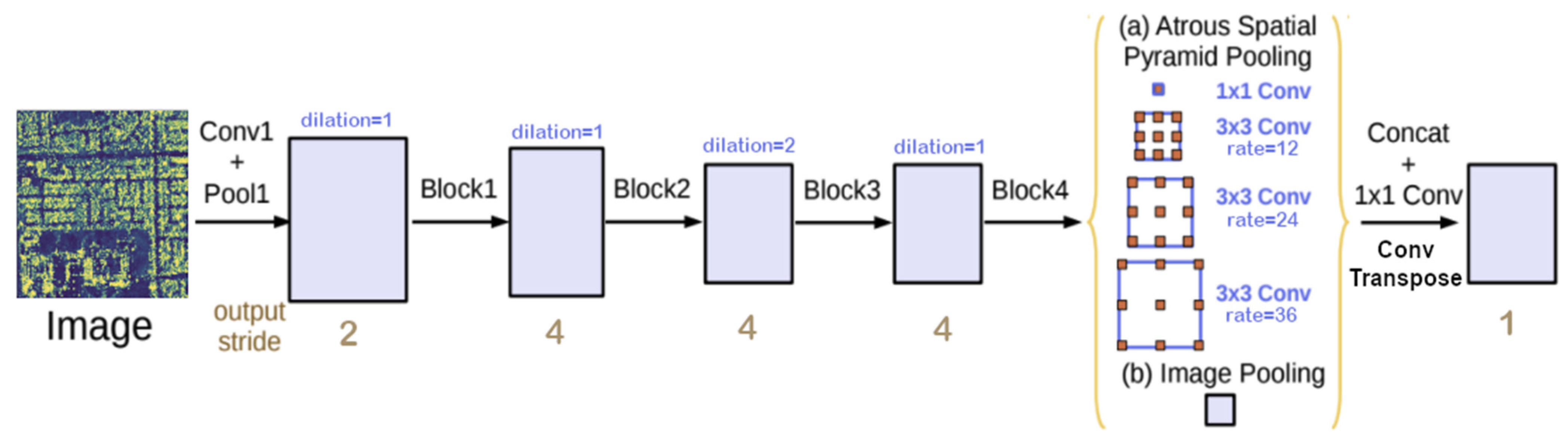
2.2. Segmentation Model
2.3. Uncertainty in Deep Learning
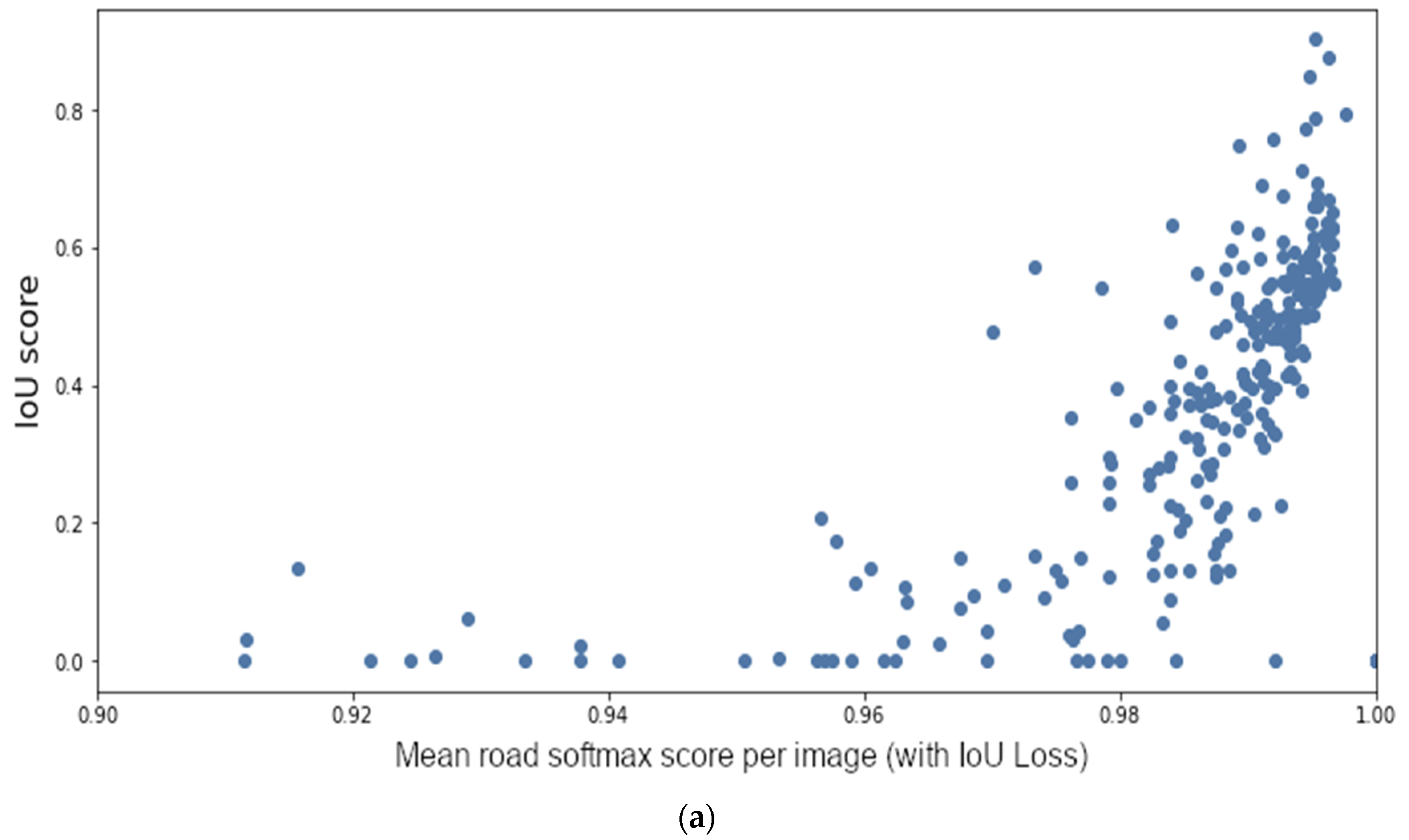
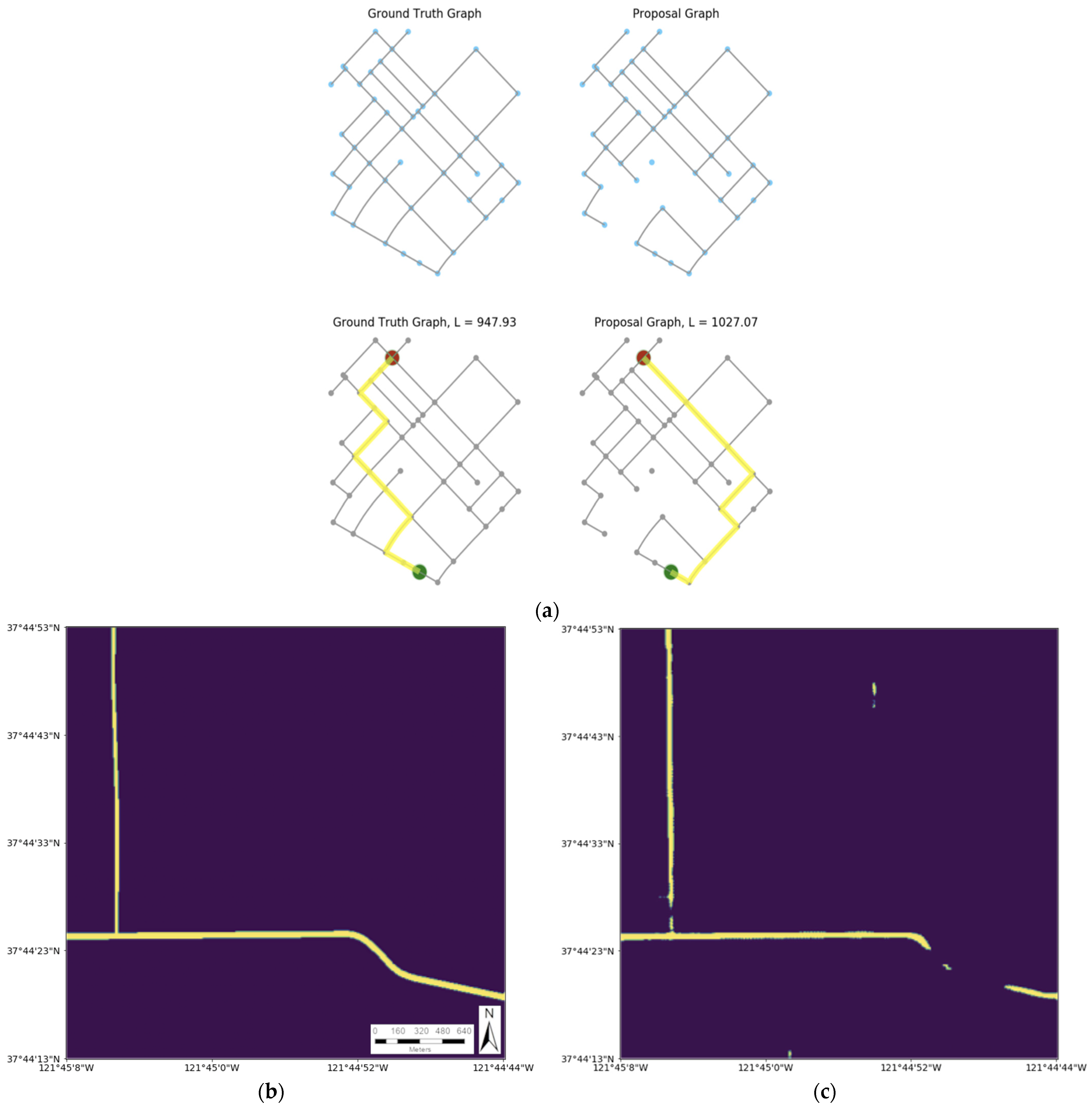
2.4. Loss Function and Segmentation Metrics
2.5. Improving Uncertainty Measurements
2.6. Training and Testing
3. Results
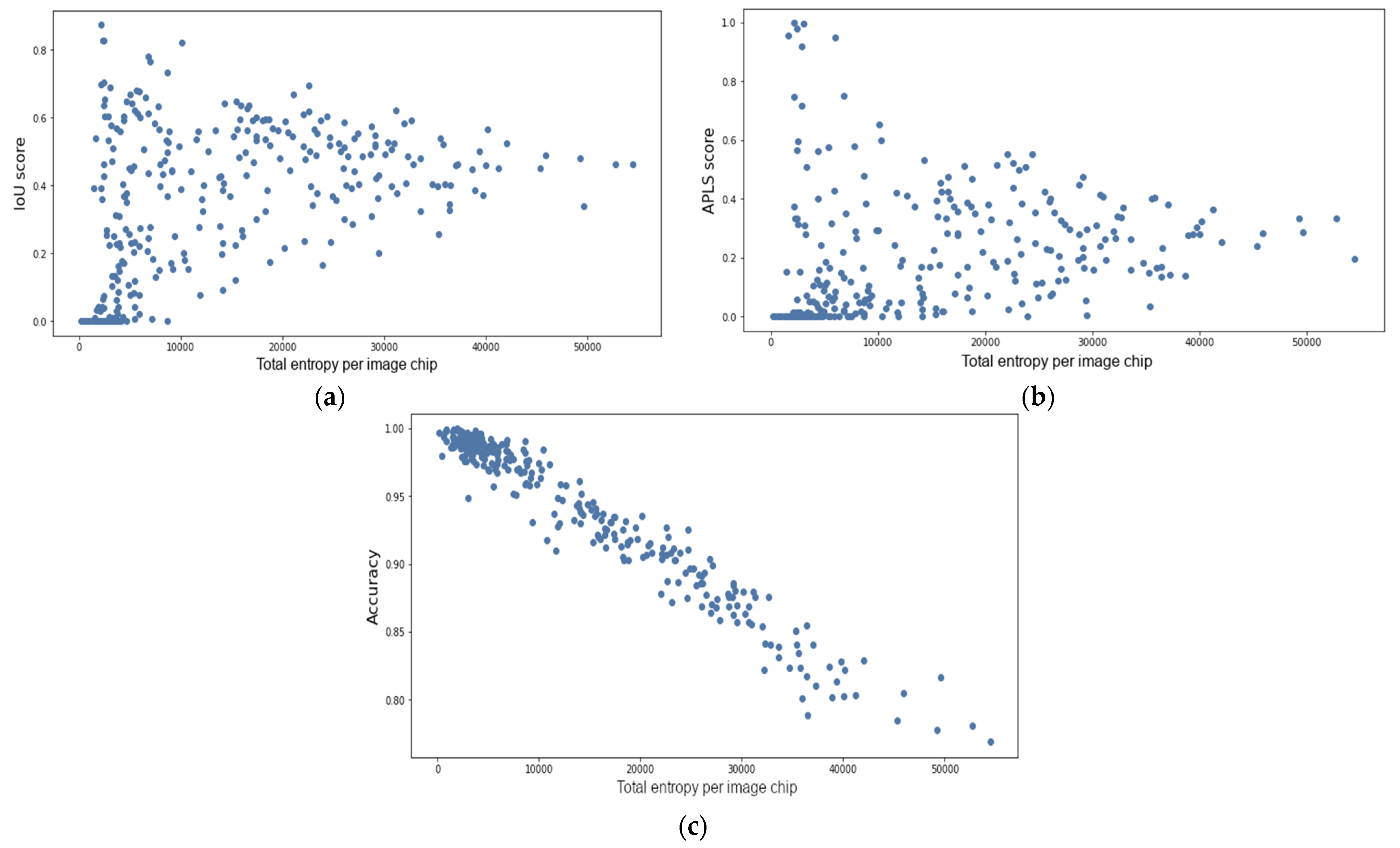
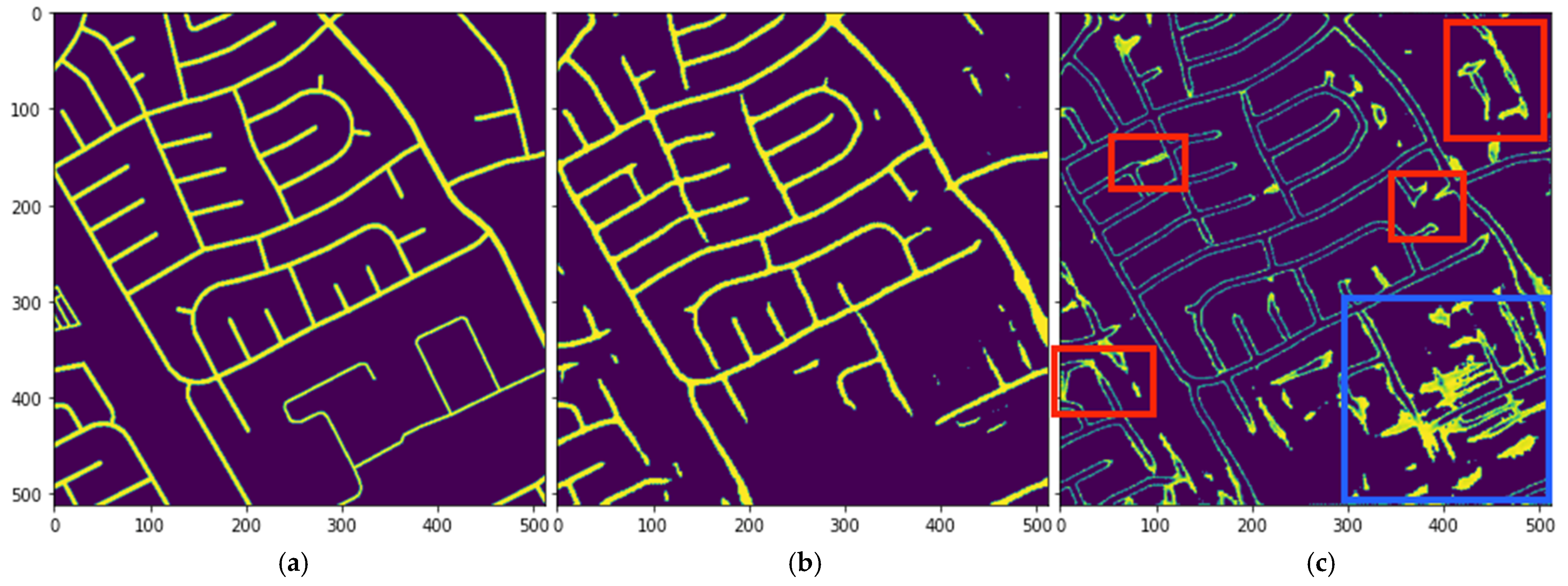
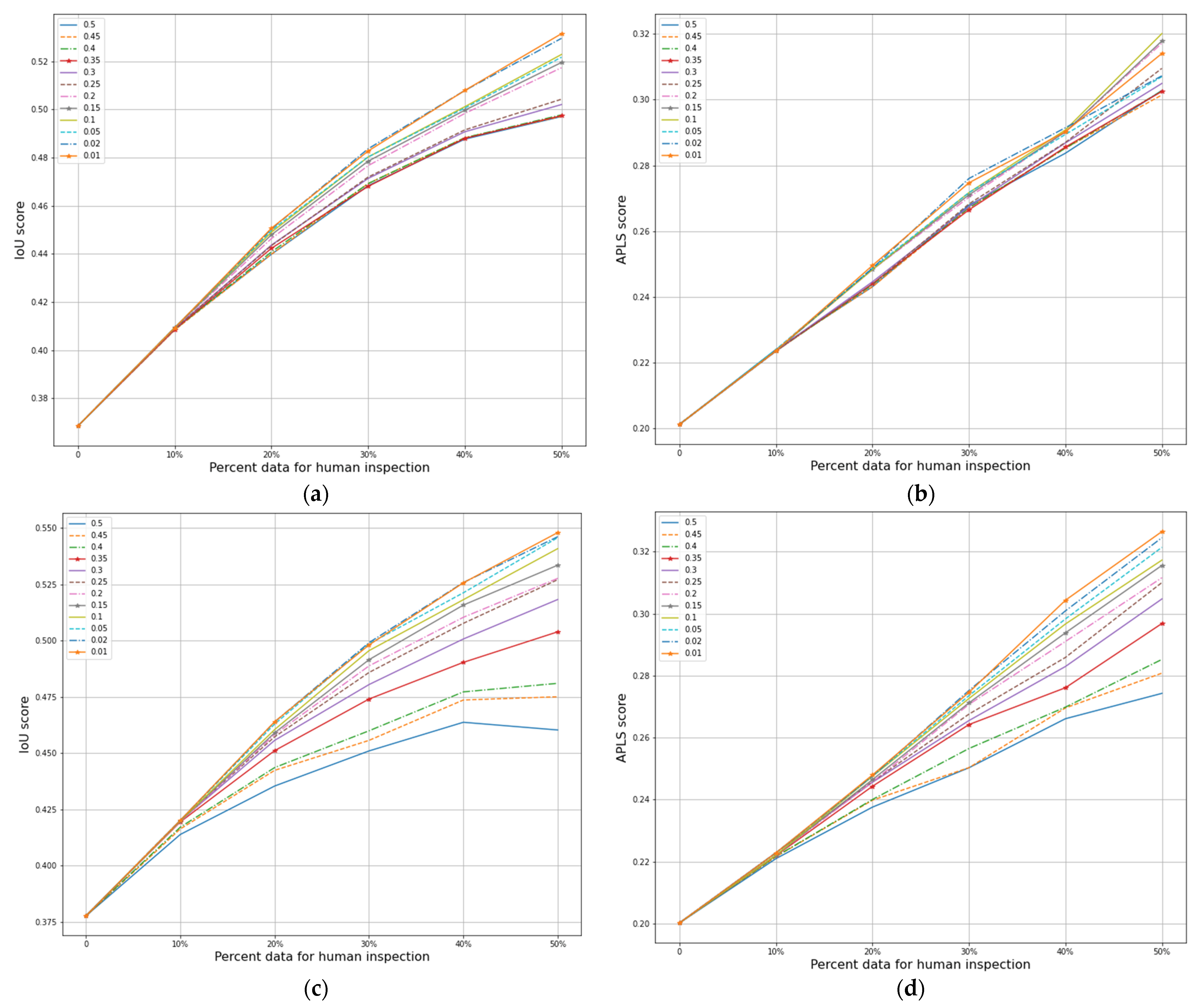
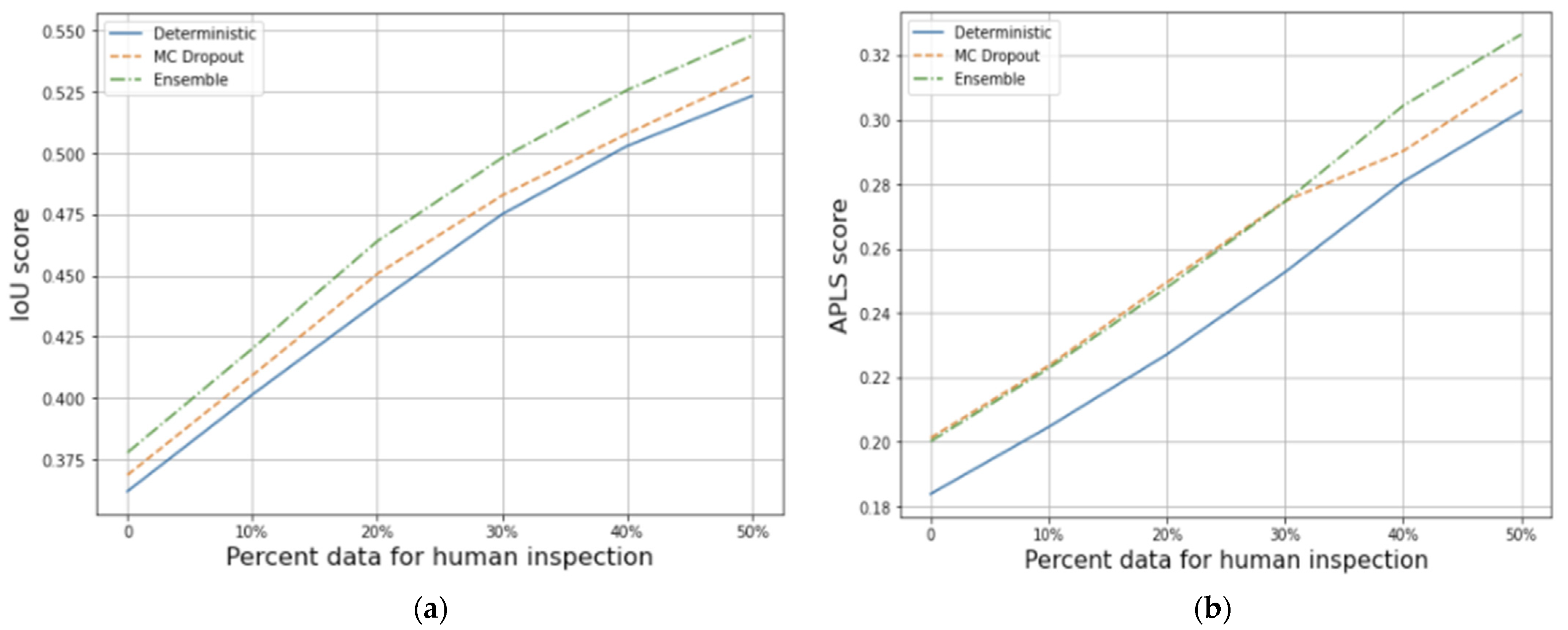
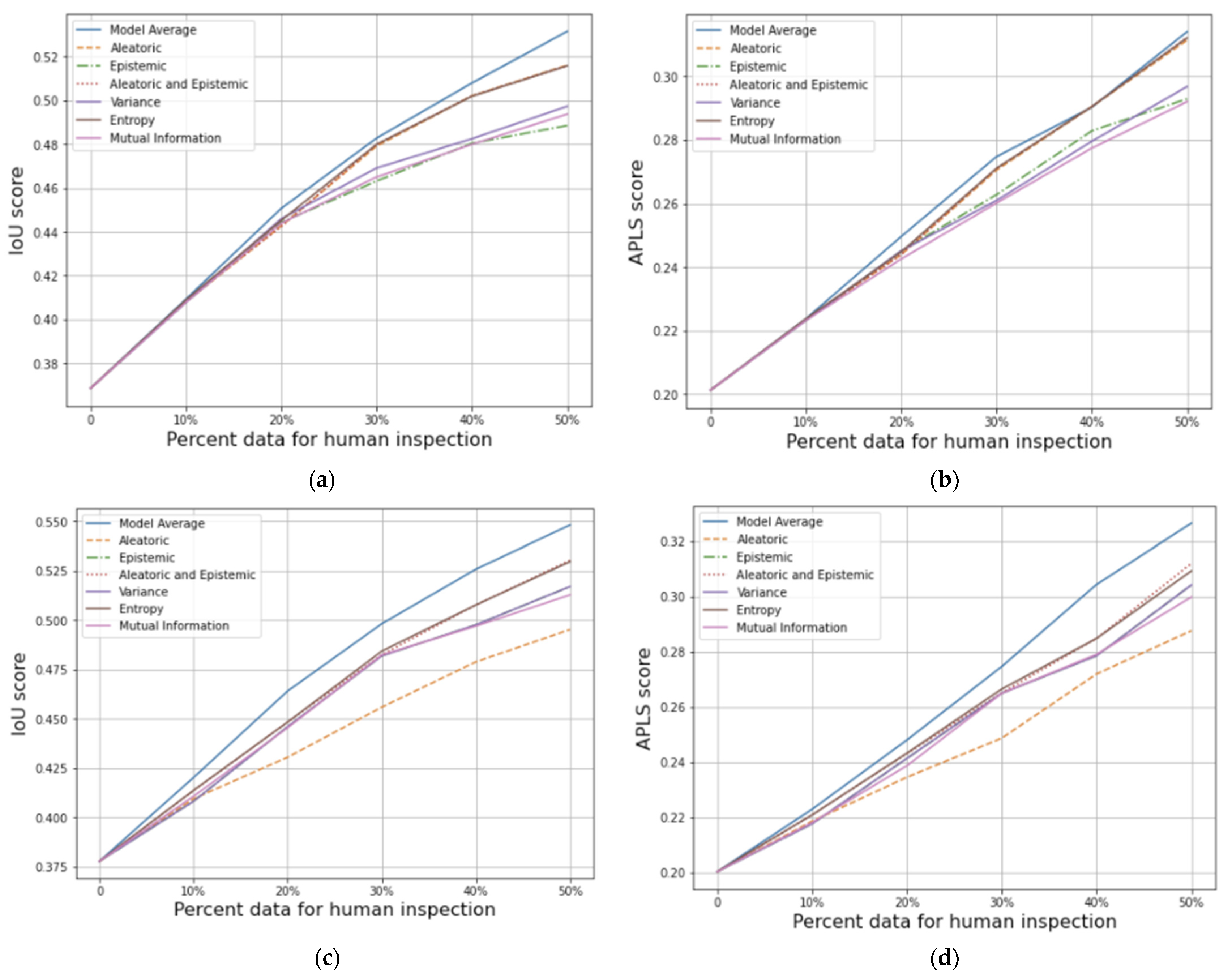
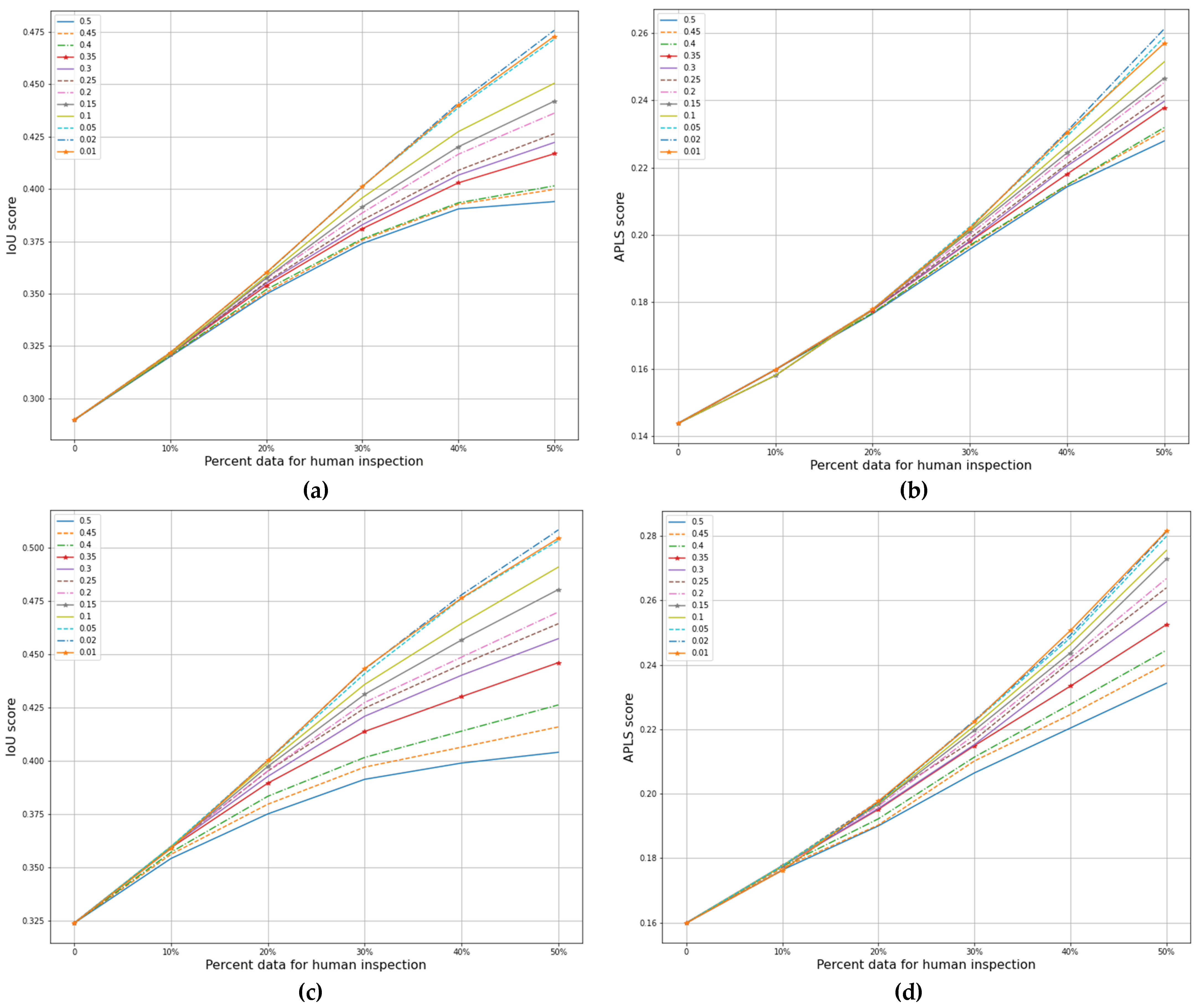
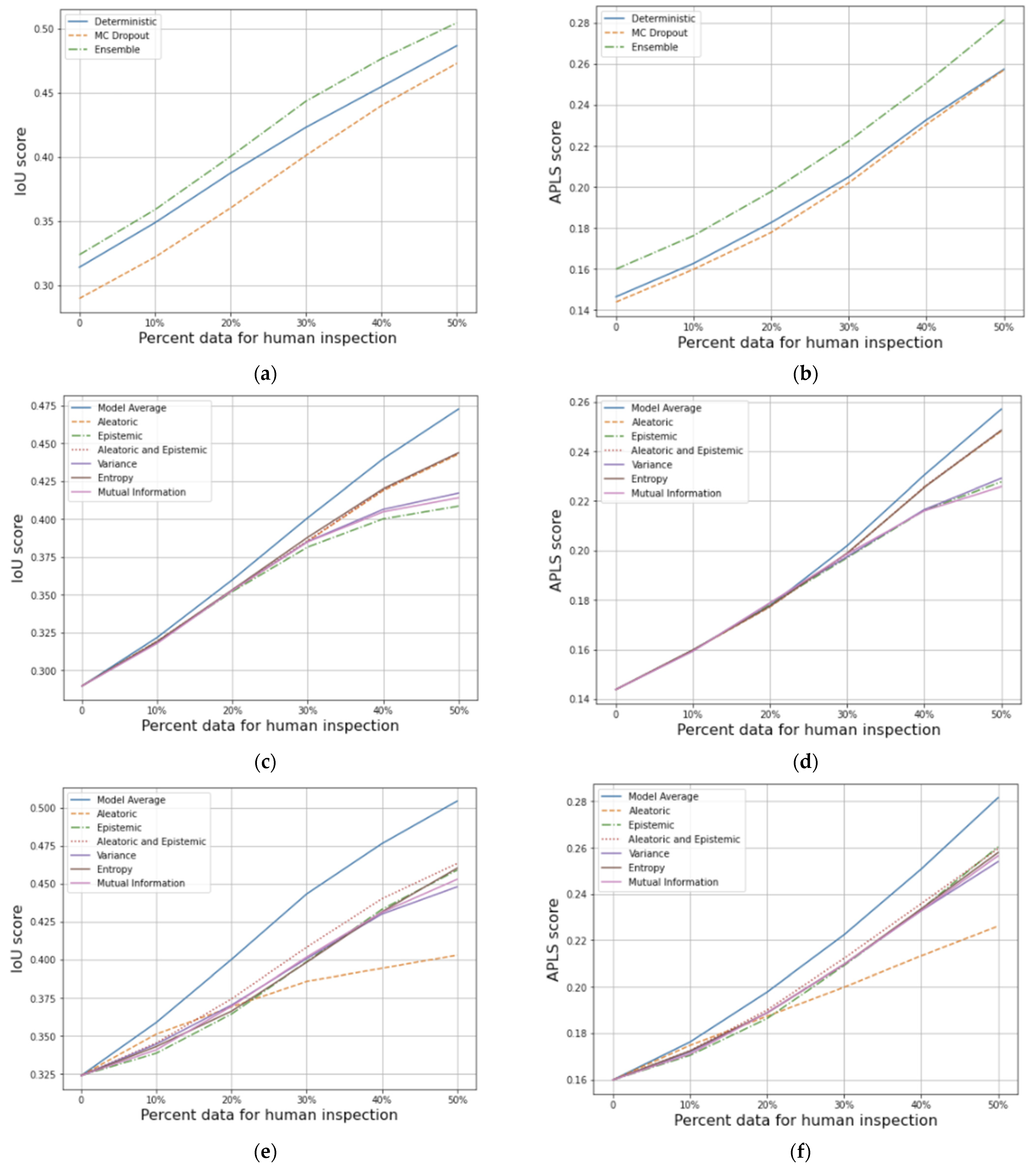
3.1. In-Distribution Test Data
3.2. Out-of-Distribution Test Data
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guo, C.; Pleiss, G.; Sun, Y.; Weinberger, K.Q. On Calibration of Modern Neural Networks. arXiv 2017, arXiv:170604599. [Google Scholar]
- Gal, Y.; Ghahramani, Z. Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning. arXiv 2016, arXiv:150602142. [Google Scholar]
- Henne, M.; Schwaiger, A.; Roscher, K.; Weiss, G. Benchmarking Uncertainty Estimation Methods for Deep Learning with Safety-Related Metrics. In Proceedings of the 34th AAAI Conference on Artificial Intelligence SafeAI, New York, NY, USA, 9–12 February 2020; p. 8. [Google Scholar]
- Loquercio, A.; Segù, M.; Scaramuzza, D. A General Framework for Uncertainty Estimation in Deep Learning. IEEE Robot. Autom. Lett. 2020, 5, 3153–3160. [Google Scholar] [CrossRef]
- Leibig, C.; Allken, V.; Ayhan, M.S.; Berens, P.; Wahl, S. Leveraging Uncertainty Information from Deep Neural Networks for Disease Detection. Sci. Rep. 2017, 7, 17816. [Google Scholar] [CrossRef] [PubMed]
- Kendall, A.; Gal, Y. What Uncertainties Do We Need in Bayesian Deep Learning for Computer Vision? arXiv 2017, arXiv:170304977. [Google Scholar]
- Ovadia, Y.; Fertig, E.; Ren, J.; Nado, Z.; Sculley, D.; Nowozin, S.; Dillon, J.V.; Lakshminarayanan, B.; Snoek, J. Can You Trust Your Model’s Uncertainty? Evaluating Predictive Uncertainty Under Dataset Shift. arXiv 2019, arXiv:190602530. [Google Scholar]
- Nixon, J.; Dusenberry, M.; Jerfel, G.; Nguyen, T.; Liu, J.; Zhang, L.; Tran, D. Measuring Calibration in Deep Learning. arXiv 2020, arXiv:190401685. [Google Scholar]
- Nalisnick, E.; Matsukawa, A.; Teh, Y.W.; Gorur, D.; Lakshminarayanan, B. Do Deep Generative Models Know What They Don’t Know? arXiv 2019, arXiv:181009136. [Google Scholar]
- Wilson, A.G.; Izmailov, P. Bayesian Deep Learning and a Probabilistic Perspective of Generalization. arXiv 2020, arXiv:200208791. [Google Scholar]
- Maddox, W.; Garipov, T.; Izmailov, P.; Vetrov, D.; Wilson, A.G. A Simple Baseline for Bayesian Uncertainty in Deep Learning. arXiv 2019, arXiv:190202476. [Google Scholar]
- Lakshminarayanan, B.; Pritzel, A.; Blundell, C. Simple and Scalable Predictive Uncertainty Estimation Using Deep Ensembles. arXiv 2017, arXiv:161201474. [Google Scholar]
- Chen, L.-C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-Decoder with Atrous Separable Convolution for Semantic Image Segmentation. arXiv 2018, arXiv:180202611. [Google Scholar]
- Kwon, Y.; Won, J.-H.; Kim, B.; Paik, M. Uncertainty Quantification Using Bayesian Neural Networks in Classification: Application to Biomedical Image Segmentation. Comput. Stat. Data Anal. 2020, 142, 106816. [Google Scholar] [CrossRef]
- Steger, C.; Glock, C.; Eckstein, W.; Mayer, H.; Radig, B. Model-Based Road Extraction from Images. In Automatic Extraction of Man-Made Objects from Aerial and Space Images; Gruen, A., Kuebler, O., Agouris, P., Eds.; Birkhäuser: Basel, Switzerland, 1995; pp. 275–284. [Google Scholar]
- Hedman, K.; Wessel, B.; Soergel, U.; Stilla, U. Automatic road extraction by fusion of multiple SAR views. In Proceedings of the 3th International Symposium: Remote Sensing and Data Fusion on Urban Areas, Tempe, AZ, USA, 14–16 March 2005. [Google Scholar]
- Hinz, S.; Baumgartner, A.; Steger, C.; Mayer, H.; Eckstein, W.; Ebner, H.; Radig, B.; Smati, S.M. Road Extraction in Rural and Urban Areas. In Semantic Modeling for the Acquisition of Topographic Information from Images and Maps; Birkhäuser: Basel, Switzerland, 1999. [Google Scholar]
- Steger, C.; Mayer, H.; Radig, B. The Role of Grouping for Road Extraction. In Automatic Extraction of Man-Made Objects from Aerial and Space Images (II); Birkhäuser: Basel, Switzerland, 1997. [Google Scholar]
- Xu, R.; He, C.; Liu, X.; Chen, D.; Qin, Q. Bayesian Fusion of Multi-Scale Detectors for Road Extraction from SAR Images. ISPRS Int. J. Geo. Inf. 2017, 6, 26. [Google Scholar] [CrossRef]
- Elguebaly, T.; Bouguila, N. A Bayesian Approach for SAR Images Segmentation and Changes Detection. In Proceedings of the 25th Biennial Symposium on Communications, Kingston, ON, Canada, 12–14 May 2010; pp. 24–27. [Google Scholar]
- Zhao, Q.; Li, Y.; Liu, Z. SAR Image Segmentation Using Voronoi Tessellation and Bayesian Inference Applied to Dark Spot Feature Extraction. Sensors 2013, 13, 14484–14499. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of Hyperspectral Remote Sensing Images with Support Vector Machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Yager, N.; Sowmya, A. Support Vector Machines for Road Extraction from Remotely Sensed Images. In Computer Analysis of Images and Patterns, Proceedings of the CAIP 2003, Groningen, The Netherlands, 25–27 August 2003; Springer: Berlin/Heidelberg, Germany; Volume 2756.
- Yousif, O.; Ban, Y. Improving SAR-Based Urban Change Detection by Combining MAP-MRF Classifier and Nonlocal Means Similarity Weights. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4288–4300. [Google Scholar] [CrossRef]
- Zeiler, M.D.; Fergus, R. Visualizing and Understanding Convolutional Networks. arXiv 2014, arXiv:abs/1311.2901. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 2012, 60, 84–90. [Google Scholar] [CrossRef]
- Kemker, R.; Salvaggio, C.; Kanan, C. Algorithms for Semantic Segmentation of Multispectral Remote Sensing Imagery Using Deep Learning. ISPRS J. Photogramm. Remote Sens. 2018, 145, 60–77. [Google Scholar] [CrossRef]
- Seo, H.; Khuzani, M.B.; Vasudevan, V.; Huang, C.; Ren, H.; Xiao, R.; Jia, X.; Xing, L. Machine Learning Techniques for Biomedical Image Segmentation: An Overview of Technical Aspects and Introduction to State-of-Art Applications. Med. Phys. 2020, 47, e148–e167. [Google Scholar] [CrossRef]
- Zhang, Q.; Kong, Q.; Zhang, C.; You, S.; Wei, H.; Sun, R.; Li, L. A New Road Extraction Method Using Sentinel-1 SAR Images Based on the Deep Fully Convolutional Neural Network. Eur. J. Remote Sens. 2019, 52, 572–582. [Google Scholar] [CrossRef]
- Henry, C.; Azimi, S.M.; Merkle, N. Road Segmentation in SAR Satellite Images with Deep Fully Convolutional Neural Networks. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1867–1871. [Google Scholar] [CrossRef]
- Xiong, D.; He, C.; Liu, X.; Liao, M. An End-To-End Bayesian Segmentation Network Based on a Generative Adversarial Network for Remote Sensing Images. Remote Sens. 2020, 12, 216. [Google Scholar] [CrossRef]
- Wen, Y.; Vicol, P.; Ba, J.; Tran, D.; Grosse, R.B. Flipout: Efficient Pseudo-Independent Weight Perturbations on Mini-Batches. arXiv 2018, arXiv:abs/1803.04386. [Google Scholar]
- Hernández-Lobato, J.M.; Adams, R. Probabilistic Backpropagation for Scalable Learning of Bayesian Neural Networks. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015. [Google Scholar]
- Nair, T.; Precup, D.; Arnold, D.; Arbel, T. Exploring Uncertainty Measures in Deep Networks for Multiple Sclerosis Lesion Detection and Segmentation. arXiv 2018, arXiv:abs/1808.01200. [Google Scholar]
- McClure, P.; Rho, N.; Lee, J.A.; Kaczmarzyk, J.R.; Zheng, C.Y.; Ghosh, S.; Nielson, D.M.; Thomas, A.G.; Bandettini, P.; Pereira, F. Knowing What You Know in Brain Segmentation Using Bayesian Deep Neural Networks. Front. Neuroinformatics 2019, 13, 67. [Google Scholar] [CrossRef] [PubMed]
- Filos, A.; Farquhar, S.; Gomez, A.N.; Rudner, T.G.J.; Kenton, Z.; Smith, L.; Alizadeh, M.; Kroon, A.D.; Gal, Y. A Systematic Comparison of Bayesian Deep Learning Robustness in Diabetic Retinopathy Tasks. arXiv 2019, arXiv:abs/1912.10481. [Google Scholar]
- Hendrycks, D.; Dietterich, T.G. Benchmarking Neural Network Robustness to Common Corruptions and Perturbations. arXiv 2019, arXiv:abs/1903.12261. [Google Scholar]
- Pu, W. Deep SAR Imaging and Motion Compensation. IEEE Trans. Image Process. 2021, 30, 2232–2247. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. arXiv 2015, arXiv:abs/1505.04597. [Google Scholar]
- Saxe, A.M.; Bansal, Y.; Dapello, J.; Advani, M.; Kolchinsky, A.; Tracey, B.D.; Cox, D. On the Information Bottleneck Theory of Deep Learning. In Proceedings of the 6th International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning (Information Science and Statistics); Springer: New York, NY, USA, 2006. [Google Scholar]
- Hinton, G.E.; Srivastava, N.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Improving Neural Networks by Preventing Co-Adaptation of Feature Detectors. arXiv 2012, arXiv:abs/1207.0580. [Google Scholar]
- Shannon, C. A Mathematical Theory of Communication. Bell. Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Fort, S.; Hu, H.; Lakshminarayanan, B. Deep Ensembles: A Loss Landscape Perspective. arXiv 2019, arXiv:abs/1912.02757. [Google Scholar]
- Jaccard, P. The Distribution of the Flora in the Alpine Zone. New Phytol. 1912, 11, 37–50. [Google Scholar] [CrossRef]
- Rahman, M.A.; Wang, Y. Optimizing Intersection-Over-Union in Deep Neural Networks for Image Segmentation. In Proceedings of the 12th International Symposium ISVC, Las Vegas, NV, USA, 12–14 December 2016. [Google Scholar]
- Etten, A.V.; Lindenbaum, D.; Bacastow, T.M. SpaceNet: A Remote Sensing Dataset and Challenge Series. arXiv 2018, arXiv:abs/1807.01232. [Google Scholar]
- D’Amour, A.; Heller, K.; Moldovan, D.; Adlam, B.; Alipanahi, B.; Beutel, A.; Chen, C.; Deaton, J.; Eisenstein, J.; Hoffman, M.D.; et al. Underspecification Presents Challenges for Credibility in Modern Machine Learning. arXiv 2020, arXiv:2011.03395. [Google Scholar]


| Method | IoU | APLS |
|---|---|---|
| Deterministic | 0.362 | 0.184 |
| MC Dropout | 0.369 | 0.201 |
| Deep Ensemble | 0.378 | 0.200 |
| Method | SUG IoU | SUG APLS | Total SUG | AuC IoU | AuC APLS | Total AuC |
|---|---|---|---|---|---|---|
| Deterministic | 0.532 | 0.349 | 0.881 | 2.26 | 1.21 | 3.47 |
| MC Dropout | 0.540 | 0.346 | 0.885 | 2.30 | 1.30 | 3.60 |
| Deep Ensemble | 0.567 | 0.375 | 0.942 | 2.37 | 1.31 | 3.69 |
| Method | SUG IoU | SUG APLS | Total SUG | AuC IoU 2 | AuC APLS | Total AuC |
|---|---|---|---|---|---|---|
| Deterministic | 0.530 | 0.308 | 0.838 | 2.01 | 0.984 | 3.00 |
| MC Dropout | 0.547 | 0.308 | 0.855 | 1.90 | 0.969 | 2.87 |
| Deep Ensemble | 0.564 | 0.329 | 0.893 | 2.09 | 1.07 | 3.16 |
| Method | 10% | 20% | 30% | 40% | 50% |
|---|---|---|---|---|---|
| Deterministic | 0.9 | 0.7 | 0.63 | 0.6 | 0.58 |
| MC Dropout | 0.9 | 0.8 | 0.73 | 0.7 | 0.66 |
| Deep Ensemble | 0.7 | 0.65 | 0.63 | 0.65 | 0.62 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haas, J.; Rabus, B. Uncertainty Estimation for Deep Learning-Based Segmentation of Roads in Synthetic Aperture Radar Imagery. Remote Sens. 2021, 13, 1472. https://doi.org/10.3390/rs13081472
Haas J, Rabus B. Uncertainty Estimation for Deep Learning-Based Segmentation of Roads in Synthetic Aperture Radar Imagery. Remote Sensing. 2021; 13(8):1472. https://doi.org/10.3390/rs13081472
Chicago/Turabian StyleHaas, Jarrod, and Bernhard Rabus. 2021. "Uncertainty Estimation for Deep Learning-Based Segmentation of Roads in Synthetic Aperture Radar Imagery" Remote Sensing 13, no. 8: 1472. https://doi.org/10.3390/rs13081472
APA StyleHaas, J., & Rabus, B. (2021). Uncertainty Estimation for Deep Learning-Based Segmentation of Roads in Synthetic Aperture Radar Imagery. Remote Sensing, 13(8), 1472. https://doi.org/10.3390/rs13081472






