Next Article in Journal
Modeling Mean Radiant Temperature Distribution in Urban Landscapes Using DART
Next Article in Special Issue
Effect of the Partitioning of Diffuse and Direct APAR on GPP Estimation
Previous Article in Journal
A Novel Vegetation Point Cloud Density Tree-Segmentation Model for Overlapping Crowns Using UAV LiDAR
Previous Article in Special Issue
Assessing Canopy Responses to Thinnings for Sweet Chestnut Coppice with Time-Series Vegetation Indices Derived from Landsat-8 and Sentinel-2 Imagery
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 13
Issue 8
10.3390/rs13081441
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Discrepancies between Global Forest Net Primary Productivity Estimates Derived from MODIS and Forest Inventory Data and Underlying Factors

by
Jin Han Park
1,
Jianbang Gan
2,* and
Chan Park
3
1
Korea Adaptation Center for Climate Change, Korea Environment Institute, Sejong 30121, Korea
2
Department of Ecology and Conservation Biology, Texas A&M University, College Station, TX 77843, USA
3
Department of Landscape Architecture, College of Urban Science, University of Seoul, Seoul 02504, Korea
*
Author to whom correspondence should be addressed.
Remote Sens. 2021, 13(8), 1441; https://doi.org/10.3390/rs13081441
Submission received: 23 February 2021 / Revised: 26 March 2021 / Accepted: 5 April 2021 / Published: 8 April 2021
(This article belongs to the Special Issue Modelling and Monitoring Vegetation Decline and Productivity with Remote Sensing)
Browse Figures
Versions Notes

Abstract

:
The net primary productivity (NPP) of a forest is an important indicator of its potential for the provision of ecosystem services such as timber, carbon, and biodiversity. However, accurately and consistently quantifying global forest NPP remains a challenge in practice. We converted carbon stock changes using the Global Forest Resources Assessment (FRA) data and carbon losses associated with disturbances and timber removals into an NPP equivalent measurement (FRA NPP*) and compared it with the NPP derived from the MODIS satellite data (MOD17 NPP) for the world’s forests. We found statistically significant differences between the two NPP estimates, with the FRA NPP* being lower than the MOD17 NPP; the differences were correlated with forest cover, normalized difference vegetation index (NDVI), and GDP per capita in countries, and may also stem from the NPP estimation methods and scopes. While the former explicitly accounts for carbon losses associated with timber removals and disturbances, the latter better reflects the principles of photosynthesis. The discrepancies between the two NPP estimates increase in countries with a low income or low forest cover, calling for enhancing their forest resource assessment capacity. By identifying the discrepancies and underlying factors, we also provide new insights into the relationships between the MOD17 NPP and global forest carbon stock estimates, motivating and guiding future research to improve the robustness of quantifying global forest NPP and carbon sequestration potential.

1. Introduction

Forest productivity is an essential indicator for gauging the capacity of a forest to provide an array of ecosystem services. In addition to the provisions of timber, water, and biodiversity, forests play an important role in the global carbon cycle by absorbing and storing carbon dioxide through photosynthesis [1,2,3], and account for about half of the carbon stocks stored in terrestrial ecosystems [4]. As a result, interest in forest carbon uptake and storage has been increasing in recent years [5,6,7,8]. The net primary productivity (NPP) of a forest refers to the amount of carbon absorbed from the atmosphere through plant growth minus carbon losses due to plant respiration [9]. It is also related to the biomass and carbon stock stored in forest biomes [8,10,11]. Many studies have attempted to quantify forest NPP at different geographic scales using various methods [12,13,14]. However, accurately quantifying the NPP of global forests remains notoriously challenging due to data limitations, uncertainties involved, and other barriers [9].
Several methods have been devised and applied to quantify forest NPP, including field measurements, remote sensing, and modeling. Most studies on global forest NPP have used hybrid approaches to take advantage of strengths of each method to overcome measurement barriers. One subset of these studies has employed model-based methods for estimating the NPP [14,15,16]. These model-based methods often involve the use of data collected from flux towers [17,18], remote sensing devices [19,20], and other sources [2,9,14,21]. On the other hand, the traditional forest inventory method, which involves statistical sampling and inferences, is still commonly used in forest resource assessments at the country level [22,23]. Based on the forest inventory statistics reported by individual countries, the Food and Agriculture Organization (FAO) of the United Nations has compiled the Global Forest Resources Assessment (FRA) reports [24,25]. The FAO data have also been used to estimate the biomass and carbon stock of the world’s forests, providing important information for global carbon accounting [26]. Different methods have been used to quantify the NPP and carbon stock of the world’s forests; therefore, inconsistencies among these estimates and methods have caused confusions, hindering the development and implementation of policies and programs to enhance the productivity and climate mitigation role of global forests.
Researchers have also examined the factors, mainly biophysical variables, which are potentially attributable to NPP or NPP estimates [2,16,21,27]. Among these factors are terrain, soil, fire, and weather [28,29,30,31,32]. In terms of remote sensing data, the issue with data inaccuracy resulting from, for example, the pre-processing process and the manual and subjective determination of the threshold of each image has also been identified [33]. Traditional forest inventory, on the other hand, can be affected by the country’s technical and/or economic capacity [22,23]. When the data of individual countries are aggregated to generate the global total, some of these issues could be amplified. However, to the best of our knowledge, no study has compared the global forest NPP or carbon stock estimates derived from different methods or data sources and analyzed the underlying factors attributable to their differences. This may be partly because the NPP or carbon stock estimates are not directly comparable given the different estimation approaches or data sources employed, although they have been used extensively for policy discussions. Given the importance of global NPP estimates for guiding policy and efforts to enhance forest sustainability and forest carbon sequestration for mitigating climate change, there is a compelling need for such comparisons and analyses. Comparative studies can uncover possible consistencies or discrepancies between different NPP estimates as well as factors that may contribute to the discrepancies, helping to improve the accuracy and consistency of global forest NPP measurements in the future.
Here, we aim to compare the global forest NPPs derived from the MOD17 satellite data of the U.S. National Aeronautics and Space Administration (NASA) and the FAO’s FRA data and to identify factors that may contribute to their discrepancies. We will refer to the former as to the MOD17 NPP and to the latter as the FRA NPP* hereafter, with the asterisk indicating that it is an NPP approximation based on carbon stock changes. Although the FRA data represent carbon stock, for the purpose of comparison, we attempt to convert carbon stock changes along with carbon losses due to timber removals and disturbances into an NPP equivalent measurement. Choosing these two NPP estimates or measurements was largely because they have been widely used for or cited in quantifying the carbon fluxes and stocks of the world’s forests. Additionally, they are obtained by aggregating the country-level estimates across all countries or territories in the world. The country-level data can allow us to examine the statistical associations between the NPP estimates and the biophysical and socioeconomic attributes of individual countries.
For the global assessments, several criteria such as relevance, accuracy, timelines, comparability, coherence, accessibility, and clarity are important to create a reliable set of national statistics [34]. However, it is unlikely to produce statistical data at the same level of standards for all the countries in the world because of differences in their technical capacity, socioeconomic development status, and political systems. We are interested in how and to what extent socioeconomic variables as well as biophysical variables affect the two forest NPP estimates and their discrepancies across countries. We also attempt to estimate the statistical relationships of the estimated NPPs, especially their discrepancies, with the biophysical and socioeconomic variables.
Please note that our intention is not to verify either of the two global forest NPP estimates, which is impossible without knowing the true value of global forest NPP. Instead, we aim to identify the discrepancies, if any, between them and the underlying factors that may contribute to the discrepancies. Hence, our findings, including the magnitude and underlying causes of the discrepancies, will provide guidance for the better use of these existing NPP and carbon stock estimates, and for improvements in future endeavors to quantify the global forest NPP and carbon sequestration potential.

2. Materials and Methods

2.1. Overall Study Approach

Our overall approach includes several major steps (Figure 1). First, we identified the variables affecting NPP through a literature review and gathered relevant data. These variables were classified into biophysical and socioeconomic factors. Secondly, we compiled two NPP measurements: one derived from the FRA data (FRA NPP*), and the other based on the MOD17 data (MOD17 NPP). Thirdly, we tested whether there was a statistically significant difference between the two NPP measurements, and analyzed the relationship between each of the NPP measurements and a specific biophysical or socioeconomic factor. Finally, we examined the effects of multiple factors on the discrepancy between the two NPP measurements by regressing it on several biophysical and socioeconomic factors together.

2.2. Variable Measurements and Data

2.2.1. Net Primary Productivity

We derived the NPP of global forests using two different sets of data: one from MOD17 and the other from the FRA report. The two datasets have been extensively used for quantifying the productivity and carbon sequestration and storage capacity of the world’s forests. The annual NPP estimates were either measured in or converted to tonnes of carbon per unit forest area (tC/km2/year) for each country or territory in 2015.
NASA use the MODIS satellite data to calculate the NPPs of the world’s terrestrial ecosystems at a 1 km2 spatial resolution of earth surface [35]. Their NPP estimate is based on the amount of solar energy absorbed by plants, which is measured by the satellite sensor, adjusted for the differences between the theoretical and practical solar energy absorption efficiencies of plants. Specifically, the MODIS algorithm is based on the original radiation use efficiency and considers vegetation type, water stress, and cold temperature conditions, as well as daily leaf and fine root maintenance respiration, annual growth respiration, and annual maintenance respiration of live cells in woody tissues [36]. The MOD17A2 data of validation stage 3, which were collected by the TERRA satellite, were used in this study. The monthly NPP data were extracted only for forests. The monthly average NPPs in 2015 were downloaded directly from the NASA Earth Observations website [37] and aggregated into annual NPP values for each country using the following formula:
M O D 17   N P P i =   ∑ m = 1 12 M o n t h l y   a v e r a g e   N P P i m    
where i represents the country or territory, and m denotes the month.
The FAO, on the other hand, has compiled statistics on the world’s forests since 1946 and has published the FRA reports every five years since 1980. These FAO statistics and reports update the state of global forests periodically and have been extensively used for research and policy discussions related to forest production, conservation, and carbon sequestration and storage. They are compiled based on the country reports prepared by the national correspondents in individual countries, and the estimates are by FAO staff in cooperation with national focal points and regional partners if a country report is unavailable. The 2015 FRA included 234 countries and territories, and the data for 155 countries and territories were reported by individual countries themselves, accounting for 98.8% of the world’s forests [24]. The FRA report did not directly provide NPP estimates but contained the quantities of forest area, biomass, and carbon stored in each of the five forest carbon pools (above-ground, below-ground, deadwood, litter, and soil carbon) [3,24]. We calculated the NPP for each country based on annual changes in the amounts of carbon stored in these pools plus the carbon removed via annual timber harvest and the carbon lost due to disturbances (fire, insects, diseases, and weather events). The FRA reports forest biomass and carbon stocks every five years; therefore, we computed and used the mean of the average annual changes between 2010 and 2015 and between 2015 and 2020 as the annual change for 2015. The volume of timber harvested in 2015, including all roundwood and wood fuel [38], was converted to carbon based on the carbon content per unit volume of wood reported in the FRA for each country. Similarly, the carbon losses due to disturbances were calculated by multiplying the area of forests damaged by disturbances in 2015 with the amount of carbon per unit forest area reported in the FRA for each country. The FRA did provide annual data on disturbances while reporting forest biomass and carbon stocks every five years, enabling us to calculate annual carbon losses due to disturbances in 2015. The annual total NPP in each country was divided by its total forest area to derive its annual NPP per unit forest area (tC/km2/year).
The formula used to calculate annual NPP based on the FRA data is as follows:
F R A   N P P i * =   ∑ p = 1 5 Δ S i p + ∑ d = 1 4 L i d + H i                        
where i represents the country or territory, p denotes each of the five forest carbon pools (above-ground, below-ground, deadwood, litter, and soil carbon), and d represents the type of disturbances (fire, insects, diseases, and weather events); ∆Sip denotes the average annual change in the carbon stock of pool p per unit forest area in country i; Lid denotes the annual carbon loss due to disturbance d per unit forest area in country i; and Hi denotes the annual carbon loss due to timber harvest/removals per unit forest area in country i.
This approach excluded the carbon losses to the atmosphere from soil respiration and decomposition and the biomass consumed by herbivores. For simplicity, we also assumed that all biomass in a forest area affected by disturbances disappears from the ground within the same year. These exclusions tend to underestimate NPP, while the simplification may overestimate NPP because not all biomass carbon in a forest affected by a disturbance will be released to the atmosphere immediately. The possible underestimates and overestimates may cancel each other out, at least partially. The major reason for the exclusions and simplification was that estimating these carbon losses and the amount of deadwood remaining after various disturbances is extremely difficult. However, the amount of biomass carbon excluded seems relatively small compared to the total amount of carbon reported in the five pools [9,39,40]. The FRA report also shows that only about 3% of the world’s forest area was damaged by disturbances in 2015, and that only one-fifth of the countries and territories reported that their forests were affected by disturbances in that year [24]. Hence, the exclusions and simplification are unlikely to have a big impact on the NPP estimate.
Although this is an indirect approach to estimating NPP, it connects NPP to the amount of carbon stored in the major forest carbon pools. Translating changes in the carbon stock in different carbon pools into NPP allows us to compare the two NPP estimates explicitly. Meanwhile, this approach enables us to implicitly compare the NPP obtained from MOD17 with the carbon stock derived from the FRA report. While NPP represents the potential of forests for carbon sequestration, the amount of carbon stored in the pools demonstrates the role of forests in carbon storage; both are critical to the global carbon cycle. Therefore, their robust estimates have important implications for understanding and leveraging the potential of global forests for climate mitigation.

2.2.2. Biophysical Factors

The biophysical factors considered in this study include latitude; forest cover; aspects of the south, southwest, and southeast; ratios of deciduous and coniferous forests to total forest area; ratios of desert area and tropical and subtropical area in an ecoregion; leaf area index (LAI); normalized difference vegetation index (NDVI); annual net radiation (W/m2); land surface temperature (LST) (°C); annual accumulated temperatures over 10 °C (°C); annual precipitation (mm); and available water storage capacity (index value from 1 to 7).
We used the Google Public Data Explorer to obtain the latitude data. Data on forest-related factors were drawn from the FRA report [24], and data on ecoregion type were downloaded from the World Wildlife Fund (WWF) [41]. The forest types or ecoregions covered in this study included tropical and subtropical moist broadleaf forests, tropical and subtropical dry broadleaf forests, tropical and subtropical coniferous forests, temperate broadleaf and mixed forests, temperate coniferous forests, and boreal forests. These forest types also resemble those included in the FRA data source. We used the Aspect tool of ArcMap 10.2.2., coupled with the elevation map provided by NASA, to derive the aspect data. The monthly LAI, NDVI, and LST data and the daily average net radiation data were made available by NASA [42]. These data were then converted to their annual means. The v5.01 data of annual precipitation and monthly temperatures were downloaded from the webpage supported by the Department of Geography at the University of Delaware and NASA [43]. We then calculated the annual accumulated temperatures over 10 °C using the monthly temperature data. Data on the available water storage capacity were obtained from the Regridded Harmonized World Soil Database v1.2 [44]. The available water storage capacity is represented by an index value ranging from 1 to 7. The lower the index value, the greater the capacity for water storage.

2.2.3. Socioeconomic Factors

We considered several socioeconomic factors that may have an impact on the capacity of a country to conduct its forest resource inventory and report its forest statistics that meet the FAO standards. These factors included gross domestic product (GDP; measured in USD) per capita, technicians in R&D (number of technicians per million people), expenditure on education (% of GDP), and the global open data index (ODI).
Data on GDP, population, technicians in R&D, and expenditure on education were acquired from the World Bank open data platform [45]. The Open Knowledge International, a non-profit organization, publishes the Global Open Data Index [46]. The index, representing the openness of government data in countries, was compiled based on crowd-sourced surveys.

2.3. Statistical Analysis

We conducted a paired t-test to compare the NPPs derived from the MOD17 and FRA data. We also estimated the statistical relationship between the NPP estimates and each of the biophysical and socioeconomic factors and generated scatter plots. Finally, we ran multiple regressions of the discrepancy between the MOD17 NPP and the FRA NPP* on various combinations of biophysical and socioeconomic factors described above. We used the percentage discrepancy between the two NPP estimates as the dependent variable. The percentage discrepancy represents the distance between the FRA NPP* and the MOD17 NPP divided by their mean. In order to compare the effects of independent variables on the NPP discrepancy, the biophysical and socioeconomic variables were normalized (i.e., converted to Z-scores). After experimenting with different function forms (linear, nonlinear, and mixed) and testing for the goodness of fit, collinearity, and robustness, we derived the final best-fit model. The sample size (n) used for the t-test and regression analysis was 151 (countries), after excluding those that did not have both MOD17 and FRA data or information on the biophysical and socioeconomic variables included in the regression analysis.

3. Results

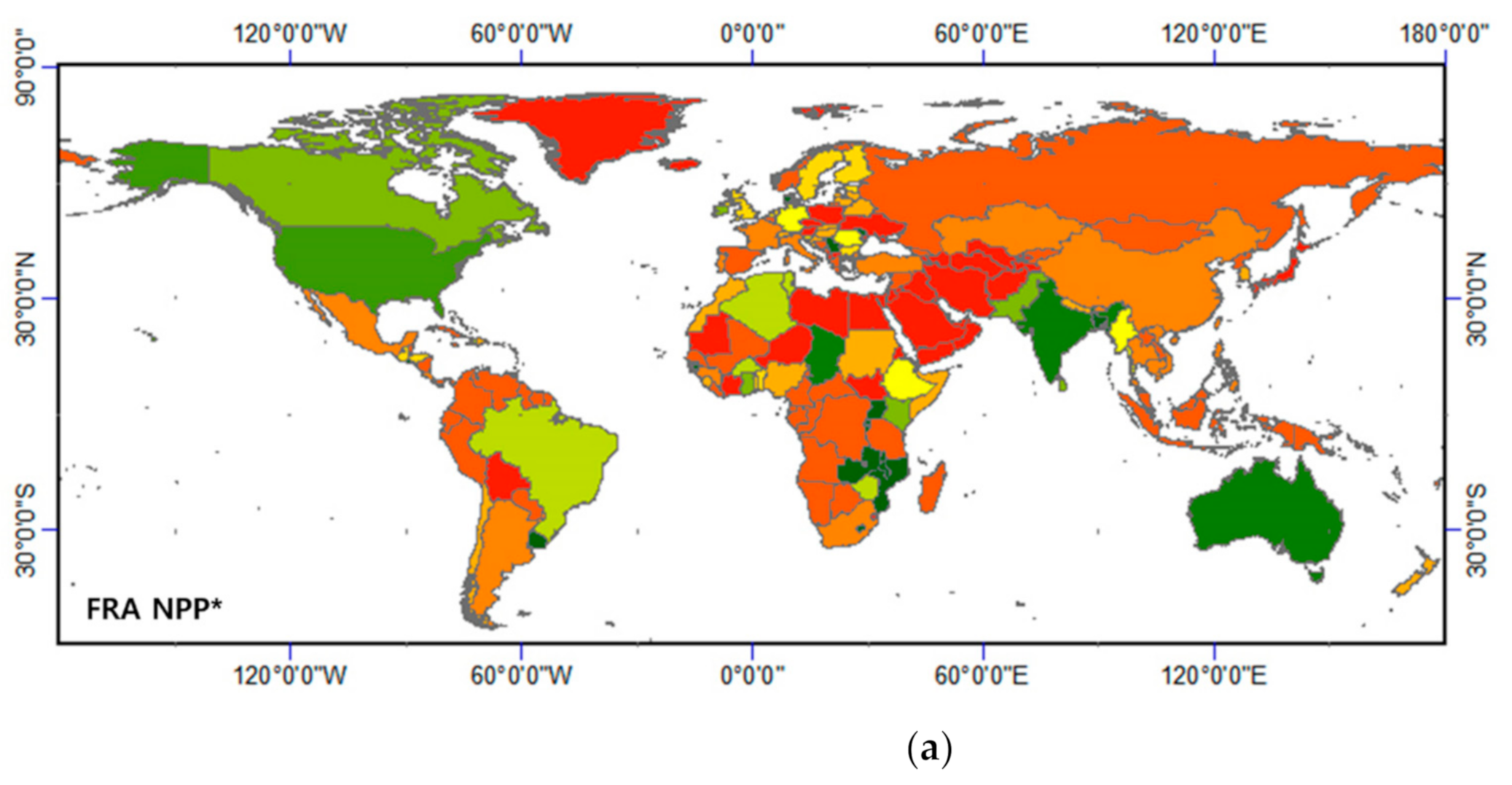
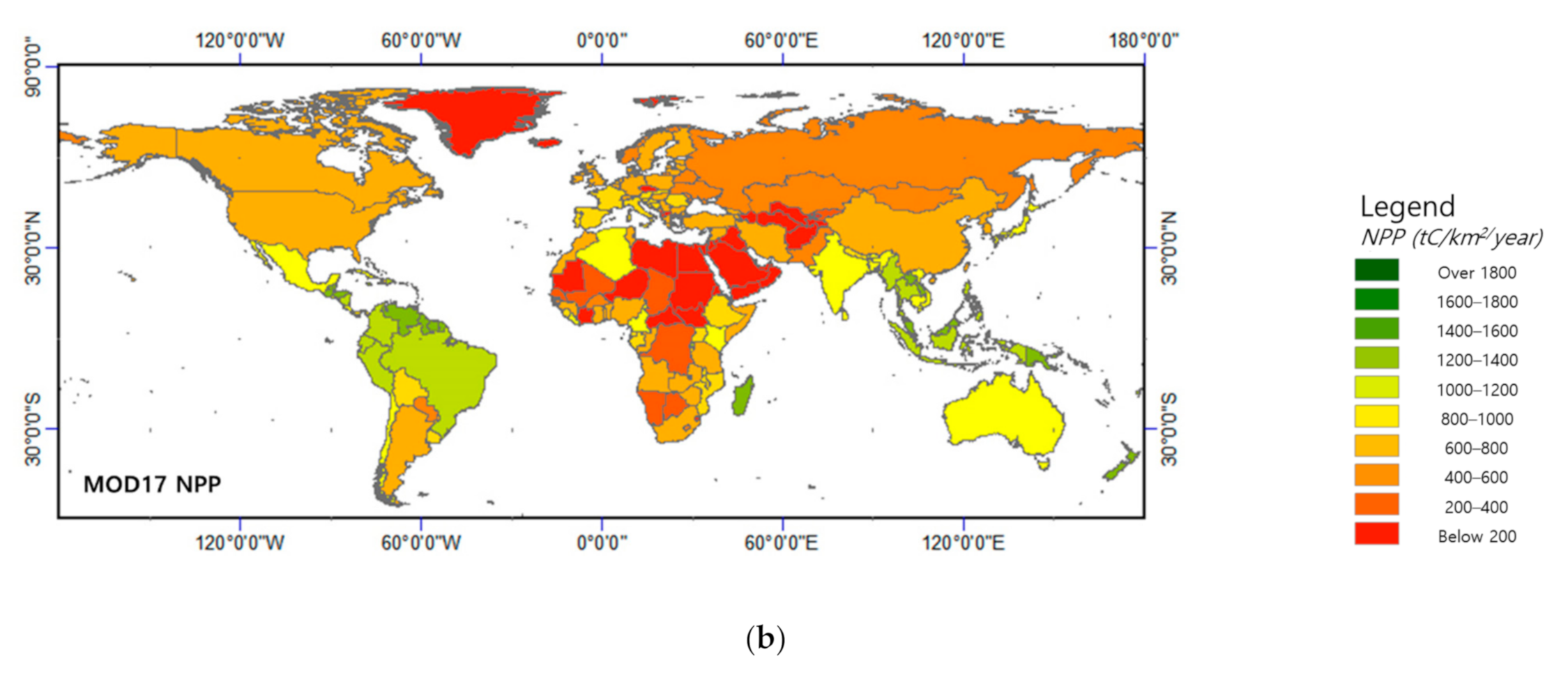
3.1. Annual NPP by Country

The estimated annual NPPs per unit forest area across countries in 2015 are shown in Figure 2, which varied considerably from country to country. The highest FRA NPP*, for countries with at least one million ha of forest area, occurred in Bangladesh, Niger, Malawi, Uganda, Mozambique, Serbia and Montenegro, Zambia, Uruguay, Guinea-Bissau, and India. On the other hand, Honduras, French Guiana, Papua New Guinea, New Zealand, Venezuela, Guatemala, Suriname, Lao, Belize, and Madagascar had the highest MOD17 NPP.

3.2. Relationships Between the MOD17 NPP and the FRA NPP*

In general, the FRA NPP* was lower than the MOD17 NPP. The paired t-test confirmed that there was a statistically significant difference between the two NPP estimates (Table 1). Their mean difference was 217.502 tC/km2/year. The difference between the two NPP estimates also varied across countries (Figure 3). The largest discrepancies (in absolute value) existed in countries such as Bangladesh, Niger, Malawi, Uganda, Serbia and Montenegro, Mozambique, Guinea-Bissau, Zambia, Chad, Japan, French Guiana, Uruguay, Venezuela, Suriname, Papua New Guinea, Belize, Solomon Islands, Guyana, and Laos.
On the other hand, the least discrepancies between the two NPP estimates occurred in Morocco, Switzerland, Slovenia, Brazil, Latvia, Croatia, Slovakia, Republic of Korea, Lithuania, Democratic Republic of the Congo, Nigeria, Ethiopia, Kazakhstan, Myanmar, Hungary, and Algeria. For these countries, the absolute value of the difference between the two NPP estimates was less than 5% of their mean. The next group of countries, including Sweden, Finland, Somalia, Bulgaria, China, Sri Lanka, Sierra Leone, Mali, Guinea, Estonia, Nepal, Kenya, Togo, Romania, Belarus, and Netherlands, showed a less than 10% discrepancy between the two NPP estimates.
The scatter plot of the MOD17 NPP versus the FRA NPP* also indicated the evidence of discrepancies between the two NPP estimates (Figure 4). Moreover, there was no strong statistical relationship between them. Surprisingly, these two NPP estimates were not even positively related. The discrepancy patterns differed across regions. For almost all countries in South America, their MOD17 NPP was higher than their FRA NPP*. Approximately an equal number of African countries had MOD17 NPP values either higher or lower than their FRA NPP*. Most countries in other regions had MOD17 NPP values higher than their FRA NPP*.

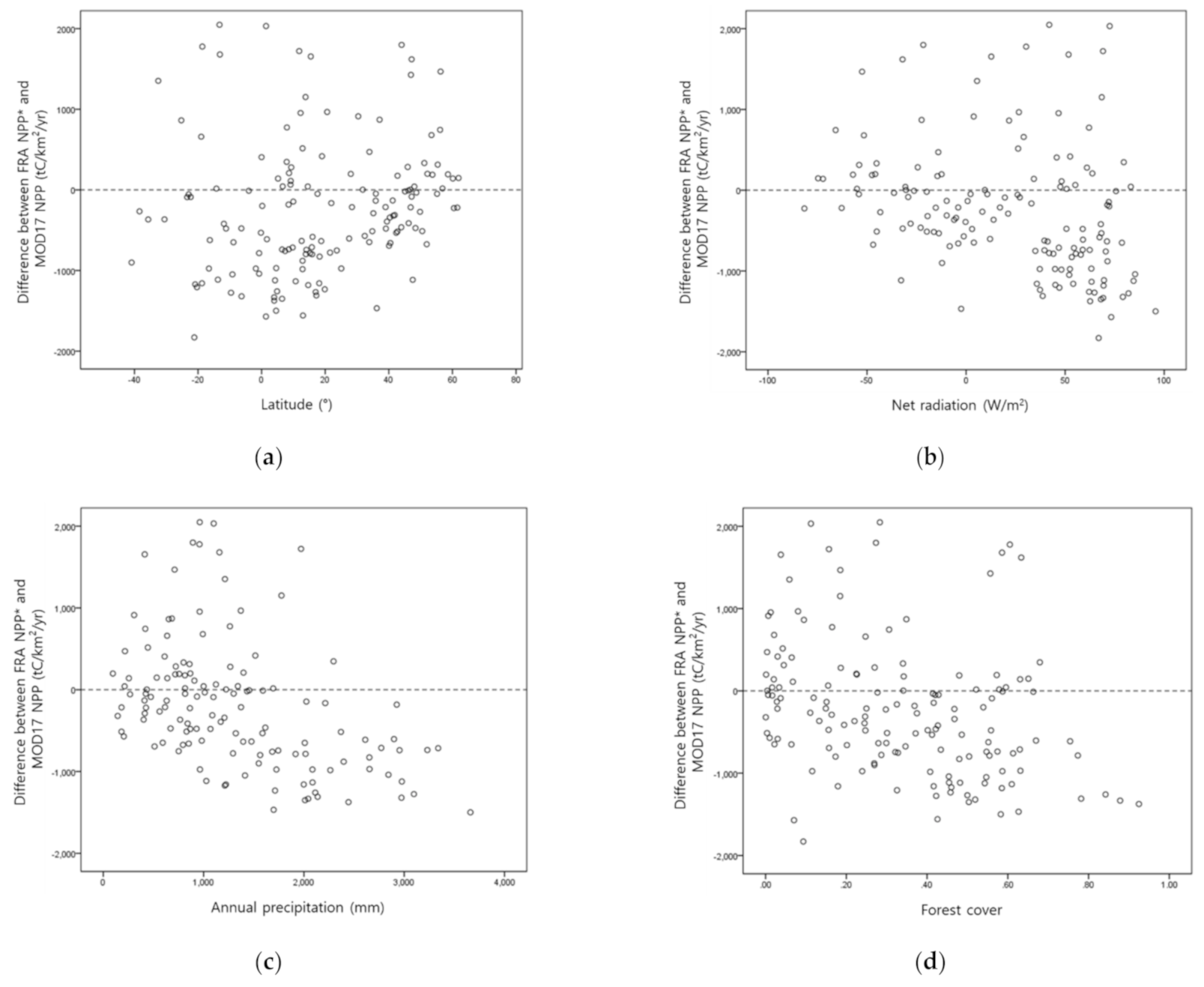
3.3. Relationships between NPP Estimates and Biophysical and Socioeconomic Factors

3.3.1. Relationships with an Individual Factor

The MOD17 NPP was nonlinearly correlated with several biophysical factors, especially NDVI, LAI, net radiation, and annual precipitation. This is consistent with the NPP definition and the principles embedded in the MODIS algorithm [35,47]. On the contrary, the FRA NPP* showed no correlation with any of these biophysical factors except forest cover. The ratio of forest cover (ratio of forest area to total land area) was moderately correlated with the FRA NPP*. Furthermore, the variations of the FRA NPP* tend to decrease as the ratio of forest cover increases.
The relationships between the discrepancy in the two estimated NPPs and each of the biophysical and socioeconomic factors are shown in Figure 5. There are a few factors that can help explain the discrepancies. They are NDVI, LAI, net radiation, annual precipitation, and forest cover, mirroring those that are correlated with the MOD17 or FRA NPP*. The magnitude (absolute value) of discrepancies between the two NPP estimates increases with a rise in the value of these factors. The MOD17 NPP is more likely to be greater than the FRA NPP* in countries with net radiation > 70 W/m, annual precipitation > 2000 mm, forest cover rate > 0.4, NVDI > 0.7, or LAI > 2.5. The variance of the discrepancies, on the other hand, tends to diminish as the values of these factors increase.

3.3.2. Relationships with Multiple Factors

The final multiple regression results are shown in Table 2. The adjusted R2 is 0.74. All variance inflation factor (VIF) values were less than 5, indicating no evidence of collinearity.
The regression results revealed several interesting relationships between the NPP discrepancy and the biophysical and socioeconomic factors. Of the four statistically significant independent variables, forest cover had the largest effect on the NPP discrepancy, followed by NDVI, ODI, and GDP per capita. In terms of simple correlation, NDVI and forest cover were also correlated with the MOD17 NPP and the FRA NPP*, respectively. Therefore, there is no surprise that they are attributable to the NPP discrepancy. The open data index and GDP per capita show no correlation with either the MOD 17 NPP or the FRA NPP* in simple correlation, but they are related to the NPP discrepancy in the multiple regression even though the absolute values of their coefficients are much smaller than those of forest cover and NDVI.
According to the sign of estimated regression coefficients, countries with a higher forest cover rate and GDP per capita tend to have smaller discrepancies between the FRA NPP* and the MOD17 NPP. The NPP discrepancy increases with an increase in NDVI. The positive sign of the NDVI coefficient is largely because NDVI is positively correlated with the MOD17 NPP but uncorrelated with the FRA NPP*. It is unexpected that ODI is positively related to the NPP discrepancy. This might be attributable to the fact that ODI does not necessarily reflect the statistical capacity or the quality of open data in different countries [46].

4. Discussion

Our findings show tremendous discrepancies and no clear relationship between the two NPP estimates (FRA NPP* and MOD17 NPP) of global forests. This calls for further efforts to understand and resolve the discrepancies, because both data sources are widely used for quantifying global forest productivity and/or carbon stocks. The discrepancies could stem from multiple factors because measuring forest NPP is a complex and challenging task in practice, especially on a global scale. These factors include differences in the NPP measurement methods and scopes, among others. The MOD17 NPP measurements were obtained by satellite sensors, which can be consistently applied across countries, while the FRA NPP* was based on forest inventories that entail extensive human involvements in data collection. Due to the differences in counties’ technical capacity and efforts committed to conducting forest inventories, the quality of forest inventory data may vary from country to country. The different criteria used for classifying forests or forestland could be another reason for the NPP discrepancies. For instance, the MODIS sensors may recognize newly harvested or cutover forestland as non-forest land with a low MOD17 NPP, while the FRA still classifies this type of land as forestland, the same as its neighboring forest or its previous/pre-harvest state. Accurately classifying forest cover, and especially forest types, remains a challenge using MODIS imageries [48]. The NPP discrepancies could also be due to the different time periods embedded in the two NPP estimates. While the MOD17 NPP represents its measurement in 2015, the FRA reports carbon stocks in every five years. As a result, the FRA NPP* reflects the mean of its annual averages for the two five-year periods before and after 2015 (i.e., 2010–2015 and 2015–2020). Additionally, measuring NPP or carbon stocks in litters and below-ground biomass is difficult although it is an important part of total forest NPP [9,47]. Litter decomposition is a complex process, and the amounts of carbon released due to heterotrophic respiration and transferred to soil carbon in the decomposition process are uncertain and vary considerably across forest types and locations [49]. This may have some influence on the FRA NPP* because it is based on carbon stock changes in the litter, below-ground, and soil carbon pools. All these factors may positively or negatively affect the NPP discrepancies.
The FRA NPP* was generally lower than the MOD17 NPP. Aside from the factors discussed above, the exclusion or inaccurate measurement of the exudates and lateral flows of carbon as well as heterotrophic respiration in the FRA NPP* seems more critical. The exudates and lateral flows of carbon or heterotrophic respiration may not be fully captured by the changes in the forest carbon stocks reported in the FRA data, but could account for large portions of NPP depending on the ecosystem [50]. Thus, carbon stock changes reported in the FRA may not be a perfect match with NPP but may more closely resemble net ecosystem exchange (NEE), which is NPP minus carbon losses in heterotrophic respiration by animals and microbes [51,52,53]. Nevertheless, litter decomposition transfers part of the carbon in the litter pool to soil carbon [49], which is included in the FRA NPP*. Together, these factors may partly explain why the FRA NPP* is lower than the MOD17 NPP. However, disturbances cause different changes in carbon stock and NPP. For example, a fire may leave a large portion of carbon in deadwood. In this situation, the total carbon stock change in all carbon pools might actually be small, while the NPP will decrease considerably after the fire. As a result, the FRA NPP* may overestimate NPP (by underestimating reductions in carbon stocks). These two types or sources of NPP estimation errors could be cancelled out, at least partially, although in some countries or ecosystems one source of errors may dominate the other.
Although we compared the NPPs estimated from the two data sources, our results could not determine which one is more accurate. Nevertheless, our findings reveal several unique features of both, gaining insights into their discrepancies and the underlying factors. Such insights foster a better understanding of the discrepancies and suggest ways to mitigate the discrepancies or to improve the consistency of NPP estimates. Our results show that the MOD17 NPP is related to biophysical factors such as LAI and NDVI but is independent of socioeconomic factors of a country, while the FRA NPP* shows no correlation with LAI or NDVI. This may at least partially explain why there is no clear statistical relationship between the NPPs estimated from the two data sources. Additionally, the MOD17 NPP can better reflect the principles of photosynthesis, but the FRA data can better represent the biomass or carbon stock accumulated or actually retained in forests with measurements of biomass growth as well as biomass losses due to timber removals and disturbances. This suggests the differences between the two data sources, on the one hand, and their potential complementarity in quantifying the carbon sequestration and storage capacity of the world’s forests, on the other.
Finally, forest cover and GDP per capita are negatively related to the NPP discrepancies. In addition, the largest discrepancies of NPP estimates occur in countries with low NDVI values, while the MOD17 NPP mirrors the photosynthesis principle represented by NDVI. All these imply the needs for improving the FRA data for countries with low forest cover rates and incomes in order to enhance the consistency of the FRA data across countries. These countries may not have adequate capacity for conducting forest resource assessments because of their economic limitations, or may not pay enough attention to their forest resource assessments because of their low forest cover. It is essential to assist or encourage these countries to strengthen their forest resource assessment capacity. Satellite-based remote sensing technology can play an important role in this endeavor as well.

5. Conclusions

We computed the FRA NPP* based on changes in carbon stocks and carbon losses associated with timber removals and disturbances and compared it with the MOD17 NPP for the world’s forests. We found statistically significant differences between the two estimated NPPs, and the FRA NPP* was generally smaller than the MOD17 NPP. Such differences could be due to many factors, including the NPP measurement methods and scopes. Although our results could not determine which NPP measurement is more accurate than the other, they do shed light on consistency within each of the two NPP estimates and the magnitude and underlying factors of their discrepancies. The MOD17 NPP seems more consistent with strong correlations with LAI and NDVI. The major statistical determinants for the NPP discrepancies are forest cover, NDVI, and GDP per capita. Countries with a low forest cover rate and income tend to have large variations in their FRA NPP* and large discrepancies between the FRA NPP* and the MOD17 NPP. Hence, improving the forest resource assessment capacity in these countries would enhance the robustness of FRA carbon stock estimates as well as the FRA NPP* of global forests.
The MOD17 NPP mirrors the principle of photosynthesis, while the FRA NPP* explicitly incorporates carbon losses associated with timber removals and disturbances. Each of these data sources has unique strengths and weaknesses, and they can complement each other. Given the complexity and importance of quantifying forest NPP and carbon stock, we hope that our work will motivate and guide future research to increase the accuracy and consistency of global forest NPP and carbon stock estimates.

Author Contributions

Conceptualization, J.G. and J.H.P.; methodology, J.G. and J.H.P.; software, J.H.P. and C.P.; validation, J.H.P., C.P. and J.G.; formal analysis, J.H.P. and J.G.; investigation, J.H.P., C.P. and J.G.; resources, J.H.P., C.P. and J.G.; data curation, J.H.P. and J.G.; writing—original draft preparation, C.P.; writing—review and editing, J.G. and C.P.; visualization, J.H.P.; supervision, J.G.; project administration, J.G.; funding acquisition, J.H.P., C.P. and J.G. All authors have read and agreed to the published version of the manuscript.

Funding

This work of J.P. and C.P. was supported by the Korea Environment Industry & Technology Institute (KEITI) through its Urban Ecological Health Promotion Technology Development Project and the Korea Ministry of Environment (MOE) (2019002760001). The work of J.G. was supported in part by the McIntire-Stennis Program of the U.S. Department of Agriculture.

Data Availability Statement

The monthly average NPPs in 2015 were downloaded directly from the NASA Earth Observations website [37]. Data on forest-related factors were drawn from the FRA report [24], and data on ecoregion type were downloaded from the World Wildlife Fund (WWF) [41]. The monthly LAI, NDVI, and LST data and the daily average net radiation data were made available by NASA [42]. The v5.01 data of annual precipitation and monthly temperatures were downloaded from the webpage supported by the Department of Geography at the University of Delaware and NASA [43]. Data on the available water storage capacity were obtained from the Regridded Harmonized World Soil Database v1.2 [44]. And we used the Google Public Data Explorer to obtain the latitude data.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

References

  1. Scurlock, J.M.O.; Cramer, W.; Olson, R.J.; Parton, W.J.; Prince, S.D. Terrestrial NPP: Toward a Consistent Data Set for Global Model Evaluation. Ecol. Appl. 1999, 9, 913–919. [Google Scholar] [CrossRef]
  2. Park, J.; Lee, D.; Gan, J.; Park, C.; Kim, S.; Sung, S.; Jung, T.; Hong, S. Effects of Climate Change and Ozone Concentration on the Net Primary Productivity of Forests in South Korea. Forests 2018, 9, 112. [Google Scholar] [CrossRef] [Green Version]
  3. Hoover, K.; Riddle, A.A. Forest Carbon Primer; Congressional Research Service: Washington, DC, USA, 2020. [Google Scholar]
  4. Dixon, R.K.; Brown, S.; Houghton, R.A.; Solomon, A.M.; Trexier, M.C.; Wisniewski, J. Carbon Pools and Flux of Global Forest Ecosystems. Science 1994, 263, 185–190. [Google Scholar] [CrossRef] [PubMed]
  5. De Groot, R.; Wilson, M.A.; Boumans, R.M.J. A typology for the classification, description and valuation of ecosystem functions, goods and services. Ecol. Econ. 2002, 41, 393–408. [Google Scholar] [CrossRef] [Green Version]
  6. Guo, L.B.; Gifford, R.M. Soil carbon stocks and land use change: A meta analysis. Glob. Chang. Biol. 2002, 8, 345–360. [Google Scholar] [CrossRef]
  7. Liski, J.; Westman, C.J. Carbon storage in forest soil of Finland. Biogeochemistry 1997, 36, 239–260. [Google Scholar] [CrossRef]
  8. Keeling, H.C.; Phillips, O.L. The global relationship between forest productivity and biomass. Glob. Ecol. Biogeogr. 2007, 16, 618–631. [Google Scholar] [CrossRef]
  9. Clark, D.A.; Brown, S.; Kicklighter, D.W.; Chambers, J.Q.; Thomlinson, J.R.; Ni, J. Measuring net primary production in forests: Concepts and field methods. Ecol. Appl. 2001, 11, 356–370. [Google Scholar] [CrossRef]
  10. Jenkins, J.C.; Birdsey, R.A.; Pan, Y. Biomass and NPP estimation for the mid-Atlantic region (USA) using plot-level forest inventory data. Ecol. Appl. 2001, 11, 1174–1193. [Google Scholar] [CrossRef]
  11. Hong, J.; Shim, C.; Lee, M.; Back, G.; Song, W.; Jeon, S.; Park, Y. Net Primary Production Changes over Korea and Climate Factors. Korean J. Remote Sens. 2011, 27, 467–480. [Google Scholar] [CrossRef] [Green Version]
  12. Cramer, W.; Kicklighter, D.W.; Bondeau, A.; Iii, B.M.; Churkina, G.; Nemry, B.; Ruimy, A.; Schloss, A.L. Comparing global models of terrestrial net primary productivity (NPP): Overview and key results. Glob. Chang. Biol. 1999, 5, 1–15. [Google Scholar] [CrossRef]
  13. Field, C.B.; Randerson, J.T.; Malmström, C.M. Global net primary production: Combining ecology and remote sensing. Remote Sens. Environ. 1995, 51, 74–88. [Google Scholar] [CrossRef] [Green Version]
  14. Ruimy, A.; Kergoat, L.; Bondeau, A. Comparing global models of terrestrial net primary productivity (NPP): Analysis of differences in light absorption and light-use efficiency. Glob. Chang. Biol. 1999, 5, 56–64. [Google Scholar] [CrossRef] [Green Version]
  15. Adams, B.; White, A.; Lenton, T.M. An analysis of some diverse approaches to modelling terrestrial net primary productivity. Ecol. Model. 2004, 177, 353–391. [Google Scholar] [CrossRef]
  16. Jiang, H.; Apps, M.J.; Zhang, Y.; Peng, C.; Woodard, P.M. Modelling the spatial pattern of net primary productivity in Chinese forests. Ecol. Model. 1999, 122, 275–288. [Google Scholar] [CrossRef]
  17. Goulden, M.L.; Mcmillan, A.M.S.; Winston, G.C.; Rocha, A.V.; Manies, K.L.; Harden, J.W.; Bond-Lamberty, B.P. Patterns of NPP, GPP, respiration, and NEP during boreal forest succession. Glob. Chang. Biol. 2011, 17, 855–871. [Google Scholar] [CrossRef] [Green Version]
  18. Turner, D.P.; Ritts, W.D.; Cohen, W.B.; Gower, S.T.; Running, S.W.; Zhao, M.; Costa, M.H.; Kirschbaum, A.A.; Ham, J.M.; Saleska, S.R.; et al. Evaluation of MODIS NPP and GPP products across multiple biomes. Remote Sens. Environ. 2006, 102, 282–292. [Google Scholar] [CrossRef]
  19. Zhang, Y.; Xu, M.; Chen, H.; Adams, J. Global pattern of NPP to GPP ratio derived from MODIS data: Effects of ecosystem type, geographical location and climate. Glob. Ecol. Biogeogr. 2009, 18, 280–290. [Google Scholar] [CrossRef]
  20. Matsushita, B.; Tamura, M. Integrating remotely sensed data with an ecosystem model to estimate net primary productivity in East Asia. Remote Sens. Environ. 2002, 81, 58–66. [Google Scholar] [CrossRef]
  21. Ito, A.; Inatomi, M. Use of a process-based model for assessing the methane budgets of global terrestrial ecosystems and evaluation of uncertainty. Biogeosciences 2012, 9, 759–773. [Google Scholar] [CrossRef] [Green Version]
  22. Oswalt, S.N.; Smith, W.B.; Miles, P.D.; Pugh, S.A. Forest Resources of the United States, 2012: A Technical Document Supporting the Forest Service Update of the 2010 RPA Assessment; USDA Forest Service: Washington, DC, USA, 2014. [Google Scholar]
  23. Korea Forest Service. 2015 Forest Basic Statistics; Korea Forest Service: Seoul, Korea, 2016.
  24. FAO. Global Forest Resources Assessment 2015; FAO: Rome, Italy, 2015. [Google Scholar]
  25. FAO. State of the World’s Forests 2016; FAO: Rome, Italy, 2016. [Google Scholar]
  26. Kindermann, G.E.; McCallum, I.; Fritz, S.; Obersteiner, M. A global forest growing stock, biomass and carbon map based on FAO statistics. Silva Fenn. 2008, 42, 387–396. [Google Scholar] [CrossRef] [Green Version]
  27. Grier, C.C.; Lee, K.M.; Nadkarni, N.M.; Klock, G.O.; Edgerton, P.J. Productivity of forests of the United States and its relation to soil and site factors and management practices: A review. Gen. Tech. Rep. 1989, 51. [Google Scholar] [CrossRef] [Green Version]
  28. Yan, H.; Zhan, J.; Jiang, Q.; Yuan, Y.; Li, Z. Multilevel modeling of NPP change and impacts of water resources in the Lower Heihe River Basin. Phys. Chem. Earth 2015, 79–82, 29–39. [Google Scholar] [CrossRef]
  29. Liu, L.B.; Yang, H.M.; Xu, Y.; Guo, Y.M.; Ni, J. Forest biomass and net primary productivity in Southwestern China: A meta-analysis focusing on environmental driving factors. Forests 2016, 7, 173. [Google Scholar] [CrossRef] [Green Version]
  30. Lu, X.; Kicklighter, D.W.; Melillo, J.M.; Reilly, J.M.; Xu, L. Land carbon sequestration within the conterminous United States: Regional-and state-level analyses. J. Geophys. Res. Biogeosciences 2015, 120, 379–398. [Google Scholar] [CrossRef]
  31. Peng, C.; Apps, M.J. Modelling the response of net primary productivity (NPP) of boreal forest ecosystems to changes in climate and fire disturbance regimes. Ecol. Model. 1999, 122, 175–193. [Google Scholar] [CrossRef]
  32. Ito, A. Evaluation of the impacts of defoliation by tropical cyclones on a Japanese forest’s carbon budget using flux data and a process-based model. J. Geophys. Res. Biogeosci. 2010, 115. [Google Scholar] [CrossRef] [Green Version]
  33. Kyriakidis, P.C.; Dungan, J.L. A geostatistical approach for mapping thematic classification accuracy and evaluating the impact of inaccurate spatial data on ecological model predictions. Environ. Ecol. Stat. 2001, 8, 311–330. [Google Scholar] [CrossRef]
  34. United Nations Statistical Commission. Fundamental Principles of Official Statistics; United Nations Statistics Division: New York, NY, USA, 2014. [Google Scholar]
  35. Running, S.W.; Zhao, M. User’s Guide Daily GPP and Annual NPP (MOD17A2/A3) Products NASA Earth Observing System MODIS Land Algorithm; NASA Press: Washington, DC, USA, 2015. [Google Scholar]
  36. Neumann, M.; Moreno, A.; Thurnher, C.; Mues, V.; Härkönen, S.; Mura, M.; Bouriaud, O.; Lang, M.; Cardellini, G.; Thivolle-Cazat, A.; et al. Creating a regional MODIS satellite-driven net primary production dataset for european forests. Remote Sens. 2016, 8, 554. [Google Scholar] [CrossRef] [Green Version]
  37. NASA Earth Observations. Net Primary Productivity. Available online: https://neo.sci.gsfc.nasa.gov/view.php?datasetId=MOD17A2_M_PSN&year=2015 (accessed on 16 November 2019).
  38. FAO. Forestry Production and Data. Available online: http://www.fao.org/faostat/en/#data/FO (accessed on 26 September 2019).
  39. Clark, D.A.; Brown, S.; Kicklighter, D.W.; Chambers, J.Q.; Thomlinson, J.R.; Ni, J.; Holland, E.A. Net primary production in tropical forests: An evaluation and synthesis of existing field data. Ecol. Appl. 2001, 11, 371–384. [Google Scholar] [CrossRef]
  40. Schowalter, T.D. Insect Ecology: An Ecosystem Approach, 3rd ed.; Elsevier/Academic: San Diego, CA, USA, 2011. [Google Scholar]
  41. Olson, D.M.; Dinerstein, E.; Wikramanayake, E.D.; Burgess, N.D.; Powell, G.V.N.; Underwood, E.C.; D’amico, J.A.; Itoua, I.; Strand, H.E.; Morrison, J.C.; et al. Terrestrial Ecoregions of the World: A New Map of Life on Earth. Bioscience 2006, 51, 933. [Google Scholar] [CrossRef]
  42. NASA. Earth Observation Data. Available online: https://earthdata.nasa.gov/earth-observation-data (accessed on 16 November 2019).
  43. Willmott, C.J.; Matsuura, K. Terrestrial Air Temperature and Precipitation: Monthly and Annual Time Series (1950–1999). Available online: http://climate.geog.udel.edu/~climate/html_pages/README.ghcn_ts2.html (accessed on 29 December 2019).
  44. Wieder, W.R.; Boehnert, J.; Bonan, G.B.; Langseth, M. Regridded Harmonized World Soil Database v1.2. Available online: https://daac.ornl.gov/SOILS/guides/HWSD.html (accessed on 3 February 2020).
  45. World Bank. World Bank Open Data. Available online: https://data.worldbank.org/ (accessed on 12 December 2019).
  46. Attard, J.; Orlandi, F.; Scerri, S.; Auer, S. A systematic review of open government data initiatives. Gov. Inf. Q. 2015, 32, 399–418. [Google Scholar] [CrossRef]
  47. Liu, C.; Westman, C.J.; Berg, B.; Kutsch, W.; Wang, G.Z.; Man, R.; Ilvesniemi, H. Variation in litterfall-climate relationships between coniferous and broadleaf forests in Eurasia. Glob. Ecol. Biogeogr. 2004, 13, 105–114. [Google Scholar] [CrossRef]
  48. Cano, E.; Denux, J.-P.; Bisquert, M.; Hubert-Moy, L.; Chéret, V. Improved forest-cover mapping based on MODIS time series and landscape stratification. Int. J. Remote Sens. 2017, 38, 1865–1888. [Google Scholar] [CrossRef] [Green Version]
  49. Krishna, M.P.; Mohan, M. Litter decomposition in forest ecosystems: A review. Energ. Ecol. Environ. 2017, 2, 236–249. [Google Scholar] [CrossRef]
  50. Tank, S.E.; Fellman, J.B.; Hood, E.; Kritzberg, E.S. Beyond respiration: Controls on lateral carbon fluxes across the terrestrial-aquatic interface. Limnol. Oceanogr. 2018, 3, 76–88. [Google Scholar] [CrossRef]
  51. Waring, R.H.; Running, S.W. Chapter 3—Carbon Cycle. In Forest Ecosystems, 3rd ed.; Waring, R.H., Running, S.W., Eds.; Academic Press: San Diego, CA, USA, 2007; pp. 59–98. [Google Scholar]
  52. Kirschbaum, M.U.F.; Eamus, D.; Gifford, R.M.; Roxburgh, S.H.; Sands, P.J. Definitions of some ecological terms commonly used in carbon accounting. In Proceedings of the Net Ecosystem Exchange CRC Workshop, Canberra, Australia, 18–20 April 2001; pp. 2–5. [Google Scholar]
  53. IPCC. The carbon budget of terrestrial ecosystems. In Land Use Land Use Change and Forestry; Watson, R.T., Noble, I.R., Bolin, B., Ravindranath, N.H., Verardo, D.J., Dokken, D.J., Eds.; Cambridge University Press: Cambridge, UK, 2000; Available online: https://archive.ipcc.ch/ipccreports/sres/land_use/index.php?idp=24 (accessed on 5 March 2021).
Remotesensing 13 01441 g001 550
Figure 1. Flowchart of the research process.
Figure 1. Flowchart of the research process.
Remotesensing 13 01441 g001
Remotesensing 13 01441 g002a 550Remotesensing 13 01441 g002b 550
Figure 2. Estimated annual forest net primary productivity (NPP) by country in 2015. (a) FRA NPP* (NPP estimated from the FRA data). (b) MOD17 NPP (NPP derived from the MOD17A2 satellite data). The legend is the same for both (a) and (b).
Figure 2. Estimated annual forest net primary productivity (NPP) by country in 2015. (a) FRA NPP* (NPP estimated from the FRA data). (b) MOD17 NPP (NPP derived from the MOD17A2 satellite data). The legend is the same for both (a) and (b).
Remotesensing 13 01441 g002aRemotesensing 13 01441 g002b
Remotesensing 13 01441 g003 550
Figure 3. Differences between the FRA NPP* and the MOD17 NPP in 2015. Difference = FRA NPP* − MOD17 NPP.
Figure 3. Differences between the FRA NPP* and the MOD17 NPP in 2015. Difference = FRA NPP* − MOD17 NPP.
Remotesensing 13 01441 g003
Remotesensing 13 01441 g004 550
Figure 4. The FRA NPP* versus the MOD17 NPP in 2015. Of the 151 countries included for NPP comparison, 11 countries were excluded from this scatterplot because their NPPs were far beyond the axis range. Their exclusion did not affect the pattern of this scatterplot.
Figure 4. The FRA NPP* versus the MOD17 NPP in 2015. Of the 151 countries included for NPP comparison, 11 countries were excluded from this scatterplot because their NPPs were far beyond the axis range. Their exclusion did not affect the pattern of this scatterplot.
Remotesensing 13 01441 g004
Remotesensing 13 01441 g005a 550Remotesensing 13 01441 g005b 550
Figure 5. Discrepancies between the FRA NPP* and the MOD17 NPP versus biophysical factors in 2015. Difference = FRA NPP* − MOD17 NPP. (a) Latitude; (b) net radiation; (c) annual precipitation; (d) forest cover (ratio of forest area to total land area); (e) mean of normalized difference vegetation index (NDVI); (f) mean of leaf area index (LAI).
Figure 5. Discrepancies between the FRA NPP* and the MOD17 NPP versus biophysical factors in 2015. Difference = FRA NPP* − MOD17 NPP. (a) Latitude; (b) net radiation; (c) annual precipitation; (d) forest cover (ratio of forest area to total land area); (e) mean of normalized difference vegetation index (NDVI); (f) mean of leaf area index (LAI).
Remotesensing 13 01441 g005aRemotesensing 13 01441 g005b
Table
Table 1. Comparison of annual global forest NPP estimates derived from the MOD17 and FRA data in 2015.
Table 1. Comparison of annual global forest NPP estimates derived from the MOD17 and FRA data in 2015.
VariableMeanStd. Dev.t-Statisticp-Value
MOD17 NPP739.745384.752
FRA NPP*522.243789.662
Difference between the two NPPs 1−217.502942.419−2.8360.005
1 Difference = FRA NPP* − MOD17 NPP. The unit of NPP is tC/km2/year, and n = 151.
Table
Table 2. Results of multiple regressions of NPP discrepancy on biophysical and socioeconomic factors.
Table 2. Results of multiple regressions of NPP discrepancy on biophysical and socioeconomic factors.
Independent Variable 1Coefficientt-Statisticp-Value
Ratio of forest cover to total land area−1.262−4.5400.001
NDVI0.7572.8610.014
Open data index (ODI)0.3622.6960.019
Ln (GDP per capita)−0.356−2.2520.044
1 Only the independent variables that are significant at the 5% level are presented here. Adjusted R2 = 0.74, and n = 151. GDP is originally measured in USD, and all other independent variables are either an index or a ratio. However, all independent variables used in this regression analysis were normalized to Z-scores in order to better compare their effect size.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Park, J.H.; Gan, J.; Park, C. Discrepancies between Global Forest Net Primary Productivity Estimates Derived from MODIS and Forest Inventory Data and Underlying Factors. Remote Sens. 2021, 13, 1441. https://doi.org/10.3390/rs13081441

AMA Style

Park JH, Gan J, Park C. Discrepancies between Global Forest Net Primary Productivity Estimates Derived from MODIS and Forest Inventory Data and Underlying Factors. Remote Sensing. 2021; 13(8):1441. https://doi.org/10.3390/rs13081441

Chicago/Turabian Style

Park, Jin Han, Jianbang Gan, and Chan Park. 2021. "Discrepancies between Global Forest Net Primary Productivity Estimates Derived from MODIS and Forest Inventory Data and Underlying Factors" Remote Sensing 13, no. 8: 1441. https://doi.org/10.3390/rs13081441

APA Style

Park, J. H., Gan, J., & Park, C. (2021). Discrepancies between Global Forest Net Primary Productivity Estimates Derived from MODIS and Forest Inventory Data and Underlying Factors. Remote Sensing, 13(8), 1441. https://doi.org/10.3390/rs13081441

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop