Detection of the Minute Variations of Total Suspended Matter in Strong Tidal Waters Based on GaoFen-4 Satellite Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Sources
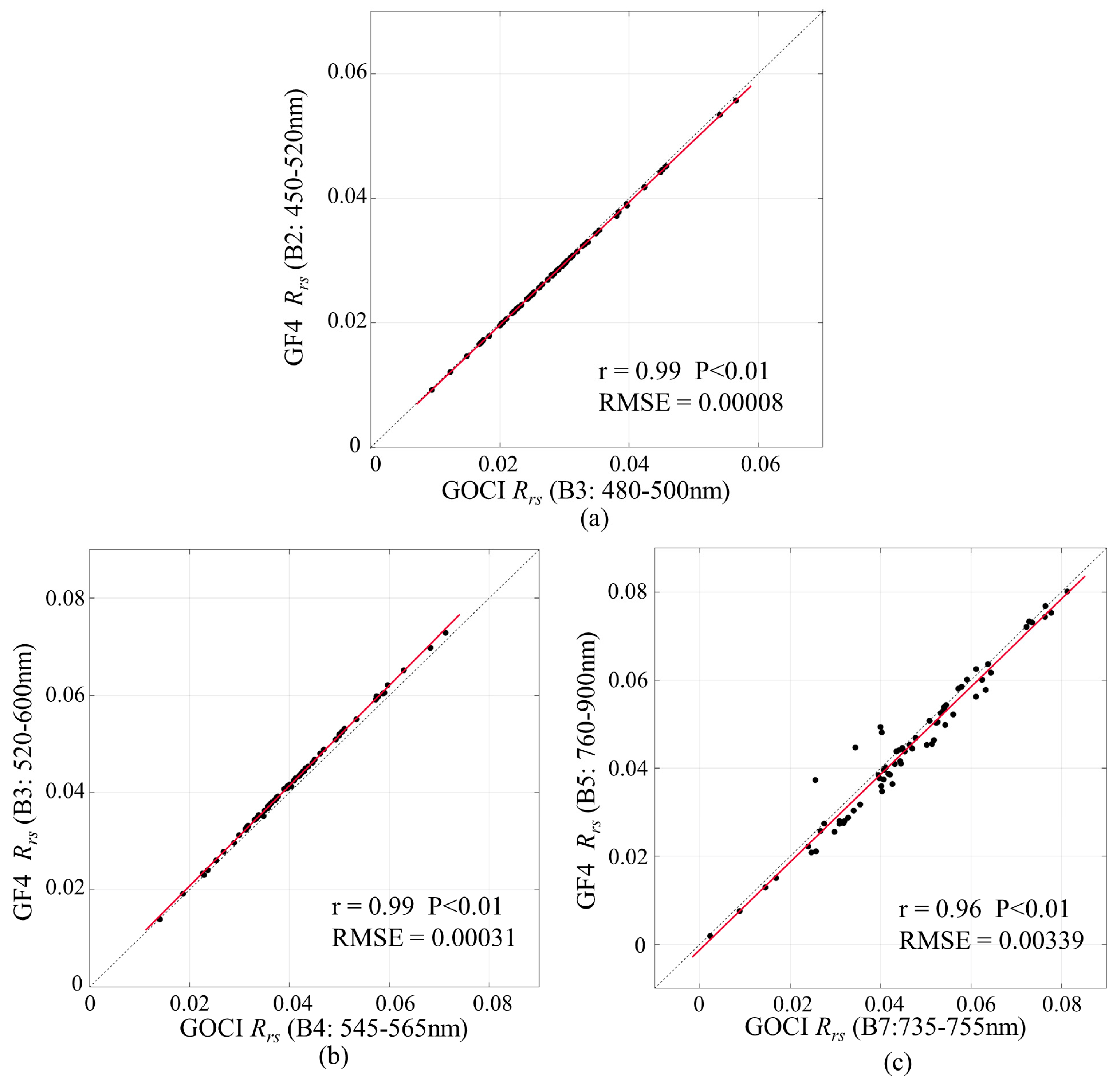
2.3. GF-4 Remote Sensing Data Processing
2.4. Remote Sensing Estimation of TSM Concentration and Current Velocity
2.4.1. The Correction of TSM Algorithm
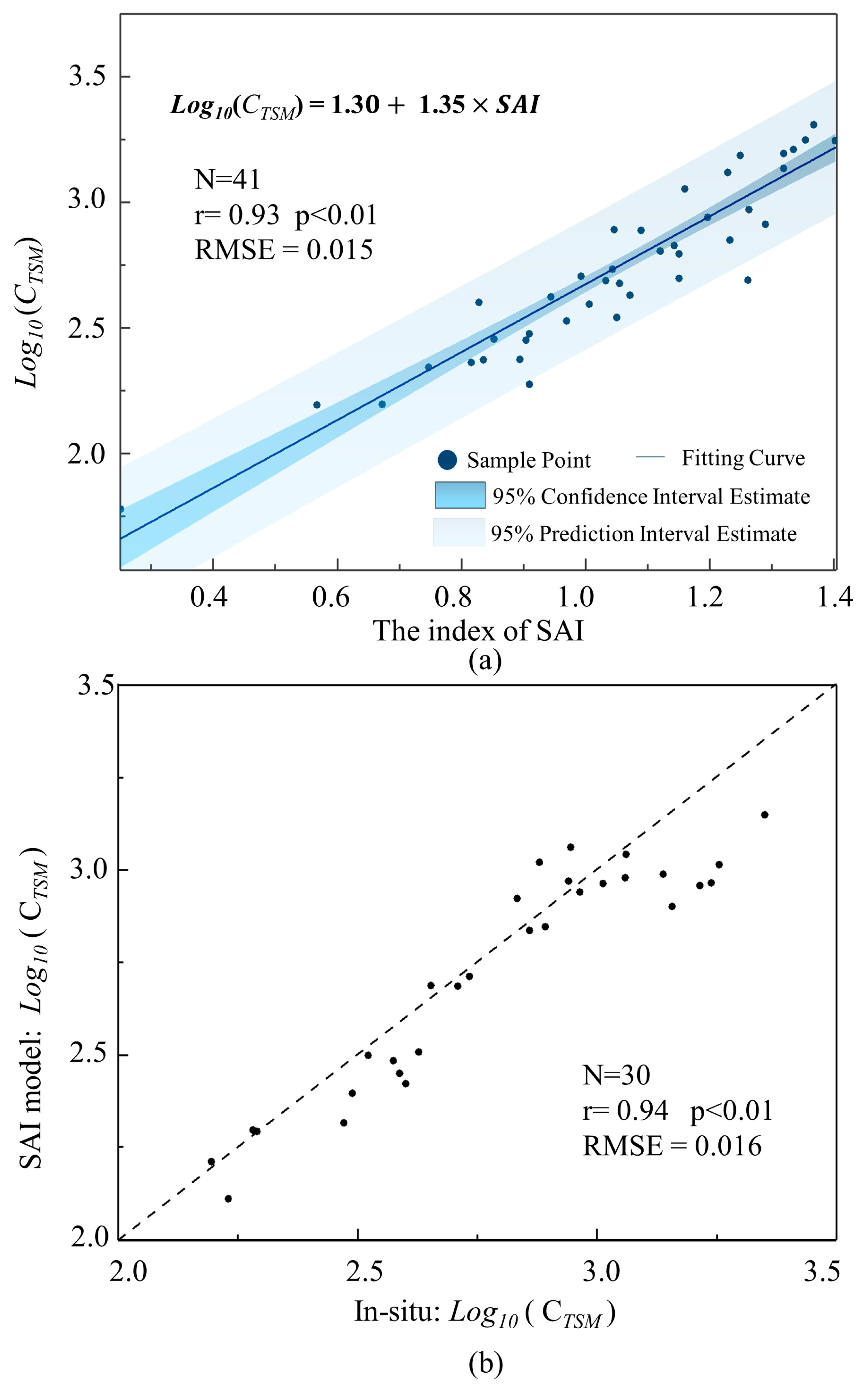
2.4.2. The Calculation of Average TSM Concentration and Current Velocity
3. Results
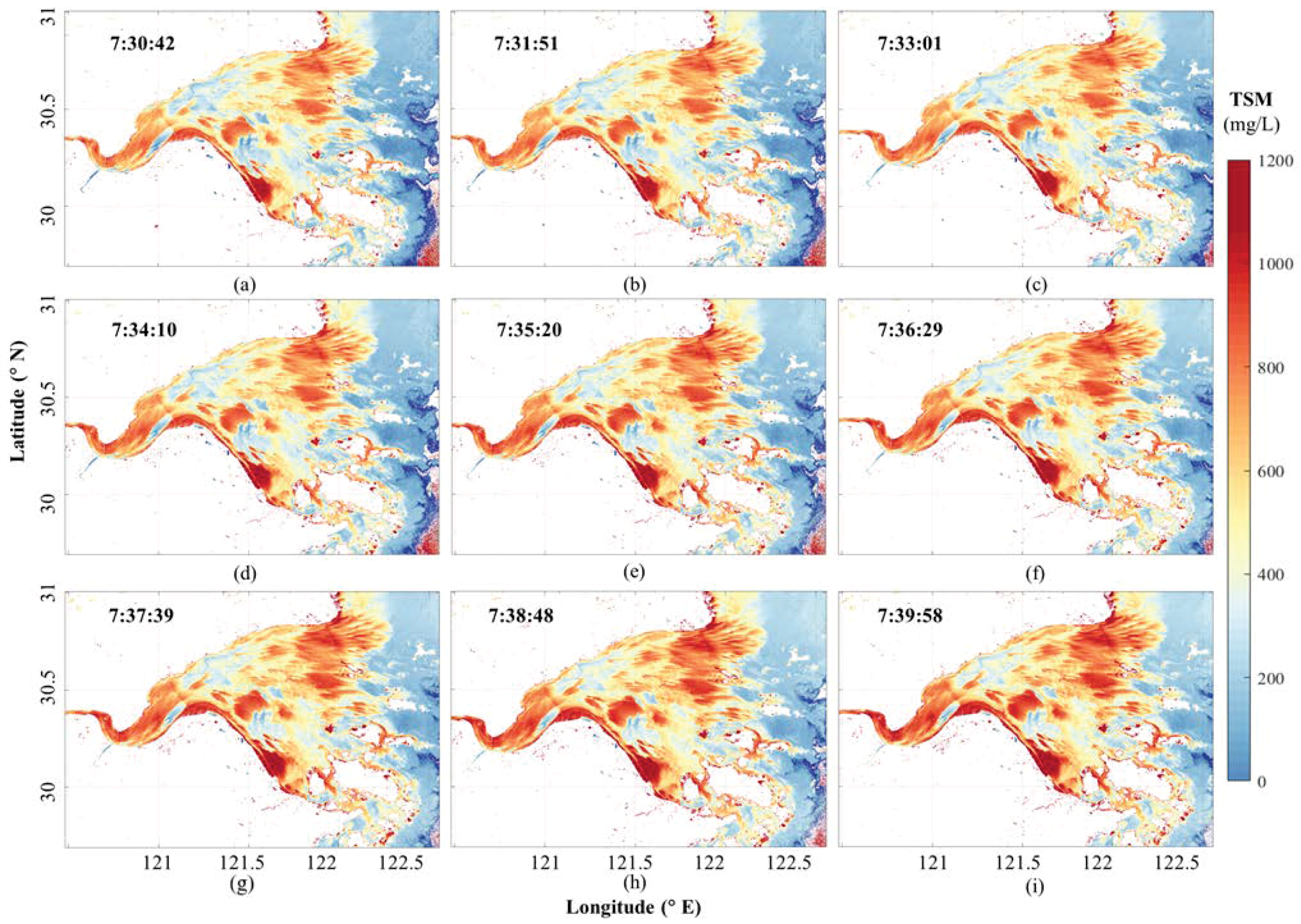
3.1. The Spatial Distribution Characteristics of TSM in HZB
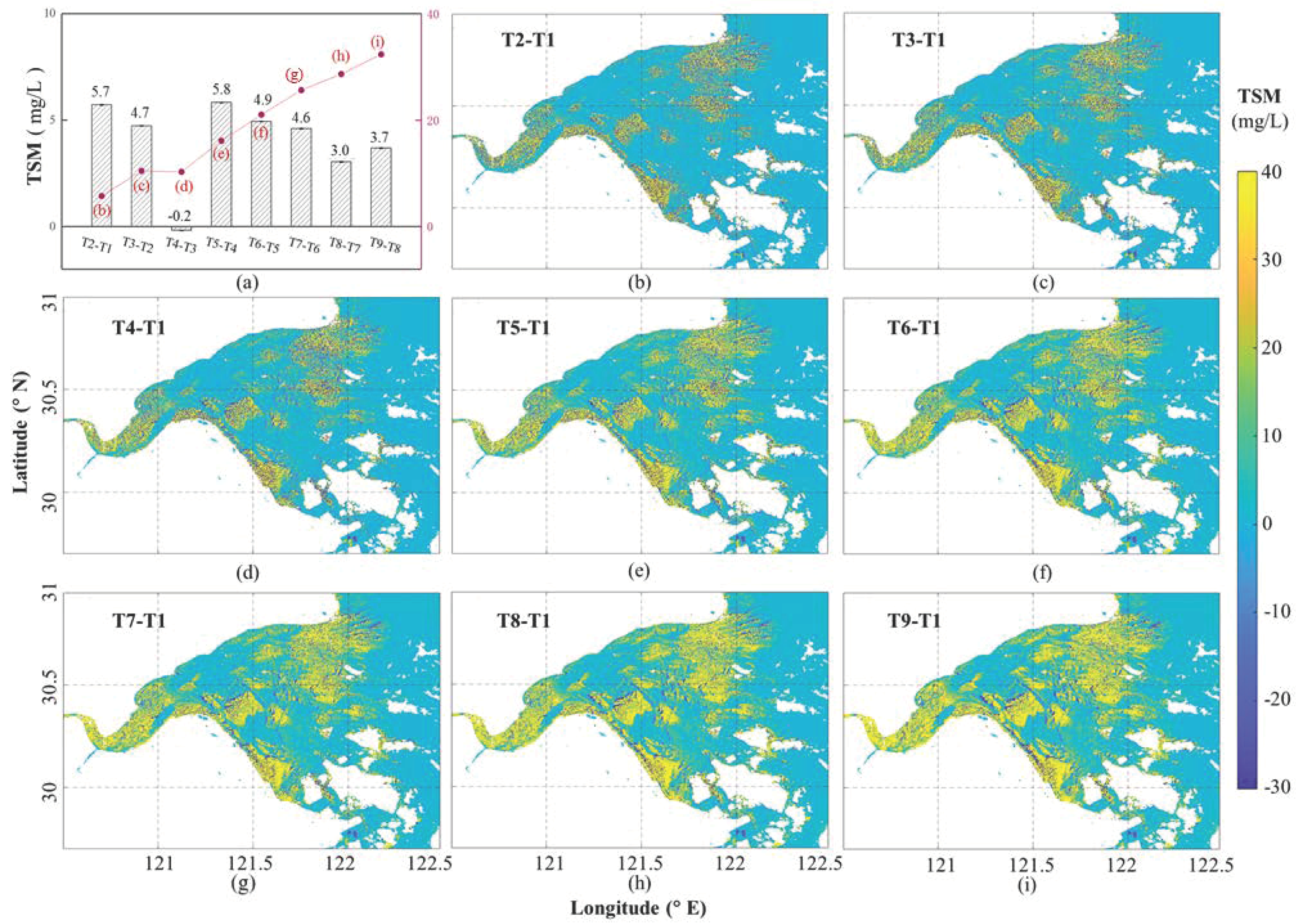
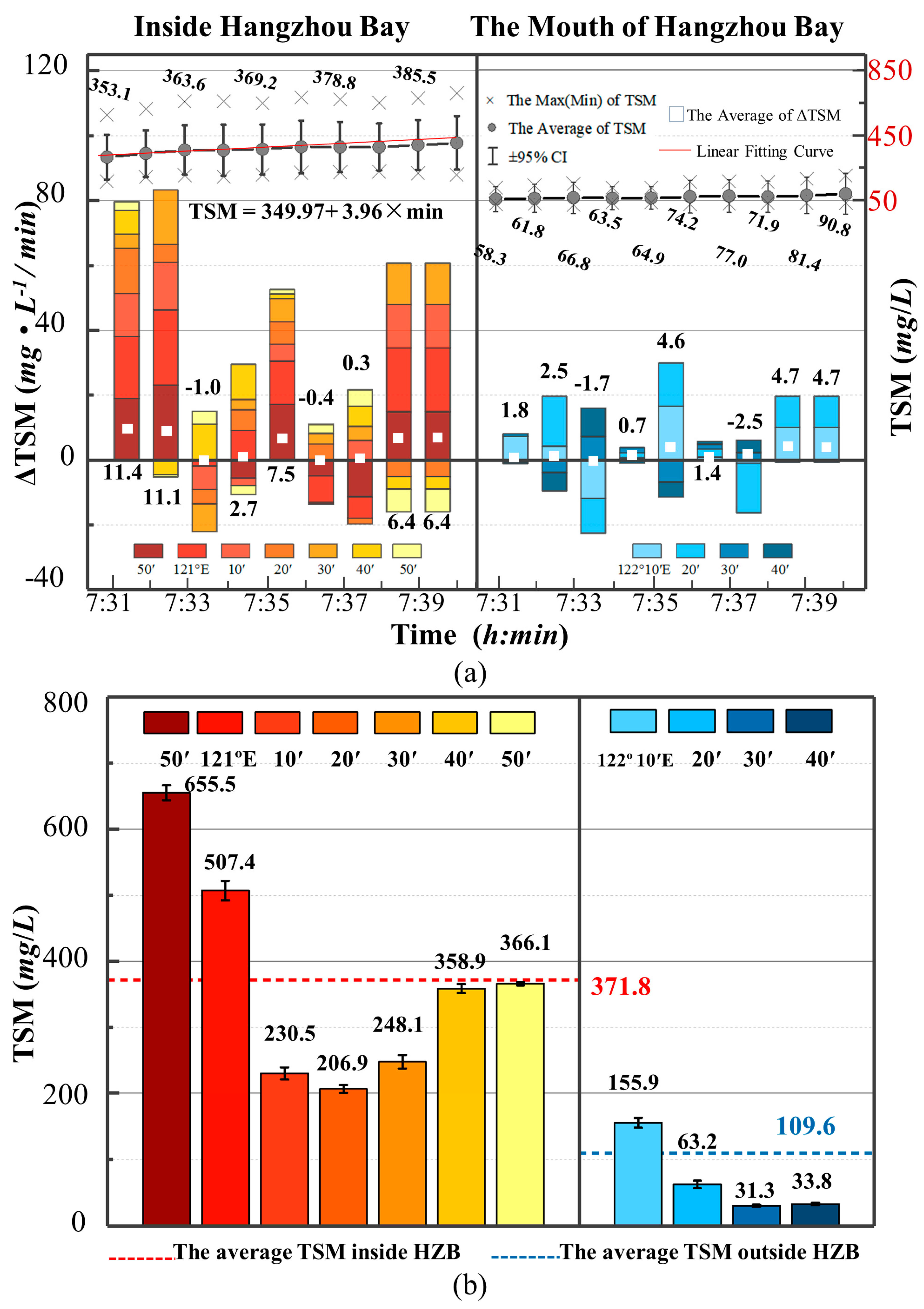
3.2. Minute Scale Dynamic Change Characteristics of TSM at Ebb Tide in HZB
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zeng, X.; He, R.; Xue, Z.; Wang, H.; Wang, Y.; Yao, Z.; Guan, W.; Warrillow, J. River-derived sediment suspension and transport in the Bohai, Yellow, and East China Seas: A preliminary modeling study. Cont. Shelf Res. 2015, 111, 112–125. [Google Scholar] [CrossRef]
- Ziegler, C.K.; Lick, W. The transport of fine-grained sediments in shallow waters. Environ. Geol. Water Sci. 1988, 11, 123–132. [Google Scholar] [CrossRef]
- Yu, Q.; Wang, Y.P.; Flemming, B.; Gao, S. Tide-induced suspended sediment transport: Depth-averaged concentrations and horizontal residual fluxes. Cont. Shelf Res. 2012, 34, 53–63. [Google Scholar] [CrossRef]
- Xiong, J.; Wang, X.H.; Wang, Y.P.; Chen, J.; Shi, B.; Gao, J.; Yang, Y.; Yu, Q.; Li, M.; Yang, L.; et al. Mechanisms of maintaining high suspended sediment concentration over tide-dominated offshore shoals in the southern Yellow Sea. Estuar. Coast Shelf Sci. 2017, 191, 221–233. [Google Scholar] [CrossRef]
- Li, J.; Gao, S.; Wang, Y. Delineating suspended sediment concentration patterns in surface waters of the Changjiang Estuary by remote sensing analysis. Acta Oceanol. Sin. 2010, 29, 38–47. [Google Scholar] [CrossRef]
- Abascal-Zorrilla, N.; Vantrepotte, V.; Huybrechts, N.; Ngoc, D.D.; Anthony, E.J.; Gardel, A. Dynamics of the Estuarine Turbidity Maximum Zone from Landsat-8 Data: The Case of the Maroni River Estuary, French Guiana. Remote Sens. 2020, 12, 2173. [Google Scholar] [CrossRef]
- Xu, X.; Chen, J.; Ye, X. Study on the seasonal migration of surface suspended sediment in the Taiwan Strait based on remote sensing. In Remote Sensing of the Ocean, Sea Ice, Coastal Waters, and Large Water Regions 2015; Bostater, C.R., Mertikas, S.P., Neyt, X., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2015; Volume 9638. [Google Scholar]
- Burenkov, V.I.; Vazyulya, S.V.; Kopelevich, O.V.; Sheberstov, S.V. Spatiotemporal variability of the suspended matter distribution in the surface layer of the white sea from the data of the SeaWiFS satellite color scanner. Oceanology 2004, 44, 472–480. [Google Scholar]
- Bai, Y.; He, X.; Pan, D.; Zhu, Q.; Lei, H.; Tao, B.; Hao, Z. The extremely high concentration of suspended particulate matter in Changjiang Estuary detected by MERIS data. In Remote Sensing of the Coastal Ocean, Land, and Atmosphere Environment; Frouin, R.J., Yoo, H.R., Won, J.S., Feng, A., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2010; Volume 7858. [Google Scholar]
- Shen, F.; Verhoef, W.; Zhou, Y.; Salama, M.S.; Liu, X. Satellite Estimates of Wide-Range Suspended Sediment Concentrations in Changjiang (Yangtze) Estuary Using MERIS Data. Estuaries Coasts 2010, 33, 1420–1429. [Google Scholar] [CrossRef]
- Li, P.; Ke, Y.; Bai, J.; Zhang, S.; Chen, M.; Zhou, D. Spatiotemporal dynamics of suspended particulate matter in the Yellow River Estuary, China during the past two decades based on time-series Landsat and Sentinel-2 data. Mar. Pollut. Bull. 2019, 149. [Google Scholar] [CrossRef]
- Scanes, P.; Coade, G.; Doherty, M.; Hill, R. Evaluation of the utility of water quality based indicators of estuarine lagoon condition in NSW, Australia. Estuar. Coast. Shelf Sci. 2007, 74, 306–319. [Google Scholar] [CrossRef]
- Wang, F.; Zhou, B.; Liu, X.; Zhou, G.; Zhao, K. Remote-sensing inversion model of surface water suspended sediment concentration based on in situ measured spectrum in Hangzhou Bay, China. Environ. Earth Sci. 2012, 67, 1669–1677. [Google Scholar] [CrossRef]
- Gordon, H.R.; Wang, M. Retrieval of water-leaving radiance and aerosol optical thickness over the oceans with SeaWiFS: A preliminary algorithm. Appl Opt. 1994, 33, 443–452. [Google Scholar] [CrossRef] [PubMed]
- Gao, F.; Wang, Y.P.; Zhang, Y.Z. Evaluation of the Crosta method for the retrieval of water quality parameters from remote sensing data in the Pearl River estuary. Water Qual. Res. J. Can. 2020, 5, 209–220. [Google Scholar] [CrossRef]
- Mayo, M.; Karnieli, A.; Gitelson, A.; Benavraham, Z. Determination of suspended sediment concentrations from CZCS data. Photogramm. Eng. Remote Sens. 1993, 59, 1265–1269. [Google Scholar]
- Burenkov, V.I.; Ershova, S.V.; Kopelevich, O.V.; Sheberstov, S.V.; Shevchenko, V.P. An estimate of the distribution of suspended matter in the Barents Sea waters on the basis of the SeaWiFS satellite ocean color scanner. Oceanology 2001, 41, 622–628. [Google Scholar]
- Tian, L.; Wai, O.W.H.; Chen, X.; Li, W.; Li, J.; Li, W.; Zhang, H. Retrieval of total suspended matter concentration from Gaofen-1 Wide Field Imager (WFI) multispectral imagery with the assistance of Terra MODIS in turbid water-case in Deep Bay. Int. J. Remote Sens. 2016, 37, 3400–3413. [Google Scholar] [CrossRef]
- Wang, F.; Zhou, B.; Xu, J.; Song, L.; Wang, X. Application of neural network and MODIS 250 m imagery for estimating suspended sediments concentration in Hangzhou Bay, China. Environ. Geol. 2009, 56, 1093–1101. [Google Scholar] [CrossRef]
- Tang, S.L.; Larouche, P.; Niemi, A.; Michel, C. Regional algorithms for remote-sensing estimates of total suspended matter in the Beaufort Sea. Int. J. Remote Sens. 2013, 34, 6562–6576. [Google Scholar] [CrossRef]
- Toming, K.; Kutser, T.; Uiboupin, R.; Arikas, A.; Vahter, K.; Paavel, B. Mapping Water Quality Parameters with Sentinel-3 Ocean and Land Colour Instrument Imagery in the Baltic Sea. Remote Sens. 2017, 9, 1070. [Google Scholar] [CrossRef]
- Chami, M.; Larnicol, M.; Migeon, S.; Minghelli, A.; Mathieu, S. Potential for nocturnal satellite detection of suspended matter concentrations in coastal waters using a panchromatic band: A feasibility study based on VIIRS (NASA/NOAA) spectral and radiometric specifications. Opt. Express 2020, 28, 15314–15330. [Google Scholar] [CrossRef]
- He, X.; Bai, Y.; Pan, D.; Huang, N.; Dong, X.; Chen, J.; Chen, C.-T.A.; Cui, Q. Using geostationary satellite ocean color data to map the diurnal dynamics of suspended particulate matter in coastal waters. Remote Sens. Environ. 2013, 133, 225–239. [Google Scholar] [CrossRef]
- Hu, Y.; Yu, Z.; Zhou, B.; Li, Y.; Yin, S.; He, X.; Peng, X.; Shum, C.K. Tidal-driven variation of suspended sediment in Hangzhou Bay based on GOCI data. Int. J. Appl. Earth Obs. Geoinf. 2019, 82. [Google Scholar] [CrossRef]
- Liu, J.; Liu, J.; He, X.; Pan, D.; Bai, Y.; Zhu, F.; Chen, T.; Wang, Y. Diurnal Dynamics and Seasonal Variations of Total Suspended Particulate Matter in Highly Turbid Hangzhou Bay Waters Based on the Geostationary Ocean Color Imager. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2170–2180. [Google Scholar] [CrossRef]
- Cheng, Z.; Wang, X.H.; Paull, D.; Gao, J. Application of the Geostationary Ocean Color Imager to Mapping the Diurnal and Seasonal Variability of Surface Suspended Matter in a Macro-Tidal Estuary. Remote Sens. 2016, 8, 244. [Google Scholar] [CrossRef]
- Pan, Y.; Shen, F.; Wei, X. Fusion of Landsat-8/OLI and GOCI Data for Hourly Mapping of Suspended Particulate Matter at High Spatial Resolution: A Case Study in the Yangtze (Changjiang) Estuary. Remote Sens. 2018, 10, 158. [Google Scholar] [CrossRef]
- Li, F.; Fu, J.; Xin, L.; Liu, Y.; Liu, Z. New developments in super-resolution for GaoFen-4. In Image and Signal Processing for Remote Sensing XXIII; Bruzzone, L., Bovolo, F., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 10427. [Google Scholar]
- Wang, D.; He, H. Observation Capability and Application Prospect of GF-4 Satellite. In 3rd International Symposium of Space Optical Instruments and Applications; Urbach, H.P., Zhang, G., Eds.; Springer Nature: Berlin, Germany, 2017; Volume 192, pp. 393–401. [Google Scholar]
- Li, F.; Xin, L.; Guo, Y.; Gao, D.; Kong, X.; Jia, X. Super-Resolution for GaoFen-4 Remote Sensing Images. IEEE Geosci. Remote Sens. Lett. 2018, 15, 28–32. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, J.; Zhang, L.; Shen, Y. Computational investigation of typhoon-induced storm surge in Hangzhou Bay, China. Estuar. Coast. Shelf Sci. 2009, 85, 530–536. [Google Scholar] [CrossRef]
- Xie, D.; Wang, Z.; Gao, S.; De Vriend, H.J. Modeling the tidal channel morphodynamics in a macro-tidal embayment, Hangzhou Bay, China. Cont. Shelf Res. 2009, 29, 1757–1767. [Google Scholar] [CrossRef]
- Lin, C.-M.; Zhuo, H.-C.; Gao, S. Sedimentary facies and evolution in the Qiantang River incised valley, eastern China. Mar. Geol. 2005, 219, 235–259. [Google Scholar] [CrossRef]
- Amante, C.; Eakins, B.W. ETOPO1 1 Arc-Minute Global Relief Model: Procedures, Data Sources and Analysis. NOAA Technical Memorandum NESDIS NGDC-24; National Geophysical Data Center, NOAA: Boulder, CO, USA, 2009.
- Normalized Multi-band Drought Index Center. Tide Tables 2020; China Ocean Press: Beijing, China, 2020; Volume 3. [Google Scholar]
- Goyens, C.; Jamet, C.; Ruddick, K.G. Spectral relationships for atmospheric correction. II. Improving NASA’s standard and MUMM near infra-red modeling schemes. Opt. Express 2013, 21, 21176–21187. [Google Scholar] [CrossRef]
- Lavender, S.J.; Pinkerton, M.H.; Moore, G.F.; Aiken, J.; Blondeau-Patissier, D. Modification to the atmospheric correction of SeaWiFS ocean colour images over turbid waters. Cont. Shelf Res. 2005, 25, 539–555. [Google Scholar] [CrossRef]
- Wang, M.H.; Shi, W. The NIR-SWIR combined atmospheric correction approach for MODIS ocean color data processing. Opt. Express 2007, 15, 15722–15733. [Google Scholar] [CrossRef] [PubMed]
- He, Q.J.; Chen, C.Q. A new approach for atmospheric correction of MODIS imagery in turbid coastal waters: A case study for the Pearl River Estuary. Remote Sens. Lett. 2014, 5, 249–257. [Google Scholar] [CrossRef]
- Ye, H.B.; Chen, C.Q.; Yang, C.Y. Atmospheric Correction of Landsat-8/OLI Imagery in Turbid Estuarine Waters: A Case Study for the Pearl River Estuary. IEEE J. Stars 2017, 10, 252–261. [Google Scholar] [CrossRef]
- Wu, J.; Chen, C.Q.; Nukapothula, S. Atmospheric Correction of GOCI Using Quasi-Synchronous VIIRS Data in Highly Turbid Coastal Waters. Remote Sens. 2020, 12, 89. [Google Scholar] [CrossRef]
- Vermote, E.F.; Tanre, D.; Deuze, J.L.; Herman, M.; Morcrette, J.J. Second Simulation of the Satellite Signal in the Solar Spectrum, 6S: An overview. IEEE Trans. Geosci. Remote Sens. 1997, 35, 675–686. [Google Scholar] [CrossRef]
- Ahmad, Z.; Franz, B.A.; McClain, C.R.; Kwiatkowska, E.J.; Werdell, J.; Shettle, E.P.; Holben, B.N. New aerosol models for the retrieval of aerosol optical thickness and normalized water-leaving radiances from the SeaWiFS and MODIS sensors over coastal regions and open oceans. Appl. Opt. 2010, 49, 5545–5560. [Google Scholar] [CrossRef]
- Yang, H.; Arnone, R.; Jolliff, J. Estimating advective near-surface currents from ocean color satellite images. Remote Sens. Environ. 2015, 158, 1–14. [Google Scholar] [CrossRef]
- Emery, W.J.; Fowler, C.; Clayson, C.A. Satellite-image derived gulf-stream currents compared with numerical-model RESULTS. J. Atmosheric Ocean. Technol. 1992, 9, 286–304. [Google Scholar] [CrossRef]
- Crocker, R.I.; Matthews, D.K.; Emery, W.J.; Baldwin, D.G. Computing coastal ocean surface currents from infrared and ocean color satellite imagery. IEEE Trans. Geosci. Remote Sens. 2007, 45, 435–447. [Google Scholar] [CrossRef]
- Wang, Z.; Li, L.; Chen, D.; Xu, K.; Wei, T.; Gao, J.; Zhao, Y.; Chen, Z.; Masabate, W. Plume front and suspended sediment dispersal off the Yangtze (Changjiang) River mouth, China during non-flood season. Estuar. Coast. Shelf Sci. 2007, 71, 60–67. [Google Scholar] [CrossRef]
- Chen, S.-L.; Zhang, G.-A.; Yang, S.-L.; Shi, J.Z. Temporal variations of fine suspended sediment concentration in the Changjiang River estuary and adjacent coastal waters, China. J. Hydrol. 2006, 331, 137–145. [Google Scholar] [CrossRef]
- Cai, L.; Tang, D.; Li, X.; Zheng, H.; Shao, W. Remote sensing of spatial-temporal distribution of suspended sediment and analysis of related environmental factors in Hangzhou Bay, China. Remote Sens. Lett. 2015, 6, 597–603. [Google Scholar] [CrossRef]
- Ralston, D.K.; Geyer, W.R.; Warner, J.C. Bathymetric controls on sediment transport in the Hudson River estuary: Lateral asymmetry and frontal trapping. J. Geophys. Res. Ocean. 2012, 117. [Google Scholar] [CrossRef]
- Normandin, C.; Lubac, B.; Sottolichio, A.; Frappart, F.; Ygorra, B.; Marieu, V. Analysis of suspended sediment variability in a large highly turbid estuary using a 5-year-long remotely sensed data archive at high resolution. J. Geophys. Res. Ocean. 2019, 124, 7661–7682. [Google Scholar] [CrossRef]

| Symbol | Description | Unit |
|---|---|---|
| M2 | One of the semi-diurnal tidal constituents, the relative amplitude is 100 cm and the period is 12.4206 h. | - |
| Rrs | Above-surface remote sensing reflectance. | 1/Sr |
| d | The Sun–Earth distance at the time of the measurement showing the relative deviation from the average Sun–Earth distance d0 equal to 1 AU. | AU |
| Lλ | The TOA radiance measured by the sensor in band λ. | W/m2/Sr/μm |
| θs | Solar zenith angles. | rad |
| F0 | The extraterrestrial solar irradiance for mean Sun–Earth distance d0. | W/ m2/μm |
| Rr | The reflectance of Rayleigh scattering. | 1/Sr |
| Ra | The reflectance of aerosol multiple scattering reflectance. | 1/Sr |
| tv | The diffuse transmittance of the atmospheric column. | - |
| SAI | The spectral absorption index, one of the absorption-band parameters. | - |
| CTSM | The total suspended matter concentration. | mg/L |
| s | The symmetry of the spectral absorption band used for calculation of the SAI index. | - |
| RMSE | Root mean square error. | - |
| r | Correlation coefficient. | - |
| ΔTSM | The difference of TSM concentration. | mg/L |
| Sensor | Parameter | Spectral Band (nm) | Resolution (m) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GOCI | Band name | B1 | B2 | B3 | B4 | B5 | B6 | B7 | B8 | |||
| Spectral range | 402~422 | 433~453 | 480~500 | 545~565 | 650~670 | 675~685 | 735~755 | 845~885 | 500 | |||
| Central wavelength | (412) | (443) | (490) * | (555) * | (660) | (680) | (745) * | (865) | ||||
| GF-4 | Band name | B1 | B2 | B3 | B4 | B5 | B6 | |||||
| Spectral range | 450~900 | 450~520 | 520~600 | 630~690 | 760~900 | 3500~4100 | 50 | |||||
| Central wavelength | - | (519) * | (550) * | (628) | (770) * | - | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Q.; Zhou, B.; Yu, Z.; Wu, J.; Tang, S. Detection of the Minute Variations of Total Suspended Matter in Strong Tidal Waters Based on GaoFen-4 Satellite Data. Remote Sens. 2021, 13, 1339. https://doi.org/10.3390/rs13071339
Chen Q, Zhou B, Yu Z, Wu J, Tang S. Detection of the Minute Variations of Total Suspended Matter in Strong Tidal Waters Based on GaoFen-4 Satellite Data. Remote Sensing. 2021; 13(7):1339. https://doi.org/10.3390/rs13071339
Chicago/Turabian StyleChen, Qiong, Bin Zhou, Zhifeng Yu, Jie Wu, and Shilin Tang. 2021. "Detection of the Minute Variations of Total Suspended Matter in Strong Tidal Waters Based on GaoFen-4 Satellite Data" Remote Sensing 13, no. 7: 1339. https://doi.org/10.3390/rs13071339
APA StyleChen, Q., Zhou, B., Yu, Z., Wu, J., & Tang, S. (2021). Detection of the Minute Variations of Total Suspended Matter in Strong Tidal Waters Based on GaoFen-4 Satellite Data. Remote Sensing, 13(7), 1339. https://doi.org/10.3390/rs13071339







