Geometry-Aware Discriminative Dictionary Learning for PolSAR Image Classification
Abstract
1. Introduction
2. Related Work
3. Preliminaries
3.1. PolSAR Coherence Matrices
3.2. Discriminative Dictionary Learning
3.3. Sparse Coding on Riemannian Manifold
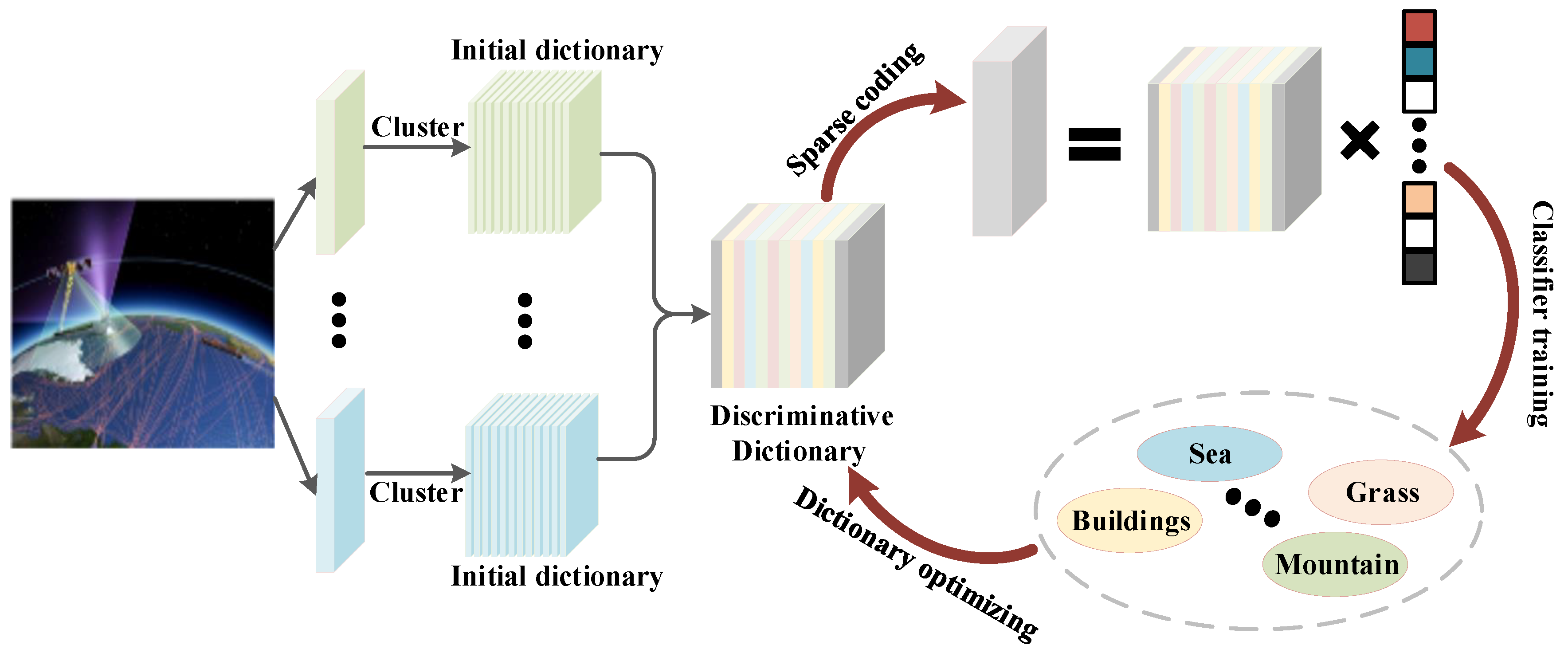
4. Proposed Method
4.1. Riemannian Discriminative Dictionary Learning for PolSAR Data
4.2. Model Optimization
4.2.1. Discriminative Dictionary Learning
4.2.2. Classifier Training
5. Experimental Results and Analysis
5.1. Description of Datasets
5.2. Experimental Results
5.2.1. Evaluation on Flevoland-1989
5.2.2. Evaluation on SanFransco
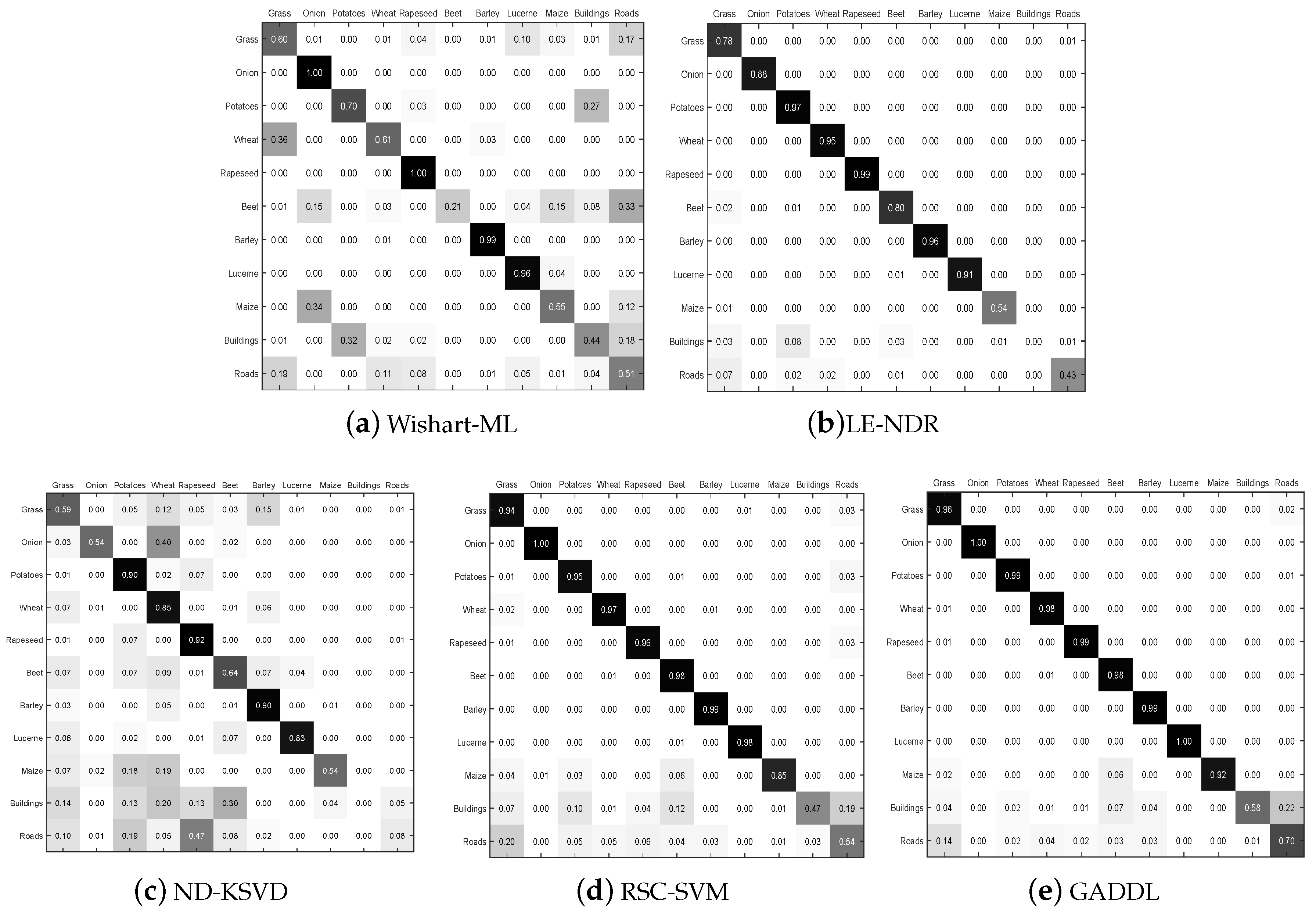
5.2.3. Evaluation on Flevoland-1991
5.3. Computational Cost
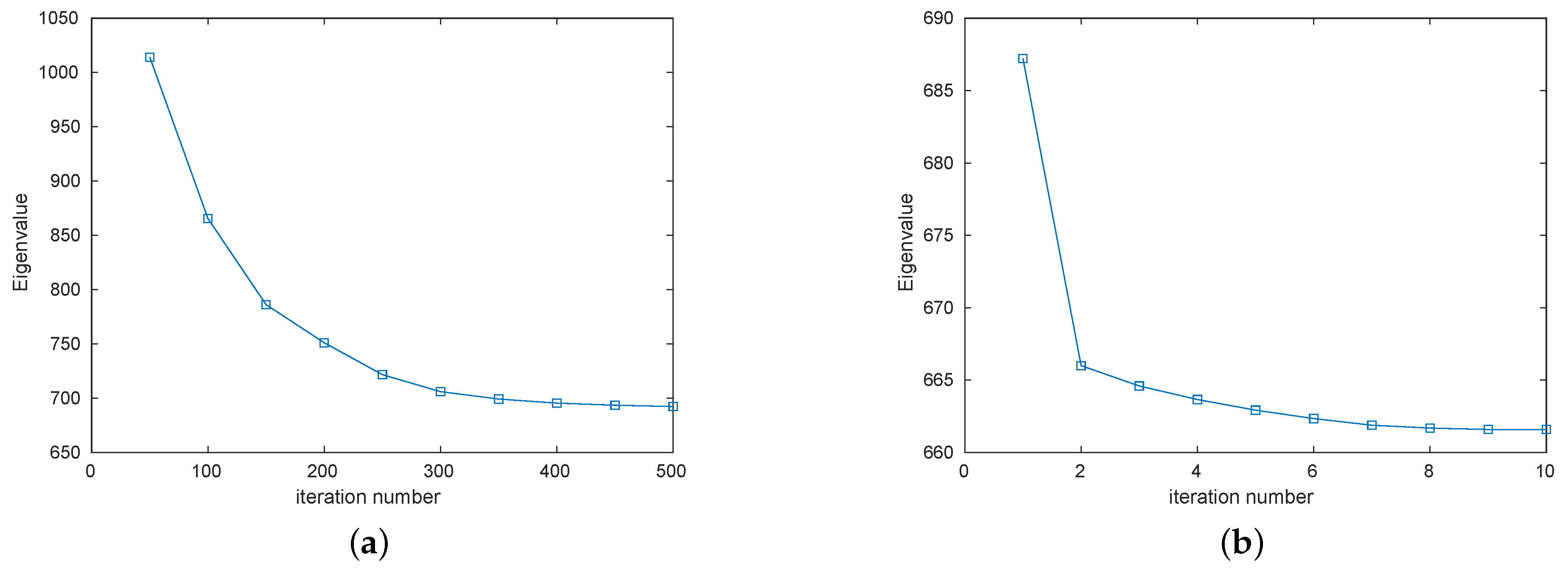
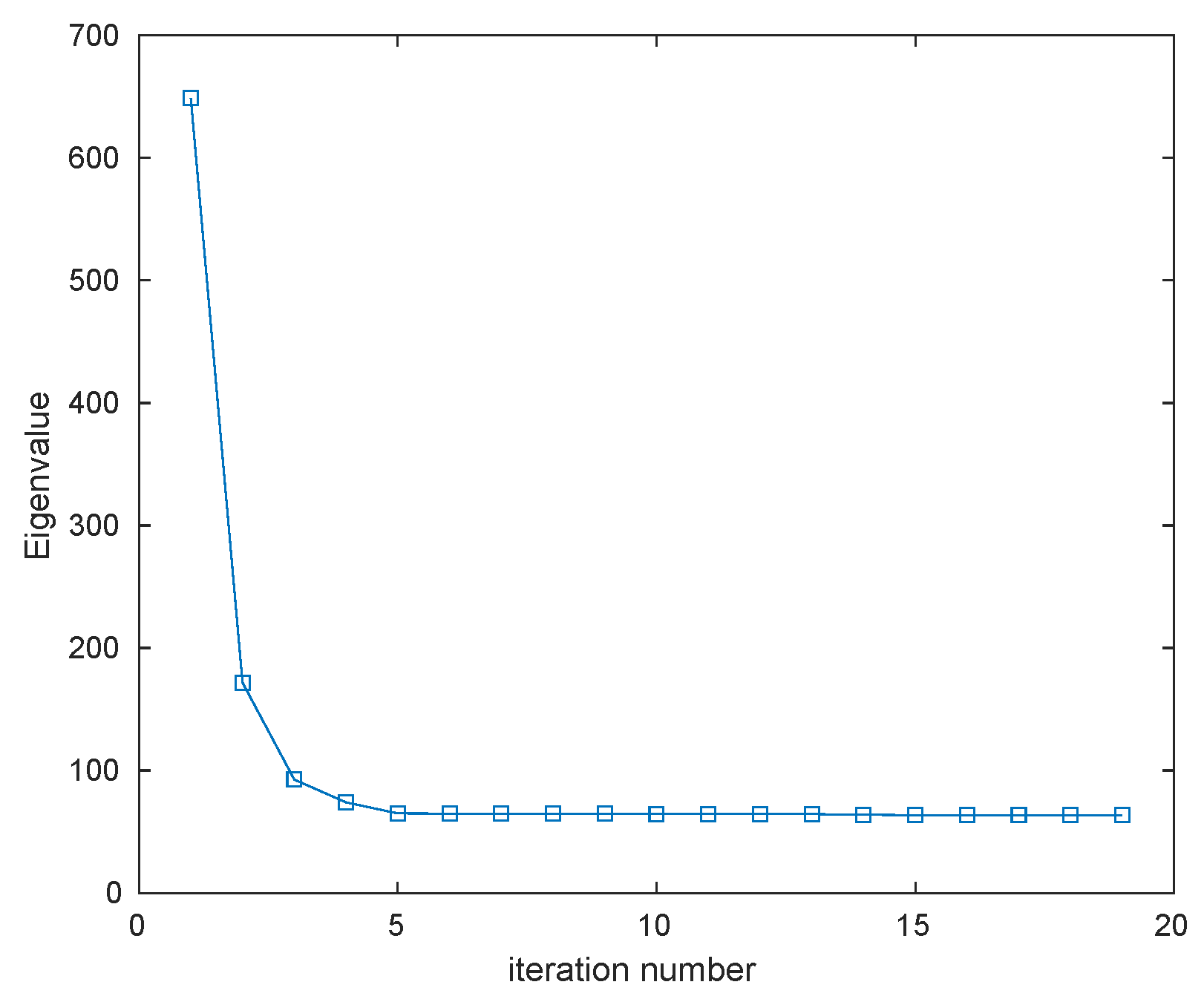
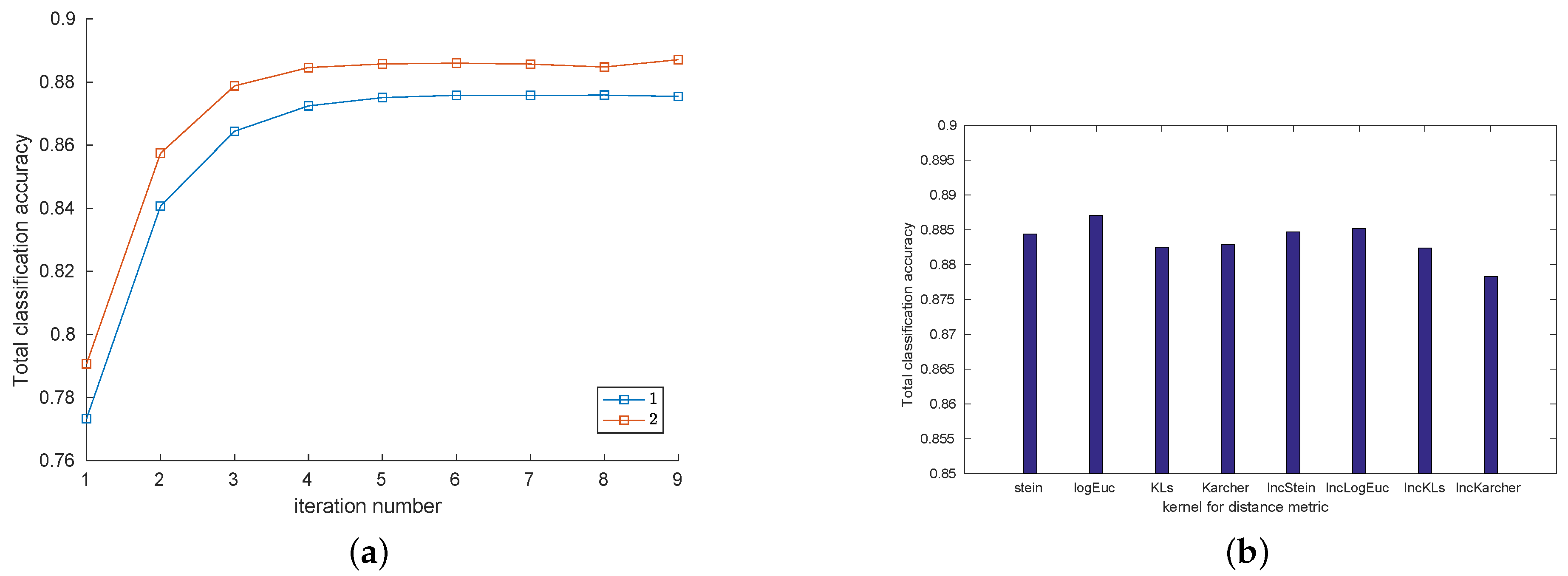
5.4. Convergence Analysis
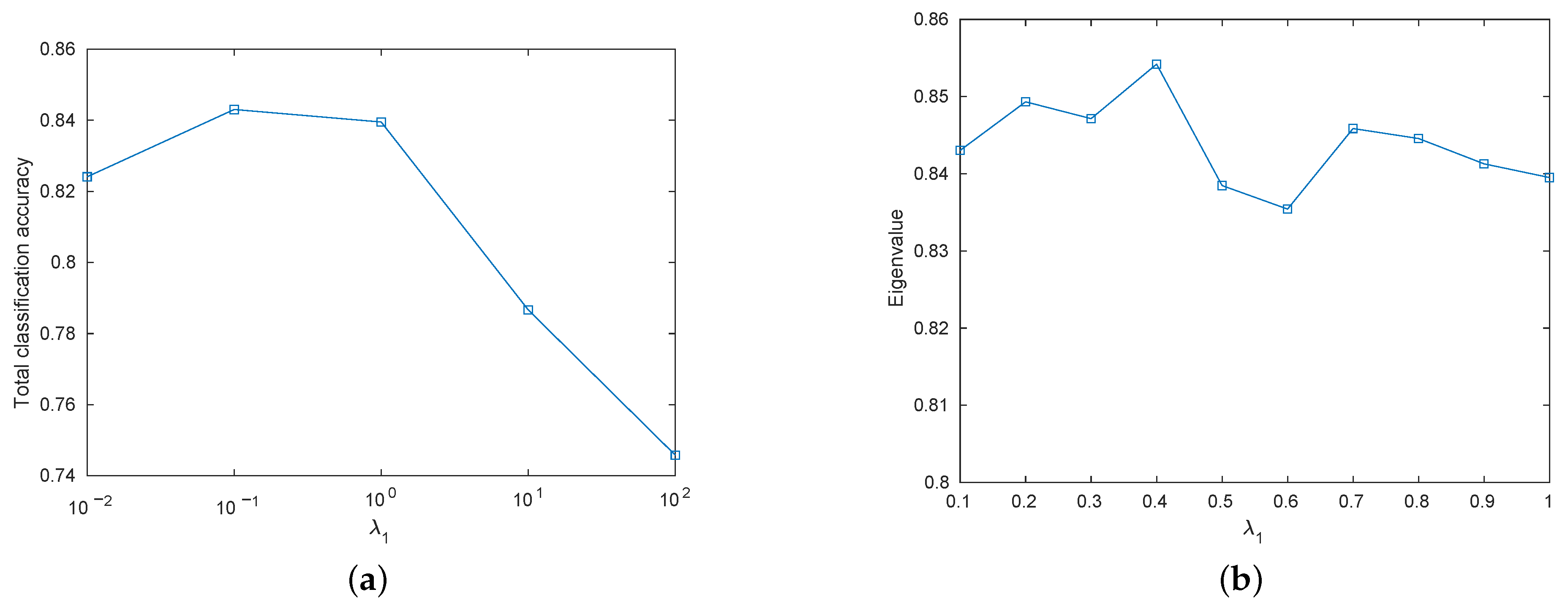
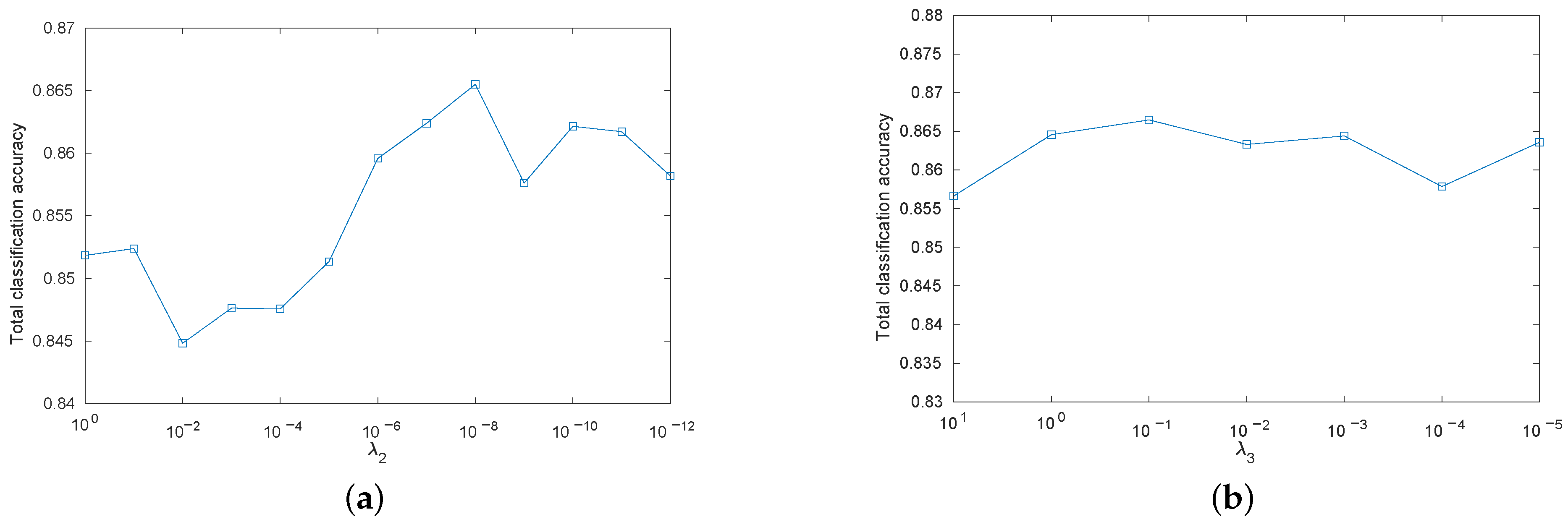
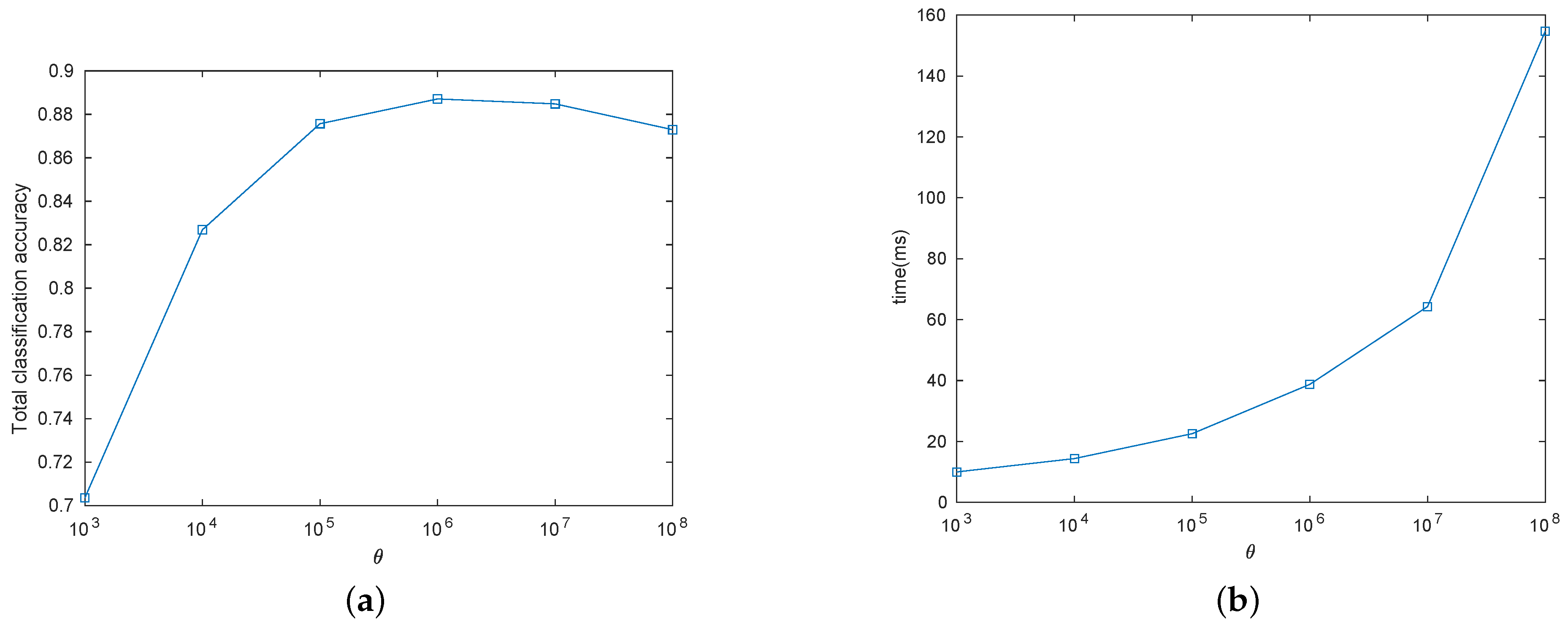
5.5. Parameter Analysis
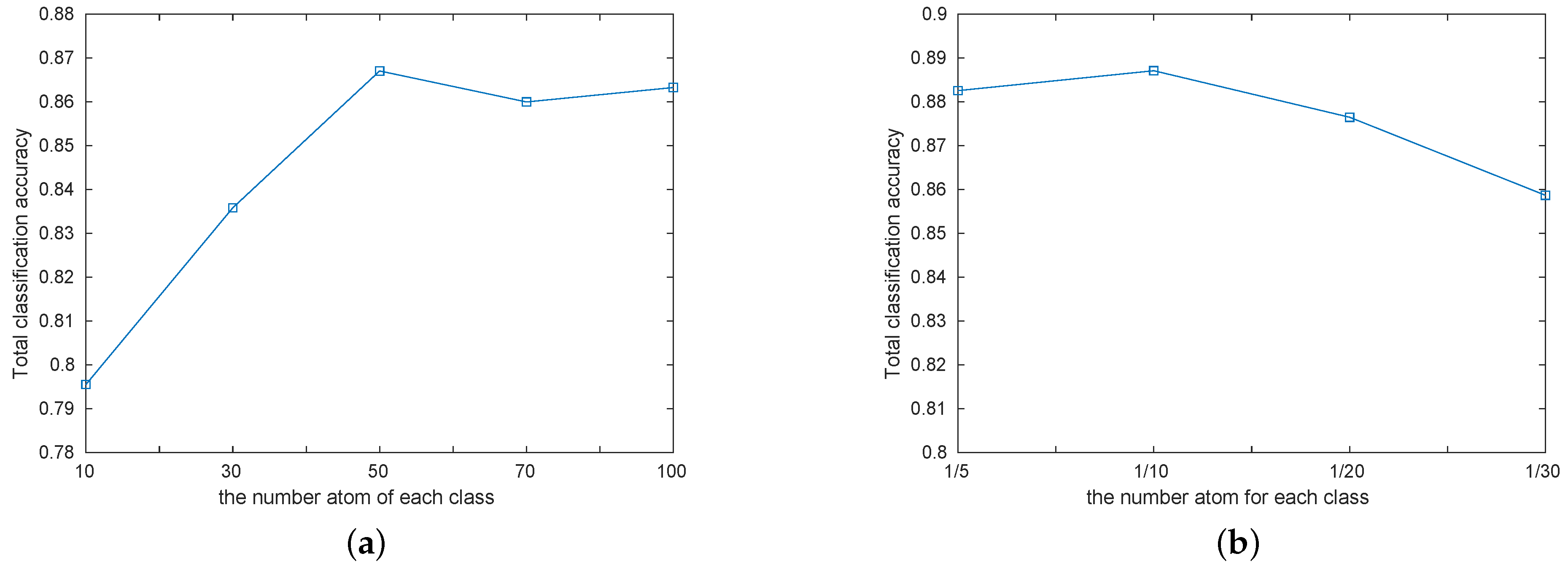
5.6. Robustness Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cloude, S.R.; Pottier, E. An entropy based classification scheme for land applications of polarimetric SAR. IEEE Trans. Geosci. Remote. Sens. 1997, 35, 68–78. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Moriyama, T.; Ishido, M.; Yamada, H. Four-component scattering model for polarimetric SAR image decomposition. IEEE Trans. Geosci. Remote. Sens. 2005, 43, 1699–1706. [Google Scholar] [CrossRef]
- Freeman, A.; Durden, S.L. A three-component scattering model for polarimetric SAR data. IEEE Trans. Geosci. Remote. Sens. 1998, 36, 963–973. [Google Scholar] [CrossRef]
- Pottier, E.; Saillard, J. On radar polarization target decomposition theorems with application to target classification, by using neural network method. In Proceedings of the 1991 Seventh International Conference on Antennas and Propagation, ICAP 91 (IEE), New York, NY, USA, 15–18 April 1991; pp. 265–268. [Google Scholar]
- Fukuda, S.; Hirosawa, H. Support vector machine classification of land cover: Application to polarimetric SAR data. In Proceedings of the IGARSS 2001. Scanning the Present and Resolving the Future. Proceedings. IEEE 2001 International Geoscience and Remote Sensing Symposium (Cat. No. 01CH37217), Sydney, NSW, Australia, 9–13 July 2001; Volume 1, pp. 187–189. [Google Scholar]
- Lardeux, C.; Frison, P.L.; Tison, C.; Souyris, J.C.; Stoll, B.; Fruneau, B.; Rudant, J.P. Support vector machine for multifrequency SAR polarimetric data classification. IEEE Trans. Geosci. Remote. Sens. 2009, 47, 4143–4152. [Google Scholar] [CrossRef]
- Ghoggali, N.; Melgani, F.; Bazi, Y. A multiobjective genetic SVM approach for classification problems with limited training samples. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1707–1718. [Google Scholar] [CrossRef]
- She, X.; Yang, J.; Zhang, W. The boosting algorithm with application to polarimetric SAR image classification. In Proceedings of the 2007 1st Asian and Pacific Conference on Synthetic Aperture Radar, Huangshan, China, 5–9 November 2007; pp. 779–783. [Google Scholar]
- Zou, T.; Yang, W.; Dai, D.; Sun, H. Polarimetric SAR image classification using multifeatures combination and extremely randomized clustering forests. EURASIP J. Adv. Signal Process. 2009, 2010, 1–9. [Google Scholar] [CrossRef]
- Tannous, O.; Kasilingam, D. Independent component analysis of polarimetric SAR data for separating ground and vegetation components. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009; Volume 4, pp. IV-93–IV-96. [Google Scholar]
- Wang, H.; Pi, Y.; Cao, Z. Unsupervised classification of polarimetric SAR images based on ICA. In Proceedings of the Third International Conference on Natural Computation (ICNC 2007), Haikou, China, 24–27 August 2007; Volume 3, pp. 576–582. [Google Scholar]
- Zhang, Y.D.; Wu, L.; Wei, G. A new classifier for polarimetric SAR images. Prog. Electromagn. Res. 2009, 94, 83–104. [Google Scholar] [CrossRef]
- Tu, S.T.; Chen, J.Y.; Yang, W.; Sun, H. Laplacian eigenmaps-based polarimetric dimensionality reduction for SAR image classification. IEEE Trans. Geosci. Remote. Sens. 2011, 50, 170–179. [Google Scholar] [CrossRef]
- He, C.; Li, S.; Liao, Z.; Liao, M. Texture Classification of PolSAR Data Based on Sparse Coding of Wavelet Polarization Textons. IEEE Trans. Geosci. Remote. Sens. 2013, 51, 4576–4590. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, L.; Zou, B.; Moon, W.M. Fully Polarimetric SAR Image Classification via Sparse Representation and Polarimetric Features. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2015, 8, 3923–3932. [Google Scholar] [CrossRef]
- Xie, W.; Jiao, L.; Zhao, J. PolSAR Image Classification via D-KSVD and NSCT-Domain Features Extraction. IEEE Geosci. Remote. Sens. Lett. 2016, 13, 227–231. [Google Scholar] [CrossRef]
- Yang, F.; Gao, W.; Xu, B.; Yang, J. Multi-Frequency Polarimetric SAR Classification Based on Riemannian Manifold and Simultaneous Sparse Representation. Remote Sens. 2015, 7, 8469–8488. [Google Scholar] [CrossRef]
- Zhong, N.; Yan, T.; Yang, W.; Xia, G. A supervised classification approach for PolSAR images based on covariance matrix sparse coding. In Proceedings of the 2016 IEEE 13th International Conference on Signal Processing (ICSP), Chengdu, China, 6–10 November 2016; pp. 213–216. [Google Scholar] [CrossRef]
- Cai, S.; Zuo, W.; Zhang, L.; Feng, X.; Wang, P. Support Vector Guided Dictionary Learning. In Proceedings of the Computer Vision—ECCV 2014, Zurich, Switzerland, 6–12 September 2014; Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 624–639. [Google Scholar]
- Cherian, A.; Sra, S. Riemannian Dictionary Learning and Sparse Coding for Positive Definite Matrices. IEEE Trans. Neural Networks Learn. Syst. 2017, 28, 2859–2871. [Google Scholar] [CrossRef]
- Birgin, E.G.; Raydan, M. SPG: Software for Convex-Constrained Optimization. Acm Trans. Math. Softw. 2001, 27, 340–349. [Google Scholar] [CrossRef]
- Hiai, F.; Petz, D. Riemannian metrics on positive definite matrices related to means. Linear Algebra Its Appl. 2012, 430, 3105–3130. [Google Scholar] [CrossRef]
- Absil, P.A.; Mahony, R.; Sepulchre, R. Optimization Algorithms on Matrix Manifolds:First-Order Geometry; Princeton University Press: Princeton, NJ, USA, 2009; pp. 17–51. [Google Scholar]
- Absil, P.A.; Baker, C.G.; Gallivan, K.A. Trust-Region Methods on Riemannian Manifolds. Found. Comput. Math. 2007, 7, 303–330. [Google Scholar] [CrossRef]
- Bertsekas, D.P. Nonlinear Programming. J. Oper. Res. Soc. 1997, 48, 334. [Google Scholar] [CrossRef]
- Yang, J.; Yu, K.; Gong, Y.; Huang, T. Linear spatial pyramid matching using sparse coding for image classification. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 1794–1801. [Google Scholar] [CrossRef]
- Schmidt, M.W.; Berg, E.V.D.; Friedlander, M.P.; Murphy, K.P. Optimizing Costly Functions with Simple Constraints: A Limited-Memory Projected Quasi-Newton Algorithm. Hansen. Int. 2009, 5, 355–357. [Google Scholar]
- He, C.; Deng, J.; Xu, L.; Li, S.; Duan, M.; Liao, M. A novel over-segmentation method for polarimetric SAR images classification. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 4299–4302. [Google Scholar]
- Hoekman, D.H.; Vissers, M.A. A new polarimetric classification approach evaluated for agricultural crops. IEEE Trans. Geosci. Remote. Sens. 2003, 41, 2881–2889. [Google Scholar] [CrossRef]
- Xiao, D.; Liu, C.; Wang, Q.; Wang, C.; Zhang, X. PolSAR Image Classification Based on Dilated Convolution and Pixel-Refining Parallel Mapping network in the Complex Domain. arXiv 2019, arXiv:1909.10783. [Google Scholar]
- Lee, J.S.; Cloude, S.R.; Papathanassiou, K.P.; Grunes, M.R.; Woodhouse, I.H. Speckle filtering and coherence estimation of polarimetric SAR interferometry data for forest applications. Geosci. Remote. Sens. IEEE Trans. 2003, 41, 2254–2263. [Google Scholar]
- Du, L.J.; Lee, J.S. Polarimetric SAR image classification based on target decomposition theorem and complex Wishart distribution. In Proceedings of the IGARSS ’96. 1996 International Geoscience and Remote Sensing Symposium, Lincoln, NE, USA, 31 May 1996; Volume 1, pp. 439–441. [Google Scholar] [CrossRef]
- Hua, W.; Wang, S.; Zhao, Y.; Yue, B.; Guo, Y. Semi-supervised PolSAR Classification Based on Improved Tri-training. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 3937–3940. [Google Scholar] [CrossRef]
- Hearst, M.A.; Dumais, S.T.; Osuna, E.; Platt, J.; Scholkopf, B. Support vector machines. IEEE Intell. Syst. Their Appl. 1998, 13, 18–28. [Google Scholar] [CrossRef]



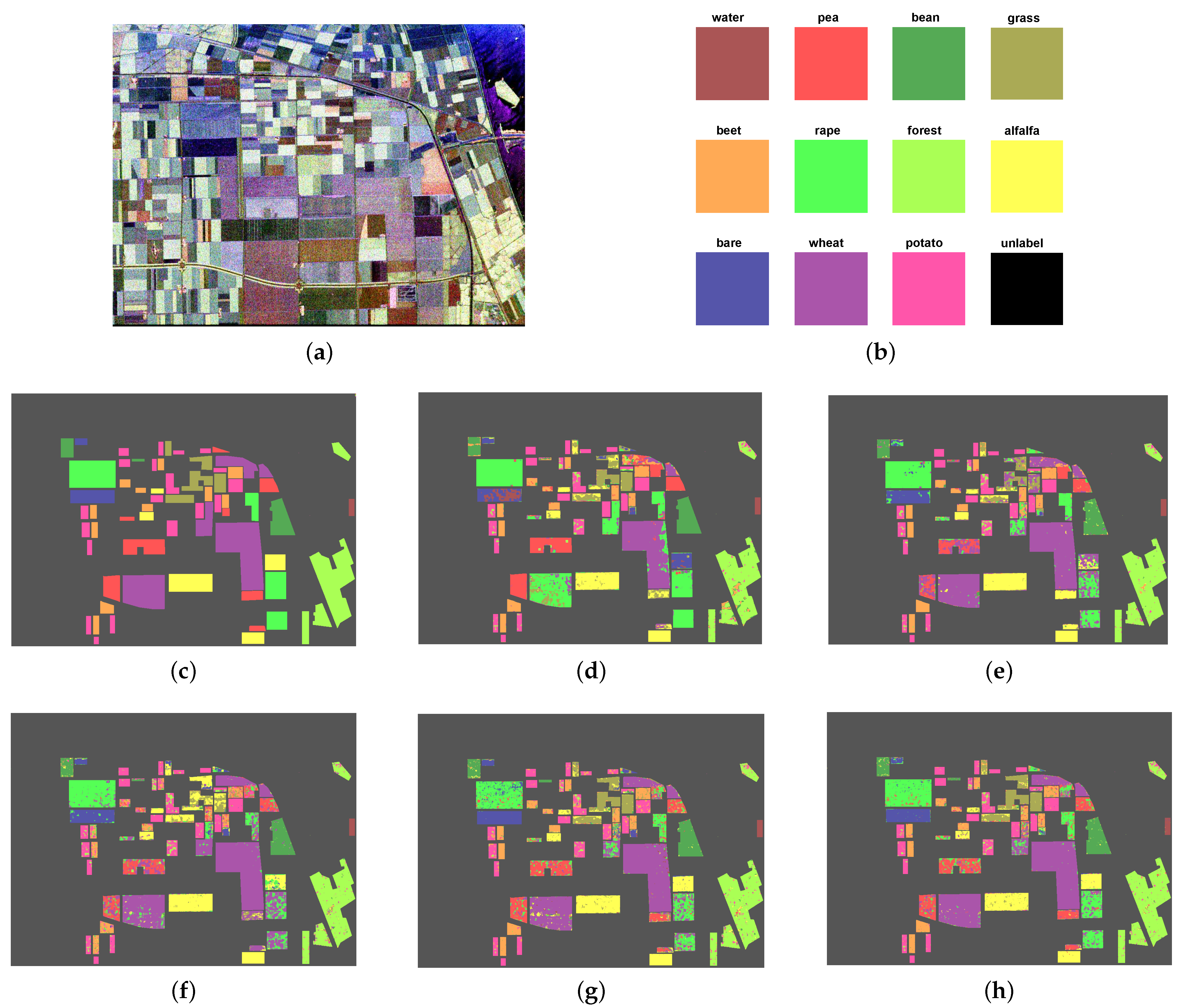

| Class | # Num. | Wishart-ML | LE-NDR | ND-KSVD | RSC-SVM | GADDL |
|---|---|---|---|---|---|---|
| Water | 867 | 1 | 1 | 1 | 1 | 0.9655 |
| Pea | 14798 | 0.6958 | 0.6856 | 0.2532 | 0.6629 | 0.7331 |
| Bean | 8098 | 0.9389 | 0.7820 | 0.8859 | 0.9554 | 0.9481 |
| Grass | 9706 | 0.6937 | 0.3091 | 0.2843 | 0.8307 | 0.8144 |
| Beet | 9895 | 0.9178 | 0.8479 | 0.6571 | 0.8773 | 0.8152 |
| Rape | 21967 | 0.9482 | 0.8320 | 0.5634 | 0.7427 | 0.8230 |
| Forest | 22639 | 0.8855 | 0.9451 | 0.9418 | 0.9124 | 0.9616 |
| Alfalfa | 13655 | 0.7216 | 0.69381 | 0.8799 | 0.9353 | 0.9129 |
| Bare | 5888 | 0.5985 | 0.8492 | 0.9562 | 0.9801 | 0.9423 |
| Wheat | 40030 | 0.5104 | 0.7549 | 0.8989 | 0.8686 | 0.9241 |
| Potato | 16434 | 0.9171 | 0.8356 | 0.8556 | 0.8311 | 0.9069 |
| OA | 0.7583 | 0.7735 | 0.7490 | 0.8483 | 0.8848 | |
| AA | 0.8025 | 0.7759 | 0.7433 | 0.8724 | 0.8861 | |
| Kappa | 0.7263 | 0.7388 | 0.7064 | 0.8258 | 0.8669 | |
| Class | # Num. | Wishart-ML | LE-NDR | ND-KSVD | RSC-SVM | GADDL |
|---|---|---|---|---|---|---|
| Sea | 352577 | 0.9814 | 0.9817 | 0.9887 | 0.9839 | 0.9871 |
| Mountain | 63419 | 0.4929 | 0.8247 | 0.7052 | 0.6821 | 0.8231 |
| Grass | 133164 | 0.8214 | 0.6578 | 0.7441 | 0.5862 | 0.6689 |
| Building | 372440 | 0.7518 | 0.9315 | 0.8193 | 0.9385 | 0.9145 |
| OA | 0.8319 | 0.9038 | 0.8654 | 0.8873 | 0.9005 | |
| AA | 0.7619 | 0.8489 | 0.8143 | 0.7977 | 0.8484 | |
| Kappa | 0.7531 | 0.8544 | 0.8012 | 0.8448 | 0.8491 | |
| Class | # Num. | Wishart-ML | LE-NDR | ND-KSVD | RSC-SVM | GADDL |
|---|---|---|---|---|---|---|
| Grass | 11890 | 0.6006 | 0.7828 | 0.5855 | 0.9443 | 0.9597 |
| Onion | 1144 | 1 | 0.8840 | 0.5376 | 0.9963 | 0.9963 |
| Potatoes | 14126 | 0.6998 | 0.9713 | 0.8973 | 0.9495 | 0.9864 |
| Wheat | 15050 | 0.6093 | 0.9458 | 0.8546 | 0.9687 | 0.9764 |
| Rapeseed | 11345 | 1 | 0.9916 | 0.9169 | 0.9621 | 0.9912 |
| Beet | 7239 | 0.2124 | 0.8033 | 0.6407 | 0.9763 | 0.9794 |
| Barley | 1681 | 0.9864 | 0.9565 | 0.8995 | 0.9880 | 0.9948 |
| Lucerne | 2129 | 0.9560 | 0.9125 | 0.8314 | 0.9822 | 0.9965 |
| Maize | 961 | 0.5482 | 0.5362 | 0.5390 | 0.8509 | 0.9156 |
| Buildings | 378 | 0.4429 | 0.0 | 0.0027 | 0.4652 | 0.5850 |
| Roads | 2532 | 0.5110 | 0.4345 | 0.0786 | 0.5410 | 0.7048 |
| OA | 0.7276 | 0.8968 | 0.7866 | 0.9498 | 0.9718 | |
| AA | 0.6879 | 0.7471 | 0.6167 | 0.8750 | 0.9078 | |
| Kappa | 0.7263 | 0.6864 | 0.7487 | 0.9410 | 0.9668 | |
| Datasets | Wishart-ML | LE-NDR | ND-KSVD | RSC-SVM | GADDL | |
|---|---|---|---|---|---|---|
| Flevoland-1989 | Test-time | 9.1 | 335.5 | 26.0 | 883.4 | 898.1 |
| OA | 0.7583 | 0.7735 | 0.749 | 0.8483 | 0.8848 | |
| SanFransco | Test-time | 20.7 | 1475.9 | 44.3 | 986.0 | 1001.8 |
| OA | 0.8319 | 0.9038 | 0.8654 | 0.8873 | 0.9005 | |
| Flevoland-1991 | Test-time | 7.1 | 147.5 | 12.3 | 428.4 | 428.6 |
| OA | 0.7276 | 0.8968 | 0.7866 | 0.9498 | 0.9718 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Lai, X.; Xie, Y.; Qu, Y.; Li, C. Geometry-Aware Discriminative Dictionary Learning for PolSAR Image Classification. Remote Sens. 2021, 13, 1218. https://doi.org/10.3390/rs13061218
Zhang Y, Lai X, Xie Y, Qu Y, Li C. Geometry-Aware Discriminative Dictionary Learning for PolSAR Image Classification. Remote Sensing. 2021; 13(6):1218. https://doi.org/10.3390/rs13061218
Chicago/Turabian StyleZhang, Yachao, Xuan Lai, Yuan Xie, Yanyun Qu, and Cuihua Li. 2021. "Geometry-Aware Discriminative Dictionary Learning for PolSAR Image Classification" Remote Sensing 13, no. 6: 1218. https://doi.org/10.3390/rs13061218
APA StyleZhang, Y., Lai, X., Xie, Y., Qu, Y., & Li, C. (2021). Geometry-Aware Discriminative Dictionary Learning for PolSAR Image Classification. Remote Sensing, 13(6), 1218. https://doi.org/10.3390/rs13061218







