Comparison of Regional Winter Wheat Mapping Results from Different Similarity Measurement Indicators of NDVI Time Series and Their Optimized Thresholds
Abstract
1. Introduction
2. Data Preparation and Preprocessing
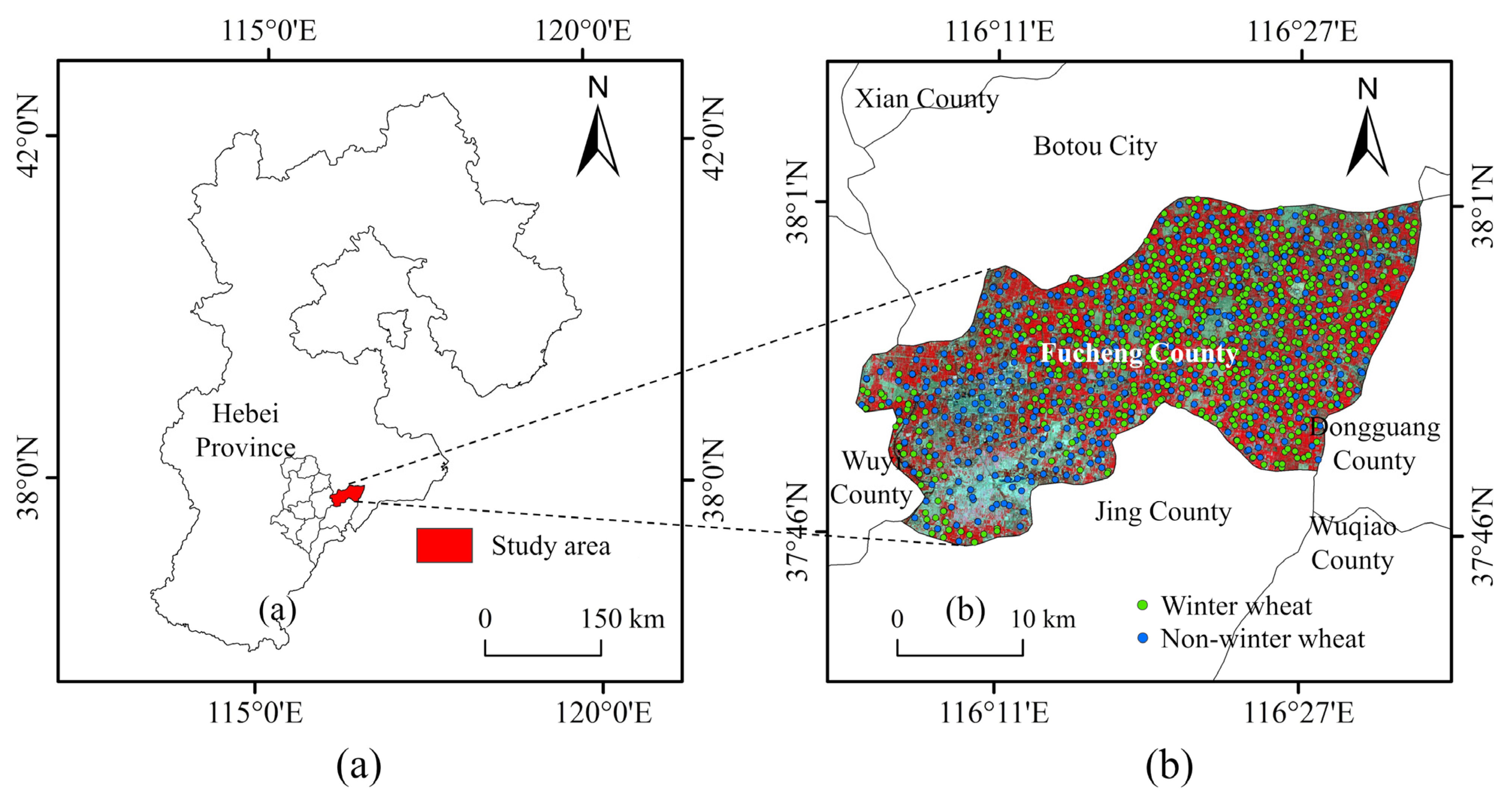
2.1. Study Area
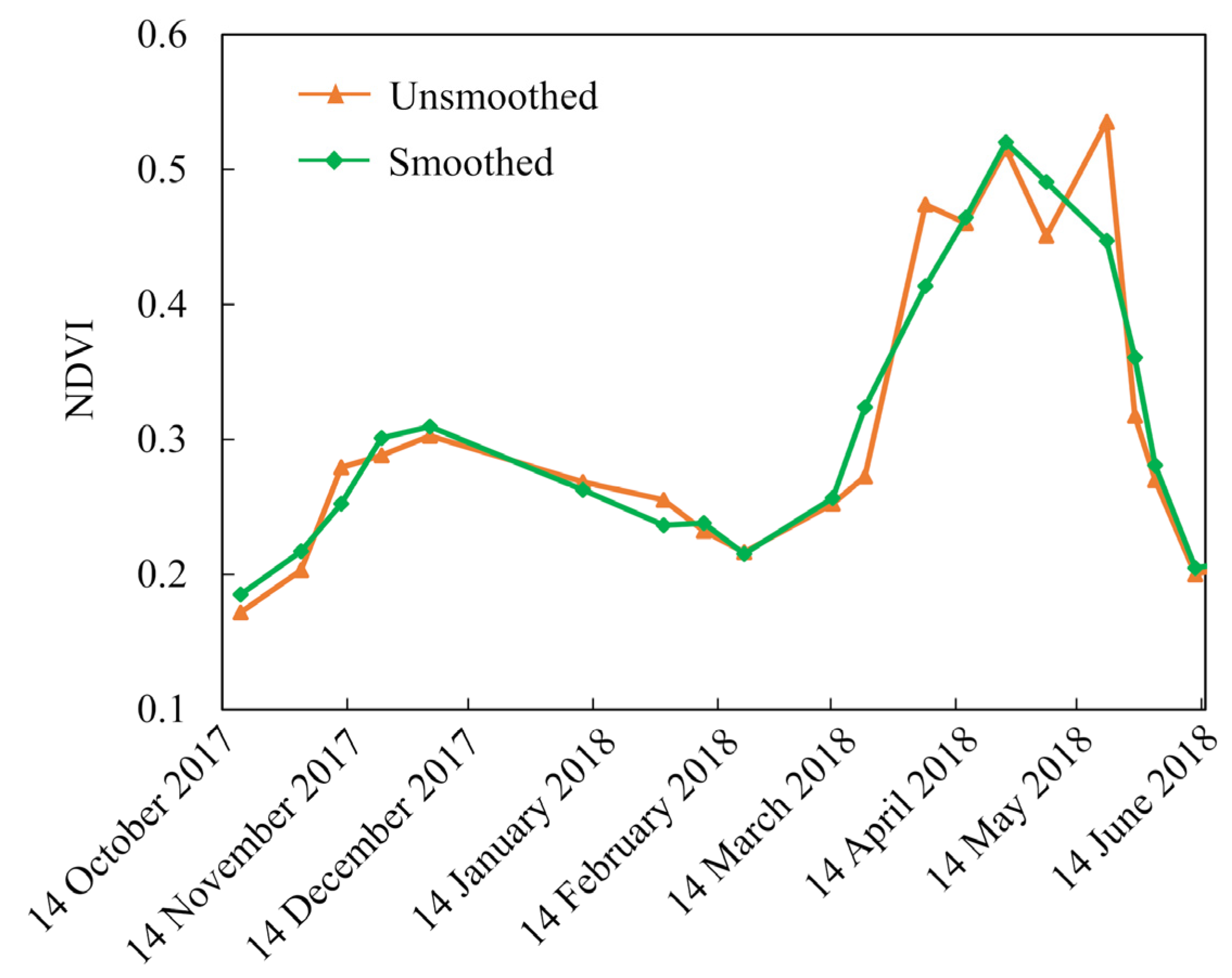
2.2. Remote Sensing Data
2.3. Sampling Point Data
2.4. Other Data
3. Methodology
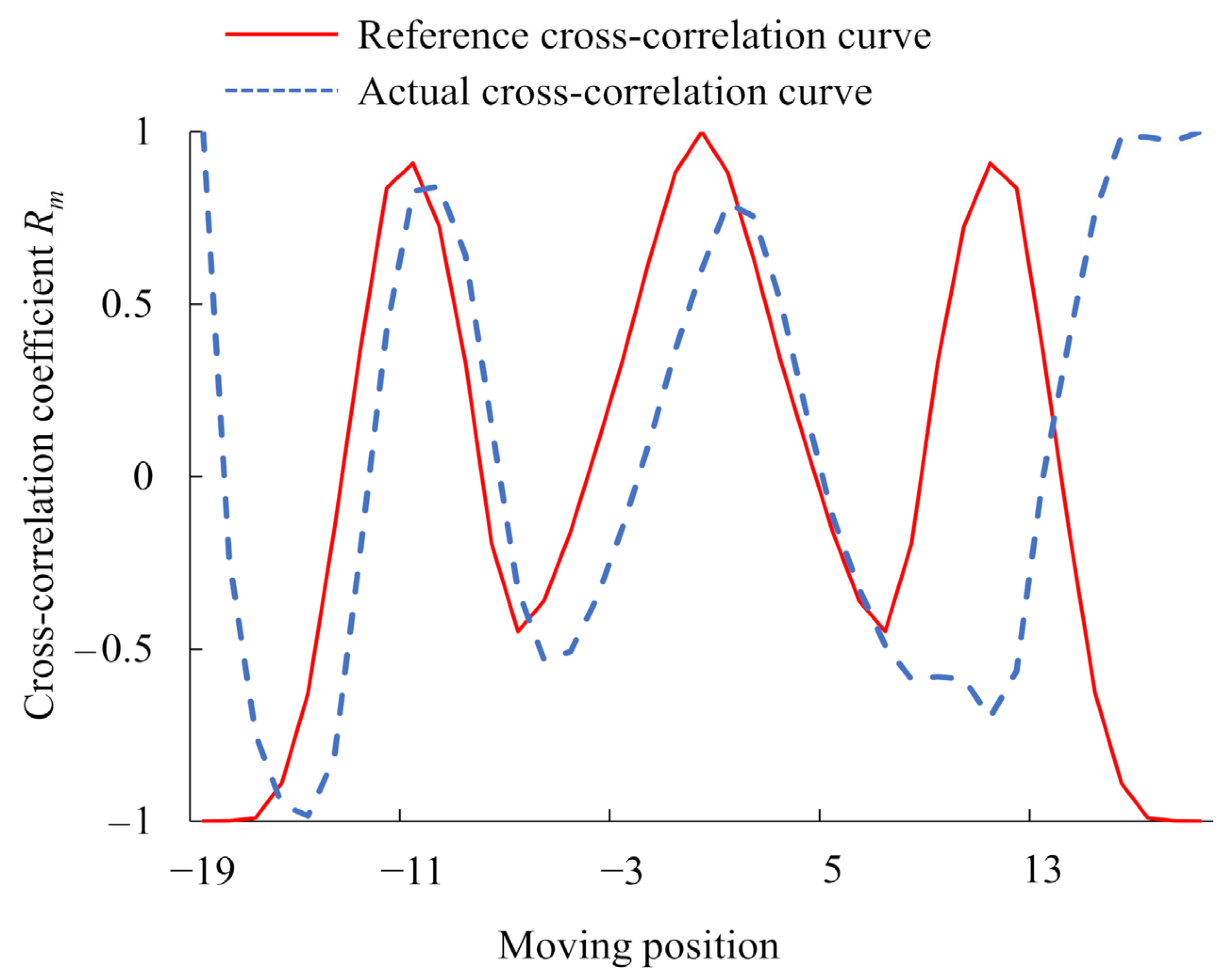
3.1. Cross Correlogram Spectral Matching (CCSM) Algorithm
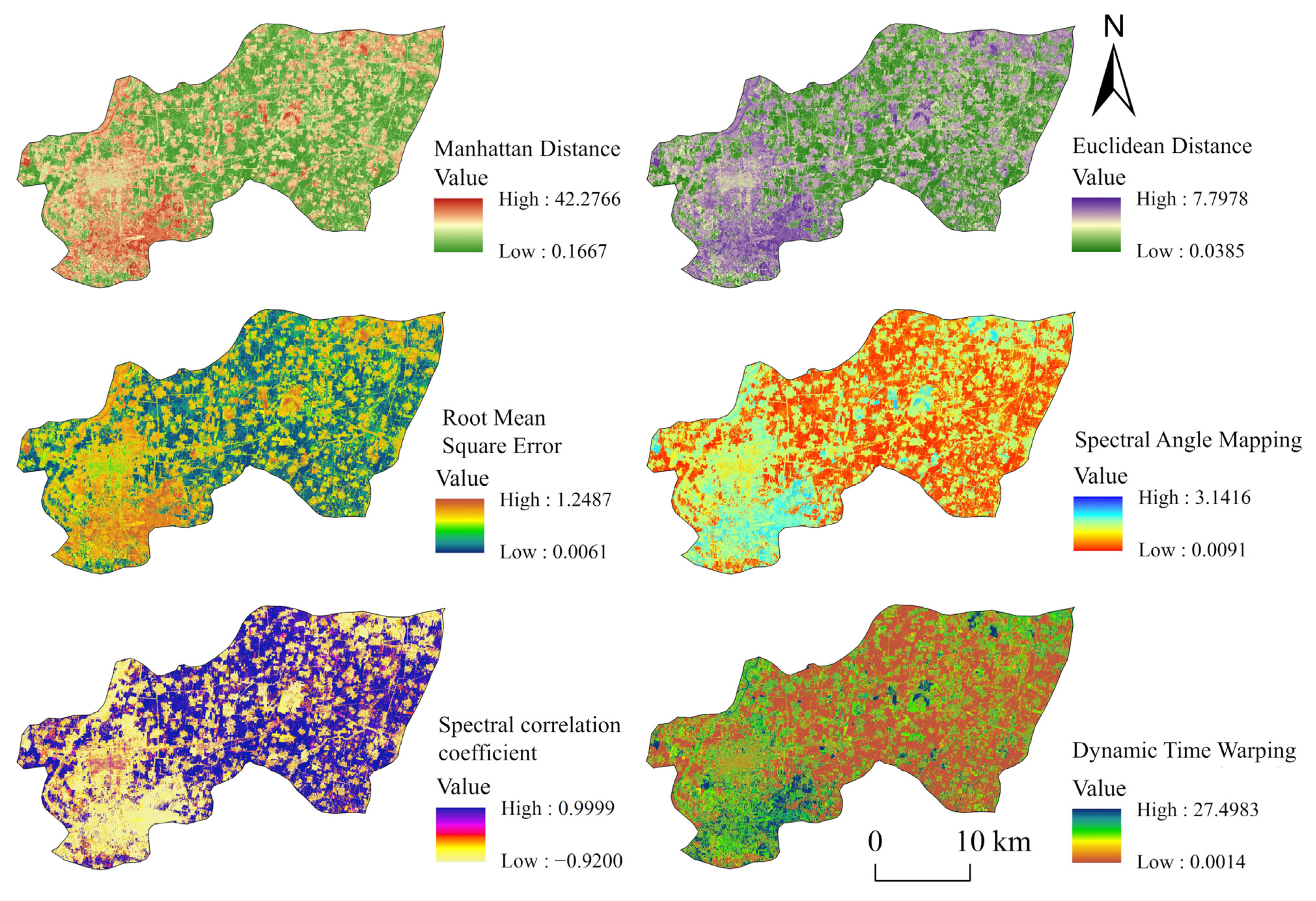
3.2. Calculation of Different Similarity Indicators
3.3. Establishment of the Winter Wheat Extraction Model
3.4. Optimization of the Threshold in the Extraction Model
3.5. Accuracy Assessment of Crop Mapping Results
4. Results and Analysis
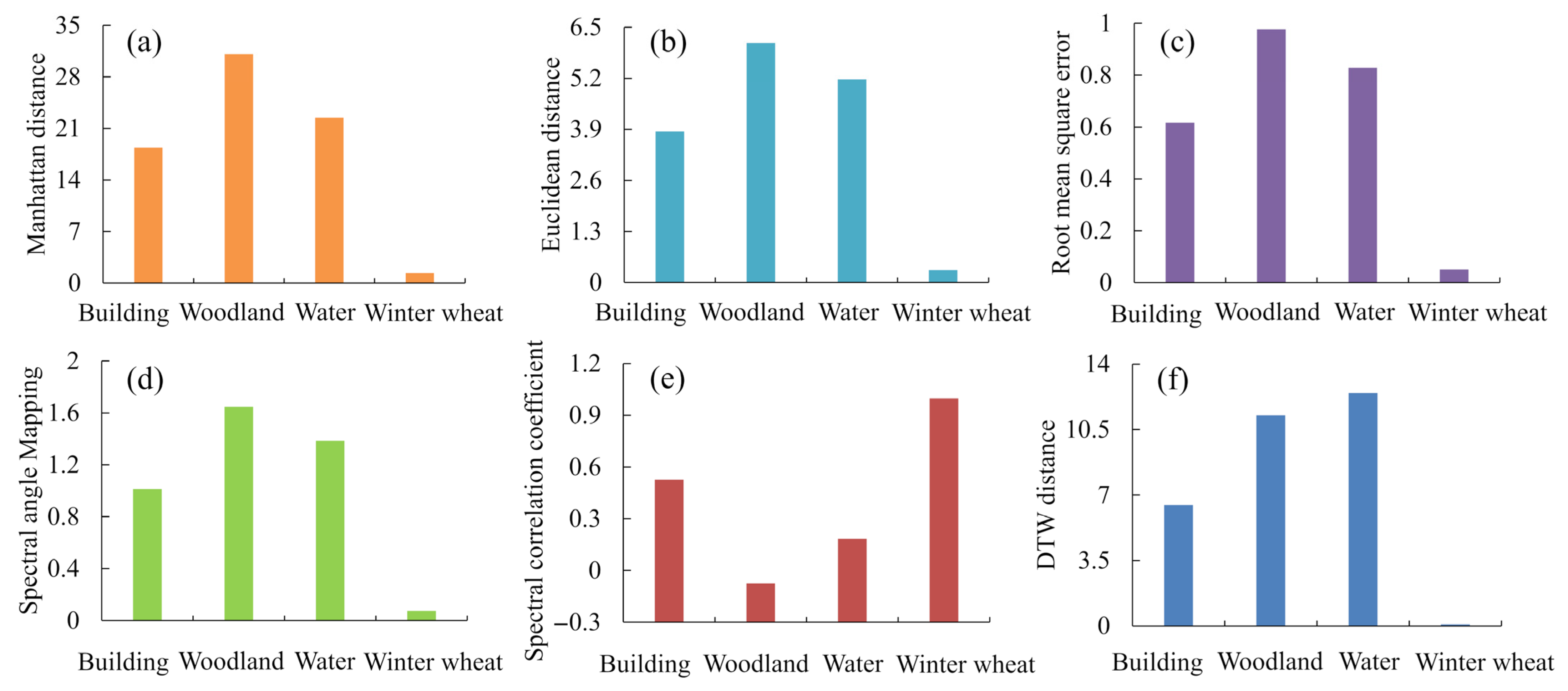
4.1. The Results of Different Similarity Indicators
4.2. Threshold Optimization Results of the Winter Wheat Extraction Model
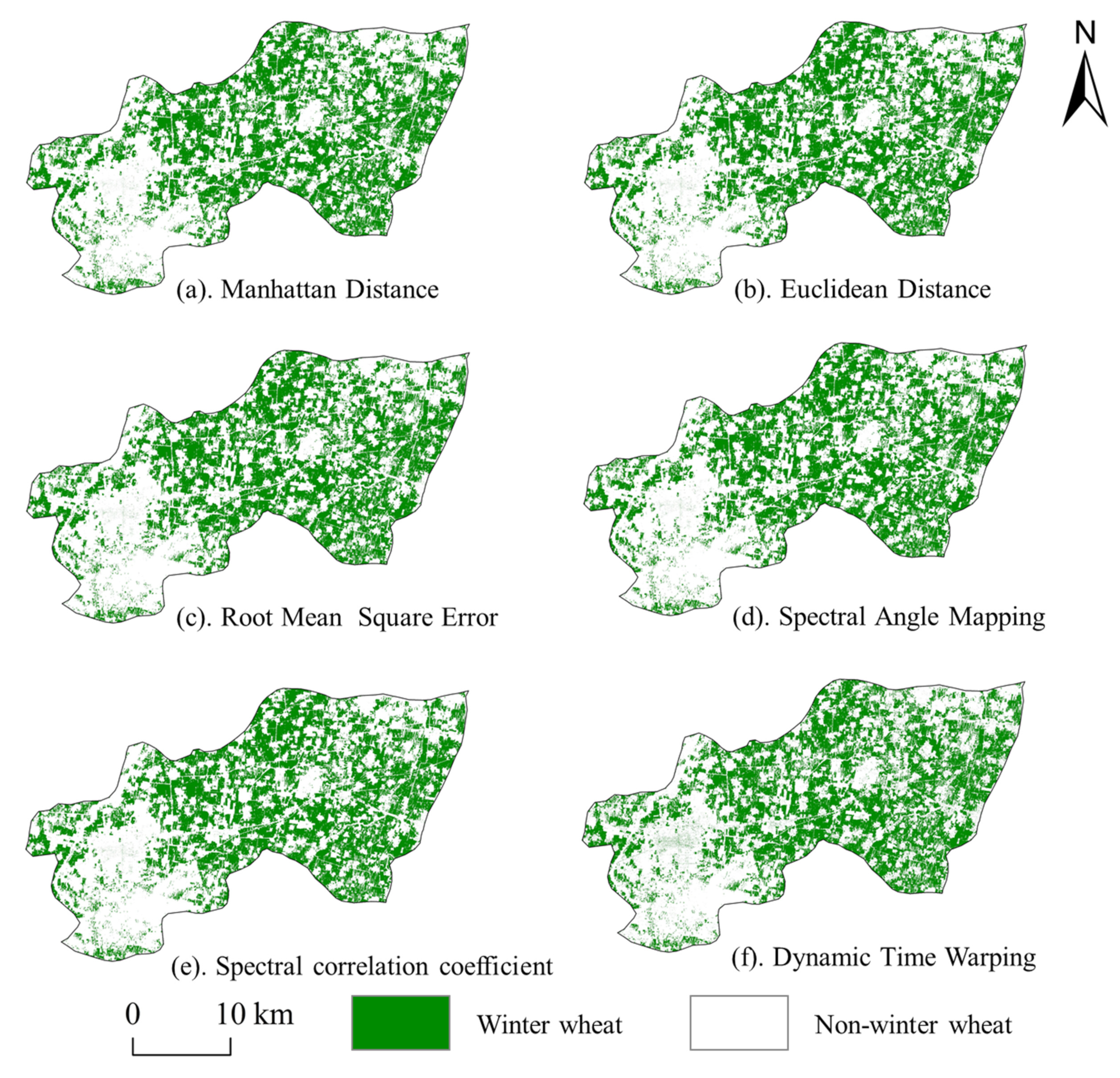
4.3. Extraction Results of Winter Wheat Spatial Distribution and Their Verification
5. Discussion
5.1. Total Amount Control of Crop Area Statistics
5.2. Threshold Optimization of the Crop Extraction Model
5.3. Shortcomings and Suggestions for Improvement
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Barnwal, P.; Kotani, K. Climatic impacts across agricultural crop yield distributions: An application of quantile regression on rice crops in Andhra Pradesh, India. Ecol. Econ. 2013, 87, 95–109. [Google Scholar] [CrossRef]
- Feng, L.; Jia, Z.; Zhang, J. The dynamic monitoring of corn planting area distribution in response to climate change from 2001 to 2010: A case study of Northeast China. Geogr. Tidsskr. -Dan. J. Geogr. 2016, 116, 44–55. [Google Scholar] [CrossRef]
- Dempewolf, J.; Adusei, B.; Becker-Reshef, I.; Hansen, M.; Potapov, P.; Khan, A.; Barker, B. Wheat Yield Forecasting for Punjab Province from Vegetation Index Time Series and Historic Crop Statistics. Remote Sens. 2014, 6, 9653–9675. [Google Scholar] [CrossRef]
- Gallego, F.J.; Stibig, H.J. Area estimation from a sample of satellite images: The impact of stratification on the clustering efficiency. Int. J. Appl. Earth Obs. Geoinf. 2013, 22, 139–146. [Google Scholar] [CrossRef]
- Khan, A.; Hansen, M.; Potapov, P.; Adusei, B.; Pickens, A.; Krylov, A.; Stehman, S.V. Evaluating Landsat and RapidEye Data for Winter Wheat Mapping and Area Estimation in Punjab, Pakistan. Remote Sens. 2018, 10, 489. [Google Scholar] [CrossRef]
- Liu, J.; Zhu, W.; Atzberger, C.; Zhao, A.; Pan, Y.; Huang, X. A Phenology-Based Method to Map Cropping Patterns under a Wheat-Maize Rotation Using Remotely Sensed Time-Series Data. Remote Sens. 2018, 10, 1203. [Google Scholar] [CrossRef]
- Song, Y.; Wang, J. Mapping Winter Wheat Planting Area and Monitoring Its Phenology Using Sentinel-1 Backscatter Time Series. Remote Sens. 2019, 11, 449. [Google Scholar] [CrossRef]
- Li, F.; Qin, Q.; Wang, H.; Hu, X.; Zhao, H. Extraction of Planting Information of Winter Wheat in a Province Based on GF-1/WFV Images. Meteor Environ. Res. 2018, 9, 100–105. [Google Scholar] [CrossRef]
- Wang, J.; Liu, J.; Zhuan, D.; Li, L.; Ge, Y. Spatial sampling design for monitoring the area of cultivated land. Int. J. Remote Sens. 2002, 23, 263–284. [Google Scholar] [CrossRef]
- Wu, M.; Yang, L.; Yu, B.; Wang, Y.; Zhao, X.; Niu, Z.; Wang, C. Mapping crops acreages based on remote sensing and sampling investigation by multivariate probability proportional to size. Trans. Chin. Soc. Agric. Eng. 2014, 30, 146–152. (In Chinese) [Google Scholar] [CrossRef]
- Gandharum, L.; Mulyani, M.E.; Hartono, D.M.; Karsidi, A.; Ahmad, M. Remote sensing versus the area sampling frame method in paddy rice acreage estimation in Indramayu regency, West Java province, Indonesia. Int. J. Remote Sens. 2021, 42, 1738–1767. [Google Scholar] [CrossRef]
- Zhang, J.; Pan, Y.; Hu, T.G.; Chen, L.; Dong, Y. Analysis of influence factors about space sampling efficiency of winter wheat planting area. Trans. Chin. Soc. Agric. Eng. 2009, 25, 169–173. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, H.; Li, Q.; Wen, N.; Du, X.; Tao, Q.; Dong, T. Analysis on estimation accuracy of crop area caused by spatial sampling factors based on remote sensing data. Trans. Chin. Soc. Agric. Eng. 2014, 30, 176–184. (In Chinese) [Google Scholar] [CrossRef]
- Tan, J.; Zhang, J.; Gao, C.; Bao, Y. Winter wheat area estimation based on structure and scale using remote sensing. Trans. Chin. Soc. Agric. Eng. 2012, 28, 114–122. (In Chinese) [Google Scholar] [CrossRef]
- Wei, M.; Qiao, B.; Zhao, J.; Zuo, X. The area extraction of winter wheat in mixed planting area based on Sentinel-2 a remote sensing satellite images. Int. J. Parallel. Emerg. Distrib. Syst. 2020, 35, 297–308. [Google Scholar] [CrossRef]
- Liu, X.; Li, F.; Guo, L. Winter Wheat Planting Information Extraction in Qingdao: Based on High-resolution Satellite Imagery. Chin. Agric. Sci. Bull. 2020, 36, 118–123. (In Chinese) [Google Scholar]
- Yang, H.; Deng, F.; Zhang, J.; Wang, X.; Ma, Q.; Xu, N. A study of information extraction of rape and winter wheat planting in Jianghan Plain based on MODIS EVI. Remote Sens. Land Resour. 2020, 32, 208–215. (In Chinese) [Google Scholar] [CrossRef]
- He, H.; Zhu, X.; Pan, Y.; Zhu, W.; Zhang, J.; Jia, B. Study on Scale Issues in Measurement of Winter Wheat Plant Area by Remote Sensing. J. Remote Sens. 2008, 12, 168–175. (In Chinese) [Google Scholar] [CrossRef]
- Abdikan, S.; Sanli, F.B.; Sunar, F.; Ehlers, M. A comparative data-fusion analysis of multi-sensor satellite images. Int. J. Digit. Earth 2014, 7, 671–687. [Google Scholar] [CrossRef]
- Zhang, W.; Li, A.; Jin, H.; Bian, J.; Zhang, Z.; Lei, G.; Qin, Z.; Huang, C. An Enhanced Spatial and Temporal Data Fusion Model for Fusing Landsat and MODIS Surface Reflectance to Generate High Temporal Landsat-Like Data. Remote Sens. 2013, 5, 5346–5368. [Google Scholar] [CrossRef]
- Esch, T.; Metz, A.; Marconcini, M.; Keil, M. Combined use of multi-seasonal high and medium resolution satellite imagery for parcel-related mapping of cropland and grassland. Int. J. Appl. Earth Obs. Geoinf. 2014, 28, 230–237. [Google Scholar] [CrossRef]
- Van Dijk, M.; You, L.; Havlik, P.; Mosnier, A. Generating high-resolution national crop distribution maps: Combining statistics, gridded data and surveys using an optimization approach. In Proceedings of the International Association of Agricultural Economists 2018 Conference, Vancouver, BC, Canada, 28 July–2 August 2018. [Google Scholar]
- Lu, J.; Huang, J.; Wang, L.; Pei, Y. Paddy rice planting information extraction based on spatial and temporal data fusion approach in Jianghan Plain. Resour. Environ. Yangtze Basin. 2017, 26, 874–881. (In Chinese) [Google Scholar] [CrossRef]
- Tan, J.; Yang, P.; Liu, Z.; Wu, W.; Zhang, L.; Li, Z.; You, L.; Tang, H.; Li, Z. Spatio-temporal dynamics of maize cropping system in Northeast China between 1980 and 2010 by using spatial production allocation model. J. Geogr. Sci. 2014, 24, 397–410. [Google Scholar] [CrossRef]
- Xia, T.; Wu, W.; Zhou, Q.; Zhou, Y.; Luo, J.; Yang, P.; Li, Z. Spatialization of Statistical Crop Planting Area Based on Geographical Regression. J. Nat. Resour. 2016, 31, 1773–1782. (In Chinese) [Google Scholar] [CrossRef]
- You, L.; Wood, S.; Wood-Sichra, U. Generating plausible crop distribution maps for Sub-Saharan Africa using a spatially disaggregated data fusion and optimization approach. Agric. Syst. 2009, 99, 126–140. [Google Scholar] [CrossRef]
- Lu, M.; Wu, W.; You, L.; Chen, D.; Zhang, L.; Yang, P.; Tang, H. A Synergy Cropland of China by Fusing Multiple Existing Maps and Statistics. Sensors 2017, 17, 1613. [Google Scholar] [CrossRef]
- Li, Q.; Wang, C.; Zhang, B.; Lu, L. Object-Based Crop Classification with Landsat-MODIS Enhanced Time-Series Data. Remote Sens. 2015, 7, 16091–16107. [Google Scholar] [CrossRef]
- Pan, Y.; Li, L.; Zhang, J.; Liang, S.; Hou, D. Crop area estimation based on MODIS-EVI time series according to distinct characteristics of key phenology phasesa case study of winter wheat area estimation in small-scale area. J. Remote Sens. 2011, 15, 578–594. [Google Scholar] [CrossRef]
- Singha, M.; Wu, B.; Zhang, M. Object-Based Paddy Rice Mapping Using HJ-1A/B Data and Temporal Features Extracted from Time Series MODIS NDVI Data. Sensors 2017, 17, 10. [Google Scholar] [CrossRef]
- Zhu, C.; Lu, D.; Victoria, D.; Dutra, L.V. Mapping Fractional Cropland Distribution in Mato Grosso, Brazil Using Time Series MODIS Enhanced Vegetation Index and Landsat Thematic Mapper Data. Remote Sens. 2015, 8, 22. [Google Scholar] [CrossRef]
- Gao, H.; Wang, C.; Wang, G.; Li, Q.; Zhu, J. A New Crop Classification Method Based on the Time-Varying Feature Curves of Time Series Dual-Polarization Sentinel-1 Data Sets. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1183–1187. [Google Scholar] [CrossRef]
- Sun, H.; Xu, A.; Lin, H.; Zhang, L.; Mei, Y. Winter wheat mapping using temporal signatures of MODIS vegetation index data. Int. J. Remote Sens. 2012, 33, 5026–5042. [Google Scholar] [CrossRef]
- Yang, Y.; Tao, B.; Ren, W.; Zourarakis, D.P.; Masri, B.E.; Sun, Z.; Tian, Q. An Improved Approach Considering Intraclass Variability for Mapping Winter Wheat Using Multitemporal MODIS EVI Images. Remote Sens. 2019, 11, 1191. [Google Scholar] [CrossRef]
- Dong, Q.; Chen, X.; Chen, J.; Zhang, C.; Liu, L.; Cao, X.; Zang, Y.; Zhu, X.; Cui, X. Mapping Winter Wheat in North China Using Sentinel 2A/B Data: A Method Based on Phenology-Time Weighted Dynamic Time Warping. Remote Sens. 2020, 12, 1274. [Google Scholar] [CrossRef]
- Yonezawa, C. Maximum likelihood classification combined with spectral angle mapper algorithm for high resolution satellite imagery. Int. J. Remote Sens 2007, 28, 3729–3737. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, Q.; Liu, G.; Huang, C. Extraction of Main Crops in Yellow River Delta Based on MODIS NDVI Time Series. J. Nat. Resour. 2017, 32, 1808–1818. (In Chinese) [Google Scholar] [CrossRef]
- Main-Knorn, M.; Pflug, B.; Louis, J.; Debaecker, V. Sen2Cor for Sentinel-2. In Proceedings of the SPIE Remote Sensing, Warschau, Poland, 11–14 September 2017; p. 1042704. [Google Scholar] [CrossRef]
- Hird, J.N.; Mcdermid, G.J. Noise reduction of NDVI time series: An empirical comparison of selected techniques. Remote Sens. Environ. 2009, 113, 248–258. [Google Scholar] [CrossRef]
- Chen, J.; Jönsson, P.; Tamura, M.; Gu, Z.; Matsushita, B.; Eklundh, L. A simple method for reconstructing a high-quality NDVI time-series data set based on the Savitzky–Golay filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]
- Van Der Meer, F.; Bakker, W. Cross correlogram spectral matching Application to surface mineralogical mapping by using AVIRIS data from Cuprite, Nevada. Remote Sens. Environ. 1997, 61, 371–382. [Google Scholar] [CrossRef]
- Van Der Meer, F.; Bakker, W. CCSM: Cross correlogram spectral matching. Int. J. Remote Sens. 2010, 18, 1197–1201. [Google Scholar] [CrossRef]
- Wang, L.; Chen, J.; Gong, P.; Shimazaki, H.; Tamura, M. Land cover change detection with a cross-correlogram spectral matching algorithm. Int. J. Remote Sens. 2010, 30, 3259–3273. [Google Scholar] [CrossRef]
- Erudel, T.; Fabre, S.; Houet, T.; Mazier, F.; Briottet, X. Criteria Comparison for Classifying Peatland Vegetation Types Using In Situ Hyperspectral Measurements. Remote Sens. 2017, 9, 748. [Google Scholar] [CrossRef]
- Da Silva, M.R.; de Carvalho, O.A., Jr.; Guimarães, R.F.; Gomes, R.A.T.; Silva, C.R. Wheat planted area detection from the MODIS NDVI time series classification using the nearest neighbour method calculated by the Euclidean distance and cosine similarity measures. Geocarto Int. 2020, 35, 1400–1414. [Google Scholar] [CrossRef]
- Ghiyamat, A.; Shafri, H.Z.M.; Mahdiraji, G.A.; Shariff, A.R.M.; Mansor, S. Hyperspectral discrimination of tree species with different classifications using single- and multiple-endmember. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 177–191. [Google Scholar] [CrossRef]
- Chauhan, H.J.; Buddhiraju, K.M. Effectiveness of Spectral Similarity Measures to Develop Precise Crop Spectra for Hyper-spectral Data Analysis. ISPRS Ann. Photogramm. Remote Sens. Spatial Inf. Sci. 2014, 2, 83–90. [Google Scholar] [CrossRef]
- Yagoub, H.; Belbachir, A.H.; Benabadji, N. Detection and mapping vegetation cover based on the Spectral Angle Mapper algorithm using NOAA AVHRR data. Adv. Space Res. 2014, 53, 1686–1693. [Google Scholar] [CrossRef]
- Abade, N.A.; Júnior, O.A.d.C.; Guimarães, R.F.; De Oliveira, S.N. Comparative Analysis of MODIS Time-Series Classification Using Support Vector Machines and Methods Based upon Distance and Similarity Measures in the Brazilian Cerrado-Caatinga Boundary. Remote Sens. 2015, 7, 12160–12191. [Google Scholar] [CrossRef]
- Guo, Z.; Yang, K.; Liu, C.; Lu, X.; Cheng, L.; Li, M. Mapping National-Scale Croplands in Pakistan by Combining Dynamic Time Warping Algorithm and Density-Based Spatial Clustering of Applications with Noise. Remote Sens. 2020, 12, 3644. [Google Scholar] [CrossRef]
- Guan, X.; Huang, C.; Liu, G.; Meng, X.; Liu, Q. Mapping Rice Cropping Systems in Vietnam Using an NDVI-Based Time-Series Similarity Measurement Based on DTW Distance. Remote Sens. 2016, 8, 19. [Google Scholar] [CrossRef]
- Csillik, O.; Belgiu, M.; Asner, G.P.; Kelly, M. Object-Based Time-Constrained Dynamic Time Warping Classification of Crops Using Sentinel-2. Remote Sens. 2019, 11, 1257. [Google Scholar] [CrossRef]
- Duan, Q.; Gupta, V.K.; Sorooshian, S. Shuffled Complex Evolution Approach for Effective and Efficient Global Minimization. J. Optim. Theory Appl. 1993, 76, 501–502. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V.K. Optimal use of the SCE-UA global optimization method for calibrating watershed models. J. Hydrol. 1994, 158, 265–284. [Google Scholar] [CrossRef]
- Huang, L.; Wang, L.; Zhang, Y.; Xing, L.; Hao, Q.; Xiao, Y.; Yang, L.; Zhu, H. Identification of Groundwater Pollution Sources by a SCE-UA Algorithm-Based Simulation/Optimization Model. Water 2018, 10, 193. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Q. Effects of Spatial Resolution on Crop Identification and Acreage Estimation. Remot Sens. Inf. 2014, 29, 36–40. (In Chinese) [Google Scholar] [CrossRef]
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- Xu, F.; Li, Z.; Zhang, S.; Huang, N.; Quan, Z.; Zhang, W.; Liu, X.; Jiang, X.; Pan, J.; Prishchepov, A.V. Mapping Winter Wheat with Combinations of Temporally Aggregated Sentinel-2 and Landsat-8 Data in Shandong Province, China. Remote Sens. 2020, 12, 2065. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, X.; Huang, Y.; Hong, C.; Zhang, Z.; Huang, X.; Zeng, J.; Tang, J.; Zhang, R. Monitoring of Winter Wheat and Summer Corn Phenology in Xiong’an New Area Based on NDVI Time Series. In Proceedings of the 2019 International Conference on Wireless Communication, Network and Multimedia Engineering (WCNME 2019), Guilin, China, 21 April 2019. [Google Scholar]
- Wang, L.; Liu, J.; Yang, G.; Fu, C.; Teng, F.; Gao, J. Early recognition of winter wheat area based on GF-1 satellite. Trans. Chin. Soc. Agric. Eng. 2015, 31, 194–201. (In Chinese) [Google Scholar] [CrossRef]
- Xun, L.; Zhang, J.; Cao, D.; Wang, J.; Zhang, S.; Yao, F. Mapping cotton cultivated area combining remote sensing with a fused representation-based classification algorithm. Comput. Electron. Agric. 2021, 181, 105940. [Google Scholar] [CrossRef]
- Zhang, J.; Feng, L.; Yao, F. Improved maize cultivated area estimation over a large-scale combining MODIS–EVI time series data and crop phenological information. ISPRS J. Photogramm. Remote Sens. 2014, 94, 102–113. [Google Scholar] [CrossRef]

| ID | Satellite | Scan Time | ID | Satellite | Scan Time |
|---|---|---|---|---|---|
| 1 | S2B | 20 October 2017 | 12 | S2B | 16 March 2018 |
| 2 | S2A | 4 November 2017 | 13 | S2A | 24 March 2018 |
| 3 | S2A | 14 November 2017 | 14 | S2B | 8 April 2018 |
| 4 | S2A | 24 November 2017 | 15 | S2B | 18 April 2018 |
| 5 | S2B | 6 December 2017 | 16 | S2B | 28 April 2018 |
| 6 | S2B | 16 December 2018 | 17 | S2B | 8 May 2018 |
| 7 | S2B | 26 December 2018 | 18 | S2A | 23 May 2018 |
| 8 | S2A | 13 January 2018 | 19 | S2A | 30 May 2018 |
| 9 | S2A | 2 February 2018 | 20 | S2B | 4 June 2018 |
| 10 | S2A | 12 February 2018 | 21 | S2B | 14 June 2018 |
| 11 | S2A | 22 February 2018 |
| Similarity Indicator | Initial Parameter Settings | Optimization Results | |||
|---|---|---|---|---|---|
| Lower T | Upper T | Initial T | Optimal T | Minimum Difference Value y (m2) | |
| MD | 0 | 16.7221 | 3.6056 | 9.9904 | 0 |
| ED | 0 | 4.5642 | 0.8725 | 2.4129 | 0 |
| RMSE | 0 | 0.7309 | 0.1397 | 0.3864 | 0 |
| SAM | 0 | 1.2071 | 0.2138 | 0.5917 | 100 |
| SCC | 0.3629 | 1 | 0.9586 | 0.8514 | 100 |
| DTW | 0 | 11.3329 | 0.8929 | 0.82626 | 0 |
| Similarity Indicator | TA (%) | OA (%) | Kappa | PA (%) | UA (%) | ||
|---|---|---|---|---|---|---|---|
| Winter Wheat | Non-Winter Wheat | Winter Wheat | Non-Winter Wheat | ||||
| MD | 100 | 93.9 | 0.8776 | 90.54 | 98.18 | 98.45 | 89.07 |
| ED | 100 | 94.1 | 0.8815 | 90.89 | 98.18 | 98.45 | 89.44 |
| RMSE | 100 | 94.5 | 0.8894 | 91.61 | 98.18 | 98.46 | 90.19 |
| SAM | 99.99 | 93.3 | 0.8657 | 89.46 | 98.18 | 98.43 | 87.98 |
| SCC | 99.99 | 92.8 | 0.8558 | 88.75 | 97.95 | 98.22 | 87.25 |
| DTW | 100 | 86.2 | 0.7256 | 80.18 | 93.86 | 94.33 | 78.82 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Ren, J.; Wu, S.; Zhao, H.; Zhang, N. Comparison of Regional Winter Wheat Mapping Results from Different Similarity Measurement Indicators of NDVI Time Series and Their Optimized Thresholds. Remote Sens. 2021, 13, 1162. https://doi.org/10.3390/rs13061162
Li F, Ren J, Wu S, Zhao H, Zhang N. Comparison of Regional Winter Wheat Mapping Results from Different Similarity Measurement Indicators of NDVI Time Series and Their Optimized Thresholds. Remote Sensing. 2021; 13(6):1162. https://doi.org/10.3390/rs13061162
Chicago/Turabian StyleLi, Fangjie, Jianqiang Ren, Shangrong Wu, Hongwei Zhao, and Ningdan Zhang. 2021. "Comparison of Regional Winter Wheat Mapping Results from Different Similarity Measurement Indicators of NDVI Time Series and Their Optimized Thresholds" Remote Sensing 13, no. 6: 1162. https://doi.org/10.3390/rs13061162
APA StyleLi, F., Ren, J., Wu, S., Zhao, H., & Zhang, N. (2021). Comparison of Regional Winter Wheat Mapping Results from Different Similarity Measurement Indicators of NDVI Time Series and Their Optimized Thresholds. Remote Sensing, 13(6), 1162. https://doi.org/10.3390/rs13061162





