A Novel Approach to Estimating Time-Averaged Volcanic SO2 Fluxes from Infrared Satellite Measurements
Abstract
1. Introduction
1.1. Basic Principles of Time-Averaged SO Flux Estimation
1.2. CrIS SO Data
2. Materials and Methods
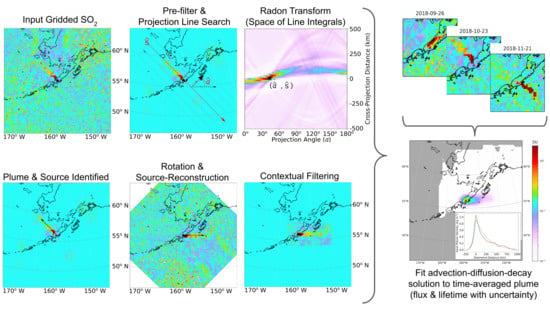
2.1. Object Detection-Based Mean Plume Construction
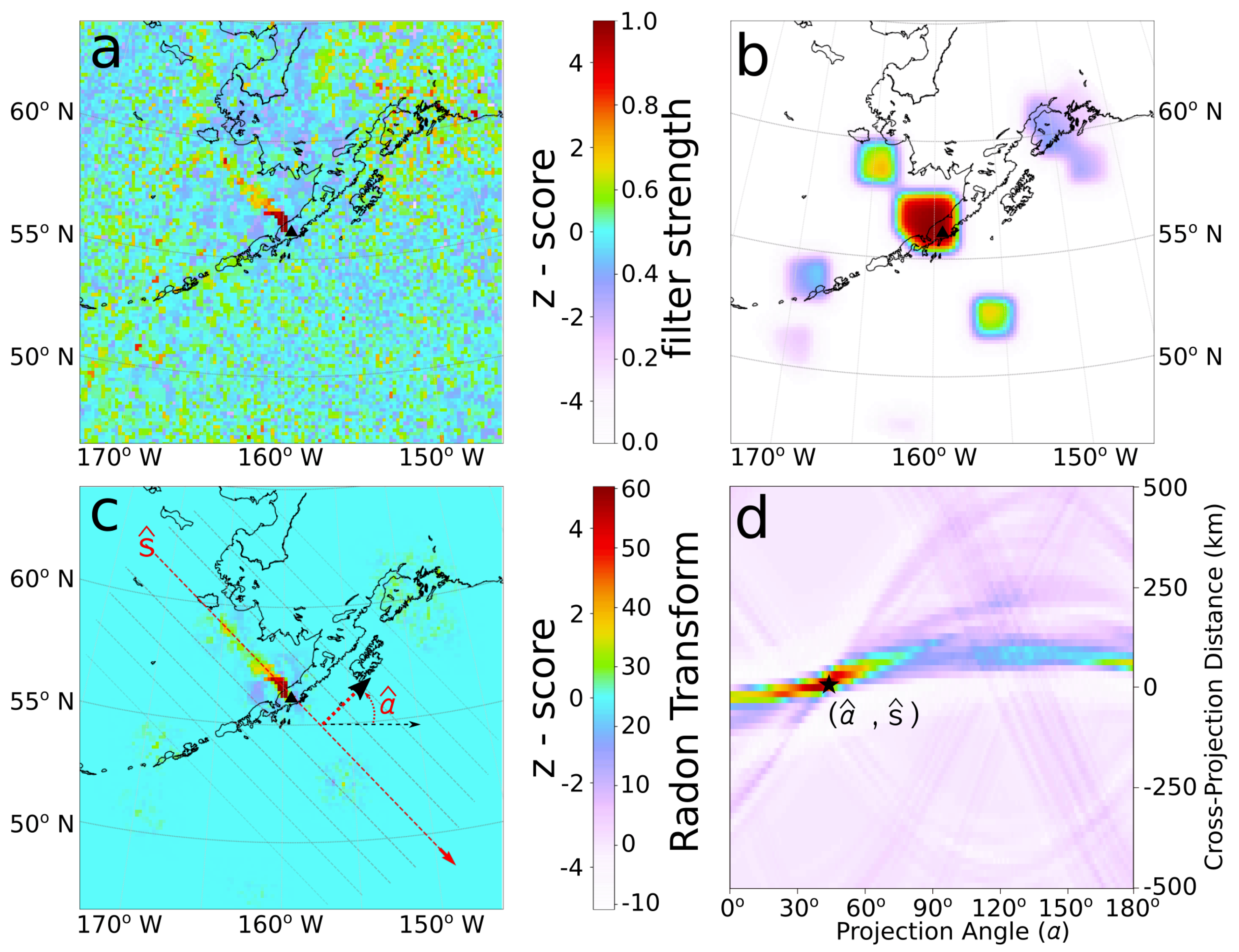
2.1.1. Plume Detection, Source Reconstruction, and Wind Rotation
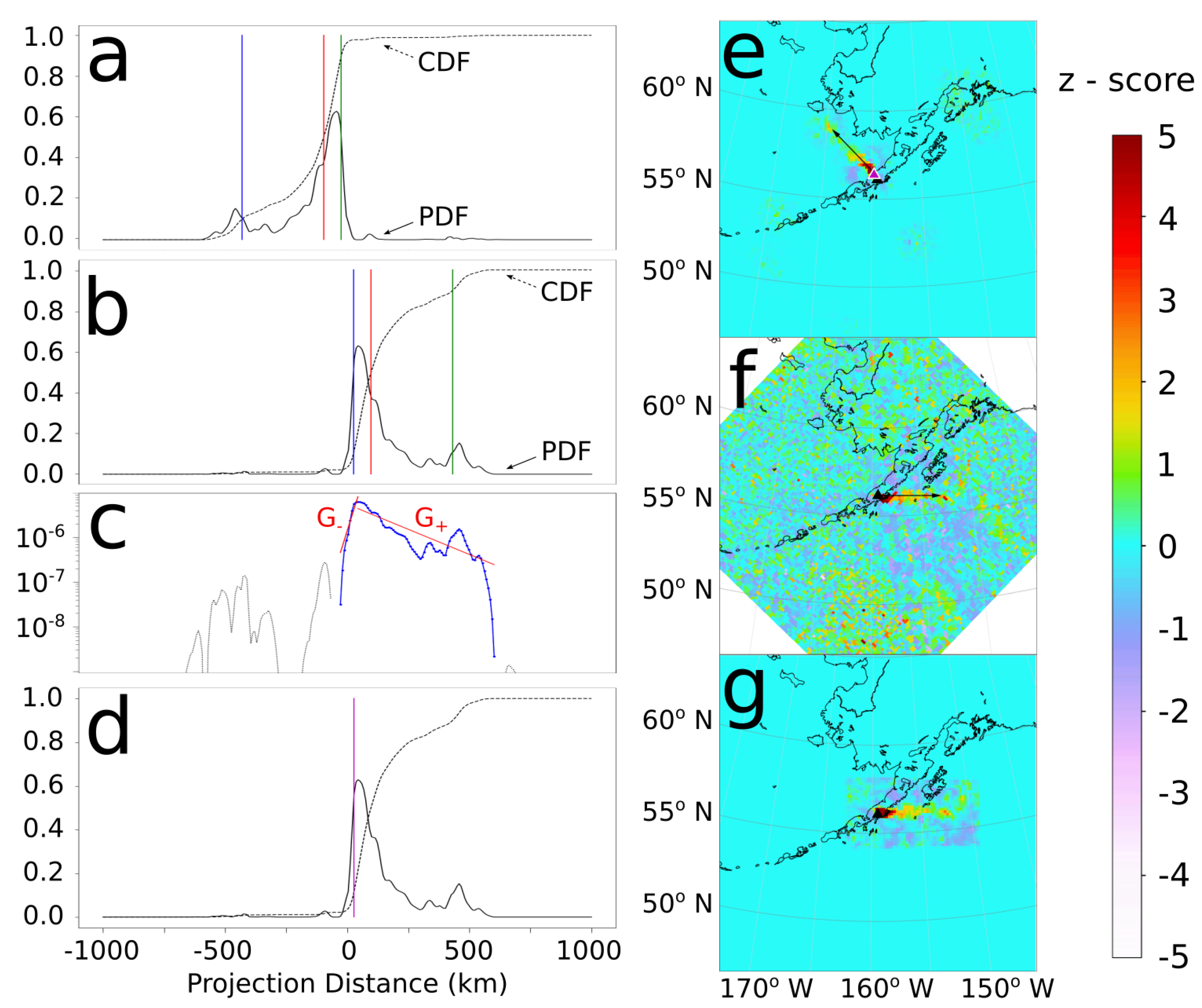
2.1.2. Filtering and Smoothing in Wind Reconstruction
2.1.3. Time-Averaging and Post-Processing
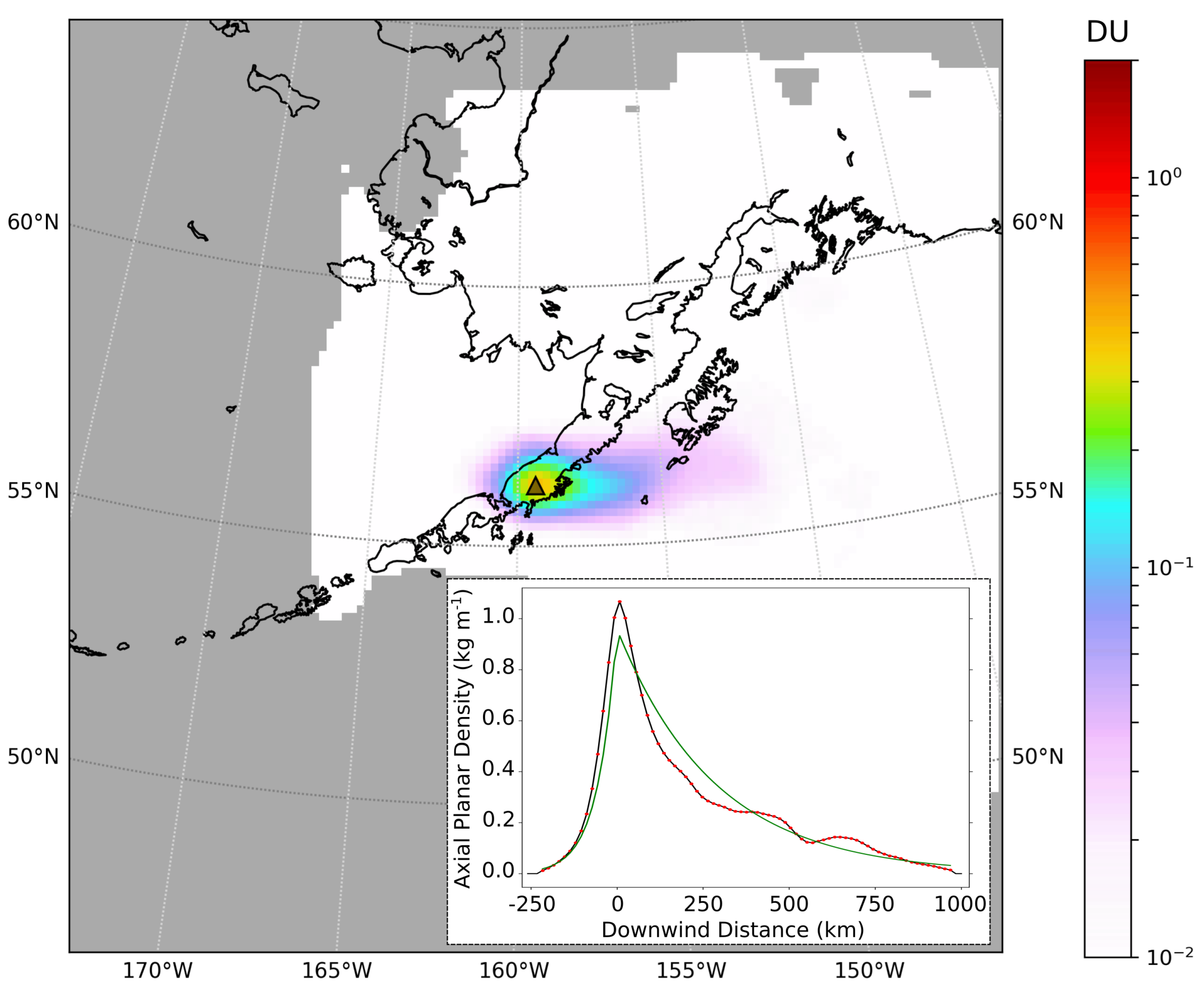
2.2. Physics-Based SO Cloud Fitting
2.2.1. Application of Simplified Theory to Satellite Measurements of Volcanic Plumes
2.2.2. Relationship to Previous Fitting Model
2.2.3. Fitting the ADRE Parameters
2.2.4. Decay Rate Estimation
2.3. Uncertainty Quantification
3. Results
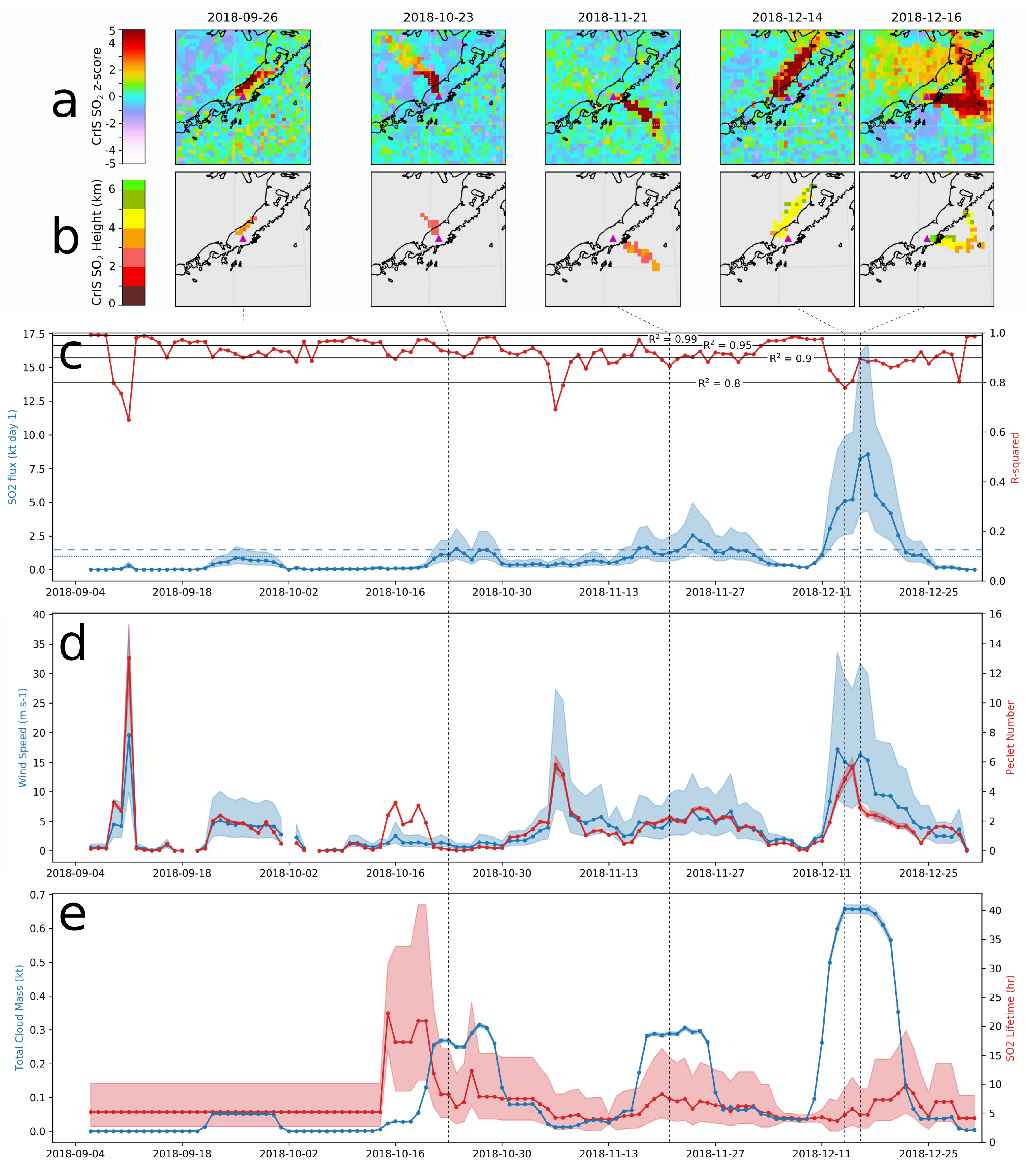
3.1. 4-Month Summary of Eruptive Sequence
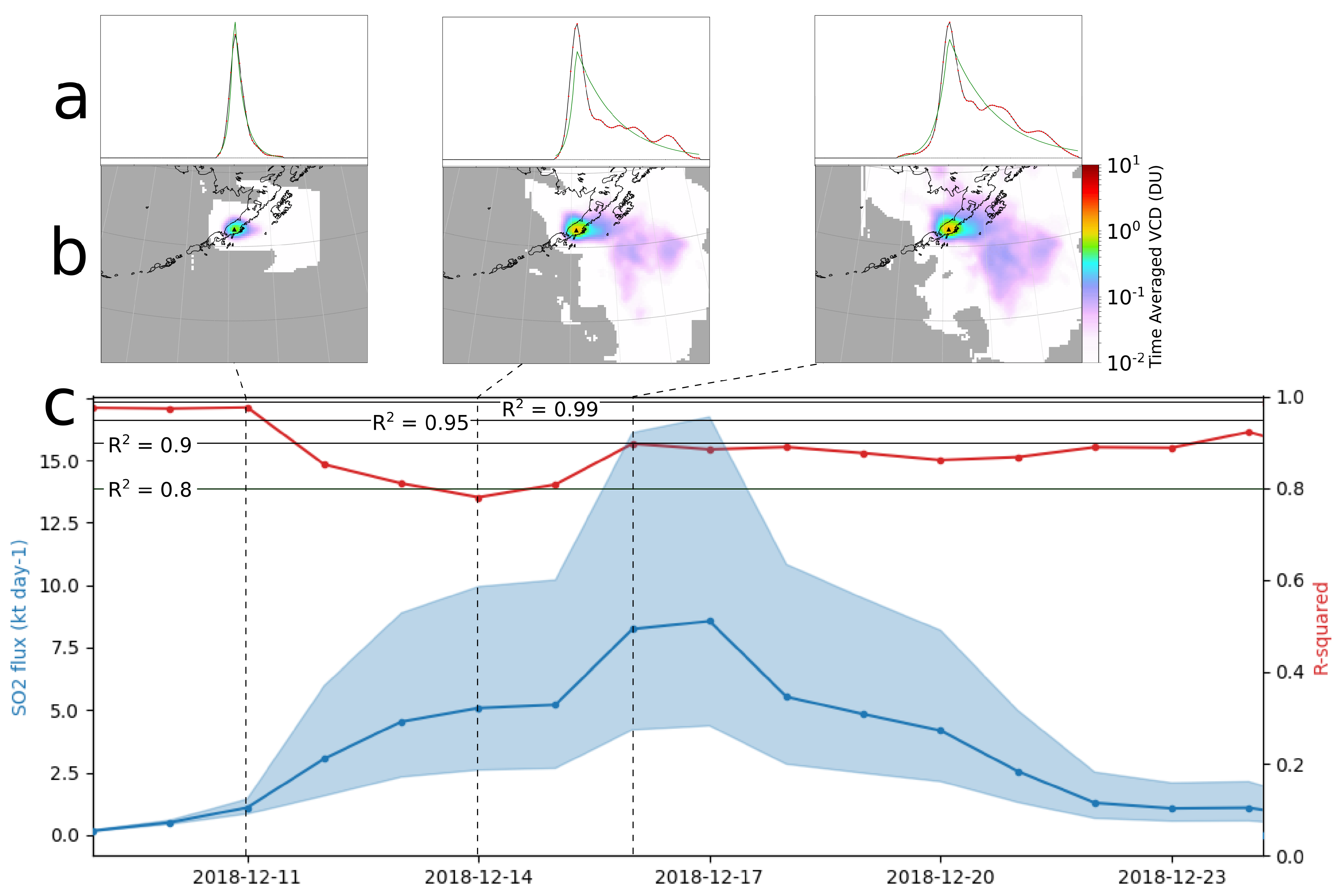
3.2. Time Series of 10-Day Running Averages
4. Discussion
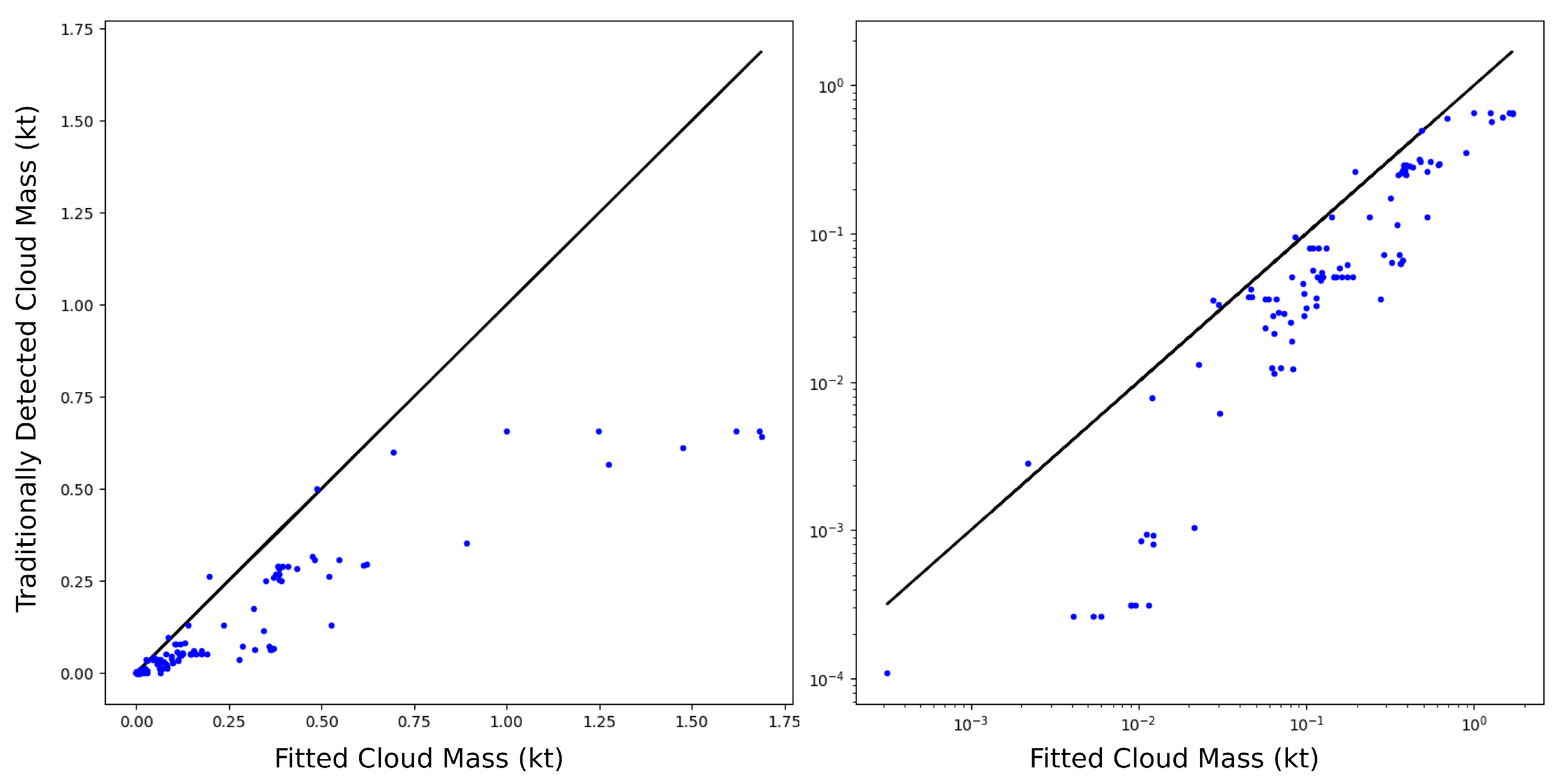
4.1. Estimated Cloud Mass
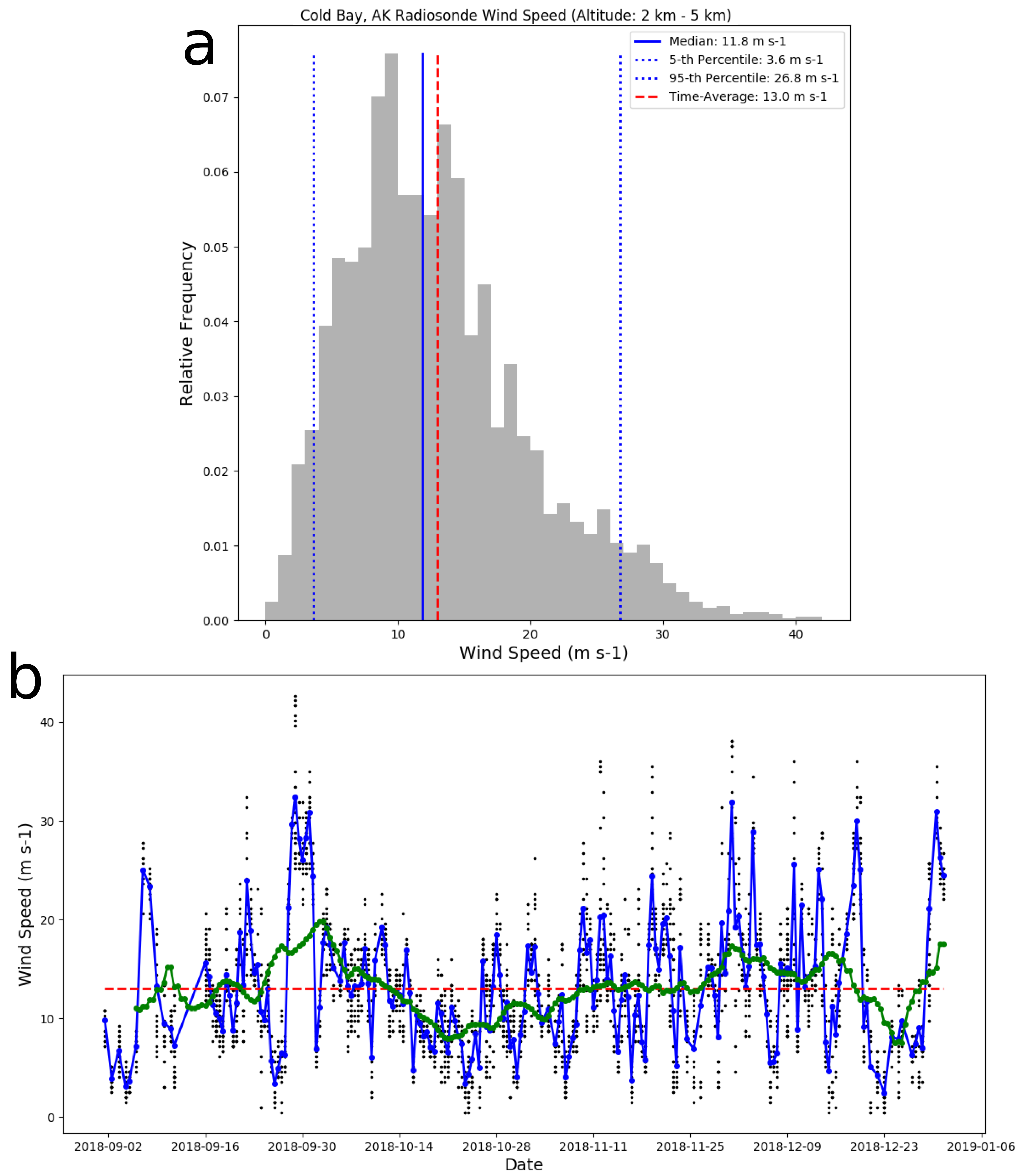
4.2. Wind Speed, Goodness of Fit, and Anomalous Flux
4.3. Comparison of Single-Sensor Results
4.4. Comparison with Other Estimates of Degassing and Lifetime
5. Conclusions
- (i)
- Time-averaged volcanic flux and lifetime estimation techniques can be successfully modified to accept newly-available hyperspectral IR data, enabling robust gas monitoring at high-latitude volcanoes in all illumination conditions, including low- or no sunlight conditions. This has the potential to fill a key observational gap in traditionally UV-based monitoring.
- (ii)
- Our technique detects weak signals of plumes in gridded data using computer vision and object-detection techniques used widely in medical and seismic tomography. It then amplifies these weak plume signals by attempting to reconstruct the wind fields dispersing them and time-averaging the results. This amplification enables the recovery of approximately twice as much mass as would be estimated by considering the cloud mass in individual plume snapshots alone. A new line-density fitting function derived directly from the time-averaged point-source dispersion physics is used to generate a well-fitting model of the time-averaged plumes.
- (iii)
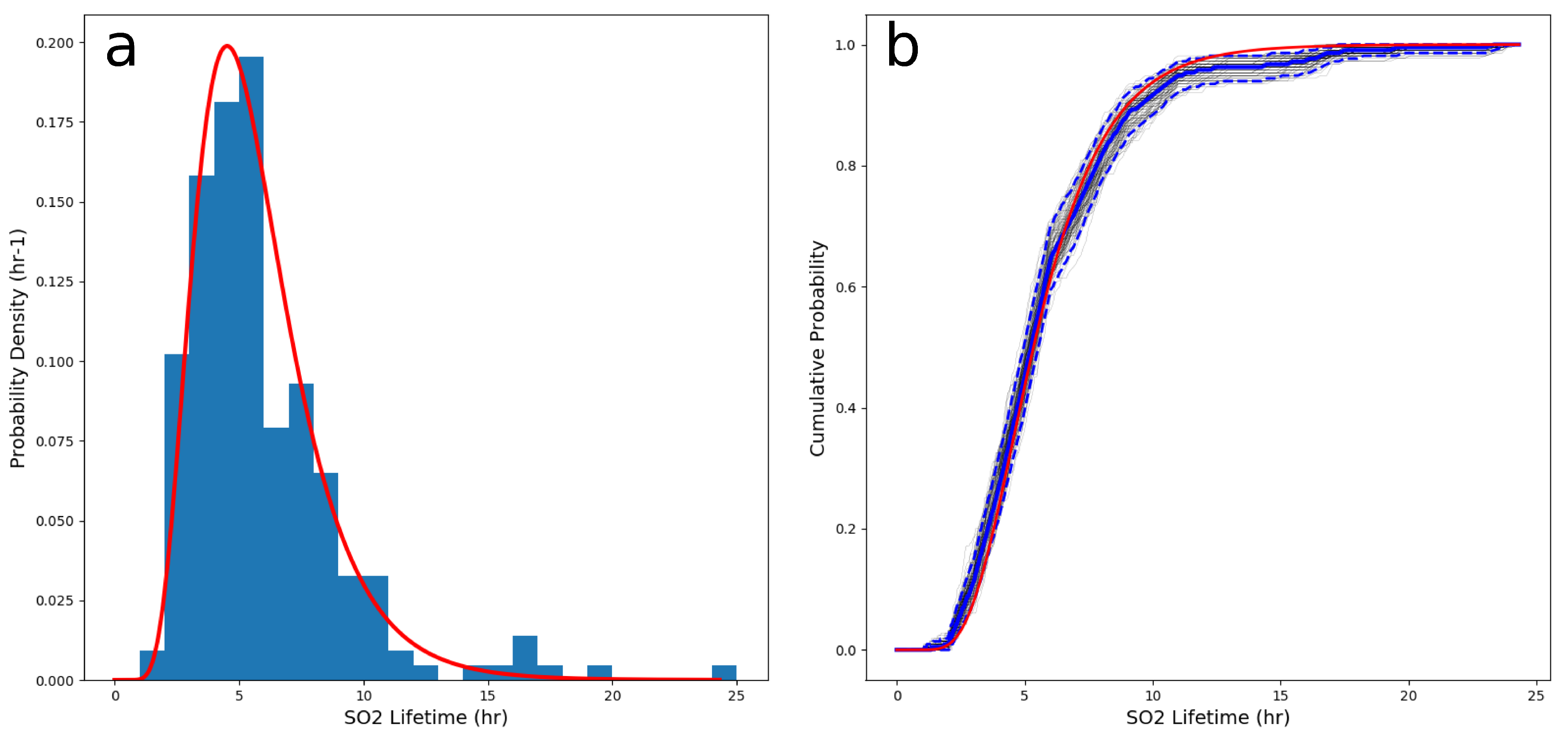
- The decay rate and lifetime (reciprocal decay rate) are estimated independently of the fitting and are shown to have lognormal statistics which agree remarkably well with previous published estimates of the distribution of lifetimes from large sources globally.
- (iv)
- This technique can be subdivided, allowing for short-timescale averages and the generation of flux monitoring time series, which could prove useful to observatories. The technique in general and the time series capability in particular have been demonstrated for the September–December 2018 period of unrest and eruption at Veniaminof volcano, Alaska, highlighting the importance of new algorithms designed for detection and characterization of in the infrared.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Plume Source Estimation for Rotation and Source-Reconstruction Scheme
Appendix B. Exponential Smoothing Filter
Appendix C. Appropriateness of Implementing a Steady State Solution
Appendix D. Aspect Ratio Estimation
Appendix E. Estimation of Decay Rate Statistics
Decay Rate Correction
- Step 1:
- Valid decay samples are computed asfor all .
- Step 2:
- The mass detection limit is estimated for a sequence of plume observations aswith the angle brackets referring to a sample mean over all pixels meeting the criteria.
- Step 3:
- The number of terms needed for each correction is estimated as
- Step 4:
- Each correction is performed:
References
- Beirle, S.; Hörmann, C.; Penning de Vries, M.; Dörner, S.; Kern, C.; Wagner, T. Estimating the volcanic emission rate and atmospheric lifetime of SO2 from space: A case study for Kīlauea volcano, Hawai‘i. Atmos. Chem. Phys. 2014, 14, 8309–8322. [Google Scholar] [CrossRef]
- Fioletov, V.E.; McLinden, C.A.; Krotkov, N.; Li, C. Lifetimes and emissions of SO2 from point sources estimated from OMI. Geophys. Res. Lett. 2015, 42, 1969–1976. [Google Scholar] [CrossRef]
- Fioletov, V.E.; McLinden, C.A.; Krotkov, N.; Li, C.; Joiner, J.; Theys, N.; Carn, S.; Moran, M.D. A global catalogue of large SO2 sources and emissions derived from the Ozone Monitoring Instrument. Atmos. Chem. Phys. 2016, 16, 11497–11519. [Google Scholar] [CrossRef]
- McLinden, C.A.; Fioletov, V.; Shephard, M.W.; Krotkov, N.; Li, C.; Martin, R.V.; Moran, M.D.; Joiner, J. Space-based detection of missing sulfur dioxide sources of global air pollution. Nat. Geosci. 2016, 9, 496–500. [Google Scholar] [CrossRef]
- Carn, S.A.; Fioletov, V.E.; McLinden, C.A.; Li, C.; Krotkov, N.A. A decade of global volcanic SO2 emissions measured from space. Sci. Rep. 2017, 7, 44095. [Google Scholar] [CrossRef]
- Hyman, D.M.; Pavolonis, M.J. Probabilistic retrieval of volcanic SO2 layer height and partial column density using the Cross-track Infrared Sounder (CrIS). Atmos. Meas. Tech. 2020, 13, 5891–5921. [Google Scholar] [CrossRef]
- Pavolonis, M.J.; Heidinger, A.K.; Sieglaff, J. Automated retrievals of volcanic ash and dust cloud properties from upwelling infrared measurements. J. Geophys. Res. Atmos. 2013, 118, 1436–1458. [Google Scholar] [CrossRef]
- Pavolonis, M.J.; Sieglaff, J.; Cintineo, J. Spectrally Enhanced Cloud Objects—A generalized framework for automated detection of volcanic ash and dust clouds using passive satellite measurements: 1. Multispectral analysis. J. Geophys. Res. Atmos. 2015, 120, 7813–7841. [Google Scholar] [CrossRef]
- Pavolonis, M.J.; Sieglaff, J.; Cintineo, J. Spectrally Enhanced Cloud Objects—A generalized framework for automated detection of volcanic ash and dust clouds using passive satellite measurements: 2. Cloud object analysis and global application. J. Geophys. Res. Atmos. 2015, 120, 7842–7870. [Google Scholar] [CrossRef]
- Pavolonis, M.J.; Sieglaff, J.; Cintineo, J. Automated Detection of Explosive Volcanic Eruptions Using Satellite-Derived Cloud Vertical Growth Rates. Earth Space Sci. 2018, 5, 903–928. [Google Scholar] [CrossRef]
- Beirle, S.; Boersma, K.F.; Platt, U.; Lawrence, M.G.; Wagner, T. Megacity Emissions and Lifetimes of Nitrogen Oxides Probed from Space. Science 2011, 333, 1737–1739. [Google Scholar] [CrossRef]
- de Foy, B.; Wilkins, J.L.; Lu, Z.; Streets, D.G.; Duncan, B.N. Model evaluation of methods for estimating surface emissions and chemical lifetimes from satellite data. Atmos. Environ. 2014, 98, 66–77. [Google Scholar] [CrossRef]
- Fioletov, V.; McLinden, C.A.; Griffin, D.; Theys, N.; Loyola, D.G.; Hedelt, P.; Krotkov, N.A.; Li, C. Anthropogenic and volcanic point source SO2 emissions derived from TROPOMI on board Sentinel-5 Precursor: First results. Atmos. Chem. Phys. 2020, 20, 5591–5607. [Google Scholar] [CrossRef]
- Han, Y.; Revercomb, H.; Cromp, M.; Gu, D.; Johnson, D.; Mooney, D.; Scott, D.; Strow, L.; Bingham, G.; Borg, L.; et al. Suomi NPP CrIS measurements, sensor data record algorithm, calibration and validation activities, and record data quality. J. Geophys. Res. Atmos. 2013, 118, 12734–12748. [Google Scholar] [CrossRef]
- Wang, L.; Tremblay, D.A.; Han, Y.; Esplin, M.; Hagan, D.E.; Predina, J.; Suwinski, L.; Jin, X.; Chen, Y. Geolocation assessment for CrIS sensor data records. J. Geophys. Res. Atmos. 2013, 118, 12690–12704. [Google Scholar] [CrossRef]
- Clarisse, L.; Coheur, P.F.; Theys, N.; Hurtmans, D.; Clerbaux, C. The 2011 Nabro eruption, a SO2 plume height analysis using IASI measurements. Atmos. Chem. Phys. 2014, 14, 3095–3111. [Google Scholar] [CrossRef]
- Carboni, E.; Grainger, R.; Walker, J.; Dudhia, A.; Siddans, R. A new scheme for sulphur dioxide retrieval from IASI measurements: Application to the Eyjafjallajökull eruption of April and May 2010. Atmos. Chem. Phys. 2012, 12, 11417–11434. [Google Scholar] [CrossRef]
- Pommier, M.; McLinden, C.A.; Deeter, M. Relative changes in CO emissions over megacities based on observations from space. Geophys. Res. Lett. 2013, 40, 3766–3771. [Google Scholar] [CrossRef]
- Radon, J. On the determination of functions from their integral values along certain manifolds. Rep. Proc. R. Saxonian Acad. Sci. Leipzig Math. Phys. Sect. 1917, 69, 262–277. Trans. by Parks, P.C. IEEE Trans. Med. Imag. 1986, 5, 170–176. [Google Scholar] [CrossRef]
- Durrani, T.S.; Bisset, D. The Radon transform and its properties. Geophysics 1984, 49, 1180–1187. [Google Scholar] [CrossRef]
- Shepp, L.A.; Kruskal, J.B. Computerized Tomography: The New Medical X-Ray Technology. Am. Math. Mon. 1978, 85, 420–439. [Google Scholar] [CrossRef]
- Ali, H.; Sritharan, V.; Hariharan, M.; Zaaba, S.K.; Elshaikh, M. Feature extraction using Radon transform and Discrete Wavelet Transform for facial emotion recognition. In Proceedings of the 2016 2nd IEEE International Symposium on Robotics and Manufacturing Automation (ROMA), Ipoh, Malaysia, 25–27 September 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Walker, J.C.; Dudhia, A.; Carboni, E. An effective method for the detection of trace species demonstrated using the MetOp Infrared Atmospheric Sounding Interferometer. Atmos. Meas. Tech. 2011, 4, 1567–1580. [Google Scholar] [CrossRef]
- Basu, M.; Su, M. Image smoothing with exponential functions. Int. J. Pattern Recognit. Artif. Intell. 2001, 15, 735–752. [Google Scholar] [CrossRef]
- Csanady, G.T. Turbulent Diffusion in the Environment; D. Reidel Pub. Co.: Dordrecht, The Netherlands; Boston, MA, USA, 1973. [Google Scholar]
- Fischer, H.B.; List, J.E.; Koh, C.R.; Imberger, J.; Brooks, N.H. Mixing in Inland and Coastal Waters; Academic Press: New York, NY, USA, 1979. [Google Scholar]
- Socolofsky, S.A.; Jirka, G.H. Special Topics in Mixing and Transport Processes in the Environment, 5th ed.; Texas A&M University: College Station, TX, USA, 2005. [Google Scholar]
- Theys, N.; Campion, R.; Clarisse, L.; Brenot, H.; van Gent, J.; Dils, B.; Corradini, S.; Merucci, L.; Coheur, P.F.; Van Roozendael, M.; et al. Volcanic SO2 fluxes derived from satellite data: A survey using OMI, GOME-2, IASI and MODIS. Atmos. Chem. Phys. 2013, 13, 5945–5968. [Google Scholar] [CrossRef]
- Spiess, A.N.; Neumeyer, N. An evaluation of R2 as an inadequate measure for nonlinear models in pharmacological and biochemical research: A Monte Carlo approach. BMC Pharmacol. 2010, 10, 6. [Google Scholar] [CrossRef] [PubMed]
- Katz, D.; Baptista, J.; Azen, S.P.; Pike, M.C. Obtaining Confidence Intervals for the Risk Ratio in Cohort Studies. Biometrics 1978, 34, 469–474. [Google Scholar] [CrossRef]
- Delgado-Granados, H.; Cárdenas González, L.; Piedad Sánchez, N. Sulfur dioxide emissions from Popocatépetl volcano (Mexico): Case study of a high-emission rate, passively degassing erupting volcano. J. Volcanol. Geotherm. Res. 2001, 108, 107–120. [Google Scholar] [CrossRef]
- Tamburello, G.; Aiuppa, A.; McGonigle, A.J.S.; Allard, P.; Cannata, A.; Giudice, G.; Kantzas, E.P.; Pering, T.D. Periodic volcanic degassing behavior: The Mount Etna example. Geophys. Res. Lett. 2013, 40, 4818–4822. [Google Scholar] [CrossRef]
- Girona, T.; Costa, F.; Taisne, B.; Aggangan, B.; Ildefonso, S. Fractal degassing from Erebus and Mayon volcanoes revealed by a new method to monitor H2O emission cycles. J. Geophys. Res. Solid Earth 2015, 120, 2988–3002. [Google Scholar] [CrossRef]
- Hyman, D.M.; Bursik, M.I.; Legorreta Paulń, G. Time Dependence of Passive Degassing at Volcán Popocatépetl, Mexico, From Infrared Measurements: Implications for Gas Pressure Distribution and Lava Dome Stability. J. Geophys. Res. Solid Earth 2018, 123, 8527–8547. [Google Scholar] [CrossRef]
- Campion, R.; Delgado-Granados, H.; Legrand, D.; Taquet, N.; Boulesteix, T.; Pedraza-Espitía, S.; Lecocq, T. Breathing and Coughing: The Extraordinarily High Degassing of Popocatépetl Volcano Investigated with an SO2 Camera. Front. Earth Sci. 2018, 6, 163. [Google Scholar] [CrossRef]
- Pering, T.D.; Ilanko, T.; Liu, E.J. Periodicity in Volcanic Gas Plumes: A Review and Analysis. Geosciences 2019, 9, 394. [Google Scholar] [CrossRef]
- Global Volcanism Program. Report on Veniaminof; Venzke, E., Ed.; Bulletin of the Global Volcanism Network, 44:1; Smithsonian Institution: Washington, DC, USA, 2019. [Google Scholar]
- Fioletov, V.; McLinden, C.; Krotkov, N.; Li, C.; Leonard, P.; Joiner, J.; Carn, S. Multi-Satellite Air Quality Sulfur Dioxide (SO2) Database Long-Term L4 Global V1; Leonard, P., Ed.; Goddard Earth Science Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2019. [CrossRef]
- Revercomb, H.; Strow, L. Suomi NPP CrIS Level-1B Full Spectral Resolution V2; Goddard Earth Science Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2018. [CrossRef]
- Revercomb, H.; Strow, L. JPSS-1 CrIS Level-1B Full Spectral Resolution V2; Goddard Earth Science Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2018. [CrossRef]
- Corless, R.M.; Gonnet, G.H.; Hare, D.E.G.; Jeffrey, D.J.; Knuth, D.E. On the Lambert W function. Adv. Comput. Math. 1996, 5, 329–359. [Google Scholar] [CrossRef]
- Berezhkovskii, A.M.; Sample, C.; Shvartsman, S.Y. How Long Does It Take to Establish a Morphogen Gradient? Biophys. J. 2010, 99, L59–L61. [Google Scholar] [CrossRef] [PubMed]
- Berezhkovskii, A.M.; Sample, C.; Shvartsman, S.Y. Formation of morphogen gradients: Local accumulation time. Phys. Rev. E 2011, 83, 051906. [Google Scholar] [CrossRef]
- Ellery, A.J.; Simpson, M.J.; McCue, S.W.; Baker, R.E. Critical time scales for advection-diffusion-reaction processes. Phys. Rev. E 2012, 85, 041135. [Google Scholar] [CrossRef] [PubMed]
- McNabb, A.; Wake, G.C. Heat Conduction and Finite Measures for Transition Times between Steady States. IMA J. Appl. Math. 1991, 47, 193–206. [Google Scholar] [CrossRef]
- Ng, E.W.; Geller, M. A table of integrals of the Error functions. J. Res. Natl. Bureau Stand. Sec. B Math. Sci. 1969, 73B, 1–9. [Google Scholar] [CrossRef]
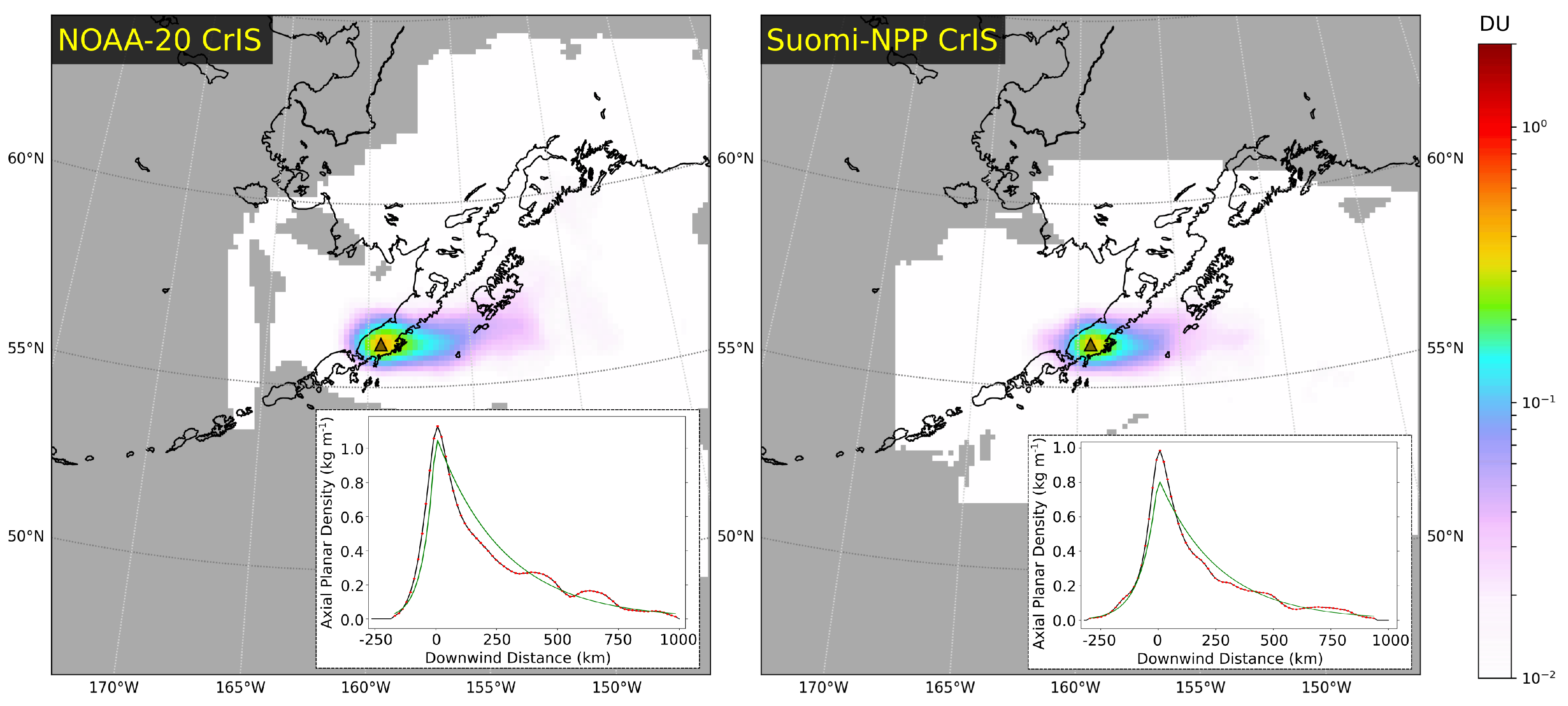
| Parameter | Units | Median | [5th, 95th] Percentiles |
|---|---|---|---|
| Flux | kt day | 1.5 | [0.8, 2.9] |
| wind speed | m s | 12.0 | [6.1, 23.4] |
| Eddy Diffusivity (downwind) | m s | 8.2 × 10 | [4.2,16.0] × 10 |
| Eddy Diffusivity (crosswind) | m s | 5.5 × 10 | [2.8, 10.8] × 10 |
| lifetime | h | 5.3 | [2.7, 10.4] |
| Plume Peclet Number | - | 3.4 | [3.2, 3.5] |
| Parameter | Units | Percentiles: Median [5th, 95th] | |
|---|---|---|---|
| NOAA-20 Only | SNPP Only | ||
| Flux | kt day | 1.6 [0.8, 3.2] | 1.0 [0.5, 2.0] |
| wind speed | m s | 12.5 [6.4, 24.4] | 8.1 [4.1, 15.8] |
| Eddy Diffusivity (downwind) | m s | 7.2 [3.7, 14.0] × 10 | 7.7 [4.0, 15.2] ×10 |
| Eddy Diffusivity (crosswind) | m s | 2.6 [1.4, 5.2] × 10 | 2.2 [1.1, 4.3] ×10 |
| lifetime | h | 5.1 [2.6, 10.0] | 6.6 [3.4, 12.9] |
| Plume Peclet Number | - | 4.0 [3.8, 4.2] | 2.0 [1.9, 2.1] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hyman, D.M.R.; Pavolonis, M.J.; Sieglaff, J. A Novel Approach to Estimating Time-Averaged Volcanic SO2 Fluxes from Infrared Satellite Measurements. Remote Sens. 2021, 13, 966. https://doi.org/10.3390/rs13050966
Hyman DMR, Pavolonis MJ, Sieglaff J. A Novel Approach to Estimating Time-Averaged Volcanic SO2 Fluxes from Infrared Satellite Measurements. Remote Sensing. 2021; 13(5):966. https://doi.org/10.3390/rs13050966
Chicago/Turabian StyleHyman, David M.R., Michael J. Pavolonis, and Justin Sieglaff. 2021. "A Novel Approach to Estimating Time-Averaged Volcanic SO2 Fluxes from Infrared Satellite Measurements" Remote Sensing 13, no. 5: 966. https://doi.org/10.3390/rs13050966
APA StyleHyman, D. M. R., Pavolonis, M. J., & Sieglaff, J. (2021). A Novel Approach to Estimating Time-Averaged Volcanic SO2 Fluxes from Infrared Satellite Measurements. Remote Sensing, 13(5), 966. https://doi.org/10.3390/rs13050966