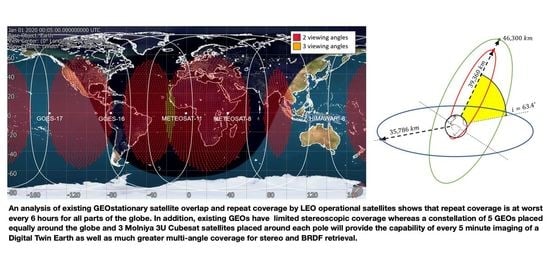
Contemporaneous Monitoring of the Whole Dynamic Earth System from Space, Part I: System Simulation Study Using GEO and Molniya Orbits
Abstract
1. Introduction
2. Materials and Methods
2.1. Simulation Structure
2.2. Camera Design
2.2.1. Nominal Constellation Architecture and Camera Parameter Definition
2.2.2. Dynamic Range Requirements
3. Results
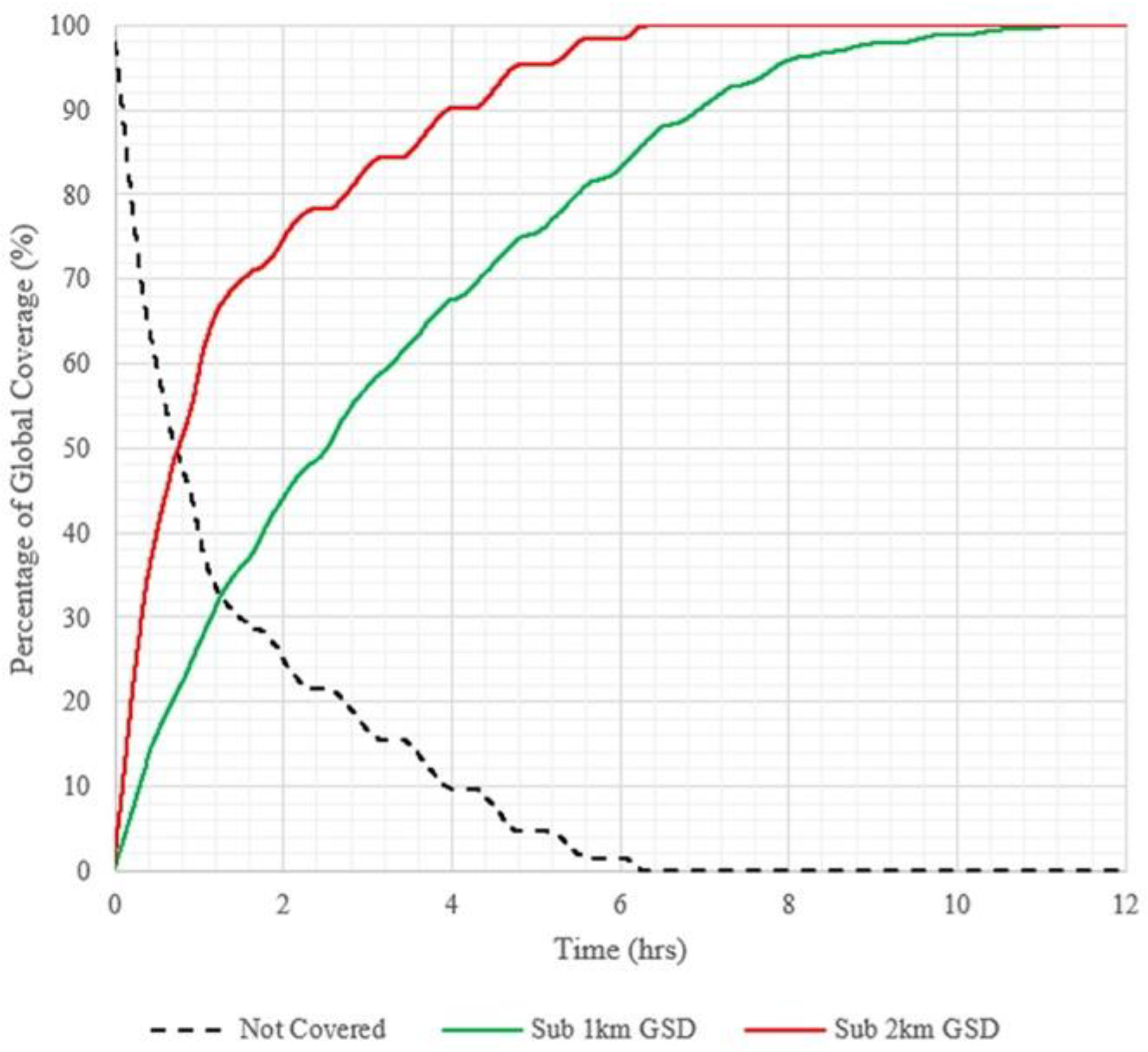
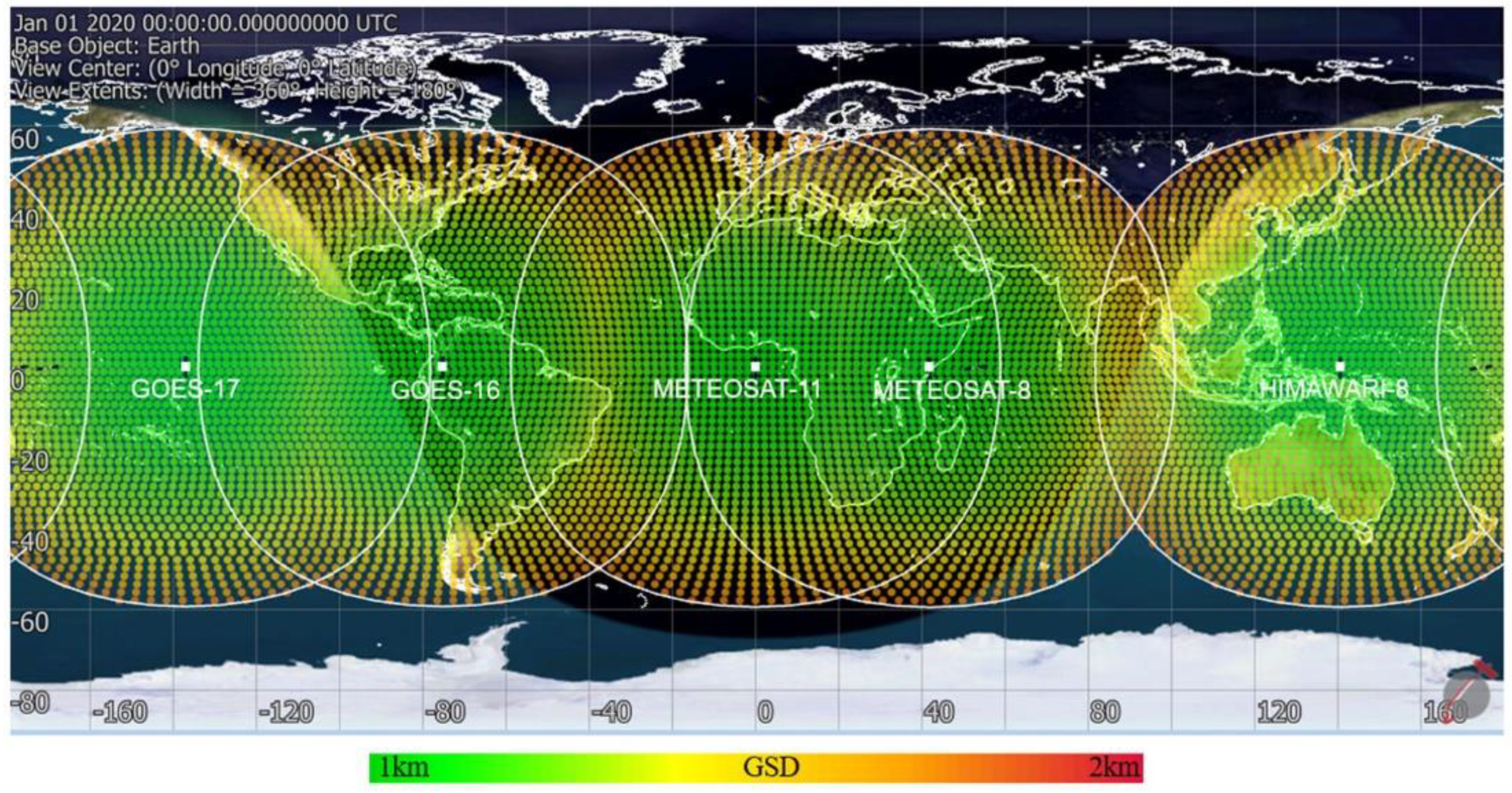
3.1. Existing GEO and LEO Earth Observers
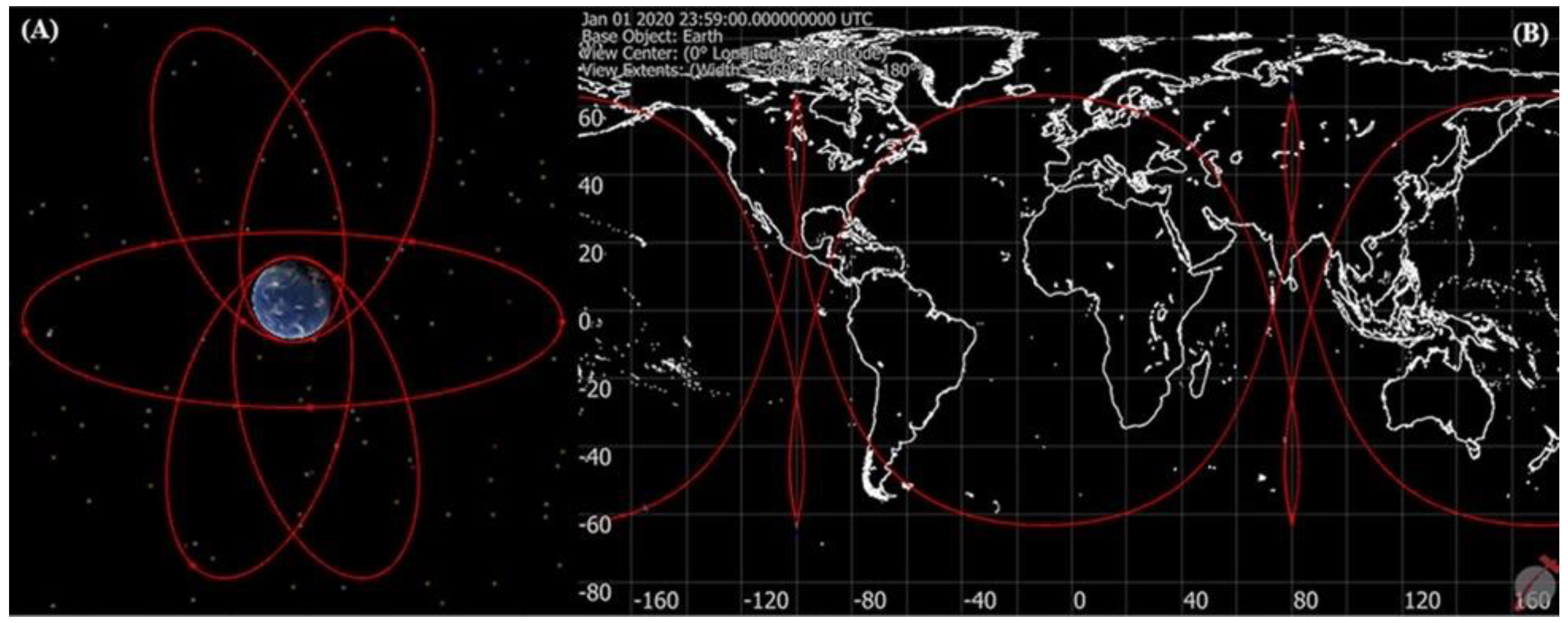
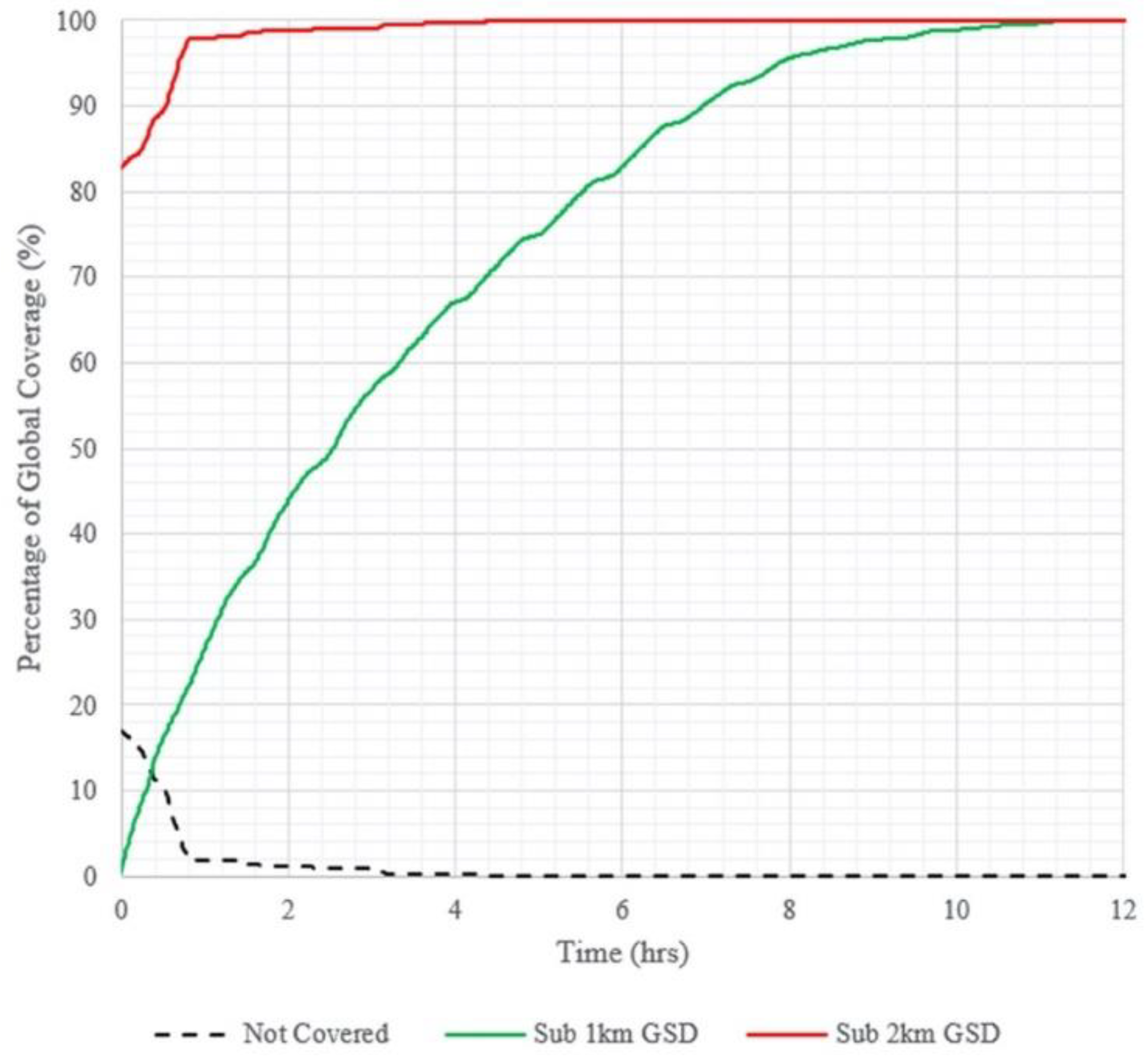
3.2. GEO and Molniya Constellation
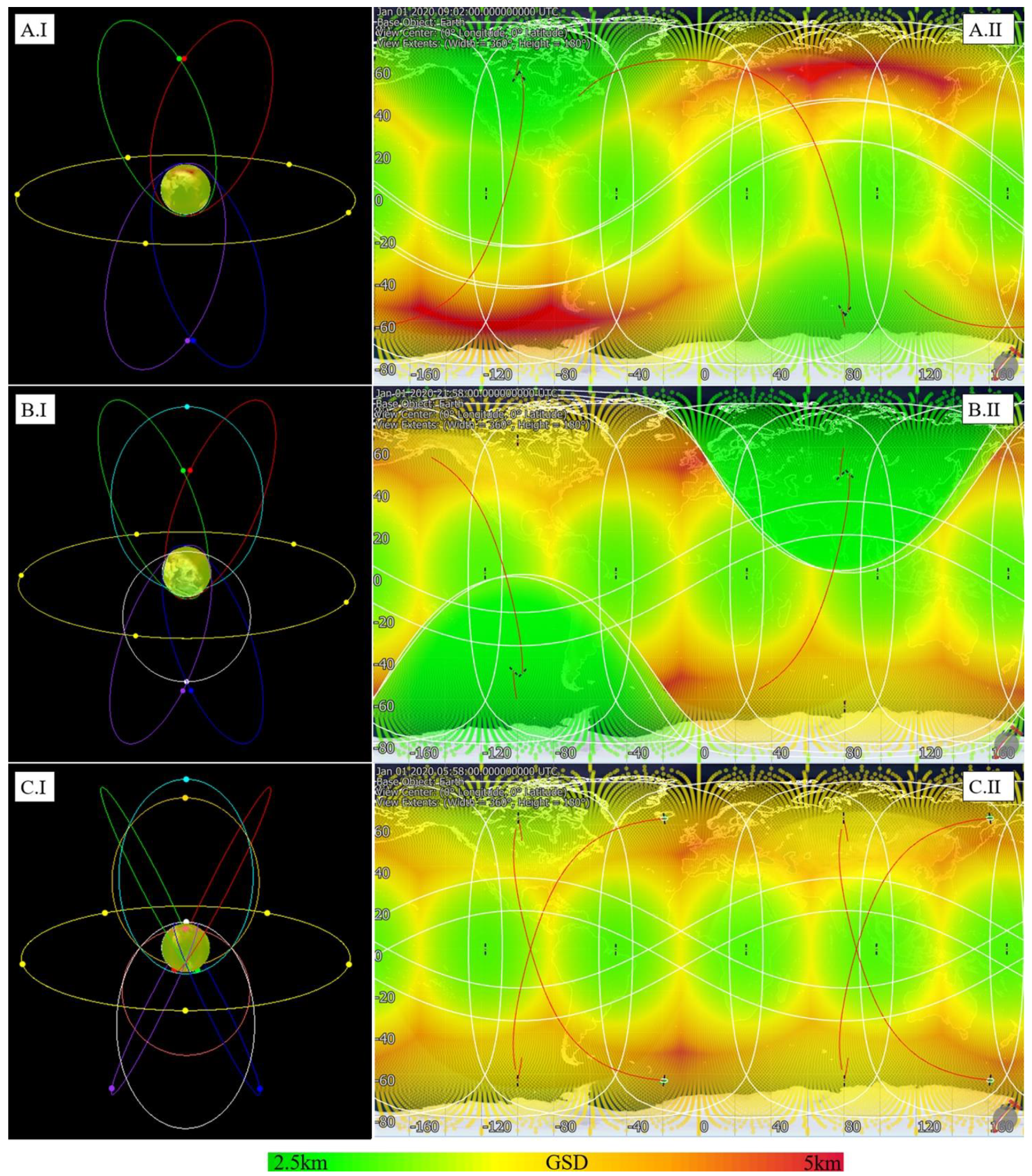
3.2.1. Four Molniya
3.2.2. Six Molniya
3.2.3. Eight Molniya
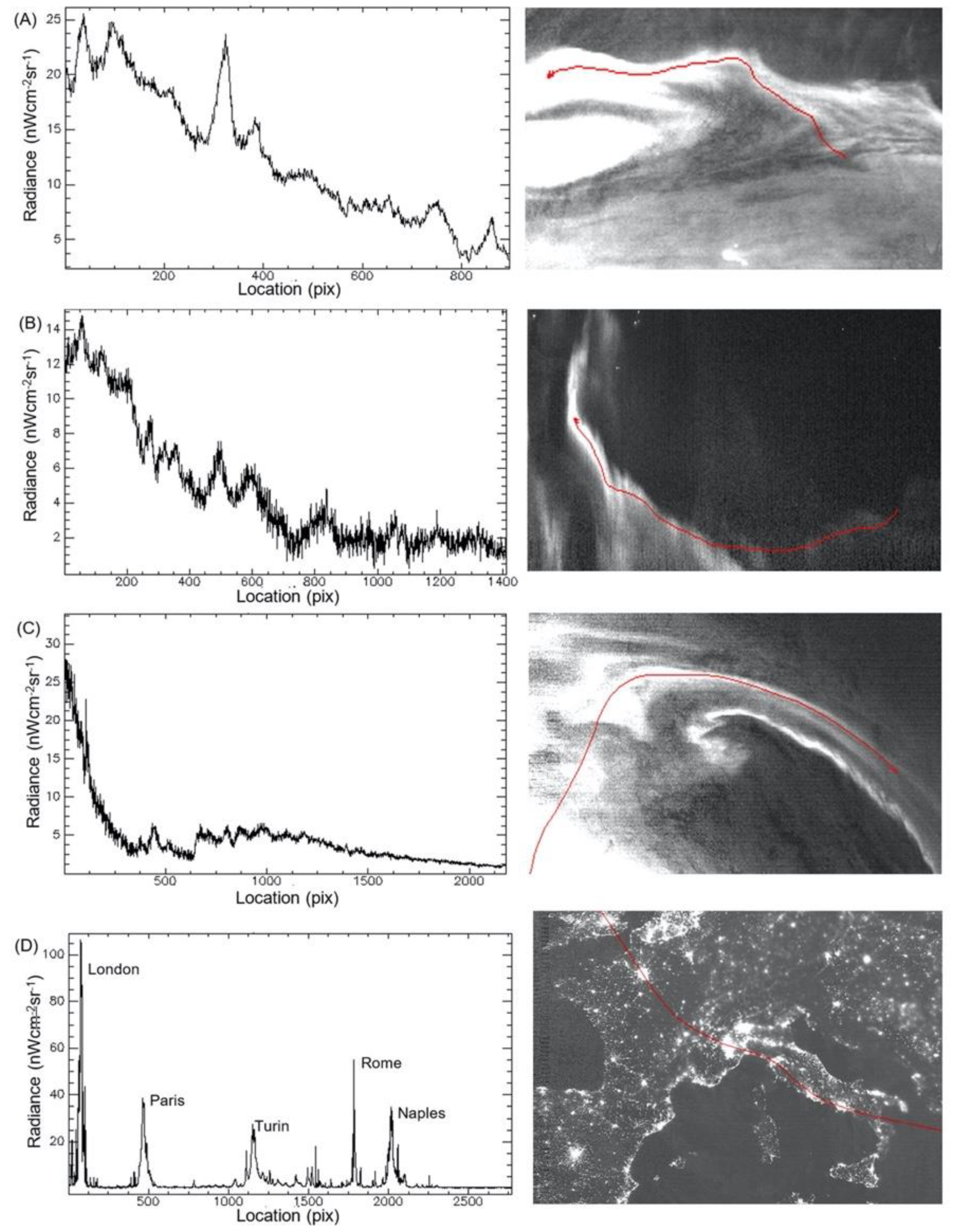
3.3. BRDF Quality
3.4. GEO Stereoscopic Potential Quality
3.5. Representational Renderings
3.6. Radiation Protection Consideration
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cosgrove, D. Contested Global Visions: One-World, Whole-Earth, and the Apollo Space Photographs. Ann. Assoc. Am. Geogr. 1994, 84, 270–294. [Google Scholar] [CrossRef]
- Available online: https://www.csiro.au/en/Research/Astronomy/Earth-observation/ASTER-map (accessed on 8 February 2021).
- Burke, M.; Lobell, D.B. Satellite-based assessment of yield variation and its determinants in smallholder African systems. Proc. Natl. Acad. Sci. USA 2017, 114, 2189–2194. [Google Scholar] [CrossRef]
- Available online: https://www.asc-csa.gc.ca/eng/satellites/everyday-lives/monitoring-and-protecting-our-ecosystems-from-space.asp (accessed on 8 February 2021).
- Available online: https://www.carbonbrief.org/interactive-satellites-used-monitor-climate-change (accessed on 8 February 2021).
- Available online: https://earthengine.google.com/timelapse/ (accessed on 8 February 2021).
- Chen, J.; Wang, Z.; Tam, C.-Y.; Lau, N.-C.; Lau, D.-S.D.; Mok, H.-Y. impacts of climate change on tropical cyclones and induced storm surges in the pearl River Delta region using pseudo-global- warming method. Sci. Rep. 2020, 10, 140. [Google Scholar] [CrossRef]
- Chadha, R.K.; Latha, G.; Yeh, H.; Peterson, C.; Katada, T. The tsunami of the great Sumatra earthquake of M 9.0 on 26 December 2004—Impact on the east coast of India. Curr. Sci. 2005, 88, 1297–1301. [Google Scholar]
- Details of the Himawari Imaging Systems (n.d.). Available online: https://www.data.jma.go.jp/mscweb/en/himawari89/space_segment/spsg_ahi.html (accessed on 3 January 2021).
- Available online: https://www.noaa.gov/organization/information-technology/list-of-big-data-program-datasets#NESDIS (accessed on 15 February 2021).
- GEO-KOMPSAT-2 (Geostationary—Korea Multi-Purpose Satellite-2) Program/Cheollian-2/GK-2 (n.d.). Available online: https://directory.eoportal.org/web/eoportal/satellite-missions/g/geo-kompsat-2 (accessed on 3 January 2021).
- FY-4 (FengYun-4) Geostationary Meteorological Satellite Series (n.d.). Available online: https://directory.eoportal.org/web/eoportal/satellite-missions/f/fy-4 (accessed on 3 January 2021).
- FY-3 (FengYun-3) 2nd Generation Polar Orbiting Meteorological Satellite Series (n.d.). Available online: https://directory.eoportal.org/web/eoportal/satellite-missions/content/-/article/fy-3 (accessed on 3 January 2021).
- Gallaher, D.; Campbell, G.G.; Meier, W.; Moses, J.; Wingo, D. The process of bringing dark data to light: The rescue of the early Nimbus satellite data. GeoResJ 2015, 6, 124–134. [Google Scholar] [CrossRef]
- Croft, T. Burning waste gas in oil fields. Nature 1973, 245, 375–376. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Baugh, K.E.; Kihn, E.A.; Kroehl, H.W.; Davis, E.R. Mapping city lights with nighttime data from the DMSP Operational Linescan System. Photogramm. Eng. Remote Sens. 1997, 63, 727–734. [Google Scholar]
- Running, S.W.; Justice, C.O.; Salomonson, V.V.; Hall, D.K.; Barker, J.L.; Kaufmann, Y.J.; Strahler, A.H.; Huete, A.R.; Muller, J.-P.; Vanderbilt, V.; et al. Terrestrial remote-sensing science and algorithms planned for EOS MODIS. Int. J. Remote Sens. 1994, 15, 3587–3620. [Google Scholar] [CrossRef]
- Levin, N.; Kyba, C.C.M.; Zhang, Q.; Sánchez de Miguel, A.; Roman, M.O.; Li, X.; Portnov, B.A.; Molthan, A.L.; Jechow, A.; Miller, S.D.; et al. Remote sensing of night lights: A review and an outlook for the future. Remote Sens. Environ. 2020, 237, 111443. [Google Scholar] [CrossRef]
- Lee, T.; Miller, S.; Turk, F.; Schueler, C.; Julian, R.; Deyo, S.; Dills, P.; Wang, S. The NPOESS VIIRS Day/Night Visible Sensor. Bull. Am. Meteorol. Soc. 2006, 191–199. [Google Scholar] [CrossRef]
- Roman, M.O.; Wang, Z.; Sun, Q.; Kalb, V.; Miller, S.D.; Molthan, A.; Schultz, L.; Bell, J.; Stokes, E.C.; Pandey, B.; et al. NASA’s Black Marble nighttime lights product suite. Remote Sens. Environ. 2018, 210, 113–143. [Google Scholar] [CrossRef]
- Diner, D.J.; Bruegge, C.J.; Martonchik, J.V.; Ackerman, T.P.; Davies, R.; Gerstl, S.A.; Gordon, H.R.; Sellers, P.J.; Clark, J.; Daniels, J.A.; et al. MISR: A multiangle imaging spectroradiometer for geophysical and climatological research from Eos. IEEE Trans. Geosci. Remote Sens. 1989, 27, 200–214. [Google Scholar] [CrossRef]
- Muller, J.-P.; Mandanayake, A.; Moroney, C.; Davies, R.; Diner, D.J.; Paradise, S. MISR stereoscopic image matchers: Techniques and results. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1547–1559. [Google Scholar] [CrossRef]
- Wanner, W.; Strahler, A.H.; Hu, B.; Lewis, P.; Muller, J.-P.; Li, X.; Schaaf, C.L.B.; Barnsley, M.J. Global retrieval of bidirectional reflectance and albedo over land from EOS MODIS and MISR data: Theory and algorithm. J. Geophys. Res. 1997, 102, 17143–17161. [Google Scholar] [CrossRef]
- MODIS Rapid Response Products. Available online: https://earthdata.nasa.gov/earth-observation-data/near-real-time/rapid-response (accessed on 4 January 2021).
- Holdaway, D.; Yang, Y. Study of the Effect of Temporal Sampling Frequency on DSCOVR Observations Using the GEOS-5 Nature Run Results (Part I): Earth’s Radiation Budget. Remote Sens. 2016, 8, 98. [Google Scholar] [CrossRef]
- Adler, R.F.; Fenn, D.D. Thunderstorm Vertical Velocities Estimated from Satellite Data. J. Atmos. Sci. 1979, 36, 1747–1754. [Google Scholar] [CrossRef]
- Bedka, K.M.; Wang, C.; Rogers, R.; Carey, L.D.; Feltz, W.; Kanak, J. Examining Deep Convective Cloud Evolution Using Total Lightning, WSR-88D, and GOES-14 Super Rapid Scan Datasets. Weather Forecast. 2015, 30, 571–590. [Google Scholar] [CrossRef]
- Fantino, E.; Flores, R.M.; Di Carlo, M.; Di Salvo, A.; Cabot, E. Geosynchronous inclined orbits for high-latitude communications. Acta Astronaut. 2017, 140, 570–582. [Google Scholar] [CrossRef]
- Mathilde, M. The Molniya Orbit and Satellites. 2020. Available online: https://www.spacelegalissues.com/the-molniya-orbit-and-satellites/ (accessed on 6 February 2021).
- FreeFlyer, A.I. Solutions. Available online: https://ai-solutions.com/freeflyer-astrodynamic-software/ (accessed on 3 January 2021).
- Barnsley, M.J.; Strahler, A.H.; Morris, K.P.; Muller, J.-P. Sampling the surface bidirectional reflectance distribution function (BRDF): 1. Evaluation of current and future satellite sensors. Remote Sens. Rev. 1994, 8, 271–311. [Google Scholar] [CrossRef]
- Song, W.; Knyazikhin, Y.; Wen, G.; Marshak, A.; Mõttus, M.; Yan, K.; Yang, B.; Xu, B.; Park, T.; Chen, C.; et al. Implications of Whole-Disc DSCOVR EPIC Spectral Observations for Estimating Earth’s Spectral Reflectivity Based on Low-Earth-Orbiting and Geostationary Observations. Remote Sens. 2018, 10, 1594. [Google Scholar] [CrossRef]
- Space Environment Information System (SPENVIS), ESA. Available online: https://www.spenvis.oma.be/ (accessed on 31 August 2020).
- Sawyer, D.M.; Vette, J.I. AP-8 Trapped Proton Model Environment for Solar Maximum and Minimum, NSSDC/WDC-A-R&S. 1976. Available online: https://ntrs.nasa.gov/citations/19770012039 (accessed on 6 February 2021).
- Vette, J.I. The AE-8 Trapped Electron Model Environment, NSSDC/WDC-A-R&S 91-24. 1991. Available online: https://ntrs.nasa.gov/citations/19920014985 (accessed on 6 February 2021).
- Jiggens, P.; Varotsou, A.; Truscott, P.; Heynderickx, D.; Lei, F.; Evans, H.; Daly, E. The Solar Accumulated and Peak Proton and Heavy Ion Radiation Environment (SAPPHIRE) Model. IEEE Trans. Nuclear Sci. 2018, 65, 698–711. [Google Scholar] [CrossRef]
- Dyer, J.; Sinclair, D. Radiation Effects and COTS Parts in SmallSats. In Proceedings of the 27th Annual AIAA/USU Conference on Small Satellites, Logan, UT, USA, 10–15 August 2013. [Google Scholar]
- Trishchenko, A.; Garand, L. Spatial and Temporal Sampling of Polar Regions from Two-Satellite System on Molniya Orbit. J. Atmos. Ocean. Technol. 2011, 28. [Google Scholar] [CrossRef]
- Carr, J.L.; Wu, D.L.; Daniels, J.; Friberg, M.D.; Bresky, W.; Madan, H. GEO-GEO Stereo-Tracking of Atmospheric Motion. Remote Sens. 2020, 12, 3779. [Google Scholar] [CrossRef]
- Carr, J.L.; Wu, D.; A Kelly, M.; Gong, J. MISR-GOES 3D Winds: Implications for Future LEO-GEO and LEO-LEO Winds. Remote Sens. 2018, 10, 1885. [Google Scholar] [CrossRef]
- Carr, J.L.; Wu, D.L.; Wolfe, R.E.; Madani, H.; Lin, G.G.; Tan, B. Joint 3D-Wind Retrievals with Stereoscopic Views from MODIS and GOES. Remote Sens. 2019, 11, 2100. [Google Scholar] [CrossRef]
- MT9D131, Data Sheet. Available online: https://www.onsemi.com/pub/Collateral/MT9D131-D.PDF (accessed on 2 January 2021).
- Pack, D.; Hardy, B. CubeSat Nighttime Lights. In Proceedings of the 30th Annual AIAA/USU Conference on Small Satellites, Logan, UT, USA, 6–11 August 2016. [Google Scholar]
- IDS UI-3590CP, Data Sheet. Available online: https://en.ids-imaging.com/store/ui-3590cp-rev-2.html (accessed on 2 January 2021).
- Lt1245R, Data Sheet. Available online: https://www.lumenera.com/media/wysiwyg/documents/datasheets/industrial/Lt1245-USB3-Datasheet.pdf (accessed on 2 January 2021).
- KA1-11002, Data Sheet. Available online: https://www.onsemi.com/pub/Collateral/KAI-11002-D.PDF (accessed on 2 January 2021).
- MT9F002, Data Sheet. Available online: https://www.onsemi.com/pub/Collateral/MT9F002-D.PDF (accessed on 2 January 2021).
- KAF-16801, Data Sheet. Available online: https://www.onsemi.com/pub/Collateral/KAF-16801-D.PDF (accessed on 2 January 2021).
- KAF-16070, Data Sheet. Available online: https://www.onsemi.com/pub/Collateral/KAI-16070-D.PDF (accessed on 2 January 2021).
- Tao, Y.; Muller, J.-P. Repeat Multiview panchromatic super-resolution restoration using the UCL MAGiGAN system. Remote Sens. 2018. [Google Scholar] [CrossRef]
- ENVI, Harris Geospatial. Available online: https://www.harrisgeospatial.com/SoftwareTechnology/ENVI (accessed on 3 January 2021).
- Seaman, C.; Miller, S. VIIRS Captures Aurora Motions. Bull. Am. Meteorol. Soc. 2013, 1491–1493. [Google Scholar] [CrossRef]
- Cheng, H.; Choubey, B.; Collins, S. A Wide Dynamic Range CMOS Image Sensor with an Adjustable Logarithmic Response. Sens. Cameras Syst. Ind. Sci. Appl. IX 2008, 6816, 681602. [Google Scholar] [CrossRef]
- HAC-HF3805G, Data Sheet. Available online: https://www.dahuasecurity.com/products/productDetail/17711 (accessed on 2 January 2021).
- Gonzalez, L.; Yamamoto, H. The Wall: The Earth in True Natural Color from Real-Time Geostationary Satellite Imagery. Remote Sens. 2020, 12, 2375. [Google Scholar] [CrossRef]
- Terra and Aqua Moderate Resolution Imaging Spectroradiometer (MODIS). 2020. Available online: https://ladsweb.modaps.eosdis.nasa.gov/missions-and-measurements/modis/ (accessed on 2 January 2021).
- Suomi National Polar-Orbiting Partnership (SNPP) Visible Infrared Imaging Suite (VIIRS) Aerosol Products User’s Guide. Version 2.0.1. 2013. Available online: https://www.star.nesdis.noaa.gov/smcd/emb/viirs_aerosol/documents/Aerosol_Product_Users_Guide_V2.0.1.pdf (accessed on 2 January 2021).
- Sentinel 3 OLCI Coverage. Available online: https://sentinel.esa.int/web/sentinel/user-guides/sentinel-3-olci/coverage (accessed on 15 February 2021).
- ESA—About AVHRR/3 (n.d.). Available online: http://www.esa.int/Applications/Observing_the_Earth/Meteorological_missions/MetOp/About_AVHRR_3 (accessed on 2 January 2021).
- NORAD Two-Line Element Sets Current Data, AGI. 2020. Available online: https://www.celestrak.com/NORAD/elements/ (accessed on 3 January 2021).
- Visible Earth: A Catalog of NASA Images and Animations of Our Home Planet. NASA. Available online: https://visibleearth.nasa.gov/collection/1484/blue-marble (accessed on 3 January 2021).
- Cloud Overlay. NASA. Available online: https://visibleearth.nasa.gov/images/57747/bluemarble-clouds (accessed on 3 January 2021).
- Night Lights Image. NASA. Available online: https://visibleearth.nasa.gov/images/55167/earths-city-lights (accessed on 3 January 2021).
- Aurora Overlay. Earth Nullschool. Available online: https://earth.nullschool.net/#current/space/surface/level/anim=off/overlay=aurora/ (accessed on 3 January 2021).
- Selva, D.; Krejci, D. A survey and assessment of the capabilities of CubeSats for Earth Observations. Acta Astronaut. 2012, 74, 50–68. [Google Scholar] [CrossRef]
- Atwell, W.; Rojdev, K.; Sukesh, A.; Sirikul, S. Mitigating the Effects of the Space Radiation Environment: A Novel Approach of Using Graded-Z Materials. In Proceedings of the AIAA Space 2013 Conference and Exposition, San Diego, CA, USA, 10–12 September 2013. [Google Scholar] [CrossRef]
- Thomsen, D.; Kim, W.; Cutler, J. Shields-1, A SmallSat Radiation Shielding Technology Demonstration. In Proceedings of the 29th Annual AIAA/USU Conference on Small Satellites, Logan, UT, USA, 8–13 August 2015. [Google Scholar]
- Available online: https://aerospaceamerica.aiaa.org/features/building-goes-r/ and https://www.goes-r.gov/resources/faqs.html; (accessed on 15 February 2021).
- Available online: https://www.bbc.co.uk/news/science-environment-12583115 (accessed on 15 February 2021).
- Available online: http://www.satmagazine.com/story.php?number=602922274 (accessed on 15 February 2021).
- Cullingworth, C. Design and Simulation of an Earth Viewing CubeSat Constellation to Image the Whole Globe on the Daylight and Night-Side Every 5–10 Minutes. Master’s Thesis, London’s Global University, London, UK, 2019, unpublished. [Google Scholar]
- Rose, T.S.; Rowen, D.W.; LaLumondiere, S.; Werner, N.I.; Linares, R.; Faler, A.; Wicker, J.; Coffman, C.M.; Maul, G.A.; Chien, D.H.; et al. Optical Communications Downlink from a 1.5U Cubesat: OCSD Program; Karafolas, N., Sodnik, Z., Cugny, B., Eds.; SPIE: Washington, DC, USA, 2019; Volume 11180, p. 18. [Google Scholar] [CrossRef]
- Wulder, M.A.; Hilker, T.; White, J.C.; Coops, N.C.; Masek, J.G.; Pflugmacher, D.; Crevier, Y. Virtual constellations for global terrestrial monitoring. Remote Sens. Environ. 2015, 170, 62–76. [Google Scholar] [CrossRef]
- Bauer, P.; Dueben, P.D.; Hoefler, T.; Quintino, T.; Schulthess, T.C.; Wedi, N.P. The digital revolution of Earth-system science. Nat. Comput. Sci. 2021, 1, 104–113. [Google Scholar] [CrossRef]
- Bauer, P.; Stevens, B.; Hazeleger, W. A digital twin of Earth for the green transition. Nat. Clim. Chang. 2021, 11, 80–83. [Google Scholar] [CrossRef]


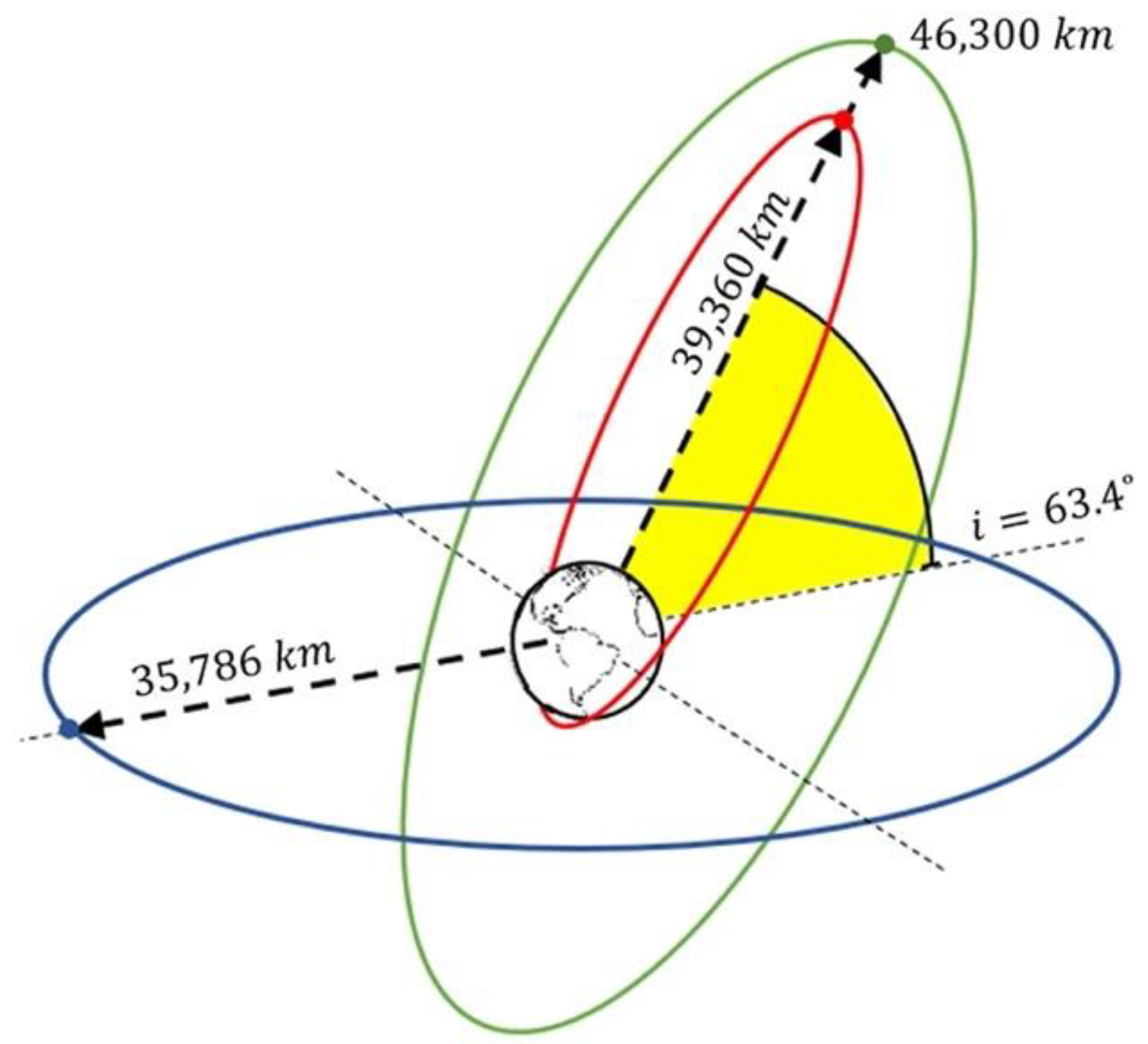

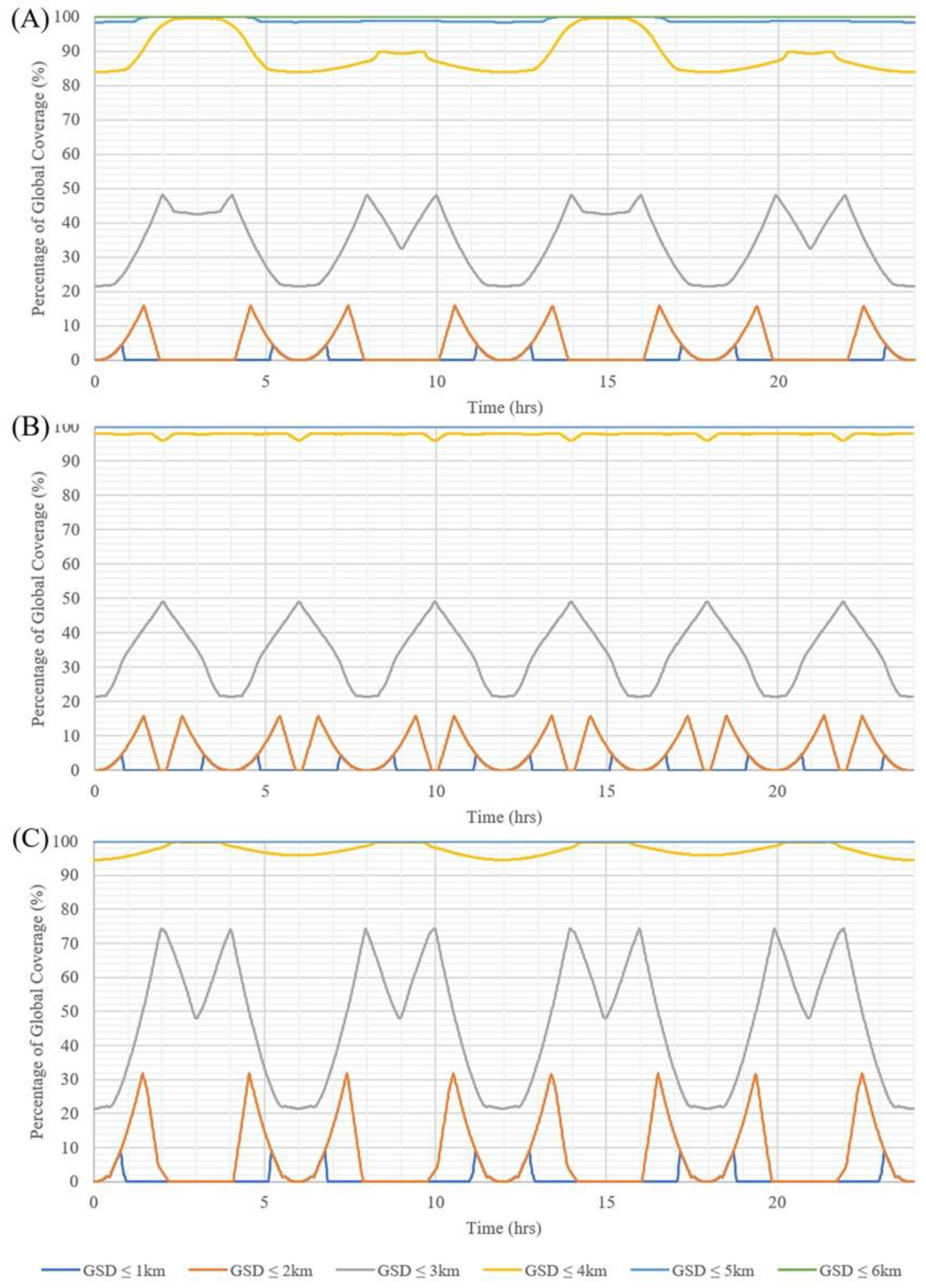

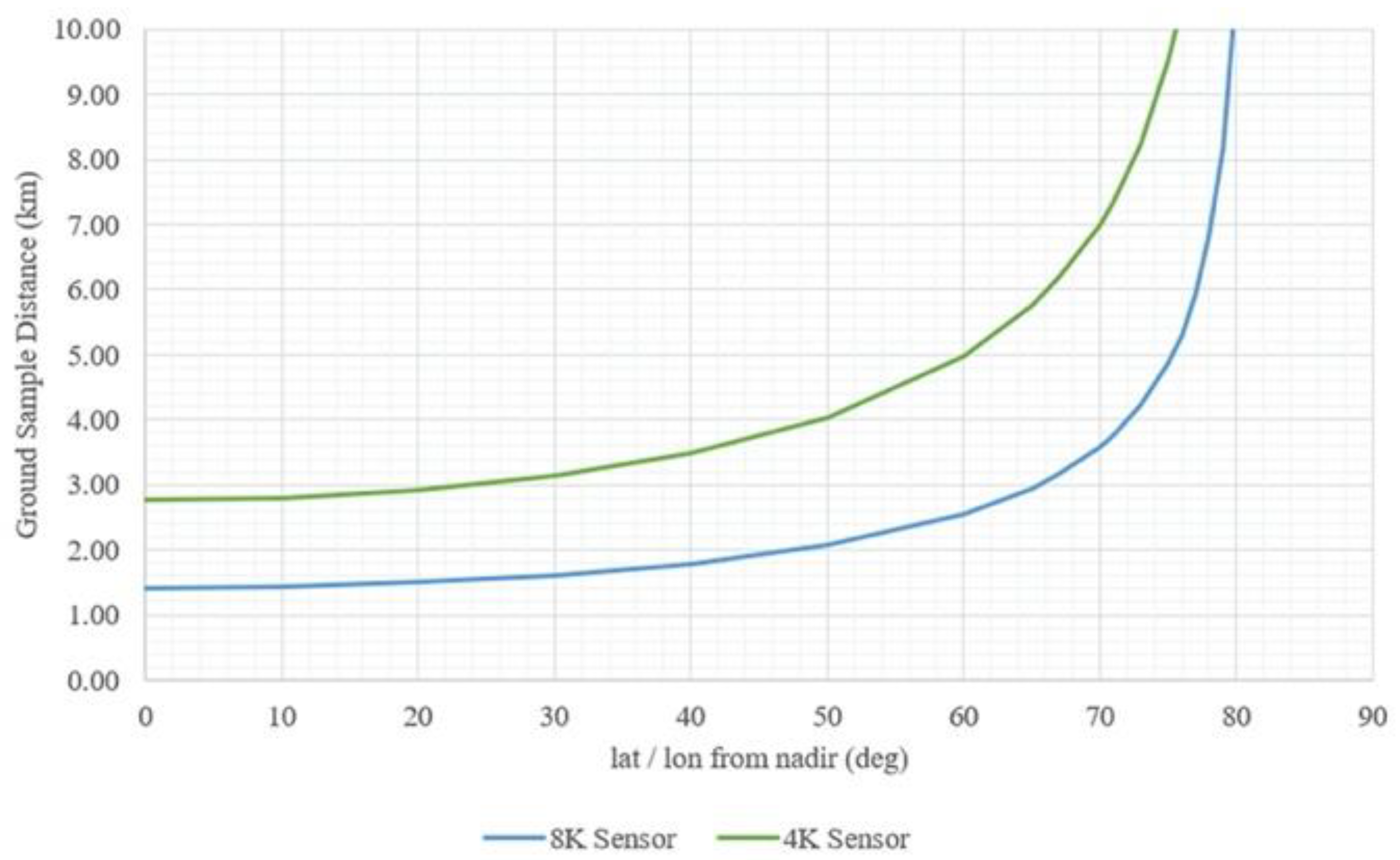
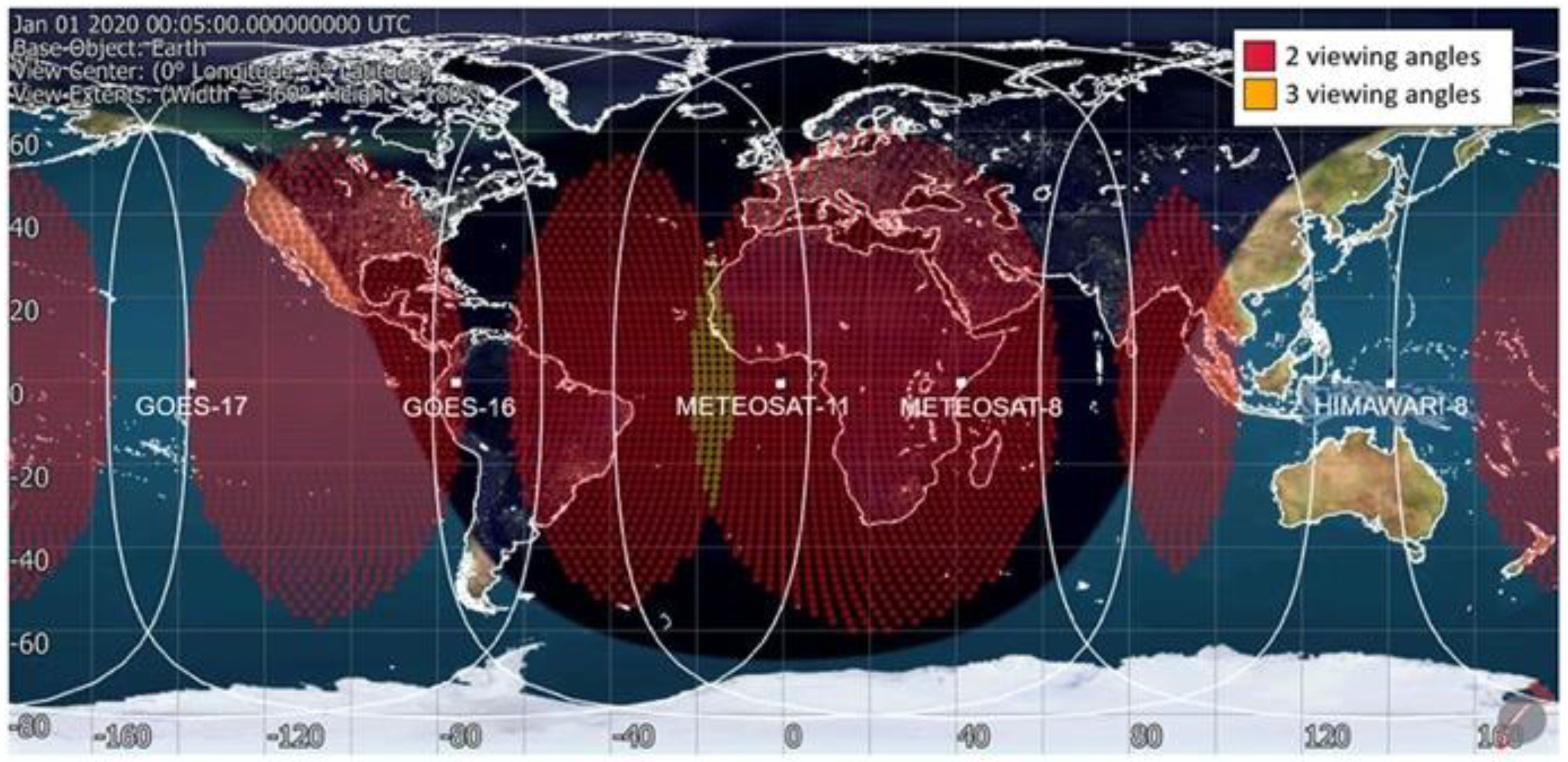
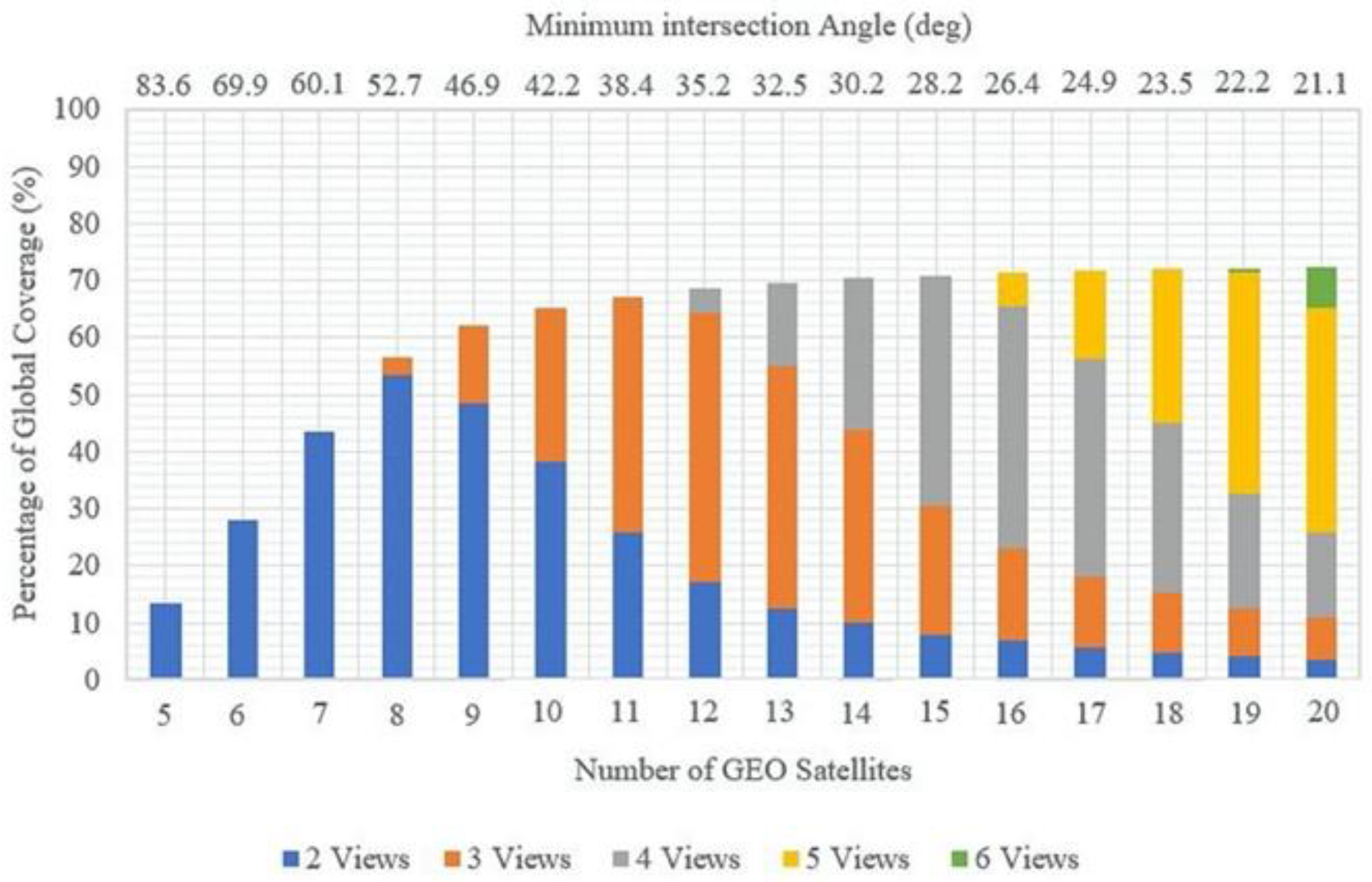

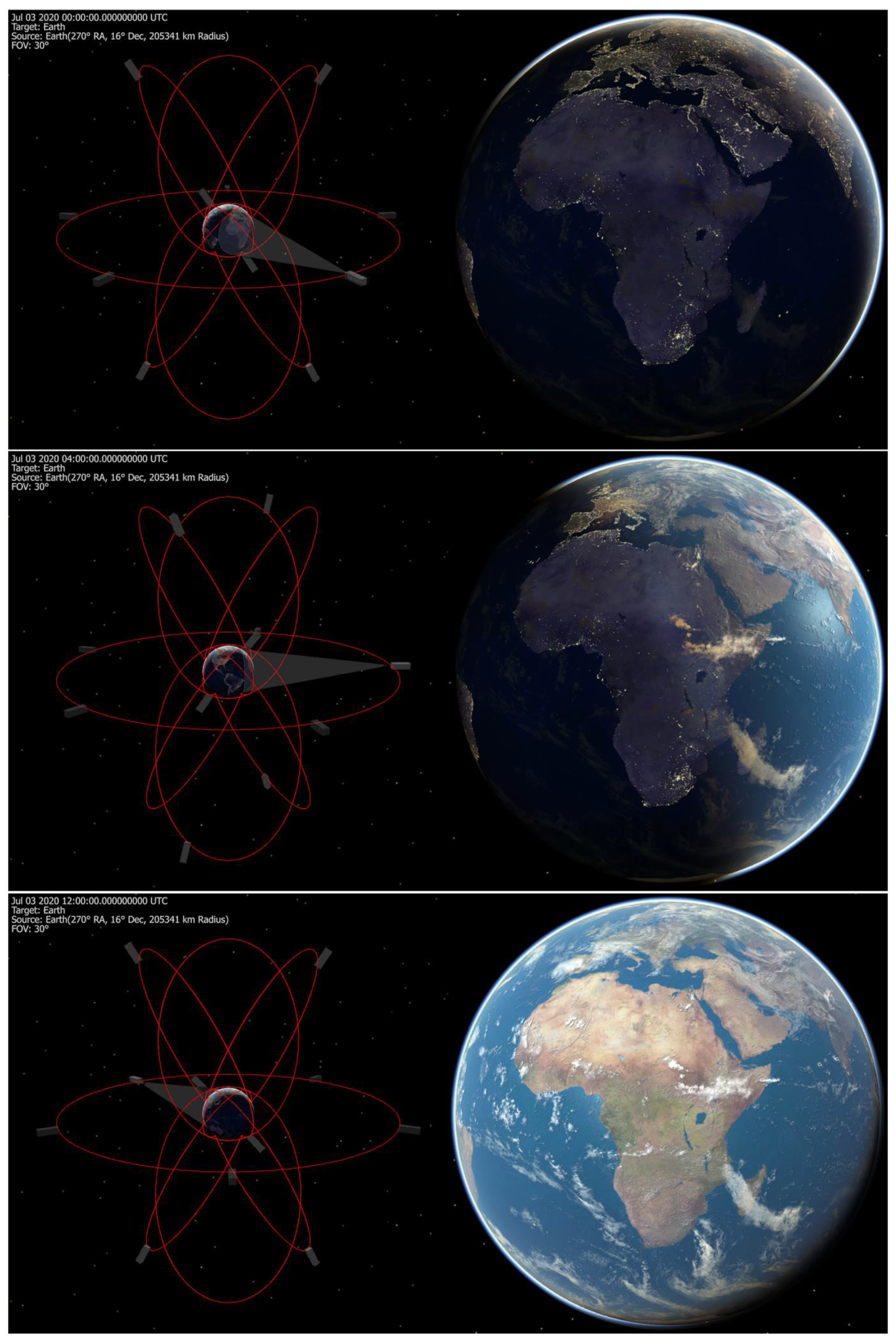
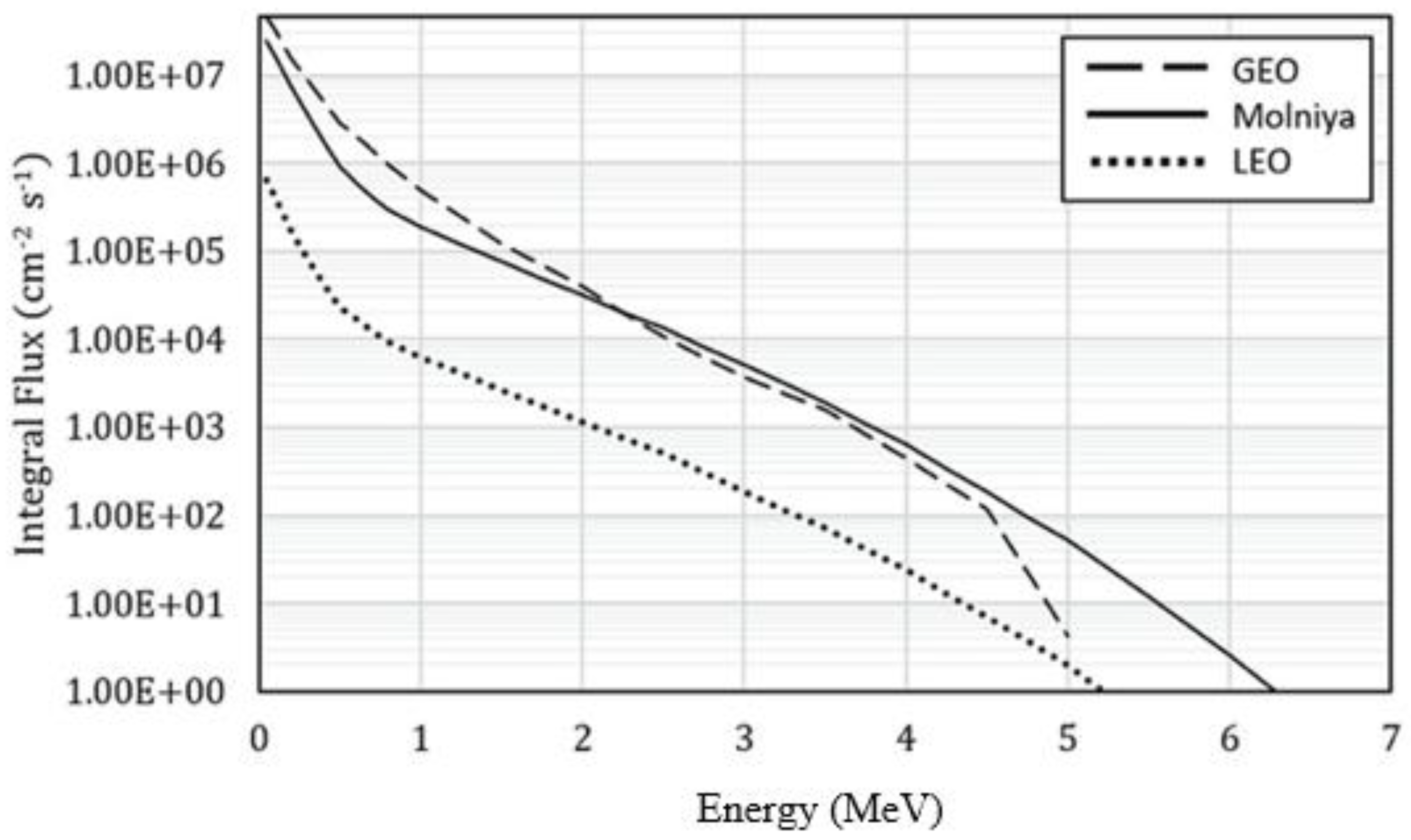

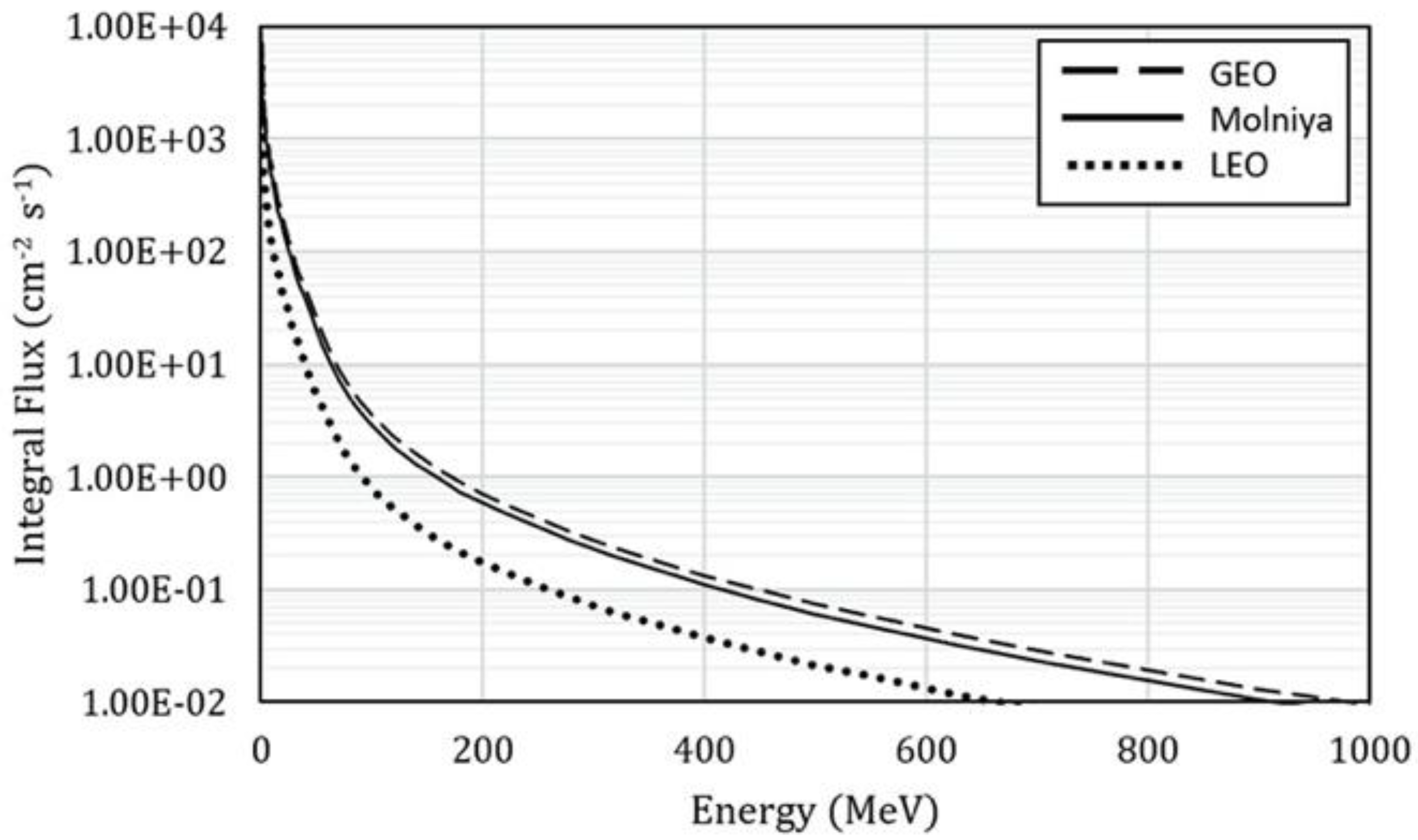
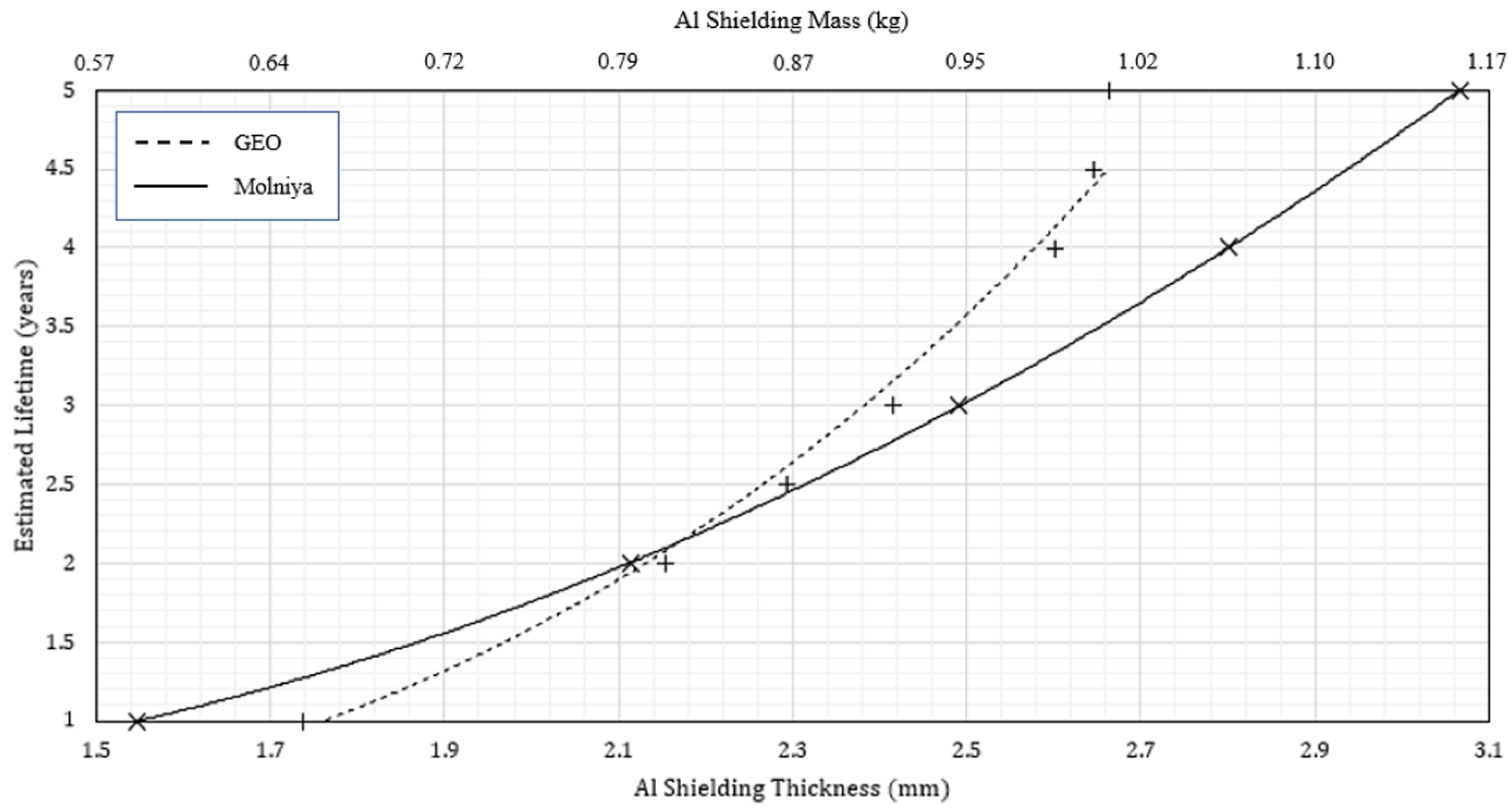
| Molniya | GEO | Tundra | |
|---|---|---|---|
| Apogee Altitude (km) | 39,850 | 35,788 | 46,300 |
| Crossing Point Altitude (km) | 31,472 | N/A | 38,339 |
| X Pixels | 4096 | 4 096 | 4096 |
| Pixel Size (μm) | 9.60 | 7.75 | 10 |
| Sensor Horizontal (mm) | 19.66 | 15.87 | 20.48 |
| Focal Length (mm) | 111.55 | 100.18 | 129.31 |
| Aperture (mm) | 55.77 | 50.09 | 64.80 |
| f/# | 2 | 2 | 2 |
| GSD from Apogee (km) | 3.43 | 2.77 | 3.58 |
| GSD from Crossing Point (km) | 2.71 | N/A | 2.97 |
| FOV (deg) | 20 | 18 | 18 |
| FOV from Apogee (km) | 16,303 | 13,357 | 14,666 |
| IDS UI-3590CP-C | Lumenera Lt1245R | Kodak KA1-11002 | MT9F002 | KAF-16801 | KAI-16070 | Aptina MT9D131 (AC-4) | |
|---|---|---|---|---|---|---|---|
| Ref | [44] | [45] | [46] | [47] | [48] | [49] | [43] |
| X Pixels | 4912 | 4112 | 4032 | 4384 | 4096 | 4864 | 1600 |
| Y Pixels | 3684 | 3008 | 2688 | 3288 | 4096 | 3232 | 1200 |
| Pixel Size (μm) | 1.25 | 3.45 | 9 | 1.4 | 9 | 7.4 | 2.8 |
| Sensor Horizontal (mm) | 3.07 | 7.09 | 18.14 | 3.07 | 18.43 | 18.00 | 2.24 |
| Sensor Vertical (mm) | 2.30 | 3.75 | 12.10 | 2.30 | 18.43 | 11.96 | 1.68 |
| Focal Length (mm) | 17.41 | 40.23 | 102.90 | 17.40 | 104.53 | 102.06 | 12.70 |
| Aperture (mm) | 8.71 | 20.11 | 51.45 | 8.70 | 52.27 | 51.03 | 6.35 |
| f/# | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| GSD at Apogee (km) | 2.86 | 3.42 | 3.49 | 3.21 | 3.43 | 2.89 | 8.78 |
| GSD at Crossing Point (km) | 2.26 | 2.70 | 2.75 | 2.53 | 2.71 | 2.28 | 6.94 |
| Horizontal FOV (km) | 16,303 | 16,303 | 16,303 | 16,303 | 16,303 | 16,303 | 16,303 |
| Vertical FOV (km) | 12,227 | 11,925 | 10,868 | 12,227 | 16,303 | 10,833 | 12,227 |
| IDS UI-3590CP-C | Lumenera Lt1245R | Kodak KA1-11002 | MT9F002 | KAF-16801 | KAI-16070 | Aptina MT9D131 (AC-4) | |
|---|---|---|---|---|---|---|---|
| Ref | [44] | [45] | [46] | [47] | [48] | [49] | [43] |
| X Pixels | 4912 | 4112 | 4032 | 4384 | 4096 | 4864 | 1600 |
| Y Pixels | 3684 | 3008 | 2688 | 3288 | 4096 | 3232 | 1200 |
| Pixel Size (μm) | 1.25 | 3.45 | 9 | 1.4 | 9 | 7.4 | 2.8 |
| Sensor Horizontal (mm) | 3.07 | 7.09 | 18.14 | 3.07 | 18.43 | 18.00 | 2.24 |
| Sensor Vertical (mm) | 2.30 | 5.19 | 12.10 | 2.30 | 18.43 | 11.96 | 1.68 |
| Focal Length (mm) | 19.38 | 44.78 | 114.56 | 19.38 | 116.38 | 113.63 | 14.14 |
| Aperture (mm) | 9.69 | 22.39 | 57.28 | 9.69 | 58.19 | 56.81 | 7.07 |
| f/# | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| GSD (km) | 2.31 | 2.76 | 2.81 | 2.59 | 2.77 | 2.33 | 7.09 |
| Horizontal FOV (km) | 13,357 | 13,357 | 13,357 | 13,357 | 13,357 | 13,357 | 13,357 |
| Vertical FOV (km) | 10,018 | 9771 | 8905 | 10,018 | 13,357 | 8875 | 10,018 |
| IDS UI-3590CP-C | Lumenera Lt1245R | Kodak KA1-11002 | MT9F002 | KAF-16801 | KAI-16070 | Aptina MT9D131 (AC-4) | |
|---|---|---|---|---|---|---|---|
| Ref | [44] | [45] | [46] | [47] | [48] | [49] | [43] |
| X Pixels | 4912 | 4112 | 4032 | 4384 | 4096 | 4864 | 1600 |
| Y Pixels | 3684 | 3008 | 2688 | 3288 | 4096 | 3232 | 1200 |
| Pixel Size (μm) | 1.25 | 3.45 | 9 | 1.4 | 9 | 7.4 | 2.8 |
| Sensor Horizontal (mm) | 3.07 | 7.09 | 18.14 | 3.07 | 18.43 | 18.00 | 2.24 |
| Sensor Vertical (mm) | 2.30 | 3.75 | 12.10 | 2.30 | 18.43 | 11.96 | 1.68 |
| Focal Length (mm) | 19.38 | 44.78 | 114.56 | 19.38 | 116.38 | 113.63 | 14.14 |
| Aperture (mm) | 9.69 | 22.39 | 57.28 | 9.69 | 58.19 | 56.81 | 7.07 |
| f/# | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| GSD at Apogee (km) | 2.99 | 3.57 | 3.64 | 3.35 | 3.58 | 3.02 | 9.17 |
| GSD at Crossing Point (km) | 2.47 | 2.95 | 3.01 | 2.77 | 2.97 | 2.50 | 7.59 |
| Horizontal FOV (km) | 14,666 | 14,666 | 14,666 | 14,666 | 14,666 | 14,666 | 14,666 |
| Vertical FOV (km) | 11,000 | 10,729 | 9778 | 11,000 | 14,666 | 9745 | 11,000 |
| Instrument | LEO Orbiter | Spatial Resolution Nadir (km) | Swath Width (km) | Global Coverage | Ref |
|---|---|---|---|---|---|
| MODIS | TERRA/AQUA | 1.000 | 2330 | 1–2 Days | [56] |
| VIIRS | NOAA 20/Suomi NPP | 0.742 | 3000 | Daily | [19,57] |
| OLCI | Sentinel-3A/Sentinel-3B | 0.300 | 1270 | 0.9 Days | [58] |
| AVHRR | MetOp-A/MetOp-B/MetOp-C | 1.100 | 2894 | Twice Daily | [59] |
| Constellation Size | No. Molniya Satellites | No. GEO Satellites | Average Percentage of Globe in View of at Least: | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 Sat | 2 Sats | 3 Sats | 4 Sats | 5 Sats | 6 Sats | 7 Sats | 8 Sats | |||
| 9 | 4 | 5 | 99.98 | 99.14 | 87.67 | 32.09 | 3.29 | 0.00 | 0.00 | 0.00 |
| 10 | 4 | 6 | 100 | 99.22 | 94.21 | 59.67 | 11.50 | 0.00 | 0.00 | 0.00 |
| 11 | 6 | 5 | 100 | 99.99 | 96.30 | 64.63 | 15.37 | 1.07 | 0.00 | 0.00 |
| 12 | 6 | 6 | 100 | 99.99 | 98.07 | 81.58 | 36.34 | 3.75 | 0.00 | 0.00 |
| 13 | 8 | 5 | 100 | 100 | 98.23 | 83.92 | 38.30 | 10.67 | 1.06 | 0.00 |
| 14 | 8 | 6 | 100 | 100 | 99.25 | 91.17 | 60.98 | 19.07 | 4.06 | 0.00 |
| Constellation Size | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|
| No Molniya Satellites | 4 | 4 | 6 | 6 | 8 | 8 |
| No GEO Satellites | 5 | 6 | 5 | 6 | 5 | 6 |
| Maximum GSD (km) | 5.760 | 5.631 | 4.738 | 4.622 | 4.710 | 4.429 |
| Average GSD (km) | 3.245 | 3.204 | 3.114 | 3.077 | 3.017 | 2.984 |
| Standard Deviation (km) | 0.145 | 0.138 | 0.098 | 0.096 | 0.202 | 0.195 |
| Average Coverage of Instantaneous Multiple BRDF Sampling (%) | 0.764 | 0.868 | 1.013 | 1.100 | 2.192 | 2.346 |
| Standard Deviation (%) | 0.811 | 0.817 | 0.839 | 0.707 | 1.562 | 1.481 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cullingworth, C.; Muller, J.-P. Contemporaneous Monitoring of the Whole Dynamic Earth System from Space, Part I: System Simulation Study Using GEO and Molniya Orbits. Remote Sens. 2021, 13, 878. https://doi.org/10.3390/rs13050878
Cullingworth C, Muller J-P. Contemporaneous Monitoring of the Whole Dynamic Earth System from Space, Part I: System Simulation Study Using GEO and Molniya Orbits. Remote Sensing. 2021; 13(5):878. https://doi.org/10.3390/rs13050878
Chicago/Turabian StyleCullingworth, Christopher, and Jan-Peter Muller. 2021. "Contemporaneous Monitoring of the Whole Dynamic Earth System from Space, Part I: System Simulation Study Using GEO and Molniya Orbits" Remote Sensing 13, no. 5: 878. https://doi.org/10.3390/rs13050878
APA StyleCullingworth, C., & Muller, J.-P. (2021). Contemporaneous Monitoring of the Whole Dynamic Earth System from Space, Part I: System Simulation Study Using GEO and Molniya Orbits. Remote Sensing, 13(5), 878. https://doi.org/10.3390/rs13050878