Automatic Target Recognition (ATR) in Synthetic Aperture Radar (SAR) images is a topic of great interest and demanding requirements [
1,
2,
3,
4]. In particular, for defense applications, the knowledge of the vehicles deployed in a specific area of interest is fundamental to the understanding of the threat that exists (e.g., Small Intercontinental Ballistic Missile launcher rather than a theatre missile launcher). As current systems have reached a high level of target classification capabilities, more demanding tasks, such as recognition and identification of the targets, pose still a fundamental technical challenge. The ATR challenge has been investigated with a number of different approaches, including
normalization [
5], where the normalization is applied to the image thereby preserving all the information of the image whilst assigning to the classifier the task of deriving the model and separation of targets. In Reference [
1], an analysis investigating both detection and classification of stationary ground targets using high resolution, fully polarimetric SAR images is provided. Many approaches use feature extractions from the detected SAR targets, such as the algorithm proposed in Reference [
6], where a relatively large number of scatterers are selected with a variability reduction technique. Discriminative graphical models have been used in Reference [
7] with the aim to fuse different features and allow good performance with small training datasets. A two-stage framework is proposed to model dependencies between different feature representations of a target image. The approach has been tested using the MSTAR dataset and the performance resulted to overcome Extended Maximum Average Correlation Height (EMACH), Support Vector Machines (SVM), AdaBoost, and Conditional Gaussian Model classifiers. Finally, in Reference [
8], a Krawtchouk moments-based approach has been introduced in order to recognize military vehicles by exploiting invariance, orthogonality, and low computational complexity. Recently, a broad set of approaches has investigated the latest advances in Artificial Intelligence (AI) applied to the SAR ATR challenge [
3,
4,
9]. Specifically, in Reference [
10], a Convolutional Neural Network (CNN) was developed for target classification and was tested in MSTAR dataset for 10 targets. The results demonstrated significant performance improvement compared to more traditional approaches, such as SVM [
5] and Bayesian compressive sensing [
11], when tested in different operational conditions. To deal with high complexity SAR ATR systems may impose, a lossless lightweight CNN design is proposed in Reference [
12], based on pruning and knowledge distillation. Results demonstrated that using all-convolutional networks (A-ConvNets) and visual geometry group network (VGGNet) on MSTAR dataset, the proposed approach can achieve 65.68× and 344× lossless compression while reducing the computational cost by 2.5 and 18 times, respectively, with minimum impact on accuracy. Furthermore, in Reference [
13], a different lightweight CNN approach was investigated utilizing two streams to extract multilevel features. Tested on MSTAR dataset, the presented approach offers
accuracy while significantly reducing the number of parameters compared to previously proposed networks. Bidirectional long short-term memory (LSTM) recurrent neural networks were also proposed for SAR ATR in Reference [
14], reaching classification accuracy of
.
Generative Adversarial Networks (GAN) have also been widely suggested in SAR ATR as at tool to generate synthetic images. In Reference [
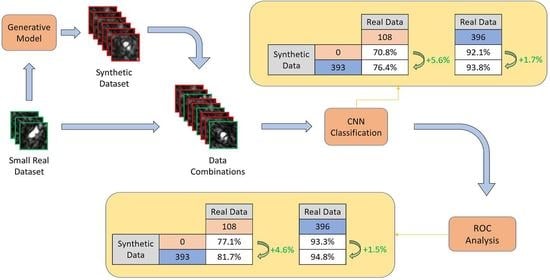
15], a Multi-Discriminator GAN (MGAN) was proposed for dataset expansion in combination with a CNN classifier. The conducted analysis demonstrated that inclusion of synthetic data in the training can improve the CNN accuracy especially when the number of real images is low. Moreover, in Reference [
16], a novel Integrated GANs (I-GAN) model for SAR image generation and recognition was presented combining the ability of the unconditional and conditional GANs for unsupervised feature extraction and supervised image-label matching, respectively. Performance analysis in the MSTAR dataset showed that the proposed framework can generate high quality SAR images outperforming previously proposed semi-supervised learning methods.
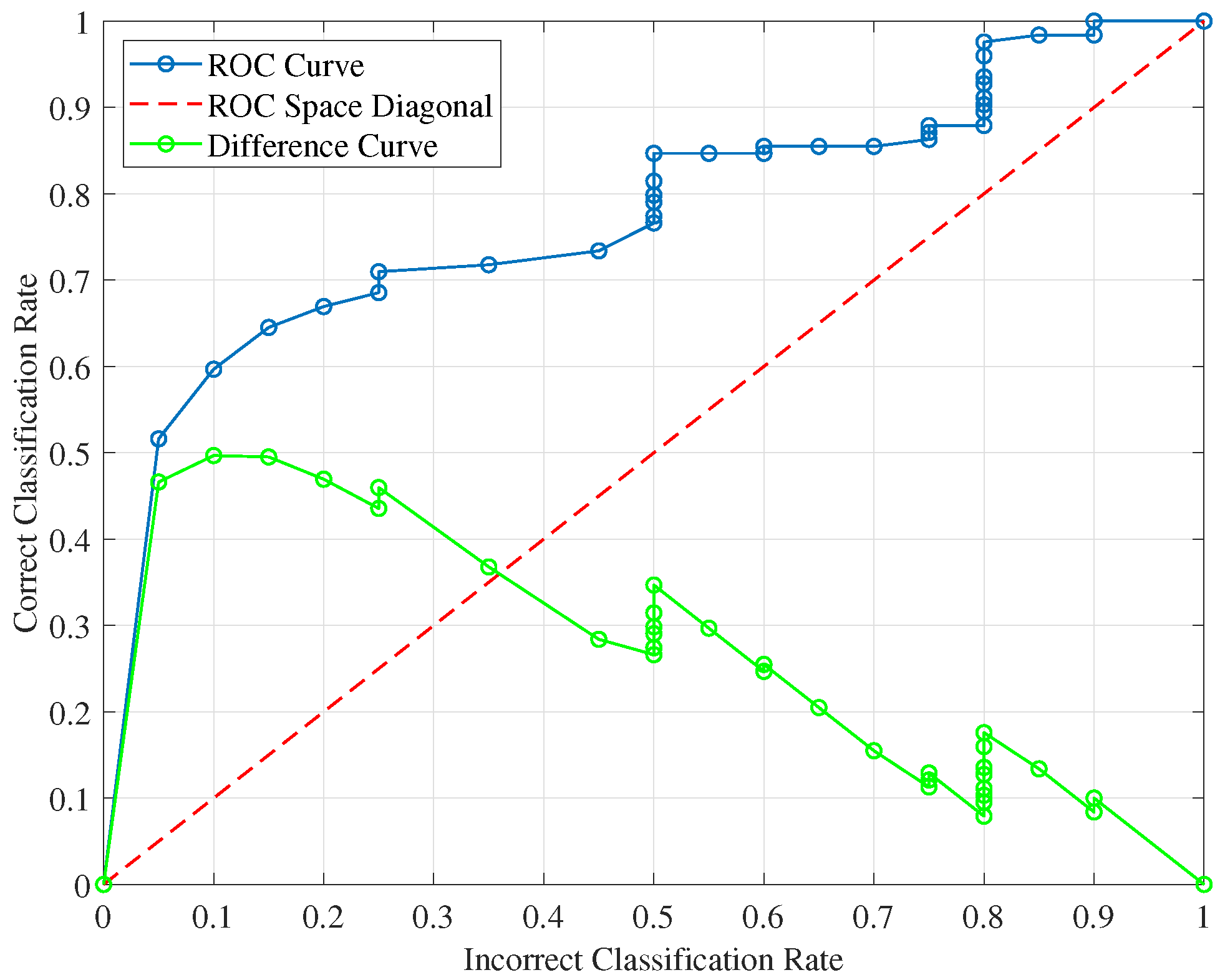
A common limitation of all the above mentioned approaches and of most of the SAR ATR literature is that these are designed and applied on high-resolution SAR images and such a scenario is not always verified. Indeed, the ATR problem becomes even more difficult when the SAR images are not acquired with high spatial resolution due to sensor’s limitations and/or to the actual SAR imaging mode used, such as in Foliage Penetrating (FOPEN) SAR [
17]. FOPEN SAR uses relatively low carrier frequencies in order to be able to penetrate canopies, and as a consequence has relatively low bandwidths in both range and cross-range directions, meaning that the final SAR image has a relatively poor spatial resolution, and while such a resolution is enough to detect extended targets, such as vehicles hidden under canopies [
18], the target recognition task become very challenging. The problem of low resolution SAR and FOPEN SAR ATR has been only marginally investigated in the literature mainly due to the lack of data availability to the research community. In Reference [
2], the performance of SAR ATR was examined using imagery of three different resolutions. Results demonstrated significant impact lowering resolution has on the classification performance, as well as the improvement super-resolution can offer. For these reasons, we are investigating whether the consolidated techniques in the area of AI, such as CNNs and GANs, can be used also in this context to provide a significant operational advantage, such as reducing the need to gather large datasets in hostile environments.