Radiometric Calibration Evaluation for FY3D MERSI-II Thermal Infrared Channels at Lake Qinghai
Abstract
1. Introduction
2. Calibration Site
3. Methods
3.1. Theory of TIR Radiometric Calibration
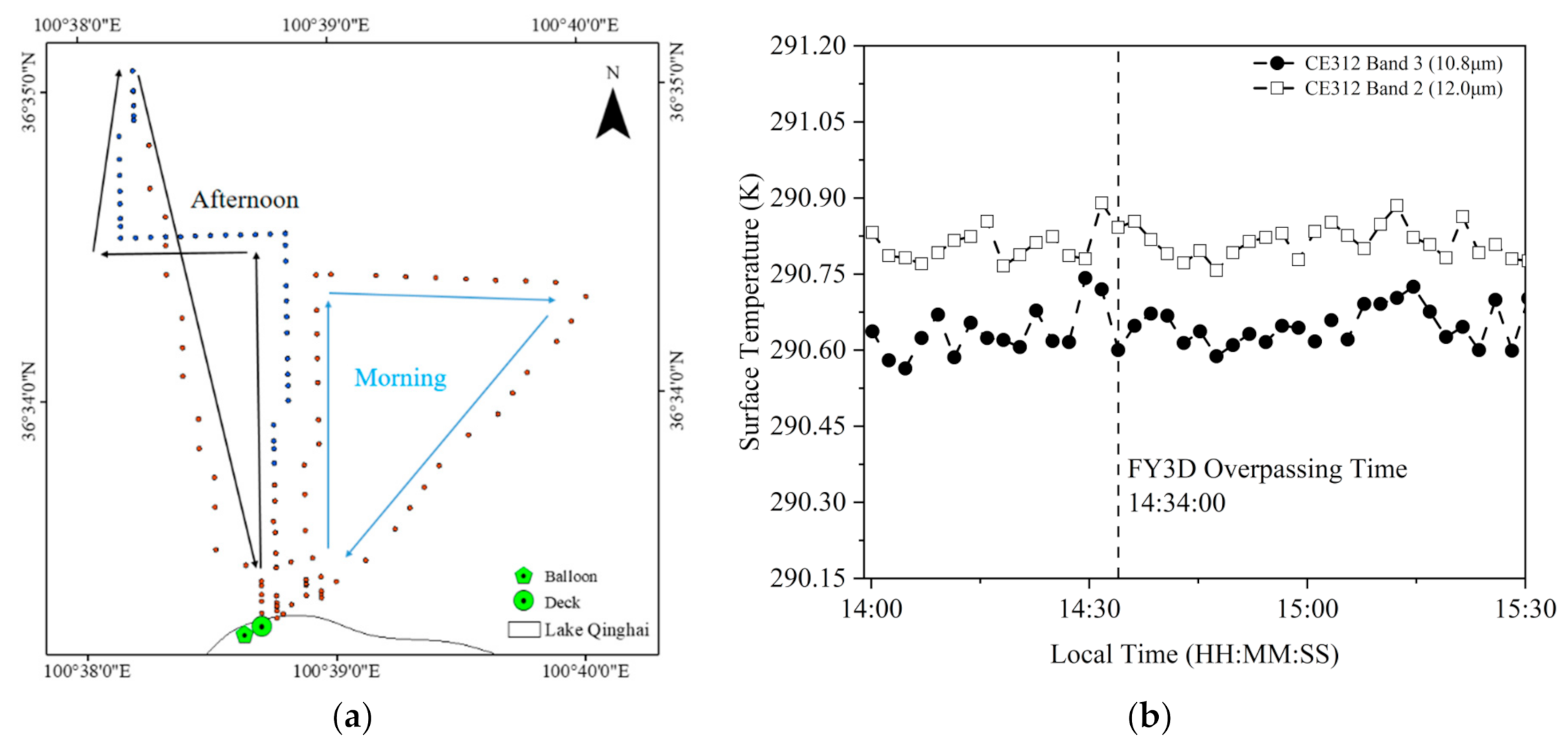
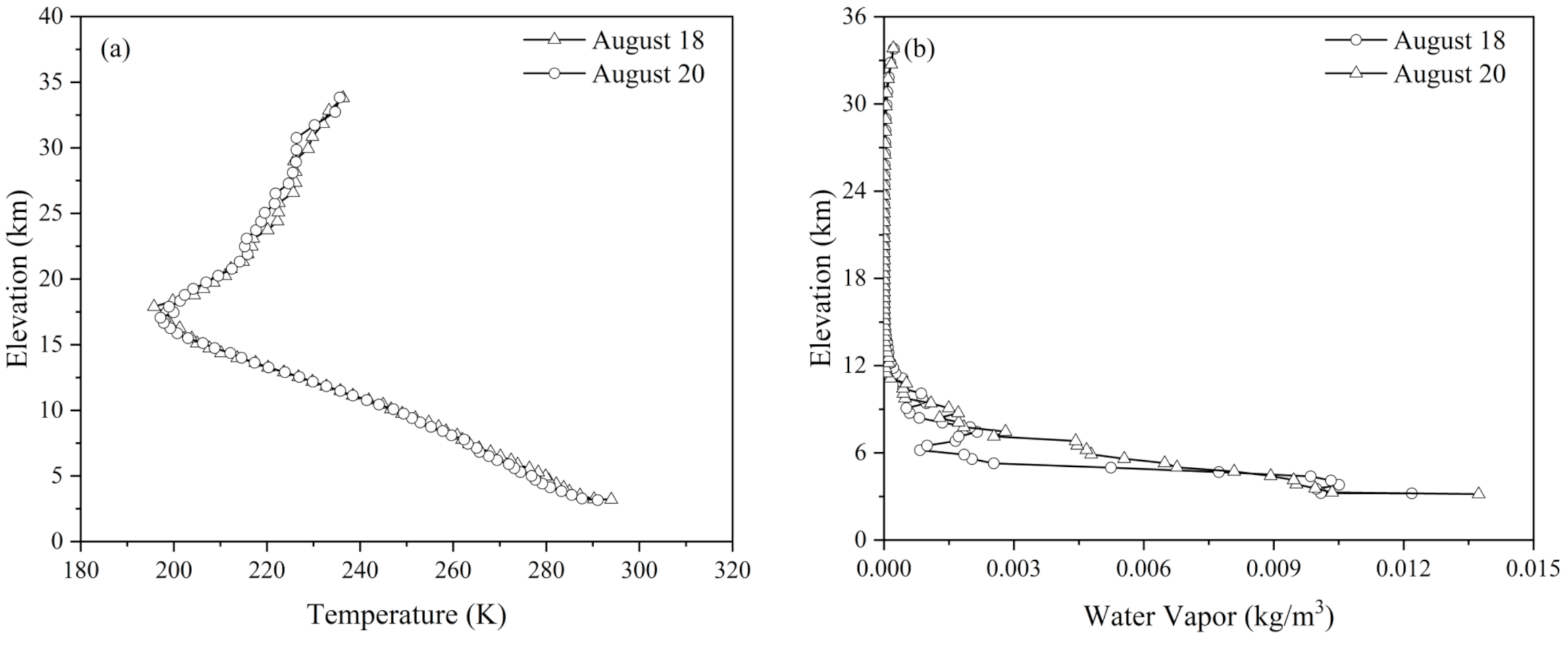
3.2. Surface Parameters Measured by an Unmanned Surface Vehicle
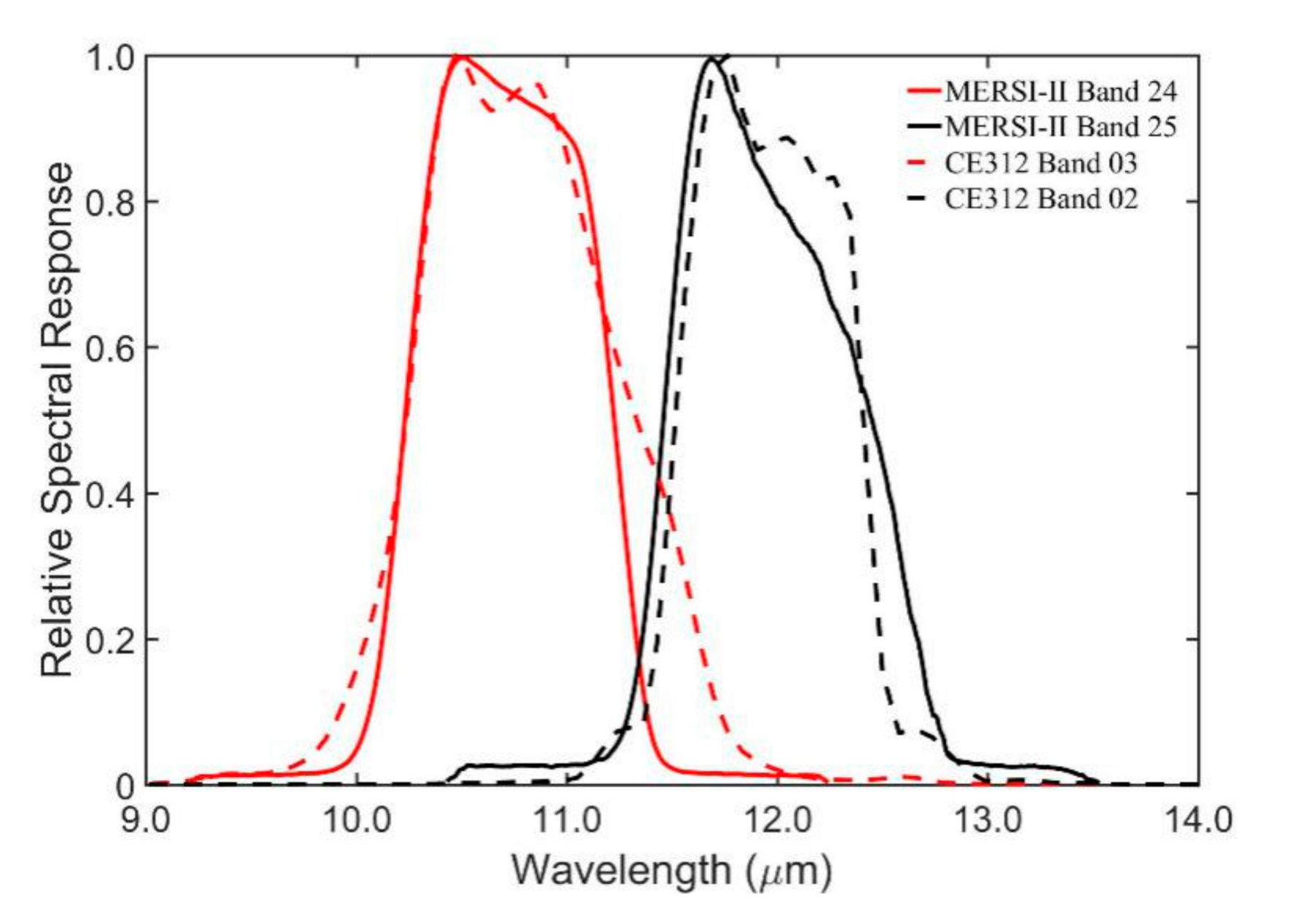
3.3. Spectral Matching
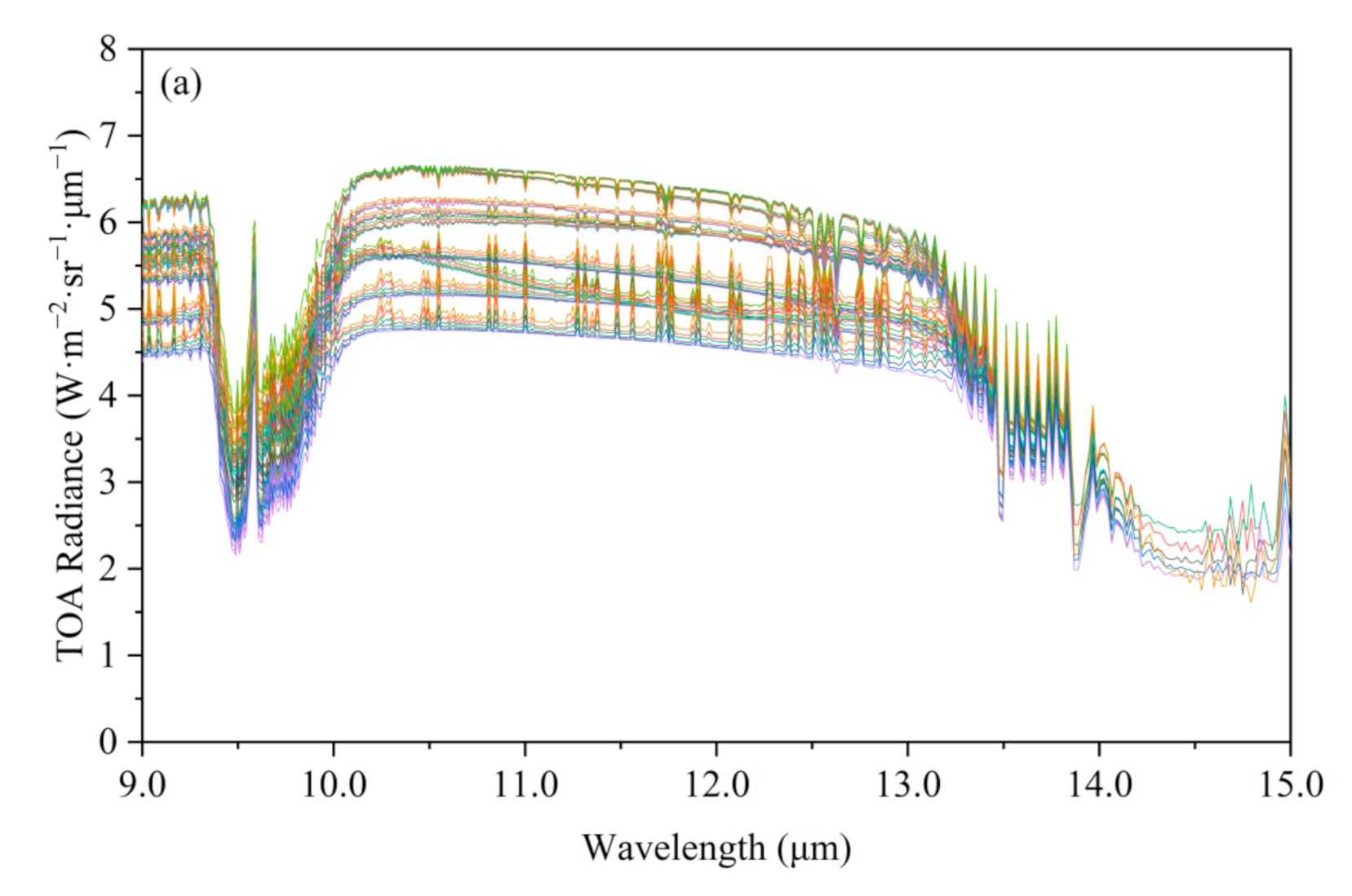
3.4. The Derivation of the Atmospheric Effects by MODTRAN Simulation
4. Results and Discussion
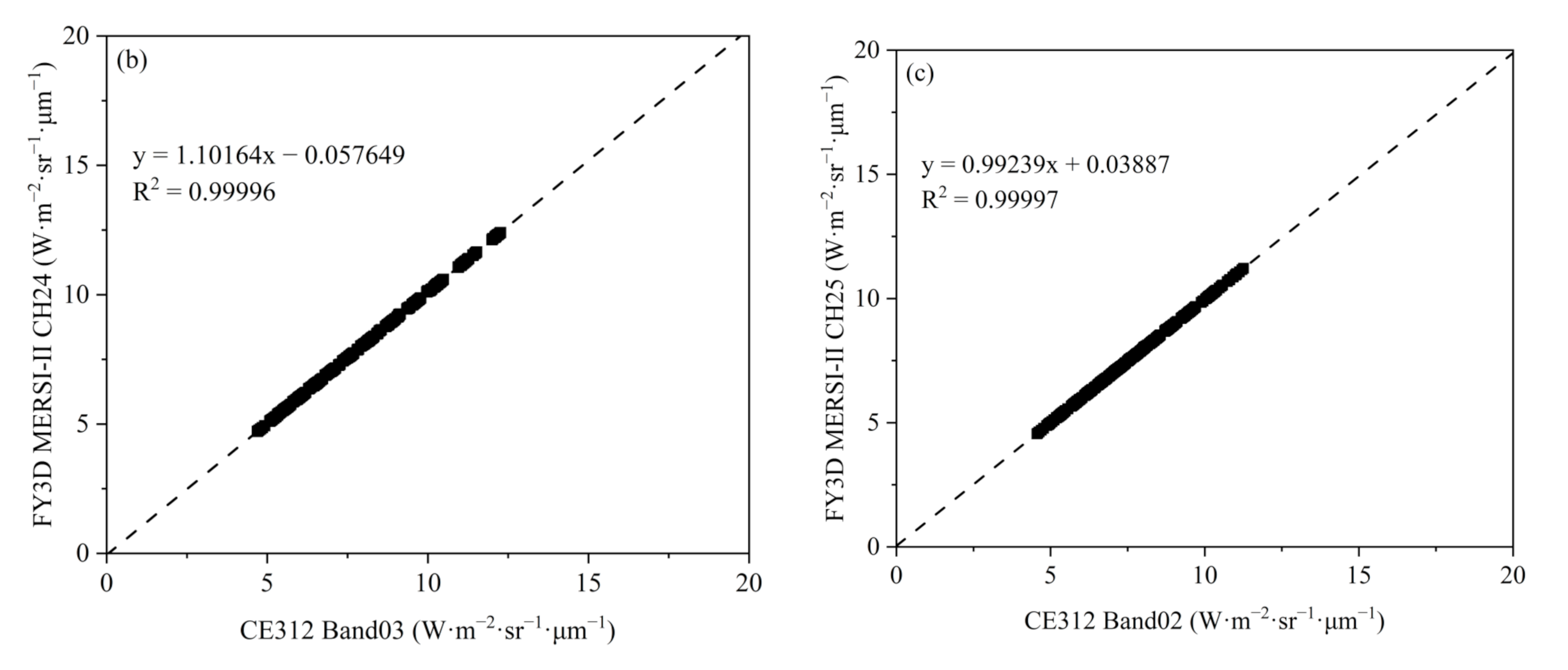
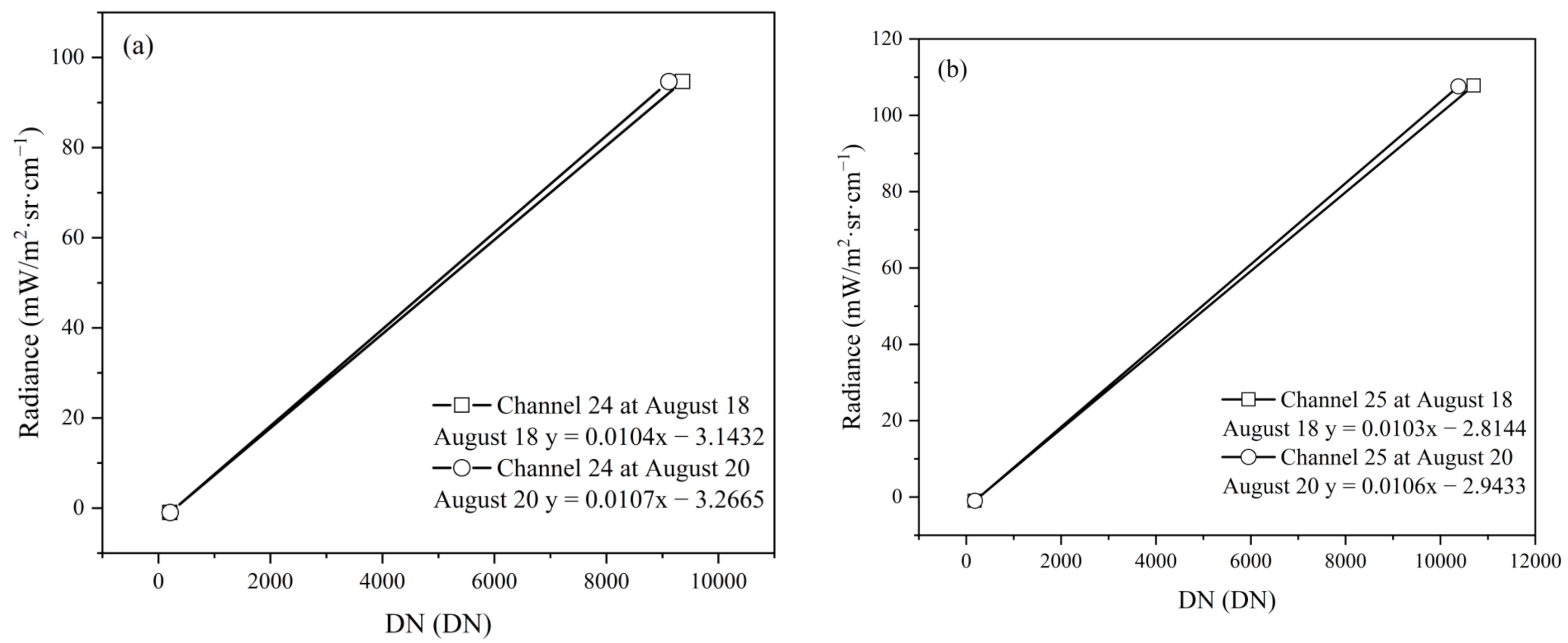
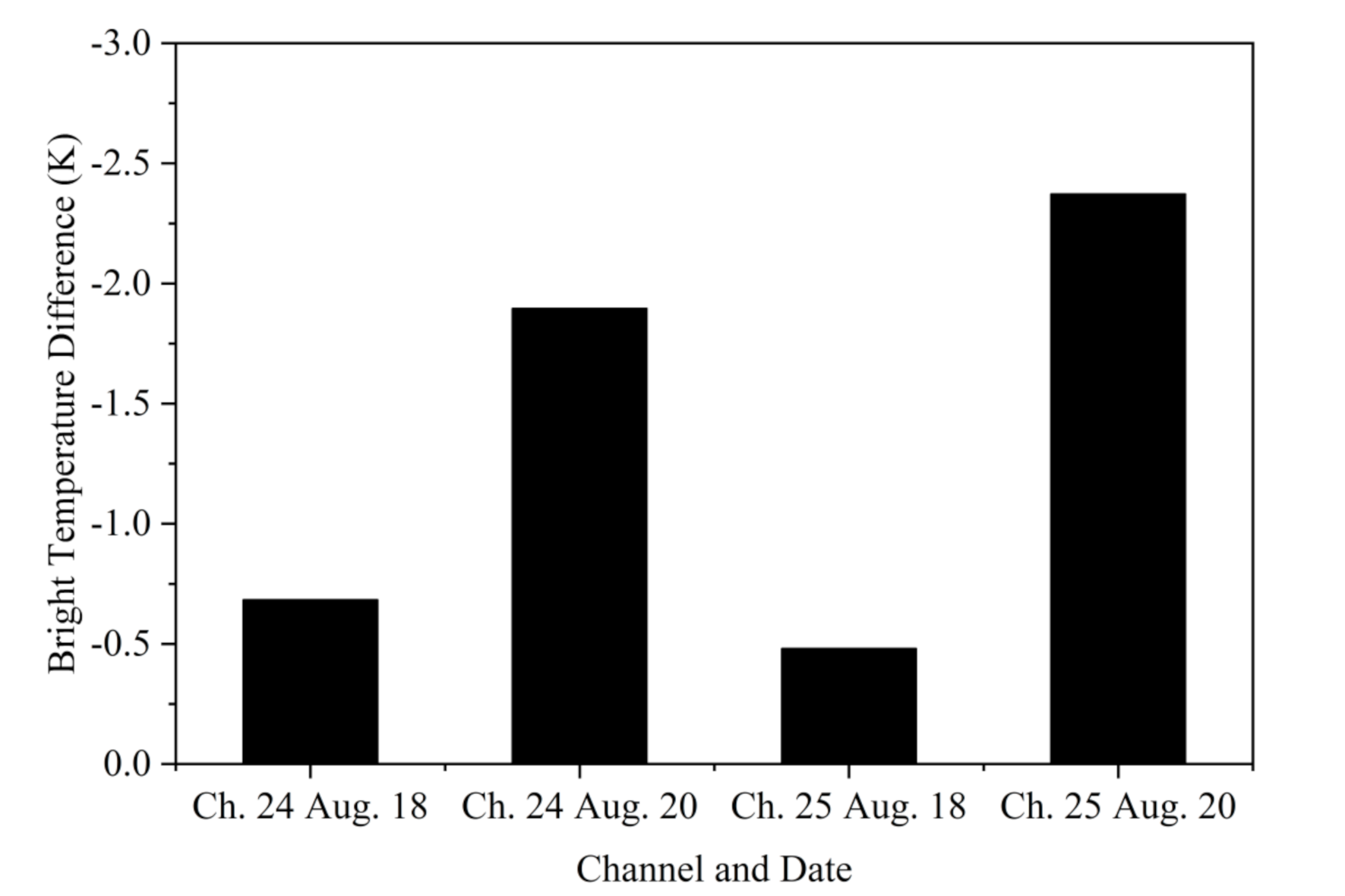
4.1. Calibration Results of the FY3D MERSI-II TIR Channels
4.2. Validation for the Vicarious Calibration Coefficient
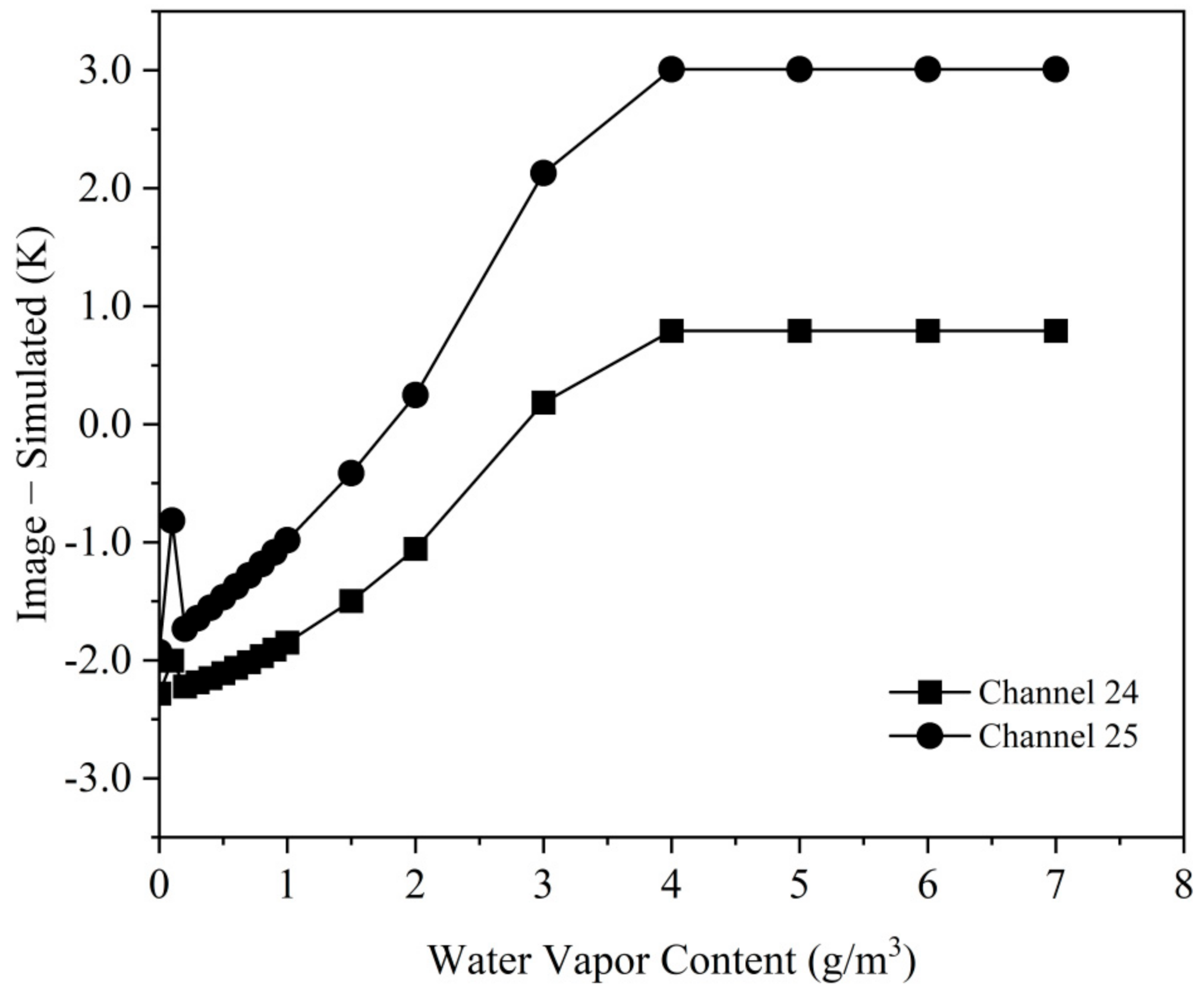
4.3. Uncertainties About Calibration Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Russell, J.E.; Haigh, J.D. Effect of Cloud Vertical Inhomogeneity on the Retrieval of Cirrus Cloud Temperature and Infrared Optical Depth Using the ASTR. J. Atmos. Sci. 1999, 56, 2601–2612. [Google Scholar] [CrossRef]
- Jedlovec, G.J.; Haines, S.L.; Lafontaine, F.J. Spatial and Temporal Varying Thresholds for Cloud Detection in GOES Imagery. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1705–1717. [Google Scholar] [CrossRef]
- Zhang, X.; Zhong, T.; Feng, X.; Wang, K. Estimation of the relationship between vegetation patches and urban land surface temperature with remote sensing. Int. J. Remote Sens. 2009, 30, 2105–2118. [Google Scholar] [CrossRef]
- Alcântara, E.H.; Stech, J.L.; Lorenzzetti, J.A.; Bonnet, M.-P.; Casamitjana, X.; Assireu, A.T.; Novo, E.M.L.D.M. Remote sensing of water surface temperature and heat flux over a tropical hydroelectric reservoir. Remote Sens. Environ. 2010, 114, 2651–2665. [Google Scholar] [CrossRef]
- Silvestro, F.; Gabellani, S.; Delogu, F.; Rudari, R.; Boni, G. Exploiting remote sensing land surface temperature in distributed hydrological modelling: The example of the Continuum model. Hydrol. Earth Syst. Sci. 2013, 17, 39–62. [Google Scholar] [CrossRef]
- Orsini, A.; Calzolari, F.; Georgiadis, T.; Levizzani, V.; Nardino, M.; Pirazzini, R.; Rizzi, R.; Sozzi, R.; Tomasi, C. Parameterisation of surface radiation flux at an Antarctic site. Atmos. Res. 2000, 54, 245–261. [Google Scholar] [CrossRef]
- Kandel, R.; Viollier, M. Observation of the Earth’s radiation budget from space. Comptes Rendus Geosci. 2010, 342, 286–300. [Google Scholar] [CrossRef]
- Hu, T.; Cao, B.; Du, Y.; Li, H.; Wang, C.; Bian, Z.; Sun, D.; Liu, Q. Estimation of Surface Upward Longwave Radiation Using a Direct Physical Algorithm. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4412–4426. [Google Scholar] [CrossRef]
- Ohring, G.; Tansock, J.; Emery, W.J.; Butler, J.; Flynn, L.E.; Weng, F.; Germain, K.S.; Wielicki, B.; Cao, C.; Goldberg, M.; et al. Achieving satellite instrument calibration for climate change. Trans. Am. Geophys. Union. 2013, 88, 136. [Google Scholar] [CrossRef]
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Gao, S.; Li, Z.; Chen, Q.; Zhou, W.; Lin, M.; Yin, X. Inter-Sensor Calibration between HY−2B and AMSR2 Passive Microwave Data in Land Surface and First Result for Snow Water Equivalent Retrieval. Sensors 2019, 19, 5023. [Google Scholar] [CrossRef] [PubMed]
- Baraldi, A. Impact of Radiometric Calibration and Specifications of Spaceborne Optical Imaging Sensors on the Development of Operational Automatic Remote Sensing Image Understanding Systems. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2009, 2, 104–134. [Google Scholar] [CrossRef]
- Gao, H.; Gu, X.; Yu, T.; Sun, Y.; Liu, Q. Cross-Calibration of GF−1 PMS Sensor with Landsat 8 OLI and Terra MODIS. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4847–4854. [Google Scholar] [CrossRef]
- Gu, X.; Tian, G.; Yu, T.; Li, X.; Gao, H.; Xie, Y. Principle and Method of Radiometric Calibration for Space Optical Remote Sensors; Science Press: Beijing, China, 2013. [Google Scholar]
- Zhang, Y.; Zheng, Z.; Hu, X.; Rong, Z.; Zhang, L. Lake Qinghai: Chinese site for radiometric calibration of satellite infrared remote sensors. Remote Sens. Lett. 2013, 4, 315–324. [Google Scholar] [CrossRef]
- Sayer, A.M.; Hsu, N.C.; Bettenhausen, C.; Jeong, M.; Meister, G. Effect of MODIS Terra radiometric calibration improvements on Collection 6 Deep Blue aerosol products: Validation and Terra/Aqua consistency. J. Geophys. Res. Atmos. 2015, 120, 12–157. [Google Scholar] [CrossRef]
- Kim, W.; He, T.; Wang, D.; Cao, C.; Liang, S. Assessment of Long-Term Sensor Radiometric Degradation Using Time Series Analysis. IEEE Trans. Geosci. Remote Sens. 2013, 52, 2960–2976. [Google Scholar] [CrossRef]
- Wang, W.; Cao, C. Assessing the VIIRS RSB Calibration Stability Using Deep Convective Clouds. In Earth Observing Missions and Sensors: Development, Implementation, and Characterization III; SPIE: Bellingham, WA, USA, 2014; Volume 9264, p. 926410. [Google Scholar]
- Wang, W.; Cao, C. DCC Radiometric Sensitivity to Spatial Resolution, Cluster Size, and LWIR Calibration Bias Based on VIIRS Observations. J. Atmos. Ocean. Technol. 2015, 32, 48–60. [Google Scholar] [CrossRef]
- Wang, W.; Cao, C. Monitoring the NOAA Operational VIIRS RSB and DNB Calibration Stability Using Monthly and Semi-Monthly Deep Convective Clouds Time Series. Remote Sens. 2016, 8, 32. [Google Scholar] [CrossRef]
- Bhatt, R.; Doelling, D.R.; Scarino, B.R.; Gopalan, A.K.S.; Haney, C.O. Toward consistent radiometric calibration of the NOAA AVHRR visible and near-infrared data record. In Earth Observing Systems XX; SPIE: Bellingham, WA, USA, 2015; Volume 9607, p. 960703. [Google Scholar]
- Qiu, S.; Shao, X.; Cao, C.; Wang, W. Vicarious Validation of Straylight Correction for VIIRS Day/Night Band Using Dome-C. In Earth Observing Systems XX; SPIE: Bellingham, WA, USA, 2015; Volume 9607. [Google Scholar] [CrossRef]
- Brown, S.W.; Flora, S.J.; Feinholz, M.E.; Yarbrough, M.A.; Houlihan, T.; Peters, D.; Kim, Y.S.; Mueller, J.L.; Johnson, B.C.; Clark, D.K. The marine optical buoy (MOBY) radiometric calibration. In Sensors, Systems, and Next-Generation Satellites XI; SPIE: Bellingham, WA, USA, 2007; p. 67441M. [Google Scholar]
- Elyouncha, A.; Acheroy, M. Radiometric cross-calibration of spaceborne scatterometers: First results. In Remote Sensing of the Ocean, Sea Ice, and Large Water Regions 2009; SPIE: Bellingham, WA, USA, 2009; Volume 7473, p. 74730B. [Google Scholar]
- Hu, X.; Zhang, Y.; Liu, Z.; Huang, Y.; Qiu, K.; Wang, Y.; Zhu, X.; Rong, Z. Optical characteristics of China Radiometric Calibration Site for Remote Sensing Satellite Sensors (CRCSRSSS). In Hyperspectral Remote Sensing of the Land and Atmosphere; SPIE: Bellingham, WA, USA, 2001; Volume 4151. [Google Scholar] [CrossRef]
- Barry, P.; Jarecke, P.J.; Pearlman, J.; Jupp, D.L.B.; Lovell, J.; Campbell, S. Radiometric calibration validation of the Hyperion instrument using ground truth at a site in Lake Frome, Australia. In Imaging Spectrometry VII; SPIE: Bellingham, WA, USA, 2002; Volume 4480. [Google Scholar]
- Li, Z.; Xingfa, G.; Yuxiang, Z.; Tao, Y.; Liangful, C.; Hui, G.; HongYan, H. A vicarious calibration for thermal infrared bands of TERRA-MODIS sensor using a new calibration test site-lake dali, China. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007. [Google Scholar]
- Wołczyński, W.; Guzik, E.; Wajda, W.; Jedrzejczyk, D.; Kania, B.; Kostrzewa, M. Cet in Solidifying Roll—Thermal Gradient Field Analysis. Arch. Met. Mater. 2012, 57, 105–117. [Google Scholar] [CrossRef]
- Williams, G.; Douglas, J. Comments on Cretaceous climatic equability in polar regions. Palaeogeogr. Palaeoclim. Palaeoecol. 1985, 49, 355–357. [Google Scholar] [CrossRef]
- Wan, Z.; Zhang, Y.; Li, Z.-L.; Wang, R.; Salomonson, V.V.; Yves, A.; Bosseno, R.; Hanocq, J.F. Preliminary estimate of calibration of the moderate resolution imaging spectroradiometer thermal infrared data using Lake Titicaca. Remote Sens. Environ. 2002, 80, 497–515. [Google Scholar] [CrossRef]
- Hook, S.J.; Vaughan, R.G.; Tonooka, H.; Schladow, S.G. Absolute Radiometric In-Flight Validation of Mid Infrared and Thermal Infrared Data from ASTER and MODIS on the Terra Spacecraft Using the Lake Tahoe, CA/NV, USA, Automated Validation Site. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1798–1807. [Google Scholar] [CrossRef]
- Hook, S.; Chander, G.; Barsi, J.; Alley, R.; Abtahi, A.; Palluconi, F.; Markham, B.L.; Richards, R.; Schladow, S.; Helder, D. In-flight validation and recovery of water surface temperature with Landsat−5 thermal infrared data using an automated high-altitude lake validation site at Lake Tahoe. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2767–2776. [Google Scholar] [CrossRef]
- Schott, J.R.; Hook, S.J.; Barsi, J.A.; Markham, B.L.; Miller, J.; Padula, F.P.; Raqueno, N.G. Thermal infrared radiometric calibration of the entire Landsat 4, 5, and 7 archive (1982–2010). Remote Sens. Environ. 2012, 122, 41–49. [Google Scholar] [CrossRef]
- Dong, C.; Yang, J.; Zhang, W.; Yang, Z.; Lu, N.; Shi, J.; Zhang, P.; Liu, Y.; Cai, B. An Overview of a New Chinese Weather Satellite FY−3A. Bull. Am. Meteorol. Soc. 2009, 90, 1531–1544. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, P.; Lu, N.; Yang, Z.; Shi, J.; Dong, C. Improvements on global meteorological observations from the current Fengyun 3 satellites and beyond. Int. J. Digit. Earth 2012, 5, 251–265. [Google Scholar] [CrossRef]
- Xu, N.; Chen, L.; Hu, X.; Zhang, L.; Zhang, P. Assessment and Correction of on-Orbit Radiometric Calibration for FY−3 VIRR Thermal Infrared Channels. Remote Sens. 2014, 6, 2884–2897. [Google Scholar] [CrossRef]
- National Satellite Meteorological Center China Meteorological Administration. Available online: http://www.nsmc.org.cn/en/nsmc/channels/FY−3SeriesSatellites.html (accessed on 1 September 2019).
- Jiang, J.; Wang, M.; Ju, S.; Xi, J. Land Surface Temperature Retrieval from FY−3D MERSI−2 Data in the Arid/Semi-Arid Area. Adv. Geosci. 2019, 9, 693–702. [Google Scholar] [CrossRef]
- Xu, N.; Niu, X.; Hu, X.; Wang, X.; Wu, R.; Chen, S.; Chen, L.; Sun, L.; Ding, L.; Yang, Z.; et al. Prelaunch Calibration and Radiometric Performance of the Advanced MERSI II on FengYun−3D. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4866–4875. [Google Scholar] [CrossRef]
- Tong, J.; Déry, S.J.; Chen, Y.; Hu, B. An alternative method for in-flight absolute radiometric calibration of thermal infrared channels of Chinese geostationary meteorological satellites. Int. J. Remote Sens. 2010, 31, 791–803. [Google Scholar] [CrossRef]
- Zhang, Y.; Gu, X.; Yu, T.; Li, X.; Li, X. In-flight method for CBERS−02 IRMSS thermal channel absolute radiometric calibration at Lake Qinghai (China). IEEE Trans. Geosci. Remote Sens. 2005, 3, 2227–2230. [Google Scholar] [CrossRef]
- Zhang, Y.; Gu, X.; Yu, T.; Li, X. Radiometric cross-calibration of CBERS−02 IRMSS thermal channel against TERRA MODIS. In Sensors, Systems, and Next-Generation Satellites IX; SPIE: Bellingham, WA, USA, 2005; Volume 5978, p. 59781V. [Google Scholar]
- Brogniez, G.E.R.; Pietras, C.; Legrand, M.; Dubuisson, P.; Haeffelin, M. A high-accuracy multiwavelength radiometer for in situ measurements in the thermal infrared. Part II: Behavior in field experiments. J. Atmos. Ocean. Technol. 2003, 20, 1023–1033. [Google Scholar] [CrossRef]
- National Satellite Meteorological Center China Meteorological Administration. FY3D Data Usage Guide. Available online: http://satellite.nsmc.org.cn/ (accessed on 12 November 2019).
- Chander, G.; Mishra, N.; Helder, D.L.; Aaron, D.; Choi, T.; Angal, A.; Xiong, X. Use of EO−1 Hyperion data to calculate spectral band adjustment factors (SBAF) between the L7 ETM+ and Terra MODIS sensors. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010. [Google Scholar] [CrossRef]
- Xu, N.; Hu, X.-Q.; Chen, L.; Zhang, Y.; Hu, J.-Y.; Sun, L. On-Orbit Radiometric Calibration Accuracy of FY−3A MERSI Thermal Infrared Channel. Spectrosc. Spectr. Anal. 2014, 34, 3429–3434. [Google Scholar] [CrossRef]
- Chander, G.; Mishra, N.; Helder, D.; Aaron, D.; Angal, A.; Choi, T.; Xiong, X.; Doelling, D.R. Applications of Spectral Band Adjustment Factors (SBAF) for Cross-Calibration. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1267–1281. [Google Scholar] [CrossRef]
- Li, Y.; Wu, J.; Fang, Y. Cross-Calibration of FY−3A/VIRR Thermal Infrared Channel with TERRA/MODIS. J. Atmos. Environ. Optics. 2016, 11, 204–210. [Google Scholar] [CrossRef]
- Hu, X.Q.; Zhang, L.Y.; Zheng, Z.J.; Zhang, Y.; Sun, L.; Ding, L.; Huang, X.X. FY−3A multi-detector radiometric calibration for infrared band of medium resolution spectral imager. Optics. Precis. Eng. 2010, 18, 1972–1980. [Google Scholar] [CrossRef]
- Chen, Y.; Sun, K.; Li, D.; Bai, T.; Huang, C. Radiometric Cross-Calibration of GF−4 PMS Sensor Based on Assimilation of Landsat−8 OLI Images. Remote Sens. 2017, 9, 811. [Google Scholar] [CrossRef]
- Wan, Z.; Li, Z.-L. A physics-based algorithm for retrieving land-surface emissivity and temperature from EOS/MODIS data. IEEE Trans. Geosci. Remote Sens. 1997, 35, 980–996. [Google Scholar] [CrossRef]
- Xiong, X.; Chiang, K.; Wu, A.; Barnes, W.; Guenther, B.; Salomonson, V.V. Multiyear On-Orbit Calibration and Performance of Terra MODIS Thermal Emissive Bands. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1790–1803. [Google Scholar] [CrossRef]
- Barsi, J.A.; Schott, J.R.; Hook, S.J.; Raqueno, N.G.; Markham, B.L.; Radocinski, R.G. Landsat−8 Thermal Infrared Sensor (TIRS) Vicarious Radiometric Calibration. Remote Sens. 2014, 6, 11607–11626. [Google Scholar] [CrossRef]



| Band Number | Center Wavelength (μm) | Bandwidth (nm) | Spatial Resolution (m) | SNR or NEΔT (K) | Maximum Reflectance ρ or Dynamic Range (K) |
|---|---|---|---|---|---|
| 1 | 0.47 | 50 | 250 | 100 | 90% |
| 2 | 0.55 | 50 | 250 | 100 | 90% |
| 3 | 0.65 | 50 | 250 | 100 | 90% |
| 4 | 0.865 | 50 | 250 | 100 | 90% |
| 5 | 1.38 | 20/30 | 1000 | 60/100 | 90% |
| 6 | 1.64 | 50 | 1000 | 200 | 90% |
| 7 | 2.13 | 50 | 1000 | 100 | 90% |
| 8 | 0.412 | 20 | 1000 | 300 | 30% |
| 9 | 0.443 | 20 | 1000 | 300 | 30% |
| 10 | 0.49 | 20 | 1000 | 300 | 30% |
| 11 | 0.555 | 20 | 1000 | 500 | 30% |
| 12 | 0.67 | 20 | 1000 | 500 | 30% |
| 13 | 0.709 | 20 | 1000 | 500 | 30% |
| 14 | 0.746 | 20 | 1000 | 500 | 30% |
| 15 | 0.865 | 20 | 1000 | 500 | 30% |
| 16 | 0.905 | 20 | 1000 | 200 | 100% |
| 17 | 0.936 | 20 | 1000 | 100 | 100% |
| 18 | 0.940 | 50 | 1000 | 200 | 100% |
| 19 | 1.030 | 20 | 1000 | 100 | 100% |
| 20 | 3.800 | 180 | 1000 | 0.25 K | 200–350 K |
| 21 | 4.050 | 155 | 1000 | 0.25 K | 200–350 K |
| 22 | 7.200 | 500 | 1000 | 0.30 K | 200–350 K |
| 23 | 8.550 | 300 | 1000 | 0.25 K | 200–350 K |
| 24 | 10.800 | 1000 | 250 | 0.40 K | 200–350 K |
| 25 | 12.000 | 1000 | 250 | 0.40 K | 200–350 K |
| Date | Parameters | |
|---|---|---|
| 18 August 2019 | 20 August 2019 | |
| Time (UTC) | 06:34:00 | 05:56:10 |
| Solar Zenith | 28.470° | 28.460° |
| Solar Azimuth | −145.770° | −149.190° |
| Satellite Zenith | 21.334° | 37.430° |
| Satellite Azimuth | 261.505° | 26.130° |
| Ground Altitude | 2.360 km | 2.360 km |
| AOD@550nm | 0.167 | 0.239 |
| Item | 18 August | 20 August | |||
|---|---|---|---|---|---|
| Channel 24 | Channel 25 | Channel 24 | Channel 25 | ||
| Before Spectral Matching | At-Sensor Radiance mW/(m2·sr·cm−1) | 93.209 | 108.587 | 93.177 | 108.345 |
| At-Sensor BT (K) | 289.105 | 289.552 | 289.083 | 289.398 | |
| Raw BT (K) | 289.734 | 288.589 | 289.336 | 287.859 | |
| Difference (K) | 0.629 | −0.964 | 0.253 | −1.539 | |
| After Spectral Matching | At-Sensor Radiance mW/(m2·sr·cm−1) | 94.680 | 107.800 | 94.647 | 107.559 |
| At-Sensor BT (K) | 290.080 | 289.049 | 290.058 | 288.895 | |
| Raw BT (K) | 289.734 | 288.589 | 289.336 | 287.859 | |
| Difference (K) | −0.346 | −0.460 | −0.722 | −1.036 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, L.; Hu, Y.; Zhang, Y.; Li, X.-M.; Dou, C.; Li, J.; Si, Y.; Zhang, L. Radiometric Calibration Evaluation for FY3D MERSI-II Thermal Infrared Channels at Lake Qinghai. Remote Sens. 2021, 13, 466. https://doi.org/10.3390/rs13030466
Yan L, Hu Y, Zhang Y, Li X-M, Dou C, Li J, Si Y, Zhang L. Radiometric Calibration Evaluation for FY3D MERSI-II Thermal Infrared Channels at Lake Qinghai. Remote Sensing. 2021; 13(3):466. https://doi.org/10.3390/rs13030466
Chicago/Turabian StyleYan, Lin, Yonghong Hu, Yong Zhang, Xiao-Ming Li, Changyong Dou, Jun Li, Yidan Si, and Lijun Zhang. 2021. "Radiometric Calibration Evaluation for FY3D MERSI-II Thermal Infrared Channels at Lake Qinghai" Remote Sensing 13, no. 3: 466. https://doi.org/10.3390/rs13030466
APA StyleYan, L., Hu, Y., Zhang, Y., Li, X.-M., Dou, C., Li, J., Si, Y., & Zhang, L. (2021). Radiometric Calibration Evaluation for FY3D MERSI-II Thermal Infrared Channels at Lake Qinghai. Remote Sensing, 13(3), 466. https://doi.org/10.3390/rs13030466










