Reduced-Complexity End-to-End Variational Autoencoder for on Board Satellite Image Compression
Abstract
1. Introduction
2. Background: Autoencoder Based Image Compression
2.1. Analysis and Synthesis Transforms
2.2. Bottleneck
2.3. Parameter Learning and Entropy Model Estimation
2.3.1. Loss Function: Rate Distortion Trade-Off
- The rate R achieved by an entropy coder is lower-bounded by the entropy derived from the actual discrete probability distribution of the quantized vector . The rate increase comes from the mismatch between the probability model required for the coder design and . The bit-rate is given by the Shannon cross entropy between the two distributions:where means distributed according to. The bit-rate is thus minimized if the distribution model is equal to the distribution arising from the actual distribution of the input image and from the analysis transform . This highlights the key role of the probability model.
- The distortion measure D is chosen to account for image quality as perceived by a human observer. Due to its many desirable computational properties, the mean square error (MSE) is generally selected. However, a measure of perceptual distortion may also be employed such as the multi-scale structural similarity index (MS-SSIM) [24].
2.3.2. Entropy Model
- Fully factorized model: For simplicity, in [13,14], the approximated quantized representation was assumed independent and identically distributed within each channel and the channels were assumed independent of each other, resulting in a fully factorized distribution:where index i runs over all elements of the representation, through channels and through spatial locations, is the distribution model parameter vector associated with each element. As mentioned previously, for back-propagation derivation during the training step, the quantization process () is approximated by the addition of an i.i.d uniform noise , whose range is defined by the quantization step. Due to the adaptive local normalization performed by GDN non-linearities, the quantization step can be set to one without loss of generality. Hence the quantized representation , which is a discrete random variable taking values in , is modelled by the continuous random vector defined by:taking values in . The addition of the uniform quantization noise leads to the following expression for defined through a convolution by a uniform distribution on the interval :For generality, in [13], the distribution is assumed non parametric, namely without predefined shape. In [13,14], the parameter vectors are learned from data during the training phase. This learning, performed once and for all, prohibits adaptivity to the input images during operational phase. Moreover, the simplifying hypothesis of a fully factorized distribution is very strong and not satisfied in practice, elements of exhibiting strong spatial dependency as observed in [16]. To overcome these limitations and thus to obtain a more realistic and more adaptive entropy model, [16] proposed a hyperprior model, derived through a variational autoencoder, which takes into account possible spatial dependency in each input image.
- Hyperprior model: Auxiliary random variables , conditioned on which the quantized representation elements are independent, are derived from by an auxiliary autoencoder, connected in parallel with the bottleneck (right column of Figure 1 (right)). The hierarchical model hyper-parameters are learned for each input image in operational phase. Firstly, the hyperprior transform analysis produces the set of auxiliary random variables . Secondly, is transformed by the hyperprior synthesis transform into a second set of random variables . In [16], distribution is assumed fully factorized and each representation element , knowing , is modeled by a zero-mean Gaussian distribution with its own standard deviation . Finally, taking into account the quantization process, the conditional distribution of each quantized representation element is given by:The rate computation must take into account the prior distribution of , which has to be transmitted to the decoder with the compressed data, as side information.
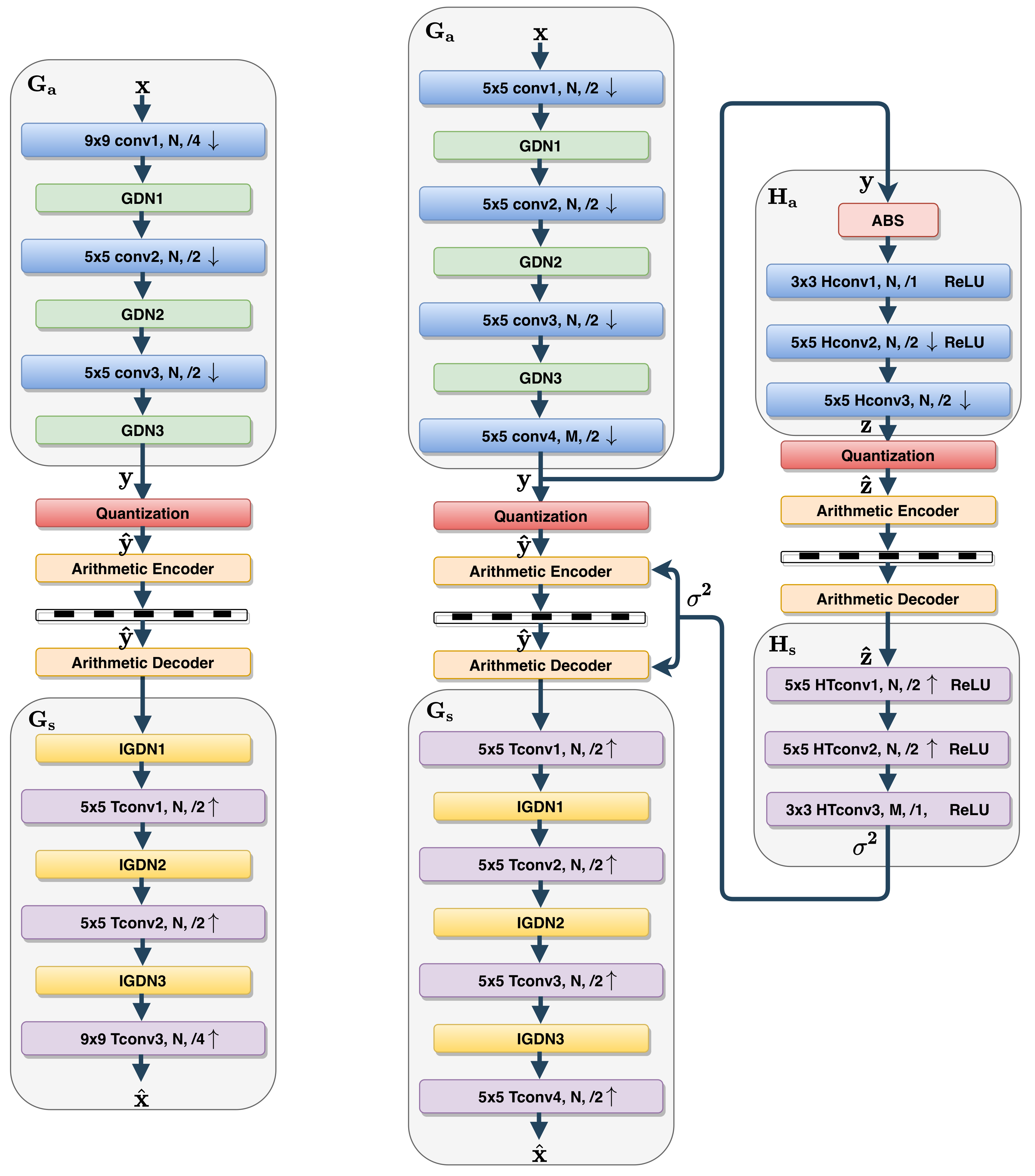
3. Reduced-Complexity Variational Autoencoder
3.1. Analysis and Synthesis Transforms
3.1.1. Complexity Assessment
3.1.2. Proposal: Simplified Analysis and Synthesis Transforms
3.2. Reduced Complexity Entropy Model
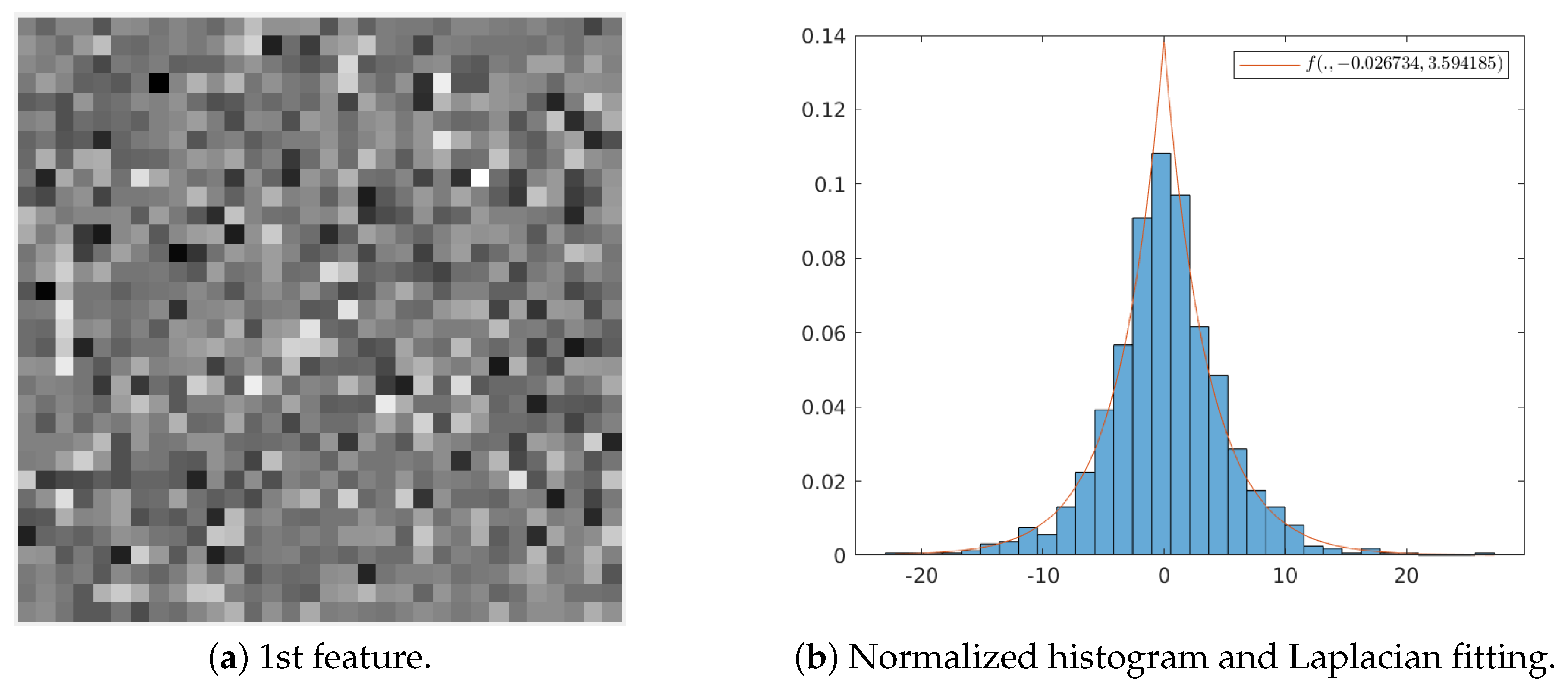
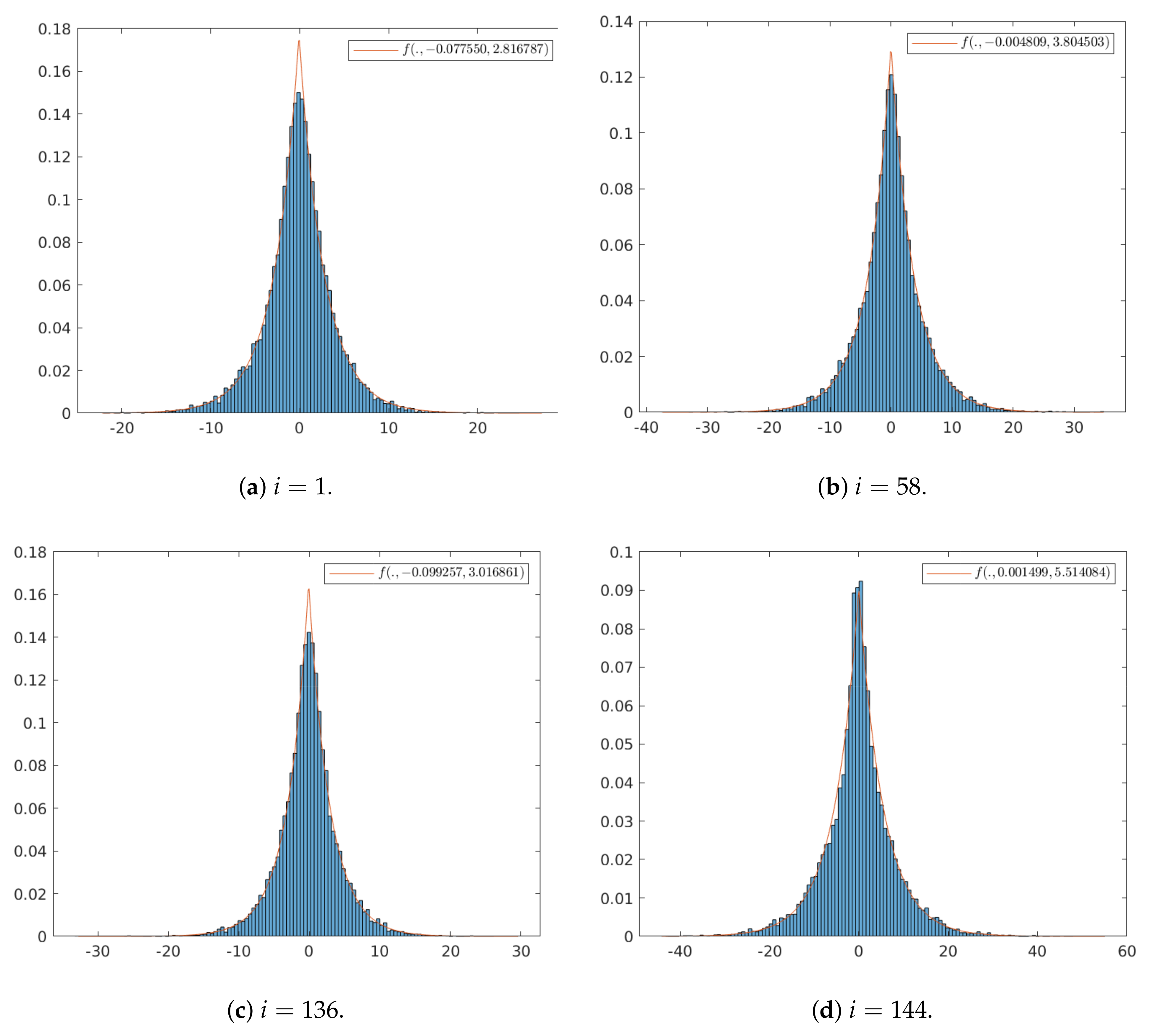
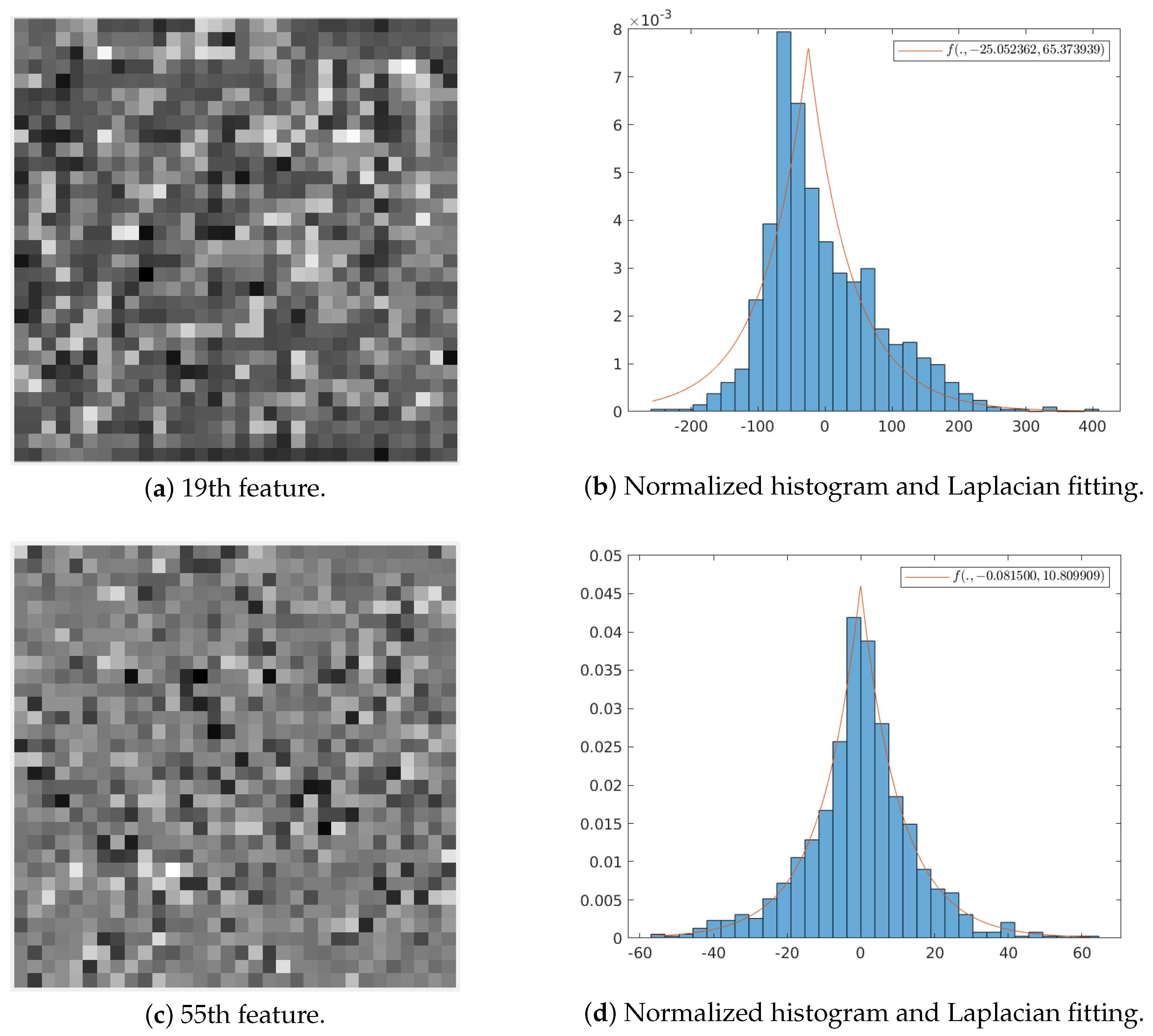
3.2.1. Statistical Analysis of the Learned Transform
3.2.2. Proposal: Simplified Entropy Model
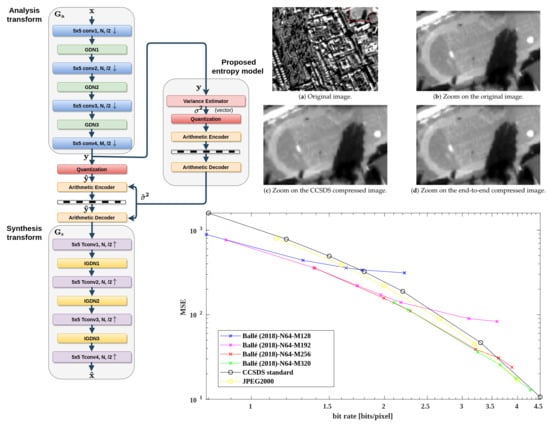
4. Performance Analysis
4.1. Implementation Setup
4.2. Subjective Image Quality Assessment
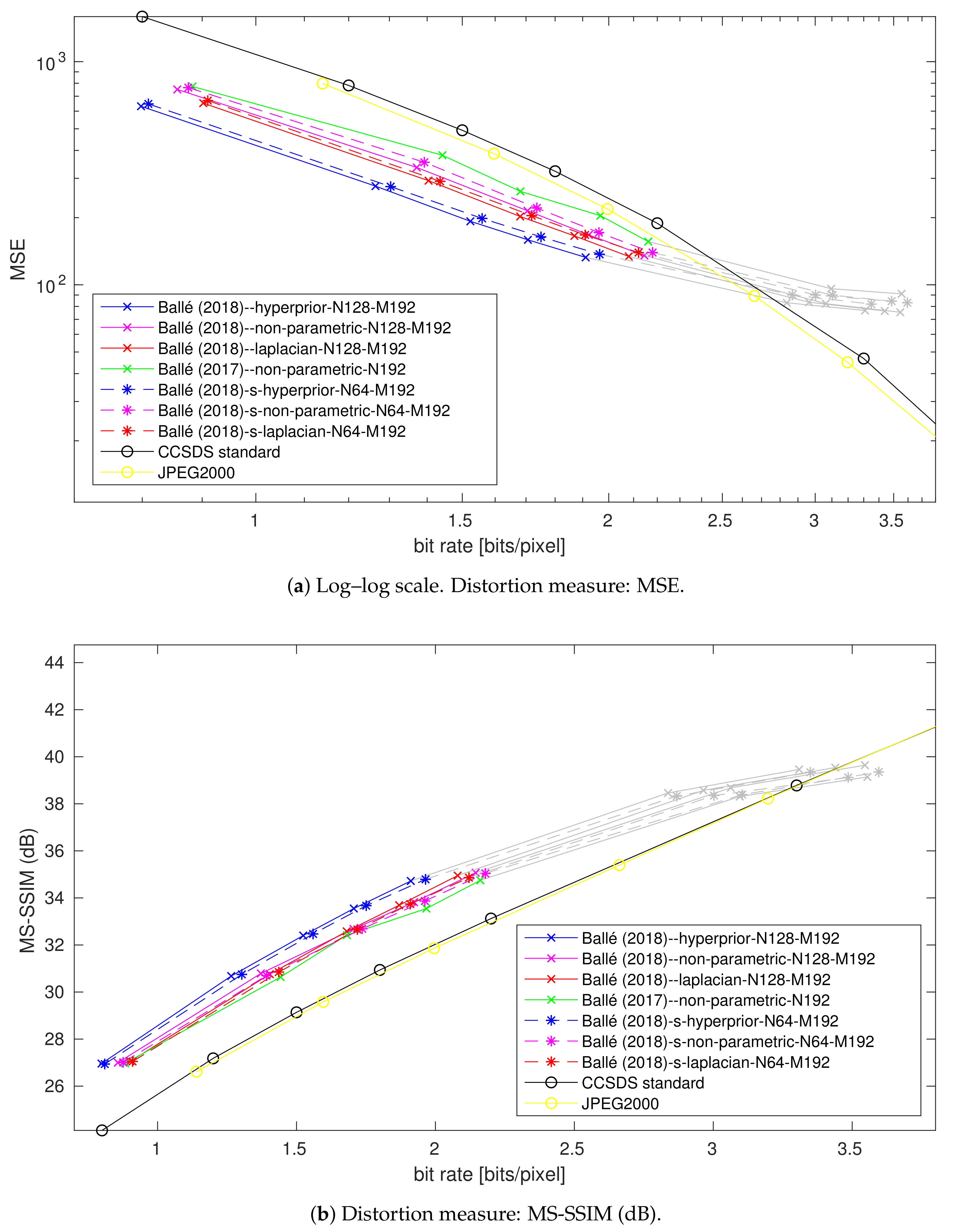
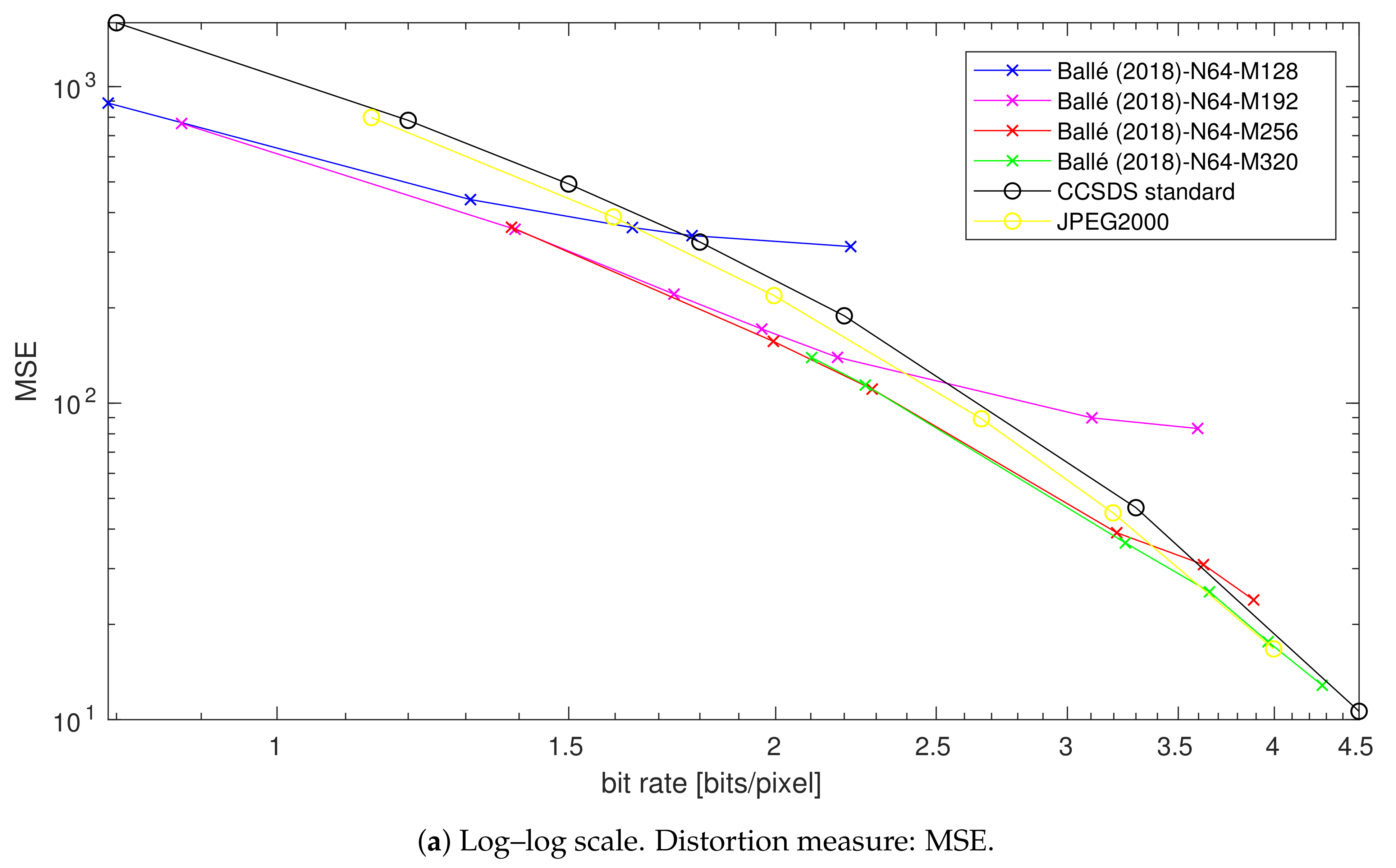
4.3. Impact of the Number of Filter Reduction
4.3.1. At Low Rates
4.3.2. At High Rates
4.3.3. Summary
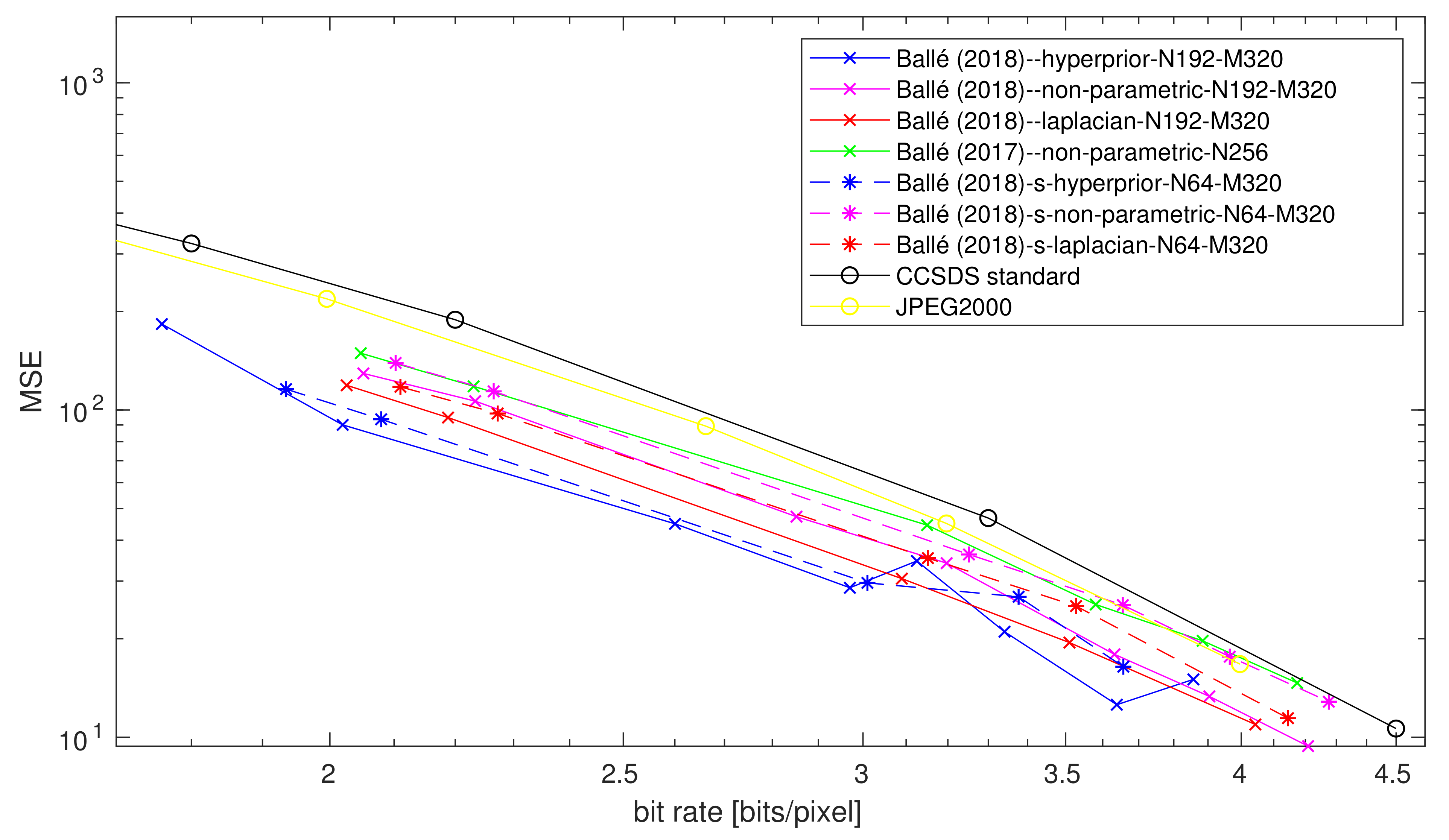
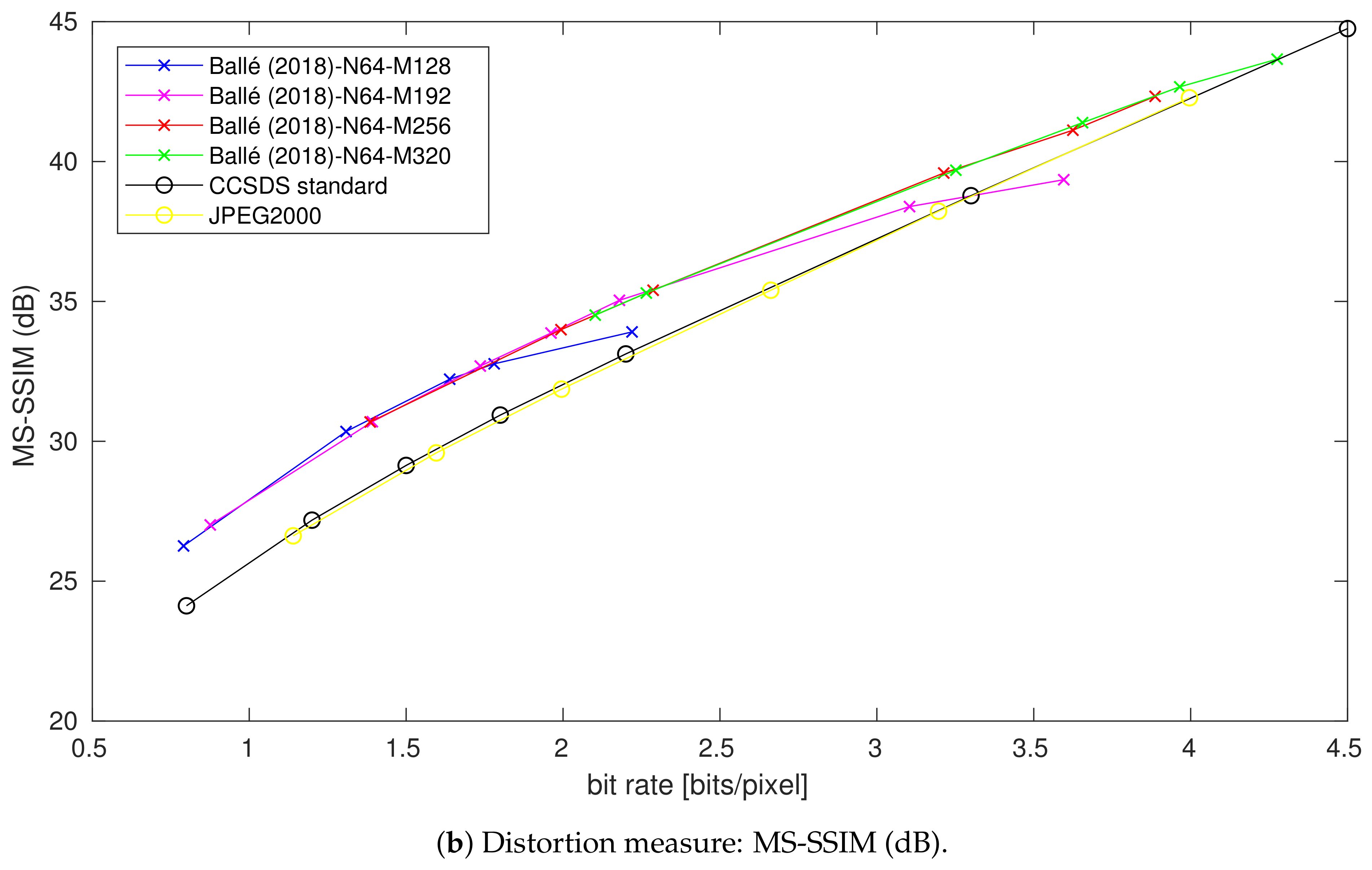
4.4. Impact of the Bottleneck Size
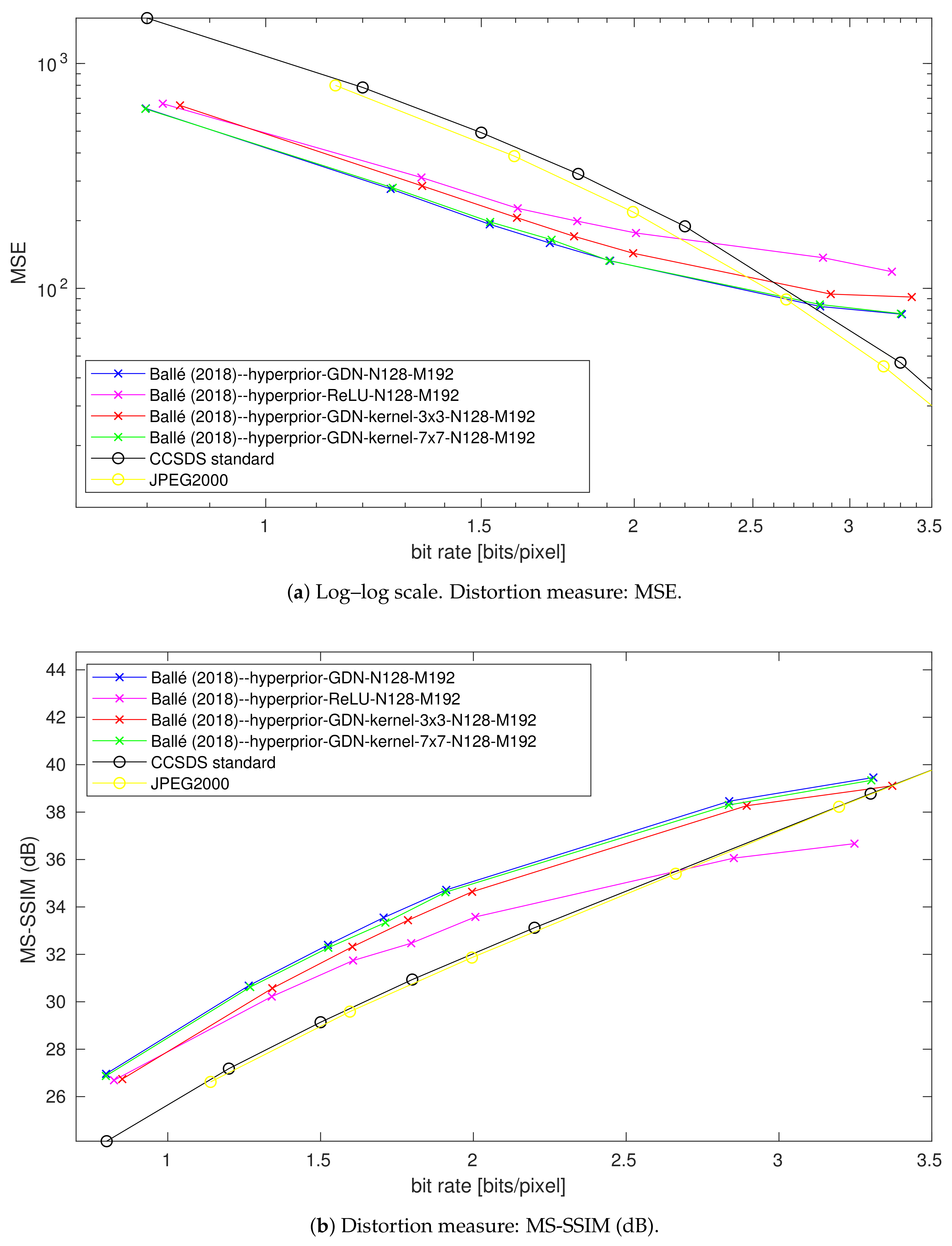
4.5. Impact of the Gdn/Igdn Replacement in the Main Autoencoder
4.6. Impact of the Filter Kernel Support in the Main Autoencoder
4.7. Impact of the Entropy Model Simplification
4.7.1. At Low Rates
4.7.2. At High Rates
4.7.3. Summary
4.8. Discussion About Complexity
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CCSDS | Consultative committee for space data systems |
| CNN | Convolutional neural networks |
| DCT | Discrete cosine transform |
| GDN | Generalized divisive normalization |
| IGDN | Inverse generalized divisive normalization |
| JPEG | Joint photographic experts group |
| MSE | Mean square error |
| MS-SSIM | Multi-scale structural similarity index |
| PCA | Principal component analysis |
| ReLU | Rectified Linear Unit |
Appendix A. Table of Symbols Used
| Symbol | Meaning | Reference |
|---|---|---|
| original image | Section 2.1 | |
| analysis transform | Section 2.1 | |
| learned representation | Section 2.1 | |
| quantized learned representation | Section 2.1 | |
| synthesis transform | Section 2.1 | |
| reconstructed image | Section 2.1 | |
| GDN | generalized divisive normalizations | Section 2.1 |
| IGDN | inverse generalized divisive normalizations | Section 2.1 |
| N | filters composing the convolutional layers | Section 2.1 |
| kernel support | Section 2.1 | |
| M | filters composing the last layer of | Section 2.1 |
| coordinate indexes of the output of the ith filter | Section 2.1 | |
| value indexed by of the output of the ith filter | Section 2.1 | |
| quantizer | Section 2.2 | |
| J | rate-distortion loss function | Section 2.3.1 |
| rate | Section 2.3.1 | |
| distortion between the original image and the reconstructed image | Section 2.3.1 | |
| parameter that tunes the rate-distortion trade-off | Section 2.3.1 | |
| actual discrete probability distribution | Section 2.3.1 | |
| probability model assigned to the quantized representation | Section 2.3.1 | |
| bit-rate given by the Shannon cross entropy | Section 2.3.1 | |
| distribution model parameter vector associated with each element | Section 2.3.2 | |
| i.i.d uniform noise | Section 2.3.2 | |
| continuous approximated quantized learned representation | Section 2.3.2 | |
| set of auxiliary random variables | Section 2.3.2 | |
| hyperprior analysis transform | Section 2.3.2 | |
| hyperprior synthesis transform | Section 2.3.2 | |
| standard deviation of a zero-mean Gaussian distribution | Section 2.3.2 | |
| number of features at the considered layer input | Section 3.1.1 | |
| number of features at the considered layer output | Section 3.1.1 | |
| number of parameters associated with the filtering part of the considered layer | Section 3.1.1 | |
| term accounting for the bias | Section 3.1.1 | |
| D | downsampling factor | Section 3.1.1 |
| channel input size | Section 3.1.1 | |
| downsampled input channel size | Section 3.1.1 | |
| number of floating points operations | Section 3.1.1 | |
| number of parameters associated with each IGDN/GDN | Section 3.1.1 | |
| number of floating points operations of each GDN/IGDN | Section 3.1.1 | |
| random variable that follows a Laplacian distribution | Section 3.2.1 | |
| mean value of a Laplacian distribution | Section 3.2.1 | |
| b | scale parameter of a Laplacian distribution | Section 3.2.1 |
| variance of a laplacian distributed random variable | Section 3.2.1 | |
| feature map elements | Section 3.2.2 | |
| set of indexes covering the jth feature | Section 3.2.2 |
References
- Yu, G.; Vladimirova, T.; Sweeting, M.N. Image compression systems on board satellites. Acta Astronaut. 2009, 64, 988–1005. [Google Scholar] [CrossRef]
- Huang, B. Satellite Data Compression; Springer Science & Business Media: New York, NY, USA, 2011. [Google Scholar]
- Qian, S.E. Optical Satellite Data Compression and Implementation; SPIE Press: Bellingham, WA, USA, 2013. [Google Scholar]
- Goyal, V.K. Theoretical foundations of transform coding. IEEE Signal Process. Mag. 2001, 18, 9–21. [Google Scholar] [CrossRef]
- Taubman, D.; Marcellin, M. JPEG2000 Image Compression Fundamentals, Standards and Practice; Springer Publishing Company: New York, NY, USA, 2013. [Google Scholar]
- Book, B. Consultative Committee for Space Data Systems (CCSDS), Image Data Compression CCSDS 122.0-B-1, Ser. Blue Book; CCSDS: Washington, DC, USA, 2005. [Google Scholar]
- Bengio, Y. Learning deep architectures for AI. Found. Trends Mach. Learn. 2009, 2, 1–127. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 7132–7141. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Kaiser, P.; Wegner, J.D.; Lucchi, A.; Jaggi, M.; Hofmann, T.; Schindler, K. Learning aerial image segmentation from online maps. IEEE Trans. Geosci. Remote. Sens. 2017, 55, 6054–6068. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a gaussian denoiser: Residual learning of deep CNN for image denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef] [PubMed]
- Wiatowski, T.; Bölcskei, H. A mathematical theory of deep convolutional neural networks for feature extraction. IEEE Trans. Inf. Theory 2017, 64, 1845–1866. [Google Scholar] [CrossRef]
- Ballé, J.; Laparra, V.; Simoncelli, E. End-to-end optimized image compression. In Proceedings of the International Conference on Learning Representations (ICLR), Toulon, France, 24–26 April 2017. [Google Scholar]
- Theis, L.; Shi, W.; Cunningham, A.; Huszár, F. Lossy image compression with compressive autoencoders. In Proceedings of the International Conference on Learning Representations (ICLR), Toulon, France, 24–26 April 2017. [Google Scholar]
- Rippel, O.; Bourdev, L. Real-Time Adaptive Image Compression. In Proceedings of the International Conference on Machine Learning (ICML), Sydney, Australia, 6–11 August 2017; pp. 2922–2930. [Google Scholar]
- Ballé, J.; Minnen, D.; Singh, S.; Hwang, S.J.; Johnston, N. Variational image compression with a scale hyperprior. In Proceedings of the International Conference on Learning Representations (ICLR), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Bellard, F. BPG Image Format. 2015. Available online: https://bellard.org/bpg (accessed on 15 December 2020).
- Cheng, Z.; Sun, H.; Takeuchi, M.; Katto, J. Deep Residual Learning for Image Compression. In Proceedings of the 2019 IEEE Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Ballé, J. Efficient Nonlinear Transforms for Lossy Image Compression. In Proceedings of the 2018 IEEE Picture Coding Symposium (PCS), San Francisco, CA, USA, 24–27 June 2018; pp. 248–252. [Google Scholar]
- Lyu, S. Divisive normalization: Justification and effectiveness as efficient coding transform. Adv. Neural Inf. Process. Syst. 2010, 23, 1522–1530. [Google Scholar]
- Rissanen, J.; Langdon, G. Universal modeling and coding. IEEE Trans. Inf. Theory 1981, 27, 12–23. [Google Scholar] [CrossRef]
- Martin, G. Range encoding: An algorithm for removing redundancy from a digitised message. In Proceedings of the Video and Data Recording Conference, Southampton, UK, 24–27 July 1979; pp. 24–27. [Google Scholar]
- Van Leeuwen, J. On the Construction of Huffman Trees. In Proceedings of the International Colloquium on Automata, Languages, and Programming (ICALP), Edinburgh, UK, 20–23 July 1976; pp. 382–410. [Google Scholar]
- Wang, Z.; Simoncelli, E.P.; Bovik, A.C. Multiscale structural similarity for image quality assessment. In Proceedings of the Thrity-Seventh Asilomar Conference on Signals, Systems & Computers, Pacific Grove, CA, USA, 9–12 November 2003; pp. 1398–1402. [Google Scholar]
- Dumas, T.; Roumy, A.; Guillemot, C. Autoencoder based image compression: Can the learning be quantization independent? In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 1188–1192. [Google Scholar]
- Lam, E.Y.; Goodman, J.W. A mathematical analysis of the DCT coefficient distributions for images. IEEE Trans. Image Process. 2000, 9, 1661–1666. [Google Scholar] [CrossRef] [PubMed]
- Pratt, J.W.; Gibbons, J.D. Kolmogorov-Smirnov two-sample tests. In Concepts of Nonparametric Theory; Springer: New York, NY, USA, 1981; pp. 318–344. [Google Scholar]
- Hu, Y.; Yang, W.; Ma, Z.; Liu, J. Learning End-to-End Lossy Image Compression: A Benchmark. arXiv 2020, arXiv:2002.03711. [Google Scholar]
- Book, G. Consultative Committee for Space Data Systems (CCSDS), Image Data Compression CCSDS 120.1-G-2, Ser. Green Book; CCSDS: Washington, DC, USA, 2015. [Google Scholar]





| Layer | Filter Size | Channels | Output | Parameters | FLOPp | |||
|---|---|---|---|---|---|---|---|---|
| n | n | |||||||
| conv1 | 5 | 5 | 1 | 64 | 256 | 256 | 1664 | |
| GDN1 | 4160 | |||||||
| conv2 | 5 | 5 | 64 | 64 | 128 | 128 | 102,464 | |
| GDN2 | 4160 | |||||||
| conv3 | 5 | 5 | 64 | 64 | 64 | 64 | 102,464 | |
| GDN3 | 4160 | |||||||
| conv4 | 5 | 5 | 64 | 192 | 32 | 32 | 307,392 | |
| Hconv1 | 3 | 3 | 192 | 64 | 32 | 32 | 110,656 | |
| Hconv2 | 5 | 5 | 64 | 64 | 16 | 16 | 102,464 | |
| Hconv3 | 5 | 5 | 64 | 64 | 8 | 8 | 102,464 | |
| HTconv1 | 5 | 5 | 64 | 64 | 16 | 16 | 102,464 | |
| HTconv2 | 5 | 5 | 64 | 64 | 32 | 32 | 102,464 | |
| HTconv3 | 3 | 3 | 64 | 192 | 32 | 32 | 110,784 | |
| Tconv1 | 5 | 5 | 192 | 64 | 64 | 64 | 307,264 | |
| IGDN1 | 4160 | |||||||
| Tconv2 | 5 | 5 | 64 | 64 | 128 | 128 | 102,464 | |
| IGDN2 | 4160 | |||||||
| Tconv3 | 5 | 5 | 64 | 64 | 256 | 256 | 102,464 | |
| IGDN3 | 4160 | |||||||
| Tconv4 | 5 | 5 | 64 | 1 | 512 | 512 | 1601 | |
| Total | 1,683,969 | |||||||
| Method | Parameters | FLOPp | Relative |
|---|---|---|---|
| Ballé(2018)–hyperprior-N128-M192 | 5,055,105 | 1.00 | |
| Ballé(2018)-s-hyperprior-N64-M192 | 1,683,969 | 0.27 | |
| Ballé(2018)-s-laplacian-N64-M192 | 1,052,737 | 0.265 |
| Method | Parameters | FLOPp | Relative |
|---|---|---|---|
| Ballé(2018)–hyperprior-N192-M320 | 11,785,217 | 1.00 | |
| Ballé(2018)-s-hyperprior-N64-M320 | 1,683,969 | 0.13 | |
| Ballé(2018)-s-laplacian-N64-M320 | 1,052,737 | 0.1273 |
| Method | Parameters | FLOPp | Relative |
|---|---|---|---|
| Ballé(2018)-s-hyperprior-N64-M192 | 1,157,696 | 1 | |
| Ballé(2018)-s-laplacian-N64-M192 | 526,464 | 0.87 |
| Method | Parameters | FLOPp | Relative |
|---|---|---|---|
| Ballé(2018)-s-hyperprior-N64-M320 | 1,715,008 | 1 | |
| Ballé(2018)-s-laplacian-N64-M320 | 731,392 | 0.8432 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alves de Oliveira, V.; Chabert, M.; Oberlin, T.; Poulliat, C.; Bruno, M.; Latry, C.; Carlavan, M.; Henrot, S.; Falzon, F.; Camarero, R. Reduced-Complexity End-to-End Variational Autoencoder for on Board Satellite Image Compression. Remote Sens. 2021, 13, 447. https://doi.org/10.3390/rs13030447
Alves de Oliveira V, Chabert M, Oberlin T, Poulliat C, Bruno M, Latry C, Carlavan M, Henrot S, Falzon F, Camarero R. Reduced-Complexity End-to-End Variational Autoencoder for on Board Satellite Image Compression. Remote Sensing. 2021; 13(3):447. https://doi.org/10.3390/rs13030447
Chicago/Turabian StyleAlves de Oliveira, Vinicius, Marie Chabert, Thomas Oberlin, Charly Poulliat, Mickael Bruno, Christophe Latry, Mikael Carlavan, Simon Henrot, Frederic Falzon, and Roberto Camarero. 2021. "Reduced-Complexity End-to-End Variational Autoencoder for on Board Satellite Image Compression" Remote Sensing 13, no. 3: 447. https://doi.org/10.3390/rs13030447
APA StyleAlves de Oliveira, V., Chabert, M., Oberlin, T., Poulliat, C., Bruno, M., Latry, C., Carlavan, M., Henrot, S., Falzon, F., & Camarero, R. (2021). Reduced-Complexity End-to-End Variational Autoencoder for on Board Satellite Image Compression. Remote Sensing, 13(3), 447. https://doi.org/10.3390/rs13030447