Moving Target Detection and Parameter Estimation via a Modified Imaging STAP with a Large Baseline in Multistatic GEO SAR

Abstract

With the development trends of multistatic spaceborne synthetic aperture radar (SAR), geosynchronous SAR (GEO SAR) employing several formation-flying small satellites also has great potential for remote sensing. The small satellites can cooperate to acquire multi-channel data for moving target detection and parameter estimation in strong clutters. However, multistatic GEO SAR has large satellite spacing and a curved trajectory, which induce the near-field effects and channels out of alignment, respectively, bringing about challenges for the spatial adaptive processing. These problems produce a high-order term in the multi-channel slant range model, making the traditional model and adaptive processing method invalid. In this paper, to meet the requirement of SAR focusing, we firstly derive a fourth-order slant range model and a third-order path difference model for multistatic GEO SAR. Secondly, based on the derived model, the principle of stationary phase and series reversion method are utilized to derive the spatial steering vector for a moving target, which is a basis of spatial adaptive processing in the range-Doppler domain. Thirdly, the time-domain match filtering is constructed based on the fourth-order slant range model to image the moving target. Additionally, the moving targets are detected in the image domain. The motion parameter is estimated by iteratively maximizing the output signal to clutter and noise ratio (SCNR) through the range of possible target velocities. Finally, considering that the GEO SAR is still in development, the computer simulations are carried out to verify the effectiveness and evaluate the performance.

1. Introduction

Geosynchronous synthetic aperture radar (GEO SAR) refers to the high-resolution imaging system running in an orbit of approximately 36,000 km [1,2]. The high orbit brings in the benefits of a large coverage area and short revisit time [3]. Therefore, GEO SAR has excellent potential in remote sensing, disaster management, marine monitoring, etc. Most GEO SAR research focuses on system design and optimization, resolution analysis, accurate imaging algorithms, and deformation retrieval [4,5,6,7,8,9,10].

With the development trends of multistatic spaceborne SAR, much research is carried out on multistatic GEO SAR formation. It was demonstrated that multistatic GEO SAR can accomplish complex space missions. One typical system is the Advanced Radar Geosynchronous Observation System (ARGOS) [11], which utilizes several GEO satellites to image at a medium resolution within the aperture time of 20–40 min. It has notable performance in detecting landslides, floods, soil moisture changes, volcanic activity, earthquakes, and facility deformation [11,12,13,14].

Some other research has discussed the system optimization, including integration time optimization for grating lobe suppression in a sparse multistatic GEO SAR [15] and orbital element optimization for minimizing the along-track baseline in a formation-flying multistatic GEO interferometry SAR (InSAR) [16]. Moreover, geosynchronous spaceborne–airborne bistatic SAR has also been studied for system configuration and imaging [17,18]. The target’s velocity estimation for GEO SAR has been investigated in [19], by exploiting the non-uniform cubic phase function (NU-CPF) algorithm, which is only applicable in high SNR. In order to improve the SNR, the generalized Radon-Fourier transform (GRFT)-based target detection and imaging method are proposed in [20]. However, these methods are studied for the monostatic case. A displaced phase center antenna (DPCA) method for GEO SAR with three antennas has been shown in [21], but the method fails in multistatic GEO SAR where the DPCA condition is not satisfied. Research related to moving target indication (MTI) in multistatic GEO SAR has not been carried out.

Multistatic GEO SAR can detect moving targets with better performance compared to a single-channel system. The spatial degrees of freedom of multistatic GEO SAR can be employed for clutter suppression. Besides, the GEO SAR formation can form a sizeable along-track baseline compared with a single GEO SAR platform with an array antenna. The large baseline can reduce the minimum detectable velocity [22]. Thus, multistatic GEO SAR can employ multi-channel MTI techniques and indicate slow-moving targets in strong clutters.

Currently, multi-channel MTI methods are well developed in airborne and low Earth orbit (LEO) SAR systems [23,24,25], especially space-time adaptive processing (STAP) [26,27,28,29,30,31]. Post-Doppler STAP techniques [32] can be used in SAR data, and they are performed on each range-Doppler cell to maximize the target signal to noise ratio (SNR). However, this method requires a short coherent processing interval (CPI), which causes the SNR loss because most of the available pulses are not involved in processing. Imaging STAP (ISTAP) [33,34,35] was put forward to integrate all the pulses coherently and obtain an optimal SNR.

Usually, ISTAP is applied in the multi-channel LEO SAR systems, which use a uniform linear array antenna with small channel spacing. However, in multistatic GEO SAR, the spatial interval between GEO SAR satellites is large enough to avoid the collision, ranging from several kilometers to a few tens of kilometers. The large baseline leads to near-field effects and curved trajectory in the multistatic SAR spatial adaptive processing [36]. Thus, different channels in multistatic GEO SAR each have a different direction of arrival (DOA). The traditional ISTAP method leads to the SNR loss and detection performance degradation. To guarantee a consistent DOA for different channels, we must compensate for the phase errors for different channels caused by near-field effects and curved trajectory during the ISTAP processing.

In this paper, a modified ISTAP considering near field effects is developed to adapt to multistatic GEO SAR characteristics. The moving target’s range model analysis for multistatic GEO SAR has been investigated in [37]. However, the accurate signal model in the frequency domain and the detailed MTI process are not given. These two issues are studied in this paper. This paper has three main goals. The first goal is to derive an accurate multi-channel signal model considering the near-field effects and curved multistatic GEO SAR trajectory. The second objective is to provide an optimal MTI processing for multistatic GEO SAR, which can achieve target detection, motion parameter estimation, and target refocusing. The final goal is to validate the proposed method’s effectiveness and investigate the multistatic GEO SAR performance.

This paper is organized as follows. Section 2 discusses special problems in multistatic GEO SAR, including near-field effects and curved trajectory. Then, a multi-channel parametric model of the moving target is constructed based on the near-field geometry and curved trajectory in Section 3. Section 4 derives the modified ISTAP processing framework in the near field, including clutter suppression, beamforming, imaging, and velocity searching. Finally, computer simulations are carried out to verify the effectiveness of the proposed model and method in Section 5. In the simulation, the background clutter is produced according to the K distribution, whose parameters are obtained based on the Ryan–Johnson model according to the radar parameters.

2. Special Problems of Multistatic GEO SAR MTI

Multistatic GEO SAR consists of several GEO satellites and can acquire multi-channel data simultaneously. We studied a multistatic GEO SAR where satellites are distributed in the along-track direction. The along-track spacing must be large enough (ranging from several kilometers to dozens of kilometers) to guarantee the satellites’ safety and formation stability. This section will discuss the near-field effects and curved trajectory of multistatic GEO SAR caused by the large channel spacing.

2.1. Geometry of Multistatic GEO SAR

In the studied multistatic GEO SAR, all the satellites can be used as transmitters and receivers. They transmit signals at the same time and receive echoes. Assuming there are N satellites, the multistatic system can generate $N\left(N+1\right)/2$ SAR data sets simultaneously.

In this paper, the moving target is thought to be a prominent point target. Therefore, the assumption was made that the waveforms are fully orthogonal. The system’s synchronization can be achieved by the direct wave. Therefore, they are not the research emphasis of this paper.

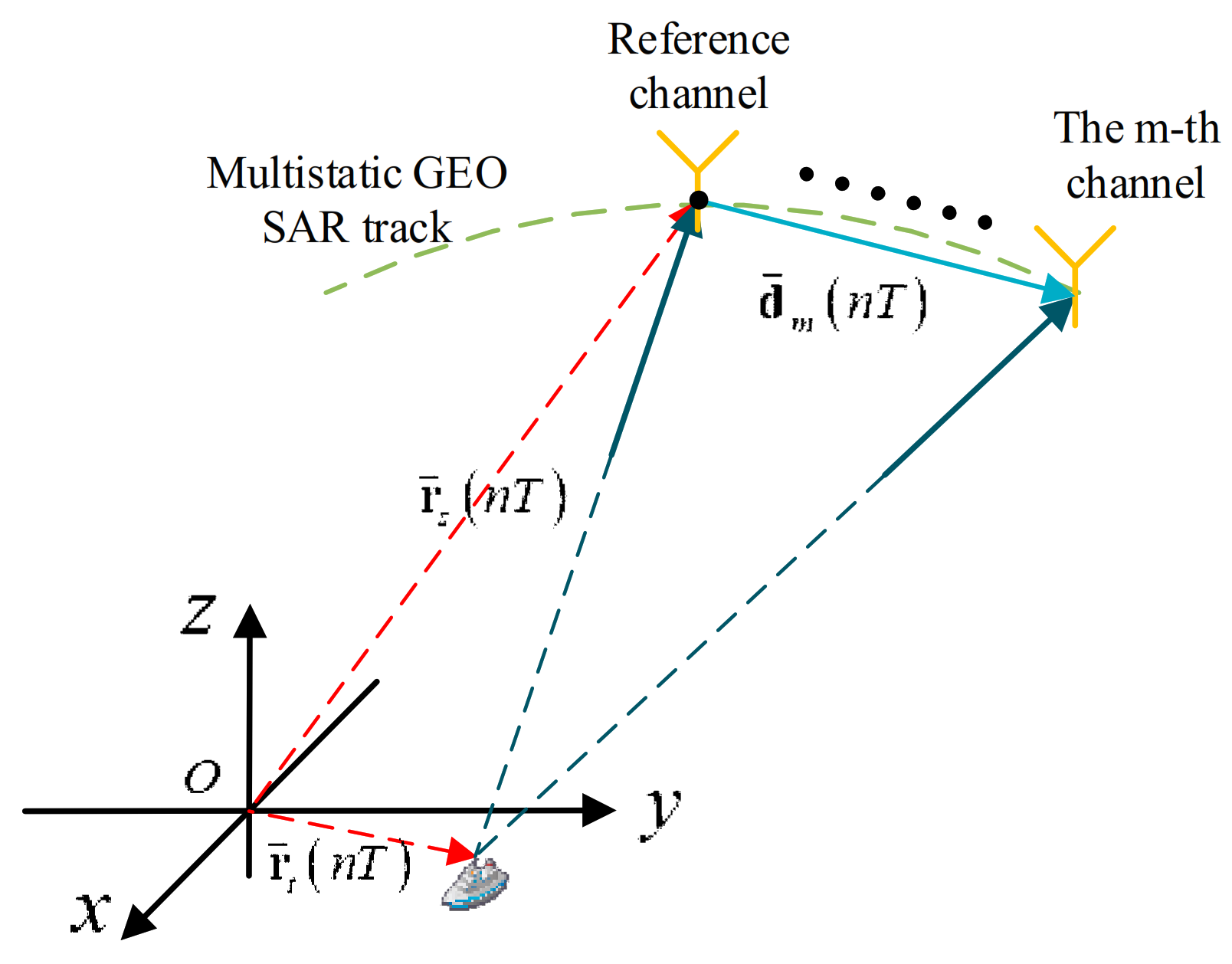
The satellites in multistatic GEO SAR distribute along the trajectory so that the multi-channel data can be used to detect and image the moving target. Figure 1 shows the geometry for moving target detection. The coordinate system OXYZ is the Earth-Centered, Earth-Fixed (ECEF) system. It is assumed that there are M channels, and the first channel is selected as the reference channel. The position of the reference channel is ${\stackrel{\rightharpoonup }{r}}_s\left(nT\right)$, and the position vector of the moving target is ${\stackrel{\rightharpoonup }{r}}_t\left(nT\right)={\stackrel{\rightharpoonup }{r}}_{t0}+\stackrel{\rightharpoonup }{v}·nT$. The baseline vector from the reference channel to the mth channel is ${\stackrel{\rightharpoonup }{d}}_m\left(nT\right)$. The notations in this paper are listed in

Table 1. Notation list of this paper.

Symbol	Explanation	Symbol	Explanation
$n$	Slow time	$T$	Pulse repetition time
$c$	Speed of light	$a_a\left(·\right)$	The envelope in the azimuth direction
$\lambda$	Wavelength	$a_r\left(·\right)$	The envelope in range direction
${\sigma }_s^m$	The amplitude of the target received by the mth channel	$k_r$	The frequency modulation rate in range direction
${\phi }_s^m$	The phase of the target received by the mth channel	${\mathbf{\vartheta }}_s$	The set of moving target’s position and its velocity
$k_1~k_4$	Coefficients of each order of the Taylor expansion of the reference channel’s slant range history	${\mathbf{\vartheta }}_c$	The set of stationary target’s position and its velocity
${\mathbf{I}}_M$	M-dimensional identity matrix	${\sigma }_n^2$	The variance of thermal noise
${\phi }_s$	The phase of the target	${\sigma }_s$	The amplitude of the target
M	Number of channels	$\Delta k_1~\Delta k_3$	Coefficients of each order of the Taylor expansion of the path difference
$r$	The range position in SAR image	$x$	The azimuth position in SAR image

.

2.2. Ship Oscillatory Motions Effects

Multistatic GEO SAR has the potential for maritime target detection. The characteristics of maritime targets for the multistatic GEO SAR system are discussed briefly in this section. Multistatic GEO SAR requires a long synthetic aperture time to obtain high-SNR and high-resolution images. During the observation time, ship targets may have non-uniform motions. Ships in the open seas have large tonnage, and their speeds are assumed to be constant during SAR observation [19]. Therefore, the non-uniform motions of ships are mainly due to oscillation.

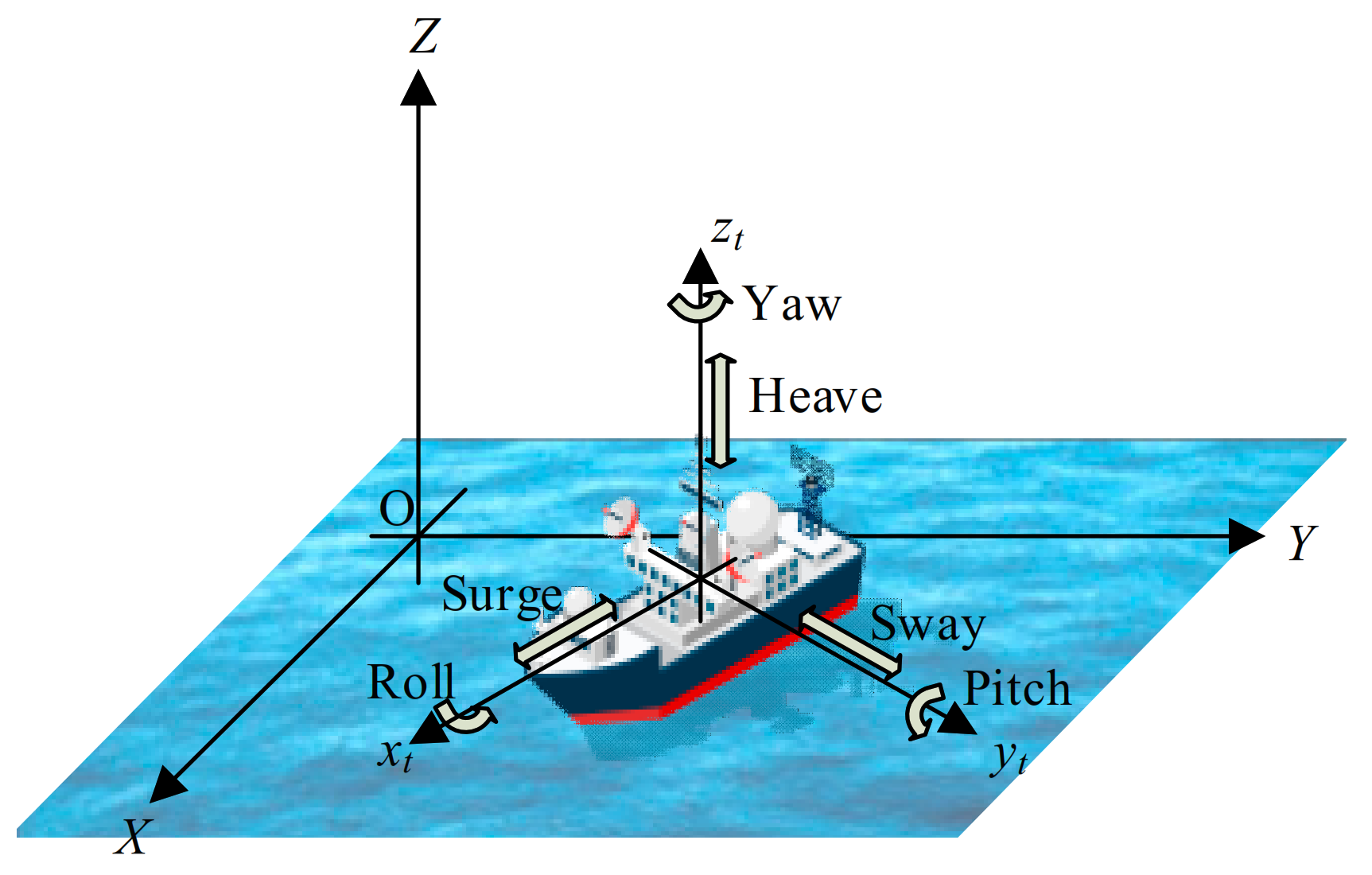
The ship oscillatory motions are mainly driven by the sea surface waves and tend to be sinusoidal. Due to the random sea waves, the vessel will exhibit six-freedom motion, as shown in Figure 2, including surge, sway, heave, roll, pitch, and yaw. Yaw, surge, and heave motions have large damping, while sway motion is relatively small, so they are not considered. Therefore, the ship’s oscillatory movements are mainly generated by roll and pitch motions [38]. In the STAP method, it is necessary to build a high-precision phase difference signal model between channels; thus, the ship oscillation’s impact on the phase difference between channels is analyzed as follow.

Firstly, two coordinate systems are constructed to describe the relative relations between the satellite and any scatter point on the ship. One is the reference coordinate system OXYZ, which does not move with the ship. Its origin locates at the center of the scene. The x-axis is parallel to the ship’s longitudinal direction at aperture center moment (ACM), the y-axis is parallel to the ship’s transverse direction at ACM, and the z-axis is vertical. Another one is the hull coordinate system $o_t{x}_t{y}_t{z}_t$, which moves with the ship. The origin is located at the ship’s center of gravity, $o_t{x}_t$ always points to the bow, $o_t{y}_t$ always points to the port side, and $o_t{z}_t$ completes the right-hand coordinate system.

According to the coordinate transformation method in [39], the mth channel position of multistatic GEO SARs in the reference coordinate system can be obtained and represented by $r_{S,m}\left(nT\right)$. It is assumed that the ship sails with constant speed, and its center of gravity is located at $r_C\left(nT\right)$ in the reference coordinate system. In the presence of the sea waves, the roll angle is ${\theta }_r$, and the pitch angle is ${\theta }_p$. Then, the mth channel position in the hull coordinate system is as follows:

$$r_{S_t,m}\left(nT\right)=P_r{P}_p\left[r_{S,m}\left(nT\right)-r_C\left(nT\right)\right]$$

(1)

where $P_r$ and $P_p$ are the rotation matrices of roll and pitch, respectively.

$$P_r=\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos {\theta }_r& \sin {\theta }_r\\ 0& -\sin {\theta }_r& \cos {\theta }_r\end{array}\right]$$

(2)

$$P_p=\left[\begin{array}{ccc}\cos {\theta }_p& 0& -\sin {\theta }_p\\ 0& 1& 0\\ \sin {\theta }_p& 0& \cos {\theta }_p\end{array}\right]$$

(3)

For any scatter point $r_t$ on the ship, considering that the ship’s size is far smaller than the slant range of GEO SAR, the mth channel slant range from the scatter point to multistatic GEO SAR can be expressed as:

$$R_m\left(nT\right)=‖r_{S_t,m}\left(nT\right)-r_t‖\approx ‖r_{S_t,m}\left(nT\right)‖-\frac{r_{S_t,m}^T\left(nT\right)r_t}{‖r_{S_t,m}\left(nT\right)‖}$$

(4)

The rotation matrices $P_r$ and $P_p$ do not change the magnitude of the vector; the ship’s oscillatory motions only affect the last term in Equation (4) and the phase difference between different channels due to oscillation is:

$$\begin{array}{c}\Delta {\varphi }_{oc,mn}\left(nT\right)=\frac{4\pi }{\lambda }\Delta R_{oc,mn}=\frac{4\pi }{\lambda }\left|\frac{r_{S_t,m}^T\left(nT\right)r_t}{‖r_{S_t,m}\left(nT\right)‖}-\frac{r_{S_t,n}^T\left(nT\right)r_t}{‖r_{S_t,n}\left(nT\right)‖}\right|\\ =\frac{4\pi }{\lambda }{\left|\frac{r_{S,m}\left(nT\right)-r_C\left(nT\right)}{‖r_{S,m}\left(nT\right)-r_C\left(nT\right)‖}-\frac{r_{S,n}\left(nT\right)-r_C\left(nT\right)}{‖r_{S,n}\left(nT\right)-r_C\left(nT\right)‖}\right|}^T{P}_r{P}_p{r}_t\end{array}$$

(5)

The typical values of roll and pitch angles are used to analyze the influence of the oscillation. In sea-state 4, a typical roll angle is several degrees with the period in the order of 10 to 20 s; a typical pitch angle is 1° to 2° with the period between one-third and two-thirds of the value of the roll period [40]. In the following simulation, it was assumed that the roll angle is 10°, the roll period is 10 s, the pitch angle is 2°, and the pitch period is 3.3 s.

For the scatter point at (200,50,30) m, the phase differences between channels caused by oscillatory motions are shown in Figure 3. It can be seen that the phase differences are less than $\pi /4$ and will have no impact on coherent accumulation between channels. However, the target’s oscillatory motions will cause the defocusing when imaging, even if the velocity has been known. Many techniques investigate the ship target’s refocusing method [40]; the oscillatory motions’ compensation was not the key point of our paper. Therefore, the oscillatory motions are ignored in multi-channel signal modeling in this paper.

2.3. Near-Field Effects

In traditional processing, the arrival signals of the linear array are plane waves in the far-field region. Then, the DOA of the signal is the same for different channels. In practice, the electromagnetic wave propagates as a spherical wave from the point source. Only when the array is far enough away from the radiation source is the far-field assumption valid.

Generally, the far-field assumption satisfies that the path difference between the edge of the array and the array’s center is equal to or less than $\lambda /16$ [39]. Considering that the channels of multistatic GEO SAR may not distribute linearly as the traditional array, the far-field boundary in multistatic GEO SAR is derived again in this part, where the parameters, such as range and baseline, are expressed based on the vector.

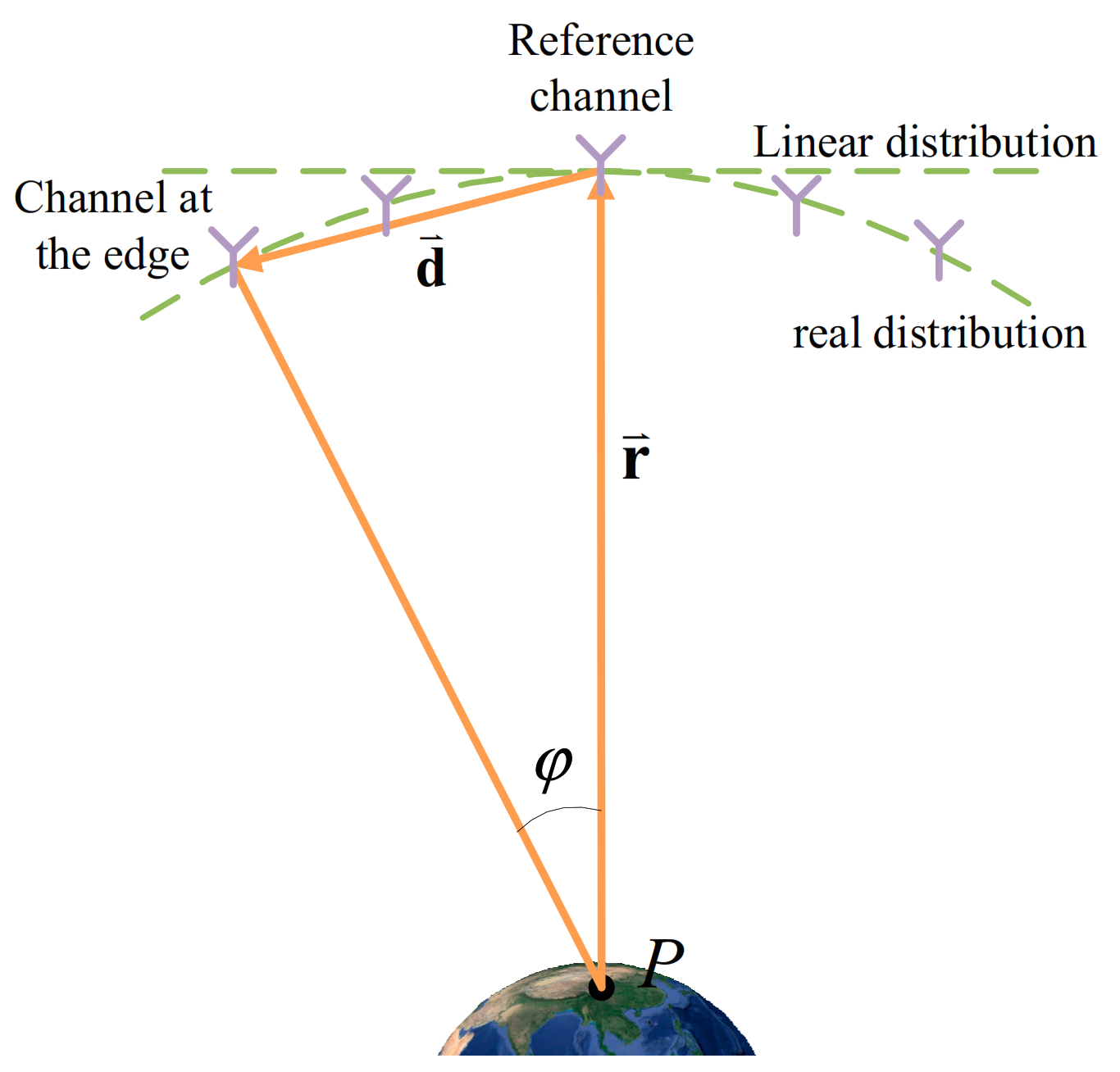
The simplified geometry diagram of multistatic GEO SAR is shown in Figure 4. Vector $\stackrel{\rightharpoonup }{d}$ is the baseline vector between the reference channel and the channel at the edge, and the range vector of the reference channel is $\stackrel{\rightharpoonup }{r}$. The path difference between the reference channel and the edge’s channel can be obtained:

$$\Delta R=\left| ‖\stackrel{\rightharpoonup }{r}+\stackrel{\rightharpoonup }{d}‖-‖\stackrel{\rightharpoonup }{r}‖ \right|$$

(6)

According to the far-field condition, the path difference $\Delta R$ satisfies that:

$$\left| ‖\stackrel{\rightharpoonup }{r}+\stackrel{\rightharpoonup }{d}‖-‖\stackrel{\rightharpoonup }{r}‖ \right|\le \frac{\lambda }{16}$$

(7)

Solving the above inequality yields:

$$\begin{array}{l}‖\stackrel{\rightharpoonup }{d}‖\le \sqrt{{‖\stackrel{\rightharpoonup }{r}‖}^2{\cos }^2\theta +\frac{\lambda }{8}‖\stackrel{\rightharpoonup }{r}‖}-‖\stackrel{\rightharpoonup }{r}‖\cos \theta , when \cos \theta >-\sqrt{\frac{\lambda }{8‖\stackrel{\rightharpoonup }{r}‖}}\\ ‖\stackrel{\rightharpoonup }{d}‖\le -\sqrt{{‖\stackrel{\rightharpoonup }{r}‖}^2{\cos }^2\theta -\frac{\lambda }{8}‖\stackrel{\rightharpoonup }{r}‖}-‖\stackrel{\rightharpoonup }{r}‖\cos \theta , otherwise\end{array}$$

(8)

where the angle $\theta$ is the angle between the baseline vector $\stackrel{\rightharpoonup }{d}$ and the range vector $\stackrel{\rightharpoonup }{r}$.

For simplicity, it is assumed that the target is in the side-looking direction and SARs distribute linearly along the track, which means that the range vector $\stackrel{\rightharpoonup }{r}$ is perpendicular to the baseline vector $\stackrel{\rightharpoonup }{d}$. Therefore, the far-field condition of the multistatic SAR system is approximated to:

$$‖d‖\le \sqrt{\frac{\lambda }{8}‖\stackrel{\rightharpoonup }{r}‖}$$

(9)

The rotation angle $\phi$ must satisfy Equation (10) to meet the far-field assumption:

$$\phi \le \sqrt{\frac{\lambda }{8‖\stackrel{\rightharpoonup }{r}‖}}$$

(10)

Table 2. Baseline length and range’s rotation angle limited by the far-field assumption of GEO SAR and a Interferometric Radar Mission (Tandem-L).

Satellite	Slant Range	Wavelength	Baseline Length Limited by the Far-Field Assumption	Range’s Rotation Angle Limited by the Far-Field Assumption
GEO SAR	~36,000 km	0.24 m	1309 m	0.0016°
Tandem-L	~745 km	0.24 m	149 m	0.011°

shows the limitation of the baseline length and the rotation angle of range under the far-field assumption in different SAR systems. For GEO SAR, the far-field assumption’s rotation angle is 0.0016°, and the baseline length is 1039 m at most. Nevertheless, the rotation angle is much higher in LEO SAR because of the lower orbit, which is 0.011°. Therefore, the far-field assumption greatly limits the application of multistatic GEO SAR.

2.4. Errors Induced by Curved Trajectories

Generally, the synthetic aperture time of an airborne or LEO SAR system is around several seconds or less, and the motion trajectory is approximated as a straight line. The second-order slant range model is usually adopted for slant range history. The traditional slant range model can be expressed as:

$$R_{tra}\left(nT\right)=R_0+\frac{v_s^2}{2R_0}{\left(nT\right)}^2$$

(11)

where $R_0$ is the shortest range and $v_s$ is the satellite velocity.

However, due to the high orbit, the synthetic aperture time of multistatic GEO SAR is several hundred seconds or even more. The employment of a traditional linear trajectory model will produce significant errors. According to the parameters in

Table 3. Orbit and system parameters of multistatic GEO SAR simulation.

Parameters	Values	Parameters	Values
Semi-major axis	42,164 km	Sample rate	20 MHz
Inclination	53°	Pulse width	20 μs
Eccentricity	0	Wavelength	0.24 m
Number of channels	5	Bandwidth	18 MHz
Look angle	4.65°	Pulse Repetition Frequency	600 Hz
Adjacent channel spacings	5368 m, 2684 m, −2618 m and −5236 m	Observation Time	60 s

, the accurate slant range of GEO SAR can be obtained by a systems tool kit (STK), which can provide the time-dynamic position and attitude of the satellite. Compared with the accurate slant range, the traditional range model’s error (Equation (11)) can reach 112 m, as shown in Figure 5a.

Besides, because of the large channel spacing, channels distribute along the curved trajectory. The path difference in the traditional multi-channel signal model, assuming that the array is linear, can be expressed as:

$$\Delta R\left(nT\right)=\frac{2\left(v_s-v_a\right)d}{R_0}·nT$$

(12)

where $v_a$ is the azimuth velocity of the moving target and $d$ is the channel spacing. Compared with the accurate path difference obtained by STK, the path difference error in multistatic GEO SAR is shown in Figure 5b. The error reaches 28 m, which has to be considered.

3. High-Precision Multi-Channel Signal Model in Multistatic GEO SAR

As shown in Section 2, the traditional range model and signal model are derived under the far-field assumption condition and straight-line distribution of channels [32,33], which is not available for multistatic GEO SAR. Thus, the multi-channel signal model with a large baseline is firstly derived in this section.

3.1. High-Precision Signal Model of Reference Channel

In this section, the reference-channel signal model of a moving target under the curved trajectory’s impact is derived first. On the one hand, the reference-channel model’s derivation can help derive the phase difference of other channels relative to it. On the other hand, it will be utilized in moving target imaging processing. Based on the geometrical relationship between the moving target and the satellite, the reference channel’s moving target signal model is deduced by exploiting high-order polynomial functions to fit the curved trajectory.

For a moving target $P$, the motion parameters are expressed as ${\mathbf{\vartheta }}_s=\left[\begin{array}{cc}{\stackrel{\rightharpoonup }{r}}_{t0}& \stackrel{\rightharpoonup }{v}\end{array}\right]$, where ${\stackrel{\rightharpoonup }{r}}_{t0}$ and $\stackrel{\rightharpoonup }{v}$ represent the position and velocity vector of the target in ECEF, respectively. Assuming that the target’s motion is uniform and linear, the velocity vector $\stackrel{\rightharpoonup }{v}$ is constant. Then, the moving-target echo of the reference channel after the range compression can be expressed as:

$$S\left(t,nT,{\mathbf{\vartheta }}_s\right)={\sigma }_s{e}^{j{\phi }_s}{a}_a\left(nT\right){\delta }_r\left(r-R\left(nT,{\mathbf{\vartheta }}_s\right)\right)\exp \left(-j\frac{4\pi R\left(nT,{\mathbf{\vartheta }}_s\right)}{\lambda }\right)$$

(13)

where $R\left(·\right)$ is the range history between the target and the reference channel. Considering that it is difficult to conduct derivation using the accurate squared range model, a high-order Taylor expansion is adopted to approximate the range model. In order to ensure that the range error is less than $\lambda /16$ (meaning the phase error is not more than $\pi /4$ and the target will not defocus), the range history is expressed by using the fourth-order Taylor expansion to:

$$R\left(nT,{\mathbf{\vartheta }}_s\right)=‖{\stackrel{\rightharpoonup }{r}}_s\left(nT\right)-{\stackrel{\rightharpoonup }{r}}_t\left(nT,{\mathbf{\vartheta }}_s\right)‖\approx R_0+k_1\left(nT\right)+k_2{\left(nT\right)}^2+k_3{\left(nT\right)}^3+k_4{\left(nT\right)}^4$$

(14)

where the expression for each derivative can be seen in Appendix A.

3.2. Multi-Channel Signal Model with Large Baseline

The approximate multi-channel signal model is deduced with a large baseline below. The echo signal of the mth channel after the range compression can be expressed as:

$$S_m\left(t,nT,{\mathbf{\vartheta }}_s\right)={\sigma }_s^m{e}^{j{\phi }_s^m}{a}_a\left(nT\right){\delta }_r\left(r-R_m\left(nT,{\mathbf{\vartheta }}_s\right)\right)\exp \left(-j\frac{4\pi R_m\left(nT,{\mathbf{\vartheta }}_s\right)}{\lambda }\right)$$

(15)

where $R_m\left(nT,{\mathbf{\vartheta }}_s\right)$ is the range history of the mth channel, and $\Delta R_m\left(nT,{\mathbf{\vartheta }}_s\right)$ is the path difference between the mth channel and the reference channel, which can be written as:

$$\Delta R_m\left(nT,{\mathbf{\vartheta }}_s\right)=R_m\left(nT,{\mathbf{\vartheta }}_s\right)-R\left(nT,{\mathbf{\vartheta }}_s\right)$$

(16)

For the multistatic GEO SAR, the large baseline results in the failure of far-field assumption and curved trajectory. In order to overcome these problems, a high-order approximation is needed to reduce the error to obtain a high precision wave-path difference. If the baseline vector from the reference channel to the mth channel is ${\stackrel{\rightharpoonup }{d}}_m\left(nT\right)$, the position of mth channel can be expressed as ${\stackrel{\rightharpoonup }{r}}_{sm}\left(nT\right)={\stackrel{\rightharpoonup }{r}}_s\left(nT\right)+{\stackrel{\rightharpoonup }{d}}_m\left(nT\right)$, and the range history of the mth channel in multistatic GEO SAR is:

$$R_m\left(nT,{\mathbf{\vartheta }}_s\right)=‖{\stackrel{\rightharpoonup }{r}}_{sm}\left(nT\right)-{\stackrel{\rightharpoonup }{r}}_t\left(nT,{\mathbf{\vartheta }}_s\right)‖=‖{\stackrel{\rightharpoonup }{r}}_s\left(nT\right)-{\stackrel{\rightharpoonup }{r}}_t\left(nT,{\mathbf{\vartheta }}_s\right)+{\stackrel{\rightharpoonup }{d}}_m\left(nT\right)‖$$

(17)

By utilizing the generalized binomial theorem to carry out the algebraic expansion, three terms are retained to ensure the range error is less than $\lambda /16$:

$$\begin{array}{c}{R}_m\left(nT,{\mathbf{\vartheta }}_s\right)\approx ‖{\stackrel{\rightharpoonup }{r}}_s\left(nT\right)-{\stackrel{\rightharpoonup }{r}}_t\left(nT,{\mathbf{\vartheta }}_s\right)‖+\frac{2\left({\stackrel{\rightharpoonup }{r}}_s\left(nT\right)-{\stackrel{\rightharpoonup }{r}}_t\left(nT\right)\right){\stackrel{\rightharpoonup }{d}}_m^T\left(nT\right)+{\stackrel{\rightharpoonup }{d}}_m\left(nT\right){\stackrel{\rightharpoonup }{d}}_m^T\left(nT\right)}{2‖{\stackrel{\rightharpoonup }{r}}_s\left(nT\right)-{\stackrel{\rightharpoonup }{r}}_t\left(nT\right)‖}\\ -\frac{{\left\{2\left[{\stackrel{\rightharpoonup }{r}}_s\left(nT\right)-{\stackrel{\rightharpoonup }{r}}_t\left(nT\right)\right]{\stackrel{\rightharpoonup }{d}}_m^T\left(nT\right)+{\stackrel{\rightharpoonup }{d}}_m\left(nT\right){\stackrel{\rightharpoonup }{d}}_m^T\left(nT\right)\right\}}^2}{8{‖{\stackrel{\rightharpoonup }{r}}_s\left(nT\right)-{\stackrel{\rightharpoonup }{r}}_t\left(nT\right)‖}^3}\end{array}$$

(18)

Then, the path difference between the mth channel and the reference channel can be obtained. The Taylor expansion is carried out to facilitate the later derivation, and three terms are reserved to ensure the deviation less than $\lambda /16$, meaning the phase error less than $\pi /4$:

$$\begin{array}{cc}\Delta R_m\left(nT,{\mathbf{\vartheta }}_s\right)& \approx \frac{2\left[{\stackrel{\rightharpoonup }{r}}_s\left(nT\right)-{\stackrel{\rightharpoonup }{r}}_t\left(nT,{\mathbf{\vartheta }}_s\right)\right]{\stackrel{\rightharpoonup }{d}}_m^T\left(nT\right)+{\stackrel{\rightharpoonup }{d}}_m\left(nT\right){\stackrel{\rightharpoonup }{d}}_m^T\left(nT\right)}{2‖{\stackrel{\rightharpoonup }{r}}_s\left(nT\right)-{\stackrel{\rightharpoonup }{r}}_t\left(nT,{\mathbf{\vartheta }}_s\right)‖}\\ & \hspace{1em}-\frac{{\left\{2\left[{\stackrel{\rightharpoonup }{r}}_s\left(nT\right)-{\stackrel{\rightharpoonup }{r}}_t\left(nT\right)\right]{\stackrel{\rightharpoonup }{d}}_m^T\left(nT\right)+{\stackrel{\rightharpoonup }{d}}_m\left(nT\right){\stackrel{\rightharpoonup }{d}}_m^T\left(nT\right)\right\}}^2}{8{‖{\stackrel{\rightharpoonup }{r}}_s\left(nT\right)-{\stackrel{\rightharpoonup }{r}}_t\left(nT\right)‖}^3}\\ & \approx \Delta R_0+\Delta k_1\left(nT\right)+\Delta k_2{\left(nT\right)}^2+\Delta k_3{\left(nT\right)}^3\end{array}$$

(19)

where the expression of each order coefficient can be seen in Appendix B. Compared with (12), (19) modifies the constant term and primary term coefficient based on the spherical wave and retains the higher-order term. Then, the range of the mth channel can be expressed as the sum of the range of the reference channel and wave-path difference:

$$\begin{array}{ll}{R}_m\left(nT,{\mathbf{\vartheta }}_s\right)& =R\left(nT,{\mathbf{\vartheta }}_s\right)+\Delta R_m\left(nT,{\mathbf{\vartheta }}_s\right)\\ & =\left(R_0+\Delta R_0\right)+\left(k_1+\Delta k_1\right)\left(nT\right)+\left(k_2+\Delta k_2\right){\left(nT\right)}^2+\left(k_3+\Delta k_3\right){\left(nT\right)}^3+k_4{\left(nT\right)}^4\\ & =R_{m0}+k_{m1}\left(nT\right)+k_{m2}{\left(nT\right)}^2+k_{m3}{\left(nT\right)}^3+k_4{\left(nT\right)}^4\end{array}$$

(20)

Thus, the multi-channel signal model of moving target after range compression can be expressed as:

$$S\left(r,nT\right)=\left[\begin{array}{c}{\sigma }_s^1{e}^{j{\phi }_s^1}{a}_a\left(nT\right){\delta }_r\left(r-R_1\left(nT,{\mathbf{\vartheta }}_s\right)\right)\exp \left(-j\frac{4\pi R_1\left(nT,{\mathbf{\vartheta }}_s\right)}{\lambda }\right)\\ ⋮\\ {\sigma }_s^M{e}^{j{\phi }_s^M}{a}_a\left(nT\right){\delta }_r\left(r-R_M\left(nT,{\mathbf{\vartheta }}_s\right)\right)\exp \left(-j\frac{4\pi R_M\left(nT,{\mathbf{\vartheta }}_s\right)}{\lambda }\right)\end{array}\right]$$

(21)

3.3. Azimuthal Spectrum of Multi-Channel Data Based on High-Order Expansion

Considering that the multistatic GEO SAR has a high-order range model and the path difference does not change linearly with the slower time, it differs from the traditional multi-channel signal model. The expression of the multi-channel signal of multistatic GEO SAR in the range-Doppler domain is re-derived in this section.

In the derivation, the principle of stationary phase and series reversion method is utilized to obtain the result after azimuth Fourier transform. The detailed deducing can be seen in Appendix D. By further separation, the expression of the multi-channel signal in the range-Doppler domain can be obtained:

$$S_m^{rd}\left(r,f_a,{\mathbf{\vartheta }}_s\right)=A_m\left(r,f_a,{\mathbf{\vartheta }}_s\right)\mathsf{\Phi }\left(f_a,{\mathbf{\vartheta }}_s\right)\Delta {\mathsf{\Phi }}_m\left(f_a,{\mathbf{\vartheta }}_s\right)$$

(22)

where $A_m\left(r,f_a,{\mathbf{\vartheta }}_s\right)$ is the envelope of the signal in the range-Doppler domain, whose expression is:

$$A_m\left(r,f_a,{\mathbf{\vartheta }}_s\right)={\sigma }_s{e}^{j{\phi }_s}{\delta }_r\left(r-R_m\left(f_a,{\mathbf{\vartheta }}_s\right)\right)A_a\left(f_a\right)$$

(23)

The common phase $\mathsf{\Phi }\left(f_a,{\mathbf{\vartheta }}_s\right)$ is determined by the range between the reference channel and moving target and can be expressed as:

$$\mathsf{\Phi }\left(f_a,{\mathbf{\vartheta }}_s\right)=\exp \left(-j\frac{4\pi R_0}{\lambda }\right)\exp \left\{j\frac{\pi \lambda }{4k_2}\mathrm{\Lambda }{\left(f_a+\frac{2k_1}{\lambda }\right)}^2\right\}$$

(24)

where $\mathrm{\Lambda }$ is the factor generated by the curved trajectory, and is related to the high-order term in range history. Its expression is in Appendix D.

The phase difference $\Delta {\mathsf{\Phi }}_m\left(f_a,{\mathbf{\vartheta }}_s\right)$ is determined by the motion parameters and baseline between the multiple channels and the reference channel:

$$\begin{array}{l}\Delta {\mathsf{\Phi }}_m\left(f_a,{\mathbf{\vartheta }}_s\right)=\underset{\mathrm{multi}-\mathrm{channel} \mathrm{squint} \mathrm{term}}{\underbrace{\exp \left(j\pi {\mathrm{\Lambda }}_1\frac{\Delta k_1^2}{\lambda k_2}\right)\exp \left(-j\frac{4\pi \Delta R_0}{\lambda }\right)}}\underset{\mathrm{along}-\mathrm{track} \mathrm{interferometric} \mathrm{phase}}{\underbrace{\exp \left(j2\pi {\mathrm{\Lambda }}_2\frac{k_1\Delta k_1}{\lambda k_2}\right)}}\\ \times \underset{\mathrm{Doppler} \mathrm{shift} \mathrm{term}}{\underbrace{\exp \left(-j2\pi {\mathrm{\Lambda }}_3\frac{\Delta k_1}{2k_2}{f}_a\right)}}\underset{\mathrm{near}-\mathrm{field} \mathrm{correction} \mathrm{term} }{\underbrace{\exp \left\{-j2\pi \left[\frac{\lambda \Delta k_2}{8k_2^2}{\mathrm{\Lambda }}_4{f}_a^2-\frac{{\lambda }^2\Delta k_3}{32k_2^3}{\mathrm{\Lambda }}_5{f}_a^3\right]\right\}}}\end{array}$$

(25)

where ${\mathrm{\Lambda }}_1$, ${\mathrm{\Lambda }}_2$, ${\mathrm{\Lambda }}_3$, ${\mathrm{\Lambda }}_4$ and ${\mathrm{\Lambda }}_5$ are all factors introduced by curved trajectory and are related to high-order terms of range history. Their expressions are in Appendix D.

According to the signal model in Section 3.1 and Section 3.2, $k_1$ represents the radial velocity of the target. The coefficient $\Delta k_1$ is determined by the along-track baseline, which generates spatial sampling and forms a multi-degree freedom system. The multi-channel phase difference in Equation (25) can be categorized into four terms related to $k_1$ and $\Delta k_1$. The multi-channel squint term is the constant phase, which is generated by the baseline. The Doppler shift term is caused by the along-track baseline. The along-track interferometric phase is related to the radial velocity of the target and along-track baseline. The near-field correction term is related to the high-order term of reference-channel range history and path difference.

For stationary clutter, the velocity is zero, and the motion parameter can be expressed as ${\mathbf{\vartheta }}_c=\left[\begin{array}{cc}\mathsf{\zeta }& 0\end{array}\right]$. However, for time-varying scenes, the scene scattering point’s velocity is regarded as a random variable and expressed as $v_s\left(f_a\right)$ in the frequency domain. Then, the motion parameter can be expressed as ${\mathbf{\vartheta }}_c=\left[\begin{array}{cc}\mathsf{\zeta }& v_s\left(f_a\right)\end{array}\right]$. For simplicity, the motion parameters of the fixed and time-varying scene are written uniformly as ${\mathbf{\vartheta }}_c$. The background clutter can be expressed as the superposition of echoes of all scattered points in the imaging region. Then, the background clutter in the range-Doppler domain can be expressed as:

$$C^{rd}\left(r,f_a\right)=\left[\begin{array}{c}{\displaystyle \sum _{{\mathbf{\vartheta }}_c}{A}_1\left(r,f_a,{\mathbf{\vartheta }}_c\right)\mathsf{\Phi }\left(f_a,{\mathbf{\vartheta }}_c\right)\Delta {\mathsf{\Phi }}_M\left(f_a,{\mathbf{\vartheta }}_c\right)}\\ ⋮\\ {\displaystyle \sum _{{\mathbf{\vartheta }}_c}{A}_M\left(r,f_a,{\mathbf{\vartheta }}_c\right)\mathsf{\Phi }\left(f_a,{\mathbf{\vartheta }}_c\right)\Delta {\mathsf{\Phi }}_M\left(f_a,{\mathbf{\vartheta }}_c\right)}\end{array}\right]$$

(26)

After considering the noise, the clutter model becomes:

$$Q\left(r,f_a\right)=C^{rd}\left(r,f_a\right)+N$$

(27)

where $N$ is the additive white Gaussian noise.

4. Modified Imaging STAP Method in Near Field

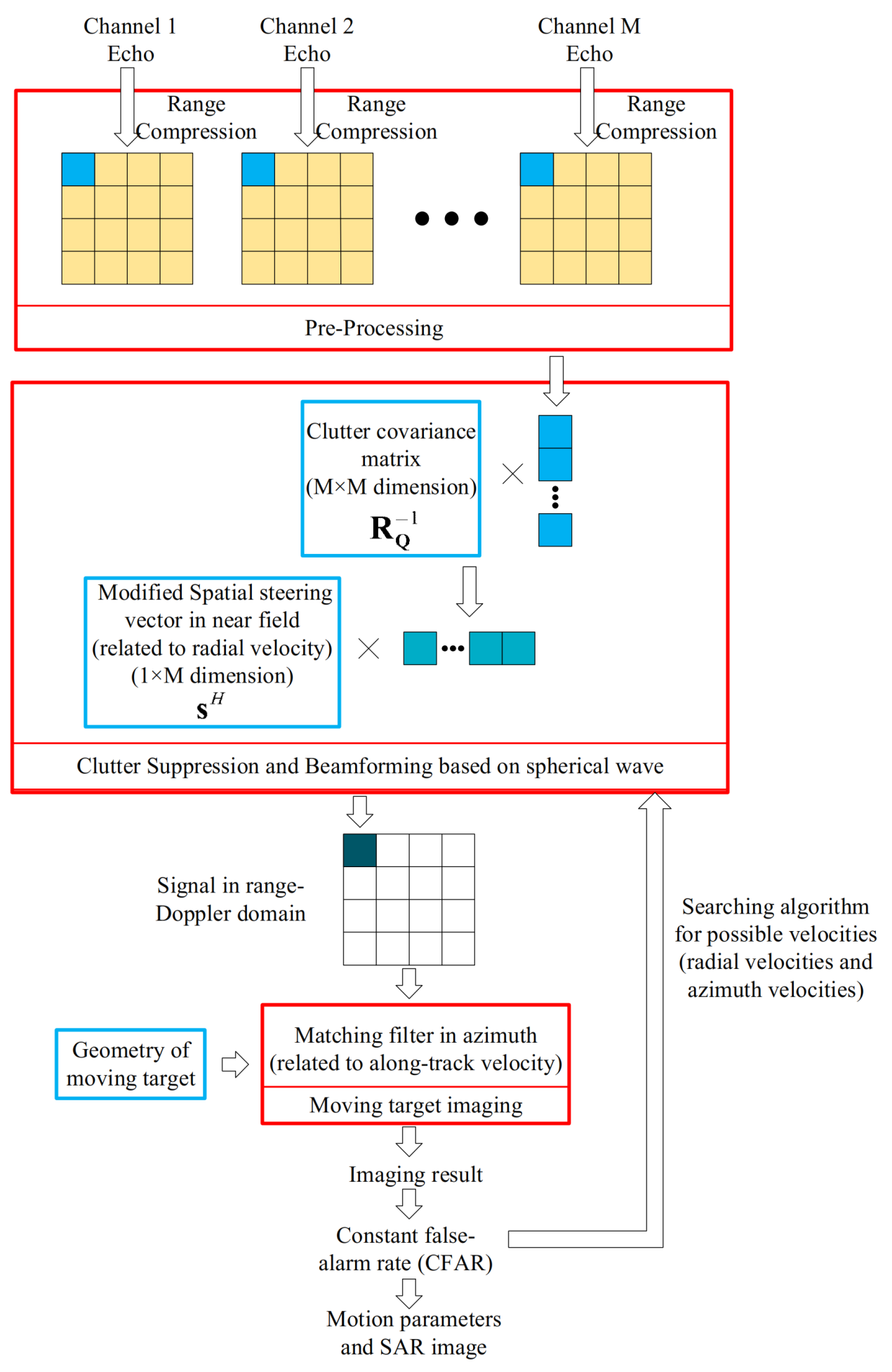
The traditional ISTAP constructs adaptive filters based on the multi-channel signal model under the far-field assumption and equivalent straight-line model, which cannot be applied to the multistatic GEO SAR. To solve these problems, a modified ISTAP considering the curved trajectory and near-field effects is proposed, whose flowchart is shown in Figure 6. Firstly, the multi-channel echo signals from several satellites are obtained. The echo signals are transformed into the range-Doppler domain based on the high-order signal model. Next, to achieve clutter suppression and beamforming, an adaptive filter is constructed by utilizing the covariance matrix of clutter and the modified spatial steering vector in the near field. The moving target imaging is then achieved by the back-projection algorithm (BPA), modified by the motion parameters. Finally, the detection and parameter estimation of the moving target is completed by searching the maximum signal to clutter and noise ratio (SCNR) through the range of possible target velocities and comparing it with a threshold. At the same time, the image of the moving target is obtained. The detail of each step is explained below.

In the preprocessing step, the data from different channels are processed separately. Firstly, the data are compressed in ranges. Then, the targets’ offset between channels can be corrected for the compressed signal [33]. Moreover, the atmospheric phase of multistatic GEO SAR can be modeled according to the global Total Electron Content (TEC) information to compensate for the phase error [41,42,43]. Finally, the signal is transformed into the range-Doppler domain.

4.1. Clutter Suppression and Beamforming

Due to the long synthetic aperture time in GEO SAR, the Doppler domain signal is only related to the instantaneous frequency. The signals of each frequency point tend to be independent of each other [28]. Therefore, the processing can be completed in the range-Doppler domain, and it only needs the spatial filtering, which reduces the dimension of the filter and the computational complexity.

Clutter suppression and beamforming are realized through the optimal adaptive processor. After optimal processing, the clutter component is whitened. The motion signal phase difference between different channels is compensated to suppress the clutter component and match the motion signal component. The expression of the optimal processor is [28]:

$$w_{opt}=R_Q^{-1}\Delta$$

(28)

where $R_Q$ is the covariance matrix of the clutter, and $\Delta$ is the spatial steering vector of the moving target, which is composed of the phase difference between different channels and the reference channel.

The covariance matrix of clutter is discussed firstly. If the background clutter is independent of the noise, and frequency units are independent of each other, the covariance matrix of the clutter $R_Q$ can be estimated by several range cells:

$$R_Q\left(f_a\right)=E\left[Q{Q}^H\right]={\sigma }_n^2{I}_M+\frac{1}{N_r}{\displaystyle \sum _{l=r}^{r+N_r-1}C\left(l,f_a\right)C{\left(l,f_a\right)}^H}$$

(29)

where $N_r$ is the number of range cells that is used to estimate the covariance matrix, which must be greater than $2M$ for accurate estimation. Considering that the clutter is homogeneous, all the range units can be used to estimate the clutter covariance matrix.

Due to the large baseline for multistatic GEO SARs, the range offset between channels caused by target movement must be considered. The range history for the moving target can be obtained according to the motion parameters; therefore, for a moving target, the data along the slant range in each channel can be extracted. The extracted data $z\left(f_a\right)$ are the input of the next step.

Then, the spatial steering vector is discussed. In the traditional ISTAP, the spatial steering vector $\Delta$ is derived based on the signal model under the far-field assumption and linear trajectory. However, it cannot be applied in the multistatic GEO SAR due to the failure of far-field assumption and curved trajectory. Therefore, the spatial steering vector should be modified first.

The modified spatial steering vector in the near-field matching with the motion parameters is:

$$\Delta \left(f_a,{\mathbf{\vartheta }}_s\right)=\left[\begin{array}{c}\Delta {\mathsf{\Phi }}_1\left(f_a,{\mathbf{\vartheta }}_s\right)\\ ⋮\\ \Delta {\mathsf{\Phi }}_M\left(f_a,{\mathbf{\vartheta }}_s\right)\end{array}\right]$$

(30)

Compared with the spatial steering vector in traditional ISTAP, the phase in Equation (30) introduces the factor of curved trajectory and adds near-field correction terms.

Then, each range gate and each frequency point are filtered to obtain the clutter suppression and beamforming result in the range-Doppler domain:

$$y\left(f_a,{\mathbf{\vartheta }}_s\right)=w_{opt}^H\left(f_a,{\mathbf{\vartheta }}_s\right)z\left(f_a\right)=\Delta {\left(f_a,{\mathbf{\vartheta }}_s\right)}^H{R}_Q^{-1}\left(f_a\right)z\left(f_a\right)$$

(31)

4.2. Moving Target Imaging

Due to the SAR system’s long synthetic aperture time, signal energy is dispersed into several range-Doppler cells. The signal needs to be accumulated coherently by the iteration of motion parameters to obtain the maximum SNR.

BPAs can image the target accurately. This paper takes the BPA as an example to image the moving target. However, the traditional BPA only images stationary targets and will cause azimuth shift and defocusing in range and azimuth direction for moving target (see Appendix C). Therefore, the BPA filter should be modified according to the parametric range model to accumulate the moving target’s energy.

Specifically, the signal $y\left(r,f_a,{\mathbf{\vartheta }}_s\right)$ in the range-Doppler domain in (31) carries out the inverse Fourier transform to obtain the signal $s_t\left(t_r,nT,{\mathbf{\vartheta }}_s\right)$ in the time domain. Then, the cells, which have a parametric range model of reference channel in (14), are collected to integrate coherently. Then, the value of the corresponding pixel on the SAR image can be expressed as:

$$f\left(r,x\right)={\displaystyle {\int }_{nT}{s}_t\left(\frac{2R\left(nT;r,x,v_r,v_x\right)}{c},nT\right)}\exp \left(j\frac{4\pi \left[R\left(nT;r,x,v_r,v_x\right)-r\right]}{\lambda }\right)d\left(nT\right)$$

(32)

4.3. Parameters Estimation

The radial velocity and along-track velocity are used to construct the spatial steering and imaging function, respectively. Thus, all ranges of possible target velocities are traversed to searching the maximum of the test statistics. If the test statistic exceeds the threshold, it is considered that the moving target exists. According to the generalized likelihood ratio test, the test statistic is:

$$T\left(r,x,{\mathbf{\vartheta }}_s\right)=\frac{{\left|f\left(r,x\right)\right|}^2}{{\displaystyle \int {\Delta }^H\left(f_a,{\mathbf{\vartheta }}_s\right)R_Q^{-1}\left(f_a\right)\Delta \left(f_a,{\mathbf{\vartheta }}_s\right)d{f}_a}}$$

(33)

Considering the computational load brought by traversing possible target velocities, it is determined that the result can still be accepted when the loss of the output SNR is no more than 3 dB [33]. Besides, compared with LEO SAR, the synthetic aperture time of GEO SAR increases greatly so that the small radial velocity will lead to a large change of range in GEO SAR. This means that the range of GEO SAR is more sensitive to the radial velocity than LEO SAR. Therefore, when the radial velocity for searching does not match the actual velocity slightly, the moving target will not focus and output low SCNR. In the modified ISTAP in the near field for multistatic GEO SAR, the radial velocity search interval should be small to prevent missing targets. The specific steps of parameters estimation are as follows.

Firstly, the azimuth velocities are set to zero, and different radial velocities are used to process the beamforming and imaging to obtain different SAR images of moving targets. The energy of the target is focused primarily and can be detected. Of course, the azimuth velocity may not match the moving target, so the SAR images may defocus in the azimuth direction.

Then, to detect the targets, we calculate the SNR of each SAR image. We find the peak value position in each SAR image, where the target is thought to be located. The target’s energy is obtained by incoherently integrating all the azimuth cells, while the noise is calculated by the mean amplitude of the resting cell. Then, the SNR of all the SAR images can be calculated.

Next, based on the SNR of each SAR image, the targets can be filtered out by setting the threshold value. The SNR threshold is determined by the NP criterion, which can detect signals in white Gaussian noise. Then, the targets are selected, and their radial velocities are obtained.

Finally, different azimuth velocities are exploited for each target to process the beamforming and imaging to find the azimuth velocities that generate the results with maximum signal energy.

4.4. Theoretical Analysis of the Proposed Method’s Performance

4.4.1. SCNR Analysis

For optimal processing, the maximum SCNR that can be achieved is:

$$SCNR\left({\mathbf{\vartheta }}_s\right)={\displaystyle {\int }_{f_a}S{\left(f_a,{\mathbf{\vartheta }}_s\right)}^H{R}_Q^{-1}\left(f_a\right)S\left(r,f_a\right)}d{f}_a$$

(34)

where $S\left(f_a,{\mathbf{\vartheta }}_s\right)$ is the spatial signal of moving target in the range-Doppler domain:

$$S\left(f_a,{\mathbf{\vartheta }}_s\right)=\left[\begin{array}{c}{S}_1^{rd}\left(f_a,{\mathbf{\vartheta }}_s\right)\\ S_2^{rd}\left(f_a,{\mathbf{\vartheta }}_s\right)\\ ⋮\\ S_M^{rd}\left(f_a,{\mathbf{\vartheta }}_s\right)\end{array}\right]$$

(35)

Based on the SCNR, the minimum detectable velocity and the ability of clutter suppression can be analyzed. We analyze these performance indicators by simulation, which can be seen in the next section.

4.4.2. Computational Complexity Analysis

The time complexity of the covariance matrix calculation, beamforming, and velocity searching are mainly analyzed. In the processing, the number of the raw data points is $N_a$ in azimuth, and $N_r$ in range; the number of channels is $M$; and the size of the scene is $L_r$ in range and $L_a$ in azimuth. For velocity searching, the number of radial velocities is $N_{vr}$, and the azimuth velocity is $N_{va}$.

The computation of clutter suppression for multistatic GEO SAR mainly consists of calculating the covariance matrix, estimated by several range units. When we calculate the covariance matrix of the $n_a$th Doppler cell, all the range units are used to estimate and the time complexity is $O\left(N_r·M^2\right)$. Then, the time complexity of inversion is $O\left(M^3\right)$. When we suppress the interference, the inverse covariance matrix and the signal are multiplied, and the time complexity is $O\left(M^2\right)$. Above all, the whole processing of clutter suppression has the time complexity of $O\left(N_a\left(N_r{M}^2+M^2+M^3\right)\right)$.

The beamforming and velocity searching is conducted simultaneously so that the time complexity is analyzed together. Firstly, the beamforming is processed by multiplying the spatial steering vector and clutter suppression results so that the time complexity is $O\left(N_a{N}_{r}M\right)$. Then, the moving target imaging achieves coherent accumulation for each pixel, and the time complexity is $O\left(L_r{L}_a{N}_a\right)$. Finally, the beamforming and moving target imaging are processed for different velocities, and the time complexity of the whole processing is $O\left(N_{vr}{N}_{va}\left(N_a{N}_{r}M+L_r{L}_a{N}_a\right)\right)$.

The computation is determined by the scene size, and the method is feasible for a small scene. However, to reduce the computational burden greatly for large scene imaging, the frequency domain method is waiting to be proposed in the future.

5. Simulation and Discussion

Some multistatic GEO SAR simulations were carried out in this section to verify the multi-channel range model’s validity and the effectiveness of the proposed modified ISTAP method in the near field.

This section takes the typical GEO SAR system as an example to simulate, and the parameters can be seen in Table 3 [44]. The two-dimensional zero Doppler control [1] was adopted to guarantee the system in side looking. Five channels formed by multistatic GEO SAR were arranged along the track. The spacing between the adjacent channels was 5368 m, 2684 m, −2618 m, and −5236 m to guarantee the correlation of clutter, and the non-uniform channel spacing was to suppress the grating lobe.

For the imaging scene, a 2 km by 2 km scenario with 16 moving targets was used. The scene’s size was small to reduce the computational cost, and all the moving targets were used to analyze the detection performance of the modified ISTAP method in the near field. The target positions were evenly distributed in the scene, and the velocities were between −30 m/s and 30 m/s, the range of which includes most moving vehicles and ships. The specific motion parameters of the moving target are shown in

Table 4. Motion parameters of moving target in the scene.

Target No.	Radial Velocity	Azimuth Velocity	Target No.	Radial Velocity	Azimuth Velocity
1	−1 m/s	−1 m/s	9	−3.0147 m/s	−3.0147 m/s
2	−5 m/s	−5 m/s	10	−6.9825 m/s	−6.9825 m/s
3	−15 m/s	−15 m/s	11	−11.4486 m/s	−11.4486 m/s
4	−30 m/s	−30 m/s	12	−24.1429 m/s	−24.1429 m/s
5	1 m/s	1 m/s	13	−29.4437 m/s	−29.4437 m/s
6	5 m/s	5 m/s	14	3.5543 m/s	3.5543 m/s
7	15 m/s	15 m/s	15	19.6818 m/s	19.6818 m/s
8	30 m/s	30 m/s	16	20.4853 m/s	20.4853 m/s

.

5.1. Error Analysis of Range Model

This section verifies the validity of the range model. The parameters of multistatic GEO SAR in Table 2 were adopted to derive the range history in theory. Then, the STK software was used to obtain the exact range history to compare. When the range model’s error, in theory, is less than $\pi /4$, the accuracy of the range model can be proved.

5.1.1. Error Analysis of Path Difference

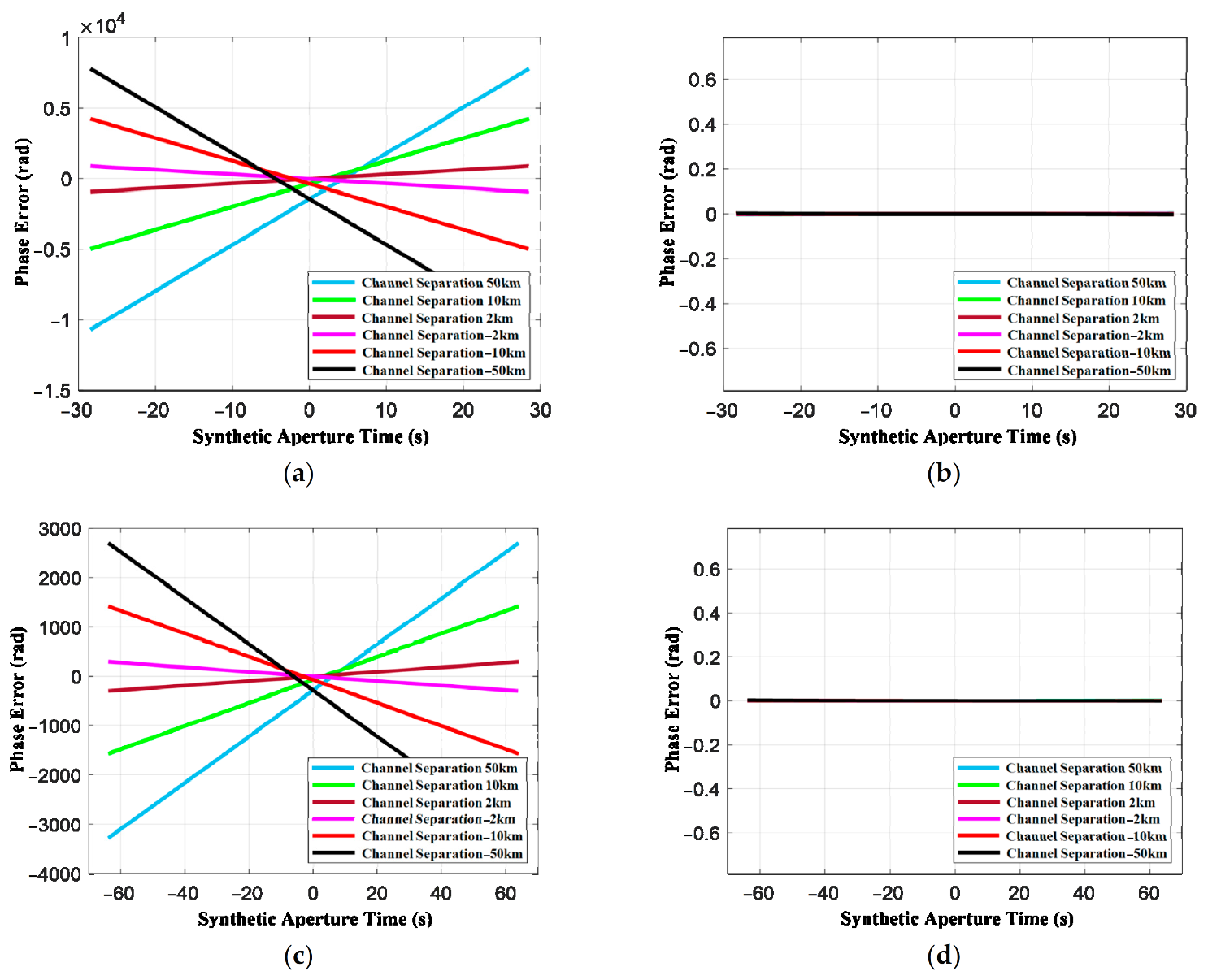
The simulation was conducted to verify the accuracy of the path difference model in Section 2. The path difference model is shown in Equation (19). It was assumed that the radial velocity and azimuth velocity are all 30 m/s. The error is shown in Figure 7. Figure 7 shows the phase errors produced by the traditional and proposed path difference model at different orbit positions. Figure 7a,c are the phase errors of the path different model based on the far-field assumption and linear trajectory (see Equation (12)), where Figure 7a is the error at the equator and Figure 7c is the error at the perigee. Whether at the equator and the perigee, the traditional path difference model will produce an intolerable error. The phase errors are different at different orbit position due to the difference in the trajectory’s curve. Figure 7b,d are the phase errors produced by the proposed path difference model. The path difference model applies to both equator position (the slightest orbital curvature) and perigee position (the most severe orbital curvature). When the channel’s spacing is 50 km, the phase error is still small. It can be seen that the wave-path difference model in the near field in this paper is still valid at the along-track baseline of 50 km because the phase error is less than $\pi /4$. However, the traditional wave-path difference model with the far-field assumption produces phase errors of 10⁴ orders of magnitude at the equator.

5.1.2. Error Analysis of Range Model

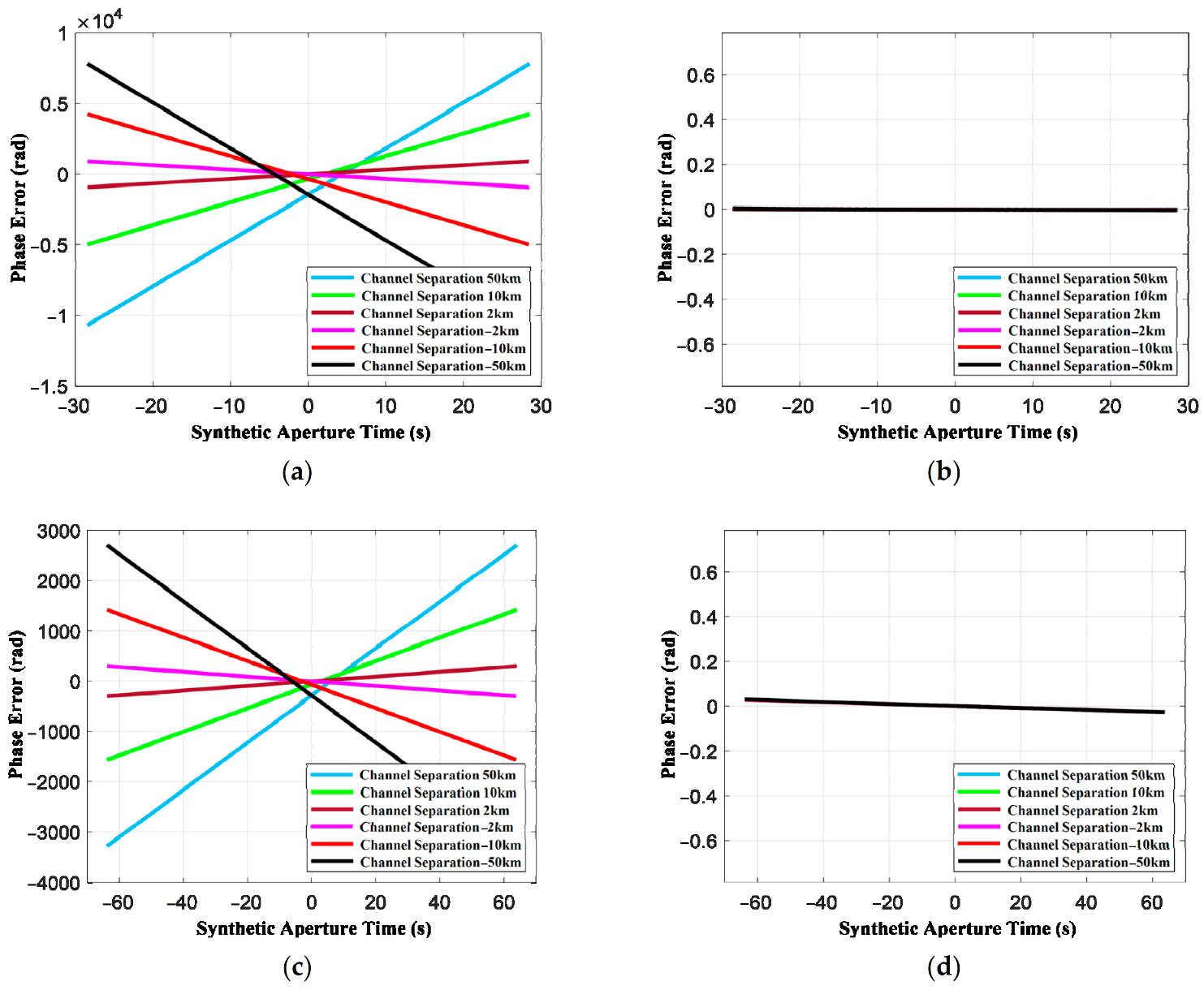
The simulation was also conducted to verify the range model’s accuracy based on the curved trajectory and near-field effects in Section 2. The range model is shown in Equation (20). It was assumed that the radial velocity and azimuth velocity were all 30 m/s, and the error is shown in Figure 8. It can be seen that the range model based on curved trajectory and near-field effects in this paper was still valid at the along-track baseline of 50 km because the phase error was less than $\pi /4$. However, the traditional range model with the assumption of linear trajectory and far-field assumption produced phase errors of 10⁴ orders of magnitude at the equator. The results in Figure 7a,c are similar to the results in Figure 8a,c because the range model’s phase errors were mainly produced by the path difference model’s errors. Thus, only the method based on the fourth-order phase signal is effective for the multistatic GEO SAR system.

5.2. Results of Modified ISTAP Method in Near Field

Taking sea clutter as an example, we obtained the amplitude of echo according to the statistical characteristics. The common statistical model of sea clutter is the K distribution [44], which synthesizes Rayleigh and exponential distribution. The K distribution is specified by the shape parameter and scale parameter.

The shape parameter can be obtained by the Ryan–Johnson model according to the radar parameters in Table 3. The expression of the Ryan–Johnson model is as follows:

$${\log }_{10}v=\frac{2}{3}{\log }_{10}\psi +\frac{5}{8}{\log }_{10}l+\delta -k+{\log }_{10}\frac{\tau }{30}{\log }_{10}\frac{50}{\psi }{\log }_{10}{\left(5.5\psi \right)}^{0.8}$$

(36)

where the shape parameter is $v$ and the grazing angle is $\psi$. The range resolution is represented by $l$, and $\delta$ satisfies $\delta =-\frac{1}{3}\cos 2\varphi$ where $\varphi$ is the wind direction ($\varphi =0^{\circ }$when it is against the wind). The parameter $k$ equals 1 for horizontal polarization and 1.7 for vertical polarization. The variable $\tau$ represents the signal pulse width. GEO SAR parameters are brought into the equation, and we obtained the shape parameter of K distribution in GEO SAR.

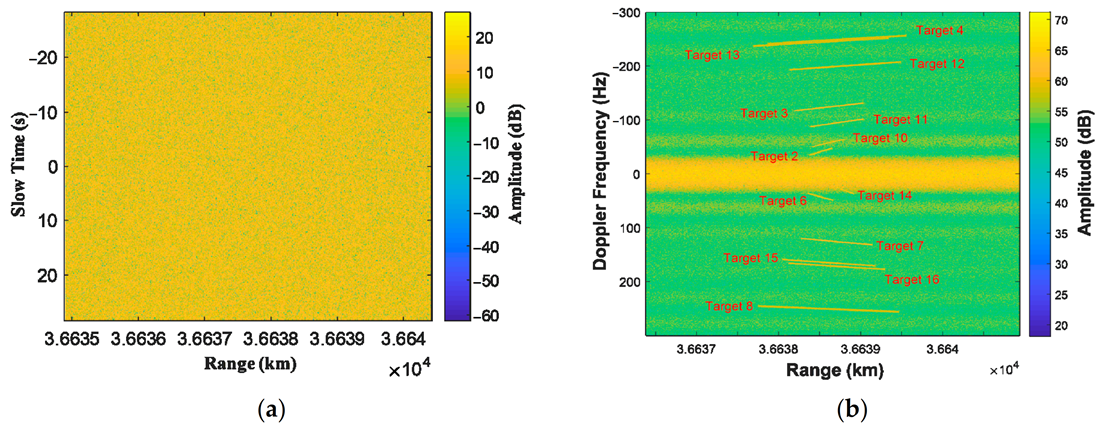
The scale parameter is calculated according to the CNR, which is set as 10 dB. The complex white noise is also added. Then, the moving targets are added to the clutter, and the SCR is −10 dB. The echo is shown in Figure 9a, and the signal in the range-Doppler domain is shown in Figure 9b. It can be seen that the moving targets are submerged in background clutter. Moreover, the clutter buries the slow targets in the range-Doppler domain. Thus, it is difficult to detect the moving target directly.

5.2.1. Clutter Suppression and Motion Parameters Estimation

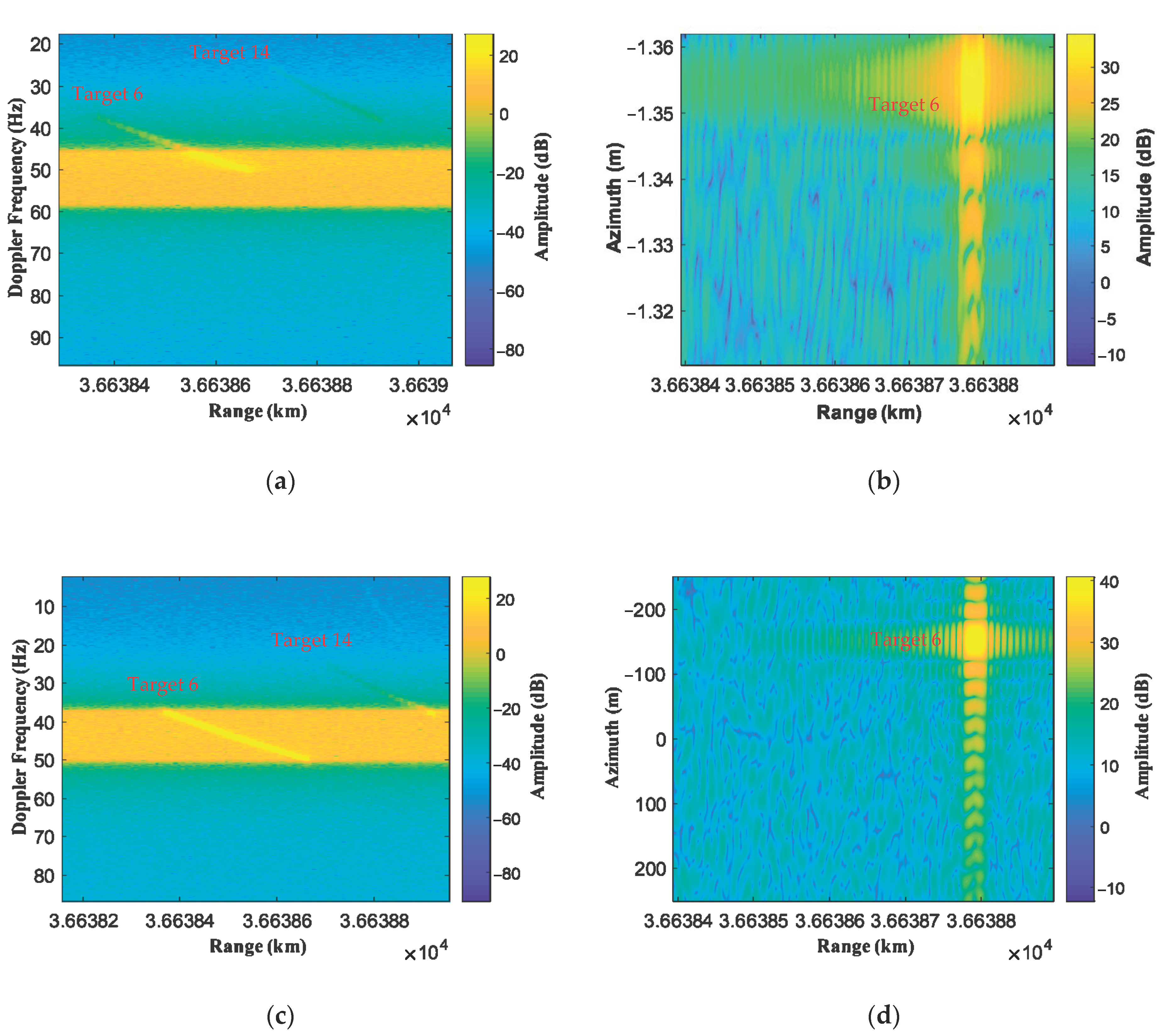
The modified ISTAP method in the near field is adopted, and the results are shown in Figure 10. Figure 10a,b show the beamforming result and target imaging result when the search parameters are inconsistent with the targets’ actual motion parameters. The radial velocity and azimuth velocity for searching are both 6 m/s. Figure 10c,d show the beamforming result and target imaging result when the search parameters are consistent with the actual motion parameters of Target 6, and the radial velocity and azimuth velocity for searching are both 5 m/s. By comparing Figure 10a with Figure 10c, only when the searching parameters are the same as the target’s motion parameters, the SNR of the whole range migration line is improved. Otherwise, the SNR of only a small part (or none) of the range migration line is improved. The imaging results in Figure 10b,d are near the highest SNR position. When the searching parameters are inconsistent, as shown in Figure 10b, the target has a serious azimuth offset, up to 13 km, and the target is defocusing. When the searching parameters are the same as Target 6, the target is focused well and located at its real position. Moreover, the target’s SNR in Figure 10d is significantly higher than that shown in Figure 10b. It can be seen from the results that the clutter is removed, and the moving target matching the searching parameters is preserved.

As shown in Figure 10, when the searching parameters do not match the actual motion parameters, the moving target defocuses and has low SNR; vice versa, the SNR can be the highest. Thus, the motion parameters can be estimated.

In this paper, to prevent missing the target and to consider the computational burden, the search interval of radial velocity was 0.1 m/s, and the search interval of azimuth velocity was 0.5 m/s. The radial velocity is not coupled with the azimuth velocity, therefore the searching can be independent.

Firstly, the azimuth velocities were set to zero, and different radial velocities were used to process the beamforming and imaging to obtain different SAR images of moving targets. Then, we calculated the SNR of each SAR image. According to the signal’s and the noise’s energy, SNRs of all the SAR images were calculated, and the result is the blue line in Figure 11a. Only when the search parameters are consistent with the target’s actual velocity can the maximum output SNR of the target be obtained. Therefore, the peaks appear at the corresponding radial velocities in the output SNR results. Many peaks appear in Figure 11a, which implies that there are many targets with different radial velocities, and the different peaks should be associated with different moving targets. The targets can be detected, and their radial velocities can be obtained simultaneously by setting a certain threshold. The targets can be filtered out by selecting the threshold value: 17 dB here and shown as the red line in Figure 11a. Besides, the output SNRs of different targets are different because their radar cross sections (RCS) are different, and their azimuth velocities lead to different defocus values. Thus, the 16 targets are selected. Their radial velocities were obtained, and the value can be seen in

Table 5. Motion parameter estimation results.

Target No.	Radial Velocity	Azimuth Velocity	Target No.	Radial Velocity	Azimuth Velocity
1	−1 m/s	−1 m/s	9	−3 m/s	−3 m/s
2	−5 m/s	−5 m/s	10	−7 m/s	−7 m/s
3	−15 m/s	−15 m/s	11	−11.5 m/s	−11.5 m/s
4	−30 m/s	−30 m/s	12	−24.1 m/s	−24 m/s
5	1 m/s	1 m/s	13	−29.4 m/s	−29.5 m/s
6	5 m/s	5 m/s	14	3.5 m/s	3.5 m/s
7	15 m/s	15 m/s	15	19.7 m/s	19.5 m/s
8	30 m/s	30 m/s	16	20.5 m/s	20.5 m/s

.

Next, different azimuth velocities were exploited for each target to process the beamforming and imaging to find the azimuth velocities that generate the results with maximum signal energy. The estimation results of azimuth velocities can be seen in Table 5, and they have high accuracy by comparing to the truth values. Figure. 11b shows the imaging results of all moving targets using the estimated motion parameters, where the red cross marks represent the actual position of the targets. It can be seen that the energy of all the targets is well gathered, and the targets are repositioned. However, due to the error in target estimation, the targets are still offset in azimuth.

Finally, the values of the parameter estimation results are shown in Table 5. The root mean square error (RMSE) of radial velocity is 0.0255 m/s and the RMSE of azimuth velocity is 0.0627 m/s. Thus, multistatic GEO SAR can obtain much more accurate velocities of the targets. According to the two-dimensional velocity of the target, the imaging results can be obtained. All the targets were placed at the same SAR image, as shown in Figure 11b.

5.2.2. Performance Analysis of SCNR and Minimum Detectable Velocity

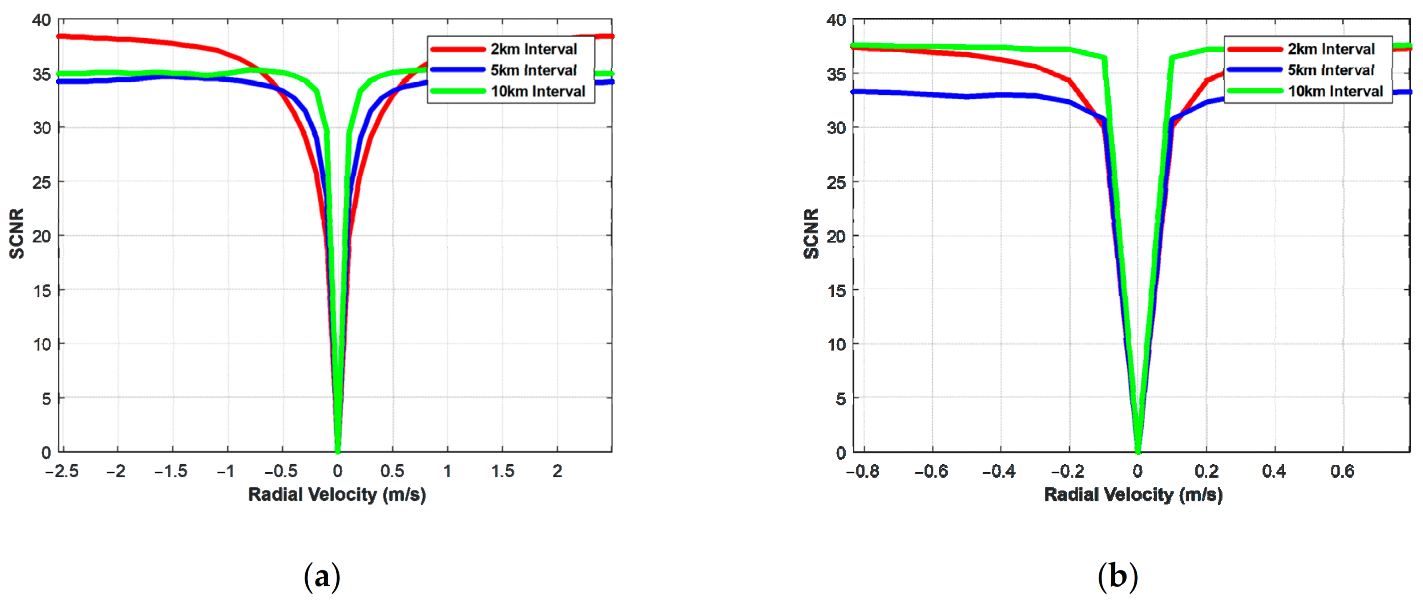
The orbital elements and imaging parameters used for simulation are shown in Table 2. Different shortest channel spacings were selected, and the satellite was in the side-looking mode. The output SCNR can be seen in Figure 12 after the whole steps of modified ISTAP in the near field for multistatic GEO SAR. It is shown that the output SCNR reached 35 dB both at the equator and at the perigee. Moreover, from the curve of output SCNR, it can be seen that the clutter was suppressed by −35 dB. This means that the proposed method can suppress the clutter effectively.

The minimum detectable velocity (MDV) under different conditions can be obtained from the output SCNR because the MDV is determined by the output SCNR’s detection threshold. It is considered that the moving target signal can be detected when the maximum allowable output SCNR loss is −5 dB [45].

From Figure 12, it can be seen that the MDV is limited by the channel spacing. The greater the channel spacing, the smaller the MDV. Besides, if the channel spacing is the same, the MDV at the perigee is smaller than the MDV at the equator. It results from the satellite velocity at the perigee being less than the equator’s satellite velocity, which causes the clutter to become narrow. Both at the equator and perigee, the MDV is less than 0.5 m/s.

6. Conclusions

Multistatic GEO SAR can realize multiple channels, which can be used to monitor moving targets. Compared with the LEO SAR system, multistatic GEO SAR has a wide coverage and short revisit time, and has the ability to observe moving targets continuously. In this paper, the modified ISTAP in the near field was proposed to detect a moving target and estimate the motion parameters, which solves the problem of curved trajectory and failure of far-field assumption and obtains the optimal output SCNR. Firstly, the multi-channel signal model for multistatic GEO SAR was derived. The simulation experiments proved that the proposed model is still valid at an along-track baseline of 50 km. Secondly, the ISTAP method was modified according to the new signal model to apply to the multistatic GEO SAR. Finally, according to the simulation results in this paper, it can be seen that multistatic GEO SAR has excellent detection performance of moving targets. The RMSE of radial velocity was 0.0255 m/s, and the RMSE of azimuth velocity was 0.0627 m/s. The MDV was less than 0.5 m/s. However, it was noticeable that the accuracy was obtained by simulated data and will degrade for experimental data. The proposed method will face performance degradation when the baseline’s length reaches hundreds of kilometers, and the clutter is heterogeneous. Besides, if the orbit determination error of GEO SARs is large, an additional correction method based on ground corner reflectors should be carried out to obtain the accurate motion parameter estimations.

Moreover, the oscillatory motions of the target will cause defocusing. When a point target swings within a short period, it will produce a phase error with sinusoidal changes, causing the target to spread in the azimuth direction in the SAR image. The technique to finely focus ship target with oscillatory motions has been investigated for monostatic case in [45,46], and the multistatic GEO SAR case will also be considered in our future research.