Estimating Stand and Fire-Related Surface and Canopy Fuel Variables in Pine Stands Using Low-Density Airborne and Single-Scan Terrestrial Laser Scanning Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data
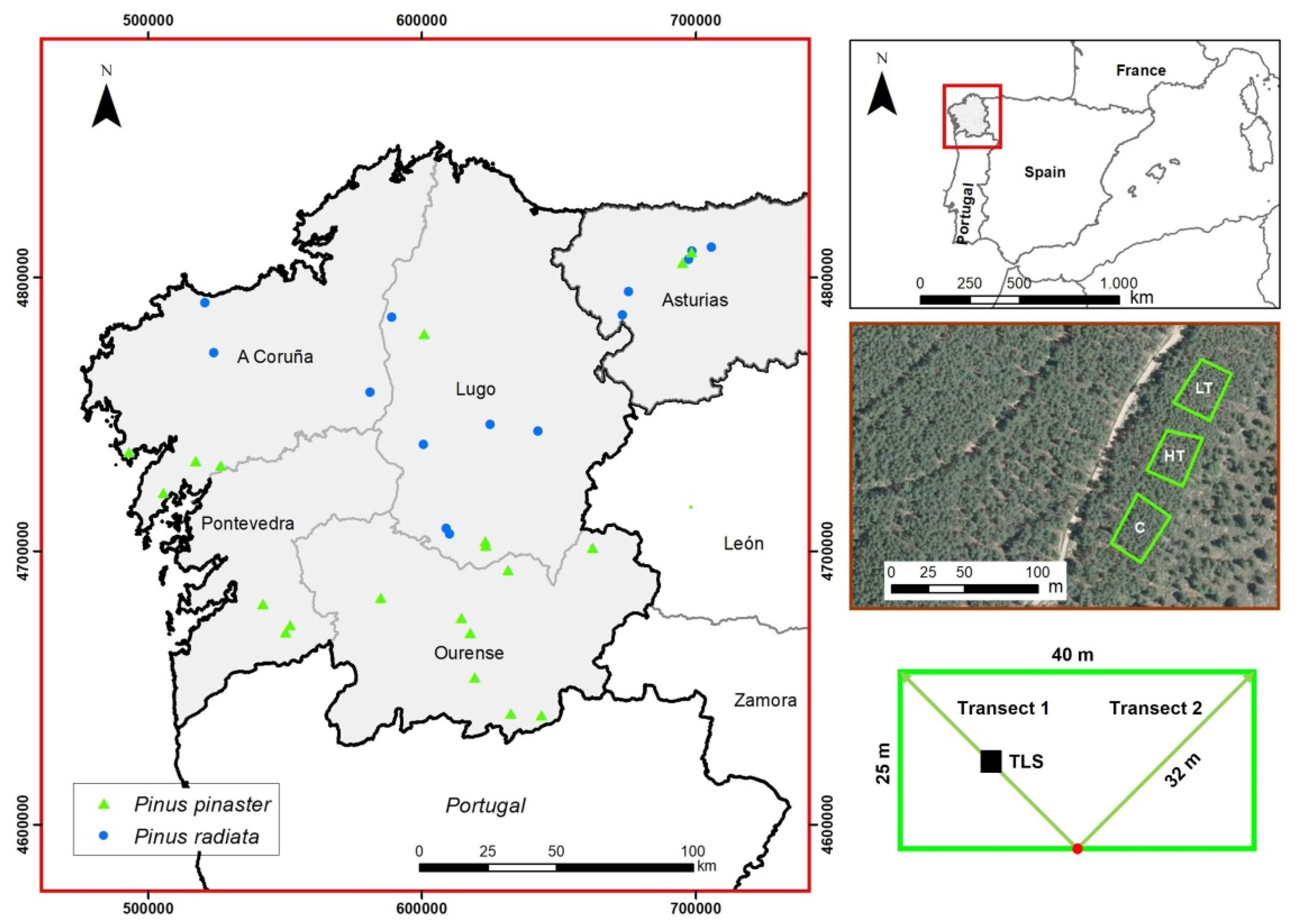
2.1.1. Study Area and Sample Plots
2.1.2. Tree and Stand Variables
2.1.3. Canopy Fuel Variables
2.1.4. Understory Fuel Variables
2.1.5. TLS Data
2.1.6. ALS Data
2.2. Model Development
3. Results and Discussion
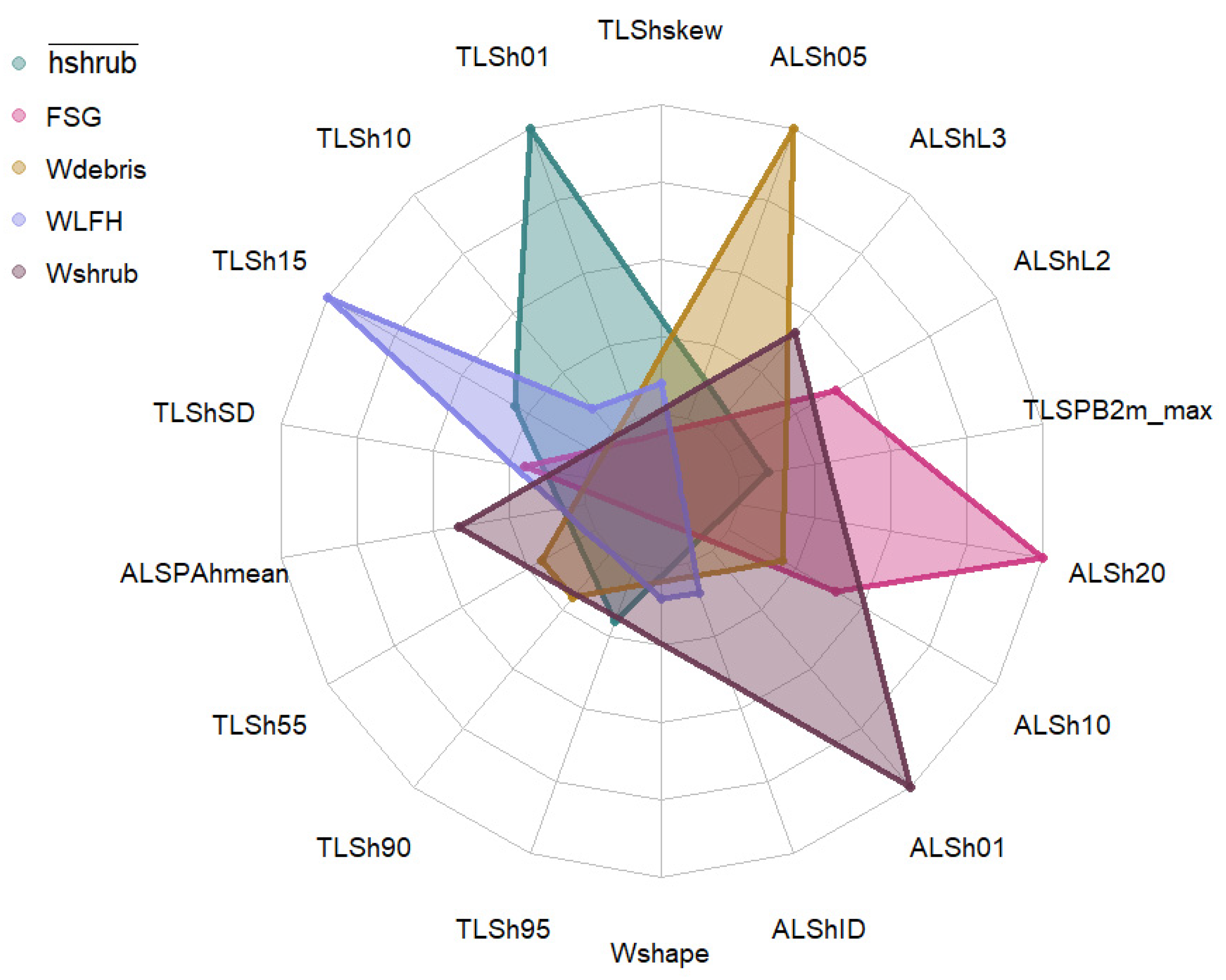
3.1. Models Based on TLS-Derived Metrics
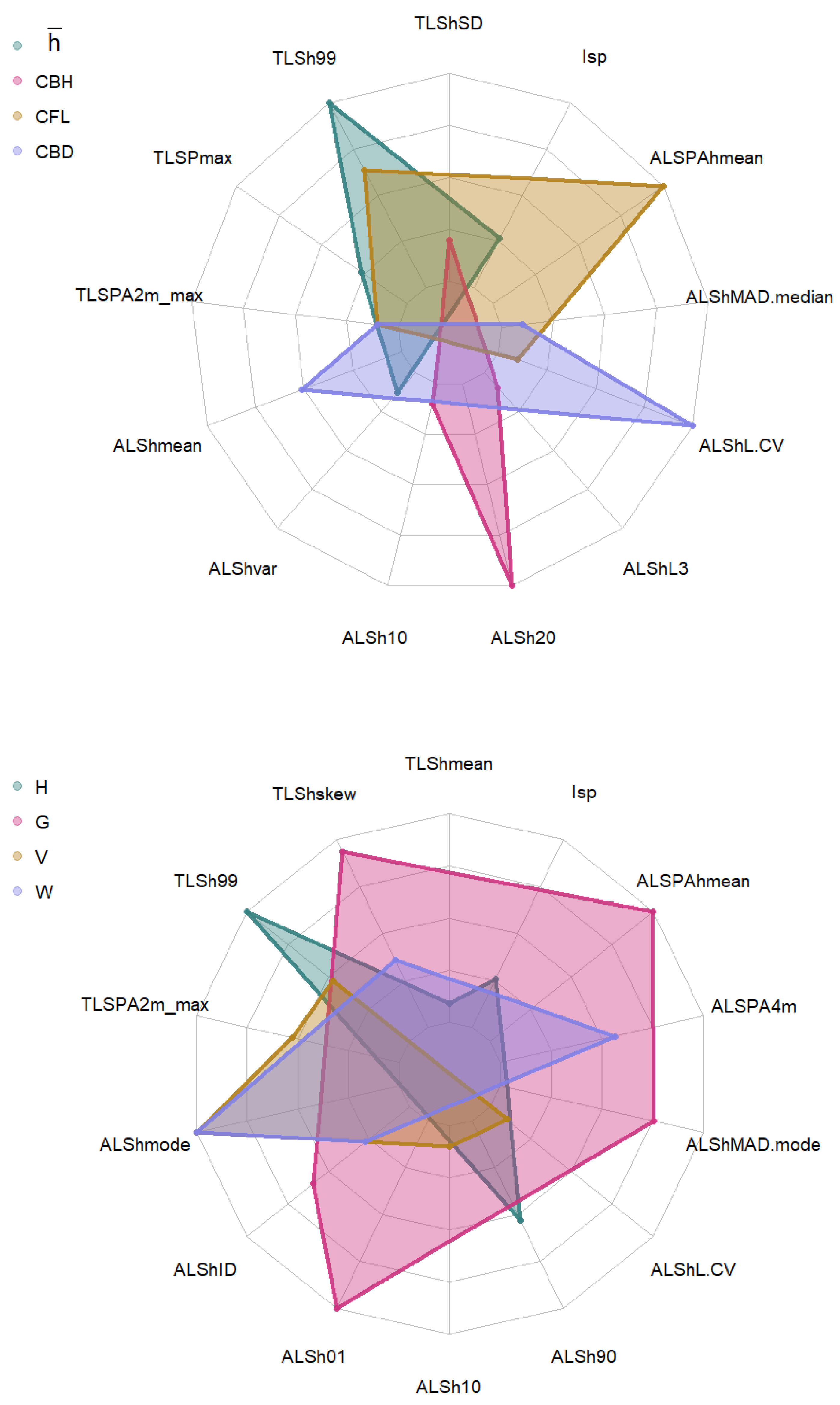
3.2. Models Based on ALS-Derived Metrics
3.3. MARS Models Combining TLS- and ALS-Derived Metrics
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Surface Fire-Related Variables | ||
|---|---|---|
| Variable | Metrics | Model |
(m) | TLS | |
| ALS | ||
| TLS + ALS | The inclusion of ALS metrics does not improve the goodness-of-fit statistics of the model using only TLS metrics | |
| FSG (m) | TLS | |
| ALS | ||
| TLS + ALS | ||
| Wdebris (Mg ha−1) | TLS | |
| ALS | ||
| TLS+ALS | ||
| WLFH (Mg ha−1) | TLS | |
| ALS | ||
| TLS + ALS | ||
| Wshrub (Mg ha−1) | TLS | |
| ALS | ||
| TLS + ALS | The inclusion of TLS metrics does not improve the goodness-of-fit statistics of the model using only ALS metrics | |
| Canopy Fire-Related Variables | ||
|---|---|---|
| Variable | Metrics | Model |
(m) | TLS | |
| ALS | ||
| TLS + ALS | ||
| CBH (m) | TLS | |
| ALS | ||
| TLS + ALS | ||
| CFL (kg m2) | TLS | |
| ALS | ||
| TLS + ALS | ||
| CBD (kg m3) | TLS | |
| ALS | ||
| TLS + ALS | ||
| Stand Variables | ||
|---|---|---|
| Variable | Metrics | Model |
| H (m) | TLS | |
| ALS | ||
| TLS + ALS | ||
| G (m2 ha−1) | TLS | |
| ALS | ||
| TLS + ALS | ||
| V (m3 ha−1) | TLS | |
| ALS | ||
| TLS + ALS | ||
| W (Mg ha−1) | TLS | |
| ALS | ||
| TLS + ALS | ||



References
- Andrews, P.L. BEHAVE: Fire Behavior Prediction and Fuel Modeling System: BURN Subsystem, Part 1; US Department of Agriculture, Forest Service, Intermountain Research Station: Ogden, UT, USA, 1986. [Google Scholar]
- Finney, M.A. FARSITE: Fire Area Simulator-Model Development and Evaluation; Res. Pap. RMRS-RP-4, Revised 2004; US Department of Agriculture, Forest Service, Rocky Mountain Research Station: Ogden, UT, USA, 1998; Volume 47, p. 4. [Google Scholar]
- Finney, M.A. An overview of FlamMap fire modeling capabilities. In Proceedings of the Fuels Management-How to Measure Success: Conference Proceedings, Portland, OR, USA, 28–30 March 2006; Andrews, P.L., Butler, B.W., Eds.; Proceedings RMRS-P-41. US Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2006; pp. 213–220. [Google Scholar]
- Arellano-Pérez, S.; Castedo-Dorado, F.; López-Sánchez, C.; González-Ferreiro, E.; Yang, Z.; Díaz-Varela, R.; Álvarez-González, J.; Vega, J.; Ruiz-González, A. Potential of Sentinel-2A Data to Model Surface and Canopy Fuel Characteristics in Relation to Crown Fire Hazard. Remote Sens. 2018, 10, 1645. [Google Scholar] [CrossRef] [Green Version]
- Hawbaker, T.J.; Keuler, N.S.; Lesak, A.A.; Gobakken, T.; Contrucci, K.; Radeloff, V.C. Improved estimates of forest vegetation structure and biomass with a LiDAR-optimized sampling design. J. Geophys. Res. Biogeosciences 2009, 114. [Google Scholar] [CrossRef]
- Maltamo, M.; Næsset, E.; Vauhkonen, J. Forestry applications of airborne laser scanning. Concepts and case studies. Manag. For. Ecosyst. 2014, 27, 460. [Google Scholar]
- Liang, X.; Kankare, V.; Hyyppä, J.; Wang, Y.; Kukko, A.; Haggrén, H.; Yu, X.; Kaartinen, H.; Jaakkola, A.; Guan, F. Terrestrial laser scanning in forest inventories. ISPRS J. Photogramm. Remote Sens. 2016, 115, 63–77. [Google Scholar] [CrossRef]
- Liang, X.; Hyyppä, J.; Kaartinen, H.; Lehtomäki, M.; Pyörälä, J.; Pfeifer, N.; Holopainen, M.; Brolly, G.; Francesco, P.; Hackenberg, J. International benchmarking of terrestrial laser scanning approaches for forest inventories. ISPRS J. Photogramm. Remote Sens. 2018, 144, 137–179. [Google Scholar] [CrossRef]
- Gale, M.G.; Cary, G.J.; Van Dijk, A.I.; Yebra, M. Forest fire fuel through the lens of remote sensing: Review of approaches, challenges and future directions in the remote sensing of biotic determinants of fire behaviour. Remote Sens. Environ. 2021, 255, 112282. [Google Scholar] [CrossRef]
- González-Ferreiro, E.; Diéguez-Aranda, U.; Miranda, D. Estimation of stand variables in Pinus radiata D. Don plantations using different LiDAR pulse densities. Forestry 2012, 85, 281–292. [Google Scholar] [CrossRef]
- González-Ferreiro, E.; Diéguez-Aranda, U.; Crecente-Campo, F.; Barreiro-Fernández, L.; Miranda, D.; Castedo-Dorado, F. Modelling canopy fuel variables for Pinus radiata D. Don in NW Spain with low-density LiDAR data. Int. J. Wildland Fire 2014, 23, 350–362. [Google Scholar]
- González-Ferreiro, E.; Arellano-Pérez, S.; Castedo-Dorado, F.; Hevia, A.; Vega, J.A.; Vega-Nieva, D.; Álvarez-González, J.G.; Ruiz-González, A.D. Modelling the vertical distribution of canopy fuel load using national forest inventory and low-density airbone laser scanning data. PLoS ONE 2017, 12, e0176114. [Google Scholar] [CrossRef]
- Hermosilla, T.; Ruiz, L.A.; Kazakova, A.N.; Coops, N.C.; Moskal, L.M. Estimation of forest structure and canopy fuel parameters from small-footprint full-waveform LiDAR data. Int. J. Wildland Fire 2013, 23, 224–233. [Google Scholar] [CrossRef] [Green Version]
- Hevia-Cabal, A.; Álvarez-González, J.G.; Ruiz Fernández, E.; Prendes, C.; Ruiz González, A.D.; Majada, J.; González-Ferreiro, E. Modelling canopy fuel and forest stand variables and characterizing the influence of thinning in the stand structure using airborne LiDAR. Rev. Teledetección 2016, 45, 41–55. [Google Scholar]
- Kelly, M.; Su, Y.; Di Tommaso, S.; Fry, D.L.; Collins, B.M.; Stephens, S.L.; Guo, Q. Impact of Error in Lidar-Derived Canopy Height and Canopy Base Height on Modeled Wildfire Behavior in the Sierra Nevada, California, USA. Remote Sens. 2018, 10, 10. [Google Scholar] [CrossRef] [Green Version]
- Botequim, B.; Fernandes, P.M.; Borges, J.G.; González-Ferreiro, E.; Guerra-Hernández, J. Improving silvicultural practices for Mediterranean forests through fire behaviour modelling using LiDAR-derived canopy fuel characteristics. Int. J. Wildland Fire 2019, 28, 823–839. [Google Scholar] [CrossRef]
- Ruiz, L.Á.; Crespo-Peremarch, P.; Torralba, J. Modelling canopy fuel properties and understory vegetation with full-waveform LiDAR. In Proceedings of the International Conference on Smart Geoinformatics Applications (ICSGA 2021), Prince of Songkla University, Phuket, Thailand, 24–25 February 2021. [Google Scholar]
- Chamberlain, C.P.; Meador, A.J.S.; Thode, A.E. Airborne lidar provides reliable estimates of canopy base height and canopy bulk density in southwestern ponderosa pine forests. For. Ecol. Manag. 2021, 481, 118695. [Google Scholar] [CrossRef]
- Hilker, T.; van Leeuwen, M.; Coops, N.; Wulder, M.A.; Newnham, G.; Jupp, D.; Culvenor, D. Comparing canopy metrics derived from terrestrial and airborne laser scanning in a Douglas-fir dominated forest stand. Trees 2010, 24, 819–832. [Google Scholar] [CrossRef]
- White, J.C.; Coops, N.C.; Wulder, M.A.; Vastaranta, M.; Hilker, T.; Tompalski, P. Remote sensing technologies for enhancing forest inventories: A review. Can. J. Remote Sens. 2016, 42, 619–641. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Zhu, X.; Yebra, M.; Harris, S.; Tapper, N. Development of a predictive model for estimating forest surface fuel load in Australian eucalypt forests with LiDAR data. Environ. Model. Softw. 2017, 97, 61–71. [Google Scholar] [CrossRef]
- Bright, B.C.; Hudak, A.T.; Meddens, A.J.; Hawbaker, T.J.; Briggs, J.S.; Kennedy, R.E. Prediction of forest canopy and surface fuels from lidar and satellite time series data in a bark beetle-affected forest. Forests 2017, 8, 322. [Google Scholar] [CrossRef] [Green Version]
- Campbell, M.J.; Dennison, P.E.; Hudak, A.T.; Parham, L.M.; Butler, B.W. Quantifying understory vegetation density using small-footprint airborne lidar. Remote Sens. Environ. 2018, 215, 330–342. [Google Scholar] [CrossRef]
- Stefanidou, A.; ZGitas, I.; Korhonen, L.; Georgopoulos, N.; Stavrakoudis, D. Multispectral lidar-based estimation of surface fuel load in a dense coniferous forest. Remote Sens. 2020, 12, 3333. [Google Scholar] [CrossRef]
- Cao, L.; Coops, N.C.; Hermosilla, T.; Innes, J.; Dai, J.; She, G. Using small-footprint discrete and full-waveform airborne LiDAR metrics to estimate total biomass and biomass components in subtropical forests. Remote Sens. 2014, 6, 7110–7135. [Google Scholar] [CrossRef] [Green Version]
- Anderson, K.; Hancock, S.; Disney, M.; Gaston, K.J. Is waveform worth it? A comparison of LiDAR approaches for vegetation and landscape characterization. Remote Sens. Ecol. Conserv. 2016, 2, 5–15. [Google Scholar] [CrossRef]
- Crespo-Peremarch, P.; Fournier, R.A.; Nguyen, V.-T.; van Lier, O.R.; Ruiz, L.Á. A comparative assessment of the vertical distribution of forest components using full-waveform airborne, discrete airborne and discrete terrestrial laser scanning data. For. Ecol. Manag. 2020, 473, 118268. [Google Scholar] [CrossRef]
- Crespo-Peremarch, P.; Ruiz, L.Á.; Balaguer-Beser, Á.; Estornell, J. Analyzing the role of pulse density and voxelization parameters on full-waveform LiDAR-derived metrics. ISPRS J. Photogramm. Remote Sens. 2018, 146, 453–464. [Google Scholar] [CrossRef]
- Loudermilk, E.L.; Hiers, J.K.; O’Brien, J.J.; Mitchell, R.J.; Singhania, A.; Fernandez, J.C.; Slatton, K.C. Ground-based LIDAR: A novel approach to quantify fine-scale fuelbed characteristics. Int. J. Wildland Fire 2009, 18, 676–685. [Google Scholar] [CrossRef] [Green Version]
- Olsoy, P.J.; Glenn, N.F.; Clark, P.E.; Derryberry, D.R. Aboveground total and green biomass of dryland shrub derived from terrestrial laser scanning. ISPRS J. Photogramm. Remote Sens. 2014, 88, 166–173. [Google Scholar]
- Owers, C.J.; Rogers, K.; Woodroffe, C.D. Terrestrial laser scanning to quantify above-ground biomass of structurally complex coastal wetland vegetation. Estuar. Coast. Shelf Sci. 2018, 204, 164–176. [Google Scholar] [CrossRef] [Green Version]
- Alonso-Rego, C.; Arellano-Pérez, S.; Cabo, C.; Ordoñez, C.; Álvarez-González, J.G.; Díaz-Varela, R.A.; Ruiz-González, A.D. Estimating fuel loads and structural characteristics of shrub communities by using terrestrial laser scanning. Remote Sens. 2020, 12, 3704. [Google Scholar] [CrossRef]
- Rowell, E.; Loudermilk, E.L.; Seielstad, C.; O’Brien, J.J. Using simulated 3D surface fuelbeds and terrestrial laser scan data to develop inputs to fire behavior models. Can. J. Remote Sens. 2016, 42, 443–459. [Google Scholar] [CrossRef]
- Rowell, E.; Loudermilk, E.L.; Hawley, C.; Pokswinski, S.; Seielstad, C.; Queen, L.L.; O’Brien, J.J.; Hudak, A.T.; Goodrick, S.; Hiers, J.K. Coupling terrestrial laser scanning with 3D fuel biomass sampling for advancing wildland fuels characterization. For. Ecol. Manag. 2020, 462, 117945. [Google Scholar] [CrossRef]
- Hudak, A.; Prichard, S.; Keane, R.; Loudermilk, L.; Parsons, R.; Seielstad, C.; Rowell, E.; Skowronski, N. Hierarchical 3D Fuel and Consumption Maps to Support Physics-Based Fire Modeling; Joint Fire Science Program Project 16-4-01-15 Final Report; US Forest Service, Rocky Mountain Research Station: Moscow, ID, USA, 2017; 38p. [Google Scholar]
- Hudak, A.T.; Kato, A.; Bright, B.C.; Loudermilk, E.L.; Hawley, C.; Restaino, J.C.; Ottmar, R.D.; Prata, G.A.; Cabo, C.; Prichard, S.J.; et al. Towards spatially explicit quantification of pre- and post-fire fuels and fuel consumption from traditional and point cloud measurements. For. Sci. 2020, 66, 428–442. [Google Scholar]
- Greaves, H.E.; Vierling, L.A.; Eitel, J.U.H.; Boelman, N.T.; Troy, S.T.; Magney, T.; Prager, C.M.; Grin, K.L. Estimating aboveground biomass and leaf area of low-stature Arctic shrubs with terrestrial LiDAR. Remote Sens. Environ. 2015, 164, 26–35. [Google Scholar] [CrossRef]
- Jupp, D.L.B.; Culvenor, D.S.; Lovell, J.L.; Newnham, G.J.; Strahler, A.H.; Woodcock, C.E. Estimating forest LAI profiles and structural parameters using a ground-based laser called ‘Echidna’. Tree Physiol. 2009, 29, 171–181. [Google Scholar] [CrossRef] [PubMed]
- Newnham, G.J.; Armston, J.D.; Calders, K.; Disney, M.I.; Lovell, J.L.; Schaaf, C.B.; Strahler, A.H.; Danson, F.M. Terrestrial laser scanning for plot-scale forest measurement. Curr. For. Rep. 2015, 1, 239–251. [Google Scholar] [CrossRef] [Green Version]
- Wezyk, P. The integration of the Terrestrial and Airborne Laser Scanning technologies in the semi-automated process of retrieving selected trees and forest stand parameters. Ambiencia 2012, 8, 533–548. [Google Scholar]
- Hilker, T.; Coops, N.C.; Newnham, G.J.; van Leeuwen, M.; Wulder, M.A.; Stewart, J.; Culvenor, D.S. Comparison of terrestrial and airborne LiDAR in describing stand structure of a thinned lodgepole pine forest. J. For. 2012, 110, 97–104. [Google Scholar] [CrossRef]
- Kankare, V.; Vauhkonen, J.; Tanhuanpaa, T.; Holopainen, M.; Vastaranta, M.; Joensuu, M.; Krooks, A.; Hyyppä, J.; Hyyppä, H.; Alho, P.; et al. Accuracy in estimation of timber assortments and stem distribution—a comparison of airborne and terrestrial laser scanning techniques. ISPRS J. Photogramm. Remote Sens. 2014, 97, 89–97. [Google Scholar] [CrossRef]
- Kankare, V.; Liang, X.; Vastaranta, M.; Yu, X.; Holopainen, M.; Hyyppä, J. Diameter distribution estimation with laser scanning based multisource single tree inventory. ISPRS J. Photogramm. Remote Sens. 2015, 108, 161–171. [Google Scholar] [CrossRef]
- Chasmer, L.; Hopkinson, C.; Treitz, P. Assessing the three dimensional frequency distribution of airborne and ground-based LiDAR data for red pine and mixed deciduous forest plots. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 36, 8. [Google Scholar]
- Jung, S.-E.; Kwak, D.-A.; Park, T.; Lee, W.-K.; Yoo, S. Estimating crown variables of individual trees using airborne and terrestrial laser scanners. Remote Sens. 2011, 3, 2346–2363. [Google Scholar] [CrossRef] [Green Version]
- Listopad, C.M.C.S.; Drake, J.B.; Masters, R.E.; Weishampel, J.F. Portable and Airborne Small Footprint LiDAR: Forest Canopy Structure Estimation of Fire Managed Plots. Remote Sens. 2011, 3, 1284–1307. [Google Scholar] [CrossRef] [Green Version]
- Zhao, F.; Yang, X.; Strahler, A.H.; Schaaf, C.L.; Yao, T.; Wang, Z.; Román, M.O.; Woodcock, C.E.; Ni-Meister, W.; Jupp, D.L.B.; et al. A comparison of foliage profiles in the Sierra National Forest obtained with a full-waveform under-canopy EVI lidar system with the foliage profiles obtained with an airborne full-waveform LVIS lidar system. Remote Sens. Environ. 2013, 136, 330–341. [Google Scholar] [CrossRef] [Green Version]
- Greaves, H.E.; Vierling, L.A.; Eitel, J.U.H.; Boelman, N.T.; Magney, T.S.; Prager, C.M.; Griffin, K.L. Applying terrestrial lidar for evaluation and calibration of airborne lidar-derived shrub biomass estimates in Arctic tundra. Remote Sens. Lett. 2017, 8, 175–184. [Google Scholar] [CrossRef]
- Liu, L.; Pang, Y.; Li, Z.; Si, L.; Liao, S. Combining Airborne and Terrestrial Laser Scanning Technologies to Measure Forest Understorey Volume. Forests 2017, 8, 111. [Google Scholar] [CrossRef] [Green Version]
- Torralba, J.; Crespo-Peremarch, P.; Ruiz, L.Á. Assessing the use of discrete, fullwaveform LiDAR and TLS to classify Mediterranean forest species composition. Rev. Teledetección 2018, 27–40. [Google Scholar] [CrossRef] [Green Version]
- Skowronski, N.S.; Clark, K.-L.; Duveneck, M.; Hom, J. Three-dimensional canopy fuel loading predicted using upward and downward sensing LiDAR systems. Remote Sens. Environ. 2011, 115, 703–714. [Google Scholar] [CrossRef]
- Lindberg, E.; Holmgren, J.; Olofsson, K.; Olsson, H. Estimation of stem attributes using a combination of terrestrial and airborne laser scanning. Eur. J. For. Res. 2012, 131, 1917–1931. [Google Scholar] [CrossRef] [Green Version]
- LaRue, E.A.; Wagner, F.W.; Fei, S.; Atkins, J.W.; Fahey, R.T.; Gough, C.M.; Hardiman, B.S. Compatibility of Aerial and Terrestrial LiDAR for Quantifying Forest Structural Diversity. Remote Sens. 2020, 12, 1407. [Google Scholar] [CrossRef]
- Hauglin, M.; Lien, V.; Næsset, E.; Gobakken, T. Geo-referencing forest field plots by co-registration of terrestrial and airborne laser scanning data. Int. J. Remote Sens. 2014, 5, 3135–3149. [Google Scholar] [CrossRef]
- Yang, B.; Zang, Y.; Dong, Z.; Huang, R. An automated method to register airborne and terrestrial laser scanning point clouds. ISPRS J. Photogramm. Remote Sens. 2015, 109, 62–76. [Google Scholar] [CrossRef]
- Paris, C.; Kelbe, D.; van Aardt, J.; Bruzzone, L. A Novel Automatic Method for the Fusion of ALS and TLS LiDAR Data for Robust Assessment of Tree Crown Structure Fellow. IEEE Transcations Geosci. Remote Sens. 2017, 55, 3679–3693. [Google Scholar] [CrossRef]
- Bazezew, M.N.; Hussin, Y.A.; Kloosterman, E.H. Integrating Airborne LiDAR and Terrestrial Laser Scanner forest parameters for accurate above-ground biomass/carbon estimation in Ayer Hitam tropical forest, Malaysia. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 638–652. [Google Scholar] [CrossRef]
- Giannetti, F.; Puletti, N.; Quatrini, V.; Travaglini, D.; Bottalico, F.; Corona, P.; Chirici, G. Integrating terrestrial and airborne laser scanning for the assessment of single-tree attributes in Mediterranean forest stands. Eur. J. Remote Sens. 2018, 51, 795–807. [Google Scholar] [CrossRef] [Green Version]
- Dai, W.; Yang, B.; Liang, X.; Dong, Z.; Huang, R.; Wang, Y.; Li, W. Automated fusion of forest airborne and terrestrial point clouds through canopy density analysis. ISPRS J. Photogramm. Remote Sens. 2019, 156, 94–107. [Google Scholar] [CrossRef]
- Arellano-Pérez, S.; Castedo-Dorado, F.; Álvarez-González, J.G.; Alonso-Rego, C.; Vega, J.A.; Ruiz-González, A.D. Mid-term effects of a thin-only treatment on fuel complex, potential fire behaviour and severity and post-fire soil erosion protection in fast-growing pine plantations. For. Ecol. Manag. 2020, 460, 117895. [Google Scholar] [CrossRef]
- Dieguez-Aranda, U.; Rojo-Alboreca, A.; Castedo-Dorado, F.; Álvarez-González, J.G.; Barrio-Anta, M.; Crecente-Campo, F.; González-González, J.M.; Pérez-Cruzado, C.; Rodriguez-Soalleiro, R.; López-Sánchez, C.A.; et al. Herramientas Selvícolas Para la Gestión Forestal Sostenible en Galicia; Xunta de Galicia: Santiago de Compostela, Spain, 2009. [Google Scholar]
- Crecente-Campo, F.; Marshall, P.; LeMay, V.; Diéguez-Aranda, U. A crown profile model for Pinus radiata D. Don in northwestern Spain. For. Ecol. Manag. 2009, 257, 2370–2379. [Google Scholar] [CrossRef]
- Crecente-Campo, F.; Álvarez-González, J.G.; Castedo-Dorado, F.; Gómez-García, E.; Diéguez-Aranda, U. Development of crown profile models for Pinus pinaster Ait. and Pinus sylvestris L. in northwestern Spain. Forestry 2013, 86, 481–491. [Google Scholar] [CrossRef] [Green Version]
- Brown, J.K. A Planar Intersect Method for Sampling Fuel Volume and Surface Area. For. Sci. 1971, 17, 96–102. [Google Scholar]
- Brown, J.K. Handbook for Inventorying Downed Woody Material; General Technical Report GTR-INT-16; USDA Forest Service, Intermountain Forest and Range Experiment Station: Ogden, UT, USA, 1974. [Google Scholar]
- Molina-Valero, J.A.; Ginzo Villamayor, M.J.; Novo Pérez, A.M.; Martínez-Calvo, A.; Álvarez-González, J.G.; Montes, F.; Pérez-Cruzado, C. FORTLS: Automatic Processing of TLS Point Cloud Data for Forestry Purposes. R Package Version 1.0.3. 2021. Available online: https://CRAN.R-project.org/package=FORTLS (accessed on 4 December 2021).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021; Available online: https://www.R-project.org/ (accessed on 4 November 2021).
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An easy-to-use airborne LiDAR data filtering method based on cloth simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Cao, Q.V.; Burkhart, H.E.; Lemin, R.C. Diameter Distributions and Yields of Thinned Loblolly Pine Plantations; FWS 1-82; School of Forestry and Wildlife Resources; Virginia Polytechnic Institute and State University: Blacksburg, VA, USA, 1982. [Google Scholar]
- McGaughey, R.J. FUSION/LDV: Software for LIDAR Data Analysis and Visualization; US Department of Agriculture, Forest Service: Pacific Northwest Research Station: Seattle, WA, USA, 2021; Available online: http://forsys.sefs.uw.edu/fusion/fusion_overview.html (accessed on 4 December 2021).
- Friedman, J.H. Multivariate adaptive regression splines (with discussion). Ann. Stat. 1991, 19, 79–141. [Google Scholar]
- Milborrow, S. Derived from Mda: Mars by Hastie T and Tibshirani R. Uses Alan Miller’s Fortran Utilities with Thomas Lumley’s Leaps Wrapper. Earth: Multivariate Adaptive Regression Splines. R Package Version 4.5.1. Available online: https://cran.r-project.org/package=earth (accessed on 4 December 2021).
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Genuer, R.; Poggi, J.M.; Tuleau-Malot, C. Variable selection using random forests. Pattern Recognit. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef] [Green Version]
- Gislason, P.O.; Benediktsson, J.A.; Sveinsson, J.R. Random Forests for land cover classification. Pattern Recognit. Lett. 2006, 27, 294–300. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Meyer, D.; Dimitriadou, E.; Hornik, K.; Weingessel, A.; Leisch, F. e1071: Misc Functions of the Department of Statistics, Probability Theory Group (Formerly: E1071), TU Wien. R Package Version 1.7-2. Available online: https://CRAN.R-project.org/package=e1071 (accessed on 4 December 2021).
- Huang, H.; Li, Z.; Gong, P.; Cheng, X.; Clinton, N.; Cao, C.; Ni, W.; Wang, L. Automated methods for measuring DBH and tree heights with a commercial scanning lidar. Photogram. Eng. Remote Sens. 2011, 77, 219–227. [Google Scholar] [CrossRef]
- Liang, X.; Hyyppa, J. Automatic Stem Mapping by Merging Several Terrestrial Laser Scans at the Feature and Decision Levels. Sensors 2013, 13, 1614–1634. [Google Scholar] [CrossRef] [Green Version]
- Srinivasan, S.; Popescu, S.; Eriksson, M.; Sheridan, R.D.; Ku, N.-W. Terrestrial Laser Scanning as an Effective Tool to Retrieve Tree Level Height, CrownWidth, and Stem Diameter. Remote Sens. 2015, 7, 1877–1896. [Google Scholar] [CrossRef] [Green Version]
- Torralba, J.; Ruiz, L.A.; Carbonell-Rivera, J.P.; Crespo-Peremarch, P. Análisis de posiciones y densidades TLS (Terrestrial Laser Scanning) para optimizar la estimación de parámetros forestales. In Teledetección: Hacia una Visión Global del Cambio Climático; Ruiz, L.A., Estornell, J., Calle, A., Antuña-Sánchez, J.C., Eds.; Universidad de Valladolid: Valladolid, Spain, 2019; pp. 443–446. [Google Scholar]
- García, M.; Danson, F.M.; Riaño, D.; Chuvieco, E.; Ramirez, F.A.; Bandugula, V. Terrestrial laser scanning to estimate plot-level forest canopy fuel properties. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 636–645. [Google Scholar] [CrossRef]
- Wilson, N.; Bradstock, R.; Bedward, M. Detecting the effects of logging and wildfire on forest fuel structure using terrestrial laser scanning (TLS). For. Ecol. Manag. 2021, 488, 119037. [Google Scholar] [CrossRef]
- Astrup, R.; Ducey, M.J.; Granhus, A.; Ritter, T.; von Lüpke, N. Approaches for estimating stand-level volume using terrestrial laser scanning in a single-scan mode. Can. J. For. Res. 2014, 44, 666–676. [Google Scholar]
- Panagiotidis, D.; Abdollahnejad, A.; Slavík, M. Assessment of Stem Volume on Plots Using Terrestrial Laser Scanner: A Precision Forestry Application. Sensors 2021, 21, 301. [Google Scholar] [CrossRef]
- Watt, P.J.; Donoghue, D.N.M. Measuring forest structure with terrestrial laser scanning. Int. J. Remote Sens. 2005, 26, 1437–1446. [Google Scholar] [CrossRef]
- Brolly, G.; Kiraly, G. Algorithms for stem mapping by means of terrestrial laser scanning. Acta Silv. Lignaria Hung. 2009, 5, 119–130. [Google Scholar]
- Liang, X.; Litkey, P.; Hyyppa, J.; Kaartinen, H.; Vastaranta, M.; Holopainen, M. Automatic stem mapping using single-scan terrestrial laser scanning. IEEE Trans. Geosci. Remote Sens. 2012, 50, 661–670. [Google Scholar] [CrossRef]
- Olofsson, K.; Holmgren, J.; Olsson, H. Tree stem and height measurements using terrestrial laser scanning and the RANSAC algorithm. Remote Sens. 2014, 6, 4323–4344. [Google Scholar] [CrossRef] [Green Version]
- Strahler, A.H.; Jupp, D.L.B.; Woodcock, C.E.; Schaaf, C.B.; Yao, T.; Zhao, F.; Yang, X.; Lovell, J.; Culvenor, D.; Newnham, G.; et al. Retrieval of forest structural parameters using a ground-based lidar instrument (Echidna®). Can. J. Remote Sens. 2008, 34, S426–S440. [Google Scholar] [CrossRef] [Green Version]
- Yao, T.; Yang, X.; Zhao, F.; Wang, Z.; Zhang, Q.; Jupp, D.; Lovell, J.; Culvenor, D.; Newnham, G.; Ni-Meister, W.; et al. Measuring forest structure and biomass in New England forest stands using Echidna ground-based lidar. Remote Sens. Environ. 2011, 115, 2965–2974. [Google Scholar] [CrossRef]
- Molina-Valero, J.A.; Ginzo-Villamayor, M.J.; Novo-Pérez, M.A.; Álvarez-González, J.G.; Pérez-Cruzado, C. Estimación del área basimétrica en masas maduras de Pinus sylvestris en base a una única medición del escáner láser terrestre (TLS). Cuad. Soc. Española Cienc. For. 2019, 45, 97–116. [Google Scholar] [CrossRef]
- Wallace, L.; Hillman, S.; Reinke, K.; Hally, B. Non-destructive estimation of above-ground surface and near-surface biomass using 3D terrestrial remote sensing techniques. Methods Ecol. Evol. 2017, 8, 1607–1616. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Wang, T.; Hou, Z.; Gong, Y.; Feng, L.; Ge, J. Harnessing terrestrial laser scanning to predict understory biomass in temperate mixed forests. Ecol. Indic. 2021, 121, 107011. [Google Scholar] [CrossRef]
- Keane, R.E.; Burgan, R.; van Wagtendonk, J. Mapping wildland fuels for fire management across multiple scales: Integrating remote sensing, GIS, and biophysical modeling. Int. J. Wildland Fire 2001, 10, 301–319. [Google Scholar] [CrossRef]
- Crespo-Peremarch, P.; Ruiz, L. Análisis comparativo del potencial del ALS y TLS en la caracterización estructural de la masa forestal basado en voxelización. In Nuevas Plataformas y Sensores de Teledetección, Proceedings of the XVII Congreso de la Asociación Española de Teledetección, Murcia, Spain, 3–7 October 2017; Ruiz, L.A., Estornell, J., Erena, M., Eds.; Universitat Politécnica de Valencia: Valencia, Spain, 2017; pp. 131–135. [Google Scholar]
- Chasmer, L.; Hopkinson, C.; Treitz, P. Investigating laser pulse penetration through a conifer canopy by integrating airborne and terrestrial lidar. Can. J. Remote Sens. 2006, 32, 116–125. [Google Scholar] [CrossRef] [Green Version]
- García-Gutiérrez, J.; Gonzalez-Ferreiro, E.; Riquelme-Santos, J.C.; Miranda, D.; Dieguez-Aranda, U.; Navarro-Cerrillo, R.M. Evolutionary feature selection to estimate forest stand variables using LiDAR. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 119–131. [Google Scholar] [CrossRef]
- Jiménez, E.; Vega, J.A.; Fernández-Alonso, J.M.; Vega-Nieva, D.; Ortiz, L.; López-Serrano, P.M.; López-Sánchez, C.A. Estimation of aboveground forest biomass in Galicia (NW Spain) by the combined use of LiDAR, LANDSAT ETM+ and National Forest Inventory data. Iforest-Biogeosci. For. 2017, 10, 590–596. [Google Scholar] [CrossRef]
- Novo-Fernández, A.; Barrio-Anta, M.; Recondo, C.; Cámara-Obregón, A.; López-Sánchez, C.A. Integration of National Forest Inventory and Nationwide Airborne Laser Scanning Data to Improve Forest Yield Predictions in North-Western Spain. Remote Sens. 2019, 11, 1693. [Google Scholar] [CrossRef] [Green Version]
- Xu, D.; Wang, H.; Xu, W.; Luan, Z.; Xu, X. LiDAR Applications to Estimate Forest Biomass at Individual Tree Scale: Opportunities, Challenges and Future Perspectives. Forests 2021, 12, 550. [Google Scholar] [CrossRef]
- Bouvier, M.; Durrieu, S.; Fournier, R.A.; Renaud, J.P. Generalizing predictive models of forest inventory attributes using an area-based approach with airborne LiDAR data. Remote Sens. Environ. 2015, 156, 322–334. [Google Scholar] [CrossRef]
- Guerra-Hernández, J.; Bastos Görgens, E.; García-Gutiérrez, J.; Estraviz Rodriguez, L.C.; Tom, M.; González-Ferreiro, E. Comparison of ALS based models for estimating aboveground biomass in three types of Mediterranean forest. Eur. J. Remote Sens. 2016, 49, 185–204. [Google Scholar] [CrossRef]
- Mauro, F.; Hudak, A.T.; Fekety, P.A.; Frank, B.; Temesgen, H.; Bell, D.M.; Gregory, M.J.; McCarley, T.R. Regional Modeling of Forest Fuels and Structural Attributes Using Airborne Laser Scanning Data in Oregon. Remote Sens. 2021, 13, 261. [Google Scholar] [CrossRef]
| Variable | Statistic | Pinus pinaster | Pinus radiata | ||||
|---|---|---|---|---|---|---|---|
| C | LT | HT | C | LT | HT | ||
| Stand Variables | |||||||
| N (stems ha−1) | Mean | 1312.57 | 945.53 | 697.70 | 1014.23 | 725.52 | 506.35 |
| Std. dev. | 384.14 | 358.82 | 228.99 | 261.14 | 144.36 | 112.60 | |
| G (m2 ha−1) | Mean | 45.75 | 38.59 | 33.19 | 39.33 | 31.94 | 27.89 |
| Std. dev. | 8.93 | 8.57 | 6.95 | 9.32 | 7.39 | 7.56 | |
| H (m) | Mean | 16.31 | 16.39 | 16.55 | 22.99 | 22.42 | 21.76 |
| Std. dev. | 2.49 | 2.85 | 2.51 | 2.97 | 2.63 | 2.94 | |
| V (m3 ha−1) | Mean | 297.51 | 256.28 | 223.39 | 349.20 | 282.46 | 245.22 |
| Std. dev. | 90.41 | 88.14 | 70.34 | 95.83 | 84.04 | 86.85 | |
| W (Mg ha−1) | Mean | 160.06 | 138.55 | 121.31 | 172.47 | 138.89 | 119.40 |
| Std. dev. | 45.54 | 44.90 | 35.66 | 46.57 | 40.10 | 41.19 | |
| Canopy fire-related variables | |||||||
(m) | Mean | 14.79 | 15.18 | 15.53 | 19.16 | 19.58 | 20.01 |
| Std. dev. | 2.28 | 2.61 | 2.57 | 2.82 | 2.38 | 3.08 | |
| CFL (kg m−2) | Mean | 1.15 | 0.99 | 0.87 | 1.20 | 0.96 | 0.82 |
| Std. dev. | 0.26 | 0.26 | 0.20 | 0.28 | 0.21 | 0.21 | |
| CBH (m) | Mean | 9.10 | 8.88 | 8.89 | 10.50 | 9.72 | 9.23 |
| Std. dev. | 2.06 | 2.36 | 2.33 | 2.66 | 1.89 | 2.83 | |
| CBD (kg m−3) | Mean | 0.21 | 0.16 | 0.13 | 0.14 | 0.10 | 0.08 |
| Std. dev. | 0.05 | 0.04 | 0.03 | 0.03 | 0.02 | 0.03 | |
| Variable | Statistic | Pinus pinaster | Pinus radiata | ||
|---|---|---|---|---|---|
| C | HT | C | HT | ||
(cm) | Mean | 30.39 | 37.57 | 46.19 | 56.96 |
| Std. dev. | 21.44 | 25.99 | 24.97 | 24.57 | |
| COVshrub (%) | Mean | 28.16 | 44.55 | 51.45 | 55.08 |
| Std. dev. | 26.13 | 27.70 | 32.61 | 32.41 | |
| FSG (m) | Mean | 8.79 | 8.52 | 10.04 | 8.66 |
| Std. dev. | 2.06 | 2.35 | 2.67 | 2.84 | |
| Wdebris (Mg ha−1) | Mean | 5.78 | 11.89 | 7.22 | 27.66 |
| Std. dev. | 3.49 | 9.99 | 5.96 | 25.01 | |
| WLFH (Mg ha−1) | Mean | 31.34 | 30.47 | 31.20 | 31.41 |
| Std. dev. | 5.23 | 4.69 | 3.93 | 4.59 | |
| Wshrub (Mg ha−1) | Mean | 4.60 | 6.11 | 7.06 | 8.57 |
| Std. dev. | 3.08 | 3.08 | 3.67 | 3.40 | |
| Metric | Description |
|---|---|
| TLShmax (cm) | maximum |
| TLShmean (cm) | mean |
| TLShmode (cm) | mode |
| TLShmedian (cm) | median |
| TLShSD (cm) | standard deviation |
| TLShvar (cm) | variance |
| TLShCV (cm) | coefficient of variation (ratio) |
| TLShskw, TLShkurt | skewness and kurtosis |
| TLShID (cm) | interquartile distance |
| TLSh01, TLSh05, TLSh10, …, TLSh90, TLSh95, TLSh99 (cm) | percentiles |
| TLSh25 and TLSh75 (cm) | first and third quartiles |
| TLShL1, TLShL2, TLShL3, TLShL4 | L-moments of order i (i = 1,…,4) |
| TLShL-CV | Ratio of L1 and L2 moments |
| TLShMAD-median | median of the absolute deviations from the overall median |
| TLShMAD-mode | mode of the absolute deviations from the overall mode |
| TLSPA2m | % of laser returns above 2 m |
| TLSPAhmean | % of laser returns above hmean |
| TLSPAhmode | % of laser returns above hmode |
| TLSCRR | canopy relief ratio (TLShmean/TLShmax) |
| Surface Fire-Related Variables | ||||||
| Variable | Statistic | MARS | SVM-L | SVM-R | SVM-P | RF |
(cm) | R2 | 0.5308 | 0.4605 | 0.3816 | 0.4679 | 0.4305 |
| RMSE(%) | 42.55 | 45.63 | 48.85 | 45.32 | 46.88 | |
| FSG (m) | R2 | 0.7662 | 0.6959 | 0.6254 | 0.6968 | 0.6556 |
| RMSE(%) | 13.30 | 15.17 | 16.84 | 15.15 | 16.14 | |
| Wdebris (Mg ha−1) | R2 | 0.3653 | 0.2395 | 0.2507 | 0.0737 | - |
| RMSE(%) | 97.07 | 106.26 | 105.47 | 117.27 | - | |
| WLFH (Mg ha−1) | R2 | 0.3496 | 0.3035 | 0.3346 | 0.4225 | 0.2987 |
| RMSE(%) | 11.96 | 12.38 | 12.10 | 11.27 | 12.42 | |
| Wshrub (Mg ha−1) | R2 | 0.3462 | 0.3270 | 0.3178 | 0.3106 | 0.3180 |
| RMSE(%) | 44.51 | 45.16 | 45.46 | 45.70 | 45.46 | |
| Canopy fire-related variables | ||||||
| Variable | Statistic | MARS | SVM-L | SVM-R | SVM-P | RF |
(m) | R2 | 0.9250 | 0.9357 | 0.9395 | 0.9318 | 0.8766 |
| RMSE(%) | 5.43 | 5.03 | 4.88 | 5.18 | 6.97 | |
| CBH (m) | R2 | 0.7715 | 0.7273 | 0.7417 | 0.7115 | 0.6670 |
| RMSE(%) | 11.92 | 13.02 | 12.67 | 13.39 | 14.39 | |
| CFL (kg m−2) | R2 | 0.4235 | 0.3498 | 0.3783 | 0.3498 | 0.2978 |
| RMSE(%) | 20.42 | 21.69 | 21.21 | 21.69 | 22.54 | |
| CBD (kg m−3) | R2 | 0.5135 | 0.4510 | 0.3604 | 0.3265 | 0.2660 |
| RMSE(%) | 26.54 | 28.16 | 30.43 | 31.21 | 32.62 | |
| Stand variables | ||||||
| Variable | Statistic | MARS | SVM-L | SVM-R | SVM-P | RF |
| H (m) | R2 | 0.9324 | 0.9200 | 0.9316 | 0.9190 | 0.9066 |
| RMSE(%) | 5.39 | 5.86 | 5.42 | 5.90 | 6.34 | |
| G (m2 ha−1) | R2 | 0.5187 | 0.2945 | 0.5125 | 0.2937 | 0.3334 |
| RMSE(%) | 18.70 | 22.64 | 18.82 | 22.66 | 22.01 | |
| V (m3 ha−1) | R2 | 0.5865 | 0.4976 | 0.5924 | 0.5236 | 0.4475 |
| RMSE(%) | 21.84 | 24.07 | 21.68 | 23.44 | 25.24 | |
| W (Mg ha−1) | R2 | 0.5607 | 0.4600 | 0.6120 | 0.4831 | 0.4603 |
| RMSE(%) | 21.29 | 23.61 | 20.01 | 23.10 | 23.60 | |
| Surface Fire-Related Variables | ||||||
| Variable | Statistic | MARS | SVM-L | SVM-R | SVM-P | RF |
(cm) | R2 | 0.3201 | 0.3144 | 0.4246 | 0.4185 | 0.2758 |
| RMSE(%) | 51.22 | 51.44 | 47.12 | 47.37 | 52.86 | |
| FSG (m) | R2 | 0.8551 | 0.7924 | 0.7310 | 0.8624 | 0.7811 |
| RMSE(%) | 10.47 | 12.53 | 14.27 | 10.20 | 12.87 | |
| Wdebris (Mg ha−1) | R2 | 0.4069 | 0.3794 | 0.3874 | 0.3244 | 0.3027 |
| RMSE(%) | 93.84 | 95.99 | 95.37 | 100.15 | 101.75 | |
| WLFH (Mg ha−1) | R2 | 0.1049 | 0.1556 | 0.1346 | 0.1750 | - |
| RMSE(%) | 14.03 | 13.63 | 13.80 | 13.47 | - | |
| Wshrub (Mg ha−1) | R2 | 0.4796 | 0.4020 | 0.4514 | 0.4333 | 0.4542 |
| RMSE(%) | 39.71 | 42.56 | 40.77 | 41.44 | 40.67 | |
| Canopy fire-related variables | ||||||
| Variable | Statistic | MARS | SVM-L | SVM-R | SVM-P | RF |
(m) | R2 | 0.8916 | 0.8457 | 0.8197 | 0.8455 | 0.8381 |
| RMSE(%) | 6.53 | 7.80 | 8.43 | 7.80 | 7.98 | |
| CBH (m) | R2 | 0.8457 | 0.8574 | 0.8381 | 0.8625 | 0.8141 |
| RMSE(%) | 9.79 | 9.41 | 10.03 | 9.25 | 10.75 | |
| CFL (kg m−2) | R2 | 0.5203 | 0.4167 | 0.3959 | 0.3985 | 0.3285 |
| RMSE(%) | 18.63 | 20.55 | 20.91 | 20.87 | 22.05 | |
| CBD (kg m−3) | R2 | 0.5587 | 0.4677 | 0.4412 | 0.5727 | 0.4590 |
| RMSE(%) | 25.26 | 27.74 | 28.45 | 24.84 | 27.95 | |
| Stand variables | ||||||
| Variable | Statistic | MARS | SVM-L | SVM-R | SVM-P | RF |
| H (m) | R2 | 0.9307 | 0.9201 | 0.8560 | 0.9105 | 0.8849 |
| RMSE(%) | 5.46 | 5.86 | 7.87 | 6.20 | 7.03 | |
| G (m2 ha−1) | R2 | 0.4939 | 0.4867 | 0.4314 | 0.5027 | 0.3849 |
| RMSE(%) | 19.18 | 19.32 | 20.33 | 19.01 | 21.14 | |
| V (m3 ha−1) | R2 | 0.6599 | 0.5749 | 0.5521 | 0.6137 | 0.5638 |
| RMSE(%) | 19.80 | 22.14 | 22.73 | 21.11 | 22.43 | |
| W (Mg ha−1) | R2 | 0.6452 | 0.5199 | 0.5620 | 0.5949 | 0.5624 |
| RMSE(%) | 19.14 | 22.26 | 21.26 | 20.45 | 21.25 | |
| Surface Fire-Related Variables | ||||
| Variable | Statistic | TLS-Data | ALS-Data | TLS + ALS-Data |
(cm) | R2 | 0.5308 | 0.3201 | 0.5308 |
| RMSE(%) | 42.55 | 51.22 | 42.55 | |
| FSG (m) | R2 | 0.7662 | 0.8551 | 0.8987 |
| RMSE(%) | 13.30 | 10.47 | 8.75 | |
| Wdebris (Mg ha−1) | R2 | 0.3653 | 0.4069 | 0.4894 |
| RMSE(%) | 97.07 | 93.84 | 87.06 | |
| WLFH (Mg ha−1) | R2 | 0.3496 | 0.1049 | 0.4311 |
| RMSE(%) | 11.96 | 14.03 | 11.19 | |
| Wshrub (Mg ha−1) | R2 | 0.3462 | 0.4796 | 0.3462 |
| RMSE(%) | 44.51 | 39.71 | 44.51 | |
| Canopy fire-related variables | ||||
| Variable | Statistic | TLS-data | ALS-data | TLS+ALS-data |
(m) | R2 | 0.9250 | 0.8916 | 0.9343 |
| RMSE(%) | 5.43 | 6.53 | 5.08 | |
| CBH (m) | R2 | 0.7715 | 0.8457 | 0.8683 |
| RMSE(%) | 11.92 | 9.79 | 9.05 | |
| CFL (kg m−2) | R2 | 0.4235 | 0.5203 | 0.5899 |
| RMSE(%) | 20.42 | 18.63 | 17.22 | |
| CBD (kg m−3) | R2 | 0.5135 | 0.5587 | 0.6383 |
| RMSE(%) | 26.54 | 25.26 | 22.86 | |
| Stand variables | ||||
| Variable | Statistic | TLS-data | ALS-data | TLS+ALS-data |
| H (m) | R2 | 0.9324 | 0.9307 | 0.9425 |
| RMSE(%) | 5.39 | 5.46 | 4.97 | |
| G (m2 ha−1) | R2 | 0.5187 | 0.4939 | 0.6163 |
| RMSE(%) | 18.7 | 19.18 | 16.70 | |
| V (m3 ha−1) | R2 | 0.5865 | 0.6599 | 0.7197 |
| RMSE(%) | 21.84 | 19.80 | 17.98 | |
| W (Mg ha−1) | R2 | 0.5607 | 0.6452 | 0.6512 |
| RMSE(%) | 21.29 | 19.14 | 18.97 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alonso-Rego, C.; Arellano-Pérez, S.; Guerra-Hernández, J.; Molina-Valero, J.A.; Martínez-Calvo, A.; Pérez-Cruzado, C.; Castedo-Dorado, F.; González-Ferreiro, E.; Álvarez-González, J.G.; Ruiz-González, A.D. Estimating Stand and Fire-Related Surface and Canopy Fuel Variables in Pine Stands Using Low-Density Airborne and Single-Scan Terrestrial Laser Scanning Data. Remote Sens. 2021, 13, 5170. https://doi.org/10.3390/rs13245170
Alonso-Rego C, Arellano-Pérez S, Guerra-Hernández J, Molina-Valero JA, Martínez-Calvo A, Pérez-Cruzado C, Castedo-Dorado F, González-Ferreiro E, Álvarez-González JG, Ruiz-González AD. Estimating Stand and Fire-Related Surface and Canopy Fuel Variables in Pine Stands Using Low-Density Airborne and Single-Scan Terrestrial Laser Scanning Data. Remote Sensing. 2021; 13(24):5170. https://doi.org/10.3390/rs13245170
Chicago/Turabian StyleAlonso-Rego, Cecilia, Stéfano Arellano-Pérez, Juan Guerra-Hernández, Juan Alberto Molina-Valero, Adela Martínez-Calvo, César Pérez-Cruzado, Fernando Castedo-Dorado, Eduardo González-Ferreiro, Juan Gabriel Álvarez-González, and Ana Daría Ruiz-González. 2021. "Estimating Stand and Fire-Related Surface and Canopy Fuel Variables in Pine Stands Using Low-Density Airborne and Single-Scan Terrestrial Laser Scanning Data" Remote Sensing 13, no. 24: 5170. https://doi.org/10.3390/rs13245170
APA StyleAlonso-Rego, C., Arellano-Pérez, S., Guerra-Hernández, J., Molina-Valero, J. A., Martínez-Calvo, A., Pérez-Cruzado, C., Castedo-Dorado, F., González-Ferreiro, E., Álvarez-González, J. G., & Ruiz-González, A. D. (2021). Estimating Stand and Fire-Related Surface and Canopy Fuel Variables in Pine Stands Using Low-Density Airborne and Single-Scan Terrestrial Laser Scanning Data. Remote Sensing, 13(24), 5170. https://doi.org/10.3390/rs13245170









