An Efficient Lightweight Neural Network for Remote Sensing Image Change Detection
Abstract
:1. Introduction
2. Proposed Method
2.1. DConv-Based Backbone Network
2.1.1. Introducing Residual Network
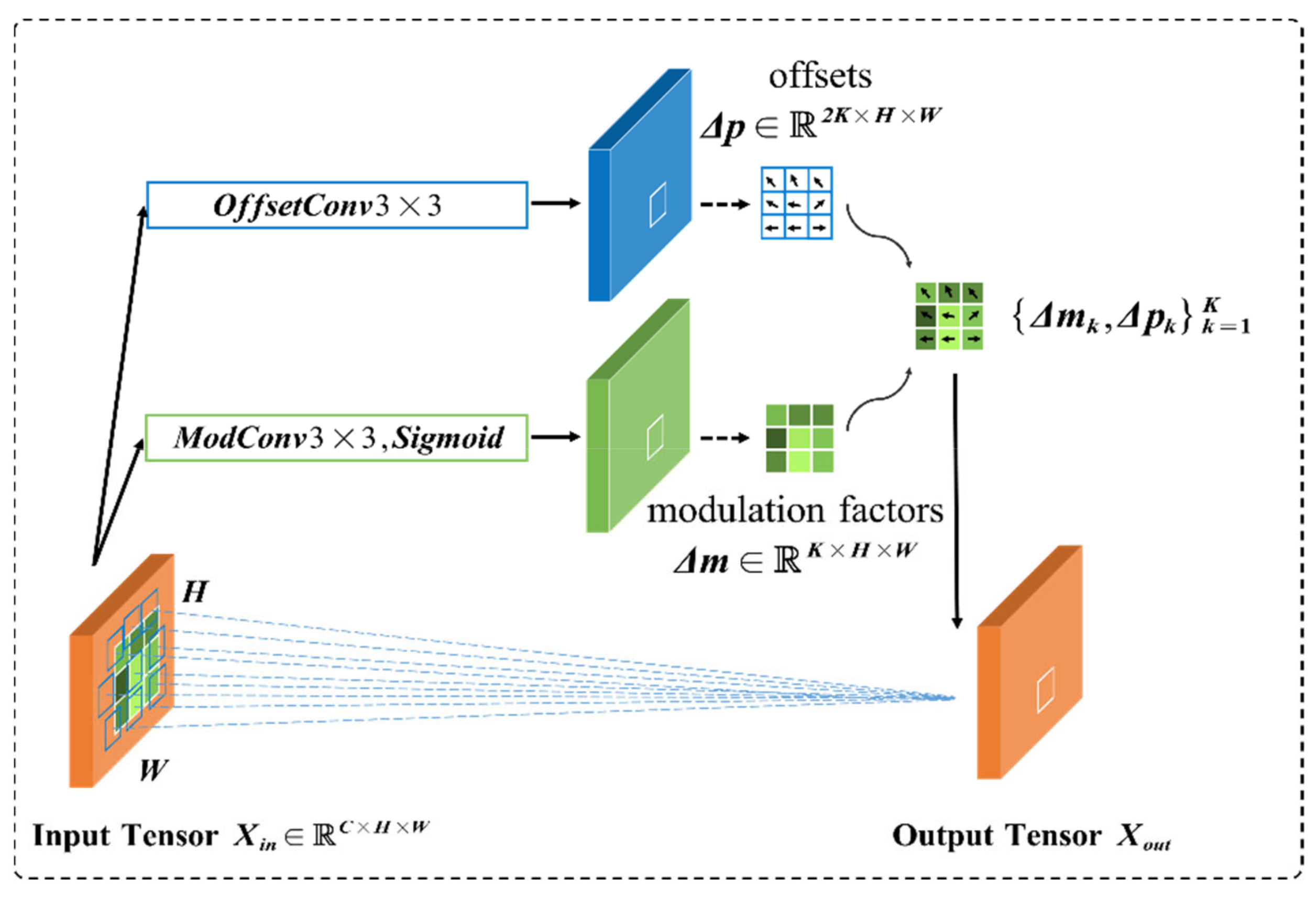
2.1.2. Introducing Deformable Convolutions
2.1.3. Multilevel Feature Fusion Strategies
2.2. Pixelwise Classifier
2.2.1. Introducing Dropout Regularization
2.2.2. Binarization
2.3. Loss Function Definition
3. Experiments and Results
3.1. Experimental Dataset
3.2. Evaluation Metrics
3.3. Experiment Settings
3.3.1. Implementation Details
3.3.2. Online Data Augmentation
3.4. Comparative Methods
- (1)
- FC-Siam-Diff [26]. A feature-level late-fusion method, which uses a pseudo-Siamese FCN to extract and fuse the bitemporal multilevel features by a feature difference operation.
- (2)
- FC-Siam-Conc [26]. It is very similar to FC-Siam-Diff. The difference lies in the way to fuse the bitemporal features by a feature concatenation operation.
- (3)
- FC-EF-Res [35]. An image-level early-fusion method. The network takes as an input the concatenated bitemporal images. It introduced the residual modules to facilitate network convergence easily.
- (4)
- CLNet [29]. A U-Net based early-fusion method, which builds the encoder part by incorporating the cross layer blocks (CLBs). An input feature map was first divided into two parallel but asymmetric branches, then CLBs apply convolution kernels with different strides to capture multi-scale context for performance improvement.
- (5)
- STANet [44]. A metric-based method, which adopts a Siamese FCN for feature extraction and learns the change map based on the distances between the bitemporal features. Inspired by the self-attention mechanism, a spatial–temporal attention module was proposed to learn the spatial–temporal relationships between the bitemporal images to generate more discriminative features.
- (6)
- DDCNN [37]. An attention-based method that adopts a simplified UNet++ architecture. Combined with the dense upsampling units, high-level features were applied to guide the selection of low-level features during the upsampling phase for performance improvement.
- (7)
- FarSeg [56]. A foreground-aware relation network for geospatial objects segmentation in RS images. From the perspective of relation, FarSeg enhances the discrimination of foreground features via foreground-correlated contexts associated by learning foreground scene relation.
- (8)
- BIT-CD [48]. A transformer-based method, which expresses the input images into a few high-level semantic tokens. By incorporating a transformer encoder in the CNN backbone network, BIT-CD models the context in a compact token-based space-time.
- (9)
- MSPP-Net [49]. A lightweight multi-scale spatial pooling (MSPP) network was used to exploit the changed information from the noisy difference image. Multi-scale pooling kernels are equipped in a convolutional network to exploit the spatial context information on changed regions from images.
- (10)
- Lite-CNN [50]. A lightweight network replaces normal convolutional layers with bottleneck layers that keep the same number of channels between input and output. It also employs dilated convolutional kernels with a few non-zero entries that reduce the running time in convolutional operators.
3.5. Experiment Results
3.5.1. Comparisons on LEVIR-CD Dataset
- (a)
- Quantitative evaluation
- (b)
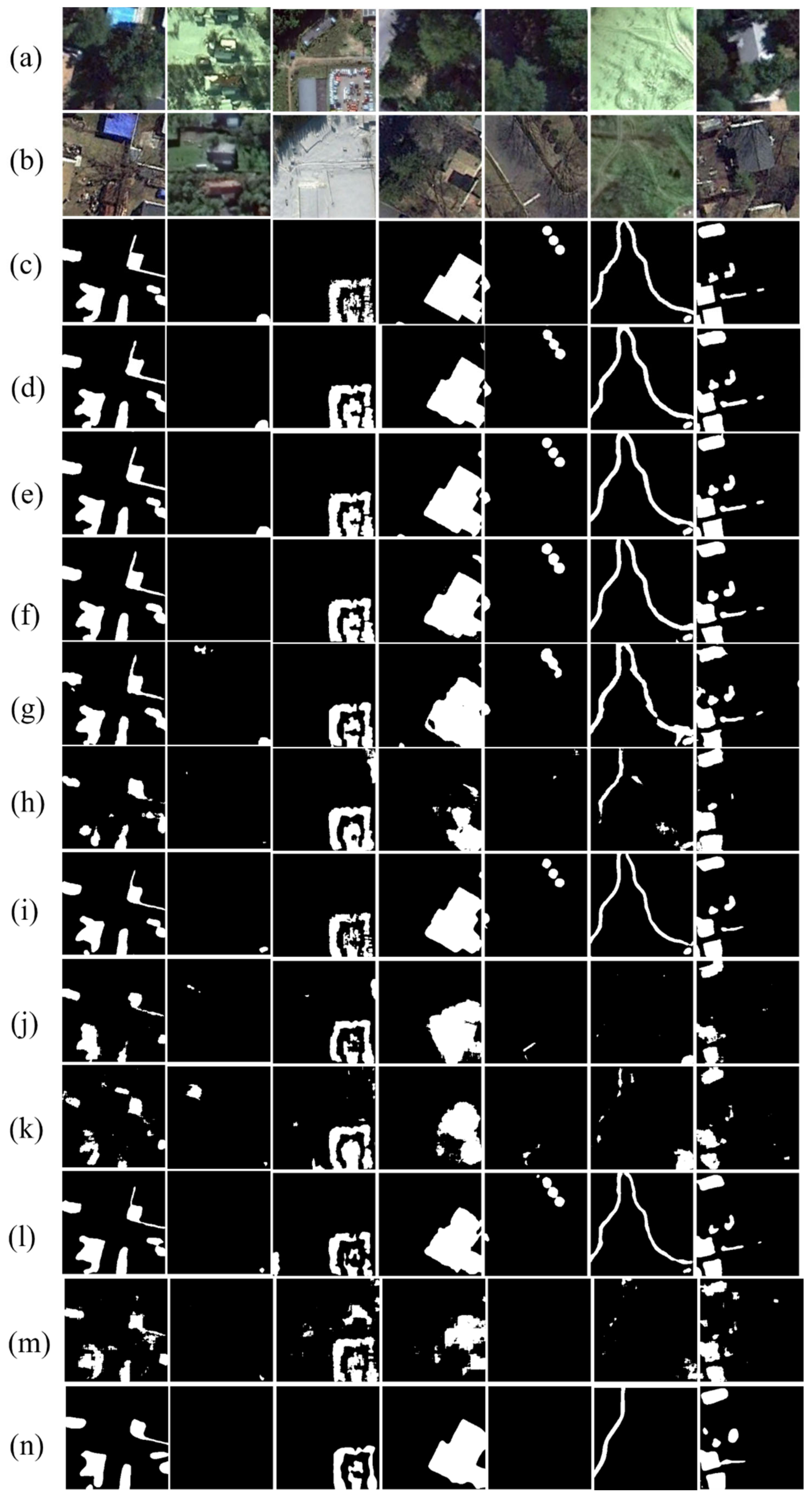
- Qualitative evaluation
3.5.2. Comparisons on Season-Varying Dataset
- (a)
- Quantitative evaluation
- (b)
- Qualitative evaluation
4. Discussion
4.1. Effectiveness of Different Multilevel Feature Fusion Strategies
4.2. Effects of Online DA, Dropout, and Dconv
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Long, Y.; Xia, G.S.; Li, S.; Yang, W.; Yang, M.Y.; Zhu, X.X.; Zhang, L.; Li, D. On Creating Benchmark Dataset for Aerial Image Interpretation: Reviews, Guidances, and Million-AID. Int. J. Remote Sens. 2021, 14, 4205–4230. [Google Scholar] [CrossRef]
- Singh, A. Review Article Digital change detection techniques using remotely-sensed data. Int. J. Remote Sens. 1989, 10, 989–1003. [Google Scholar] [CrossRef] [Green Version]
- Bouziani, M.; Goïta, K.; He, D.-C. Automatic change detection of buildings in urban environment from very high spatial resolution images using existing geodatabase and prior knowledge. ISPRS J. Photogramm. Remote Sens. 2010, 65, 143–153. [Google Scholar] [CrossRef]
- Deng, J.S.; Wang, K.; Deng, Y.H.; Qi, G.J. PCA-based land-use change detection and analysis using multitemporal and multisensor satellite data. Int. J. Remote Sens. 2008, 29, 4823–4838. [Google Scholar] [CrossRef]
- Gupta, R.; Hosfelt, R.; Sajeev, S.; Patel, N.; Goodman, B.; Doshi, J.; Heim, E.; Choset, H.; Gaston, M. xBD: A Dataset for Assessing Building Damage from Satellite Imagery. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Long Beach, CA, USA, 16–20 June 2019; pp. 10–17. [Google Scholar]
- Shi, W.; Min, Z.; Zhang, R.; Chen, S.; Zhan, Z. Change Detection Based on Artificial Intelligence: State-of-the-Art and Challenges. Int. J. Remote Sens. 2020, 12, 1688. [Google Scholar] [CrossRef]
- Xiao, P.; Zhang, X.; Wang, D.; Yuan, M.; Feng, X.; Kelly, M. Change detection of built-up land: A framework of combining pixel-based detection and object-based recognition. ISPRS J. Photogramm. Remote Sens. 2016, 119, 402–414. [Google Scholar] [CrossRef]
- Hussain, M.; Chen, D.; Cheng, A.; Wei, H.; Stanley, D. Change detection from remotely sensed images: From pixel-based to object-based approaches. ISPRS J. Photogramm. Remote Sens. 2013, 80, 91–106. [Google Scholar] [CrossRef]
- Chen, J.; Gong, P.; He, C.; Pu, R.; Shi, P. Land-Use/Land-Cover Change Detection Using Improved Change-Vector Analysis. ISPRS J. Photogramm. Remote Sens. 2003, 69, 369–379. [Google Scholar] [CrossRef] [Green Version]
- Nielsen, A.A. The Regularized Iteratively Reweighted MAD Method for Change Detection in Multi- and Hyperspectral Data. IEEE Trans. Image Process. 2007, 16, 463–478. [Google Scholar] [CrossRef] [Green Version]
- Liu, Q.; Liu, L. Unsupervised Change Detection for Multispectral Remote Sensing Images Using Random Walks. Int. J. Remote Sens. 2017, 9, 438. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, A.; Mishra, N.S.; Ghosh, S. Fuzzy clustering algorithms for unsupervised change detection in remote sensing images. Inf. Sci. 2011, 181, 699–715. [Google Scholar] [CrossRef]
- Celik, T. Unsupervised Change Detection in Satellite Images Using Principal Component Analysis and k-Means Clustering. IEEE Geosci. Remote Sens. Lett. 2009, 6, 772–776. [Google Scholar] [CrossRef]
- Lv, P.; Zhong, Y.; Zhao, J.; Zhang, L. Unsupervised Change Detection Based on Hybrid Conditional Random Field Model for High Spatial Resolution Remote Sensing Imagery. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4002–4015. [Google Scholar] [CrossRef]
- Han, Y.; Javed, A.; Jung, S.; Liu, S. Object-Based Change Detection of Very High Resolution Images by Fusing Pixel-Based Change Detection Results Using Weighted Dempster–Shafer Theory. Int. J. Remote Sens. 2020, 12, 983. [Google Scholar] [CrossRef] [Green Version]
- Tan, K.; Zhang, Y.; Wang, X.; Chen, Y. Object-Based Change Detection Using Multiple Classifiers and Multi-Scale Uncertainty Analysis. Int. J. Remote Sens. 2019, 11, 359. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Liu, S.; Du, P.; Liang, H.; Xia, J.; Li, Y. Object-Based Change Detection in Urban Areas from High Spatial Resolution Images Based on Multiple Features and Ensemble Learning. Int. J. Remote Sens. 2018, 10, 276. [Google Scholar] [CrossRef] [Green Version]
- Touazi, A.; Bouchaffra, D. A k-Nearest Neighbor approach to improve change detection from remote sensing: Application to optical aerial images. In Proceedings of the 2015 15th International Conference on Intelligent Systems Design and Applications (ISDA), Marrakech, Morocco, 14–16 December 2015; pp. 98–103. [Google Scholar]
- Feng, W.; Sui, H.; Tu, J.; Huang, W.; Sun, K. A novel change detection approach based on visual saliency and random forest from multi-temporal high-resolution remote-sensing images. Int. J. Remote Sens. 2018, 39, 7998–8021. [Google Scholar] [CrossRef]
- Bovolo, F.; Bruzzone, L.; Marconcini, M. A Novel Approach to Unsupervised Change Detection Based on a Semisupervised SVM and a Similarity Measure. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2070–2082. [Google Scholar] [CrossRef] [Green Version]
- Benedek, C.; Szirányi, T. Change Detection in Optical Aerial Images by a Multilayer Conditional Mixed Markov Model. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3416–3430. [Google Scholar] [CrossRef] [Green Version]
- Wu, C.; Du, B.; Cui, X.; Zhang, L. A post-classification change detection method based on iterative slow feature analysis and Bayesian soft fusion. Remote Sens. Environ. 2017, 199, 241–255. [Google Scholar] [CrossRef]
- Hou, B.; Wang, Y.; Liu, Q. Change Detection Based on Deep Features and Low Rank. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2418–2422. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Zhou, Z.; Rahman Siddiquee, M.M.; Tajbakhsh, N.; Liang, J. UNet++: A Nested U-Net Architecture for Medical Image Segmentation. In Proceedings of the Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support, Granada, Spain, 20 September 2018; pp. 3–11. [Google Scholar]
- Daudt, R.C.; Saux, B.L.; Boulch, A. Fully Convolutional Siamese Networks for Change Detection. In Proceedings of the 2018 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; pp. 4063–4067. [Google Scholar]
- Peng, D.; Zhang, Y.; Wanbing, G. End-to-End Change Detection for High Resolution Satellite Images Using Improved UNet++. Int. J. Remote Sens. 2019, 11, 1382. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Chen, X.; Jiang, M.; Du, S.; Xu, B.; Wang, J. ADS-Net:An Attention-Based deeply supervised network for remote sensing image change detection. Int. J. Appl. Earth Obs. Geoinf. 2021, 101, 102348. [Google Scholar] [CrossRef]
- Zheng, Z.; Wan, Y.; Zhang, Y.; Xiang, S.; Peng, D.; Zhang, B. CLNet: Cross-layer convolutional neural network for change detection in optical remote sensing imagery. ISPRS J. Photogramm. Remote Sens. 2021, 175, 247–267. [Google Scholar] [CrossRef]
- Zhang, C.; Yue, P.; Tapete, D.; Jiang, L.; Shangguan, B.; Huang, L.; Liu, G. A deeply supervised image fusion network for change detection in high resolution bi-temporal remote sensing images. ISPRS J. Photogramm. Remote Sens. 2020, 166, 183–200. [Google Scholar] [CrossRef]
- Hou, B.; Liu, Q.; Wang, H. From W-Net to CDGAN: Bitemporal Change Detection via Deep Learning Techniques. IEEE Trans. Geosci. Remote Sens. 2019, 58, 1790–1802. [Google Scholar] [CrossRef] [Green Version]
- Woo, S.; Park, J.; Lee, J.-Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Proceedings of the Computer Vision—ECCV 2018, Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Fang, S.; Li, K.; Shao, J.; Li, Z. SNUNet-CD: A Densely Connected Siamese Network for Change Detection of VHR Images. IEEE Geosci. Remote Sens. Lett. 2021, 1–5. [Google Scholar] [CrossRef]
- Zhang, Y.; Fu, L.; Li, Y.; Zhang, Y. HDFNet: Hierarchical Dynamic Fusion Network for Change Detection in Optical Aerial Images. Int. J. Remote Sens. 2021, 13, 1440. [Google Scholar] [CrossRef]
- Caye Daudt, R.; Le Saux, B.; Boulch, A.; Gousseau, Y. Multitask learning for large-scale semantic change detection. Comput. Vis. Image. Underst. 2019, 187, 102783. [Google Scholar] [CrossRef] [Green Version]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Peng, X.; Zhong, R.; Li, Z.; Li, Q. Optical Remote Sensing Image Change Detection Based on Attention Mechanism and Image Difference. IEEE Trans. Geosci. Remote Sens. 2020, 59, 7296–7307. [Google Scholar] [CrossRef]
- Zhang, X.; Yue, Y.; Gao, W.; Yun, S.; Su, Q.; Yin, H.; Zhang, Y. DifUnet++: A Satellite Images Change Detection Network Based on Unet++ and Differential Pyramid. IEEE Geosci. Remote Sens. Lett. 2021, 1–5. [Google Scholar] [CrossRef]
- Yu, X.; Fan, J.; Chen, J.; Zhang, P.; Zhou, Y.; Han, L. NestNet: A multiscale convolutional neural network for remote sensing image change detection. Int. J. Remote Sens. 2021, 42, 4902–4925. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar]
- Wang, X.; Girshick, R.B.; Gupta, A.; He, K. Non-Local Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7794–7803. [Google Scholar]
- Hu, J.; Shen, L.; Albanie, S.; Sun, G.; Wu, E. Squeeze-and-Excitation Networks. IEEE Trans. Pattern. Anal. Mach. Intell. 2020, 42, 2011–2023. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fu, J.; Liu, J.; Tian, H.; Li, Y.; Bao, Y.; Fang, Z.; Lu, H. Dual Attention Network for Scene Segmentation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 3141–3149. [Google Scholar]
- Chen, H.; Shi, Z. A Spatial-Temporal Attention-Based Method and a New Dataset for Remote Sensing Image Change Detection. Int. J. Remote Sens. 2020, 12, 1662. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16 × 16 Words: Transformers for Image Recognition at Scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Zhu, X.; Su, W.; Lu, L.; Li, B.; Wang, X.; Dai, J. Deformable DETR: Deformable Transformers for End-to-End Object Detection. In Proceedings of the International Conference on Learning Representations, Vienna, Austria, 4 May 2021. [Google Scholar]
- Zheng, S.; Lu, J.; Zhao, H.; Zhu, X.; Luo, Z.; Wang, Y.; Fu, Y.; Feng, J.; Xiang, T.; Torr, P.; et al. Rethinking Semantic Segmentation from a Sequence-to-Sequence Perspective with Transformers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 6881–6890. [Google Scholar]
- Chen, H.; Qi, Z.; Shi, Z. Remote Sensing Image Change Detection With Transformers. IEEE Trans. Geosci. Remote Sens. 2021, 10, 1–14. [Google Scholar] [CrossRef]
- Chen, J.-W.; Wang, R.; Ding, F.; Liu, B.; Jiao, L.; Zhang, J. A Convolutional Neural Network with Parallel Multi-Scale Spatial Pooling to Detect Temporal Changes in SAR Images. Remote Sens. 2020, 12, 1619. [Google Scholar] [CrossRef]
- Wang, R.; Ding, F.; Chen, J.W.; Jiao, L.; Wang, L. A Lightweight Convolutional Neural Network for Bitemporal Image Change Detection. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 2551–2554. [Google Scholar]
- Dai, J.; Qi, H.; Xiong, Y.; Li, Y.; Zhang, G.; Hu, H.; Wei, Y. Deformable Convolutional Networks. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 764–773. [Google Scholar]
- Zhu, X.; Hu, H.; Lin, S.; Dai, J. Deformable ConvNets V2: More Deformable, Better Results. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, 15–20 June 2019; pp. 9300–9308. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Bolya, D.; Zhou, C.; Xiao, F.; Lee, Y. YOLACT++: Better Real-time Instance Segmentation. IEEE Trans. Pattern. Anal. Mach. Intell. 2020. [Google Scholar] [CrossRef]
- Lebedev, M.; Vizilter, Y.; Vygolov, O.; Knyaz, V.; Rubis, A. Change Detection in Remote Sensing Images Using Conditional Advertisal Networks. Int. Arch. Photogramm. Remote Sens. 2018, 42, 565–571. [Google Scholar] [CrossRef] [Green Version]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Proceedings of the NeurlPS, Vancouver, BC, Canada, 8–11 December 2019. [Google Scholar]
- Loshchilov, I.; Hutter, F. Decoupled Weight Decay Regularization. In Proceedings of the ICLR, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Zheng, Z.; Zhong, Y.; Wang, J.; Ma, A. Foreground-Aware Relation Network for Geospatial Object Segmentation in High Spatial Resolution Remote Sensing Imagery. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 4095–4104. [Google Scholar]
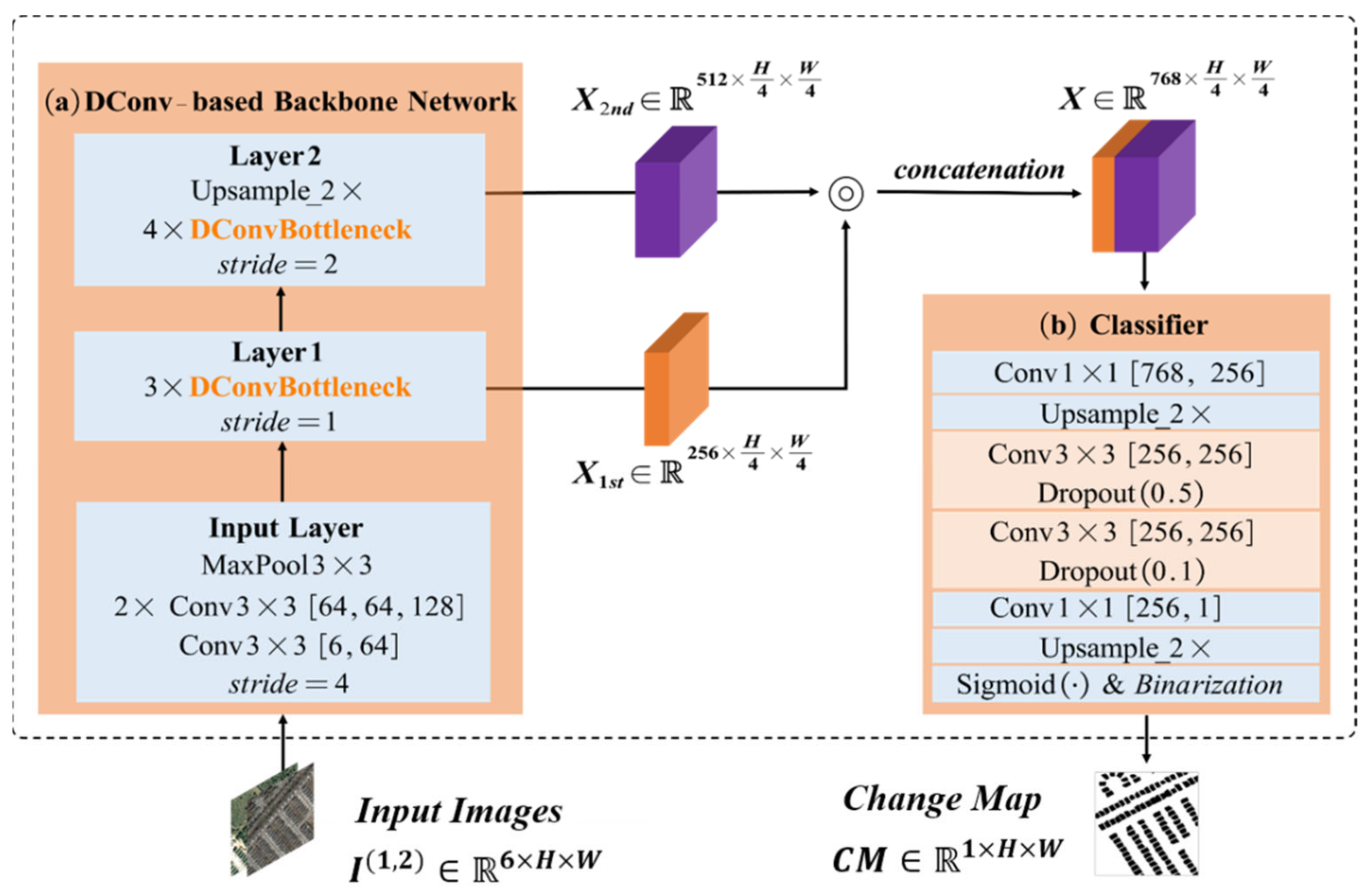
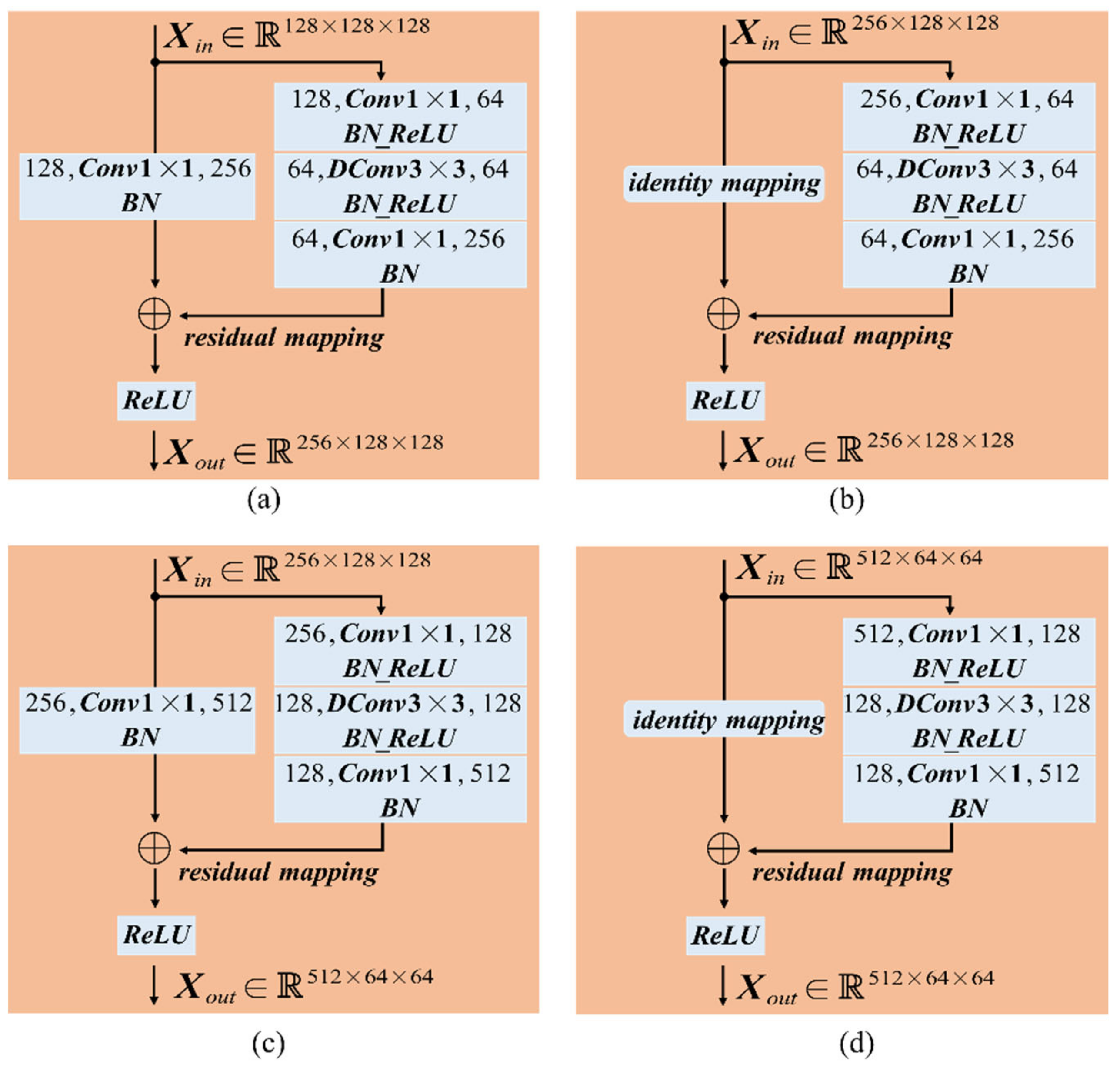

| Layer Name | Components, Kernel Size, Filters | Stride | |
|---|---|---|---|
| Input Layer | 2 | ||
| 1 | |||
| 1 | |||
| 2 | |||
| Layer1 | 1 | ||
| Layer2 | 2 | ||
| Layer2_Upsample_2×, —, — | — |
| Layer Name | Components, Kernel Size, Filters | Stride | |
|---|---|---|---|
| Classifier | 1 | ||
| Upsample_2× | — | ||
| 1 | |||
| Dropout_0.5 | — | ||
| 1 | |||
| Dropout_0.1 | — | ||
| 1 | |||
| Upsample_2× | — | ||
| Sigmoid | — |
| Layer Name | Components, Kernel Size, Filters | Stride | |
|---|---|---|---|
| Classifier | 1 | ||
| Upsample_2× | — | ||
| Dropout_0.5 | — | 256 × 256 × 256 | |
| 1 | 64 × 256 × 256 | ||
| Dropout_0.1 | — | 64 × 256 × 256 | |
| 1 | |||
| Upsample_2× | — | ||
| Sigmoid | — |
| Method | Number of Parameters (M) | Computational Costs (GFLOPs) w/bs = 1 | Runtime (ms) w/bs = 1 | Runtime (ms) w/bs = 16 | |||
|---|---|---|---|---|---|---|---|
| 512 × 512 | 256 × 256 | 512 × 512 | 256 × 256 | 512 × 512 | 256 × 256 | ||
| DDCNN [37] | 60.21 | 856.63 | 214.16 | 151.07 | 44.67 | - | 477.73 |
| STANet [44] | 16.93 | 206.68 | 32.42 | 12.07 | 11.49 | - | - |
| FarSeg [56] | 31.38 | 47.45 | 11.86 | 13.71 | 8.79 | 168.55 | 44.68 |
| CLNet [29] | 8.53 | 35.65 | 8.91 | 11.12 | 4.92 | 128.46 | 33.22 |
| BIT-CD [48] | 3.05 | 62.68 | 15.67 | 16.22 | 12.89 | 259.15 | 65.24 |
| FC-Siam-Diff [26] | 1.35 | 20.74 | 5.18 | 8.72 | 4.05 | 128.46 | 32.30 |
| FC-Siam-Conc [26] | 1.55 | 20.75 | 5.19 | 8.73 | 3.77 | 130.19 | 32.32 |
| FC-EF-Res [35] | 1.10 | 6.94 | 1.73 | 7.73 | 4.85 | 90.98 | 23.78 |
| MSPP-Net [49] | 6.245 | 66.16 | 16.54 | 13.38 | 6.42 | 186.66 | 47.58 |
| Lite-CNN [50] | 3.876 | 19.17 | 4.79 | 10.15 | 9.76 | 116.78 | 29.49 |
| 1M-CDNet | 1.26 | 18.43 | 4.61 | 8.02 | 4.07 | 126.79 | 33.58 |
| 3M-CDNet | 3.12 | 94.83 | 23.71 | 16.62 | 7.28 | 327.60 | 55.65 |
| Method | Pr (%) | Re (%) | OA (%) | IoU | F1 |
|---|---|---|---|---|---|
| STANet [44] | 85.01 | 91.38 | 98.74 | 0.7869 | 0.8808 |
| FC-EF-Res [35] | 91.48 | 88.04 | 98.97 | 0.8137 | 0.8973 |
| FC-Siam-Conc [26] | 89.49 | 89.18 | 98.92 | 0.8072 | 0.8933 |
| FC-Siam-Diff [26] | 91.25 | 88.18 | 98.97 | 0.8130 | 0.8969 |
| BIT-CD [48] | 90.38 | 89.69 | 98.99 | 0.8187 | 0.9003 |
| DDCNN [37] | 92.15 | 89.07 | 99.06 | 0.8279 | 0.9059 |
| FarSeg [56] | 91.04 | 90.22 | 99.05 | 0.8286 | 0.9063 |
| CLNet [29] | 90.85 | 90.53 | 99.05 | 0.8297 | 0.9069 |
| MSPP-Net [48] | 89.65 | 86.73 | 98.81 | 0.7883 | 0.8816 |
| Lite-CNN [49] | 90.77 | 89.96 | 99.02 | 0.8242 | 0.9036 |
| 1M-CDNet | 92.32 | 90.06 | 99.11 | 0.8379 | 0.9118 |
| 3M-CDNet | 91.99 | 91.24 | 99.15 | 0.8452 | 0.9161 |
| Method | Pr (%) | Re (%) | OA(%) | IoU | F1 |
|---|---|---|---|---|---|
| FC-Siam-Conc [26] | 91.94 | 82.06 | 96.90 | 0.7656 | 0.8672 |
| FC-Siam-Diff [26] | 93.98 | 81.05 | 97.02 | 0.7705 | 0.8704 |
| FC-EF-Res [35] | 89.91 | 87.37 | 97.25 | 0.7956 | 0.8862 |
| BIT-CD [48] | 98.49 | 92.34 | 98.88 | 0.9105 | 0.9531 |
| STANet [44] | 93.13 | 93.59 | 98.36 | 0.8755 | 0.9336 |
| DDCNN [37] | 96.71 | 92.32 | 98.64 | 0.8951 | 0.9446 |
| CLNet [29] | 98.62 | 94.46 | 99.15 | 0.9323 | 0.9650 |
| FarSeg [56] | 95.12 | 98.13 | 99.15 | 0.9343 | 0.9660 |
| MSPP-Net [49] | 92.95 | 85.93 | 97.46 | 0.8067 | 0.8930 |
| Lite-CNN [50] | 96.58 | 89.76 | 98.34 | 0.8700 | 0.9305 |
| 1M-CDNet | 95.05 | 98.61 | 99.19 | 0.9379 | 0.9680 |
| 3M-CDNet | 95.88 | 99.16 | 99.37 | 0.9510 | 0.9749 |
| Method | LEVIR-CD | Season-Varying | ||||
|---|---|---|---|---|---|---|
| OA (%) | IoU | F1 | OA (%) | IoU | F1 | |
| w/two-level | 99.15 | 0.8452 | 0.9161 | 99.37 | 0.9510 | 0.9749 |
| w/one-level | 99.03 | 0.8243 | 0.9037 | 99.14 | 0.9340 | 0.9659 |
| w/three-level | 99.05 | 0.8291 | 0.9066 | 99.20 | 0.9384 | 0.9682 |
| Method | LEVIR-CD | Season-Varying | ||||
|---|---|---|---|---|---|---|
| OA (%) | IoU | F1 | OA (%) | IoU | F1 | |
| 3M-CDNet | 99.15 | 0.8452 | 0.9161 | 99.37 | 0.9510 | 0.9749 |
| w/o DA | 99.01 | 0.8212 | 0.9018 | 99.18 | 0.9363 | 0.9671 |
| w/o DA/Dropout | 98.95 | 0.8109 | 0.8956 | 99.13 | 0.9331 | 0.9654 |
| w/o DA/DConv | 98.92 | 0.8069 | 0.8932 | 98.73 | 0.9021 | 0.9486 |
| w/o DConv | 99.04 | 0.8283 | 0.9061 | 99.02 | 0.9251 | 0.9611 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, K.; Cui, F.; Jiang, J. An Efficient Lightweight Neural Network for Remote Sensing Image Change Detection. Remote Sens. 2021, 13, 5152. https://doi.org/10.3390/rs13245152
Song K, Cui F, Jiang J. An Efficient Lightweight Neural Network for Remote Sensing Image Change Detection. Remote Sensing. 2021; 13(24):5152. https://doi.org/10.3390/rs13245152
Chicago/Turabian StyleSong, Kaiqiang, Fengzhi Cui, and Jie Jiang. 2021. "An Efficient Lightweight Neural Network for Remote Sensing Image Change Detection" Remote Sensing 13, no. 24: 5152. https://doi.org/10.3390/rs13245152
APA StyleSong, K., Cui, F., & Jiang, J. (2021). An Efficient Lightweight Neural Network for Remote Sensing Image Change Detection. Remote Sensing, 13(24), 5152. https://doi.org/10.3390/rs13245152






