Multimodal Remote Sensing Image Registration Methods and Advancements: A Survey
Abstract
1. Introduction
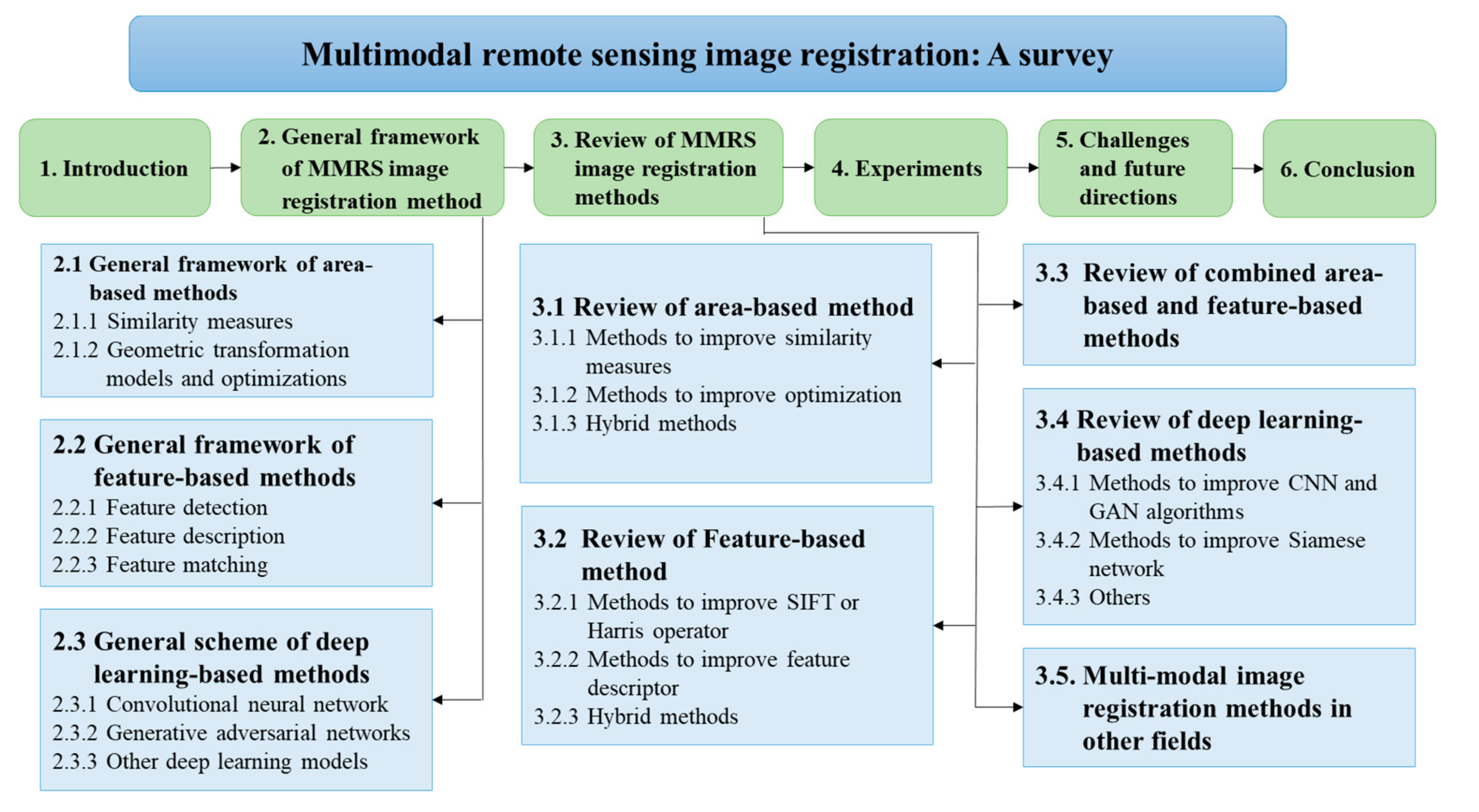
2. General Framework of MMRS Image Registration Methods
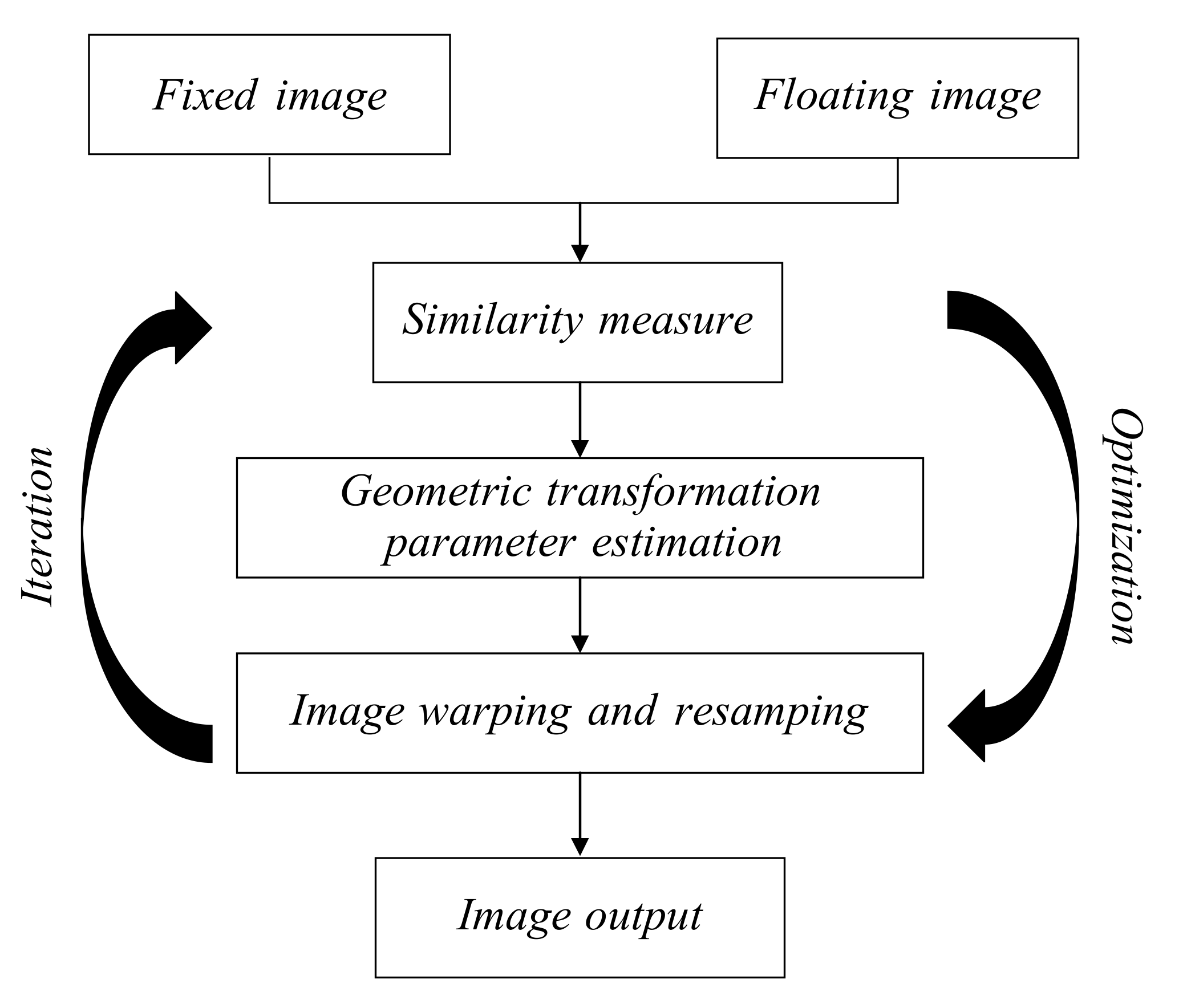
2.1. General Framework of Area-Based Methods
2.1.1. Similarity Measures
2.1.2. Geometric Transformation Models and Optimizations
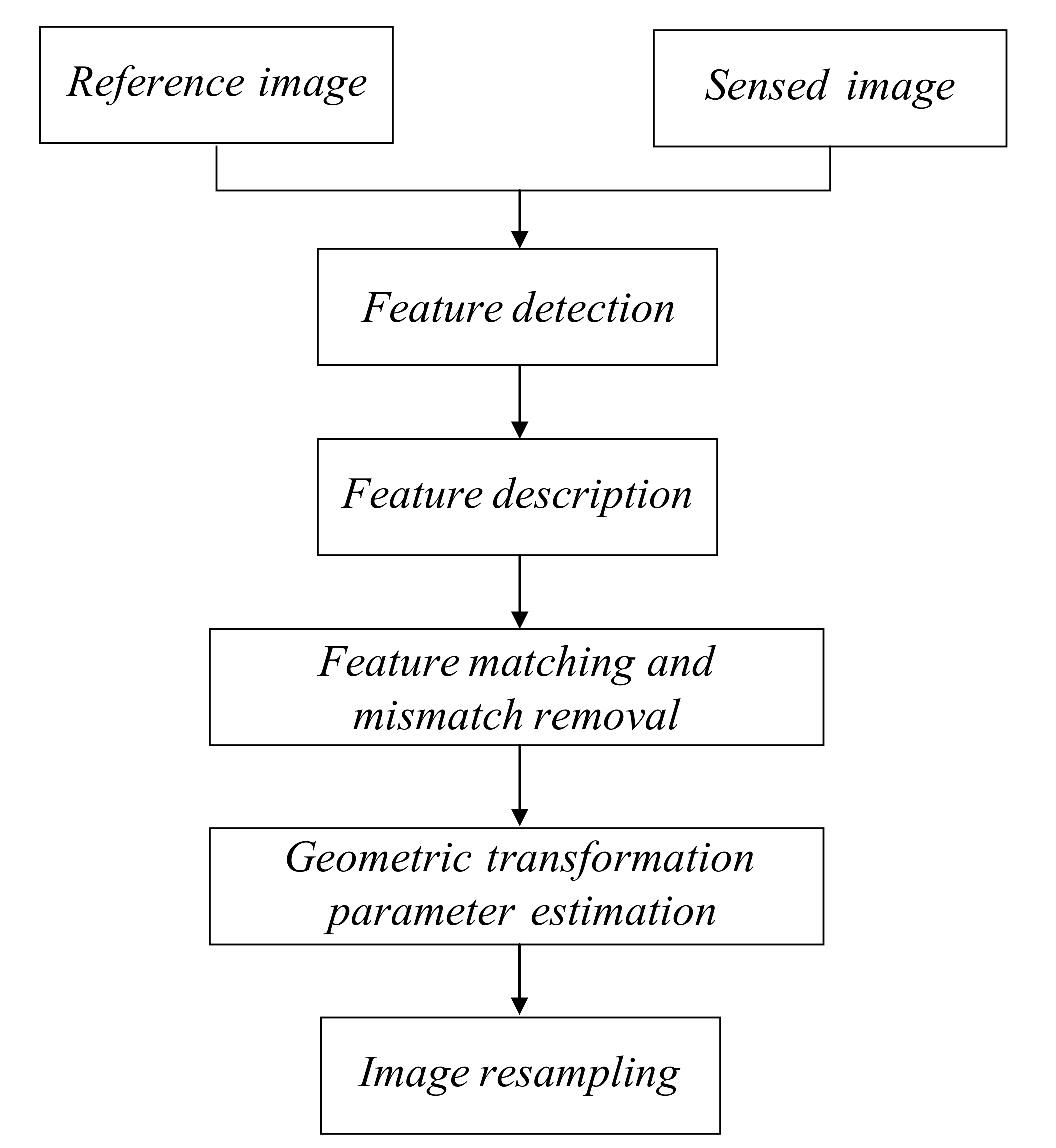
2.2. General Framework of Feature-Based Methods
2.2.1. Feature Detection
2.2.2. Feature Description
2.2.3. Feature Matching
2.3. General Framework of Deep Learning-Based Methods
2.3.1. Convolutional Neural Network
2.3.2. Generative Adversarial Networks
2.3.3. Other Deep Learning Models
3. Review of MMRS Image Registration Methods
3.1. Review of Area-Based Methods
- Improving the similarity measure MI that is the most suitable for MMRS image registration;
- Establishing a similarity measure to eliminate modal differences based on the shape and structure of an image;
- Improving the optimization method for high-resolution and noise-affected images to enhance registration performance.
3.1.1. Methods to Improve Similarity Measures
3.1.2. Methods to Improve Optimization
3.1.3. Hybrid Methods
3.2. Review of Feature-Based Methods
3.2.1. Methods to Improve SIFT or Harris Operator
3.2.2. Methods to Improve Feature Descriptor
3.2.3. Hybrid Methods
3.3. Review of Combined Area-Based and Feature-Based Methods
3.4. Review of Deep Learning-Based Methods
3.4.1. Methods to Improve CNN and GAN Algorithms
3.4.2. Methods to Improve Siamese Network
3.4.3. Others
3.5. Multi-Modal Image Registration Methods in Other Fields
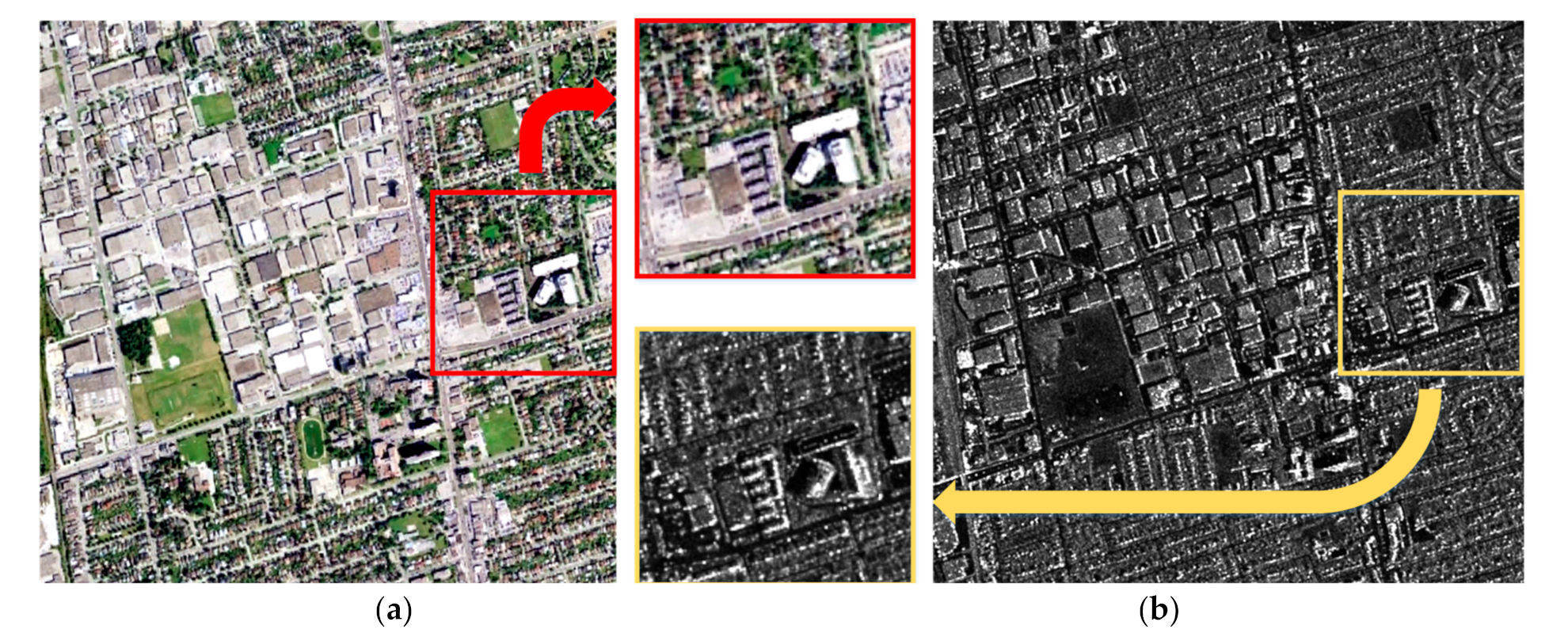
4. Experiments
5. Challenges and Future Directions
- There is insufficient data for different modal conditions in the field of remote sensing, and there is no complete and comprehensive database containing all types of MMRS image pairs. Therefore, for deep learning methods that are developing rapidly and showing great progress, most of the work uses this technology for feature detection and feature description. The lack of training and test data greatly limits its application in MMRS image registration.
- With the development of remote sensing technology, images from different sensors will have higher resolution. The details within high-resolution images are complex, the amount of data is large, and the local geometric deformation caused by the undulation of the terrain cannot be ignored. This results in a significant challenge for image registration.
- By comparing existing methods on MMRS image registration, we found that there are many registration strategies for optical-to-SAR and infrared-to-visible. However, learning-based methods can only learn the characteristics and differences between specific multi-modal image pairs. In the future, how to fuse and learn the data between multi-modalities should become the focus. For example, rather than eliminating the modal difference between two images, the registration method should be suitable for remote sensing images with multiple modalities.
- Area-based methods still face the impact of overlapping block regions and low computational efficiency on the registration performance, whereas feature-based methods face the challenge of nonlinear intensity differences.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zitová, B.; Flusser, J. Image registration methods: A survey. Image Vis. Comput. 2003, 21, 977–1000. [Google Scholar] [CrossRef]
- Yan, X.H.; Zhang, D.J.; Hou, N. Multimodal image registration using histogram of oriented gradient distance and data-driven grey wolf optimizer. Neurocomputing 2020, 392, 108–120. [Google Scholar] [CrossRef]
- Gong, M.G.; Zhao, S.M.; Jiao, L.C.; Tian, D.Y.; Wang, S. A novel coarse-to-fine scheme for automatic image registration based on SIFT and mutual information. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4328–4338. [Google Scholar] [CrossRef]
- Ye, Y.X.; Shan, J.; Bruzzone, L.; Shen, L. Robust registration of multimodal remote sensing images based on structural similarity. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2941–2958. [Google Scholar] [CrossRef]
- Fan, B.; Huo, C.; Pan, C.; Kong, Q. Registration of optical and SAR satellite images by exploring the spatial relationship of the improved SIFT. IEEE Geosci. Remote Sens. Lett. 2013, 10, 657–661. [Google Scholar] [CrossRef]
- Ma, J.; Jiang, X.; Fan, A.; Jiang, J.; Yan, J. Image matching from handcrafted to deep features: A survey. Int. J. Comput. Vis. 2021, 129, 23–79. [Google Scholar] [CrossRef]
- Dawn, S.; Saxena, V.; Sharma, B. Remote sensing image registration techniques: A survey. In Proceedings of the International Conference on Image and Signal Processing, Québec, QC, Canada, 30 June–2 July 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 103–112. [Google Scholar]
- Wu, Y.; Liu, J.W.; Zhu, C.Z.; Bai, Z.F.; Miao, Q.G.; Ma, W.P.; Gong, M.G. Computational Intelligence in Remote Sensing Image Registration: A survey. Int. J. Autom. Comput. 2020, 18, 1–17. [Google Scholar] [CrossRef]
- Haskins, G.; Kruger, U.; Yan, P. Deep learning in medical image registration: A survey. Mach. Vis. Appl. 2020, 31, 8. [Google Scholar] [CrossRef]
- Sotiras, A.; Davatzikos, C.; Paragios, N. Deformable medical image registration: A survey. IEEE Trans. Med. Imaging 2013, 32, 1153–1190. [Google Scholar] [CrossRef] [PubMed]
- Fu, Y.; Lei, Y.; Wang, T.; Curran, W.J.; Liu, T.; Yang, X. Deep learning in medical image registration: A review. Phys. Med. Biol. 2020, 65, 20TR01. [Google Scholar] [CrossRef]
- Xiang, Y.M.; Wang, F.; You, H.J. OS-SIFT: A robust SIFT-like algorithm for high-resolution optical-to-SAR image registration in suburban areas. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3078–3093. [Google Scholar] [CrossRef]
- Sui, H.G.; Xu, C.; Liu, J.Y.; Hua, F. Automatic optical-to-SAR image registration by iterative line extraction and Voronoi integrated spectral point matching. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6058–6072. [Google Scholar] [CrossRef]
- Xu, C.; Sui, H.; Li, H.; Liu, J. An automatic optical and SAR image registration method with iterative level set segmentation and SIFT. Int. J. Remote Sens. 2015, 36, 3997–4017. [Google Scholar] [CrossRef]
- Liu, X.; Ai, Y.; Zhang, J.; Wang, Z. A novel affine and contrast invariant descriptor for infrared and visible image registration. Remote Sens. 2018, 10, 658. [Google Scholar] [CrossRef]
- Du, Q.; Fan, A.; Ma, Y.; Fan, F.; Huang, J.; Mei, X. Infrared and visible image registration based on scale-invariant piifd feature and locality preserving matching. IEEE Access 2018, 6, 64107–64121. [Google Scholar] [CrossRef]
- Min, C.; Gu, Y.; Li, Y.; Yang, F. Non-rigid infrared and visible image registration by enhanced affine transformation. Pattern Recognit. 2020, 106, 107377. [Google Scholar] [CrossRef]
- Jiang, X.; Ma, J.; Xiao, G.; Shao, Z.; Guo, X. A review of multimodal image matching: Methods and applications. Inf. Fusion 2021, 73, 22–71. [Google Scholar] [CrossRef]
- Zhao, F.; Huang, Q.M.; Gao, W. Image matching by normalized cross-correlation. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Toulouse, France, 14–19 May 2006; Volume 2. [Google Scholar]
- Luo, J.W.; Konofagou, E.E. A fast normalized cross-correlation calculation method for motion estimation. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2010, 57, 1347–1357. [Google Scholar]
- Cole-Rhodes, A.A.; Johnson, K.L.; LeMoigne, J.; Zavorin, I. Multiresolution registration of remote sensing imagery by optimization of mutual information using a stochastic gradient. IEEE Trans. Image Process. 2003, 12, 1495–1511. [Google Scholar] [CrossRef]
- Chen, H.M.; Arora, M.K.; Varshney, P.K. Mutual information-based image registration for remote sensing data. Int. J. Remote Sens. 2003, 24, 3701–3706. [Google Scholar] [CrossRef]
- Chen, H.M.; Varshney, P.K.; Arora, M.K. Performance of mutual information similarity measure for registration of multitemporal remote sensing images. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2445–2454. [Google Scholar] [CrossRef]
- Yang, W.; Han, C.Z.; Sun, H.; Cao, Y.F. Registration of high resolution SAR and optical images based on multiple features. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Seoul, Korea, 29 July 2005; Volume 5, pp. 3542–3544. [Google Scholar]
- Lehureau, G.; Tupin, F.; Tison, C.; Guillaume, O.; Petit, D. Registration of metric resolution SAR and optical images in urban areas. In Proceedings of the European Conference on Synthetic Aperture Radar, Friedrichshafen, Germany, 2–5 June 2008; pp. 1–4. [Google Scholar]
- Yan, X.H.; Zhang, Y.J.; Zhang, D.J.; Hou, N.; Zhang, B. Registration of multimodal remote sensing images using transfer optimization. IEEE Geosci. Remote Sens. Lett. 2020, 17, 2060–2064. [Google Scholar] [CrossRef]
- Tondewad, P.S.; Dale, M.P. Remote sensing image registration methodology: Review and discussion. Procedia Comput. Sci. 2020, 171, 2390–2399. [Google Scholar] [CrossRef]
- Yu, L.; Zhang, D.R.; Holden, E.J. A fast and fully automatic registration approach based on point features for multi-source remote sensing images. Comput. Geosci. 2008, 34, 838–848. [Google Scholar] [CrossRef]
- Gonçalves, H.; Gonçalves, J.; Corte-Real, L. HAIRIS: A method for automatic image registration through histogram-based image segmentation. IEEE Trans. Image Process. 2011, 20, 776–789. [Google Scholar] [CrossRef] [PubMed]
- Moravec, H. Obstacle Avoidance and Navigation in the Real World by a Seeing Robot Rover. Ph.D. Thesis, Standford University, Stanford, CA, USA, 1980. [Google Scholar]
- Harris, C.; Stephens, M. A combined corner and edge detector. In Proceedings of the Alvey Vision Conference, Manchester, UK, 31 August–2 September 1988; pp. 147–151. [Google Scholar]
- Mikolajczyk, K.; Schmid, C. Scale & affine invariant interest point detectors. Int. J. Comput. Vis. 2004, 60, 63–86. [Google Scholar]
- Lowe, D.G. Object recognition from local scale-invariant features. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; pp. 1150–1157. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Sedaghat, A.; Mokhtarzade, M.; Ebadi, H. Uniform robust scale-invariant feature matching for optical remote sensing images. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4516–4527. [Google Scholar] [CrossRef]
- Sun, H.; Lei, L.; Zou, H.; Wang, C. Multimodal remote sensing image registration using multiscale self-similarities. In Proceedings of the IEEE International Conference on Computer Vision in Remote Sensing, Xiamen, China, 16–18 December 2012; pp. 199–202. [Google Scholar]
- Zeng, Q.; Adu, J.; Liu, J.; Yang, J.; Xu, Y.; Gong, M. Real-time adaptive visible and infrared image registration based on morphological gradient and C_SIFT. J. Real-Time Image Process. 2020, 17, 1103–1115. [Google Scholar] [CrossRef]
- Bay, H.; Tuytelaars, T.; Van Gool, L. SURF: Speeded up robust features. In Proceedings of the European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; pp. 404–417. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Litjens, G.; Kooi, T.; Bejnordi, B.E.; Setio, A.A.A.; Ciompi, F.; Ghafoorian, M.; Sanchez, C.I. A survey on deep learning in medical image analysis. Med. Image Anal. 2017, 42, 60–88. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, I.; Abadie, J.; Mirza, M.; Xu, B.; Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. arXiv 2014, arXiv:1406.2661v1. [Google Scholar]
- Oliehoek, F.A.; Savani, R.; Gallego-Posada, J.; Van der Pol, E.; De Jong, E.D.; Groß, R. GANGs: Generative adversarial network games. arXiv 2017, arXiv:1712.00679v2. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep learning in remote sensing: A comprehensive review and list of resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Hinton, G.E. A Practical Guide to Training Restricted Boltzmann Machines. In Neural Networks: Tricks of the Trade. Lecture Notes in Computer Science; Montavon, G., Orr, G.B., Müller, K.R., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; p. 7700. [Google Scholar]
- Sutskever, I.; Martens, J.; Hinton, G.E. Generating text with recurrent neural networks. In Proceedings of the 28th International Conference on Machine Learning, Washington, DC, USA, 28 June–2 July 2011; pp. 1017–1024. [Google Scholar]
- Abdi, G.; Samadzadegan, F.; Reinartz, P. Spectral-spatial feature learning for hyperspectral imagery classification using deep stacked sparse autoencoder. J. Appl. Remote Sens. 2017, 11, 042604. [Google Scholar]
- Gong, M.; Yang, H.; Zhang, P. Feature learning and change feature classification based on deep learning for ternary change detection in SAR images. ISPRS J. Photogramm. Remote Sens. 2017, 129, 212–225. [Google Scholar] [CrossRef]
- Zabalza, J.; Ren, J.; Zheng, J.; Zhao, H.; Qing, C.; Yang, Z.; Du, P.; Marshall, S. Novel segmented stacked autoencoder for effective dimensionality reduction and feature extraction in hyperspectral imaging. Neurocomputing 2016, 185, 1–10. [Google Scholar] [CrossRef]
- Mou, L.; Ghamisi, P.; Zhu, X.X. Deep recurrent neural networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3639–3655. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, L.; Wei, W.; Zhang, Y. When low rank representation based hyperspectral imagery classification meets segmented stacked denoising auto-encoder based spatial-spectral feature. Remote Sens. 2018, 10, 284. [Google Scholar] [CrossRef]
- Lin, D.; Fu, K.; Wang, Y.; Xu, G.; Sun, X. MARTA GANs: Unsupervised representation learning for remote sensing image classification. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2092–2096. [Google Scholar] [CrossRef]
- Zhan, Y.; Hu, D.; Wang, Y.; Yu, X. Semisupervised hyperspectral image classification based on Generative Adversarial Networks. IEEE Geosci. Remote Sens. Lett. 2018, 15, 212–216. [Google Scholar] [CrossRef]
- Shadaydeh, M.; Sziranyi, T. An improved mutual information similarity measure for registration of multi-modal remote sensing images. In Image and Signal Processing for Remote Sensing XXI; Bruzzone, L., Ed.; International Society for Optics and Photonics: Washington, DC, USA, 2015; Volume 9643, p. 96430F. [Google Scholar]
- Xu, X.; Li, X.; Liu, X.; Shen, H.; Shi, Q. Multimodal registration of remotely sensed images based on jeffrey’s divergence. ISPRS J. Photogramm. Remote Sens. 2016, 122, 97–115. [Google Scholar] [CrossRef]
- Xie, X.; Zhang, Y.; Ling, X.; Wang, X. A new registration algorithm for multimodal remote sensing images. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 7011–7014. [Google Scholar]
- Xie, X.; Zhang, Y.; Ling, X.; Wang, X. A novel extended phase correlation algorithm based on log-gabor filtering for multimodal remote sensing image registration. Int. J. Remote Sens. 2019, 40, 5429–5453. [Google Scholar] [CrossRef]
- Hasan, M.; Pickering, M.R.; Jia, X. Robust automatic registration of multimodal satellite images using ccre with partial volume interpolation. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4050–4061. [Google Scholar] [CrossRef]
- Dame, A.; Marchand, E. Second-order optimization of mutual information for real-time image registration. IEEE Trans. Image Process. 2012, 21, 4190–4203. [Google Scholar] [CrossRef] [PubMed]
- Liang, J.; Liu, X.; Huang, K.; Li, X.; Wang, D.; Wang, X. Automatic registration of multisensor images using an integrated spatial and mutual information (SMI) metric. IEEE Trans. Geosci. Remote Sens. 2014, 52, 603–615. [Google Scholar] [CrossRef]
- Wu, Y.; Ma, W.; Miao, Q.; Wang, S. Multimodal continuous ant colony optimization for multisensor remote sensing image registration with local search. Swarm Evol. Comput. 2019, 47, 89–95. [Google Scholar] [CrossRef]
- Liu, X.; Chen, S.; Zhuo, L.; Li, J.; Huang, K. Multi-sensor image registration by combining local self-similarity matching and mutual information. Front. Earth Sci. 2018, 12, 779–790. [Google Scholar] [CrossRef]
- Ye, Y.; Bruzzone, L.; Shan, J.; Bovolo, F.; Zhu, Q. Fast and robust matching for multimodal remote sensing image registration. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9059–9070. [Google Scholar] [CrossRef]
- Liang, D.; Ding, J.; Zhang, Y. Efficient Multisource Remote Sensing Image Matching Using Dominant Orientation of Gradient. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2194–2205. [Google Scholar] [CrossRef]
- De Castro, E.; Morandi, C. Registration of translated and rotated images using finite fourier transforms. IEEE Trans. Pattern Anal. Mach. Intell. 1987, 9, 700–703. [Google Scholar] [CrossRef]
- Reddy, B.S.; Chatterji, B.N. An FFT-based technique for translation, rotation, and scale-invariant image registration. IEEE Trans. Image Process. 1996, 5, 1266–1271. [Google Scholar] [CrossRef] [PubMed]
- Foroosh, H.; Zerubia, J.B.; Berthod, M. Extension of phase correlation to subpixel registration. IEEE Trans. Image Process. 2002, 11, 188–200. [Google Scholar] [CrossRef]
- Thevenaz, P.; Unser, M. Optimization of mutual information for multiresolution image registration. IEEE Trans. Image Process. 2020, 9, 2083–2099. [Google Scholar]
- Hossain, M.T.; Lv, G.; Teng, S.; Lu, G.; Lackmann, M. Improved symmetric-SIFT for multi-modal image registration. In Proceedings of the International Conference on Digital Image Computing: Techniques and Applications, Noosa, Australia, 6–8 December 2011; pp. 197–202. [Google Scholar]
- Huang, L.; Li, Z.; Zhang, R. SAR and optical images registration using shape context. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 1007–1010. [Google Scholar]
- Aguilera, C.; Barrera, F.; Lumbreras, F.; Sappa, A.D.; Toledo, R. Multispectral image feature points. Sensors 2012, 12, 12661–12672. [Google Scholar] [CrossRef]
- Ye, Y.; Shan, J. A local descriptor based registration method for multispectral remote sensing images with non-linear intensity differences. ISPRS J. Photogramm. Remote Sens. 2014, 90, 83–95. [Google Scholar] [CrossRef]
- Sedaghat, A.; Ebadi, H. Distinctive order based self-similarity descriptor for multi-sensor remote sensing image matching. ISPRS J. Photogramm. Remote Sens. 2015, 108, 62–71. [Google Scholar] [CrossRef]
- Ye, Y.; Li, S.; Hao, M.; Wang, J.; Xu, Z. Robust optical-to-SAR image matching based on shape properties. IEEE Geosci. Remote Sens. 2017, 14, 564–568. [Google Scholar] [CrossRef]
- Xiong, X.; Xu, Q.; Jin, G.; Zhang, H.; Gao, X. Rank-based local self-similarity descriptor for optical-to-SAR image matching. IEEE Geosci. Remote Sens. 2020, 17, 1742–1746. [Google Scholar] [CrossRef]
- Cui, S.; Zhong, Y. Multi-modal remote sensing image registration based on multi-scale phase congruency. In Proceedings of the 10th IAPR Workshop on Pattern Recognition in Remote Sensing (PRRS), Beijing, China, 19–20 August 2018. [Google Scholar]
- Ye, Y.; Shan, J.; Hao, S.; Bruzzone, L.; Qin, Y. A local phase based invariant feature for remote sensing image matching. ISPRS J. Photogramm. Remote Sens. 2018, 142, 205–221. [Google Scholar] [CrossRef]
- Fan, J.; Wu, Y.; Li, M.; Liang, W.; Cao, Y. SAR and optical image registration using nonlinear diffusion and phase congruency structural descriptor. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5368–5379. [Google Scholar] [CrossRef]
- Li, J.; Hu, Q.; Ai, M. RIFT: Multi-modal image matching based on radiation-variation insensitive feature transform. IEEE Trans. Image Process. 2020, 29, 3296–3310. [Google Scholar] [CrossRef]
- Zhao, C.; Zhao, H.; Lv, J.; Sun, S.; Li, B. Multimodal image matching based on multimodality robust line segment descriptor. Neurocomputing 2016, 177, 290–303. [Google Scholar] [CrossRef]
- Xu, G.; Wu, Q.; Cheng, Y.; Yan, F.; Li, Z.; Yu, Q. A robust deformed image matching method for multi-source image matching. Infrared Phys. Technol. 2021, 115, 103691. [Google Scholar] [CrossRef]
- Chen, J.; Tian, J. Real-time multi-modal rigid registration based on a novel symmetric-SIFT descriptor. Prog. Nat. Sci. 2009, 19, 643–651. [Google Scholar] [CrossRef]
- Fjortoft, R.; Lopes, A.; Marthon, P.; Cubero-Castan, E. An optimal multiedge detector for SAR image segmentation. IEEE Trans. Geosci. Remote Sens. 1998, 36, 793–802. [Google Scholar] [CrossRef]
- Xiang, Y.; Wang, F.; Wan, L.; Jiao, N.; You, H. Os-flow: A robust algorithm for dense optical and SAR image registration. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6335–6354. [Google Scholar] [CrossRef]
- Xiang, Y.; Tao, R.; Wan, L.; Wang, F.; You, H. Os-pc: Combining feature representation and 3-D phase correlation for subpixel optical and SAR image registration. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6451–6466. [Google Scholar] [CrossRef]
- Shechtman, E.; Irani, M. Matching local self-similarities across images and videos. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; Volume 1, pp. 1–8. [Google Scholar]
- Tola, E.; Lepetit, V.; Fua, P. DAISY: An efficient dense descriptor applied to wide-baseline stereo. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 815–830. [Google Scholar] [CrossRef]
- Perona, P.; Malik, J. Scale-space and edge detection using anisotropic diffusion. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 629–639. [Google Scholar] [CrossRef]
- Alcantarilla, P.F.; Bartoli, A.; Davison, A.J. KAZE features. In Proceedings of the European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; pp. 214–227. [Google Scholar]
- von Gioi, R.; Jakubowicz, J.; Morel, J.M.; Randall, G. LSD: A fast line segment detector with a false detection control. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 722–732. [Google Scholar] [CrossRef] [PubMed]
- Xiong, B.; Li, W.; Zhao, L.; Lu, J.; Zhang, X.; Kuang, G. Registration for SAR and optical images based on straight line features and mutual information. In Proceedings of the IGARSS, IEEE International Geoscience and Remote Sensing Symposium, Beijing, China, 10–15 July 2016; pp. 2582–2585. [Google Scholar]
- Zhang, M.X.; Wang, Z.G.; Bai, R.Y. A coarse-to-fine optical and SAR remote sensing image registration algorithm. J. Geo-Inf. Sci. 2020, 22, 2238–2246. [Google Scholar]
- Ye, F.; Su, Y.; Xiao, H.; Zhao, X.; Min, W. Remote sensing image registration using convolutional neural network features. IEEE Geosci. Remote Sens. Lett. 2018, 15, 232–236. [Google Scholar] [CrossRef]
- Ma, W.; Zhang, J.; Wu, Y.; Jiao, L.; Zhu, H.; Zhao, W. A novel two-step registration method for remote sensing images based on deep and local features. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4834–4843. [Google Scholar] [CrossRef]
- Yang, Z.; Dan, T.; Yang, Y. Multi-temporal remote sensing image registration using deep convolutional features. IEEE Access. 2018, 6, 38544–38555. [Google Scholar] [CrossRef]
- Quan, D.; Wang, S.; Liang, X.F.; Wang, R.J.; Fang, S.; Hou, B.; Jiao, L.C. Deep generative matching network for optical and SAR image registration. Proceedings of The IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 6215–6218. [Google Scholar]
- Merkle, N.; Auer, S.; Müller, R.; Reinartz, P. Exploring the potential of conditional adversarial networks for optical and SAR image matching. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1811–1820. [Google Scholar] [CrossRef]
- Hughes, L.H.; Schmitt, M.; Mou, L.C.; Wang, Y.Y.; Zhu, X.X. Identifying corresponding patches in SAR and optical images with a pseudo-Siamese CNN. IEEE Geosci. Remote Sens. Lett. 2018, 15, 784–788. [Google Scholar] [CrossRef]
- Zhang, H.; Ni, W.; Yan, W.; Xiang, D.; Wu, J.; Yang, X.; Bian, H. Registration of multimodal remote sensing image based on deep fully convolutional neural network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3028–3042. [Google Scholar] [CrossRef]
- Merkle, N.; Luo, W.J.; Auer, S.; Muller, R.; Urtasun, R. Exploiting deep matching and sar data for the geo-localization accuracy improvement of optical satellite images. Remote Sens. 2017, 9, 586. [Google Scholar] [CrossRef]
- He, H.; Chen, M.; Chen, T.; Li, D. Matching of remote sensing images with complex background variations via siamese convolutional neural network. Remote Sens. 2018, 10, 355. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, W.; Wu, Y.; Jiao, L. Multimodal Remote Sensing Image Registration Based on Image Transfer and Local Features. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1210–1214. [Google Scholar] [CrossRef]
- Wang, S.; Quan, D.; Liang, X.; Ning, M.; Guo, Y.; Jiao, L. A deep learning framework for remote sensing image registration. ISPRS J. Photogramm. Remote Sens. 2018, 145, 148–164. [Google Scholar] [CrossRef]
- Zampieri, A.; Charpiat, G.; Girard, N.; Tarabalka, Y. Multimodal Image Alignment through a Multiscale Chain of Neural Networks with Application to Remote Sensing. 2018. Available online: http://openaccess.thecvf.com/content_ECCV_2018/papers/Armand_Zampieri_Multimodal_image_alignment_ECCV_2018_paper.pdf (accessed on 14 December 2021).
- Luo, W.J.; Schwing, A.G.; Urtasun, R. Efficient deep learning for stereo matching. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 5695–5703. [Google Scholar]
- Tombari, F.; Stefano, L.D. The Maximal Self-dissimilarity Interest Point Detector. IPSJ Trans. Comput. Vis. Appl. 2015, 7, 175–188. [Google Scholar] [CrossRef][Green Version]
- Sedghi, A.; Luo, J.; Mehrtash, A.; Pieper, S.; Tempany, C.M.; Kapur, T.; Mousavi, P.; Wells, W.M., III. Semi-supervised deep metrics for image registration. arXiv 2018, arXiv:1804.01565. [Google Scholar]
- Wang, Y.; Zhang, J.K.; Cavichini, M.; Bartsch, D.G.; Freeman, W.R.; Nguyen, T.Q.; An, C. Robust Content-Adaptive Global Registration for Multimodal Retinal Images Using Weakly Supervised Deep-Learning Framework. IEEE Trans. Image Process. 2021, 30, 3167–3178. [Google Scholar] [CrossRef]
- Huang, W.; Yang, H.; Liu, X.; Li, C.; Zhang, I.; Wang, R.; Zheng, H.; Wang, S. A Coarse-to-Fine Deformable Transformation Framework for Unsupervised Multi-Contrast MR Image Registration with Dual Consistency Constraint. IEEE Trans. Med. Imaging 2021, 40, 2589–2599. [Google Scholar] [CrossRef]
- Jhan, J.P.; Rau, J. A Generalized Tool for Accurate and Efficient Image Registration of UAV Multi-lens Multispectral Cameras by N-SURF Matching. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 6353–6362. [Google Scholar] [CrossRef]
- Zhou, H.; Ma, J.; Tan, C.C.; Zhang, Y.; Ling, H. Cross-weather image alignment via latent generative model with intensity consistency. IEEE Trans. Image Process. 2020, 29, 5216–5228. [Google Scholar] [CrossRef]
- Dellinger, F.; Delon, J.; Gousseau, Y.; Michel, J.; Tupin, F. Sar-Sift: A Sift-Like Algorithm for Sar Images. IEEE Trans. Geosci. Remote Sens. 2015, 53, 453–466. [Google Scholar] [CrossRef]
- Ma, W.; Wen, Z.; Wu, Y.; Jiao, L.; Gong, M.; Zheng, Y.; Liu, L. Remote Sensing Image Registration with Modified SIFT and Enhanced Feature Matching. IEEE Geosci. Remote Sens. Lett. 2017, 14, 3–7. [Google Scholar] [CrossRef]
- Ma, J.; Zhou, H.; Zhao, J.; Gao, Y.; Jiang, J.; Tian, J. Robust Feature Matching for Remote Sensing Image Registration via Locally Linear Transforming. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6469–6481. [Google Scholar] [CrossRef]
- Li, Y.; Ma, J.; Zhang, Y. Image retrieval from remote sensing big data: A survey. Inf. Fusion 2021, 67, 94–115. [Google Scholar] [CrossRef]


| Author | Method Category | Method Improvement | Conclusion |
|---|---|---|---|
| Cole-Rhodes et al. [21] | Methods to improve similarity measures | Improve the joint histogram of MI and propose the simultaneous perturbation stochastic approximation (SPSA) algorithm. | The algorithm relies on gradient approximation instead of the target gradient value and finds the global maximum value through the local extrema of the objective function, which greatly speeds up the entire registration process. |
| Chen et al. [23] | Methods to improve similarity measures | A new joint histogram estimation algorithm is proposed, called Generalized Partial Volume Estimation (GPVE, with a second-order B-spline function). | Overcome the problem of interpolation-induced artifacts. |
| Shadaydeh et al. [54] | Methods to improve similarity measures | Propose a weight-based joint histogram estimation method (WJH-MI). | Reduces the peaks in the joint histogram caused by the background or homogeneous regions by assigning more weight to the high gradient pixels containing more registration related information. |
| Xu et al. [55] | Methods to improve similarity measures | Propose using the symmetric form of Kullback-Leiber divergence, namely Jeffrey’s divergence as similarity measure. | The registration model based on Jeffrey’s divergence can provide a larger feasible search space and solve the problem of MI facing insufficient image overlapping area. |
| Xie et al. [56] | Methods to improve similarity measures | MLPC method combining multi-scale Log-Gabor filter and phase consistency | Effectively resolving the non-linear intensity difference in MMRS image registration. |
| Xie et al. [57] | Methods to improve similarity measures | Based on the extended phase correlation of log-Gabor, an improved LGEPC method is proposed | Use the overall structure information to eliminate the influence of radiation differences as much as possible. |
| Hasan et al. [58] | Methods to improve optimization | Using CCRE to align SAR and Google satellite images and applying partial volume interpolation to calculate the gradient of the similarity measure. | Directly implement the optimization process based on partial volume interpolation. |
| Dame and Marchand [59] | Methods to improve optimization | Define a new inverse combinatorial optimization method to handle the quasi-concave shape of MI, where the required derivative can be pre-calculated allowing the Hessian matrix to be estimated after convergence. | Reduce the calculation time and estimate an accurate parameter. |
| Liang et al. [60] and Wu et al. [61] | Methods to improve optimization | The authors used the ant colony optimization (ACO) algorithm to optimize the similarity measure to maximize MI. | The similarity curve of MI has been proved to have many local optimal values. |
| Yan et al. [26] | Methods to improve optimization | Propose a method of using transfer optimization (TO) to maximize MI, optimize conversion parameters and transfer better results to another optimizer in the iterative process. | Enhance the global search capability of TO and avoid a local optima. |
| Liu et al. [62] | Hybrid methods | Propose an image registration method that combines local self-similarity (LSS) and MI, which combined local internal features and global intensity information. | The proposed method can register multi-sensor images with different resolutions and handle the geometric differences between grayscale and corresponding pixels and regions. |
| Ye et al. [63] | Hybrid methods | A fast and robust template matching framework for MMRS images called channel features of orientated gradients (CFOG). | A new general scheme of template matching based on pixel feature representation, suitable for all kinds of multi-modal image registration. |
| Yan et al. [2] | Hybrid methods | Introduced the histogram of oriented gradient distance (HOGD) and the grey wolf optimizer (GWO). | It avoids falling into the local optimum and reduces the calculation time. |
| Liang et al. [64] | Hybrid methods | A variable template matching method based on DOG features and the sum of cosine difference. | The proposed matching method has good robustness to nonlinear light intensity changes, and effectively improves the matching accuracy. |
| Author | Method Category | Method Improvement | Conclusion |
|---|---|---|---|
| Yu et al. [28] | Methods to improve SIFT or Harris operator | Combine the advantages of SIFT and Harris to propose a coarse to fine MMRS image registration. | The proposed method is more suitable for MMRS image registration. |
| Sedaghat et al. [35] | Methods to improve SIFT or Harris operator | Propose a registration method, called Uniform Robust SIFT (UR-SIFT), suitable for a variety of optical multi-source remote sensing images with illumination, rotation and up to five times the scale difference. | In the process of descriptor merging, this algorithm led to many other combinations to be merged into the same final descriptor, which greatly reduced the registration accuracy. |
| Hossain et al. [69] | Methods to improve SIFT or Harris operator | An improved symmetric SIFT method. | The descriptor merging step in symmetric SIFT can be skipped to obtain excellent matching accuracy. |
| Fan et al. [5] | Methods to improve SIFT or Harris operator | A novel spatial consensus matching (SCM) algorithm. | Using improved SIFT and K-nearest neighbors (KNN) to obtain an initial set of matching features and utilized spatial consistency constraints for refinement. |
| Huang et al. [70] | Methods to improve SIFT or Harris operator | A new algorithm for improving feature extraction and feature matching was introduced. | Using Harris operator, Canny operator and shape context descriptor to match multimodal images. |
| Xiang et al. [12] | Methods to improve SIFT or Harris operator | Propose a SIFT-like algorithm (OS-SIFT), which introduce multi-scale ratio of exponentially weighted averages (ROEWA) and multi-scale Sobel operators. | By calculating the consistent gradients of SAR and optical images, it is proved that the algorithm is robust to noise and has excellent registration performance and accuracy. |
| Aguilera et al. [71] | Methods to improve feature descriptor | The edge-oriented histogram (EOH) descriptor | The descriptor contained the information of the contour near each feature point without using the gradient information to describe the shape and contour of the image. |
| Ye et al. [72] | Methods to improve feature descriptor | Combine Harris and LSS descriptors to establish a piecewise linear transformation | The impact of the low discriminability of the LSS descriptor is reduced, and the reliable registration of multi-spectral remote sensing images is realized. |
| Sedaghat et al. [73] | Methods to improve feature descriptor | An advanced version of the self-similarity descriptor, which has high distinguishability, called distinctive order based self similarity (DOBSS) descriptor. | The DOBSS descriptor has better recall, precision and positioning accuracy. |
| Ye et al. [74] | Methods to improve feature descriptor | Based on the internal self-similarity of images, the author introduced a shape descriptor of dense local self-similarity (DLSS). | Using the internal structure information of the image to construct the descriptor is more suitable for multi-mode image registration. |
| Xiong et al. [75] | Methods to improve feature descriptor | A rank-based local self-similarity (RLSS) to describe the local shape of an image in a distinguishable manner. | The rank value was used as a substitute for the correlation value to indicate the relative relationship of the correlation value, which further improved distinguishability of feature descriptors. |
| Cui et al. [76] | Methods to improve feature descriptor | A multi-scale phase-congruency descriptor (MS-PC), which captured the shape and structural characteristics of an image. | The descriptor compensates for the sensitivity of traditional descriptors to radiation differences. |
| Ye et al. [4] | Methods to improve feature descriptor | Combine the PC describing structural features with the histogram of gradient directions (HOG) as a feature descriptor, called HOPC. | Using the structure information of the image to construct the descriptor can eliminate modal differences and is more suitable for multi-mode image registration. |
| Liu et al. [15] | Methods to improve feature descriptor | A maximum stable phase congruency (MSPC), which combined affine invariant region extraction and image structural features. | The algorithm extracted structural features by merging phase congruency images in multiple orientations. Registration was achieved according to the correspondence of the descriptors. |
| Ye et al. [77] | Hybrid methods | A local invariant feature that was robust to geometric distortion and radiation changes, which consisted of a feature detector named MMPC-lap and a feature descriptor named local histogram of orientated phase congruency (LHOPC). | This method also solved the radiation differences caused by spectral and time changes between MMRS images. |
| Fan et al. [78] | Hybrid methods | An UND-Harris detector that introduced nonlinear diffusion, feature ratio and block strategy. | Experimental results on different SAR and optical image pairs showed the effectiveness of this method, which can obtain better registration results and improve registration accuracy. |
| Zeng et al. [37] | Hybrid methods | An infrared-to-visible image registration method based on morphological gradient and C-SIFT. | The algorithm uses morphological methods to preserve the gray-scale edges of the image and improve the similarity of infrared and visible images. |
| Li et al. [79] | Hybrid methods | A radiation insensitive image registration method based on phase congruency (PC) and a maximum index image (MIM), which was called radiation variation insensitive feature transform (RIFT). | This method realizes the insensitivity and rotation invariance to multi-modal image radiation changes. |
| Sui et al. [13] | Hybrid methods | An iterative process combining line segment extraction and line intersection matching based online segment extraction, and integrated Voronoi polygons into spectral point matching (SPM) to obtain the correspondences between line intersections. | An iterative strategy of “re-extraction” and “re-matching” mechanisms was adopted to enhance feature extraction and matching performance. |
| Zhao et al. [80] | Hybrid methods | Using Kovesi corner point extraction and line segment detection methods based on phase congruency and local direction. | Compared to other edge extraction methods, this method extracted more equivalent line segments. |
| Xu et al. [81] | Hybrid methods | A new contour segment representation method based on local histogram of maximal edge orientation and defined angles is proposed, and the Fréchet distance is defined as the weighting parameter of combined histograms to enhance the descriptive ability. | The proposed method can effectively reduce the impacts of radiation distortion and is superior to some current popular multi-source image matching methods. |
| Author | Method Category | Method Improvement | Conclusion |
|---|---|---|---|
| Gong et al. [3] | Combined area-based and feature-based methods | A novel coarse-to-fine scheme for automatic image registration. | In coarse registration (pre-registration), the scale histogram was used to remove the outliers detected by SIFT. Due to the robustness of MI to noise and its adaptability to different image intensity values, adopted it to refine the pre-registration results in the multiresolution framework. |
| Ye et al. [72] | Combined area-based and feature-based methods | A local descriptor-based registration method for multispectral remote sensing images. | Pre-registration used SR-SIFT and projection transformation to eliminate the obvious rotation and scale differences between the reference and sensed images. Then the second stage uses LSS as a new similarity measure. |
| Xiong et al. [91] | Combined area-based and feature-based methods | Coarse registration based on intersections of straight lines and fine registration based on MI from separated patches. | Using the stable and consistent edge information of the optical and SAR images, the registration accuracy is improved. |
| Zhang et al. [92] | Combined area-based and feature-based methods | Using the feature-based SAR-SIFT algorithm to complete the coarse registration, and then utilize the area-based ROEWA-HOG method to complete the fine registration. | Achieve high-precision automatic registration of the hybrid model. |
| Author | Method Category | Method Improvement | Conclusion |
|---|---|---|---|
| Ye et al. [93] | Methods to improve CNN and GAN algorithms | Using CNN to extract the middle and high-level features of an image and combined them with the low-level features extracted by SIFT. | Features of CNN and SIFT were incorporated into the PSO-SIFT algorithm for registration. |
| Ma et al. [94] | Methods to improve CNN and GAN algorithms | Using VGG-16 to approximate spatial relationships and proposed a new point matching strategy based on spatial relationships and combined the local feature-based methods. | Due to the powerful feature extraction capabilities of CNN and the consideration of spatial relationships, the matching results are robust and accurate. |
| Yang et al. [95] | Methods to improve CNN and GAN algorithms | Adopting a pre-trained VGG network to generate multi-scale descriptors through high-level convolution information features. | Optimize the registration details by increasing the number of feature points. |
| Quan et al. [96] | Methods to improve CNN and GAN algorithms | Applying GAN for MMRS images data augmentation, which could immensely enhance the accuracy and robust of registration process. | A dual-channel deep network and CNN can save the spatial information of the image. |
| Merkle et al. [97] | Methods to improve CNN and GAN algorithms | A GAN-based method for dealing with optical and SAR image registration. | The generator in GAN accurately and reliably retained the geometric structure of the optical image, opening up new possibilities for MMRS. |
| Hughes et al. [98] | Methods to improve Siamese network | A specific pseudo-Siamese network to register the optical and SAR images. | The two convolutional streams of this network are identical and independent, and there is no parameter sharing to process the different intensity information of the two images. |
| Zhang et al. [99] | Methods to improve Siamese network | A fully convolutional Siamese network, which used an end-to-end training process. It built a general framework for MMRS image registration based on depth features. | Sharing parameters between the two branches to solve the problem of lack of data sets. |
| Merkle et al. [100] | Methods to improve Siamese network | By training the Siamese network to learn the spatial transformation between optical and SAR images. | The effectiveness of this approach for the generation of reliable and robust matching points between optical and SAR images had been demonstrated by experiment. |
| He et al. [101] | Methods to improve Siamese network | A novel multi-scale remote sensing image registration deep network, which includes the following three steps: corner detection based on s-Harris, a search strategy based on Gaussian pyramid coupled quadtree. Finally, global to local quadratic polynomial constraints and RANSAC were utilized to remove mismatches. | This algorithm can realize the scale comparison of multi-scale conjugate patches, make the matching evenly distributed, and obtain satisfactory matching accuracy. The most important thing is to avoid the influence of complex background changes on the registration results. |
| Zhang et al. [102] | Others | Extending the image visual attribute transfer method to pre-process an image. | Eliminate the intensity differences between the multi-modal image pairs, and make the color, texture and other characteristics consistent in a similar structural area. |
| Wang et al. [103] | Others | A remote sensing image registration framework based on deep learning, which directly learns the mapping function between image patch pairs and their matching labels through closed-loop information. | A self-learning method was introduced to avoid a few image data and can learn the mapping function from itself without relying on other data. At the same time, the application of transfer learning further improves the registration accuracy and reduces training costs. |
| Zampieri et al. [104] | Others | Designing a neural network with a specific scale to learn image features. | Complete the alignment between remote sensing images and maps |
| Author | Method Category | Method Improvement | Conclusion |
|---|---|---|---|
| Tombari et al. [106] | Multimodal registration of photogrammetric images | The local maximum feature of the Contextual Self-dissimilarity (CSD) operator is detected through the non-maximum suppression (NMS) stage, which is called the Maximal Self-Dissimilarity interest point detector (MSD). | MSD is taking the lead for photogrammetric based multimodal registration. |
| Sedghi et al. [107] | Multimodal registration of medical images | Building a five-layer neural network to learn a similarity metric that can measure the level of registration and using Powell’s method to optimize the learned metric in an iterative manner. | The results demonstrate the feasibility of learning a useful deep metric from substantially misaligned training data, and results are significantly better than from Mutual Information. |
| Wang et al. [108] | Multimodal registration of medical images | A content-adaptive weakly-supervised deep learning framework is constructed for multi-modal retinal image registration. The framework is composed of three neural networks for blood vessel segmentation, feature detection and description, and outlier elimination. | This method is superior to other learning-based methods, achieved the highest success rate and Dice coefficient, and has significant robustness in poor quality images. |
| Huang et al. [109] | Multimodal registration of medical images | An end-to-end network architecture composed of affine transformation and deformable transformation is proposed. | Double consistency constraints and a new loss function based on prior knowledge have been developed to achieve accurate and efficient multi-contrast MR image registration. |
| Jhan et al. [110] | Multimodal registration of computer vision images | A new N-SURF matching method for multi-spectral camera (MSCs) image registration and a general tool for image registration of various MSCs. | This method has good accuracy and can obtain more the number of correct matches (CMs) that are evenly distributed, which has the advantages of accuracy and efficiency. |
| Zhou et al. [111] | Multimodal registration of computer vision images | A potential generation model for cross-weather image alignment based on intensity constancy and image manifold characteristics. | Experimental results demonstrate that this approach can significantly outperform the state-of-the-art methods. |
| Image Pairs | Depth-Opti. | Opti-Opti. | IR-Opti. | Map-Opti. | Night-Day | SAR-Opti. | |
|---|---|---|---|---|---|---|---|
| Method | |||||||
| SIFT | 7/122 | 15/83 | 6/103 | 35/146 | 6/37 | / | |
| SURF | 42/830 | 81/1025 | 23/943 | 65/375 | / | 20/1297 | |
| SAR-SIFT | 4/43 | 25/127 | / | / | 4/20 | / | |
| PSO-SIFT | 4/137 | 12/113 | 7/64 | 16/124 | 5/49 | / | |
| RIFT | 258/1152 | 285/956 | 319/800 | 554/1351 | 238/958 | 596/1520 | |
| RIFT-LAF | 607/1152 | 496/956 | 283/800 | 410/1351 | 387/958 | 897/1520 | |
| HOPC | 89/219 | 8/186 | 128/230 | 174/498 | 153/202 | 286/328 | |
| CFOG | 98/258 | 213/956 | 135/319 | 193/554 | 168/238 | 303/596 | |
| Image Pairs | Depth-Opti. | Opti-Opti. | IR-Opti. | Map-Opti. | Night-Day | SAR-Opti. | |
|---|---|---|---|---|---|---|---|
| Method | |||||||
| SIFT | 0.44 | 0.52 | 0.49 | 0.58 | 0.22 | / | |
| SURF | 0.34 | 0.14 | 0.24 | 0.20 | / | 0.21 | |
| SAR-SIFT | 0.12 | 0.62 | / | / | 0.06 | / | |
| PSO-SIFT | 0.35 | 0.64 | 0.55 | 0.56 | 0.63 | / | |
| RIFT | 0.64 | 0.63 | 0.64 | 0.70 | 0.68 | 0.66 | |
| RIFT-LAF | 0.30 | 0.36 | 0.53 | 0.59 | 0.38 | 0.40 | |
| HOPC | / | / | / | / | / | / | |
| CFOG | / | / | / | / | / | / | |
| Image Pairs | Depth-Opti. | Opti-Opti. | IR-Opti. | Map-Opti. | Night-Day | SAR-Opti. | |
|---|---|---|---|---|---|---|---|
| Method | |||||||
| SIFT | 13.69 | 14.04 | 8.39 | 12.90 | 11.44 | / | |
| SURF | 2.69 | 2.24 | 2.15 | 1.69 | / | 2.55 | |
| SAR-SIFT | 15.02 | 12.59 | / | / | 11.66 | / | |
| PSO-SIFT | 12.91 | 12.86 | 9.17 | 10.28 | 9.34 | / | |
| RIFT | 10.93 | 9,31 | 8.32 | 13.04 | 9.63 | 11.03 | |
| RIFT-LAF | 11.04 | 9.41 | 8.65 | 13.25 | 9.87 | 11.31 | |
| HOPC | 61.65 | 61.50 | 40.24 | 55.60 | 62.69 | 62.99 | |
| CFOG | 10.93 | 4.29 | 1.30 | 3.95 | 2.73 | 2.47 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Leng, C.; Hong, Y.; Pei, Z.; Cheng, I.; Basu, A. Multimodal Remote Sensing Image Registration Methods and Advancements: A Survey. Remote Sens. 2021, 13, 5128. https://doi.org/10.3390/rs13245128
Zhang X, Leng C, Hong Y, Pei Z, Cheng I, Basu A. Multimodal Remote Sensing Image Registration Methods and Advancements: A Survey. Remote Sensing. 2021; 13(24):5128. https://doi.org/10.3390/rs13245128
Chicago/Turabian StyleZhang, Xinyue, Chengcai Leng, Yameng Hong, Zhao Pei, Irene Cheng, and Anup Basu. 2021. "Multimodal Remote Sensing Image Registration Methods and Advancements: A Survey" Remote Sensing 13, no. 24: 5128. https://doi.org/10.3390/rs13245128
APA StyleZhang, X., Leng, C., Hong, Y., Pei, Z., Cheng, I., & Basu, A. (2021). Multimodal Remote Sensing Image Registration Methods and Advancements: A Survey. Remote Sensing, 13(24), 5128. https://doi.org/10.3390/rs13245128









