GNSS-IR Measurements of Inter Annual Sea Level Variations in Thule, Greenland from 2008–2019
Abstract
:1. Introduction
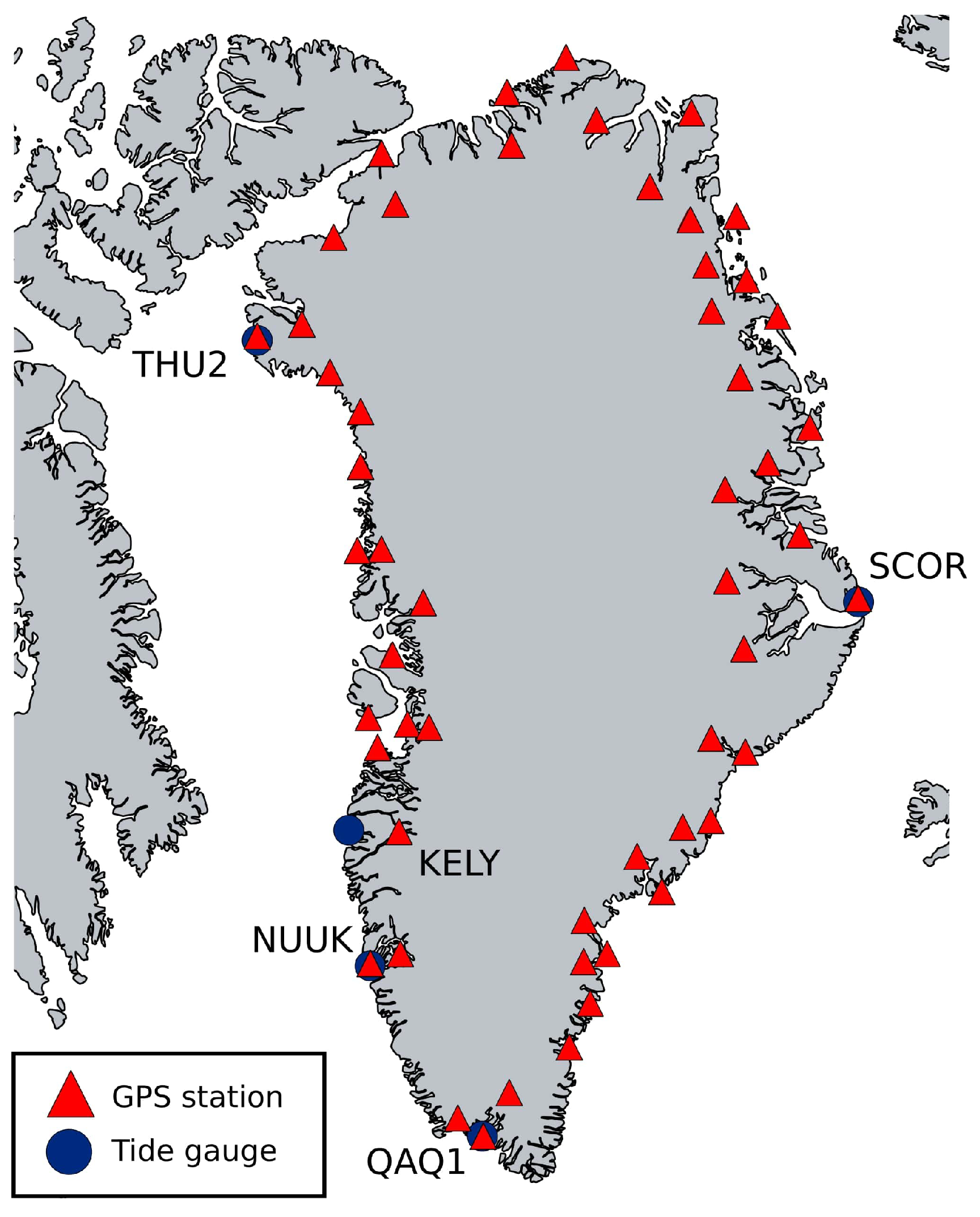
2. Materials and Methods
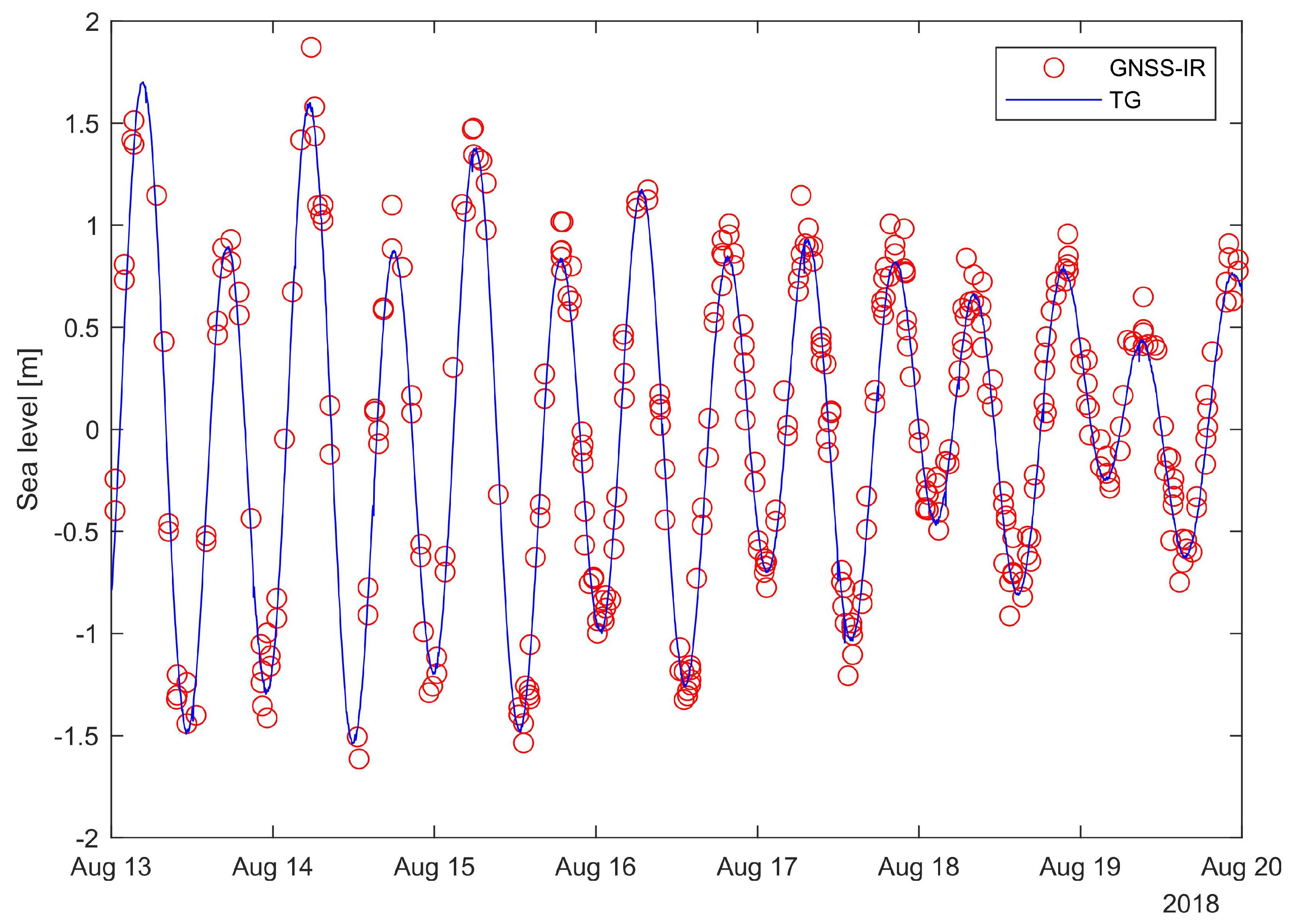
2.1. Sea Level Measurements
2.2. Sea Level Change Due to Reduced Gravity
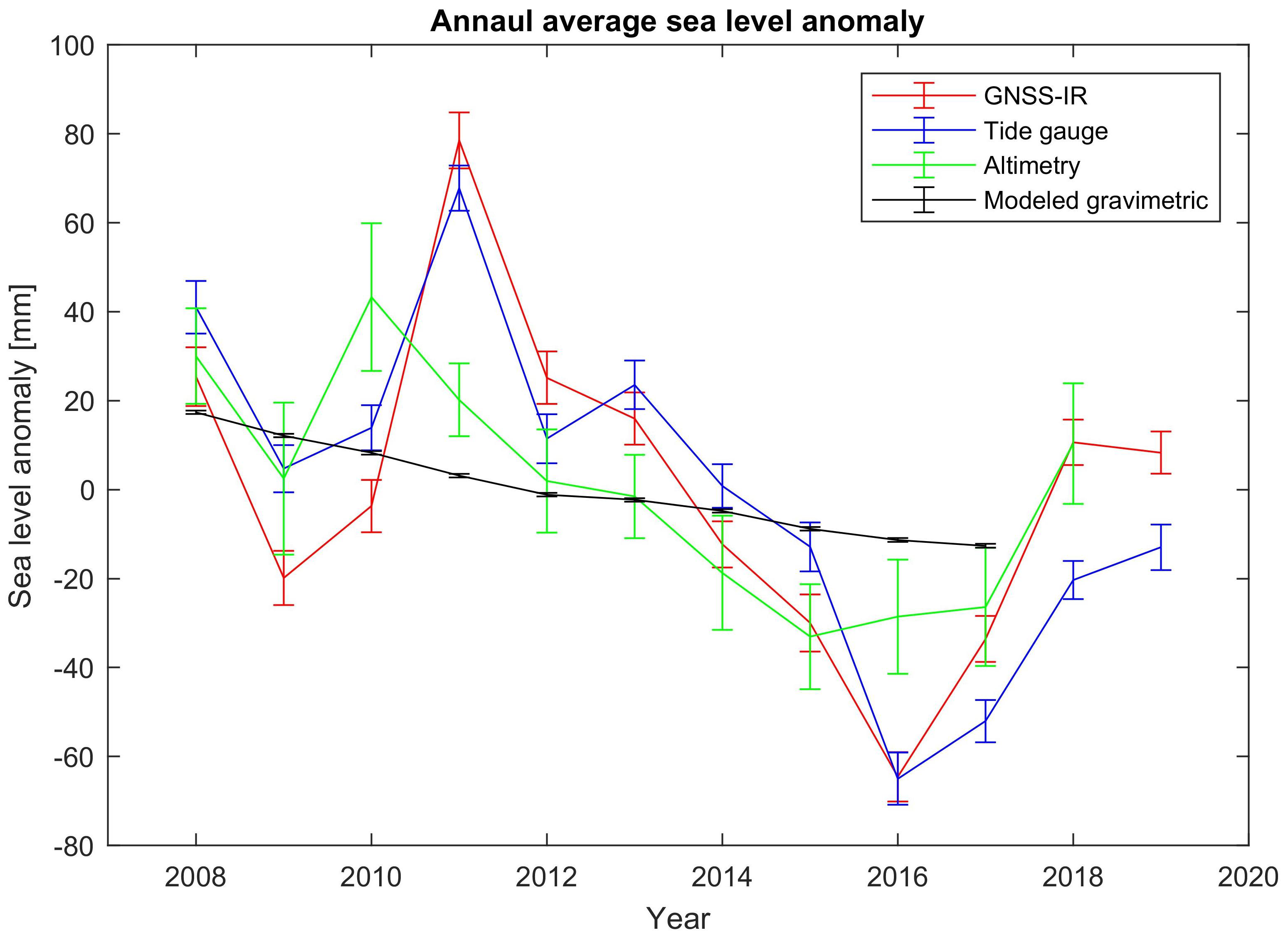
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Spada, G.; Galassi, G. New estimates of secular sea level rise from tide gauge data and GIA modelling. Geophys. J. Int. 2012, 191, 1067–1094. [Google Scholar] [CrossRef] [Green Version]
- Church, J.; White, N.; Coleman, R.; Lambeck, K.; Mitrovica, J. Estimates of the regional distribution of sea level rise over the 1950–2000 period. J. Clim. 2004, 17, 2609–2625. [Google Scholar] [CrossRef]
- Hsu, C.W.; Velicogna, I. Detection of sea level fingerprints derived from GRACE gravity data. Geophys. Res. Lett. 2017, 44, 8953–8961. [Google Scholar] [CrossRef]
- Woeppelmann, G.; Letetrel, C.; Santamaria, A.; Bouin, M.N.; Collilieux, X.; Altamimi, Z.; Williams, S.D.P.; Miguez, B.M. Rates of sea-level change over the past century in a geocentric reference frame. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Lofgren, J.S.; Haas, R.; Scherneck, H.G. Sea level time series and ocean tide analysis from multipath signals at five GPS sites in different parts of the world. J. Geodyn. 2014, 80, 66–80. [Google Scholar] [CrossRef] [Green Version]
- Larson, K.M.; Ray, R.D.; Williams, S.D.P. A 10-Year Comparison of Water Levels Measured with a Geodetic GPS Receiver versus a Conventional Tide Gauge. J. Atmos. Ocean. Technol. 2017, 34, 295–307. [Google Scholar] [CrossRef] [Green Version]
- Strandberg, J.; Hobiger, T.; Haas, R. Improving GNSS-R sea level determination through inverse modeling of SNR data. Radio Sci. 2016, 51, 1286–1296. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.K.; Park, J. Monitoring Sea Level Change in Arctic using GNSS-Reflectometry. In Proceedings of the 2019 International Technical Meeting of the Institute of Navigation, Reston, VA, USA, 28–31 January 2019; pp. 665–675. [Google Scholar] [CrossRef]
- Khan, S.A.; Sasgen, I.; Bevis, M.; van Dam, T.; Bamber, J.L.; Wahr, J.; Willis, M.; Kjaer, K.H.; Wouters, B.; Helm, V.; et al. Geodetic measurements reveal similarities between post-Last Glacial Maximum and present-day mass loss from the Greenland ice sheet. Sci. Adv. 2016, 2, e1600931. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bevis, M.; Wahr, J.; Khan, S.A.; Madsen, F.B.; Brown, A.; Willis, M.; Kendrick, E.; Knudsen, P.; Box, J.E.; van Dam, T.; et al. Bedrock displacements in Greenland manifest ice mass variations, climate cycles and climate change. Proc. Natl. Acad. Sci. USA 2012, 109, 11944–11948. [Google Scholar] [CrossRef] [Green Version]
- Tabibi, S.; Geremia-Nievinski, F.; Francis, O.; van Dam, T. Tidal analysis of GNSS reflectometry applied for coastal sea level sensing in Antarctica and Greenland. Remote Sens. Environ. 2020, 248, 111959. [Google Scholar] [CrossRef]
- Williams, S.D.P.; Bell, P.S.; McCann, D.L.; Cooke, R.; Sams, C. Demonstrating the Potential of Low-Cost GPS Units for the Remote Measurement of Tides and Water Levels Using Interferometric Reflectometry. J. Atmos. Ocean. Technol. 2020, 37, 1925–1935. Available online: https://journals.ametsoc.org/jtech/article-pdf/37/10/1925/5010618/jtechd200063.pdf (accessed on 1 December 2021). [CrossRef]
- Larson, K.M.; Ray, R.D.; Nievinski, F.G.; Freymueller, J.T. The Accidental Tide Gauge: A GPS Reflection Case Study From Kachemak Bay, Alaska. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1200–1204. [Google Scholar] [CrossRef] [Green Version]
- Williams, S.D.P.; Nievinski, F.G. Tropospheric delays in ground-based GNSS Multipath Reflectometry— Experimental evidence from coastal sites. J. Geophys. Res. Solid Earth 2017, 122, 2310–2327. [Google Scholar] [CrossRef] [Green Version]
- Rose, S.K.; Andersen, O.B.; Passaro, M.; Ludwigsen, C.A.; Schwatke, C. Arctic Ocean Sea Level Record from the Complete Radar Altimetry Era: 1991–2018. Remote Sens. 2019, 11, 1672. [Google Scholar] [CrossRef] [Green Version]
- Andersen, O. Shallow water tides in the northwest European shelf region from TOPEX/POSEIDON altimetry. J. Geophys. Res.-Ocean. 1999, 104, 7729–7741. [Google Scholar] [CrossRef]
- Khan, S.A.; Wahr, J.; Leuliette, E.; van Dam, T.; Larson, K.M.; Francis, O. Geodetic measurements of postglacial adjustments in Greenland. J. Geophys. Res.-Solid Earth 2008, 113. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Xiang, L.; Jia, L.; Jiang, L.; Wang, Z.; Hu, B.; Gao, P. Load Love numbers and Green’s functions for elastic Earth models PREM, iasp91, ak135, and modified models with refined crustal structure from Crust 2.0. Comput. Geosci. 2012, 49, 190–199. [Google Scholar] [CrossRef]
- Groh, A.; Horwath, M. The method of tailored sensitivity kernels for GRACE mass change estimates. Geophys. Res. Abstr. 2016, 18, EGU2016-12065. [Google Scholar]
- Krabill, W. IceBridge ATM L2 Icessn Elevation, Slope, and Roughness, [1994–2010]; National Snow and Ice Data Center: Boulder, CO, USA, 2011. [Google Scholar]
- Zwally, H.J.; Schutz, R.; Bentley, C.; Bufton, J.; Herring, T.; Minster, J.; Spinhirne, J.; Thomas, R. GLAS/ICESat L2 Antarctic and Greenland Ice Sheet Altimetry Data, Version 34; Indicate Subset Used; NASA National Snow and Ice Data Center: Boulder, CO, USA, 2014. [Google Scholar] [CrossRef]
- Helm, V.; Humbert, A.; Miller, H. Elevation and elevation change of Greenland and Antarctica derived from CryoSat-2. Cryosphere 2014, 8, 1539–1559. Available online: https://tc.copernicus.org/articles/8/1539/2014/tc-8-1539-2014.pdf (accessed on 1 December 2021). [CrossRef] [Green Version]
- Khan, S.A.; Kjaer, K.H.; Korsgaard, N.J.; Wahr, J.; Joughin, I.R.; Timm, L.H.; Bamber, J.L.; van den Broeke, M.R.; Stearns, L.A.; Hamilton, G.S.; et al. Recurring dynamically induced thinning during 1985 to 2010 on Upernavik Isstrom, West Greenland. J. Geophys. Res.-Earth Surf. 2013, 118, 111–121. [Google Scholar] [CrossRef] [Green Version]
- Marzeion, B.; Jarosch, A.H.; Hofer, M. Past and future sea-level change from the surface mass balance of glaciers. Cryosphere 2012, 6, 1295–1322. [Google Scholar] [CrossRef] [Green Version]
- RGI Consortium. Randolph Glacier Inventory—A Dataset of Global Glacier Outlines: Version 6.0. In Global Land Ice Measurements from Space; Technical Report; Digital Media: Denver, CO, USA, 2017. [Google Scholar] [CrossRef]
- Khan, S.A.; Kjaer, K.H.; Bevis, M.; Bamber, J.L.; Wahr, J.; Kjeldsen, K.K.; Bjork, A.A.; Korsgaard, N.J.; Stearns, L.A.; van den Broeke, M.R.; et al. Sustained mass loss of the northeast Greenland ice sheet triggered by regional warming. Nat. Clim. Chang. 2014, 4, 292–299. [Google Scholar] [CrossRef]
- Strandberg, J.; Hobiger, T.; Haas, R. Coastal Sea Ice Detection Using Ground-Based GNSS-R. IEEE Geosci. Remote. Sens. Lett. 2017, 14, 1552–1556. [Google Scholar] [CrossRef]
- Larson, K.M.; Lofgren, J.S.; Haas, R. Coastal sea level measurements using a single geodetic GPS receiver. Adv. Space Res. 2013, 51, 1301–1310. [Google Scholar] [CrossRef] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dahl-Jensen, T.S.; Andersen, O.B.; Williams, S.D.P.; Helm, V.; Khan, S.A. GNSS-IR Measurements of Inter Annual Sea Level Variations in Thule, Greenland from 2008–2019. Remote Sens. 2021, 13, 5077. https://doi.org/10.3390/rs13245077
Dahl-Jensen TS, Andersen OB, Williams SDP, Helm V, Khan SA. GNSS-IR Measurements of Inter Annual Sea Level Variations in Thule, Greenland from 2008–2019. Remote Sensing. 2021; 13(24):5077. https://doi.org/10.3390/rs13245077
Chicago/Turabian StyleDahl-Jensen, Trine S., Ole B. Andersen, Simon D. P. Williams, Veit Helm, and Shfaqat A. Khan. 2021. "GNSS-IR Measurements of Inter Annual Sea Level Variations in Thule, Greenland from 2008–2019" Remote Sensing 13, no. 24: 5077. https://doi.org/10.3390/rs13245077
APA StyleDahl-Jensen, T. S., Andersen, O. B., Williams, S. D. P., Helm, V., & Khan, S. A. (2021). GNSS-IR Measurements of Inter Annual Sea Level Variations in Thule, Greenland from 2008–2019. Remote Sensing, 13(24), 5077. https://doi.org/10.3390/rs13245077





