Spatial Representativeness of Gross Primary Productivity from Carbon Flux Sites in the Heihe River Basin, China
Abstract
:1. Introduction
2. Materials and Methods
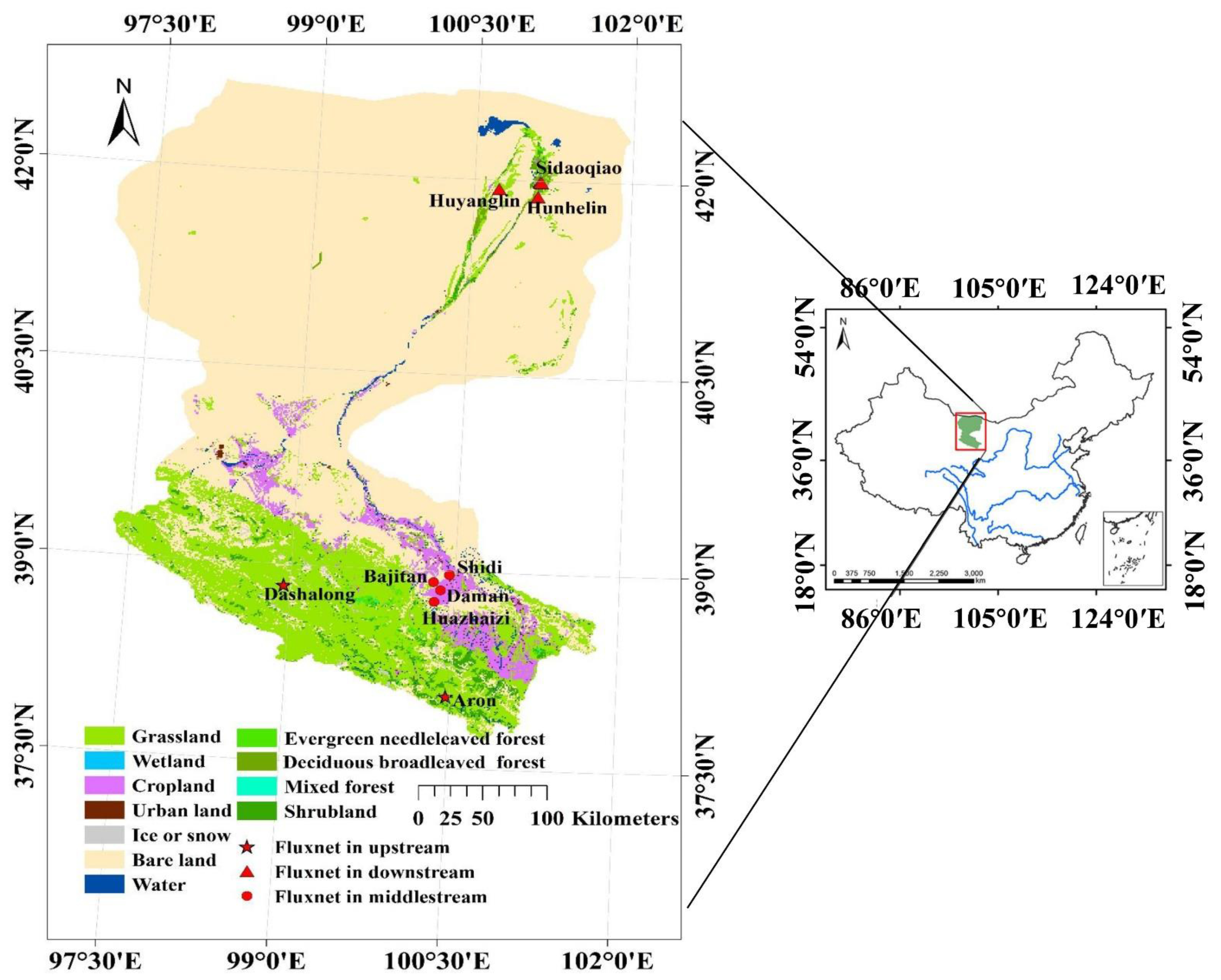
2.1. Study Area
2.2. Data and Data Processing
2.2.1. Carbon Flux Observed Data
2.2.2. Meteorological Data
2.2.3. Land Cover Data
2.2.4. Multi-Scale GPP Products
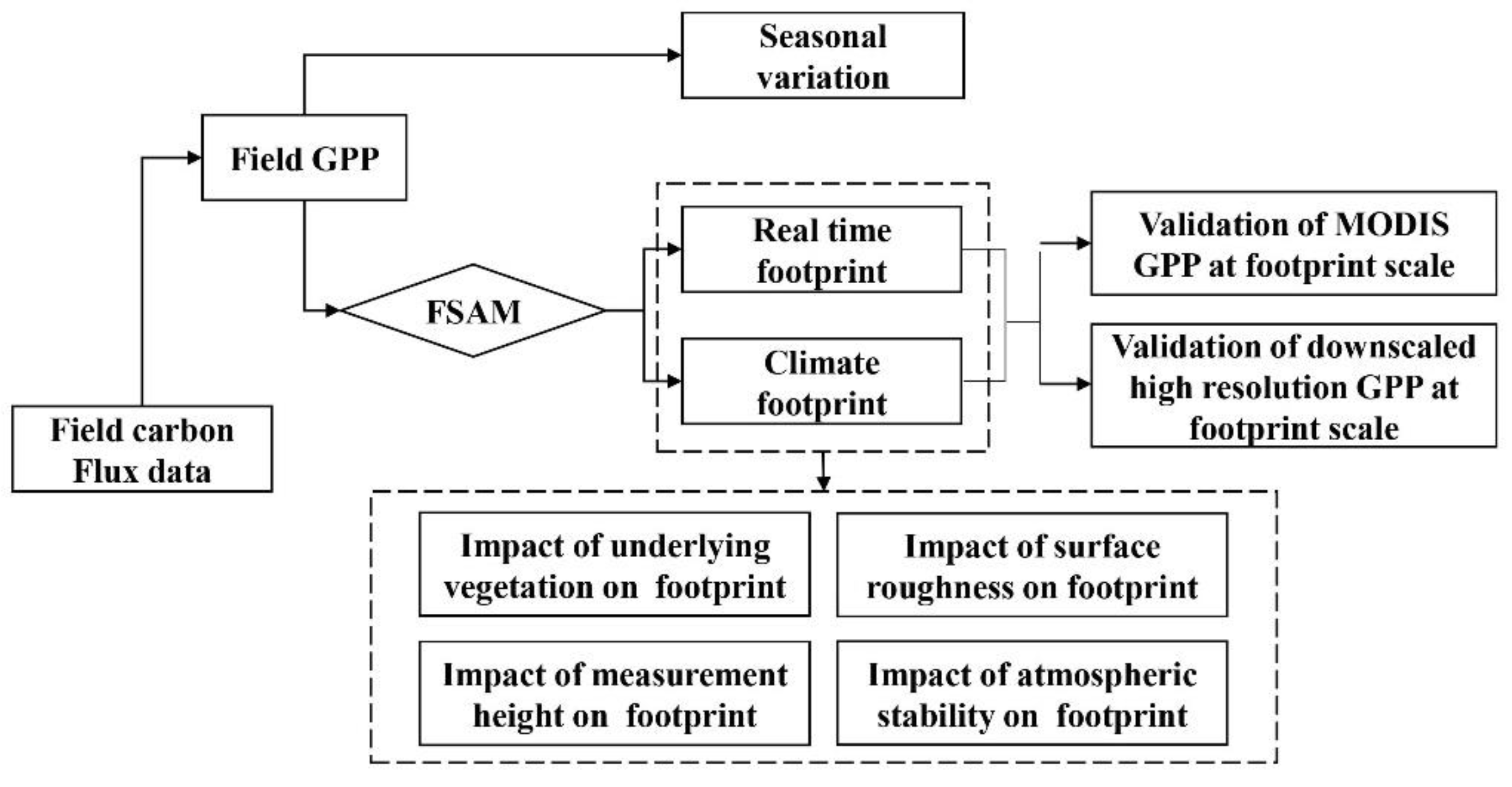
2.3. Methods
2.3.1. Real-Time Footprint of Field GPP
2.3.2. Climate Footprint of Field GPP
2.3.3. Validation of Multiple GPP Products at Footprint Scale
3. Results
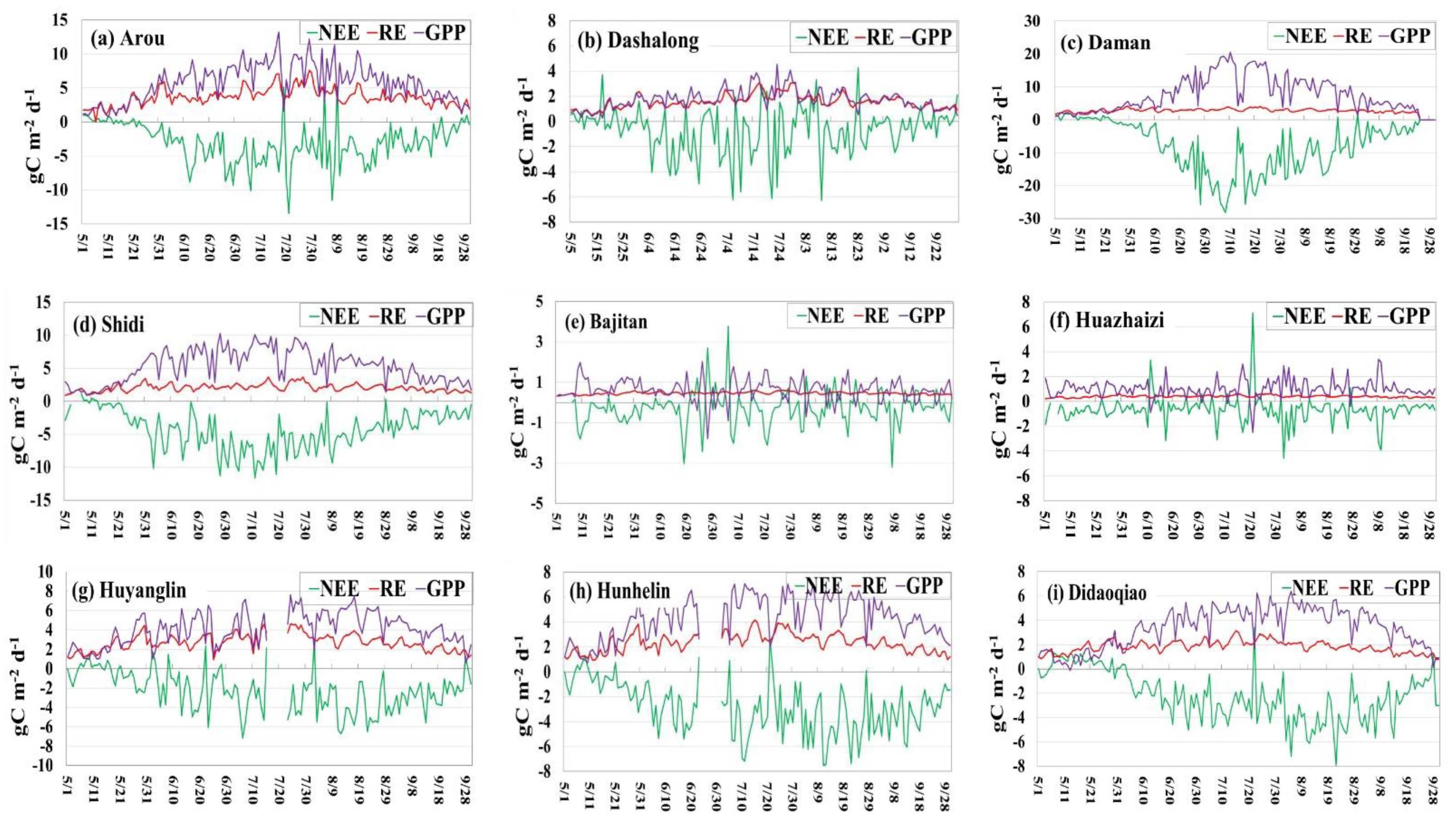
3.1. Seasonal Variation in Field GPP
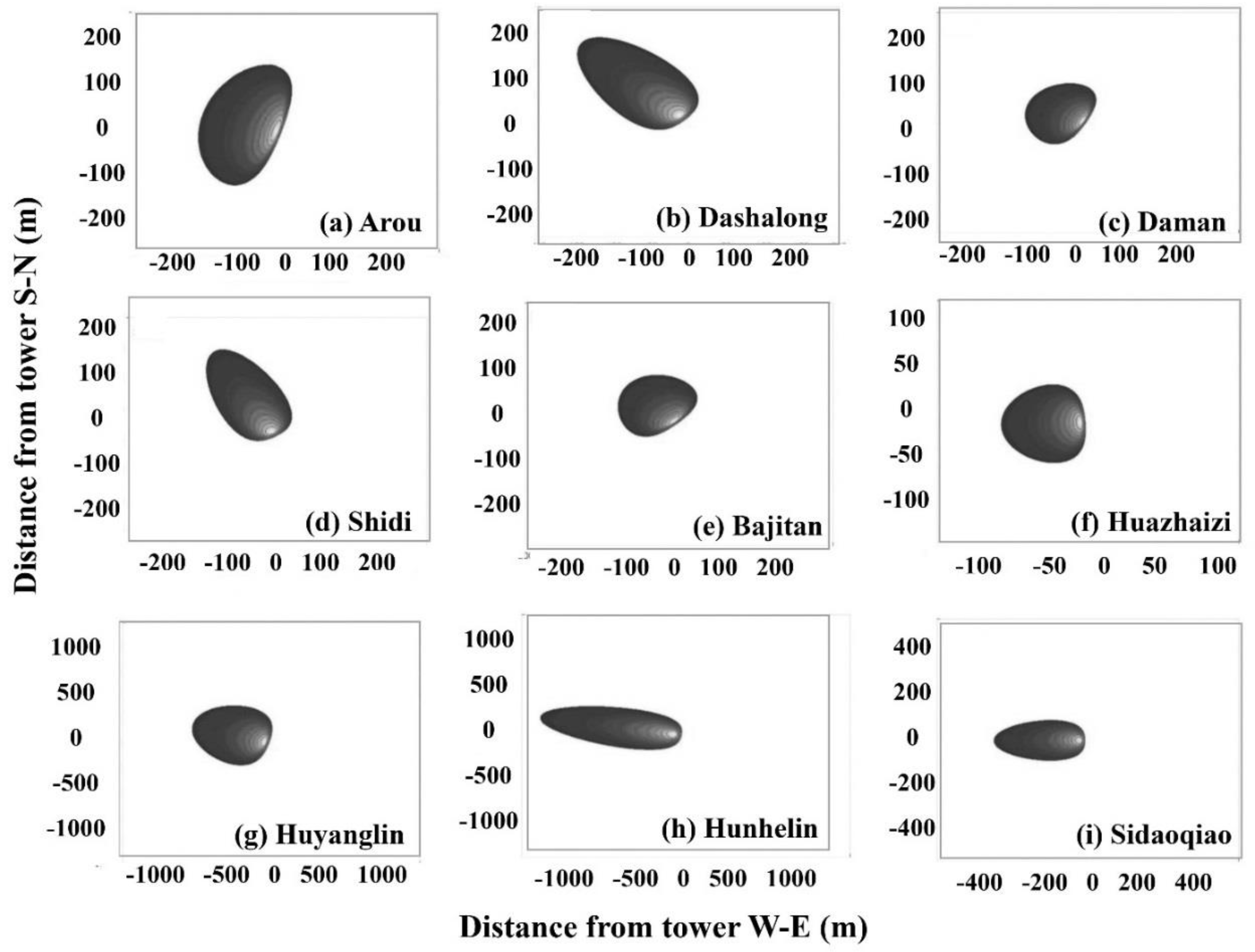
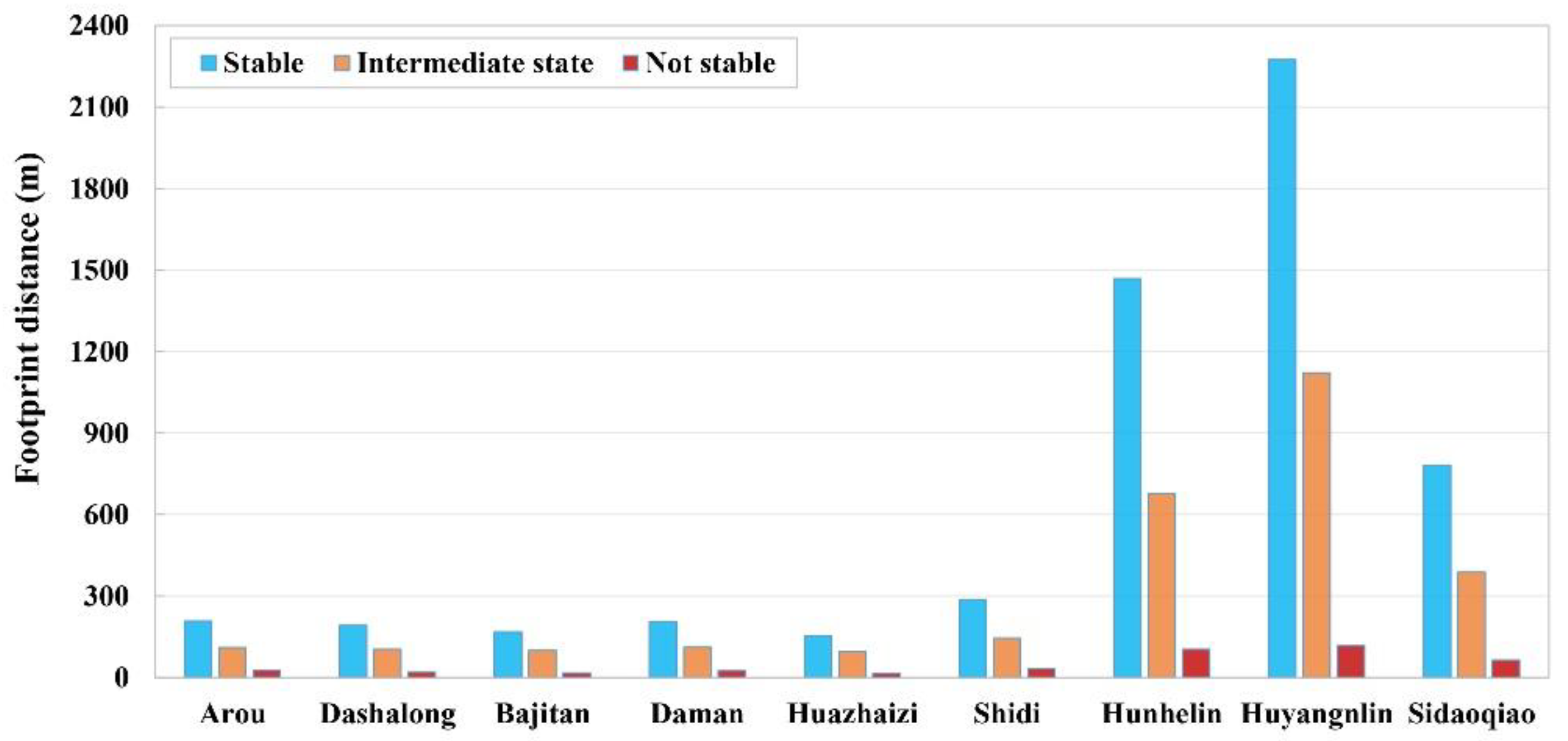
3.2. Footprint of Field GPP
3.2.1. Real-Time Footprint of Field GPP
3.2.2. Seasonal Variation in Climate Footprint of Field GPP
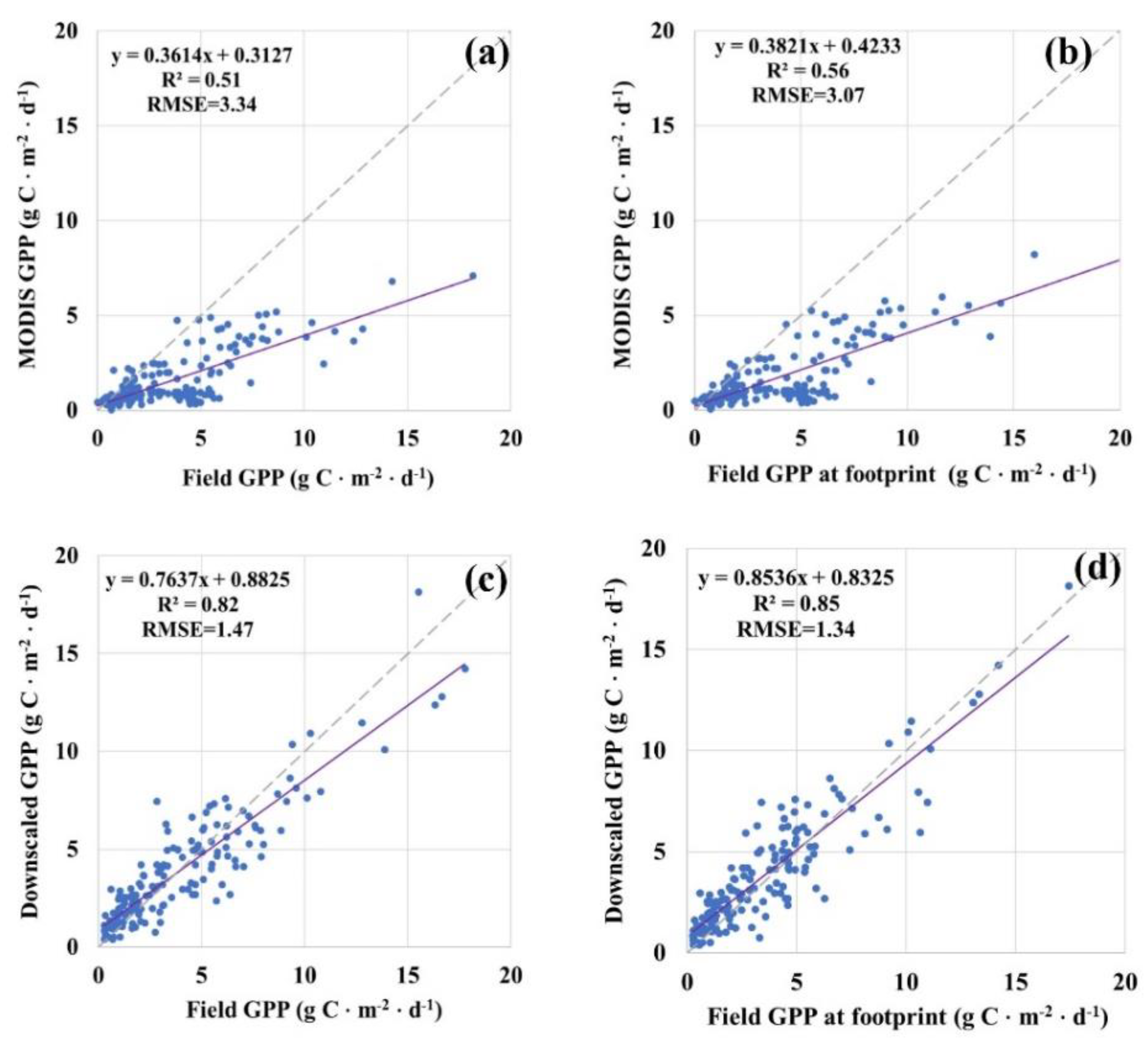
3.3. Comparison of Validation Multi-Scale GPP Products at Field Scale and at Footprint Scale
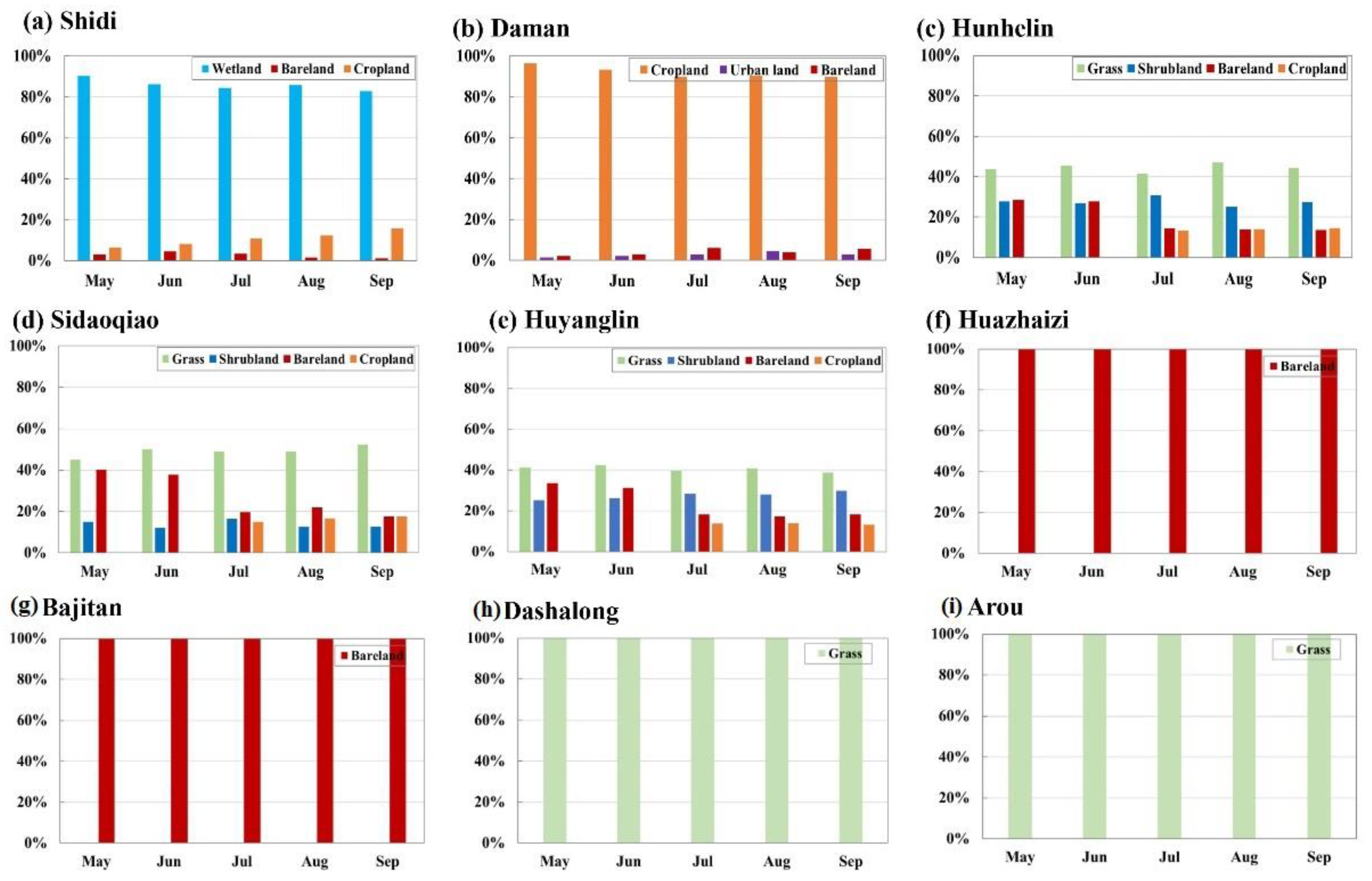
3.4. Land Cover Types in the Footprint
3.5. Main Impact Factors of the Field GPP Footprint
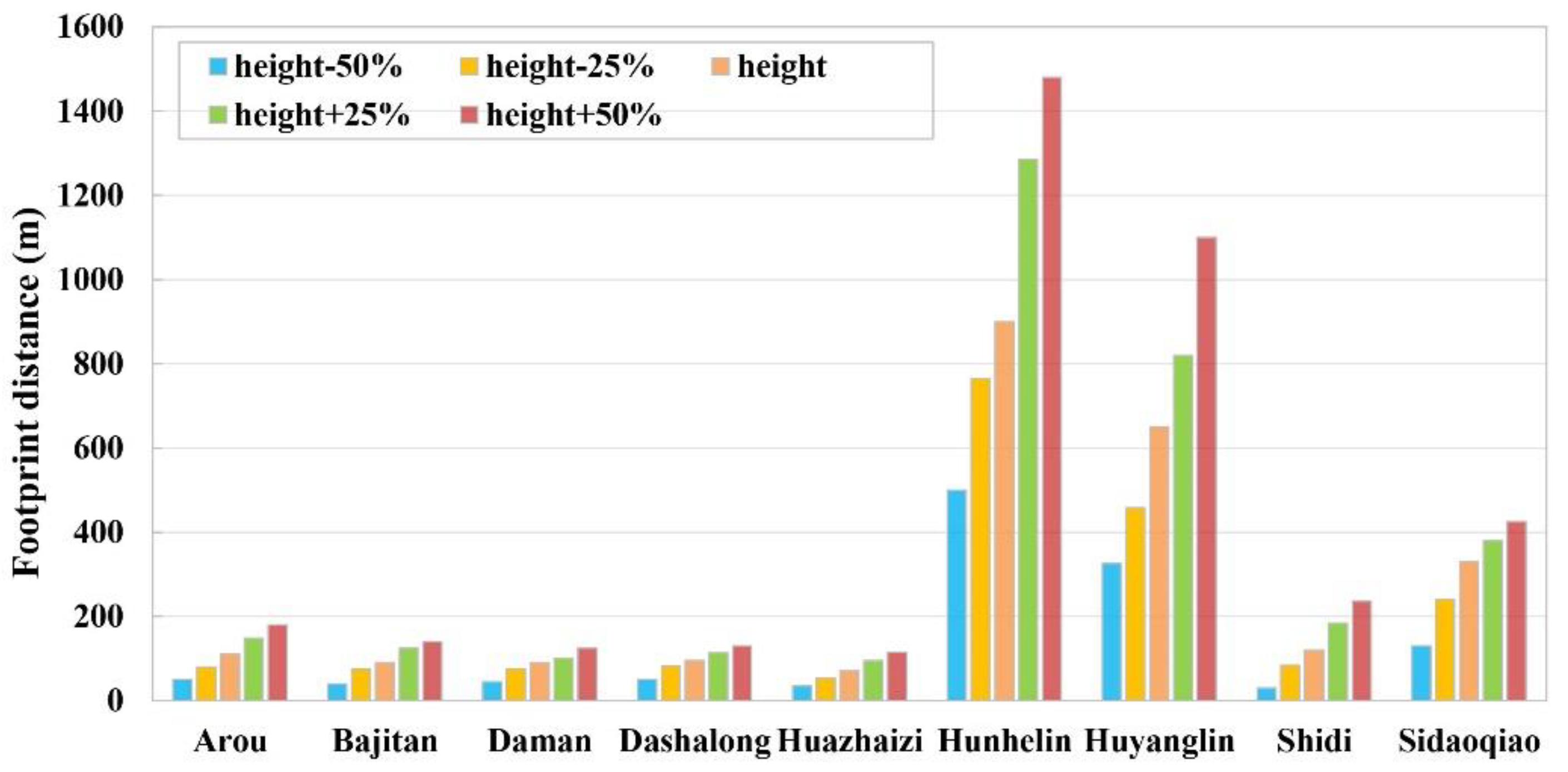
3.5.1. Influence of Measurement Height on Footprint of Field GPP
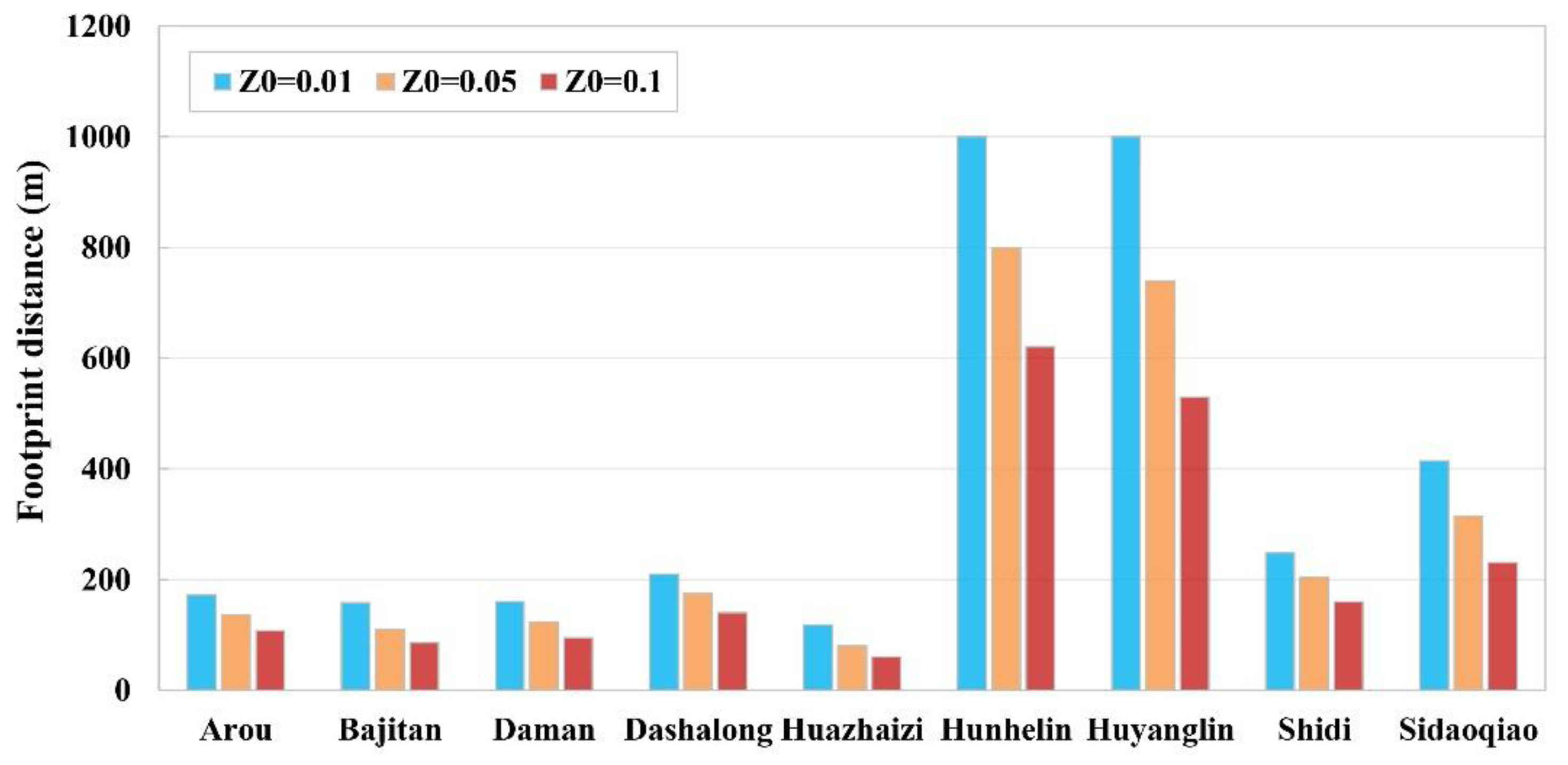
3.5.2. Influence of Surface Roughness on Footprint of Field GPP
3.5.3. Influence of Atmospheric Stability on Footprint of Field GPP
4. Discussion
4.1. Scale Mismatching between Satellte GPP and Ground Observed GPP
4.2. Limitations and Future Work
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Baldocchi, D.; Chu, H.; Reichstein, M. Inter-annual variability of net and gross ecosystem carbon fluxes: A review. Agric. For. Meteorol. 2018, 249, 520–533. [Google Scholar] [CrossRef] [Green Version]
- Biudes, M.S.; Vourlitis, G.L.; Velasque, M.C.S.; Machado, N.G.; de Morais Danelichen, V.H.; Pavão, V.M.; Arruda, P.H.Z.; de Souza Nogueira, J. Gross primary productivity of Brazilian Savanna (Cerrado) estimated by different remote sensing-based models. Agric. For. Meteorol. 2021, 307, 108456. [Google Scholar] [CrossRef]
- Yu, T.; Zhang, Q.; Sun, R. Comparison of machine learning methods to up-scale gross primary production. Remote Sens. 2021, 13, 2448. [Google Scholar] [CrossRef]
- Chu, H.; Luo, X.; Ouyang, Z.; Chan, W.; Dengel, S.; Biraud, S.C.; Torna, M.S.; Metzger, S.; Kumar, J.; Arain, M.A.; et al. Representativeness of eddy-covariance flux footprints for areas surrounding AmeriFlux sites. Agric. For. Meteorol. 2021, 301, 108350. [Google Scholar] [CrossRef]
- Durden, D.J.; Metzger, S.; Chu, H.; Collier, N.; Davis, K.J.; Desai, A.R.; Kumar, J.; Wieder, W.R.; Xu, M.; Hoffman, F.M. Automated integration of continentalscale observations in near-real time for simulation and analysis of biosphere–atmosphere interactions. In Driving Scientific and Engineering Discoveries through the Convergence of HPC, Big Data and AI; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Villarreal, S.; Guevara, M.; Alcaraz-Segura, D.; Brunsell, N.A.; Hayes, D.; Loescher, H.W.; Vargas, R. Ecosystem functional diversity and the representativeness of environmental networks across the conterminous United States. Agric. For. Meteorol. 2018, 262, 423–433. [Google Scholar] [CrossRef]
- Villarreal, S.; Vargas, R. Representativeness of FLUXNET sites across Latin America. J. Geophys. Res. Biogeosci. 2021, 126, e2020JG006090. [Google Scholar] [CrossRef]
- Pallandt, M.; Kumar, J.; Mauritz, M.; Schuur, E.; Virkkala, A.M.; Celis, G.; Hoffman, F.; Göckede, M. Representativeness assessment of the pan-Arctic eddy-covariance site network, and optimized future enhancements. Biogeosci. Discuss. 2021, 133, 1–42. [Google Scholar]
- Schmid, H.P. Experimental design for flux measurements: Matching scales of observations and fluxes. Agric. For. Meteorol. 1997, 87, 179–200. [Google Scholar] [CrossRef]
- Chen, B.; Zhang, H.; Coops, N.C.; Fu, D.; Worthy, D.E.J.; Xu, G.; Black, T.A. Assessing scalar concentration footprint climatology and land surface impacts on tall-tower CO2, concentration measurements in the boreal forest of central Saskatchewan, Canada. Theor. Appl. Climatol. 2014, 118, 115–132. [Google Scholar] [CrossRef]
- Schmid, H.P. Source areas for scalars and scalar fluxes. Bound. Layer Meteorol. 1994, 67, 293–318. [Google Scholar] [CrossRef]
- Schmid, H.P.; Lloyd, C.R. Spatial representativeness and the location bias of flux footprints over inhomogeneous areas. Agric. For. Meteorol. 1999, 93, 195–209. [Google Scholar] [CrossRef]
- Hsieh, C.I.; Katul, G.; Chi, T.W. An approximate analytical model for footprint estimation of scalar fluxes in thermally stratified atmospheric flows. Adv. Water Rerour. 2000, 23, 765–772. [Google Scholar] [CrossRef]
- Horst, T.W.; Weil, J. Footprint estimation for scalar flux measurements in the atmospheric surface layer. Bound. Layer Meteorol. 1992, 59, 279–296. [Google Scholar] [CrossRef]
- Järvi, L.; Rannik, Ü.; Kokkonen, T.V.; Kurppa, M.; Karppinen, A.; Kouznetsov, R.D.; Pekka, R.; Timo, V.; Wood, C.R. Uncertainty of eddy covariance flux measurements over an urban area based on two towers. Atmos. Meas. Tech. 2018, 11, 5421–5438. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Hwang, T.; Schaaf, C.L.; Kljun, N.; Munger, J.W. Seasonal variation of source contributions to eddy-covariance CO2 measurements in a mixed hardwood-conifer forest. Agric. For. Meteorol. 2018, 253, 71–83. [Google Scholar] [CrossRef]
- Rana, G.; Martinelli, N.; Famulari, D.; Pezzati, F.; Muschitiello, C.; Ferrara, R.M.M. Representativeness of carbon dioxide fluxes measured by eddy covariance over a mediterranean urban district with equipment setup restrictions. Atmosphere 2021, 12, 197. [Google Scholar] [CrossRef]
- Zhao, J.; Li, J.; Liu, Q.; Fan, W.; Zhong, B.; Wu, S.; Yang, L.; Zeng, Y.; Xu, B.; Yin, G. Leaf area index retrieval combining HJ1/CCD and Landsat8/OLI data in the Heihe River Basin, China. Remote Sens. 2015, 7, 6862–6885. [Google Scholar] [CrossRef] [Green Version]
- Fan, W.; Liu, Y.; Xu, X.; Chen, G.; Zhang, B. A new FAPAR analytical model based on the law of energy conservation: A case study in China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3945–3955. [Google Scholar] [CrossRef]
- Li, X.; Liu, S.M.; Xiao, Q.; Ma, M.G.; Jin, R.; Che, T.; Wang, W.Z.; Hu, X.L.; Xu, Z.W.; Wen, J.G.; et al. A multiscale dataset for understanding complex eco-hydrological processes in a heterogeneous oasis system. Sci. Data 2017, 4, 170083. [Google Scholar] [CrossRef] [Green Version]
- Pan, X.; Li, X.; Yang, K.; He, J.; Zhang, Y.; Han, X. Comparison of downscaled precipitation data over a mountainous watershed: A case study in the Heihe River Basin. J. Hydrometeorol. 2014, 15, 1560–1574. [Google Scholar] [CrossRef]
- Griebel, A.; Metzen, D.; Pendall, E.; Burba, G.; Metzger, S. Generating spatially robust carbon budgets from flux tower observations. Geophys. Res. Lett. 2020, 47, e2019GL085942. [Google Scholar] [CrossRef]
- Stoy, P.C.; Mauder, M.; Foken, T.; Marcolla, B.; Boegh, E.; Ibrom, A.; Arain, M.A.; Arneth, A.; Aurela, M.; Bernhofer, C.; et al. A data-driven analysis of energy balance closure across FLUXNET research sites: The role of landscape scale heterogeneity. Agric. For. Meteorol. 2013, 171–172, 137–152. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Tu, G.; Fu, C. Three-year variations of water, energy and CO2 fluxes of cropland and degraded grassland surfaces in a semi-arid area of Northeastern China. Adv. Atmos. Sci. 2008, 25, 1009–1020. [Google Scholar] [CrossRef] [Green Version]
- Cui, Y.; Song, L.; Fan, W. Generation of spatio-temporally continuous evapotranspiration and its components by coupling a two-source energy balance model and a deep neural network over the Heihe River Basin. J. Hydrol. 2021, 597, 126176. [Google Scholar] [CrossRef]
- Li, Y.; Huang, C.; Kustas, W.P.; Nieto, H.; Sun, L.; Hou, J. Evapotranspiration partitioning at field scales using TSEB and multi-satellite data fusion in the middle reaches of Heihe River Basin, Northwest China. Remote Sens. 2020, 12, 3223. [Google Scholar] [CrossRef]
- Gao, N.N.; Li, F.; Zeng, H.; Zheng, Y.R. The impact of human activities, natural factors and climate time-lag effects over 33 years in Heihe River Basin, China. Appl. Ecol. Environ. Res. 2021, 19, 1589–1606. [Google Scholar] [CrossRef]
- Liu, Q.; Niu, J.; Sivakumar, B.; Ding, R.; Li, S. Accessing future crop yield and crop water productivity over the Heihe River basin in northwest China under a changing climate. Geosci. Lett. 2021, 8, 2. [Google Scholar] [CrossRef]
- Li, X.; Cheng, G.; Liu, S.; Xiao, Q.; Ma, M.; Jin, R.; Che, T.; Liu, Q.; Wang, W.; Qi, Y.; et al. Heihe watershed allied telemetry experimental research (hiwater): Scientific objectives and experimental design. Bull. Am. Meteorol. Soc. 2013, 94, 1145–1160. [Google Scholar] [CrossRef]
- Liu, S.M.; Xu, Z.W.; Wang, W.; Jia, Z.Z.; Zhu, M.J.; Bai, J.; Wang, J.M. A comparison of eddy-covariance and large aper-ture scintillometer measurements with respect to the energy balance closure problem. Hydrol. Earth Syst. Sci. 2011, 15, 1291–1306. [Google Scholar] [CrossRef] [Green Version]
- Xu, Z.; Liu, S.; Li, X.; Shi, S.; Wang, J.; Zhu, Z.; Xu, T.; Wang, W.; Ma, M. Intercomparison of surface energy flux measurement systems used during the HiWATER-MUSOEXE. J. Geophys. Res. 2013, 118, 13140–13157. [Google Scholar] [CrossRef]
- Wilczak, J.M.; Oncley, S.P.; Stage, S.A. Sonic anemometer tilt correction algorithms. Bound. Layer Meteorol. 2001, 99, 127–150. [Google Scholar] [CrossRef]
- Liu, S.; Xu, Z.; Zhu, Z.; Jia, Z.; Zhu, M. Measurements of evapotranspiration from eddy-covariance systems and large aperture scintillometers in the Hai River Basin, China. J. Hydrol. 2013, 487, 24–38. [Google Scholar] [CrossRef]
- Papale, D.; Reichstein, M.; Aubinet, M.; Canfora, E.; Bernhofer, C.; Kutsch, W.; Longdoz, B.; Rambal, S.; Valentini, R.; Vesala, T.; et al. Towards a standardized processing of Net Ecosystem Exchange measured with eddy covariance technique: Algo-rithms and uncertainty estimation. Biogeosciences 2006, 3, 571–583. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Z.; Sun, X.; Wen, X.; Zhou, Y.; Tian, J.; Yuan, G. Study on the processing method of nighttime CO2 eddy covariance flux data in ChinaFLUX. Sci. China Ser. D 2006, 49, 36–46. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, R.; Xu, Z.; Qiao, C.; Jiang, G. Diurnal and seasonal variations in carbon dioxide exchange in ecosystems in the Zhangye oasis area, Northwest China. PLoS ONE 2015, 10, e0120660. [Google Scholar]
- Coops, N.C.; Black, T.A.; Jassal, R.P.S.; Trofymow, J.T.; Morgenstern, K. Comparison of MODIS, eddy covariance deter-mined and physiologically modelled gross primary production (GPP) in a Douglas-fir forest stand. Remote Sens. Environ. 2007, 107, 385–401. [Google Scholar] [CrossRef]
- Wang, H.; Saigusa, N.; Yamamoto, S.; Kondo, H.; Hirano, T.; Toriyama, A.; Fujinuma, Y. Net ecosystem CO2 exchange over a larch forest in Hokkaido, Japan. Atmos. Environ. 2004, 38, 7021–7032. [Google Scholar] [CrossRef]
- Landuse/Landcover Data of the Heihe River Basin. Available online: https://westdc.westgis.ac.cn (accessed on 5 October 2021).
- Zhong, B.; Yang, A.; Nie, A.; Yao, Y.; Zhang, H.; Wu, S.; Liu, Q. Finer resolution land-cover mapping using multiple classifiers and multisource remotely sensed data in the heihe river basin. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4973–4992. [Google Scholar] [CrossRef]
- Zhong, B.; Ma, P.; Nie, A.H.; Yang, A.X.; Yao, Y.J.; Lv, W.B.; Zhang, H.; Liu, Q.H. Land cover mapping using time series HJ-1/CCD data. Sci. China Earth Sci. 2014, 57, 1790–1799. [Google Scholar] [CrossRef]
- Heinsch, F.A.; Reeves, M.; Bowker, C.F. User’s Guide, GPP and NPP (MOD 17A2/A3) Products, NASA MODIS Land Algorithm. Available online: https://www.researchgate.net/publication/242118371_User\T1\textquoterights_guide_GPP_and_NPP_MOD17A2A3_products_NASA_MODIS_land_algorithm (accessed on 5 October 2021).
- Yu, T.; Sun, R.; Xiao, Z.; Zhang, Q.; Wang, J.; Liu, G. Generation of high resolution vegetation productivity from a downscaling method. Remote Sens. 2018, 10, 1748. [Google Scholar] [CrossRef] [Green Version]
- Schmid, H.P. Footprint modeling for vegetation atmosphere exchange studies: A review and perspective. Agric. For. Meteorol. 2002, 113, 159–183. [Google Scholar] [CrossRef]
- Kljun, N.; Kastner-Klein, P.; Fedorovich, E.; Rotach, M.W. Evaluation of Lagrangian footprint model using data from wind tunnel convective boundary layer. Agric. For. Meteorol. 2004, 127, 189–201. [Google Scholar] [CrossRef]
- Kljun, N.; Calanca, P.; Rotach, M.W.; Schmid, H.P. A simple two-dimensional parameterisation for Flux Footprint Predic-tion (FFP). Geosci. Model Dev. 2015, 8, 3695–3713. [Google Scholar] [CrossRef] [Green Version]
- He, H.; Zhang, L.; Gao, Y.; Ren, X.; Zhang, L.; Yu, G.; Wang, S. Regional representativeness assessment and improvement of eddy flux observations in China. Sci. Total Environ. 2015, 502, 688–698. [Google Scholar] [CrossRef]
- Yu, G.; Ren, W.; Chen, Z.; Zhang, L.; Wang, Q.; Wen, X.; He, N.; Zhang, L.; Fang, H.; Zhu, X.; et al. Construction and progress of Chinese terrestrial ecosystem carbon, nitrogen and water fluxes coordinated observation. J. Geogr. Sci. 2016, 26, 803–826. [Google Scholar] [CrossRef] [Green Version]
- Cui, T.; Wang, Y.; Sun, R.; Qiao, C.; Fan, W.; Jiang, G.; Hao, L.; Zhang, L. Estimating vegetation primary production in the Heihe River Basin of China with multi-source and multi-scale data. PLoS ONE 2016, 11, e0153971. [Google Scholar] [CrossRef] [Green Version]
- Turner, D.P.; Ollinger, S.; Smith, M.L.; Krankina, O.; Gregory, M. Scaling net primary production to a MODIS footprint in support of Earth observing system product validation. Int. J. Remote Sens. 2004, 25, 1961–1979. [Google Scholar] [CrossRef]
- Ramoelo, A.; Majozi, N.; Mathieu, R.; Jovanovic, N.; Nickless, A.; Dzikiti, S. Validation of global evapotranspiration product (MOD16) using flux tower data in the African savanna, South Africa. Remote Sens. 2014, 6, 7406–7423. [Google Scholar] [CrossRef] [Green Version]
- Battles, J.J.; Robards, T.; Das, A.; Waring, K.; Gilless, J.K.; Biging, G.; Schurr, F. Climate change impacts on forest growth and tree mortality: A data-driven modeling study in the mixedconifer forest of the Sierra Nevada, California. Clim. Chang. 2008, 87, 193–213. [Google Scholar] [CrossRef]
- Foley, J.A.; DeFries, R.; Asner, G.P.; Barford, C.; Bonan, G.; Carpenter, S.R.; Chapin, F.S.; Coe, M.T.; Daily, G.C.; Gibbs, H.K.; et al. Global Consequences of Land Use. Science 2005, 309, 570–574. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chu, H.; Baldocchi, D.D.; Poindexter, C.; Abraha, M.; Desai, A.R.; Bohrer, G.; Arain, M.A.; Griffis, T.; Blanken, P.D.; O’Halloran, T.H.; et al. Temporal dynamics of aerodynamic canopy height derived from eddy covariance momentum flux data across North American Flux Networks. Geophys. Res. Lett. 2018, 45, 9275–9287. [Google Scholar] [CrossRef]
- Lees, K.J.; Khomik, M.; Quaife, T.; Clark, J.M.; Hill, T.; Klein, D.; Ritson, J.; Artz, R.R. Assessing the reliability of peatland GPP measurements by remote sensing: From plot to landscape scale. Sci. Total Environ. 2021, 766, 142613. [Google Scholar] [CrossRef] [PubMed]
- Xiao, J.; Chevallier, F.; Gomez, C.; Guanter, L.; Hicke, J.A.; Huete, A.R.; Ichii, K.; Ni, W.; Pang, Y.; Rahman, A.F.; et al. Remote sensing of the terrestrial carbon cycle: A review of advances over 50 years. Remote Sens. Environ. 2019, 233, 111383. [Google Scholar] [CrossRef]
- Duan, Z.; Yang, Y.; Zhou, S.; Gao, Z.; Zong, L.; Fan, S.; Yin, J. Estimating gross primary productivity (GPP) over rice–wheat-rotation croplands by using the random forest model and eddy covariance measurements: Upscaling and comparison with the MODIS product. Remote Sens. 2021, 13, 4229. [Google Scholar] [CrossRef]
- Huang, Y.; Nicholson, D.; Huang, B.; Cassar, N. Global estimates of marine gross primary production based on machine learning upscaling of field observations. Glob. Biogeochem. Cycles 2021, 35, e2020GB006718. [Google Scholar] [CrossRef]
- Virkkala, A.M.; Aalto, J.; Rogers, B.M.; Tagesson, T.; Treat, C.C.; Natali, S.M.; Watts, J.D.; Potter, S.; Lehtonen, A.; Mauritz, M.; et al. Statistical upscaling of ecosystem CO2 fluxes across the terrestrial tundra and boreal domain: Regional patterns and uncertainties. Glob. Chang. Biol. 2021, 27, 4040–4059. [Google Scholar] [CrossRef]
- Kormann, R.; Meixner, F. An analytical footprint model for non-neutral stratification. Bound. Layer Meteorol. 2001, 99, 207–224. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, T.; Zhang, Q.; Sun, R. Spatial Representativeness of Gross Primary Productivity from Carbon Flux Sites in the Heihe River Basin, China. Remote Sens. 2021, 13, 5016. https://doi.org/10.3390/rs13245016
Yu T, Zhang Q, Sun R. Spatial Representativeness of Gross Primary Productivity from Carbon Flux Sites in the Heihe River Basin, China. Remote Sensing. 2021; 13(24):5016. https://doi.org/10.3390/rs13245016
Chicago/Turabian StyleYu, Tao, Qiang Zhang, and Rui Sun. 2021. "Spatial Representativeness of Gross Primary Productivity from Carbon Flux Sites in the Heihe River Basin, China" Remote Sensing 13, no. 24: 5016. https://doi.org/10.3390/rs13245016
APA StyleYu, T., Zhang, Q., & Sun, R. (2021). Spatial Representativeness of Gross Primary Productivity from Carbon Flux Sites in the Heihe River Basin, China. Remote Sensing, 13(24), 5016. https://doi.org/10.3390/rs13245016






