Hybrids of Support Vector Regression with Grey Wolf Optimizer and Firefly Algorithm for Spatial Prediction of Landslide Susceptibility
Abstract
:1. Introduction
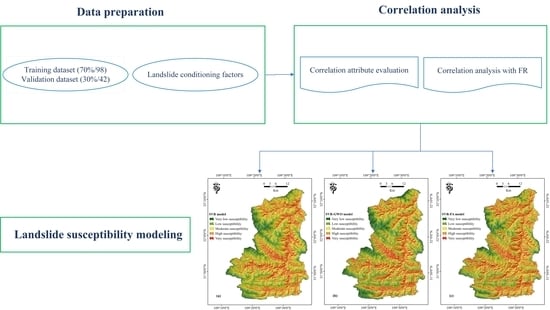
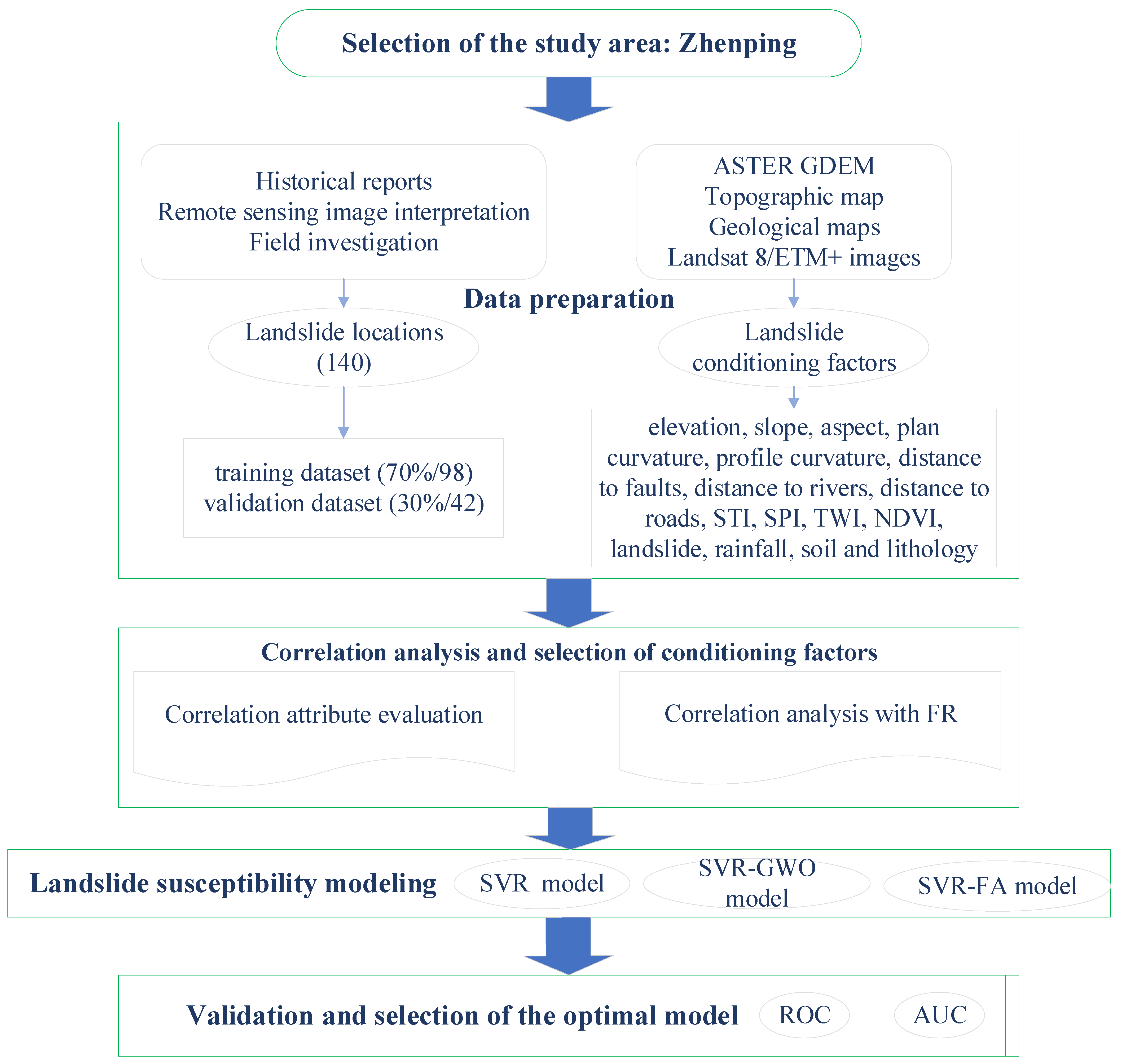
2. Study Area and Data Preparation
3. Methodology
3.1. Frequency Ratio (FR)
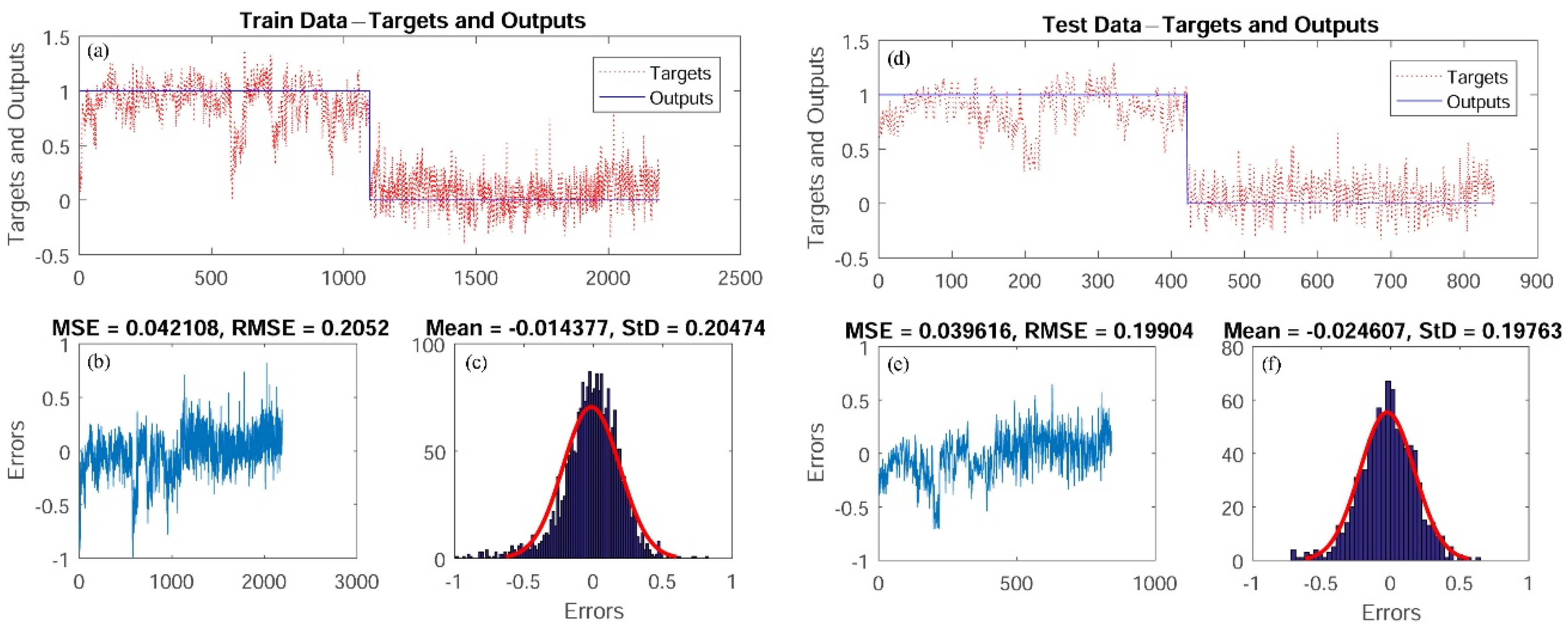
3.2. Support Vector Regression (SVR)
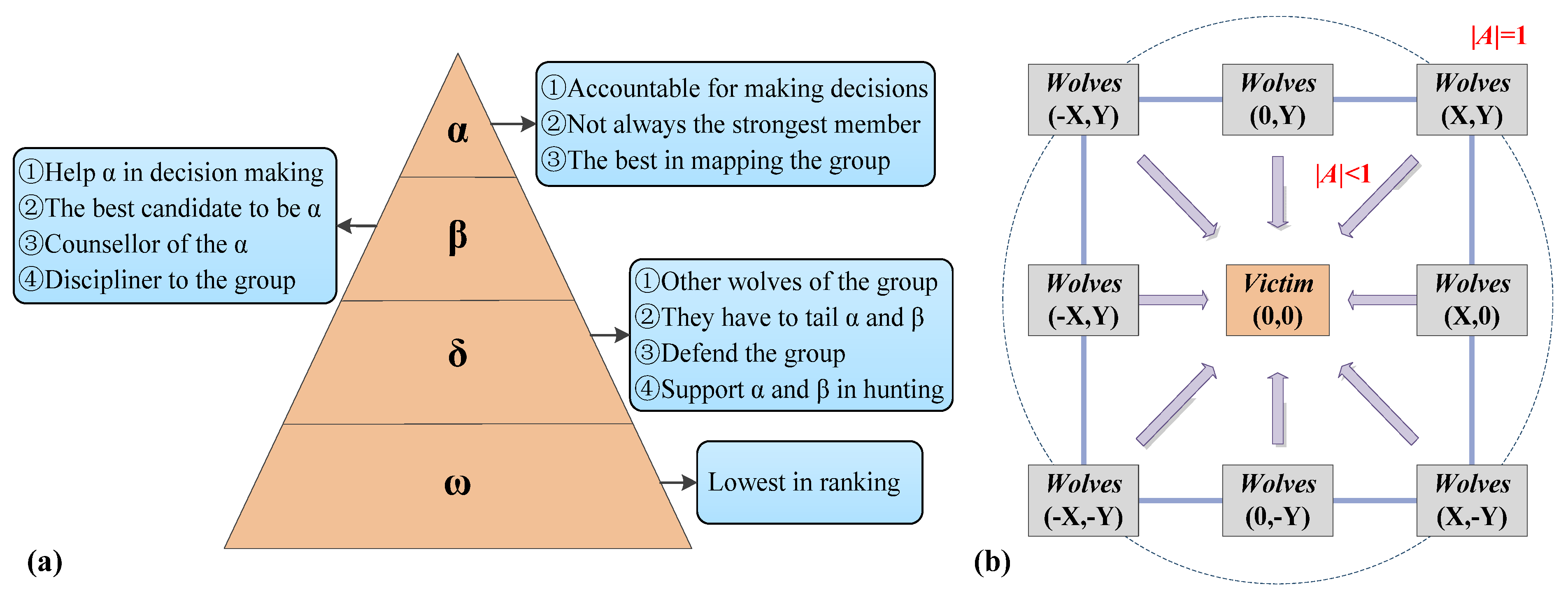
3.3. Grey Wolf Optimizer (GWO)
3.4. Firefly Algorithm (FA)
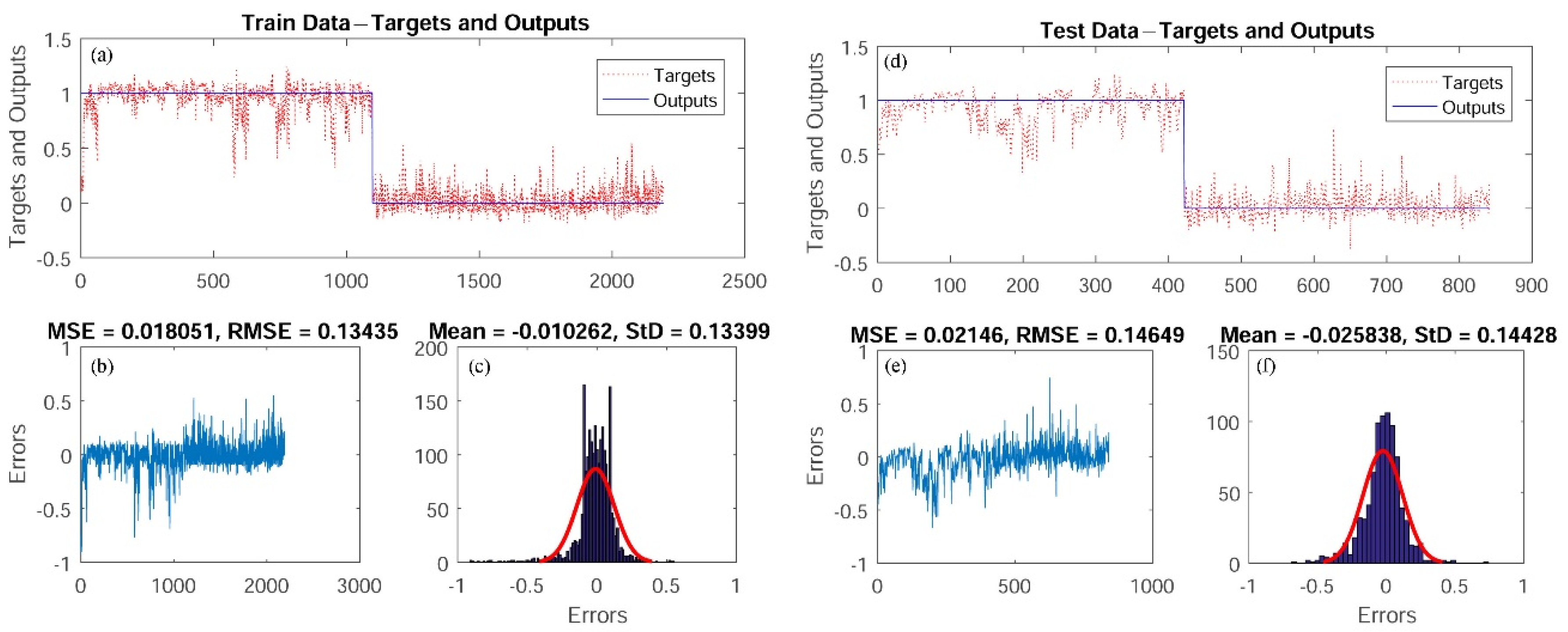
4. Results
4.1. Correlation Analysis and Selection of Conditioning Factors
4.2. Application of Hybrid Models
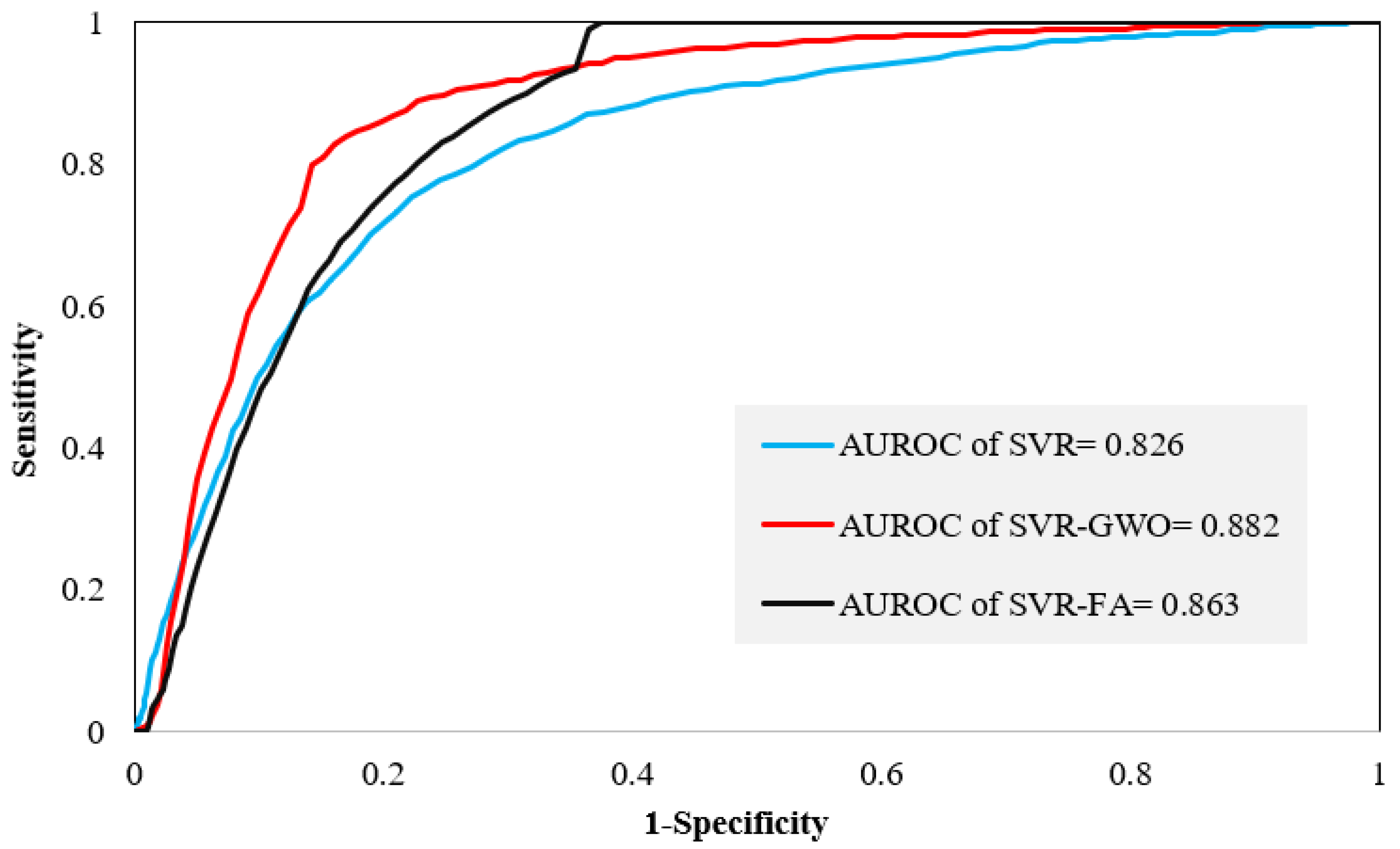
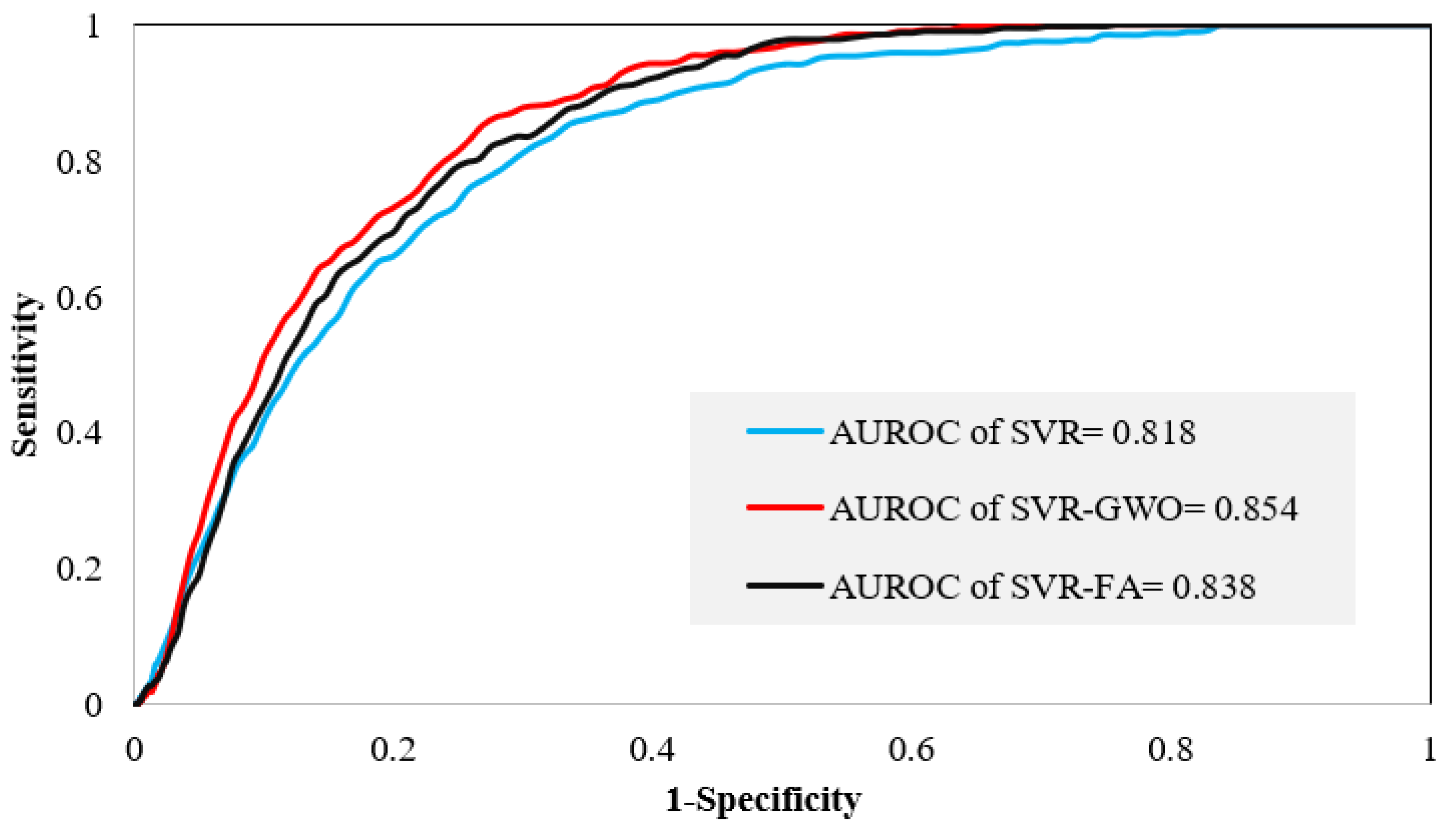
4.3. Validation and Comparison of Models
4.4. Generation of Landslide Susceptibility Maps
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pham, B.T.; Tien Bui, D.; Prakash, I. Bagging based Support Vector Machines for spatial prediction of landslides. Environ. Earth Sci. 2018, 77, 146. [Google Scholar] [CrossRef]
- Varnes, D.J. Landslide Hazard Zonation: A Review of Principles and Practice; TRID: Jacksonville, FL, USA, 1984. [Google Scholar]
- Zhou, C.; Yin, K.; Cao, Y.; Ahmed, B.; Li, Y.; Catani, F.; Pourghasemi, H.R. Landslide susceptibility modeling applying machine learning methods: A case study from Longju in the Three Gorges Reservoir area, China. Comput. Geosci. 2018, 112, 23–37. [Google Scholar] [CrossRef] [Green Version]
- Mahalingam, R.; Olsen, M.J. Evaluation of the influence of source and spatial resolution of DEMs on derivative products used in landslide mapping. Geomat. Nat. Hazards Risk 2015, 7, 1835–1855. [Google Scholar] [CrossRef]
- Pham, B.T.; Tien Bui, D.; Pourghasemi, H.R.; Indra, P.; Dholakia, M.B. Landslide susceptibility assesssment in the Uttarakhand area (India) using GIS: A comparison study of prediction capability of naïve bayes, multilayer perceptron neural networks, and functional trees methods. Theor. Appl. Climatol. 2017, 128, 255–273. [Google Scholar] [CrossRef]
- Pham, B.T.; Nguyen, V.-T.; Ngo, V.-L.; Trinh, P.T.; Ngo, H.T.T.; Tien Bui, D. A novel hybrid model of rotation forest based functional trees for landslide susceptibility mapping: A case study at kon tum province, vietnam. In Advances and Applications in Geospatial Technology and Earth Resources; Tien Bui, D., Ngoc Do, A., Bui, H.-B., Hoang, N.-D., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; pp. 186–201. [Google Scholar]
- Ercanoglu, M.; Gokceoglu, C.; Van Asch, T.W.J. Landslide Susceptibility Zoning North of Yenice (NW Turkey) by Multivariate Statistical Techniques. Nat. Hazards 2004, 32, 1–23. [Google Scholar] [CrossRef]
- Rasyid, A.; Bhandary, N.; Yatabe, R. Performance of frequency ratio and logistic regression model in creating GIS based landslides susceptibility map at Lompobattang Mountain, Indonesia. Geoenviron. Disasters 2016, 3, 19. [Google Scholar] [CrossRef] [Green Version]
- Bălteanu, D.; Micu, M.; Jurchescu, M.; Malet, J.-P.; Sima, M.; Kucsicsa, G.; Dumitrică, C.; Petrea, D.; Mărgărint, M.C.; Bilaşco, Ş.; et al. National-scale landslide susceptibility map of Romania in a European methodological framework. Geomorphology 2020, 371, 107432. [Google Scholar] [CrossRef]
- Aditian, A.; Kubota, T.; Shinohara, Y. Comparison of GIS-based landslide susceptibility models using frequency ratio, logistic regression, and artificial neural network in a tertiary region of Ambon, Indonesia. Geomorphology 2018, 318, 101–111. [Google Scholar] [CrossRef]
- Clerici, A.; Perego, S.; Tellini, C.; Vescovi, P. A procedure for landslide susceptibility zonation by the conditional analysis method. Geomorphology 2002, 48, 349–364. [Google Scholar] [CrossRef]
- Süzen, M.L.; Doyuran, V. Data driven bivariate landslide susceptibility assessment using geographical information systems: A method and application to Asarsuyu catchment, Turkey. Eng. Geol. 2004, 71, 303–321. [Google Scholar] [CrossRef]
- Al-Najjar, H.A.H.; Pradhan, B.; Sarkar, R.; Beydoun, G.; Alamri, A. A New Integrated Approach for Landslide Data Balancing and Spatial Prediction Based on Generative Adversarial Networks (GAN). Remote Sens. 2021, 13, 4011. [Google Scholar] [CrossRef]
- Pradhan, B. A comparative study on the predictive ability of the decision tree, support vector machine and neuro-fuzzy models in landslide susceptibility mapping using GIS. Comput. Geosci. 2013, 51, 350–365. [Google Scholar] [CrossRef]
- Westen, C.J.V.; Rengers, N.; Terlien, M.T.J.; Soeters, R. Prediction of the occurrence of slope instability phenomenal through GIS-based hazard zonation. Geol. Rundsch. 1997, 86, 404–414. [Google Scholar] [CrossRef]
- Sestraș, P.; Bilașco, Ș.; Roșca, S.; Naș, S.; Bondrea, M.V.; Gâlgău, R.; Vereș, I.; Sălăgean, T.; Spalević, V.; Cîmpeanu, S.M. Landslides Susceptibility Assessment Based on GIS Statistical Bivariate Analysis in the Hills Surrounding a Metropolitan Area. Sustainability 2019, 11, 1362. [Google Scholar] [CrossRef] [Green Version]
- Razandi, Y.; Pourghasemi, H.R.; Neisani, N.S.; Rahmati, O. Application of analytical hierarchy process, frequency ratio, and certainty factor models for groundwater potential mapping using GIS. Earth Sci. Inform. 2015, 8, 867–883. [Google Scholar] [CrossRef]
- Wang, X.L.; Zhang, L.Q.; Ding, J.X.; Meng, Q.F.; Iqbal, J.; Li, L.H.; Yang, Z.F. Comparison of rockfall susceptibility assessment at local and regional scale: A case study in the north of Beijing (China). Environ. Earth Sci. 2014, 72, 4639–4652. [Google Scholar] [CrossRef]
- Choi, J.; Oh, H.J.; Lee, H.J.; Lee, C.; Lee, S. Combining landslide susceptibility maps obtained from frequency ratio, logistic regression, and artificial neural network models using ASTER images and GIS. Eng. Geol. 2012, 124, 12–23. [Google Scholar] [CrossRef]
- Yilmaz, I. Landslide susceptibility mapping using frequency ratio, logistic regression, artificial neural networks and their comparison: A case study from Kat landslides (Tokat—Turkey). Comput. Geosci. 2009, 35, 1125–1138. [Google Scholar] [CrossRef]
- Pradhan, B. Landslide susceptibility mapping of a catchment area using frequency ratio, fuzzy logic and multivariate logistic regression approaches. J. Indian Soc. Remote Sens. 2010, 38, 301–320. [Google Scholar] [CrossRef]
- Dou, J.; Oguchi, T.; Hayakawa, Y.S.; Uchiyama, S.; Saito, H.; Paudel, U. Gis-based landslide susceptibility mapping using a certainty factor model and its validation in the chuetsu area, central japan. In Landslide Science for a Safer Geoenvironment; Sassa, K., Canuti, P., Yin, Y., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2014; pp. 419–424. [Google Scholar]
- Wang, Q.; Li, W.; Chen, W.; Bai, H. GIS-based assessment of landslide susceptibility using certainty factor and index of entropy models for the Qianyang County of Baoji city, China. J. Earth Syst. Sci. 2015, 124, 1399–1415. [Google Scholar] [CrossRef]
- Sujatha, E.R.; Rajamanickam, G.V.; Kumaravel, P. Landslide susceptibility analysis using Probabilistic Certainty Factor Approach: A case study on Tevankarai stream watershed, India. J. Earth Syst. Sci. 2012, 121, 1337–1350. [Google Scholar] [CrossRef] [Green Version]
- Devkota, K.C.; Regmi, A.D.; Pourghasemi, H.R.; Yoshida, K.; Pradhan, B.; Ryu, I.C.; Dhital, M.R.; Althuwaynee, O.F. Landslide susceptibility mapping using certainty factor, index of entropy and logistic regression models in GIS and their comparison at Mugling–Narayanghat road section in Nepal Himalaya. Nat. Hazards 2013, 65, 135–165. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Pradhan, B. Application of weights-of-evidence and certainty factor models and their comparison in landslide susceptibility mapping at Haraz watershed, Iran. Arab. J. Geosci. 2013, 6, 2351–2365. [Google Scholar] [CrossRef]
- Jebur, M.N.; Pradhan, B.; Tehrany, M.S. Optimization of landslide conditioning factors using very high-resolution airborne laser scanning (LiDAR) data at catchment scale. Remote Sens. Environ. 2014, 152, 150–165. [Google Scholar] [CrossRef]
- Kayastha, P.; Dhital, M.R.; De Smedt, F. Landslide susceptibility mapping using the weight of evidence method in the Tinau watershed, Nepal. Nat. Hazards 2012, 63, 479–498. [Google Scholar] [CrossRef]
- Ozdemir, A.; Altural, T. A comparative study of frequency ratio, weights of evidence and logistic regression methods for landslide susceptibility mapping: Sultan Mountains, SW Turkey. J. Asian Earth Sci. 2013, 64, 180–197. [Google Scholar] [CrossRef]
- Lee, S.; Choi, J. Landslide susceptibility mapping using GIS and the weight-of-evidence model. Int. J. Geogr. Inf. Sci. 2004, 18, 789–814. [Google Scholar] [CrossRef]
- Regmi, N.R.; Giardino, J.R.; Vitek, J.D. Modeling susceptibility to landslides using the weight of evidence approach: Western Colorado, USA. Geomorphology 2010, 115, 172–187. [Google Scholar] [CrossRef]
- Pradhan, B. Use of GIS-based fuzzy logic relations and its cross application to produce landslide susceptibility maps in three test areas in Malaysia. Environ. Earth Sci. 2011, 63, 329–349. [Google Scholar] [CrossRef]
- Aksoy, B.; Ercanoglu, M. Landslide identification and classification by object-based image analysis and fuzzy logic: An example from the Azdavay region (Kastamonu, Turkey). Comput. Geosci. 2012, 38, 87–98. [Google Scholar] [CrossRef]
- Saboya, F.; Alves, M.D.G.; Pinto, W.D. Assessment of failure susceptibility of soil slopes using fuzzy logic. Eng. Geol. 2006, 86, 211–224. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Pradhan, B.; Gokceoglu, C. Application of fuzzy logic and analytical hierarchy process (AHP) to landslide susceptibility mapping at Haraz watershed, Iran. Nat. Hazards 2012, 63, 965–996. [Google Scholar] [CrossRef]
- Zhu, A.X.; Wang, R.; Qiao, J.; Qin, C.-Z.; Chen, Y.; Liu, J.; Du, F.; Lin, Y.; Zhu, T. An expert knowledge-based approach to landslide susceptibility mapping using GIS and fuzzy logic. Geomorphology 2014, 214, 128–138. [Google Scholar] [CrossRef]
- Ahmed, B. Landslide susceptibility mapping using multi-criteria evaluation techniques in Chittagong Metropolitan Area, Bangladesh. Landslides 2015, 12, 1077–1095. [Google Scholar] [CrossRef] [Green Version]
- Komac, M. A landslide susceptibility model using the analytical hierarchy process method and multivariate statistics in perialpine Slovenia. Geomorphology 2006, 74, 17–28. [Google Scholar] [CrossRef]
- Rozos, D.; Bathrellos, G.D.; Skillodimou, H.D. Comparison of the implementation of rock engineering system and analytic hierarchy process methods, upon landslide susceptibility mapping, using GIS: A case study from the Eastern Achaia County of Peloponnesus, Greece. Environ. Earth Sci. 2011, 63, 49–63. [Google Scholar] [CrossRef]
- Yalcin, A. GIS-based landslide susceptibility mapping using analytical hierarchy process and bivariate statistics in Ardesen (Turkey): Comparisons of results and confirmations. Catena 2008, 72, 1–12. [Google Scholar] [CrossRef]
- Mohammady, M.; Pourghasemi, H.R.; Pradhan, B. Landslide susceptibility mapping at Golestan Province, Iran: A comparison between frequency ratio, Dempster–Shafer, and weights-of-evidence models. J. Asian Earth Sci. 2012, 61, 221–236. [Google Scholar] [CrossRef]
- Pourghasemi, H.; Pradhan, B.; Gokceoglu, C.; Moezzi, K.D. A comparative assessment of prediction capabilities of Dempster–Shafer and Weights-of-evidence models in landslide susceptibility mapping using GIS. Geomat. Nat. Hazards Risk 2013, 4, 93–118. [Google Scholar] [CrossRef]
- Park, N.-W. Application of Dempster-Shafer theory of evidence to GIS-based landslide susceptibility analysis. Environ. Earth Sci. 2011, 62, 367–376. [Google Scholar] [CrossRef]
- Tangestani, M.H. A comparative study of Dempster–Shafer and fuzzy models for landslide susceptibility mapping using a GIS: An experience from Zagros Mountains, SW Iran. J. Asian Earth Sci. 2009, 35, 66–73. [Google Scholar] [CrossRef]
- Gorsevski, P.V.; Jankowski, P.; Gessler, P.E. Spatial Prediction of Landslide Hazard Using Fuzzy k-means and Dempster-Shafer Theory. Trans. GIS 2005, 9, 455–474. [Google Scholar] [CrossRef]
- Sarkar, S.; Roy, A.K.; Martha, T.R. Landslide susceptibility assessment using Information Value Method in parts of the Darjeeling Himalayas. J. Geol. Soc. India 2013, 82, 351–362. [Google Scholar] [CrossRef]
- van Westen, C.J.; Rengers, N.; Soeters, R. Use of Geomorphological Information in Indirect Landslide Susceptibility Assessment. Nat. Hazards 2003, 30, 399–419. [Google Scholar] [CrossRef]
- Sharma, L.P.; Patel, N.; Ghose, M.K.; Debnath, P. Development and application of Shannon’s entropy integrated information value model for landslide susceptibility assessment and zonation in Sikkim Himalayas in India. Nat. Hazards 2015, 75, 1555–1576. [Google Scholar] [CrossRef]
- Che, V.B.; Kervyn, M.; Suh, C.E.; Fontijn, K.; Ernst, G.G.J.; del Marmol, M.A.; Trefois, P.; Jacobs, P. Landslide susceptibility assessment in Limbe (SW Cameroon): A field calibrated seed cell and information value method. Catena 2012, 92, 83–98. [Google Scholar] [CrossRef]
- Ayalew, L.; Yamagishi, H. The application of GIS-based logistic regression for landslide susceptibility mapping in the Kakuda-Yahiko Mountains, Central Japan. Geomorphology 2005, 65, 15–31. [Google Scholar] [CrossRef]
- Irigaray, C.; Fernández, T.; El Hamdouni, R.; Chacón, J. Evaluation and validation of landslide-susceptibility maps obtained by a GIS matrix method: Examples from the Betic Cordillera (southern Spain). Nat. Hazards 2007, 41, 61–79. [Google Scholar] [CrossRef]
- Jiménez-Perálvarez, J.D.; Irigaray, C.; El Hamdouni, R.; Chacón, J. Building models for automatic landslide-susceptibility analysis, mapping and validation in ArcGIS. Nat. Hazards 2009, 50, 571–590. [Google Scholar] [CrossRef]
- Panahi, M.; Gayen, A.; Pourghasemi, H.R.; Rezaie, F.; Lee, S. Spatial prediction of landslide susceptibility using hybrid support vector regression (SVR) and the adaptive neuro-fuzzy inference system (ANFIS) with various metaheuristic algorithms. Sci. Total Environ. 2020, 741, 139937. [Google Scholar] [CrossRef]
- Dehnavi, A.; Aghdam, I.N.; Pradhan, B.; Morshed Varzandeh, M.H. A new hybrid model using step-wise weight assessment ratio analysis (SWARA) technique and adaptive neuro-fuzzy inference system (ANFIS) for regional landslide hazard assessment in Iran. Catena 2015, 135, 122–148. [Google Scholar] [CrossRef]
- Aghdam, I.N.; Varzandeh, M.H.M.; Pradhan, B. Landslide susceptibility mapping using an ensemble statistical index (Wi) and adaptive neuro-fuzzy inference system (ANFIS) model at Alborz Mountains (Iran). Environ. Earth Sci. 2016, 75, 553. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Blaschke, T.; Aryal, J.; Gholaminia, K. A new GIS-based technique using an adaptive neuro-fuzzy inference system for land subsidence susceptibility mapping. J. Spat. Sci. 2020, 65, 401–418. [Google Scholar] [CrossRef] [Green Version]
- Aghdam, I.N.; Pradhan, B.; Panahi, M. Landslide susceptibility assessment using a novel hybrid model of statistical bivariate methods (FR and WOE) and adaptive neuro-fuzzy inference system (ANFIS) at southern Zagros Mountains in Iran. Environ. Earth Sci. 2017, 76, 22. [Google Scholar] [CrossRef]
- Meten, M.; Bhandary, N.P.; Yatabe, R. GIS-based frequency ratio and logistic regression modelling for landslide susceptibility mapping of Debre Sina area in central Ethiopia. J. Mt. Sci. 2015, 12, 1355–1372. [Google Scholar] [CrossRef]
- Al-Juaidi, A.E.M.; Nassar, A.M.; Al-Juaidi, O.E.M. Evaluation of flood susceptibility mapping using logistic regression and GIS conditioning factors. Arab. J. Geosci. 2018, 11, 10. [Google Scholar] [CrossRef]
- Sahana, M.; Sajjad, H. Evaluating effectiveness of frequency ratio, fuzzy logic and logistic regression models in assessing landslide susceptibility: A case from Rudraprayag district, India. J. Mt. Sci. 2017, 14, 2150–2167. [Google Scholar] [CrossRef]
- Steger, S.; Brenning, A.; Bell, R.; Glade, T. The propagation of inventory-based positional errors into statistical landslide susceptibility models. Nat. Hazards Earth Syst. Sci. 2016, 16, 2729–2745. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.J.; Guo, M.; Sawada, K.; Lin, J.; Zhang, J.C. Landslide susceptibility mapping in Mizunami City, Japan: A comparison between logistic regression, bivariate statistical analysis and multivariate adaptive regression spline models. Catena 2015, 135, 271–282. [Google Scholar] [CrossRef]
- Tsangaratos, P.; Ilia, I. Comparison of a logistic regression and Naïve Bayes classifier in landslide susceptibility assessments: The influence of models complexity and training dataset size. Catena 2016, 145, 164–179. [Google Scholar] [CrossRef]
- Hong, H.; Liu, J.; Zhu, A.X.; Shahabi, H.; Pham, B.T.; Chen, W.; Pradhan, B.; Tien Bui, D. A novel hybrid integration model using support vector machines and random subspace for weather-triggered landslide susceptibility assessment in the Wuning area (China). Environ. Earth Sci. 2017, 76, 652. [Google Scholar] [CrossRef]
- Feng, X.; Li, S.; Yuan, C.; Zeng, P.; Sun, Y. Prediction of Slope Stability using Naive Bayes Classifier. KSCE J. Civ. Eng. 2018, 22, 941–950. [Google Scholar] [CrossRef]
- Pham, B.; Prakash, I. Machine Learning Methods of Kernel Logistic Regression and Classification and Regression Trees for Landslide Susceptibility Assessment at Part of Himalayan Area, India. Indian J. Sci. Technol. 2018, 11, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Hong, H.; Pradhan, B.; Xu, C.; Tien Bui, D. Spatial prediction of landslide hazard at the Yihuang area (China) using two-class kernel logistic regression, alternating decision tree and support vector machines. Catena 2015, 133, 266–281. [Google Scholar] [CrossRef]
- Pham, B.T.; Shirzadi, A.; Shahabi, H.; Omidvar, E.; Singh, S.K.; Sahana, M.; Asl, D.T.; Bin Ahmad, B.; Quoc, N.K.; Lee, S. Landslide Susceptibility Assessment by Novel Hybrid Machine Learning Algorithms. Sustainability 2019, 11, 4386. [Google Scholar] [CrossRef] [Green Version]
- Tien Bui, D.; Le, K.T.T.; Nguyen, V.C.; Le, H.D.; Revhaug, I. Tropical Forest Fire Susceptibility Mapping at the Cat Ba National Park Area, Hai Phong City, Vietnam, Using GIS-Based Kernel Logistic Regression. Remote Sens. 2016, 8, 347. [Google Scholar] [CrossRef] [Green Version]
- Park, S.J.; Lee, C.W.; Lee, S.; Lee, M.J. Landslide Susceptibility Mapping and Comparison Using Decision Tree Models: A Case Study of Jumunjin Area, Korea. Remote Sens. 2018, 10, 1545. [Google Scholar] [CrossRef] [Green Version]
- Zhang, K.; Wu, X.; Niu, R.; Yang, K.; Zhao, L. The assessment of landslide susceptibility mapping using random forest and decision tree methods in the Three Gorges Reservoir area, China. Environ. Earth Sci. 2017, 76, 405. [Google Scholar] [CrossRef]
- Zhao, H.L.; Yao, L.H.; Mei, G.; Liu, T.Y.; Ning, Y.S. A Fuzzy Comprehensive Evaluation Method Based on AHP and Entropy for a Landslide Susceptibility Map. Entropy 2017, 19, 396. [Google Scholar] [CrossRef]
- Tien Bui, D.; Tuan, T.A.; Hoang, N.D.; Thanh, N.Q.; Nguyen, D.B.; Liem, N.V.; Pradhan, B. Spatial prediction of rainfall-induced landslides for the Lao Cai area (Vietnam) using a hybrid intelligent approach of least squares support vector machines inference model and artificial bee colony optimization. Landslides 2017, 14, 447–458. [Google Scholar] [CrossRef]
- Feizizadeh, B.; Roodposhti, M.S.; Blaschke, T.; Aryal, J. Comparing GIS-based support vector machine kernel functions for landslide susceptibility mapping. Arab. J. Geosci. 2017, 10, 13. [Google Scholar] [CrossRef]
- Hong, H.; Pourghasemi, H.R.; Pourtaghi, Z.S. Landslide susceptibility assessment in Lianhua County (China): A comparison between a random forest data mining technique and bivariate and multivariate statistical models. Geomorphology 2016, 259, 105–118. [Google Scholar] [CrossRef]
- Kim, J.-C.; Lee, S.; Jung, H.-S.; Lee, S. Landslide susceptibility mapping using random forest and boosted tree models in Pyeong-Chang, Korea. Geocarto Int. 2018, 33, 1000–1015. [Google Scholar] [CrossRef]
- Kadirhodjaev, A.; Kadavi, P.R.; Lee, C.W.; Lee, S. Analysis of the relationships between topographic factors and landslide occurrence and their application to landslide susceptibility mapping: A case study of Mingchukur, Uzbekistan. Geosci. J. 2018, 22, 1053–1067. [Google Scholar] [CrossRef]
- Lai, C.G.; Chen, X.H.; Wang, Z.L.; Xu, C.Y.; Yang, B. Rainfall-induced landslide susceptibility assessment using random forest weight at basin scale. Hydrol. Res. 2018, 49, 1363–1378. [Google Scholar] [CrossRef]
- Arabameri, A.; Pourghasemi, H.R.; Yamani, M. Applying different scenarios for landslide spatial modeling using computational intelligence methods. Environ. Earth Sci. 2017, 76, 20. [Google Scholar] [CrossRef]
- Tsangaratos, P.; Benardos, A. Estimating landslide susceptibility through a artificial neural network classifier. Nat. Hazards 2014, 74, 1489–1516. [Google Scholar] [CrossRef]
- Tian, Y.; Xu, C.; Hong, H.; Zhou, Q.; Wang, D. Mapping earthquake-triggered landslide susceptibility by use of artificial neural network (ANN) models: An example of the 2013 Minxian (China) Mw 5.9 event. Geomat. Nat. Hazards Risk 2019, 10, 1–25. [Google Scholar] [CrossRef] [Green Version]
- Conforti, M.; Pascale, S.; Robustelli, G.; Sdao, F. Evaluation of prediction capability of the artificial neural networks for mapping landslide susceptibility in the Turbolo River catchment (northern Calabria, Italy). Catena 2014, 113, 236–250. [Google Scholar] [CrossRef]
- Abbaszadeh Shahri, A.; Spross, J.; Johansson, F.; Larsson, S. Landslide susceptibility hazard map in southwest Sweden using artificial neural network. Catena 2019, 183, 104225. [Google Scholar] [CrossRef]
- Oh, H.J.; Lee, S. Shallow Landslide Susceptibility Modeling Using the Data Mining Models Artificial Neural Network and Boosted Tree. Appl. Sci. 2017, 7, 1000. [Google Scholar] [CrossRef] [Green Version]
- Kumar, D.; Thakur, M.; Dubey, C.S.; Shukla, D.P. Landslide susceptibility mapping & prediction using Support Vector Machine for Mandakini River Basin, Garhwal Himalaya, India. Geomorphology 2017, 295, 115–125. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, L. Review on landslide susceptibility mapping using support vector machines. Catena 2018, 165, 520–529. [Google Scholar] [CrossRef]
- Tien Bui, D.; Pradhan, B.; Nampak, H.; Bui, Q.T.; Tran, Q.A.; Nguyen, Q.P. Hybrid artificial intelligence approach based on neural fuzzy inference model and metaheuristic optimization for flood susceptibilitgy modeling in a high-frequency tropical cyclone area using GIS. J. Hydrol. 2016, 540, 317–330. [Google Scholar] [CrossRef]
- Colkesen, I.; Sahin, E.K.; Kavzoglu, T. Susceptibility mapping of shallow landslides using kernel-based Gaussian process, support vector machines and logistic regression. J. Afr. Earth Sci. 2016, 118, 53–64. [Google Scholar] [CrossRef]
- Rahmati, O.; Yousefi, S.; Kalantari, Z.; Uuemaa, E.; Teimurian, T.; Keesstra, S.; Pham, T.D.; Tien Bui, D. Multi-Hazard Exposure Mapping Using Machine Learning Techniques: A Case Study from Iran. Remote Sens. 2019, 11, 1943. [Google Scholar] [CrossRef] [Green Version]
- Garosi, Y.; Sheklabadi, M.; Pourghasemi, H.R.; Besalatpour, A.A.; Conoscenti, C.; Van Oost, K. Comparison of differences in resolution and sources of controlling factors for gully erosion susceptibility mapping. Geoderma 2018, 330, 65–78. [Google Scholar] [CrossRef]
- Youssef, A.M.; Pourghasemi, H.R.; Pourtaghi, Z.S.; Al-Katheeri, M.M. Landslide susceptibility mapping using random forest, boosted regression tree, classification and regression tree, and general linear models and comparison of their performance at Wadi Tayyah Basin, Asir Region, Saudi Arabia. Landslides 2016, 13, 839–856. [Google Scholar] [CrossRef]
- Camilo, D.C.; Lombardo, L.; Mai, P.M.; Dou, J.; Huser, R. Handling high predictor dimensionality in slope-unit-based landslide susceptibility models through LASSO-penalized Generalized Linear Model. Environ. Model. Softw. 2017, 97, 145–156. [Google Scholar] [CrossRef] [Green Version]
- Miao, F.; Wu, Y.; Xie, Y.; Li, Y. Prediction of landslide displacement with step-like behavior based on multialgorithm optimization and a support vector regression model. Landslides 2018, 15, 475–488. [Google Scholar] [CrossRef]
- Khosravi, K.; Panahi, M.; Tien Bui, D. Spatial prediction of groundwater spring potential mapping based on an adaptive neuro-fuzzy inference system and metaheuristic optimization. Hydrol. Earth Syst. Sci. 2018, 22, 4771–4792. [Google Scholar] [CrossRef] [Green Version]
- Razavizadeh, S.; Solaimani, K.; Massironi, M.; Kavian, A. Mapping landslide susceptibility with frequency ratio, statistical index, and weights of evidence models: A case study in northern Iran. Environ. Earth Sci. 2017, 76, 499. [Google Scholar] [CrossRef]
- Oh, H.J.; Lee, S.; Chotikasathien, W.; Kim, C.H.; Kwon, J.H. Predictive landslide susceptibility mapping using spatial information in the Pechabun area of Thailand. Environ. Geol. 2009, 57, 641. [Google Scholar] [CrossRef]
- Solaimani, K.; Mousavi, S.Z.; Kavian, A. Landslide susceptibility mapping based on frequency ratio and logistic regression models. Arab. J. Geosci. 2013, 6, 2557–2569. [Google Scholar] [CrossRef]
- Wei, X.; Zhang, L.; Luo, J.; Liu, D. A hybrid framework integrating physical model and convolutional neural network for regional landslide susceptibility mapping. Nat. Hazards 2021, 109, 471–497. [Google Scholar] [CrossRef]
- Hong, H.Y.; Liu, J.Z.; Zhu, A.X. Modeling landslide susceptibility using LogitBoost alternating decision trees and forest by penalizing attributes with the bagging ensemble. Sci. Total Environ. 2020, 718, 137231. [Google Scholar] [CrossRef] [PubMed]
- Pradhan, A.M.S.; Kim, Y.T. Evaluation of a combined spatial multi-criteria evaluation model and deterministic model for landslide susceptibility mapping. Catena 2016, 140, 125–139. [Google Scholar] [CrossRef]
- Yuan, R.; Deng, Q.; Cunningham, D.; Han, Z.; Zhang, D.; Zhang, B. Erratum to: Newmark displacement model for landslides induced by the 2013 Ms 7.0 Lushan earthquake, China. Front. Earth Sci. 2017, 11, 202. [Google Scholar] [CrossRef] [Green Version]
- Pham, B.T.; Khosravi, K.; Prakash, I. Application and comparison of decision tree-based machine learning methods in landside susceptibility assessment at Pauri Garhwal Area, Uttarakhand, India. Environ. Process. 2017, 4, 711–730. [Google Scholar] [CrossRef]
- Khosravi, K.; Pham, B.T.; Chapi, K.; Shirzadi, A.; Shahabi, H.; Revhaug, I.; Prakash, I.; Tien Bui, D. A comparative assessment of decision trees algorithms for flash flood susceptibility modeling at Haraz watershed, northern Iran. Sci. Total Environ. 2018, 627, 744–755. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Kornejady, A.; Kerle, N.; Shabani, F. Investigating the effects of different landslide positioning techniques, landslide partitioning approaches, and presence-absence balances on landslide susceptibility mapping. Catena 2020, 187, 104364. [Google Scholar] [CrossRef]
- Lorang, M.S. Predicting the crest height of a gravel beach. Geomorphology 2002, 48, 87–101. [Google Scholar] [CrossRef]
- Rahmati, O.; Pourghasemi, H.R.; Melesse, A.M. Application of GIS-based data driven random forest and maximum entropy models for groundwater potential mapping: A case study at Mehran Region, Iran. Catena 2016, 137, 360–372. [Google Scholar] [CrossRef]
- Chang, K.-T.; Merghadi, A.; Yunus, A.P.; Pham, B.T.; Dou, J. Evaluating scale effects of topographic variables in landslide susceptibility models using GIS-based machine learning techniques. Sci. Rep. 2019, 9, 12296. [Google Scholar] [CrossRef] [Green Version]
- Dahal, R.K.; Hasegawa, S.; Nonomura, A.; Yamanaka, M.; Masuda, T.; Nishino, K. GIS-based weights-of-evidence modelling of rainfall-induced landslides in small catchments for landslide susceptibility mapping. Environ. Geol. 2008, 54, 311–324. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Rahmati, O. Prediction of the landslide susceptibility: Which algorithm, which precision? Catena 2018, 162, 177–192. [Google Scholar] [CrossRef]
- Oh, H.-J.; Pradhan, B. Application of a neuro-fuzzy model to landslide-susceptibility mapping for shallow landslides in a tropical hilly area. Comput. Geosci. 2011, 37, 1264–1276. [Google Scholar] [CrossRef]
- Yesilnacar, E.; Topal, T. Landslide susceptibility mapping: A comparison of logistic regression and neural networks methods in a medium scale study, Hendek region (Turkey). Eng. Geol. 2005, 79, 251–266. [Google Scholar] [CrossRef]
- Tien Bui, D.; Pradhan, B.; Lofman, O.; Revhaug, I.; Dick, O.B. Landslide susceptibility assessment in the Hoa Binh province of Vietnam: A comparison of the Levenberg–Marquardt and Bayesian regularized neural networks. Geomorphology 2012, 171, 12–29. [Google Scholar] [CrossRef]
- Yalcin, A.; Reis, S.; Aydinoglu, A.C.; Yomralioglu, T. A GIS-based comparative study of frequency ratio, analytical hierarchy process, bivariate statistics and logistics regression methods for landslide susceptibility mapping in Trabzon, NE Turkey. Catena 2011, 85, 274–287. [Google Scholar] [CrossRef]
- Coelho-Netto, A.L.; Avelar, A.S.; Fernandes, M.C.; Lacerda, W.A. Landslide susceptibility in a mountainous geoecosystem, Tijuca Massif, Rio de Janeiro: The role of morphometric subdivision of the terrain. Geomorphology 2007, 87, 120–131. [Google Scholar] [CrossRef]
- Conforti, M.; Aucelli, P.P.C.; Robustelli, G.; Scarciglia, F. Geomorphology and GIS analysis for mapping gully erosion susceptibility in the Turbolo stream catchment (Northern Calabria, Italy). Nat. Hazards 2011, 56, 881–898. [Google Scholar] [CrossRef]
- Vorpahl, P.; Elsenbeer, H.; Märker, M.; Schröder, B. How can statistical models help to determine driving factors of landslides? Ecol. Model. 2012, 239, 27–39. [Google Scholar] [CrossRef]
- Jaafari, A.; Najafi, A.; Pourghasemi, H.R.; Rezaeian, J.; Sattarian, A. GIS-based frequency ratio and index of entropy models for landslide susceptibility assessment in the Caspian forest, northern Iran. Int. J. Environ. Sci. Technol. 2014, 11, 909–926. [Google Scholar] [CrossRef] [Green Version]
- Hall, F.G.; Townshend, J.R.; Engman, E.T. Status of remote sensing algorithms for estimation of land surface state parameters. Remote Sens. Environ. 1995, 51, 138–156. [Google Scholar] [CrossRef]
- Zhao, C.; Zhang, L.; Kong, W.; Liang, J.; Xu, X.; Wu, H.; Feng, X.; Hua, B.; Wang, H.; Sun, L. Umbilical Cord-Derived Mesenchymal Stem Cells Inhibit Cadherin-11 Expression by Fibroblast-Like Synoviocytes in Rheumatoid Arthritis. J. Immunol. Res. 2015, 2015, 137695. [Google Scholar] [CrossRef]
- Martelloni, G.; Segoni, S.; Fanti, R.; Catani, F. Rainfall thresholds for the forecasting of landslide occurrence at regional scale. Landslides 2012, 9, 485–495. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T.; Han, L.; Han, J.; Li, X.; Zhang, H.; Wang, H. Assessment of Landslide Susceptibility Using Integrated Ensemble Fractal Dimension with Kernel Logistic Regression Model. Entropy 2019, 21, 218. [Google Scholar] [CrossRef] [Green Version]
- Basher, L.; Betts, H.; Lynn, I.; Marden, M.; McNeill, S.; Page, M.; Rosser, B. A preliminary assessment of the impact of landslide, earthflow, and gully erosion on soil carbon stocks in New Zealand. Geomorphology 2017, 307. [Google Scholar] [CrossRef]
- Rossi, L.M.W.; Rapidel, B.; Roupsard, O.; Villatoro-sánchez, M.; Mao, Z.; Nespoulous, J.; Perez, J.; Prieto, I.; Roumet, C.; Metselaar, K.; et al. Sensitivity of the landslide model LAPSUS_LS to vegetation and soil parameters. Ecol. Eng. 2017, 109, 249–255. [Google Scholar] [CrossRef]
- Cheng, C.-H.; Hsiao, S.-C.; Huang, Y.-S.; Hung, C.-Y.; Pai, C.-W.; Chen, C.-P.; Menyailo, O.V. Landslide-induced changes of soil physicochemical properties in Xitou, Central Taiwan. Geoderma 2016, 265, 187–195. [Google Scholar] [CrossRef]
- Thomas, M.A.; Mirus, B.B.; Collins, B.D.; Lu, N.; Godt, J.W. Variability in soil-water retention properties and implications for physics-based simulation of landslide early warning criteria. Landslides 2018, 15, 1265–1277. [Google Scholar] [CrossRef]
- Oh, H.J.; Kim, Y.S.; Choi, J.K.; Park, E.; Lee, S. GIS mapping of regional probabilistic groundwater potential in the area of Pohang City, Korea. J. Hydrol. 2011, 399, 158–172. [Google Scholar] [CrossRef]
- Lee, S.; Pradhan, B. Landslide hazard mapping at Selangor, Malaysia using frequency ratio and logistic regression models. Landslides 2007, 4, 33–41. [Google Scholar] [CrossRef]
- Chen, X.; Chen, W. Gis-based landslide susceptibility assessment using optimized hybrid machine learning methods. CATENA 2021, 196, 104833. [Google Scholar] [CrossRef]
- Zhang, F.; O’Donnell, L.J. Chapter 7—Support vector regression. In Machine Learning; Mechelli, A., Vieira, S., Eds.; Academic Press: Cambridge, MA, USA, 2020; pp. 123–140. [Google Scholar] [CrossRef]
- Vapnik, V.N. StatisticaLearning Theory; John Wiey SonsTnc: New York, NY, USA, 1998. [Google Scholar]
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A training algorithm for optimal margin classifiers. In COLT ’92: Proceedings of the Fifth Annual Workshop on Computational Learning Theory, Pittsburgh, PA, USA, 27–29 July 1992; ACM: New York, NY, USA, 1992; pp. 144–152. [Google Scholar]
- Drucker, H.; Burges, C.J.C.; Kaufman, L.; Chris, J.C.; Kaufman, B.L.; Smola, A.; Vapnik, V. Support Vector Regression Machines; MIT Press: Cambridge, MA, USA, 1997; Volume 28, pp. 779–784. [Google Scholar]
- Panahi, M.; Sadhasivam, N.; Pourghasemi, H.R.; Rezaie, F.; Lee, S. Spatial prediction of groundwater potential mapping based on convolutional neural network (CNN) and support vector regression (SVR). J. Hydrol. 2020, 588, 125033. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Sulaiman, M.H.; Mustaffa, Z.; Mohamed, M.R.; Aliman, O. Using the gray wolf optimizer for solving optimal reactive power dispatch problem. Appl. Soft Comput. 2015, 32, 286–292. [Google Scholar] [CrossRef] [Green Version]
- Sahoo, A.; Chandra, S. Multi-objective Grey Wolf Optimizer for improved cervix lesion classification. Appl. Soft Comput. 2016, 52, 64–80. [Google Scholar] [CrossRef]
- Pradhan, M.; Roy, P.K.; Pal, T. Oppositional based grey wolf optimization algorithm for economic dispatch problem of power system. Ain Shams Eng. J. 2018, 9, 2015–2025. [Google Scholar] [CrossRef]
- Moayedi, H.; Osouli, A.; Tien Bui, D.; Foong, L. Spatial Landslide Susceptibility Assessment Based on Novel Neural-Metaheuristic Geographic Information System Based Ensembles. Sensors 2019, 19, 4698. [Google Scholar] [CrossRef] [Green Version]
- Bozorg-Haddad, O. (Ed.) Advanced Optimization by Nature-Inspired Algorithms; Springer: Singapore, 2018; Volume 720. [Google Scholar]
- Dehghani, M.; Riahi-Madvar, H.; Hooshyaripor, F.; Mosavi, A.; Shamshirband, S.; Zavadskas, E.; Chau, K.W. Prediction of Hydropower Generation Using Grey Wolf Optimization Adaptive Neuro-Fuzzy Inference System. Energies 2019, 12, 289. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Zhou, Y. Template Matching Using Grey Wolf Optimizer with Lateral Inhibition. Optik 2016, 130, 1229–1243. [Google Scholar] [CrossRef] [Green Version]
- Zhiwen, L.; Xin, Z.; Zhengjia, H.; Qiang, M. An adaptive stochastic resonance method based on grey wolf optimizer algorithm and its application to machinery fault diagnosis. ISA Trans. 2017, 71, 206–214. [Google Scholar]
- Muro, C.; Escobedo, R.; Spector, L.; Coppinger, R.P. Wolf-pack (Canis lupus) hunting strategies emerge from simple rules in computational simulations. Behav. Process. 2011, 88, 192–197. [Google Scholar] [CrossRef]
- Bian, X.Q.; Zhang, L.; Du, Z.M.; Chen, J.; Zhang, J.Y. Prediction of sulfur solubility in supercritical sour gases using grey wolf optimizer-based support vector machine. J. Mol. Liq. 2018, 261, 431–438. [Google Scholar] [CrossRef]
- Yang, X.-S. Nature-Inspired Metaheuristic Algorithms; Luniver Press: Beckington, UK, 2008. [Google Scholar]
- Nguyen, H.-L.; Pham, B.; Son, L.; Thang, N.; Ly, H.-B.; Le, T.-T.; Lanh, H.; Le, T.-H.; Tien Bui, D. Adaptive Network Based Fuzzy Inference System with Meta-Heuristic Optimizations for International Roughness Index Prediction. Appl. Sci. 2019, 9, 4715. [Google Scholar] [CrossRef] [Green Version]
- Jiang, M.; Jiang, L.; Jiang, D.; Xiong, J.; Shen, J.; Ahmed, S.H.; Luo, J.; Song, H. Dynamic measurement errors prediction for sensors based on firefly algorithm optimize support vector machine. Sustain. Cities Soc. 2017, 35, 250–256. [Google Scholar] [CrossRef]
- Dey, N.; Chaki, J.; Moraru, L.; Fong, S.; Yang, X.-S. Firefly Algorithm and Its Variants in Digital Image Processing: A Comprehensive Review. In Applications of Firefly Algorithm and Its Variants: Case Studies and New Developments; Dey, N., Ed.; Springer: Singapore, 2020; pp. 1–28. [Google Scholar]
- Asl, P.F.; Monjezi, M.; Hamidi, J.K.; Armaghani, D.J. Optimization of flyrock and rock fragmentation in the Tajareh limestone mine using metaheuristics method of firefly algorithm. Eng. Comput. 2017, 34, 241–251. [Google Scholar] [CrossRef]
- Zang, H.; Zhang, S.; Hapeshi, K. A Review of Nature-Inspired Algorithms. J. Bionic Eng. 2010, 7, S232–S237. [Google Scholar] [CrossRef]
- Alexandridis, A.K.; Zapranis, A.D. Wavelet neural networks: A practical guide. Neural Netw. 2013, 42, 1–27. [Google Scholar] [CrossRef] [PubMed]
- Eibe, F.; Hall, M.A.; Witten, I.H. The WEKA Workbench. Online Appendix for “Data Mining: Practical Machine Learning Tools and Techniques”. In Morgan Kaufmann, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Shahabi, H.; Khezri, S.; Ahmad, B.B.; Hashim, M. Landslide susceptibility mapping at central Zab basin, Iran: A comparison between analytical hierarchy process, frequency ratio and logistic regression models. Catena 2014, 115, 55–70. [Google Scholar] [CrossRef]
- Hong, H.; Shahabi, H.; Shirzadi, A.; Chen, W.; Chapi, K.; Ahmad, B.B.; Roodposhti, M.S.; Yari Hesar, A.; Tian, Y.; Tien Bui, D. Landslide susceptibility assessment at the Wuning area, China: A comparison between multi-criteria decision making, bivariate statistical and machine learning methods. Nat. Hazards 2019, 96, 173–212. [Google Scholar] [CrossRef]
- Abramson, L.W. Slope Stability and Stabilization Methods; Wiley: Hoboken, NJ, USA, 1995. [Google Scholar]
- Oh, H.-J.; Kadavi, P.R.; Lee, C.-W.; Lee, S. Evaluation of landslide susceptibility mapping by evidential belief function, logistic regression and support vector machine models. Geomat. Nat. Hazards Risk 2018, 9, 1053–1070. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Ke, Y.; Chen, Z.; Liang, S.; Zhao, H.; Hong, H. Application of alternating decision tree with AdaBoost and bagging ensembles for landslide susceptibility mapping. Catena 2020, 187, 104396. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Mohammady, M.; Pradhan, B. Landslide susceptibility mapping using index of entropy and conditional probability models in GIS: Safarood Basin, Iran. Catena 2012, 97, 71–84. [Google Scholar] [CrossRef]
- Zhao, X.; Chen, W. Optimization of Computational Intelligence Models for Landslide Susceptibility Evaluation. Remote Sens. 2020, 12, 2180. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Kornejady, A.; Zhang, N. Landslide spatial modeling: Introducing new ensembles of ANN, MaxEnt, and SVM machine learning techniques. Geoderma 2017, 305, 314–327. [Google Scholar] [CrossRef]
- Pontius, R.G.; Schneider, L.C. Land-cover change model validation by an ROC method for the Ipswich watershed, Massachusetts, USA. Agric. Ecosyst. Environ. 2001, 85, 239–248. [Google Scholar] [CrossRef]
- Visser, H.; Nijs, T.D. The Map Comparison Kit. Environ. Model. Softw. 2006, 21, 346–358. [Google Scholar] [CrossRef]
- Meliho, M.; Khattabi, A.; Mhammdi, N. A GIS-based approach for gully erosion susceptibility modelling using bivariate statistics methods in the Ourika watershed, Morocco. Environ. Earth Ences 2018, 77, 655. [Google Scholar] [CrossRef]
- Tien Bui, D.; Ho, T.C.; Pradhan, B.; Pham, B.T.; Nhu, V.H.; Revhaug, I. GIS-based modeling of rainfall-induced landslides using data mining-based functional trees classifier with AdaBoost, Bagging, and MultiBoost ensemble frameworks. Environ. Earth Sci. 2016, 75, 1101. [Google Scholar] [CrossRef]
- Landis, J.R.; Koch, G.G. JSTOR: Biometrics. Biometrics 1977, 33, 159–174. [Google Scholar] [CrossRef] [Green Version]
- Fell, R.; Corominas, J.; Bonnard, C.; Cascini, L.; Leroi, E.; Savage, W. Guidelines for landslide susceptibility, hazard and risk zoning for land use planning—ScienceDirect. Eng. Geol. 2008, 102, 83–84. [Google Scholar]
- Chen, W.; Pourghasemi, H.R.; Panahi, M.; Kornejady, A.; Wang, J.; Xie, X.; Cao, S. Spatial prediction of landslide susceptibility using an adaptive neuro-fuzzy inference system combined with frequency ratio, generalized additive model, and support vector machine techniques. Geomorphology 2017, 297, 69–85. [Google Scholar] [CrossRef]
- Singh, A.K. Bioengineering techniques of slope stabilization and landslide mitigation. Disaster Prev. Manag. 2010, 19, 384–397. [Google Scholar] [CrossRef]
- Chen, W.; Peng, J.; Hong, H.; Shahabi, H.; Pradhan, B.; Liu, J.; Zhu, A.-X.; Pei, X.; Duan, Z. Landslide susceptibility modelling using GIS-based machine learning techniques for Chongren County, Jiangxi Province, China. Sci. Total Environ. 2018, 626, 1121–1135. [Google Scholar] [CrossRef]






| Group | Lithology | Geologic Ages |
|---|---|---|
| 1 | Trachyte | Silurian |
| 2 | Volcanic rock, diabase, diabase porphyrite | Silurian |
| 3 | Diabase | Palaeozoic |
| 4 | Metamorphic rhyolite, quartz porphyry, volcanic clastic rocks, phyllite, metamorphic sandstone | Proterozoic |
| 5 | Yellow-green and dark gray sandy slate, argillaceous slate, silty sericite phyllite, sandstone, siltstone, carbonaceous slate, tuff sandstone | Silurian |
| 6 | Slate, argillaceous limestone, banded slate, carbonaceous slate, silt sandstone, sandstone | Silurian |
| 7 | Gray-black siliceous rock, carbonaceous slate, yellow-green phyllite, schist, marl, limestone, calcareous slate, dolomite, breccia limestone | Cambrian |
| 8 | Dolomite, marl, shale, conglomerate, sandstone, limestone, carbonaceous slate | Ediacaran |
| 9 | Silty slate, siltstone, sandstone, tuff sandstone, glacial mud | Ediacaran |
| 10 | Metamorphic basic volcanic rocks, carbonaceous phyllite, marble, siliceous rocks, metamorphic terrigenous clastic rocks | Ediacaran |
| Conditioning Factors | Classes | Percentage of Domain (a) | Percentage of Landslides (b) | FR (b/a) |
|---|---|---|---|---|
| Elevation (m) | 547–700 | 0.7 | 0.6 | 0.90 |
| 700–900 | 3.5 | 10.9 | 3.09 | |
| 900–1100 | 9.4 | 35.7 | 3.80 | |
| 1100–1300 | 14.9 | 24.0 | 1.61 | |
| 1300–1500 | 17.2 | 11.9 | 0.70 | |
| 1500–1700 | 16.6 | 7.8 | 0.47 | |
| 1700–1900 | 14.8 | 1.3 | 0.09 | |
| 1900–2100 | 10.6 | 2.7 | 0.26 | |
| 2100–2300 | 6.7 | 1.9 | 0.29 | |
| 2300–2500 | 4.0 | 3.2 | 0.80 | |
| 2500–2700 | 1.4 | 0.0 | 0.00 | |
| 2700–2911 | 0.2 | 0.0 | 0.00 | |
| Slope (°) | 0–10 | 5.8 | 0.0 | 0.00 |
| 10–20 | 19.6 | 11.8 | 0.60 | |
| 20–30 | 30.9 | 31.7 | 1.03 | |
| 30–40 | 28.1 | 35.3 | 1.26 | |
| 40–50 | 13.4 | 17.7 | 1.32 | |
| 50–60 | 2.2 | 3.6 | 1.62 | |
| 60–72.77 | 0.1 | 0.0 | 0.00 | |
| Aspect (°) | Flat (−1) | 0.0 | 0.0 | 0.00 |
| North (0°–22.5°) | 13.1 | 0.1 | 0.01 | |
| Northeast (22.5°–67.5°) | 14.3 | 0.8 | 0.06 | |
| East (67.5°–112.5°) | 13.8 | 15.6 | 1.13 | |
| Southeast (112.5°–157.5°) | 12.5 | 42.8 | 3.42 | |
| South (157.5°–202.5°) | 12.2 | 31.5 | 2.60 | |
| Southwest (202.5°–247.5°) | 12.0 | 7.0 | 0.59 | |
| West (247.5°–292.5°) | 11.6 | 2.0 | 0.17 | |
| Northwest (292.5°–337.5°) | 10.6 | 0.2 | 0.02 | |
| Plan curvature (m/100) | Concave | 47.5 | 52.6 | 1.11 |
| Plan | 4.3 | 3.7 | 0.87 | |
| Convex | 48.3 | 43.7 | 0.90 | |
| Profile curvature (m/100) | Concave | 47.6 | 40.8 | 0.86 |
| Plan | 3.0 | 1.9 | 0.63 | |
| Convex | 49.4 | 57.3 | 1.16 | |
| Distance to faults (m) | 0–500 | 25.4 | 21.4 | 0.84 |
| 500–1000 | 19.2 | 32.5 | 1.69 | |
| 1000–1500 | 14.9 | 12.0 | 0.81 | |
| 1500–2000 | 11.5 | 23.3 | 2.03 | |
| >2000 | 29.0 | 10.8 | 0.37 | |
| Distance to rivers (m) | 0–200 | 23.8 | 49.5 | 2.08 |
| 200–400 | 19.5 | 27.2 | 1.39 | |
| 400–600 | 16.9 | 7.3 | 0.43 | |
| 600–800 | 14.6 | 6.7 | 0.46 | |
| >800 | 25.2 | 9.4 | 0.37 | |
| Distance to roads (m) | 0–200 | 6.8 | 26.8 | 3.95 |
| 200–400 | 5.5 | 19.1 | 3.48 | |
| 400–600 | 5.1 | 6.8 | 1.34 | |
| 600–800 | 4.9 | 2.2 | 0.45 | |
| >800 | 77.7 | 45.0 | 0.58 | |
| STI | 0–10 | 42.8 | 30.1 | 0.70 |
| 10–20 | 27.7 | 28.8 | 1.04 | |
| 20–30 | 10.9 | 13.4 | 1.23 | |
| 30–40 | 5.0 | 6.6 | 1.32 | |
| >40 | 13.7 | 21.2 | 1.55 | |
| SPI | 0–10 | 32.7 | 23.1 | 0.71 |
| 10–20 | 16.9 | 14.6 | 0.86 | |
| 20–30 | 11.3 | 12.7 | 1.12 | |
| 30–40 | 6.8 | 7.1 | 1.05 | |
| >40 | 32.3 | 42.6 | 1.32 | |
| TWI | <1.5 | 25.8 | 26.7 | 1.04 |
| 1.5–2 | 36.8 | 33.8 | 0.92 | |
| 2–2.5 | 16.5 | 14.6 | 0.88 | |
| 2.5–3 | 9.3 | 14.6 | 1.57 | |
| >3 | 11.6 | 10.3 | 0.89 | |
| NDVI | −0.12–0.16 | 6.6 | 1.4 | 0.21 |
| 0.16–0.24 | 16.2 | 4.4 | 0.27 | |
| 0.24–0.31 | 23.9 | 8.8 | 0.37 | |
| 0.31–0.38 | 26.3 | 24.0 | 0.91 | |
| 0.38–0.53 | 26.9 | 61.5 | 2.29 | |
| Landuse | Farmland | 11.0 | 26.3 | 2.40 |
| Forestland | 43.3 | 13.0 | 0.30 | |
| Grassland | 45.5 | 60.6 | 1.33 | |
| Water bodies | 0.0 | 0.0 | 0.00 | |
| Construction land | 0.2 | 0.0 | 0.00 | |
| Bare land | 0.0 | 0.0 | 0.00 | |
| Rainfall (mm/yr) | <800 | 0.1 | 0.5 | 4.60 |
| 800–850 | 0.2 | 0.0 | 0.00 | |
| 850–900 | 1.3 | 0.0 | 0.00 | |
| 900–950 | 4.2 | 3.1 | 0.75 | |
| 950–1000 | 35.0 | 22.1 | 0.63 | |
| 1000–1050 | 48.6 | 63.5 | 1.31 | |
| 1050–1100 | 7.4 | 7.7 | 1.04 | |
| 1100–1150 | 2.4 | 3.0 | 1.24 | |
| 1150–1200 | 0.8 | 0.2 | 0.24 | |
| >1200 | 0.2 | 0.0 | 0.00 | |
| Soil | Type 1 (Yellow-brown soil) | 23.4 | 28.7 | 1.23 |
| Type 2 (Dark-yellow-brown soil) | 13.9 | 21.1 | 1.52 | |
| Type 3 (Yellow-browning soil) | 0.0 | 0.0 | 0.00 | |
| Type 4 (Albic yellow cinnamon soil) | 0.5 | 3.7 | 7.79 | |
| Type 5 (Brown soil) | 55.0 | 21.7 | 0.39 | |
| Type 6 (Alluvial soil) | 2.9 | 19.4 | 6.81 | |
| Type 7 (Calcareous soil) | 1.5 | 0.4 | 0.24 | |
| Type 8 (Skeletal soil) | 2.3 | 5.0 | 2.22 | |
| Type 9 (Mountain scrubby-meadow soil) | 0.6 | 0.0 | 0.00 | |
| Lithology | Group 1 | 2.5 | 0.2 | 0.07 |
| Group 2 | 6.9 | 5.7 | 0.84 | |
| Group 3 | 1.2 | 0.0 | 0.00 | |
| Group 4 | 0.9 | 1.5 | 1.62 | |
| Group 5 | 1.8 | 1.1 | 0.60 | |
| Group 6 | 24.7 | 36.0 | 1.46 | |
| Group 7 | 44.6 | 40.2 | 0.90 | |
| Group 8 | 7.8 | 7.4 | 0.95 | |
| Group 9 | 7.9 | 7.3 | 0.92 | |
| Group 10 | 1.8 | 0.6 | 0.35 |
| Landslide Susceptibility Map | Very Low | Low | Moderate | High | Very High | All |
|---|---|---|---|---|---|---|
| SVR vs. SVR-GWO | ||||||
| Kappa index | 1.000 | 0.680 | 0.477 | 0.426 | 0.747 | 0.586 |
| Kappa location | 1.000 | 0.878 | 0.491 | 0.476 | 0.780 | 0.640 |
| Kappa histogram | 1.000 | 0.775 | 0.972 | 0.896 | 0.957 | 0.916 |
| SVR vs. SVR-FA | ||||||
| Kappa index | 1.000 | 0.608 | 0.418 | 0.326 | 0.659 | 0.503 |
| Kappa location | 1.000 | 0.612 | 0.446 | 0.349 | 0.725 | 0.539 |
| Kappa histogram | 1.000 | 0.937 | 0.937 | 0.934 | 0.909 | 0.934 |
| SVR-GWO vs. SVR-FA | ||||||
| Kappa index | 1.000 | 0.658 | 0.413 | 0.339 | 0.711 | 0.536 |
| Kappa location | 1.000 | 0.843 | 0.454 | 0.352 | 0.821 | 0.604 |
| Kappa histogram | 1.000 | 0.780 | 0.909 | 0.962 | 0.856 | 0.888 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, R.; Peng, J.; Leng, Y.; Lee, S.; Panahi, M.; Chen, W.; Zhao, X. Hybrids of Support Vector Regression with Grey Wolf Optimizer and Firefly Algorithm for Spatial Prediction of Landslide Susceptibility. Remote Sens. 2021, 13, 4966. https://doi.org/10.3390/rs13244966
Liu R, Peng J, Leng Y, Lee S, Panahi M, Chen W, Zhao X. Hybrids of Support Vector Regression with Grey Wolf Optimizer and Firefly Algorithm for Spatial Prediction of Landslide Susceptibility. Remote Sensing. 2021; 13(24):4966. https://doi.org/10.3390/rs13244966
Chicago/Turabian StyleLiu, Ru, Jianbing Peng, Yanqiu Leng, Saro Lee, Mahdi Panahi, Wei Chen, and Xia Zhao. 2021. "Hybrids of Support Vector Regression with Grey Wolf Optimizer and Firefly Algorithm for Spatial Prediction of Landslide Susceptibility" Remote Sensing 13, no. 24: 4966. https://doi.org/10.3390/rs13244966
APA StyleLiu, R., Peng, J., Leng, Y., Lee, S., Panahi, M., Chen, W., & Zhao, X. (2021). Hybrids of Support Vector Regression with Grey Wolf Optimizer and Firefly Algorithm for Spatial Prediction of Landslide Susceptibility. Remote Sensing, 13(24), 4966. https://doi.org/10.3390/rs13244966