SDFCNv2: An Improved FCN Framework for Remote Sensing Images Semantic Segmentation
Abstract
:1. Introduction
- 1.
- We design a novel FCN backbone network with hybrid basic convolutional (HBC) blocks and spatial-channel-fusion squeeze-and-excitation (SCFSE) modules for feature recalibration to obtain larger receptive field and reduce network parameters.
- 2.
- We propose the SDFCNv2 framework, which includes a data augmentation method based on spectral-specific stochastic-gamma-transform (SSSGT) to improve generalizability of our model, and a mask-weighted voting decision fusion postprocessing algorithm on overlarge RS image segmentation, in order to balance the final prediction accuracy and computational cost.
2. Related Works
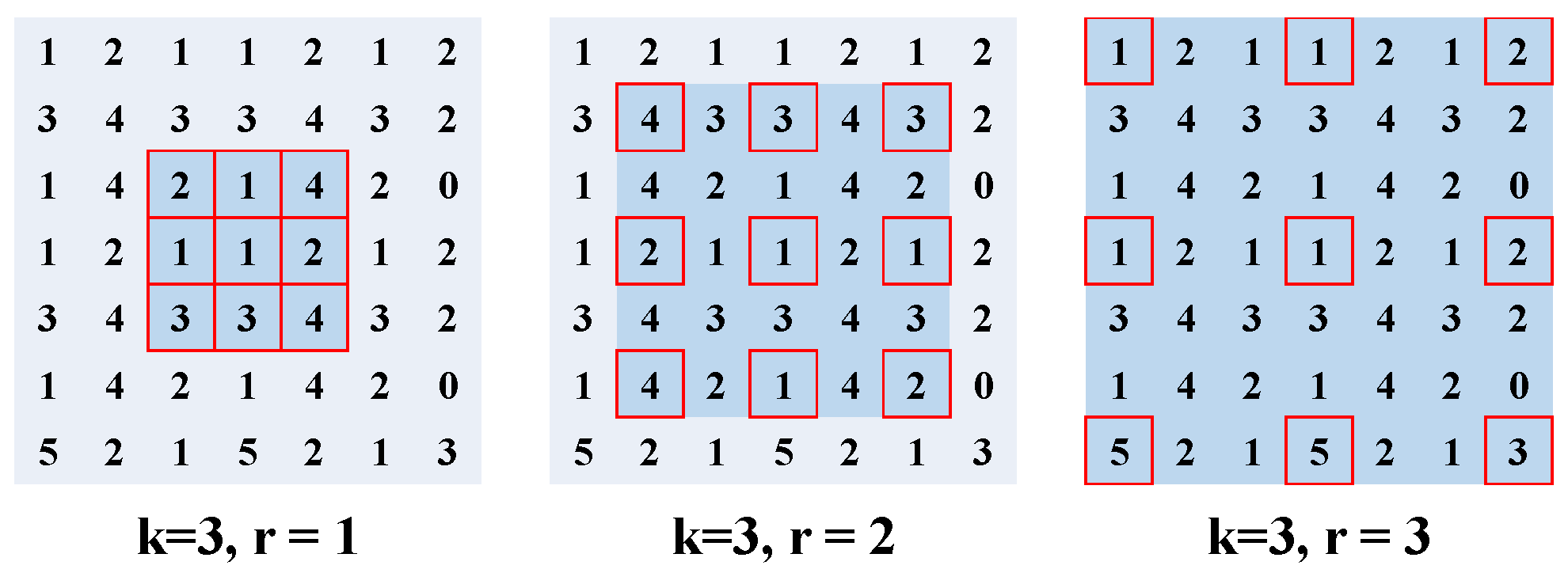
2.1. Receptive Field (RF) of FCNS
2.2. Feature Recalibration Modules
2.3. Sdfcnv1 Model
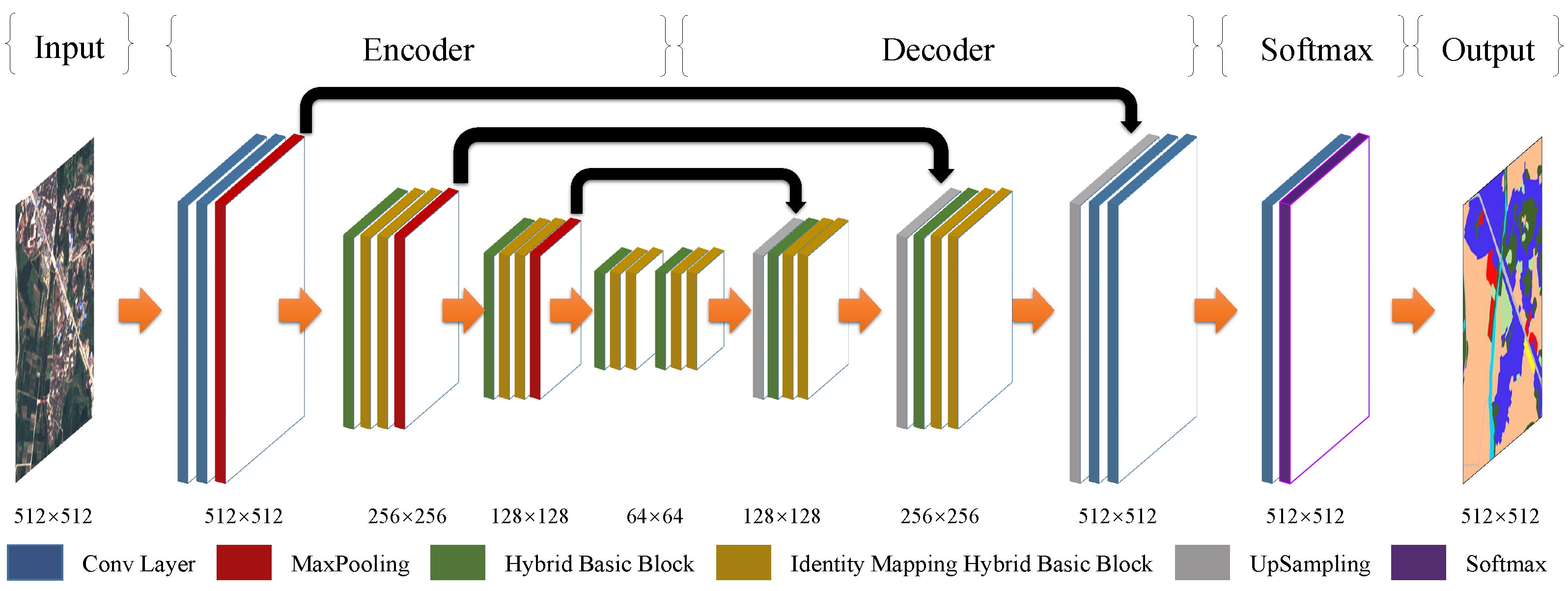
3. SDFCNv2 Architecture
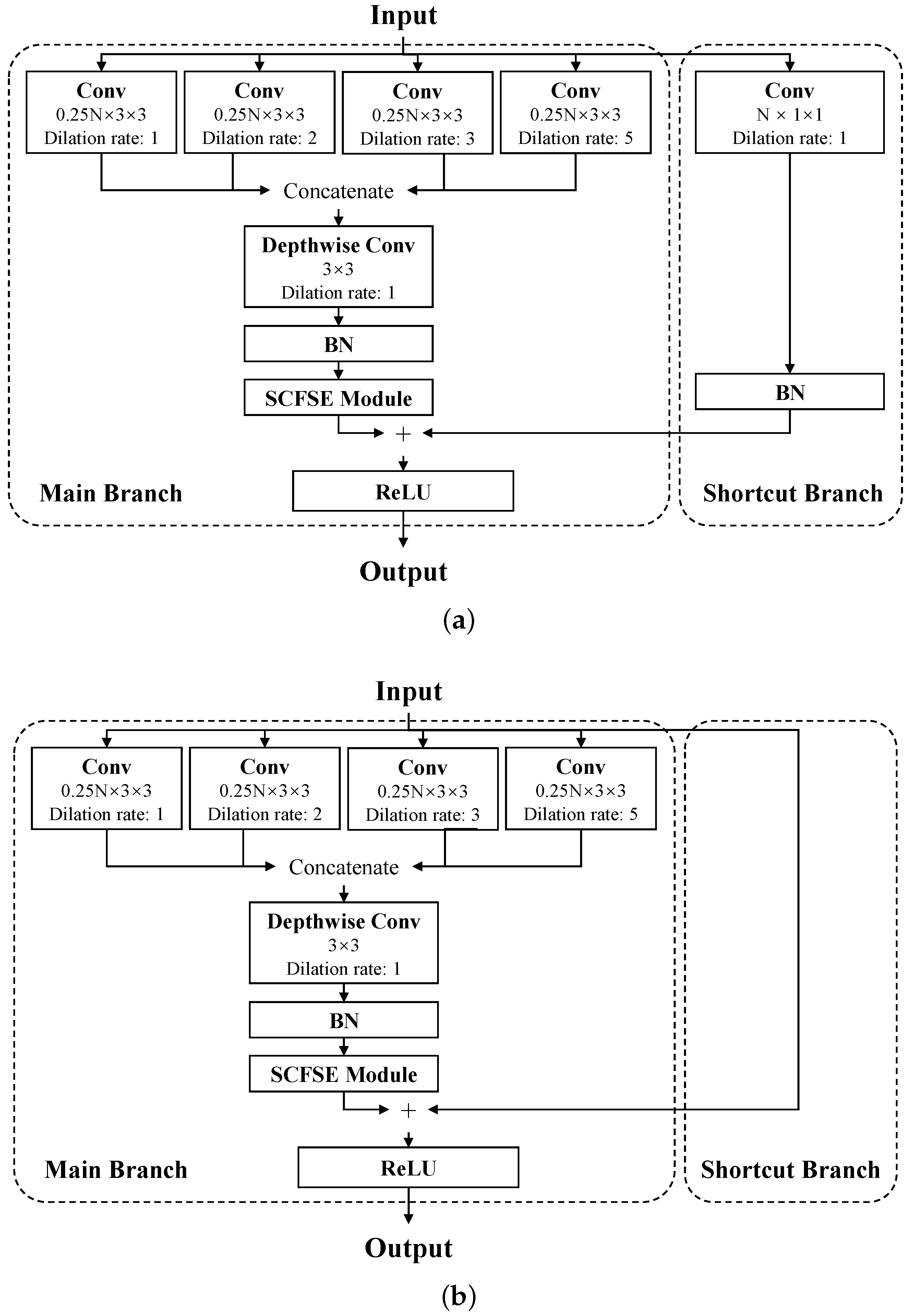
3.1. Hybrid Basic Convolutional (HBC) Block
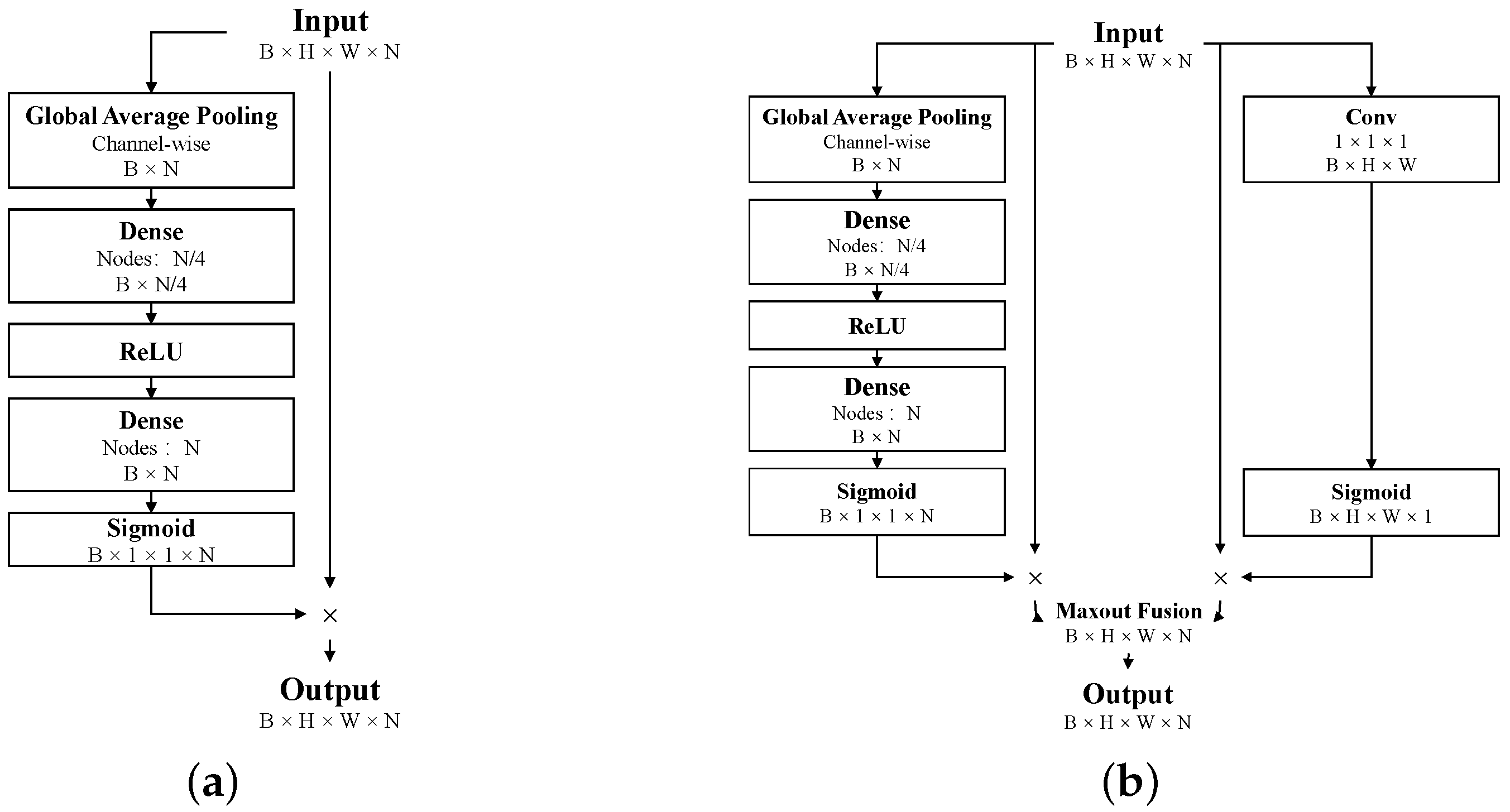
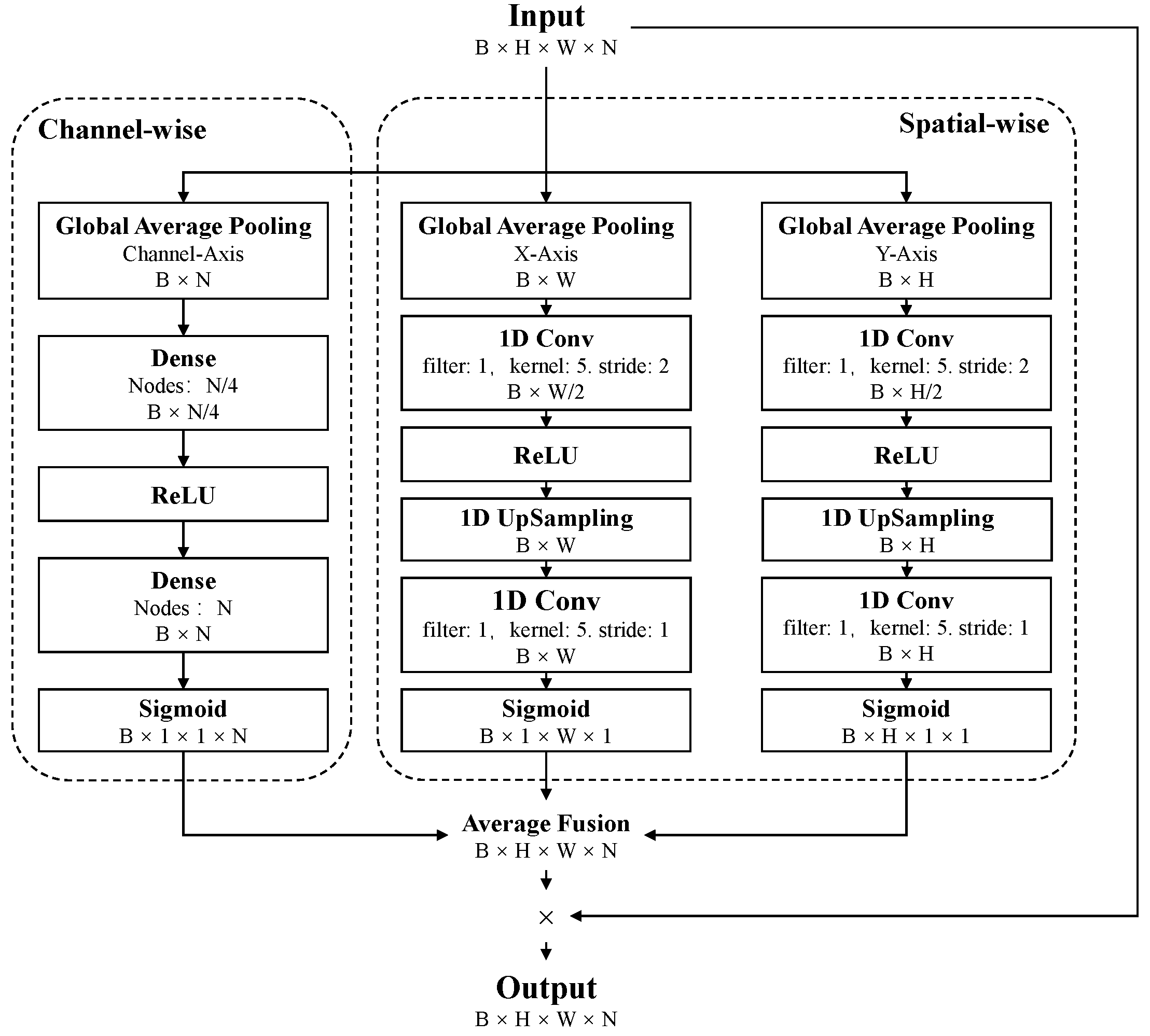
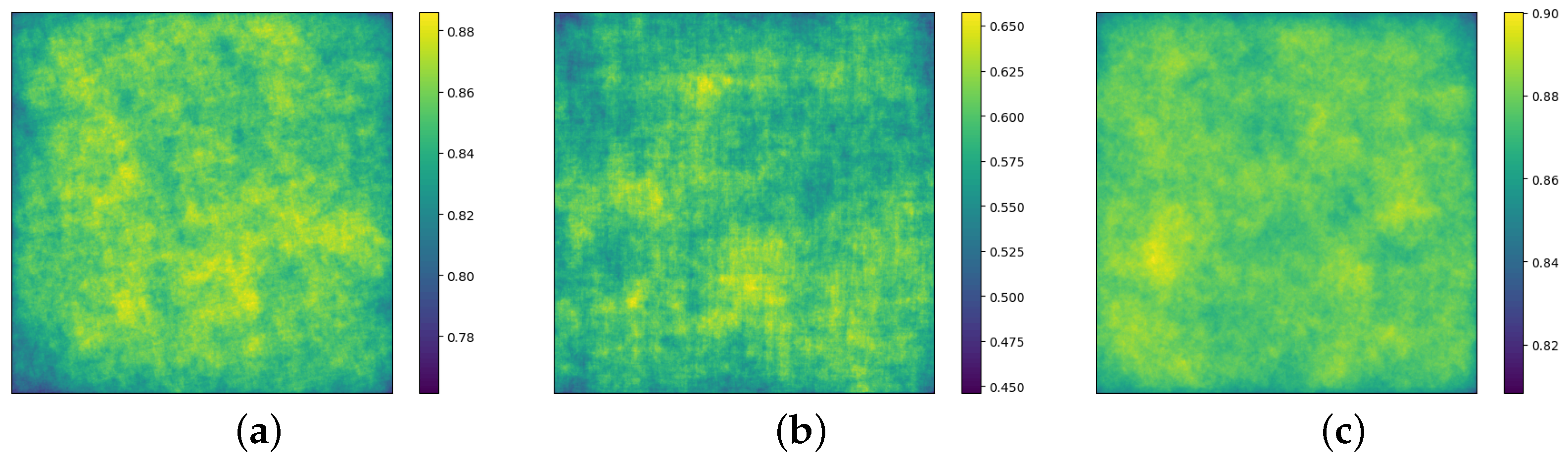
3.2. Spatial and Channel Fusion Squeeze-and-Excitation (SCFSE) Module
3.3. Spectral-Specific Stochastic-Gamma-Transform-Based Data Augmentation
- Random scaling in the range of [1, 1.2];
- Random translation by [−5, 5] pixels;
- Random vertically and horizontally flipping.
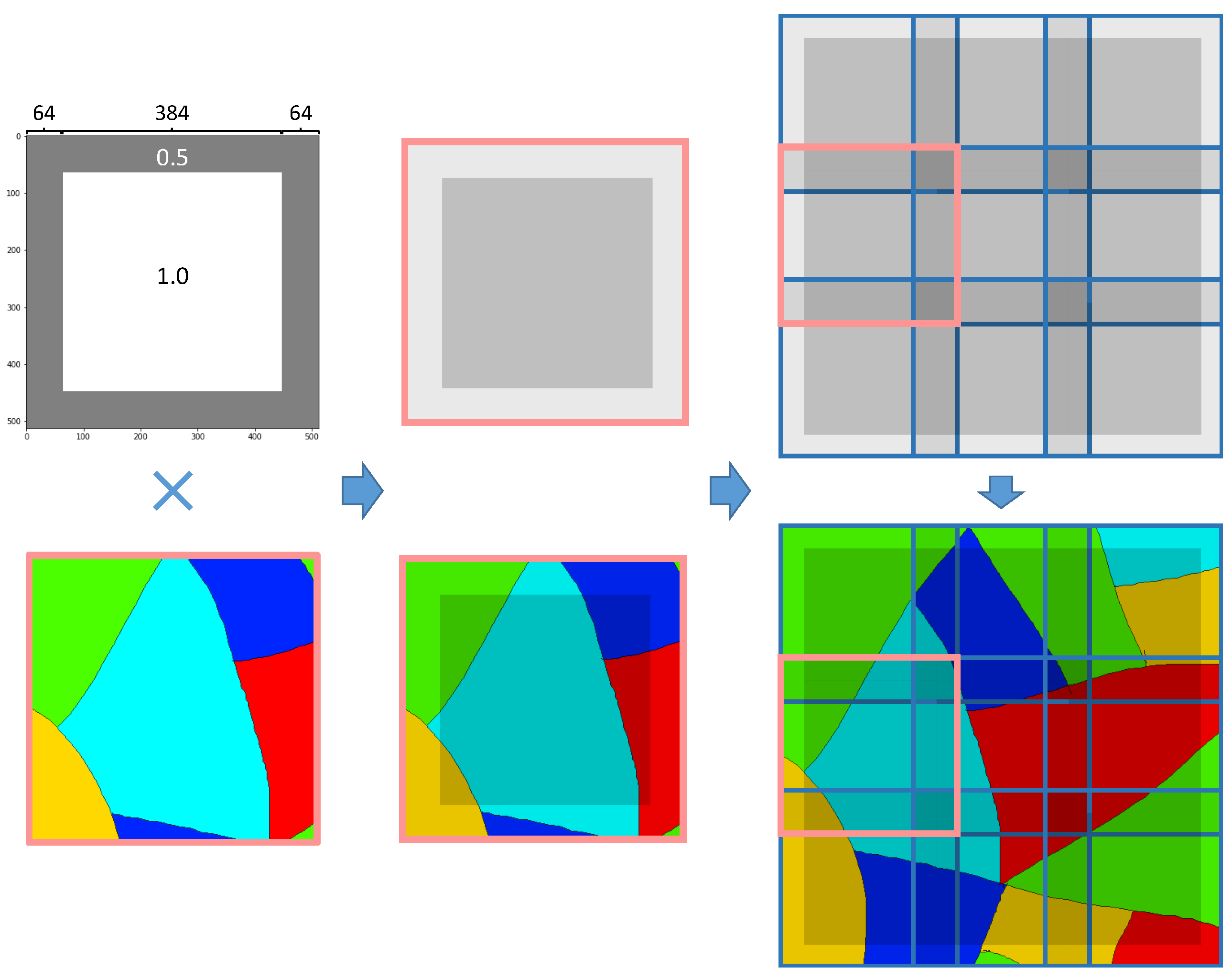
3.4. Decision Fusion Postprocessing via Mask-Weighted Voting
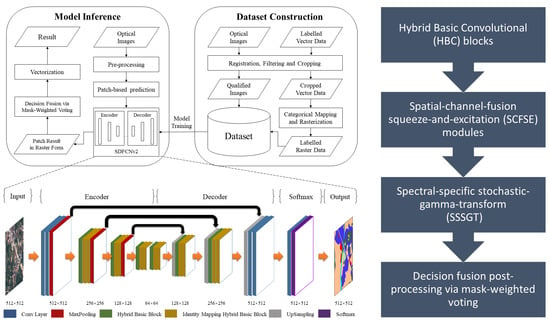
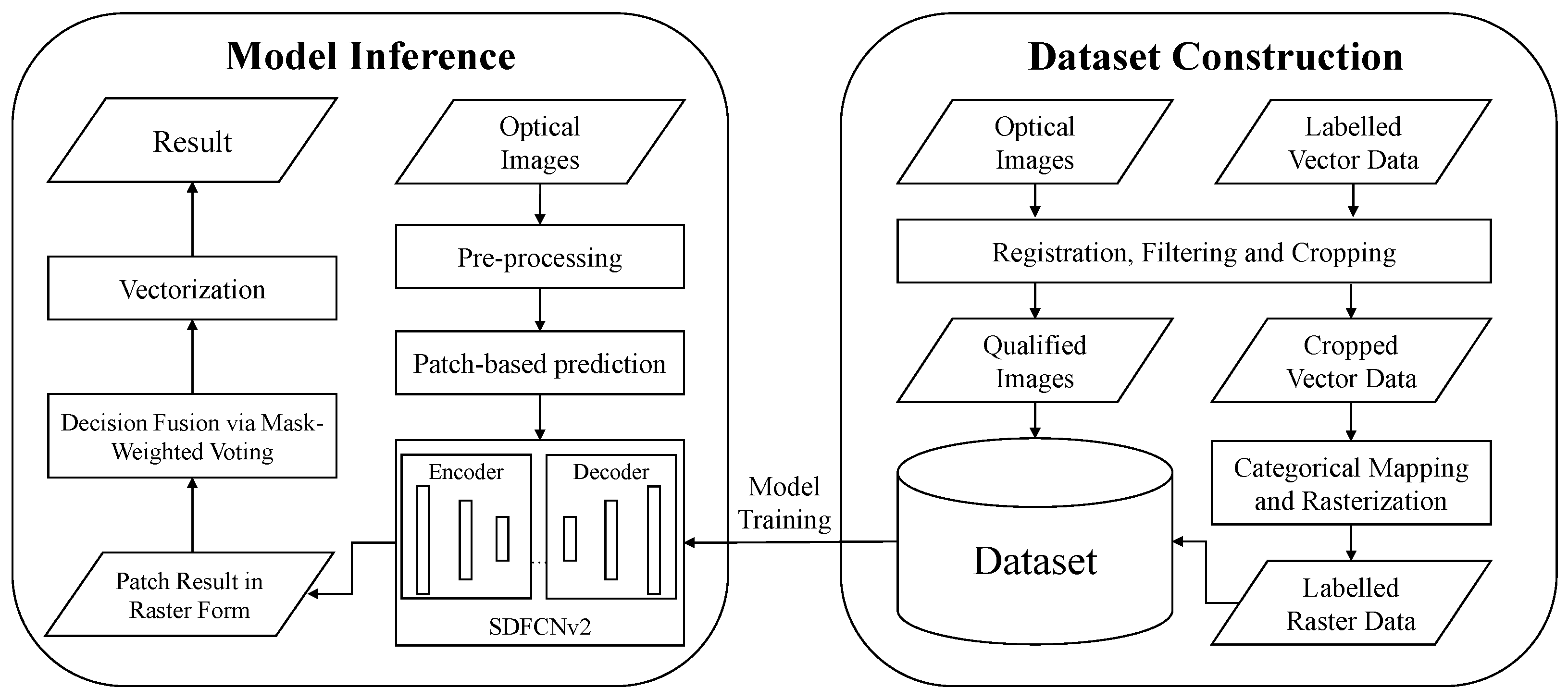
4. Dataset Construction and the Whole Framework
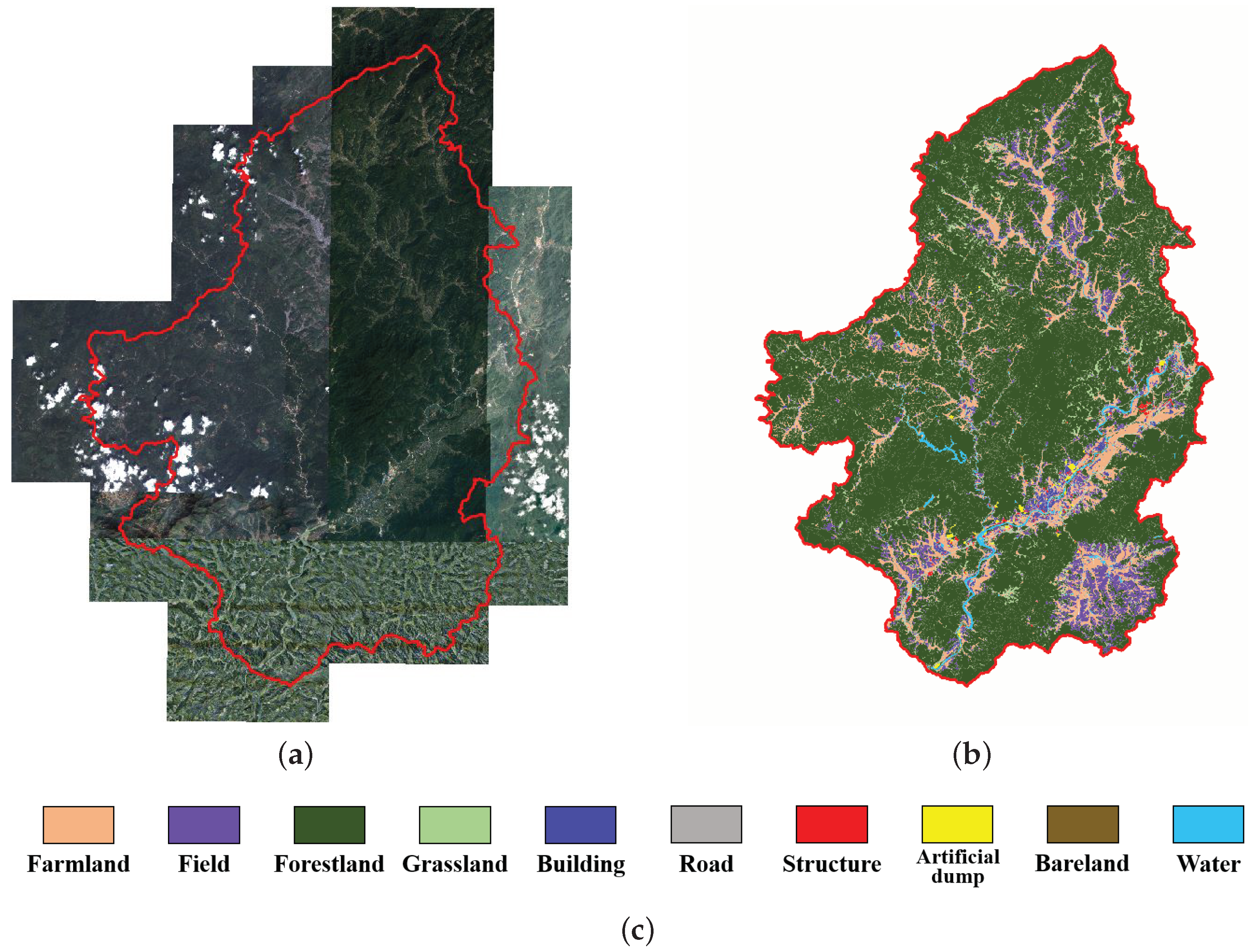
4.1. Dataset Construction
- 1.
- Data registration. RS images are first aligned with the corresponding label vector data in the identical coordinate system. For optical RS images, we need to further unify their spatial resolution, radiometric resolution and image spectral bands. In this paper, we convert all RS images into 8-bit raster data with a spatial resolution of 0.5 m, containing three spectral bands of red, green, and blue. Besides, we crop the vector data according to the rectangular area of the RS raster data, and we need to filter out the partly overlapping area.
- 2.
- Categorical mapping. We extract the attributes of the category codes from the cropped vector data, convert them into category labels and encode them. (For example we encode ten categories from 0 to 9).
- 3.
- Rasterization. We rasterize the cropped vector data according to the spatial resolution of the RS images and generate labeled raster data, where each pixel value represents a specific category code.
- 4.
- Invalid label cleaning. In full-covered label vector data, invalid labels due to incomplete coverage, edge connection errors, and label errors may appear with extremely low probability. Therefore, it is necessary to classify invalid labels into a certain category for cleaning up.
- 5.
- Data partition. The image–label pairs are divided into training set, validation set, and test set according to the designed proportion.
- 6.
- Generating metadata. In accordance with the partitioned dataset, we need to record the dataset name, partition results, basic attributes of images, categories, file naming rules as metadata to facilitate dataset management and model training.
- 7.
- Manual verification. Check the generated dataset to avoid problems in the above process.
4.2. The Whole Sdfcnv2 Framework
5. Experimental Results and Analysis
5.1. Experiment Datasets
5.2. Model Implementation
- Random rotation by 0°, 90°, 180° or 270°;
- Random vertically and horizontally flipping;
- Random offset (Maximum offset range is consistent with the model input patch size.);
- Selective gamma-transform-based augmentation methods, including GGT, SIGT and SSSGT.
- Overlap fusion strategy with majority voting.
- Mask-weighted voting decision fusion.
- Rotation by four kinds of degrees (0°, 90°, 180° or 270°).
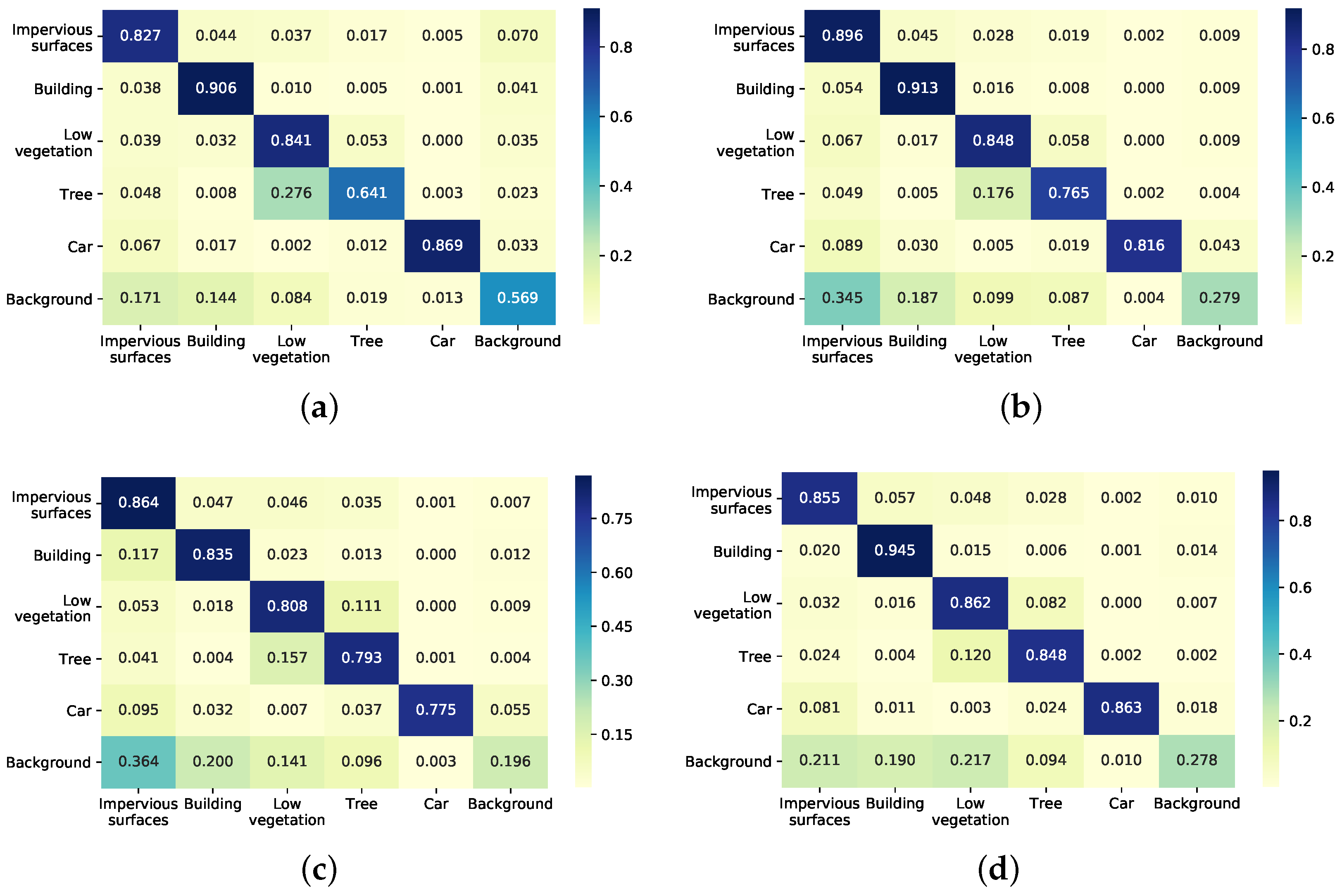
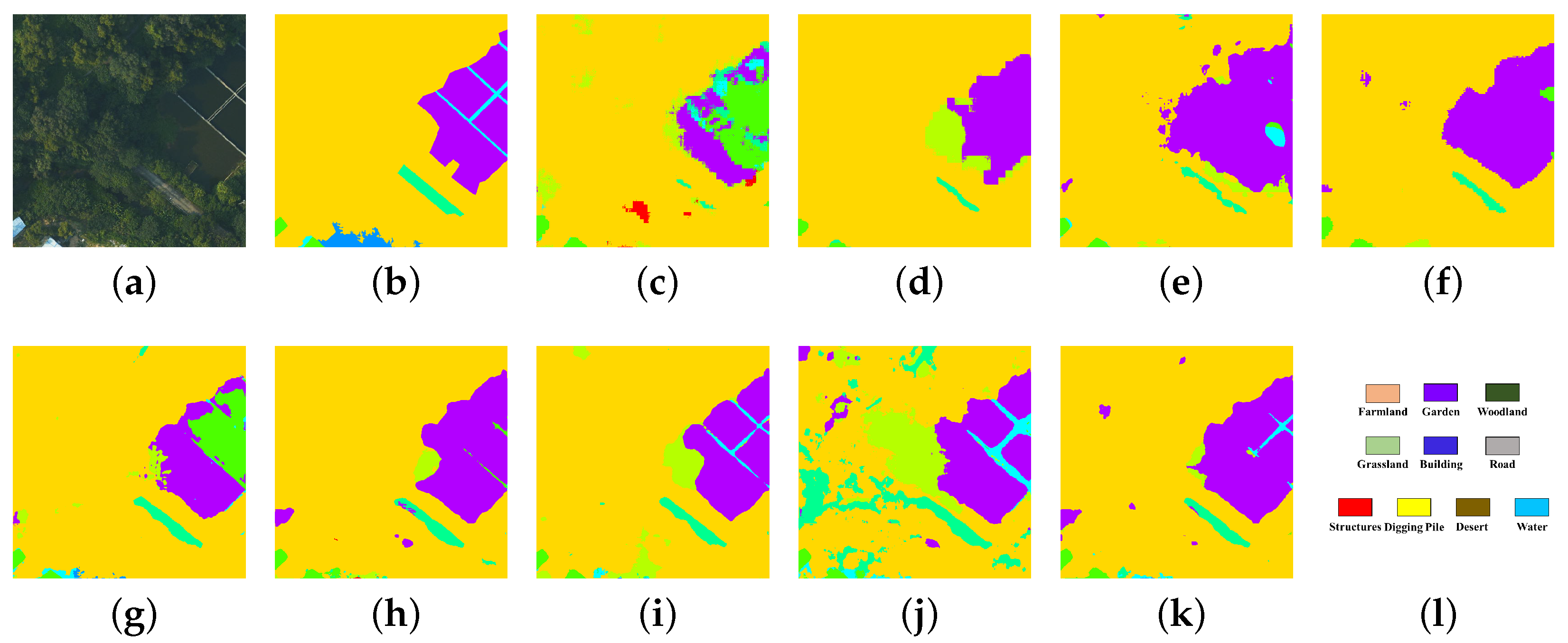
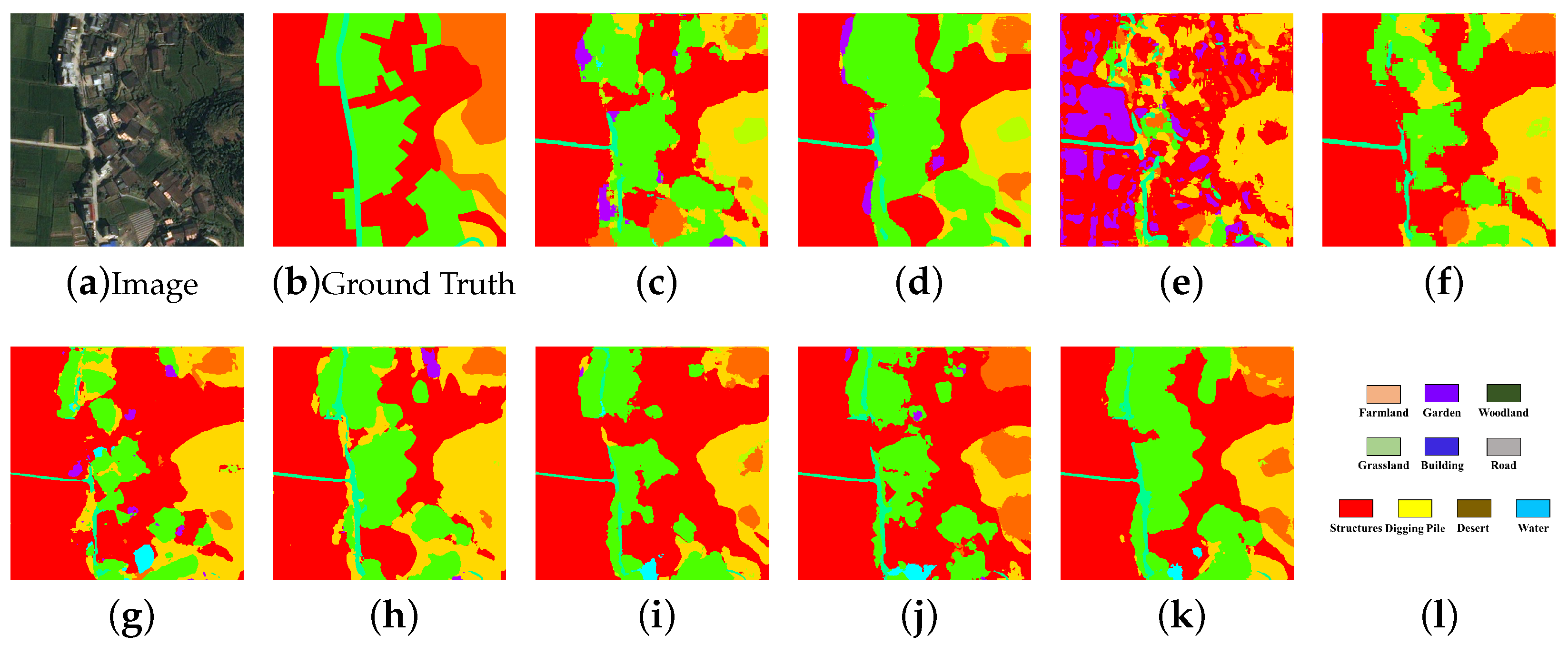
5.3. Experiments on Model Structures and Different Feature Recalibration Modules
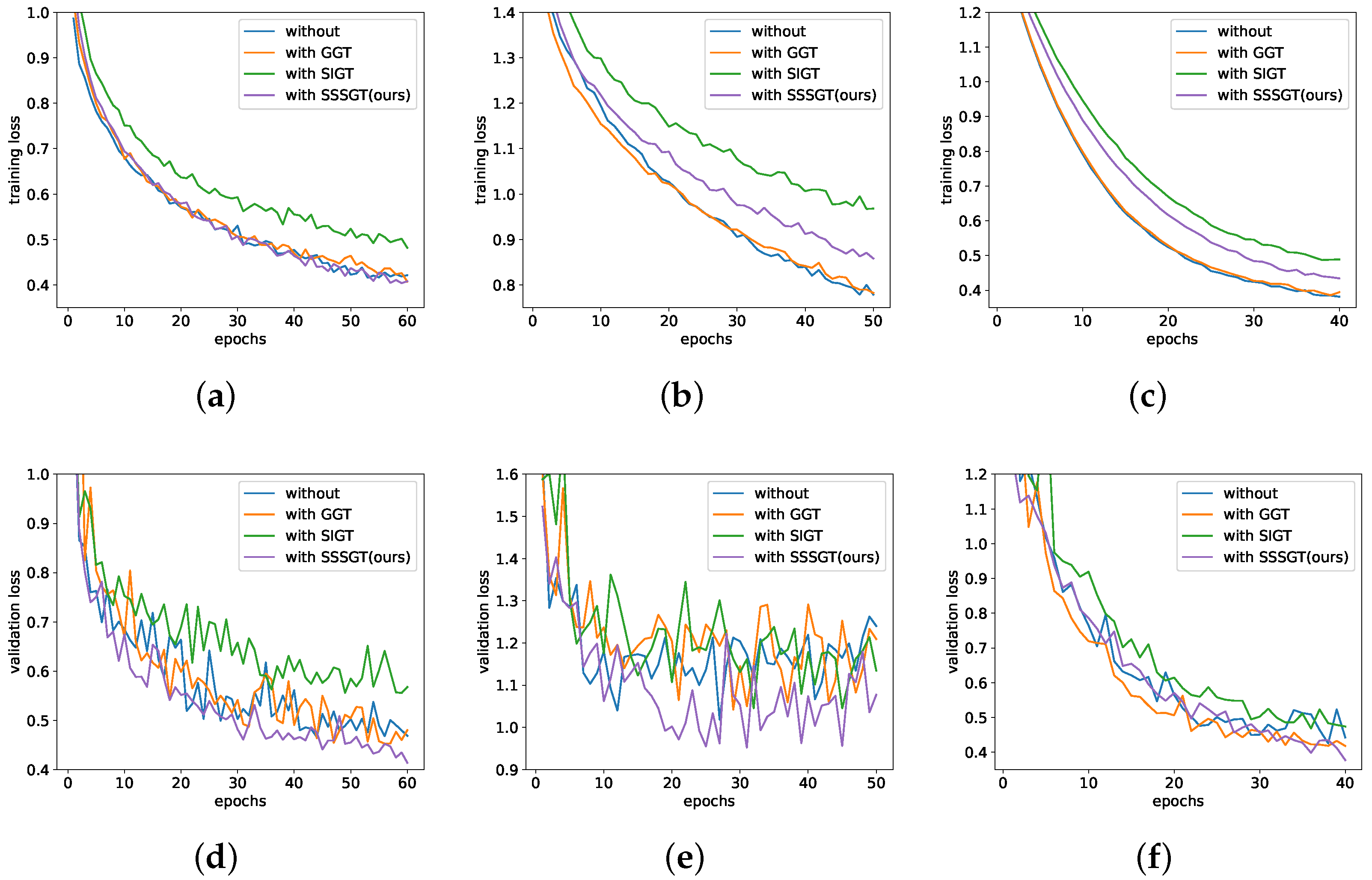
5.4. Experiments on Data Augmentation
5.5. Experiments on Decision Fusion via Mask-Weighted Voting
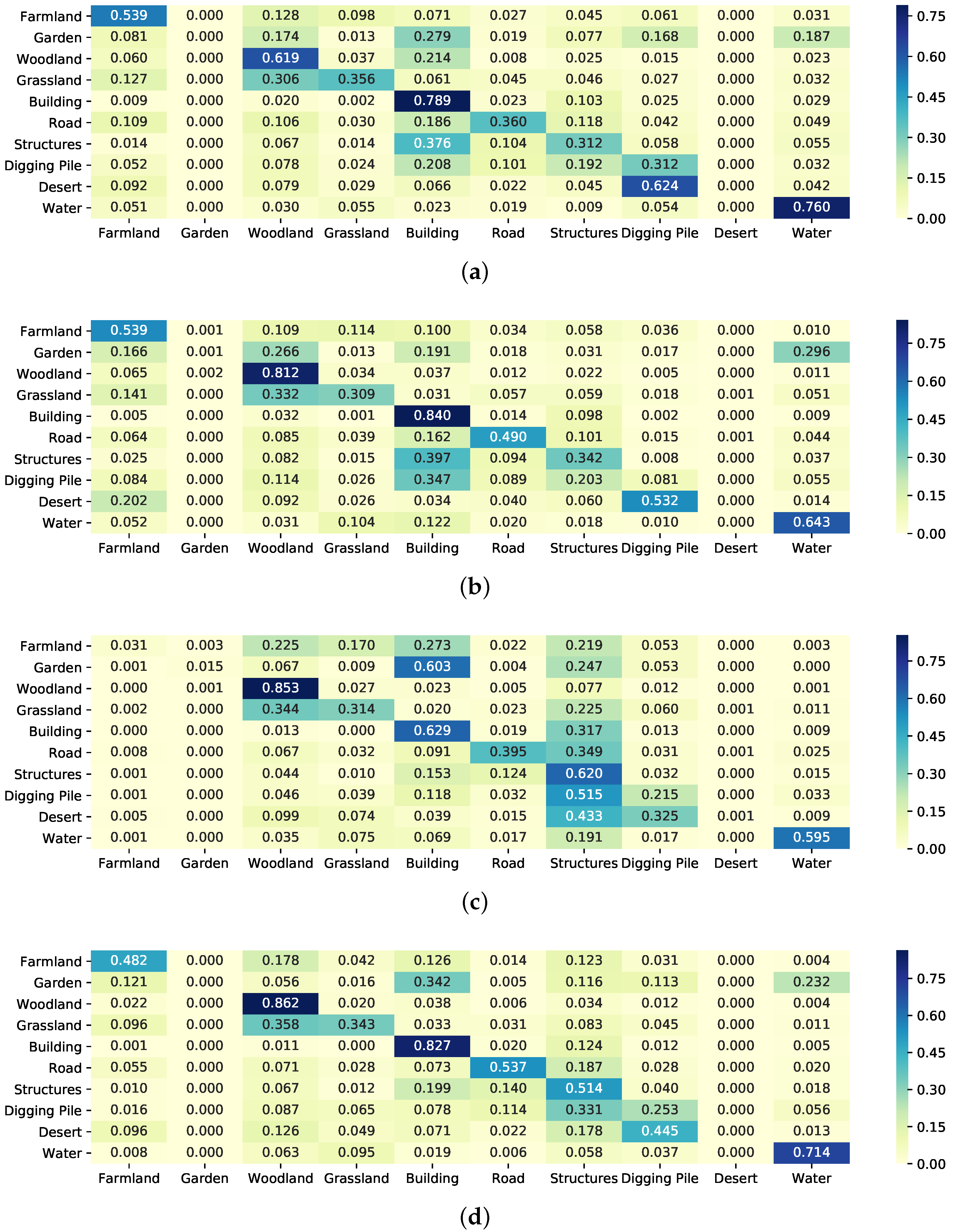
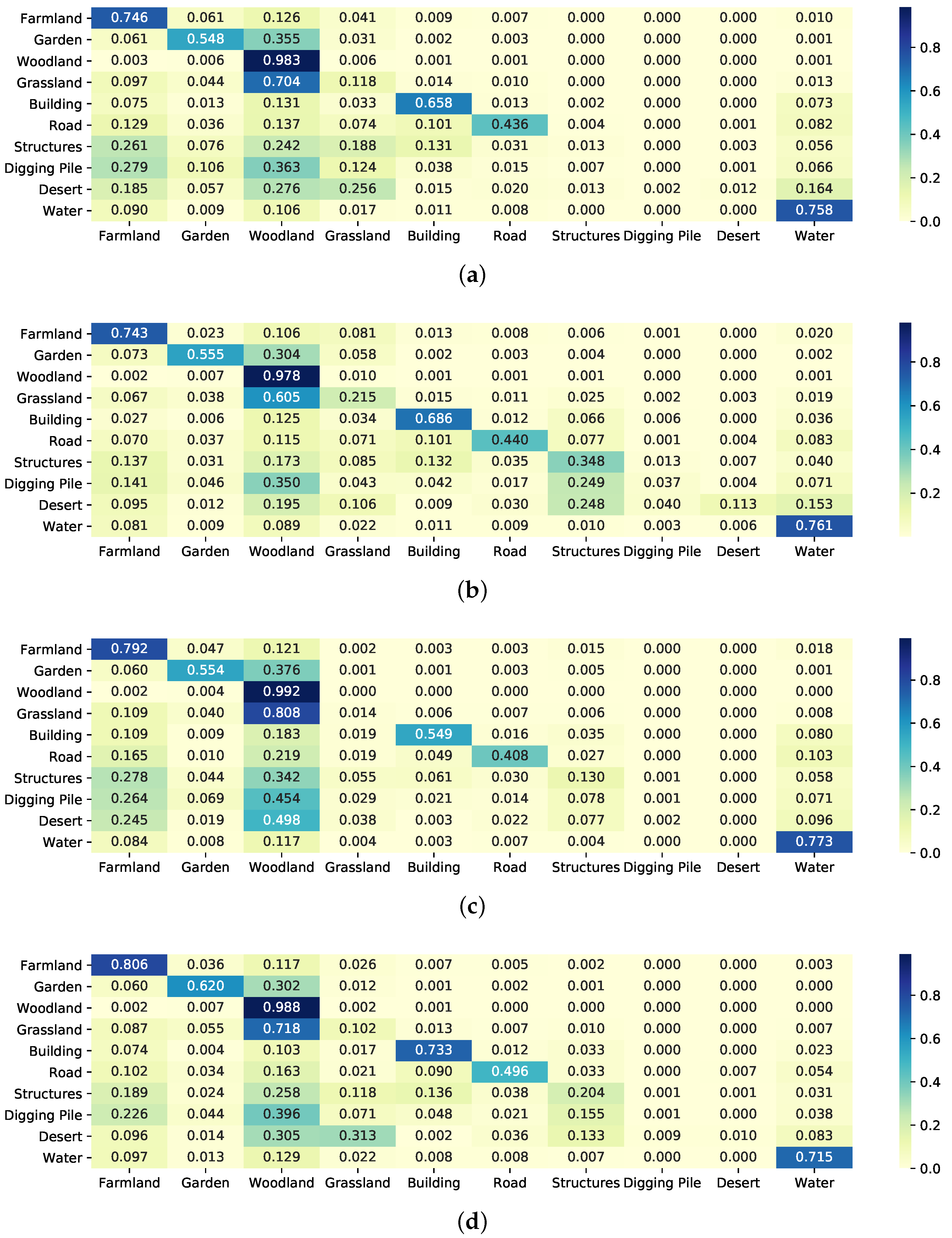
5.6. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cheng, G.; Xie, X.; Han, J.; Guo, L.; Xia, G.S. Remote sensing image scene classification meets deep learning: Challenges, methods, benchmarks, and opportunities. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3735–3756. [Google Scholar] [CrossRef]
- Cheng, G.; Yang, C.; Yao, X.; Guo, L.; Han, J. When deep learning meets metric learning: Remote sensing image scene classification via learning discriminative CNNs. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2811–2821. [Google Scholar] [CrossRef]
- Helber, P.; Bischke, B.; Dengel, A.; Borth, D. Introducing eurosat: A novel dataset and deep learning benchmark for land use and land cover classification. Int. Geosci. Remote Sens. Symp. 2018, 2018, 204–207. [Google Scholar] [CrossRef]
- Metzger, M.J.; Bunce, R.G.; Jongman, R.H.; Sayre, R.; Trabucco, A.; Zomer, R. A high-resolution bioclimate map of the world: A unifying framework for global biodiversity research and monitoring. Glob. Ecol. Biogeogr. 2013, 22, 630–638. [Google Scholar] [CrossRef] [Green Version]
- Taylor, J.R.; Lovell, S.T. Mapping public and private spaces of urban agriculture in Chicago through the analysis of high-resolution aerial images in Google Earth. Landsc. Urban Plan. 2012, 108, 57–70. [Google Scholar] [CrossRef]
- Benediktsson, J.; Chanussot, J.; Moon, W.M. Advances in Very-High-Resolution Remote Sensing. Proc. IEEE 2013, 101, 566–569. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, T.; Chen, G.; Tan, X.; Zhu, K. Convective Clouds Extraction From Himawari-8 Satellite Images Based on Double-Stream Fully Convolutional Networks. IEEE Geosci. Remote Sens. Lett. 2019, 17, 553–557. [Google Scholar] [CrossRef]
- Lateef, F.; Ruichek, Y. Survey on semantic segmentation using deep learning techniques. Neurocomputing 2019, 338, 321–348. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 39, 640–651. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation; Miccai; Springer: Berlin, Germany, 2015; pp. 234–241. [Google Scholar] [CrossRef] [Green Version]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid scene parsing network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2881–2890. [Google Scholar]
- Lin, G.; Milan, A.; Shen, C.; Reid, I. RefineNet: Multi-path refinement networks for high-resolution semantic segmentation. In Proceedings of the 30th IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5168–5177. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 834–848. [Google Scholar] [CrossRef]
- Sun, K.; Zhao, Y.; Jiang, B.; Cheng, T.; Xiao, B.; Liu, D.; Mu, Y.; Wang, X.; Liu, W.; Wang, J. High-resolution representations for labeling pixels and regions. arXiv 2019, arXiv:1904.04514. [Google Scholar]
- Ma, L.; Liu, Y.; Zhang, X.; Ye, Y.; Yin, G.; Johnson, B.A. Deep learning in remote sensing applications: A meta-analysis and review. ISPRS J. Photogramm. Remote Sens. 2019, 152, 166–177. [Google Scholar] [CrossRef]
- Yuan, Q.; Shen, H.; Li, T.; Li, Z.; Li, S.; Jiang, Y.; Xu, H.; Tan, W.; Yang, Q.; Wang, J.; et al. Deep learning in environmental remote sensing: Achievements and challenges. Remote Sens. Environ. 2020, 241, 111716. [Google Scholar] [CrossRef]
- Talukdar, S.; Singha, P.; Mahato, S.; Shahfahad; Pal, S.; Liou, Y.A.; Rahman, A. Land-use land-cover classification by machine learning classifiers for satellite observations—A review. Remote Sens. 2020, 12, 1135. [Google Scholar] [CrossRef] [Green Version]
- Vali, A.; Comai, S.; Matteucci, M. Deep learning for land use and land cover classification based on hyperspectral and multispectral earth observation data: A review. Remote Sens. 2020, 12, 2495. [Google Scholar] [CrossRef]
- Hoeser, T.; Bachofer, F.; Kuenzer, C. Object detection and image segmentation with deep learning on earth observation data: A review-part II: Applications. Remote Sens. 2020, 12, 1667. [Google Scholar] [CrossRef]
- Saha, S.; Mou, L.; Qiu, C.; Zhu, X.X.; Bovolo, F.; Bruzzone, L. Unsupervised Deep Joint Segmentation of Multitemporal High-Resolution Images. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8780–8792. [Google Scholar] [CrossRef]
- Mou, L.; Hua, Y.; Zhu, X.X. Relation Matters: Relational Context-Aware Fully Convolutional Network for Semantic Segmentation of High-Resolution Aerial Images. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7557–7569. [Google Scholar] [CrossRef]
- Hua, Y.; Marcos, D.; Mou, L.; Zhu, X.X.; Tuia, D. Semantic Segmentation of Remote Sensing Images With Sparse Annotations. IEEE Geosci. Remote Sens. Lett. 2021. [Google Scholar] [CrossRef]
- Zhong, Y.; Fei, F.; Liu, Y.; Zhao, B.; Jiao, H.; Zhang, L. SatCNN: Satellite image dataset classification using agile convolutional neural networks. Remote Sens. Lett. 2017, 8, 136–145. [Google Scholar] [CrossRef]
- Ni, W.; Gao, X.; Wang, Y. Single satellite image dehazing via linear intensity transformation and local property analysis. Neurocomputing 2016, 175, 25–39. [Google Scholar] [CrossRef]
- Yu, H.; Yang, W.; Xia, G.S.; Liu, G. A Color-Texture-Structure Descriptor for High-Resolution Satellite Image Classification. Remote Sens. 2016, 8, 259. [Google Scholar] [CrossRef] [Green Version]
- Mohammadimanesh, F.; Salehi, B.; Mahdianpari, M.; Gill, E.; Molinier, M. A new fully convolutional neural network for semantic segmentation of polarimetric SAR imagery in complex land cover ecosystem. ISPRS J. Photogramm. Remote Sens. 2019, 151, 223–236. [Google Scholar] [CrossRef]
- Diakogiannis, F.I.; Waldner, F.; Caccetta, P.; Wu, C. ResUNet-a: A deep learning framework for semantic segmentation of remotely sensed data. ISPRS J. Photogramm. Remote Sens. 2020, 162, 94–114. [Google Scholar] [CrossRef] [Green Version]
- Flood, N.; Watson, F.; Collett, L. Using a U-net convolutional neural network to map woody vegetation extent from high resolution satellite imagery across Queensland, Australia. Int. J. Appl. Earth Obs. Geoinf. 2019, 82, 101897. [Google Scholar] [CrossRef]
- Miyoshi, G.T.; Arruda, M.d.S.; Osco, L.P.; Junior, J.M.; Gonçalves, D.N.; Imai, N.N.; Tommaselli, A.M.G.; Honkavaara, E.; Gonçalves, W.N. A novel deep learning method to identify single tree species in UAV-based hyperspectral images. Remote Sens. 2020, 12, 1294. [Google Scholar] [CrossRef] [Green Version]
- Chen, G.; Zhang, X.; Wang, Q.; Dai, F.; Gong, Y.; Zhu, K. Symmetrical Dense-Shortcut Deep Fully Convolutional Networks for Semantic Segmentation of Very-High-Resolution Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1633–1644. [Google Scholar] [CrossRef]
- Lan, M.; Zhang, Y.; Zhang, L.; Du, B. Global context based automatic road segmentation via dilated convolutional neural network. Inf. Sci. 2020, 535, 156–171. [Google Scholar] [CrossRef]
- Rottensteiner, F.; Sohn, G.; Jung, J.; Gerke, M.; Baillard, C.; Benitez, S.; Breitkopf, U. The isprs benchmark on urban object classification and 3D building reconstruction. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 1, 293–298. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Dou, X.; Peng, J.; Li, W.; Sun, B.; Li, H. EFCNet: Ensemble Full Convolutional Network for Semantic Segmentation of High-Resolution Remote Sensing Images. IEEE Geosci. Remote Sens. Lett. 2021. [Google Scholar] [CrossRef]
- Huang, Z.; Qi, H.; Kang, C.; Su, Y.; Liu, Y. An ensemble learning approach for urban land use mapping based on remote sensing imagery and social sensing data. Remote Sens. 2020, 12, 3254. [Google Scholar] [CrossRef]
- Li, J.; Meng, Y.; Dorjee, D.; Wei, X.; Zhang, Z.; Zhang, W. Automatic Road Extraction from Remote Sensing Imagery Using Ensemble Learning and Postprocessing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 10535–10547. [Google Scholar] [CrossRef]
- Luo, W.; Li, Y.; Urtasun, R.; Zemel, R. Understanding the effective receptive field in deep convolutional neural networks. In Proceedings of the 30th International Conference on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2019; pp. 4967–4970. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the Inception Architecture for Computer Vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 2818–2826. [Google Scholar] [CrossRef] [Green Version]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016. [Google Scholar] [CrossRef] [Green Version]
- Tolias, G.; Sicre, R.; Jégou, H. Particular object retrieval with integral max-pooling of CNN activations. arXiv 2015, arXiv:1511.05879. [Google Scholar]
- Chen, L.C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-decoder with atrous separable convolution for semantic image segmentation. Lect. Notes Comput. Sci. 2018, 11211, 833–851. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.C.; Papandreou, G.; Schroff, F.; Adam, H. Rethinking Atrous Convolution for Semantic Image Segmentation. arXiv 2017, arXiv:1706.05587. [Google Scholar]
- Yu, F.; Koltun, V. Multi-scale context aggregation by dilated convolutions. arXiv 2015, arXiv:1511.07122. [Google Scholar]
- Yu, F.; Koltun, V.; Funkhouser, T. Dilated residual networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 636–644. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Huang, D.; Wang, Y. Receptive Field Block Net for Accurate and Fast Object Detection. Lect. Notes Comput. Sci. 2018, 11215, 404–419. [Google Scholar] [CrossRef] [Green Version]
- Mehta, S.; Rastegari, M.; Shapiro, L.; Hajishirzi, H. ESPNetv2: A light-weight, power efficient, and general purpose convolutional neural network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 9182–9192. [Google Scholar] [CrossRef] [Green Version]
- Takikawa, T.; Acuna, D.; Jampani, V.; Fidler, S. Gated-scnn: Gated shape cnns for semantic segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 5229–5238. [Google Scholar]
- Li, Y.; Chen, Y.; Wang, N.; Zhang, Z.X. Scale-aware trident networks for object detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 6053–6062. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Lee, J. A 3-D Atrous Convolution Neural Network for Hyperspectral Image Denoising. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5701–5715. [Google Scholar] [CrossRef]
- Chen, H.; Lin, M.; Zhang, H.; Yang, G.; Xia, G.S.; Zheng, X.; Zhang, L. Multi-level fusion of the multi-receptive fields contextual networks and disparity network for pairwise semantic stereo. In Proceedings of the 2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 4967–4970. [Google Scholar]
- Chen, X.; Li, Z.; Jiang, J.; Han, Z.; Deng, S.; Li, Z.; Fang, T.; Huo, H.; Li, Q.; Liu, M. Adaptive Effective Receptive Field Convolution for Semantic Segmentation of VHR Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2021, 59, 3532–3546. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 2017, 5999–6009. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-Excitation Networks. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7132–7141. [Google Scholar] [CrossRef] [Green Version]
- Roy, A.G.; Navab, N.; Wachinger, C. Recalibrating fully convolutional networks with spatial and channel “squeeze and excitation” blocks. IEEE Trans. Med. Imaging 2018, 38, 540–549. [Google Scholar] [CrossRef] [PubMed]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. CBAM: Convolutional block attention module. Lect. Notes Comput. Sci. 2018, 11211, 3–19. [Google Scholar] [CrossRef] [Green Version]
- Fu, J.; Liu, J.; Tian, H.; Li, Y.; Bao, Y.; Fang, Z.; Lu, H. Dual attention network for scene segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 3141–3149. [Google Scholar] [CrossRef] [Green Version]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Identity Mappings in Deep Residual Networks. In European Conference on Computer Vision; Leibe, B., Matas, J., Sebe, N., Welling, M., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 630–645. [Google Scholar]
- Zhang, M.; Hu, X.; Zhao, L.; Lv, Y.; Luo, M.; Pang, S. Learning dual multi-scale manifold ranking for semantic segmentation of high-resolution images. Remote Sens. 2017, 9, 500. [Google Scholar] [CrossRef] [Green Version]
- Kingma, D.P.; Ba, J.L. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015—Conference Track Proceedings, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Thompson, W.D.; Walter, S.D. A rEAPPRAISAL of the kappa coefficient. J. Clin. Epidemiol. 1988, 41, 949–958. [Google Scholar] [CrossRef]
- Berman, M.; Rannen Triki, A.; Blaschko, M.B. The lovász-softmax loss: A tractable surrogate for the optimization of the intersection-over-union measure in neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 4413–4421. [Google Scholar]



| Model | # of Parameters | Model File Size |
|---|---|---|
| FCN-8s | 184,631,780 | 704.39 MB |
| PSPNet | 47,346,560 | 181.15 MB |
| Deeplab v3+ | 41,254,358 | 158.39 MB |
| HRNetV2 | 9,524,696 | 37.12 MB |
| SDFCNv1 | 44,705,118 | 170.86 MB |
| SDFCNv2 | 18,606,430 | 71.42 MB |
| SDFCNv2 + SE | 19,638,622 | 75.47 MB |
| SDFCNv2 + scSE | 19,643,998 | 75.59 MB |
| SDFCNv2 + SCFSE | 19,638,982 | 75.88 MB |
| Dataset | Source | GSD | Spectral Band | Category | Number of Image and Division (Train, Val and Test) |
|---|---|---|---|---|---|
| Potsdam | Aerial | 0.05 m | IRRGB | 6 | 38 (18, 6, 14) |
| Evlab | Satellite & Aerial | 0.1–1 m | RGB | 10 | 45 (28, 9, 8) |
| Songxi | Satellite & Aerial | 0.5 m | RGB | 10 | 26 (12, 5, 9) |
| Model | Potsdam Dataset | EvLab Dataset | Songxi Dataset | ||||||
|---|---|---|---|---|---|---|---|---|---|
| OA | K | mIoU | OA | K | mIoU | OA | K | mIoU | |
| FCN-8s | 0.7444 | 0.7021 | 0.5586 | 0.4730 | 0.4313 | 0.2067 | 0.8567 | 0.7215 | 0.3456 |
| PSPNet | 0.8059 | 0.7687 | 0.6364 | 0.4956 | 0.4647 | 0.2559 | 0.8602 | 0.7307 | 0.3833 |
| Deeplab V3+ | 0.7436 | 0.6989 | 0.5263 | 0.5492 | 0.5085 | 0.2733 | 0.7708 | 0.5758 | 0.2042 |
| HRNet V2 | 0.8380 | 0.8029 | 0.6584 | 0.5288 | 0.4831 | 0.2453 | 0.8584 | 0.7208 | 0.3448 |
| SDFCN V1 | 0.8006 | 0.7615 | 0.6081 | 0.5083 | 0.4641 | 0.2448 | 0.8627 | 0.7280 | 0.3440 |
| SDFCNv2 | 0.8473 | 0.8140 | 0.6741 | 0.5773 | 0.5380 | 0.2963 | 0.8461 | 0.6955 | 0.3458 |
| SDFCNv2+SE | 0.8419 | 0.8077 | 0.6744 | 0.5631 | 0.5301 | 0.3017 | 0.8657 | 0.7340 | 0.3708 |
| SDFCNv2+scSE | 0.8262 | 0.7920 | 0.6685 | 0.4883 | 0.4532 | 0.2496 | 0.8697 | 0.7471 | 0.3621 |
| SDFCNv2+SCFSE | 0.8503 | 0.8177 | 0.6782 | 0.5945 | 0.5539 | 0.3208 | 0.8762 | 0.7562 | 0.3980 |
| Gamma Augmentation | Potsdam Dataset | EvLab Dataset | Songxi Dataset | ||||||
|---|---|---|---|---|---|---|---|---|---|
| OA | K | mIoU | OA | K | mIoU | OA | K | mIoU | |
| No | 0.8306 | 0.7952 | 0.6531 | 0.5398 | 0.4963 | 0.2623 | 0.8501 | 0.7073 | 0.3153 |
| GGT | 0.8287 | 0.7927 | 0.6508 | 0.4572 | 0.4263 | 0.2204 | 0.8336 | 0.6714 | 0.3160 |
| SIGT | 0.8261 | 0.7897 | 0.6574 | 0.5181 | 0.4769 | 0.2310 | 0.8718 | 0.7483 | 0.3895 |
| SSSGT (ours) | 0.8503 | 0.8177 | 0.6782 | 0.5945 | 0.5539 | 0.3208 | 0.8762 | 0.7562 | 0.3980 |
| Overlap Rate | rot90° ×4 | Weigthed-Mask (Ours) | Potsdam Dataset | EvLab Dataset | Songxi Dataset | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| OA | K | mIoU | OA | K | mIoU | OA | K | mIoU | |||
| 0% | × | × | 0.8503 | 0.8177 | 0.6782 | 0.5945 | 0.5539 | 0.3208 | 0.8762 | 0.7562 | 0.3980 |
| 25% | × | × | 0.8573 | 0.8256 | 0.6867 | 0.6016 | 0.5611 | 0.3277 | 0.8784 | 0.7602 | 0.4032 |
| × | ✓ | 0.8576 | 0.8259 | 0.6871 | 0.6025 | 0.5619 | 0.3287 | 0.8787 | 0.7608 | 0.4040 | |
| ✓ | × | 0.8639 | 0.8331 | 0.6973 | 0.6137 | 0.5730 | 0.3380 | 0.8815 | 0.7659 | 0.4096 | |
| ✓ | ✓ | 0.8642 | 0.8334 | 0.6978 | 0.6145 | 0.5738 | 0.3392 | 0.8818 | 0.7665 | 0.4102 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, G.; Tan, X.; Guo, B.; Zhu, K.; Liao, P.; Wang, T.; Wang, Q.; Zhang, X. SDFCNv2: An Improved FCN Framework for Remote Sensing Images Semantic Segmentation. Remote Sens. 2021, 13, 4902. https://doi.org/10.3390/rs13234902
Chen G, Tan X, Guo B, Zhu K, Liao P, Wang T, Wang Q, Zhang X. SDFCNv2: An Improved FCN Framework for Remote Sensing Images Semantic Segmentation. Remote Sensing. 2021; 13(23):4902. https://doi.org/10.3390/rs13234902
Chicago/Turabian StyleChen, Guanzhou, Xiaoliang Tan, Beibei Guo, Kun Zhu, Puyun Liao, Tong Wang, Qing Wang, and Xiaodong Zhang. 2021. "SDFCNv2: An Improved FCN Framework for Remote Sensing Images Semantic Segmentation" Remote Sensing 13, no. 23: 4902. https://doi.org/10.3390/rs13234902
APA StyleChen, G., Tan, X., Guo, B., Zhu, K., Liao, P., Wang, T., Wang, Q., & Zhang, X. (2021). SDFCNv2: An Improved FCN Framework for Remote Sensing Images Semantic Segmentation. Remote Sensing, 13(23), 4902. https://doi.org/10.3390/rs13234902