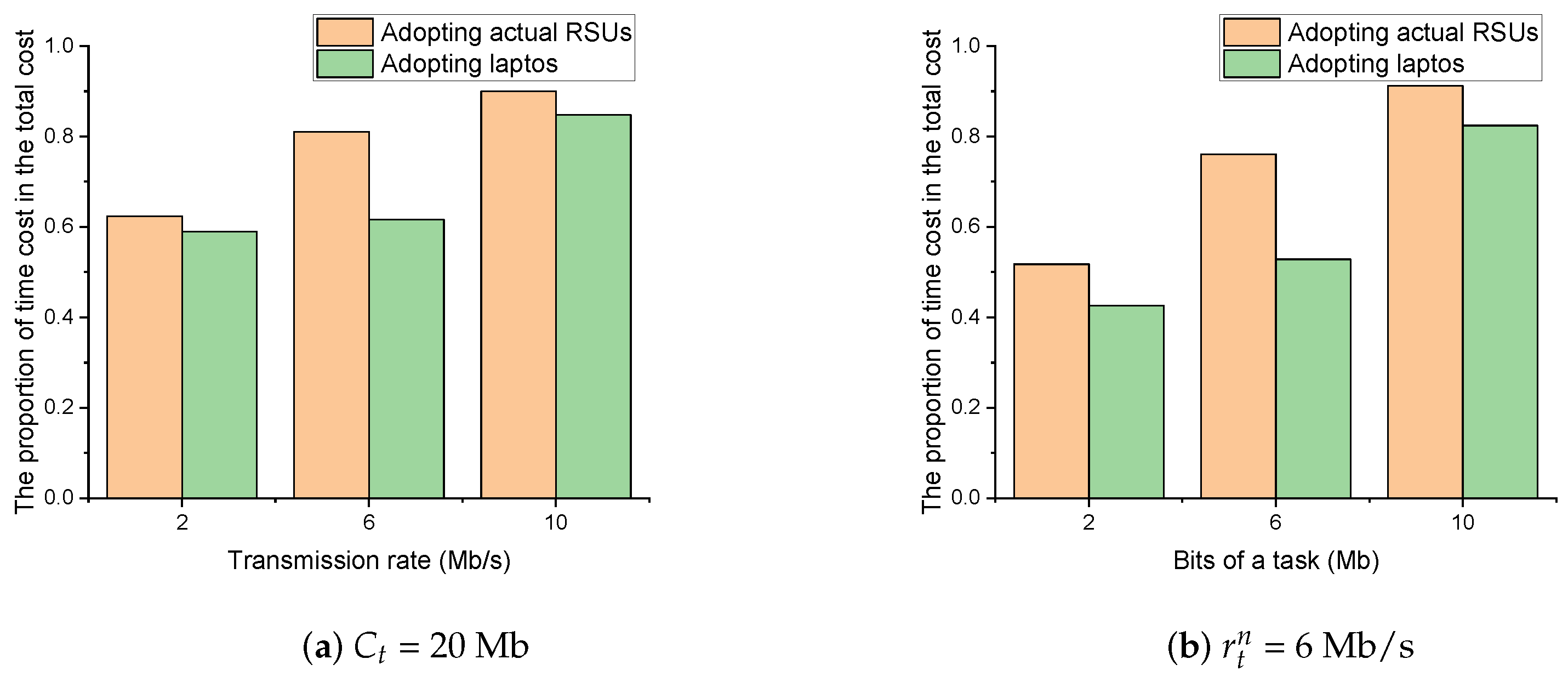Abstract
Unmanned aerial vehicle (UAV) plays a more and more important role in Internet of Things (IoT) for remote sensing and device interconnecting. Due to the limitation of computing capacity and energy, the UAV cannot handle complex tasks. Recently, computation offloading provides a promising way for the UAV to handle complex tasks by deep reinforcement learning (DRL)-based methods. However, existing DRL-based computation offloading methods merely protect usage pattern privacy and location privacy. In this paper, we consider a new privacy issue in UAV-assisted IoT, namely computation offloading preference leakage, which lacks through study. To cope with this issue, we propose a novel privacy-preserving online computation offloading method for UAV-assisted IoT. Our method integrates the differential privacy mechanism into deep reinforcement learning (DRL), which can protect UAV’s offloading preference. We provide the formal analysis on security and utility loss of our method. Extensive real-world experiments are conducted. Results demonstrate that, compared with baseline methods, our method can learn cost-efficient computation offloading policy without preference leakage and a priori knowledge of the wireless channel model.
1. Introduction
With the rapid development of unmanned aerial vehicles (UAVs), they are applied in the various applications, such as data collection and remote sensing among Internet of Things (IoT) sensors [1]. Although the benefits of high mobility, swift deployment, and low economic cost, large-scale application of UAV is limited by the computation capacity and energy. Recently, computation offloading is regarded as a promising solution for enabling UAV-assisted IoT to process huge data produced by IoT sensors [2,3].
Existing computation offloading methods for IoT focus on two main categories, i.e., one-shot optimization methods [4,5] and DRL-based methods [6,7]. Compared with one-shot optimization methods, the DRL-based methods can assist devices to learn computation offloading policy with higher energy efficiency and low time delay. Besides this benefit, DRL-based methods allow the devices to learn computation offloading policy without a priori knowledge of wireless channel model, which can be applied to solve the wireless channel dynamic between the UAV and IoT sensors [8].
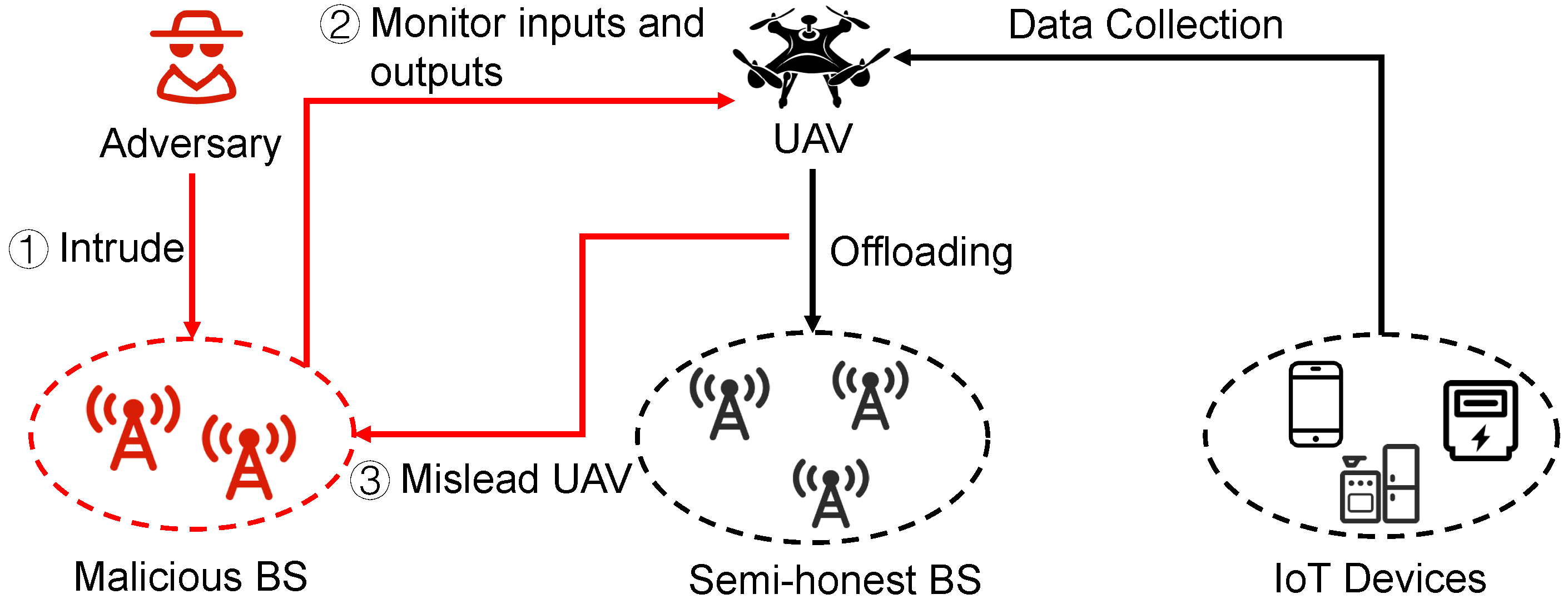
Although the benefits of applying DRL into computation offloading, the vulnerabilities in DRL can be exploited by adversaries to interfere the UAV with learning policy [9], which hinders it from being applied to the real world. Figure 1 provides a case of computation offloading preference leakage over UAV-assisted IoT. The adversary misleads the UAV to offload tasks to malicious BSs by inversing the RL algorithm based on the observations of the offloading decision and the transmission radio link status.
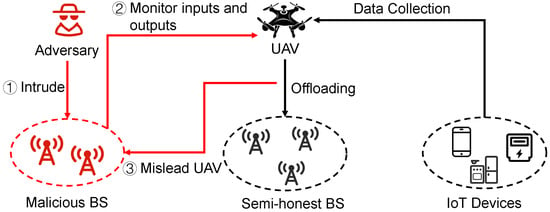
Figure 1.
The offloading performance leakage problem in UAV-assisted online computation offloading.
1.1. Related Works and Challenges
(1) DRL-based Computation Offloading in UAV-Assisted MEC Networks: Zhou et al. [10] formulated the computing task scheduling problem as a constrained Markov decision process (CMDP) and solved it by proposing a novel risk-sensitive DRL method, where the UAV’s energy consumption violation is defined as the risk metric. Liu et al. [11] modified the vanilla Q-Learning algorithm to maximize the profit of the UAV under the constant cruising path. Recently, multi-UAV scenario also has been taken into consideration. Wei et al. [12] proposed a distributed DRL-based method that is enhanced by prioritized experience replay (PER), denoted as DDRL-PER. In their work, the proposed DDRL-PER method is adopted to solve the computation offloading problem over multi-UAV MEC network. Zhu et al. [13] decomposed the complex task and proposed a DRL-based method for the task offloading over UAV group, which optimizes the policy under the constraints of energy, dynamic network state. Seid et al. [14] designed a collaborative learning framework for computation offloading and resource allocation over multi-UAV-assisted IoT, where the UAV group was divided into multiple clusters. Then, the distributed deep deterministic policy gradient (DDPG) algorithms was adopted to solve the multi-cluster computation offloading problem. Sacco et al. [15] also proposed a multi-agent DRL-based method to solve the multi-tasks offloading problem over multi-UAV networks. Moreover, Gao et al. [16] combined game theory with DRL to solve the joint optimization of task offloading and multi-UAV trajectories.
Challenge 1: Existing DRL-based methods for computation offloading over UAV-assisted IoT take protecting computation offloading preference into consideration.
(2) Privacy Preserving in MEC: Considering the privacy preserving has not been widely researched over UAV-assisted MEC networks, we extend our review to the architectures of MEC networks that are not limited to UAV-assisted MEC networks. The privacy issues related to DRL-based offloading method were firstly investigated by He et al. [17]. The privacy constraints were generated in the value function, and the computation offloading policy was learned within several training episodes. Then, the authors adopted Q-learning method to solve the private problem. Furthermore, an active suppression method was proposed in Reference [18], which can prevent adversaries from eavesdropping. However, this method needs to modify the hardware, such as the antenna of mobile devices, in order to effectively suppress adversaries with different signal types. In addition, this active suppression method leads to excessive hardware modification costs when it is applied on a large scale UAV-assisted IoT. To improve the privacy-preserving learning efficiency of computation offloading policy, Min et al. [19] utilized the transfer learning and Dyna architecture to accelerate the learning speed, while He et al. [20] proposed the RL- and DRL-based methods based on generic framework of Lyapunov optimization, which is resistant to user presence inference attack. Existing works holds the assumption that there is no malicious BSs; thus, they mainly generate private constraints in value function to preserve the privacy. However, malicious BSs cannot be completely avoided in the real world. Once the value function is obtained by adversaries, the adversaries can compromise the mobile devices to offload computation tasks to malicious BSs.
Challenge 2: Existing privacy-preserving works that are designed for the DRL-based computation cannot prevent the malicious BSs from inferring the value function of the DRL algorithm.
1.2. Contributions
To solve the aforementioned privacy issues in existing works, we propose a differential privacy (DP)-based deep Q-learning (DP-DQL) method to solve the computation offloading preference leakage issue over UAV-assisted IoT. Our contributions can be summarized as follows.
- We investigate a new privacy leakage issue within the online computation offloading over UAV-assisted IoT, namely computation offloading preference leakage.
- We propose a differential privacy-based deep Q-learning (DP-DQL) method to protect computation offloading preference over UAV-assisted IoT. In the proposed DP-DQL method, the DQL is adopted as the basic framework for efficiently learning computation offloading policy without the a priori knowledge of the wireless channel model. Then, a generated Gaussian noise is generated in the policy updating process of DQL, which can protect the computation offloading preference. Finally, the learning speed of DP-DQL is accelerated by the PER technique [21] by replying the experience with high temporal-difference error.
- We provide theoretical analysis for the differential privacy guarantee and utility loss. Then, the convergence, privacy protection, and cost efficiency of our method is demonstrated by extensive real-world experiments. The results show that our method can help UAV learn the cost-efficient computation offloading policy with the differential privacy guarantee.
The rest of this paper is organized as follows. Section 2 gives the necessary background, system model and problem formulation, details of the proposed method and theoretical analysis. Then, we design and conduct the experiments in Section 3. We discuss the impact of key parameters on the convergence and the limitations of the proposed method in Section 4. Finally, we conclude this paper in Section 5.
2. Materials and Methods
In this section, we first provide the background techniques. Then, we describe the system model and formulate the research problem of this paper. Finally, we show the proposed DP-DQL method and give the theoretical analysis in terms of privacy guarantee and utility loss.
2.1. Background Techniques
2.1.1. Differential Privacy
Differential privacy [22,23] establishes a strong standard for privacy guarantees in knowledge transfer, which aims to disable data analysis algorithms from distinguishing between two neighboring inputs. The key definitions are provided in the following.
Definition 1.
For any two neighboring inputs and subset of outputs , the ()-differential privacy can be guaranteed once the mechanism satisfies the inequality
The definition of output’s global sensitivity is shown as follows.
Definition 2.
Given as neighboring inputs, the output’s global sensitivity can be computed as
where represents the norm function in .
2.1.2. Deep Q-Learning
Deep Q-learning [24] leverages the deep neural network to approximate the value function, which aims to find a policy that can minimize the Bellman error as follows.
2.2. System Model and Problem Formulation
2.2.1. System Model
Figure 1 shows a UAV-assisted MEC system for IoT, which contains N fixed base stations (BSs), denoted as a set and a UAV. is the coordinate of BS n, and is the coordinate of the UAV, where h indicates the flight height of UAV. Referring to Reference [25], UAV adopts Wi-Fi or LTE technology to communicate with BS and smart factories. At each time slot t, a computation task (e.g., pattern recognition) is collected by the UAV from a smart factory, where . The task is described as , where is the maximum execution time, and is the bits of task . Morevoer, every CPU cycles can process a bit in the task.
Due to the binary computation offloading is the special case of partial computation offloading [26,27], we investigate partial offloading in this paper for generality. To process a task, the UAV needs to decide how much of a task should be offload to BSs. Formally, represents the offloaded proportion of a task . To improve the performance of computation offloading decision, the UAV can adjust the offloaded proportion of a task. We define the CPU frequency of the BS and UAV as and f, respectively. We assume that the each BS has the same CPU frequency, which can avoid some of fallacies of computing during BS parallel processes tasks [28]. Hence, the cost model is shown in the following. The time spent for locally processing a task is
The local energy consumption is
where the is a coefficient related to the CPU architecture [29].
The cost on offloading task to BS n consists of two parts, i.e., the time cost and the energy cost. The time for offloading and processing task is
where the is the time for transmitting the task to BSs, and represents the processing time in the BS.
Based on References [30,31], the energy consumption on transmitting a task to BS n depends on the transmit power , which can be shown as
In this paper, we assume that the BSs have sufficient energy. This is reasonable that fixed BSs are usually deployed in the area that has wired power supplied by grid. Hence, the energy consumption on the BS is not considered in this paper. For convenience, the major notations used in this paper are summarized in Table 1.

Table 1.
List of major notations.
2.2.2. Threat Model and Privacy Issue
In this paper, we consider a new privacy leakage issue over UAV-assisted IoT, namely computation offloading preference leakage, which is shown in Figure 1. In this paper, we assume that the adversary knows the inputs and formats of UAV’s computation offloading policy in advance. It is reasonable to make the assumption because:
- The BSs can provide customized services for UAV based on the formats of UAV’s computation offloading policy and the inputs of the policy.
- Once the adversary induce the BS, it can monitor the inputs and formats of UAV’s computation offloading policy.
In accordance with above assumptions, the adversaries monitor UAV’s computation offloading decision and the input of computation offloading policy, e.g., radio link transmission rate between UAV and BSs. The adversaries utilize an algorithm, such as inverse reinforcement learning algorithm, to infer the UAV’s computation offloading preference based on monitoring results. Furthermore, the adversaries construct specific inputs for UAV’s computation offloading policy, e.g., improving radio link transmission rate with the help of malicious BSs, which can mislead UAV to offload computation tasks onto the malicious BSs.
2.2.3. Design Goals
To solve above privacy issues, our proposed method should reach the goals as follows.
- Differential privacy guarantee: DP-DQL method should provide -differential privacy for UAV during learning process so that the value function of the UAV’s computation offloading policy will not be inferred by the adversaries based on the system state and offloading decision.
- Minor utility loss: DP-DQL method should guarantee that, compared with the traditional DQL method, the performance of the DP-DQL method will not be significantly degraded by adding the differential privacy mechanism.
2.2.4. Problem Formulation
As claimed in Section 2.1.2, we formulate the problem of privacy-preserving computation offloading in UAV-assisted MEC network for IoT as the Markov decision process (MDP), which is defined as a tuple .
- (1)
- System state: The system state is the offloaded proportion. Formally, ranges from 0 to 1.
- (2)
- Action space: The UAV adjusts the offloaded proportion of a task by increasing or decreasing from 0 to 0.25. Formally, .
- (3)
- Reward function: The weighted average of energy and time costs is adopted as the reward function, which is given as follows:
2.3. DP-Based Deep Q-Learning for Computation Offloading
In this section, we firstly give an overview of the DP-DQL. Then, the details for the DP-DQL are provided.
2.3.1. Overview
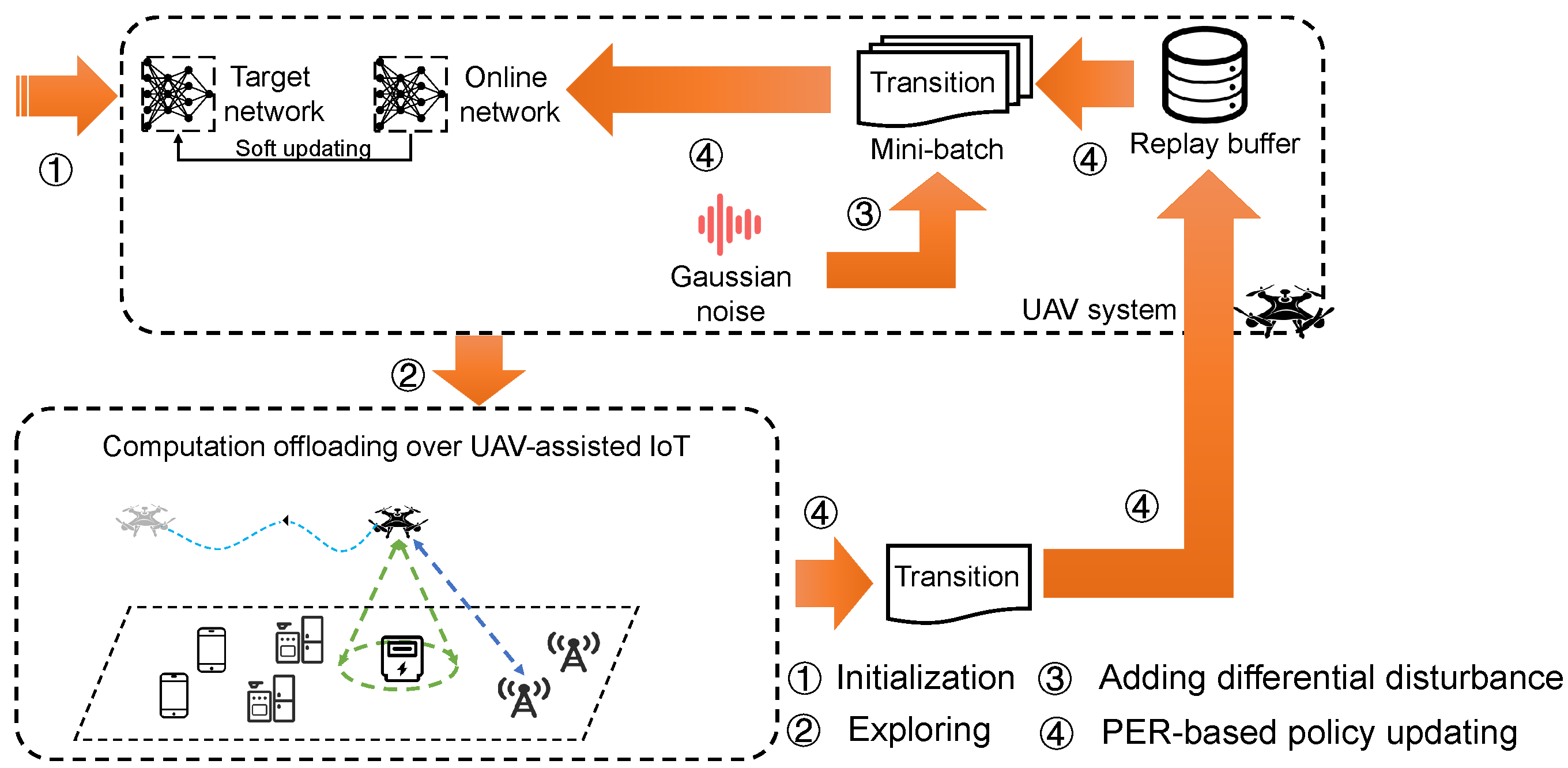
The steps of online learning are shown in Figure 2, which consists of four stages.
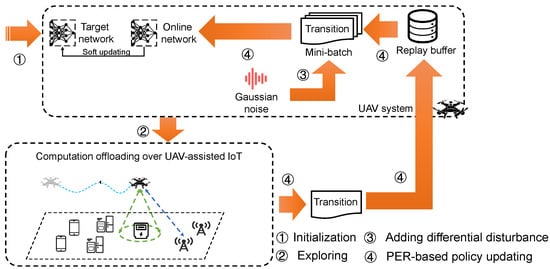
Figure 2.
The overview of the proposed DP-DQL approach.
- Initialization: Initializing the parameters used in DP-DQL approach.
- Exploring: The UAV executes offloading action and obtains reward from the environment.
- Generating differential disturbance: The UAV generates the specific Gaussian noise to prevent the computation offloading preference leakage.
- PER-based policy updating: The UAV updates computation offloading policy with the help of PER technique.
Algorithm 1 shows the details of the DP-DQL method, and its description is given as follows.
| Algorithm 1 Differential Privacy-based Deep Q-Learning for computation offloading method |
|
2.3.2. Initialization (Lines 1–4)
The online policy and target policy are initialized with random weights and (Lines 1), where the target policy is used to slow the updating rate of online policy and, hence, improve the stability of the algorithm. The environment is constructed for learning computation offloading policy. Then, the differential dict is initialized and reset to every training episodes. (Line 4). The differential dict is defined as a Dictionary structure, where the key size and value size are set to and 2, respectively.
2.3.3. Exploring (Lines 5–8)
If a task is collected by UAV at time slot t, the UAV makes offloading decision by online computation offloading policy under differential disturbance (Line 6). After receiving the reward (Line 6), the UAV obtains a new state (Line 7). Based on old state , action , new state , and reward , the UAV constructs a transition. Then, the UAV compute the priority and store it in replay buffer with the transition (Line 8). Based on Reference [21], the priority can be computed as follows:
The in Equation (9) is given as follows:
where .
2.3.4. Generating Differential Disturbance (Lines 9–11)
Once replay buffer is filled with the transitions (Line 9), a mini-batch of the transitions will be sampled from replay buffer to update online and target policies (Line 10). Gaussian process generates a differential disturbance for each action (Line 11). The differential disturbance is appended to differential dict , then is sorted. The and are given below based on [32]:
where , represents the balance factor, , , and .
2.3.5. PER-Based Policy Updating (Lines 12–21)
In this stage, the accumulated policy gradient is calculated based on PER technique. Specifically, the sampling probability of a transition is computed by (Line 12)
where the is the index of a transition. Then, the function of importance sampling weight (Line 13) is to decrease bias referred to Reference [21], which is given as follows:
where is the sampled probability, represents the replay buffer size, is used to determine how much priority affects the sampling probability, and is an importance factor of transition. Hence, the TD-error is calculated via Equation (9) (Lines 14), and the absolute TD-error value is adopted to update the ith transition priority (Lines 15). Finally, the accumulated policy gradient is computed based on a chain rule in Reference [33] as shown below (Line 16):
where is the gradient of the online policy for vector . Then, the online policy is softly update as follows:
where is a soft update coefficient (Line 18). Then, set . Finally, the target policy is updated (Line 18).
2.4. Theoretical Analysis
2.4.1. Differential Privacy Guarantee
To analyze the differential privacy guarantee of the DP-DQL method under the adversary model in Section 2.2.2, we firstly provide a necessary theorem.
Theorem 1.
Given the sample path k from Gaussian process , exists with high probability. For each in Sobolev space , we have
where the .
Proof.
Firstly, we define some necessary notations. For a sample path k, we define and , where , , .
Then, we consider the base case that the sample path k contains two elements, i.e., . Therefore, the expectation is
which is based on .
Finally, we consider the case of . Specifically, we aim to bound the expectation for all . Referring to Chernoff bound, we have
where is the p independent Gaussian random variables based on . Let , we have .
Let . Due to , the series is non-decreasing. Then, we derive the upper bound of . Referring to Reference [32], we have . The bound of is given as follows.
Hence,
Finally, we have
Based on induction, we can get ,
Referring to Reference [34], shares the same upper bound of almost surely when k is continuous with probability one. Hence, Theorem 1 follows. □
Theorem 2.
The proposed DP-DQL method ensures the ()-differential privacy once neighboring rewards , if
and
where , , X represents the Lipschitz constant, A is the mini-batch size, and V is the training episodes.
Proof.
To prove this theorem, we firstly prove that the neighboring value functions cannot be distinguished with differential privacy guarantee in one policy updating step. Then, we extend conclusion to multiple policy updating steps. Referring to Reference [35], we have
where is the value function from u and is the value function from . Note that . The inequality holds with at least probability of , where is the neighboring value function of , according to Theorem 1. Then, for each , holds based on triangle inequality with the same . Let , we can obtain Equation (27) in the Sobolev space.
Let , and the Equation (27) can be rewritten as
Referring to Reference [36], we can get
by adding Gaussian disturbance to within a policy updating step on the basis of Equation (25). This conclusion can be generalized to multiple policy updating steps by the theorem in Reference [37]. Hence, Theorem 2 is proved. □
2.4.2. Minor Utility Loss
Before giving the final proof of utility loss, we show a necessary theorem and its proof.
Theorem 3.
Assume that is the optimal result of the inequality constraint problem
and we can obtain
Proof.
Given , we can get Equation (32) based on the strong duality and non-negativity in (♠) and (▪), respectively.
□
Finally, we prove the convergence of the proposed method through Theorem 4.
Theorem 4.
Compared with vanilla DQL, the utility loss of the our DP-DQL method tends to be 0 even under the worst case, where .
Proof.
We have Equation (33) by solving Equation (30)
according to Theorem 3. Further, according to Reference [32], the equation holds. Based on the strong duality, we have . As . Considering state space is infinity, the upper bound of tends to be zero. Moreover, Reference [24] guarantees the convergence of vanilla DQL. Therefore, our DP-DQL method achieves minor utility loss compared with vanilla DQL and converges within finite training episodes. □
3. Results
In this section, we design four experiments to evaluate the convergence, privacy protection and cost efficiency of the DP-DQL method.
3.1. Experiment Settings
Scenario: In this paper, the UAV flies around the area at a constant height to collect data and make computation offloading decision based on its offloading policy. The device for locally processing task is a Raspberry Pi 3B+, which is adopted as the airborne computer. Figure 3a shows the architecture of UAV used for experiments, and the flying area is shown in Figure 3b. In this paper, we firstly randomly deploy three laptops in Figure 3b to represent the BSs. Then, we deploy three actual rodeside units (RSU) to evaluate the variation of results. Because the computing power of actual RSU is similar to that of Raspberry Pi [38,39], the actual RSU is represented by the Raspberry Pi 4.

Figure 3.
The illustration of real-world experiment.
Parameter settings: The radio link transmission rate from n-th BS to the UAV is {2 Mb/s, 6 Mb/s, 10 Mb/s}. At each time slot t, the values of data size for the task is {20 Mb, 40 Mb, 60 Mb}, and each task should be processed within s. During task processing, each bit needs CPU cycles to process [40]. As defined in Reference [41], the transmit power form BSs to the UAV is W. The proposed DP-DQL method is implemented by Pytorch 1.1 and Python 3.6. We adopt a four-layer fully-connected feedforward neural network to implement the online and target policies. The learning rate is set to 0.001, while the discounted factor is set to 0.999. The replay buffer size is 1024. The size of mini-batch A is 128. During online learning, there are training episodes and learning steps in every training episode. For convenience, the all values of parameters are summarized in Table 2.

Table 2.
Parameter values.
3.2. Baseline Methods
We evaluate the efficiency of our DP-DQL method by comparing it with two baseline methods:
- Greedy: This method has been widely adopted as a baseline method, where all tasks are fully offloaded to the BSs.
- Deep Q-learning with non-differentially-private mechanism (DQL-non-DP) [19]: We adopt a model-free method designed for healthcare IoT network [19] and adjust it according to the system state space of this paper. This method can learn the cost-efficient computation offloading policy and serve as the baseline of cost efficiency for the DP-DQL method. The DQL-non-DP method shares the same hyperparameters with the DP-DQL method in the following experiments.
3.3. The Convergence of the DP-DQL Method
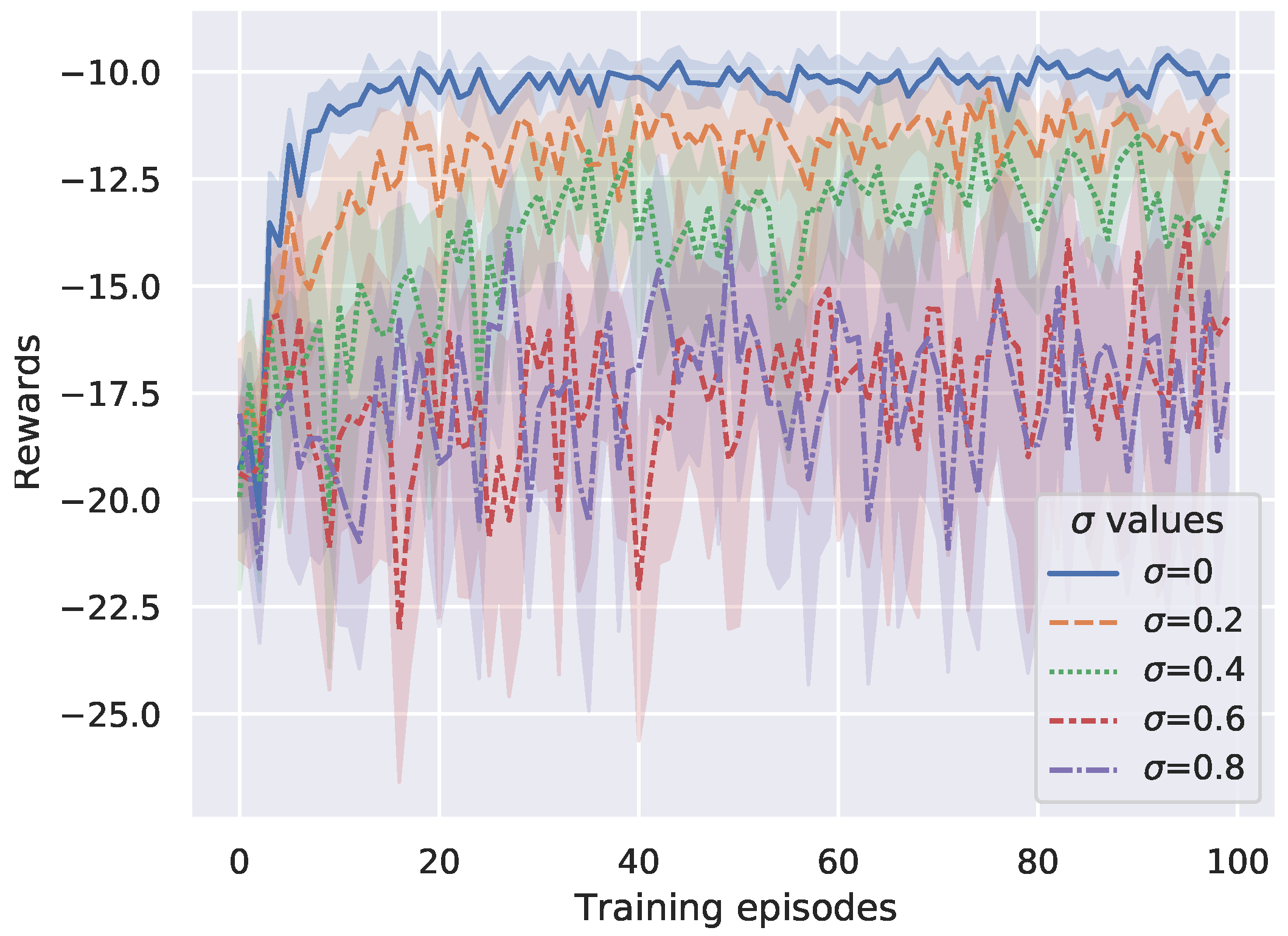
In this paper, the proposed DP-DQL method is modified at the action selection step in exploring and the accumulated policy gradient computing step in PER-based policy updating with the aim of protecting computation offloading preference. However, these two modifications may affect the learning performance of the proposed method. To evaluate the potential effect, we vary the to test the impact of the modifications on the learning performance of the proposed method. According to Theorem 2, once the other hyperparameters and experiment parameters are determined, will be an important parameter in the DP-DQL method to determine privacy level. In this paper, we set . Note that is a special case that privacy-preserving mechanism is not applied. Figure 4 shows the results. The results indicate that, with increasing, DP-DQL method needs more training episodes to approximate the learning performance than the non-privacy case. It raises a problem that what value of should we choose to achieve the best learning performance while preserving computation offloading preference. From Figure 4, it can be seen that the DP-DQL method allows UAV to learn the a stability computation offloading policy within 20 TPs, 20 TPs, and 34 TPs under the case of , , and , respectively. When , the DP-DQL method will continue to oscillate with no sign of convergence. Hence, we can see that DP-DQL method performs well when .
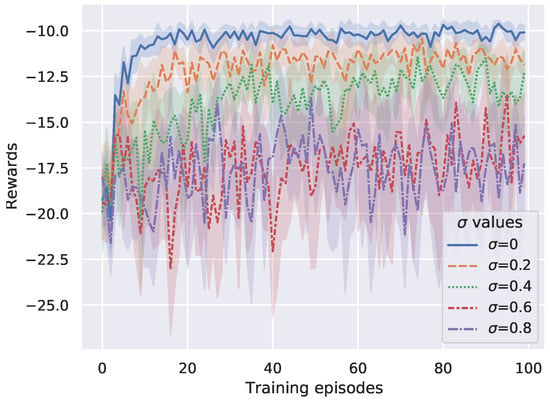
Figure 4.
Convergence performance versus different .
3.4. The Privacy Protection of the DP-DQL Method
According to the threat model in Section 2.2.2, the adversary tries to increase the similarity of the distributions of the vanilla value function and recovered value function in the state space . In this paper, we adopt the t-test to quantitatively evaluate the above similarity. To conduct the t-test, we firstly make a set of hypotheses, including and . Note that the subscript 0 is the null hypothesis, and is the alternative hypothesis.
- : The distributions of the vanilla value function is the same as that of recovered value function in the state space .
- : The distributions of the vanilla value function is not the same as that of recovered value function in the state space .
Referring to Section 3.3, we set the value function with as the vanilla value function, while the value function with , , , , and is set as recovered value function. We randomly generate the twenty pairs (, ), and input them to the vanilla value function and recovered value function, respectively. Then, we obtain two sets of values. Finally, we calculate the p-value of two sets. Table 3 shows the results. It can be seen that the p-value is less than 0.001 in most cases, except the case of . Hence, the null hypothesis is accepted with strong evidence. It indicates that the value function of proposed DP-DRL method cannot be recovered by inverse RL.

Table 3.
The results of t-test.
3.5. The Cost Efficiency of the DP-DQL Method
In this experiment, our aim is to evaluate how much the privacy preserving mechanism in the proposed method affects its cost efficiency, compared to the baseline methods. We adopt the weighted average of the cost and as the comparing metric, which is calculated based on Equation (8). Note that, due to the different ranges of the cost and , they are normalized as Equation (8). According to Section 3.3, we set and in the experiments. To avoid statistical deviation, we perform each experiment with 10 random seeds.
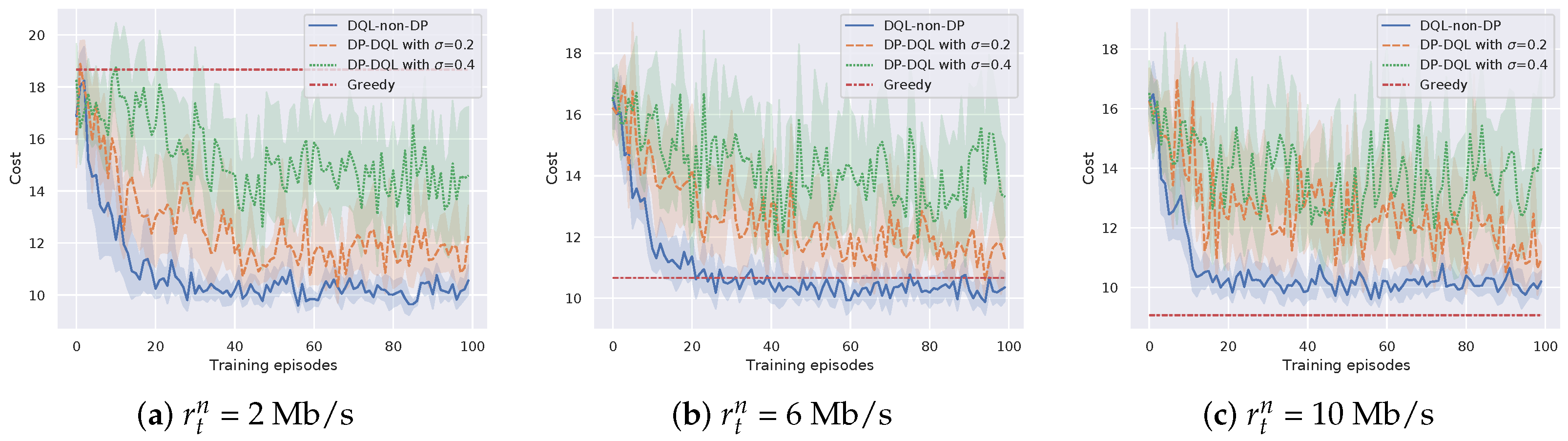
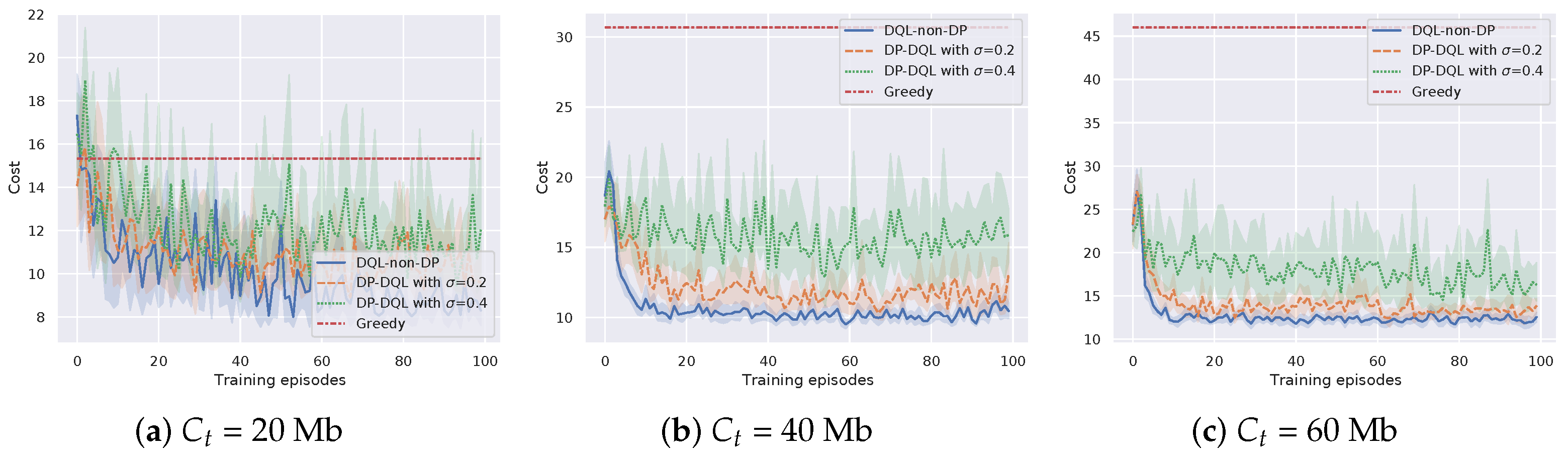
Figure 5 shows the influence of the radio transmission rate on the cost efficiency of DP-DQL and baseline methods. The radio transmission rate is set to be 2 Mb/s, 6 Mb/s, and 10 Mb/s, respectively, while the bits of a task is = 40 Mb. Compred with the baseline method, i.e., DQL-non-DP method, we can see that DP-DQL method has little cost efficiency reduction. For instance, we select the DP-DQL method with to compare with DQL-non-DP method. When two methods converge, the average cost of DP-DQL method is 15%, 18%, and 20% less than that of DQL-non-DP method in the case of Mb/s, Mb/s, and Mb/s. Moreover, we observe that the proposed DP-DQL method requires more training episodes, which varies from 20 TPs to 35 TPs, to achieve the similar cost than DQL-non-DP method. The extra training episodes used by the proposed DP-DQL method indicate the tradeoff between privacy and cost. Furthermore, we can find that, with the increase of radio transmission rate , the Greedy method can achieve better the cost efficiency of DP-DQL method in the cases of Mb/s and 10 Mb/s. The reason is that promising wireless channel status reduces the transmitting cost. However, compared with DP-DQL method, the Greedy method cannot preserve computation offloading preference.
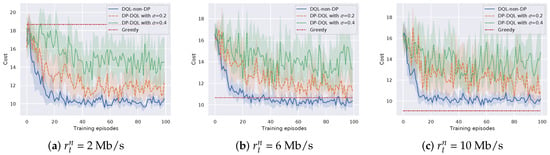
Figure 5.
Cost efficiency of the proposed method versus different transmission rate .
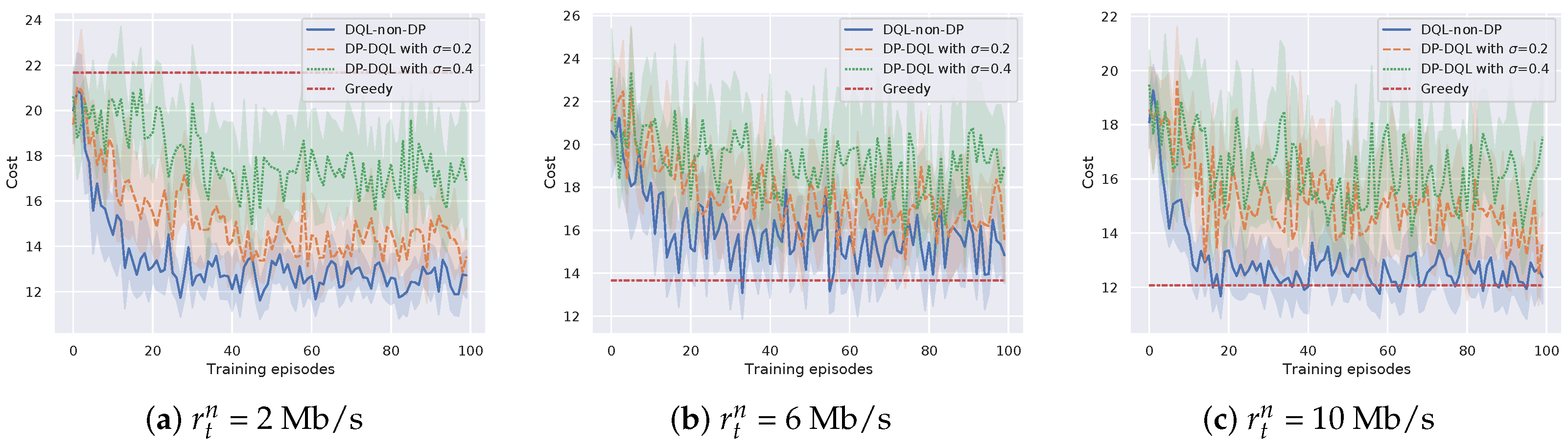
Moreover, the cost efficiency of DP-DQL is evaluated under different task bits , compared with baseline methods. The bits of a task is set to be 20 Mb, 40 Mb, and 60 Mb, while the radio transmission rate is 10 Mb/s. The results in Figure 6 show that DP-DQL method and DQL-non-DP method outperform the Greedy method in most cases, except the early learning stage of the case of Mb. The largest improvement of rewards is in the case of = 60 Mb, which is 260%. We can see that the difference in rewards between the DP-DQL method and DQL-non-DP method varies relatively little with . The maximum difference is only 12%, indicating that the proposed method is not overly affected by privacy-preserving mechanisms in terms of cost efficiency and can learn a cost-efficient computation offloading policy. The reason is that offloading all of a task to the BS will not cause too much cost in transmission time when the size of a task is small. With the size of a task increases, transmission time becomes the bottleneck of the cost efficiency of the Greedy method.
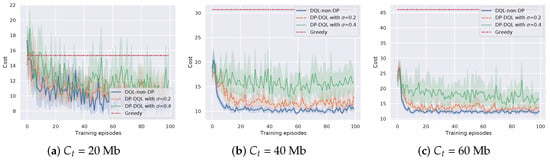
Figure 6.
Cost efficiency of the proposed method versus different bits of a task .
3.6. The Performance of the DP-DQL Method Deployed in a Realistic Scenario
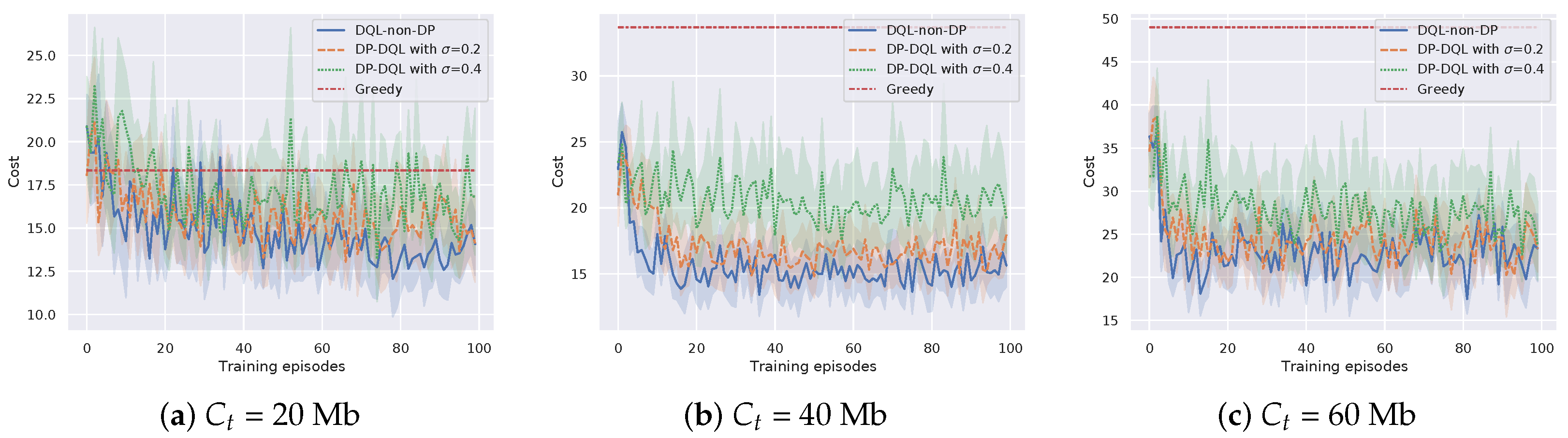
Through changing the laptops to the actual RSUs in the scenario, we re-examine the performance of the proposed method and DQL-non-DRL method in terms of cost efficiency. The parameters are set the same as Section 3.5. Figure 7 and Figure 8 show the cost efficiency of the proposed method and baseline methods under different transmission rate and bits of a task , respectively. It can be seen that the proposed method can still converge with finite TPs. However, by pairwise comparing Figure 5 with Figure 7, and Figure 6 with Figure 8, we can see that the experiments with actual RSUs increase the cost. The reason is that the weaker CPU computing power of the actual RSU increases the time cost and eventually leads to an increase in the total cost. Specifically, based on the assumption that the BS energy consumption is not considered in Section 2.2.1, the energy cost does not change when the actual RSUs are used to replace the laptops, which is still the local energy cost plus the transmission energy cost . However, the time for offloading and processing will increase due to the weaker CPU computing power of the actual RSUs. To further verify our point, setting , Figure 9 shows the proportion of time cost in the total cost. It can be seen that the proportion of time cost to the total cost increases after replacing with actual RSUs. Hence, changing laptops to the actual RSUs will increase the time cost and eventually lead to an increase in the total cost.
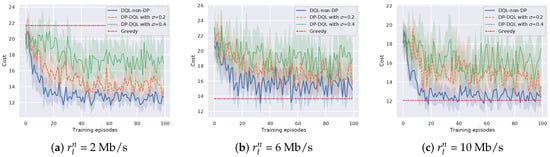
Figure 7.
Cost efficiency of the proposed method versus different transmission rate .
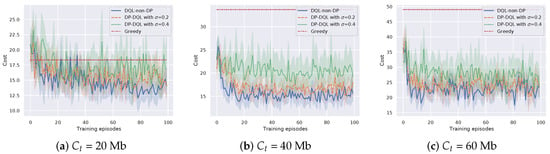
Figure 8.
Cost efficiency of the proposed method versus different bits of a task .
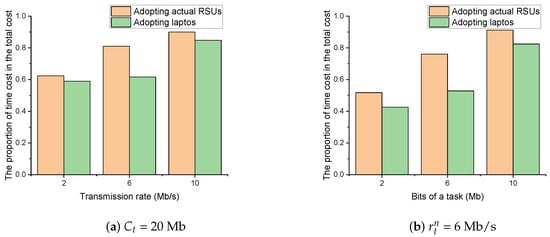
Figure 9.
The proportion of time cost in the total cost versus (a) different transmission rate and (b) different bits of a task .
4. Discussion
In this section, we firstly discuss the impact of the parameter value on the learning performance of the proposed method. Then, we discuss the limitations of the proposed method.
4.1. Impact of the Key Parameters on the Convergence of DP-DQL Method
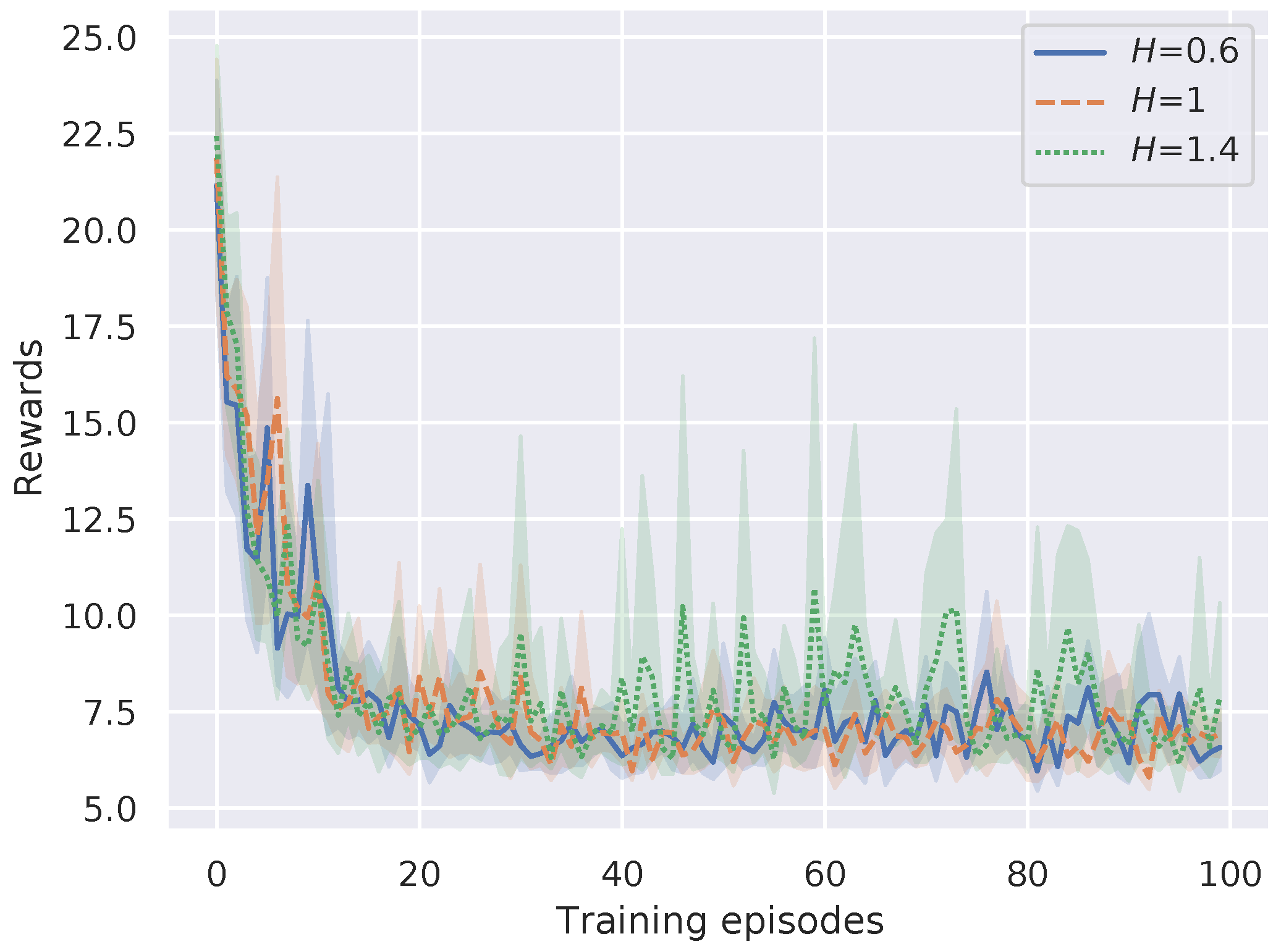
As shown in Line 4, Algorithm 1, the reset factor H is the updating frequency of the differential dict , which can affect the convergence of the proposed method. In this experiment, we evaluate the influence of value selection of reset factor H on DP-DQL performance by setting the . Figure 10 shows the results. In the figure, it can be seen that the average reward is not influenced by the value of reset factor H.
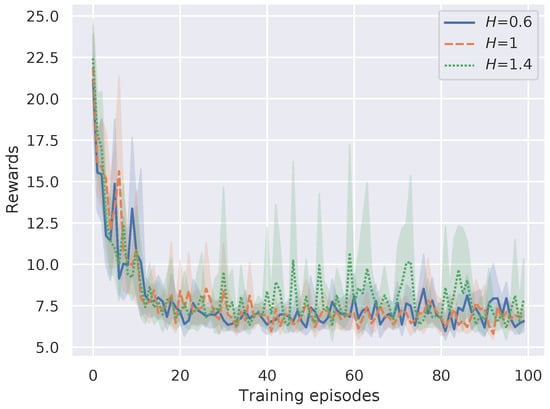
Figure 10.
Convergence performance versus different H.
4.2. Limitations and Future Works
The proposed method supports only one UAV to offload the task to single BS at one time slot. This can cover most of the existing daily application scenarios, such as grid inspection, remote sensing, etc. However, the limited endurance of a single UAV limits its ability to perform more complex tasks. Multi-UAV collaboration provides a viable idea, but the proposed method is not able to support privacy-preserving computation offloading in multi-UAV-assisted IoT scenarios. In the future, techniques, such as distributed reinforcement learning and local differential privacy, offer potential solutions to the above needs.
5. Conclusions
In this paper, we propose a differential privacy-based deep Q-learning method for computation offloading over UAV-assisted IoT, which can protect UAV’s computation offloading preference. The formal analysis shows that the proposed DP-DQL method meets the design goals, i.e., differential privacy guarantee and minor utility loss. Furthermore, we evaluate the convergence and privacy of DP-DQL method by the real-world experiment. The results indicate that our DP-DQL method can achieve long-term energy performance under the privacy guarantee, compared with baseline methods. In the future, we will further investigate various privacy issues on DRL-based computation offloading methods.
Author Contributions
Conceptualization, D.W. and N.X.; methodology, D.W.; software, L.H.; validation, D.W. and L.H.; formal analysis, D.W.; investigation, D.W.; writing—original draft preparation, D.W.; writing—review and editing, N.X.; visualization, D.W.; supervision, J.M.; funding acquisition, N.X. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Key R&D Program of China (Grant No. 2018YFE0207600), National Natural Science Foundation of China (No. 61902291), the Fundamental Research Funds for the Central Universities (Project No. XJS201503) and China Postdoctoral Science Foundation Funded Project (2019M653567).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fraga-Lamas, P.; Ramos, L.; Mondéjar-Guerra, V.M.; Fernández-Caramés, T.M. A Review on IoT Deep Learning UAV Systems for Autonomous Obstacle Detection and Collision Avoidance. Remote Sens. 2019, 11, 2144. [Google Scholar] [CrossRef] [Green Version]
- Qiu, T.; Chi, J.; Zhou, X.; Ning, Z.; Atiquzzaman, M.; Wu, D.O. Edge Computing in Industrial Internet of Things: Architecture, Advances and Challenges. IEEE Commun. Surv. Tutor. 2020, 22, 2462–2488. [Google Scholar] [CrossRef]
- Zhou, F.; Hu, R.Q.; Li, Z.; Wang, Y. Mobile Edge Computing in Unmanned Aerial Vehicle Networks. IEEE Wirel. Commun. 2020, 27, 140–146. [Google Scholar] [CrossRef] [Green Version]
- Hong, Z.; Chen, W.; Huang, H.; Guo, S.; Zheng, Z. Multi-Hop Cooperative Computation Offloading for Industrial IoT-Edge-Cloud Computing Environments. IEEE Trans. Parallel Distrib. Syst. 2019, 30, 2759–2774. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, Z.; Hong, Z.; Chen, C.; Wu, J.; Maharjan, S.; Zheng, Z.; Zhang, Y. Cooperative and Distributed Computation Offloading for Blockchain-Empowered Industrial Internet of Things. IEEE Internet Things J. 2019, 6, 8433–8446. [Google Scholar] [CrossRef]
- Dai, Y.; Zhang, K.; Maharjan, S.; Zhang, Y. Deep Reinforcement Learning for Stochastic Computation Offloading in Digital Twin Networks. IEEE Trans. Ind. Inform. 2021, 17, 4968–4977. [Google Scholar] [CrossRef]
- Ren, Y.; Sun, Y.; Peng, M. Deep Reinforcement Learning Based Computation Offloading in Fog Enabled Industrial Internet of Things. IEEE Trans. Ind. Inform. 2021, 17, 4978–4987. [Google Scholar] [CrossRef]
- Yang, L.; Li, M.; Si, P.; Yang, R.; Sun, E.; Zhang, Y. Energy-Efficient Resource Allocation for Blockchain-Enabled Industrial Internet of Things with Deep Reinforcement Learning. IEEE Internet Things J. 2021, 8, 2318–2329. [Google Scholar] [CrossRef]
- Pan, X.; Wang, W.; Zhang, X.; Li, B.; Yi, J.; Song, D. How You Act Tells a Lot: Privacy-Leaking Attack on Deep Reinforcement Learning. In Proceedings of the International Foundation for Autonomous Agents and Multiagent Systems, AAMAS 2019, Montreal, QC, Canada, 13–17 May 2019; pp. 368–376. [Google Scholar]
- Zhou, C.; Wu, W.; He, H.; Yang, P.; Lyu, F.; Cheng, N.; Shen, X. Deep Reinforcement Learning for Delay-Oriented IoT Task Scheduling in SAGIN. IEEE Trans. Wirel. Commun. 2021, 20, 911–925. [Google Scholar] [CrossRef]
- Liu, P.; He, H.; Fu, T.; Lu, H.; Alelaiwi, A.; Wasi, M.W.I. Task offloading optimization of cruising UAV with fixed trajectory. Comput. Netw. 2021, 199, 108397. [Google Scholar] [CrossRef]
- Wei, D.; Ma, J.; Luo, L.; Wang, Y.; He, L.; Li, X. Computation offloading over multi-UAV MEC network: A distributed deep reinforcement learning approach. Comput. Netw. 2021, 199, 108439. [Google Scholar] [CrossRef]
- Zhu, S.; Gui, L.; Zhao, D.; Cheng, N.; Zhang, Q.; Lang, X. Learning-Based Computation Offloading Approaches in UAVs-Assisted Edge Computing. IEEE Trans. Veh. Technol. 2021, 70, 928–944. [Google Scholar] [CrossRef]
- Seid, A.M.; Boateng, G.O.; Anokye, S.; Kwantwi, T.; Sun, G.; Liu, G. Collaborative Computation Offloading and Resource Allocation in Multi-UAV-Assisted IoT Networks: A Deep Reinforcement Learning Approach. IEEE Internet Things J. 2021, 8, 12203–12218. [Google Scholar] [CrossRef]
- Sacco, A.; Esposito, F.; Marchetto, G.; Montuschi, P. Sustainable Task Offloading in UAV Networks via Multi-Agent Reinforcement Learning. IEEE Trans. Veh. Technol. 2021, 70, 5003–5015. [Google Scholar] [CrossRef]
- Gao, A.; Wang, Q.; Chen, K.; Liang, W. Multi-UAV Assisted Offloading Optimization: A Game Combined Reinforcement Learning Approach. IEEE Commun. Lett. 2021, 25, 2629–2633. [Google Scholar] [CrossRef]
- He, X.; Liu, J.; Jin, R.; Dai, H. Privacy-Aware Offloading in Mobile-Edge Computing. In Proceedings of the 2017 IEEE Global Communications Conference (GLOBECOM 2017), Singapore, 4–8 December 2017; pp. 1–6. [Google Scholar]
- He, X.; Jin, R.; Dai, H. Physical-Layer Assisted Privacy-Preserving Offloading in Mobile-Edge Computing. In Proceedings of the 2019 IEEE International Conference on Communications (ICC 2019), Shanghai, China, 20–24 May 2019; pp. 1–6. [Google Scholar]
- Min, M.; Wan, X.; Xiao, L.; Chen, Y.; Xia, M.; Wu, D.; Dai, H. Learning-Based Privacy-Aware Offloading for Healthcare IoT with Energy Harvesting. IEEE Internet Things J. 2019, 6, 4307–4316. [Google Scholar] [CrossRef]
- He, X.; Jin, R.; Dai, H. Deep PDS-Learning for Privacy-Aware Offloading in MEC-Enabled IoT. IEEE Internet Things J. 2019, 6, 4547–4555. [Google Scholar] [CrossRef]
- Schaul, T.; Quan, J.; Antonoglou, I.; Silver, D. Prioritized Experience Replay. In Proceedings of the 4th International Conference on Learning Representations, (ICLR 2016), San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Dwork, C.; McSherry, F.; Nissim, K.; Smith, A.D. Calibrating Noise to Sensitivity in Private Data Analysis. Lecture Notes in Computer Science. In Proceedings of the Theory of Cryptography, Third Theory of Cryptography Conference, TCC 2006, New York, NY, USA, 4–7 March 2006; Springer: Berlin/Heidelberg, Germany, 2006; Volume 3876, pp. 265–284. [Google Scholar]
- Dwork, C.; Roth, A. The Algorithmic Foundations of Differential Privacy. Found. Trends Theor. Comput. Sci. 2014, 9, 211–407. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.A.; Fidjeland, A.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Messous, M.A.; Senouci, S.; Sedjelmaci, H.; Cherkaoui, S. A Game Theory Based Efficient Computation Offloading in an UAV Network. IEEE Trans. Veh. Technol. 2019, 68, 4964–4974. [Google Scholar] [CrossRef]
- Li, K.; Tao, M.; Chen, Z. Exploiting Computation Replication for Mobile Edge Computing: A Fundamental Computation-Communication Tradeoff Study. IEEE Trans. Wirel. Commun. 2020, 19, 4563–4578. [Google Scholar] [CrossRef] [Green Version]
- Zhou, F.; Hu, R.Q. Computation Efficiency Maximization in Wireless-Powered Mobile Edge Computing Networks. IEEE Trans. Wirel. Commun. 2020, 19, 3170–3184. [Google Scholar] [CrossRef] [Green Version]
- Tiwari, N.; Bellur, U.; Sarkar, S.; Indrawan, M. CPU Frequency Tuning to Improve Energy Efficiency of MapReduce Systems. In Proceedings of the 2016 IEEE 22nd International Conference on Parallel and Distributed Systems (ICPADS), Wuhan, China, 13–16 December 2016; pp. 1015–1022. [Google Scholar]
- He, X.; Jin, R.; Dai, H. Peace: Privacy-Preserving and Cost-Efficient Task Offloading for Mobile-Edge Computing. IEEE Trans. Wirel. Commun. 2020, 19, 1814–1824. [Google Scholar] [CrossRef]
- Min, M.; Xiao, L.; Chen, Y.; Cheng, P.; Wu, D.; Zhuang, W. Learning-Based Computation Offloading for IoT Devices with Energy Harvesting. IEEE Trans. Veh. Technol. 2019, 68, 1930–1941. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Jiao, L.; Li, W.; Fu, X. Efficient Multi-User Computation Offloading for Mobile-Edge Cloud Computing. IEEE/ACM Trans. Netw. 2016, 24, 2795–2808. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Hegde, N. Privacy-Preserving Q-Learning with Functional Noise in Continuous Spaces. arXiv 2019, arXiv:1901.10634. [Google Scholar]
- Silver, D.; Lever, G.; Heess, N.; Degris, T.; Wierstra, D.; Riedmiller, M.A. Deterministic Policy Gradient Algorithms. In Proceedings of the 31st International Conference on Machine Learning, Beijing, China, 21–26 June 2014; Volume 32, pp. 387–395. [Google Scholar]
- MacKay, D.J. Introduction to Gaussian processes. NATO ASI Ser. F Comput. Syst. Sci. 1998, 168, 133–166. [Google Scholar]
- Wei, D.; Xi, N.; Ma, J.; Li, J. Protecting Your Offloading Preference: Privacy-aware Online Computation Offloading in Mobile Blockchain. In Proceedings of the 2021 IEEE/ACM 29th International Symposium on Quality of Service (IWQOS), Tokyo, Japan, 25–28 June 2021; pp. 1–10. [Google Scholar]
- Hall, R.; Rinaldo, A.; Wasserman, L.A. Differential privacy for functions and functional data. J. Mach. Learn. Res. 2013, 14, 703–727. [Google Scholar]
- Kairouz, P.; Oh, S.; Viswanath, P. The Composition Theorem for Differential Privacy. IEEE Trans. Inf. Theory 2017, 63, 4037–4049. [Google Scholar] [CrossRef]
- Patel, A.; Shah, N.; Limbasiya, T.; Das, D. VehicleChain: Blockchain-based Vehicular Data Transmission Scheme for Smart City. In Proceedings of the 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC), Bari, Italy, 6–9 October 2019; pp. 661–667. [Google Scholar]
- Sakuraba, A.; Sato, G.; Uchida, N.; Shibata, Y. Performance Evaluation of Improved V2X Wireless Communication Based on Gigabit WLAN. Lecture Notes in Networks and Systems. In Proceedings of the International Conference on Broadband and Wireless Computing, Communication and Applications, Yonago, Japan, 28–30 October 2020; Springer: Cham, Switzerland, 2020; Volume 159, pp. 131–142. [Google Scholar]
- You, C.; Huang, K.; Chae, H.; Kim, B. Energy-Efficient Resource Allocation for Mobile-Edge Computation Offloading. IEEE Trans. Wirel. Commun. 2017, 16, 1397–1411. [Google Scholar] [CrossRef]
- Cheng, X.; Lyu, F.; Quan, W.; Zhou, C.; He, H.; Shi, W.; Shen, X. Space/Aerial-Assisted Computing Offloading for IoT Applications: A Learning-Based Approach. IEEE J. Sel. Areas Commun. 2019, 37, 1117–1129. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).