Performance Assessment of BDS-2/BDS-3/GPS/Galileo Attitude Determination Based on the Single-Differenced Model with Common-Clock Receivers
Abstract
1. Introduction
2. Method
2.1. Functional Model
2.2. Stochastic Model
2.3. Direct Computation of Attitude
3. Results
3.1. Data Collection
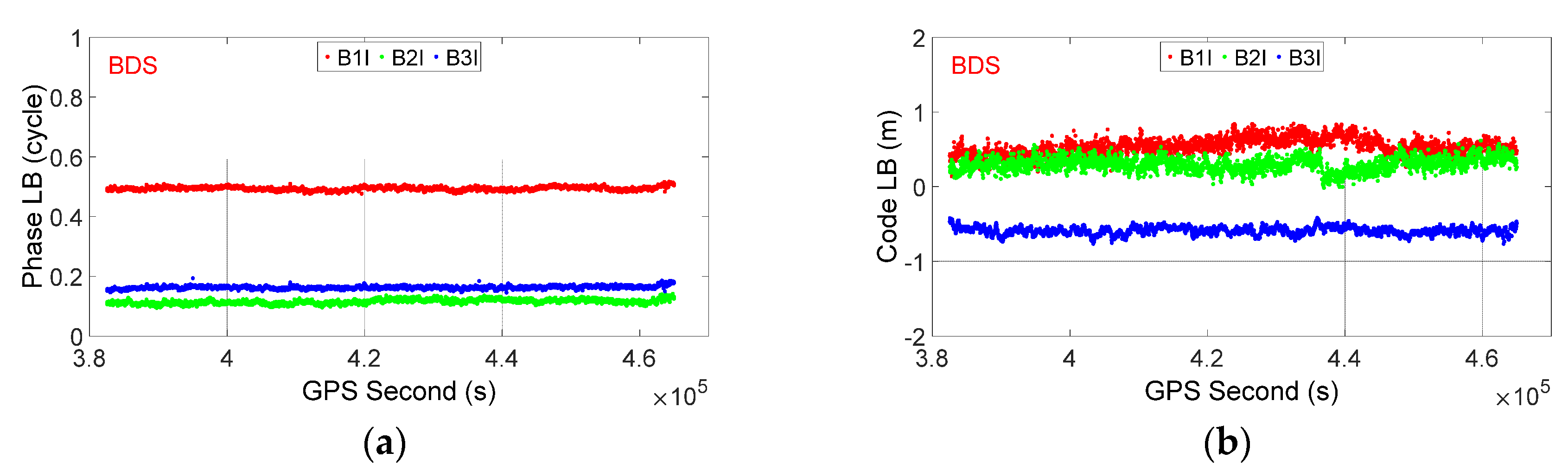
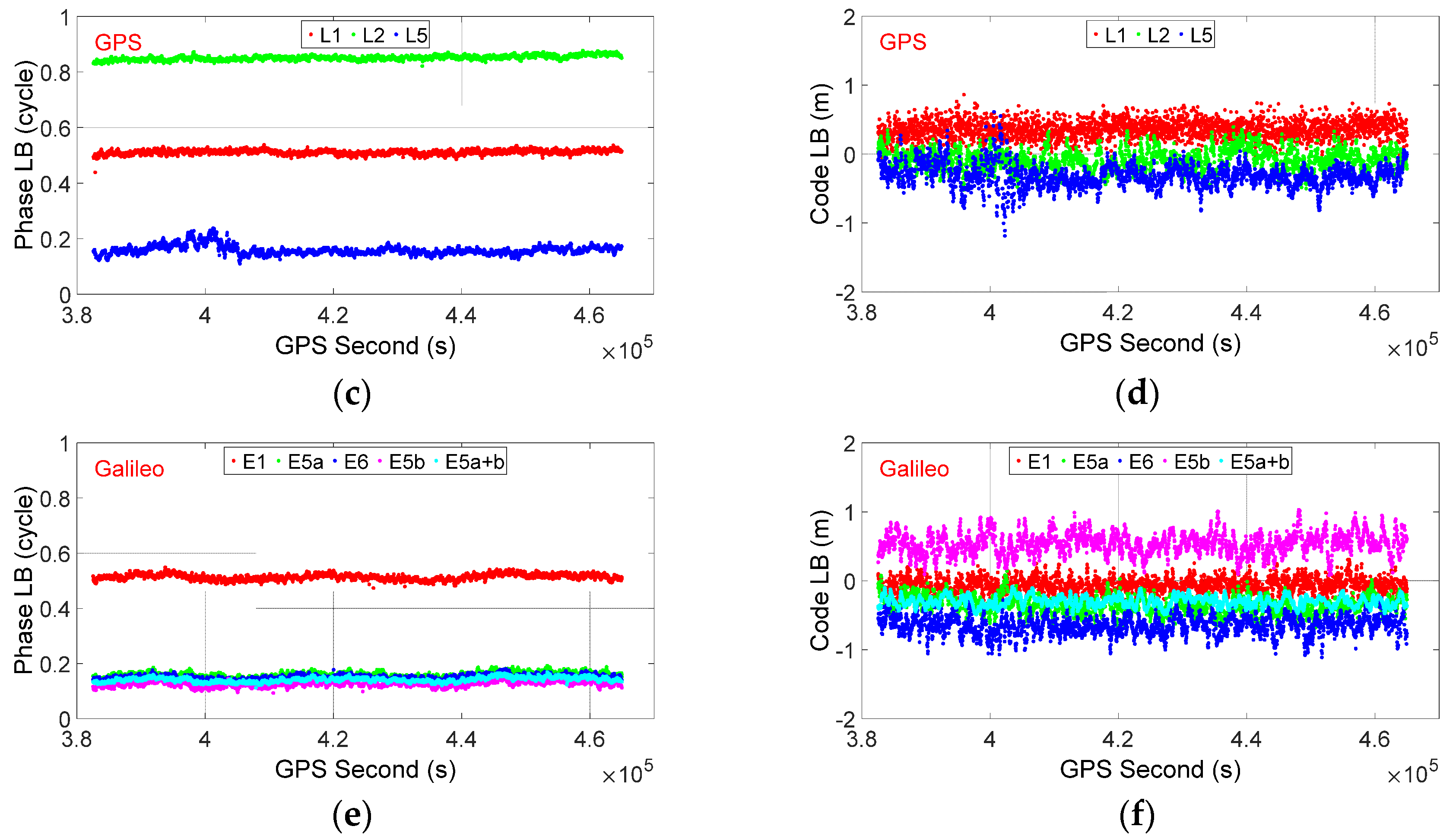
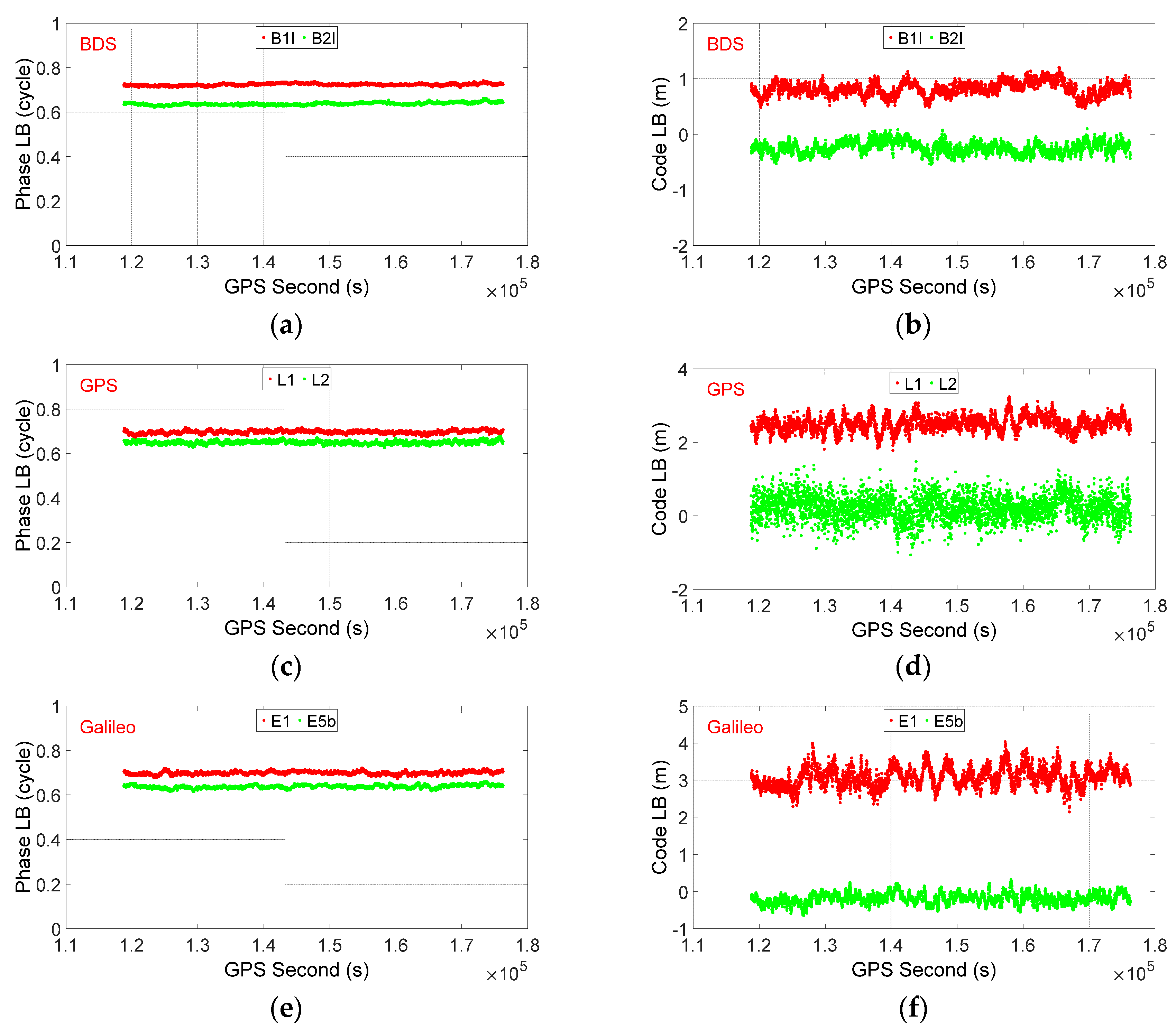
3.2. LB Estimation and Characterization
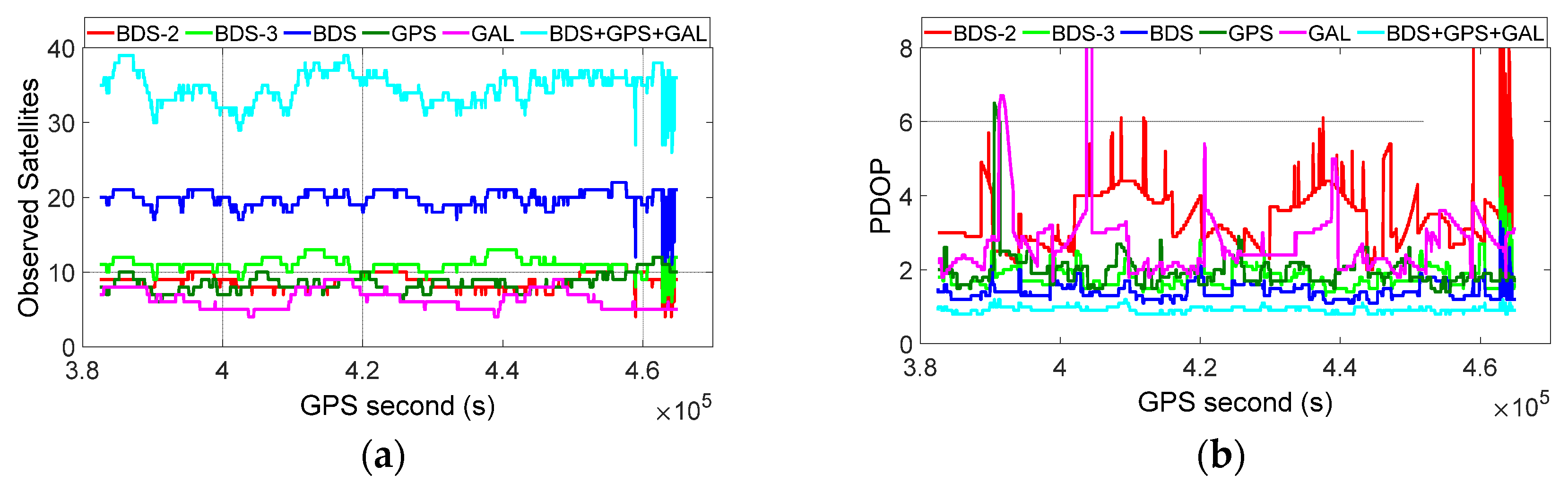
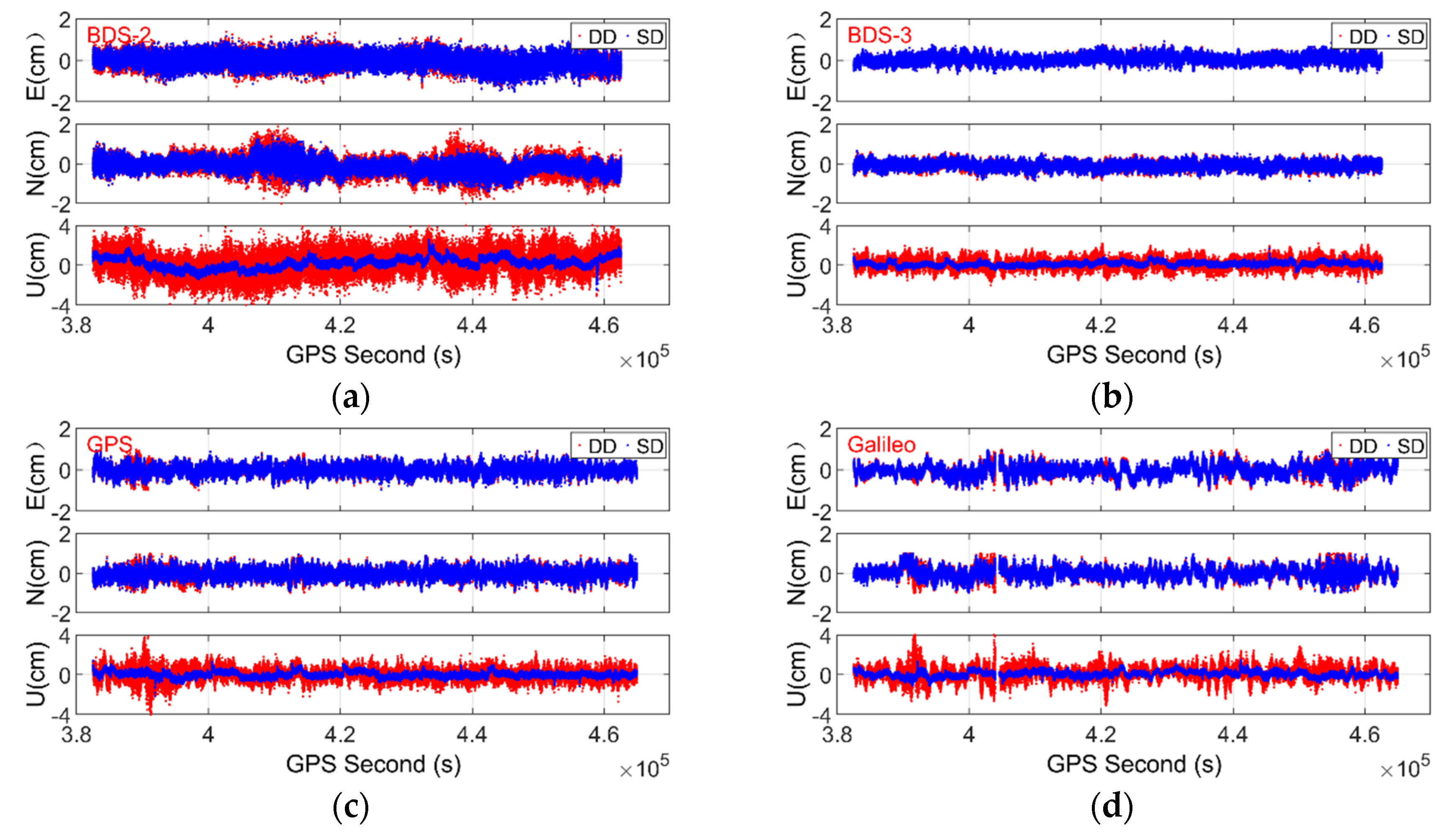
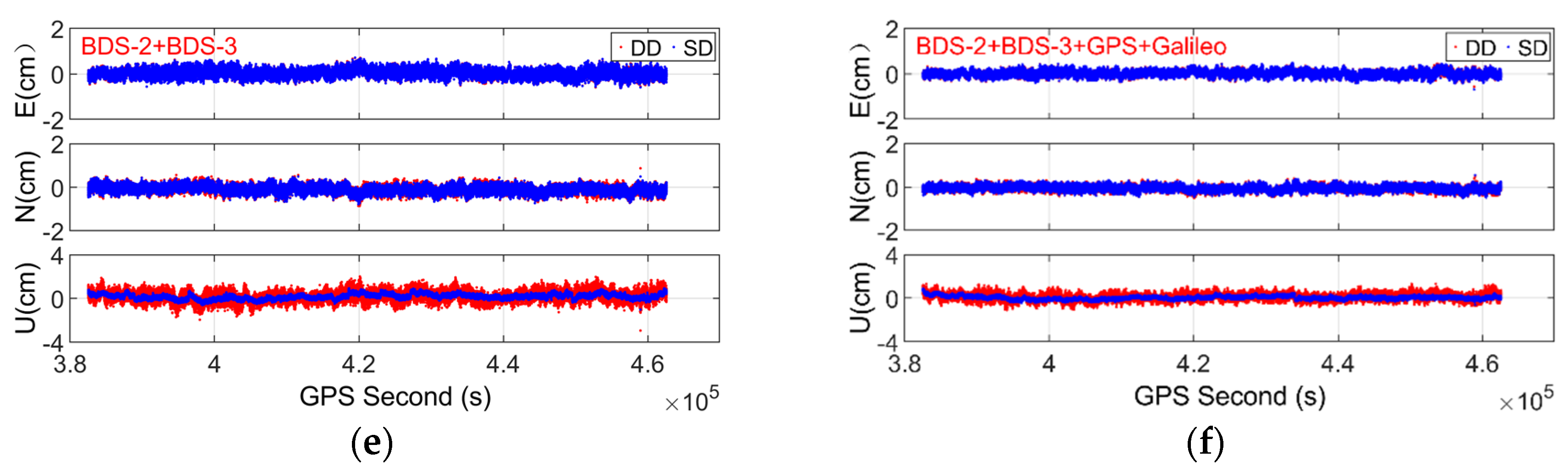
3.3. Performance Assessment of Attitude Determination with SD and DD Models
4. Discussions
5. Conclusions
- (1)
- Experimental results with Trimble BD992 and Unicore UB482 receivers have confirmed that both the phase and code LBs are relatively stable in the time domain once the receivers have started. However, the phase LB could change to an arbitrary value after each restart of the common-clock receivers. It is also found that the LBs for signals with overlapping frequencies, but from different GNSS systems (e.g., GPS/Galileo L1-E1 and L5-E5a), are equal, which implies that the observations from overlapping frequencies of different GNSS systems can be simply treated as if they are from one constellation in the SD model.
- (2)
- The positioning accuracy of the SD model is comparable to that of the DD model in the east and north components but significantly higher in the up component, whether for BDS-2, BDS-3, GPS, and Galileo only or combined solutions. The positioning RMS errors of the SD model are reduced by approximately 21.0–47.1% for single-frequency solutions and 40.0–58.0% for dual-frequency solutions with respect to the DD model.
- (3)
- Compared with the DD model, the SD model can deliver comparable accuracy for yaw and significantly higher accuracy for pitch, whether for BDS-2, BDS-3, GPS, and Galileo alone or a combination of them. The RMS errors of pitch are reduced by approximately 20.8–47.5% and 40.7–57.5% with single- and dual-frequency observations, respectively.
- (4)
- The BDS-3 can deliver relatively better positioning and attitude accuracy with respect to GPS and Galileo, due to its better geometry. Compared with BDS-2, BDS-3, GPS, and Galileo-only solutions, the three-dimensional positioning and attitude (including yaw and pitch) accuracy for both the DD and SD models can be remarkably improved by a combination of multi-GNSS systems.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Teunissen, P.J.G.; Giorgi, G.; Buist, P.J. Testing of a new single-frequency GNSS carrier phase attitude determination method: Land, ship and aircraft experiments. GPS Solut. 2011, 15, 15–28. [Google Scholar] [CrossRef]
- Giorgi, G.; Teunissen, P.J.G.; Gourlay, T.P. Instantaneous global navigation satellite system (GNSS)-based attitude determination for maritime applications. IEEE J. Ocean. Eng. 2012, 37, 348–362. [Google Scholar] [CrossRef]
- Sabatini, R.; Kaharkar, A.; Bartel, C.; Shaid, T. Carrier-phase GNSS attitude determination and control for small UAV applications. J. Aeronaut. Aerosp. Eng. 2013, 2, 1–11. [Google Scholar]
- Willi, D.; Rothacher, M. GNSS attitude determination with non-synchronized receivers and short baselines onboard a spacecraft. GPS Solut. 2017, 21, 1605–1617. [Google Scholar] [CrossRef]
- Hauschild, A.; Mohr, U.; Markgraf, M.; Montenbruck, O. Flight results of GPS-based attitude determination for the microsatellite Flying Laptop. Navigation 2019, 66, 277–287. [Google Scholar] [CrossRef]
- Wang, Y.; Zhan, X.; Zhang, Y. Improved ambiguity function method based on analytical resolution for GPS attitude determination. Meas. Sci. Technol. 2007, 18, 2985–2990. [Google Scholar] [CrossRef]
- Li, Z.; Liu, W.; Lou, Y.; Zhou, Z. Heading determination algorithm with single epoch dual frequency GPS data. Geomat. Inf. Sci. Wuhan Univ. 2007, 32, 753–756. [Google Scholar]
- Dai, Z.; Knedlik, S.; Loffeld, O. A MATLAB toolbox for attitude determination with GPS multi-antenna systems. GPS Solut. 2009, 13, 241–248. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. Integer least-squares theory for the GNSS compass. J. Geod. 2010, 84, 433–447. [Google Scholar] [CrossRef]
- Giorgi, G.; Teunissen, P.J.G.; Verhagen, S.; Buist, P.J. Testing a new multivariate GNSS carrier phase attitude determination method for remote sensing platforms. Adv. Space Res. 2010, 46, 118–129. [Google Scholar] [CrossRef]
- Nadarajah, N.; Teunissen, P.J.G.; Raziq, N. Instantaneous BeiDou–GPS attitude determination: A performance analysis. Adv. Space Res. 2014, 54, 851–862. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, M.; Liu, W. Receiver time misalignment correction for GPS-based attitude determination. J. Navig. 2015, 68, 646–664. [Google Scholar] [CrossRef]
- Gan, Y.; Sui, L.; Xiao, G.; Zhang, Q.; Wang, L. Real-time GNSS attitude determination by a direct approach with efficiency and robustness. Meas. Sci. Technol. 2021, 32, 115904. [Google Scholar] [CrossRef]
- Wang, X.; Yao, Y.; Xu, C.; Zhao, Y.; Lv, D. An Improved Single-Epoch Attitude Determination Method for Low-Cost Single-Frequency GNSS Receivers. Remote Sens. 2021, 13, 2746. [Google Scholar] [CrossRef]
- Wu, S.; Zhao, X.; Pang, C.; Zhang, L.; Xu, Z.; Zou, K. Improving ambiguity resolution success rate in the joint solution of GNSS-based attitude determination and relative positioning with multivariate constraints. GPS Solut. 2020, 24, 31. [Google Scholar] [CrossRef]
- Santerre, R.; Beutler, G. A proposed GPS method with multi-antennae and single receiver. J. Geod. 1993, 67, 210–223. [Google Scholar] [CrossRef]
- Macias-Valadez, D.; Santerre, R.; Larochelle, S.; Landry, R. Improving vertical GPS precision with a GPS-over-fiber architecture and real-time relative delay calibration. GPS Solut. 2012, 16, 449–462. [Google Scholar] [CrossRef]
- Chen, W.; Qin, H.; Zhang, Y.; Tian, J. Accuracy assessment of single and double difference models for the single epoch GPS compas. Adv. Space Res. 2012, 49, 725–738. [Google Scholar] [CrossRef]
- Dong, D.; Chen, W.; Cai, M.; Zhou, F.; Wang, M.; Yu, C.; Zheng, Z.; Wang, Y. Multi-antenna synchronized global navigation satellite system receiver and its advantages in high-precision positioning applications. Front. Earth Sci. 2016, 10, 772–783. [Google Scholar] [CrossRef]
- Chen, W. A remark on the GNSS single difference model with common clock scheme for attitude determination. J. Appl. Geod. 2016, 10, 167–173. [Google Scholar] [CrossRef]
- Chen, W.; Yu, C.; Dong, D.; Cai, M.; Zhou, F.; Wang, Z.; Zhang, L.; Zheng, Z. Formal Uncertainty and Dispersion of Single and Double Difference Models for GNSS-Based Attitude Determination. Sensors 2017, 17, 408. [Google Scholar] [CrossRef] [PubMed]
- Keong, J.; Lachapelle, G. Heading and pitch determination using GPS/GLONASS. GPS Solut. 2000, 3, 26–36. [Google Scholar] [CrossRef]
- Alban, S. Design and Performance of a Robust GPS/INS Attitude System for Automobile Applications. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2004. [Google Scholar]
- Li, Y.; Zhang, K.; Roberts, C.; Murata, M. On-the-fly GPS-based attitude determination using single-and double-differenced carrier phase measurements. GPS Solut. 2004, 8, 93–102. [Google Scholar] [CrossRef]
- Park, K.; Crassidis, J.L. A Robust GPS receiver self-survey algorithm. Navigation 2006, 53, 259–268. [Google Scholar] [CrossRef]
- Zhang, L.; Hou, Y.; Wu, J. A drift line bias estimator: ARMA-based filter or calibration method, and its application in BDS/GPS-based attitude determination. J. Geod. 2016, 90, 1331–1343. [Google Scholar]
- Schön, S.; Pham, H.K.; Kersten, T.; Leute, J.; Bauch, A. Potential of GPS common clock single-differences for deformation monitoring. J. Appl. Geod. 2016, 10, 45–52. [Google Scholar] [CrossRef][Green Version]
- Zhang, L.; Chen, W.; Yu, C.; Dong, D. Attitude Determination based on Common Reference Clock GPS/BDS Dual Antenna. In Proceedings of the 4th International Conference on Information Systems and Computing Technology (ISCT 2016), Advances in Computer Science Research, Shanghai, China, 22–23 December 2016. [Google Scholar]
- Nadarajah, N.; Teunissen, P.J.G. Instantaneous GPS/Galileo/QZSS/SBAS attitude determination: A single-frequency (L1/E1) robustness analysis under constrained environments. Navigation 2014, 61, 65–75. [Google Scholar] [CrossRef]
- Li, X.; Ge, M.; Dai, X.; Ren, X.; Fritsche, M.; Wickert, J.; Schuh, H. Accuracy and reliability of multi-GNSS real-time precise positioning: GPS, GLONASS, BeiDou, and Galileo. J. Geod. 2015, 89, 607–635. [Google Scholar] [CrossRef]
- Odolinski, R.; Teunissen, P.J.G. Low-cost, 4-system, precise GNSS positioning: A GPS, Galileo, BDS and QZSS ionosphere-weighted RTK analysis. Meas. Sci. Technol. 2017, 28, 125801. [Google Scholar] [CrossRef]
- Constellation Status. Available online: http://www.csno-tarc.cn/system/constellation (accessed on 26 September 2021).
- Wu, W.; Guo, F.; Zheng, J. Analysis of Galileo signal-in-space range error and positioning performance during 2015–2018. Sat. Nav. 2020, 1, 6. [Google Scholar] [CrossRef]
- Constellation Information. Available online: https://www.gsc-europa.eu/system-service-status/constellation-information (accessed on 26 September 2021).
- Meindl, M. Combined Analysis of Observations from Different Global Navigation Satellite Systems. Ph.D. Thesis, University of Bern, Bern, Swiss, 2011. [Google Scholar]
- Herring, T.A.; King, R.W.; Floyd, M.A.; McClusky, S.C. GAMIT Reference Manual: GPS Analysis at MIT (Release 10.7). Massachusetts Institute of Technology (MIT). 2018. Available online: http://geoweb.mit.edu/gg/GAMIT_Ref.pdf (accessed on 26 September 2021).
- Hofmann-Wellenhof, B.; Lichtenegger, H.; Wasle, E. GNSS–Global Navigation Satellite Systems: GPS, GLONASS, Galileo, and More, 1st ed.; Springer: Wien, Austria; Berlin, Germany, 2007; p. 442. [Google Scholar]
- Teunissen, P.J.G. The least-squares ambiguity decorrelation adjustment: A method for fast GPS integer ambiguity estimation. J. Geod. 1995, 70, 1–2. [Google Scholar] [CrossRef]
- Euler, H.J.; Schaffrin, B. On a measure for the discernibility between different ambiguity solutions in the static-kinematic GPS-mode. In Kinematic Systems in Geodesy, Surveying, and Remote Sensing. Proceedings of the International Association of Geodesy Symposia, Banff, AL, Canada, 10–13 September 1990; Schwarz, K.P., Lachapelle, G., Eds.; Springer: New York, NY, USA, 1990; Volume 107. [Google Scholar]


| Option | Dataset 1 | Dataset 2 |
|---|---|---|
| Site | On the roof of teaching experiment building, Wuhan University | On the roof of teaching experiment building, Wuhan University |
| Time | 1 April to 2 April 2021 GPST | 26 July to 27 July 2021 GPST |
| Duration | About 25 h | About 17 h |
| Sampling interval | 1 s | 1 s |
| Elevation cutoff angle | 10° | 10° |
| Receiver | Trimble BD992 | Unicore UB482 |
| Antenna | Trimble Zephyr Model2 | Trimble Zephyr Model2 |
| Cable | Two the same Coaxial cables with length of 30 m | Two the same Coaxial cables with length of 33 m |
| Observations | GPS L1/L2/L5 | GPS L1/L2 |
| BDS-2 B1I/B2I/B3I | BDS-2 B1I/B2I | |
| BDS-3 B1I/B3I | BDS-3 B1I | |
| Galileo E1/E5a/E5b/E6/E5a+b | Galileo E1/E6 | |
| Baseline length | About 1.71 m | About 0.71 m |
| System | Frequency | Phase LB (Cycle) | Code LB (m) | ||
|---|---|---|---|---|---|
| Mean | STD | Mean | STD | ||
| GPS | L1 | 0.512 | 0.008 | 0.36 | 0.13 |
| L2 | 0.851 | 0.008 | −0.08 | 0.15 | |
| L5 | 0.159 | 0.016 | −0.32 | 0.17 | |
| BDS | B1I | 0.494 | 0.006 | 0.54 | 0.11 |
| B2I | 0.115 | 0.007 | 0.30 | 0.09 | |
| B3I | 0.163 | 0.005 | −0.59 | 0.05 | |
| Galileo | E1 | 0.514 | 0.010 | −0.07 | 0.11 |
| E5a | 0.159 | 0.010 | −0.36 | 0.13 | |
| E6 | 0.150 | 0.009 | −0.65 | 0.14 | |
| E5b | 0.126 | 0.010 | 0.54 | 0.15 | |
| E5a+b | 0.141 | 0.008 | −0.30 | 0.08 | |
| System | Frequency | Phase LB (Cycle) | Code LB (m) | ||
|---|---|---|---|---|---|
| Mean | STD | Mean | STD | ||
| GPS | L1 | 0.697 | 0.007 | 2.51 | 0.20 |
| L2 | 0.650 | 0.007 | 0.22 | 0.33 | |
| BDS | B1I | 0.724 | 0.005 | 0.82 | 0.12 |
| B2I | 0.638 | 0.006 | −0.24 | 0.11 | |
| Galileo | E1 | 0.699 | 0.007 | 3.08 | 0.27 |
| E5b | 0.638 | 0.007 | −0.19 | 0.15 | |
| System | Frequency | Session 1 | Session 2 | ||
|---|---|---|---|---|---|
| Phase LB (Cycle) | Code LB (m) | Phase LB (Cycle) | Code LB (m) | ||
| Mean | Mean | Mean | Mean | ||
| GPS | L1 | 0.984 | 0.30 | 0.229 | 0.32 |
| L2 | 0.190 | −0.29 | 0.418 | −0.25 | |
| L5 | 0.714 | −0.10 | 0.203 | 0.01 | |
| BDS | B1I | 0.951 | 0.35 | 0.198 | 0.36 |
| B2I | 0.660 | 0.25 | 0.139 | 0.30 | |
| B3I | 0.676 | 0.06 | 0.926 | 0.02 | |
| Galileo | E1 | 0.984 | 0.19 | 0.226 | 0.21 |
| E5a | 0.717 | −0.14 | 0.199 | −0.01 | |
| E6 | 0.691 | −1.26 | 0.937 | −1.25 | |
| E5b | 0.667 | 0.44 | 0.149 | 0.53 | |
| E5a+b | 0.688 | −0.43 | 0.174 | −0.12 | |
| Option | DD Model | SD Model |
|---|---|---|
| Positioning mode | Moving-baseline | Moving-baseline |
| Observations | BDS-2 B1I/B3I | BDS-2 B1I/B3I |
| BDS-3 B1I/B3I | BDS-3 B1I/B3I | |
| GPS L1/L2 | GPS L1/L2 | |
| Galileo E1/E5a | Galileo E1/E5a | |
| Elevation cutoff angle | 10° | 10° |
| Ephemeris | Broadcast | Broadcast |
| Ionospheric delay | Neglected | Neglected |
| Tropospheric delay | Neglected | Neglected |
| Stochastic model | Elevation-dependent model in Equation (6) | Elevation-dependent model in Equation (6) |
| Parameter estimator | Kalman filter | Kalman filter |
| Phase LB | Cancelled out | Estimate, random walk with process noise: 1 × 10−6 m/sqrt(s) |
| Code LB | Cancelled out | Estimate, random walk with process noise: 1 × 10−4 m/sqrt(s) |
| Ambiguity resolution | LAMBDA | LAMBDA |
| Ambiguity validation | Ratio test with a critical value of 2.0 for GPS, Galileo, BDS-2, BDS-3 alone and 1.5 for a combination of them | Ratio test with a critical value of 2.0 for GPS, Galileo, BDS-2, BDS-3 alone and 1.5 for a combination of them |
| Attitude computation | Direct computation with Equation (7) | Direct computation with Equation (7) |
| Frequency | System | AR Success Rate (%) | E (cm) | N (cm) | U (cm) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| DD | SD | DD | SD | DD | SD | DD | SD | Imp. (%) 1 | ||
| Single-frequency | BDS-2 | 98.99 | 99.66 | 0.32 | 0.30 | 0.43 | 0.40 | 1.24 | 0.98 | 21.0 |
| BDS-3 | 99.99 | 99.99 | 0.24 | 0.24 | 0.20 | 0.20 | 0.59 | 0.32 | 45.8 | |
| GPS | 99.99 | 99.99 | 0.28 | 0.28 | 0.27 | 0.26 | 0.70 | 0.37 | 47.1 | |
| Galileo | 99.67 | 99.94 | 0.35 | 0.34 | 0.35 | 0.31 | 0.87 | 0.47 | 46.0 | |
| BDS-2/BDS-3 | 100 | 99.99 | 0.18 | 0.18 | 0.18 | 0.16 | 0.54 | 0.40 | 25.9 | |
| BDS/GPS | 100 | 100 | 0.16 | 0.16 | 0.14 | 0.14 | 0.44 | 0.30 | 31.8 | |
| BDS/GPS/Galileo | 100 | 100 | 0.15 | 0.15 | 0.12 | 0.12 | 0.40 | 0.25 | 37.5 | |
| Dual-frequency | BDS-2 | 99.92 | 99.94 | 0.31 | 0.29 | 0.40 | 0.32 | 1.08 | 0.58 | 46.3 |
| BDS-3 | 99.99 | 99.99 | 0.20 | 0.20 | 0.19 | 0.19 | 0.49 | 0.24 | 51.0 | |
| GPS | 100 | 100 | 0.22 | 0.21 | 0.24 | 0.23 | 0.57 | 0.26 | 54.4 | |
| Galileo | 99.79 | 100 | 0.28 | 0.26 | 0.28 | 0.26 | 0.69 | 0.29 | 58.0 | |
| BDS-2/BDS-3 | 100 | 100 | 0.16 | 0.16 | 0.19 | 0.18 | 0.45 | 0.27 | 40.0 | |
| BDS/GPS | 100 | 100 | 0.13 | 0.13 | 0.14 | 0.13 | 0.35 | 0.18 | 48.6 | |
| BDS/GPS/Galileo | 100 | 100 | 0.11 | 0.11 | 0.12 | 0.12 | 0.31 | 0.16 | 48.4 | |
| Frequency | System | Yaw (Degree) | Pitch (Degree) | |||
| DD | SD | DD | SD | Imp. (%) 1 | ||
| Single-frequency | BDS-2 | 0.19 | 0.18 | 0.72 | 0.57 | 20.8 |
| BDS-3 | 0.15 | 0.14 | 0.34 | 0.18 | 47.1 | |
| GPS | 0.17 | 0.16 | 0.40 | 0.21 | 47.5 | |
| Galileo | 0.21 | 0.20 | 0.50 | 0.27 | 46.0 | |
| BDS-2/BDS-3 | 0.11 | 0.11 | 0.31 | 0.22 | 29.0 | |
| BDS/GPS | 0.09 | 0.09 | 0.25 | 0.17 | 32.0 | |
| BDS/GPS/Galileo | 0.09 | 0.09 | 0.23 | 0.14 | 39.1 | |
| Dual-frequency | BDS-2 | 0.18 | 0.18 | 0.63 | 0.34 | 46.0 |
| BDS-3 | 0.11 | 0.11 | 0.28 | 0.14 | 50.0 | |
| GPS | 0.13 | 0.12 | 0.33 | 0.15 | 54.5 | |
| Galileo | 0.16 | 0.15 | 0.40 | 0.17 | 57.5 | |
| BDS-2/BDS-3 | 0.09 | 0.09 | 0.27 | 0.16 | 40.7 | |
| BDS/GPS | 0.07 | 0.07 | 0.20 | 0.10 | 50.0 | |
| BDS/GPS/Galileo | 0.06 | 0.06 | 0.18 | 0.09 | 50.0 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, M.; Luo, S.; Wang, W.; Liu, W. Performance Assessment of BDS-2/BDS-3/GPS/Galileo Attitude Determination Based on the Single-Differenced Model with Common-Clock Receivers. Remote Sens. 2021, 13, 4845. https://doi.org/10.3390/rs13234845
Wu M, Luo S, Wang W, Liu W. Performance Assessment of BDS-2/BDS-3/GPS/Galileo Attitude Determination Based on the Single-Differenced Model with Common-Clock Receivers. Remote Sensing. 2021; 13(23):4845. https://doi.org/10.3390/rs13234845
Chicago/Turabian StyleWu, Mingkui, Shuai Luo, Wang Wang, and Wanke Liu. 2021. "Performance Assessment of BDS-2/BDS-3/GPS/Galileo Attitude Determination Based on the Single-Differenced Model with Common-Clock Receivers" Remote Sensing 13, no. 23: 4845. https://doi.org/10.3390/rs13234845
APA StyleWu, M., Luo, S., Wang, W., & Liu, W. (2021). Performance Assessment of BDS-2/BDS-3/GPS/Galileo Attitude Determination Based on the Single-Differenced Model with Common-Clock Receivers. Remote Sensing, 13(23), 4845. https://doi.org/10.3390/rs13234845





