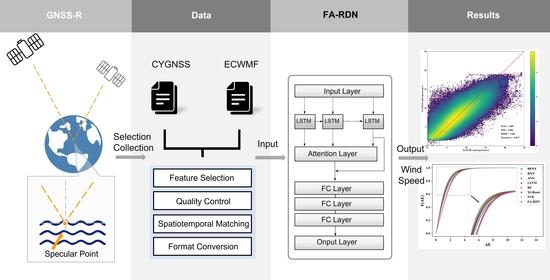
FA-RDN: A Hybrid Neural Network on GNSS-R Sea Surface Wind Speed Retrieval
Abstract
:1. Introduction
- It provides a new feature reference for GNSS-R sea surface wind speed retrieval through feature engineering;
- A new network structure is devised to extract the feature time dimension information in GNSS-R sea surface wind speed retrieval for the first time;
- The feature attention mechanism is added to implement attention weighting factors from the dimensions of feature types.
2. Data
2.1. Data Acquisition
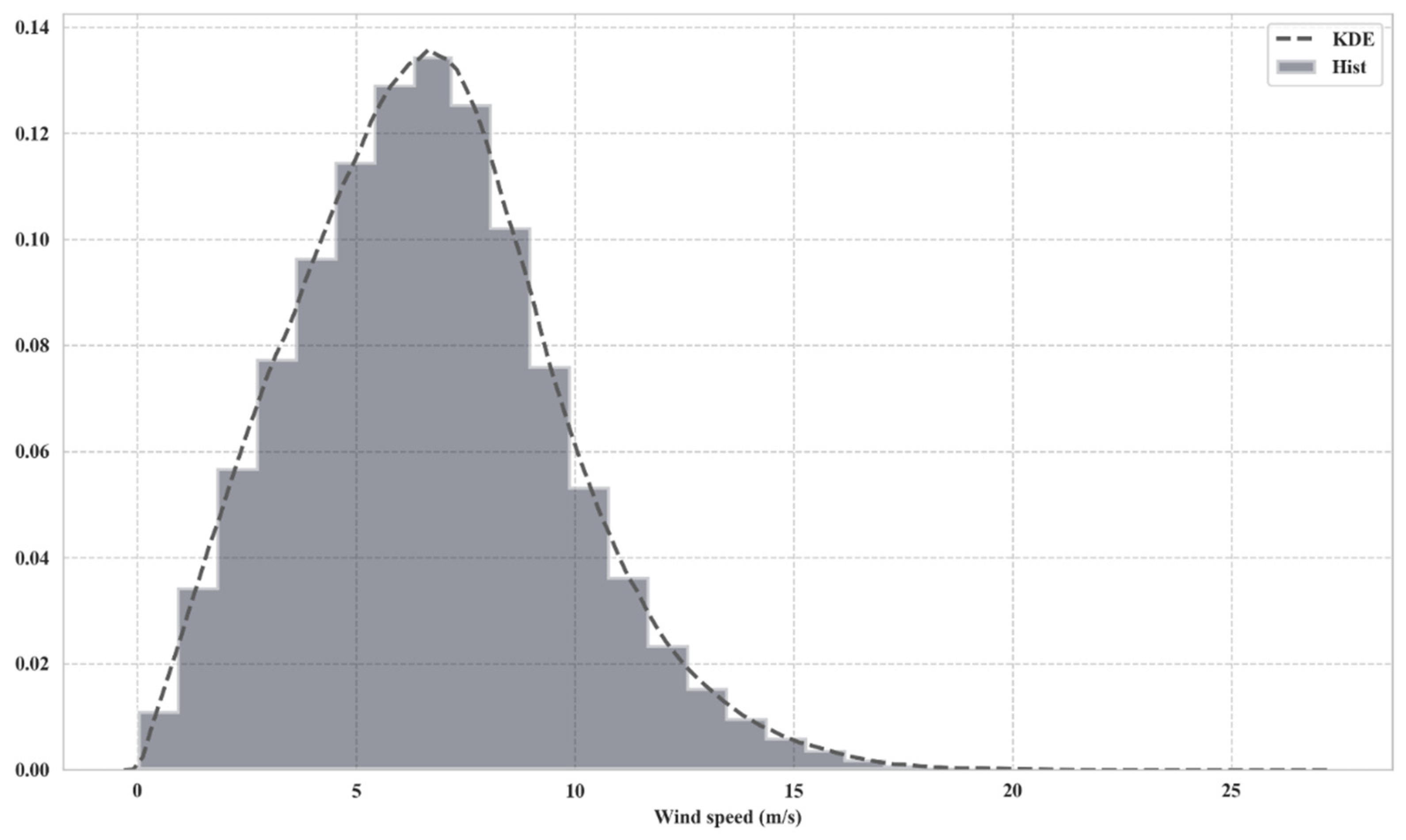
2.2. Data Pre-Processing
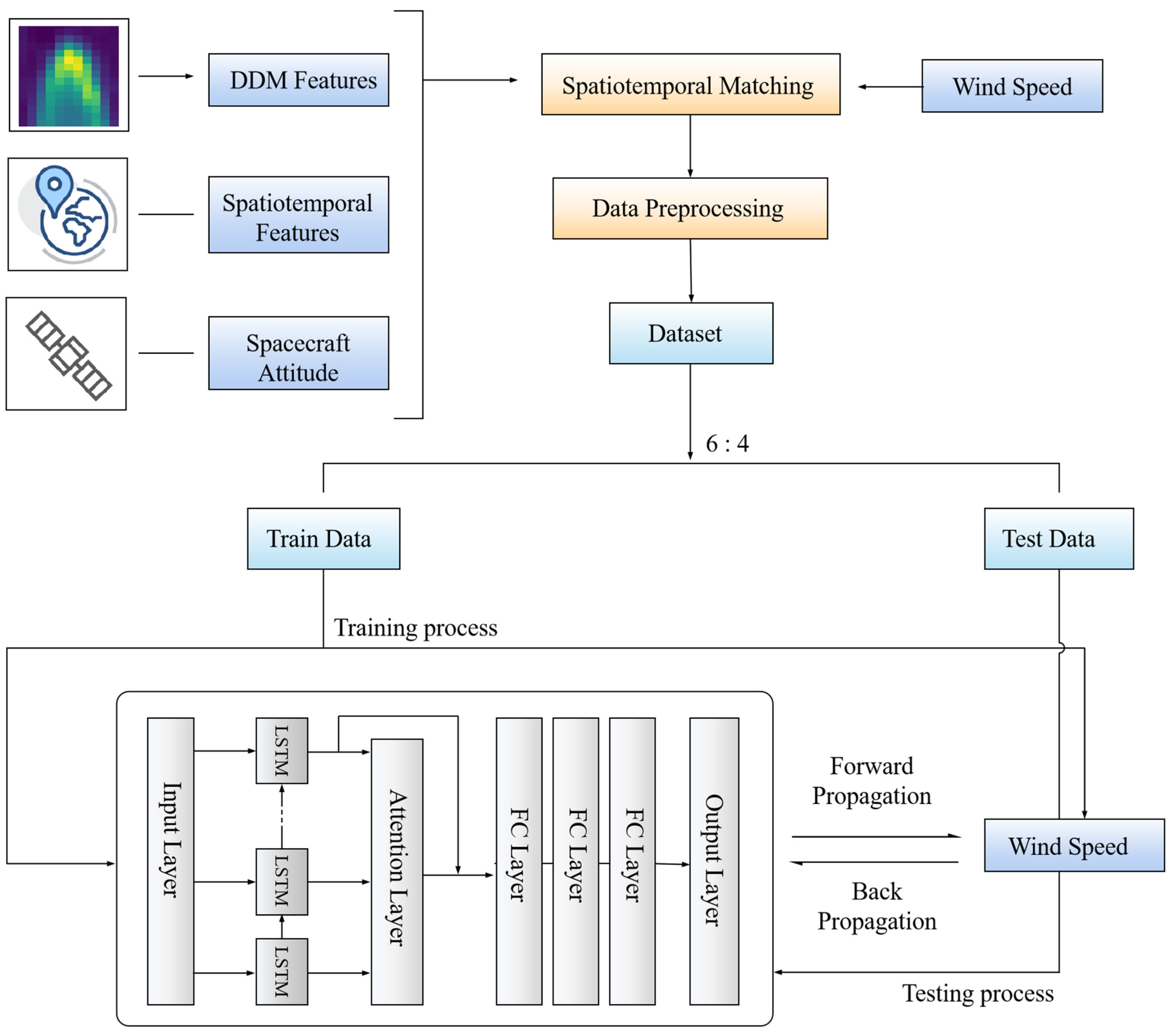
3. Method
3.1. Objective
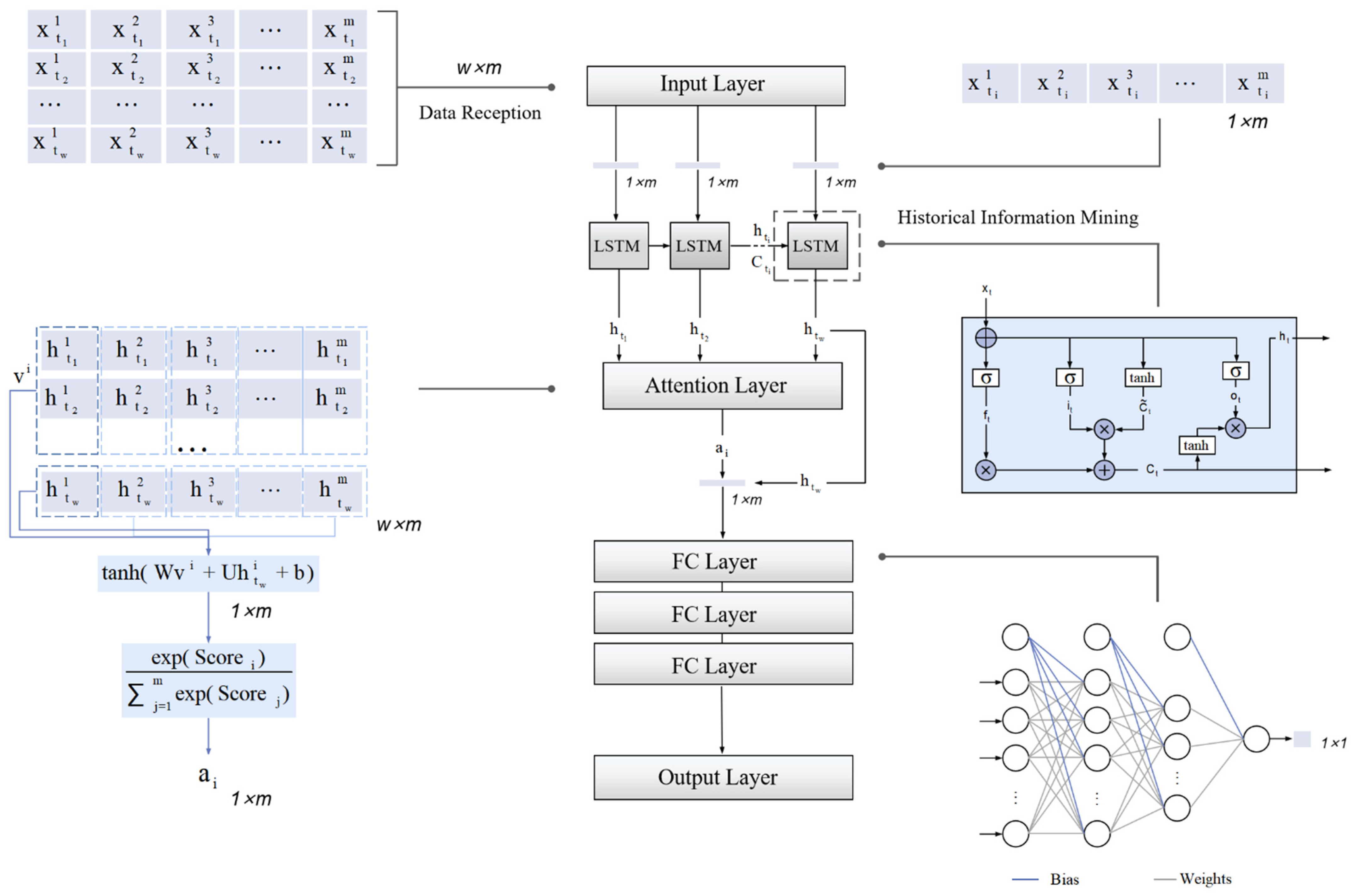
3.2. Model and Algorithm
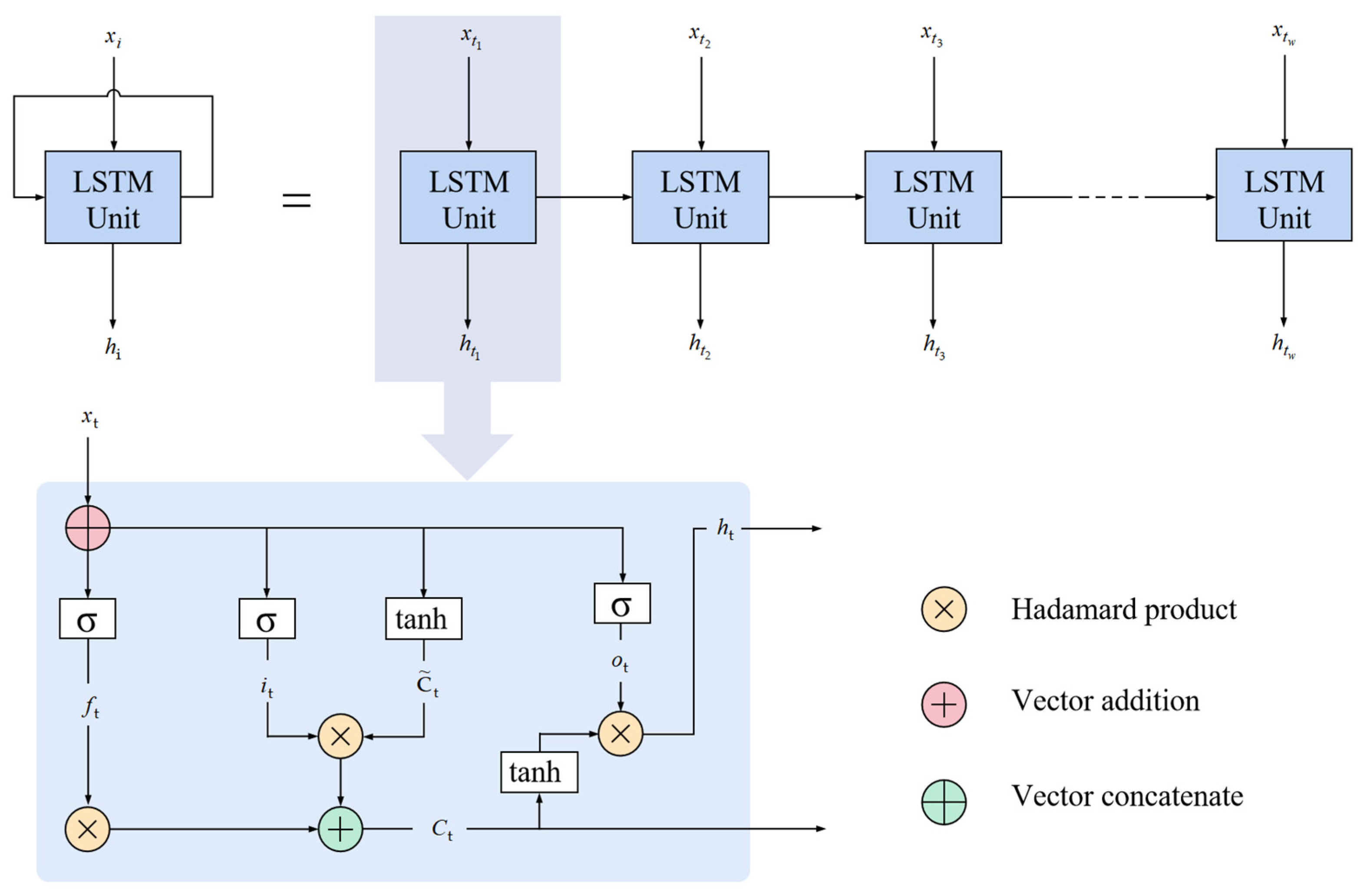
3.2.1. Lstm Layer
3.2.2. Attention Mechanism
3.3. Realization
4. Experiment
4.1. Evaluation Criteria
4.2. Comparison Model
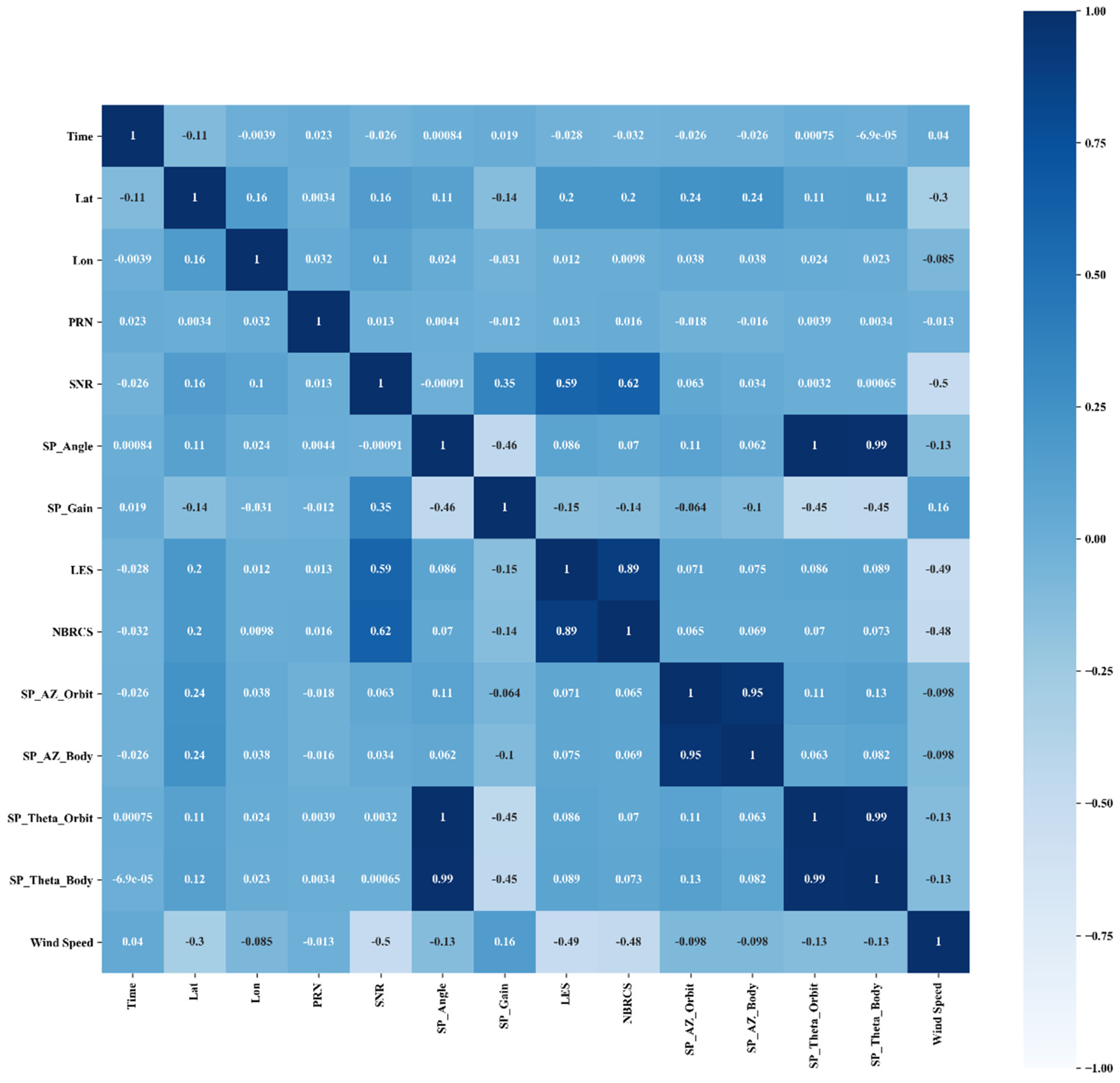
4.3. Feature Engineering
4.4. Experimental Design
- A.
- Performance evaluation
- B.
- Validity verification
- C.
- Stability analysis
5. Experimental Results and Analysis
5.1. Feature Analysis
5.2. Comparative Verification Experiments
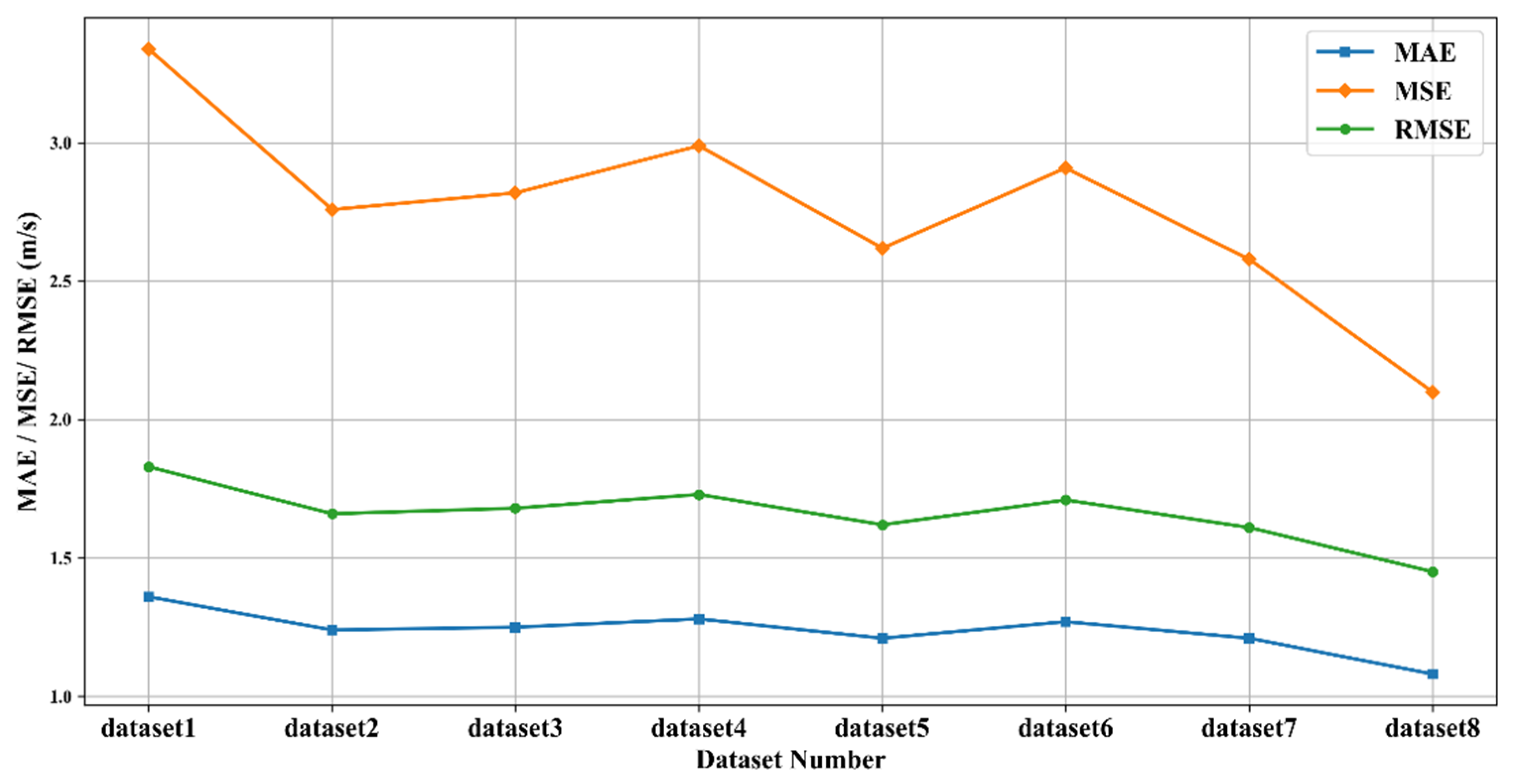
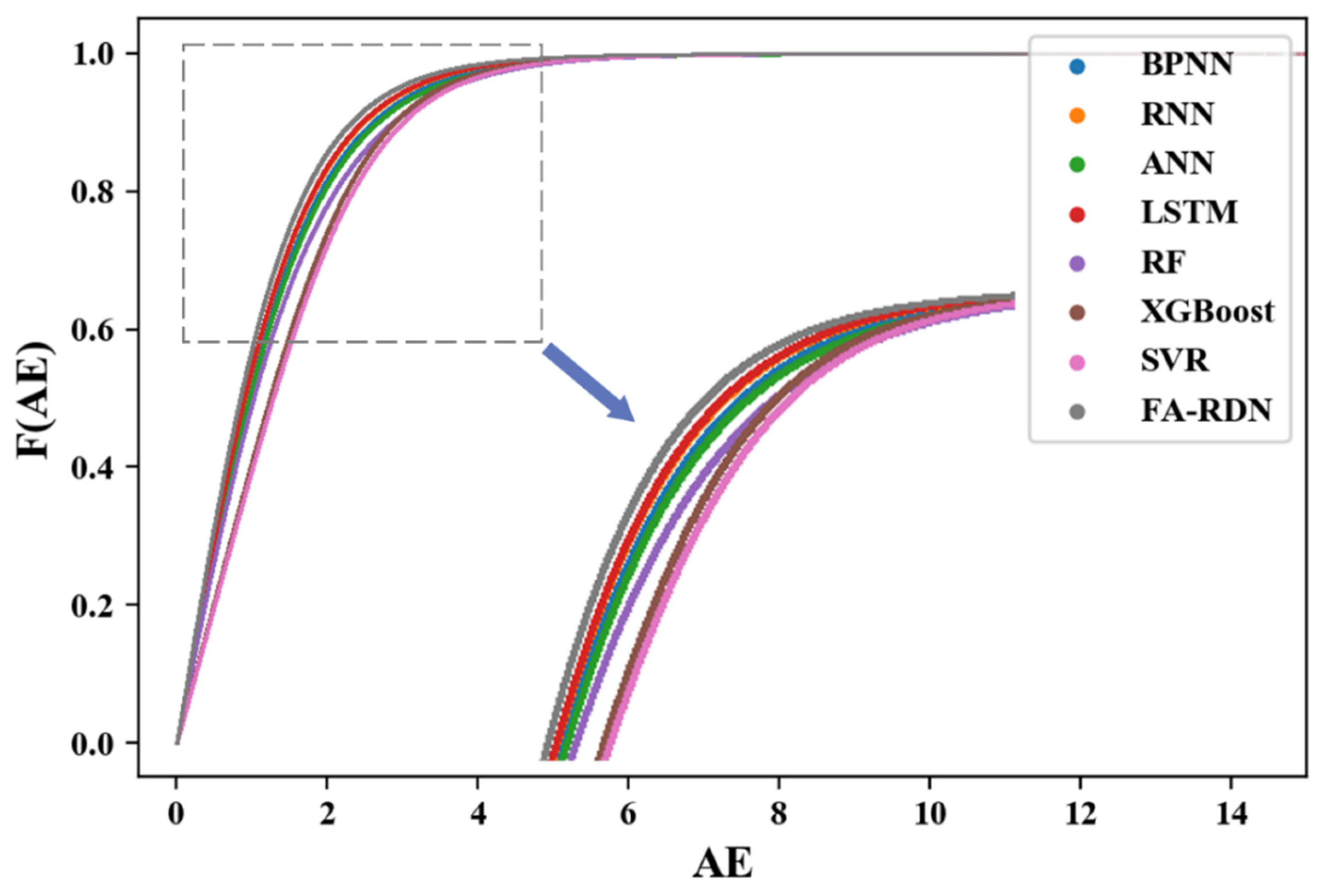
5.2.1. Performance Evaluation
5.2.2. Validity Verification
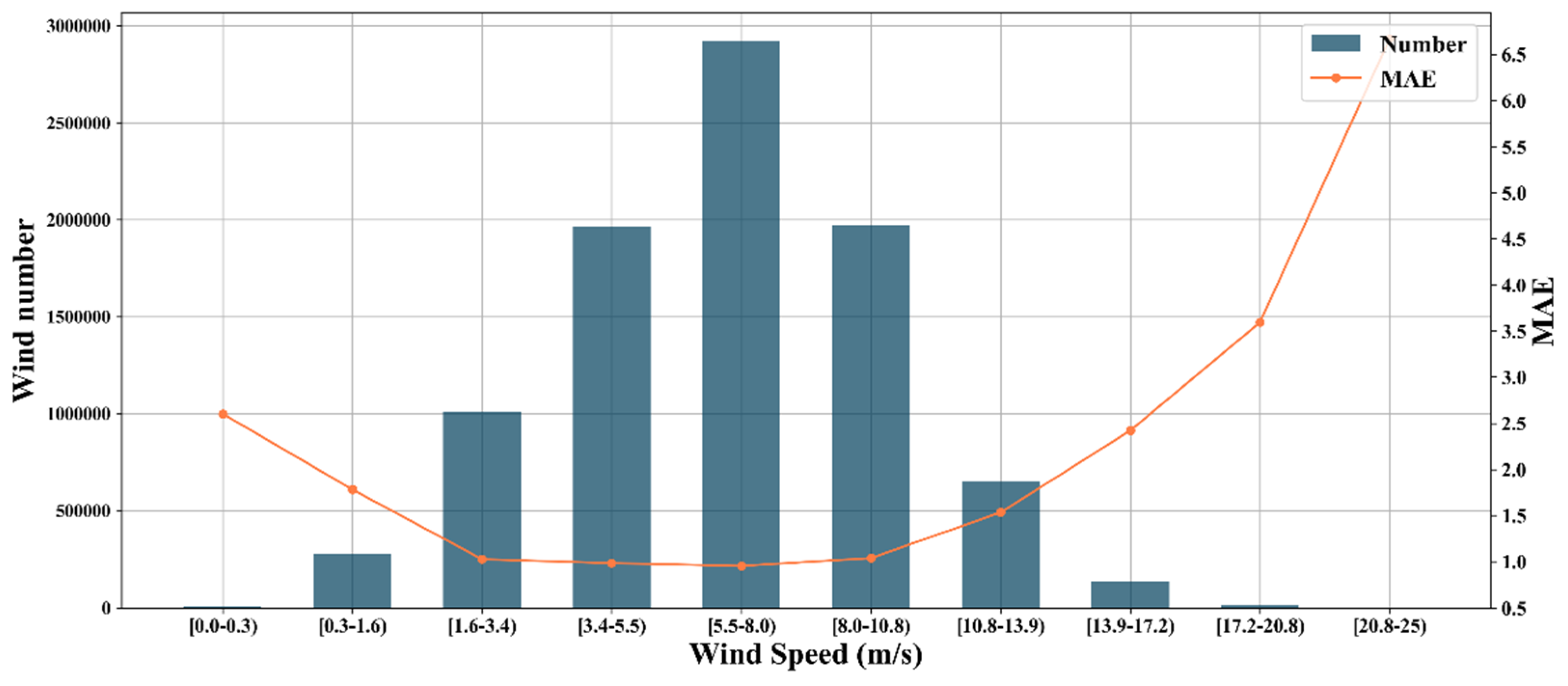
5.2.3. Stability Analysis
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AE | Absolute error |
| ANN | Artificial Neural Network |
| BPNN | Backpropagation neural network |
| CDF | Cumulative distribution function |
| CYGNSS | Cyclone Global Navigation Satellite System |
| DDM | Delay-Doppler map |
| GMF | Geophysical model function |
| FA-RDN | Recurrent deep neural network using feature attention mechanism |
| LES | Leading edge of the slope |
| LSTM | Long-short term memory |
| MAE | Mean absolute error |
| MLP | Multilayer Perceptron |
| MSE | Mean square error |
| NBRCS | Normalized bistatic radar cross-section |
| NLP | Natural Language Processing |
| Pearson’s r | Pearson correlation coefficient |
| Percent improvement in MAE | |
| Percent improvement in MSE | |
| Percent improvement in RMSE | |
| PRN | GPS pseudo random noise code |
| RMSE | Root mean square error |
| RNN | Recurrent Neural Network |
| RF | Random Forest |
| SM | Soil moisture |
| SNR | DDM signal to noise ratio |
| SP_Angle | The angle between the transmitter to specular point ray and the surface normal |
| SP_AZ_body | The azimuth angle of the specular point to receiver vector in the receiver’s body reference frame |
| SP_AZ_orbit | The azimuth angle of the specular point to receiver vector in the receiver’s orbit reference frame |
| SP_gain | The antenna gain towards specular point |
| SP_Lat | The latitude of the specular point |
| SP_Lon | The longitude of the specular point |
| SP_Theta_body | The theta angle of the specular point to receiver vector in the receiver’s body reference frame |
| SP_Theta_orbit | The theta angle of the specular point to receiver vector in the receiver’s orbit reference frame |
| SP_Time | The time of the specular point |
| SVM | Support Vector Machine |
| SVR | Support Vector Regression |
| TDS-1 | Demonstration Satellite-1 |
| UK-DMC | United Kingdom-Disaster Monitoring Constellation Technology |
| XGBoost | eXtreme Gradient Boosting |
References
- Martín-Neira, M. A passive reflectometry and interferometry system (PARIS) application to ocean altimetry. ESA J. 1993, 17, 331–355. [Google Scholar]
- Auber, J.; Bibaut, A.; Rigal, J. Characterization of Multipath on Land and Sea at GPS Frequencies. In Proceedings of the 7th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS 1994), Salt Lake City, UT, USA, 20–23 September 1994; pp. 1155–1171. [Google Scholar]
- Garrison, J.; Katzberg, S.; Hill, M. Effect of sea roughness on bistatically scattered range coded signals from the Global Positioning System. Geophys. Res. Lett. 1998, 25, 2257–2260. [Google Scholar] [CrossRef] [Green Version]
- Clarizia, M.P.; Gommenginger, C.; Bisceglie, M.; Galdi, C.; Srokosz, M. Simulation of L-Band Bistatic Returns from the Ocean Surface: A Facet Approach with Application to Ocean GNSS Reflectometry. IEEE Trans. Geosci. Remote Sens. 2012, 50, 960–971. [Google Scholar] [CrossRef]
- Gleason, S.; Hodgart, S.; Sun, Y.P.; Gommenginger, C.; Mackin, S.; Adjrad, M.; Unwin, M. Detection and Processing of bistatically reflected GPS signals from low Earth orbit for the purpose of ocean remote sensing. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1229–1241. [Google Scholar] [CrossRef] [Green Version]
- Foti, G.; Gommenginger, C.; Jales, P.; Unwin, M.; Shaw, A.; Robertson, C.; Roselló, J. Spaceborne GNSS Reflectometry for Ocean Winds: First Results from the UK TechDemoSat-1 Mission. Geophys. Res. Lett. 2015, 42, 5435–5441. [Google Scholar] [CrossRef] [Green Version]
- Foti, G.; Gommenginger, C.; Unwin, M.; Jales, P.; Tye, J.; Roselló, J. An Assessment of Non-Geophysical Effects in Spaceborne GNSS Reflectometry Data from the UK TechDemoSat-1 Mission. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3418–3429. [Google Scholar] [CrossRef] [Green Version]
- Soisuvarn, S.; Jelenak, Z.; Said, F.; Chang, P.; Egido, A. The GNSS Reflectometry Response to the Ocean Surface Winds and Waves. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4678–4699. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Ruf, C. Wind Speed Retrieval Algorithm for the Cyclone Global Navigation Satellite System (CYGNSS) Mission. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4419–4432. [Google Scholar] [CrossRef]
- Unwin, M.; Jales, P.; Blunt, P.; Duncan, S.; Brummitt, M.; Ruf, C. The SGR-ReSI and its application for GNSS reflectometry on the NASA EV-2 CYGNSS mission. In Proceedings of the 2013 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2013; pp. 1–6. [Google Scholar]
- Komjathy, A.; Armatys, M.; Masters, D.; Axelrad, P.; Zavorotny, V.; Katzberg, S. Retrieval of Ocean Surface Wind Speed and Wind Direction Using Reflected GPS Signals. J. Atmos. Ocean Technol. 2004, 21, 515–526. [Google Scholar] [CrossRef] [Green Version]
- Cardellach, E.; Fabra, F.; Nogués-Correig, O.; Oliveras, S.; Ribó, S.; Rius, A. GNSS-R ground-based and airborne campaigns for ocean, land, ice, and snow techniques: Application to the GOLD-RTR data sets. Radio Sci. 2011, 46, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Yan, Q.; Huang, W.; Jin, S.; Jia, Y. Pan-tropical soil moisture mapping based on a three-layer model from CYGNSS GNSS-R data. Remote Sens. Environ. 2020, 247, 111944. [Google Scholar] [CrossRef]
- Stilla, D.; Zribi, M.; Pierdicca, N.; Baghdadi, N.; Huc, M. Desert Roughness Retrieval Using CYGNSS GNSS-R Data. Remote Sens. 2020, 12, 743. [Google Scholar] [CrossRef] [Green Version]
- Carreno-Luengo, H.; Luzi, G.; Crosetto, M. Above-Ground Biomass Retrieval over Tropical Forests: A Novel GNSS-R Approach with CyGNSS. Remote Sens. 2020, 12, 1368. [Google Scholar] [CrossRef]
- Jacobson, M.; Emery, W.; Westwater, E. Oceanic wind vector determination using a dual-frequency microwave airborne radiometer theory and experiment. In Proceedings of the 1996 International Geoscience and Remote Sensing Symposium (IGARSS ’96.), Lincoln, NE, USA, 31 May 1996; Volume 2, pp. 1138–1140. [Google Scholar]
- Monaldo, F.; Thompson, D.R.; Beal, R.; Pichel, W.; Clemente-Colon, P. Comparison of SAR-derived wind speed with model predictions and ocean buoy measurements. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2587–2600. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Ruf, C.; Jales, P.; Gommenginger, C. Spaceborne GNSS-R Minimum Variance Wind Speed Estimator. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6829–6843. [Google Scholar] [CrossRef]
- Frate, F.; Pacifici, F.; Schiavon, G.; Solimini, C. Use of Neural Networks for Automatic Classification from High-Resolution Images. IEEE Trans. Geosci. Remote Sens. 2007, 45, 800–809. [Google Scholar] [CrossRef]
- Chi, M.; Feng, R.; Bruzzone, L. Classification of hyperspectral remote-sensing data with primal SVM for small-sized training dataset problem. Adv. Space Res. 2008, 41, 1793–1799. [Google Scholar] [CrossRef]
- Eroglu, O.; Kurum, M.; Boyd, D.; Gürbüz, A.C. High Spatio-Temporal Resolution CYGNSS Soil Moisture Estimates Using Artificial Neural Networks. Remote Sens. 2019, 11, 2272. [Google Scholar] [CrossRef] [Green Version]
- Reynolds, J.; Clarizia, M.P.; Santi, E. Wind Speed Estimation from CYGNSS Using Artificial Neural Networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 708–716. [Google Scholar] [CrossRef]
- Asgarimehr, M.; Zhelavskaya, I.; Foti, G.; Reich, S.; Wickert, J. A GNSS-R Geophysical Model Function: Machine Learning for Wind Speed Retrievals. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1333–1337. [Google Scholar] [CrossRef]
- Liu, Y.; Collett, I.; Morton, Y. Application of Neural Network to GNSS-R Wind Speed Retrieval. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9756–9766. [Google Scholar] [CrossRef]
- Chu, X.; He, J.; Song, H.; Qi, Y.; Sun, Y.; Bai, W.; Li, W.; Wu, Q. Multimodal Deep Learning for Heterogeneous GNSS-R Data Fusion and Ocean Wind Speed Retrieval. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5971–5981. [Google Scholar] [CrossRef]
- Balasubramaniam, R.; Ruf, C. Neural Network Based Quality Control of CYGNSS Wind Retrieval. Remote Sens. 2020, 12, 2859. [Google Scholar] [CrossRef]
- Gleason, S.; Ruf, C.S.; O’Brien, A.J.; McKague, D.S. The CYGNSS Level 1 Calibration Algorithm and Error Analysis Based on On-Orbit Measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 37–49. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Kastner, S.; Ungerleider, L.G. Mechanisms of Visual Attention in the Human Cortex. Annu. Rev. Neurosci. 2000, 23, 315–341. [Google Scholar]
- Zhou, Z.-H. Ensemble Methods: Foundations and Algorithms; Chapman and Hall/CRC: London, UK, 2012; Volume 14, ISBN 978-1-4398-3003-1. [Google Scholar]
- Rodriguez-Galiano, V.F.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An Assessment of the Effectiveness of a Random Forest Classifier for Land-Cover Classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Senyurek, V.; Lei, F.; Boyd, D.; Kurum, M.; Gurbuz, A.C.; Moorhead, R. Machine Learning-Based CYGNSS Soil Moisture Estimates over ISMN Sites in CONUS. Remote Sens. 2020, 12, 1168. [Google Scholar] [CrossRef] [Green Version]
- Cutler, A.; Cutler, D.; Stevens, J. Random Forests. In Machine Learning—ML; Springer: Boston, MA, USA, 2011; Volume 45, pp. 157–176. ISBN 978-1-4419-9325-0. [Google Scholar]
- Benali, L.; Notton, G.; Fouilloy, A.; Voyant, C.; Dizene, R. Solar Radiation Forecasting Using Artificial Neural Network and Random Forest Methods: Application to Normal Beam, Horizontal Diffuse and Global Components. Renew. Energy 2019, 132, 871–884. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef] [Green Version]
- Bhattacharya, S.; Maddikunta, P.K.R.; Kaluri, R.; Singh, S.; Gadekallu, T.R.; Alazab, M.; Tariq, U. A Novel PCA-Firefly Based XGBoost Classification Model for Intrusion Detection in Networks Using GPU. Electronics 2020, 9, 219. [Google Scholar] [CrossRef] [Green Version]
- Zamani Joharestani, M.; Cao, C.; Ni, X.; Bashir, B.; Talebiesfandarani, S. PM2.5 Prediction Based on Random Forest, XGBoost, and Deep Learning Using Multisource Remote Sensing Data. Atmosphere 2019, 10, 373. [Google Scholar] [CrossRef] [Green Version]
- Drucker, H.; Burges, C.J.C.; Kaufman, L.; Smola, A.; Vapnik, V. Support Vector Regression Machines. In Proceedings of the 9th International Conference on Neural Information Processing Systems, Denver, CO, USA, 3 December 1996; MIT Press: Cambridge, MA, USA, 1996; pp. 155–161. [Google Scholar]
- Ruf, C.S.; Balasubramaniam, R. Development of the CYGNSS Geophysical Model Function for Wind Speed. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 66–77. [Google Scholar] [CrossRef]
- Asgarimehr, M.; Wickert, J.; Reich, S. TDS-1 GNSS Reflectometry: Development and Validation of Forward Scattering Winds. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4534–4541. [Google Scholar] [CrossRef]
- Ferreira, A.J.; Figueiredo, M.A.T. Efficient Feature Selection Filters for High-Dimensional Data. Pattern Recognit. Lett. 2012, 33, 1794–1804. [Google Scholar] [CrossRef] [Green Version]
- Ruf, C.S.; Gleason, S.; McKague, D.S. Assessment of CYGNSS Wind Speed Retrieval Uncertainty. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 87–97. [Google Scholar] [CrossRef]

| NO | Name | Type |
|---|---|---|
| 1 | SNR | Signal attribute |
| 2 | NBRCS | Signal attribute |
| 3 | LES | Signal attribute |
| 4 | SP_gain | Instrument attribute |
| 5 | PRN | Instrument attribute |
| 6 | SP_Lon | Spatio-temporal attribute |
| 7 | SP_Lat | Spatio-temporal attribute |
| 8 | SP_Time | Spatio-temporal attribute |
| 9 | SP_Angle | Geometry attribute |
| 10 | SP_AZ_orbit | Geometry attribute |
| 11 | SP_AZ_body | Geometry attribute |
| 12 | SP_Theta_orbit | Geometry attribute |
| 13 | SP_Theta_body | Geometry attribute |
| Hyperparameter | Size/Type | Definition/Application |
|---|---|---|
| Batch size | 64 | The size of the dataset that uses part of the training data to complete the training once and update the network weights. |
| Activation function | It is used for model computation, providing nonlinearity to the model, and improving the expressiveness of the network. | |
| Loss function | MSE | The way of measuring the difference between the computed output of the network and the true value in the training process. |
| Optimizer | Adam | The way to calculate the optimal weights as well as bias of neural network through loss function. |
| Epoch | In this article, it is determined by early termination. | The number of a complete traversal of the entire train dataset at training time. |
| Model | Parameter | Value |
|---|---|---|
| BPNN | Hidden neurons Number of hidden layers | {32,16,16} {3} |
| RNN | Hidden neurons Number of RNN layers Number of FC layers | {13,16,16,8} {1} {3} |
| LSTM | Hidden neurons Number of LSTM layers Number of FC layers | {13,16,16,8} {1} {3} |
| ANN | Hidden neurons Number of hidden layers | {16,16} {2} |
| Scheme | Dataset | Features |
|---|---|---|
| 1 | Dataset 1 | SNR, BNRES, and LES (benchmark dataset) |
| 2 | Dataset 2 | Benchmark dataset + spatio-temporal attribute |
| Dataset 3 | All features − spatio-temporal attribute | |
| 3 | Dataset 4 | Benchmark dataset + instrument attribute |
| Dataset 5 | All features − instrument attribute | |
| 4 | Dataset 6 | Benchmark dataset + geometry attribute |
| Dataset 7 | All features − geometry attribute | |
| 5 | Dataset 8 | All features |
| Metrics | Improvement | |||||
|---|---|---|---|---|---|---|
| MAE | MSE | RMSE | PMAE | PMSE | PRMSE | |
| Dataset 1 | 1.36 | 3.34 | 1.83 | \ | \ | \ |
| Dataset 2 | 1.24 | 2.76 | 1.66 | 8.56% | 17.38% | 9.11% |
| Dataset 4 | 1.28 | 2.99 | 1.73 | 5.60% | 10.43% | 5.36% |
| Dataset 6 | 1.27 | 2.91 | 1.71 | 6.35% | 12.68% | 6.56% |
| Dataset 3 | 1.25 | 2.82 | 1.68 | 13.55% | 25.65% | 13.77% |
| Dataset 5 | 1.21 | 2.62 | 1.62 | 10.64% | 20.12% | 10.63% |
| Dataset 7 | 1.21 | 2.58 | 1.61 | 10.30% | 18.73% | 9.85% |
| Dataset 8 | 1.08 | 2.10 | 1.45 | \ | \ | \ |
| Metrics | Improvement | |||||
|---|---|---|---|---|---|---|
| MAE | MSE | RMSE | PMAE | PMSE | PRMSE | |
| BPNN | 1.21 | 2.61 | 1.62 | 10.71% | 19.67% | 10.38% |
| RNN | 1.17 | 2.40 | 1.55 | 6.95% | 12.73% | 6.58% |
| ANN | 1.25 | 2.79 | 1.67 | 13.05% | 24.80% | 13.28% |
| FA_RDN | 1.08 | 2.10 | 1.45 | \ | \ | \ |
| Metrics | Improvement | |||||
|---|---|---|---|---|---|---|
| MAE | MSE | RMSE | PMAE | PMSE | PRMSE | |
| RF | 1.32 | 3.11 | 1.76 | 18.10% | 32.57% | 17.89% |
| XGBoost | 1.45 | 3.30 | 1.82 | 24.94% | 36.42% | 20.26% |
| SVR | 1.50 | 3.55 | 1.88 | 27.55% | 40.92% | 23.14% |
| FA-RDN | 1.08 | 2.10 | 1.45 | \ | \ | \ |
| Metrics | Improvement | |||||
|---|---|---|---|---|---|---|
| MAE | MSE | RMSE | PMAE | PMSE | PRMSE | |
| LSTM | 1.15 | 2.34 | 1.53 | 5.78% | 10.45% | 5.37% |
| FA_RDN | 1.08 | 2.10 | 1.45 | \ | \ | \ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Bai, W.; Xia, J.; Huang, F.; Yin, C.; Sun, Y.; Du, Q.; Meng, X.; Liu, C.; Hu, P.; et al. FA-RDN: A Hybrid Neural Network on GNSS-R Sea Surface Wind Speed Retrieval. Remote Sens. 2021, 13, 4820. https://doi.org/10.3390/rs13234820
Liu X, Bai W, Xia J, Huang F, Yin C, Sun Y, Du Q, Meng X, Liu C, Hu P, et al. FA-RDN: A Hybrid Neural Network on GNSS-R Sea Surface Wind Speed Retrieval. Remote Sensing. 2021; 13(23):4820. https://doi.org/10.3390/rs13234820
Chicago/Turabian StyleLiu, Xiaoxu, Weihua Bai, Junming Xia, Feixiong Huang, Cong Yin, Yueqiang Sun, Qifei Du, Xiangguang Meng, Congliang Liu, Peng Hu, and et al. 2021. "FA-RDN: A Hybrid Neural Network on GNSS-R Sea Surface Wind Speed Retrieval" Remote Sensing 13, no. 23: 4820. https://doi.org/10.3390/rs13234820
APA StyleLiu, X., Bai, W., Xia, J., Huang, F., Yin, C., Sun, Y., Du, Q., Meng, X., Liu, C., Hu, P., & Tan, G. (2021). FA-RDN: A Hybrid Neural Network on GNSS-R Sea Surface Wind Speed Retrieval. Remote Sensing, 13(23), 4820. https://doi.org/10.3390/rs13234820