Abstract
This paper proposes a new approach based on an unsupervised deep learning (DL) model for landslide detection. Recently, supervised DL models using convolutional neural networks (CNN) have been widely studied for landslide detection. Even though these models provide robust performance and reliable results, they depend highly on a large labeled dataset for their training step. As an alternative, in this paper, we developed an unsupervised learning model by employing a convolutional auto-encoder (CAE) to deal with the problem of limited labeled data for training. The CAE was used to learn and extract the abstract and high-level features without using training data. To assess the performance of the proposed approach, we used Sentinel-2 imagery and a digital elevation model (DEM) to map landslides in three different case studies in India, China, and Taiwan. Using minimum noise fraction (MNF) transformation, we reduced the multispectral dimension to three features containing more than 80% of scene information. Next, these features were stacked with slope data and NDVI as inputs to the CAE model. The Huber reconstruction loss was used to evaluate the inputs. We achieved reconstruction losses ranging from 0.10 to 0.147 for the MNF features, slope, and NDVI stack for all three study areas. The mini-batch K-means clustering method was used to cluster the features into two to five classes. To evaluate the impact of deep features on landslide detection, we first clustered a stack of MNF features, slope, and NDVI, then the same ones plus with the deep features. For all cases, clustering based on deep features provided the highest precision, recall, F1-score, and mean intersection over the union in landslide detection.
1. Introduction
Landslides are one of the most dangerous and complicated natural disasters that usually cause severe destruction in natural areas and settlements and loss of human life and property [1], which occur in different types, frequencies, and intensities worldwide [2]. Therefore, studying and analyzing this natural hazard is highly necessary to find appropriate solutions to mitigate its adverse consequences. Rapid detection and mapping of such events are notably necessary for immediate response and rescue operations. Field surveys and visual interpretation of aerial photographs are the prevailing methods to map landslides [3]. However, the mentioned approaches are limited because of the accessibility to remote areas for field surveys. Moreover, these approaches depend on the visual interpretation of expert experience and knowledge [4].
Moreover, these methods are time-consuming, costly, and inefficient to apply to large areas for landslide inventory mapping. However, in recent years, the significant advancements in Earth Observation (EO) technologies have resulted in a considerable variety and velocity of remote sensing (RS) data with different spatial and temporal resolutions [5,6]. On large scales, RS data are the most accessible and reliable source that can provide near real-time information on spatio-temporal changes of the land surface, particularly on landslides [7].
The application of machine learning (ML) models for detecting the landslide from the RS data such as the annotation of other natural and anthropogenic geographical features has mainly been carried out based on two main supervised and unsupervised techniques. On one hand, in the former technique, ML models including decision tree (DT) [8], support vector machine (SVM) [4,9], artificial neural network (ANN) [10,11], and random forest (RF) [4,12] have been widely used for mapping and modeling landslides. In these ML and any other supervised model, a landslide inventory map of previous landslide events is required for the training process. All mentioned models provide reliable results when there is adequate labeled data for training. Therefore, the performance of supervised ML models is highly dependent on the quality and quantity of the training data [13]. Thus, it is necessary to have access to an accurate and reliable landslide inventory dataset for training and validating supervised ML models [14]. Although these methods have proven to be more effective in image classification and complex feature detection such as landslides, they are sensitive to some issues including overlearning (over-fitting), the quality of training data, and the model configuration parameters [4].
On the other hand, in unsupervised image classification techniques, pixels that share similar or common characteristics are grouped into the same cluster [15]. However, unsupervised image classification techniques are performed without introducing any labeled data to the classifier, and it is only based on the similarity between pixel values [16,17]. Moreover, the analyst only provides the number of classes or clusters of interest to be mapped as land covers. Since there is no previous training procedure, the number of classes is not always equal to the exact number of land-use/landcover types [17]. Although supervised methods offer higher accuracy and precision, unsupervised methods do not require training data, and on images with large ground pixel size, they demonstrate a good performance [17,18,19]. The most commonly used unsupervised method for land-use/landcover and landslide mapping is K-means [20,21]. In some other studies [19], unsupervised and threshold-based methods including normalized difference vegetation index (NDVI), change vector analysis, spectral features variance, principal component analysis (PCA), and image rationing have been applied on multi-temporal images to map land surface changes, in particular landslides [22]. Although these approaches have proven to be easy and fast to implement, their accuracy is relatively low compared to supervised methods because they cannot handle complex and multi-dimensional data and cannot map non-linear patterns [19].
During the last decade, deep learning (DL) models such as convolutional neural networks (CNNs) have attracted scientific attention for many applications, particularly in image processing. Their successful performance in satellite image classification and object detection compared to conventional ML methods is due to the availability and access to the vast amount of labeled data and significant development in computer vision and graphics processing units (GPUs) [4]. In natural hazard assessment studies, CNNs have recently been used for landslide detection by some publications pioneered by [4], and the results indicated that CNNs present a decent performance in this task. In this study, Ghorbanzadeh et al. [4] applied CNNs on Rapid-Eye satellite imagery for landslide detection in the higher Himalayas and compared the results with some common supervised ML models ANN, SVM, and RF. Their accuracy assessment results showed that the CNN model outperformed other ML models in the discrimination of landslides from non-landslide areas.
Nevertheless, the authors conclude that the performance and accuracy of CNN models significantly depend on their design (i.e., input window sizes, layer depth, and amount of labeled data for training). Therefore, although CNNs provide excellent results for supervised image classification and object detection, they require a significant amount of labeled data, training time, and powerful hardware for training and testing. Thus, lacking any of these elements, particularly adequate training data, would be problematic to properly run a DL model for RS applications [3]. However, unsupervised DL models can be an alternative solution for image clustering and feature extraction [23].
Autoencoders (AEs) are one of the unsupervised architectures in deep neural networks and have been used in many applications in the field of RS. Therefore, some researchers have employed AEs to solve critical image processing challenges such as image classification [24,25,26], clustering [23,27,28], spectral unmixing [29] and image segmentation [30,31]. AEs have also been applied to deal with other important problems such as image fusion [32], change detection [33,34,35], pansharpening [36,37], anomaly detection [38,39], and image retrieval [40]. In recent years, the application of AE for clustering purposes has gained much attention in the RS community. One of the first studies that used AE for clustering was developed by [41]. They presented results that demonstrated the potential of AEs in learning more distinctive and informative representations from data. Zhang et al. [42] investigated the potential of a dual AE consisting of convolutional and LSTM layers for clustering on Landsat-8 imagery. Mousavi et al. [23] clustered seismic data over the features produced by their proposed CAE. This study achieved a reliable precision against supervised methods and provided a model to facilitate the early warning of earthquake. In [43], the authors introduced a 3D-CAE to encode embedded representations of the hyperspectral dataset, then applied clustering over them. Rahimzad et al. [28] proposed a boosted CAE to learn and extract deep features for automatic RS image clustering in urban areas.
To the best of our knowledge, no study has yet explored the possibility of unsupervised AEs for landslide detection from Sentinel-2A imageries. Therefore, our main aim in this study was to use an unsupervised DL model based on the AE for landslide detection from different geographical areas in India, China, and Taiwan. Using this model, we brought into play an AE consisting of the convolutional layers known as the convolutional auto-encoder (CAE) model. This proposed CAE was trained on Sentinel-2A images to extract discriminative features from the image and cluster them using mini-batch K-means [44]. Some studies [45,46] have proven that using irrelevant features is the main reason for overfitting, whereas cooperating of the most relevant features usually positively influences the overall image classification performance [47,48]. Therefore, selecting the most landslide-relevant features can significantly improve the landslide discrimination from non-landslide areas [48]. Stumpf and Kerle (2011) [49] concluded that reducing features led to higher landslide detection accuracy. Therefore, in this study, to improve the performance of the proposed CAE, we applied minimum noise fraction (MNF) on Sentinel-2A multispectral bands to reduce the dimensionality and separate noise in the data. Additionally, the effectiveness of some auxiliary data such as the topographic factor of slope and normalized difference vegetation index (NDVI) for landslide detection were investigated [48,50]. The resulting features of the MNF transformation were then stacked with slope and NDVI layers in this study. We designed and trained a CAE over the stacked and prepared features. CAE’s learned features were then considered ultimate deep features and clustered in classes according to deep feature pixel values.
Moreover, to compare the impact of deep features on unsupervised landslide detection, the clustering was performed twice for each study area. First, clustering was conducted based only on MNF features stacked with slope and NDVI. Second, it was carried out on the former features plus the deep features generated by CAE. Finally, for accuracy assessment, the detected landslides were evaluated by validation measures such as overall accuracy, precision, recall, f1 measure, and mean intersection-over-union (mIOU) validation using ground truth data.
2. Study Areas
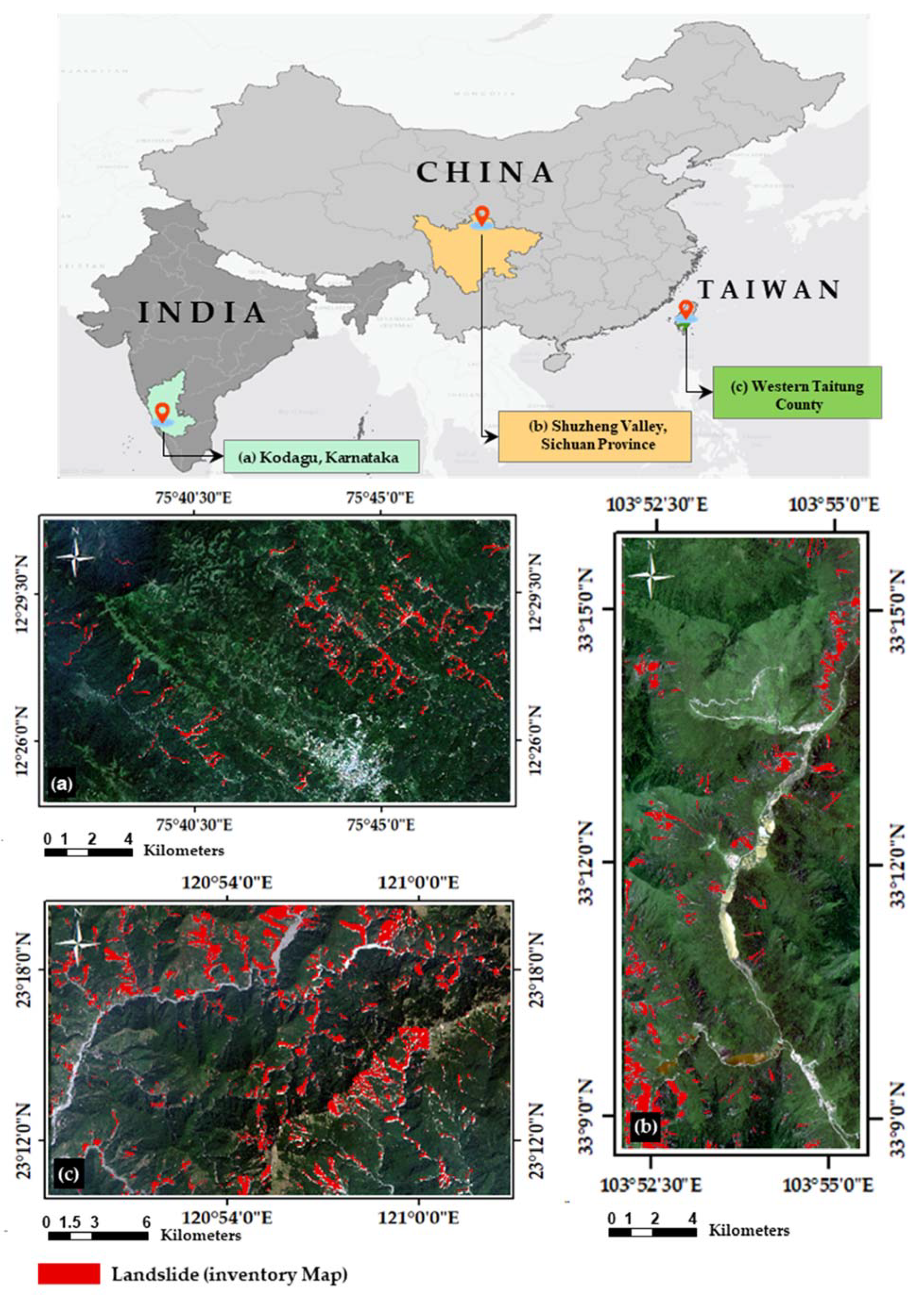
2.1. Kodagu, Karnataka (India)
During the monsoon season, which starts from early July and goes to almost the end of August, there are always heavy rainfalls in Kodagu, Karnataka, India (Figure 1a). During August 2018, heavy rainfall of more than 1200 mm occurred [51,52], while this annual figure for 2018, according to the India Meteorological Department, Customized Rainfall Information System (CRIS), reached almost 3650 mm. This event led to severe small and massive landslides in the region. As a result, over 200 villages were severely affected, sixteen people lost their lives, and around 40 were listed as missing [53]. Our selected area (250 km2) is a part of Kodagu, which contains several landslides. The geomorphological settings of Kodagu are predominated by hill ranges, which are covered by dense forests and agricultural fields. The elevation varies from approximately 45 m above mean sea level (AMSL) to more than 1726 m AMSL.
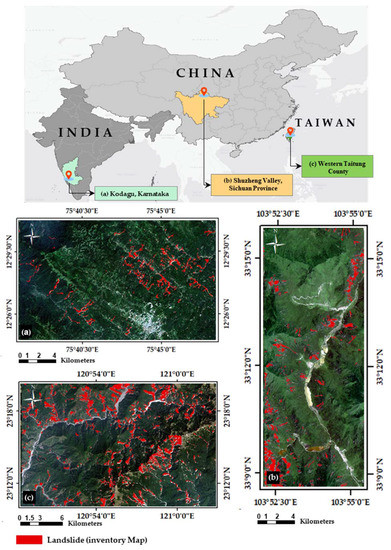
Figure 1.
The geographical location of study areas and corresponding landslide inventory map. (a) India, (b) China, and (c) Taiwan. The background image for all three cases is the Sentinel-2 natural color composite.
2.2. Shuzheng Valley, Sichuan Province, (China)
The second study area was Shuzheng Valley, located in Sichuan Province (Figure 1b), which is an area with many scenic spots. Because of its rich ecosystems, lakes, and landscapes, the region is one of the leading tourist destinations in Sichuan Province [54]. On 8 August 2017, Shuzheng Valley and its scenic areas were hit by an earthquake with a magnitude of 7 Mw, resulting in 25 deaths, 525 injuries, and a USD 21 million economic loss on top of the devastated tourism resorts [55]. In addition to economic loss, there were numerous destructive accidents following the earthquake such as dam breaks, landslides, and rockfalls. The earthquake, mostly on steep slopes, triggered nearly 1780 landslides. The elevation of this study area ranges from almost 2000 m AMSL to less than 4500 m AMSL. The climate of the Shuzheng Valley is dominated by semi-humid, and the monsoon season in this area starts in May and continues until September. In addition, most of the landslides and debris flows also take place during this season [55]. For this site, an area of 69.78 km2 with several landslides was selected.
2.3. Western Taitung County (Taiwan)
The other selected study area was Western Taitung County in Taiwan (Figure 1c). The most powerful and destructive typhoon in Taiwan’s recorded history, the Morakot typhoon, struck the island in August 2009. In five days, the tropical storm Morakot dumped an aggregate of 2884 mm of rain on southern Taiwan, leading to floods and landslides affecting a region of 274 km2 [56]. Consequently, this disaster left 652 people dead, 47 missing, and over three billion dollars of damage [56]. The Morakot typhoon caused more than 22,700 landslides in the mountainous areas. Most of the landslides were shallow, while some were characterized as deep-seated landslides [57]. Like previous study areas, an area of 348.12 km2 with sufficient landslides was chosen for this site. The elevation of this study area is up to 3950 m AMSL.
3. Methodology and Data
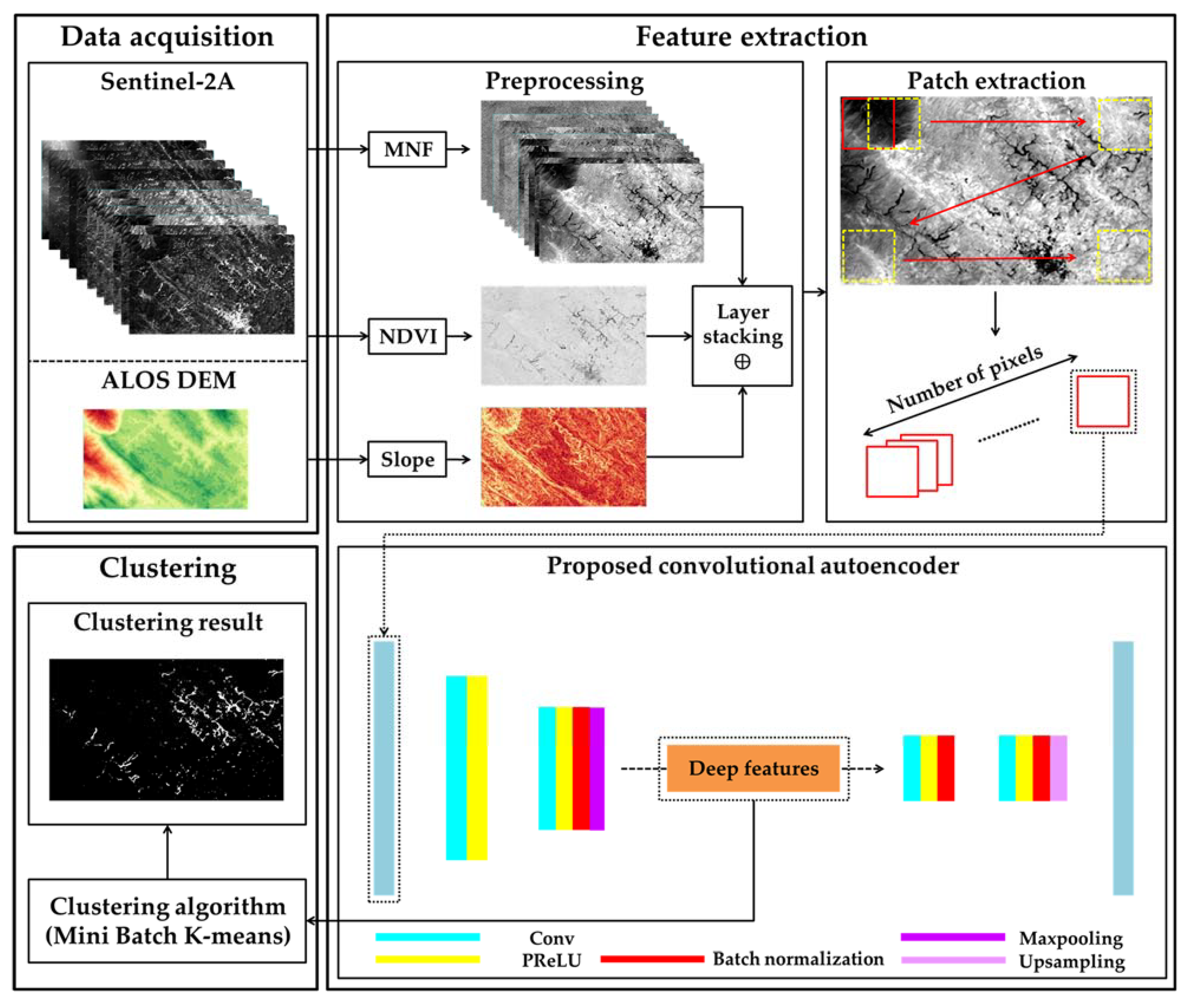
3.1. Overall Workflow
In this study, Sentinel-2 multispectral images freely available in 11 bands (B2–B8A, B10–B12) were used along with slope factors for landslide detection. The overall workflow of this study is as follows (see Figure 2):
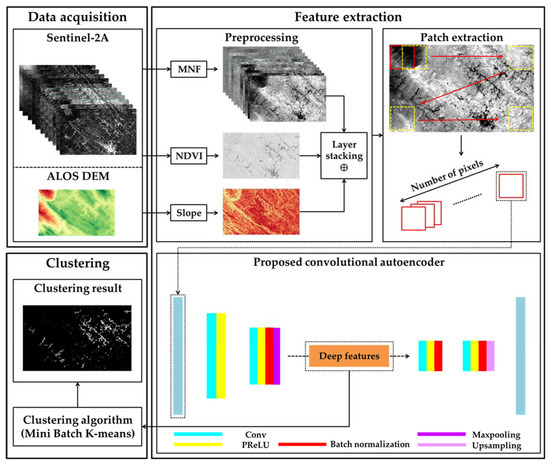
Figure 2.
Workflow of the methodology for landslide detection using CAE.
- ▪ Preparing and resampling multispectral images, NDVI, and slope factor;
- ▪ Applying MNF on multispectral images for dimensionality reduction;
- ▪ Stacking slope factor and NDVI with resulting features from the MNF;
- ▪ Feeding CAE with stacked data;
- ▪ Clustering CAE deep features using mini-batch K-means; and
- ▪ Evaluating clustering results for landslide detection through various accuracy assessment metrics.
3.2. Datasets
3.2.1. Sentinel-2A Data
In this study, Sentinel-2A multispectral images were used for landslide detection. The image acquisition dates for study areas in India, China, and Taiwan were 14 September 2018, 15 May 2018, and 30 June 2019, respectively, which had the lowest percentage of cloud cover (less than five percent) in the given areas. Furthermore, the Google Earth Engine (GEE) environment was used to search, acquire, and mask images according to the study areas. In GEE, there are two types of sentinel-2A data, namely Level-1C and Level-2A. The former dataset has global coverage. It provides top of atmosphere (TOA) reflectance images but without atmospheric terrain and cirrus correction.
At the same time, the latter does include all these corrections [58]. Although Level-2A seems like the best product for remote sensing applications, GEE’s coverage is not global. Therefore, we applied such corrections using the Sen2Cor [59] plugin in SNAP software by European Space Agency (ESA). Sentinel-2A data include 13 bands in various electromagnetic spectrums and spatial resolutions including 10, 20, and 60 m. More information on Sentinel-2A images is available in the Sentinel User Handbook [58]. Following the corrections, since Sentinel-2A image bands including aerosols (B1) and water vapor (B9) are used for coastal aquatic applications [60] and atmospheric corrections [61], we excluded them from the final image stack because they do not provide relevant information for landslide detection. Sentinel-2 images and DEM data had different coordinate systems and spatial resolution. In the pre-processing stage, the slope factor generated from DEM was resampled to 10 m to match the corresponding satellite image spatial resolution. Furthermore, in each case study, the same UTM coordinate system was used for satellite images and slope factor, and then the slope factor was georeferenced based on Sentinel-2 images to be spatially matched together. Finally, a NDVI layer was generated, matching both images and slope factors in terms of dimension, spatial resolution, and coordinate system. Finally, due to spatial resolution variation in multispectral bands, all images were resampled to 10-m spatial resolution as input for MNF.
3.2.2. Landslide Inventory Data
In contrast to the supervised DL models in which inventory data are used for training and testing, we only prepared the inventory data to test our applied unsupervised model. The post-landslide PlanetScope VHR imagery from Planet Company and Google Earth images were used to digitize the landslides visually. PlanetScope consists of more than 120 optical satellites; Dove provides VHR multispectral images in four bands, namely Blue, Green, Red, and NIR, with a spatial resolution of 3 m [62]. PlanetScope images were used for landslide digitizing; however, for the study area in Taiwan, since there were no available PlanetScope images, we used Google Earth images to digitize landslides in the QGIS 3.10 software. Table 1 provides detailed information regarding landslide features in each study area.

Table 1.
Landslide statistic information of each study area.
3.2.3. Slope Factor
Surface topography is one of the critical factors in landslides, particularly in hilly and mountainous areas [63]. Since the probability of landslides in steep slopes is very high, the slope factor can play a significant role in landslide susceptibility modeling and landslide detection [64]. In our cases, the topography of study areas in China and Taiwan is associated with steep slopes, while the study area in India is mostly hilly. Therefore, we chose the slope factor as another essential layer for landslide detection to be fed into the CAE. The steepness of the surface or terrain can be presented through slope angles, and has a direct correlation with the probability of landslides. Thus, for three cases, we extracted slope angle data from a digital elevation model (DEM) with the spatial resolution of 12.5 m generated by the ALOS PALSAR sensor [65]. In addition, the slope factor was then resampled to 10 m to be consistent with other layers fed into our CAE model.
3.2.4. Normalized Difference Vegetation Index (NDVI)
NDVI is a numerical indicator for analyzing and mapping vegetation cover and other ecological applications [66,67]. However, it can be used as an asset in landslide detection because landslide-affected areas are mostly not vegetated. Therefore, a landslide can be better distinguished or separated from non-landslide areas [10]. This index is derived from Red and NIR bands (Equation (1)) of multispectral satellite images such as the Landsat series and Sentinel 2 constellation. Since it is a standard ratio, its values range from −1 to 1, values less than zero and closer to 1 are considered as water and higher vegetation cover, respectively. In this case, we derived the NDVI index using band Red (4), and NIR (8) of Sentinel-2A images was generated using the Sen2Cor plugin in the QGIS environment (https://plugins.qgis.org/plugins/sen2cor_adapter/, accessed on 7 November 2021).
NDVI = (NIR − Red)/(NIR + Red)
3.3. Minimum Noise Fraction (MNF) Transformation
To reduce noise, computational requirements, and dimensionality, MNF transformation was applied on Sentinel-2A multispectral data before extracting deep features through CAEs. This transformation, a modified version of PCA, was proposed by Green et al., systematically reduces and segregates noise from the data through a normalized linear combination by maximizing the ratio of the signal to noise [68]. The MNF transformation method reduces spectral band dimensions through a linear transformation. During this transformation, data are rotated twice using PCA. First, a de-correlation and rescaling are performed to remove correlations and results in data with unit variance and no band-to-band correlations. After noise-whitening by the first rotation, the second rotation uses the PCA to make the original image data [69]. Based on their variance, projected components from a MNF transformation are formed, where the first component has the highest variation and, therefore, the highest information content and vice versa. [70]. In PCA, ranking is based on the variance in each component, and by increasing the component, the number variance decreases, while in MNF, images are ranked based on their quality. The measure of image quality is the signal-to-noise ratio (SNR), and MNF orders images based on SNR, representing image quality, while in PCA, there is no such ranking in terms of noise [70,71]. The mathematical expression of MNF is as follows [72]:
Let us assume noisy data as with -bands in the form of where and and are the uncorrelated signals and noise components of . Then, the covariance matrices of and should be calculated and related as (Equation (2)):
is the ratio of the noise variance to the total variance for that band. In the following, the MNF transform chooses the linear transformation by (Equation (3)).
where y is a new dataset (-bands) , which is a linear transform of the original data, and the linear transform coefficients are obtained by solving the eigenvalue equation (Equation (4)).
where is a diagonal matrix of the eigenvalues and , the eigenvalue corresponding to , equals the noise fraction in . We performed MNF transformation using the Spectral Python 0.21 library.
3.4. Convolutional Auto-Encoder (CAE)
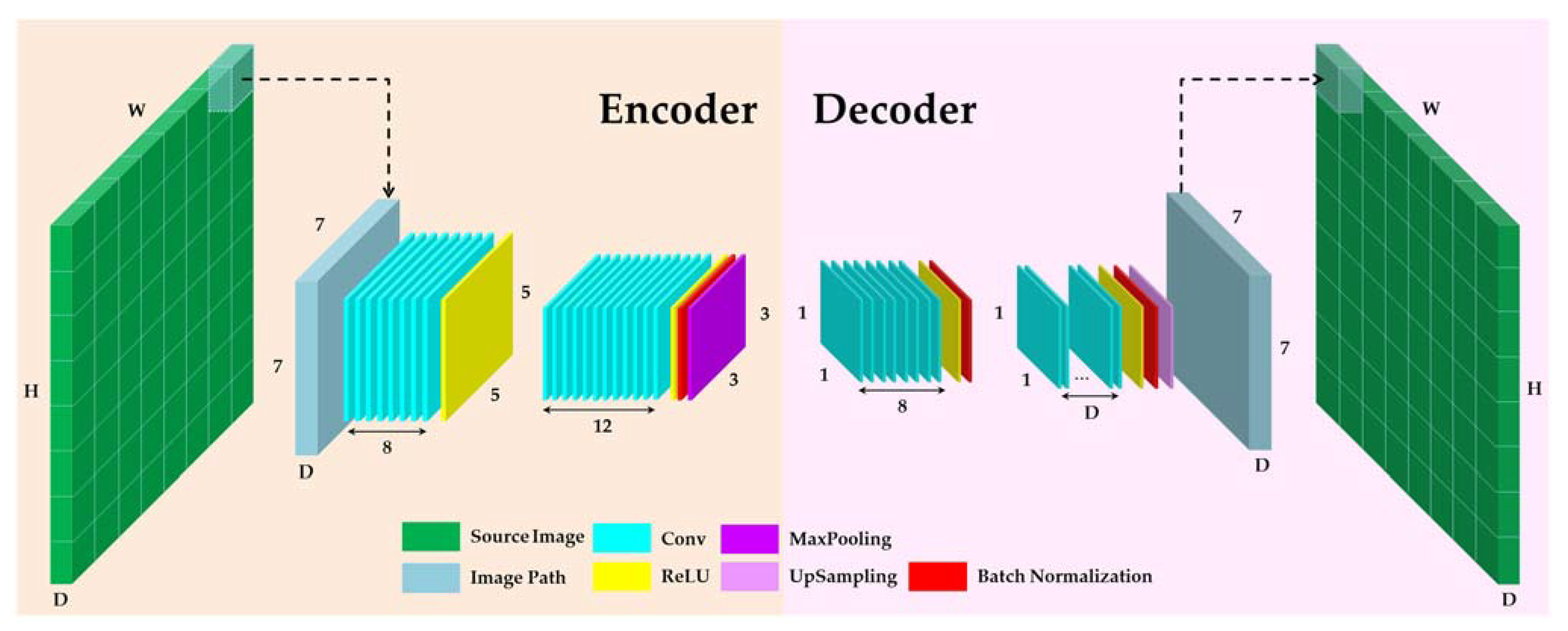
AEs are a widely used deep neural network architecture, which uses its input as a label. Then, the network tries to reconstruct its input during the learning process; for this purpose, it automatically extracts and generates the most representative features during sufficient time iterations [25,73,74]. This type of network is constructed by stacking deep layers in an AE form, consisting of two main parts of an encoder and a decoder (see Figure 3). The encoder transforms input data into a new feature space through a mapping function. At the same time, the latter tries to rebuild the original input data using the encoded features with the minimum loss [23,75,76]. The middle hidden layer of the network (bottleneck) is considered to be the layer of interest employed as deep discriminative features [77]. Since the bottleneck is the layer that AE reconstructs from and usually has smaller dimensionality than the original data, the network forces the learned representations to find the most salient features of data [74]. CAE is a type of AE employing convolutional layers to discover the inner information of images [76]. In CAE, structure weights are shared among all locations within each feature map, thus preserving the spatial locality and reducing parameter redundancy [78]. More detail on the applied CAE is described in Section 3.4.1.
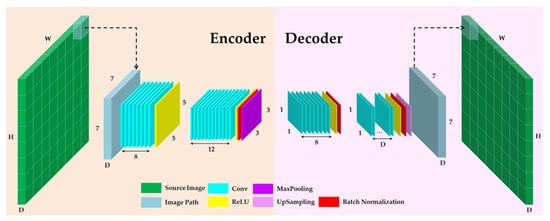
Figure 3.
The architecture of the CAE.
To extract deep features, let us assume D, W, and H indicate the depth (i.e., number of bands), width, and height of the data, respectively, and n is the number of pixels. For each member of X set, the image patches with the size are extracted, where is its centered pixel. Accordingly, the X set can be represented as the image patches, each patch, , is fed into the encoder block. For the input , the hidden layer mapping (latent representation) of the feature map is given by (Equation (5)) [79]:
where is the bias; is an activation function, which in this case, is a parametric rectified linear unit (PReLU), and the symbol corresponds to the 2D-convolution. The reconstruction is obtained using (Equation (6)):
where there is bias for each input channel, and identifies the group of latent feature maps. The corresponds to the flip operation over both dimensions of the weights . The is the predicted value [80]. To determine the parameter vector representing the complete CAE structure, one can minimize the following cost function represented by (Equation (7)) [25]:
To minimize this function, we should calculate the gradient of the cost function concerning the convolution kernel () and bias () parameters [80] (see Equations (8) and (9)):
where and are the deltas of the hidden states and the reconstruction, respectively. The weights are then updated using the optimization method [81]. Finally, the CAE parameters can be calculated once the loss function convergence is achieved. The output feature maps of the encoder block are considered as the deep features. In this work, batch normalization (BN) [82] was applied to tackle the internal covariant shift phenomenon and improve the performance of the network through normalization of the input layer by rescaling and re-centering [83]. The BN helps the network learn faster as well as increase accuracy [84].
3.4.1. Parameter Setting
Before introducing the proposed CAE’s hyperparameter setting, we demonstrated the network’s framework and configuration for image paths in detail (Table 2). In the encoder block, the number of filters of CNN1 and CNN2 are considered as 8 and 12, respectively. Simultaneously, the kernel sizes of CNN1 and CNN2 are also set as . In the decoder block, the kernel size is set as 1 × 1 to use the complete spatial information of the input cube. In this block, we chose 8 and D (i.e., number of bands) for the output of the convolutional layers (CNN3 and CNN4, respectively) in our proposed model. Based on trial and error of different combinations by Keras Tuner, for three experiment datasets, the learning rate and batch size and epochs were set to 0.1, 10,000, and 100, respectively. For the next step, we set the parameters of the regularization techniques. In the proposed network model, regularization techniques (BN) [82] are taken into account. As already mentioned, BN is used to tackle the internal covariant shift phenomenon [85]. Accordingly, BN is applied to the third dimension of each layer output to make the training process more efficient. The Adam optimizer [86] was used to optimize the Huber loss function in the training process. Afterward, the optimized hyperparameters were applied for the predicting procedure, which provides the ultimate deep features.

Table 2.
The configuration of the proposed CAE for the feature.
3.5. Mini-Batch K-Means
One of the most widely used methods in remote sensing imagery clustering is K-means because it is easy to implement and does not require any labeled data to be trained. However, as the size of the dataset starts to increase, it loses its performance in clustering such a large dataset since it requires the whole dataset in the main memory [44]. In most cases, such computational resources are not available. To overcome this challenge, Scully [44] introduced a new clustering method called mini-batch K means, a modified clustering model based on K-means, a fast and memory-efficient clustering algorithm. The main idea behind the mini-batch K-means algorithm is to reduce the computational cost using small random batches of data with a fixed size that standard computers can handle. This algorithm provides lower stochastic noise and less computational time in clustering large datasets compared to general K-means. More information on mini-batch K-means can be found in [44,86]. In this case, a mini-batch K-means algorithm with a batch size of 150, the initial size of 500, and the learning rate based on the inverse of the number of samples was used to cluster features that the CAE generated. We performed clustering with two, three, and four classes to categorize landslide features, and then the most optimal classification was selected through visual inspection. However, non-landslide areas were merged in the final step to obtain only two landslide and background classes.
4. Results
4.1. MNF Transformation
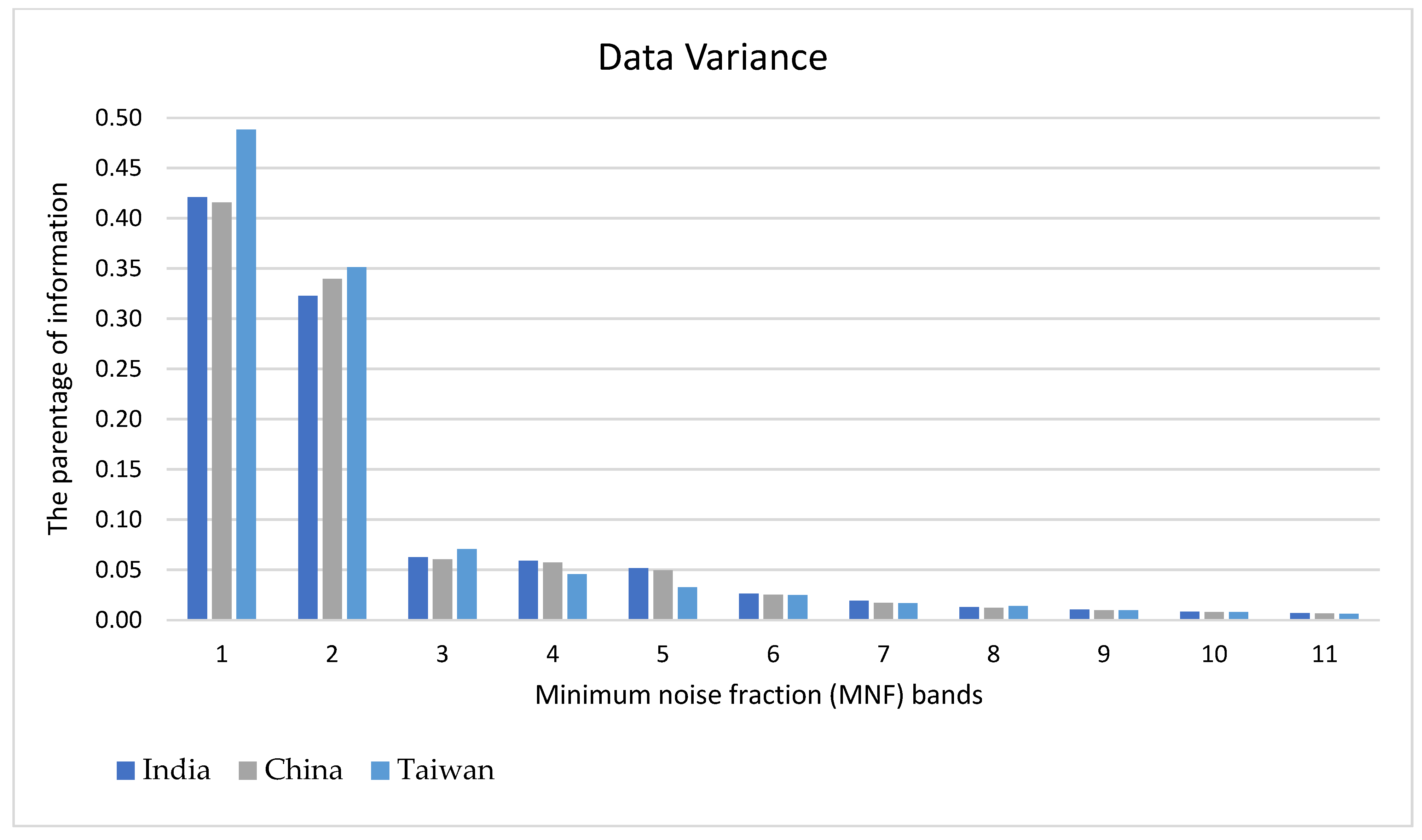
The MNF transformation was applied for the pre-processing stage. We carried out this transformation in the python platform for each case study with the help of the Scikit-Learn 1.0 package that led to a list of 11 corresponding images from informative bands to noisy ones by the size of the original dataset. In all case studies, from Table 3 and Figure 4, it was noticeable that after the third band of MNF features, the others became noisy and contained no explicit information on features. On the other hand, considering the statistical information about the transformed components, it can be perceived that the first three layers (Figure 5) comprise 80% of the information of 11 image bands. Therefore, to reduce redundancy and noise, the first three bands of MNF were selected, then stacked NDVI with the slope layer, derived from DEM in QGIS 3.10, to be fed into the CAE model.

Table 3.
Statistics of MNF bands.
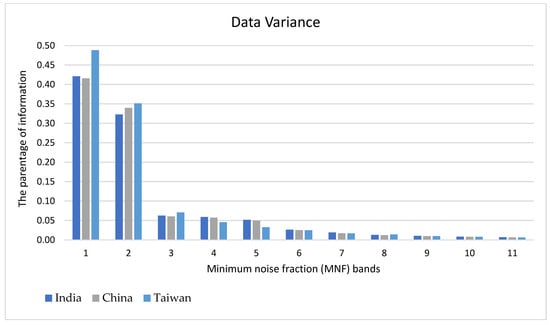
Figure 4.
Visual illustration of the MNF bands’ data variance for the satellite images of each case study. Y-axes on the left and right sides of the graph show the parentage of information in each MNF band, and X-axis is the MNF bands.

Figure 5.
Representation of three MNF features and their corresponding color composite for study areas of (a) India, (b) China, and (c) Taiwan. The numbers 1, 2, and 3 show the MNF features and number 4 indicates their color composite. The order of composition is in red (1), green (2), and blue (3).
4.2. Experimental Results from the Proposed CAE Model
Achieving an optimal model requires tuning many inter-dependent parameters [28]. In this work, the optimal parameters for the learning process, especially the number of filters of encoder output, learning rate, and batch size were obtained via the Keras Tuner optimizer developed by the Google team [87]. Therefore, we used values between 0.1, 0.01, and 0.001 for the learning rate and values of 100, 1000, and 10,000 for the batch size. Additionally, a range of 10 to 15 was selected for the number of feature maps in the last layer of the encoder for three cases. As a result, in all cases, the optimal values for learning rate, batch size, and feature maps were 0.1, 10,000, and 12, respectively.
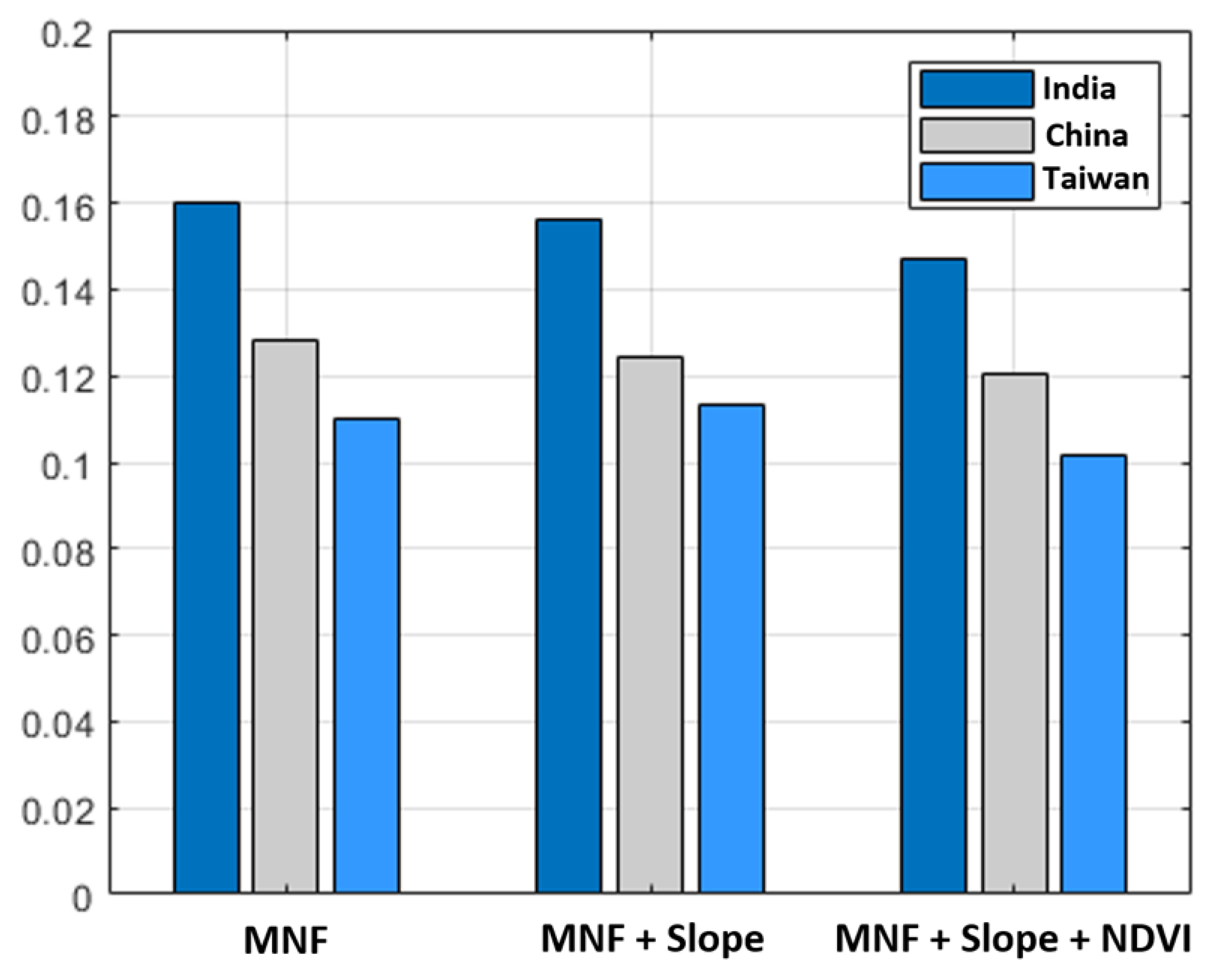
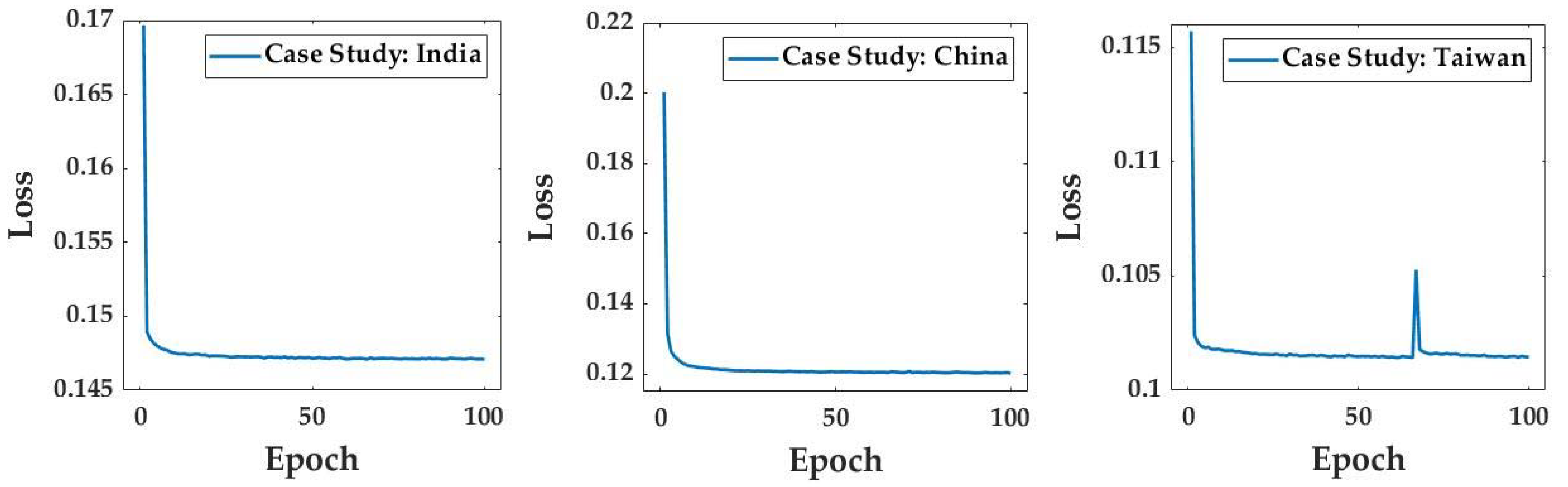
Furthermore, a loss function, namely Huber, was used to evaluate the reconstruction loss of the inputs. Since a conventional loss function such as the mean squared error (MSE) is influenced by an outlier, the loss value is dependent on outlier data. However, Huber performs as a robust loss function that is less sensitive and does not allocate higher weights to outliers [88]. To evaluate the impacts of slope and NDVI on the loss function value, we applied Huber on three different sets of data including MNF, MNF + slope, and MNF + slope + NDVI. The results (see Figure 6) indicated that the Huber loss function provides the lowest reconstruction loss for a stack of MNF features, slope, and NDVI layers in each case. Figure 7 shows an improvement in the reconstruction loss based on the Huber loss function for each study area based on 100 epochs. All the experiments here were conducted on a machine with an Intel (R) Core (TM) i9-7900X 3.31 GHz CPU, 32 GB RAM, and NVIDIA GeForce GTX 1080 12 GB GPU, and applying CAEs on our dataset was carried out in Python 3.7 using the TensorFlow 2.1.0 package.
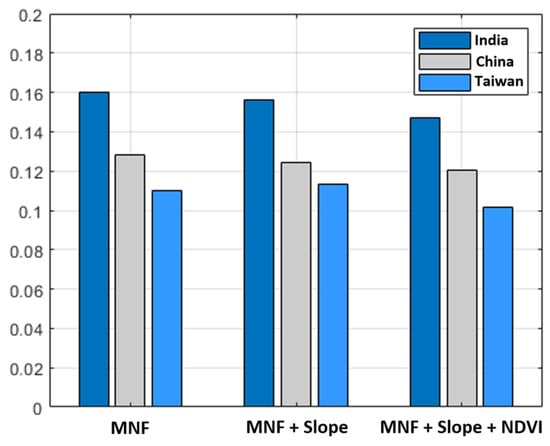
Figure 6.
The final reconstruction loss of the proposed CAEs for different input features in all study areas.
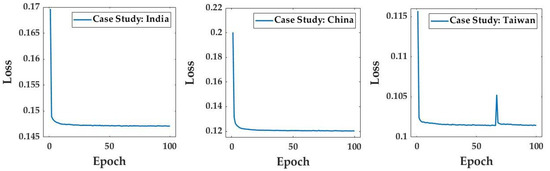
Figure 7.
Reconstruction loss improvement during the training of the proposed CAEs in 100 epochs for cases in India, China, and Taiwan.
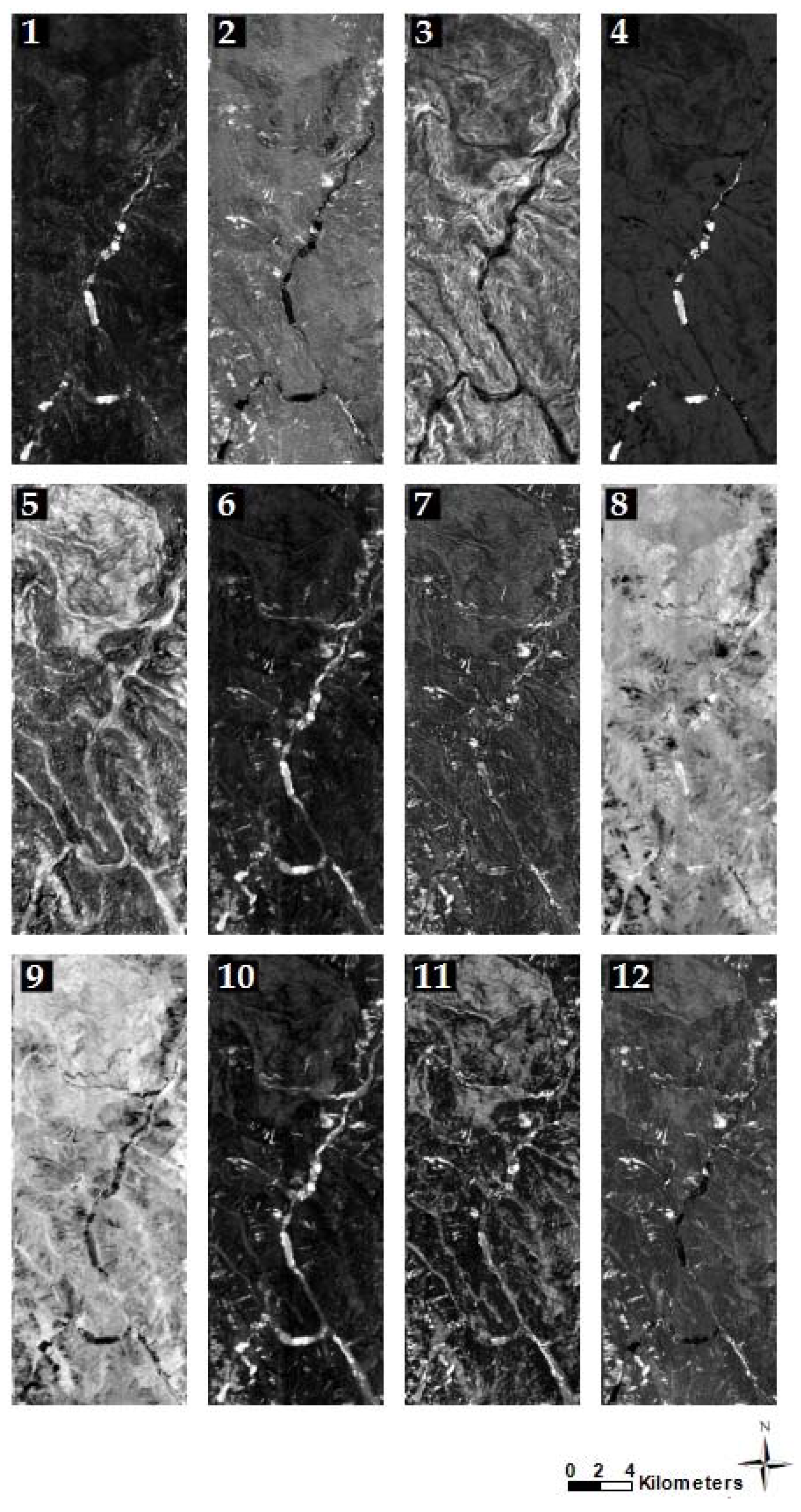
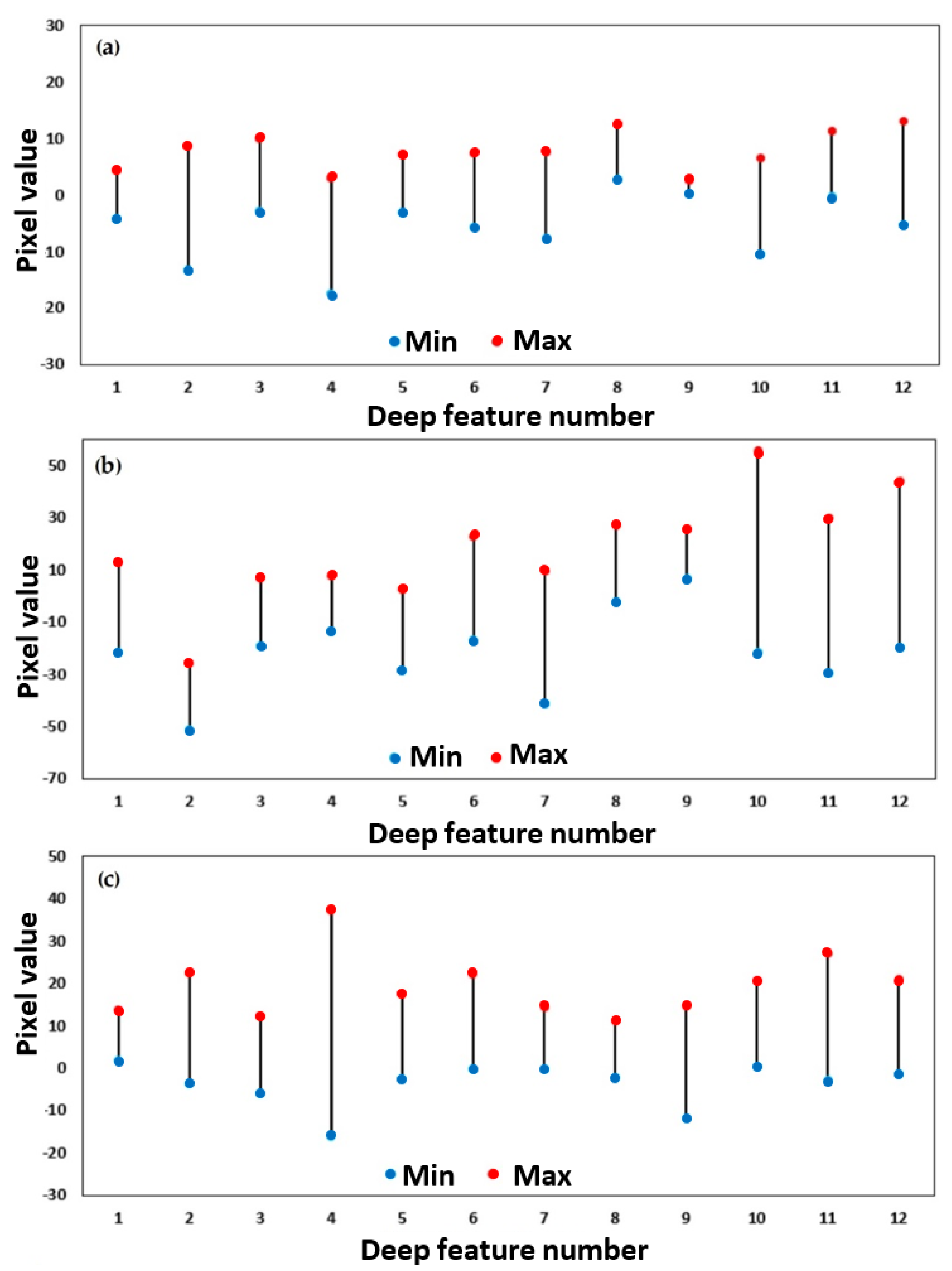
Figure 8, Figure 9 and Figure 10 represent the reconstructed deep features based on a stack of MNF features, slope, and NDVI layers of case studies in India, China, and Taiwan, respectively. In addition, Figure 11 shows the minimum and maximum values for each deep feature of different case studies.

Figure 8.
Reconstructed deep features of India’s case study. The stack of MNF features, slope, and NDVI layers were fed to our optimized CAE model (optimal parameters achieved in the tuning process), and the model’s outputs were 12 reconstructed features of the input data.
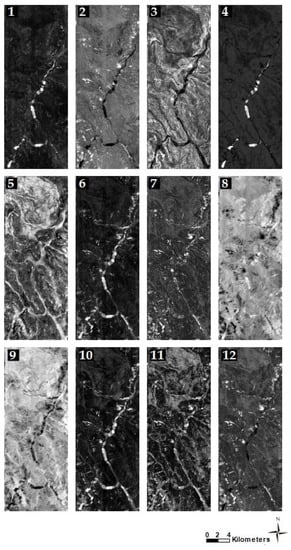
Figure 9.
Reconstructed deep features of China’s case study. The stack of MNF features, slope, and NDVI layers were fed to our optimized CAE model (optimal parameters achieved in the tuning process), and the model’s outputs were 12 reconstructed features of the input data.

Figure 10.
Reconstructed deep features of Taiwan’s case study. The stack of MNF features, slope, and NDVI layers were fed to our optimized CAE model (optimal parameters achieved in the tuning process), and the model’s outputs were 12 reconstructed features of the input data.
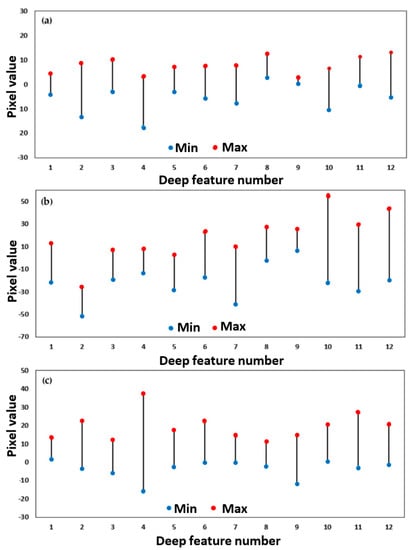
Figure 11.
Pixel values range of reconstructed deep features of case studies in India (a), China (b), and Taiwan (c). Numbers 1–12 indicate the number of image features.
4.3. Clustering Deep Features Using Mini-Batch K-Means
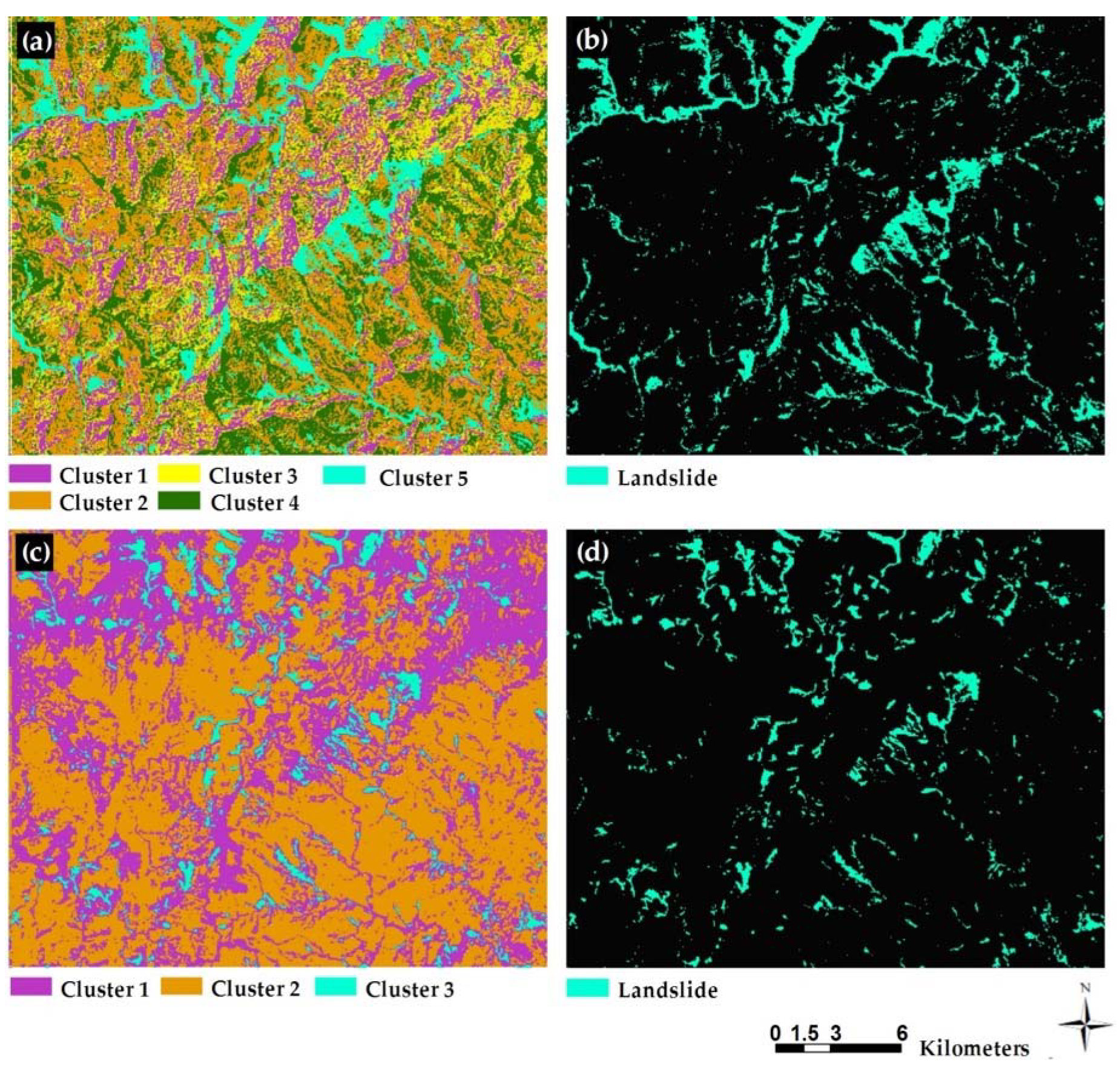
Mini-batch K-means available in the Scikit-learn 1.0 package was used to separately cluster input data and deep features into two to six categories. Since landslide inventory data were not used to train the model, the number of classes was unknown. Thus, we clustered input data and deep features into four clusters with a minimum of two to a maximum of five classes/categories. Through visual analysis of clustering maps, we chose clustering maps that had the best result compared to others. For example, in all cases, clustering MNF features stacked with slope and NDVI provided the best result with five classes, while the same scenario did not occur for clustering based on deep features. The best results were obtained with four classes using deep features for mapping landslides in India (Figure 12) and China (Figure 13). However, for Taiwan (Figure 14), clustering with three classes provided the highest accuracy. More information on the accuracy assessment is available in Section 4.3.

Figure 12.
Clustering landslides in India’s case study. (a,b) Clustering and binary landslide map based on MNF features, slop, and NDVI, while (c,d) show the same features as well as the deep features.

Figure 13.
Clustering landslides in China’s case study. (a,b) Clustering and binary landslide map based on MNF features, slop, and NDVI, while that of (c,d) show the same features as well as the deep features.
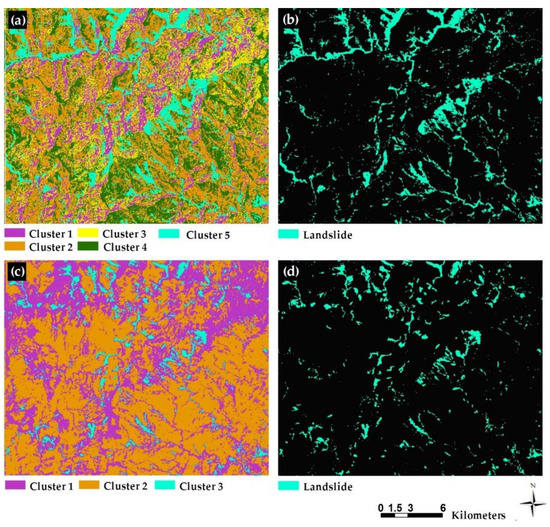
Figure 14.
Clustering landslides in Taiwan’s case study. (a,b) Clustering and binary landslide map based on MNF features, slope, and NDVI, while (c,d) show the same features as well as the deep features.
4.4. Accuracy Assessment
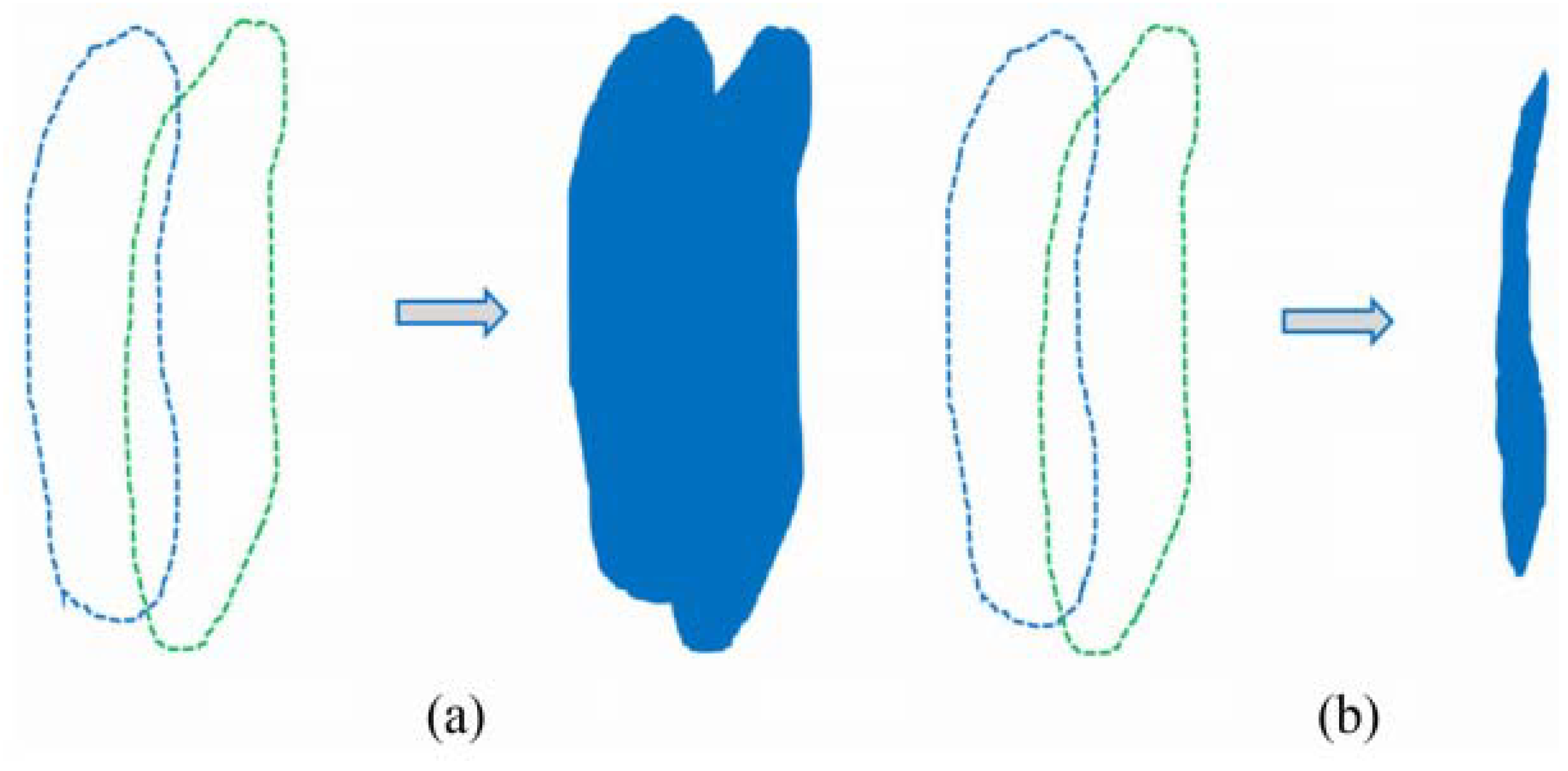
In this study, the accuracy of detected landslides was evaluated based on four wildly applied metrics, namely precision, recall, and f1-score [89]. Precision is used to measure the model’s performance in detecting landslides, recall indicates the number of accurately detected landslides, and f1-score shows the balance between precision and recall metrics. In addition, the mIOU [4] (Figure 15), which is commonly used in computer vision, is applied to evaluate the detected landslides’ accuracy. Where the inventory datasets are polygon-based, mIOU is considered an appropriate metric that can illustrate the accuracy of a model in detecting objects and landslides. Generally, the mean area of overlap is divided on the mean area of the union of detected landslides and inventory map in polygon format. The mentioned metrics are mathematically expressed as follows in Equations (10)–(13):
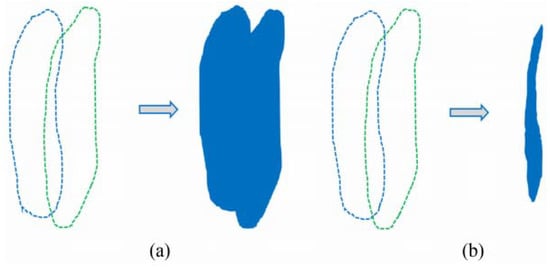
Figure 15.
Illustration of the (a) area of union and that of the (b) overlap [48].
Parameters including TP (true positive), FP (false positive), and FN (false negative) stand for correctly detected landslides, and features detected as landslides. However, according to the inventory map, they are not landslides and undetected landslides, respectively.
According to the inventory map of the case study in India, landslide detection precision through clustering MNF features stacked with slope and NDVI was 28%. In comparison, its recall metric reached 73%, which shows that clustering accuracy was relatively good in mapping actual landslides. However, due to low precision value, f1-score became 41%. On the other hand, the precision value of detected landslides through deep clustering features reached 76%, three times higher than the previous one, and recall significantly increased to 91%, resulting in an f1-score of 83%. In the following, although the precision value for India’s case was low, it was better for the case in China. This reached 44%, but the recall was not promising at 34%, indicating that only one-third of landslides were correctly detected.
Furthermore, precision, recall, and f1-score values for landslides mapped through the clustering of deep features for China’s case were 72%, 87%, and 79%, respectively. Finally, clustering based on MNF features, slope, and NDVI for Taiwan’s case provided much better results than other cases with the same clustering scenario. For example, precision and recall achieved 58% and 70%, respectively, which led to an F1 score of 63%, higher than the same metric in the other cases. In this case, clustering using deep features, similar to the other cases, presented higher precision, recall, and f1-score values, 77%, 82%, and 79%, respectively. Another metric used for accuracy assessment is mIOU, which shows that clustering with deep features provides more solid results than only the MNF features and auxiliary datasets such as slope and NDVI. For instance, for cases in India, and China, mIOU for clustering based on deep features were calculated as 70% and 60%, respectively. However, the same values for clustering without deep features were 26% and 24%, respectively. In contrast, mIOU for Taiwan’s landslide map was relatively better for both clustering maps, primarily because of higher precision values in both clustering scenarios. For example, clustering using MNF features, slope, and NDVI resulted in a mIOU of 50% and for deep features, it reached 81%. More details are available in Table 4.

Table 4.
Accuracy assessment results for both the background and landslide classes.
5. Discussion
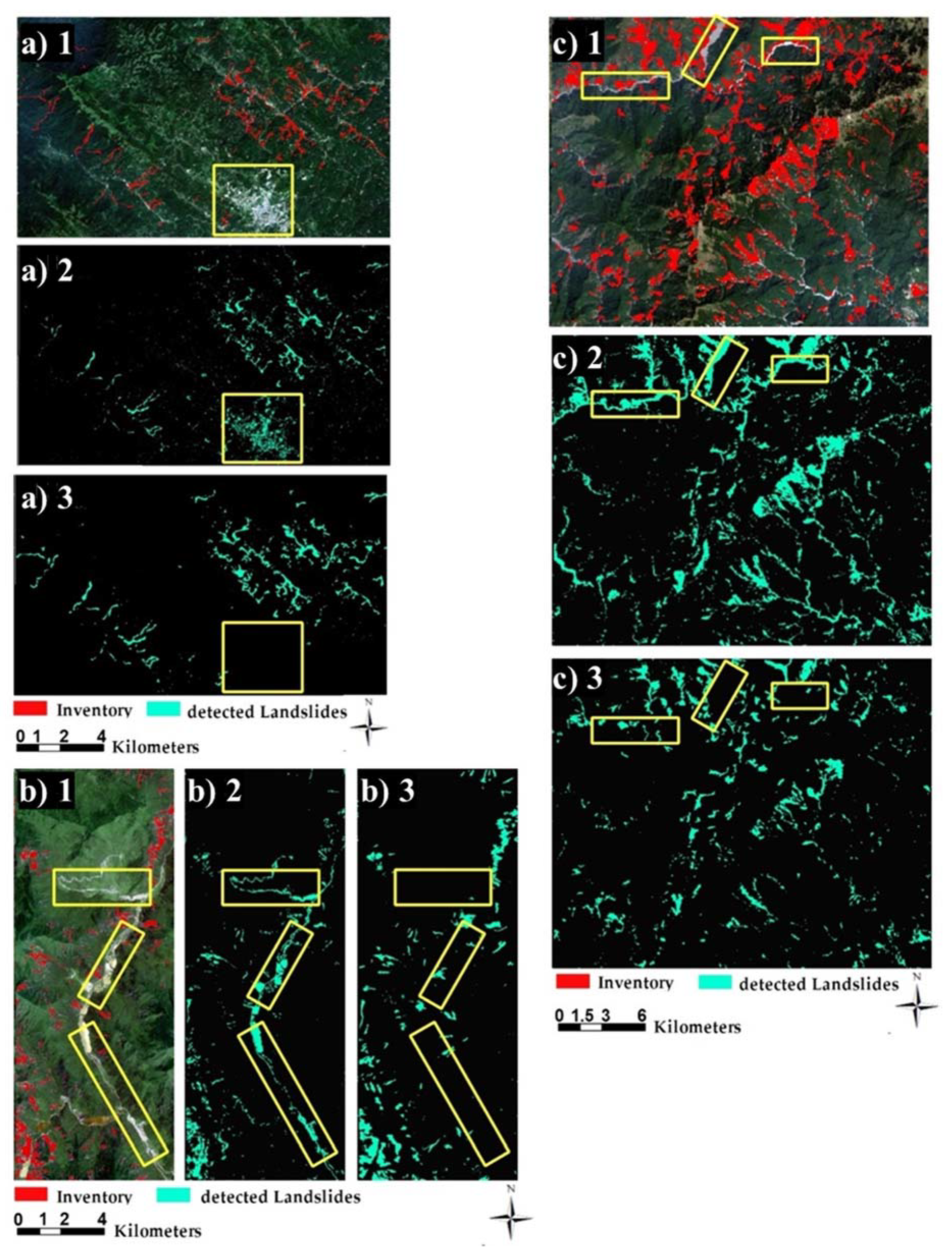
This study used an unsupervised model called CAE with a mini-batch K-means clustering algorithm to detect landslides. The main novelty of the present study was transforming and using multi-source data in a deep learning model that can extract features, which are helpful in mapping landsides without the supervision of labeled training data. Applying MNF to multispectral data helped us to reduce the dimensions from 13 to three layers but contained more than 80% of the information in all cases. Then, stacking with layers such as slope and NDVI and training a CAE with them as mid-level features resulted in feature maps that increased the overall accuracy in clustering landslides. This study clearly showed that using relevant data and appropriate methods can improve the results, even in unsupervised clustering problems. Additionally, it indicates that a similar dataset with different processing techniques can produce different results in mapping phenomena such as landslides. According to inventory data, applying clustering on MNF features along with slope and NDVI layers generated lower accuracy than clustering based on deep features learned by them. For example, in the case study in India, despite adding slope, which is an essential factor in landslide detection [4], to MNF features, the residential area was still clustered with a landslide in the same cluster Figure 16(a2). In contrast, there was no such issue in clustering maps based on deep features Figure 16(a3).
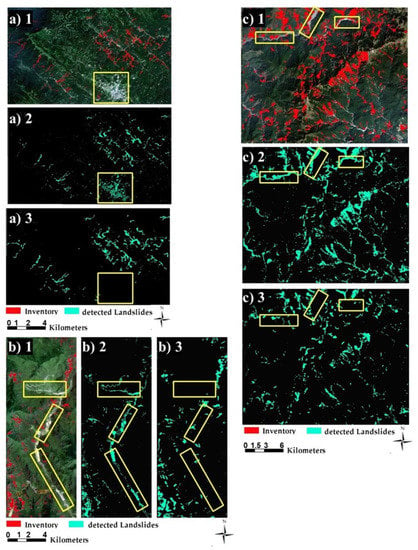
Figure 16.
Illustration the landslide detection results for (a) India, (b) China, and (c) Taiwan. The numbers of 1, 2, and 3 are represent the Sentinel-2 image, detected landslides based on clustering of MNF features, slope, and NDVI, and detected landslides based on clustering of deep features, respectively. Yellow box in (a) indicates a residential area, while (b,c) show the riverbeds.
Furthermore, the same issue exists in clustering for landslides in China and Taiwan, but instead of residential areas, most rivers are clustered with landslides into the same classes. For example, in Figure 16(b2), which is related to landslides in China, almost all rivers were clustered with landsides into the same class, while in Figure 16(c2), which is clustering based on deep features, such an issue has not occurred. Rivers are not in the same class as landslides. The same scenario occurred for landslides in Taiwan (Figure 16(b3)), and clustering-based deep features solved this problem. Clustering with deep features provides relatively good results because the CAEs learned and extracted multiple features from five inputs (three layers of MNF features, slope, and NDVI), enabling clustering to be more precise with more input data, particularly in clustering landslides. Landslides in some deep features in all cases were separable from residential areas and rivers, which explains the parameters that autoencoders learned from input data were able to capture spatial and spectral information, consequently leading to much better clustering maps compared to the ones based on MNF features, slope, and NDVI. Therefore, the results rely on deep features that could extract more consistent landslide segment boundaries. As shown in Figure 16(b1,2), detecting landslides with smaller, narrow-shaped areas does have some difficulties. However, our proposed CAE overcomes this issue and extracted landslides with spatial conditions (Figure 16(c1,2)).
In a similar study to our case, Brbu et al. [90] applied CAE on Landsat multi-temporal images for landslide change detection in Valcea County, Romania. They achieved an accuracy of 96.13% for landslide change detection through extracting features from pre- and post-landslide images. Although they achieved higher accuracy than our accuracy scores, we only used single-pass images and our study areas. In addition, our results proved their claim that CAE models are great in extracting meaningful features from satellite imagery with medium resolution such as Sentinel-2 and Landsat 8. Despite the outstanding performance of both unsupervised and supervised deep learning models in feature extraction and classification, they still suffer from some issues. For example, there is no standard procedure to define a deep learning model.
In most cases, different parameters such as window size and kernel size, somehow the activation function and loss function and input dataset should be examined to achieve a good one. For instance, we tried three different loss functions and gained the lowest loss value by the Huber function. This indicates that choosing the wrong parameters can adversely affect the performance of the deep learning model. Finally, achieving relatively high precision and recall scores in our study using sentinel-2 data and, more importantly, through an unsupervised procedure, show that CAE models have remarkable capabilities in satellite image processing, handling multi-source data, and extraction features that need further attention.
6. Conclusions
Supervised DL and ML models have demonstrated their potential for landslide mapping investigation in terms of accuracy. However, the transferability of a DL-trained model depends on the data used for training. Moreover, the accuracy is also related to the quality and quantity of the training data. Generally, remote sensing image classification and object detection using supervised ML and DL models are associated with two main issues: providing sufficient labeled data to train the model and relatively long training time due to many training parameters to be adjusted and optimized. Therefore, mapping and updating landslide inventories are still challenging issues in the RS community using supervised DL and ML models. In this study, to address this issue, we used the CAE model to extract deep features from Sentinel-2A images, spectral data such as NDVI and slope, and then clustered them to detect landslides. Our results explicitly indicate that a clustering map based on deep features is acceptable compared to the state-of-the-art results.
Moreover, this study shows that in an emergency, a combination of satellite imagery with topographical data with CAE and the Mini-batch K-means clustering algorithm can be a reliable approach for rapid mapping of landslides and provide a primary inventory map. Future studies will focus on designing (almost) similar networks and implementing them in supervised and unsupervised procedures for landslide detection. Comparing the results of these same networks may help to improve the unsupervised one to obtain results more accurate than the supervised network.
Author Contributions
Conceptualization, H.S., M.R. and O.G.; Data curation, H.S. and O.G.; Investigation, H.S., M.R. and S.T.P.; Methodology, H.S., M.R. and S.T.P.; Supervision, S.H., T.B., S.L. and P.G.; Validation, H.S., M.R. and S.T.P.; Visualization, H.S., M.R. and O.G.; Writing—original draft, H.S., M.R., S.T.P. and O.G.; Writing—review & editing, H.S., M.R., O.G., S.H., T.B., S.L. and P.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Institute of Advanced Research in Artificial Intelligence (IARAI) GmbH.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data available on request.
Acknowledgments
This research was funded by the Institute of Advanced Research in Artificial Intelligence (IARAI). The authors are grateful to three anonymous referees for their useful comments/suggestions that have helped us to improve an earlier version of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lee, S.; Ryu, J.-H.; Won, J.-S.; Park, H.-J. Determination and application of the weights for landslide susceptibility mapping using an artificial neural network. Eng. Geol. 2004, 71, 289–302. [Google Scholar] [CrossRef]
- Kornejady, A.; Pourghasemi, H.R.; Afzali, S.F. Presentation of RFFR new ensemble model for landslide susceptibility assessment in Iran. In Landslides: Theory, Practice and Modelling; Springer: Berlin/Heidelberg, Germany, 2019; pp. 123–143. [Google Scholar]
- Soares, L.P.; Dias, H.C.; Grohmann, C.H. Landslide Segmentation with U-Net: Evaluating Different Sampling Methods and Patch Sizes. arXiv 2020, arXiv:2007.06672. [Google Scholar]
- Ghorbanzadeh, O.; Blaschke, T.; Gholamnia, K.; Meena, S.R.; Tiede, D.; Aryal, J. Evaluation of Different Machine Learning Methods and Deep-Learning Convolutional Neural Networks for Landslide Detection. Remote Sens. 2019, 11, 196. [Google Scholar] [CrossRef] [Green Version]
- Ambrosi, C.; Strozzi, T.; Scapozza, C.; Wegmüller, U. Landslide hazard assessment in the Himalayas (Nepal and Bhutan) based on Earth-Observation data. Eng. Geol. 2018, 237, 217–228. [Google Scholar] [CrossRef]
- Mondini, A.; Guzzetti, F.; Reichenbach, P.; Rossi, M.; Cardinali, M.; Ardizzone, F. Semi-automatic recognition and mapping of rainfall induced shallow landslides using optical satellite images. Remote Sens. Environ. 2011, 115, 1743–1757. [Google Scholar] [CrossRef]
- Chen, Y.; Wei, Y.; Wang, Q.; Chen, F.; Lu, C.; Lei, S. Mapping Post-Earthquake Landslide Susceptibility: A U-Net Like Approach. Remote Sens. 2020, 12, 2767. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, S.; Li, R.; Shahabi, H. Performance evaluation of the GIS-based data mining techniques of best-first decision tree, random forest, and naïve Bayes tree for landslide susceptibility modeling. Sci. Total Environ. 2018, 644, 1006–1018. [Google Scholar] [CrossRef]
- Dou, J.; Yunus, A.P.; Bui, D.T.; Merghadi, A.; Sahana, M.; Zhu, Z.; Chen, C.-W.; Han, Z.; Pham, B.T. Improved landslide assessment using support vector machine with bagging, boosting, and stacking ensemble machine learning framework in a mountainous watershed, Japan. Landslides 2020, 17, 641–658. [Google Scholar] [CrossRef]
- Tavakkoli Piralilou, S.; Shahabi, H.; Jarihani, B.; Ghorbanzadeh, O.; Blaschke, T.; Gholamnia, K.; Meena, S.R.; Aryal, J. Landslide Detection Using Multi-Scale Image Segmentation and Different Machine Learning Models in the Higher Himalayas. Remote Sens. 2019, 11, 2575. [Google Scholar] [CrossRef] [Green Version]
- Kalantar, B.; Pradhan, B.; Naghibi, S.A.; Motevalli, A.; Mansor, S. Assessment of the effects of training data selection on the landslide susceptibility mapping: A comparison between support vector machine (SVM), logistic regression (LR) and artificial neural networks (ANN). Geomat. Nat. Hazards Risk 2018, 9, 49–69. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Sharma, M.; Kite, J.S.; Donaldson, K.A.; Thompson, J.A.; Bell, M.L.; Maynard, S.M. Slope failure prediction using random forest machine learning and LiDAR in an eroded folded mountain belt. Remote Sens. 2020, 12, 486. [Google Scholar] [CrossRef] [Green Version]
- Yu, B.; Chen, F.; Xu, C.; Wang, L.; Wang, N. Matrix SegNet: A Practical Deep Learning Framework for Landslide Mapping from Images of Different Areas with Different Spatial Resolutions. Remote Sens. 2021, 13, 3158. [Google Scholar] [CrossRef]
- Thi Ngo, P.T.; Panahi, M.; Khosravi, K.; Ghorbanzadeh, O.; Kariminejad, N.; Cerda, A.; Lee, S. Evaluation of deep learning algorithms for national scale landslide susceptibility mapping of Iran. Geosci. Front. 2021, 12, 505–519. [Google Scholar] [CrossRef]
- Tran, C.J.; Mora, O.E.; Fayne, J.V.; Lenzano, M.G. Unsupervised classification for landslide detection from airborne laser scanning. Geosciences 2019, 9, 221. [Google Scholar] [CrossRef] [Green Version]
- Seber, G.A. Multivariate Observations; John Wiley & Sons: Hoboken, NJ, USA, 2009; Volume 252. [Google Scholar]
- Movia, A.; Beinat, A.; Crosilla, F. Shadow detection and removal in RGB VHR images for land use unsupervised classification. ISPRS J. Photogramm. Remote Sens. 2016, 119, 485–495. [Google Scholar] [CrossRef]
- Wang, L.; Sousa, W.P.; Gong, P.; Biging, G.S. Comparison of IKONOS and QuickBird images for mapping mangrove species on the Caribbean coast of Panama. Remote Sens. Environ. 2004, 91, 432–440. [Google Scholar] [CrossRef]
- Solano-Correa, Y.T.; Bovolo, F.; Bruzzone, L. An approach for unsupervised change detection in multitemporal VHR images acquired by different multispectral sensors. Remote Sens. 2018, 10, 533. [Google Scholar] [CrossRef] [Green Version]
- Wan, S.; Chang, S.-H.; Chou, T.-Y.; Shien, C.M. A study of landslide image classification through data clustering using bacterial foraging optimization. J. Chin. Soil Water Conserv. 2018, 49, 187–198. [Google Scholar]
- Abbas, A.W.; Minallh, N.; Ahmad, N.; Abid, S.A.R.; Khan, M.A.A. K-Means and ISODATA clustering algorithms for landcover classification using remote sensing. Sindh Univ. Res. J. Sci. Ser. 2016, 48. Available online: https://sujo-old.usindh.edu.pk/index.php/SURJ/article/view/2358 (accessed on 7 November 2021).
- Ramos-Bernal, R.N.; Vázquez-Jiménez, R.; Romero-Calcerrada, R.; Arrogante-Funes, P.; Novillo, C.J. Evaluation of unsupervised change detection methods applied to landslide inventory mapping using ASTER imagery. Remote Sens. 2018, 10, 1987. [Google Scholar] [CrossRef] [Green Version]
- Mousavi, S.M.; Zhu, W.; Ellsworth, W.; Beroza, G. Unsupervised clustering of seismic signals using deep convolutional autoencoders. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1693–1697. [Google Scholar] [CrossRef]
- Tao, C.; Pan, H.; Li, Y.; Zou, Z. Unsupervised spectral–spatial feature learning with stacked sparse autoencoder for hyperspectral imagery classification. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2438–2442. [Google Scholar]
- Othman, E.; Bazi, Y.; Alajlan, N.; Alhichri, H.; Melgani, F. Using convolutional features and a sparse autoencoder for land-use scene classification. Int. J. Remote Sens. 2016, 37, 2149–2167. [Google Scholar] [CrossRef]
- Ahmad, M.; Khan, A.M.; Mazzara, M.; Distefano, S. Multi-layer Extreme Learning Machine-based Autoencoder for Hyperspectral Image Classification. In Proceedings of the VISIGRAPP (4: VISAPP) 2019, Prague, Czech Republic, 25–27 February 2019; pp. 75–82. [Google Scholar]
- Kalinicheva, E.; Sublime, J.; Trocan, M. Unsupervised Satellite Image Time Series Clustering Using Object-Based Approaches and 3D Convolutional Autoencoder. Remote Sens. 2020, 12, 1816. [Google Scholar] [CrossRef]
- Rahimzad, M.; Homayouni, S.; Alizadeh Naeini, A.; Nadi, S. An Efficient Multi-Sensor Remote Sensing Image Clustering in Urban Areas via Boosted Convolutional Autoencoder (BCAE). Remote Sens. 2021, 13, 2501. [Google Scholar] [CrossRef]
- Rasti, B.; Koirala, B.; Scheunders, P.; Ghamisi, P. Spectral Unmixing Using Deep Convolutional Encoder-Decoder. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium IGARSS 2021, Brussels, Belgium, 11–16 July 2021; pp. 3829–3832. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
- Li, L. Deep Residual Autoencoder with Multiscaling for Semantic Segmentation of Land-Use Images. Remote Sens. 2019, 11, 2142. [Google Scholar] [CrossRef] [Green Version]
- Azarang, A.; Manoochehri, H.E.; Kehtarnavaz, N. Convolutional autoencoder-based multispectral image fusion. IEEE Access 2019, 7, 35673–35683. [Google Scholar] [CrossRef]
- Xu, Y.; Xiang, S.; Huo, C.; Pan, C. Change detection based on auto-encoder model for VHR images. In Proceedings of the MIPPR 2013: Pattern Recognition and Computer Vision, Wuhan, China, 26–27 October 2013; p. 891902. [Google Scholar]
- Lv, N.; Chen, C.; Qiu, T.; Sangaiah, A.K. Deep learning and superpixel feature extraction based on contractive autoencoder for change detection in SAR images. IEEE Trans. Ind. Inform. 2018, 14, 5530–5538. [Google Scholar] [CrossRef]
- Mesquita, D.B.; dos Santos, R.F.; Macharet, D.G.; Campos, M.F.; Nascimento, E.R. Fully Convolutional Siamese Autoencoder for Change Detection in UAV Aerial Images. IEEE Geosci. Remote Sens. Lett. 2019, 17, 1455–1459. [Google Scholar] [CrossRef]
- He, G.; Zhong, J.; Lei, J.; Li, Y.; Xie, W. Hyperspectral Pansharpening Based on Spectral Constrained Adversarial Autoencoder. Remote Sens. 2019, 11, 2691. [Google Scholar] [CrossRef] [Green Version]
- Shao, Z.; Lu, Z.; Ran, M.; Fang, L.; Zhou, J.; Zhang, Y. Residual Encoder-Decoder Conditional Generative Adversarial Network for Pansharpening. IEEE Geosci. Remote Sens. Lett. 2019, 17, 1573–1577. [Google Scholar] [CrossRef]
- Zhao, C.; Li, X.; Zhu, H. Hyperspectral anomaly detection based on stacked denoising autoencoders. J. Appl. Remote Sens. 2017, 11, 042605. [Google Scholar] [CrossRef]
- Chang, S.; Du, B.; Zhang, L. A sparse autoencoder based hyperspectral anomaly detection algorihtm using residual of reconstruction error. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 5488–5491. [Google Scholar]
- Mukhtar, T.; Khurshid, N.; Taj, M. Dimensionality Reduction Using Discriminative Autoencoders for Remote Sensing Image Retrieval. In Proceedings of the International Conference on Image Analysis and Processing, Trento, Italy, 9–13 September 2019; pp. 499–508. [Google Scholar]
- Song, C.; Liu, F.; Huang, Y.; Wang, L.; Tan, T. Auto-encoder based data clustering. In Proceedings of the Iberoamerican Congress on Pattern Recognition, Havana, Cuba, 20–23 November 2013; pp. 117–124. [Google Scholar]
- Zhang, R.; Yu, L.; Tian, S.; Lv, Y. Unsupervised remote sensing image segmentation based on a dual autoencoder. J. Appl. Remote Sens. 2019, 13, 038501. [Google Scholar] [CrossRef]
- Nalepa, J.; Myller, M.; Imai, Y.; Honda, K.-i.; Takeda, T.; Antoniak, M. Unsupervised segmentation of hyperspectral images using 3-D convolutional autoencoders. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1948–1952. [Google Scholar] [CrossRef]
- Sculley, D. Web-scale k-means clustering. In Proceedings of the 19th International Conference on World Wide Web, Raleigh, NC, USA, 26–30 April 2010; pp. 1177–1178. [Google Scholar]
- Borghuis, A.; Chang, K.; Lee, H. Comparison between automated and manual mapping of typhoon-triggered landslides from SPOT-5 imagery. Int. J. Remote Sens. 2007, 28, 1843–1856. [Google Scholar] [CrossRef]
- Kursa, M.B.; Rudnicki, W.R. Feature selection with the Boruta package. J. Stat. Softw. 2010, 36, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Mezaal, M.R.; Pradhan, B.; Sameen, M.I.; Mohd Shafri, H.Z.; Yusoff, Z.M. Optimized neural architecture for automatic landslide detection from high-resolution airborne laser scanning data. Appl. Sci. 2017, 7, 730. [Google Scholar] [CrossRef] [Green Version]
- Ghorbanzadeh, O.; Meena, S.R.; Abadi, H.S.S.; Piralilou, S.T.; Zhiyong, L.; Blaschke, T. Landslide Mapping Using Two Main Deep-Learning Convolution Neural Network (CNN) Streams Combined by the Dempster—Shafer (DS) model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 14, 452–463. [Google Scholar] [CrossRef]
- Stumpf, A.; Kerle, N. Object-oriented mapping of landslides using Random Forests. Remote Sens. Environ. 2011, 115, 2564–2577. [Google Scholar] [CrossRef]
- Su, Z.; Chow, J.K.; Tan, P.S.; Wu, J.; Ho, Y.K.; Wang, Y.-H. Deep convolutional neural network–based pixel-wise landslide inventory mapping. Landslides 2020, 18, 1421–1443. [Google Scholar] [CrossRef]
- Sachin Kumar, M.; Gurav, M.; Kushalappa, C.; Vaast, P. Spatial and temporal changes in rainfall patterns in coffee landscape of Kodagu, India. Int. J. Environ. Sci. 2012, 1, 168–172. [Google Scholar]
- Shreyas, R.; Punith, D.; Bhagirathi, L.; Krishna, A.; Devagiri, G. Exploring Different Probability Distributions for Rainfall Data of Kodagu-An Assisting Approach for Food Security. Int. J. Curr. Microbiol. Appl. Sci. 2020, 9, 2972–2980. [Google Scholar] [CrossRef]
- Thomas, J.J.; Prakash, B.; Kulkarni, P.; MR, N.M. Exploring the psychiatric symptoms among people residing at flood affected areas of Kodagu district, Karnataka. Clin. Epidemiol. Glob. Health 2020, 9, 245–250. [Google Scholar] [CrossRef]
- Hu, X.; Hu, K.; Tang, J.; You, Y.; Wu, C. Assessment of debris-flow potential dangers in the Jiuzhaigou Valley following the August 8, 2017, Jiuzhaigou earthquake, western China. Eng. Geol. 2019, 256, 57–66. [Google Scholar] [CrossRef]
- Zhao, B.; Wang, Y.-S.; Luo, Y.-H.; Li, J.; Zhang, X.; Shen, T. Landslides and dam damage resulting from the Jiuzhaigou earthquake (August 8 2017), Sichuan, China. R. Soc. Open Sci. 2018, 5, 171418. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, C.-W.; Chang, W.-S.; Liu, S.-H.; Tsai, T.-T.; Lee, S.-P.; Tsang, Y.-C.; Shieh, C.-L.; Tseng, C.-M. Landslides triggered by the August 7 2009 Typhoon Morakot in southern Taiwan. Eng. Geol. 2011, 123, 3–12. [Google Scholar] [CrossRef]
- Lin, C.-W.; Tseng, C.-M.; Tseng, Y.-H.; Fei, L.-Y.; Hsieh, Y.-C.; Tarolli, P. Recognition of large scale deep-seated landslides in forest areas of Taiwan using high resolution topography. J. Asian Earth Sci. 2013, 62, 389–400. [Google Scholar] [CrossRef]
- Sentinel, E. User Handbook; ESA Standard Document 64; ESA: Darmstadt, Germany, 2015. [Google Scholar]
- Main-Knorn, M.; Pflug, B.; Louis, J.; Debaecker, V.; Müller-Wilm, U.; Gascon, F. Sen2Cor for sentinel-2. In Proceedings of the Image and Signal Processing for Remote Sensing XXIII, Warsaw, Poland, 11–13 September 2017; p. 1042704. [Google Scholar]
- Poursanidis, D.; Traganos, D.; Reinartz, P.; Chrysoulakis, N. On the use of Sentinel-2 for coastal habitat mapping and satellite-derived bathymetry estimation using downscaled coastal aerosol band. Int. J. Appl. Earth Obs. Geoinf. 2019, 80, 58–70. [Google Scholar] [CrossRef]
- Makarau, A.; Richter, R.; Schläpfer, D.; Reinartz, P. APDA water vapor retrieval validation for Sentinel-2 imagery. IEEE Geosci. Remote Sens. Lett. 2016, 14, 227–231. [Google Scholar] [CrossRef] [Green Version]
- Team, P. Planet Imagery Product Specifications; Planet Team: San Francisco, CA, USA, 2018. [Google Scholar]
- Nhu, V.-H.; Mohammadi, A.; Shahabi, H.; Ahmad, B.B.; Al-Ansari, N.; Shirzadi, A.; Geertsema, M.; Kress, V.R.; Karimzadeh, S.; Valizadeh Kamran, K. Landslide Detection and Susceptibility Modeling on Cameron Highlands (Malaysia): A Comparison between Random Forest, Logistic Regression and Logistic Model Tree Algorithms. Forests 2020, 11, 830. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Rahmati, O. Prediction of the landslide susceptibility: Which algorithm, which precision? Catena 2018, 162, 177–192. [Google Scholar] [CrossRef]
- ASF DAAC. ALOS PALSAR_Radiometric_Terrain_Corrected_low_res. Includes Material© JAXA/METI 2007. Available online: https://asf.alaska.edu:2015 (accessed on 7 November 2021).
- Pettorelli, N. The Normalized Difference Vegetation Index; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Cihlar, J.; Laurent, L.S.; Dyer, J. Relation between the normalized difference vegetation index and ecological variables. Remote Sens. Environ. 1991, 35, 279–298. [Google Scholar] [CrossRef]
- Green, A.A.; Berman, M.; Switzer, P.; Craig, M.D. A transformation for ordering multispectral data in terms of image quality with implications for noise removal. IEEE Trans. Geosci. Remote Sens. 1988, 26, 65–74. [Google Scholar] [CrossRef] [Green Version]
- Ghorbanzadeh, O.; Dabiri, Z.; Tiede, D.; Piralilo, S.T.; Blaschke, T.; Lang, S. Evaluation of Minimum Noise Fraction Transformation and Independent Component Analysis for Dwelling Annotation in Refugee Camps Using Convolutional Neural Network. In Proceedings of the 39th Annual EARSeL Symposium, Salzurg, Austria, 1–4 July 2019. [Google Scholar]
- Luo, G.; Chen, G.; Tian, L.; Qin, K.; Qian, S.-E. Minimum noise fraction versus principal component analysis as a pre-processing step for hyperspectral imagery denoising. Can. J. Remote Sens. 2016, 42, 106–116. [Google Scholar] [CrossRef]
- Yang, M.-D.; Huang, K.-H.; Tsai, H.-P. Integrating MNF and HHT Transformations into Artificial Neural Networks for Hyperspectral Image Classification. Remote Sens. 2020, 12, 2327. [Google Scholar] [CrossRef]
- Lixin, G.; Weixin, X.; Jihong, P. Segmented minimum noise fraction transformation for efficient feature extraction of hyperspectral images. Pattern Recognit. 2015, 48, 3216–3226. [Google Scholar] [CrossRef]
- Affeldt, S.; Labiod, L.; Nadif, M. Spectral clustering via ensemble deep autoencoder learning (SC-EDAE). Pattern Recognit. 2020, 108, 107522. [Google Scholar] [CrossRef]
- Min, E.; Guo, X.; Liu, Q.; Zhang, G.; Cui, J.; Long, J. A survey of clustering with deep learning: From the perspective of network architecture. IEEE Access 2018, 6, 39501–39514. [Google Scholar] [CrossRef]
- Vincent, P.; Larochelle, H.; Lajoie, I.; Bengio, Y.; Manzagol, P.-A.; Bottou, L. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion. J. Mach. Learn. Res. 2010, 11, 3371–3408. [Google Scholar]
- Tang, X.; Zhang, X.; Liu, F.; Jiao, L. Unsupervised deep feature learning for remote sensing image retrieval. Remote Sens. 2018, 10, 1243. [Google Scholar] [CrossRef] [Green Version]
- Tharani, M.; Khurshid, N.; Taj, M. Unsupervised deep features for remote sensing image matching via discriminator network. arXiv 2018, arXiv:1810.06470. [Google Scholar]
- Li, F.; Qiao, H.; Zhang, B. Discriminatively boosted image clustering with fully convolutional auto-encoders. Pattern Recognit. 2018, 83, 161–173. [Google Scholar] [CrossRef] [Green Version]
- Ribeiro, M.; Lazzaretti, A.E.; Lopes, H.S. A study of deep convolutional auto-encoders for anomaly detection in videos. Pattern Recognit. Lett. 2018, 105, 13–22. [Google Scholar] [CrossRef]
- Zhao, W.; Guo, Z.; Yue, J.; Zhang, X.; Luo, L. On combining multiscale deep learning features for the classification of hyperspectral remote sensing imagery. Int. J. Remote Sens. 2015, 36, 3368–3379. [Google Scholar] [CrossRef]
- Masci, J.; Meier, U.; Cireşan, D.; Schmidhuber, J. Stacked convolutional auto-encoders for hierarchical feature extraction. In Proceedings of the International Conference on Artificial Neural Networks, Espoo, Finland, 14–17 June 2011; pp. 52–59. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Song, C.; Huang, Y.; Liu, F.; Wang, Z.; Wang, L. Deep auto-encoder based clustering. Intell. Data Anal. 2014, 18, S65–S76. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Y.; Gu, Y.; He, X.; Ghamisi, P.; Jia, X. Deep learning ensemble for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1882–1897. [Google Scholar] [CrossRef]
- Khan, S.; Rahmani, H.; Shah, S.A.A.; Bennamoun, M. A guide to convolutional neural networks for computer vision. Synth. Lect. Comput. Vis. 2018, 8, 1–207. [Google Scholar] [CrossRef]
- Xiao, B.; Wang, Z.; Liu, Q.; Liu, X. SMK-means: An improved mini batch k-means algorithm based on mapreduce with big data. Comput. Mater. Contin. 2018, 56, 365–379. [Google Scholar]
- O’Malley, T.; Bursztein, E.; Long, J.; Chollet, F.; Jin, H.; Invernizzi, L. Keras Tuner. 2020. Available online: https://keras.io/keras_tuner/ (accessed on 7 November 2021).
- Lobry, S.; Tuia, D. Deep learning models to count buildings in high-resolution overhead images. In Proceedings of the 2019 Joint Urban Remote Sensing Event (JURSE), Vannes, France, 22–24 May 2019; pp. 1–4. [Google Scholar]
- Shahabi, H.; Jarihani, B.; Tavakkoli Piralilou, S.; Chittleborough, D.; Avand, M.; Ghorbanzadeh, O. A Semi-Automated Object-Based Gully Networks Detection Using Different Machine Learning Models: A Case Study of Bowen Catchment, Queensland, Australia. Sensors 2019, 19, 4893. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barbu, M.; Radoi, A.; Suciu, G. Landslide Monitoring using Convolutional Autoencoders. In Proceedings of the 2020 12th International Conference on Electronics, Computers and Artificial Intelligence (ECAI), Bucharest, Romania, 25–27 June 2020; pp. 1–6. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).