Validation of Multi-Year Galileo Orbits Using Satellite Laser Ranging

Abstract

Satellite laser ranging (SLR) observations provide an independent validation of the global navigation satellite system (GNSS) orbits derived using microwave measurements. SLR residuals have also proven to be an important indicator of orbit radial accuracy. In this study, SLR validation is conducted for the precise orbits of eight Galileo satellites covering four to eight years (the current longest span), provided by multiple analysis centers (ACs) participating in the multi-GNSS experiment (MGEX). The purpose of this long-term analysis (the longest such study to date), is to provide a comprehensive evaluation of orbit product quality, its influencing factors, and the effect of perturbation model updates on precise orbit determination (POD) processing. A conventional ECOM solar radiation pressure (SRP) model was used for POD. The results showed distinct periodic variations with angular arguments in the SRP model, implying certain defects in the ECOM system. Updated SRP descriptions, such as ECOM2 or the Box-Wing model, led to significant improvements in SLR residuals for orbital products from multiple ACs. The standard deviation of these residuals decreased from 8–10 cm, before the SRP update, to about 3 cm afterward. The systematic bias of the residuals was also reduced by 2–4 cm and the apparent variability decreased significantly. In addition, the effects of gradual SRP model updates in the POD were evident in orbit comparisons. Orbital differences between ACs in the radial direction were reduced from the initial 10 cm to better than 3 cm, which is consistent with the results of SLR residual analysis. These results suggest SLR validation to be a powerful technique for evaluating the quality of POD strategies in GNSS orbits. Furthermore, this study has demonstrated that perturbation models, such as SRP, provide a better orbit modeling for the Galileo satellites.

1. Introduction

Satellite laser ranging (SLR) is a space geodetic technique that offers sub-centimeter single-shot precision for ground site-to-satellite distance measurements. SLR is an independent metrology system that can provide high accuracy measurements to evaluate orbits of the global navigation satellite system (GNSS) obtained from microwave observations. The international laser ranging service (ILRS) is responsible for coordinating global SLR observation sites monitoring multiple navigation satellite systems, including the American global positioning satellite (GPS), Russian GLONASS, European Galileo, and Chinese BeiDou constellation systems [1]. SLR tracking campaigns have proven to be valuable tools for GNSS orbital accuracy assessments.

SLR validation of multi-year orbit products revealed certain characteristics that are not easily identified in short-term data. For example, the analysis of multi-year GPS data has demonstrated that both the standard deviation (STD) and systematic bias, for differences between GPS precise orbits and SLR observations, significantly exceed the common cm-level precision of SLR observations. This discrepancy may be the result of deficiencies in GPS-based precise orbit determination (POD) models [2]. Further research has shown that SLR residual time series for GPS orbits exhibit periodic variations with an amplitude of 10 cm, which peak as the satellite nears its eclipse season [3]. Residual values are related to the relative geometric relationship between the Sun and the satellite orbit. Residual distribution characteristics are caused by defects in the dynamic models of GPS-based POD strategies [4].

Galileo satellites utilize a POD strategy similar to that of GPS satellites. In the initial stages, the extended CODE model (ECOM) solar radiation pressure (SRP) model was commonly used, with the satellite’s argument of latitude, u, as the primary angular term [5]. During the analysis of long-sequence orbital accuracy, it was found that orbital SLR residuals exhibit obvious long-period variations of ~6 months, with a strong dependency on the solar elevation over the satellite orbital plane β [6,7,8]. A pronounced correlation has also been observed with the satellite–Sun elongation angle, γ. As such, deficiencies in the ECOM model are the primary cause of errors in residual terms [9]. These findings prompted the development of the ECOM2 model, with the satellite latitude with respect to the Sun Δu as the angular argument. The subsequent update of the SRP model, used by the Galileo satellites, significantly reduced dependence on angular arguments such as β and Δu [10]. However, the update did not eliminate SLR orbital residuals, which several studies have attributed to a neglect of smaller perturbations, such as Earth’s albedo radiation pressure [11] and antenna thrust [12]. The accurate modeling of these effects could help to further reduce SLR residuals [13,14,15,16]. In addition, some studies have suggested the distribution characteristics of SLR residuals in observation local time could also be related to perturbation modeling [17,18]. These studies have demonstrated that SLR validation is not only an important technique for verifying the orbital accuracy of Galileo satellites, but also a valuable tool for the improvement of dynamic GNSS POD modeling.

Differences between orbital positions and SLR residuals can be attributed to orbit calculation errors, primarily caused by defects in perturbation models. This study represents the first investigation of the relationship between SLR residuals and the angle u in local time. In addition, few has been reported on the effects of SRP updates at varying stages and the associated changes in Δu or γ. Furthermore, previous research has primarily involved data ranging from only a few months to 1–2 years. As such, this study utilizes long-term SLR observations, provided by the ILRS, to conduct SLR validation of Galileo orbital products produced as part of the multi-GNSS experiment (MGEX). The characteristics of these SLR validation results for multi-year orbits are analyzed and corroborated from multiple perspectives. In addition, their significance for quality evaluation of POD modeling, particularly SRP modeling, is assessed.

2. Data and Methods

2.1. Availability of Orbital Products

The launch of the Galileo navigation system began in 2005, with two Galileo in-orbit validation element (GIOVE) satellites launched in 2005 and 2006. Four in-orbit validation (IOV) satellites were later launched in 2011 and 2012. The launch of full operational capability (FOC) satellites began in August 2014 [19]. Due to a technical problem, the first two FOC satellites did not enter the predetermined orbit, but an elliptical orbit with an eccentricity of 0.16 [20].

Four IOV satellites (IOV-1—PRN no. E11, IOV-2—PRN no. E12, IOV-3—PRN no. E19, and IOV-4—PRN no. E20) and four FOC satellites (FOC-3—PRN no. E26, FOC-4—PRN no. E22, FOC-5—PRN no. E24, and FOC-6—PRN no. E30) with the longest orbital time spans (four to eight years) were selected to assess SLR validation for long-term MGEX orbit products. These satellites exhibit near-circular orbits with a semi-major axis of 29,600 km, an inclination of 56°, and a period of 14.08 h. The launch dates and primary orbital characteristics for these satellites are shown in Table 1. The right ascension of the ascending node, calculated according to orbital position, shows that these eight satellites are distributed in three different orbital planes (A, B, and C). Detailed naming rules for orbital planes and slots can been found in [19]. More intuitive spatial configurations for the eight satellites are shown in Figure 1, in which the two coordinates represent the right ascension of ascending node Ω and the argument of latitude u, respectively. The angle between the two coordinate axes represents the orbital inclination i. The retrograde speed of the ascending node is ~10°/year, due primarily to oblate perturbations from Earth’s gravitational field.

Table 1. Orbital elements for the Galileo satellites.

PRN	Launch Date	Orbital Slot	Right Ascension (on 1 May 2013)	Right Ascension (on 1 May 2017)
E11 (IOV-1)	21 October 2011	B5	113.9°	72.8°
E12 (IOV-2)	21 October 2011	B6	113.9°	72.8°
E19 (IOV-3)	12 October 2012	C4	233.8°	193.0°
E20 (IOV-4)	12 October 2012	C5	233.7°	-
E26 (FOC-3)	27 March 2015	B8	-	73.1°
E22 (FOC-4)	27 March 2015	B3	-	73.1°
E24 (FOC-5)	11 September 2015	A8	-	313.2°
E30 (FOC-6)	11 September 2015	A5	-	313.2°

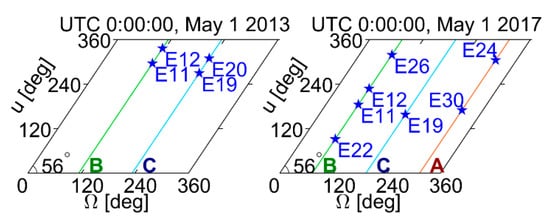
Figure 1. Schematic diagram of location distribution of orbital planes A/B/C and slots of four IOV and four FOC Galileo satellites at two epochs four years apart.

The international GNSS service (IGS) organizes the multi-GNSS experiment (MGEX), which provides high-quality data products for major navigation system satellites [13,14]. In May 2012, major analysis centers (ACs) around the world began providing precise orbital information for navigation satellites. The Galileo precise orbit products included in this study were acquired from the following MGEX ACs:

• Centre National d’Etudes Spatiales—Collecte Localisation Satellites (CNES/CLS, France, ID GRM).
• Center for Orbit Determination in Europe (CODE, Switzerland, ID COM).
• GeoForschungsZentrum Potsdam (GFZ, Germany, ID GBM).
• Technische Universität München (TUM, Germany, ID TUM).
• Wuhan University (WU, China, ID WUM).

A literature review suggested that, although POD strategies varied, orbital perturbation models at each AC improved significantly during the period ranging from the implementation of MGEX to the end of 2019 (particularly the SRP model). SLR residual time series analysis was divided into two or three stages according to the update time for POD models (see Table 2).

Table 2. Stage divisions for SRP models used by MGEX ACs.

AC	Time Boundary and Model Description	References
COM	Three stages Stage 1: ECOM model. From beginning to 4 January 2015. Stage 2: ECOM2 model. From 4 January 2015 to 6 August 2017. Stage 3: Models in Stage 2 + antenna thrust and Earth albedo model. Since 6 August 2017.	[10,17]
WUM	Three stages Stage 1: ECOM model + along-tracking empirical constant acceleration bias. For IOV: From beginning to 4 January 2015. For FOC: From beginning to 31 October 2016. Stage 2: ECOM2 model + along-tracking empirical constant acceleration bias. For IOV: From 4 January 2015 to 10 September 2017. For FOC: From 31 October 2016 to 10 September 2017. Stage 3: Models in Stage 2 + antenna thrust and Earth albedo model. Since 10 September 2017.	[14,15]
GRM	Two stages Stage 1: BW model. From beginning to 4 January 2015. Stage 2: BW + ECOM2 model. Since 4 January 2015.	[21,22]
GBM	Two stages Stage 1: ECOM model. From beginning to 25 October 2016. Stage 2: BW + ECOM model. Since 25 October 2016.	[23,24]
TUM	Two stages Stage 1: ECOM model. From beginning to 30 November 2016. Stage 2: BW + ECOM model. Since 30 November 2016.	[25,26]

The radio frequency, differencing, observation sampling, elevation cutoff, ground network, arc length, SRP model, and estimated parameters varied between each AC providing the orbit products [23,25]. As such, multiple products were used for a comparative analysis of accuracy-related factors. Figure 2 shows the time coverage for eight satellite orbits from five ACs, representing the majority of the satellite lifespan, with some small gaps included.

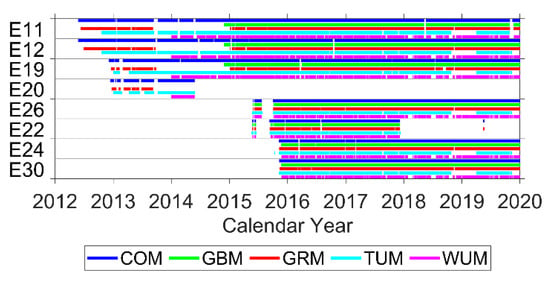
Figure 2. Availability of Galileo orbit products provided by MGEX ACs as of 31 December 2019. No orbit product of E20 was provided by GBM.

2.2. SLR Observation Status

Global SLR sites typically start tracking satellites after they enter predetermined orbits. The ILRS has previously organized three global intensive monitoring campaigns for navigation systems, in order to increase the number of SLR observations available for research. This included the laser ranging to GNSS spacecraft experiment (LARGE), with activities conducted in 2014–2015, 2017, and 2018, each of which spanned several months. As of December 2019, a total of 43 SLR sites have provided worldwide SLR observations from four IOV and four FOC satellites, with time spans ranging from four to eight years. Fourteen of these sites were selected for this study, based on ILRS system performance data and both the quantity and quality of observations performed at each site. Basic information for the selected sites is shown in Table 3. The geographic distribution of these sites was relatively uniform, as shown in Figure 3. SLR observation data were provided by two data centers, the American Crustal Dynamics Data Information System (CDDIS) and the EUROLAS Data Center (EDC). Monthly quantities, global shares, and the proportion of daytime observations at selected sites are shown in Figure 4.

Table 3. Basic information list of the selected SLR sites.

Site ID	Location Name	Country	Continent
7090	Yarragadee	Australia	Oceania
7105	Greenbelt	USA	North America
7110	Monument Peak	USA	North America
7237	Changchun	China	Asia
7406	San Juan	Argentina	South America
7501	Hartebeesthoek	South Africa	Africa
7810	Zimmerwald	Switzerland	Europe
7821	Shanghai	China	Asia
7825	Mt. Stromlo	Australia	Oceania
7839	Graz	Austria	Europe
7840	Herstmonceux	United Kingdom	Europe
7841	Potsdam	Germany	Europe
7941	Matera	Italy	Europe
8834	Wettzell	Germany	Europe

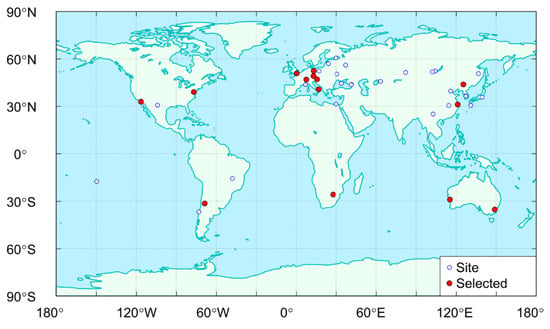
Figure 3. Geographical distribution of SLR tracking sites for Galileo satellites.

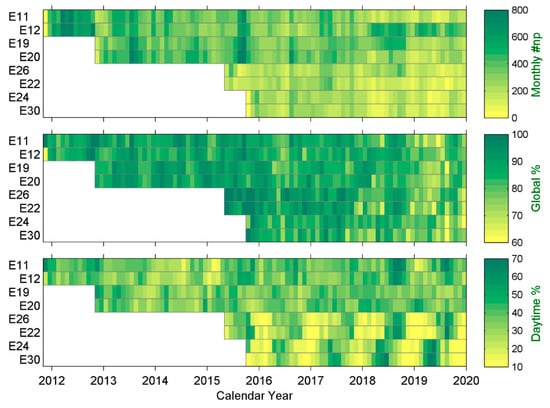
Figure 4. Number of monthly SLR normal points (np), their proportion in global observations, and the proportion of daytime observations at selected sites.

As seen in the Figure 4, the monthly average for SLR observations at 14 selected sites mostly exceeded 200 normal points. This accounted for more than 80% of observations at each of the 43 sites, as shown in Table 4. The proportion and quality of observations at selected locations were high and the geographical distributions were relatively uniform. More than half of the selected sites offered strong daytime observation capabilities. Daytime measurements accounted for ~25–40% of total tracking data, of which IOV satellites constituted a higher percentage than FOC satellites. SLR data from the selected sites were used for subsequent analysis.

Table 4. Statistical SLR tracking information for Galileo satellites, as of 31 December 2019. Each column of the table represented the satellite PRN, duration of SLR observation, total number of normal points for all sites, proportion of selected site observations, monthly average of selected site observations, and proportion of daytime observations at selected sites.

PRN	Duration	Total #np	Selected%	Monthly #np	Daytime%
E11	8.1 years	39,663	86.8%	355	39.14
E12	8.1 years	46,457	86.1%	412	36.32
E19	7.2 years	36,351	86.1%	364	36.16
E20	7.2 years	36,456	86.6%	367	36.92
E26	4.7 years	13,647	87.3%	213	27.66
E22	4.7 years	11,906	87.0%	185	27.61
E24	4.2 years	12,415	83.5%	207	28.07
E30	4.2 years	11,639	81.6%	190	27.19

2.3. Angular Argument Definitions

As discussed previously, understanding the relationship between SLR residuals and angular arguments is of great importance for the analysis of orbital accuracy in the SRP model. As such, it is necessary to clarify the definitions of relevant angular arguments, four of which are discussed below.

1.

Solar elevation over the satellite orbital plane (β)—This term represents the elevation angle for the Sun–Earth connection with respect to the satellite orbital plane. In the Galileo system, β is a slow variable that completes approximately one cycle each year, but will reach its zero value twice from the positive and negative directions. When $\left|\beta \right|$ is less than the critical value ${\beta }_{\mathrm{c}}=\mathrm{asin}\left(R_{\mathrm{E}}/r\right)$, where R_E is the radius of the Earth and r is the satellite orbital radius, the satellite will enter an eclipse season. During this period, part of the satellite orbital motion will experience a shadow from the Earth. This angle definition has been used in prior SRP models [24] and exhibits a maximum allowable range of [−23.5°, 23.5°].

2.

The satellite–Sun elongation angle (γ)—This term describes the elongation of positions of the Earth and the Sun relative to the satellite. In this study, γ is a fast variable that completes approximately one cycle in each satellite orbital period. It is only approximate because the position of the Sun will change slightly during one satellite orbital period. This angle definition has been used in previous SRP models, such as the ROCK [26] and Box-Wing (BW) models [13] and it exhibits a maximum allowable range of [0°, 180°].

3.

The argument of latitude (u)—This term denotes the angle between the satellite position and the ascending node of the satellite orbit. Here, u is a fast variable that completes exactly one 360° cycle in each satellite orbital period. This definition has been used in prior SRP models, such as ECOM [5].

4.

The argument of satellite latitude relative to the Sun (Δu)—This argument is defined as the difference between the argument of latitude (u) of the satellite and the solar argument of latitude in the satellite orbital plane (u₀). The angle Δu = u − 0 is a fast variable that completes approximately one 360° cycle in each satellite orbital period. This definition has been used in previous SRP models, such as ECOM2 [10]. The geometric meaning of each angle is represented in Figure 5.

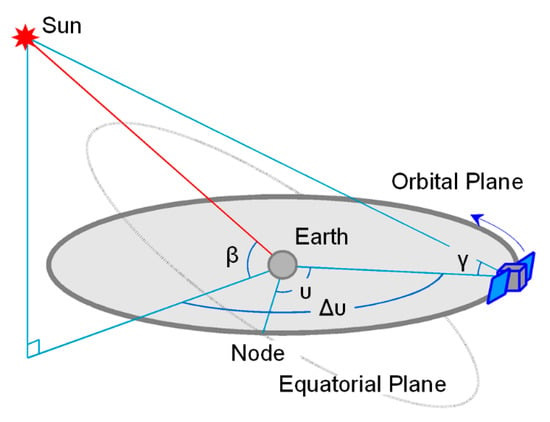Figure 5. Schematic diagram of the satellite–Earth–Sun geometry and corresponding angular arguments.

3. Results and Disscusion

3.1. SLR Residuals for COM Orbits

Precise orbits and SLR normal point data from the longest spans (as of December 2019) were selected for Galileo orbit validation. The orbital SLR residual time series for two IOV and two FOC satellites are shown for COM orbits in Figure 6, the evolution of which can be divided into three stages. Residuals in the first stage (prior to 4 January 2015) showed a non-zero mean value with a systematic bias of −6 cm, an amplitude of ~20 cm, and a standard deviation (STD) of ~8 cm. These residual terms improved significantly in the second stage (between 4 January 2015 and 6 August 2017), exhibiting a bias of roughly −4 cm, an STD of only ~4 cm, and an amplitude of less than 10 cm. In the third stage (after 6 August 2017), the bias and STD were further reduced to approximately −1 cm and 3 cm, respectively.

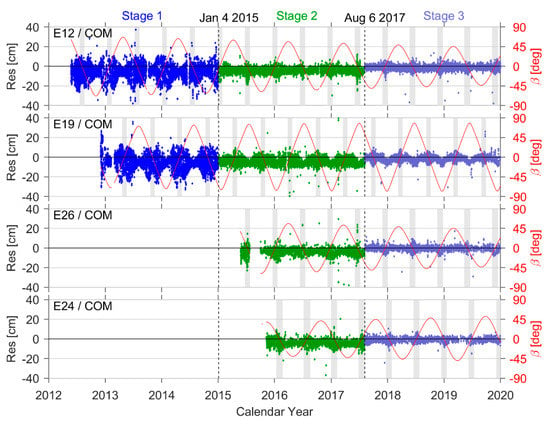
Figure 6. SLR residuals for COM orbits. The red curve represents changes in the Sun elevation angle (β) over time, with the grey area indicating the eclipse season.

Modifications to the Galileo satellite POD strategy caused significant changes in SLR validation. Prior to 4 January 2015, COM orbit products used the ECOM SRP model. The updated ECOM2 SRP model was then adopted. This update had obvious effects on improvements to orbital accuracy, which reduced residuals by 50%. After 6 August 2017, updated Earth albedo radiation pressure and satellite antenna thrust models were used in the orbit determination process [17], leading to evident improvements in the systematic bias of SLR residuals (~3 cm). Table 5 summarizes the validation results for three-stage COM orbits from all eight Galileo satellites.

Table 5. Statistical information for SLR residuals calculated from COM orbits. Duration refers to the accumulated effective time for orbit products, in which the period of interruption is subtracted. Only the number of SLR normal points over the accumulated effective time were included in orbit validation calculations.

PRN	Stage 1				Stage 2				Stage 3
	Duration (Day)	#np	Bias (cm)	STD (cm)	Duration (Day)	#np	Bias (cm)	STD (cm)	Duration (Day)	#np	Bias (cm)	STD (cm)
E11	905	12,970	−5.7	8.5	946	11,177	−4.2	3.5	857	5851	−1.0	3.1
E12	928	13,173	−5.8	8.3	931	10,123	−4.4	3.5	882	12,287	−1.4	2.7
E19	736	9916	−5.4	7.4	937	11,332	−4.3	3.8	880	9459	−1.6	3.1
E20	471	7183	−5.4	7.3	-	-	-	-	-	-	-	-
E26	-	-	-	-	728	5654	−3.7	4.0	882	5865	−0.4	2.7
E22	-	-	-	-	706	5807	−3.8	4.5	133	914	−0.2	2.6
E24	-	-	-	-	625	5358	−4.1	4.1	882	4878	−1.0	2.3
E30	-	-	-	-	636	4836	−4.2	3.5	882	4636	−0.8	2.9
Average	-	-	−5.6	7.9	-	-	−4.1	3.8	-	-	−0.9	2.8

The red curve in Figure 6 represents changes in the Sun elevation angle (β) over time, with the grey area indicating the eclipse season. It is evident from the plot that changes in the amplitude of SLR residuals follow a synchronization pattern for satellites in the same orbital plane (e.g., E12 and E26 in plane B), since variations in the angle β are temporally synchronized. Orbital accuracy is also low, while SLR residuals are high during the eclipse season. SLR residuals could exhibit a local maximum when the angle β is close to 0° (i.e., when the Sun passes through the satellite orbital plane). This is possibly due to sharp increases in the yaw rate of the Galileo satellites (when β = 0°), inducing attitude control system mechanisms and corrective maneuvers. This is reflected in both the SRP model and the estimation of D0 (a fitting coefficient in the satellite–Sun vector direction). It also produced local abnormalities [13], which in turn caused satellite orbital errors to increase in the radial direction and eventually led to local increases in SLR residual amplitudes, which are typically small when the angle β is large. In contrast, these residuals were only 25–50% of their value during the eclipse season (when β was at its maximum).

The SLR residuals of satellites in different orbital planes showed similar changes. In addition, the eclipse season and maximum value of residuals manifested in different temporal regions, due to varying trends in the angle β with time. SLR residuals also became less dependent on β from the first to the third stage of the orbit determination strategy. However, in the third stage, the residuals from some orbit products still exhibited a weak dependence on β, suggesting imperfections in current orbital perturbation models and a need for further refinement.

3.2. SLR Residuals for GBM Orbits

The residual time series for GBM orbit products from four satellites is shown in Figure 7. This sequence was divided into two stages using 25 October 2016 as the boundary. The ECOM SRP model was applied in the first stage [8] and an a priori Box-Wing (BW) model was adopted (in addition to ECOM) in the second stage [27]. The orbital SLR residual STD in Stage 2 (after 25 October) was significantly smaller than that of Stage 1. In addition, the dependence of Stage 2 residuals on the angle β was nearly eliminated, indicating the SRP model update was successful. Systematic bias in GBM residuals was also reduced significantly after adopting the a priori BW model, indicating a partial correction of model errors caused by albedo radiation pressure from the Earth and satellite antenna thrust. Table 6 summarizes these validation results for GBM orbits.

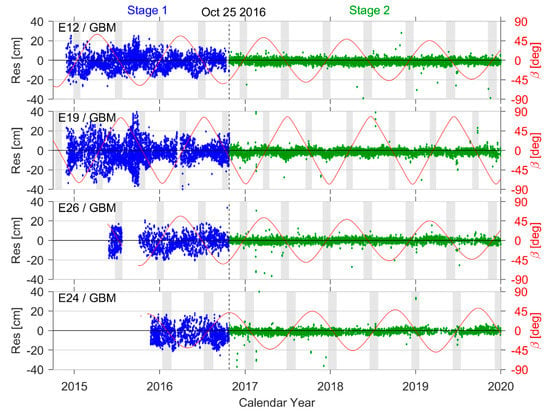
Figure 7. SLR residuals for GBM orbits.

Table 6. Statistical information for SLR residuals calculated from GBM orbits.

PRN	Stage 1				Stage 2
	Duration (Day)	#np	Bias (cm)	STD (cm)	Duration (Day)	#np	Bias (cm)	STD (cm)
E11	693	8078	−0.5	8.2	1131	9155	−0.9	2.7
E12	677	7224	−1.0	7.7	1165	15,363	−1.2	2.9
E19	678	8396	−2.7	10.6	1163	12,754	−1.6	2.8
E26	439	3252	−2.1	8.8	1165	8210	−0.2	2.7
E22	408	3071	−2.0	9.3	410	3574	−0.6	3.8
E24	329	2841	−4.0	7.9	1161	7204	−0.8	4.2
E30	338	2573	−3.6	7.8	1164	6758	−0.7	2.9
Average	-	-	−2.3	8.6	-	-	−0.9	3.1

3.3. Radial Differences in the COM and GBM Orbits

In the Galileo system observation geometry, the line of sight from the ground to satellite is always at an angle of less than 14° from the radial orbit direction. In addition, SLR residuals were highly consistent with orbital clock corrections, which map orbital radial errors [13,22]. This suggests that SLR residuals can generally be regarded as a measure of radial errors for Galileo satellites, which were investigated in this study using orbital comparisons. Figure 8 shows radial differences in the COM and GBM orbits of the four Galileo satellites. This comparison also demonstrates an obvious dependence on β and indicates that orbital errors increased significantly during eclipse season.

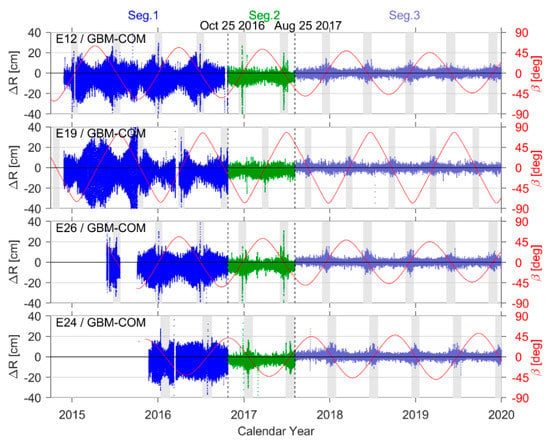
Figure 8. A COM-GBM orbit comparison in the radial direction.

This orbit comparison also demonstrates the existence of three distinct time segments, separated by boundaries occurring on 25 October 2016 (when the GBM SRP model was updated) and 6 August 2017 (the Earth albedo radiation pressure and satellite antenna thrust model updates for COM orbit products). The STD of differences in radial components were ~10 cm in Segment 1, generally reduced below 5 cm in Segment 2, and further improved to less than 3 cm in Segment 3. The absolute value of systematic biases along orbital radial directions was also reduced from 4 cm to nearly less than 1 cm, representing a significant improvement. Table 7 summarizes the statistical results of orbit comparison for each of these three segments. Comparing Table 7 with Table 5 and Table 6 suggests that SLR residuals are in good agreement with radial orbit errors.

Table 7. Statistical information for COM-GBM orbit differences in the radial direction.

PRN	Segment 1			Segment 2			Segment 3
	Duration (Day)	Mean (cm)	STD (cm)	Duration (Day)	Mean (cm)	STD (cm)	Duration (Day)	Mean (cm)	STD (cm)
E11	691	−4.8	8.1	285	−3.7	3.8	845	−0.1	2.1
E12	674	−4.8	8.5	285	−3.7	4.1	880	−0.0	2.2
E19	676	−4.4	11.1	285	−3.0	3.4	876	−0.1	2.5
E26	436	−4.0	9.2	285	−3.6	4.2	880	0.3	2.2
E22	403	−3.6	9.7	285	−3.5	4.8	125	1.1	3.3
E24	327	−3.7	9.9	280	−3.2	5.8	880	0.6	2.6
E30	337	−3.8	9.1	284	−3.2	3.2	880	0.6	2.2
Average	-	−4.2	9.4	-	−3.4	4.2	-	0.3	2.4

3.4. SLR Residuals Results for WUM, GRM, and TUM Orbits

In addition to the residual validation results for COM and GBM orbits listed above, Table 8, Table 9 and Table 10 summarize results for WUM, GRM, and TUM products. Improvements in the orbit product quality, due to SRP model updates, were reflected in the SLR validation process as the STD of residuals generally decreased from about 10 cm to 3–4 cm. The absolute value of systematic biases also improved, decreasing by 2–4 cm from the initial to the latter stages. In addition, the bias in some orbit products was close to zero and the residual STD using the ECOM2 model was significantly lower than that of the ECOM model. Orbits processed using only ECOM2 exhibited small but obvious bias, while orbits processed using both BW and ECOM models showed significantly lower bias.

Table 8. Statistical information for SLR residuals calculated from WUM orbits.

PRN	Stage 1				Stage 2				Stage 3
	Duration (Day)	SLR Points	Mean (cm)	STD (cm)	Duration (Day)	SLR Points	Mean (cm)	STD (cm)	Duration (day)	SLR Points	Mean (cm)	STD (cm)
E11	319	4140	−4.3	8.5	931	10,918	−2.8	3.2	663	4412	−1.0	3.5
E12	336	4000	−4.8	8.3	910	9885	−3.1	3.5	694	9711	−1.3	3.1
E19	346	4302	−4.2	7.8	919	11,147	−2.8	3.9	694	7024	−1.9	3.2
E20	145	1828	−3.9	7.3	-	-	-	-	-	-	-	-
E26	409	3038	−4.8	9.6	299	2416	−3.4	3.3	690	4400	0.5	3.6
E22	378	2814	−4.3	8.4	301	2764	−3.8	3.1	81	582	0.1	2.0
E24	300	2562	−6.7	7.8	292	2432	−4.3	3.9	693	3639	−0.1	2.4
E30	310	2351	−6.4	8.3	300	2242	−4.0	3.0	693	3606	−0.1	3.2
Average	-	-	−4.9	8.3	-	-	−3.5	3.4	-	-	−0.5	3.0

Table 9. Statistical information for SLR residuals calculated from GRM orbits.

PRN	Stage 1				Stage 2
	Duration (Day)	SLR Points	Mean (cm)	STD (cm)	Duration (Day)	SLR Points	Mean (cm)	STD (cm)
E11	439	6639	−4.1	14.0	1775	16,739	−0.4	3.8
E12	430	6718	−3.9	13.5	1791	22,161	−0.6	3.5
E19	238	3582	−3.0	11.3	1775	20,142	−0.9	3.9
E20	209	3569	−3.7	13.9	-	-	-	-
E26	-	-	-	-	1593	11,403	0.0	3.7
E22	-	-	-	-	827	6631	−0.7	4.0
E24	-	-	-	-	1490	10,126	−0.8	4.0
E30	-	-	-	-	1500	9321	−0.6	4.4
Average	-	-	−3.7	13.2	-	-	−0.6	3.9

Table 10. Statistical information for SLR residuals calculated from TUM orbits.

PRN	Stage 1				Stage 2
	Duration (Day)	SLR (Points)	Mean (cm)	STD (cm)	Duration (Day)	SLR (Points)	Mean (cm)	STD (cm)
E11	1454	18,211	−5.0	8.9	869	7465	−1.2	3.5
E12	1470	17,389	−5.2	8.6	890	11,944	−2.0	3.7
E19	1365	17,692	−5.4	8.5	883	10,489	−2.1	4.1
E20	413	6277	−5.4	9.2	-	-	-	-
E26	485	3558	−4.5	8.5	887	6630	−0.5	3.7
E22	467	3487	−4.4	9.3	355	3144	−0.6	3.9
E24	384	3353	−6.1	6.8	886	5661	−1.0	4.0
E30	386	2985	−5.8	6.9	887	5295	−0.8	3.6
Average	-	-	−5.2	8.3	-	-	−1.2	3.8

3.5. Relationship between Orbital SLR Residuals and the Satellite–Sun Elongation Angle

Figure 9 shows the relationship between SLR residuals for COM and GBM orbits and the satellite–Sun elongation angle γ at each stage. These residuals showed a pronounced correlation with γ before the SRP model update and were typically positive when the satellite was near the Sun (compared to the Earth), corresponding to γ > 90°. Conversely, residuals were typically negative when the satellite was in the far-Sun position (γ < 90°). This correlation between SLR residuals and the angle γ was reduced significantly after the SRP model update. The combined BW-ECOM model used for GBM was more effective in reducing the correlation with orbital residuals than that of the ECOM2 model for COM. The dispersion and systematic residual bias were further reduced when the COM orbit was supplemented with albedo radiation pressure and antenna thrust model updates.

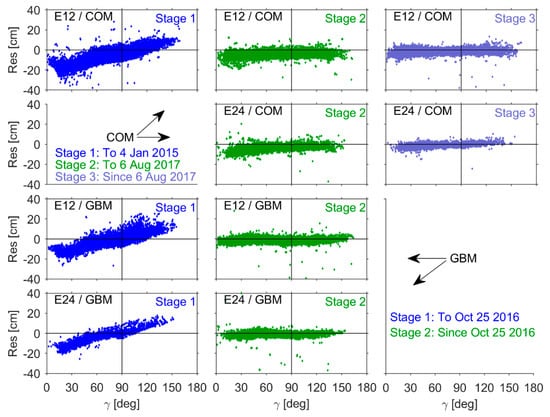
Figure 9. SLR residuals as a function of the Earth–satellite–Sun elongation γ.

3.6. Relationship between Orbital SLR Residuals on the Argument of Satellite Latitude

Figure 10 shows the relationship between SLR residuals and the satellite argument of latitude u. Prior to the SRP model update, residuals from both COM and GBM orbit products varied with the angle u (using the ECOM model). This period of fluctuation was equal to the period of the satellite’s orbital motion, but variations existed in the amplitude and phase of the fluctuations. Although the ECOM model includes u as an angular variable, the presence of such obvious fluctuations is a clear indication of model deficiencies. However, the SRP update significantly reduced the magnitude of such fluctuations to the extent that practically no systematic residual variations with the angle u can be observed when using the latest perturbation models.

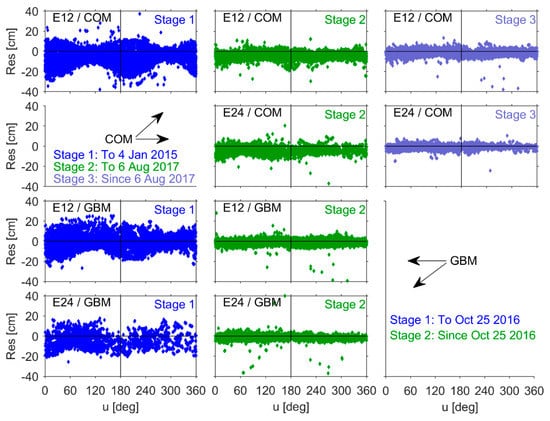
Figure 10. SLR residuals as a function of the argument of latitude u. Prior to the update, SLR residuals also exhibited a clear dependence on the argument of satellite latitude with respect to the Sun (Δu), as shown in Figure 11. As a result, residuals were mostly positive, with a maximum value of ~15–20 cm, when Δu was close to 0° or 360° (i.e., the satellite and the Sun were aligned in approximately the same direction). In contrast, residuals were mostly negative, with a minimum value of roughly −20 cm to −25 cm, when Δu was close to 180° (i.e., the satellite and the Sun were aligned in approximately opposite directions relative to the Earth). Some studies attributed the relationship between the sign of the SLR residuals (positive or negative) and the angle Δu to surface area characteristics on the X- and Z-side of the satellite body [18,28,29]. This correlation decreased significantly after the SRP model update.

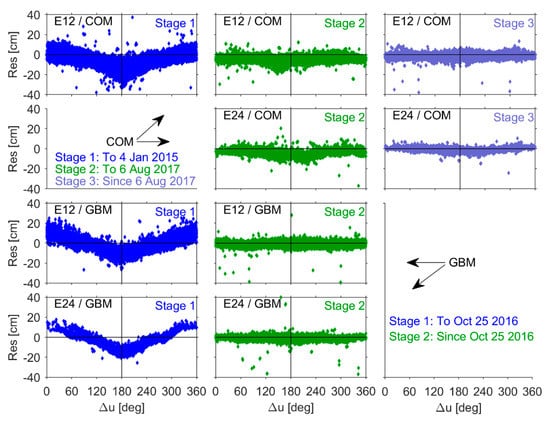
Figure 11. SLR residuals as a function of relative Sun–satellite latitude Δu.

3.7. Dependence of Orbital SLR Residuals on the Local Time of Observation

The dependence of orbital SLR residuals on the local time of observation is shown in Figure 12. The satellite and Sun were both above the horizon of the tracking site when conducting daytime observations (i.e., on the same side of the Earth). This was similar to the relative positions of the satellite and the Sun when |Δu−180°| > 90° and γ > 90°. In this configuration, most of the orbital residuals are positive. During nighttime observations, the position of the Sun is on the other side of the tracking site, similar to the relative position of the satellite and the Sun when |Δu−180°| < 90° and γ < 90°. In this configuration, most of the residuals are negative. Residual variations with a site’s local time were reduced significantly after the updates. This is similar to the relationship between orbital SLR residuals and the angles Δu or γ. Daytime observations accounted for ~25–40% of the total data, as mentioned previously. In other words, the share of day and night observations was roughly equal and such residual distributions could not be attributed to observation time. These results suggest that diurnal variations in the SLR residuals from Galileo satellite orbits are strongly correlated with the quality of SRP modeling. In fact, the included model appears to be the primary factor affecting the dependence of orbital residuals on local time, as opposed to differences in the accuracy of SLR observations during both daytime and nighttime measurements.

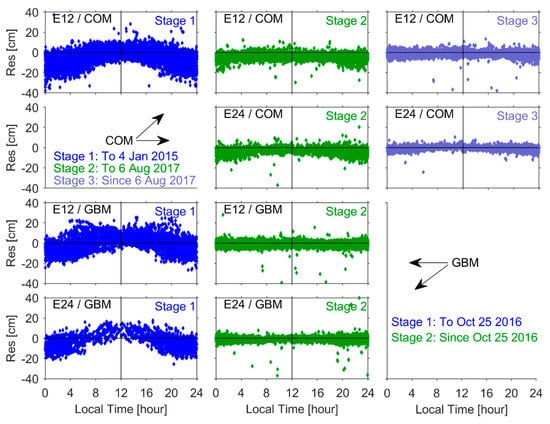
Figure 12. SLR residuals as a function of local time at various tracking sites.

4. Conclusions

In this study, SLR observations were used to validate the accuracy of orbit products for Galileo satellites with the longest temporal spans currently provided by MGEX analysis centers. The characteristics of these residual time series were analyzed, with orbital comparisons used as auxiliary support for SLR validation. The relationship between residuals and solar elevation, satellite–Sun elongation angle, the argument of satellite latitude, the argument of satellite latitude with respect to the Sun, and local observation time were discussed in detail. The results showed that multi-year SLR validation is of great benefit for accuracy assessment in Galileo satellite orbits. The presented methodology is also critical for evaluating the quality of orbit determination models such as SRP and other POD perturbation modeling strategies. As demonstrated, the SRP update significantly improved the quality of Galileo satellite orbit products. The STD of current SLR residuals, produced using updated perturbations, was reduced from 8–10 cm in the early data products to 3–4 cm in the recent products. The systematic bias was also reduced significantly (~2–4 cm). However, the Galileo SRP model and other perturbation techniques should be improved and evaluated further.

Both the quantity and quality of SLR tracking data have an obvious effect on the orbit evaluation. As such, this study only selected site data exhibiting sufficiently high observation quality and uniform spatial distributions for orbital SLR validation. Even so, at SLR sites using multi-photon detectors, beams along the direction of inclination for the on-board retro-reflector array can cause asymmetric broadening of the echo pulse. This produced a functional relationship between the mean value of SLR residuals and the satellite nadir angle, known as the SLR signature effect [30], which resulted in a difference of ~1 cm between the bias at single-photon and multi-photon sites [18]. This small discrepancy does not affect the overall conclusion of the study, but it is likely worthy of further investigation. It should also be given more attention in the process of orbital SLR validation, due to recent improvements in GNSS orbital accuracy.