Remote Sensing Imagery Segmentation: A Hybrid Approach
Abstract
:1. Introduction
1.1. Background
1.2. Related Work
1.3. Contribution
2. Multilevel Thresholding Functions
2.1. Energy Curve—Otsu Method
2.2. Multilevel Minimum Cross Entropy
2.2.1. Cross Entropy
2.2.2. Recursive MCE
2.3. Gray-Level Co-Occurrence Matrix
3. Modified Cuckoo Search Algorithm

4. Proposed Algorithm
4.1. Multilevel Rényi’s Entropy
4.2. Steps for Rényi’s Entropy–MCS-Based Multilevel Thresholding
| Algorithm 2 Proposed Algorithm |
Input:
|
5. Experimental Results and Comparison of Performances
5.1. Fidelity Parameters for Quantitative Evaluation of the Results
5.1.1. Computation Time (in Seconds)
5.1.2. PSNR and MSE
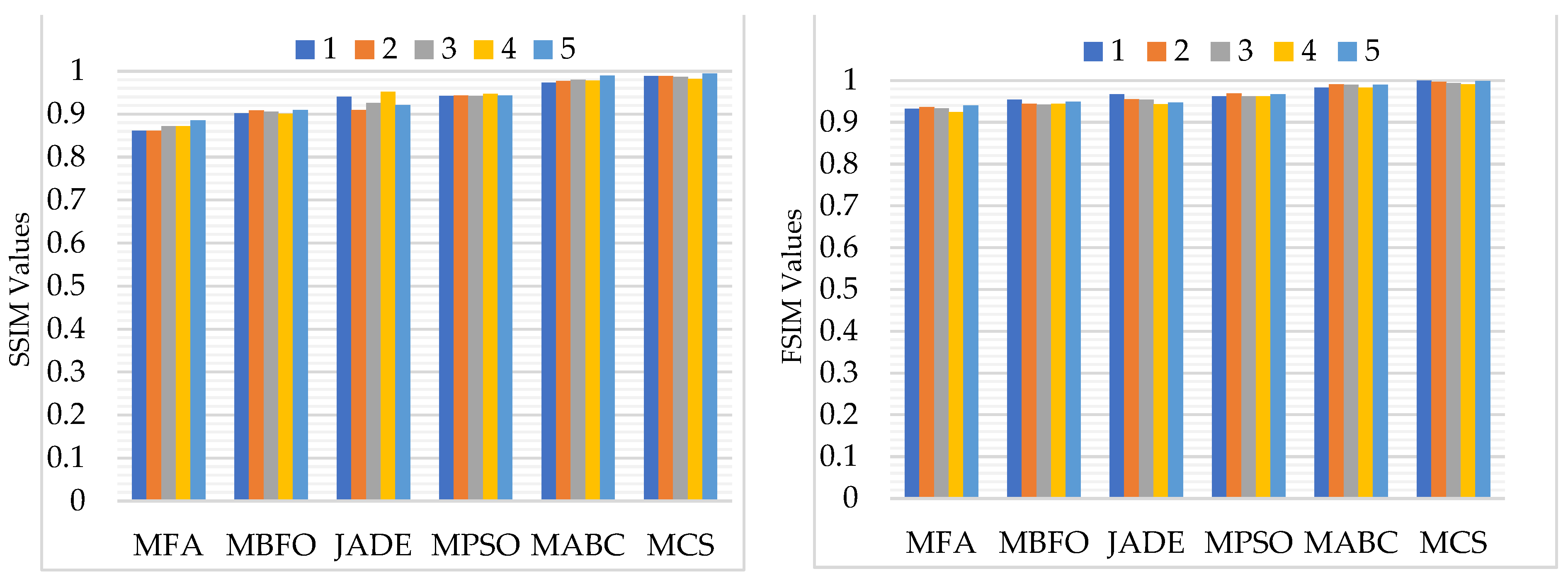
5.1.3. SSIM and FSIM
5.2. Comparison Using the Otsu Energy (EC-Otsu) Method as an Objective Function
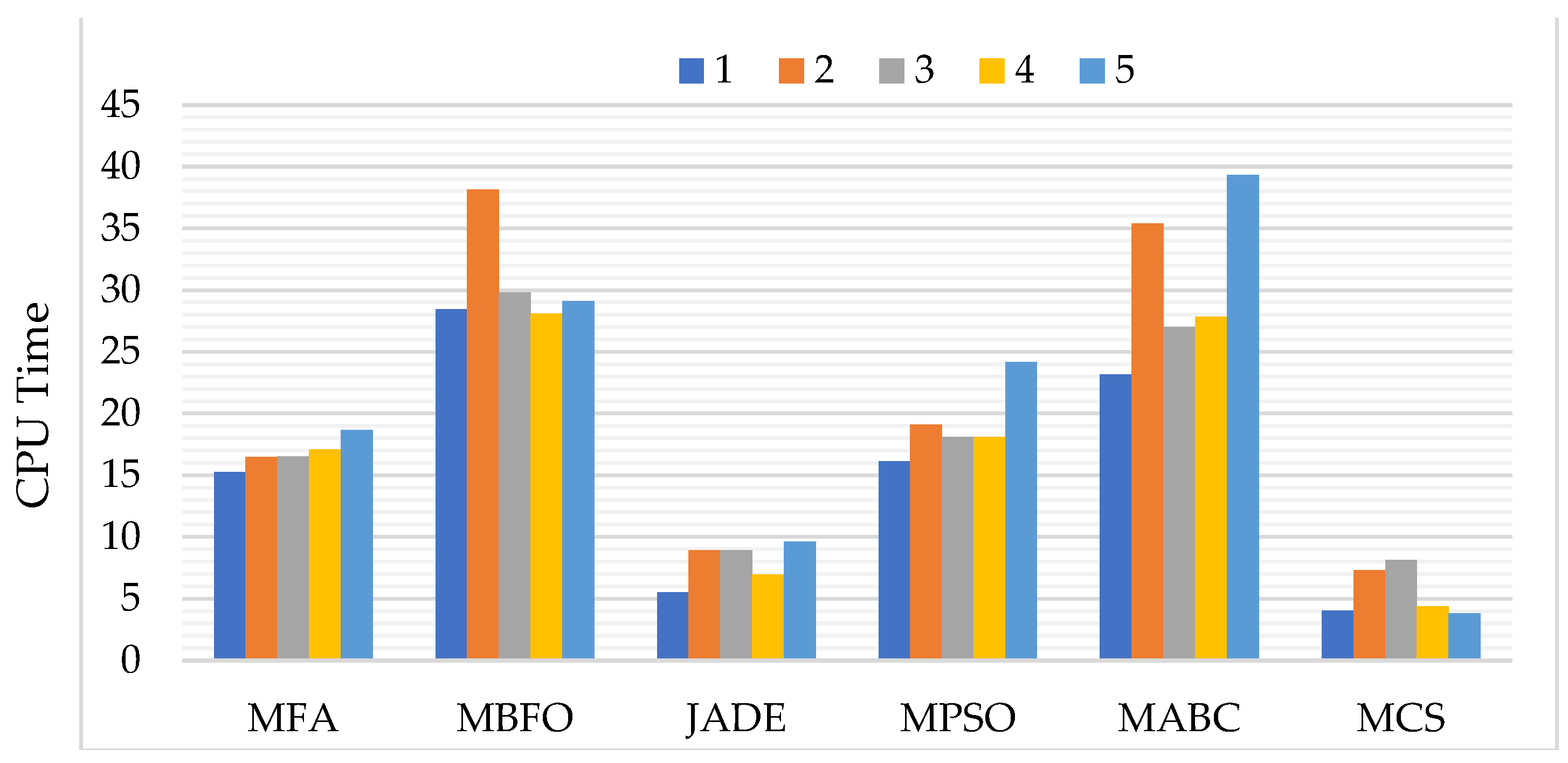
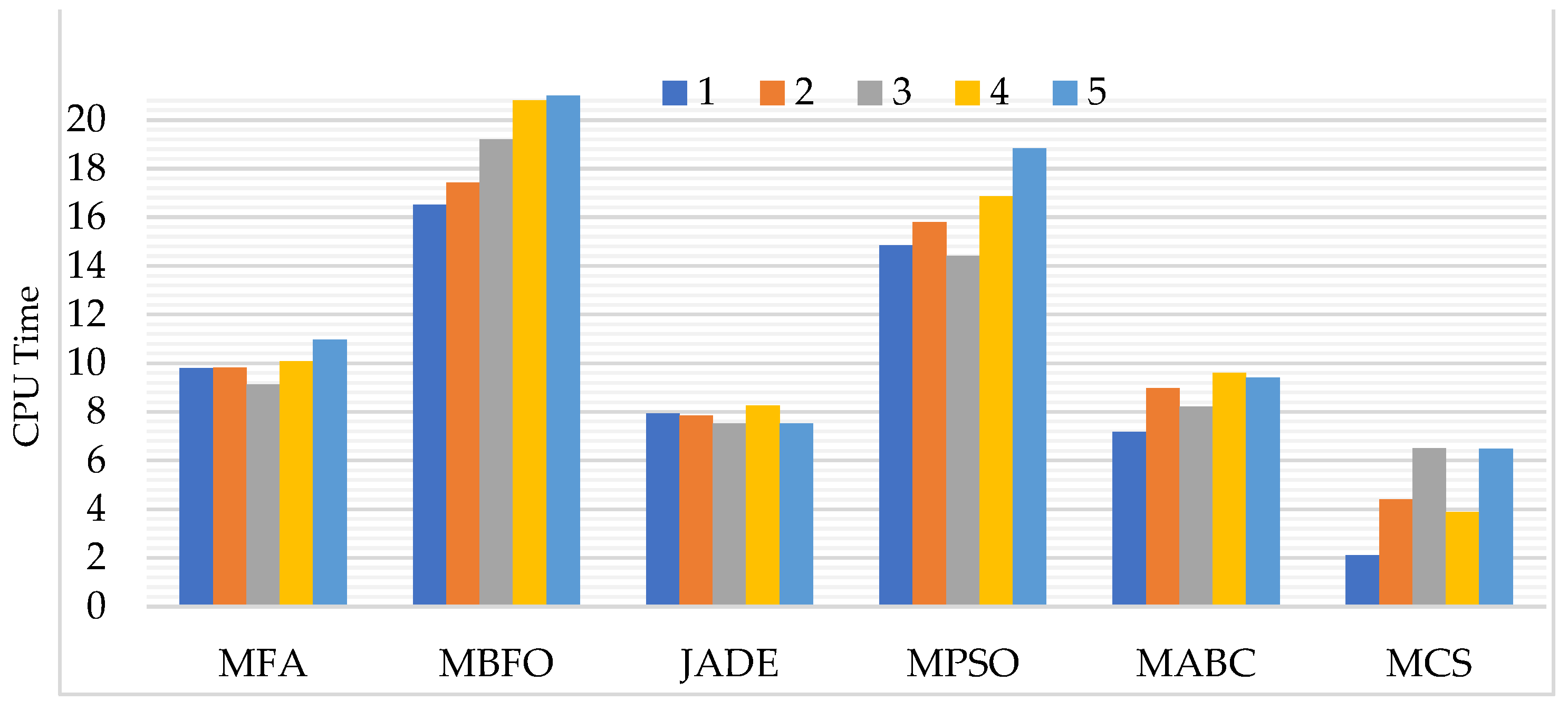
5.2.1. Assessment Based on Computation Time (CPU Time)
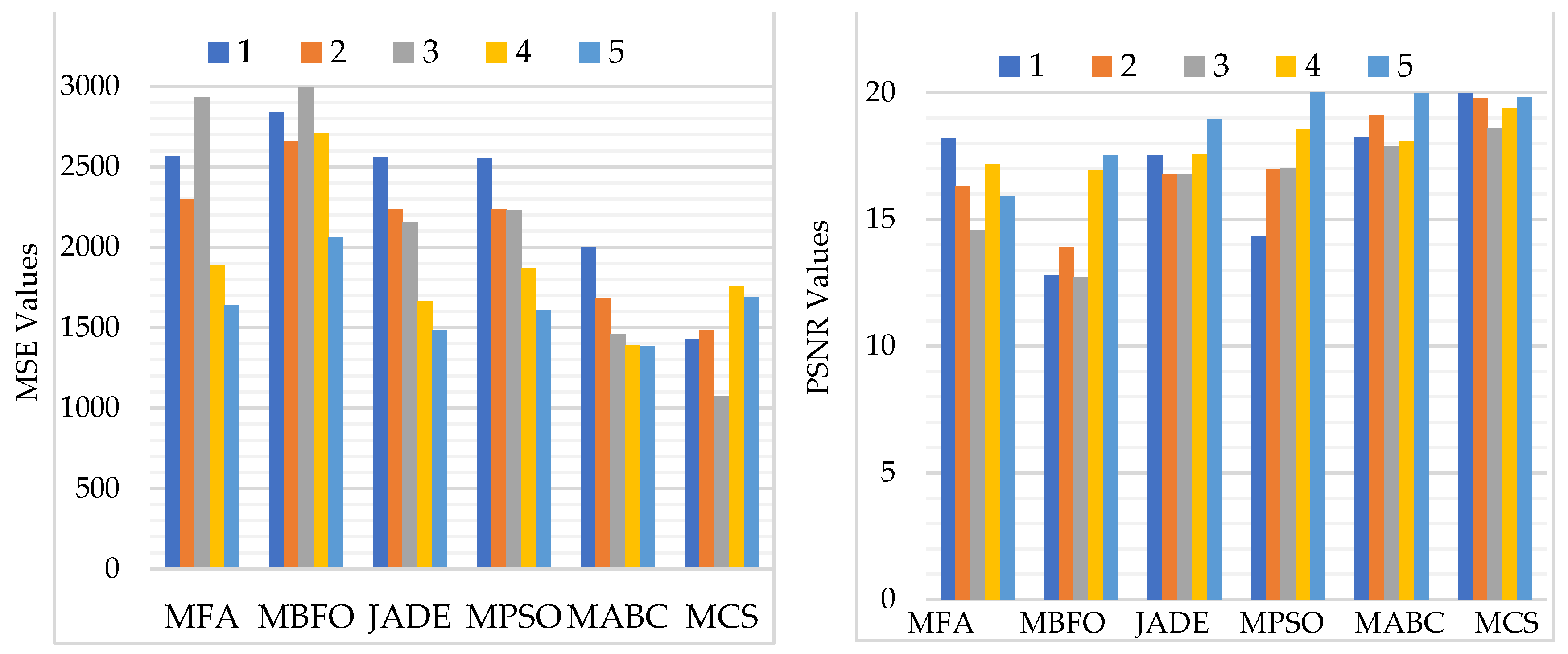
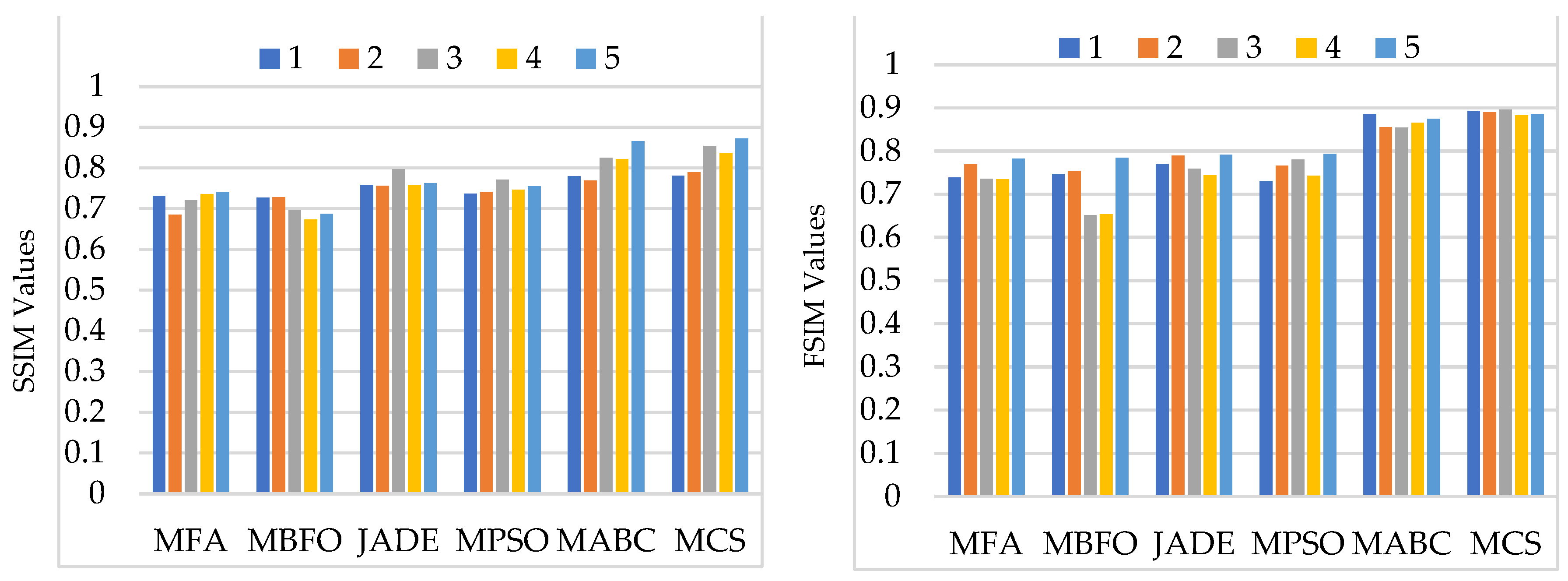
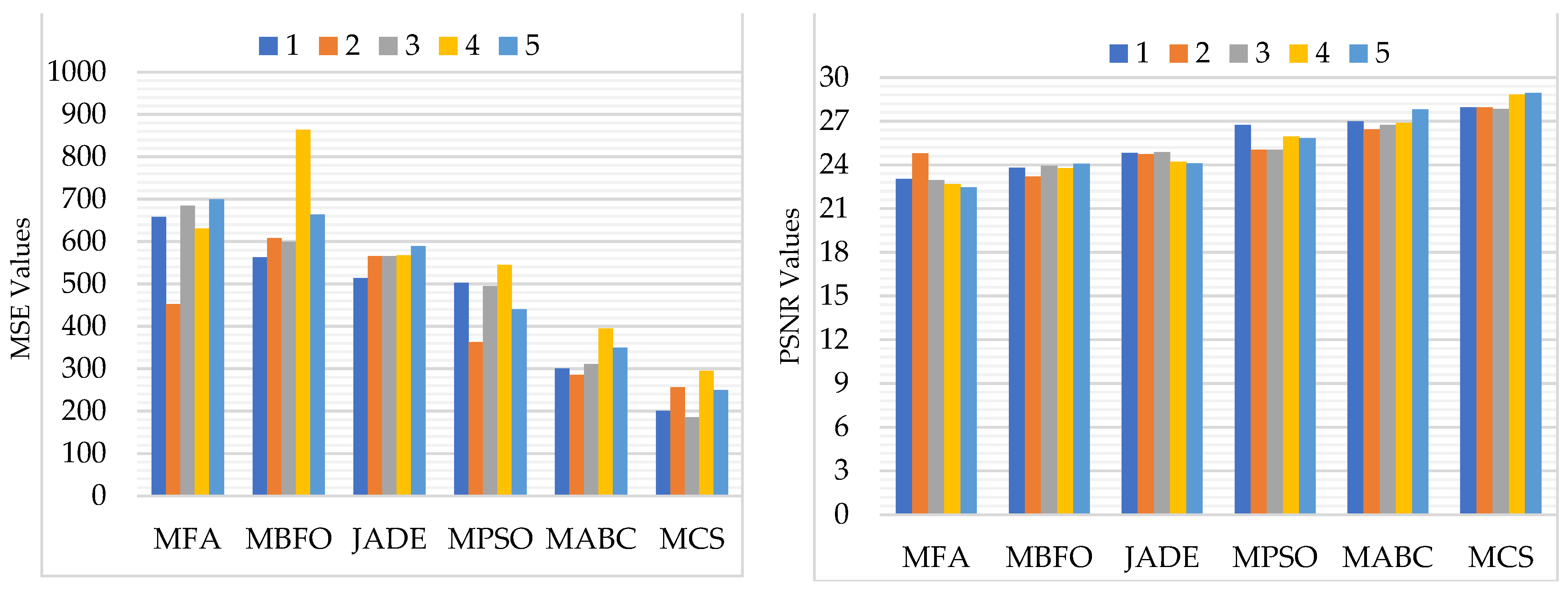
5.2.2. Assessment Based on PSNR, MSE, SSIM, and FSIM
5.2.3. Visual Analysis of the Results
5.3. Comparison Using MCE Method as an Objective Function
5.3.1. Assessment Based on Computation Time (in Seconds)
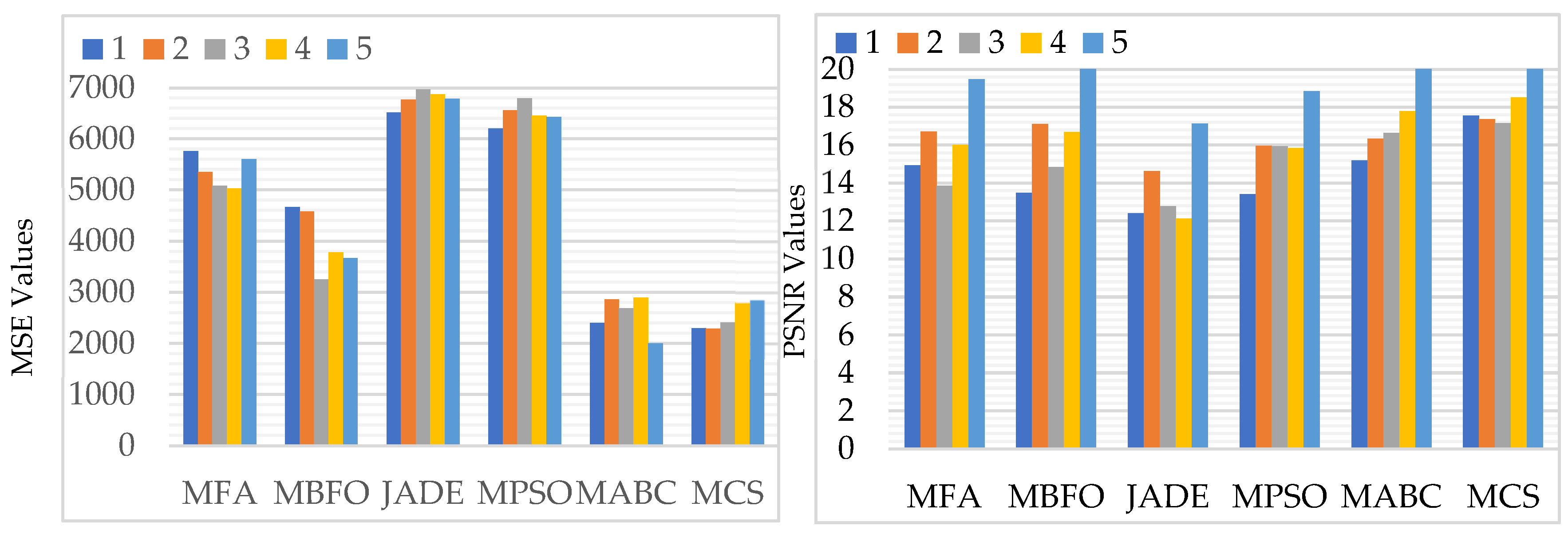
5.3.2. Assessment Based on PSNR, MSE, SSIM, and FSIM
5.3.3. Visual Analysis of the Results
5.4. Comparison Using GLCM as an Objective Function
5.4.1. Assessment Based on Computation Time (in Seconds)
5.4.2. Assessment Based on PSNR, MSE, SSIM, and FSIM
5.4.3. Visual Analysis of the Results
5.5. Comparison Using Rényi’s Entropy as an Objective Function
5.5.1. Assessment Based on Computation Time (in Seconds)
5.5.2. Assessment Based on PSNR, MSE, SSIM, and FSIM
5.5.3. Visual Analysis of the Results
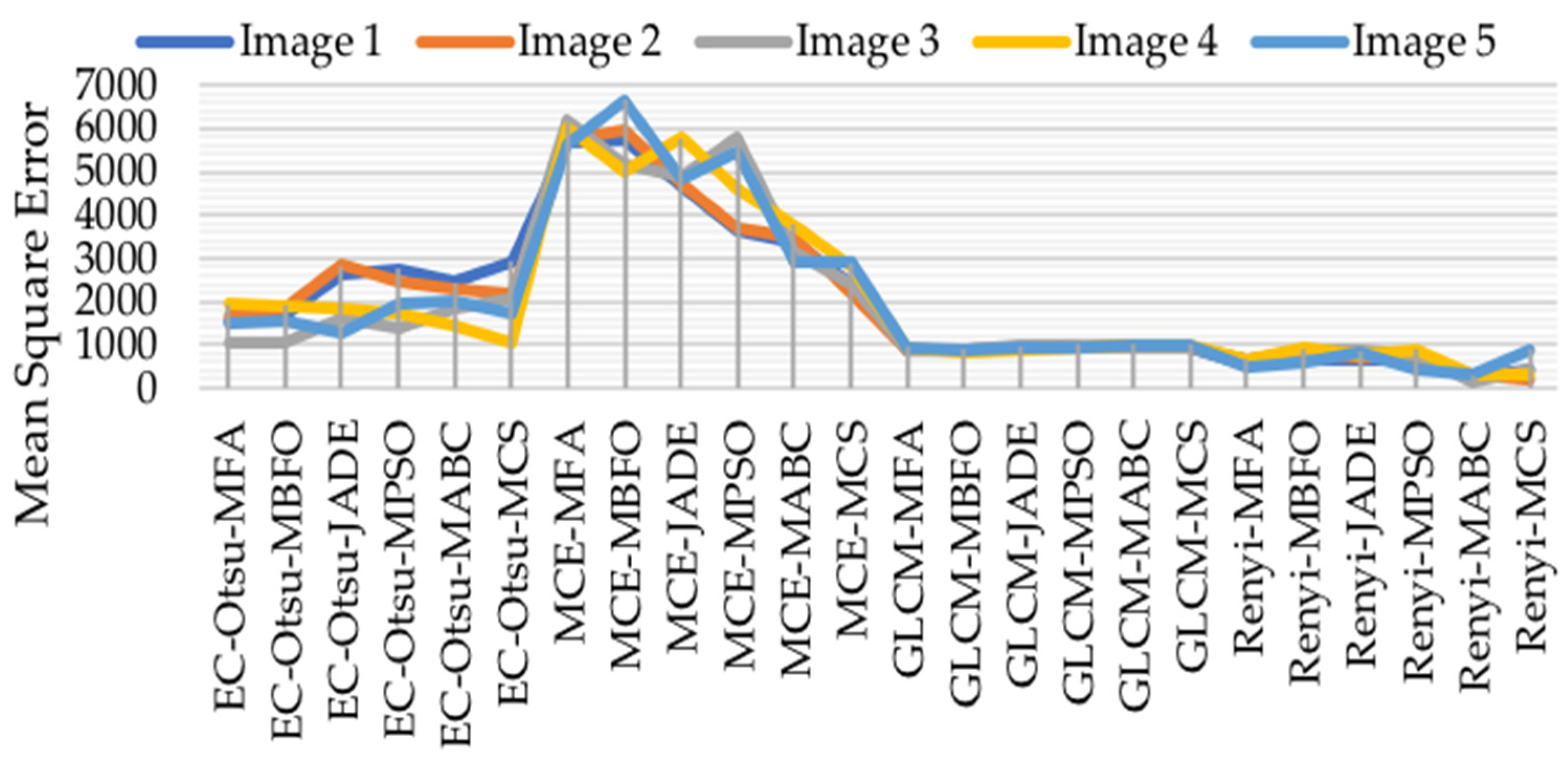
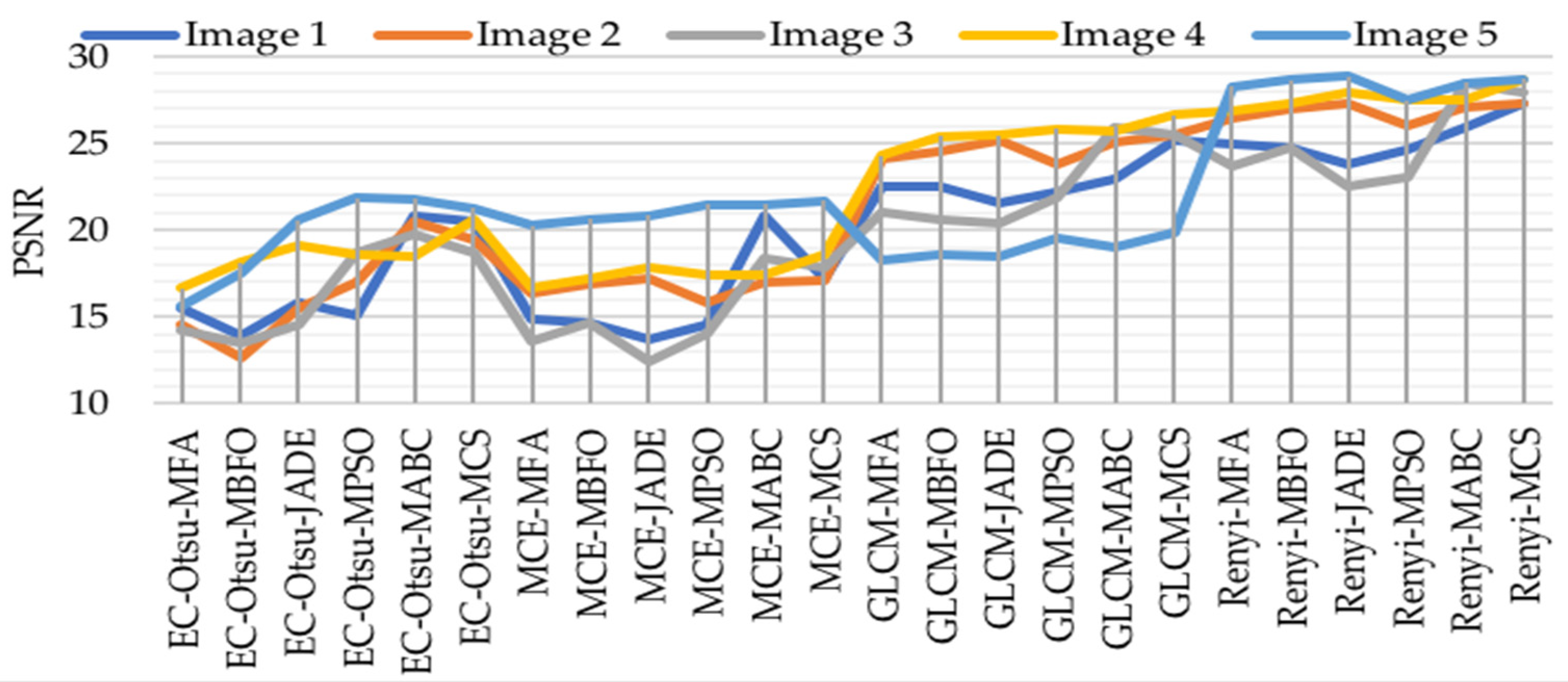
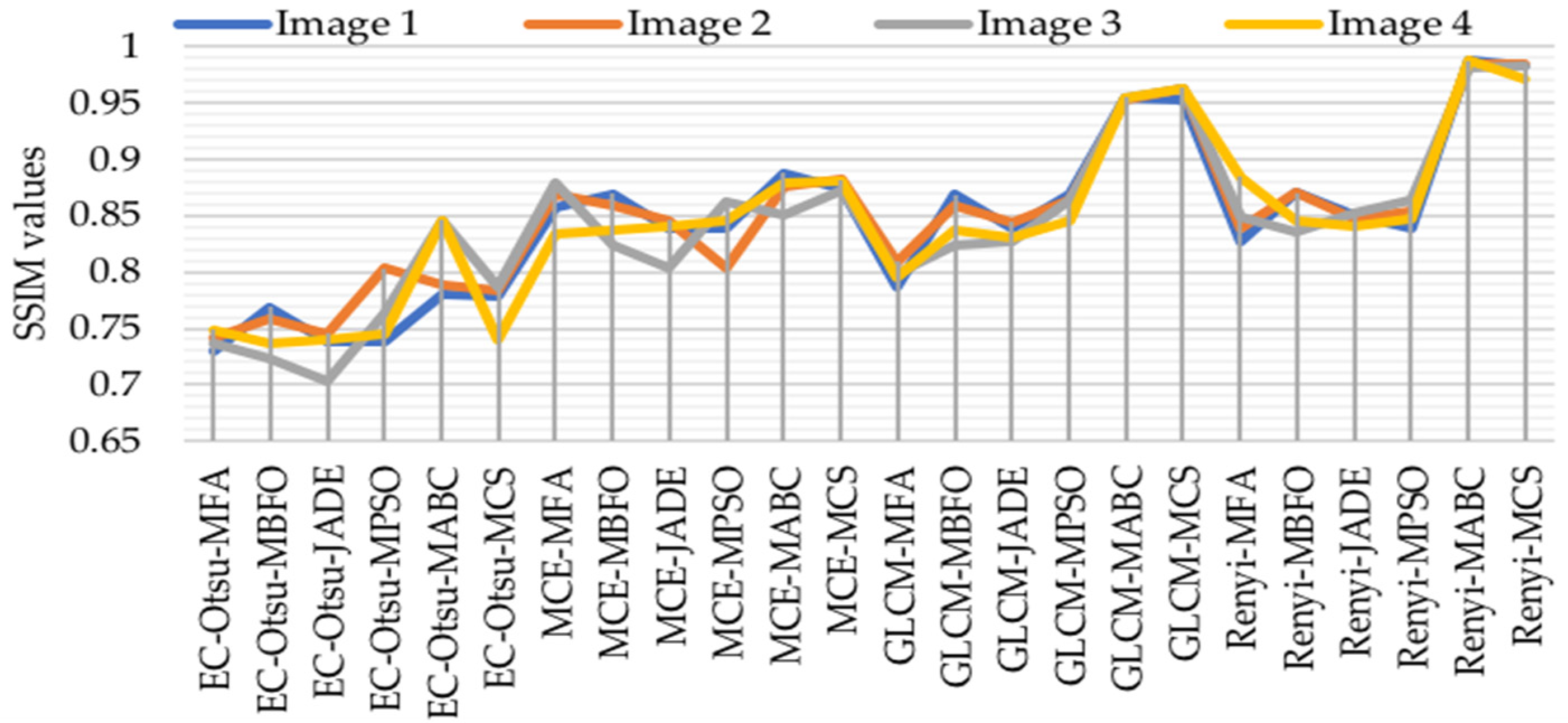
5.6. Comparison between Rényi’s Entropy, Energy-Otsu Method, MCE, and GLCM
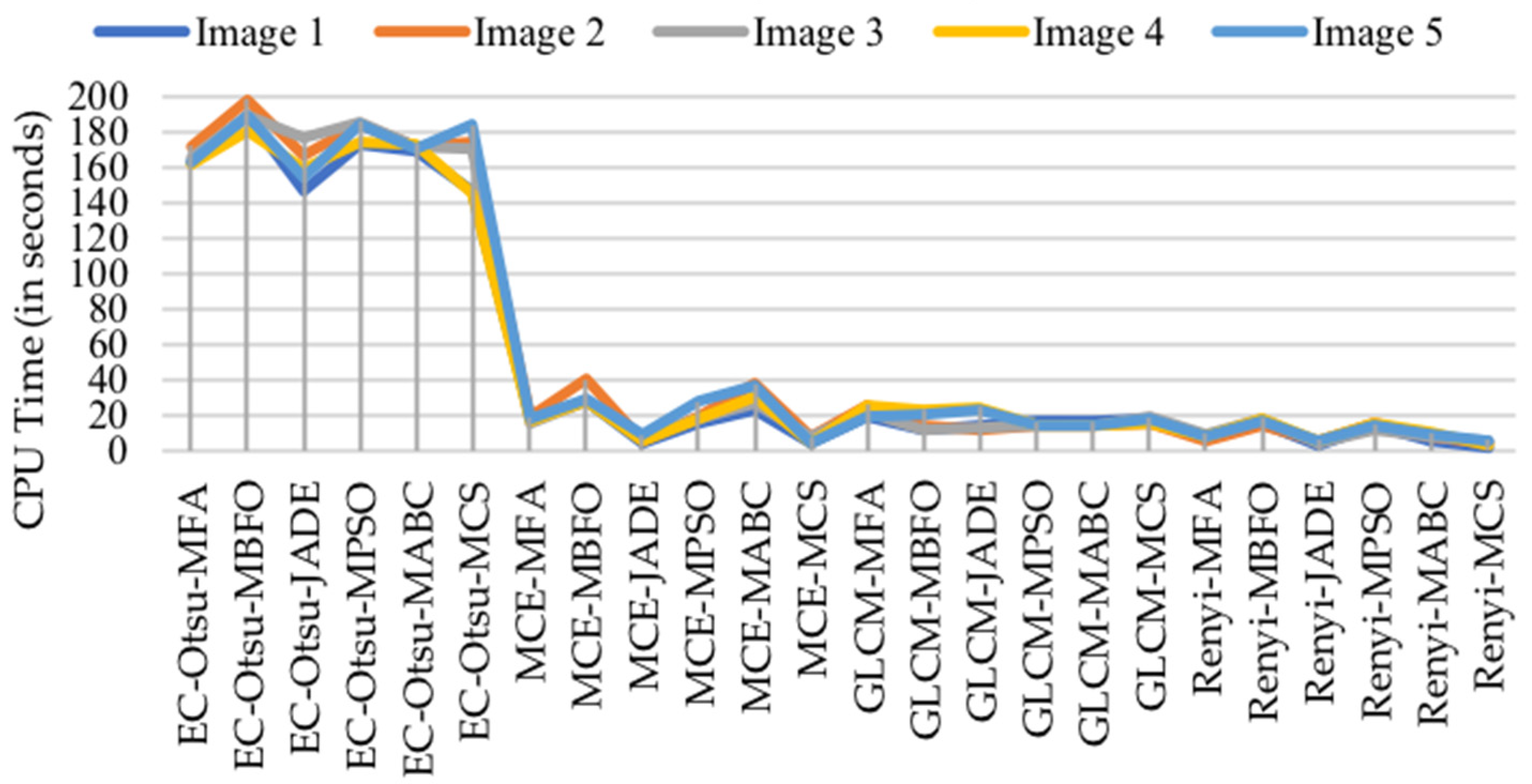
5.6.1. Assessment Based on Computation Time (in Seconds)
5.6.2. Assessment Based on PSNR, MSE, SSIM, and FSIM
5.6.3. Visual Analysis of the Results
5.7. Statistical Analysis Test
6. Conclusions and Future Work
6.1. Conclusions
6.2. Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Images | m | EC-Otsu | Minimum Cross Entropy | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MFA | MBFO | JADE | MPSO | MABC | MCS | MFA | MBFO | JADE | MPSO | MABC | MCS | ||
| 1 | 2 | 161.408 | 181.39 | 146.256 | 167.512 | 163.846 | 141.291 | 10.562 | 22.411 | 5.213 | 12.826 | 16.047 | 4.227 |
| 5 | 161.376 | 188.249 | 146.428 | 167.963 | 168.227 | 144.871 | 12.654 | 25.821 | 5.084 | 14.044 | 18.011 | 4.183 | |
| 8 | 163.102 | 188.993 | 146.658 | 173.425 | 169.519 | 146.931 | 18.854 | 28.005 | 5.367 | 16.441 | 24.117 | 4.634 | |
| 12 | 164.142 | 190.182 | 146.989 | 174.324 | 170.265 | 144.415 | 20.845 | 32.411 | 6.589 | 16.511 | 32.152 | 6.863 | |
| 2 | 2 | 168.8 | 189.068 | 165.225 | 175.429 | 166.229 | 171.707 | 12.865 | 34.54 | 5.852 | 13.66 | 21.15 | 5.871 |
| 5 | 170.736 | 189.539 | 167.285 | 178.321 | 167.539 | 170.565 | 15.652 | 36.469 | 5.485 | 15.823 | 30.472 | 7.36 | |
| 8 | 172.058 | 198.587 | 167.484 | 183.867 | 171.284 | 173.962 | 19.5 | 40.34 | 5.458 | 19.28 | 38.4 | 7.984 | |
| 12 | 172.815 | 200.958 | 168.182 | 188.216 | 171.689 | 184.275 | 20.798 | 43.809 | 7.809 | 19.4 | 46.676 | 10.086 | |
| 3 | 2 | 160.322 | 187.419 | 175.958 | 175.427 | 169.605 | 174.447 | 11.658 | 23.514 | 7.273 | 10.007 | 11.42 | 5.871 |
| 5 | 160.567 | 188.4 | 176.153 | 179.541 | 170 | 170.541 | 10.851 | 26.915 | 7.206 | 13.854 | 20.31 | 7.36 | |
| 8 | 165.335 | 188.839 | 176.282 | 186.147 | 171.387 | 170.147 | 16.125 | 28.754 | 8.972 | 18.074 | 27.572 | 8.1 | |
| 12 | 166.735 | 189.265 | 176.862 | 186.865 | 171.958 | 181.254 | 20.425 | 30.632 | 8.982 | 21.198 | 35.245 | 8.086 | |
| 4 | 2 | 160.67 | 180.437 | 156.624 | 166.156 | 167.369 | 144.106 | 12.652 | 21.981 | 6.031 | 10.751 | 18.089 | 4.227 |
| 5 | 161.667 | 188.213 | 156.858 | 171.102 | 167.475 | 145.101 | 17.465 | 24.351 | 6.386 | 13.792 | 25.768 | 4.183 | |
| 8 | 162.535 | 180.157 | 158.901 | 174.728 | 173.297 | 145.301 | 17.487 | 27.9 | 6.393 | 18.098 | 30.702 | 4.634 | |
| 12 | 163.789 | 192.658 | 149.265 | 175.524 | 173.689 | 145.458 | 20.854 | 30.098 | 8.621 | 19.86 | 36.016 | 6.863 | |
| 5 | 2 | 161.037 | 178.301 | 150.258 | 180.265 | 166.394 | 180.686 | 12.285 | 23.264 | 8.148 | 17.748 | 31.353 | 2.973 |
| 5 | 163.174 | 179.312 | 151.648 | 183.795 | 166.976 | 182.57 | 14.285 | 26.662 | 9.321 | 23.371 | 29.389 | 2.216 | |
| 8 | 163.135 | 189.339 | 155.021 | 184.543 | 171.102 | 183.783 | 18.865 | 29.624 | 9.754 | 28.097 | 37.612 | 4.725 | |
| 12 | 165.893 | 190.256 | 156.958 | 195.425 | 172.524 | 194.201 | 20.825 | 33.241 | 10.253 | 31.399 | 45.971 | 5.83 | |
| Images | m | MSE | PSNR | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MFA | MBFO | JADE | MPSO | MABC | MCS | MFA | MBFO | JADE | MPSO | MABC | MCS | ||
| 1 | 2 | 1954.548 | 1075.554 | 2855.01 | 2465.452 | 2846.154 | 2085.551 | 19.215 | 11.133 | 13.524 | 12.534 | 17.991 | 19.592 |
| 5 | 1745.154 | 1415.842 | 2455.026 | 2945.515 | 2236.658 | 2736.442 | 14.598 | 12.594 | 13225 | 14.557 | 17.224 | 19.558 | |
| 8 | 1564.846 | 1658.013 | 2655.324 | 2761.445 | 2454.954 | 2918.841 | 15.484 | 13.866 | 15.866 | 15.135 | 20.807 | 20.522 | |
| 12 | 1658.562 | 1563.325 | 2123.756 | 2193.045 | 2150.151 | 2860.152 | 15.549 | 13.527 | 15527 | 15.156 | 20.596 | 20.263 | |
| 2 | 2 | 1856.794 | 1203.774 | 2324.954 | 2375.336 | 2622.155 | 2341.111 | 16.902 | 14.534 | 17.527 | 15.465 | 17.328 | 19.264 |
| 5 | 1765.984 | 1418.015 | 2014.856 | 2044.995 | 2950.481 | 2163.145 | 16.527 | 12.135 | 14.468 | 16.855 | 17.801 | 19.861 | |
| 8 | 1645.215 | 1845.351 | 2850.852 | 2465.145 | 2305.848 | 2198.484 | 14.523 | 12.658 | 15.532 | 16.987 | 20.52 | 19.461 | |
| 12 | 1453.345 | 1478.759 | 2956.154 | 2053.985 | 2756.442 | 2495.922 | 17.228 | 16.321 | 15.546 | 18.669 | 20.853 | 20.573 | |
| 3 | 2 | 1567.021 | 1003.751 | 2755.256 | 2006.143 | 1425.454 | 1768.461 | 14.542 | 10.263 | 13.322 | 15.493 | 15.375 | 17.523 |
| 5 | 1215.341 | 1085.953 | 2256.181 | 2883.954 | 1106.853 | 2166.222 | 14.862 | 13.852 | 13.158 | 15.695 | 16.845 | 18.527 | |
| 8 | 1065.278 | 1065.153 | 1635.754 | 1395.354 | 1850.945 | 2078.896 | 14.216 | 13.466 | 14.554 | 18.699 | 19.803 | 18.658 | |
| 12 | 1984.182 | 1150.351 | 1966.784 | 1445.845 | 1205.656 | 2921.145 | 14.669 | 13.258 | 14.187 | 18.159 | 19.556 | 19.661 | |
| 4 | 2 | 1745.068 | 1352.254 | 1745.215 | 1111.654 | 1965.784 | 1350.333 | 17.494 | 15.863 | 17.462 | 17.794 | 17.866 | 18.125 |
| 5 | 1945.042 | 1895.256 | 1148.55 | 1953.784 | 1748.446 | 1814.951 | 16.116 | 15.225 | 18.266 | 18.632 | 17.551 | 18.165 | |
| 8 | 1943.986 | 1912.854 | 1820.848 | 1735.955 | 1425.494 | 1054 | 16.637 | 18.152 | 19.158 | 18.594 | 18.483 | 20.657 | |
| 12 | 1930.227 | 1874.856 | 1938.484 | 1915.748 | 1685.205 | 1345.142 | 18.505 | 18.596 | 19.432 | 19.158 | 18.507 | 20.535 | |
| 5 | 2 | 1909.984 | 1878.951 | 1717.446 | 1256.451 | 1757.942 | 1196.365 | 17.825 | 13.822 | 16.511 | 18.534 | 17.151 | 18.546 |
| 5 | 1654.001 | 1745.159 | 1170.985 | 1749.454 | 1862.145 | 1315.256 | 14.497 | 14.257 | 17.264 | 18.499 | 19.341 | 18.189 | |
| 8 | 1500.215 | 1567.852 | 1298.448 | 1965.648 | 1989.215 | 1705.142 | 15.572 | 17.566 | 20.558 | 21.864 | 21.815 | 21.296 | |
| 12 | 1500.571 | 1564.456 | 1739.552 | 1460.948 | 2625.551 | 1310.896 | 15.684 | 17.299 | 21.535 | 21.558 | 21.638 | 21.258 | |
| Images | m | SSIM | FSIM | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MFA | MBFO | JADE | MPSO | MABC | MCS | MFA | MBFO | JADE | MPSO | MABC | MCS | ||
| 1 | 2 | 0.6114 | 0.7456 | 0.7134 | 0.7261 | 0.7567 | 0.7523 | 0.7123 | 0.6805 | 0.7612 | 0.7315 | 0.8116 | 0.8535 |
| 5 | 0.6713 | 0.7568 | 0.7256 | 0.7345 | 0.7823 | 0.7634 | 0.7234 | 0.7356 | 0.7645 | 0.7302 | 0.8589 | 0.8478 | |
| 8 | 0.7301 | 0.7689 | 0.7389 | 0.739 | 0.7798 | 0.7789 | 0.7567 | 0.7517 | 0.7689 | 0.737 | 0.8875 | 0.8734 | |
| 12 | 0.7512 | 0.7702 | 0.7398 | 0.7412 | 0.7825 | 0.7881 | 0.7615 | 0.7597 | 0.7705 | 0.7381 | 0.8812 | 0.8821 | |
| 2 | 2 | 0.6257 | 0.7144 | 0.7298 | 0.7592 | 0.7655 | 0.7645 | 0.7267 | 0.6824 | 0.7587 | 0.7545 | 0.8238 | 0.8016 |
| 5 | 0.6735 | 0.7457 | 0.7345 | 0.7991 | 0.7774 | 0.7765 | 0.7568 | 0.7872 | 0.7789 | 0.7698 | 0.8546 | 0.8654 | |
| 8 | 0.7417 | 0.7589 | 0.7456 | 0.8034 | 0.7889 | 0.7834 | 0.7689 | 0.8349 | 0.7867 | 0.7712 | 0.8769 | 0.8829 | |
| 12 | 0.7425 | 0.759 | 0.7484 | 0.8125 | 0.7952 | 0.7852 | 0.7714 | 0.8365 | 0.7899 | 0.7825 | 0.8789 | 0.8882 | |
| 3 | 2 | 0.6003 | 0.7089 | 0.7592 | 0.749 | 0.8034 | 0.8145 | 0.7665 | 0.6357 | 0.7945 | 0.7245 | 0.8055 | 0.8073 |
| 5 | 0.6051 | 0.7246 | 0.7991 | 0.7519 | 0.8245 | 0.7209 | 0.7678 | 0.7297 | 0.8167 | 0.7356 | 0.8356 | 0.8998 | |
| 8 | 0.7374 | 0.7238 | 0.7034 | 0.7629 | 0.8456 | 0.7876 | 0.7789 | 0.7502 | 0.7478 | 0.7467 | 0.8504 | 0.8726 | |
| 12 | 0.7425 | 0.7245 | 0.7144 | 0.7714 | 0.8526 | 0.7825 | 0.7112 | 0.7525 | 0.7512 | 0.7524 | 0.8584 | 0.8755 | |
| 4 | 2 | 0.627 | 0.7078 | 0.7245 | 0.7256 | 0.8256 | 0.7267 | 0.7024 | 0.6539 | 0.7397 | 0.7423 | 0.8243 | 0.8064 |
| 5 | 0.673 | 0.7234 | 0.7359 | 0.7378 | 0.8345 | 0.7356 | 0.7124 | 0.6754 | 0.7413 | 0.7534 | 0.8544 | 0.8703 | |
| 8 | 0.7486 | 0.7367 | 0.7398 | 0.7456 | 0.8456 | 0.7398 | 0.7345 | 0.7874 | 0.7477 | 0.7612 | 0.8783 | 0.8804 | |
| 12 | 0.7512 | 0.7412 | 0.7412 | 0.7475 | 0.8526 | 0.7416 | 0.7412 | 0.7892 | 0.7512 | 0.7648 | 0.8812 | 0.8812 | |
| 5 | 2 | 0.6539 | 0.7821 | 0.7682 | 0.768 | 0.8878 | 0.7813 | 0.7867 | 0.8672 | 0.7815 | 0.7845 | 0.8515 | 0.8228 |
| 5 | 0.6754 | 0.7823 | 0.7612 | 0.7688 | 0.8867 | 0.7834 | 0.7867 | 0.7978 | 0.7902 | 0.7898 | 0.864 | 0.8838 | |
| 8 | 0.6874 | 0.7912 | 0.7642 | 0.7801 | 0.8978 | 0.7912 | 0.7923 | 0.7982 | 0.799 | 0.7967 | 0.8892 | 0.8904 | |
| 12 | 0.6985 | 0.7925 | 0.7702 | 0.7622 | 0.8995 | 0.7958 | 0.7952 | 0.7956 | 0.7982 | 0.7971 | 0.8899 | 0.8918 | |
| Images | m | MSE | PSNR | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MFA | MBFO | JADE | MPSO | MABC | MCS | MFA | MBFO | JADE | MPSO | MABC | MCS | ||
| 1 | 2 | 3054.122 | 6975.124 | 4745.428 | 5845.225 | 3156.347 | 2815.622 | 12.162 | 12.321 | 12.415 | 13.425 | 15.189 | 17.5621 |
| 5 | 5645.548 | 6515.784 | 4895.485 | 5695.452 | 3256.116 | 2516.664 | 13.975 | 13.485 | 12.512 | 13.745 | 16.412 | 16.845 | |
| 8 | 5664.123 | 5758.12 | 4645.855 | 3641.155 | 3354.099 | 2408.002 | 14.844 | 14.658 | 13.658 | 14.521 | 20.798 | 17.215 | |
| 12 | 5758.324 | 5663.072 | 4513.584 | 3203.093 | 2400.645 | 2300.365 | 14.935 | 14.715 | 13.715 | 14.641 | 20.685 | 17.352 | |
| 2 | 2 | 5956.732 | 5303.425 | 4654.653 | 3945.572 | 3102.276 | 2651.741 | 15.296 | 15.425 | 15.715 | 14.554 | 15.813 | 16.452 |
| 5 | 5865.124 | 5518.455 | 4684.411 | 3654.596 | 3350.828 | 2103.325 | 15.265 | 16.521 | 16.854 | 15.548 | 15.198 | 17.158 | |
| 8 | 5745.155 | 5945.128 | 4710.569 | 3715.185 | 3485.629 | 2198.823 | 16.315 | 16.846 | 17.225 | 15.879 | 17.015 | 17.154 | |
| 12 | 5353.061 | 5578.005 | 4766.252 | 3563.295 | 2856.142 | 2285.231 | 16.712 | 17.113 | 17.635 | 16.956 | 17.348 | 17.365 | |
| 3 | 2 | 6667.759 | 5103.785 | 5105.378 | 6416.448 | 3205.365 | 1658.244 | 13.235 | 13.352 | 11.213 | 12.384 | 14.563 | 17.9315 |
| 5 | 5315.765 | 5185.894 | 5006.122 | 4103.394 | 3026.372 | 2486.812 | 13.258 | 14.248 | 11.841 | 13.586 | 15.215 | 14.715 | |
| 8 | 6165.563 | 5165.645 | 4865.471 | 5785.439 | 3140.593 | 2398.773 | 13.602 | 14.654 | 12.445 | 13.986 | 18.398 | 17.846 | |
| 12 | 6084.854 | 5250.151 | 4966.12 | 3795.172 | 3685.216 | 2411.589 | 13.856 | 14.842 | 12.771 | 13.941 | 18.645 | 17.156 | |
| 4 | 2 | 5545.372 | 5552.577 | 4985.468 | 4951.495 | 2285.601 | 1620.312 | 15.384 | 16.358 | 15.254 | 15.487 | 16.658 | 17.511 |
| 5 | 6055.57 | 5705.566 | 5798.456 | 4523.577 | 2898.492 | 1024.09 | 16.501 | 16.512 | 16.652 | 16.126 | 17.145 | 17.251 | |
| 8 | 6043.572 | 5022.563 | 5790.663 | 4595.554 | 3785.498 | 2784.526 | 16.726 | 17.241 | 17.841 | 17.385 | 17.374 | 18.566 | |
| 12 | 6030.843 | 5774.451 | 4868.256 | 5455.256 | 3895.2 | 2795.253 | 17.595 | 17.685 | 18.124 | 17.841 | 17.795 | 18.525 | |
| 5 | 2 | 6009.567 | 5778.348 | 4767.345 | 5686.456 | 3997.353 | 2976.182 | 16.518 | 17.228 | 18.105 | 19.425 | 16.14 | 12.635 |
| 5 | 6754.345 | 5845.902 | 4890.567 | 5589.456 | 3882.659 | 2935.967 | 18.784 | 17.742 | 18.452 | 19.984 | 18.133 | 18.971 | |
| 8 | 5600.565 | 6667.156 | 4808.123 | 5445.686 | 2889.189 | 2885.16 | 20.265 | 20.655 | 20.845 | 21.458 | 21.508 | 21.682 | |
| 12 | 6600.028 | 6664.432 | 4789.526 | 6430.256 | 2850.263 | 2850.263 | 21.476 | 21.982 | 21.125 | 21.845 | 21.826 | 21.842 | |
| Images | m | SSIM | FSIM | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MFA | MBFO | JADE | MPSO | MABC | MCS | MFA | MBFO | JADE | MPSO | MABC | MCS | ||
| 1 | 2 | 0.8124 | 0.8457 | 0.8135 | 0.8263 | 0.8617 | 0.8634 | 0.8676 | 0.8732 | 0.8721 | 0.8851 | 0.8802 | 0.8915 |
| 5 | 0.8235 | 0.8569 | 0.8257 | 0.8346 | 0.858 | 0.8479 | 0.8632 | 0.8643 | 0.8754 | 0.882 | 0.8831 | 0.8965 | |
| 8 | 0.8568 | 0.869 | 0.839 | 0.8391 | 0.8876 | 0.8735 | 0.8689 | 0.8698 | 0.8798 | 0.8807 | 0.8831 | 0.8971 | |
| 12 | 0.8616 | 0.8701 | 0.8399 | 0.8413 | 0.8813 | 0.8822 | 0.8652 | 0.8618 | 0.875 | 0.8818 | 0.8902 | 0.8979 | |
| 2 | 2 | 0.8268 | 0.8145 | 0.8299 | 0.8593 | 0.8239 | 0.8817 | 0.8655 | 0.8654 | 0.8778 | 0.8854 | 0.8875 | 0.8842 |
| 5 | 0.8569 | 0.8458 | 0.8346 | 0.8992 | 0.8547 | 0.8653 | 0.8647 | 0.8656 | 0.8798 | 0.8889 | 0.8853 | 0.8827 | |
| 8 | 0.869 | 0.859 | 0.8457 | 0.8035 | 0.876 | 0.882 | 0.8698 | 0.8643 | 0.8876 | 0.8821 | 0.8871 | 0.8894 | |
| 12 | 0.8715 | 0.8591 | 0.8485 | 0.8126 | 0.878 | 0.8883 | 0.8625 | 0.8625 | 0.889 | 0.8852 | 0.8852 | 0.8956 | |
| 3 | 2 | 0.8666 | 0.859 | 0.8593 | 0.8491 | 0.8656 | 0.8074 | 0.8643 | 0.8657 | 0.8754 | 0.8854 | 0.873 | 0.8975 |
| 5 | 0.8679 | 0.8247 | 0.8992 | 0.851 | 0.8357 | 0.8997 | 0.8654 | 0.869 | 0.8876 | 0.8865 | 0.8815 | 0.8979 | |
| 8 | 0.879 | 0.8239 | 0.8035 | 0.863 | 0.8505 | 0.8727 | 0.8665 | 0.8667 | 0.8887 | 0.8876 | 0.8947 | 0.892 | |
| 12 | 0.8113 | 0.8246 | 0.8145 | 0.8715 | 0.8585 | 0.8756 | 0.8662 | 0.8652 | 0.8821 | 0.8842 | 0.8952 | 0.8952 | |
| 4 | 2 | 0.8025 | 0.8079 | 0.8246 | 0.8257 | 0.8244 | 0.8065 | 0.8665 | 0.8676 | 0.8807 | 0.8832 | 0.8898 | 0.8929 |
| 5 | 0.8125 | 0.8235 | 0.836 | 0.8379 | 0.8545 | 0.8704 | 0.8654 | 0.8665 | 0.8803 | 0.8843 | 0.8831 | 0.8945 | |
| 8 | 0.8346 | 0.8368 | 0.8399 | 0.8457 | 0.8784 | 0.8805 | 0.8665 | 0.8689 | 0.8868 | 0.8821 | 0.8878 | 0.8947 | |
| 12 | 0.8413 | 0.8413 | 0.8413 | 0.8476 | 0.8813 | 0.8813 | 0.8662 | 0.8661 | 0.8821 | 0.8884 | 0.8921 | 0.8993 | |
| 5 | 2 | 0.8868 | 0.8322 | 0.8683 | 0.8681 | 0.8516 | 0.8229 | 0.9878 | 0.8631 | 0.8893 | 0.8854 | 0.8951 | 0.8927 |
| 5 | 0.8868 | 0.8824 | 0.8613 | 0.8689 | 0.8641 | 0.8839 | 0.9867 | 0.8643 | 0.8745 | 0.8889 | 0.892 | 0.8987 | |
| 8 | 0.8924 | 0.8913 | 0.8645 | 0.8802 | 0.8893 | 0.8901 | 0.9978 | 0.8621 | 0.8847 | 0.8876 | 0.899 | 0.8928 | |
| 12 | 0.8953 | 0.8926 | 0.8701 | 0.8623 | 0.889 | 0.8919 | 0.9995 | 0.8685 | 0.8858 | 0.8817 | 0.8982 | 0.8965 | |
| Images | m | GLCM | Rényi’s Entropy | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MFA | MBFO | JADE | MPSO | MABC | MCS | MFA | MBFO | JADE | MPSO | MABC | MCS | ||
| 1 | 2 | 16.339 | 10.562 | 10.047 | 15.824 | 16.026 | 12.114 | 8.072 | 12.826 | 4.728 | 10.562 | 5.625 | 2.159 |
| 5 | 20.135 | 12.654 | 11.111 | 16.327 | 17.042 | 15.821 | 6.149 | 12.44 | 4.79 | 12.654 | 6.541 | 2.635 | |
| 8 | 20.811 | 15.854 | 12.321 | 17.21 | 17.667 | 18.5 | 8.207 | 15.441 | 4.002 | 14.854 | 6.521 | 2.628 | |
| 12 | 23.697 | 14.512 | 17.152 | 18.867 | 18.57 | 18.214 | 9.807 | 16.511 | 7.933 | 14.854 | 7.175 | 2.109 | |
| 2 | 2 | 15.867 | 10.224 | 10.15 | 11.845 | 11.709 | 14.54 | 6.145 | 12.006 | 3.429 | 12.115 | 8.224 | 4.62 |
| 5 | 20.475 | 11.652 | 11.472 | 15.327 | 14.962 | 16.469 | 6.629 | 13.823 | 4.762 | 14.652 | 8.345 | 4.216 | |
| 8 | 26.972 | 15.521 | 12.14 | 15.21 | 16.922 | 15.403 | 6.151 | 15.28 | 6.366 | 15.502 | 9.098 | 4.549 | |
| 12 | 24.21 | 16.798 | 15.667 | 17.867 | 18.846 | 16.098 | 7.812 | 15.422 | 7.84 | 17.798 | 8.968 | 4.402 | |
| 3 | 2 | 20.988 | 11.658 | 12.42 | 15.066 | 15.913 | 13.514 | 4.738 | 10.37 | 4.574 | 11.658 | 8.294 | 6.642 |
| 5 | 20.994 | 12.851 | 12.31 | 15.262 | 16.154 | 16.915 | 4.266 | 13.854 | 4.657 | 12.851 | 5.106 | 6.284 | |
| 8 | 22.007 | 12.521 | 14.572 | 15.964 | 16.409 | 19.745 | 9.863 | 18.074 | 4.417 | 12.521 | 8.856 | 6.569 | |
| 12 | 24.006 | 16.425 | 19.245 | 17.847 | 18.739 | 20.632 | 7.125 | 19.198 | 8.521 | 14.425 | 8.227 | 6.512 | |
| 4 | 2 | 16.137 | 21.652 | 20.089 | 13.468 | 15.14 | 10.981 | 9.145 | 11.751 | 5.844 | 11.652 | 9.492 | 2.254 |
| 5 | 20.905 | 21.465 | 25.768 | 15.685 | 16.995 | 13.351 | 7.447 | 14.792 | 5.256 | 15.465 | 9.326 | 2.502 | |
| 8 | 26.643 | 24.487 | 25.721 | 15.51 | 17.824 | 16.009 | 8.534 | 19.098 | 5.854 | 15.487 | 10.429 | 3.201 | |
| 12 | 26.443 | 24.854 | 26.016 | 16.811 | 18.35 | 11.098 | 6.082 | 20.806 | 7.251 | 16.854 | 10.593 | 3.872 | |
| 5 | 2 | 17.001 | 20.285 | 21.335 | 14.253 | 10.448 | 12.264 | 6.315 | 14.348 | 5.685 | 12.285 | 9.194 | 6.598 |
| 5 | 20.143 | 20.285 | 21.389 | 15.586 | 12.248 | 17.662 | 7.723 | 14.371 | 5.286 | 13.285 | 9.476 | 6.625 | |
| 8 | 20.729 | 21.865 | 23.612 | 15.452 | 17.845 | 18.624 | 9.085 | 17.097 | 5.546 | 14.865 | 10.379 | 6.514 | |
| 12 | 22.749 | 22.825 | 23.971 | 18.869 | 19.541 | 20.241 | 9.962 | 20.993 | 7.512 | 18.825 | 10.399 | 6.486 | |
| Images | m | MSE | PSNR | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MFA | MBFO | JADE | MPSO | MABC | MCS | MFA | MBFO | JADE | MPSO | MABC | MCS | ||
| 1 | 2 | 865.232 | 886.415 | 956.218 | 945.524 | 967.732 | 926.266 | 20.613 | 20.232 | 20.146 | 21.246 | 23.81 | 23.262 |
| 5 | 856.557 | 826.473 | 925.846 | 906.246 | 967.318 | 927.666 | 21.796 | 21.446 | 20.153 | 21.876 | 24.143 | 24.486 | |
| 8 | 875.129 | 869.014 | 956.581 | 952.516 | 965.902 | 918.006 | 22.485 | 22.569 | 21.569 | 22.252 | 22.979 | 25.126 | |
| 12 | 869.238 | 874.206 | 924.852 | 914.308 | 911.564 | 800.634 | 22.396 | 22.176 | 21.176 | 22.462 | 22.866 | 25.533 | |
| 2 | 2 | 867.378 | 814.541 | 965.564 | 956.254 | 913.624 | 962.473 | 23.927 | 23.246 | 23.715 | 22.545 | 23.184 | 24.543 |
| 5 | 876.218 | 829.543 | 995.147 | 965.658 | 961.89 | 914.235 | 23.626 | 24.252 | 24.585 | 23.459 | 23.919 | 25.519 | |
| 8 | 861.51 | 856.218 | 921.653 | 926.513 | 996.961 | 909.284 | 24.136 | 24.487 | 25.226 | 23.78 | 25.106 | 25.515 | |
| 12 | 864.609 | 889.812 | 977.524 | 974.521 | 967.213 | 996.329 | 24.173 | 25.114 | 25.366 | 24.597 | 25.439 | 25.636 | |
| 3 | 2 | 878.573 | 814.879 | 916.73 | 927.842 | 916.531 | 969.429 | 21.326 | 21.533 | 19.124 | 20.835 | 22.654 | 25.136 |
| 5 | 826.673 | 896.982 | 917.218 | 914.437 | 937.234 | 997.182 | 21.529 | 20.429 | 19.482 | 21.857 | 23.126 | 22.176 | |
| 8 | 876.657 | 876.463 | 976.743 | 996.945 | 951.356 | 909.779 | 21.063 | 20.565 | 20.446 | 21.897 | 25.939 | 25.487 | |
| 12 | 895.586 | 861.518 | 966.218 | 906.212 | 996.621 | 922.851 | 21.587 | 22.493 | 20.772 | 21.492 | 25.466 | 25.517 | |
| 4 | 2 | 856.731 | 863.752 | 996.642 | 962.541 | 985.652 | 912.13 | 23.835 | 24.539 | 23.525 | 23.848 | 24.569 | 25.152 |
| 5 | 966.759 | 806.656 | 909.657 | 934.752 | 909.943 | 935.102 | 24.052 | 24.153 | 24.563 | 24.217 | 25.416 | 25.522 | |
| 8 | 954.753 | 823.659 | 901.665 | 906.555 | 996.949 | 995.257 | 24.277 | 25.422 | 25.482 | 25.836 | 25.735 | 26.657 | |
| 12 | 941.484 | 885.547 | 979.527 | 956.527 | 906.021 | 906.524 | 25.956 | 25.866 | 26.215 | 25.482 | 25.976 | 26.256 | |
| 5 | 2 | 910.658 | 889.436 | 978.436 | 997.547 | 997.534 | 987.813 | 24.159 | 25.229 | 26.016 | 27.246 | 24.411 | 20.366 |
| 5 | 965.436 | 856.09 | 901.658 | 990.547 | 993.56 | 946.698 | 26.784 | 25.473 | 26.543 | 27.895 | 26.314 | 26.792 | |
| 8 | 911.656 | 878.517 | 919.214 | 956.867 | 980.81 | 996.611 | 18.265 | 18.566 | 18.486 | 19.549 | 19.059 | 19.863 | |
| 12 | 911.209 | 875.347 | 990.257 | 942.527 | 961.624 | 961.624 | 19.476 | 19.893 | 19.216 | 19.486 | 19.287 | 19.483 | |
| Images | m | SSIM | FSIM | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MFA | MBFO | JADE | MPSO | MABC | MCS | MFA | MBFO | JADE | MPSO | MABC | MCS | ||
| 1 | 2 | 0.7823 | 0.8457 | 0.8144 | 0.8661 | 0.9521 | 0.9521 | 0.8533 | 0.8622 | 0.8325 | 0.9724 | 0.9801 | 0.9825 |
| 5 | 0.7834 | 0.8568 | 0.8276 | 0.8645 | 0.9536 | 0.9567 | 0.8644 | 0.8656 | 0.8312 | 0.9702 | 0.9813 | 0.9846 | |
| 8 | 0.7867 | 0.8687 | 0.838 | 0.869 | 0.9542 | 0.9534 | 0.8799 | 0.8699 | 0.838 | 0.977 | 0.9804 | 0.9871 | |
| 12 | 0.7885 | 0.8705 | 0.8388 | 0.8692 | 0.955 | 0.9601 | 0.8991 | 0.8715 | 0.8381 | 0.9781 | 0.9825 | 0.9597 | |
| 2 | 2 | 0.8067 | 0.817 | 0.8298 | 0.8612 | 0.9504 | 0.9526 | 0.8755 | 0.8597 | 0.8555 | 0.9745 | 0.9867 | 0.9894 |
| 5 | 0.8068 | 0.8456 | 0.8355 | 0.8641 | 0.9518 | 0.9601 | 0.8875 | 0.8799 | 0.8608 | 0.9788 | 0.9865 | 0.9873 | |
| 8 | 0.8089 | 0.8586 | 0.8446 | 0.8634 | 0.9526 | 0.9621 | 0.8844 | 0.8807 | 0.8723 | 0.9732 | 0.9827 | 0.9889 | |
| 12 | 0.8114 | 0.8595 | 0.8474 | 0.8625 | 0.9564 | 0.9622 | 0.8962 | 0.8899 | 0.8835 | 0.9735 | 0.9835 | 0.9895 | |
| 3 | 2 | 0.7965 | 0.8083 | 0.8682 | 0.841 | 0.9587 | 0.9615 | 0.8254 | 0.8155 | 0.8355 | 0.9755 | 0.9803 | 0.9867 |
| 5 | 0.7978 | 0.8244 | 0.8391 | 0.8529 | 0.9563 | 0.9624 | 0.8319 | 0.8477 | 0.8466 | 0.9766 | 0.9841 | 0.9808 | |
| 8 | 0.7989 | 0.8237 | 0.8264 | 0.8639 | 0.9546 | 0.9629 | 0.8389 | 0.8588 | 0.8577 | 0.9777 | 0.9864 | 0.9813 | |
| 12 | 0.7912 | 0.8246 | 0.8294 | 0.8724 | 0.9587 | 0.9734 | 0.8399 | 0.8622 | 0.8534 | 0.9734 | 0.9875 | 0.9835 | |
| 4 | 2 | 0.7924 | 0.8075 | 0.8255 | 0.8255 | 0.9518 | 0.9645 | 0.9268 | 0.8497 | 0.8433 | 0.9713 | 0.986 | 0.9849 |
| 5 | 0.7924 | 0.8232 | 0.8369 | 0.8377 | 0.9526 | 0.9635 | 0.9366 | 0.8523 | 0.8544 | 0.9743 | 0.984 | 0.9864 | |
| 8 | 0.7945 | 0.8369 | 0.8308 | 0.8455 | 0.9546 | 0.9621 | 0.9499 | 0.8587 | 0.8622 | 0.9732 | 0.9876 | 0.9884 | |
| 12 | 0.7912 | 0.8416 | 0.8422 | 0.8474 | 0.9554 | 0.9643 | 0.9527 | 0.8622 | 0.8658 | 0.9758 | 0.9832 | 0.9892 | |
| 5 | 2 | 0.7967 | 0.8521 | 0.8672 | 0.8559 | 0.9515 | 0.9648 | 0.9824 | 0.8825 | 0.8855 | 0.9785 | 0.9849 | 0.9782 |
| 5 | 0.7967 | 0.8523 | 0.8622 | 0.8595 | 0.964 | 0.9685 | 0.9845 | 0.8912 | 0.8808 | 0.9788 | 0.9845 | 0.9783 | |
| 8 | 0.7923 | 0.8512 | 0.8652 | 0.8623 | 0.9648 | 0.9684 | 0.9923 | 0.8991 | 0.8977 | 0.9777 | 0.9874 | 0.9883 | |
| 12 | 0.7952 | 0.8525 | 0.8712 | 0.8621 | 0.9679 | 0.9712 | 0.9969 | 0.8981 | 0.8981 | 0.9781 | 0.9877 | 0.9846 | |
| Images | m | MSE | PSNR | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MFA | MBFO | JADE | MPSO | MABC | MCS | MFA | MBFO | JADE | MPSO | MABC | MCS | ||
| 1 | 2 | 754.122 | 575.149 | 745.428 | 845.252 | 815.625 | 256.377 | 22.262 | 22.421 | 22.515 | 23.525 | 25.289 | 27.662 |
| 5 | 745.547 | 415.747 | 895.486 | 695.428 | 516.667 | 256.134 | 23.075 | 23.585 | 22.612 | 23.845 | 26.512 | 26.945 | |
| 8 | 564.125 | 658.105 | 645.857 | 641.156 | 408.008 | 254.098 | 24.944 | 24.758 | 23.758 | 24.621 | 25.898 | 27.315 | |
| 12 | 658.328 | 563.029 | 513.586 | 603.037 | 300.362 | 200.656 | 24.035 | 24.815 | 23.815 | 24.741 | 25.985 | 27.452 | |
| 2 | 2 | 856.737 | 603.457 | 654.654 | 945.526 | 651.748 | 202.267 | 25.396 | 25.525 | 25.815 | 24.654 | 25.913 | 26.552 |
| 5 | 765.123 | 718.456 | 684.418 | 654.564 | 103.327 | 250.888 | 25.365 | 26.621 | 26.954 | 25.648 | 25.298 | 27.258 | |
| 8 | 645.151 | 845.124 | 710.565 | 715.155 | 198.826 | 285.694 | 26.415 | 26.946 | 27.325 | 25.979 | 27.115 | 27.254 | |
| 12 | 453.068 | 878.009 | 766.254 | 563.252 | 285.234 | 256.126 | 26.812 | 27.213 | 27.735 | 26.056 | 27.448 | 27.465 | |
| 3 | 2 | 567.754 | 803.783 | 805.373 | 416.485 | 658.248 | 205.357 | 23.335 | 23.452 | 21.313 | 22.484 | 24.663 | 29.415 |
| 5 | 715.762 | 885.898 | 806.127 | 803.348 | 486.817 | 126.325 | 23.358 | 24.348 | 21.941 | 23.686 | 25.315 | 24.815 | |
| 8 | 665.565 | 865.643 | 865.475 | 785.497 | 398.779 | 140.537 | 23.702 | 24.754 | 22.545 | 23.086 | 28.498 | 27.946 | |
| 12 | 684.857 | 850.157 | 966.124 | 795.123 | 411.585 | 185.265 | 23.956 | 24.942 | 22.871 | 23.041 | 28.745 | 27.256 | |
| 4 | 2 | 745.378 | 852.575 | 985.465 | 951.454 | 620.316 | 285.561 | 25.484 | 26.458 | 25.354 | 25.587 | 26.758 | 27.611 |
| 5 | 645.57 | 895.564 | 798.456 | 523.575 | 224.094 | 298.492 | 26.601 | 26.612 | 26.752 | 26.226 | 27.245 | 27.351 | |
| 8 | 643.572 | 912.568 | 790.663 | 895.554 | 284.525 | 285.498 | 26.826 | 27.341 | 27.941 | 27.485 | 27.474 | 28.666 | |
| 12 | 630.843 | 874.456 | 868.256 | 745.256 | 295.254 | 295.2 | 27.695 | 27.785 | 28.224 | 27.941 | 27.895 | 28.625 | |
| 5 | 2 | 709.567 | 878.345 | 767.345 | 686.456 | 276.187 | 297.353 | 26.518 | 27.228 | 28.105 | 27.425 | 26.14 | 28.635 |
| 5 | 654.345 | 745.909 | 890.567 | 589.456 | 235.968 | 282.659 | 28.784 | 27.742 | 28.452 | 27.984 | 28.133 | 28.971 | |
| 8 | 500.565 | 567.156 | 808.123 | 445.686 | 885.162 | 289.189 | 28.265 | 28.655 | 28.845 | 27.458 | 28.508 | 28.682 | |
| 12 | 500.028 | 564.436 | 789.526 | 430.256 | 850.268 | 250.263 | 28.476 | 28.982 | 28.125 | 27.845 | 28.826 | 28.842 | |
| Images | m | SSIM | FSIM | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MFA | MBFO | JADE | MPSO | MABC | MCS | MFA | MBFO | JADE | MPSO | MABC | MCS | ||
| 1 | 2 | 0.8523 | 0.8466 | 0.8244 | 0.8361 | 0.9806 | 0.9835 | 0.8567 | 0.9577 | 0.9623 | 0.9622 | 0.9814 | 0.9915 |
| 5 | 0.8234 | 0.8678 | 0.8266 | 0.8355 | 0.9879 | 0.9878 | 0.8523 | 0.9513 | 0.9643 | 0.9655 | 0.9923 | 0.9966 | |
| 8 | 0.8267 | 0.8699 | 0.8499 | 0.838 | 0.9875 | 0.9834 | 0.8598 | 0.9588 | 0.9669 | 0.9699 | 0.9901 | 0.9927 | |
| 12 | 0.8315 | 0.8812 | 0.8399 | 0.8422 | 0.9832 | 0.9881 | 0.8525 | 0.9535 | 0.9671 | 0.9615 | 0.9822 | 0.9996 | |
| 2 | 2 | 0.8267 | 0.8234 | 0.8208 | 0.8302 | 0.9837 | 0.9836 | 0.8634 | 0.9565 | 0.9655 | 0.9677 | 0.9867 | 0.9934 |
| 5 | 0.8468 | 0.8567 | 0.8355 | 0.8381 | 0.9836 | 0.9864 | 0.8644 | 0.9584 | 0.9645 | 0.9699 | 0.9945 | 0.9982 | |
| 8 | 0.8389 | 0.8699 | 0.8466 | 0.8544 | 0.985 | 0.9839 | 0.8652 | 0.9579 | 0.9648 | 0.9677 | 0.9927 | 0.9949 | |
| 12 | 0.8414 | 0.868 | 0.8494 | 0.8532 | 0.9869 | 0.9883 | 0.8659 | 0.9542 | 0.9652 | 0.9689 | 0.9935 | 0.9965 | |
| 3 | 2 | 0.8665 | 0.829 | 0.8502 | 0.858 | 0.9845 | 0.9883 | 0.8634 | 0.9524 | 0.9655 | 0.9635 | 0.9813 | 0.9968 |
| 5 | 0.8678 | 0.8336 | 0.8901 | 0.8529 | 0.9846 | 0.9898 | 0.8645 | 0.9535 | 0.9619 | 0.9687 | 0.9861 | 0.9907 | |
| 8 | 0.8489 | 0.8348 | 0.8524 | 0.8639 | 0.9813 | 0.9836 | 0.8656 | 0.9546 | 0.9686 | 0.9687 | 0.9884 | 0.9912 | |
| 12 | 0.8412 | 0.8352 | 0.8254 | 0.8724 | 0.9894 | 0.9865 | 0.8626 | 0.9516 | 0.9635 | 0.9622 | 0.9935 | 0.9935 | |
| 4 | 2 | 0.8824 | 0.8368 | 0.8255 | 0.8366 | 0.9833 | 0.9864 | 0.9246 | 0.9546 | 0.9967 | 0.9687 | 0.988 | 0.9949 |
| 5 | 0.8824 | 0.8344 | 0.8469 | 0.8388 | 0.9834 | 0.9714 | 0.9245 | 0.9535 | 0.9666 | 0.9623 | 0.984 | 0.9964 | |
| 8 | 0.8845 | 0.8457 | 0.8408 | 0.8466 | 0.9873 | 0.9713 | 0.9254 | 0.9546 | 0.9678 | 0.9687 | 0.9896 | 0.9984 | |
| 12 | 0.8812 | 0.8402 | 0.8522 | 0.8465 | 0.9879 | 0.9712 | 0.9236 | 0.9536 | 0.9626 | 0.9622 | 0.9823 | 0.9901 | |
| 5 | 2 | 0.8867 | 0.8202 | 0.8782 | 0.869 | 0.9823 | 0.9883 | 0.9278 | 0.9588 | 0.9623 | 0.9625 | 0.9849 | 0.9982 |
| 5 | 0.8867 | 0.8301 | 0.8722 | 0.8698 | 0.983 | 0.9849 | 0.9267 | 0.9577 | 0.9644 | 0.9612 | 0.9864 | 0.9988 | |
| 8 | 0.8923 | 0.8329 | 0.8752 | 0.8821 | 0.9882 | 0.9904 | 0.9278 | 0.9568 | 0.9622 | 0.968 | 0.9884 | 0.9983 | |
| 12 | 0.8952 | 0.8395 | 0.8812 | 0.8732 | 0.9889 | 0.9939 | 0.9295 | 0.9589 | 0.9668 | 0.9672 | 0.9895 | 0.9986 | |
References
- Sezgin, M.; Sankur, B. Survey over image thresholding techniques and quantitative performance evaluation. J. Electron. Imaging 2004, 13, 146–165. [Google Scholar]
- Pun, T. New method for gray-level picture thresholding using the entropy of the histogram. Signal Process. 1980, 2, 223–237. [Google Scholar] [CrossRef]
- Kapur, J.N.; Sahoo, P.K.; Wong, A.K.C. New method for gray-level picture thresholding using the entropy of the histogram. Comput. Vis. Graph. Image Process 1985, 29, 273–285. [Google Scholar] [CrossRef]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef] [Green Version]
- Kittler, J.; Illingworth, J. Minimum error thresholding. Pattern Recognit. 1986, 19, 41–47. [Google Scholar] [CrossRef]
- De Albuquerque, M.P.; Esquef, I.; Mello, A.G. Image thresholding using Tsallis entropy. Pattern Recognit. Lett. 2004, 25, 1059–1065. [Google Scholar] [CrossRef]
- Li, C.; Lee, C. Minimum cross entropy thresholding. Pattern Recognit. 1993, 26, 617–625. [Google Scholar] [CrossRef]
- Lim, Y.K.; Lee, S.U. On the color image segmentation algorithm based on the thresholding and the fuzzy c-means techniques. Pattern Recognit. 1990, 23, 935–952. [Google Scholar]
- Sahoo, P.; Wilkins, C.; Yeager, J. Threshold selection using Rényi’s entropy. Pattern Recognit. 1997, 30, 71–84. [Google Scholar] [CrossRef]
- Yen, J.C.; Chang, F.-J.; Chang, S. A new criterion for automatic multilevel thresholding. IEEE Trans. Image Process. 1995, 4, 370–378. [Google Scholar]
- Srikanth, R.; Bikshalu, K. Multilevel thresholding image segmentation based on energy curve with harmony Search Algorithm. Ain Shams Eng. J. 2021, 12, 1–20. [Google Scholar] [CrossRef]
- Choudhury, A.; Samanta, S.; Pratihar, S.; Bandyopadhyay, O. Multilevel segmentation of Hippocampus images using global steered quantum inspired firefly algorithm. Appl. Intell. 2021, 1–34. [Google Scholar] [CrossRef]
- Kalyani, R.; Sathya, P.D.; Sakthivel, V.P. Image segmentation with Kapur, Otsu and minimum cross entropy based multilevel thresholding aided with cuckoo search algorithm. IOP Conf. Ser. : Mater. Sci. Eng. 2021, 1119, 012019. [Google Scholar] [CrossRef]
- Liang, H.; Jia, H.; Xing, Z.; Ma, J.; Peng, X. Modified Grasshopper Algorithm-Based Multilevel Thresholding for Color Image Segmentation. IEEE Access 2019, 7, 11258–11295. [Google Scholar] [CrossRef]
- Kurban, R.; Durmus, A.; Karakose, E. A comparison of novel metaheuristic algorithms on color aerial image multilevel thresholding. Eng. Appl. Artif. Intell. 2021, 105, 104410. [Google Scholar] [CrossRef]
- Elaziz, M.A.; Ewees, A.A.; Oliva, D. Hyper-heuristic method for multilevel thresholding image segmentation. Expert Syst. Appl. 2020, 146, 113201. [Google Scholar] [CrossRef]
- Xiong, L.; Zhang, D.; Li, K.; Zhang, L. The extraction algorithm of color disease spot image based on Otsu and watershed. Soft Comput. 2019, 24, 7253–7263. [Google Scholar] [CrossRef]
- Xiong, L.; Chen, R.S.; Zhou, X.; Jing, C. Multi-feature fusion and selection method for an improved particle swarm optimization. J. Ambient Intell. Humaniz. Comput. 2019, 1–10. [Google Scholar] [CrossRef]
- Horng, M.-H. Multilevel thresholding selection based on the artificial bee colony algorithm for image segmentation. Expert Syst. Appl. 2011, 38, 13785–13791. [Google Scholar] [CrossRef]
- Suresh, S.; Lal, S. An efficient cuckoo search algorithm based multilevel thresholding for segmentation of satellite images using different objective functions. Expert Syst. Appl. 2016, 58, 184–209. [Google Scholar] [CrossRef]
- Chakraborty, R.; Sushil, R.; Garg, M.L. Hyper-spectral image segmentation using an improved PSO aided with multilevel fuzzy entropy. Multimed. Tools Appl. 2019, 78, 34027–34063. [Google Scholar] [CrossRef]
- Tan, Z.; Zhang, D. A fuzzy adaptive gravitational search algorithm for two-dimensional multilevel thresholding image segmentation. J. Ambient. Intell. Humaniz. Comput. 2020, 11, 4983–4994. [Google Scholar] [CrossRef]
- Bao, X.; Jia, H.; Lang, C. A Novel Hybrid Harris Hawks Optimization for Color Image Multilevel Thresholding Segmentation. IEEE Access 2019, 7, 76529–76546. [Google Scholar] [CrossRef]
- Hemeida, A.M.; Mansour, R.; Hussein, M.E. Multilevel thresholding for image segmentation using an improved electromagnetism optimization algorithm. IJIMAI 2019, 5, 102–112. [Google Scholar] [CrossRef]
- Kotte, S.; Pullakura, R.K.; Injeti, S.K. Optimal multilevel thresholding selection for brain MRI image segmentation based on adaptive wind driven optimization. Measurement 2018, 130, 340–361. [Google Scholar] [CrossRef]
- Upadhyay, P.; Chhabra, J.K. Kapur’s entropy based optimal multilevel image segmentation using Crow Search Algorithm. Appl. Soft Comput. 2019, 97, 105522. [Google Scholar] [CrossRef]
- Li, K.; Tan, Z. An Improved Flower Pollination Optimizer Algorithm for Multilevel Image Thresholding. IEEE Access 2019, 7, 165571–165582. [Google Scholar] [CrossRef]
- Erwin, S.; Saputri, W. Hybrid multilevel thresholding and improved harmony search algorithm for segmentation. Int. J. Electr. Comput. Eng. 2018, 8, 4593–4602. [Google Scholar] [CrossRef]
- Xing, Z. An improved emperor penguin optimization based multilevel thresholding for color image segmentation. Knowl. -Based Syst. 2020, 194, 105570. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.S.; Alavi, A.H. Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems. Eng. Comput. 2013, 29, 17–35. [Google Scholar] [CrossRef]
- El Aziz, M.A.; Hassanien, A.E. Modified cuckoo search algorithm with rough sets for feature selection. Neural Comput. Appl. 2016, 29, 925–934. [Google Scholar] [CrossRef]
- Thirugnanasambandam, K.; Prakash, S.; Subramanian, V.; Pothula, S.; Thirumal, V. Reinforced cuckoo search algorithm-based multimodal optimization. Appl. Intell. 2019, 49, 2059–2083. [Google Scholar] [CrossRef]
- Boushaki, S.I.; Kamel, N.; Bendjeghaba, O. A new quantum chaotic cuckoo search algorithm for data clustering. Expert Syst. Appl. 2018, 96, 358–372. [Google Scholar] [CrossRef]
- Mondal, A.; Dey, N.; Ashour, A.S. Cuckoo Search and Its Variants in Digital Image Processing: A Comprehensive Review. In Applications of Cuckoo Search Algorithm and Its Variants; Springer: Berlin/Heidelberg, Germany, 2021; pp. 1–20. [Google Scholar]
- Jia, H.; Lang, C.; Oliva, D.; Song, W.; Peng, X. Dynamic Harris Hawks Optimization with Mutation Mechanism for Satellite Image Segmentation. Remote Sens. 2019, 11, 1421. [Google Scholar] [CrossRef] [Green Version]
- Pal, P.; Bhattacharyya, S.; Agrawal, N. Grayscale Image Segmentation with Quantum-Inspired Multilayer Self-Organizing Neural Network Architecture Endorsed by Context Sensitive Thresholding. In Research Anthology on Advancements in Quantum Technology; IGI Global: Hershey, PA, USA, 2021; pp. 197–227. [Google Scholar]
- Wu, B.; Zhou, J.; Ji, X.; Yin, Y.; Shen, X. An ameliorated teaching–learning-based optimization algorithm based study of image segmentation for multilevel thresholding using Kapur’s entropy and Otsu’s between class variance. Inf. Sci. 2020, 533, 72–107. [Google Scholar] [CrossRef]
- Naik, M.K.; Panda, R.; Abraham, A. An opposition equilibrium optimizer for context-sensitive entropy dependency based multilevel thresholding of remote sensing images. Swarm Evol. Comput. 2021, 65, 100907. [Google Scholar] [CrossRef]
- Kaur, T.; Saini, B.S.; Gupta, S. Optimized multi threshold brain tumor image segmentation using two dimensional minimum cross entropy based on co-occurrence matrix. In Medical Imaging in Clinical Applications; Springer: Cham, Switzerland, 2016; Volume 651, pp. 461–486. [Google Scholar]
- Pare, S.; Prasad, M.; Puthal, D.; Gupta, D.; Malik, A.; Saxena, A. Multilevel Color Image Segmentation using Modified Fuzzy Entropy and Cuckoo Search Algorithm. In Proceedings of the IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Luxembourg, 11–14 July 2021; pp. 1–7. [Google Scholar]
- Abed, H.I. Image segmentation with a multilevel threshold using backtracking search optimization algorithm. Tikrit J. Pure Sci. 2020, 25, 102–109. [Google Scholar] [CrossRef]
- Zhao, S.; Wang, P.; Heidari, A.A.; Chen, H.; Turabieh, H.; Mafarja, M.; Li, C. Multilevel threshold image segmentation with diffusion association slime mould algorithm and Renyi’s entropy for chronic obstructive pulmonary disease. Comput. Biol. Med. 2021, 134, 104427. [Google Scholar] [CrossRef]
- Liu, W.; Huang, Y.; Ye, Z.; Cai, W.; Yang, S.; Cheng, X.; Frank, I. Renyi’s Entropy Based Multilevel Thresholding Using a Novel Meta-Heuristics Algorithm. Appl. Sci. 2020, 10, 3225. [Google Scholar] [CrossRef]
- Manohar, V.; Laxminarayana, G.; Savithri, T.S. Image compression using explored bat algorithm by Renyi 2-d histogram based on multilevel thresholding. Evol. Intell. 2019, 14, 75–85. [Google Scholar] [CrossRef]
- Borjigin, S.; Sahoo, P.K. Color image segmentation based on multilevel Tsallis–Havrda–Charvát entropy and 2D histogram using PSO algorithms. Pattern Recognit. 2019, 92, 107–118. [Google Scholar] [CrossRef]
- He, L.; Huang, S. Modified firefly algorithm based multilevel thresholding for color image segmentation. Neurocomputing 2017, 240, 152–174. [Google Scholar] [CrossRef]
- Sathya, P.; Kayalvizhi, R. Modified bacterial foraging algorithm based multilevel thresholding for image segmentation. Eng. Appl. Artif. Intell. 2011, 24, 595–615. [Google Scholar] [CrossRef]
- Zhang, J.; Sanderson, A.C. JADE: Adaptive Differential Evolution With Optional External Archive. IEEE Trans. Evol. Comput. 2009, 13, 945–958. [Google Scholar] [CrossRef]
- Liu, Y.; Mu, C.; Kou, W.; Liu, J. Modified particle swarm optimization-based multilevel thresholding for image segmentation. Soft Comput. 2015, 19, 1311–1327. [Google Scholar] [CrossRef]
- Zhang, S.; Jiang, W.; Satoh, S. Multilevel Thresholding Color Image Segmentation Using a Modified Artificial Bee Colony Algorithm. IEICE Trans. Inf. Syst. 2018, 101, 2064–2071. [Google Scholar] [CrossRef] [Green Version]
- Baraldi, A.; Panniggiani, F. An investigation of the textural characteristics associated with gray level co-occurrenceco-occurrence matrix statistical parameters. IEEE Trans. Geosci. Remote Sens. 1995, 33, 293–304. [Google Scholar] [CrossRef]
- Kalyani, R.; Sathya, P.D.; Sakthivel, V.P. Multilevel thresholding for image segmentation with exchange market algorithm. Multimed. Tools Appl. 2021, 1, 1–39. [Google Scholar] [CrossRef]
- Walton, S.; Hassan, O.; Morgan, K.; Brown, R. Modified cuckoo search: A new gradient free optimisation algorithm. Chaos Solitons Fractals 2011, 44, 710–718. [Google Scholar] [CrossRef]












| Parameter Values for Optimization Algorithms | ||
|---|---|---|
| MPSO | Initial value of inertia weight | 0.95 |
| Minimum inertia weight (Wmin) | 0.4 | |
| Maximum inertia weight (Wmax) | 0.9 | |
| Acceleration coefficients (c1,c2) K consecutive generations | 2.0 3.0 | |
| Fraction of max. iterations for which W is linearly varied | 0.7 | |
| Value of velocity weight at the end of PSO iterations | 0.4 | |
| MBFO | Bacterium no. (s) | 20 |
| Reproduction steps no. (Nre) | 10 | |
| Chemotactic steps no. (Nc) | 10 | |
| Swimming length no. (Ns) Elimination of dispersal events no. (Ned) | 10 10 | |
| Height of repellent (hrepellant) Width of repellent (wrepellant) | 0.1 10 | |
| Depth of attractant (dattract) Width of attract (wattract) | 0.1 0.2 | |
| Elimination and dispersal probability (Ped) | 0.9 | |
| JADE | Scaling factor (f) | 0.5 |
| Crossover probability | 0.2 | |
| Maximum allowed speed or velocity limit | 0.3 | |
| MFA | Randomization(α) | 0.01 |
| Attractiveness (β0) | 1.0 | |
| Light absorption coefficient at the source (γ) | 1.0 | |
| MABC | Value of Fi(φ) | [0,1] |
| Max trial limit | 10 | |
| Lower bound Upper bound | 1 256 | |
| MCS | Scale factor (β) | 1.5 |
| Mutation probability (Pa) | 0.25 | |
| Images | EC-Otsu | MCE | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MFA | MBFO | JADE | MPSO | MABC | MCS | MFA | MBFO | JADE | MPSO | MABC | MCS | |
| 1 | 162.251 | 186.753 | 146.257 | 168.441 | 168.088 | 140.656 | 15.245 | 28.450 | 5.511 | 16.144 | 23.167 | 4.0367 |
| 2 | 173.145 | 200.451 | 167.592 | 187.262 | 171.054 | 165.471 | 16.480 | 380.146 | 8.912 | 19.082 | 35.400 | 7.285 |
| 3 | 172.481 | 188.415 | 176.481 | 186.842 | 171.287 | 170.210 | 16.524 | 29.810 | 8.927 | 18.074 | 27.019 | 8.125 |
| 4 | 162.574 | 185.670 | 157.426 | 172.254 | 168.963 | 145.011 | 17.080 | 28.099 | 6.933 | 18.089 | 27.851 | 4.364 |
| 5 | 163.275 | 189.933 | 155.210 | 183.352 | 172.401 | 150.417 | 18.662 | 29.126 | 9.612 | 24.171 | 39.353 | 3.812 |
| Images | MSE | PSNR | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MFA | MBFO | JADE | MPSO | MABC | MCS | MFA | MBFO | JADE | MPSO | MABC | MCS | |
| 1 | 2564.258 | 2836.548 | 2555.8412 | 2554.012 | 2000.125 | 1428.183 | 18.211 | 12.781 | 17.535 | 14.345 | 18.254 | 19.983 |
| 2 | 2299.665 | 2658.731 | 2236.704 | 2234.865 | 1680.325 | 1486.474 | 16.295 | 13.912 | 16.768 | 16.994 | 19.125 | 19.789 |
| 3 | 2933.681 | 2997.227 | 2153.493 | 2232.824 | 1457.955 | 1076.302 | 14.572 | 12.709 | 16.805 | 17.011 | 17.894 | 18.592 |
| 4 | 1891.080 | 2706.232 | 1663.274 | 1871.285 | 1391.106 | 1758.850 | 17.188 | 16.959 | 17.579 | 18.545 | 18.101 | 19.370 |
| 5 | 1641.192 | 2058.713 | 1481.607 | 1608.255 | 1381.914 | 1689.140 | 15.894 | 17.526 | 18.967 | 20.113 | 19.986 | 19.822 |
| Images | SSIM | FSIM | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MFA | MBFO | JADE | MPSO | MABC | MCS | MFA | MBFO | JADE | MPSO | MABC | MCS | |
| 1 | 0.7310 | 0.7268 | 0.7584 | 0.7361 | 0.7791 | 0.7806 | 0.7381 | 0.7465 | 0.7698 | 0.7307 | 0.8857 | 0.8921 |
| 2 | 0.6845 | 0.7282 | 0.7558 | 0.7402 | 0.7684 | 0.7892 | 0.7684 | 0.7541 | 0.7891 | 0.7654 | 0.8547 | 0.8899 |
| 3 | 0.7200 | 0.6954 | 0.7963 | 0.7708 | 0.8245 | 0.8541 | 0.7354 | 0.6511 | 0.7587 | 0.7798 | 0.8541 | 0.8951 |
| 4 | 0.7355 | 0.6733 | 0.7584 | 0.7456 | 0.8208 | 0.8359 | 0.7341 | 0.6531 | 0.7435 | 0.7424 | 0.8650 | 0.8824 |
| 5 | 0.7411 | 0.6874 | 0.7624 | 0.7542 | 0.8654 | 0.8714 | 0.7822 | 0.7841 | 0.7909 | 0.7932 | 0.8740 | 0.8854 |
| Images | MSE | PSNR | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MFA | MBFO | JADE | MPSO | MABC | MCS | MFA | MBFO | JADE | MPSO | MABC | MCS | |
| 1 | 5758.324 | 4663.072 | 6513.584 | 6203.093 | 2400.645 | 2300.365 | 14.935 | 13.485 | 12.415 | 13.425 | 15.189 | 17.5621 |
| 2 | 5353.061 | 4578.005 | 6766.252 | 6563.295 | 2856.142 | 2285.231 | 16.712 | 17.113 | 14.635 | 15.956 | 16.348 | 17.365 |
| 3 | 5084.854 | 3250.151 | 6966.120 | 6795.172 | 2685.216 | 2411.589 | 13.856 | 14.842 | 12.771 | 15.941 | 16.645 | 17.156 |
| 4 | 5030.843 | 3774.451 | 6868.256 | 6455.256 | 2895.200 | 2795.253 | 16.000 | 16.685 | 12.124 | 15.841 | 17.795 | 18.525 |
| 5 | 5600.028 | 3664.432 | 6789.526 | 6430.256 | 2000.263 | 2850.263 | 19.476 | 20.002 | 17.125 | 18.845 | 20.826 | 21.842 |
| Images | SSIM | FSIM | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MFA | MBFO | JADE | MPSO | MABC | MCS | MFA | MBFO | JADE | MPSO | MABC | MCS | |
| 1 | 0.8516 | 0.8601 | 0.8399 | 0.8413 | 0.8713 | 0.8822 | 0.8652 | 0.8718 | 0.8350 | 0.8518 | 0.8902 | 0.8979 |
| 2 | 0.8415 | 0.8591 | 0.8385 | 0.8426 | 0.8780 | 0.8883 | 0.8725 | 0.8800 | 0.8490 | 0.8552 | 0.8852 | 0.8956 |
| 3 | 0.8313 | 0.8446 | 0.8145 | 0.8415 | 0.8585 | 0.8756 | 0.8562 | 0.8652 | 0.8421 | 0.8442 | 0.8852 | 0.8952 |
| 4 | 0.8513 | 0.8613 | 0.8213 | 0.8476 | 0.8713 | 0.8813 | 0.8662 | 0.8761 | 0.8421 | 0.8584 | 0.8821 | 0.8993 |
| 5 | 0.8553 | 0.8600 | 0.8201 | 0.8423 | 0.8690 | 0.8919 | 0.8695 | 0.8785 | 0.8458 | 0.8517 | 0.8982 | 0.9065 |
| Images | GLCM | Rényi’s Entropy | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MFA | MBFO | JADE | MPSO | MABC | MCS | MFA | MBFO | JADE | MPSO | MABC | MCS | |
| 1 | 23.697 | 17.512 | 14.214 | 18.867 | 18.570 | 17.902 | 9.807 | 16.511 | 7.933 | 14.854 | 7.175 | 2.109 |
| 2 | 24.210 | 16.798 | 15.098 | 18.867 | 18.846 | 17.667 | 9.812 | 17.422 | 7.840 | 15.798 | 8.968 | 4.402 |
| 3 | 24.006 | 19.425 | 16.632 | 19.847 | 18.739 | 20.099 | 9.125 | 19.198 | 7.521 | 14.425 | 8.227 | 6.512 |
| 4 | 26.443 | 16.854 | 11.098 | 19.811 | 18.350 | 17.016 | 10.082 | 20.806 | 8.251 | 16.854 | 9.593 | 3.872 |
| 5 | 22.749 | 21.825 | 20.241 | 20.869 | 22.541 | 21.971 | 10.962 | 20.993 | 7.512 | 18.825 | 9.399 | 6.486 |
| Images | MSE | PSNR | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MFA | MBFO | JADE | MPSO | MABC | MCS | MFA | MBFO | JADE | MPSO | MABC | MCS | |
| 1 | 974.206 | 1024.852 | 1011.564 | 994.308 | 869.238 | 800.634 | 20.396 | 19.176 | 18.176 | 22.462 | 23.866 | 25.533 |
| 2 | 989.812 | 1077.524 | 1007.213 | 994.521 | 864.609 | 896.329 | 20.173 | 19.114 | 18.366 | 22.597 | 25.439 | 26.636 |
| 3 | 961.518 | 1066.218 | 1116.621 | 996.212 | 895.586 | 822.851 | 21.587 | 20.493 | 18.772 | 24.492 | 25.466 | 25.517 |
| 4 | 985.547 | 1079.527 | 1014.021 | 996.527 | 941.484 | 806.524 | 20.956 | 19.866 | 19.215 | 23.482 | 25.076 | 26.256 |
| 5 | 975.347 | 1090.257 | 1000.624 | 992.527 | 911.209 | 861.624 | 20.476 | 19.893 | 18.216 | 16.486 | 19.287 | 20.483 |
| Images | SSIM | FSIM | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MFA | MBFO | JADE | MPSO | MABC | MCS | MFA | MBFO | JADE | MPSO | MABC | MCS | |
| 1 | 0.8388 | 0.8705 | 0.7885 | 0.9092 | 0.9550 | 0.9601 | 0.8491 | 0.9215 | 0.8381 | 0.9481 | 0.9597 | 0.9825 |
| 2 | 0.8474 | 0.8595 | 0.8114 | 0.9125 | 0.9564 | 0.9622 | 0.8462 | 0.9299 | 0.8835 | 0.9599 | 0.9680 | 0.9735 |
| 3 | 0.8294 | 0.9046 | 0.7912 | 0.9124 | 0.9587 | 0.9734 | 0.8499 | 0.9222 | 0.8534 | 0.9594 | 0.9735 | 0.9775 |
| 4 | 0.8422 | 0.8616 | 0.7912 | 0.9274 | 0.9554 | 0.9643 | 0.8427 | 0.9222 | 0.8658 | 0.9698 | 0.9792 | 0.9732 |
| 5 | 0.8712 | 0.8525 | 0.7952 | 0.9321 | 0.9679 | 0.9712 | 0.8469 | 0.9281 | 0.8981 | 0.9699 | 0.9746 | 0.9777 |
| Images | MSE | PSNR | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MFA | MBFO | JADE | MPSO | MABC | MCS | MFA | MBFO | JADE | MPSO | MABC | MCS | |
| 1 | 658.328 | 563.029 | 513.586 | 503.037 | 300.362 | 200.656 | 23.035 | 23.815 | 24.815 | 26.741 | 26.985 | 27.952 |
| 2 | 453.068 | 608.009 | 566.254 | 363.252 | 285.234 | 256.126 | 24.812 | 23.213 | 24.735 | 25.056 | 26.448 | 27.965 |
| 3 | 684.857 | 600.157 | 566.124 | 495.123 | 311.585 | 185.265 | 22.956 | 23.942 | 24.871 | 25.041 | 26.745 | 27.856 |
| 4 | 630.843 | 864.456 | 568.256 | 545.256 | 395.254 | 295.200 | 22.695 | 23.785 | 24.224 | 25.941 | 26.895 | 28.825 |
| 5 | 700.028 | 664.436 | 589.526 | 440.256 | 350.268 | 250.263 | 22.476 | 24.082 | 24.125 | 25.845 | 27.826 | 28.942 |
| Images | SSIM | FSIM | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MFA | MBFO | JADE | MPSO | MABC | MCS | MFA | MBFO | JADE | MPSO | MABC | MCS | |
| 1 | 0.8615 | 0.9012 | 0.9399 | 0.9422 | 0.9732 | 0.9881 | 0.9325 | 0.9535 | 0.9671 | 0.9615 | 0.9822 | 0.9996 |
| 2 | 0.8614 | 0.9080 | 0.9094 | 0.9432 | 0.9769 | 0.9883 | 0.9359 | 0.9442 | 0.9552 | 0.9689 | 0.9905 | 0.9965 |
| 3 | 0.8712 | 0.9052 | 0.9254 | 0.9424 | 0.9794 | 0.9865 | 0.9326 | 0.9416 | 0.9535 | 0.9622 | 0.9900 | 0.9935 |
| 4 | 0.8712 | 0.9002 | 0.9522 | 0.9465 | 0.9779 | 0.9812 | 0.9236 | 0.9436 | 0.9426 | 0.9622 | 0.9823 | 0.9901 |
| 5 | 0.8852 | 0.9095 | 0.9212 | 0.9432 | 0.9889 | 0.9939 | 0.9395 | 0.9489 | 0.9468 | 0.9672 | 0.9895 | 0.9986 |
| Images | Threshold Levels | MCS | Rényi’s Entropy | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rényi’s vs. MCE | Rényi’s vs. GLCM | Rényi’s vs. EC-Otsu | MCS vs. MFA | MCS vs. MBFO | MCS vs. JADE | MCS vs. MPSO | MCS vs. MABC | ||||||||||
| p | h | p | h | p | h | p | h | p | h | p | h | p | h | p | h | ||
| 1 | 2 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 |
| 5 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 8 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | 0.084 | 0 | <0.05 | 1 | <0.05 | 1 | |
| 12 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 2 | 2 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 |
| 5 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 8 | <0.05 | 1 | 0.079 | 0 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | 0.085 | 0 | <0.05 | 1 | |
| 12 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 3 | 2 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 |
| 5 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 8 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | 0.067 | 0 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 12 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | 0.09 | 0 | <0.05 | 1 | <0.05 | 1 | |
| 4 | 2 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 |
| 5 | <0.05 | 1 | <0.05 | 1 | 0.061 | 0 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 8 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 12 | <0.05 | 1 | 0.072 | 0 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | 0.075 | 0 | <0.05 | 1 | |
| 5 | 2 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 |
| 5 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 8 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | 0.069 | 0 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 12 | <0.05 | 1 | 0.062 | 0 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pare, S.; Mittal, H.; Sajid, M.; Bansal, J.C.; Saxena, A.; Jan, T.; Pedrycz, W.; Prasad, M. Remote Sensing Imagery Segmentation: A Hybrid Approach. Remote Sens. 2021, 13, 4604. https://doi.org/10.3390/rs13224604
Pare S, Mittal H, Sajid M, Bansal JC, Saxena A, Jan T, Pedrycz W, Prasad M. Remote Sensing Imagery Segmentation: A Hybrid Approach. Remote Sensing. 2021; 13(22):4604. https://doi.org/10.3390/rs13224604
Chicago/Turabian StylePare, Shreya, Himanshu Mittal, Mohammad Sajid, Jagdish Chand Bansal, Amit Saxena, Tony Jan, Witold Pedrycz, and Mukesh Prasad. 2021. "Remote Sensing Imagery Segmentation: A Hybrid Approach" Remote Sensing 13, no. 22: 4604. https://doi.org/10.3390/rs13224604
APA StylePare, S., Mittal, H., Sajid, M., Bansal, J. C., Saxena, A., Jan, T., Pedrycz, W., & Prasad, M. (2021). Remote Sensing Imagery Segmentation: A Hybrid Approach. Remote Sensing, 13(22), 4604. https://doi.org/10.3390/rs13224604








