Spaceborne GNSS-R for Sea Ice Classification Using Machine Learning Classifiers
Abstract
:1. Introduction
2. Dataset Description
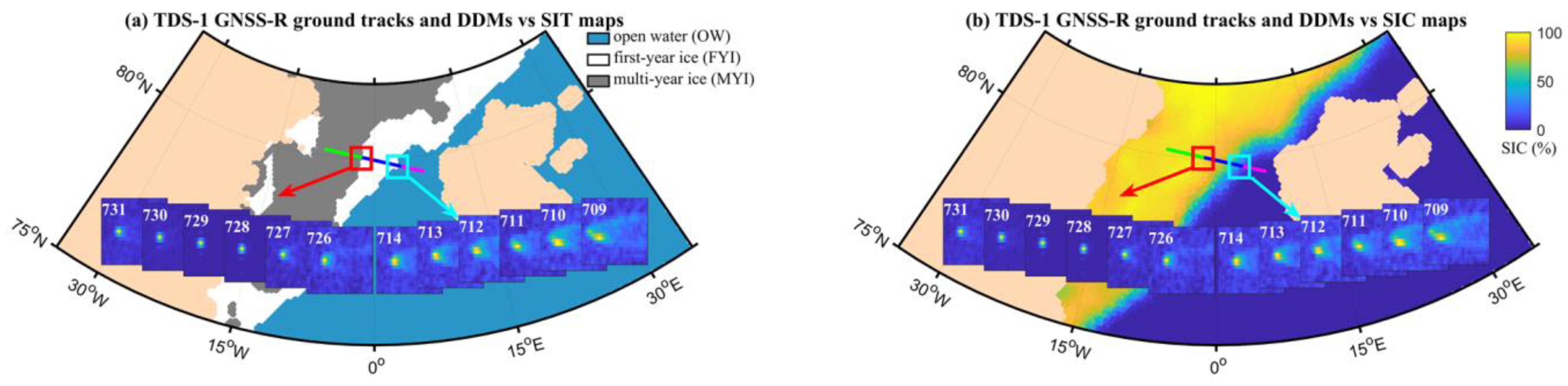
2.1. TDS-1 Mission and Dataset
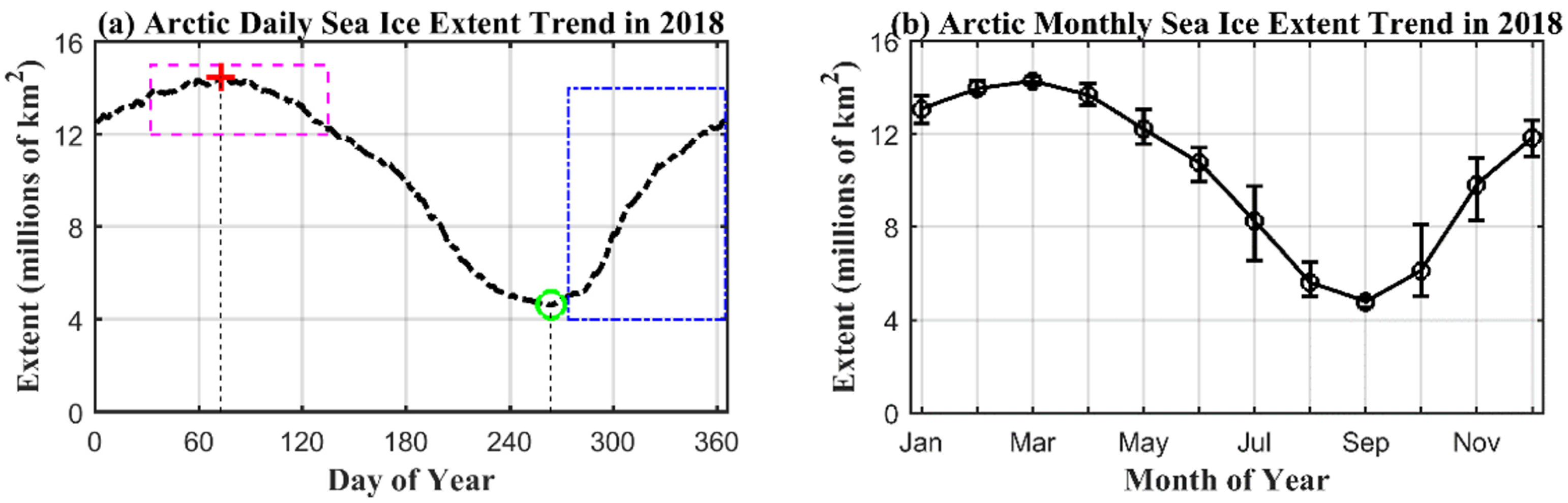
2.2. Reference Sea Ice Data
3. Theory and Methods
3.1. Spaceborne GNSS-R Features
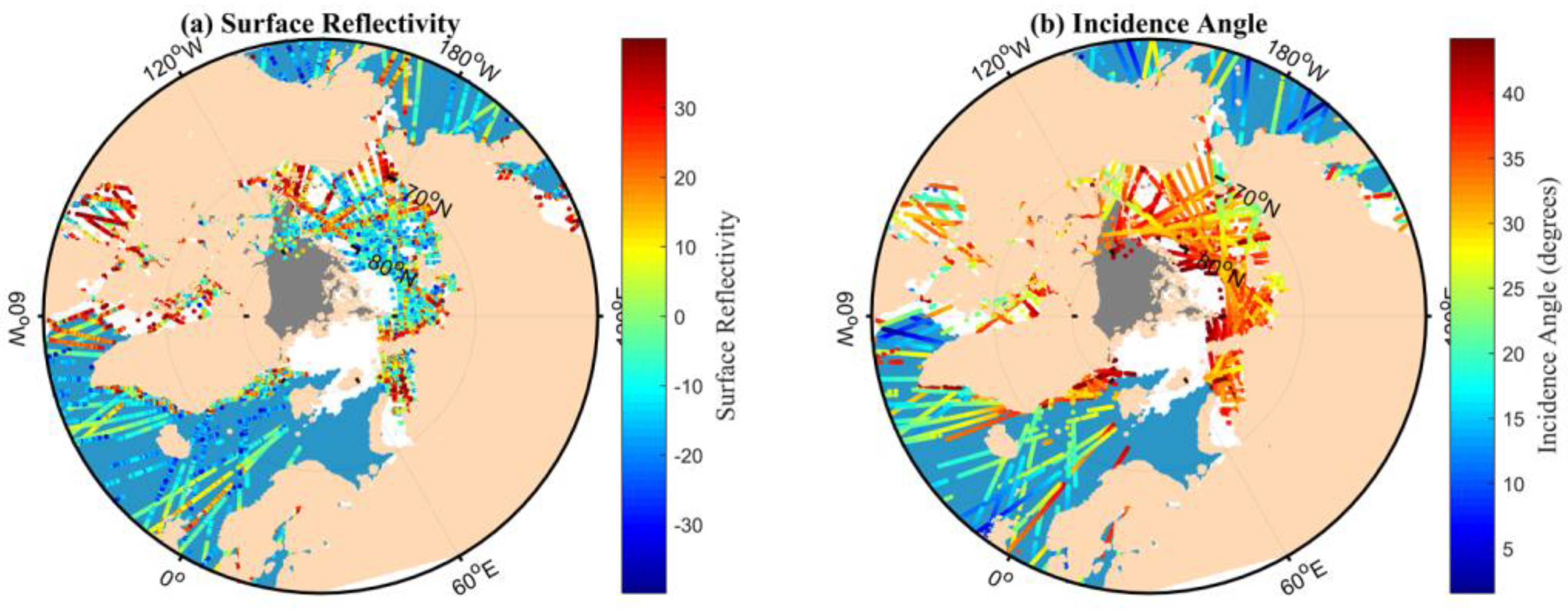
3.1.1. Surface Reflectivity
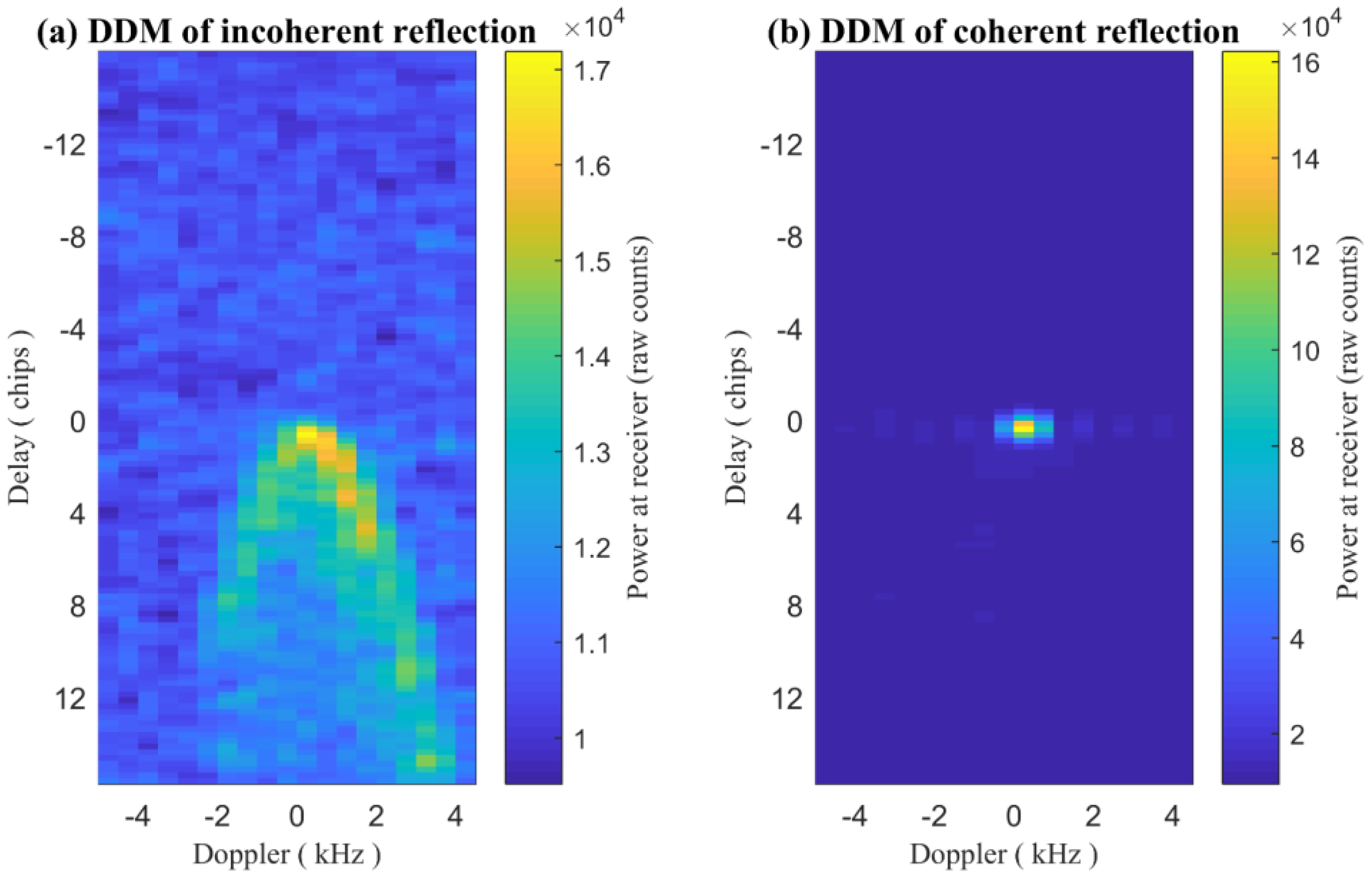
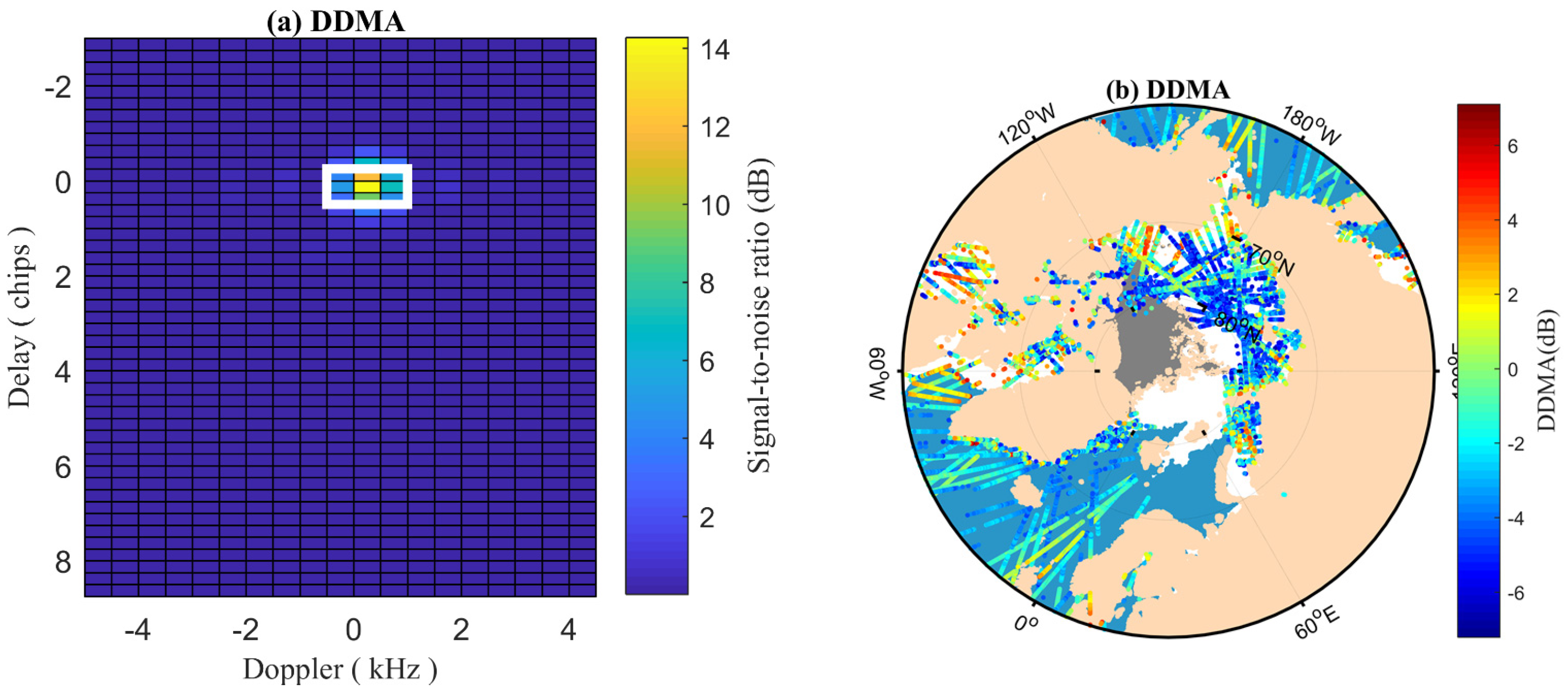
3.1.2. Features Derived from DDM
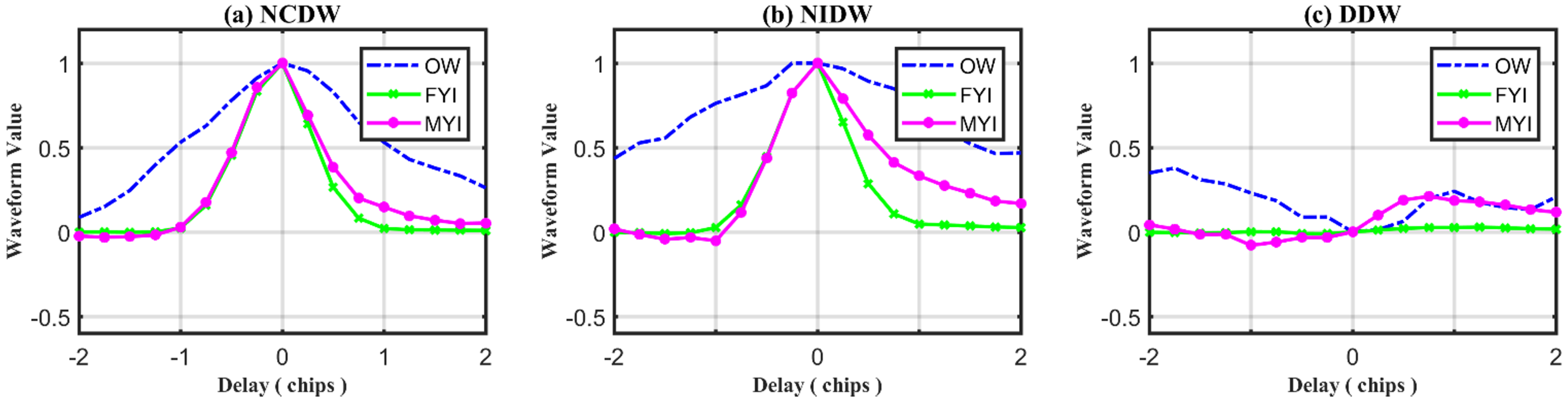
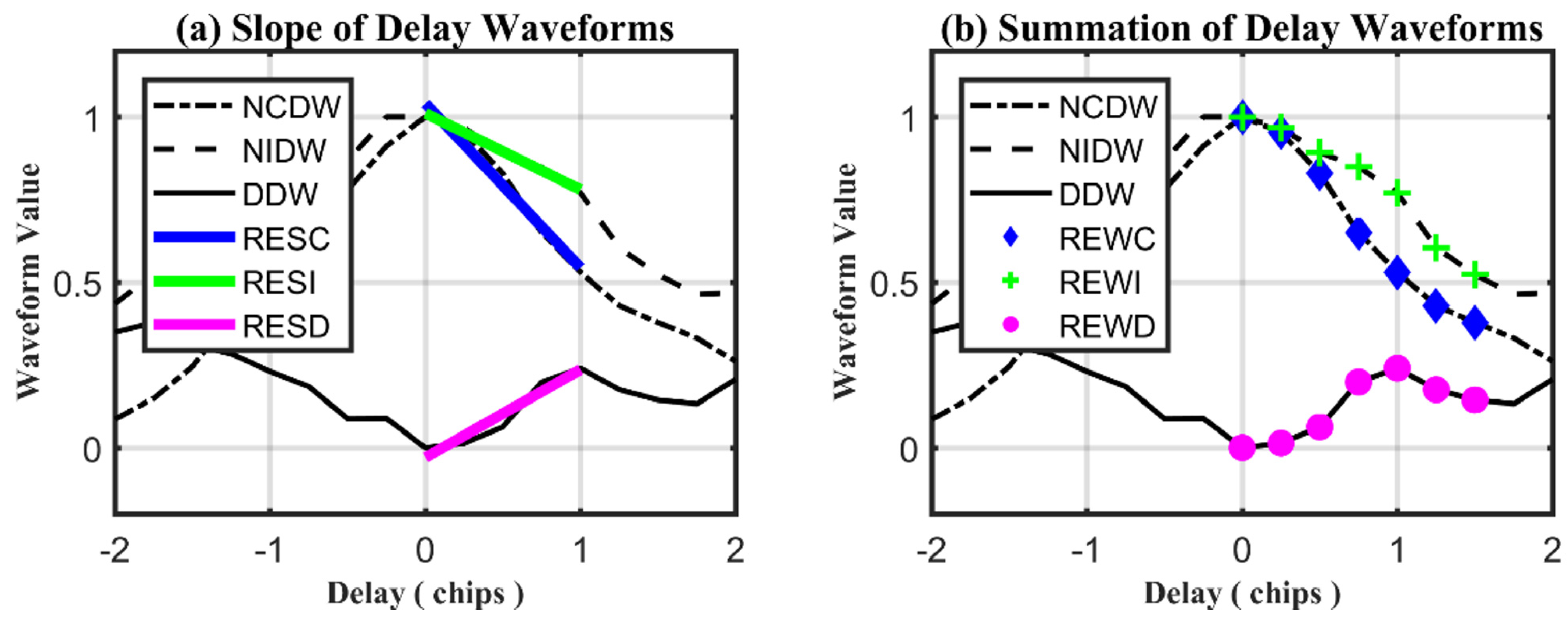
- RESC (Right Edge Slope of CDW). The fitting slope of NCDW with 5 delay bins starting from the zero delay one is defined as RESC, which is depicted by the slope of the blue line in Figure 6a.
- RESI (Right Edge Slope of IDW). The fitting slope of NIDW with 5 delay bins starting from the zero delay one is defined as RESI, which is depicted by the slope of the green line in Figure 6a.
- RESD (Right Edge Slope of DDW). The fitting slope of DDW with 5 delay bins starting from the zero delay one is defined as RESD, which is depicted by the slope of the magenta line in Figure 6a.
- REWC (Right Edge Waveform Summation of CDW). The summation of NCDW values (marked with blue diamond dots in Figure 6b) from the delay bins 0 to 6 is defined as REWC.
- REWI (Right Edge Waveform Summation of IDW)}. The summation of NCDW values (marked with green cross dots in Figure 6b) from the delay bins 0 to 6 is defined as REWI.
- REWD (Right Edge Waveform Summation of DDW)}. The summation of DDW values (marked with magenta circle dots in Figure 6b) from the delay bins 0 to 6 is defined as REWD.
3.2. Sea Ice Classification Method
3.2.1. Random Forest (RF)
3.2.2. Support Vector Machine (SVM)
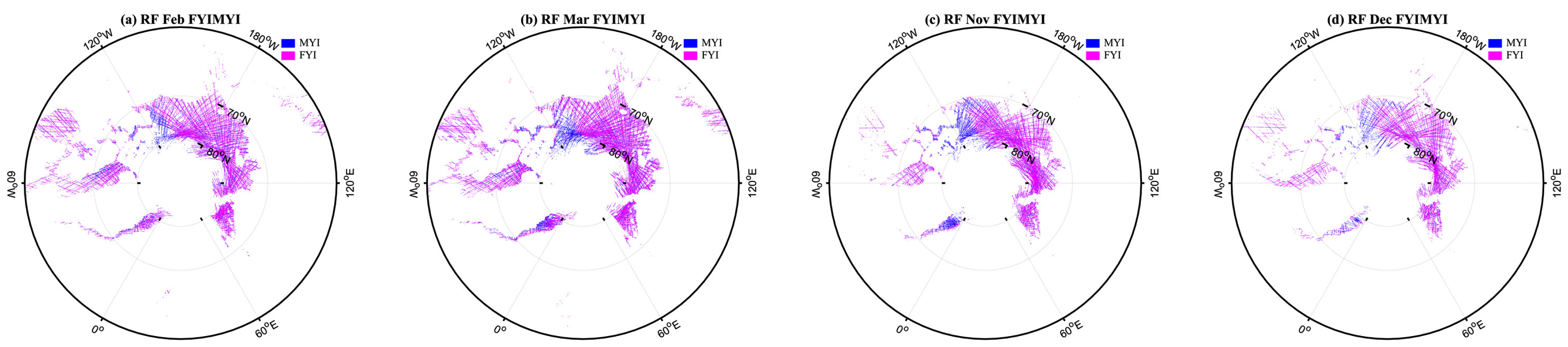
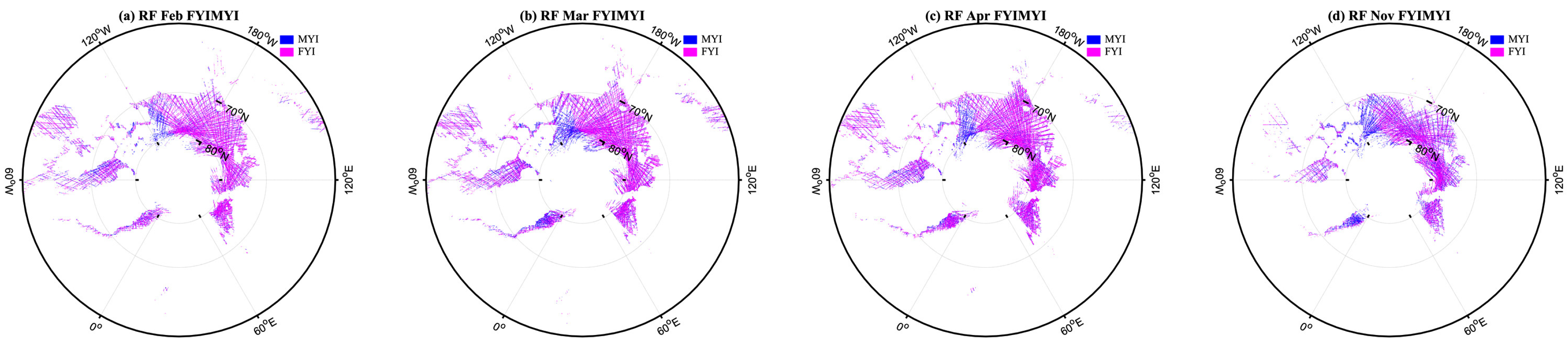
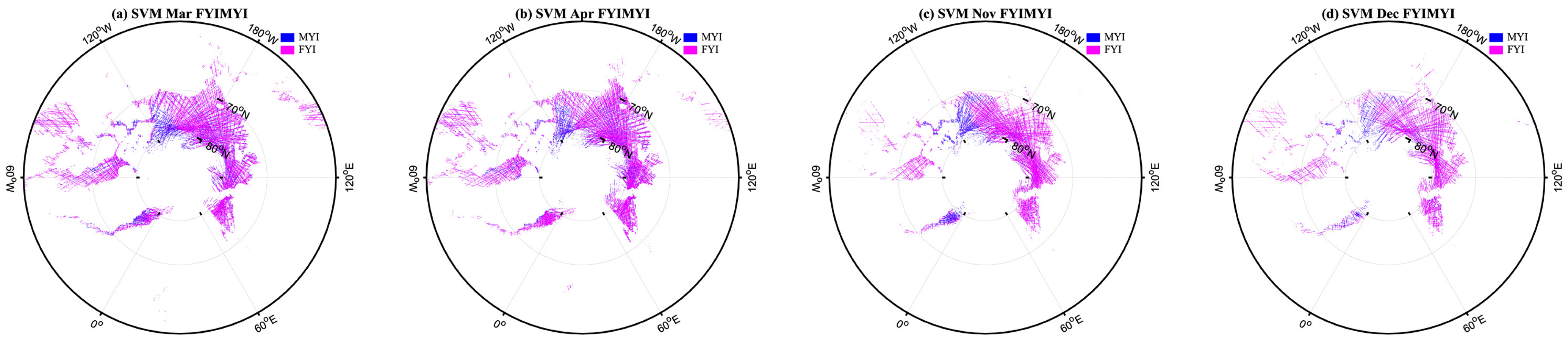
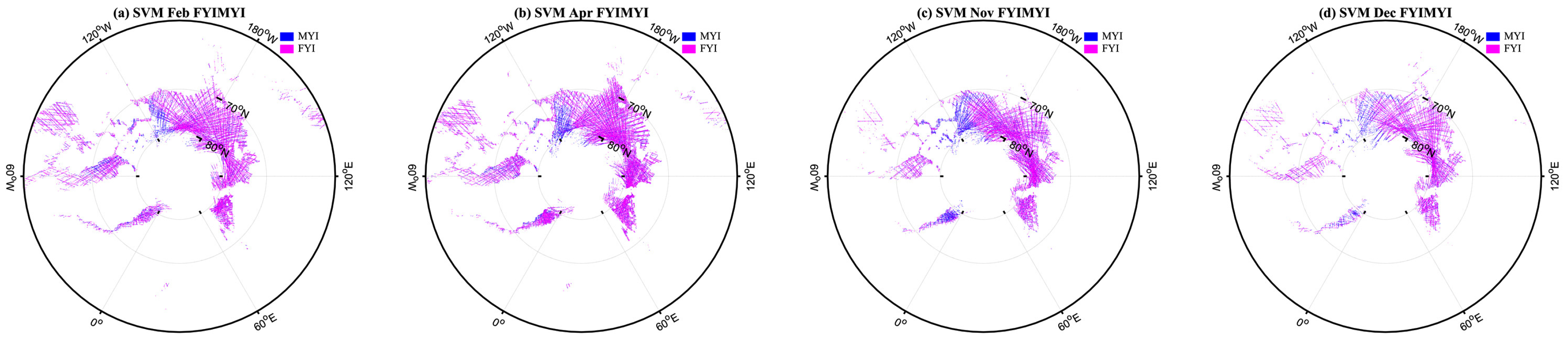
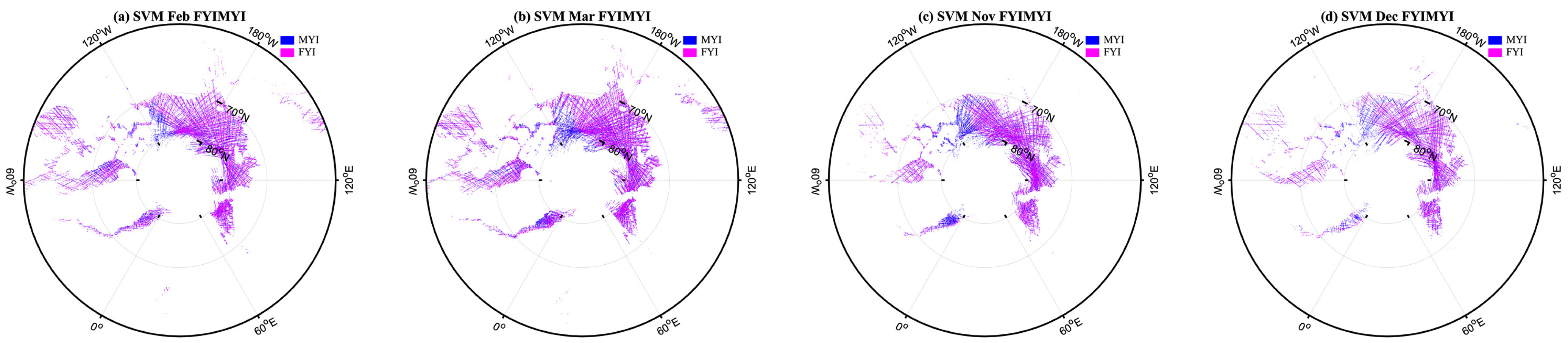
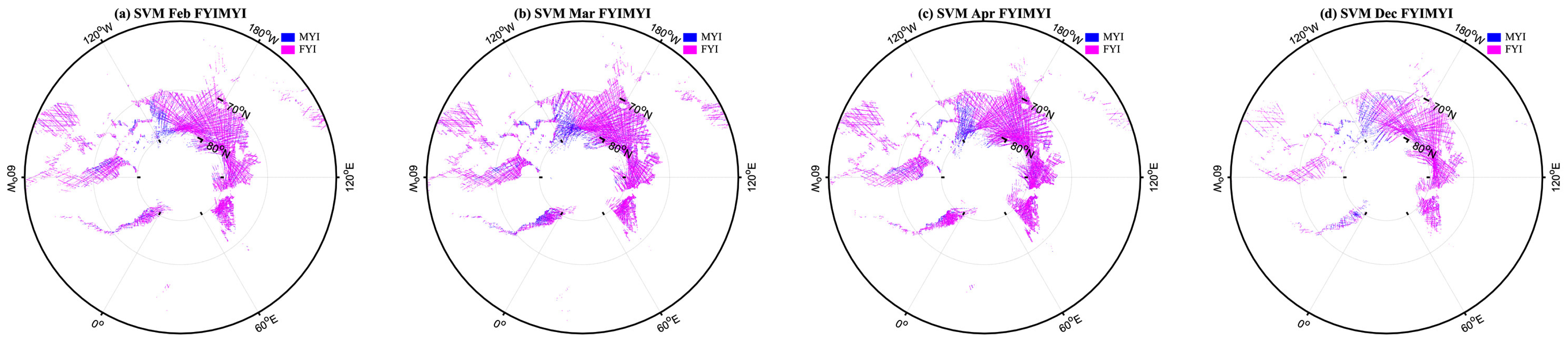
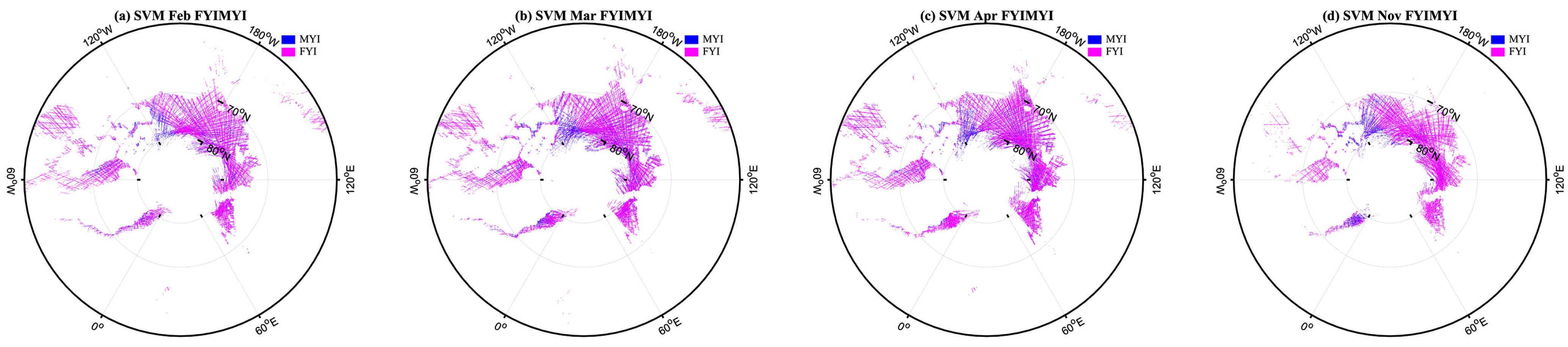
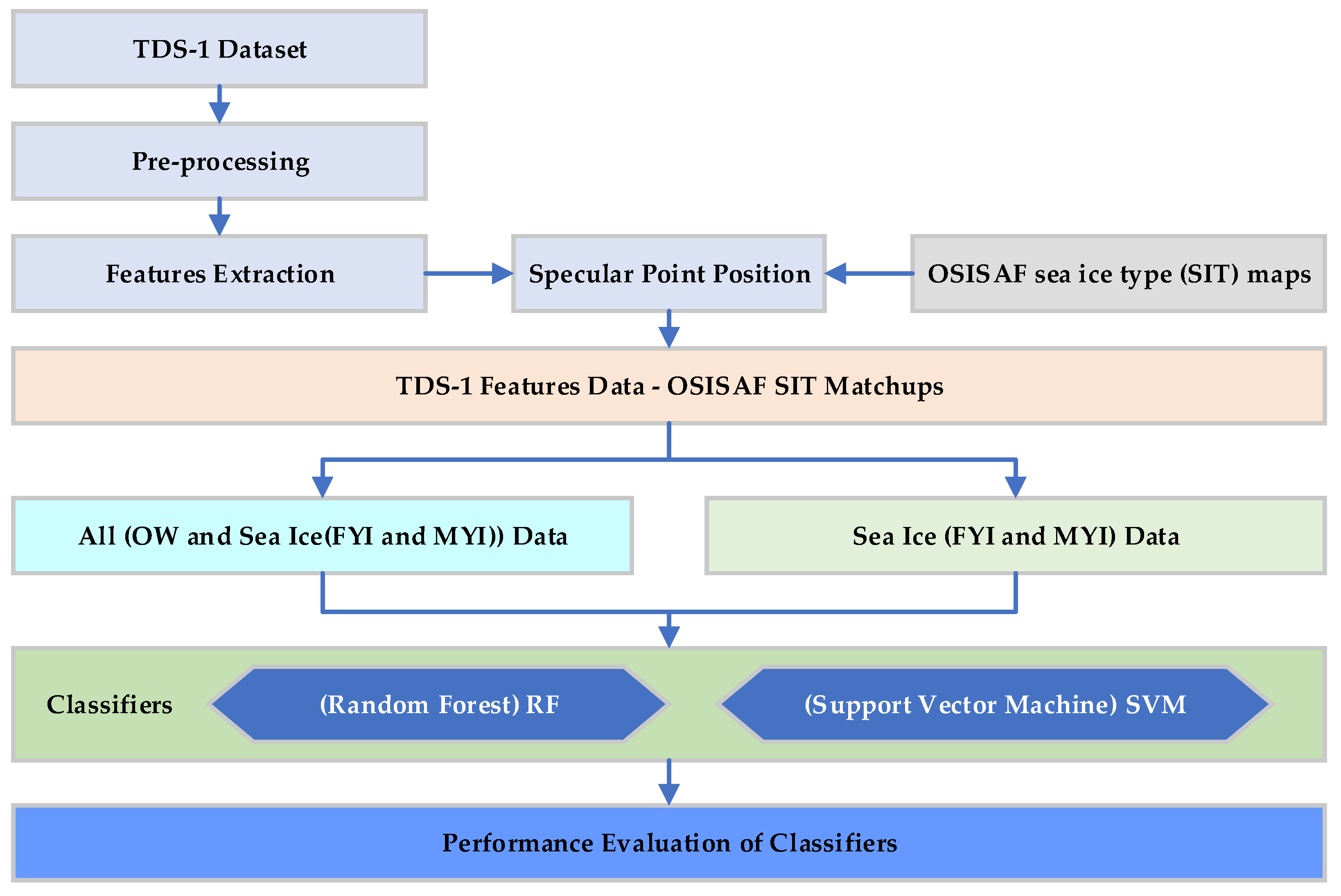
3.2.3. Sea Ice Classification Based on RF and SVM
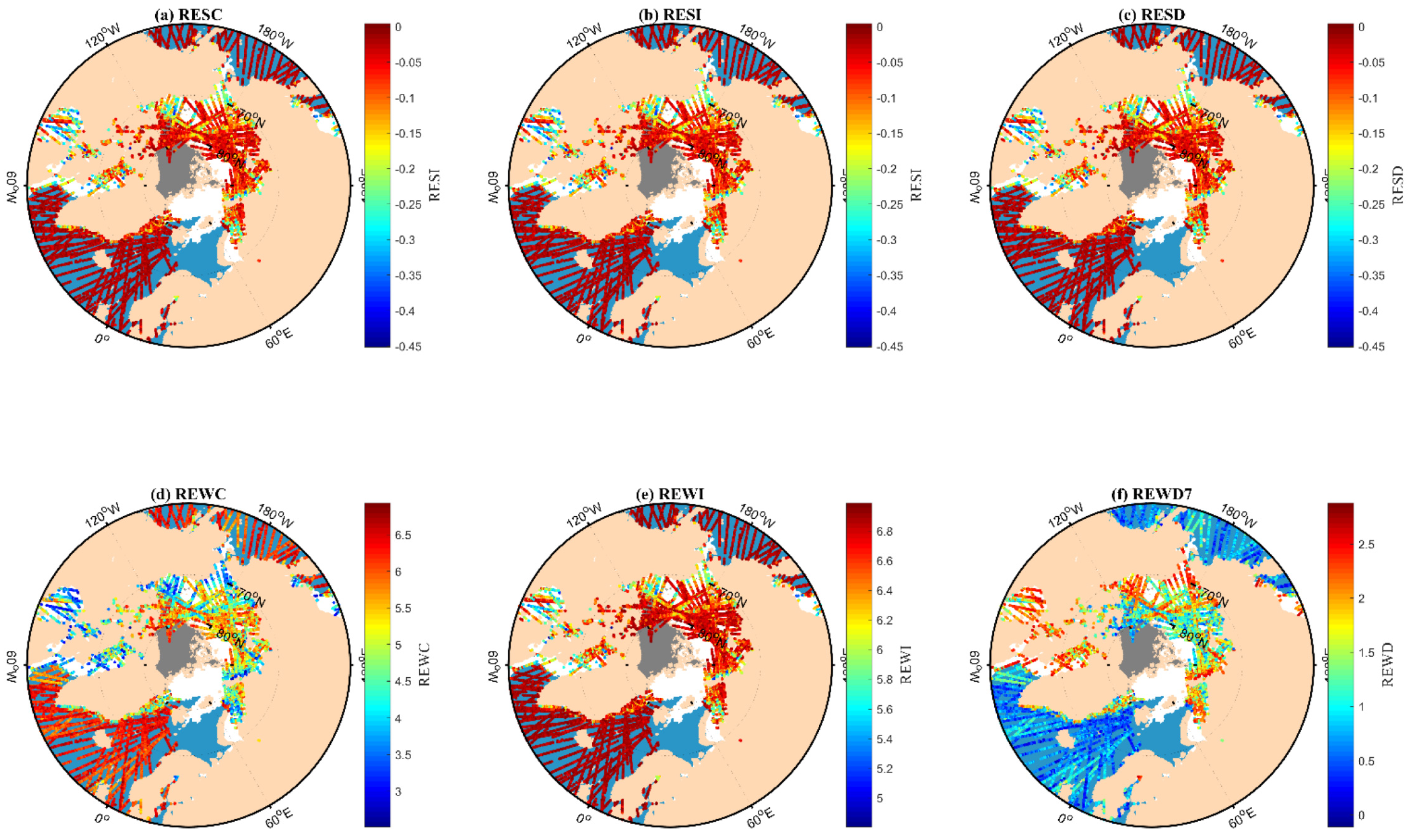
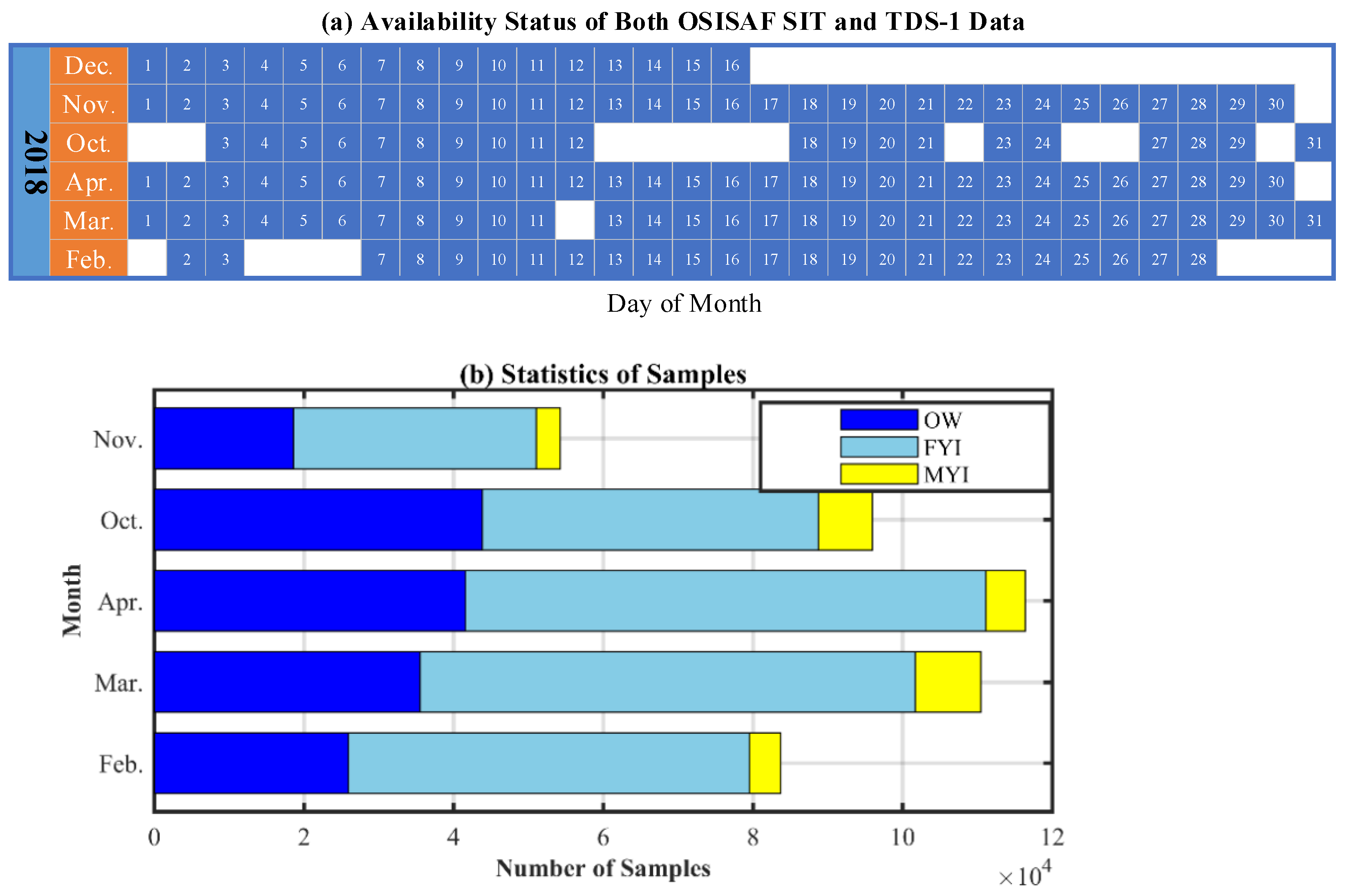
- TDS-1 data preprocessing and features extraction. Firstly, the TDS-1 data with a latitude above 55°N and peak SNR above −3 dB is adopted to extract delay waveforms, which are further normalized to extract features. A total of eight features, namely SR, DDMA, RESC, RESI, RESD, REWC, REWI, and REWD, are extracted from the TDS-1 data. Then the TDS-1 features are matched with OSISAF SIT maps based on the data collection date and specular point position through a bilinear interpolation approach.
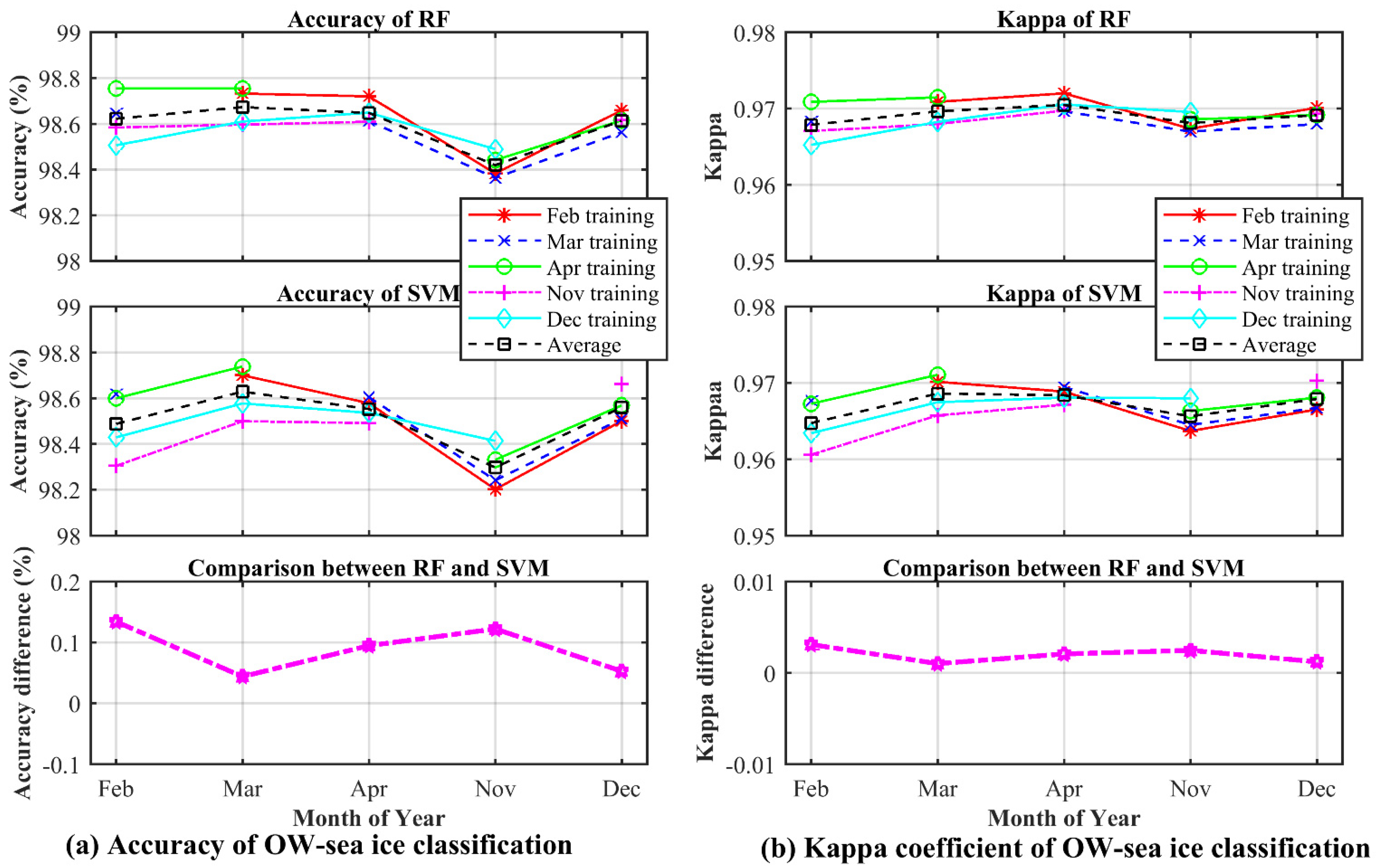
- OW-sea ice classification. In this step, the FYI and MYI are regarded as one category (i.e., sea ice). 30% of samples are randomly selected as training set and the rest 70% of samples are used to test the OW-sea ice classification results.
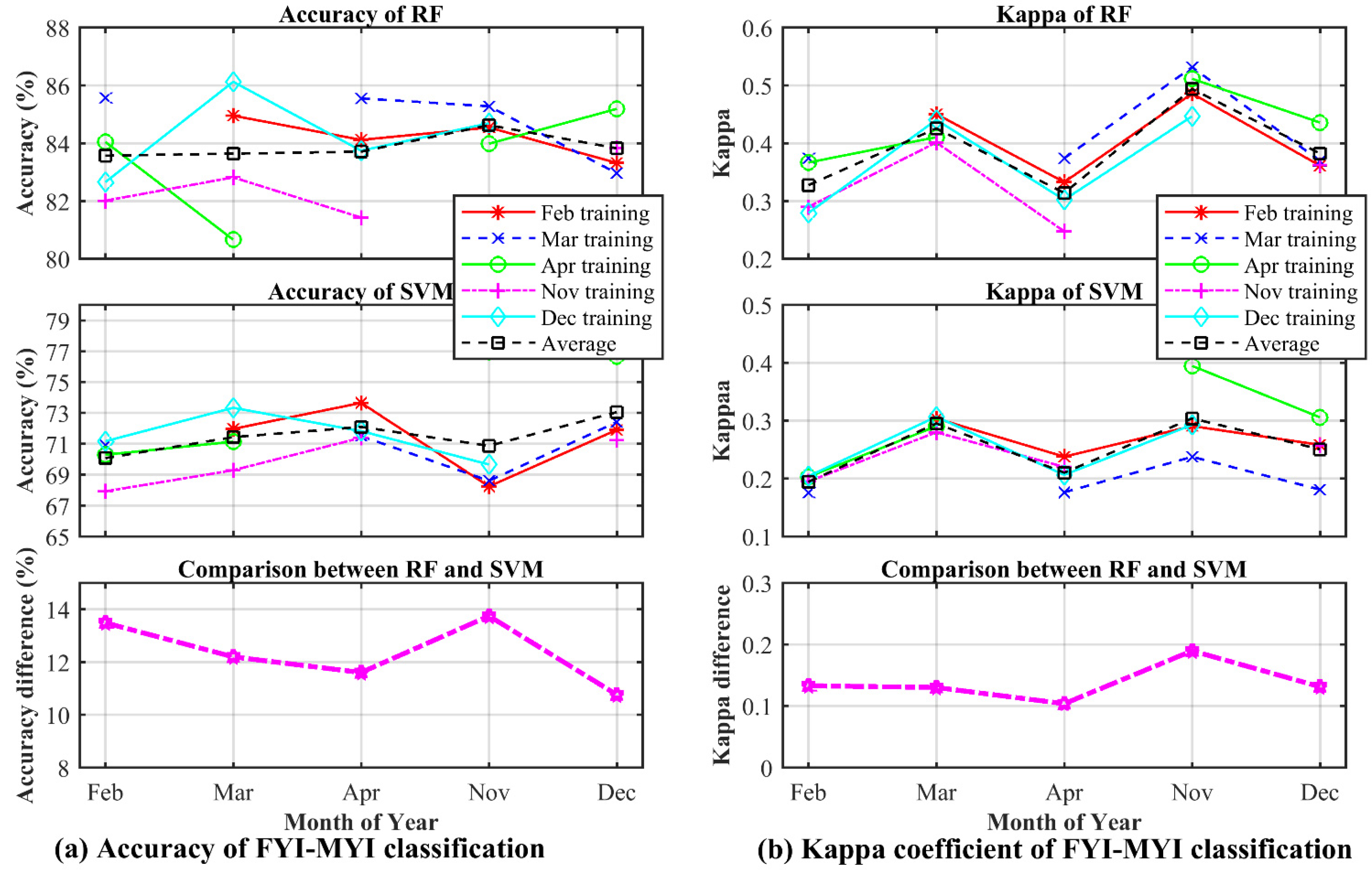
- FYI-MYI classification. The sea ice datasets are applied in this step to classify FYI and MYI. As with the process of OW-sea ice classification, sea ice samples are randomly selected as training and test sets to classify FYI and MYI.
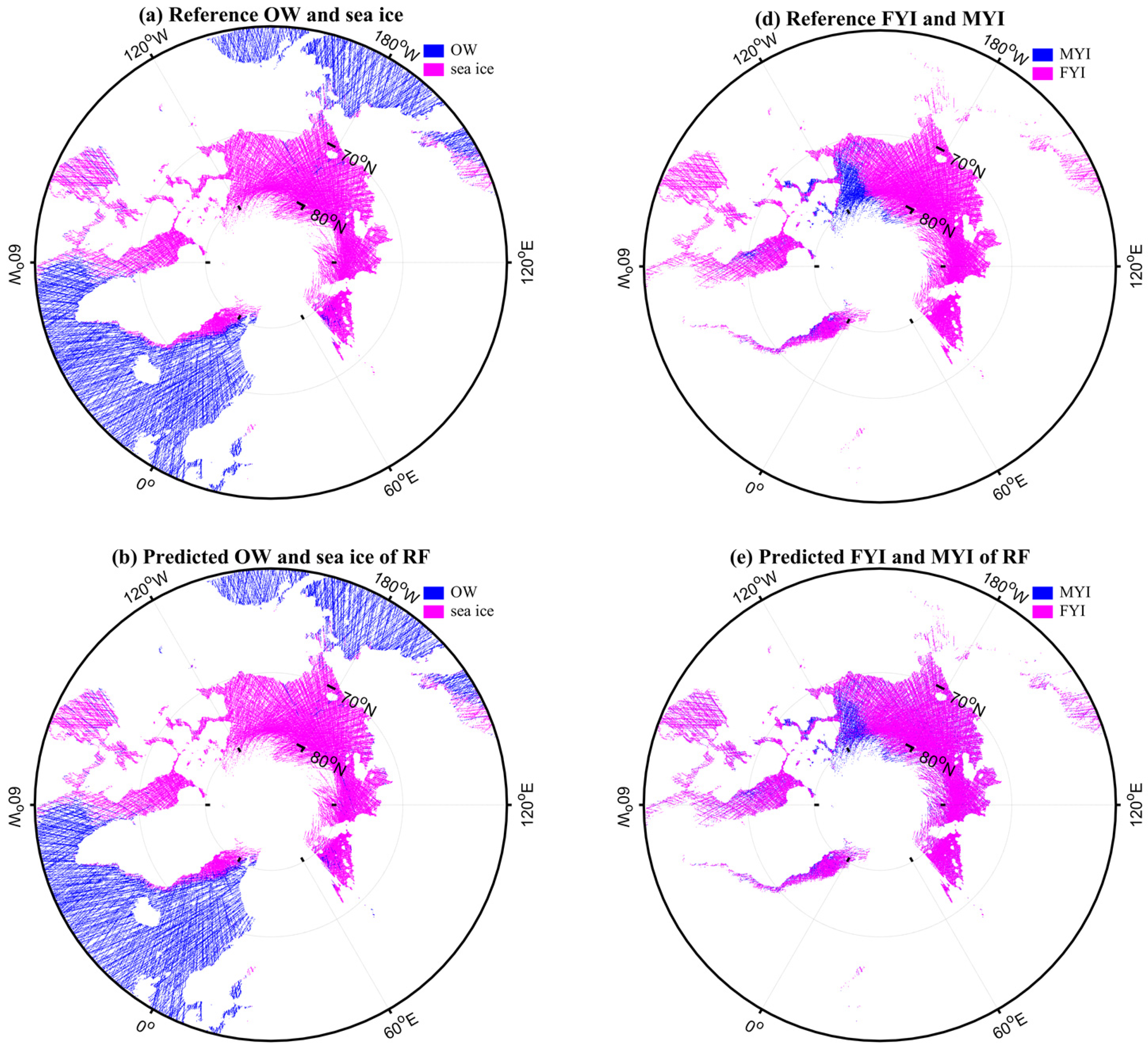
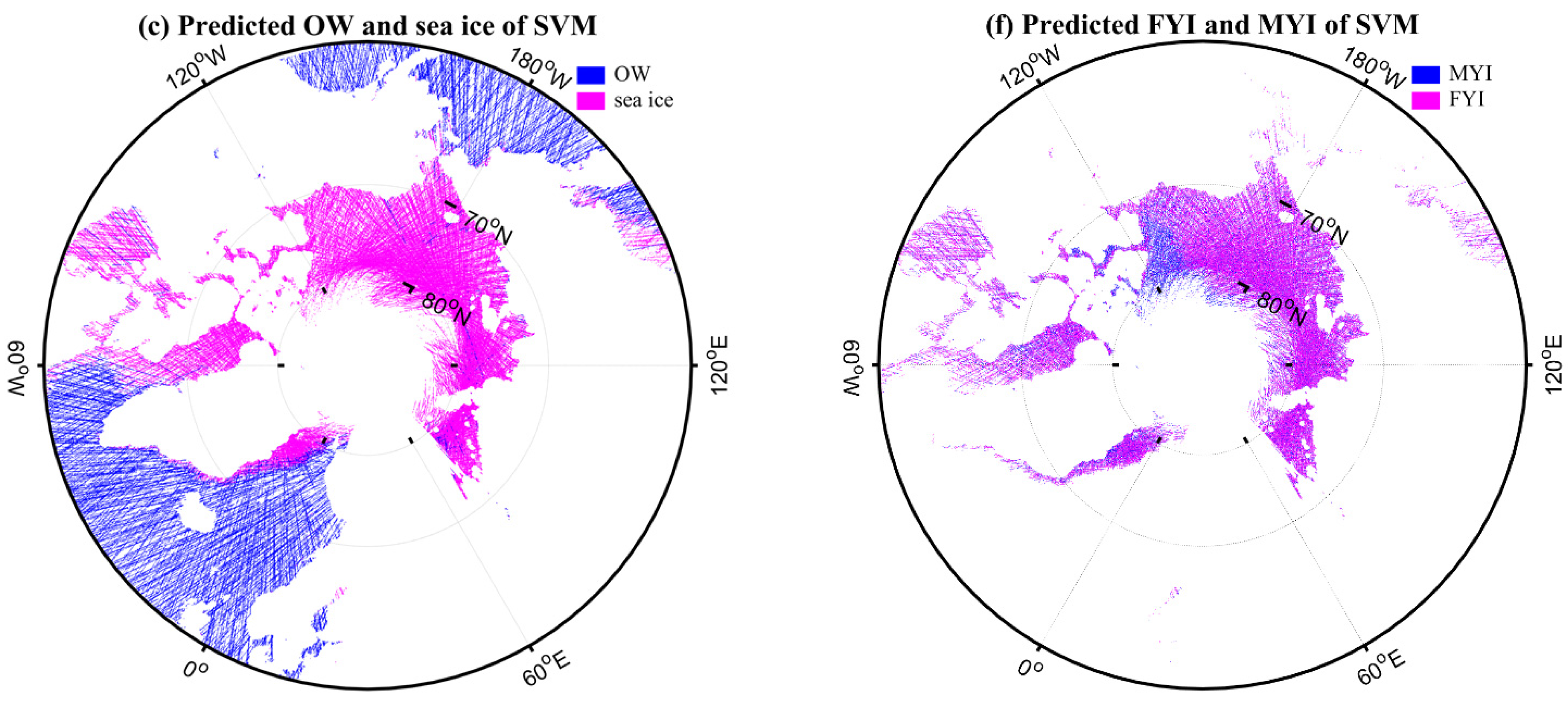
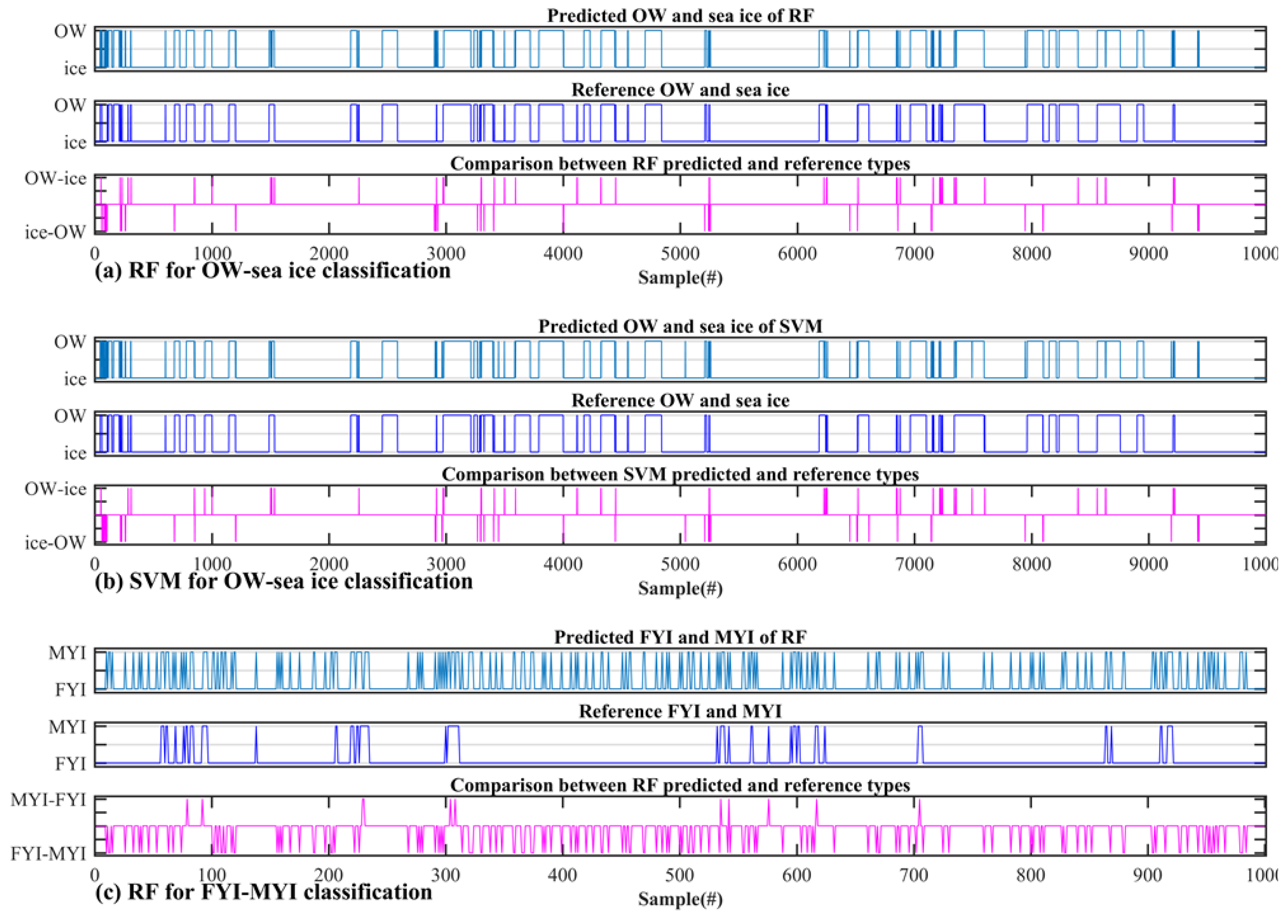
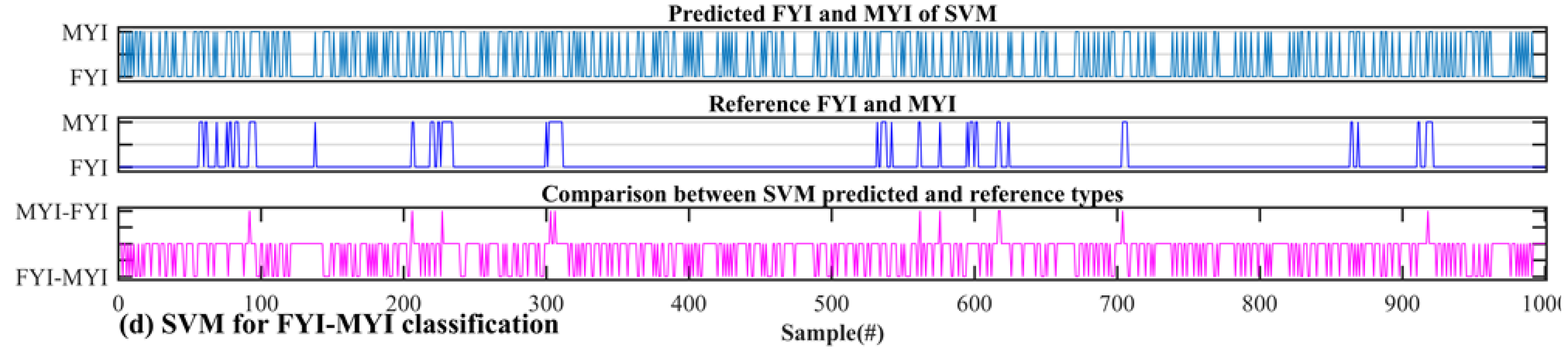
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CDW | Central Delay Waveform |
| CYGNSS | Cyclone Global Navigation Satellite System |
| DDM | Delay-Doppler Map |
| DDMA | Delay-Doppler Map Average |
| DDW | Differential Delay Waveform |
| EIRP | Effective Isotropic Radiated Power |
| EUMETSAT | European Organization for the Exploitation of Meteorological Satellites |
| FYI | First-Year Ice |
| GNSS | Global Navigation Satellite System |
| GNSS-R | Global Navigation Satellite System Reflectometry |
| IDW | Integrated Delay Waveform |
| ML | Machine Learning |
| MYI | Multi-Year Ice |
| NCDW | Normalized Central Delay Waveform |
| NIDW | Normalized Integrated Delay Waveform |
| NSIDC | National Snow and Ice Data Center |
| OSI SAF | Ocean and Sea Ice Satellite Application Facility |
| OW | Open Water |
| RESC | Right Edge Slope of CDW |
| RESD | Right Edge Slope of DDW |
| RESI | Right Edge Slope of IDW |
| REWC | Right Edge Waveform Summation of CDW |
| REWD | Right Edge Waveform Summation of DDW |
| REWI | Right Edge Waveform Summation of IDW |
| RF | Random Forest |
| SIC | Sea Ice Concentration |
| SIT | Sea Ice Type |
| SNR | Signal-to-Noise Ratio |
| SP | Specular Point |
| SSMIS | Special Sensor Microwave Imager Sounder |
| SVM | Support Vector Machine |
| TDS-1 | TechDemoSat-1 |
Appendix A
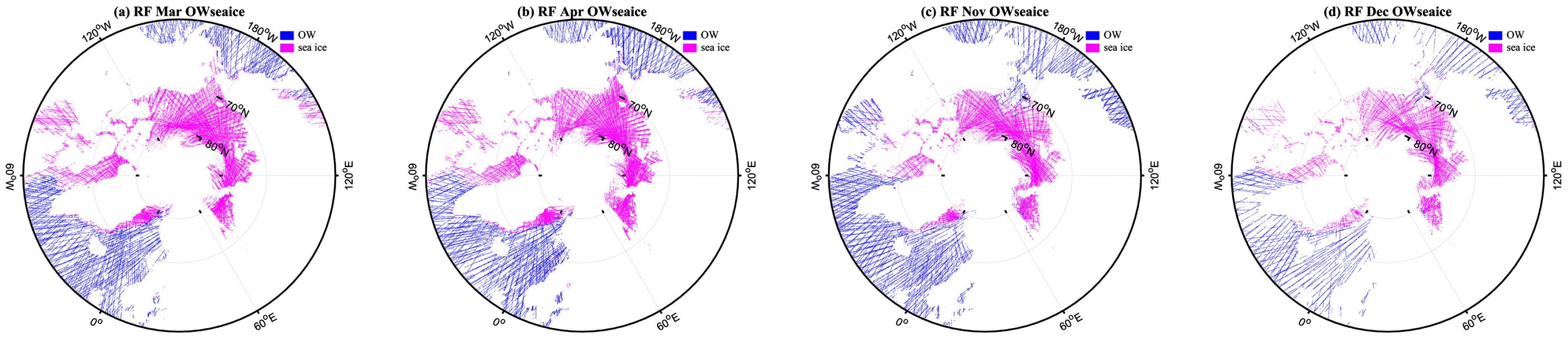
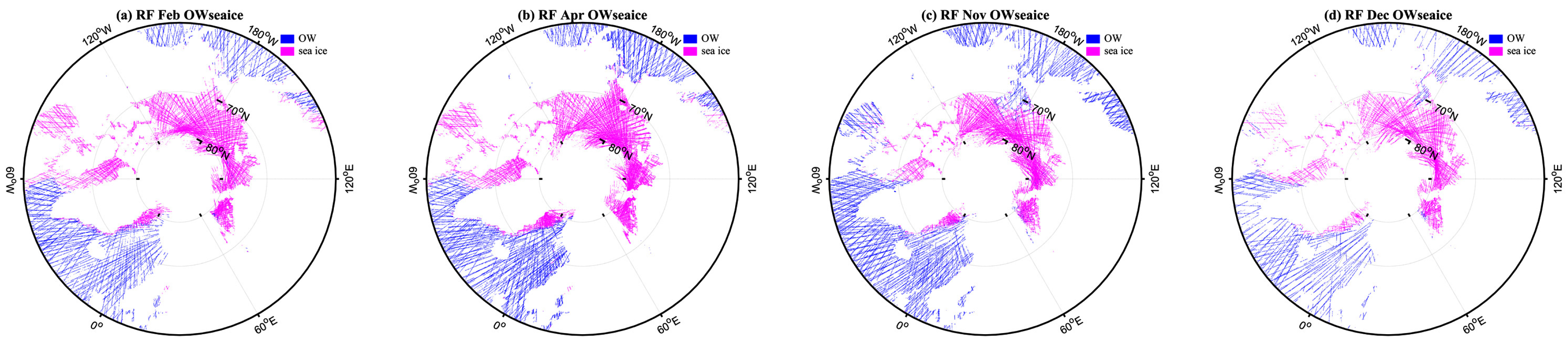
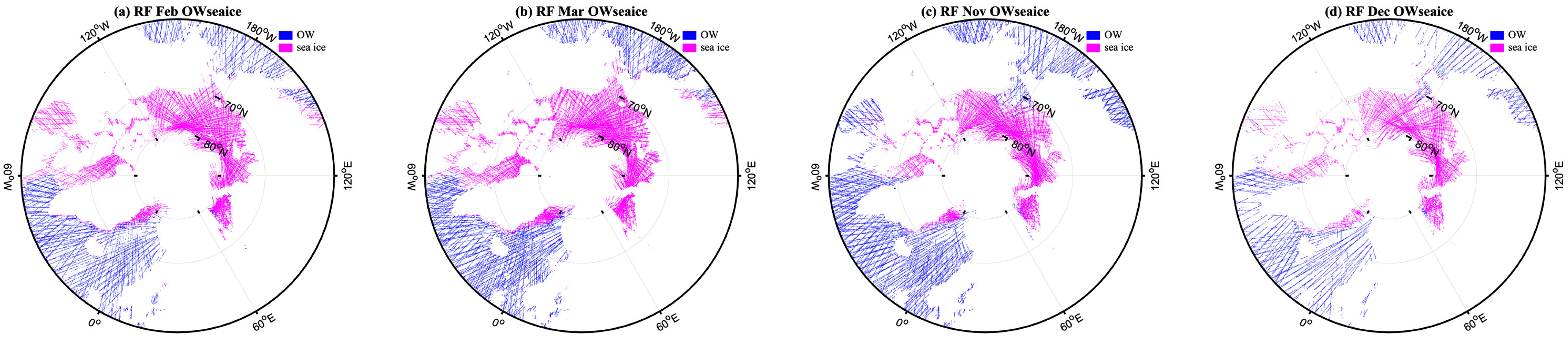
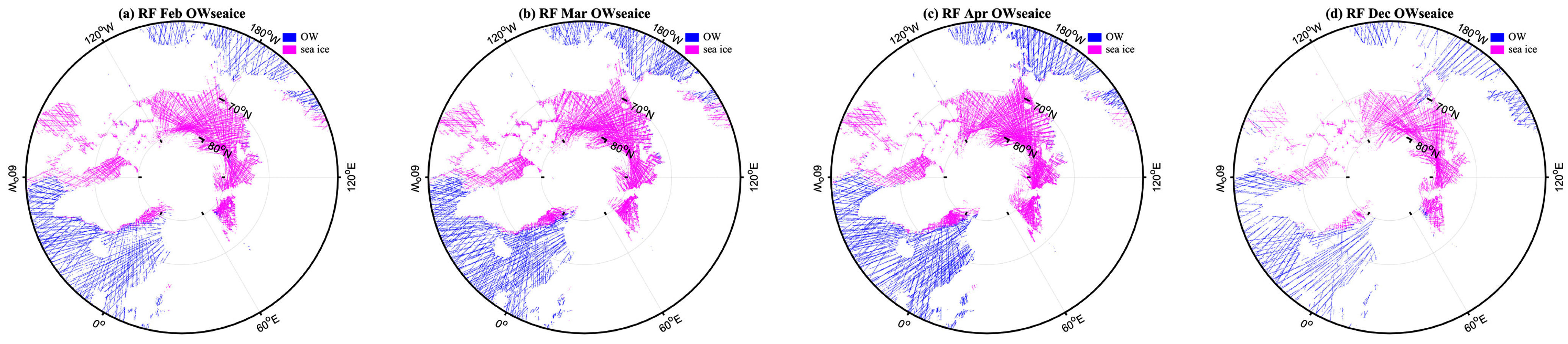
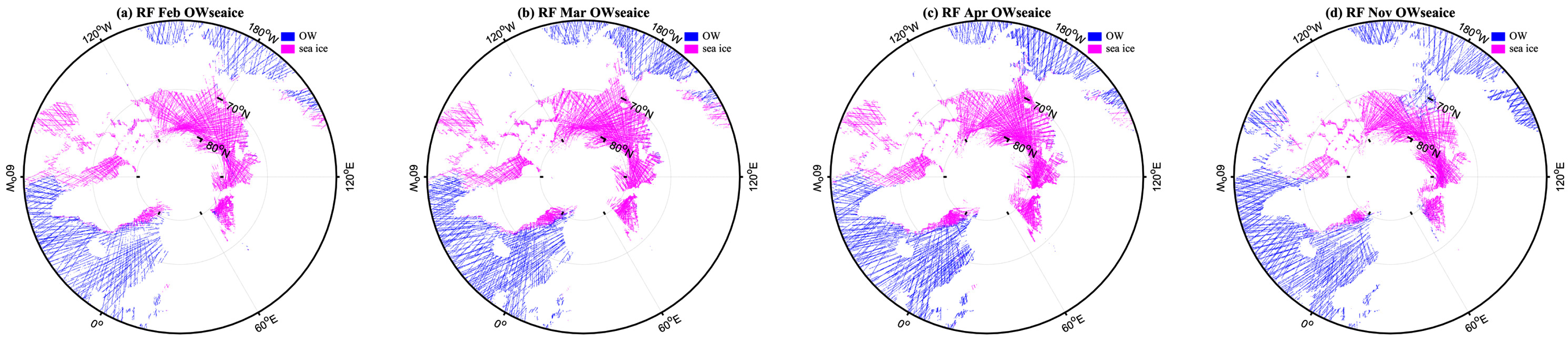
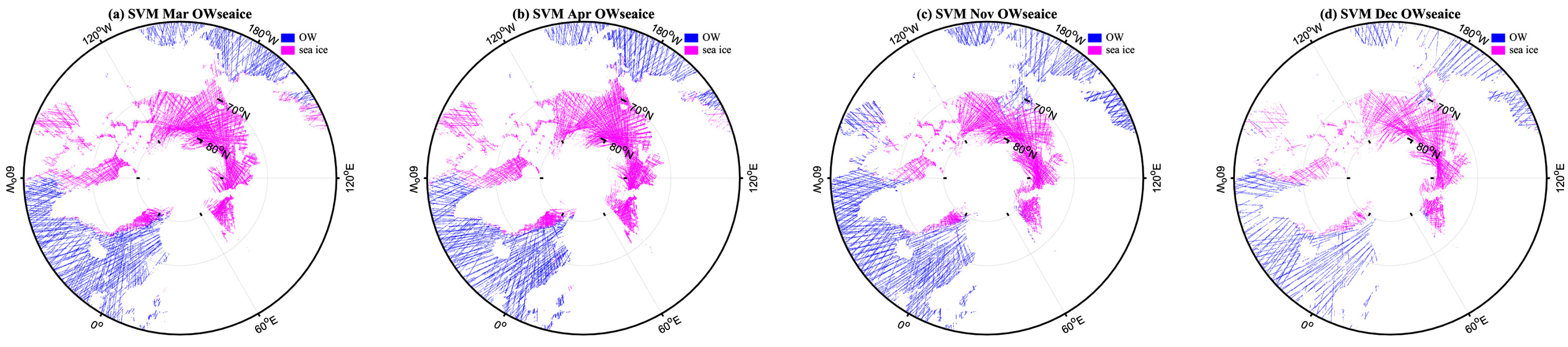

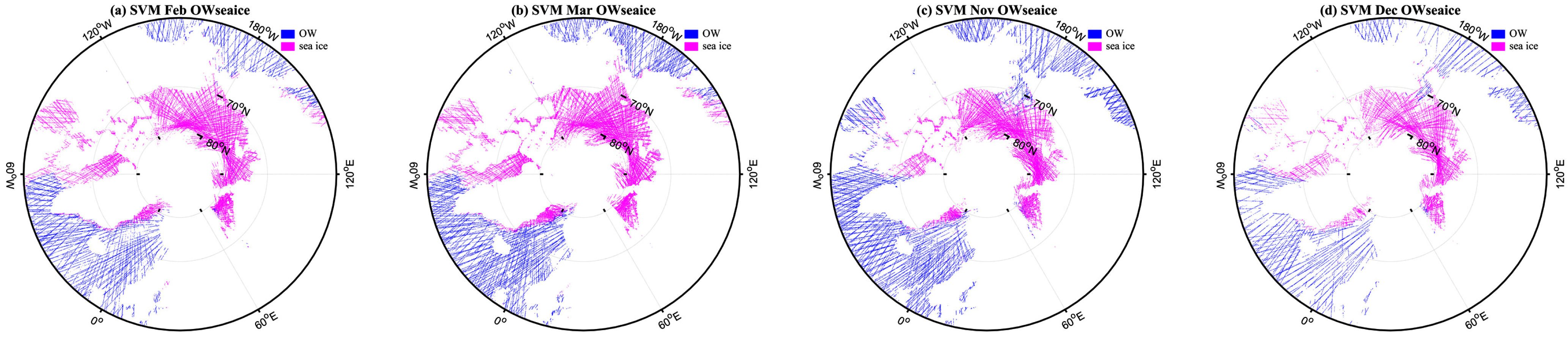
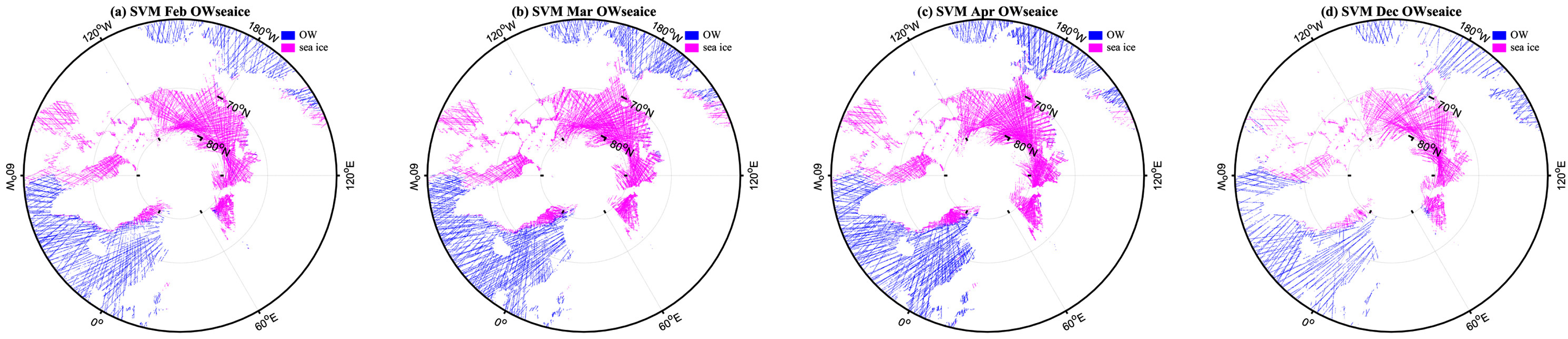

Appendix B



References
- Screen, J.A.; Simmonds, I. The central role of diminishing sea ice in recent Arctic temperature amplification. Nature 2010, 464, 1334–1337. [Google Scholar] [CrossRef] [Green Version]
- Park, J.-W.; Korosov, A.A.; Babiker, M.; Won, J.-S.; Hansen, M.W.; Kim, H.-C. Classification of sea ice types in sentinel-1 SAR images. Cryosphere Discuss 2019, 2019, 1–23. [Google Scholar]
- Dabboor, M.; Geldsetzer, T. Towards sea ice classification using simulated RADARSAT Constellation Mission compact polarimetric SAR imagery. Remote Sens. Environ. 2014, 140, 189–195. [Google Scholar] [CrossRef]
- Leisti, H.; Riska, K.; Heiler, I.; Eriksson, P.; Haapala, J. A method for observing compression in sea ice fields using IceCam. Cold Reg. Sci. Technol. 2009, 59, 65–77. [Google Scholar] [CrossRef]
- Kern, S.; Lavergne, T.; Notz, D.; Pedersen, L.T.; Tonboe, R.T.; Saldo, R.; Sørensen, A.M. Satellite passive microwave sea-ice concentration data set intercomparison: Closed ice and ship-based observations. Cryosphere 2019, 13, 3261–3307. [Google Scholar] [CrossRef] [Green Version]
- Kurtz, N.T.; Farrell, S.L.; Studinger, M.; Galin, N.; Harbeck, J.P.; Lindsay, R.; Onana, V.D.; Panzer, B.; Sonntag, J.G. Sea ice thickness, freeboard, and snow depth products from Operation IceBridge airborne data. Cryosphere 2013, 7, 1035–1056. [Google Scholar] [CrossRef] [Green Version]
- Lindsay, R.; Schweiger, A. Arctic sea ice thickness loss determined using subsurface, aircraft, and satellite observations. Cryosphere 2015, 9, 269–283. [Google Scholar] [CrossRef] [Green Version]
- Cardellach, E.; Fabra, F.; Nogués-Correig, O.; Oliveras, S.; Ribó, S.; Rius, A. GNSS-R ground-based and airborne campaigns for ocean, land, ice, and snow techniques: Application to the GOLD-RTR data sets. Radio Sci. 2011, 46, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Martin-Neira, M. A passive reflectometry and interferometry system (PARIS): Application to ocean altimetry. ESA J. 1993, 17, 331–355. [Google Scholar]
- Hall, C.D.; Cordey, R.A. Multistatic Scatterometry; IEEE: Piscataway, NJ, USA, 1988; pp. 561–562. [Google Scholar]
- Liu, Y.; Collett, I.; Morton, Y.J. Application of neural network to gnss-r wind speed retrieval. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9756–9766. [Google Scholar] [CrossRef]
- Yu, K.; Li, Y.; Chang, X. Snow depth estimation based on combination of pseudorange and carrier phase of GNSS dual-frequency signals. IEEE Trans. Geosci. Remote Sens. 2018, 57, 1817–1828. [Google Scholar] [CrossRef]
- Camps, A.; Park, H.; Pablos, M.; Foti, G.; Gommenginger, C.P.; Liu, P.-W.; Judge, J. Sensitivity of GNSS-R spaceborne observations to soil moisture and vegetation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4730–4742. [Google Scholar] [CrossRef] [Green Version]
- Cardellach, E.; Rius, A.; Martín-Neira, M.; Fabra, F.; Nogués-Correig, O.; Ribó, S.; Kainulainen, J.; Camps, A.; D’Addio, S. Consolidating the precision of interferometric GNSS-R ocean altimetry using airborne experimental data. IEEE Trans. Geosci. Remote Sens. 2013, 52, 4992–5004. [Google Scholar] [CrossRef]
- Alonso-Arroyo, A.; Zavorotny, V.U.; Camps, A. Sea ice detection using UK TDS-1 GNSS-R data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4989–5001. [Google Scholar] [CrossRef] [Green Version]
- Unwin, M.; Jales, P.; Tye, J.; Gommenginger, C.; Foti, G.; Rosello, J. Spaceborne GNSS-reflectometry on TechDemoSat-1: Early mission operations and exploitation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4525–4539. [Google Scholar] [CrossRef]
- Ruf, C.S.; Chew, C.; Lang, T.; Morris, M.G.; Nave, K.; Ridley, A.; Balasubramaniam, R. A new paradigm in earth environmental monitoring with the CYGNSS small satellite constellation. Sci. Rep. 2018, 8, 1–13. [Google Scholar]
- Jing, C.; Niu, X.; Duan, C.; Lu, F.; Di, G.; Yang, X. Sea Surface Wind Speed Retrieval from the First Chinese GNSS-R Mission: Technique and Preliminary Results. Remote Sens. 2019, 11, 3013. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Wang, X.; Du, Q.; Bai, W.; Xia, J.; Cai, Y.; Wang, D.; Wu, C.; Meng, X.; Tian, Y. The Status and Progress of Fengyun-3e GNOS II Mission for GNSS Remote Sensing. In Proceedings of the IGARSS 2019–2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 2 August 2019; pp. 5181–5184. [Google Scholar]
- Yan, Q.; Huang, W. Spaceborne GNSS-R sea ice detection using delay-Doppler maps: First results from the UK TechDemoSat-1 mission. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4795–4801. [Google Scholar] [CrossRef]
- Zhu, Y.; Yu, K.; Zou, J.; Wickert, J. Sea ice detection based on differential delay-Doppler maps from UK TechDemoSat-1. Sensors 2017, 17, 1614. [Google Scholar] [CrossRef] [Green Version]
- Schiavulli, D.; Frappart, F.; Ramillien, G.; Darrozes, J.; Nunziata, F.; Migliaccio, M. Observing sea/ice transition using radar images generated from TechDemoSat-1 Delay Doppler Maps. IEEE Geosci. Remote Sens. Lett. 2017, 14, 734–738. [Google Scholar] [CrossRef]
- Zhu, Y.; Tao, T.; Yu, K.; Li, Z.; Qu, X.; Ye, Z.; Geng, J.; Zou, J.; Semmling, M.; Wickert, J. Sensing Sea Ice Based on Doppler Spread Analysis of Spaceborne GNSS-R Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 217–226. [Google Scholar] [CrossRef]
- Cartwright, J.; Banks, C.J.; Srokosz, M. Sea ice detection using GNSS-R data from TechDemoSat-1. J. Geophys. Res. Ocean. 2019, 124, 5801–5810. [Google Scholar] [CrossRef]
- Li, W.; Cardellach, E.; Fabra, F.; Rius, A.; Ribó, S.; Martín-Neira, M. First spaceborne phase altimetry over sea ice using TechDemoSat-1 GNSS-R signals. Geophys. Res. Lett. 2017, 44, 8369–8376. [Google Scholar] [CrossRef]
- Hu, C.; Benson, C.; Rizos, C.; Qiao, L. Single-pass sub-meter space-based GNSS-R ice altimetry: Results from TDS-1. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3782–3788. [Google Scholar] [CrossRef]
- Li, W.; Cardellach, E.; Fabra, F.; Ribó, S.; Rius, A. Measuring Greenland ice sheet melt using spaceborne GNSS reflectometry from TechDemoSat-1. Geophys. Res. Lett. 2020, 47, e2019GL086477. [Google Scholar] [CrossRef]
- Yan, Q.; Huang, W. Sea ice thickness measurement using spaceborne GNSS-R: First results with TechDemoSat-1 data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 577–587. [Google Scholar] [CrossRef]
- Zhu, Y.; Tao, T.; Zou, J.; Yu, K.; Wickert, J.; Semmling, M. Spaceborne GNSS Reflectometry for Retrieving Sea Ice Concentration Using TDS-1 Data. IEEE Geosci. Remote Sens. Lett. 2020, 18, 612–616. [Google Scholar] [CrossRef]
- Rodriguez-Alvarez, N.; Holt, B.; Jaruwatanadilok, S.; Podest, E.; Cavanaugh, K.C. An Arctic sea ice multi-step classification based on GNSS-R data from the TDS-1 mission. Remote Sens. Environ. 2019, 230, 111202. [Google Scholar] [CrossRef]
- Lary, D.J.; Alavi, A.H.; Gandomi, A.H.; Walker, A.L. Machine learning in geosciences and remote sensing. Geosci. Front. 2016, 7, 3–10. [Google Scholar] [CrossRef] [Green Version]
- Maxwell, A.E.; Warner, T.A.; Fang, F. Implementation of machine-learning classification in remote sensing: An applied review. Int. J. Remote Sens. 2018, 39, 2784–2817. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Guo, H.; Zhang, L. SVM-based sea ice classification using textural features and concentration from RADARSAT-2 dual-pol ScanSAR data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 8, 1601–1613. [Google Scholar] [CrossRef]
- Deng, Z.; Sun, H.; Zhou, S.; Zhao, J.; Lei, L.; Zou, H. Multi-scale object detection in remote sensing imagery with convolutional neural networks. ISPRS J. Photogramm. Remote Sens. 2018, 145, 3–22. [Google Scholar] [CrossRef]
- Hafeez, S.; Wong, M.S.; Ho, H.C.; Nazeer, M.; Nichol, J.; Abbas, S.; Tang, D.; Lee, K.H.; Pun, L. Comparison of machine learning algorithms for retrieval of water quality indicators in case-II waters: A case study of Hong Kong. Remote Sens. 2019, 11, 617. [Google Scholar] [CrossRef] [Green Version]
- Yan, Q.; Huang, W.; Moloney, C. Neural networks based sea ice detection and concentration retrieval from GNSS-R delay-Doppler maps. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3789–3798. [Google Scholar] [CrossRef]
- Yan, Q.; Huang, W. Sea ice sensing from GNSS-R data using convolutional neural networks. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1510–1514. [Google Scholar] [CrossRef]
- Yan, Q.; Huang, W. Detecting sea ice from TechDemoSat-1 data using support vector machines with feature selection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1409–1416. [Google Scholar] [CrossRef]
- Zhu, Y.; Tao, T.; Yu, K.; Qu, X.; Li, S.; Wickert, J.; Semmling, M. Machine Learning-Aided Sea Ice Monitoring Using Feature Sequences Extracted from Spaceborne GNSS-Reflectometry Data. Remote Sens. 2020, 12, 3751. [Google Scholar] [CrossRef]
- Llaveria, D.; Munoz-Martin, J.F.; Herbert, C.; Pablos, M.; Park, H.; Camps, A. Sea Ice Concentration and Sea Ice Extent Mapping with L-Band Microwave Radiometry and GNSS-R Data from the FFSCat Mission Using Neural Networks. Remote Sens. 2021, 13, 1139. [Google Scholar] [CrossRef]
- Herbert, C.; Munoz-Martin, J.F.; Llaveria, D.; Pablos, M.; Camps, A. Sea Ice Thickness Estimation Based on Regression Neural Networks Using L-Band Microwave Radiometry Data from the FSSCat Mission. Remote Sens. 2021, 13, 1366. [Google Scholar] [CrossRef]
- Shu, S.; Zhou, X.; Shen, X.; Liu, Z.; Tang, Q.; Li, H.; Ke, C.; Li, J. Discrimination of different sea ice types from CryoSat-2 satellite data using an Object-based Random Forest (ORF). Mar. Geod. 2020, 43, 213–233. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Aaboe, S.; Breivik, L.-A.; Sørensen, A.; Eastwood, S.; Lavergne, T. Global Sea Ice Edge and Type Product User’s Manual OSI-402-c & OSI-403-c v2.3; EUMETSAT OSISAF: France, 2018. [Google Scholar]
- Jales, P.; Unwin, M. MERRByS Product Manual: GNSS Reflectometry on TDS-1 with the SGR-ReSI; Surrey Satellite Technol. Ld.: Guildford, UK, 2019. [Google Scholar]
- Zavorotny, V.U.; Voronovich, A.G. Scattering of GPS signals from the ocean with wind remote sensing application. IEEE Trans. Geosci. Remote Sens. 2000, 38, 951–964. [Google Scholar] [CrossRef] [Green Version]
- Voronovich, A.G.; Zavorotny, V.U. Bistatic radar equation for signals of opportunity revisited. IEEE Trans. Geosci. Remote Sens. 2017, 56, 1959–1968. [Google Scholar] [CrossRef]
- Hajj, G.A.; Zuffada, C. Theoretical description of a bistatic system for ocean altimetry using the GPS signal. Radio Sci. 2003, 38. [Google Scholar] [CrossRef]
- Comite, D.; Cenci, L.; Colliander, A.; Pierdicca, N. Monitoring Freeze-Thaw State by Means of GNSS Reflectometry: An Analysis of TechDemoSat-1 Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 2996–3005. [Google Scholar] [CrossRef]
- Tsang, L.; Newton, R.W. Microwave emissions from soils with rough surfaces. J. Geophys. Res. Ocean. 1982, 87, 9017–9024. [Google Scholar] [CrossRef]
- Camps, A.; Park, H.; Portal, G.; Rossato, L. Sensitivity of TDS-1 GNSS-R reflectivity to soil moisture: Global and regional differences and impact of different spatial scales. Remote Sens. 2018, 10, 1856. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Dietterich, T.G. An experimental comparison of three methods for constructing ensembles of decision trees: Bagging, boosting, and randomization. Mach. Learn. 2000, 40, 139–157. [Google Scholar] [CrossRef]
- Lerman, R.I.; Yitzhaki, S. A note on the calculation and interpretation of the Gini index. Econ. Lett. 1984, 15, 363–368. [Google Scholar] [CrossRef]
- Ghimire, B.; Rogan, J.; Miller, J. Contextual land-cover classification: Incorporating spatial dependence in land-cover classification models using random forests and the Getis statistic. Remote Sens. Lett. 2010, 1, 45–54. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez-Galiano, V.F.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Muller, K.R.; Mika, S.; Ratsch, G.; Tsuda, K.; Scholkopf, B. An introduction to kernel-based learning algorithms. IEEE Trans. Neural Netw. 2001, 12, 181–201. [Google Scholar] [CrossRef] [Green Version]
- Anand, R.; Mehrotra, K.; Mohan, C.K.; Ranka, S. Efficient classification for multiclass problems using modular neural networks. IEEE Trans. Neural Netw. 1995, 6, 117–124. [Google Scholar] [CrossRef]
- Adnan, M.N.; Islam, M.Z. One-Vs-All Binarization Technique in the Context of Random Forest. In Proceedings of the European symposium on artificial neural networks, computational intelligence and machine learning, Bruges, Belgium, 22–24 April 2015; 2015; pp. 385–390. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Wong, T.-T.; Yeh, P.-Y. Reliable accuracy estimates from k-fold cross validation. IEEE Trans. Knowl. Data Eng. 2019, 32, 1586–1594. [Google Scholar] [CrossRef]


| Source | Algorithms | Purpose | Data Time Span | Overall Performance |
|---|---|---|---|---|
| Rodriguez-Alvarez et al. (2019) [30] | CART | Sea ice classification | 10 days of TDS-1 data in 2015 | Seawater 97% First-year ice 70% Multi-year ice 82% Young ice 81% |
| Yan et al. (2017) [36] | NN | Sea ice detection and SIC retrieval | 15 days of TDS-1 data in 2015 | ice detection:98.4% SIC retrieval error: 0.09 |
| Yan and Huang (2018) [37] | CNN | Sea ice detection and SIC retrieval | 15 days of TDS-1 data in 2015 | ice detection: 98.73% SIC retrieval error: 0.16 |
| Yan and Huang (2019) [38] | SVM | Sea ice detection | 15 days of TDS-1 data in 2015 | ice detection: 98.56% |
| Zhu et al. (2020) [39] | DT and RF | Sea ice detection | Four years of available TDS-1 data from 2015 to 2018 | DT: 97.51% in Arctic RF: 98.03% in Arctic |
| Llaveria et al. (2021) [40] | NN | Sea ice extent and Sea ice concentration | Two months data from FSSCat | Sea ice extent: 99% Sea ice concentration: 0.03 |
| Herbert et al. (2021) [41] | NN | Sea ice Thickness | Two months data from FSSCat | thin ice: 6.5 cm full-range: 23 cm |
| Parameter | Value |
|---|---|
| Orbit | quasi-Sun synchronous |
| Altitude | ~635 km |
| Inclination | 98.4° |
| Delay pixels/resolution | 128/244 ns |
| Doppler pixels/resolution | 20/500 Hz |
| Coherent integration time | 1 ms |
| Incoherent integration time | 1 s |
| Evaluation Metrics | Equation |
|---|---|
| Accuracy | |
| Precision | |
| Recall | |
| F-value | |
| G-mean | |
| Kappa coefficient |
| Evaluation Metrics | OW-Sea Ice Classification | FYI-MYI Classification | ||
|---|---|---|---|---|
| RF | SVM | RF | SVM | |
| Accuracy (%) | 98.83 | 98.60 | 84.82 | 71.71 |
| Precision (%) | 98.47 | 98.30 | 98.57 | 98.83 |
| Recall (%) | 98.07 | 97.56 | 84.79 | 70.19 |
| F1-value | 0.98 | 0.98 | 0.91 | 0.82 |
| G-mean | 0.99 | 0.98 | 0.85 | 0.79 |
| Kappa coefficient | 0.97 | 0.97 | 0.39 | 0.23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Tao, T.; Li, J.; Yu, K.; Wang, L.; Qu, X.; Li, S.; Semmling, M.; Wickert, J. Spaceborne GNSS-R for Sea Ice Classification Using Machine Learning Classifiers. Remote Sens. 2021, 13, 4577. https://doi.org/10.3390/rs13224577
Zhu Y, Tao T, Li J, Yu K, Wang L, Qu X, Li S, Semmling M, Wickert J. Spaceborne GNSS-R for Sea Ice Classification Using Machine Learning Classifiers. Remote Sensing. 2021; 13(22):4577. https://doi.org/10.3390/rs13224577
Chicago/Turabian StyleZhu, Yongchao, Tingye Tao, Jiangyang Li, Kegen Yu, Lei Wang, Xiaochuan Qu, Shuiping Li, Maximilian Semmling, and Jens Wickert. 2021. "Spaceborne GNSS-R for Sea Ice Classification Using Machine Learning Classifiers" Remote Sensing 13, no. 22: 4577. https://doi.org/10.3390/rs13224577
APA StyleZhu, Y., Tao, T., Li, J., Yu, K., Wang, L., Qu, X., Li, S., Semmling, M., & Wickert, J. (2021). Spaceborne GNSS-R for Sea Ice Classification Using Machine Learning Classifiers. Remote Sensing, 13(22), 4577. https://doi.org/10.3390/rs13224577








