Monitoring and Forecasting of Urban Expansion Using Machine Learning-Based Techniques and Remotely Sensed Data: A Case Study of Gharbia Governorate, Egypt
Abstract
:1. Introduction
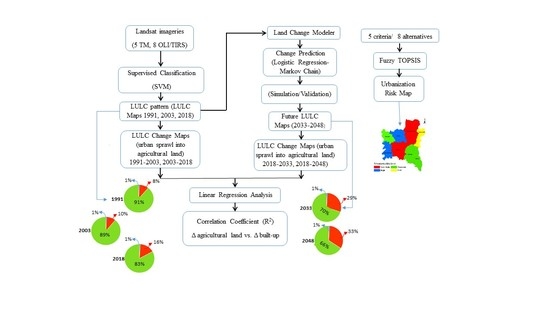
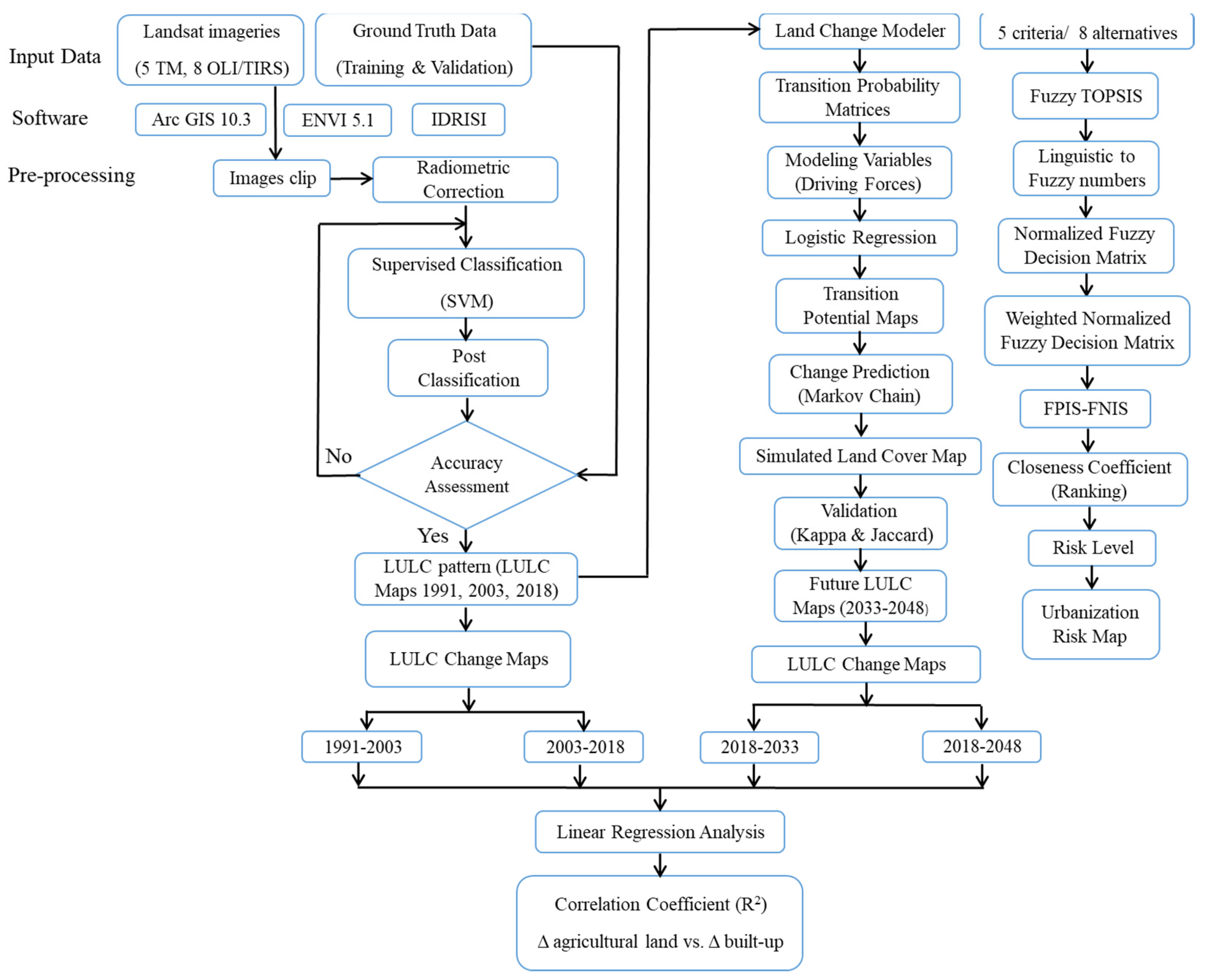
2. Materials and Methods
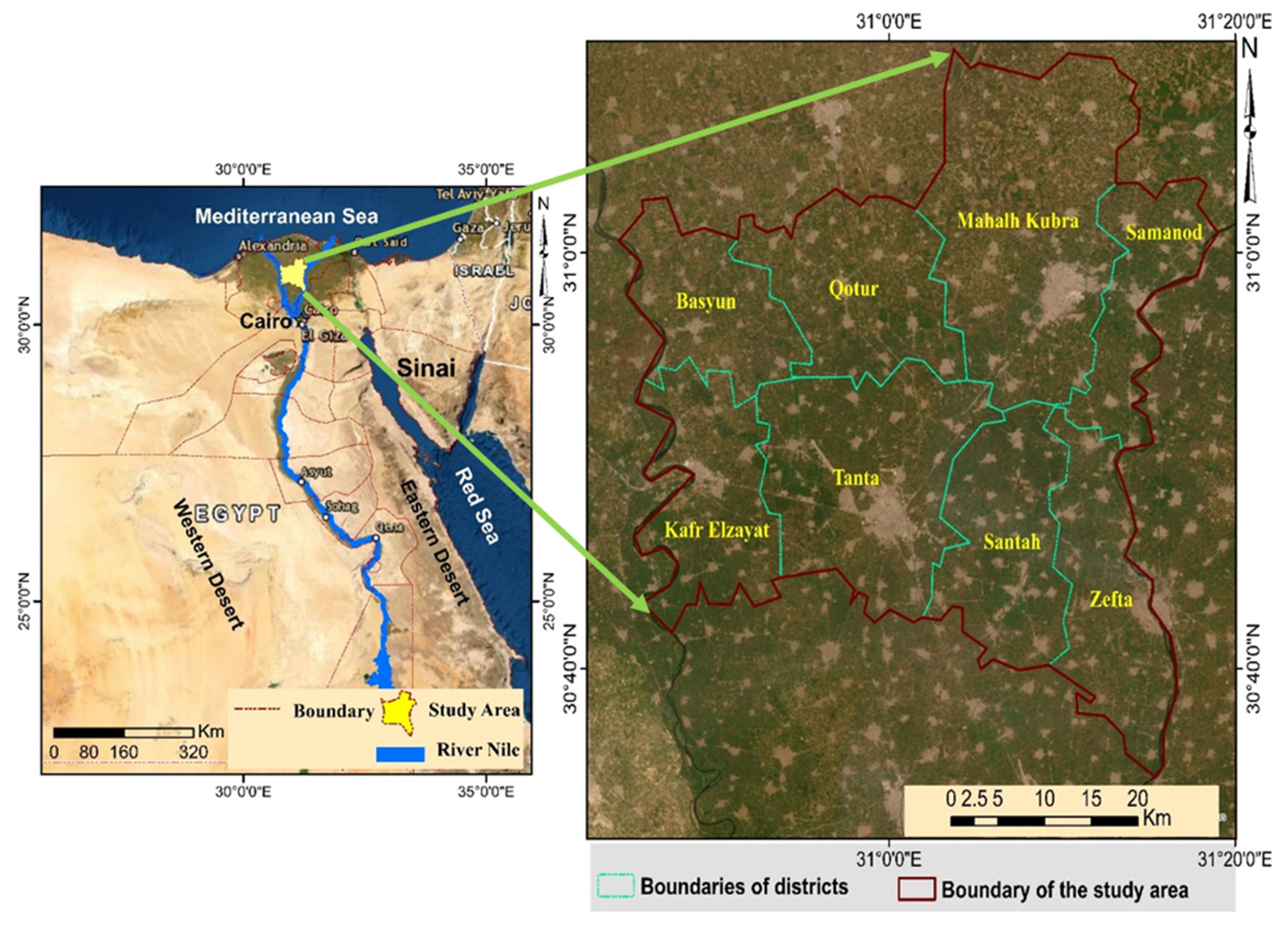
2.1. Study Area
2.2. Data Collection and Processing
2.3. LULC Classification
2.4. Accuracy Assessment
2.5. LULC Change Modeling
2.5.1. Model Calibration (1991–2003)
- a.
- The distance from roads: Roads can provide access to previously remote areas promoting urbanization near roadways.
- b.
- The distance from urban centers: Urban centers tend to grow and expand as the human population increases, such that the areas surrounding current urban centers are frequently susceptible to land change.
- c.
- The distance from persistent built-up areas: Areas that have already been disturbed by humans often have the infrastructure in place to promote further urbanization along current persistent built-up edges.
- d.
- The distance from railway stations: This is the same effect of the driver of “distance from roads”.
- e.
- Digital Elevation Model (DEM): Because of the environmental gradient, characteristics such as temperature and rainfall alter with elevation; elevation is a proper indicator of areas that are appropriate for cultivation (and thus are prone to transition to agricultural land) and for subsequent development (for instance, the lowland area is more disposed to evolution).
- f.
- Slope: The slope is the principal of determining whether the land is advantageous to humans. For example, agriculture and building require fairly gentle slopes, such that areas with these slopes may be more likely to experience land cover change.
2.5.2. LULC Simulation and Model Validation (2003–2018)
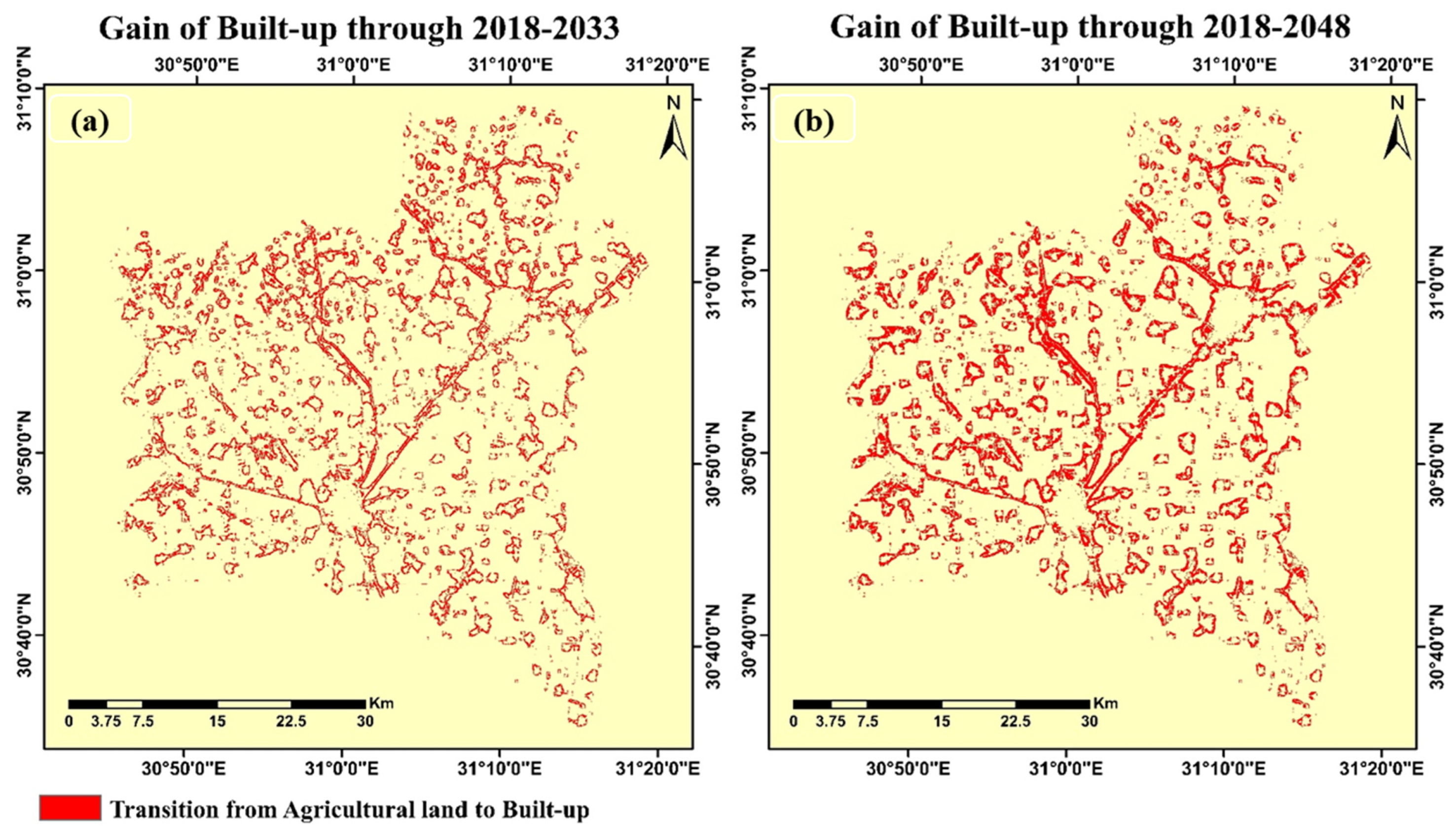
2.5.3. Projecting Future LULC Changes (2018–2033/2048)
2.6. Fuzzy TOPSIS Analysis
- Step 1: Alternatives rating by decision-makers and applying for fuzzy numbers.
- Step 2: Normalizing the fuzzy decision matrix using Equation (2).
- Step 3: Computing the weighted normalized fuzzy decision matrix using Equation (3).
- Step 4: Computing the Fuzzy Positive Ideal Solution (FPIS) using Equation (4) and the Fuzzy Negative Ideal Solution (FNIS) using Equation (5).
- Step 5: Computing the distance from each alternative to the FPIS and to the FNIS using Equation (6).
- Step 6: Compute the Closeness Coefficient (CCi) for each alternative using Equation (9).
3. Results
3.1. Accuracy of the LULC Maps
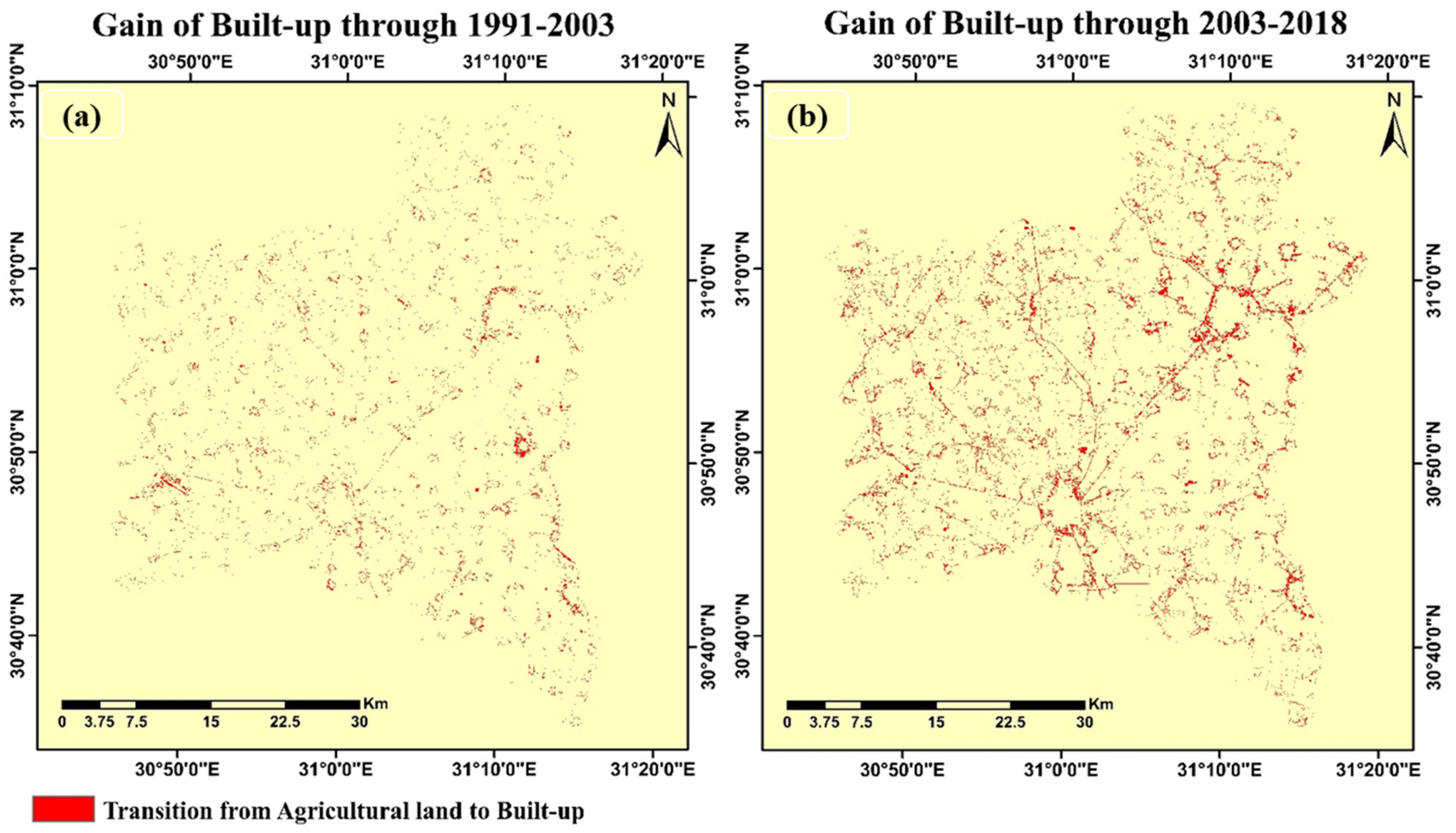
3.2. Spatiotemporal Analysis of LULCC
3.3. LULC Change Modeling, Simulation, and Projection
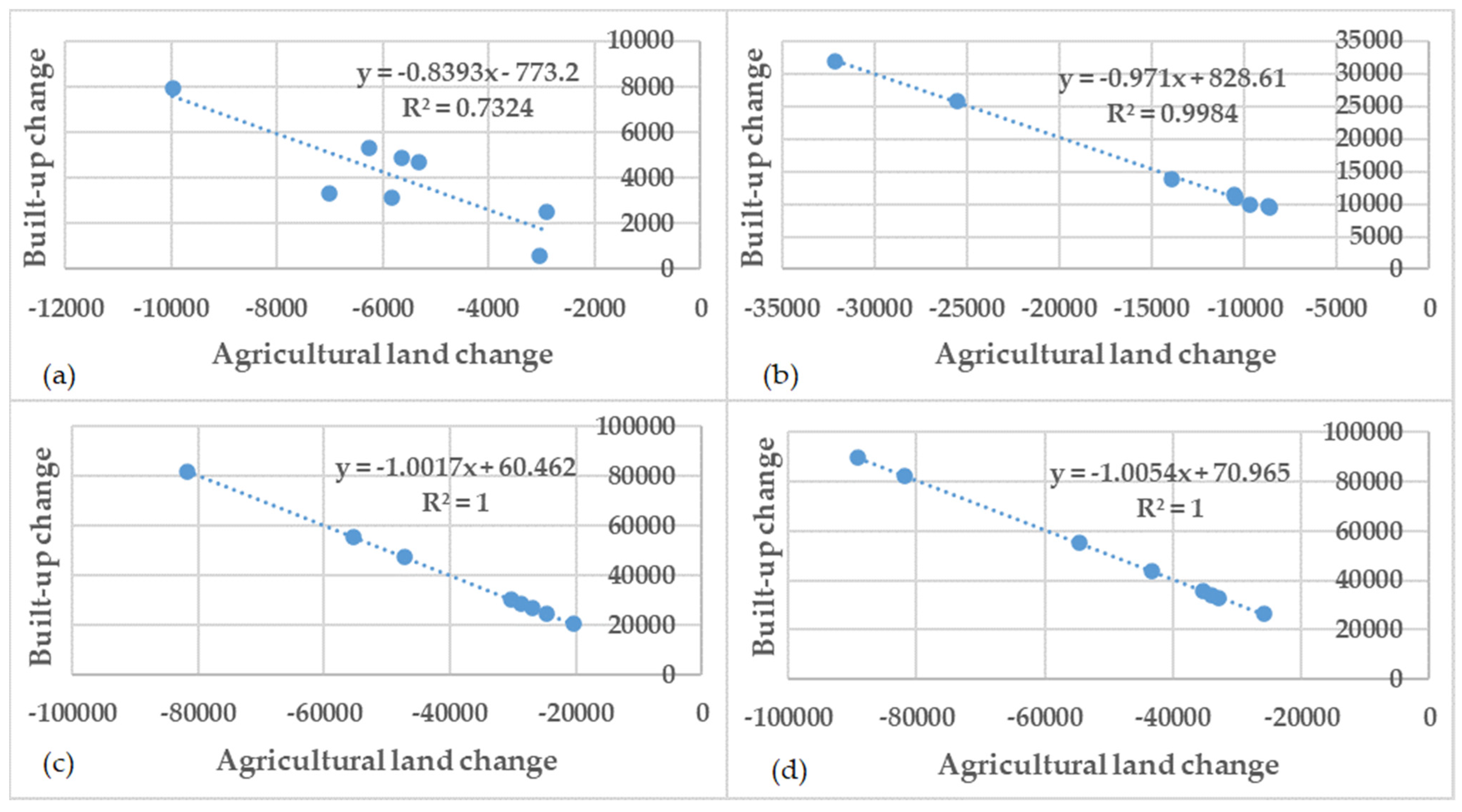
3.4. Linear Regression Analysis
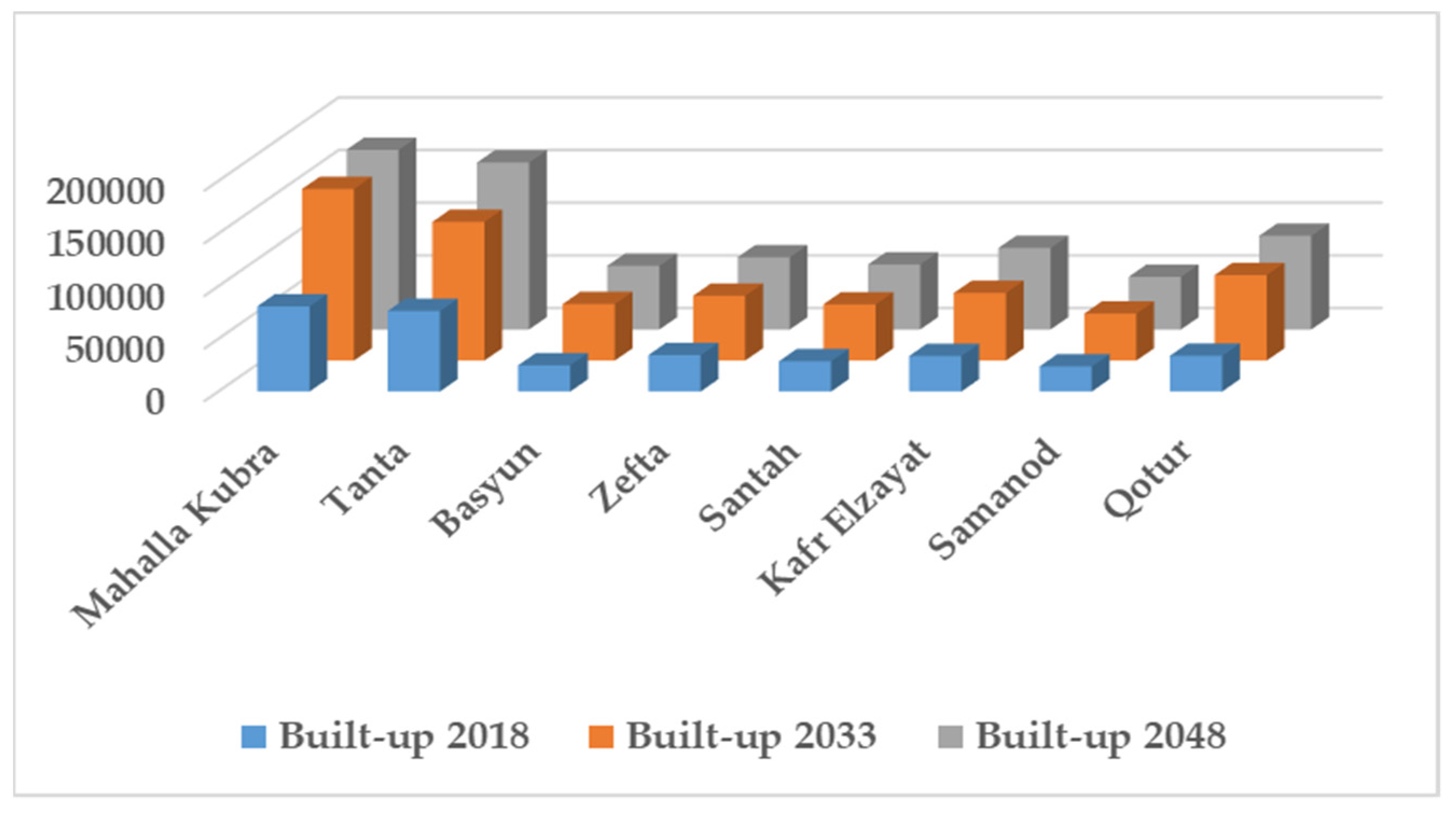
3.5. Analysis of Fuzzy TOPSIS
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Seto, K.C.; Güneralp, B.; Hutyra, L.R. Global forecasts of urban expansion to 2030 and direct impacts on biodiversity and carbon pools. Proc. Natl. Acad. Sci. USA 2012, 109, 16083–16088. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bakr, N.; Bahnassy, M.H. Egyptian Natural Resources. In The Soils of Egypt, 1st ed.; El-Ramady, H., Alshaal, T., Bakr, N., Elbana, T., Mohamed, E., Belal, A.A., Eds.; Springer: Cham, Switzerland, 2019; pp. 33–49. [Google Scholar]
- Van Vliet, J.; Eitelberg, D.A.; Verburg, P.H. A global analysis of land take in cropland areas and production displacement from urbanization. Glob. Environ. Chang. 2017, 43, 107–115. [Google Scholar] [CrossRef]
- Zhao, S.; Da, L.; Tang, Z.; Fang, H.; Song, K.; Fang, J. Ecological consequences of rapid urban expansion: Shanghai, China. Front. Ecol. Environ. 2006, 4, 341–346. [Google Scholar] [CrossRef]
- Grimm, N.B.; Faeth, S.H.; Golubiewski, N.E.; Redman, C.L.; Wu, J.; Bai, X.; Briggs, J.M. Global change and the ecology of cities. Science 2008, 319, 756–760. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Linard, C.; Tatem, A.J.; Gilbert, M. Modelling spatial patterns of urban growth in africa. Appl. Geogr. 2013, 44, 23–32. [Google Scholar] [CrossRef]
- Wu, Y.; Li, S.; Yu, S. Monitoring urban expansion and its effects on land use and land cover changes in Guangzhou city, China. Environ. Monit. Assess. 2016, 188, 1–15. [Google Scholar] [CrossRef]
- Guan, D.; Li, H.; Inohae, T.; Su, W.; Nagaie, T.; Hokao, K. Modeling urban land use change by the integration of cellular automaton and Markov model. Ecol. Model. 2011, 222, 3761–3772. [Google Scholar] [CrossRef]
- Ranagalage, M.; Wang, R.; Gunarathna, M.H.J.P.; Dissanayake, D.M.S.L.B.; Murayama, Y.; Simwanda, M. Spatial forecasting of the landscape in rapidly urbanizing hill stations of South Asia: A case study of Nuwara Eliya, Sri Lanka (1996–2037). Remote Sens. 2019, 11, 1743. [Google Scholar] [CrossRef] [Green Version]
- Rimal, B.; Sloan, S.; Keshtkar, H.; Sharma, R.; Rijal, S.; Shrestha, U.B. Patterns of historical and future urban expansion in Nepal. Remote Sens. 2020, 12, 628. [Google Scholar] [CrossRef] [Green Version]
- Dewan, A.M.; Corner, R.J. Spatiotemporal analysis of urban growth, sprawl and structure. In Dhaka Megacity, Geospatial Perspectives on Urbanization, Environment and Health; Springer: New York, NY, USA, 2013. [Google Scholar]
- El-Eraqi, M.B.; Shehata, M.S. The Urban Sprawl on Agricultural Lands in Gharbia Govornorate. Ar. Univ. J. Agric. Sci. 2019, 27, 1771–1781. [Google Scholar]
- Radwan, T.M.; Blackburn, G.A.; Whyatt, J.D.; Atkinson, P.M. Dramatic loss of agricultural land due to urban expansion threatens food security in the Nile Delta, Egypt. Remote Sens. 2019, 11, 332. [Google Scholar] [CrossRef] [Green Version]
- Abd El-Kawy, O.R.; Rød, J.K.; Ismail, H.A.; Suliman, A.S. Land use and land cover change detection in the western Nile delta of Egypt using remote sensing data. Appl. Geogr. 2011, 31, 483–494. [Google Scholar] [CrossRef]
- Bratley, K.; Ghoneim, E. Modeling Urban Encroachment on the Agricultural Land of the Eastern Nile Delta Using Remote Sensing and a GIS-Based Markov Chain Model. Land 2018, 7, 114. [Google Scholar] [CrossRef] [Green Version]
- Bakr, N.; Weindorf, D.C.; Bahnassy, M.H.; Marei, S.M.; El-Badawi, M.M. Monitoring land cover changes in a newly reclaimed area of Egypt using multi-temporal Landsat data. Appl. Geogr. 2010, 30, 592–605. [Google Scholar] [CrossRef]
- Sarker, I.H.; Hoque, M.M.; Uddin, M.K.; Alsanoosy, T. Mobile data science and intelligent apps: Concepts, ai-based modeling and research directions. Mob. Netw. Appl. 2021, 26, 285–303. [Google Scholar] [CrossRef]
- Rai, R.; Zhang, Y.; Paudel, B.; Acharya, B.; Basnet, L. Land use and land cover dynamics and assessing the ecosystem service values in the trans-boundary gandaki river basin, central himalayas. Sustainability 2018, 10, 3052. [Google Scholar] [CrossRef] [Green Version]
- Liping, C.; Yujun, S.; Saeed, S. Monitoring and predicting land use and land cover changes using remote sensing and gis techniques—A case study of a hilly area, Jiangle, China. PLoS ONE 2018, 13, e0200493. [Google Scholar] [CrossRef] [PubMed]
- Sarker, I.H.; Kayes, A.S.M.; Badsha, S.; Alqahtani, H.; Watters, P.; Ng, A. Cybersecurity data science: An overview from machine learning perspective. J. Big Data 2020, 7, 1–29. [Google Scholar] [CrossRef]
- Han, J.; Pei, J.; Kamber, M. Data Mining: Concepts and Techniques; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Bray, M.; Han, D. Identification of support vector machines for runoff modelling. J. Hydroinform. 2004, 6, 265–280. [Google Scholar] [CrossRef] [Green Version]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learning 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Moghaddamnia, A.; Gosheh, M.; Nuraie, M.; Mansuri, M.; Han, D.; Schmitter, E. Performance evaluation of LLR, SVM, CGNN and BFGSNN models to evaporation estimation. Water Geosci. 2010, 9, 108–113. [Google Scholar]
- Han, D.; Chan, L.; Zhu, N. Flood forecasting using support vector machines. J. Hydroinform. 2007, 9, 267–276. [Google Scholar] [CrossRef]
- Taati, A.; Sarmadian, F.; Mousavi, A.; Pour, C.T.H.; Shahir, A.H.E. Land use classification using support vector machine and maximum likelihood algorithms by Landsat 5 TM images. Walailak J. Sci. Tech. (WJST) 2015, 12, 681–687. [Google Scholar]
- Yousefi, S.; Tazeh, M.; Mirzaee, S.; Moradi, H.R.; Tavangar, S.H. Comparison of different classification algorithms in satellite imagery to produce land use maps (Case study: Noor city). J. Appl. RS GIS Tech. Nat. Res. Sci. 2011, 2, 15–25. [Google Scholar]
- Clarke, K.C. Land use change modeling with sleuth: Improving calibration with a genetic algorithm. In Geomatic Approaches for Modeling Land Change Scenarios; Camacho Olmedo, M.T., Paegelow, M., Mas, J.-F., Escobar, F., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 139–161. [Google Scholar]
- Verburg, P.H.; Overmars, K.P. Dynamic simulation of land-use change trajectories with the clue-s model. In Modelling Land-Use Change: Progress and Applications; Koomen, E., Stillwell, J., Bakema, A., Scholten, H.J., Eds.; Springer: Dordrecht, The Netherlands, 2007; pp. 321–337. [Google Scholar]
- Kuo, H.-F.; Tsou, K.-W. Modeling and simulation of the future impacts of urban land use change on the natural environment by sleuth and cluster analysis. Sustainability 2018, 10, 72. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Son, N.; Chang, N.; Chen, C.; Chang, L.; Valdez, M.; Centeno, G.; Thompson, C.A.; Aceituno, J.L. Multi-decadal mangrove forest change detection and prediction in Honduras, Central America, with Landsat imagery and a Markov Chain Model. Remote Sens. 2013, 5, 6408–6426. [Google Scholar] [CrossRef] [Green Version]
- Weiguo, J.; Zheng, C.; Xuan, L.E.I.; Kai, J.I.A.; Yongfeng, W.U. Simulating urban land use change by incorporating an autologistic regression model into a CLUE-S model. J. Geogr. Sci. 2015, 25, 836–850. [Google Scholar]
- Arsanjani, J.J.; Helbich, M.; Kainz, W.; Boloorani, A.D. Integration of logistic regression, markov chain and cellular automata models to simulate urban expansion. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 265–275. [Google Scholar] [CrossRef]
- Hamdy, O.; Zhao, S.; Osman, T.; Salheen, M.A.; Eid, Y.Y. Applying a hybrid model of Markov chain and logistic regression to identify future urban sprawl in Abouelreesh, Aswan: A case study. Geosciences 2016, 6, 43. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, V.T.; Le, T.T.H.; La, P.H. Predicting land use change affected by population growth by integrating logistic regression, Markov chain and cellular automata models. J. Korean Soc. Surv. Geod. Photogramm Cart. 2017, 35, 221–230. [Google Scholar]
- Verhagen, P. Case Studies in Archaeological Predictive Modeling; Amsterdam University Press: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Dewan, A.M.; Yamaguchi, Y. Land use and land cover change in Greater Dhaka, Bangladesh: Using remote sensing to promote sustainable urbanization. Appl. Geogr. 2009, 29, 390–401. [Google Scholar] [CrossRef]
- Negm, A.M.; Saavedra, O.; El-Adawy, A. Nile Delta Biography: Challenges and Opportunities. In The Nile Delta; Negm, A., Ed.; The Handbook of Environmental Chemistry; Springer: Cham, Switzerland, 2016; Volume 55. [Google Scholar]
- Erkan, U.; Gökrem, L. A new method based on pixel density in salt and pepper noise removal. Turk. J. Electr. Eng. Comput. Sci. 2018, 26, 162–171. [Google Scholar] [CrossRef]
- Sakthidasan, K.; Nagappan, N.V. Noise free image restoration using hybrid filter with adaptive genetic algorithm. Comput. Electr. Eng. 2016, 54, 382–392. [Google Scholar] [CrossRef]
- Vivekananda, G.N.; Swathi, R.; Sujith, A.V.L.N. Multi-temporal image analysis for LULC classification and change detection. Eur. J. Remote. Sens. 2021, 54 (Suppl. S2), 189–199. [Google Scholar] [CrossRef]
- Talukdar, S.; Singha, P.; Mahato, S.; Pal, S.; Liou, Y.A.; Rahman, A. Land-use land-cover classification by machine learning classifiers for satellite observations—A review. Remote Sens. 2020, 12, 1135. [Google Scholar] [CrossRef] [Green Version]
- Foody, G.M. Status of land cover classification accuracy assessment. Remote Sens. Environ. 2002, 80, 185–201. [Google Scholar] [CrossRef]
- Bharatkar, P.S.; Patel, R. Approach to accuracy assessment tor RS image classification techniques. Int. J. Sci. Eng. Res. 2013, 4, 79–86. [Google Scholar]
- Li, C. Monitoring and Analysis of Urban Growth Process Using Remote Sensing, GIS and Cellular Automata Modeling: A Case Study of Xuzhou City, China. Ph.D. Thesis, Universitätsbibliothek, Dortmund, Germany, September 2014. [Google Scholar]
- Ramachandra, T.V.; Aithal, H.B.; Vinay, S.; Joshi, N.V.; Kumar, U.; Rao, K.V. Modelling urban revolution in Greater Bangalore, India. In Proceedings of the 30th Annual In-House Symposium on Space Science and Technology, Bangalore, India, 7–8 November 2013; pp. 7–8. [Google Scholar]
- Sang, L.; Zhang, C.; Yang, J.; Zhu, D.; Yun, W. Simulation of land use spatial pattern of towns and villages based on CA-Markov model. Math. Comput. Model. 2011, 54, 938–943. [Google Scholar] [CrossRef]
- Kore, N.B.; Ravi, K.; Patil, S.B. A simplified description of fuzzy TOPSIS method for multi criteria decision making. Int. Res. J. Eng. Tech. (IRJET) 2017, 4, 2047–2050. [Google Scholar]
- Gutiérrez, S.; Tardaguila, J.; Fernández-Novales, J.; Diago, M.P. Support vector machine and artificial neural network models for the classification of grapevine varieties using a portable NIR spectrophotometer. PLoS ONE 2015, 10, e0143197. [Google Scholar] [CrossRef]
- Mustafa, E.K.; Co, Y.; Liu, G.; Kaloop, M.R.; Beshr, A.A.; Zarzoura, F.; Sadek, M. Study for Predicting Land Surface Temperature (LST) Using Landsat Data: A Comparison of Four Algorithms. Adv. Civ. Eng. 2020, 2020, 7363546. [Google Scholar] [CrossRef]
- Sadek, M.; Li, X. Low-cost solution for assessment of urban flash flood impacts using sentinel-2 satellite images and fuzzy analytic hierarchy process: A case study of ras ghareb city, Egypt. Adv. Civ. Eng. 2019, 2019, 2561215. [Google Scholar] [CrossRef] [Green Version]
- Almouctar, M.A.S.; Wu, Y.; Kumar, A.; Zhao, F.; Mambu, K.J.; Sadek, M. Spatiotemporal analysis of vegetation cover changes around surface water based on NDVI: A case study in Korama basin, Southern Zinder, Niger. Appl. Water Sci. 2020, 11, 1–14. [Google Scholar] [CrossRef]
- Kamusoko, C.; Aniya, M. Hybrid classification of Landsat data and GIS for land use/cover change analysis of the Bindura district, Zimbabwe. Int. J. Remote Sens. 2008, 30, 97–115. [Google Scholar] [CrossRef]
- Sadek, M.; Li, X.; Mostafa, E.; Freeshah, M.; Kamal, A.; Sidi Almouctar, M.A.; Mustafa, E.K. Low-Cost Solutions for Assessment of Flash Flood Impacts Using Sentinel-1/2 Data Fusion and Hydrologic/Hydraulic Modeling: Wadi El-Natrun Region, Egypt. Adv. Civ. Eng. 2020. [Google Scholar] [CrossRef]
- Dossou, J.; Li, X.; Sadek, M.; Mostafa, E. Hybrid model of ecological vulnerability assessment in Benin. Sci. Rep. 2021. Available online: https://www.nature.com/articles/s41598-021-81742-2 (accessed on 21 June 2021). [CrossRef]
- Rousta, I.; Sarif, M.O.; Gupta, R.D.; Olafsson, H.; Ranagalage, M.; Murayama, Y.; Zhang, H.; Mushore, T.D. Spatiotemporal analysis of land use/land cover and its effects on surface urban heat island using Landsat data: A case study of metropolitan city Tehran (1988–2018). Sustainability 2018, 10, 4433. [Google Scholar] [CrossRef] [Green Version]
- Dissanayake, D.; Morimoto, T.; Murayama, Y.; Ranagalage, M. Impact of landscape structure on the variation of land surface temperature in sub-saharan region: A case study of Addis Ababa using Landsat data (1986–2016). Sustainability 2019, 11, 2257. [Google Scholar] [CrossRef] [Green Version]
- Hamdy, O.; Zhao, S.; Salheen, M.A.; Eid, Y.Y. Analyses the driving forces for urban growth by using IDRISI® Selva Models Abouelreesh Aswan as a Case Study. Int. J. Eng. Technol. 2017, 9, 226. [Google Scholar] [CrossRef] [Green Version]
- Eastman, J.R. Manual for Using Terrset; Clark Labs, Clark University: Worcester, MA, USA, 2018. [Google Scholar]
- CLARK LAB. Available online: https://clarklabs.org (accessed on 8 September 2019).
- Rizk, I.; Rashed, M. Monitoring urban growth and land use change detection with GIS and remote sensing techniques in Daqahlia governorate Egypt. Int. J. Sustain. Built Environ. 2015, 4, 117–124. [Google Scholar]
- Rimal, B.; Zhang, L.; Keshtkar, H.; Wang, N.; Lin, Y. Monitoring and modeling of spatiotemporal urban expansion and land-use/land-cover change using integrated Markov chain cellular automata model. ISPRS Int. J. Geo-Inf. 2017, 6, 288. [Google Scholar] [CrossRef] [Green Version]
- Keshtkar, H.; Voigt, W. Potential impacts of climate and landscape fragmentation changes on plant distributions: Coupling multi-temporal satellite imagery with gis-based cellular automata model. Ecol. Inform. 2016, 32, 145–155. [Google Scholar] [CrossRef]
- Hou, H.; Wang, R.; Murayama, Y. Scenario-based modelling for urban sustainability focusing on changes in cropland under rapid urbanization: A case study of Hangzhou from 1990 to 2035. Sci. Total Environ. 2019, 661, 422–431. [Google Scholar] [CrossRef]
- Wang, R.; Derdouri, A.; Murayama, Y. Spatiotemporal simulation of future land use/cover change scenarios in the Tokyo metropolitan area. Sustainability 2018, 10, 2056. [Google Scholar] [CrossRef] [Green Version]
- Subasinghe, S.; Estoque, R.C.; Murayama, Y. Spatiotemporal analysis of urban growth using GIS and remote sensing: A case study of the Colombo Metropolitan Area, Sri Lanka. ISPRS Int. J. Geo-Inf. 2016, 5, 197. [Google Scholar] [CrossRef] [Green Version]
- Thapa, R.B.; Murayama, Y. Scenario based urban growth allocation in Kathmandu Valley, Nepal. Landsc. Urban Plan. 2012, 105, 140–148. [Google Scholar] [CrossRef]
- Mishra, V.N.; Rai, P.K. A remote sensing aided multi-layer perceptron-Markov chain analysis for land use and land cover change prediction in Patna district (Bihar), India. Arab. J. Geosci. 2016, 9, 249. [Google Scholar] [CrossRef]
- Estoque, R.C.; Murayama, Y. Examining the potential impact of land use/cover changes on the ecosystem services of Baguio city, the Philippines: A scenario-based analysis. Appl. Geogr. 2012, 35, 316–326. [Google Scholar] [CrossRef]
- Ahmed, B.; Ahmed, R.; Zhu, X. Evaluation of model validation techniques in land cover dynamics. ISPRS Int. J. Geo-Inf. 2013, 2, 577–597. [Google Scholar] [CrossRef]
- Van Vliet, J.; Bregt, A.K.; Hagen-zanker, A. Revisiting Kappa to account for change in the accuracy assessment of land-use change models. Ecol. Model. 2011, 222, 1367–1375. [Google Scholar] [CrossRef]
- Landis, J.R.; Koch, G.G. The measurement of observer agreement for categorical Data. Biometrics 1977, 33, 159–174. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Flo, J.; Landmark, B.; Hatlevik, O.E.; Fagerström, L. Using a new interrater reliability method to test the modified oulu patient classification instrument in home health care. Nurs. Open 2018, 5, 167–175. [Google Scholar] [CrossRef] [Green Version]
- Pontius, R.G., Jr.; Millones, M. Death to Kappa: Birth of quantity disagreement and allocation disagreement for accuracy assessment. Int. J. Remote Sens. 2011, 32, 4407–4429. [Google Scholar] [CrossRef]
- Sadek, M.; Li, X.; Mostafa, E.; Dossou, J. Monitoring Flash Flood Hazard Using Modeling-Based Techniques and Multi-Source Remotely Sensed Data in Ras Ghareb City, Egypt. Arab. J. Geosci. 2021, 14, 1–16. [Google Scholar] [CrossRef]
- Ghar, M.A.; Shalaby, A.; Tateishi, R. Agricultural land monitoring in the Egyptian Nile Delta using landsat data. Int. J. Environ. Stud. 2004, 61, 651–657. [Google Scholar] [CrossRef]
- Hwang, C.L.; Yoon, K.P. Multiple Attribute Decision Making: Methods and Applications, A State-of-the-Art Survey; Springer-Verlang: Berlin, Germany, 1981. [Google Scholar]
- Chen, C.T. Extension of the TOPSIS for group decision-making under fuzzy environment. Fuzzy Sets Syst. 2000, 114, 1–9. [Google Scholar] [CrossRef]
- Nădăban, S.; Dzitac, S.; Dzitac, I. Fuzzy TOPSIS: A general view. Procedia Comput. Sci. 2016, 91, 823–831. [Google Scholar] [CrossRef] [Green Version]
- Brownlee, J. Probability for Machine Learning: Discover How to Harness Uncertainty with Python. Machine Learning Mastery. 2019. Available online: https://machinelearningmastery.com/uncertainty-in-machine-learning/ (accessed on 29 September 2021).
- Hammer, B.; Villmann, T. How to process uncertainty in machine learning? In Proceedings of the ESANN’2007—European Symposium on Artificial Neural Networks, Bruges, Belgium, 25–27 April 2007; pp. 79–90. [Google Scholar]
- Towards Data Science, The Limitations of Machine Learning. Available online: https://towardsdatascience.com/the-limitations-of-machine-learning-a00e0c3040c6 (accessed on 29 September 2021).
- Zhu, X.; Vondrick, C.; Fowlkes, C.C.; Ramanan, D. Do we need more training data? Int. J. Comput. Vis. 2016, 119, 76–92. [Google Scholar] [CrossRef] [Green Version]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Mastorakis, G. Human-like machine learning: Limitations and suggestions. arXiv 2018, arXiv:1811.06052. [Google Scholar]
- Ying, X. An overview of overfitting and its solutions. J. Phys. Conf. Ser. 2019, 1168, 02202. [Google Scholar] [CrossRef]
- Cawley, G.C.; Talbot, N.L. On over-fitting in model selection and subsequent selection bias in performance evaluation. J. Mach. Learn. Res. 2010, 11, 2079–2107. [Google Scholar]
- Lever, J.; Krzywinski, M.; Altman, N. Points of significance: Model selection and overfitting. Nat. Methods 2016, 13, 703–705. [Google Scholar] [CrossRef]
- CFI. Available online: https://corporatefinanceinstitute.com/resources/knowledge/other/overfitting/ (accessed on 29 October 2021).
- Towards Data Science. Available online: https://towardsdatascience.com/8-simple-techniques-to-prevent-overfitting-4d443da2ef7d (accessed on 29 October 2021).
- Li, S.; Song, W.; Fang, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Deep learning for hyperspectral image classification: An overview. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6690–6709. [Google Scholar] [CrossRef] [Green Version]




| Data Type | Capture Date | Resolution | Source | Output |
|---|---|---|---|---|
| Landsat 1991TM | 27 June 1991 | 30 m | USGS | LULC map |
| Landsat 2003TM | 28 June 2003 | 30 m | USGS | LULC map |
| Landsat 2018OLI-TIRS | 21 June 2018 | 30 m | USGS | LULC map |
| Training Samples | Google Earth Pro | Training/Validation | ||
| Road Network layer | OSM | Distance to nearest road |
| Linguistic Term | Fuzzy Number |
|---|---|
| Very high | 7, 9, 9 |
| High | 5, 7, 9 |
| Moderate | 3, 5, 7 |
| Low | 1, 3, 5 |
| Very low | 1, 1, 3 |
| Weightage | 7, 9, 9 | 7, 9, 9 | 5, 7, 9 | 5, 7, 9 | 3, 5, 7 |
|---|---|---|---|---|---|
| Criteria Alternatives | Population Growth | Employment | Local Development | Area | Socio-Economic Conditions |
| Mahalla Kubra | 7, 9, 9 | 7, 9, 9 | 5, 7, 9 | 7, 9, 9 | 5, 7, 9 |
| Tanta | 7, 9, 9 | 7, 9, 9 | 5, 7, 9 | 7, 9, 9 | 5, 7, 9 |
| Basyun | 1, 4, 7 | 1, 3, 5 | 1, 4, 7 | 3, 5, 7 | 1, 4, 7 |
| Zefta | 3, 6, 9 | 1, 4, 7 | 1, 4, 7 | 3, 5, 7 | 1, 3, 5 |
| Santah | 1, 4, 7 | 1, 4, 7 | 1, 4, 7 | 3, 5, 7 | 1, 4, 7 |
| Kafr Elzayat | 5, 7, 9 | 5, 7, 9 | 3, 5, 7 | 5, 7, 9 | 1, 4, 7 |
| Samanod | 1, 4, 7 | 1, 3, 5 | 3, 5, 7 | 3, 5, 7 | 1, 3, 5 |
| Qotur | 5, 7, 9 | 3, 5, 7 | 3, 5, 7 | 5, 7, 9 | 1, 4, 7 |
| Accuracy | LULC Class | 1991 | 2003 | 2018 |
|---|---|---|---|---|
| User’s Accuracy (%) | Built-up | 85.7 | 90.7 | 91.8 |
| Water | 88.9 | 76.2 | 92.3 | |
| Agricultural land | 94.8 | 95.3 | 94.8 | |
| Producer’s Accuracy (%) | Built-up | 67.8 | 78.5 | 83.1 |
| Water | 64.0 | 66.7 | 54.5 | |
| Agricultural land | 98.3 | 97.9 | 98.1 | |
| Overall Accuracy (%) | 93.9 | 94.3 | 94.3 | |
| Kappa Coefficient | 0.73 | 0.79 | 0.82 |
| LULC | 1991 | 2003 | 2018 | |||
|---|---|---|---|---|---|---|
| Area (km2) | % | Area (km2) | % | Area (km2) | % | |
| Built-up | 156.75 | 7.8 | 193.37 | 9.7 | 303.75 | 15.2 |
| Water | 19.57 | 1.0 | 24.48 | 1.2 | 21.56 | 1.1 |
| Agricultural land | 1832.01 | 91.2 | 1781.48 | 89.1 | 1674.02 | 83.7 |
| Total | 1999.33 | 100 | 1999.33 | 100 | 1999.33 | 100 |
| RD % | 1991–2003 | 2003–2018 | 1991–2018 |
|---|---|---|---|
| Built-up | +23.4 | +57.1 | +93.8 |
| Water | +25.1 | −11.9 | +10.2 |
| Agricultural land | −2.8 | −6.0 | −8.6 |
| LULC | 2018 | 2033 | 2048 | RD% 2018–2033 | RD% 2018–2048 | |||
|---|---|---|---|---|---|---|---|---|
| Area (km2) | % | Area (km2) | % | Area (km2) | % | |||
| Built-up | 279.48 | 14.0 | 588.24 | 29.4 | 663.68 | 33.2 | +110.5 | +137.5 |
| Water | 48.59 | 2.4 | 20.65 | 1.1 | 19.11 | 1.0 | −57.5 | −60.7 |
| Agricultural land | 1671.26 | 83.6 | 1390.44 | 69.5 | 1316.54 | 65.8 | −16.8 | −21.2 |
| Total | 1999.33 | 100 | 1999.33 | 100 | 1999.33 | 100 | ||
| Criteria | CCi | Rank | Risk Level |
|---|---|---|---|
| Mahalla Kubra | 1 | 1 | V. High |
| Tanta | 1 | 2 | V. High |
| Basyun | 0.055 | 7 | Moderate |
| Zefta | 0.19 | 5 | Moderate |
| Santah | 0.132 | 6 | Moderate |
| Kafr Elzayat | 0.577 | 3 | High |
| Samanod | 0.049 | 8 | Low |
| Qotur | 0.472 | 4 | High |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mostafa, E.; Li, X.; Sadek, M.; Dossou, J.F. Monitoring and Forecasting of Urban Expansion Using Machine Learning-Based Techniques and Remotely Sensed Data: A Case Study of Gharbia Governorate, Egypt. Remote Sens. 2021, 13, 4498. https://doi.org/10.3390/rs13224498
Mostafa E, Li X, Sadek M, Dossou JF. Monitoring and Forecasting of Urban Expansion Using Machine Learning-Based Techniques and Remotely Sensed Data: A Case Study of Gharbia Governorate, Egypt. Remote Sensing. 2021; 13(22):4498. https://doi.org/10.3390/rs13224498
Chicago/Turabian StyleMostafa, Eman, Xuxiang Li, Mohammed Sadek, and Jacqueline Fifame Dossou. 2021. "Monitoring and Forecasting of Urban Expansion Using Machine Learning-Based Techniques and Remotely Sensed Data: A Case Study of Gharbia Governorate, Egypt" Remote Sensing 13, no. 22: 4498. https://doi.org/10.3390/rs13224498
APA StyleMostafa, E., Li, X., Sadek, M., & Dossou, J. F. (2021). Monitoring and Forecasting of Urban Expansion Using Machine Learning-Based Techniques and Remotely Sensed Data: A Case Study of Gharbia Governorate, Egypt. Remote Sensing, 13(22), 4498. https://doi.org/10.3390/rs13224498