Abstract
With the rapid process of urbanization, the urban heat island (UHI), the phenomenon where urban regions become hotter than their surroundings, is increasingly aggravated. The UHI is affected by multiple factors overall. However, it is difficult to dissociate the effect of one aspect by widely used approaches such as the remote-sensing-based method. To qualify the response of surface UHI to the land use and land cover (LULC) changes, this study took the numerical land model named u-HRLDAS (urbanized high-resolution land data assimilation system) as the modeling tool to investigate the effect of LULC changes on the UHI from 1980 to 2013 in Wuhan city, China. Firstly, the simulation accuracy of the model was improved, and the summer urban heat environment was simulated for the summer of 2013. Secondly, taking the simulation in 2013 as the control case (CNTL), the LULC in 1980, 1990, and 2000 were replaced by the LULC while the other conditions kept the same as the CNTL to explore the effect of LULC on UHI. The results indicate that the proper configuration of the modeling setup and accurate surface input data are considered important for the simulated results of the u-HRLDAS. The response intensity of UHI to LULC changes after 2000 was stronger than that of before 2000. From the spatial perspective, the part that had the strongest response intensity of land surface temperature to LULC changes was the region between the third ring road and the inner ring road of Wuhan. This study can provide a reference for cognizing the urban heat environment and guide policy making for urban development.
1. Introduction
The urban heat island (UHI) effect is a well-known phenomenon where urban regions are significantly warmer than their surroundings [1,2]. With rapid urbanization, UHI becomes increasingly prominent and affects the development of high-quality human settlement environments enormously [3]. Abundant studies have been conducted to investigate the UHI in different scales and different regions. Generally, these studies mainly focus on the following aspects: (1) the spatial and temporal evolution of UHI [4,5,6,7,8,9]; (2) mitigation of the urban heat and cooling of cities [10,11,12], and the mitigation methods are highly corrected with the driving factors; (3) The driving factors and the mechanism of UHI [9,13]. Many studies have investigated the driving factors of UHI in some specific regions. The UHI is indeed a comprehensive effect involving many factors [13,14,15]. For example, Zhao et al. [13] regarded that anthropogenic heat, convection, radiation, evaporation, and heat storage are the main five aspects of the causes of UHI. However, it is not easy to quantify the effect of specific aspect.
With the process of urbanization, the UHI is aggravated even if they differ in spatial distribution [16,17,18]. Many factors can contribute to the aggravation of UHI with the development of urbanization, for example, the land use and land cover (LULC) changes, the albedo changes from natural surfaces to man-made surfaces, the configuration of building spatial patterns, anthropogenic heat emissions with more people living in city, and climate changes. It is difficult to detach the effect of one aspect (such as LULC changes in the progress of urbanization) on the urban heat environment. However, the LULC has changed much since the last century, and it is essential to qualify the effect of LULC changes on the urban heat environment.
Generally, there are mainly two methods to investigate the surface UHI based on land surface temperature (LST) [3,19]: the remotely sensed method and the numerical modeling method. Remote sensing is a popular way to study the surface UHI effect on a larger scale because it is easy to obtain data covering a larger region [20], but the observed images capture the composite effect with all the influencing factors. Although some studies have investigated the driving factors of UHI qualitatively [5,15]; still, it is hard to detach the effect of one aspect quantificationally based on the remotely sensed data. Meanwhile, the model simulation method, driven by the initial conditions and forcing conditions, can simulate the results using a numerical model with the built-in mechanism of the of physics, biology, and chemistry and their progress toward understanding the Earth [21,22,23,24]. The model can output the continuous spatiotemporal state parameters [25,26]. In addition, it offers the opportunity to qualify the effect of specific factors through a hypothesis experiment. Specifically, it can easily qualify the effect of each aspect by changing the input of the specific aspect in the hypothesis experiment and compare them with the control simulation (the simulation of the real case). Therefore, it is convenient to qualify the contribution of LULC changes on UHI in the process of urbanization based on the numerical model.
There are various numerical models developed [24,27,28,29]. Among them, compared with the coupled model, such as WRF, the uncoupled model by offline forcing factors costs fewer computational resources. The u-HRLDAS (urbanized high-resolution land data assimilation system), developed by NCAR [29], is an uncoupled model and widely used in urban studies [26,30,31]; therefore, the u-HRLDAS was chosen to explore the response of the urban heat environment to LULC changes. As a model tool, the simulation accuracy of the land model is easily affected by multiple input variables and model settings [32,33,34,35,36]. The description of the surface is a non-negligible factor for the model’s simulation, especially in urban regions. For the model with its released physical progress, improving the accuracy of the input data source and setting-up suitable parameters for the model are considered valid methods for improving the accuracy of the simulated results. Although several studies have tried to improve the model simulation in different ways for a specific region, the regional differences, themselves, are the reason that there are usually no universal model setups directly suitable for all regions. It is necessary to improve the model simulation before further using it as a tool.
To qualify the response of UHI to LULC changes, Wuhan, a city well known for its high temperatures in China, was taken as the case study in this following work. The main purpose of this study was: (1) to try to improve the simulation accuracy of the urban heat environment for Wuhan city in the summer of 2013 based on the u-HRLDAS model by adjusting the simulation setups and using for more accurate inputs; (2) the optimized simulation case of summer in 2013 was taken as the referential case. The LULC data in different stages (1980, 1990, and 2000) were used to replace the LULC in 2013, while keeping all the other conditions the same as the referential case, to evaluate the effect of LULC changes on the urban heat environment quantitatively.
2. Materials and Methods
2.1. Study Region
Wuhan (113°41′E–115°05′E, 29°58′N–31°22′N, Figure 1), which is the capital city of Hubei Province, China, is approximately 134 km from east to west and approximately 155 km from south to north. The area of Wuhan is approximately 8495 km2, and the Yangtze River crosses through the city. In the summer, Wuhan has high temperatures and high humidity, which makes it very uncomfortable for citizens to live. However, more than 10 million people live in this city, and it is famous as one of the hottest cities in China.
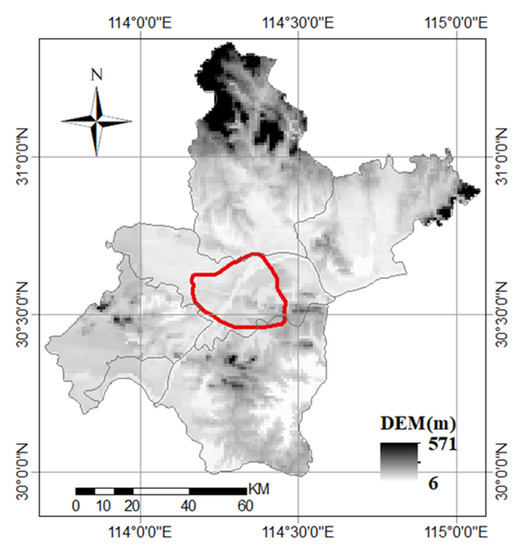
Figure 1.
The map of the Wuhan city; the red line is the third ring road of Wuhan.
2.2. Model and Data
2.2.1. u-HRLDAS Model
The u-HRLDAS includes the land models coupled with urban canopy models [29]. To be specific, two land models (i.e., Noah and Noah-MP) and three urban canopy models (i.e., UCM, BEP, and BEM) are included in the u-HRLDAS [29]. Compared with the WRF/Urban model, which is coupled to the atmosphere process, the u-HRLDAS is forced use offline atmospheric data sets, and it can save computational time. In addition, it is convenient to detach the impact of a single factor from the model simulated results by conducting the hypothesis experiment. Therefore, it is suitable for a study with the purpose of investigating the response of the urban heat effect to land cover changes. Moreover, the forcing data and the initial data are essential for u-HRLDAS model simulation. With the input of forcing data (such as precipitation, wind, air pressure, etc.), the fine scale of surface data (land use and land cover, the soil texture data, etc.), and other dynamic surface information (the fraction of vegetation cover, etc.), the model can calculate and output the spatial and temporal continuous surface state parameters such as LST and soil moisture.
2.2.2. Forcing Data Sets
China meteorological forcing data set (CMFD) [37,38,39] developed by the Institute of Tibetan Plateau Research and Chinese Academy of Sciences (ITPCAS) has been widely used in forcing land model [40,41], and it has been proved with high accuracy in China [32]. The data set contains seven factors, namely, near-surface air temperature, near-surface air pressure, relative humidity, wind speed, downward shortwave radiation, and downward longwave radiation. The spatial resolution of CMFD is 0.1 arc degree and its temporal resolution is 3 h. The data set comes from the fusion of the in-situ observation, the Princeton reanalysis, GLDAS data, GEWEX-SRB radiation information and TRMM precipitation data. The details of the CMFD can be found in [38] and [39]. In this study, the CMFD data set is resampled to 1 km and 30 min before forcing the u-HRLDAS model.
2.2.3. Remotely Sensed Data
Two types of remotely sensed data are used in this study: the LULC data set for input and the LST data set for the model simulated evaluation. The LULC used in this study comes from Chinese multi-period land use and land cover change remote sensing monitoring data set (CNLUCC) [42]. The data set is derived from Landsat images with manual–visual interpretation, and it provides the LULC data from the 1980s, 1990s, 1995, 2000, 2005, 2010, 2015, and 2018. The spatial resolution was 30 m, and it has been validated with an accuracy higher than 90% [43]. Various studies on the urbanization and urban heat environment employed this data set for its fine spatial resolution and high accuracy [44,45]. The 30 m data in 1980, 1990, 2000, and 2010 were used in this study to update the land use and land covers. The model simulated resolution was set to 1 km in this study; therefore, the data were resampled to 1 km beforehand. The dominant type of each 1 km grid was regarded as the new type of the 1 km grid; meanwhile, the urban fraction used in this model was calculated by the fraction of the 30 m impervious data in each 1 km grid.
Besides the LULC data set, MODIS land surface temperature products [46], version 6, with a 1 km spatial resolution (MOD11A1 and MYD11A1) were used to compare the simulated LST results in this study. Both MOD11A1 and MYD11A1 have a pair value in daytime and nighttime. The data sets have been proved with a bias of less than 1 K in most regions [46].
2.3. Experiment Design
Considering the availability of the validation data (MODIS LST) and the hot period of summer in Wuhan, 1 August 2013 to 15 August 2013, was selected as the simulated period. The 12 cases listed in Table 1 were designed to test how to configure the model to obtain a higher simulation accuracy. These cases can be divided into four groups: (1) The spin-up period test group. For numerical model simulation, the spin-up period is a necessary process to reach the quasi-equilibrium state [19,24]. It is different in different periods to obtain the quasi-equilibrium state in different regions, different models, and different land types [47]. To test the spin-up effect on the u-HRLDAS simulation for Wuhan, a series of spin-up periods (1, 2, 4, 6, 12, 24, 36, and 48 months) were set in CMFD-1M, CMFD-2M, CMFD-4M, CMFD-6M, CMFD-12M, CMFD-24M, CMFD-36M, and CMFD-48M. The simulated LST of each case was compared with the results of CMFD-48M to test if the model reached the quasi-equilibrium state. (2) The test group for time step size. Time steps can be in minutes, hours, days, or years in a climate model. When the size of time step is larger, the truncation error is larger, which may make it not appropriate for the specific simulation. While the small size of a time step generates too much computational cost. Therefore, the appropriate size for the time step is necessary. Three different sizes of time step (120, 600, and 1800 s) were tested in CMFD-6M, CMFD-6M-600s, and CMFD-6M-1800s. (3) For the LULC test group, the LULC data in 2013 was updated in CMFD-6M-LULC to test the effect of land cover on the simulated accuracy. The default LULC provided by the u-HRLDAS model came from the 500 m MODIS data of 2005; thus, it is not accurate for the surface description of Wuhan. In this stage, at first, the LULC of 2010 in the CNLULC data sets were used to update the land covers for the whole region; then, the impervious data derived from the Landsat 8 [48] image for July 2013 was used to update the impervious surface for the 2013 simulation. The ULULC used here is shown in Figure 2d. (4) For the parameters test group, the main parameters for urban simulation were updated in CMFD-6M-PAR to test the suitability of the parameters compared with CMFD-6M. The parameters before and after being updated are shown in Table 2. The building height for low residence, high-residence, and commercial were 5, 7.5, and 10 m in default, which was not suitable for Wuhan. Heights of 8, 15, and 24 m were used in the updated case. Irrigation for urban vegetation was turned on in Wuhan over summer; therefore, the irrigation process was turned on in the updated parameters. In addition, the urban fraction in the model default for three urban categories was 0.5, 0.9, and 0.95, respectively. The impervious fractions of each 1 km grid based on Landsat 30 m data were updated in the CMFD-6M-PAR case. Overall, the parameters settings are listed in Table 2.

Table 1.
The experimental setup for accuracy improvement of the model simulated.
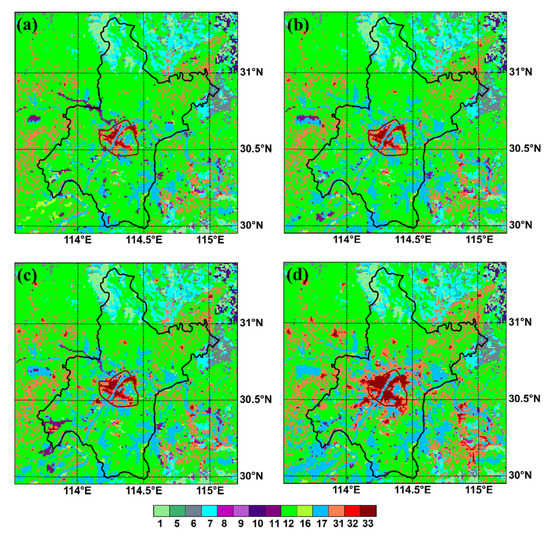
Figure 2.
The land use and land cover in different periods of Wuhan: (a) LULC1980; (b) ULC1990; (c) LULC2000; (d) CNTL. 1: evergreen needleleaf forest, 5: mixed forest, 6: closed shrublands, 7: open shrublands, 8: woody savannas, 9: savanna, 10: grasslands, 11: permanent wetlands, 12: croplands, 16: barren or sparsely vegetated, 17: water, 31: low-density residential, 32: high-density residential, and 33: commercial; black line: the administrative boundary of Wuhan, dark-red line: the third ring road of Wuhan.

Table 2.
The comparison of parameters in the update and default.
The case of Table 1 with the highest simulated accuracy was regarded as the control case (CNTL) in the following. To investigate the effect of LULC changes on the urban heat environment, the experiments in Table 3 were designed. Except for the LULC data, the other settings of the model simulation listed in Table 3 remained the same. Thus, these cases were designed with all the same conditions as the CNTL case for 2013, but the LULC data were changed from 1980 to 2013 in different cases. Therefore, Table 3 can be used to qualify the effect of LULC changes in urban heat excluding the fusion effect of other factors such as climate changing and population increase. The LULC used in LULC1980, LULC1990, LULC2000, and CNTL are shown in Figure 2a–d.

Table 3.
The experiment design for the response of SUHI to LULC.
2.4. Evaluation Metrics
The RMSE (root mean square error) and MBE (mean bias error) were used to evaluate the accuracy of model simulated. A smaller RMSE and MBE indicate a better model simulation performance. In addition, the UHII (urban heat island intensity) used to evaluate the urban heat environment can be formulated with Equation (1), corresponding to the previous UHI study on Wuhan [4].
where UHII is the urban heat island intensity, LST(outside) is the averaged LST over the region outside the third ring road but within the administrative boundary of Wuhan, and LST(inside) is the average LST over the region inside the third ring road as shown in Figure 1.
UHII = LST(inside) − LST(outside),
To qualify the response of SUHI to the LULC changes, UHI_RI (the response intensity of UHI) is calculated by Equation (2) to clarify the response intensity of UHI to the LULC.
where UHI_RI is the response intensity of UHI to LULC changes from t1 to t2. t1 and t2 denote two different times. UHI(t1) and UHI(t2) are the UHI intensity of time t1 and time t2. Similarly, the LST_RI calculated by (2) is used to qualify the response intensity of LST to LULC changes.
where LST_RI is the response intensity of LST to LULC changes from time t1 to t2, and the LST(t1) and LST(t2) denote the LST of time t1 and t2, respectively. Moreover, URB_RC (urbanization ratio changes) from time t1 to t2 is calculated by Equation (4).
where ARE_U(t1) and ARE_U(t2) represent the total area of urban pixels in time t1 and t2. ARE_TOTAL is the total area of the study region.
UHI_RI = UHI(t1) − UHI(t2),
LST_RI = LST(t1) − LST(t2),
URB_RC = (ARE_U(t1) − ARE_U(t2)/ARE_TOTAL,
3. Results and Analysis
3.1. Model Simulations with Different Setups
3.1.1. The Effect of the Spin-Up Period
To test the effectiveness of different spin-up periods for the model, the RMSE was calculated for each simulated LST in the different cases compared with the simulated LST in the case of CMFD-48M. The differently colored bars in Figure 3 indicate different experimental cases. According to the criterion of Chen et al. [29], when the RMSE is less than 0.5 K, it can regarded that the simulation reached the quasi-equilibrium state as can be seen from Figure 3. (1) It is not the same time for different land types to reach a stable state, which agrees with the conclusion of Gao et al. [47] that the different land types in different regions need different spin-up times to make it stable. Compared with the land types of 1, 3, 7, 11, 14, and 16, the land types of 4, 5, 6, 8, 9, 10, 12, and 32 needed longer time to reach the stable state over Wuhan region. (2) When the spin-up time was 4 months (CMFD-4M), most of the land types reached the stable state, but there were still some land types that had a larger RMSE, for example, the RMSE of type 9 was larger than 0.5 K. When the spin-up time was longer than six months, the RMSE of all the land types were less than 0.5 K. Overall, the results of Figure 3 indicate that the spin-up period needs a time of 6 months at least when the u-HRLDAS are used to simulate the urban heat environment for Wuhan.
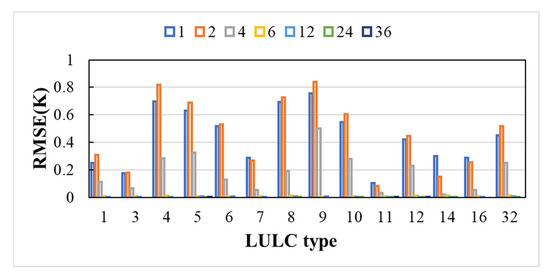
Figure 3.
The evaluation results of the spin-up period test group. The numbers on the horizontal axis represent the land cover types: 1: evergreen needleleaf forest, 3: deciduous needleleaf forest, 4: deciduous broadleaf forest, 5: mixed forest, 6: closed shrublands, 7: open shrublands, 8: woody savannas, 9: savanna, 10: grasslands, 11: permanent wetlands, 12: croplands, 14: cropland/natural vegetation mosaic, 16: barren or sparsely vegetated, 32: high-density residential. The different colors of the bars with the sign of 1, 2, 4, 6, 12, 24, and 36 represent the results of the CMFD-1M, CMFD-2M, CMFD-4M, CMFD-6M, CMFD-12M, CMFD-24M, and CMFD-36M.
3.1.2. The Effect of the Model Time Step Size
The statistical results of the maximum, minimum, and mean LST from 1 August to 15 August 2013 are shown in Table 4. Compared with MODIS LST, the maximum of LST in CMFD-6M-600s, CMFD-6M-1800s was obviously larger than MODIS LST and CMFD-6M. Meanwhile, the minimum LST of CMFD-6M, CMFD-6M-600s, and CMFD-6M-1800s were the same. The mean LST of the CMFD-6M was also the closest to MODIS LST compared with the other two cases. Therefore, the model run step of 120 s employed by CMFD-6M was more suitable for the simulation of Wuhan than the other two settings.

Table 4.
The results of cases with different model time step sizes compared with MODIS LST.
3.1.3. The Effect of LULC and Parameters Adjustment
In the daytime (Figure 4a,b), after updating the land covers of 2013 in CMFD-6M-LULC, the orange line representing the CMFD-6M-LULC is located inside the blue line representing the CMFD-6M, which means the update of LULC had a positive contribution to the model simulation’s accuracy. Based on the above configuration with updated parameters in the CMFD-6M-PAR, the RMSE and MBE are represented by the gray line inside the orange line, which indicates the model simulation’s accuracy was better in the CMFD-6M-PAR than in the CMFD-6M-LULC, especially in urban regions. At nighttime (Figure 4c,d), it was obvious that the model’s simulation over urban regions in the CMFD-6M-PAR achieved the best performance than in the other two cases. Although the MBE in rural regions was lower in the CMFD-6M than in the other two cases, the indexes in these three cases were quite close in rural regions. Overall, updating the near-real-time LULC and adopting suitable parameters had a positive effect on the model simulation’s accuracy for Wuhan. The CMFD-6M-PAR showed the best performance for the above cases, and the simulation’s accuracy was significantly improved, especially for urban regions.
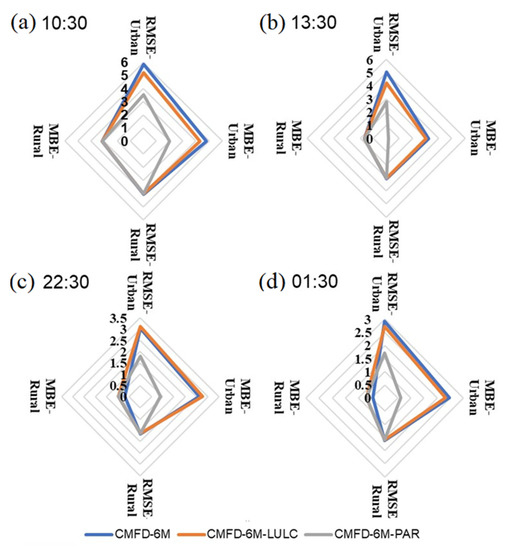
Figure 4.
Comparison of simulated accuracy in CMFD-6M, CMFD-6M-LULC, and CMFD-6M-PAR (Unit: K), the subfigures (a–d) are for the local time of 10:30, 13.30, 22.30 and 01:30 respectively.
3.1.4. The Evaluation of Model Simulated LST and UHI
According to the above comparison in Section 3.1.3, the performance of the CMFD-6M-PAR was best. Therefore, the CMFD-6M-PAR was regarded as the control case (CNTL) in the following. The UHII based on LST simulated with the CMFD-6M-PAR was compared with UHII based on MODIS LST. The UHII was calculated after data filtering according to the quality control method proposed by Hu et al. [26]. The water bodies were extracted in both MODIS UHII and simulated UHII calculations. With the specific moment, when the two-source data (MODIS LST and u-HRLDAS LST) were valid simultaneously, the data at this moment were involved in the UHII calculation. Finally, the UHII was 2.36 K and 2.52 K for MODIS and the model, respectively. The relative bias of UHII was less than 7% and satisfied the standard of less than 15%. The mean MODIS LST within the third ring road, outside the third ring road but within the administrative boundary was 306.59 K and 304.22 K, respectively. Meanwhile, the mean simulated LST was 308.16 K for the region within the third ring road and 305.63 K for the region outside the third ring road but within the administrative boundary. The relative bias of LST was less than 1% for both regions. The spatial distribution pattern of the LST from the MODIS and model were similar (Figure 5), although the averaged simulated LST was higher than the averaged MODIS-derived LST.
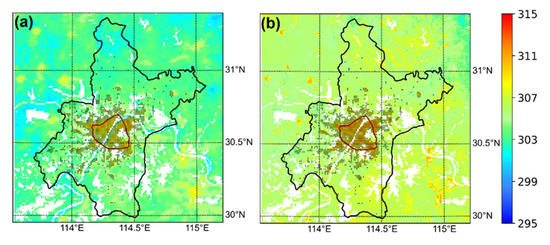
Figure 5.
The spatial distribution of LST for MODIS (a) and u-HRLDAS (b), averaged from 1 August 2013 to 15 August 2013 (the black points represents the urban grid).
3.2. The Response of the Urban Heat Environment to LULC Changes
3.2.1. Temporal Analysis
Figure 6 shows the average LST and UHII in the cases with the configuration of different LULCs. The LST inside the third ring road of Wuhan increased by just changing the LULC, while the averaged LST caused by LULC changes outside the third ring road of Wuhan to slowly increase from 1980 to 2013. For the UHII represented by the red line, it rapidly increased with the LULC changes from 1980 (in CNTL1980) to 2013 (in CNTL). The UHII influenced by LULC increased by 1.48 K from 1980 to 2013. Moreover, it yields similar outcomes to that of the changes of UHII and LST caused by the LULC inside the third ring road from 1980 to 1990, and from 1990 to 2000, while the changes of UHII and LST from 2000 to 2013 are greater than before. The response intensity of the urban heat environment to the LULC changes was further investigated in Figure 7. Note that the UHII was calculated by using the outputs by u-HRLDAS in 30 min, which took each moment of the study period into full consideration; therefore, the value was different from the UHII in Section 3.1.4. when considering the moments when both u-HRLDAS and MODIS LST were valid.
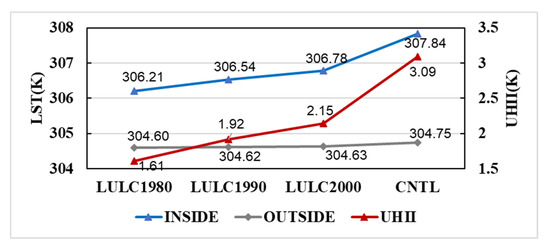
Figure 6.
The LST (Unit: K) and UHII (Unit: K) for the cases LULC1980, LULC1990, LULC2000, and CNTL. The blue line is the averaged LST inside the third ring road; the gray line shows the averaged LST outside the third ring road but within the administrative boundary; the red line represents the UHII.
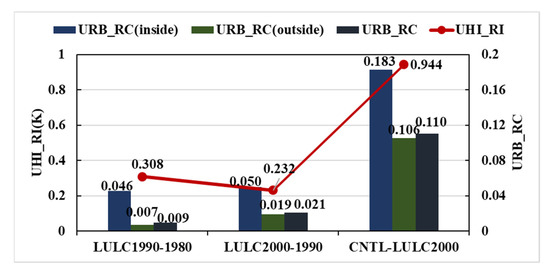
Figure 7.
The response intensity of UHI and the changes in the urbanization ratio over every decade. The UHI_RI (Unit: K) was the UHII changes of two cases, and the URB_RC (inside), URB_RC (outside), and URB_RC represent the changes in the urbanization ratio of the region inside the third ring road, outside the third ring road, and the whole region of Wuhan, respectively.
The changes in the urbanization ratios from 1980 to 1990 (URB_RC was 0.009) were lower than that from 1990 to 2000 (URB_RC was 0.021) as shown in Figure 7. Meanwhile, the changes in the urbanization ratio inside and outside the third ring road from 1990 to 2000 were also greater than that from 1980 to 1990, because the UHI was calculated by subtracting the mean LST inside the third ring road from that of outside the third ring road, and it could be determined that the speed of urbanization outside the third ring road was faster than it inside the third ring road when comparing the two periods (from 1980 to 1990 and from 1990 to 2000), the UHI response of LULC was stronger from 1980 to 1990 (UHI_RI was 0.308 K) than it was from 1990 to 2000 (UHI_RI was 0.232 K). The urbanization ratio after 2000 was fast both inside and outside the third ring road, consequently, the final result was that the UHI_RI reached 0.944 K from the case LULC2000 to the case CNTL.
3.2.2. Spatial Analysis
For the spatial distribution of LST with the changes of LULC from 1980 to 2013, the regions with high LST in red color in Wuhan become larger as shown in Figure 8a–d. In the case LULC1980, the region with high LST in red was concentrated inside the third ring road, which was the same as LULC1990. Only part of the region inside the third ring road was hot in the two cases. The high LST region extended to cover most of the region inside the third ring road in LULC2000. In the CNTL case, the whole region inside the third ring road was hot, and the high LST region was still expanding outside.
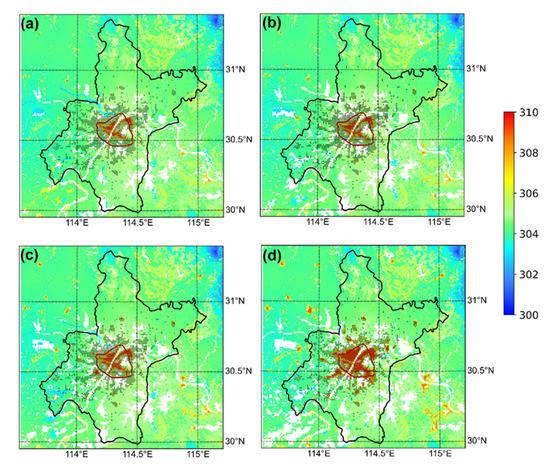
Figure 8.
The spatial distribution of LST (Unit: K) in the case LULC1980 (a), LULC1990 (b), LULC2000 (c), and CNTL (d) averaged from 1 August to 15 August (the black point represents the urban grid in the CNTL).
The statistics of the LST changes for each decade are shown in Figure 9. The green, yellow, and red bars represent the LST differences for LULC1990 minus LULC1980, LULC2000 minus LULC1990, and LST for the CNTL minus LULC2000, respectively. It is obvious that the quick LST response speed mainly occurs in the region inside the third ring road and outside the inner ring road. The LST_RI over this region from 2000 to 2013 was 1.214 K due to the LULC changes, while the LST_RI was 0.384 K from 1980 to 1990 and 0.245 K from 1990 to 2000. The change in LST_RI over the region outside the third ring road and within the outer ring road was also significant, especially after 2000 with the LST_RI was 0.510 K. For the region within the inner ring road and the region outside the outer ring road, the LST_RI was very small. It may be because the urban region inside the inner ring road was highly developed a long time ago. For the region outside the outer ring road, urbanization was also not as rapid as the region within the outer ring road; therefore, the change in the LST_RI of LULC was relatively small.
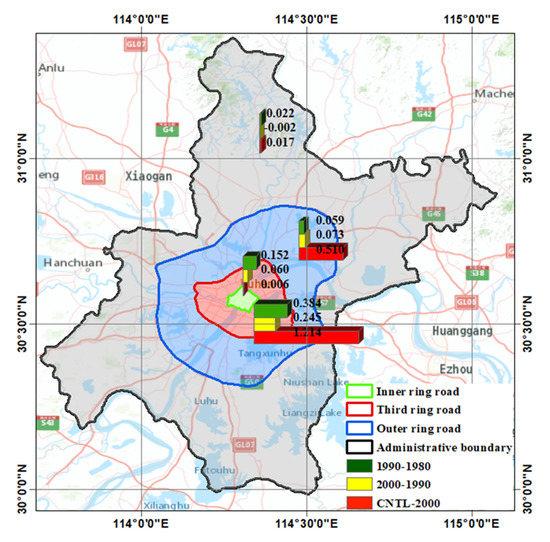
Figure 9.
The statistics of LST_RI (Unit: K) of every decade (each bar chart represents the statistical results within the region where it is located. i.e., the bar chart located between the third ring road and the outer ring road represents the statistical results outside the third ring road but inside the outer ring road).
3.3. The Reason Why Changes in LULC Alter the Heat Environment of Wuhan
It can be concluded that the response of the urban heat environment to LULC changes was strongest after the year of 2000, especially over the region within the third ring road for Wuhan from Section 3.2. To further analyze how the changes in LULC have altered the urban heat environment of Wuhan since 1980. The fraction of each LULC type in different cases is shown in Figure 10. Because the lake effect was not considered in this study, the results are demonstrated after removing the information of lake areas. There are many LULC types expressed in the simulation shown in Figure 2; briefly, the types of 1, 5, 6, and 7 in Figure 2 were combined as the forest type here. The types 8, 9, and 10 were regarded as grassland. While the types 11, 12, and 16 are the wetland, cropland, and bare land, respectively. The urban type consisted of the types 31, 32, and 33 in Figure 2. For both the regions within the third ring road of Wuhan (Figure 10a) and outside the third ring road (Figure 10b), the main changes in the LULC type were that the cropland area decreased significantly, while the urban areas increased rapidly, especially after the year of 2000. The areas of forest, grassland, wetland, and bare land have also decreased since 1980 to present. However, compared with cropland areas, the fraction of these LULC types was small. Therefore, abundant cropland has been replaced by urban areas since 1980 to 2013 in Wuhan.
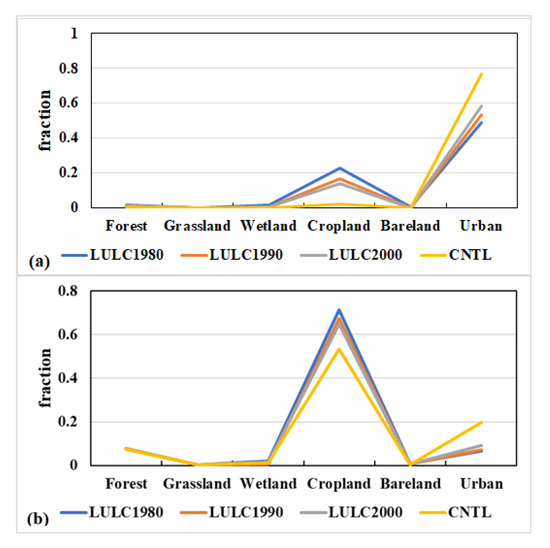
Figure 10.
The fraction of each LULC type in different periods within the third ring road (a) and the fraction of each land cover type outside the third ring road but inside the administrative boundary of Wuhan (b).
Table 5 lists the mean LST for each LULC type in different simulated cases over the whole region of Wuhan. The mean LST of wetland and cropland were lower than the mean LST over the study region for each simulation case. The LST over the urban type was higher than the mean LST for the study region in each case. Therefore, the decrease in cropland and the increase in urban areas (Figure 10) mainly caused the phenomenon that the UHI response to the LULC changes being intense since the 1980s, especially after the year 2000. To further explore the energy changes with the LULC changes, the simulated latent heat flux (LH) and sensible heat flux (HFX) averaged by the simulated results with the temporal resolution of 30 min during 1–15 August over the different statistical zones (the whole region of Wuhan, the region inside the third ring road, and the region outside the third ring road but within the administrative boundary) are shown in Figure 11. With more cropland replaced by the impervious areas, the evaporation of soil water, and the transpiration of vegetation can convert less radiation to latent heat flux; therefore, the latent heat flux decreased from 1980 to 2013, then sensible heat flux increased over both the region inside the third ring road and the region outside the third ring road (Figure 11). It can also be found that with the LULC changes, the averaged HFX (inside) increased to 81.24 W/m2 in the CNTL case, while the LH (inside) decreased to 58.19 W/m2 in the CNTL case. For the whole region of Wuhan, the averaged LH decreased 5.41 W/m2, while the HFX increased 5.59 W/m2 due to the LUCL changes from 2000–2013 and, consequently, the LST changed with the LULC changes.

Table 5.
The averaged LST for each LULC type in different simulations (Unit: K).
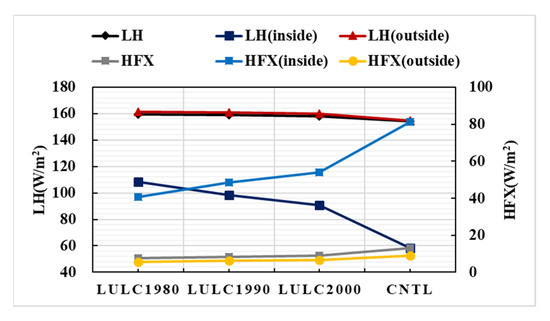
Figure 11.
The averaged latent heat flux (LH, Unit: W/m2) and sensible heat flux (HFX, Unit: W/m2) over different statistical zones averaged from 1–15 August for the different simulation cases. LH, LH (inside) and LH (outside) (HFX, HFX (inside), and HFX (outside)) is the latent heat flux (sensible heat flux) over “the whole region of Wuhan”, over “the region within the third ring road” and “the region outside the third ring road but within the Wuhan administrative boundary”, respectively.
4. Conclusions
This study investigated the effect of the LULC changes on the urban heat environment based on the u-HRLDAS. Firstly, taking Wuhan as the study region, and the time from 1 August 2013 to 15 August 2013 as the study period, the u-HRLDAS model was optimized to improve the simulated accuracy of the summer urban heat environment by adjusting the setups and the inputs. Secondly, the optimized simulation case was taken as the referential case (CNTL) to study the response of UHI to LULC changes. The LULC data in different stages (1980, 1990, and 2000) were used to replace the LULC in the CNTL simulation, keeping all the other conditions the same as the CNTL, to qualify the effect of LULC changes on the urban heat environment. The main results are as follows.
(1) The model can reach its quasi-equilibrium state after spin up for 6 months for Wuhan. The time step for the model should not be set too large to avoid extreme data, and 120 s was a valid value in this study. In addition, the accurate and near real-time surface parameters were of great importance for the simulated results, for example, the real-time LULC, the urban fraction in each grid, and the irrigation process were positive to improve the model simulation’s accuracy. Therefore, the setup of the model (such as the spin-up time and the run step) should be adjusted for a specific region. The more real-time, the higher accurate input data is, the better for the model’s simulation;
(2) From a temporal perspective, the LULC changes caused a significant increase in UHI from 1980 to 2013, and the effect became intensive after 2000 due to the rapid urbanization after that time. To be specific, the UHII caused by the LULC changes from 1980 to 2013 increased by 1.48 K, and the UHII caused by the LULC changes from 2000 to 2013 increase by 0.94 K. From the spatial perspective, the response of the LST was the strongest over the region inside the third ring road and outside the inner ring road, followed by the LST_RI over the region outside the third ring road but inside the outer ring road.
This study optimized the model simulated results for the urban heat environment based on the u-HRLDAS and investigated the response of UHII to LULC changes. The results of this study can provide references for the cognition of the UHI mechanism, which is helpful for the urban development policy maker. The magnitude of LST and UHI in this study may have some differences with the remotely sensed method. The main reason is that the model simulation’s results obtained the LST every 30 min in this study. However, the results based on remotely sensed data are only acquired at some moments corresponding to the satellite overpass time. It also differs from the in situ observed urban heat island due to the following two reasons. One is that most in situ observation are the near-surface air temperature rather than the land surface temperature. On the other hand, an observation-based study uses sparse data points to represent the urban or rural regions, which, of course, lacks spatial details. This work only qualifies the effect of the LULC changes on the urban heat environment. The others aspect of UHI-related reasons can be qualified in the future to better cognize urban warming.
Author Contributions
M.G., H.S. and Z.L. designed the method; M.G. conducted the experiment and wrote the paper; M.G., Z.T. and Q.L. performed data preprocessing and result analysis; Z.L., Z.T. and H.S. revised the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 42001382). Part of this work was also supported by the Natural Science Basic Research Program of Shaanxi (No. 2021JQ-238), the Major Projects of Technological Innovation of Hubei Province (No. 2019AAA046), the Fundamental Research Funds for the Central Universities, CHD (Ref. 300102260301 and 300102261108), and by the European Space Agency through the ESA-MOST DRAGON-5 project (Ref. 59339).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
We gratefully thank anonymous reviewers and editors for their constructive comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Oke, T.R.; Mills, G.; Christen, A.; Voogt, J.A. Urban Climates; Cambridge University Press: Cambridgeshire, UK, 2017. [Google Scholar]
- Oke, T.R. City size and the urban heat island. Atmos. Environ. 1973, 7, 769–779. [Google Scholar] [CrossRef]
- Zhou, D.; Xiao, J.; Bonafoni, S.; Berger, C.; Deilami, K.; Zhou, Y.; Frolking, S.; Yao, R.; Qiao, Z.; Sobrino, J.A. Satellite Remote Sensing of Surface Urban Heat Islands: Progress, Challenges, and Perspectives. Remote Sens. 2019, 11, 48. [Google Scholar] [CrossRef] [Green Version]
- Shen, H.; Huang, L.; Zhang, L.; Wu, P.; Zeng, C. Long-term and fine-scale satellite monitoring of the urban heat island effect by the fusion of multi-temporal and multi-sensor remote sensed data: A 26-year case study of the city of Wuhan in China. Remote Sens. Environ. 2016, 172, 109–125. [Google Scholar] [CrossRef]
- Tepanosyan, G.; Muradyan, V.; Hovsepyan, A.; Pinigin, G.; Medvedev, A.; Asmaryan, S. Studying spatial-temporal changes and relationship of land cover and surface Urban Heat Island derived through remote sensing in Yerevan, Armenia. Build. Environ. 2021, 187, 107390. [Google Scholar] [CrossRef]
- Xian, G.; Shi, H.; Auch, R.; Gallo, K.; Zhou, Q.; Wu, Z.; Kolian, M. The effects of urban land cover dynamics on urban heat Island intensity and temporal trends. GIScience Remote Sens. 2021, 58, 501–515. [Google Scholar] [CrossRef]
- Peng, S.; Piao, S.; Ciais, P.; Friedlingstein, P.; Ottle, C.; Bréon, F.-M.; Nan, H.; Zhou, L.; Myneni, R. Surface Urban Heat Island Across 419 Global Big Cities. Environ. Sci. Technol. 2011, 46, 696–703. [Google Scholar] [CrossRef] [PubMed]
- Menberg, K.; Bayer, P.; Zosseder, K.; Rumohr, S.; Blum, P. Subsurface urban heat islands in German cities. Sci. Total Environ. 2013, 442, 123–133. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.; Huang, X.; Yang, J.; Liu, Y. The relationship between land surface temperature and artificial impervious surface fraction in 682 global cities: Spatiotemporal variations and drivers. Environ. Res. Lett. 2021, 16, 024032. [Google Scholar] [CrossRef]
- Li, D.; Bou-Zeid, E.; Oppenheimer, M. The effectiveness of cool and green roofs as urban heat island mitigation strategies. Environ. Res. Lett. 2014, 9, 055002. [Google Scholar] [CrossRef]
- Zhou, W.; Wang, J.; Cadenasso, M.L. Effects of the spatial configuration of trees on urban heat mitigation: A comparative study. Remote Sens. Environ. 2017, 195, 1–12. [Google Scholar] [CrossRef]
- Gao, M.; Chen, F.; Shen, H.; Li, H. A tale of two cities: Different urban heat mitigation efficacy with the same strategies. Theor. Appl. Clim. 2020, 142, 1625–1640. [Google Scholar] [CrossRef]
- Zhao, L.; Lee, X.; Smith, R.B.; Oleson, K. Strong contributions of local background climate to urban heat islands. Nat. Cell Biol. 2014, 511, 216–219. [Google Scholar] [CrossRef] [PubMed]
- Dewan, A.; Kiselev, G.; Botje, D.; Mahmud, G.I.; Bhuian, H.; Hassan, Q.K. Surface urban heat island intensity in five major cities of Bangladesh: Patterns, drivers and trends. Sustain. Cities Soc. 2021, 71, 102926. [Google Scholar] [CrossRef]
- Deilami, K.; Kamruzzaman, M.; Liu, Y. Urban heat island effect: A systematic review of spatio-temporal factors, data, methods, and mitigation measures. Int. J. Appl. Earth Obs. Geoinf. 2018, 67, 30–42. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, M.; Zhu, J.; Wang, Y.; Skorokhod, A. Modeling Impacts of Urbanization and Urban Heat Island Mitigation on Boundary Layer Meteorology and Air Quality in Beijing Under Different Weather Conditions. J. Geophys. Res. Atmos. 2018, 123, 4323–4344. [Google Scholar] [CrossRef]
- Yao, R.; Wang, L.; Huang, X.; Guo, X.; Niu, Z.; Liu, H. Investigation of Urbanization Effects on Land Surface Phenology in Northeast China during 2001–2015. Remote Sens. 2017, 9, 66. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.; Chen, H. Impact of urbanization-related land use land cover changes and urban morphology changes on the urban heat island phenomenon. Sci. Total Environ. 2018, 635, 1467–1476. [Google Scholar] [CrossRef] [PubMed]
- Gao, M.; Shen, H.; Han, X.; Chen, W. Numerical simulation of diurnal variation of urban land surface temperature based on CLM4.5. In Proceedings of the 2016 4th International Workshop on Earth Observation and Remote Sensing Applications (EORSA), Guangzhou, China, 4–6 July 2016; pp. 183–187. [Google Scholar] [CrossRef]
- Zhou, D.; Zhao, S.; Liu, S.; Zhang, L.; Zhu, C. Surface urban heat island in China’s 32 major cities: Spatial patterns and drivers. Remote Sens. Environ. 2014, 152, 51–61. [Google Scholar] [CrossRef]
- Miao, S.; Chen, F.; LeMone, M.A.; Tewari, M.; Li, Q.; Wang, Y. An Observational and Modeling Study of Characteristics of Urban Heat Island and Boundary Layer Structures in Beijing. J. Appl. Meteorol. Clim. 2009, 48, 484–501. [Google Scholar] [CrossRef]
- Kusaka, H.; Kondo, H.; Kikegawa, Y.; Kimura, F. A simple single-layer urban canopy model for atmospheric models: Comparison with multi-layer and slab models. Bound.-Layer Meteorol. 2001, 101, 329–358. [Google Scholar] [CrossRef]
- Jackson, T.L.; Feddema, J.J.; Oleson, K.W.; Bonan, G.B.; Bauer, J.T. Parameterization of Urban Characteristics for Global Climate Modeling. Ann. Assoc. Am. Geogr. 2010, 100, 848–865. [Google Scholar] [CrossRef]
- Chen, F.; Kusaka, H.; Bornstein, R.; Ching, J.; Grimmond, S.; Grossman-Clarke, S.; Loridan, T.; Manning, K.W.; Martilli, A.; Miao, S.; et al. The integrated WRF/urban modelling system: Development, evaluation, and applications to urban environmental problems. Int. J. Clim. 2011, 31, 273–288. [Google Scholar] [CrossRef]
- Oleson, K.W.; Bonan, G.B.; Feddema, J.; Jackson, T. An examination of urban heat island characteristics in a global climate model. Int. J. Clim. 2011, 31, 1848–1865. [Google Scholar] [CrossRef] [Green Version]
- Hu, L.; Brunsell, N.A.; Monaghan, A.J.; Barlage, M.; Wilhelmi, O.V. How can we use MODIS land surface temperature to validate long-term urban model simulations? J. Geophys. Res. Atmos. 2014, 119, 3185–3201. [Google Scholar] [CrossRef] [Green Version]
- Chen, F.; Manning, K.W.; Yates, D.N.; LeMone, M.A.; Trier, S.B.; Cuenca, R.; Niyogi, D. Development of high resolution land data assimilation system and its application to WRF. In Proceedings of the 16th Conference on Numerical Weather Prediction, Seattle, WA, USA, 11–15 January 2004. [Google Scholar]
- Grimmond, C.S.B.; Blackett, M.; Best, M.; Barlow, J.; Baik, J.-J.; Belcher, S.E.; Bohnenstengel, S.I.; Calmet, I.; Chen, F.; Dandou, A.; et al. The International Urban Energy Balance Models Comparison Project: First Results from Phase 1. J. Appl. Meteorol. Clim. 2010, 49, 1268–1292. [Google Scholar] [CrossRef]
- Chen, F.; Manning, W.J.; LeMone, M.A.; Trier, S.B.; Alfieri, J.G.; Roberts, R.; Tewari, M.; Niyogi, D.; Horst, T.W.; Oncley, S.P.; et al. Description and Evaluation of the Characteristics of the NCAR High-Resolution Land Data Assimilation System. J. Appl. Meteorol. Clim. 2007, 46, 694–713. [Google Scholar] [CrossRef] [Green Version]
- Meng, C.; Zhang, C.; Miao, S.; Chen, F. Localization and validation of an urbanized high-resolution land data assimilation system (u-HRLDAS). Sci. China Earth Sci. 2013, 56, 1071–1078. [Google Scholar] [CrossRef]
- Gao, M.; Chen, F.; Shen, H.; Barlage, M.; Li, H.; Tan, Z.; Zhang, L. Efficacy of Possible Strategies to Mitigate the Urban Heat Island Based on Urbanized High-Resolution Land Data Assimilation System (u-HRLDAS). J. Meteorol. Soc. Jpn. 2019, 97, 1075–1097. [Google Scholar] [CrossRef] [Green Version]
- Yang, F.; Lu, H.; Yang, K.; He, J.; Wang, W.; Wright, J.S.; Li, C.; Han, M.; Li, Y. Evaluation of multiple forcing data sets for precipitation and shortwave radiation over major land areas of China. Hydrol. Earth Syst. Sci. 2017, 21, 5805–5821. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Wang, Z.-H.; Georgescu, M.; Chen, F.; Tewari, M. Assessing the Impact of Enhanced Hydrological Processes on Urban Hydrometeorology with Application to Two Cities in Contrasting Climates. J. Hydrometeorol. 2016, 17, 1031–1047. [Google Scholar] [CrossRef]
- Doan, V.Q.; Kusaka, H.; Nguyen, T.M. Roles of past, present, and future land use and anthropogenic heat release changes on urban heat island effects in Hanoi, Vietnam: Numerical experiments with a regional climate model. Sustain. Cities Soc. 2019, 47, 101479. [Google Scholar] [CrossRef]
- Xue, Y.; Wang, Y.; Peng, H.; Wang, H.; Shen, J. The impact of building configurations and anthropogenic heat on daily urban air temperature cycles. Build. Environ. 2020, 169, 106564. [Google Scholar] [CrossRef]
- Chen, R.; Yang, M.; Wang, X.; Wan, G. Review on simulation of land-surface processes on the Tibetan Plateau. Sci. Cold Arid. Reg. 2019, 11, 93–115. [Google Scholar]
- Chen, Y.; Yang, K.; He, J.; Qin, J.; Shi, J.; Du, J.; He, Q. Improving land surface temperature modeling for dry land of China. J. Geophys. Res. Space Phys. 2011, 116, 116. [Google Scholar] [CrossRef]
- Yang, K.; He, J.; Tang, W.; Qin, J.; Cheng, C.C. On downward shortwave and longwave radiations over high altitude regions: Observation and modeling in the Tibetan Plateau. Agric. For. Meteorol. 2010, 150, 38–46. [Google Scholar] [CrossRef]
- He, J.; Yang, K.; Tang, W.; Lu, H.; Qin, J.; Chen, Y.; Li, X. The first high-resolution meteorological forcing dataset for land process studies over China. Sci. Data 2020, 7, 1–11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, G.; Chen, F.; Gan, Y. Assessing uncertainties in the Noah-MP ensemble simulations of a cropland site during the Tibet Joint International Cooperation program field campaign. J. Geophys. Res. Atmos. 2016, 121, 9576–9596. [Google Scholar] [CrossRef]
- Liu, M.; Tang, R.; Li, Z.-L.; Yan, G. Integration of two semi-physical models of terrestrial evapotranspiration using the China Meteorological Forcing Dataset. Int. J. Remote Sens. 2018, 40, 1966–1980. [Google Scholar] [CrossRef]
- Xinliang, X.; Jiyuan, L.; Shuwen, Z.; Rednong, L.; Changzhen, Y.; Shixin, W. China Land Use and Land Cover Change Database (CNLUCC). Data Center for Resources and Environmental Sciences. Chinese Academy of Sciences. 2018. Available online: http://www.resdc.cn (accessed on 20 September 2021).
- Jiyuan, L.; Wenhui, K.; Zengxiang, Z.; Xinliang, X. Spatiaotemporal characteristics, patterns and causes of land-use changes in China since the late 1980s. J. Geogr. Sci. 2014, 69, 3–14. [Google Scholar]
- Xu, C.; Jiang, W.; Huang, Q.; Wang, Y. Ecosystem services response to rural-urban transitions in coastal and island cities: A comparison between Shenzhen and Hong Kong, China. J. Clean. Prod. 2020, 260, 121033. [Google Scholar] [CrossRef]
- Wang, X.; Yan, F.; Su, F. Impacts of Urbanization on the Ecosystem Services in the Guangdong-Hong Kong-Macao Greater Bay Area, China. Remote Sens. 2020, 12, 3269. [Google Scholar] [CrossRef]
- Wan, Z. New refinements and validation of the collection-6 MODIS land-surface temperature/emissivity product. Remote Sens. Environ. 2014, 140, 36–45. [Google Scholar] [CrossRef]
- Gao, Y.; Li, K.; Chen, F.; Jiang, Y.; Lu, C. Assessing and improving Noah-MP land model simulations for the central Tibetan Plateau. J. Geophys. Res. Atmos. 2015, 120, 9258–9278. [Google Scholar] [CrossRef]
- Shen, Y.; Shen, H.; Li, H.; Cheng, Q. Long-term urban impervious surface monitoring using spectral mixture analysis: A case study of Wuhan city in China. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 6754–6757. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).