Next Article in Journal
Microscale and Mesoscale Aeolian Processes of Sandy Coastal Foredunes from Background to Extreme Conditions
Previous Article in Journal
Spatiotemporal Characterization of the Urban Expansion Patterns in the Yangtze River Delta Region
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 13
Issue 21
10.3390/rs13214487
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Precise Relative Orbit Determination for Chinese TH-2 Satellite Formation Using Onboard GPS and BDS2 Observations

by
Bin Yi
1,
Defeng Gu
2,3,*,
Kai Shao
2,4,
Bing Ju
5,
Houzhe Zhang
1,
Xianping Qin
6,
Xiaojun Duan
1 and
Zhiyong Huang
7
1
College of Liberal Arts and Sciences, National University of Defense Technology, Changsha 410073, China
2
MOE Key Laboratory of TianQin Mission, TianQin Research Center for Gravitational Physics, Frontiers Science Center for TianQin, CNSA Research Center for Gravitational Waves, Sun Yat-sen University (Zhuhai Campus), Zhuhai 519082, China
3
School of Artificial Intelligence, Sun Yat-sen University (Zhuhai Campus), Zhuhai 519082, China
4
School of Physics and Astronomy, Sun Yat-sen University (Zhuhai Campus), Zhuhai 519082, China
5
Beijing Aerospace Control Center, National Key Laboratory of Science and Technology on Aerospace Flight Dynamics, Beijing 100094, China
6
Xi’an Research Institute of Surveying and Mapping, Xi’an 710054, China
7
Institute of Surveying and Mapping, Information Engineering University, Zhengzhou 450000, China
*
Author to whom correspondence should be addressed.
Remote Sens. 2021, 13(21), 4487; https://doi.org/10.3390/rs13214487
Submission received: 10 October 2021 / Revised: 5 November 2021 / Accepted: 5 November 2021 / Published: 8 November 2021
Browse Figures
Review Reports Versions Notes

Abstract

:
TH-2 is China’s first short-range satellite formation system used to realize interferometric synthetic aperture radar (InSAR) technology. In order to achieve the mission goal of InSAR processing, the relative orbit must be determined with high accuracy. In this study, the precise relative orbit determination (PROD) for TH-2 based on global positioning system (GPS), second-generation BeiDou navagation satellite system (BDS2), and GPS + BDS2 observations was performed. First, the performance of onboard GPS and BDS2 measurements were assessed by analyzing the available data, code multipath errors and noise levels of carrier phase observations. The differences between the National University of Defense Technology (NDT) and the Xi’an Research Institute of Surveying and Mapping (CHS) baseline solutions exhibited an RMS of 1.48 mm outside maneuver periods. The GPS-based orbit was used as a reference orbit to evaluate the BDS2-based orbit and the GPS + BDS2-based orbit. It is the first time BDS2 has been applied to the PROD of low Earth orbit (LEO) satellite formation. The results showed that the root mean square (RMS) of difference between the PROD results using GPS and BDS2 measurements in 3D components was 2.89 mm in the Asia-Pacific region. We assigned different weights to geostationary Earth orbit (GEO) satellites to illustrate the impact of GEO satellites on PROD, and the accuracy of PROD was improved to 7.08 mm with the GEO weighting strategy. Finally, relative orbits were derived from the combined GPS and BDS2 data. When BDS2 was added on the basis of GPS, the average number of visible navigation satellites from TH-2A and TH-2B improved from 7.5 to 9.5. The RMS of the difference between the GPS + BDS2-based orbit and the GPS-based orbit was about 1.2 mm in 3D. The overlap comparison results showed that the combined orbit consistencies were below 1 mm in the radial (R), along-track (T), and cross-track (N) directions. Furthermore, when BDS2 co-worked with GPS, the average of the ambiguity dilution of precision (ADOP) reduced from 0.160 cycle to 0.153 cycle, which was about a 4.4% reduction. The experimental results indicate that millimeter-level PROD results for TH-2 satellite formation can be obtained by using onboard GPS and BDS2 observations, and multi-GNSS can further improve the accuracy and reliability of PROD.

Graphical Abstract

1. Introduction

The Chinese TH-2 satellite formation is the second microwave interferometric surveying satellite system in the world after TanDEM-X [1]. It is composed of two almost identical satellites, namely TH-2A and TH-2B. The primary goal of TH-2 is to generate a high-accuracy and -resolution digital elevation model (DEM) of the Earth. It is similar to the TanDEM-X mission; the essential requirement for achieving the expected DEM is to achieve millimeter-level relative orbit of two formation-flying satellites [2].
In order to achieve high-precision precise relative orbit determination (PROD) results, both TH-2A and TH-2B satellites are equipped with the same global navigation satellite system (GNSS) receiver, which tracks BDS2 and GPS satellites simultaneously. The collected pseudo-range and carrier phase observations onboard are used for PROD. The receivers contain many key technologies such as GNSS observation pre-processing, empirical forces modeling, maneuver parameterization and fixing double differenced (DD) integer ambiguities [3,4]. Research results show that relative orbit determination at the millimeter to sub-millimeter level can be achieved through carrier-phase differential GNSS (CDGNSS) observations [5,6].
BDS3 is independently developed and operated by China [7,8]. At present, the third- generation BDS (BDS3) provides global positioning, navigation and timing service. Centimeter-level precision orbits of Tianping-1B [9] and Loujia-1A [10] were obtained by using only BDS measurements. With the rapid development of navigation satellite systems [11], multi-GNSS has become a hot research issue. Multi-GNSS improves the satellite numbers and geometric strength, which could further improve the accuracy of the LEO orbits. Yang et al. showed that when GPS was jointed with BDS, the global geometric dilution of precision (GDOP) was increased by 50% on the basis of GPS [12]. Liu et al. studied precise point positioning (PPP) based on GPS and BDS; the results showed that the ambiguity fixing rate within 10 min for GPS was only 17.6%; however, adding inclined geosynchronous orbit (IGSO) satellites and medium Earth orbit (MEO) satellites, the percentage improved significantly to 42.8% [13]. Li et al. used the FengYun-3C onboard BDS and GPS data of 2013, 2015, and 2017 to solve the precise orbit determination (POD) of FengYun-3C; the results showed that, without GEO satellites, the accuracy of BDS + GPS POD was slightly better than that of GPS-only POD [14].
In the past, the GNSS receivers carried by the LEO formation flying satellites could not receive BDS signals; research in multi-GNSS PROD was based on simulation data. Simulation experiments were carried out by Liu et al. to show that BDS2 can realize the PROD of LEO formation flying satellites in global and the accuracy of the Asia-Pacific region can reach 3.4 mm [15]. Verhagen and Teunissen showed that GPS + BDS was more conducive to real-time relative orbit determination than GPS-only or BDS-only [16]. Yi et al. found that the influence of GEOs’ meter-level ephemeris errors on PROD of short-range formations could be ignored [17]. TH-2 is the first satellite formation system, which tracks both GPS and BDS2 signals. These GPS and BDS2 observations allow us to evaluate the PROD performances based on multi-GNSS. It is also the first time BDS has been applied to PROD of LEO satellites formation.
The GRACE mission is equipped with a K-band ranging system, which enables a direct evaluation of the baseline precision [18]. However, for TanDEM-X and TH-2, no independent measurement system will be available to validate the PROD results. Therefore, how to check the accuracy of PROD becomes a problem. Montenbruck et al. [19] and Moon et al. [20] discussed the TanDEM-X mission by using the GRACE as a reference case to illustrate the processing concept and expected accuracy. Montenbruck et al. [21] and Allende-Alba and Montenbruck [22] adopted an internal consistency check, which compared the baseline solutions resulting from the differential carrier phase processing against the relative positions derived from differential POD (dPOD) solutions. In 2012, an inter-agency comparison of the TanDEM-X mission baseline solution was performed by three institutions; the bias in each direction was better than 1 mm excluding the maneuver periods [23]. Today, many agencies in China are able to determine the precise orbit of LEOs, such as the National University of Defense Technology (NDT) [24], Wuhan University [25], and the Xi’an Research Institute of Surveying and Mapping (CHS) [26]. In this study, we used internal consistency checks and inter-agency (NDT and CHS) comparisons to access the accuracy of the GPS-based orbit.
We briefly introduce the quality of onboard GPS and BDS2 data. Then, the methods for PROD at NDT and CHS are introduced. Subsequently, the GPS-based, BDS2-based and combined PROD of TH-2 is provided. Finally, conclusions are drawn.

2. Data Collection and Quality Evaluation

High-quality GNSS observations are the prerequisite for achieving high-precision relative orbit. Therefore, it is necessary to analyze the quality of the onboard GNSS observations before performing PROD. In this section, the information of TH-2 satellite formation system is introduced, and the quality of the observation data is analyzed from the available data, code multipath, and carrier phase noise.

2.1. TH-2 Satellite Formation System

The TH-2 satellite system was developed by the Shanghai Academy of Spaceflight Technology and launched by the Taiyuan Satellite Launch Center on 30 April 2019 [27]. They travel in a solar-synchronous orbit at ≈518 km altitude and the incidence angle ranges from 35° to 46°, separated from each other only a few hundred meters in space [28]. TH-2A and TH-2B carried a multi-GNSS receiver, which can be used for POD and PROD. The onboard GNSS data include GPS L1 and L2 frequencies data, and BDS2 B1 and B3 frequencies data. This study analyzes the onboard GNSS observations of TH-2 during day of year (DOY) 305–332 in 2019, with an interval of 10 s. The days (DOY 323) when both TH-2A and TH-2B performed maneuvers is excluded from the analysis. Taking the GNSS observations of TH-2A as an example for analysis in this section, the result of TH-2B was similar to that of TH-2A.

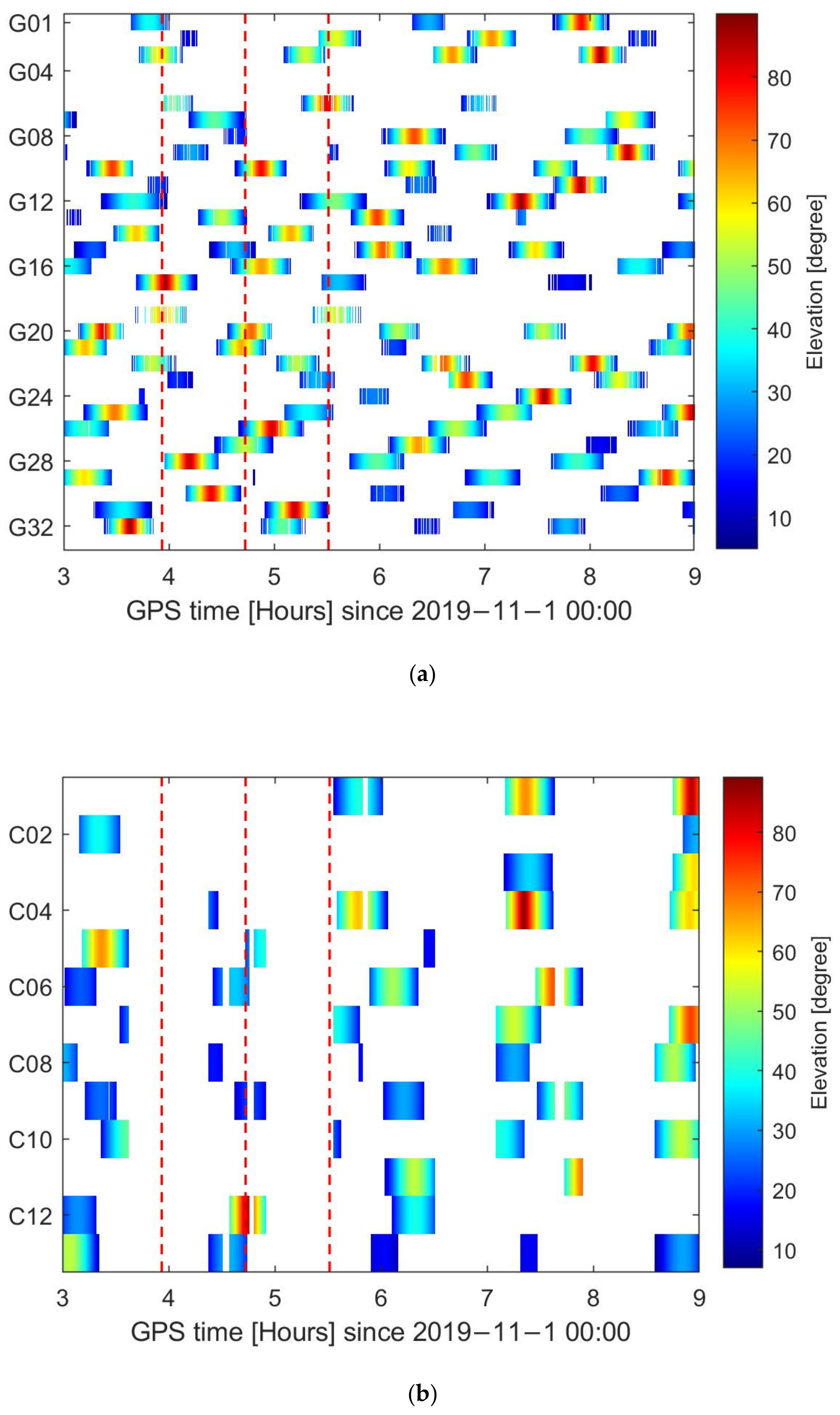
2.2. Performance of Onboard GNSS Receiver

We evaluated the availability of TH-2 onboard GNSS data by analyzing the numbers of BDS2 and GPS observations. At present, the receivers can only track the first 14 BDS2 satellites, including five GEOs (C01–C05), six IGSOs (C06–C10 and C13), and three MEOs (C11, C12, and C14). Figure 1 shows the number of observations for GPS satellites. For GPS, the L1 observations numbered slightly more than those of L2, because the signal to noise ratio (SNR) of the L1 frequency was stronger than that of the L2 frequency [29]. Figure 2 shows the number of observations for BDS2 satellites. For BDS2, the number of IGSOs observations was slightly larger than that of GEOs and MEOs, which was the result of IGSOs’ higher orbit altitude and better observation geometry. If both the dual-frequency code and carrier phase observations were present in an epoch, then that was an available epoch. The daily average numbers of available epochs were 2340 for the BDS2 MEO, 2226 for the BDS2 GEO, 2867 for the BDS2 IGSO, and 2376 for the GPS satellite.

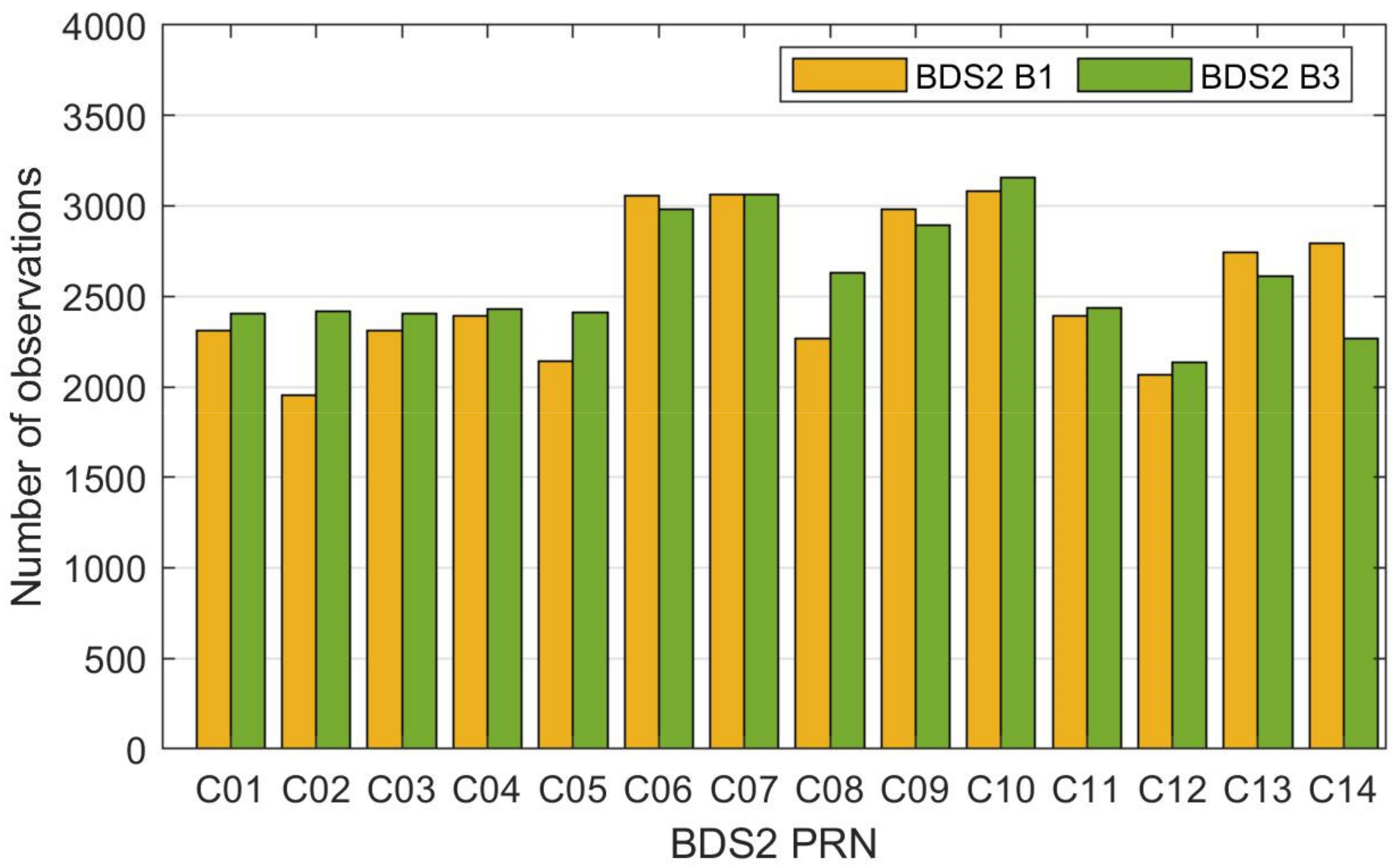
2.3. Data Quality of Multi-GNSS Observations

Figure 3 shows the magnitude of the onboard code multipath errors with respect to elevation. In Figure 3, each value represents the RMS of the data falling within the range of 3°. For GPS satellites, the multipath error decreases as the elevation increases. The average multipath error of GPS L1 and L2 was 0.26 m and 0.20 m, respectively. The data characteristics of BDS2 were different from that of GPS. When the elevation angle was greater than 45°, the average multipath error of B1/B3 decreased as the elevation increased. MEOs B1 and B3 were 0.39 m and 0.15 m, respectively, IGSOs B1 and B3 were 0.21 m and 0.13 m, respectively, and GEOs B1 and B3 were 0.22 m and 0.14 m, respectively.
High-precision carrier-phase observation is essential for GNSS-based orbit solutions, as the accuracy of carrier phase measurements is at the millimeter-level. The fitting residuals of the L1–L2 combinations are often used to evaluate the noise level of the carrier phase [24]. The average value of the daily RMS of GPS, BDS2 MEOs, IGSOs and GEOs was 4.7 mm, 3.8 mm, 4.0 mm, and 2.6 mm, respectively (see Table 1). The quality of the BDS2 observations was comparable to that of GPS. This provided a good condition for orbit determination using GPS and BDS2 observations.

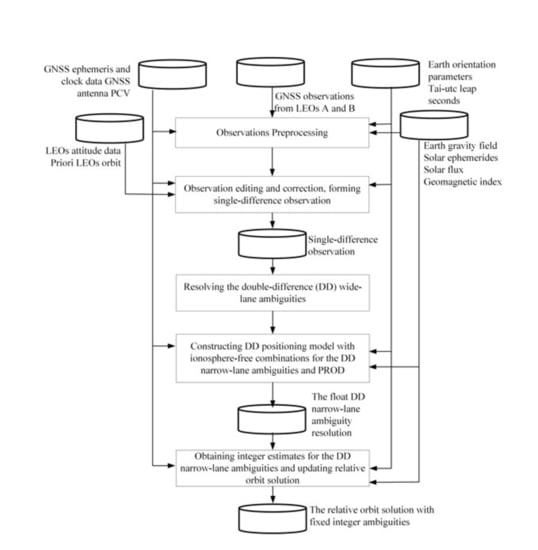
3. Methods for Precise Relative Orbit Determination

Independent precise relative orbits of TH-2 were generated by NDT and CHS with different software and strategies. The following briefly introduces the methods of PROD of NDT and CHS. The strategy of NDT and CHS software packages for baseline determination are displayed in Table 2.

3.1. National University of Defense Technology (NDT) Approach

The PROD results of NDT were generated by the National University of Defense Technology Orbit Determination Toolkit (NUDTTK) software, which has been successfully used in POD and PROD of LEOs, such as Tiangong-2 [24], GRACE [30], and GRACE-FO [31]. The NDT solutions of POD and PROD are described in detail by Gu et al. [30].
The NDT adopts a reduced-dynamic approach and a batch least-squares estimation method to perform POD and PROD. The TH-2B satellite keeps the result of POD unchanged; POD processing uses a zero-difference ionosphere-free code and carrier phase combination. TH-2A adopts a double-difference (DD) ionosphere-free carrier phase combination, where the DD ambiguity needs to be fixed in order to obtain high-precision PROD results. First, the DD wide-lane ambiguities were solved by analyzing the Melbourne-Wubbena linear combination. Then, the wide-lane ambiguities were introduced as known in order to resolve the narrow-lane ambiguities. Both the wide-lane and narrow-lane ambiguities used the LAMBDA method [32,33,34] to search for integer values. In order to maintain orbit and formation, three maneuvers are performed by TH-2A per day during 04:00–07:00; all maneuvers must be considered to obtain continuous and high-precision PROD results. In the NUDTTK software, each orbit maneuver is modeled as constant acceleration in the R, T, and N directions over a predefined thrust interval, an 11th-order Adams–Cowell multi-step integrator for normal arcs, and an eighth-order Runge–Kutta single-step integrator around maneuver arcs [35]. The estimation orbit parameters are: initial states of TH-2A, Z component of the phase center offset (PCO), a solar pressure coefficient, piecewise constant atmospheric drag coefficients over 3 h intervals, piecewise linear empirical accelerations in T and N directions over 15 min intervals, and maneuver parameters.

3.2. Xi’an Research Institute of Surveying and Mapping (CHS) Approach

The accuracy of POD and PROD for LEOs based on CHS is centimeter-level and millimeter-level, respectively [36]. The CHS solutions of POD and PROD for TH-2 are also based on reduced-dynamic approach and batch least-squares estimation method. Differences to the NDT approach mainly include the following. Within the CHS software, piecewise constant empirical accelerations are performed in the R, T, and N directions over 6 min intervals. Orbital maneuvers are considered as a series of velocity pulses in the R, T, and N directions at specified epochs. In addition, the ambiguities are resolved to their integer values by the search strategy [37] instead of LAMBDA method. Considering the use of different software and dynamical models, the NDT and CHS solutions have a certain degree of independence despite the use of common observations. This enables an accurate evaluation of PROD results through an inter-agency comparison.

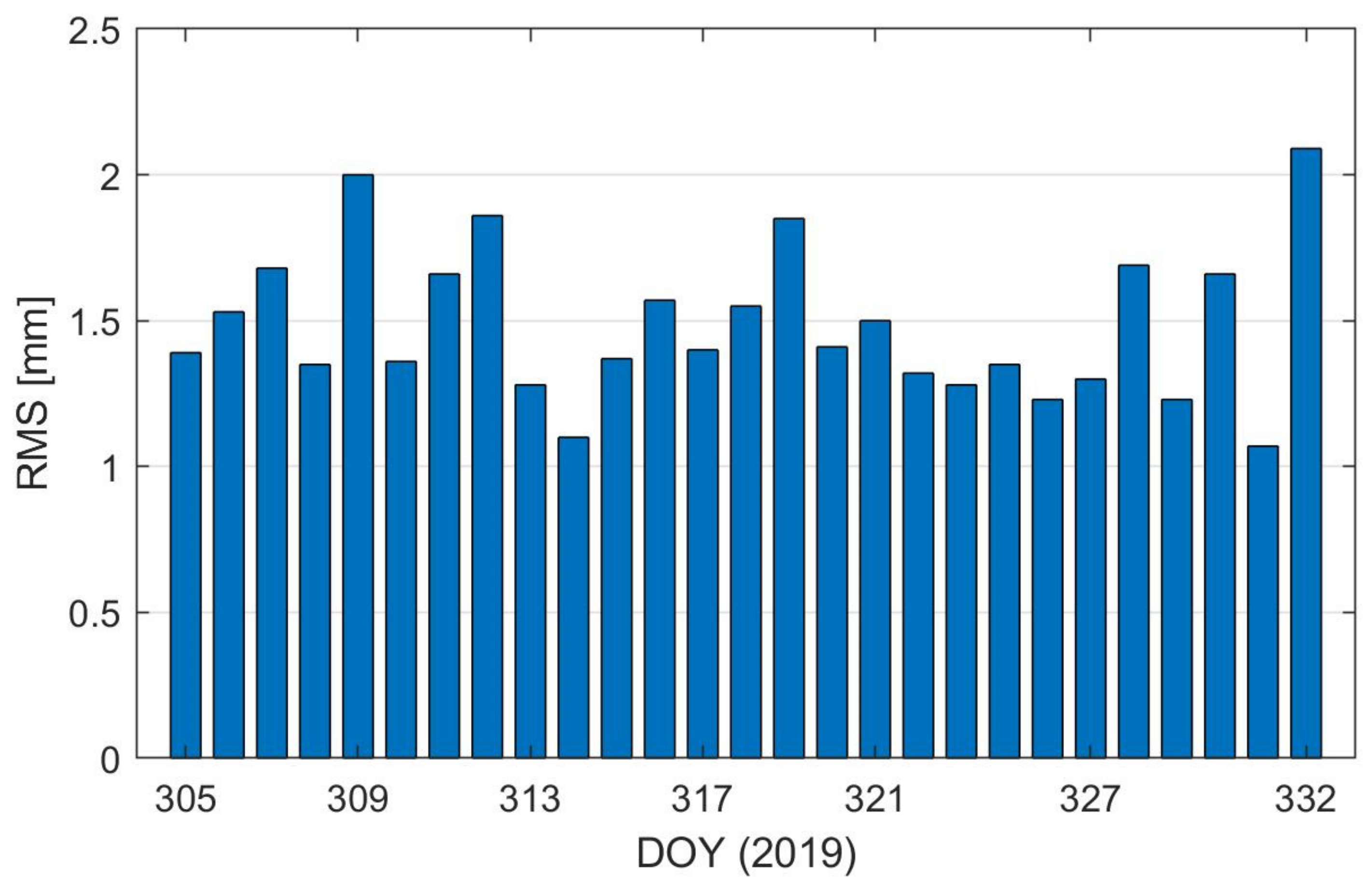
4. Results

A 30 h arc length was used for PROD, from 21:00 on the previous day to 03:00 on the following day. The middle 24 h arc was used as a precision orbit product. A description of the accuracy of GPS-based PROD is provided in Section 4.1. Then, a brief discussion about the BDS2-based PROD results and the contribution of GEOs is conducted in Section 4.2. The focus of Section 4.3 is on the performance of PROD by both GPS and BDS2.

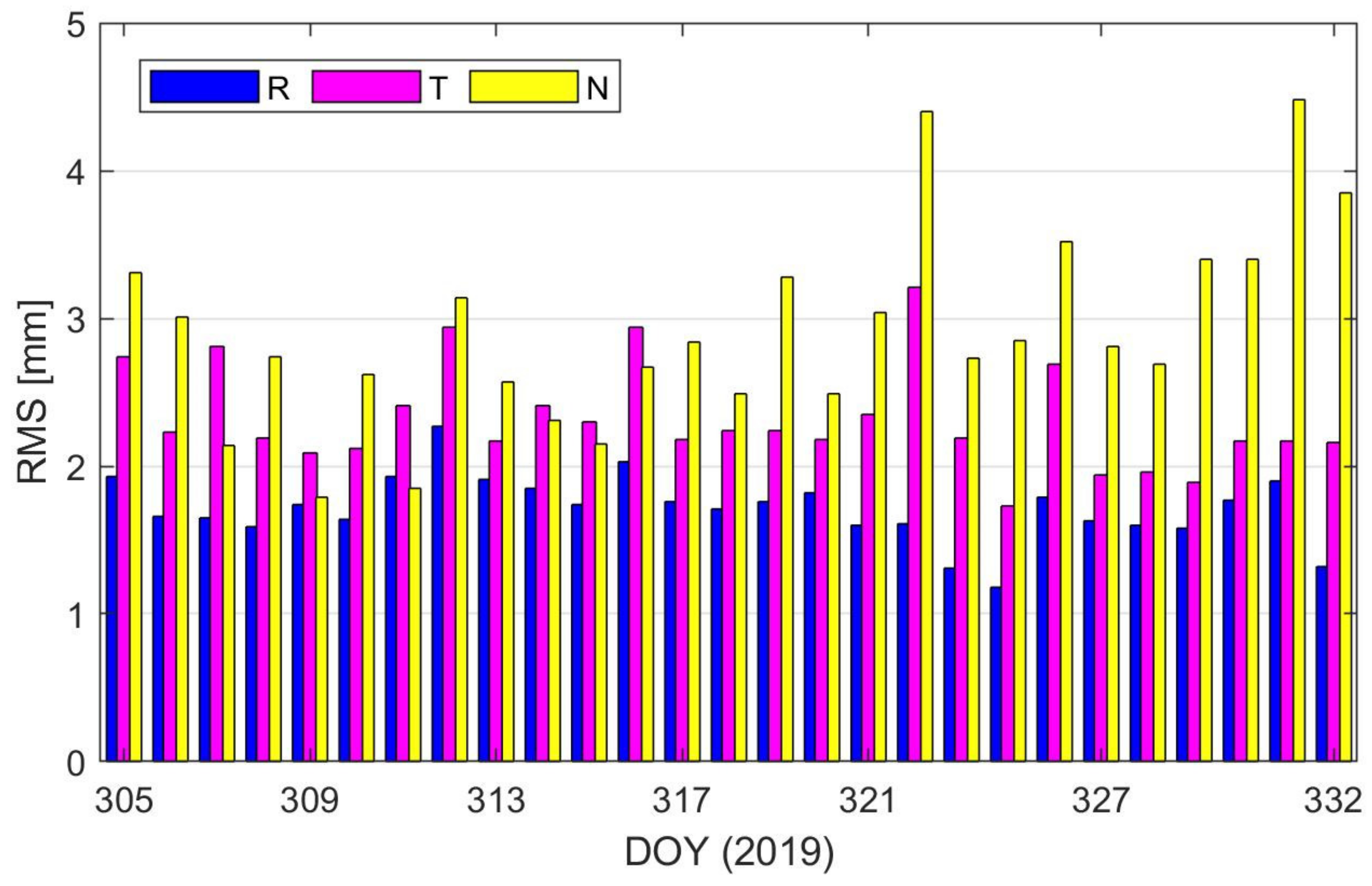
4.1. GPS-Based Precise Relative Orbit Determination (PROD)

Due to lack of direct measures for precision assessment, the PROD results were discussed by inter-agency comparison. The difference in 3D between the NDT and CHS solutions was better than 2 mm when excluding maneuver time periods [38]. Here, we excluded time intervals for each day from midnight to 1 h after the third maneuver. Figure 4 shows the difference in 3D between the NDT and CHS solutions outside the maneuver periods. The average value of the daily RMS was 1.48 mm. The differences between the NDT and CHS solutions on DOY 305 in 2019 are displayed in Figure 5. The difference between the NDT and CHS solutions in the T direction was larger than that in the R and N directions. This may be the result of the fact that the empirical forces are modeled differently at NDT and CHS. CHS has different software packages for orbit determination from NDT, which can provide independent PROD results. The PROD results provided by CHS corresponded to those provided by NDT. By inter-agency comparison, a conclusion can be drawn that the accuracy of GPS-based PROD is millimeter-level, which would be used as a reference to analyze the BDS2-based and combined PROD results.
The GPS-based PROD was evaluated by a self-consistency test and inter-agency comparison. The difference between the dPOD results and PROD results can reflect the correctness of GNSS data processing and orbit determination strategy. Figure 6 shows the RMS of the difference between the dPOD and PROD solutions in the R, T, and N directions. The RMS of orbit differences was 1.71 mm, 2.32 mm, 2.91 mm, and 4.13 mm in the R, T, N, and 3D directions, respectively. The DD ambiguity fixed rate was 100% based on GPS-only. The method of POD was different from that of PROD. However, the difference between the dPOD and PROD solutions was only several millimeters, indicating that the accuracy of a relative orbit determined by NDT was millimeter-level.

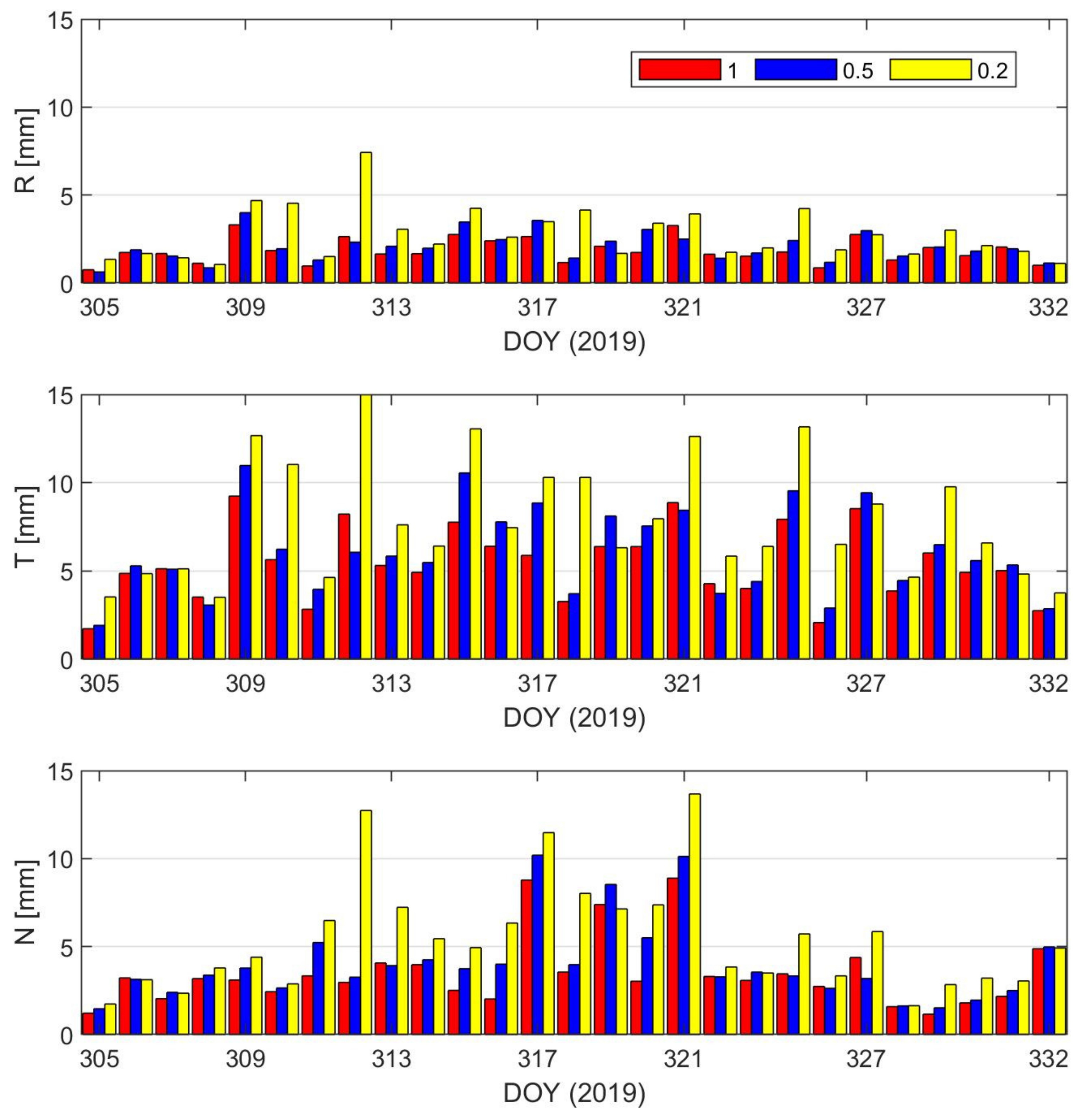
4.2. BDS2-Based Precise Relative Orbit Determination (PROD)

As BDS2 is a regional navigation satellite system, the amount of BDS2 observations was much less than that of GPS. The carrier phase tracking arcs from TH-2A and TH-2B satellites on DOY 305 in 2019 are displayed in Figure 7, where the color bar represents the elevation and the red dashed lines indicate the center of burn time. The average of continuous tracking arcs was 410 for GPS satellites, while that it was only 179 for BDS2 satellites. The average duration of continuous tracking arcs was 31.5 min, while it was only 26.2 min for BDS2 satellites. Therefore, for the BDS2-based PROD we excluded the time intervals for each day from midnight to 1 h after the third maneuver. In addition, considering the small number of BDS2 observations, the threshold for the number of visible satellites was reduced from 3 to 2, and the threshold for the duration of continuous tracking arc was reduced from 400 s to 200 s. The piecewise periodic empirical accelerations in T and N directions were estimated every 3 h.
Due to the worse ephemeris and poor geometry of GEOs [39,40], three different weighting strategies were designed to analyze the effect of GEOs on PROD. The IGSOs and MEOs were treated as unit weight and the weight of GEOs was relative to the IGSOs and MEOs. Figure 8 and Table 3 show the difference between the GPS-based PROD and BDS2-based PROD in the R, T, and N directions with the different weight of GEOs. The differences increased with the decrease in the GEOs’ weight. The average value of the daily RMS differed between the GPS-based and BDS2-based PROD. The average value of the daily RMS was 7.08 mm, 8.00 mm and 11.40 mm in 3D (global) when the weight of GEOs was 1, 0.5, and 0.2, respectively. The results showed that GEO satellites play important roles when BDS2 are applied to the PROD of LEO satellite formation. The relative position between TH-2A and TH-2B is only a few hundred meters, and the influence of ephemeris errors on PROD can be ignored, which agrees with Yi et al. [17]. It can be concluded that the accuracy of BDS2-based PROD can reach millimeter-level. In the following analysis, the MEOs, IGSOs, and GEOs are treated as equal weight.
Considering that BDS2 is a regional constellation, the difference in the accuracy of PROD in different regions needs to be analyzed. The spatial distribution of difference between the GPS-based and BDS2-based PROD in 3D is presented in Figure 9, the mean 3D accuracy of each 5° × 5° zone was calculated. The accuracies of BDS2-based PROD in different regions were apparently different. The Asia-Pacific region was defined as longitudes from 55° E to 180° E and latitudes from 55° S to 55° N. The RMS values of difference between the GPS-based and BDS2-based PROD in the Asia-Pacific region and non-Asia-Pacific region were 2.89 mm and 7.96 mm, respectively. The results are basically consistent with Liu et al. [15]. There were some arcs with large residuals in Figure 7, which were caused by the failure of integer ambiguity resolution. The ambiguity fixed rate was only 92.6% based on BDS2-only. The main reason is that there are not enough observations in some batches to ensure the ambiguities were estimated correctly. The average number of ambiguities was 11.6 per processing batch based on GPS-only, while it was only 5.0 for BDS2-only.

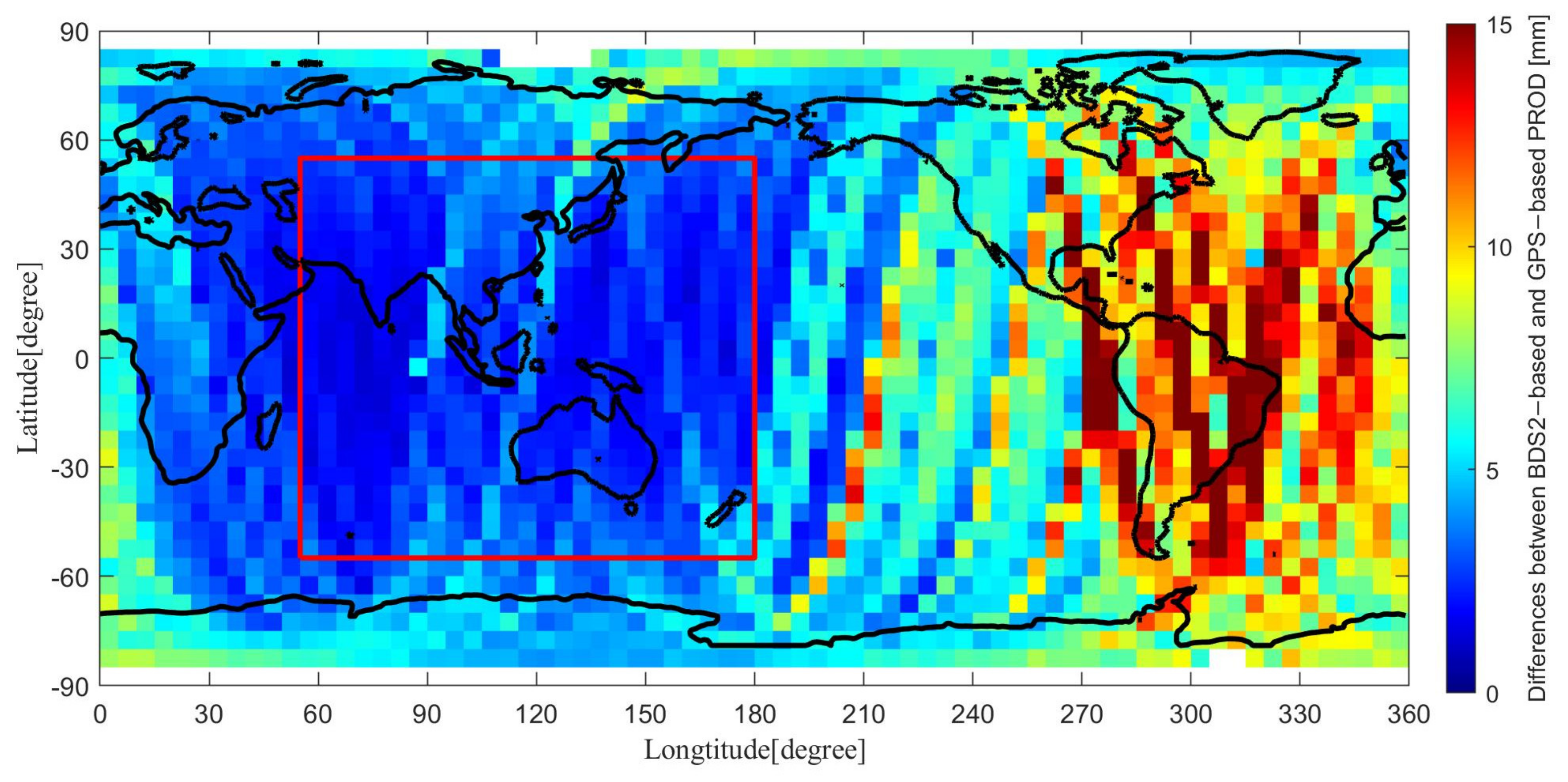
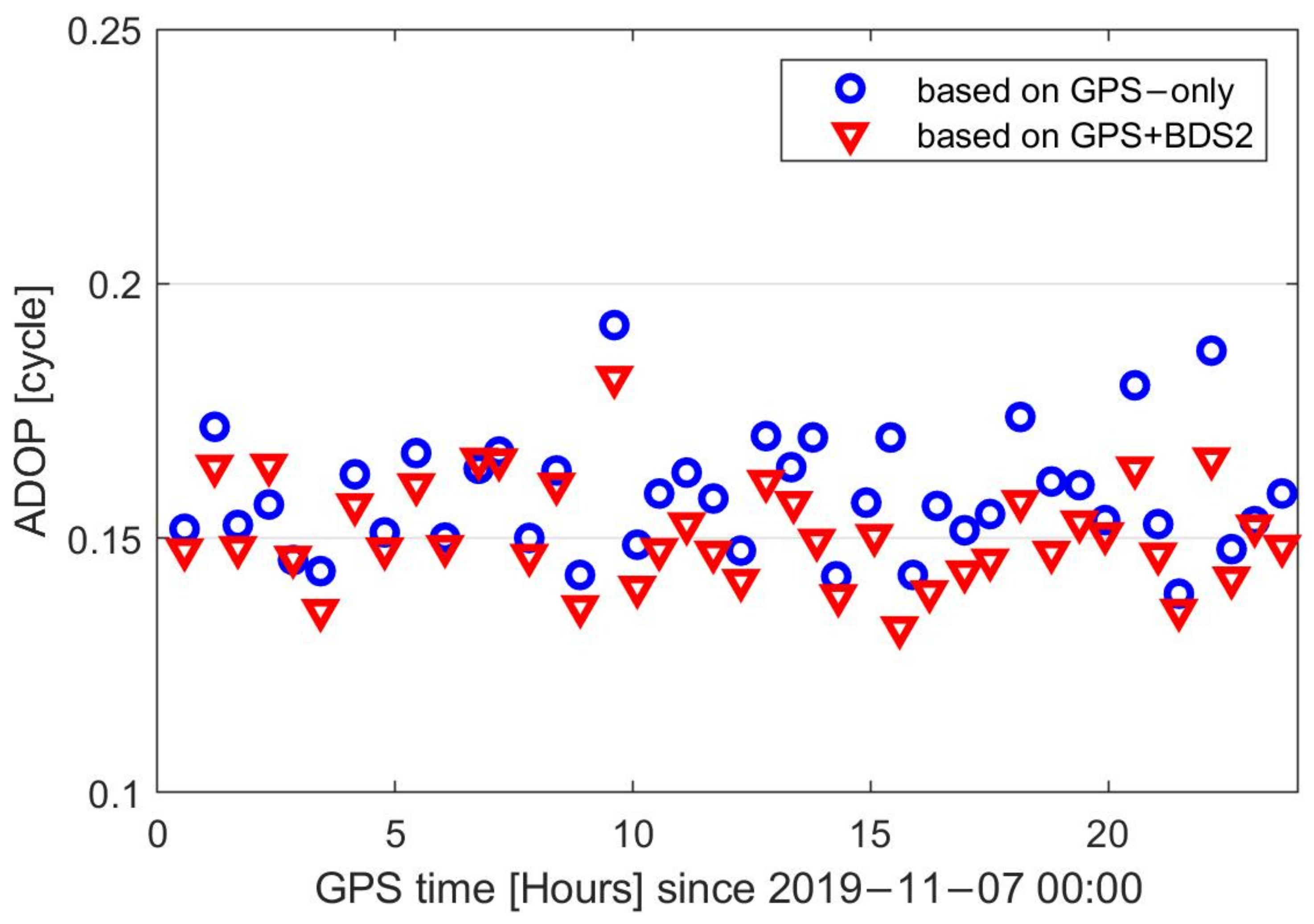
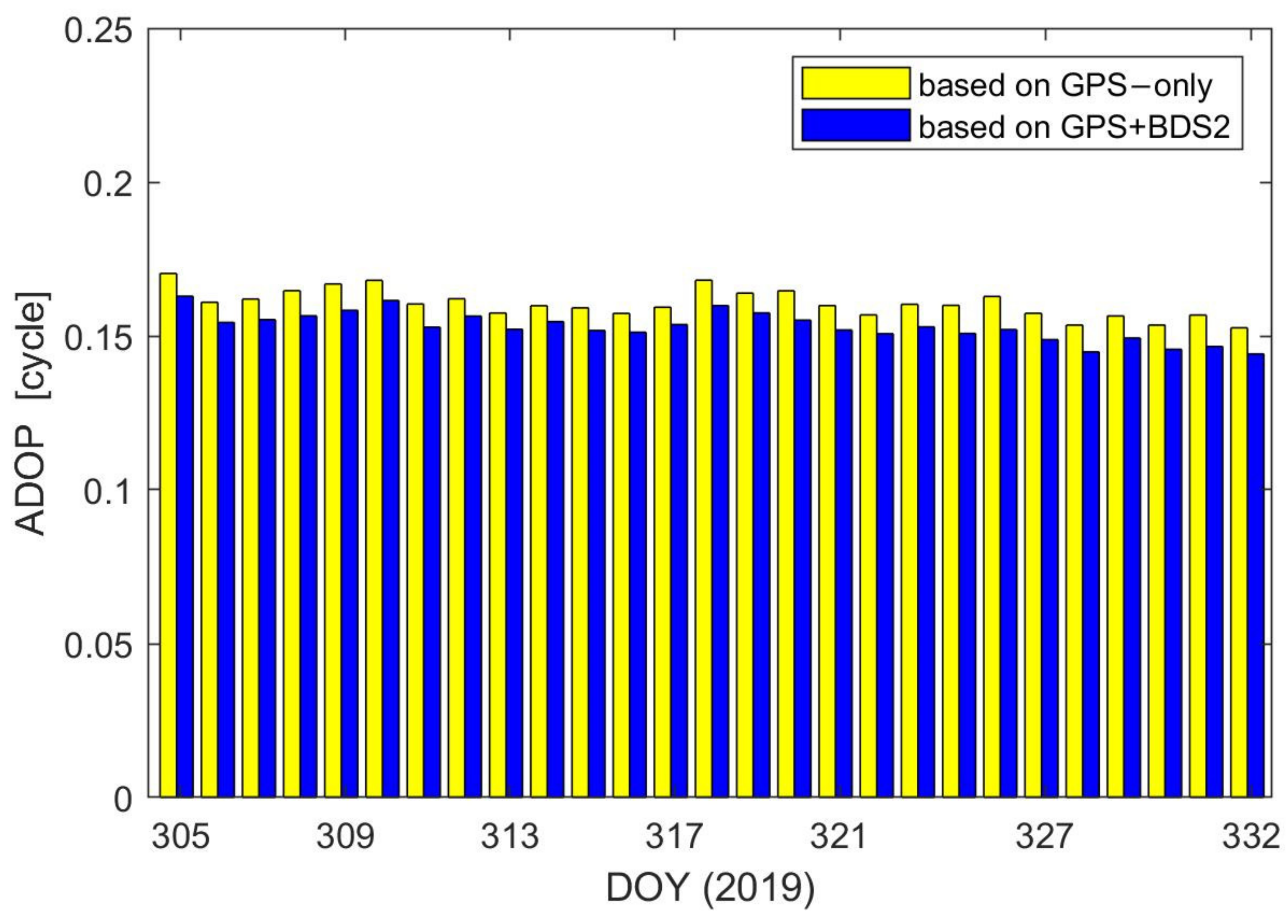
4.3. Combined GPS/BDS2 PROD

Figure 10 is the GPS-based and combined position dilution of precision (PDOP) of TH-2A on DOY 307 in 2019. For GPS-based PDOP, the total ration of less than 4 in an epoch was 96.8%, and it was 99.5% for combined PDOP. Figure 11 shows the daily average of the GPS-based and combined PDOP. Adding BDS2 to GPS, the PDOP improved from 2.42 to 1.94, an improvement of 19.8%. Figure 12 displays the visible navigation satellites from TH-2A and TH-2B based on GPS-only and GPS + BDS2. Adding BDS2 to GPS, the average number of visible satellites increased from 7.5 to 9.5, and the maximum could reach 18. All of these are beneficial to further enhance the accuracy of PROD.
Here, GPS and BDS2 each had a reference satellite to construct the DD observations, as the frequencies of GPS and BDS2 were different. The ambiguity per system was solved separately. Figure 13 displays the difference between the GPS-based and combined PROD. The averages of the daily RMS of orbit differences in the R, T, and N directions were 0.48 mm, 1.01 mm, and 0.35 mm, respectively. The GPS-based and combined PROD results were consistent, which indicated that adding BDS2 to GPS did not cause pollution of the PROD result. Figure 14 shows the DD ionospheric-free phase residuals on DOY 305 in 2019. The RMS of the DD ionospheric-free observation minus computation (O-C) phase residual of GPS and BDS2 was 4.2 mm and 8.5 mm, respectively. There were no large deviations in the vicinity of the maneuver, which shows that maneuver accommodated orbits fit the GPS and BDS2 observations well. An orbit overlap comparison was adopted to reflect the orbit consistency. The result shows the average of daily RMS values of the residuals of 6 h relative orbit overlapping for combined PROD in the R, T, and N directions were 0.53 mm, 0.97 mm, and 0.33 mm, respectively.
The success rate of the integer ambiguity has a great influence on the PROD’s accuracy, and it depends largely on the accuracy of the float ambiguity; the lower the accuracy of the float ambiguity, the longer the search time. The ambiguity dilution of precision (ADOP) measures the average precision of the ambiguities and is invariant for the class of admissible ambiguity transformations [41,42]. It is based on the determinant of the ambiguity variance matrix. Here, ADOP can be used to evaluate the accuracy of the float ambiguity, which depends on the number of visible satellites and the quality of their phase and code observations [43]. Figure 15 displays the GPS ADOP on DOY 311 in 2019 and Figure 16 shows the daily value of GPS ADOP. When BDS2 co-worked with GPS, the average of GPS ADOP reduced from 0.160 cycle to 0.153 cycle. This showed that the accuracy of the float ambiguity was effectively improved when BDS2 co-worked with GPS. The ambiguity fixed rate of GPS and BDS2 were both 100.0%. Although the ambiguity of GPS and BDS were resolved separately, the orbital and dynamic parameters were the same. By integrating BDS2 and GPS, the number of visible satellites and observations greatly increased, which can effectively improve the accuracy of orbital parameters, dynamic parameters, and float ambiguities.

5. Discussion

Since BDS2 is a regional navigation constellation and has only 14 satellites, there is still a large gap in the accuracy of relative orbit of TH-2 based on BDS2 compared with that based on GPS. The results showed that the accuracy of the relative orbit of TH-2 based on BDS2 in the Asia-Pacific region could reach 2.89 mm, which was comparable to the existing simulation results. Research on the precise orbit determination of LEO satellite based on BDS obtained the same conclusion; the addition of GEO would dramatically degrade the accuracy of orbit. However, the results of this paper show that GEO can significantly improve the accuracy of the relative orbit of TH-2 satellite formations. This is because in the precise relative orbit determination process, the ephemeris error can be greatly weakened by CDGNSS technology. The relative position between TH-2A and TH-2B satellites is only a few hundred meters; hence, the influence of GEOs’ ephemeris errors on the precise relative orbit determination of TH-2 could be ignored.
The BDS3 has been officially opened. Compared to BDS2, BDS3 has many advantages, such as 30 satellites, the ability to broadcast four civil signals, a more stable atomic clock, and inter-satellite links. The performance of relative orbit determination based on BDS3 is expected to be better than that based on BDS2. The effect of GEO satellites on the precise relative orbit determination of the LEO satellites with a several-hundred-kilometer separation and the improvement of the precise relative orbit determination by integrating BDS3 and GPS will be studied further in the future.

6. Conclusions

The collected GPS and BDS2 observations of TH-2 satellites provide a good platform for analyzing the PROD based on multi-GNSS. The onboard GPS and BDS2 observations were analyzed; the amount of GPS observations was far greater than that of BDS2, but the signal quality of the BDS2 was comparable with that of GPS.
The RMS of difference between the NDT and CHS solutions in 3D was smaller than 1.5 mm outside the maneuver periods. Different weights of GEOs observations were adopted to discuss the contribution of GEOs. The result showed that the average value of the daily RMS of difference between the GPS-based and BDS2-based PROD increased with the decrease in the GEOs’ weight. When assigning the same weight to MEO, IGSO, and GEO satellites, the RMS of difference between the GPS-based and BDS2-based PROD in 3D components was 7.08 mm, 2.89 mm, and 7.96 mm in the global, Asia-Pacific region and non-Asia-Pacific region, respectively.
After adding BDS2 to GPS, the number of visible satellites from TH-2A and TH-2B increased by 21.1%, and the PDOP improved by 19.8%. The DD ionospheric-free OC phase residual showed that the applied models fit the GPS and BDS2 observations well. The average of the daily RMS of the 6 h orbit overlapping differences in the R, T, and N were all within 1 mm. The average of GPS ADOP reduced from 0.160 cycle to 0.153 cycle; BDS2 combined with GPS can further enhance the accuracy of the float ambiguity. This study can be used as a reference for PROD based on multi-GNSS.

Author Contributions

Conceptualization, B.Y. and D.G.; methodology, B.Y. and B.J.; software, B.Y., K.S. and X.Q.; validation, B.Y., H.Z. and Z.H.; formal analysis, B.Y.; writing—original draft preparation, B.Y.; writing—review and editing, D.G., K.S., B.J., H.Z. and Z.H.; visualization, B.Y.; supervision, X.D.; project administration, D.G.; funding acquisition, D.G., B.J. and X.D. All authors have read and agreed to the published version of the manuscript.

Funding

This study was funded by the National Key R&D program of China (Nos. 2020YFA0713502) and the National Natural Science Foundation of China (Nos. 41874028 and 61803018).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Lou, L.; Liu, Z.; Zhang, H.; Qian, F.; Huang, Y. TH-2 satellite engineering design and implementation. Acta Geod. Cartogr. Sin. 2020, 49, 1252–1264. [Google Scholar] [CrossRef]
  2. Kahle, R.; Schlepp, B.; Aida, S.; Kirschner, M.; Wermuth, M. Flight Dynamics Operations of the Tandem-X Formation. In Proceedings of the SpaceOps 2012 Conference, Stockholm, Sweden, 11–15 June 2012; pp. 1–12. [Google Scholar]
  3. Barneveld, P.W.L. Orbit Determination of Satellite Formations. Ph.D. Thesis, Technische Universiteit Delft, Delft, The Netherlands, 2012. [Google Scholar]
  4. Kroes, R.; Montenbruck, O.; Bertiger, W.; Visser, P. Precise GRACE baseline determination using GPS. GPS Solut. 2005, 9, 21–31. [Google Scholar] [CrossRef]
  5. Kroes, R. Precise Relative Positioning of Formation Flying Spacecraft Using GPS. Ph.D. Thesis, Netherlands Geodetic Commission, Delft, The Netherlands, 2006. [Google Scholar]
  6. Jäggi, A.; Hugentobler, U.; Bock, H.; Beutler, G. Precise orbit determination for GRACE using undifferenced or doubly differenced GPS data. Adv. Space Res. 2007, 39, 1612–1619. [Google Scholar] [CrossRef]
  7. Yang, Y.; Mao, Y.; Sun, B. Basic performance and future developments of BeiDou global navigation satellite system. Satell. Navig. 2020, 1, 1–8. [Google Scholar] [CrossRef] [Green Version]
  8. China Satellite Navigation Office. Development of the BeiDou Navigation Satellite System (Version 4.0); China Satellite Navigation Office: Shanghai, China, 2019. [Google Scholar]
  9. Zhao, X.; Zhou, S.; Ci, Y.; Hu, X.; Cao, J.; Chang, Z.; Tang, C.; Guo, D.; Guo, K.; Liao, M. High-precision orbit determination for a LEO nanosatellite using BDS-3. GPS Solut. 2020, 24, 1–14. [Google Scholar] [CrossRef]
  10. Wang, L.; Xu, B.; Fu, W.; Chen, R.; Li, T.; Han, Y.; Zhou, H. Centimeter-Level Precise Orbit Determination for the Luojia-1A Satellite Using BeiDou Observations. Remote Sens. 2020, 12, 2063. [Google Scholar] [CrossRef]
  11. Guenter, W.H. Status, perspectives and trends of satellite navigation. Satell. Navig. 2020, 1, 22. [Google Scholar]
  12. Yang, Y.; Li, J.; Xu, J.; Tang, J.; Guo, H.; He, H. Contribution of the Compass satellite navigation system to global PNT users. Chin. Sci. Bull. 2011, 56, 2813–2819. [Google Scholar] [CrossRef] [Green Version]
  13. Liu, Y.; Ye, S.; Song, W.; Lou, Y.; Chen, D. Integrating GPS and BDS to shorten the initialization time for ambiguity-fixed PPP. GPS Solut. 2017, 21, 333–343. [Google Scholar] [CrossRef]
  14. Li, X.; Zhang, K.; Meng, X.; Zhang, W.; Zhang, Q.; Zhang, X.; Li, X. Precise Orbit Determination for the FY-3C Satellite Using Onboard BDS and GPS Observations from 2013, 2015, and 2017. Engineering 2019, 6, 904–912. [Google Scholar] [CrossRef]
  15. Liu, J.; Gu, D.; Ju, B.; Yao, J.; Duan, X.; Yi, D. Basic performance of BeiDou-2 navigation satellite system used in LEO satellites precise orbit determination. Chin. J. Aeronaut. 2014, 27, 1251–1258. [Google Scholar] [CrossRef] [Green Version]
  16. Verhagen, S.; Teunissen, P.J.G. Ambiguity resolution performance with GPS and BeiDou for LEO formation flying. Adv. Space Res. 2014, 54, 830–839. [Google Scholar] [CrossRef] [Green Version]
  17. Yi, B.; Gu, D.; Chang, X.; Shao, K. Integrating BDS and GPS for precise relative orbit determination of LEO formation flying. Chin. J. Aeronaut. 2018, 31, 2013–2022. [Google Scholar] [CrossRef]
  18. Kang, Z.; Tapley, B.; Bettadpur, S.; Ries, J.; Nagel, P.; Pastor, R. Precise orbit determination for the GRACE mission using only GPS data. J. Geod. 2006, 80, 322–331. [Google Scholar] [CrossRef]
  19. Montenbruck, O.; Barneveld, P.W.L.; Yoon, Y.; Visser, P.N.A.M. GPS-Based Precision Baseline Reconstruction for the TanDEM-X SAR-Formation. In Proceedings of the 2007 20th International Symposium on Space Flight Dynamics, Annapolis, MD, USA, 24–28 September 2007; pp. 1–13. [Google Scholar]
  20. Moon, Y.; Koenig, R.; Michalak, G.; Rothacher, M. Precise Orbit and Baseline Determination for TerraSAR-X and TanDEM-X. In Proceedings of the IGARSS 2008—2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008; Volume 2, pp. 121–124. [Google Scholar] [CrossRef]
  21. Montenbruck, O.; Wermuth, M.; Kahle, R. GPS Based Relative Navigation for the TanDEM-X Mission—First Flight Results. Navigation 2011, 58, 293–304. [Google Scholar] [CrossRef]
  22. Allende-Alba, G.; Montenbruck, O. Robust and precise baseline determination of distributed spacecraft in LEO. Adv. Space Res. 2016, 57, 46–63. [Google Scholar] [CrossRef]
  23. Jäggi, A.; Montenbruck, O.; Moon, Y.; Wermuth, M.; König, R.; Michalak, G.; Bock, H.; Bodenmann, D. Inter-agency comparison of TanDEM-X baseline solutions. Adv. Space Res. 2012, 50, 260–271. [Google Scholar] [CrossRef]
  24. Shao, K.; Gu, D.; Ju, B.; Wang, W.; Wei, C.; Duan, X.; Wang, Z. Analysis of Tiangong-2 orbit determination and prediction using onboard dual-frequency GNSS data. GPS Solut. 2019, 24, 11. [Google Scholar] [CrossRef]
  25. Guo, X.; Zhao, Q. M-estimation-based robust and precise baseline determination for formation-flying satellites. GPS Solut. 2021, 25, 1–12. [Google Scholar] [CrossRef]
  26. Qing, X. Research on Precision Orbit Determination Theory and Method of Low Earth Orbiter Based on GPS Technique. Ph.D. Thesis, Information Engineering University, Zhengzhou, China, 2009. [Google Scholar]
  27. Yang, C. LM-4B Sends Tianhui 2 Satellite into Orbit. Aerosp. China 2019, 20, 59. [Google Scholar]
  28. Qian, F.; Chen, G.; Lu, J.; Chen, X.; Lou, L.; Jiang, T.; Liu, W.; Wang, S. Correcting method of slant-range error for the TH-2 satellites. Remote Sens. Lett. 2021, 12, 142–149. [Google Scholar] [CrossRef]
  29. Montenbruck, O.; Kroes, R. In-flight performance analysis of the CHAMP BlackJack GPS Receiver. GPS Solut. 2003, 7, 74–86. [Google Scholar] [CrossRef]
  30. Gu, D.; Ju, B.; Liu, J.; Tu, J. Enhanced GPS-based GRACE baseline determination by using a new strategy for ambiguity resolution and relative phase center variation corrections. Acta Astronaut. 2017, 138, 176–184. [Google Scholar] [CrossRef]
  31. Yi, B.; Gu, D.; Ju, B.; Shao, K.; Zhang, H. Enhanced baseline determination for formation flying LEOs by relative corrections of phase center and code residual variations. Chin. J. Aeronaut. 2021. [Google Scholar] [CrossRef]
  32. Teunissen, P.J.G. The least-squares ambiguity decorrelation adjustment: A method for fast GPS integer ambiguity estimation. J. Geod. 1995, 70, 65–82. [Google Scholar] [CrossRef]
  33. De Jonge, P.J.; Tiberius, C.C.J.M. The LAMBDA Method for Integer Ambiguity Estimation: Implementation Aspects; Delft Geodetic Computing Centre LGR Series, No.12; Delft University of Technology; Faculty of Geodetic Engineering: Delft, The Netherlands, 1996. [Google Scholar]
  34. Teunissen, P.J.G.; de Jonge, P.J.; Tiberius, C.C.J.M. Performance of the LAMBDA method for fast GPS ambiguity resolution. Navigation 1997, 44, 373–383. [Google Scholar] [CrossRef]
  35. Ju, B.; Gu, D.; Herring, T.A.; Allende-Alba, G.; Montenbruck, O.; Wang, Z. Precise orbit and baseline determination for maneuvering low earth orbiters. GPS Solut. 2015, 21, 53–64. [Google Scholar] [CrossRef] [Green Version]
  36. Qing, X.; Yang, Y. Millimeter-level relative positioning of formation flying satellites onboard GPS. J. Astronaut. 2010, 31, 369–372. [Google Scholar] [CrossRef]
  37. Frei, E.; Beutler, G. Rapid static positioning based on the fast ambiguity resolution approach “FARA”: Theory and first results. Manuscr. Geod. 1990, 15, 325–356. [Google Scholar]
  38. Shao, K.; Zhang, H.; Qin, X.; Huang, Z.; Yi, B.; Gu, D. Precise absolute and relative orbit determination for distributed InSAR satellite system. Acta Geod. Cartogr. Sin. 2021, 50, 580–588. [Google Scholar] [CrossRef]
  39. Guo, F.; Li, X.; Zhang, X.; Wang, J. Assessment of precise orbit and clock products for Galileo, BeiDou, and QZSS from IGS Multi-GNSS Experiment (MGEX). GPS Solut. 2017, 21, 279–290. [Google Scholar] [CrossRef]
  40. Qing, Y.; Lin, J.; Liu, Y.; Dai, X.; Lou, Y.; Gu, S. Precise Orbit Determination of the China Seismo-Electromagnetic Satellite (CSES) Using Onboard GPS and BDS Observations. Remote Sens. 2020, 12, 3234. [Google Scholar] [CrossRef]
  41. Teunissen, P.J.G.; Odijk, D. Ambiguity Dilution of Precision: Definition, properties and application. In Proceedings of the Institute of Navigation’s ION GPS-1997, Kansas City, MO, USA, 16–19 September 1997; pp. 891–899. [Google Scholar]
  42. Teunissen, P.J.G. A canonical theory for short GPS baselines. Part IV: Precision versus reliability. J. Geod. 1997, 71, 513–525. [Google Scholar] [CrossRef] [Green Version]
  43. Verhagen, S. On the Reliability of Integer Ambiguity Resolution. Navigation 2005, 52, 99–110. [Google Scholar] [CrossRef]
Remotesensing 13 04487 g001 550
Figure 1. The number of observations for Global Positioning System (GPS) satellites.
Figure 1. The number of observations for Global Positioning System (GPS) satellites.
Remotesensing 13 04487 g001
Remotesensing 13 04487 g002 550
Figure 2. The number of observations for BDS2 satellites.
Figure 2. The number of observations for BDS2 satellites.
Remotesensing 13 04487 g002
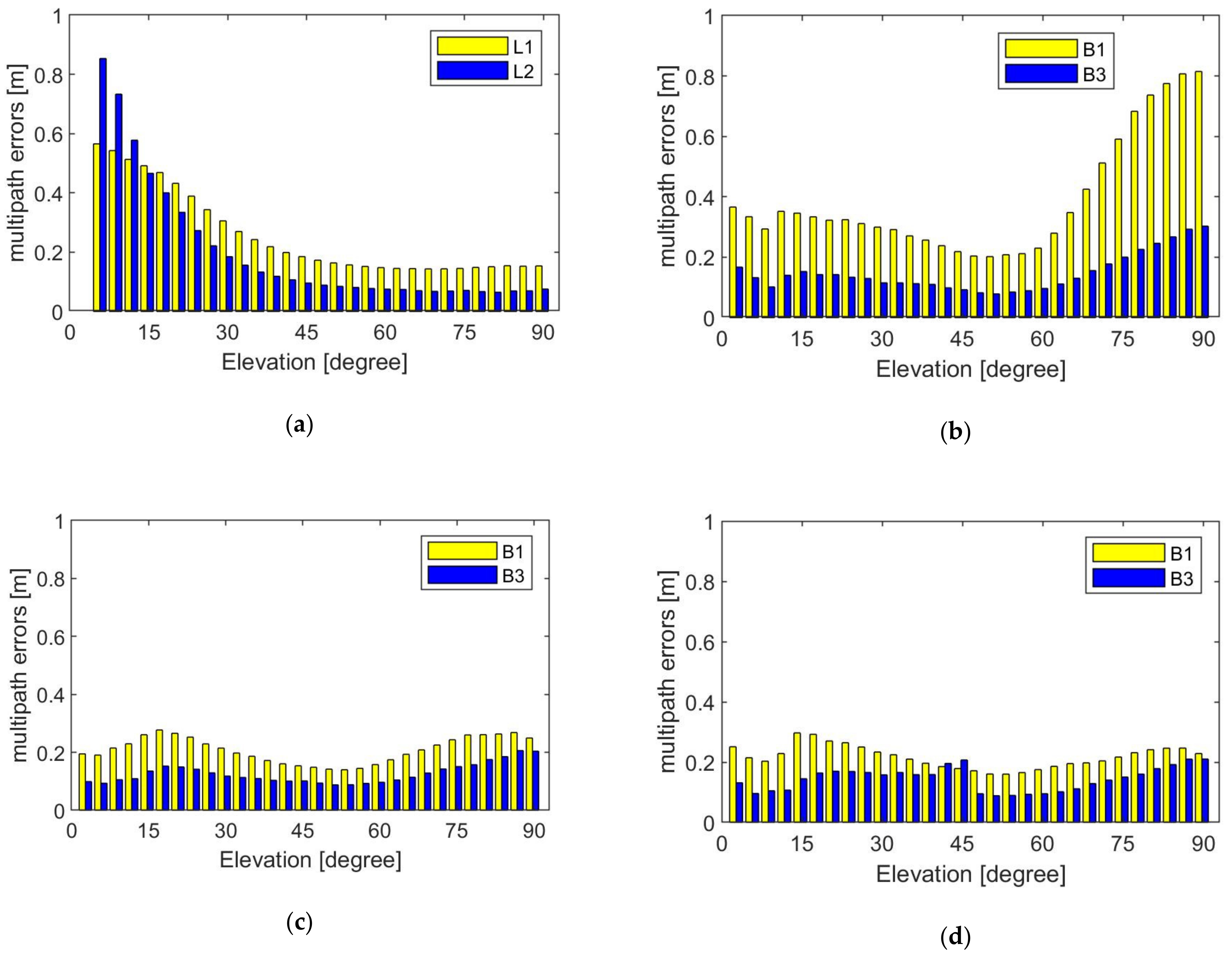
Remotesensing 13 04487 g003 550
Figure 3. Variation in code multipath error with elevation angle for different satellites: (a) GPS satellites, (b) BDS2 Medium Earth Orbit satellites (MEO) satellites, (c) BDS2 Inclined Geosynchro-nous Orbit satellites (IGSO) satellites, and (d) BDS2 Geostationary Earth Orbit (GEO) satellites.
Figure 3. Variation in code multipath error with elevation angle for different satellites: (a) GPS satellites, (b) BDS2 Medium Earth Orbit satellites (MEO) satellites, (c) BDS2 Inclined Geosynchro-nous Orbit satellites (IGSO) satellites, and (d) BDS2 Geostationary Earth Orbit (GEO) satellites.
Remotesensing 13 04487 g003
Remotesensing 13 04487 g004 550
Figure 4. Difference in 3D between the National University of Defense Technology (NDT) and Xi’an Research Institute of Surveying and Mapping (CHS) solutions (excluding maneuver periods).
Figure 4. Difference in 3D between the National University of Defense Technology (NDT) and Xi’an Research Institute of Surveying and Mapping (CHS) solutions (excluding maneuver periods).
Remotesensing 13 04487 g004
Remotesensing 13 04487 g005 550
Figure 5. Difference between the NDT and CHS solutions on day of year (DOY) 305 in 2019 (excluding maneuver periods).
Figure 5. Difference between the NDT and CHS solutions on day of year (DOY) 305 in 2019 (excluding maneuver periods).
Remotesensing 13 04487 g005
Remotesensing 13 04487 g006 550
Figure 6. Difference between the differential POD (dPOD) and precise relative orbit determination (PROD) solutions of TH-2.
Figure 6. Difference between the differential POD (dPOD) and precise relative orbit determination (PROD) solutions of TH-2.
Remotesensing 13 04487 g006
Remotesensing 13 04487 g007 550
Figure 7. Duration and common elevation of continuous carrier phase tracking arcs for navigation satellites of the two TH-2 satellites: (a) GPS satellites; (b) BDS2 satellites.
Figure 7. Duration and common elevation of continuous carrier phase tracking arcs for navigation satellites of the two TH-2 satellites: (a) GPS satellites; (b) BDS2 satellites.
Remotesensing 13 04487 g007
Remotesensing 13 04487 g008 550
Figure 8. Difference between the GPS-based and BDS2-based PROD with different weights of GEOs (excluding maneuver periods).
Figure 8. Difference between the GPS-based and BDS2-based PROD with different weights of GEOs (excluding maneuver periods).
Remotesensing 13 04487 g008
Remotesensing 13 04487 g009 550
Figure 9. Global distribution of difference between the GPS-based and BDS2-based PROD in 3D components (excluding maneuver periods).
Figure 9. Global distribution of difference between the GPS-based and BDS2-based PROD in 3D components (excluding maneuver periods).
Remotesensing 13 04487 g009
Remotesensing 13 04487 g010 550
Figure 10. GPS-based and combined PDOP of TH-2A on DOY 307 in 2019.
Figure 10. GPS-based and combined PDOP of TH-2A on DOY 307 in 2019.
Remotesensing 13 04487 g010
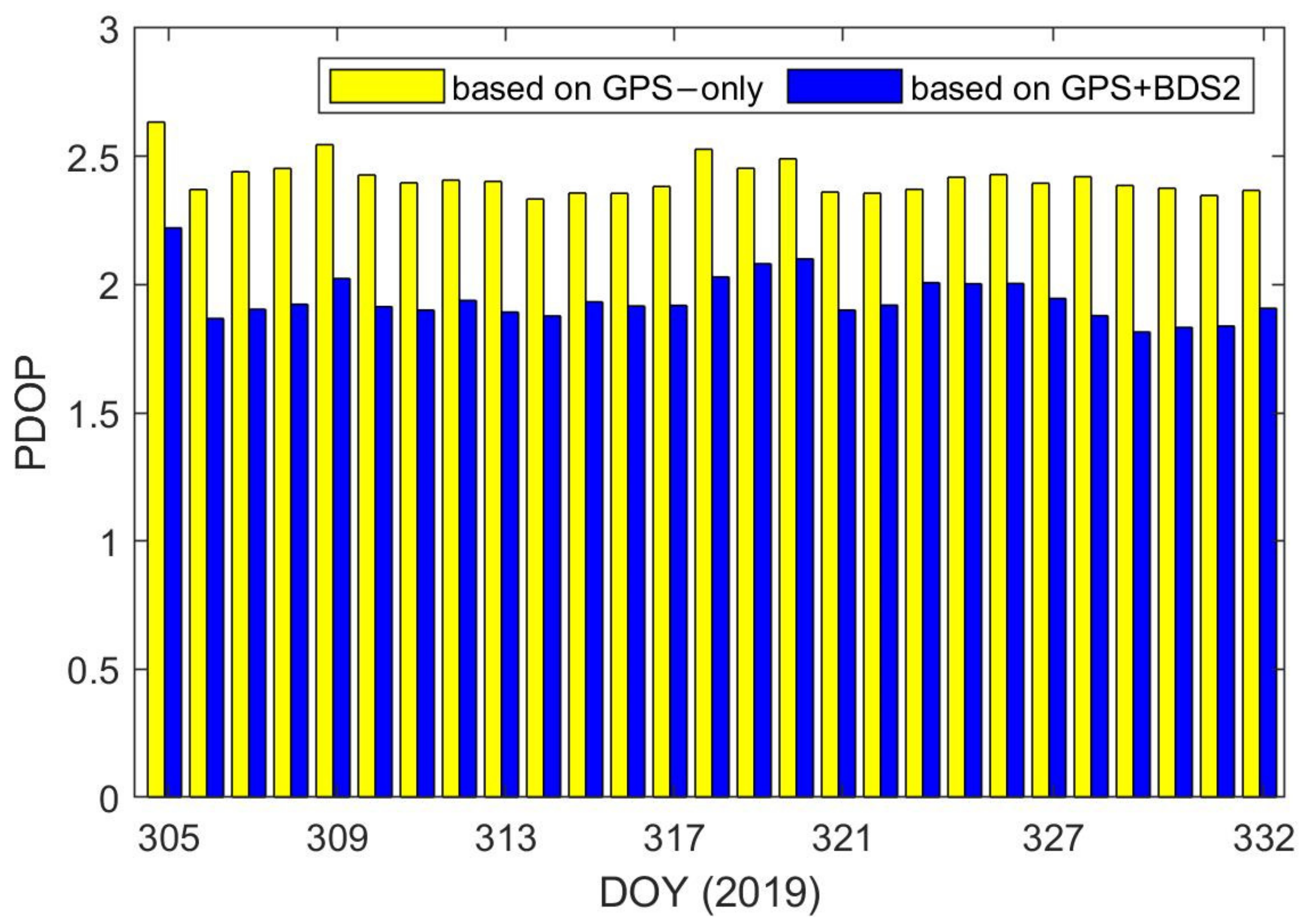
Remotesensing 13 04487 g011 550
Figure 11. GPS-based and combined PDOP of TH-2A.
Figure 11. GPS-based and combined PDOP of TH-2A.
Remotesensing 13 04487 g011
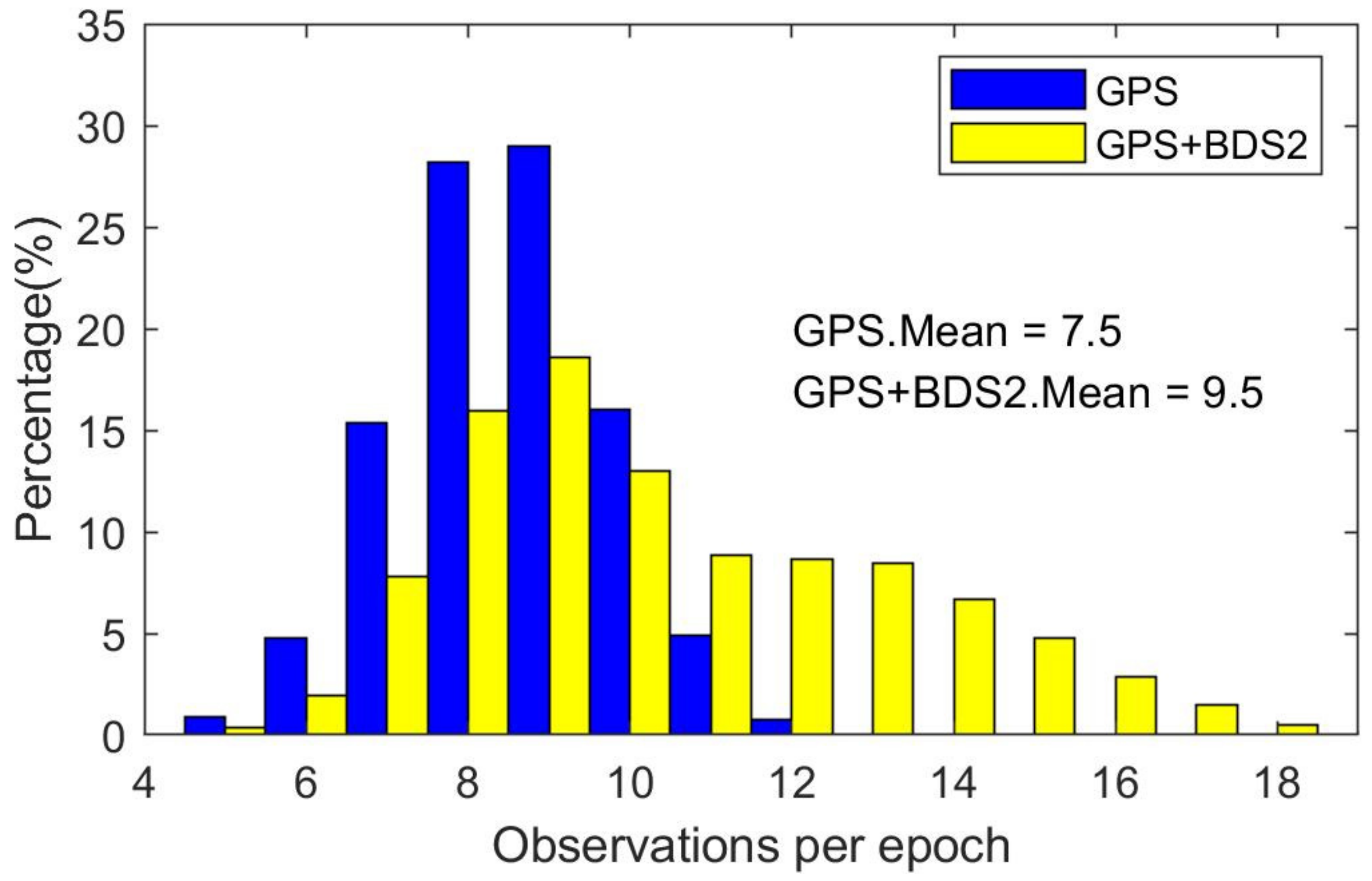
Remotesensing 13 04487 g012 550
Figure 12. Visible navigation satellites from TH-2A and TH-2B.
Figure 12. Visible navigation satellites from TH-2A and TH-2B.
Remotesensing 13 04487 g012
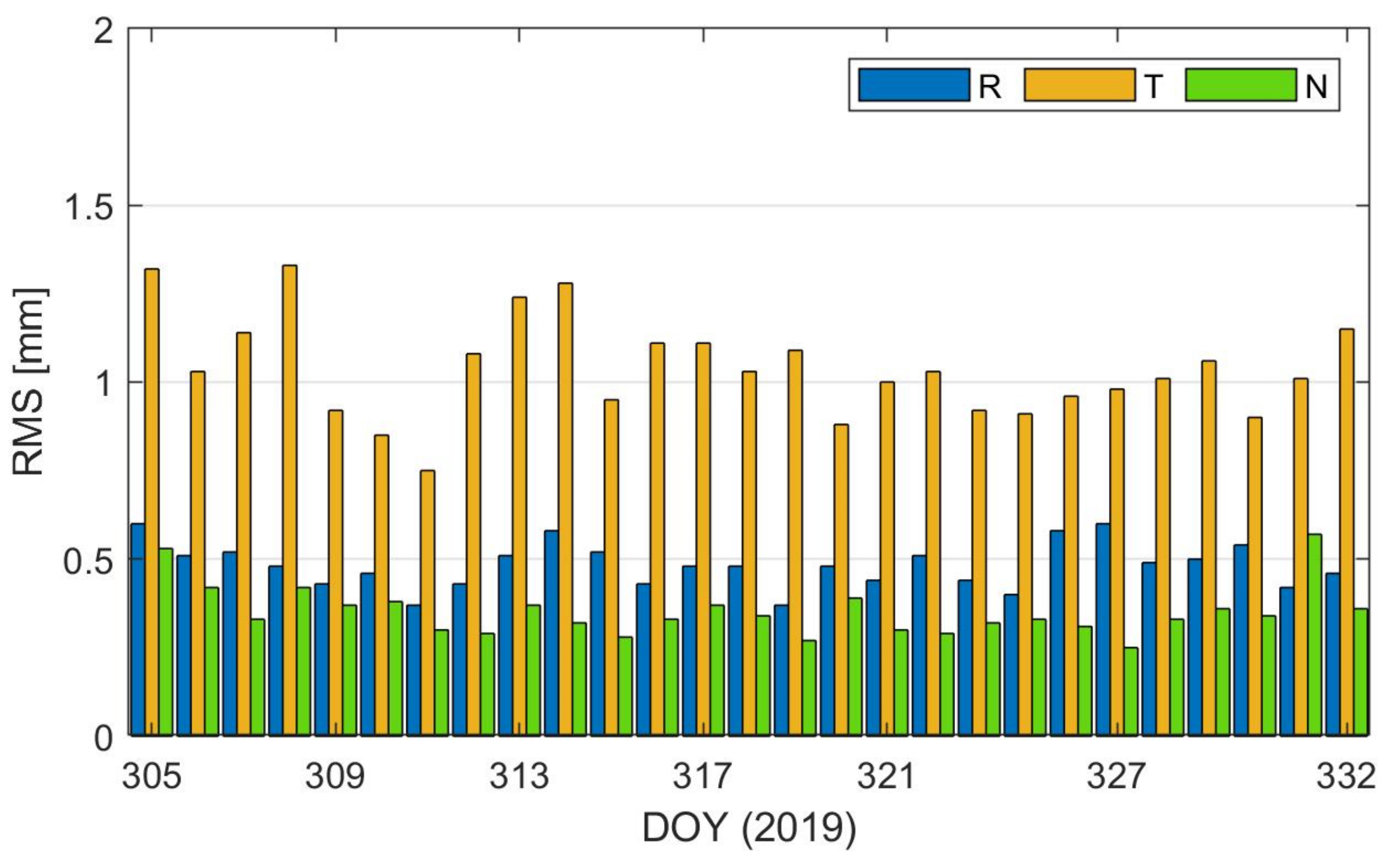
Remotesensing 13 04487 g013 550
Figure 13. Difference between the GPS-based and combined PROD results.
Figure 13. Difference between the GPS-based and combined PROD results.
Remotesensing 13 04487 g013
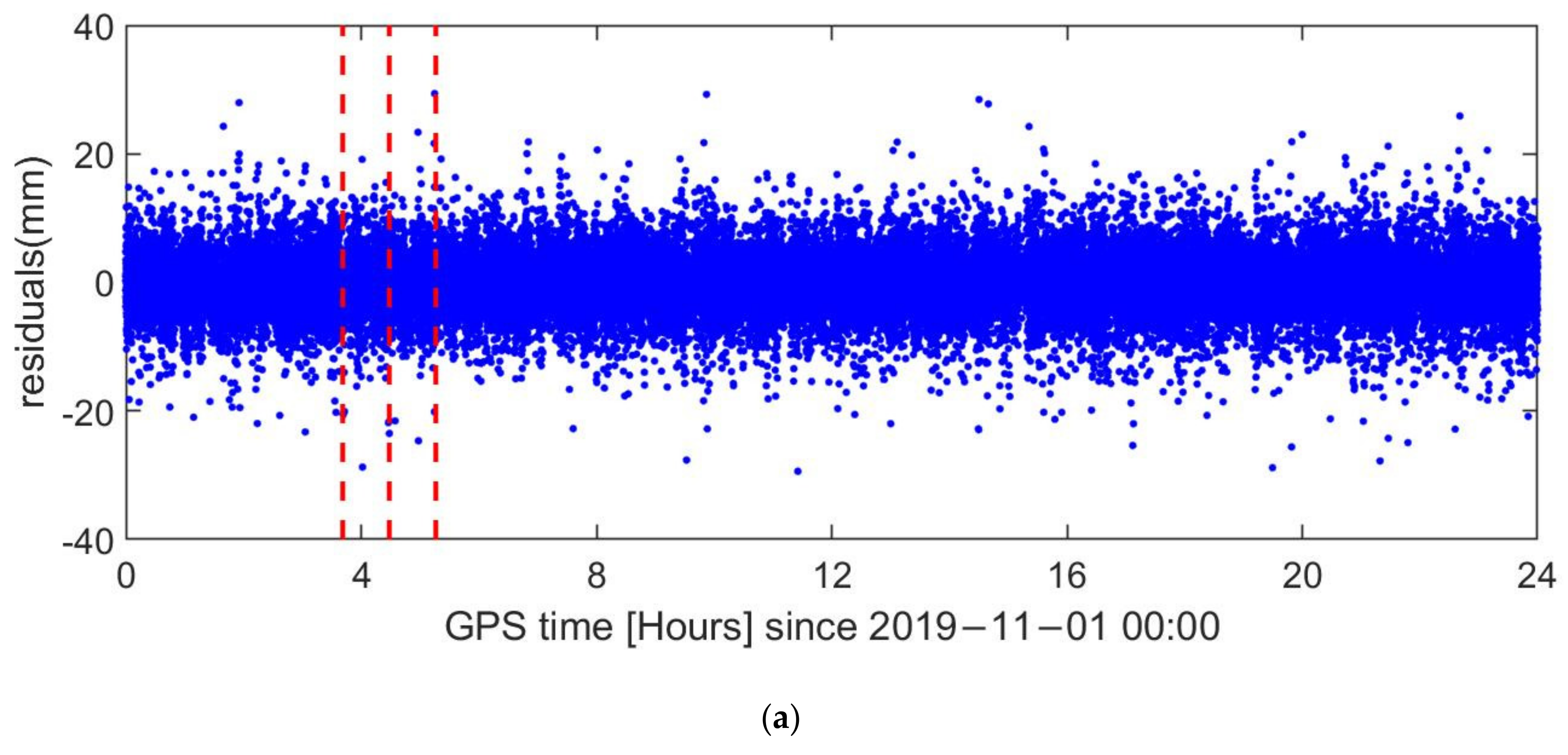
Remotesensing 13 04487 g014a 550Remotesensing 13 04487 g014b 550
Figure 14. Double-difference ionospheric-free phase residuals on DOY 305 in 2019; the red dashed lines indicate the center of burn time: (a) GPS satellites; (b) BDS2 satellites.
Figure 14. Double-difference ionospheric-free phase residuals on DOY 305 in 2019; the red dashed lines indicate the center of burn time: (a) GPS satellites; (b) BDS2 satellites.
Remotesensing 13 04487 g014aRemotesensing 13 04487 g014b
Remotesensing 13 04487 g015 550
Figure 15. GPS ambiguity dilution of precision (ADOP) on DOY 311 in 2019.
Figure 15. GPS ambiguity dilution of precision (ADOP) on DOY 311 in 2019.
Remotesensing 13 04487 g015
Remotesensing 13 04487 g016 550
Figure 16. Daily value of GPS ADOP.
Figure 16. Daily value of GPS ADOP.
Remotesensing 13 04487 g016
Table
Table 1. Average value of the daily root mean square (RMS) of multipath error and carrier phase fitting residuals.
Table 1. Average value of the daily root mean square (RMS) of multipath error and carrier phase fitting residuals.
ItemGlobal Positioning System Satellites (GPS)Medium Earth Orbit Satellites (MEO) Inclined Geosynchronous Orbit Satellites (IGSO)Geostationary Earth Orbit Satellites (GEO)
L1\B1 (m)0.260.39 0.21 0.22
L2\B3 (m)0.200.15 0.13 0.14
carrier phase fitting residuals (mm)4.7 3.8 4.0 2.6
Table
Table 2. Strategy of National University of Defense Technology (NDT) and Xi’an Research Institute of Surveying and Mapping (CHS) software packages for baseline determination.
Table 2. Strategy of National University of Defense Technology (NDT) and Xi’an Research Institute of Surveying and Mapping (CHS) software packages for baseline determination.
ItemNDTCHS
Global Navigation Satellite System (GNSS) measurement modelDouble-differenced ionosphere-free code and phase observations; 10 s sampling; igs14_2108.atx PCO and phase center variations (PCVs) correction of GNSS transmitter antennas; GeoForschungsZentrum (GFZ) GPS orbits and 30 s clocks; Relativity correctionDouble-differenced ionosphere-free code and phase observations; 30 s sampling; igs08.atx PCO and PCVs correction of GNSS transmitter antennas;
center for orbit determination in europe (CODE) final GPS orbits and 30 s clocks; No relativity correction
Gravitational
forces		GRACE Gravity Model 02C (GGM02C) gravity (100 × 100); solid-earth, pole, and ocean tides (international Earth rotation and reference systems service (IERS) 2003); luni-solar-planetary (Jet Propulsion Laboratory development ephemeris 405 (JPL DE405))European Improved Gravity Field Model of the Earth by New Techniques (EIGEN2) gravity (120 × 120); solid-earth, pole, and ocean tides (IERS 2000); luni-solar-planetary (JPL DE405)
Non-gravitationalforcesJacchia 71 density model, CD is estimated per 3 h; ball, CR is estimated; piecewise linear accelerations in T and N directions, estimated per 15 min; maneuvers (constant thrust arc)No drag model; Emprical CODE Orbit Model (ECOM) 9; pseudo-stochastic R, T and N pulses at 6-min intervals; maneuvers (additional set of pulses)
Reference
frames		International Terrestrial Reference Frame (ITRF) 2008 reference frame; IERS Standard Rapid earth orientation parameters (EOPs); International Astronomical Union (IAU) 2000A;ITRF 2008 reference frame; CODE final Earth rotation parameters (ERPs); IAU 2000A;
Ambiguities resolutionLeast-squares Ambiguity Decorrelation Adjustment (LAMBDA)Integer rounding
Table
Table 3. Difference between the GPS-based and BDS2-based PROD with different weights of GEOs (excluding maneuver periods).
Table 3. Difference between the GPS-based and BDS2-based PROD with different weights of GEOs (excluding maneuver periods).
Weight of GEO Satellites10.50.2
Global/mmR2.012.253.23
T5.856.619.26
N3.443.905.80
3D7.088.0011.40
The non-Asia-Pacific region/mmR2.162.423.41
T6.627.4910.43
N3.874.376.73
3D7.969.0012.69
The Asia-Pacific region/mmR1.441.632.61
T2.042.323.73
N1.451.743.40
3D2.893.325.69
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Yi, B.; Gu, D.; Shao, K.; Ju, B.; Zhang, H.; Qin, X.; Duan, X.; Huang, Z. Precise Relative Orbit Determination for Chinese TH-2 Satellite Formation Using Onboard GPS and BDS2 Observations. Remote Sens. 2021, 13, 4487. https://doi.org/10.3390/rs13214487

AMA Style

Yi B, Gu D, Shao K, Ju B, Zhang H, Qin X, Duan X, Huang Z. Precise Relative Orbit Determination for Chinese TH-2 Satellite Formation Using Onboard GPS and BDS2 Observations. Remote Sensing. 2021; 13(21):4487. https://doi.org/10.3390/rs13214487

Chicago/Turabian Style

Yi, Bin, Defeng Gu, Kai Shao, Bing Ju, Houzhe Zhang, Xianping Qin, Xiaojun Duan, and Zhiyong Huang. 2021. "Precise Relative Orbit Determination for Chinese TH-2 Satellite Formation Using Onboard GPS and BDS2 Observations" Remote Sensing 13, no. 21: 4487. https://doi.org/10.3390/rs13214487

APA Style

Yi, B., Gu, D., Shao, K., Ju, B., Zhang, H., Qin, X., Duan, X., & Huang, Z. (2021). Precise Relative Orbit Determination for Chinese TH-2 Satellite Formation Using Onboard GPS and BDS2 Observations. Remote Sensing, 13(21), 4487. https://doi.org/10.3390/rs13214487

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop