Unsupervised Classification of Crop Growth Stages with Scattering Parameters from Dual-Pol Sentinel-1 SAR Data
Abstract
1. Introduction
2. Methodology
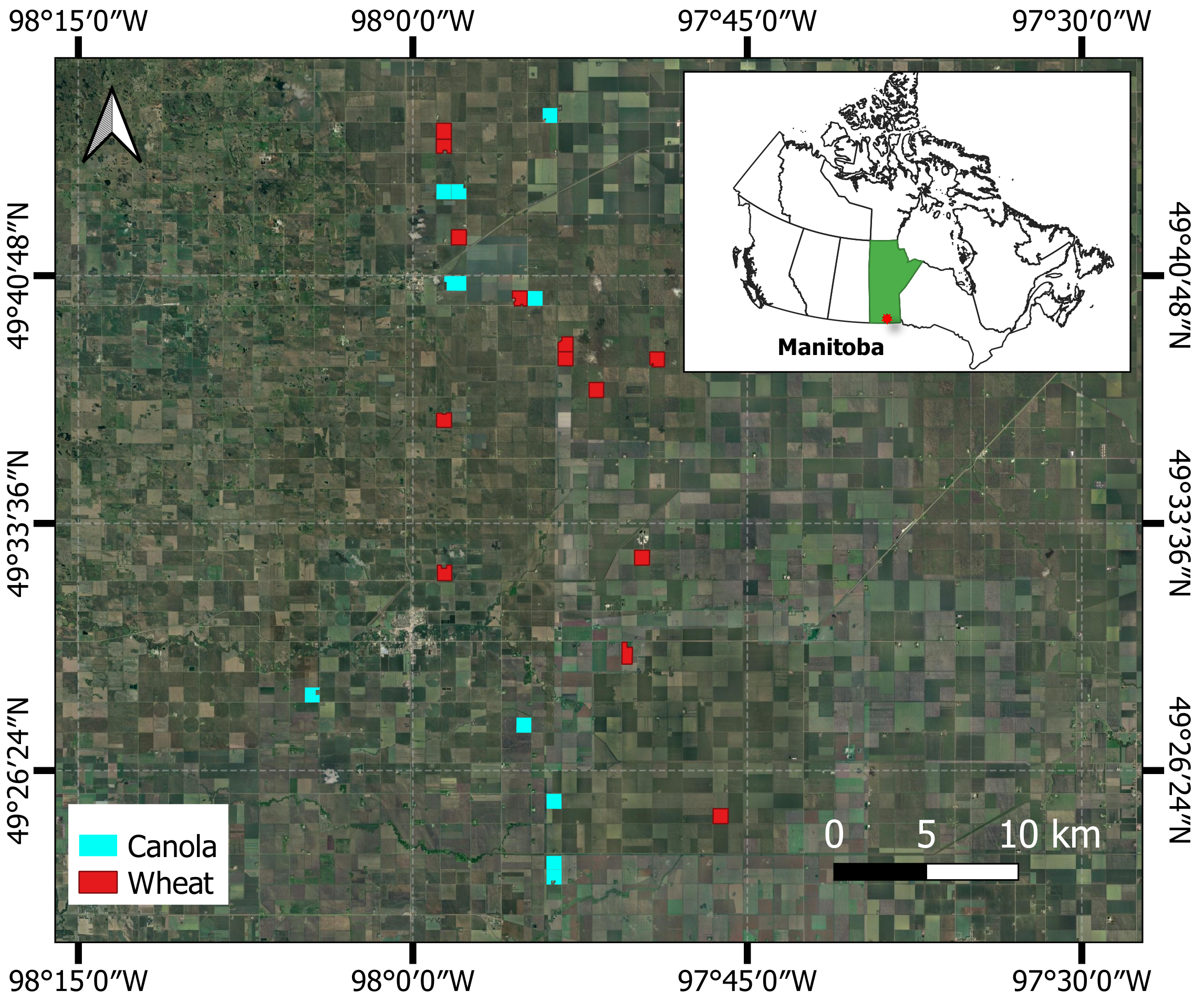
2.1. Study Area and Dataset
2.2. SAR Data Pre-Processing
2.3. Target Characterization Parameter
2.4. Bound
- (i.e., when there exists no polarization structure in the scattered EM wave), then characterize random scattering from targets.
- , and , characterize coherent scattering from deterministic targets (i.e., trihedral or dihedral).
- , and , characterize cross-polarized scattering from complex targets.
2.5. Example of Variation of and
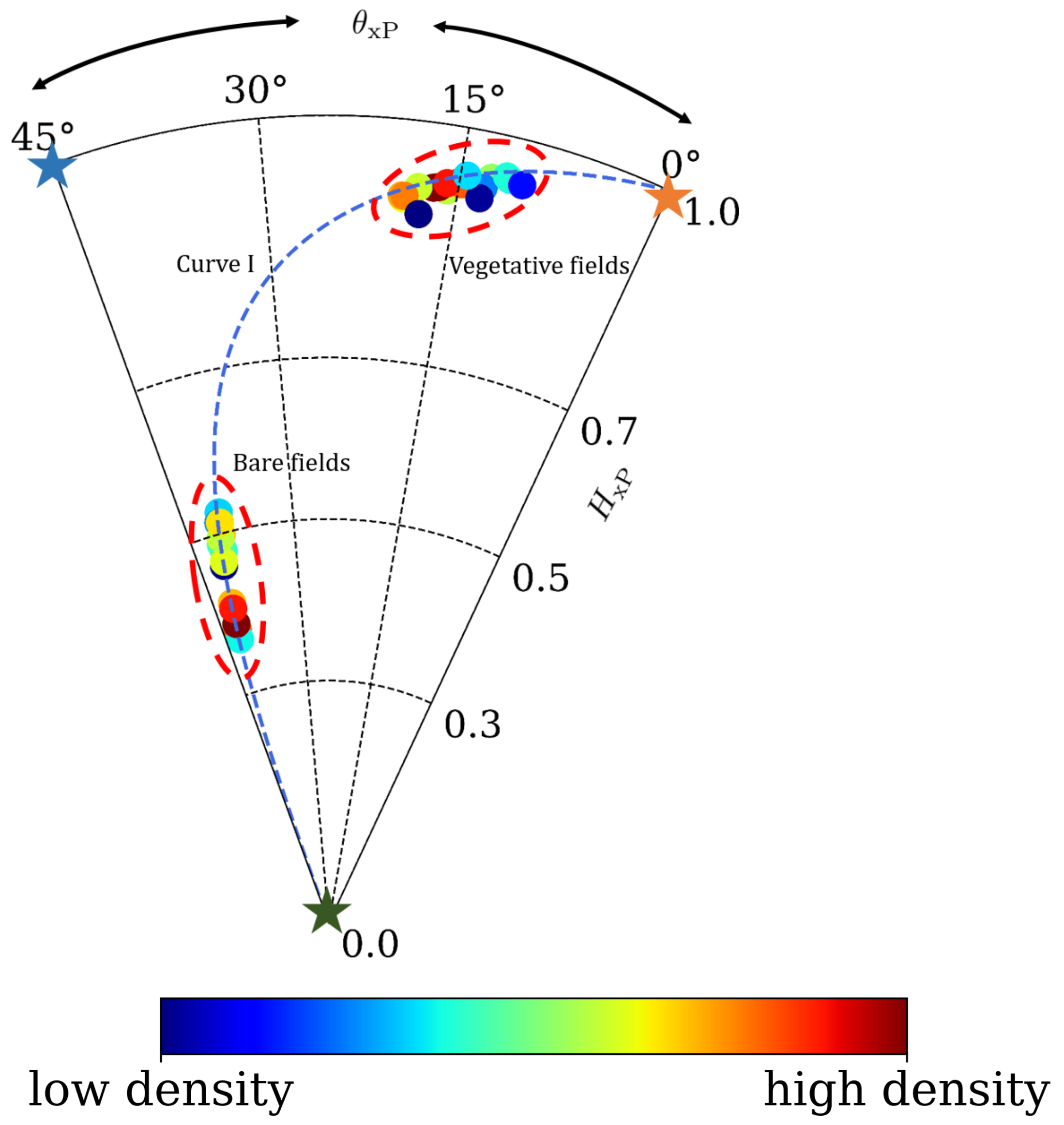
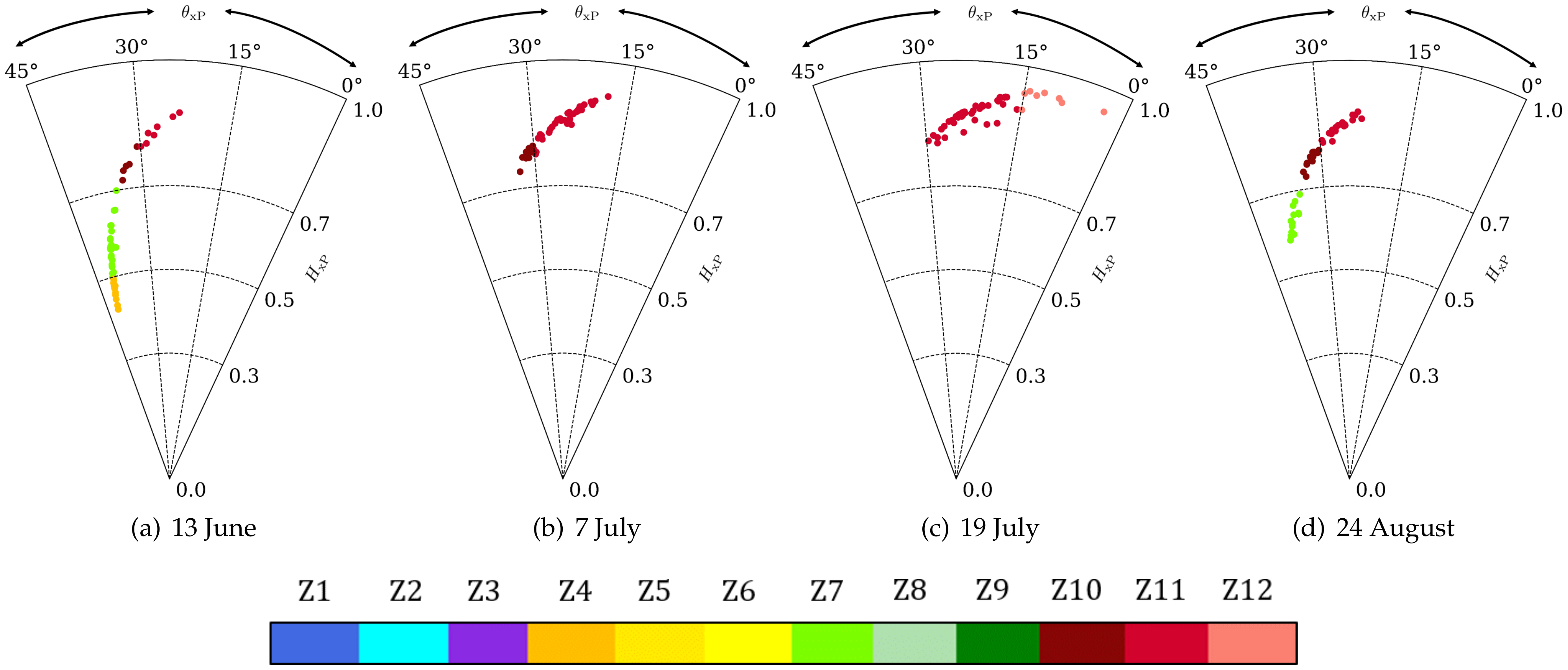
2.6. Unsupervised Clustering Zones over Vegetative Surface
- For a pure diffused target, , implies, .
- For pure or point scatterer, and , implies .
- Infeasible scattering: and .
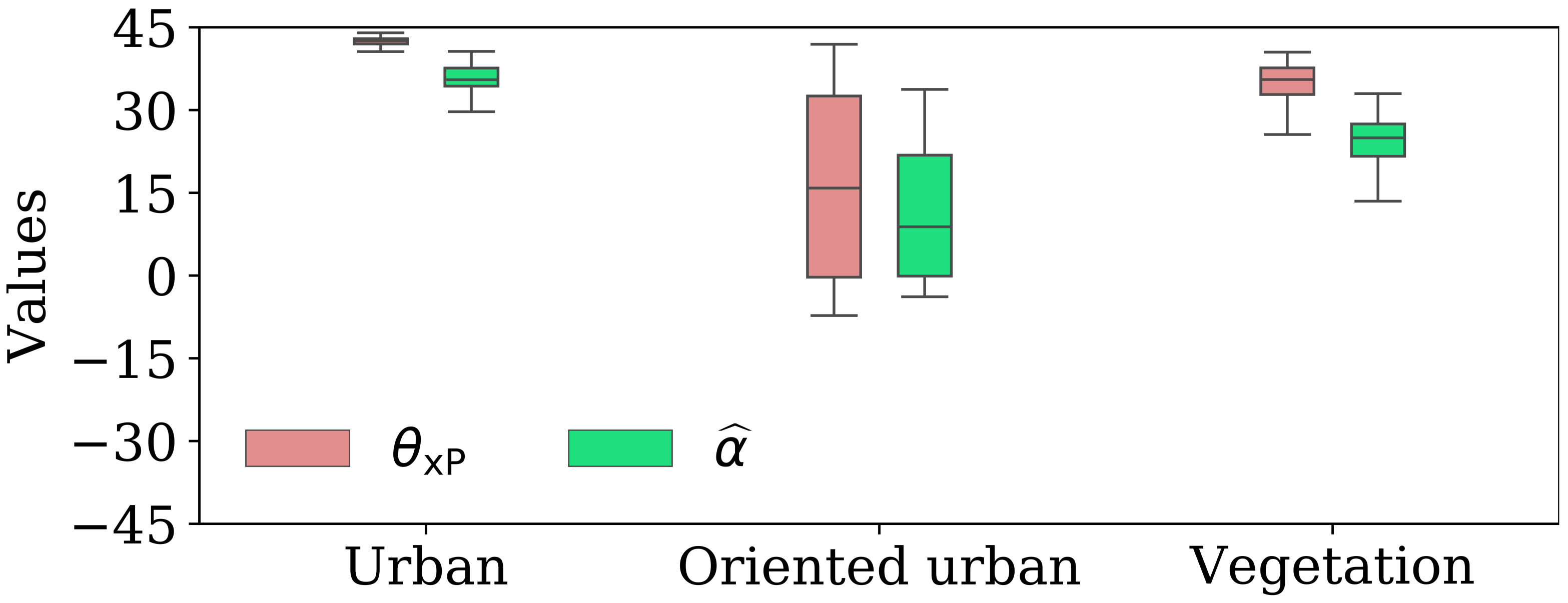
3. Results and Discussion
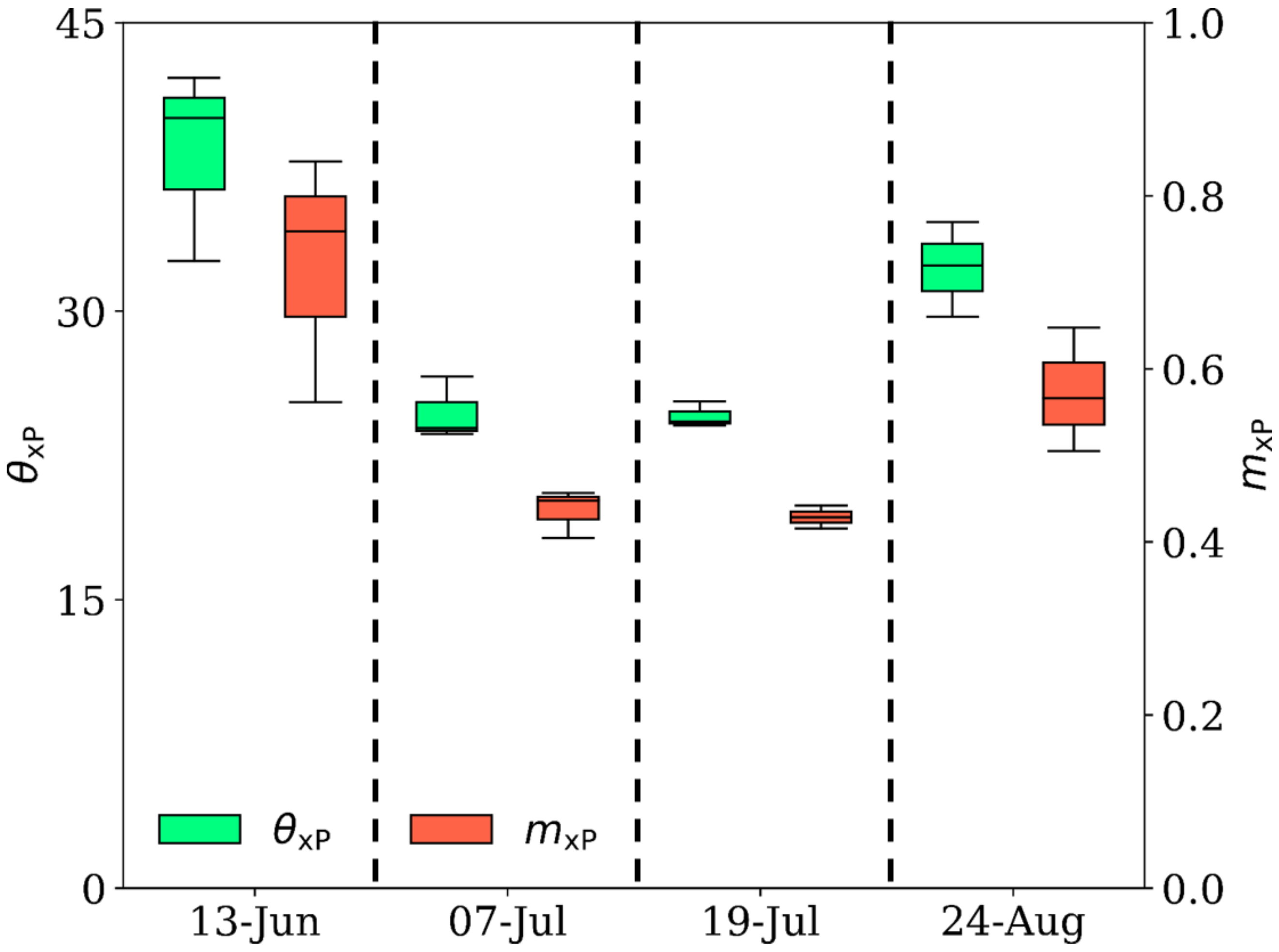
3.1. Canola
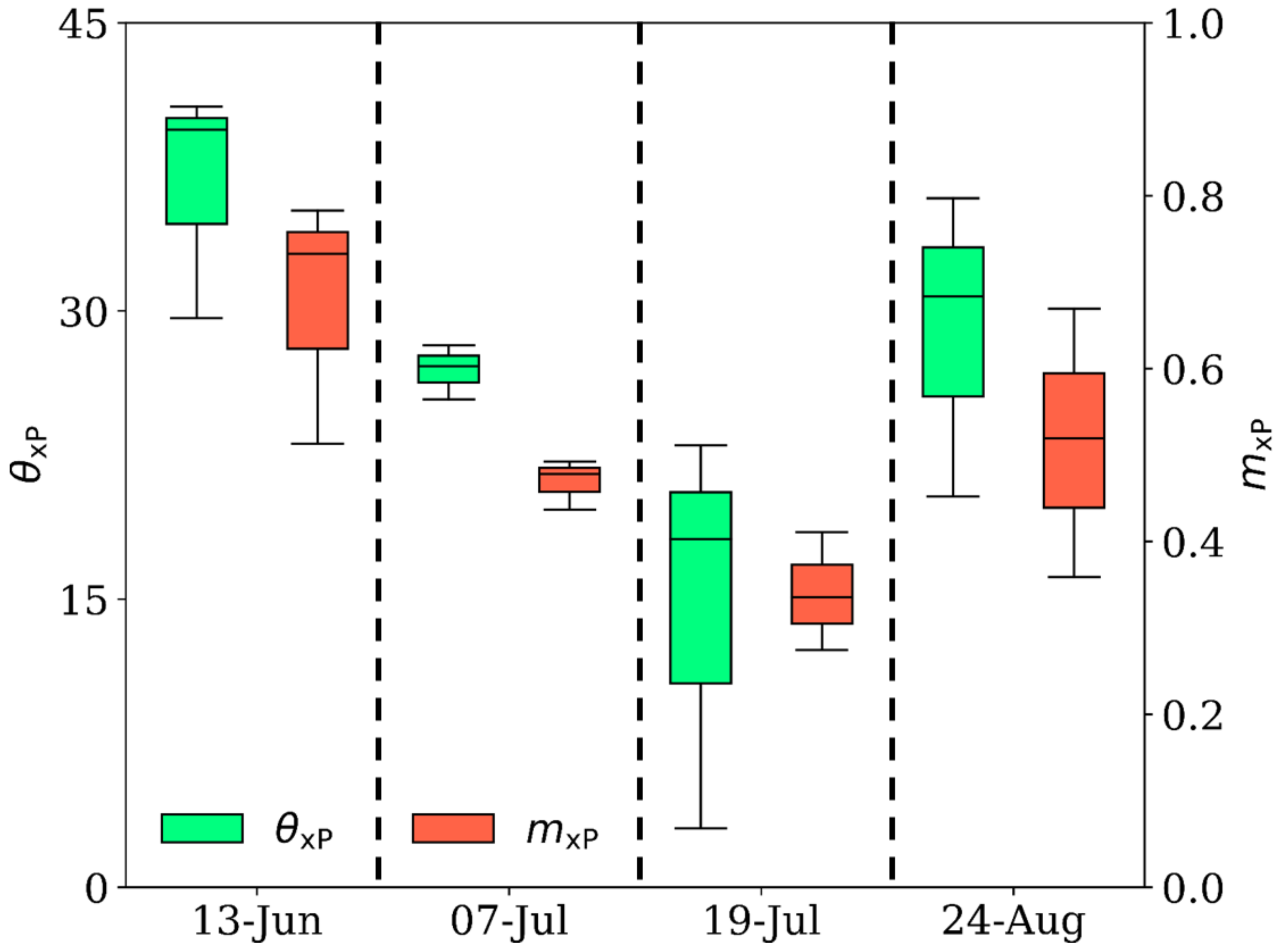
3.2. Wheat
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
| Date | Data ID |
| 13 June | S1A_IW_SLC__1SDV_20160613T001529_20160613T001556_011685_011E64_4083 |
| 7 July | S1A_IW_SLC__1SDV_20160707T001530_20160707T001557_012035_01298D_9FD9 |
| 19 July | S1A_IW_SLC__1SDV_20160719T001540_20160719T001604_012210_012F46_1DED |
| 24 August | S1A_IW_SLC__1SDV_20160824T001533_20160824T001600_012735_0140AB_4BC9 |
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Relationship with Cloude’s α i ’s
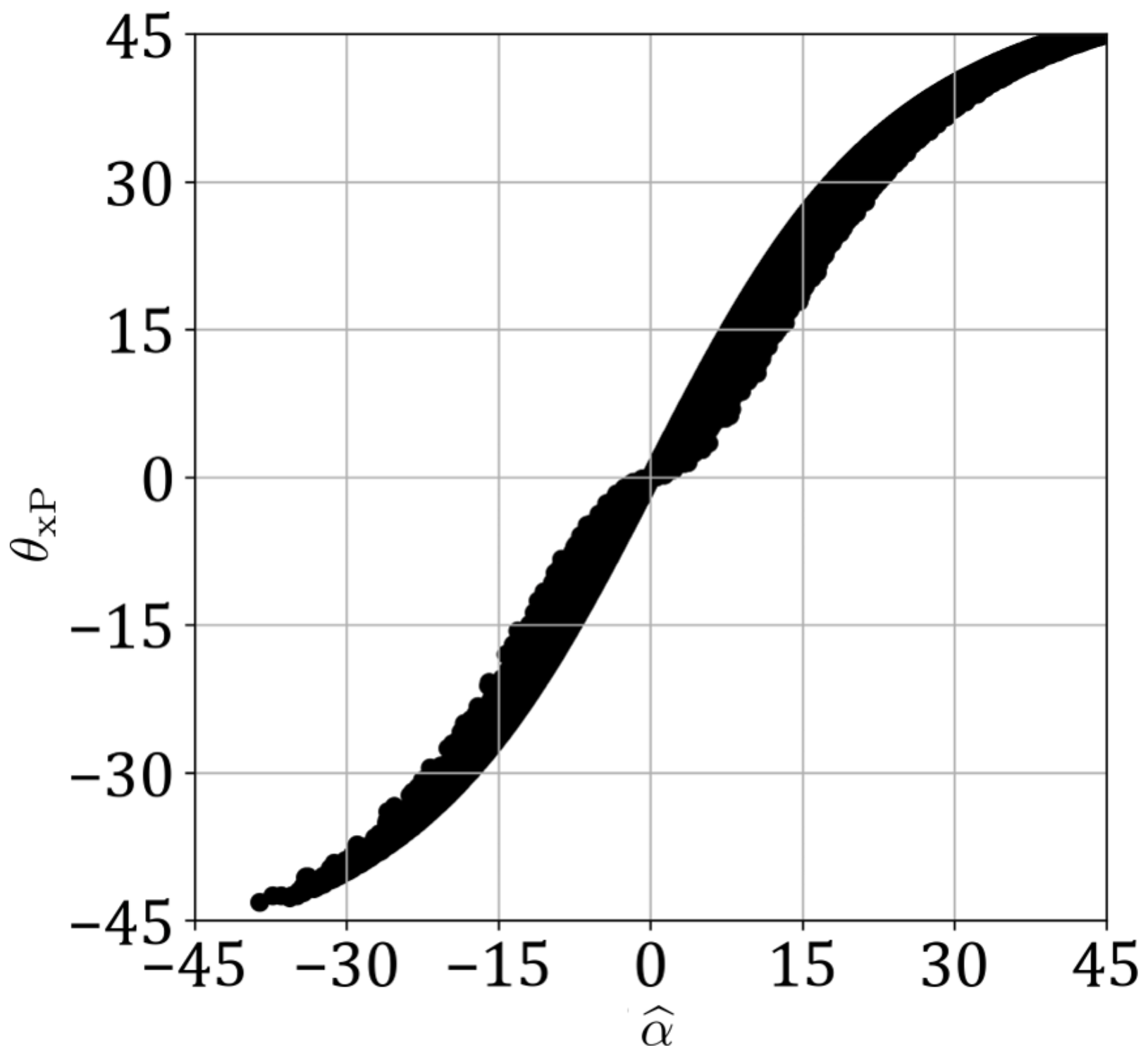
Appendix A.2. Temporal Variations of θ xP and α ^
| 13 June | 7 July | 19 July | 24 August | ||
|---|---|---|---|---|---|
| Canola | 40° | 20° | 18° | 34° | |
| 37° | 18° | 16° | 32° | ||
| Wheat | 39° | 27° | 20° | 34° | |
| 37° | 26° | 15° | 28° |
Appendix A.3. Temporal Variations of In-Situ Measurements of Crops
| 13 June | 7 July | 19 July | 24 August | ||
|---|---|---|---|---|---|
| Canola | Phenology | Leaf development | Flowering stage | Pod development | Maturity/ harvest |
| PAI | 1.82 ± 0.43 | 4.02 ± 0.62 | 6.32 ± 0.16 | N/A | |
| dry biomass | 0.21 ± 0.08 | 0.43 ± 0.04 | 0.76 | N/A | |
| VWC | 1.20 ± 0.13 | 5.82 ± 0.32 | 5.96 | N/A | |
| Wheat | Phenology | Tillering stage | Early flowering stage | Early dough stage | Maturity/ harvest |
| PAI | 2.78 ± 0.31 | 5.92 ± 0.22 | 6.52 ± 0.11 | N/A | |
| dry biomass | 0.23 ± 0.04 | 0.57 ± 0.02 | 0.98 | N/A | |
| VWC | 2.21 ± 0.12 | 5.74 ± 0.24 | 6.11 | N/A |
References
- Mandal, D.; Kumar, V.; Bhattacharya, A.; Rao, Y.S.; Siqueira, P.; Bera, S. Sen4Rice: A processing chain for differentiating early and late transplanted rice using time-series Sentinel-1 SAR data with Google Earth Engine. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1947–1951. [Google Scholar] [CrossRef]
- Dey, S.; Mandal, D.; Robertson, L.D.; Banerjee, B.; Kumar, V.; McNairn, H.; Bhattacharya, A.; Rao, Y. In-season crop classification using elements of the Kennaugh matrix derived from polarimetric RADARSAT-2 SAR data. Int. J. Appl. Earth Obs. Geoinf. 2020, 88, 102059. [Google Scholar] [CrossRef]
- Mandal, D.; Kumar, V.; McNairn, H.; Bhattacharya, A.; Rao, Y. Joint estimation of Plant Area Index (PAI) and wet biomass in wheat and soybean from C-band polarimetric SAR data. Int. J. Appl. Earth Obs. Geoinf. 2019, 79, 24–34. [Google Scholar] [CrossRef]
- Mandal, D.; Kumar, V.; Lopez-Sanchez, J.M.; Bhattacharya, A.; McNairn, H.; Rao, Y. Crop biophysical parameter retrieval from Sentinel-1 SAR data with a multi-target inversion of Water Cloud Model. Int. J. Remote Sens. 2020, 41, 5503–5524. [Google Scholar] [CrossRef]
- Mandal, D.; Hosseini, M.; McNairn, H.; Kumar, V.; Bhattacharya, A.; Rao, Y.; Mitchell, S.; Robertson, L.D.; Davidson, A.; Dabrowska-Zielinska, K. An investigation of inversion methodologies to retrieve the leaf area index of corn from C-band SAR data. Int. J. Appl. Earth Obs. Geoinf. 2019, 82, 101893. [Google Scholar] [CrossRef]
- Mandal, D.; Ratha, D.; Bhattacharya, A.; Kumar, V.; McNairn, H.; Rao, Y.S.; Frery, A.C. A radar vegetation index for crop monitoring using compact polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6321–6335. [Google Scholar] [CrossRef]
- Mandal, D.; Kumar, V.; Ratha, D.; Lopez-Sanchez, J.M.; Bhattacharya, A.; McNairn, H.; Rao, Y.; Ramana, K. Assessment of rice growth conditions in a semi-arid region of India using the Generalized Radar Vegetation Index derived from RADARSAT-2 polarimetric SAR data. Remote Sens. Environ. 2020, 237, 111561. [Google Scholar] [CrossRef]
- Bhogapurapu, N.; Dey, S.; Bhattacharya, A.; Mandal, D.; Lopez-Sanchez, J.M.; McNairn, H.; López-Martínez, C.; Rao, Y.S. Dual-polarimetric descriptors from Sentinel-1 GRD SAR data for crop growth assessment. ISPRS J. Photogramm. Remote Sens. 2021, 178, 20–35. [Google Scholar] [CrossRef]
- Ferrazzoli, P.; Paloscia, S.; Pampaloni, P.; Schiavon, G.; Solimini, D.; Coppo, P. Sensitivity of microwave measurements to vegetation biomass and soil moisture content: A case study. IEEE Trans. Geosci. Remote Sens. 1992, 30, 750–756. [Google Scholar] [CrossRef]
- Davidson, M.W.; Le Toan, T.; Mattia, F.; Satalino, G.; Manninen, T.; Borgeaud, M. On the characterization of agricultural soil roughness for radar remote sensing studies. IEEE Trans. Geosci. Remote Sens. 2000, 38, 630–640. [Google Scholar] [CrossRef]
- Wiseman, G.; McNairn, H.; Homayouni, S.; Shang, J. RADARSAT-2 polarimetric SAR response to crop biomass for agricultural production monitoring. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4461–4471. [Google Scholar] [CrossRef]
- Lee, J.S.; Grunes, M.R.; Pottier, E. Quantitative comparison of classification capability: Fully polarimetric versus dual and single-polarization SAR. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2343–2351. [Google Scholar]
- Kussul, N.; Lemoine, G.; Gallego, F.J.; Skakun, S.V.; Lavreniuk, M.; Shelestov, A.Y. Parcel-based crop classification in Ukraine using Landsat-8 data and Sentinel-1A data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2500–2508. [Google Scholar] [CrossRef]
- Nguyen, D.B.; Gruber, A.; Wagner, W. Mapping rice extent and cropping scheme in the Mekong Delta using Sentinel-1A data. Remote Sens. Lett. 2016, 7, 1209–1218. [Google Scholar] [CrossRef]
- Bargiel, D. A new method for crop classification combining time series of radar images and crop phenology information. Remote Sens. Environ. 2017, 198, 369–383. [Google Scholar] [CrossRef]
- Van Tricht, K.; Gobin, A.; Gilliams, S.; Piccard, I. Synergistic use of radar Sentinel-1 and optical Sentinel-2 imagery for crop mapping: A case study for Belgium. Remote Sens. 2018, 10, 1642. [Google Scholar] [CrossRef]
- Whelen, T.; Siqueira, P. Time-series classification of Sentinel-1 agricultural data over North Dakota. Remote Sens. Lett. 2018, 9, 411–420. [Google Scholar] [CrossRef]
- Minasny, B.; Shah, R.M.; Che Soh, N.; Arif, C.; Indra Setiawan, B. Automated Near-Real-Time Mapping and Monitoring of Rice Extent, Cropping Patterns, and Growth Stages in Southeast Asia Using Sentinel-1 Time Series on a Google Earth Engine Platform. Remote Sens. 2019, 11, 1666. [Google Scholar]
- Arias, M.; Campo-Bescós, M.Á.; Álvarez-Mozos, J. Crop Classification Based on Temporal Signatures of Sentinel-1 Observations over Navarre Province, Spain. Remote Sens. 2020, 12, 278. [Google Scholar] [CrossRef]
- Bousbih, S.; Zribi, M.; Lili-Chabaane, Z.; Baghdadi, N.; El Hajj, M.; Gao, Q.; Mougenot, B. Potential of Sentinel-1 radar data for the assessment of soil and cereal cover parameters. Sensors 2017, 17, 2617. [Google Scholar] [CrossRef]
- Kumar, P.; Prasad, R.; Gupta, D.; Mishra, V.; Vishwakarma, A.; Yadav, V.; Bala, R.; Choudhary, A.; Avtar, R. Estimation of winter wheat crop growth parameters using time series Sentinel-1A SAR data. Geocarto Int. 2018, 33, 942–956. [Google Scholar] [CrossRef]
- Dey, S.; Bhogapurapu, N.; Bhattacharya, A.; Mandal, D.; Lopez-Sanchez, J.M.; McNairn, H.; Frery, A.C. Rice phenology mapping using novel target characterization parameters from polarimetric SAR data. Int. J. Remote Sens. 2021, 42, 5519–5543. [Google Scholar] [CrossRef]
- Dey, S.; Bhattacharya, A.; Ratha, D.; Mandal, D.; McNairn, H.; Lopez-Sanchez, J.M.; Rao, Y. Novel clustering schemes for full and compact polarimetric SAR data: An application for rice phenology characterization. ISPRS J. Photogramm. Remote Sens. 2020, 169, 135–151. [Google Scholar] [CrossRef]
- Cloude, S. The dual polarisation entropy/alpha decomposition. In Proceedings of the 3rd International Workshop on Science and Applications of SAR Polarimetry and Polarimetric Interferometry, Frascati, Italy, 22–26 January 2007; pp. 22–26. [Google Scholar]
- Ainsworth, T.; Schuler, D.; Lee, J.S. Polarimetric SAR characterization of man-made structures in urban areas using normalized circular-pol correlation coefficients. Remote Sens. Environ. 2008, 112, 2876–2885. [Google Scholar] [CrossRef]
- Sugimoto, M.; Ouchi, K.; Nakamura, Y. On the similarity between dual-and quad-eigenvalue analysis in SAR polarimetry. Remote Sens. Lett. 2013, 4, 956–964. [Google Scholar] [CrossRef]
- Freeman, A.; Durden, S.L. A three-component scattering model for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 1998, 36, 963–973. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Moriyama, T.; Ishido, M.; Yamada, H. Four-component scattering model for polarimetric SAR image decomposition. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1699–1706. [Google Scholar] [CrossRef]
- Shan, Z.; Wang, C.; Zhang, H.; Chen, J. H-alpha decomposition and alternative parameters for dual Polarization SAR data. In Proceedings of the PIERS, Suzhou, China, 12–16 September 2011. [Google Scholar]
- Xie, L.; Zhang, H.; Wang, C.; Wu, F.; Zhang, B.; Tang, Y. Maritime application using Ha decomposition in compact and dual-pol SAR. In Proceedings of the 2013 Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Tsukuba, Japan, 23–27 September 2013; pp. 563–566. [Google Scholar]
- Sugimoto, M.; Ouchi, K.; Yang, C.S. On the eigenvalue analysis using HH-VV dual-polarization SAR data and its applications to monitoring of coastal oceans. In Ocean Sensing and Monitoring V; International Society for Optics and Photonics: Bellingham, WA, USA, 2013; Volume 8724, p. 87240G. [Google Scholar]
- Trudel, M.; Charbonneau, F.; Leconte, R. Using RADARSAT-2 polarimetric and ENVISAT-ASAR dual-polarization data for estimating soil moisture over agricultural fields. Can. J. Remote Sens. 2012, 38, 514–527. [Google Scholar]
- Periasamy, S. Significance of dual polarimetric synthetic aperture radar in biomass retrieval: An attempt on Sentinel-1. Remote Sens. Environ. 2018, 217, 537–549. [Google Scholar] [CrossRef]
- Mandal, D.; Kumar, V.; Ratha, D.; Dey, S.; Bhattacharya, A.; Lopez-Sanchez, J.M.; McNairn, H.; Rao, Y.S. Dual polarimetric radar vegetation index for crop growth monitoring using sentinel-1 SAR data. Remote Sens. Environ. 2020, 247, 111954. [Google Scholar] [CrossRef]
- Dey, S.; Chaudhuri, U.; Mandal, D.; Bhattacharya, A.; Banerjee, B.; McNairn, H. BiophyNet: A Regression Network for Joint Estimation of Plant Area Index and Wet Biomass From SAR Data. IEEE Geosci. Remote Sens. Lett. 2020, 18, 1701–1705. [Google Scholar] [CrossRef]
- Dey, S.; Chaudhuri, U.; Bhogapurapu, N.R.; Lopez-Sanchez, J.M.; Banerjee, B.; Bhattacharya, A.; Mandal, D.; Rao, Y. Synergistic Use of TanDEM-X and Landsat-8 Data for Crop-type Classification and Monitoring. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8744–8760. [Google Scholar] [CrossRef]
- Nasrallah, A.; Baghdadi, N.; El Hajj, M.; Darwish, T.; Belhouchette, H.; Faour, G.; Darwich, S.; Mhawej, M. Sentinel-1 data for winter wheat phenology monitoring and mapping. Remote Sens. 2019, 11, 2228. [Google Scholar] [CrossRef]
- Wali, E.; Tasumi, M.; Moriyama, M. Combination of Linear Regression Lines to Understand the Response of Sentinel-1 Dual Polarization SAR Data with Crop Phenology—Case Study in Miyazaki, Japan. Remote Sens. 2020, 12, 189. [Google Scholar] [CrossRef]
- Schlund, M.; Erasmi, S. Sentinel-1 time series data for monitoring the phenology of winter wheat. Remote Sens. Environ. 2020, 246, 111814. [Google Scholar] [CrossRef]
- Lopez-Sanchez, J.M.; Cloude, S.R.; Ballester-Berman, J.D. Rice phenology monitoring by means of SAR polarimetry at X-band. IEEE Trans. Geosci. Remote Sens. 2011, 50, 2695–2709. [Google Scholar] [CrossRef]
- Lopez-Sanchez, J.M.; Vicente-Guijalba, F.; Ballester-Berman, J.D.; Cloude, S.R. Polarimetric Response of Rice Fields at C-Band: Analysis and Phenology Retrieval. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2977–2993. [Google Scholar] [CrossRef]
- McNairn, H.; Jiao, X.; Pacheco, A.; Sinha, A.; Tan, W.; Li, Y. Estimating canola phenology using synthetic aperture radar. Remote Sens. Environ. 2018, 219, 196–205. [Google Scholar] [CrossRef]
- Dey, S.; Bhattacharya, A.; Ratha, D.; Mandal, D.; Frery, A.C. Target Characterization and Scattering Power Decomposition for Full and Compact Polarimetric SAR Data. IEEE Trans. Geosci. Remote Sens. 2020, 59, 3981–3998. [Google Scholar] [CrossRef]
- Dey, S.; Bhattacharya, A.; Frery, A.C.; López-Martínez, C.; Rao, Y.S. A Model-Free Four Component Scattering Power Decomposition for Polarimetric SAR Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 3887–3902. [Google Scholar] [CrossRef]
- Barakat, R. n-fold polarization measures and associated thermodynamic entropy of N partially coherent pencils of radiation. Opt. Acta Int. J. Opt. 1983, 30, 1171–1182. [Google Scholar] [CrossRef]
- McNairn, H.; Tom, J.; Powers, J.; Bélair, J.; Berg, A.; Bullock, A.; Colliander, A.; Cosh, A.; Kim, M.; Ramata, S.; et al. Experimental Plan SMAP Validation Experiment 2016 in Manitoba, Canada (SMAPVEX16-MB). 2016. Available online: http://smapvex16-mb.espaceweb.usherbrooke.ca/ (accessed on 10 October 2021).
- Mandal, D.; Vaka, D.S.; Bhogapurapu, N.R.; Vanama, V.; Kumar, V.; Rao, Y.S.; Bhattacharya, A. Sentinel-1 SLC preprocessing workflow for polarimetric applications: A generic practice for generating dual-pol covariance matrix elements in SNAP S-1 toolbox. Preprints 2019. [Google Scholar] [CrossRef]
- Bhogapurapu, N.; Dey, S.; Mandal, D.; Bhattacharya, A.; Rao, Y.S. PolSAR tools: A QGIS plugin for generating SAR descriptors. J. Open Source Softw. 2021, 6, 2970. [Google Scholar] [CrossRef]
- Barakat, R. Degree of polarization and the principal idempotents of the coherency matrix. Opt. Commun. 1977, 23, 147–150. [Google Scholar] [CrossRef]
- Cloude, S. Polarisation: Applications in Remote Sensing; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Brosseau, C. Polarization transfer and entropy transformation. Optik 1991, 88, 109–117. [Google Scholar]
- Bicout, D.; Brosseau, C. Multiply scattered waves through a spatially random medium: Entropy production and depolarization. J. Phys. I 1992, 2, 2047–2063. [Google Scholar] [CrossRef][Green Version]
- Wu, L.k.; Moore, R.K.; Zoughi, R. Sources of scattering from vegetation canopies at 10 Ghz. IEEE Trans. Geosci. Remote Sens. 1985, 5, 737–745. [Google Scholar] [CrossRef]
- Cloude, S.R.; Pottier, E. An entropy based classification scheme for land applications of polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 1997, 35, 68–78. [Google Scholar] [CrossRef]


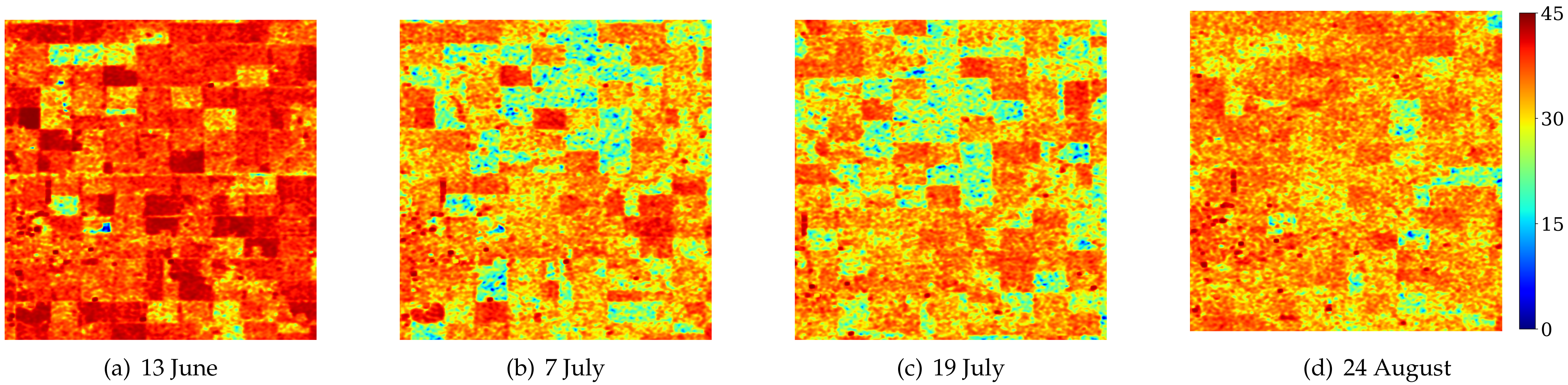

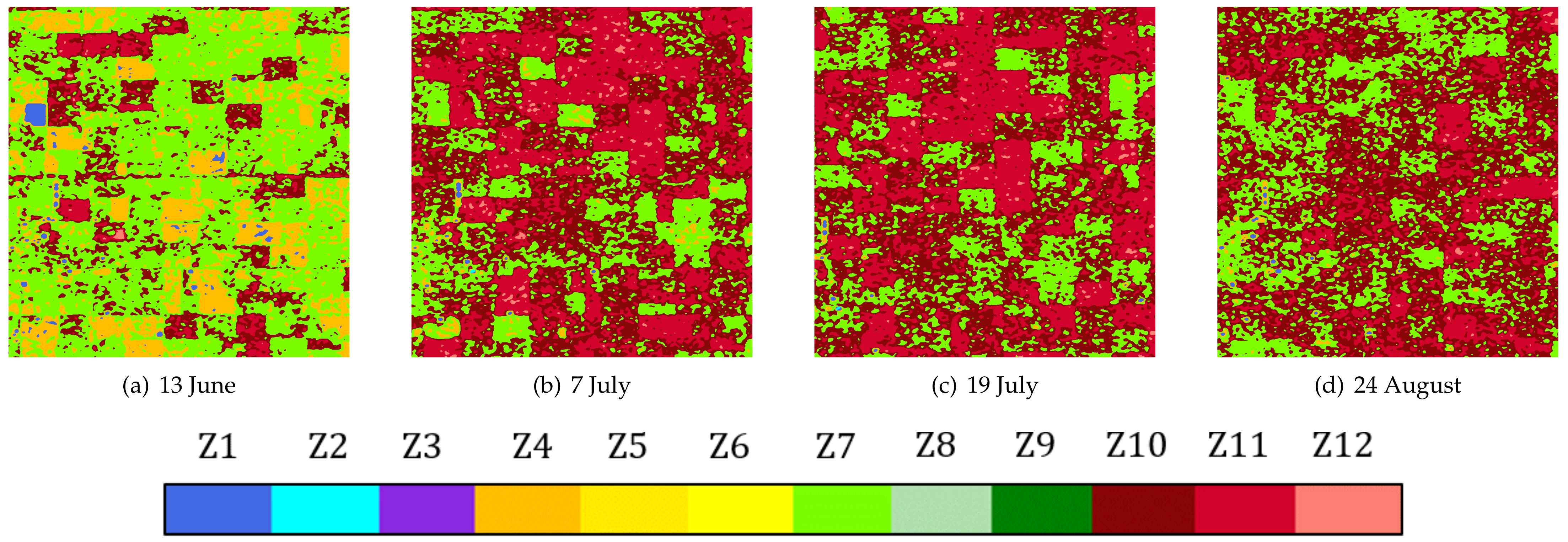
| Acquisition Date | Beam Mode | Incidence Angle Range (Deg.) | Orbit | |
|---|---|---|---|---|
| 13 June 2016 | IW | 30.22–32.47 | Ascending | |
| 07 July 2016 | IW | 30.22–32.47 | Ascending | |
| 19 July 2016 | IW | 30.22–32.47 | Ascending | |
| 24 August 2016 | IW | 30.22–32.47 | Ascending |
| Dates | Z1 | Z2 | Z3 | Z4 | Z5 | Z6 | Z7 | Z8 | Z9 | Z10 | Z11 | Z12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 13 June | 2.0 | 0.0 | 0.0 | 58.0 | 0.0 | 0.0 | 35.4 | 0.0 | 0.0 | 4.6 | 0.0 | 0.0 |
| 7 July | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 6.2 | 91.6 | 2.2 |
| 19 July | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 6.2 | 93.8 | 0.0 |
| 24 August | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 12.6 | 0.0 | 0.0 | 64.6 | 22.8 | 0.0 |
| Dates | Z1 | Z2 | Z3 | Z4 | Z5 | Z6 | Z7 | Z8 | Z9 | Z10 | Z11 | Z12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 13 June | 0.0 | 0.0 | 0.0 | 27.0 | 0.0 | 0.0 | 47.9 | 0.0 | 0.0 | 10.4 | 14.7 | 0.0 |
| 7 July | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 18.8 | 81.2 | 0.0 |
| 19 July | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 83.3 | 16.7 |
| 24 August | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 31.3 | 0.0 | 0.0 | 29.1 | 39.6 | 0.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dey, S.; Bhogapurapu, N.; Homayouni, S.; Bhattacharya, A.; McNairn, H. Unsupervised Classification of Crop Growth Stages with Scattering Parameters from Dual-Pol Sentinel-1 SAR Data. Remote Sens. 2021, 13, 4412. https://doi.org/10.3390/rs13214412
Dey S, Bhogapurapu N, Homayouni S, Bhattacharya A, McNairn H. Unsupervised Classification of Crop Growth Stages with Scattering Parameters from Dual-Pol Sentinel-1 SAR Data. Remote Sensing. 2021; 13(21):4412. https://doi.org/10.3390/rs13214412
Chicago/Turabian StyleDey, Subhadip, Narayanarao Bhogapurapu, Saeid Homayouni, Avik Bhattacharya, and Heather McNairn. 2021. "Unsupervised Classification of Crop Growth Stages with Scattering Parameters from Dual-Pol Sentinel-1 SAR Data" Remote Sensing 13, no. 21: 4412. https://doi.org/10.3390/rs13214412
APA StyleDey, S., Bhogapurapu, N., Homayouni, S., Bhattacharya, A., & McNairn, H. (2021). Unsupervised Classification of Crop Growth Stages with Scattering Parameters from Dual-Pol Sentinel-1 SAR Data. Remote Sensing, 13(21), 4412. https://doi.org/10.3390/rs13214412









