Nineteen Years of Trophic State Variation in Large Lakes of the Yangtze River Delta Region Derived from MODIS Images
Abstract
:1. Introduction
2. Materials and Methods
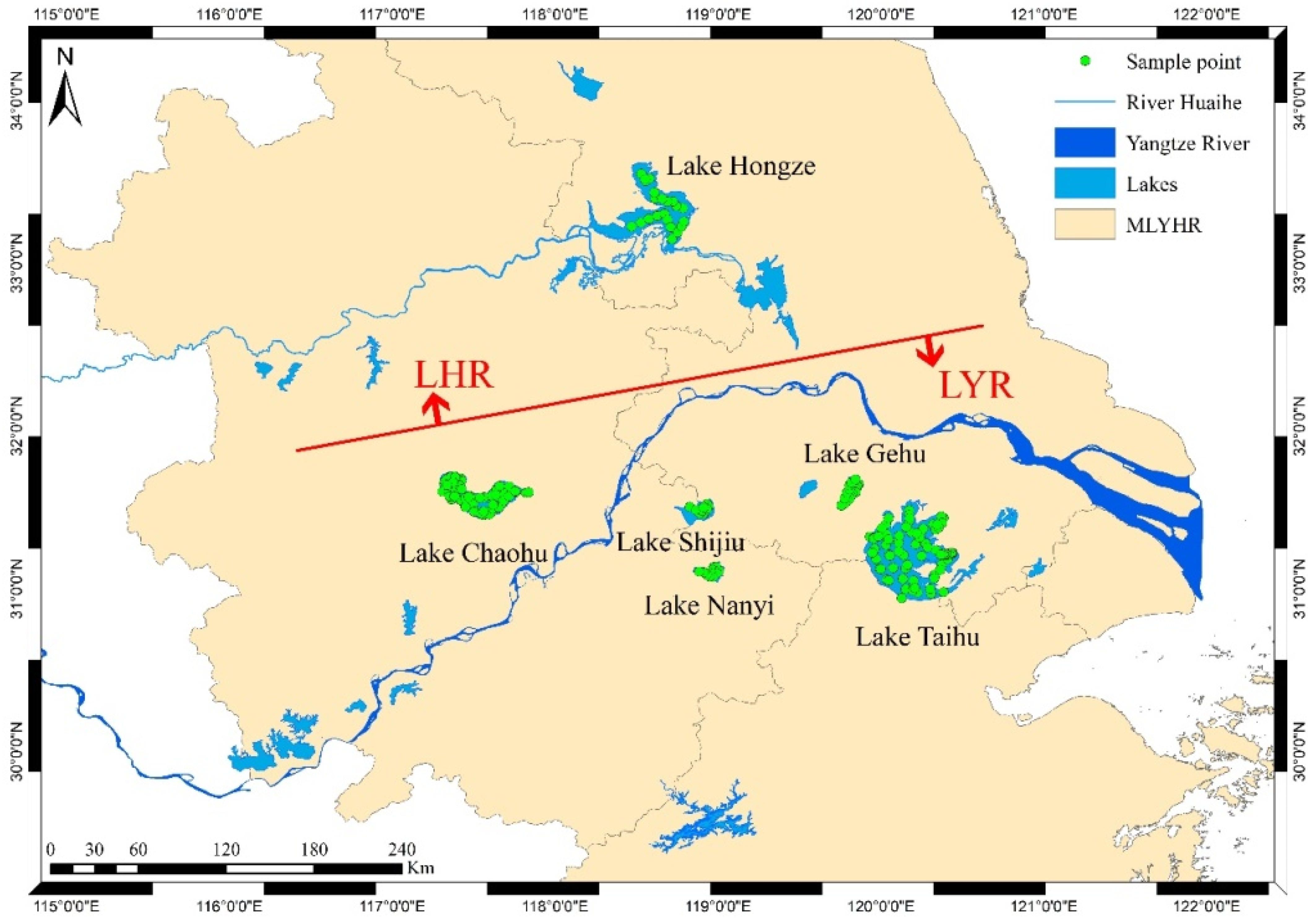
2.1. Study Area and Datasets
2.2. MODIS Image Preprocessing
2.3. Trophic State Index
2.4. The Analysis Method and Data for Long-Term Changes of TSI
2.5. The Derivation of the Particle Absorption Coefficient
2.6. Accuracy Assessment
3. Results
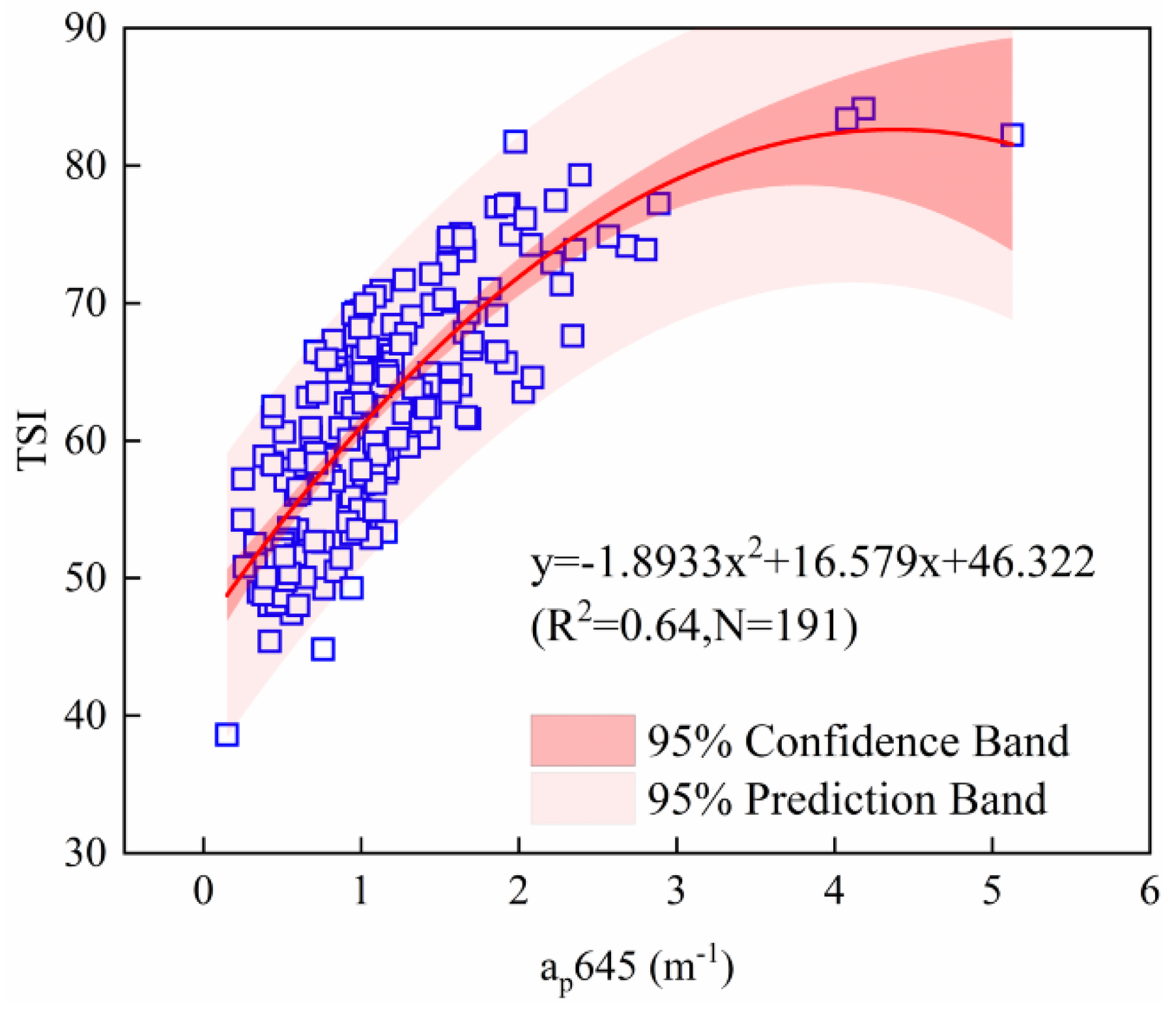
3.1. The Development of the TSI Estimation Algorithm
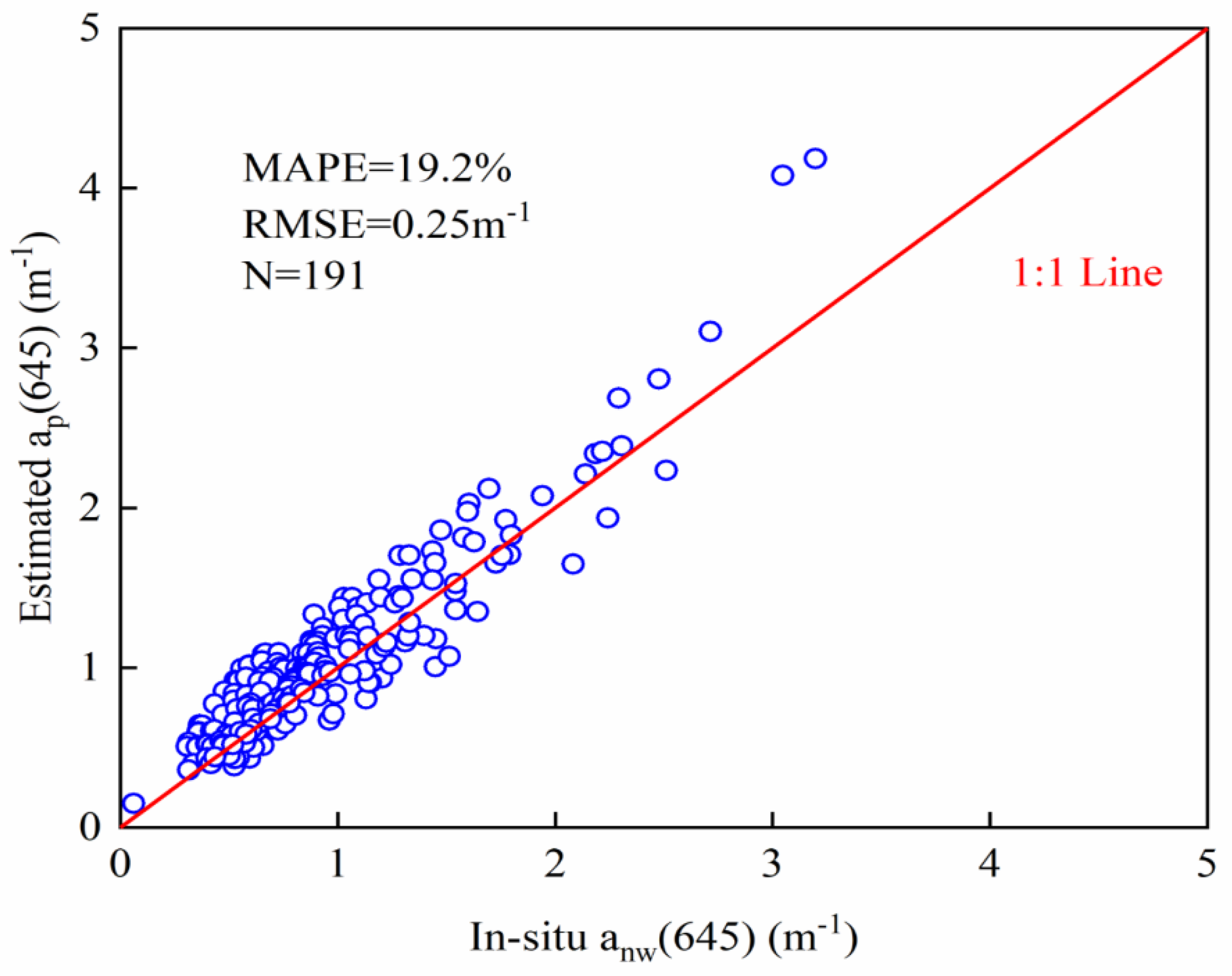
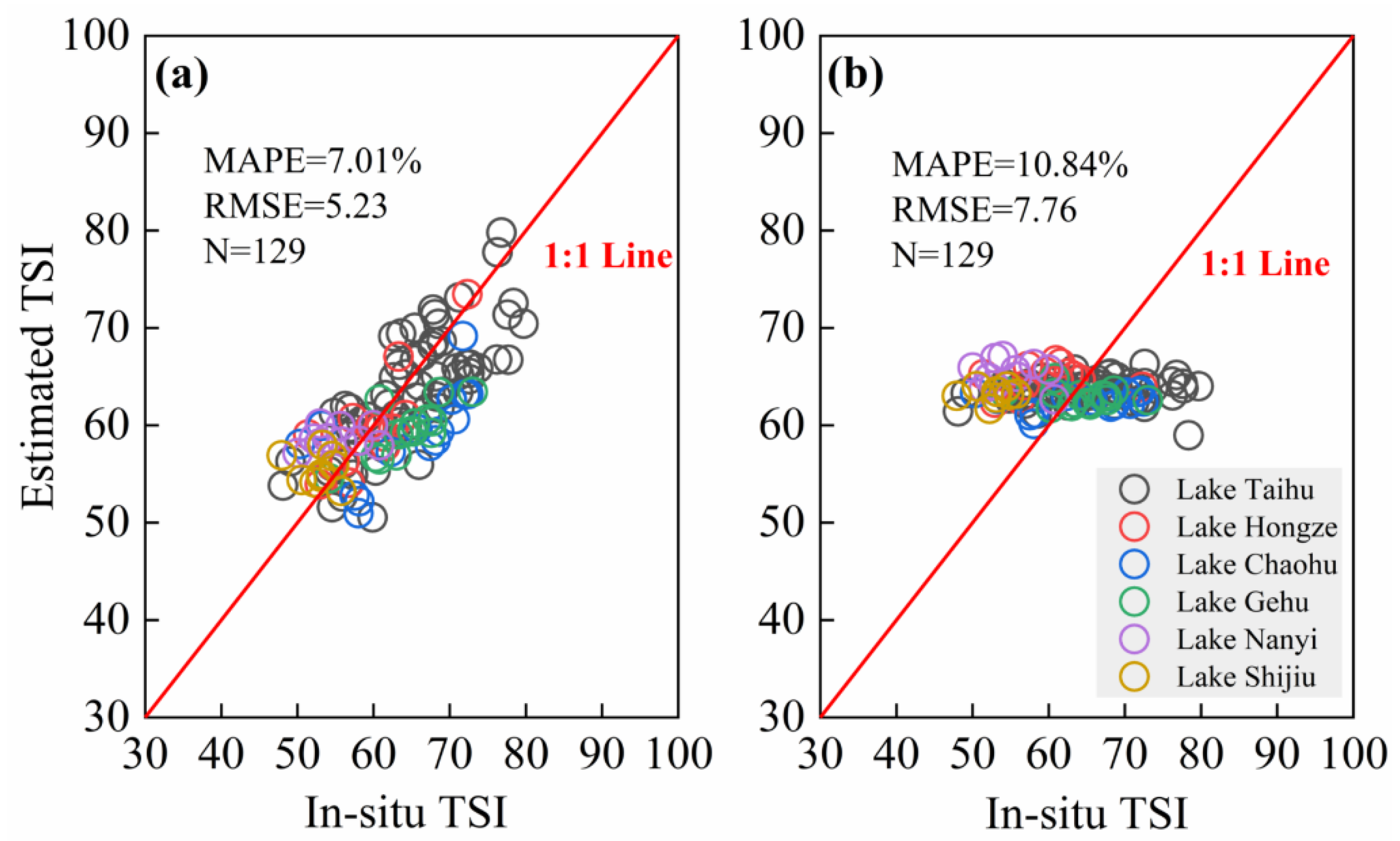
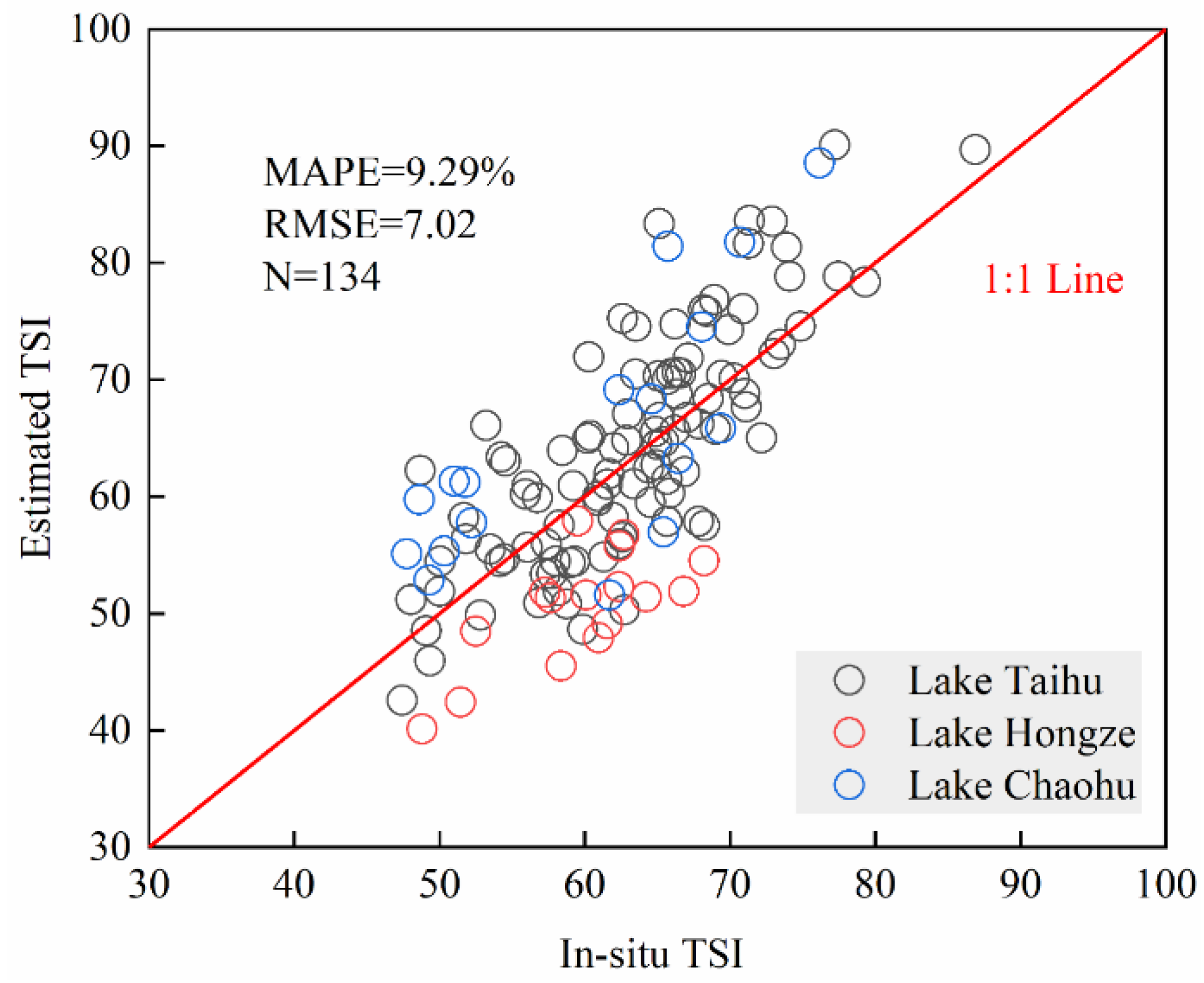
3.2. The Accuracy Evaluation of the TSI Estimating Algorithm
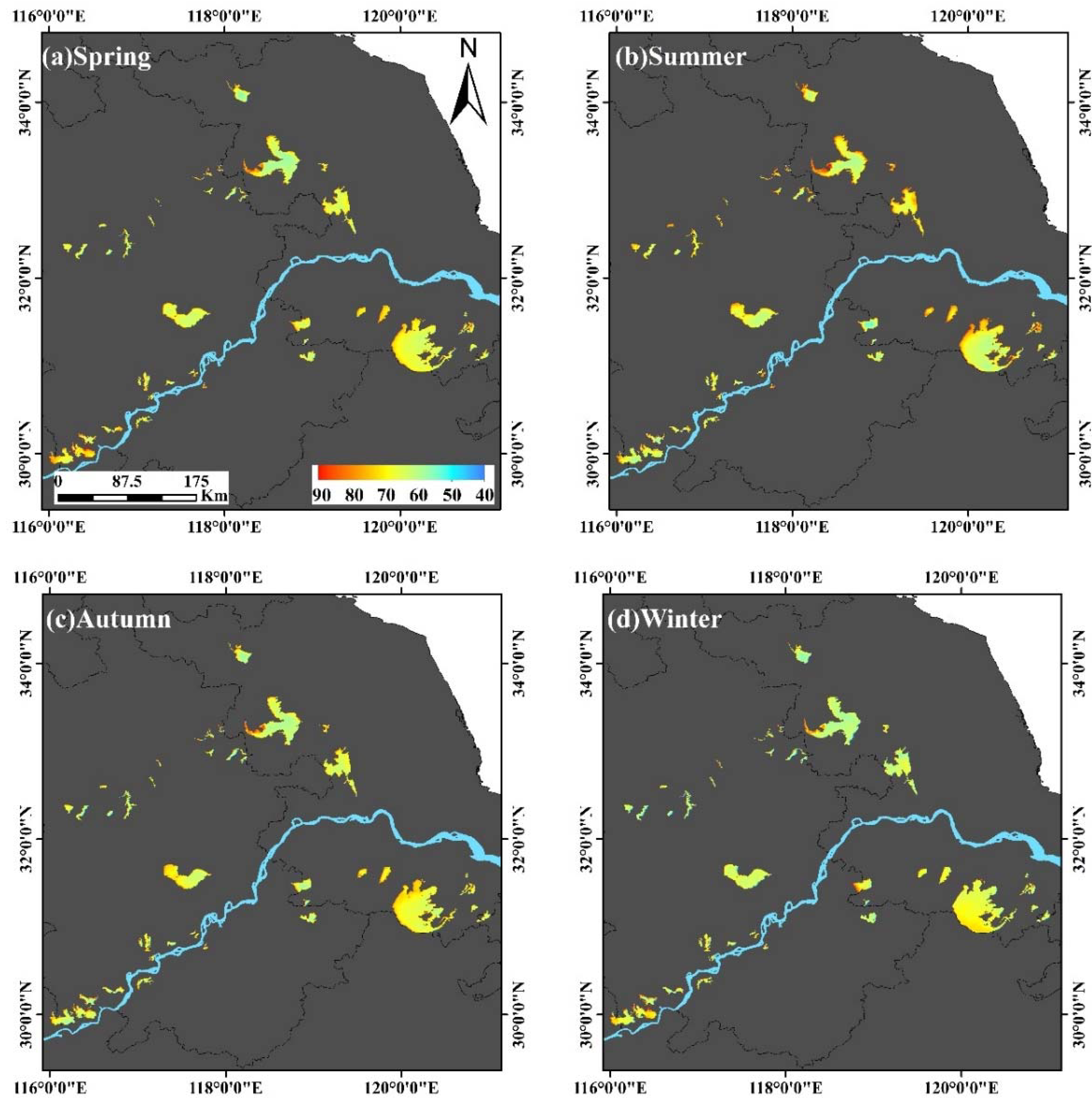
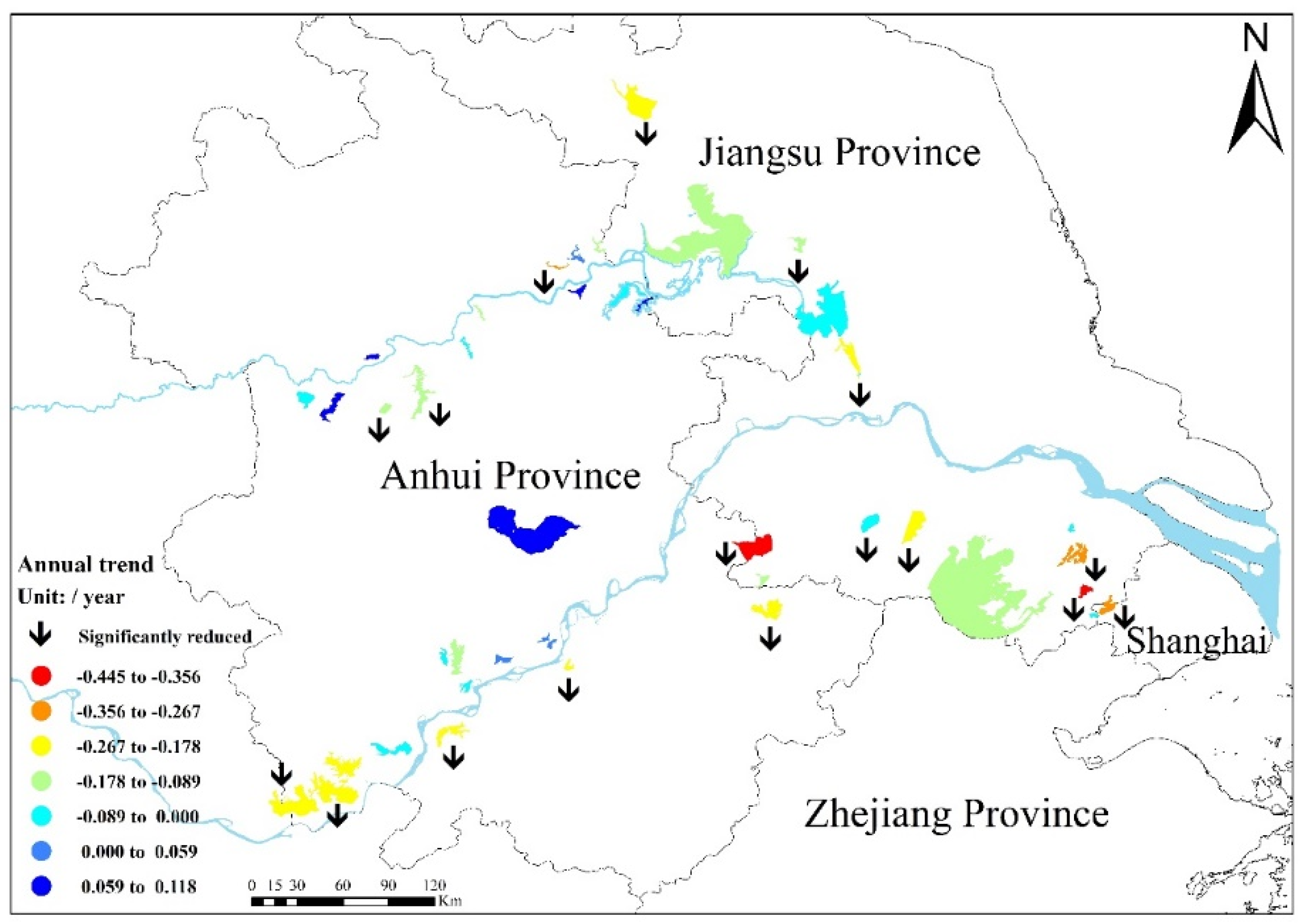
3.3. Spatial Distribution of Lake Trophic State in the YRD
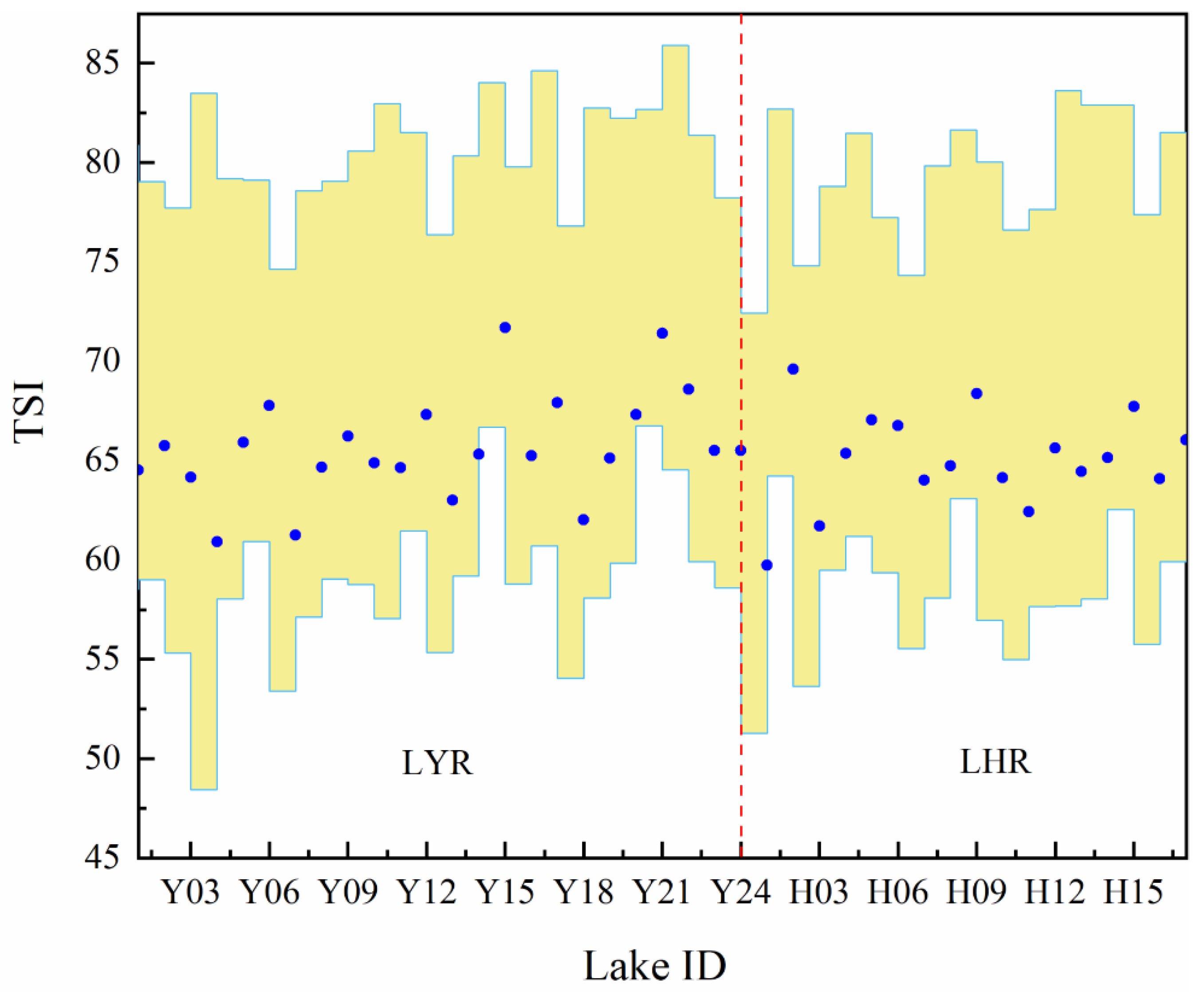
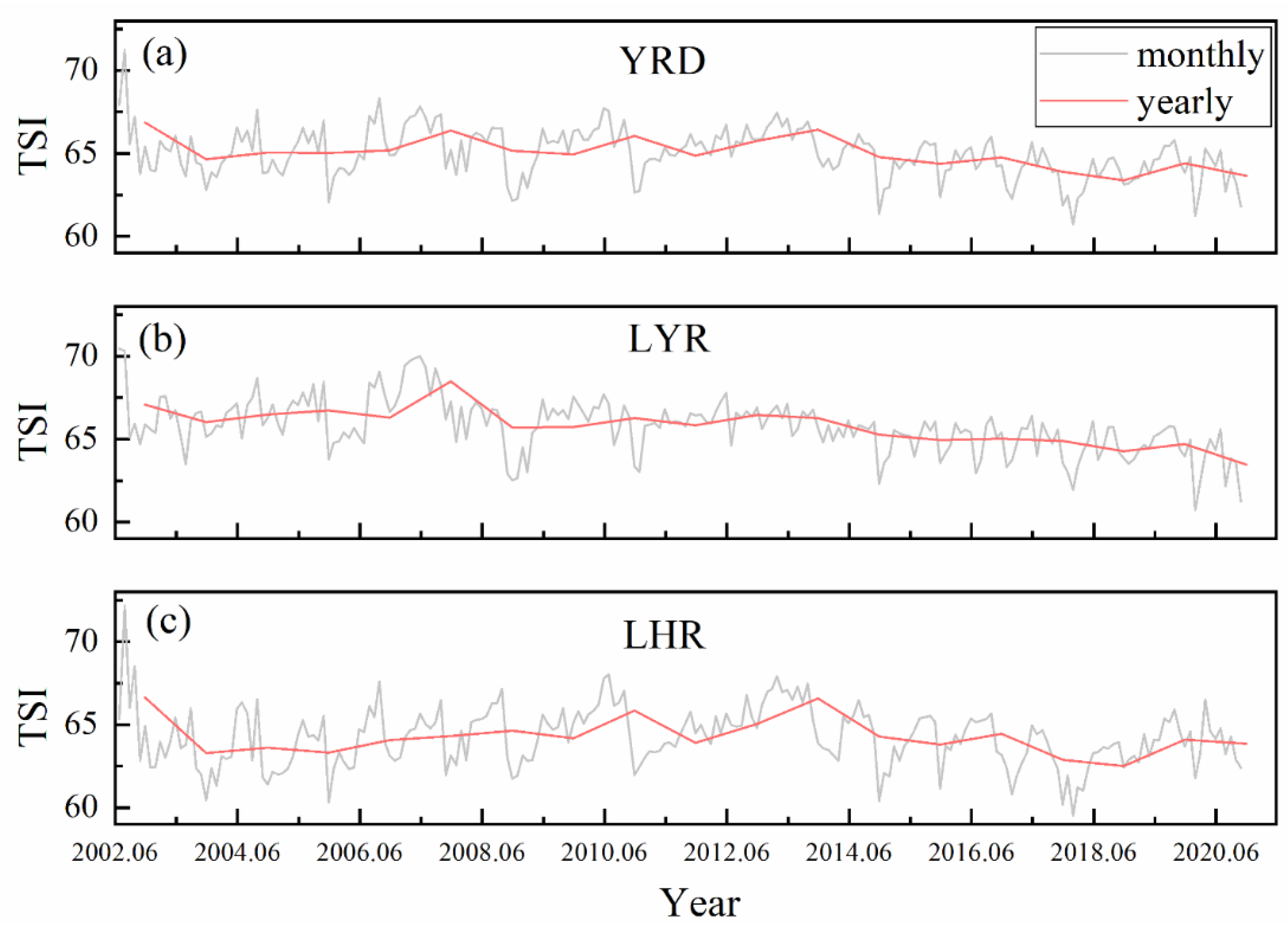
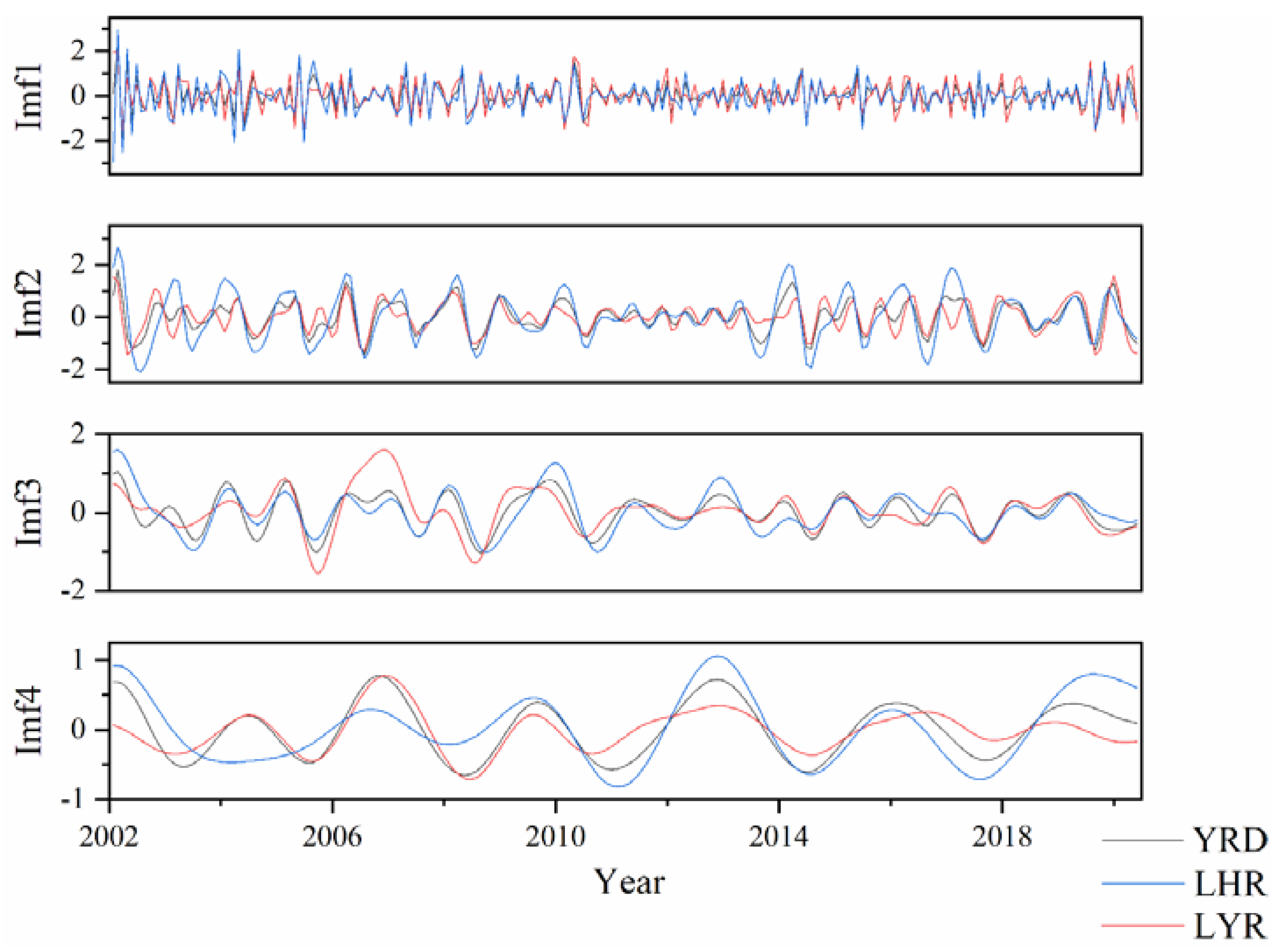
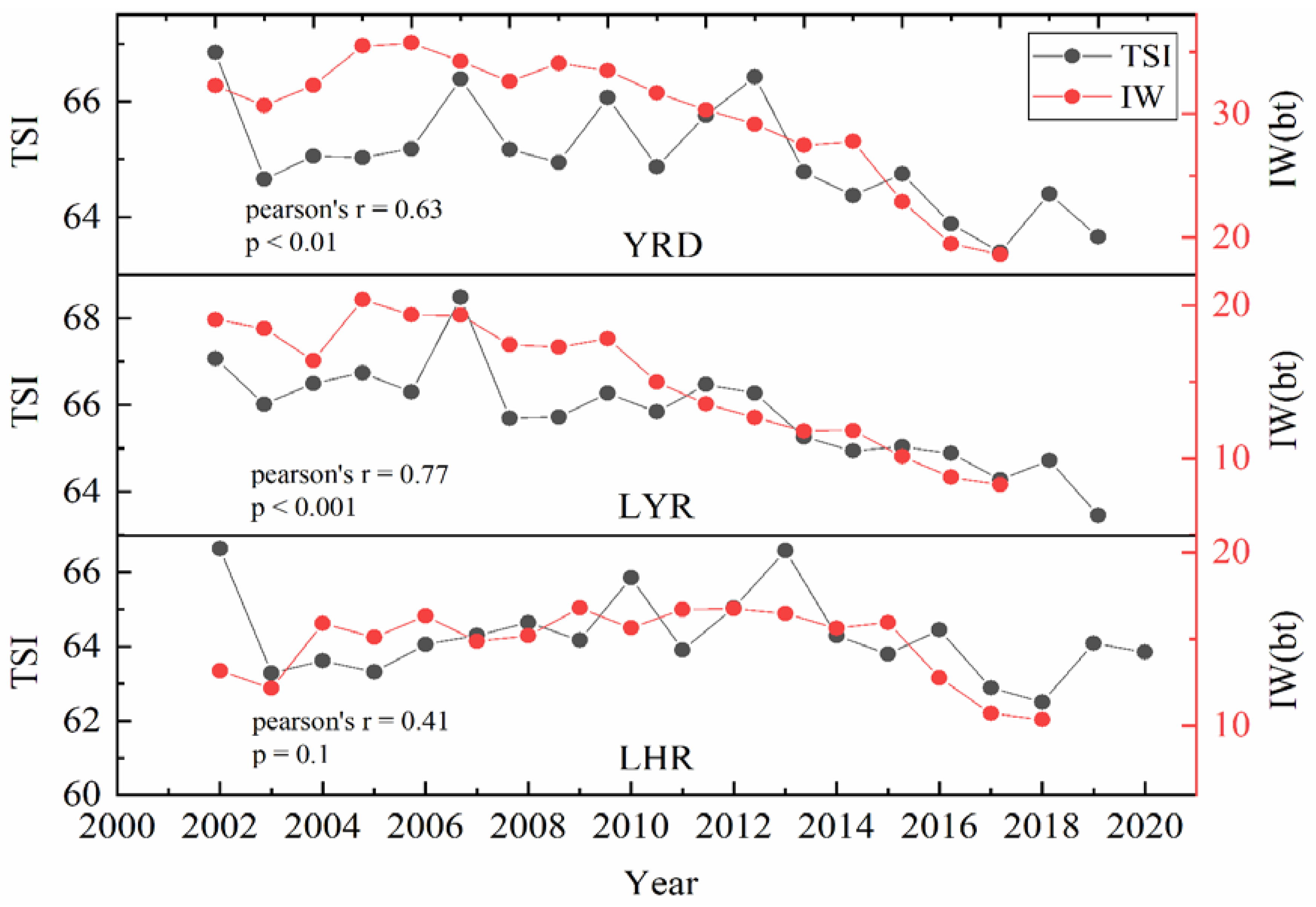
3.4. Temporal Changing Characteristics of the Lake Trophic State in the YRD
4. Discussion
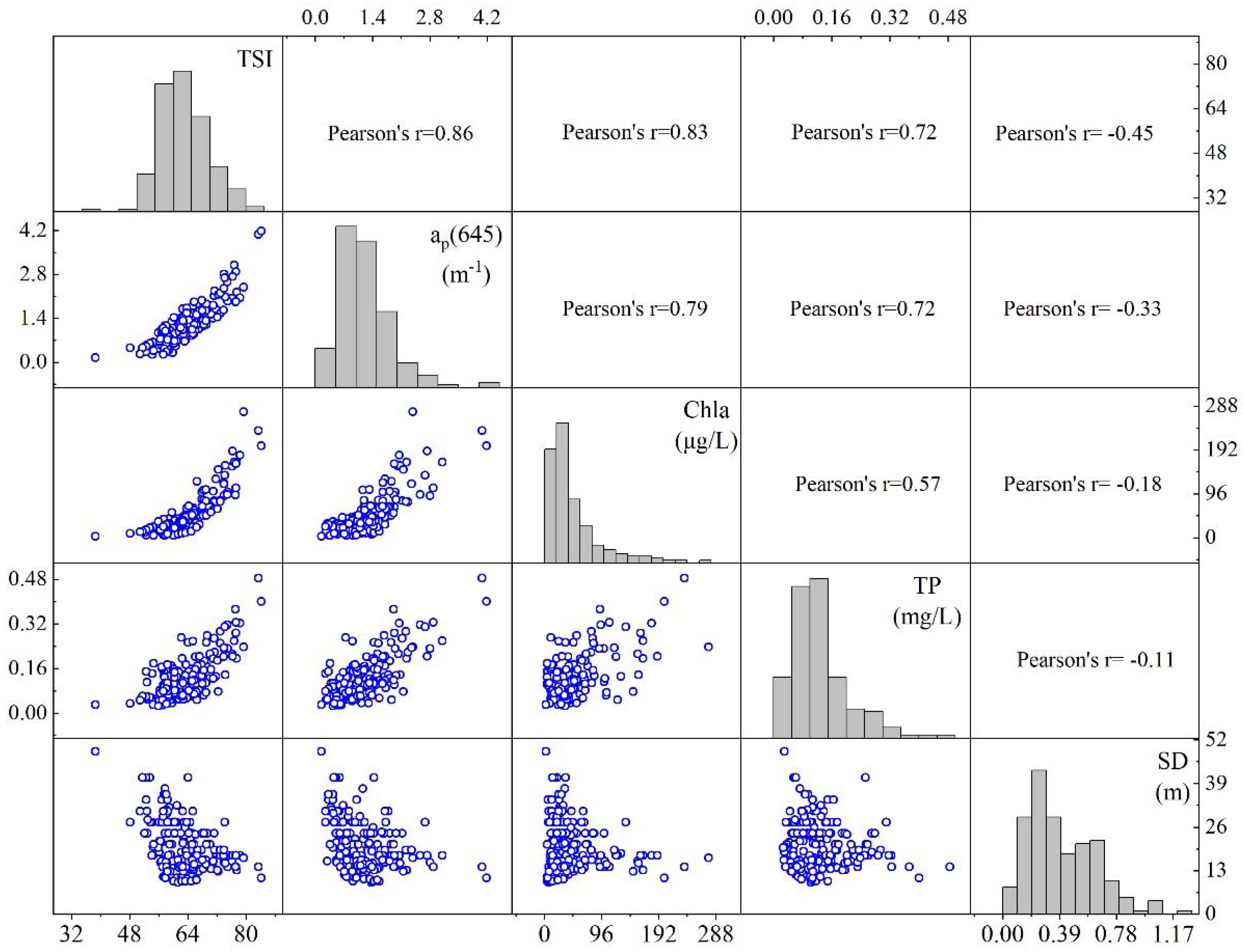
4.1. Why ap(645) Was Selected for TSI Retrievals
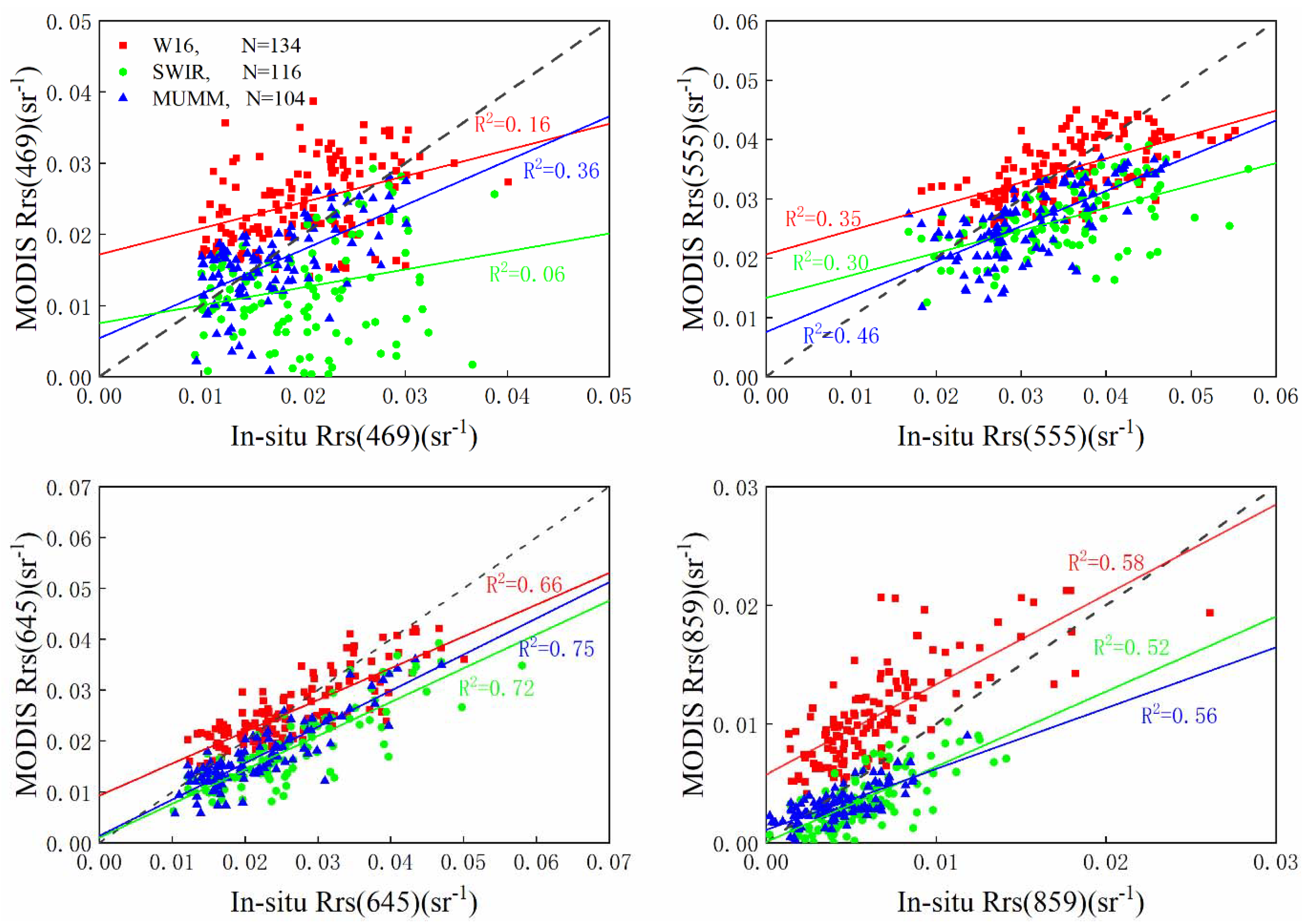
4.2. Evaluation of the Accuracy of the Simple and Operational Correction Method on MODIS Surface Reflectance Products
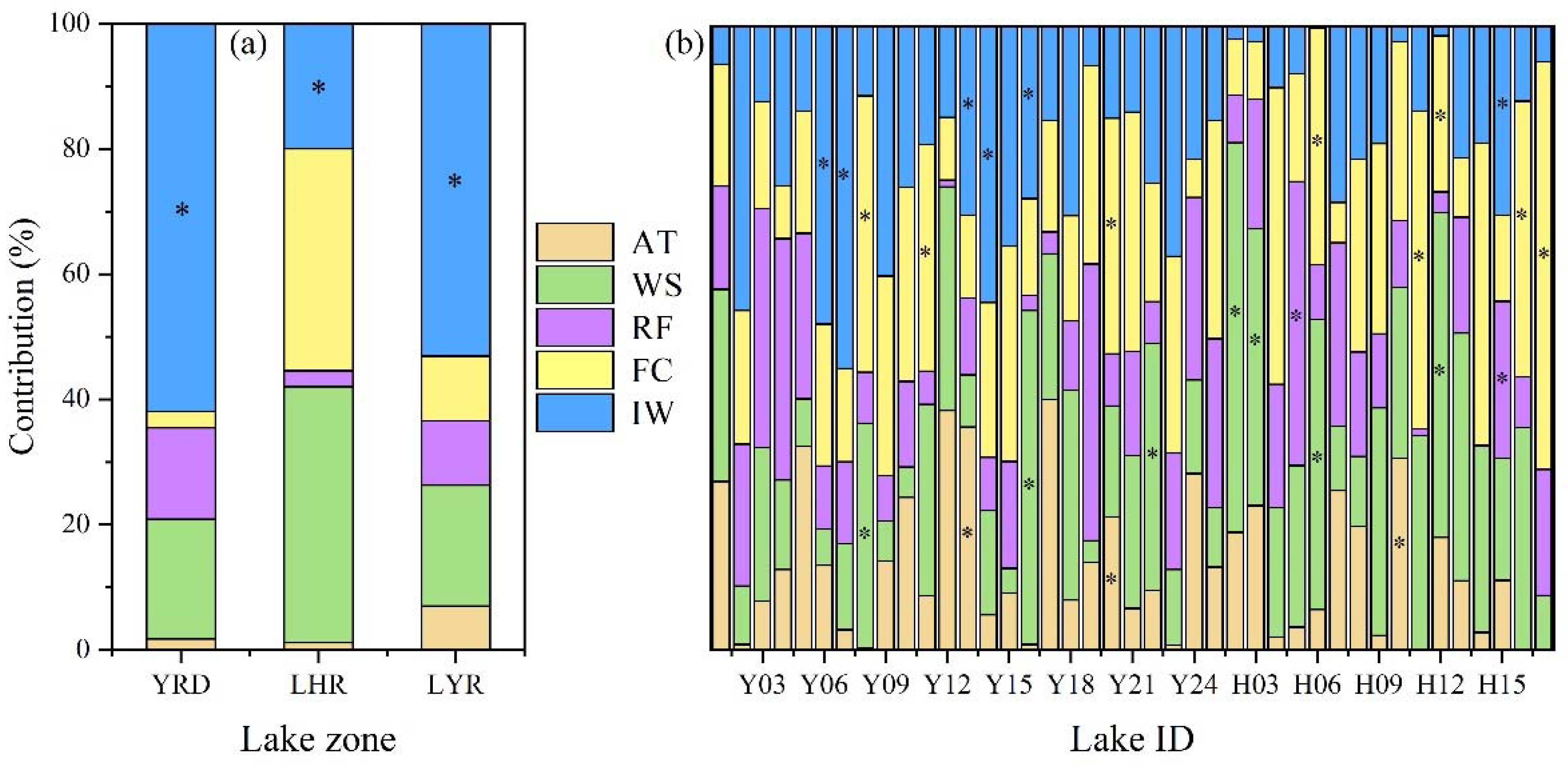
4.3. Analysis of the Driving Factors of Lake Trophic State Temporal Patterns in the YRD
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xiao, Y.; Ferreira, J.G.; Bricker, S.B.; Nunes, J.P.; Zhu, M.; Zhang, X. Trophic Assessment in Chinese coastal systems-review of methods and application to the Changjiang (Yangtze) Estuary and Jiaozhou Bay. Estuaries Coasts 2007, 30, 901–918. [Google Scholar] [CrossRef]
- Shi, K.; Zhang, Y.; Zhou, Y.; Liu, X.; Zhu, G.; Qin, B.; Gao, G. Long-term MODIS observations of cyanobacterial dynamics in Lake Taihu: Responses to nutrient enrichment and meteorological factors. Sci. Rep. 2017, 7. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Ma, R.; Zhang, M.; Duan, H.; Loiselle, S.; Xu, J. Fourteen-Year Record (2000–2013) of the Spatial and Temporal Dynamics of Floating Algae Blooms in Lake Chaohu, Observed from Time Series of MODIS Images. Remote Sens. 2015, 7, 10523–10542. [Google Scholar] [CrossRef] [Green Version]
- Guan, Q.; Feng, L.; Hou, X.; Schurgers, G.; Zheng, Y.; Tang, J. Eutrophication changes in fifty large lakes on the Yangtze Plain of China derived from MERIS and OLCI observations. Remote Sens. Environ. 2020, 246. [Google Scholar] [CrossRef]
- Huang, C.; Wang, X.; Yang, H.; Li, Y.; Wang, Y.; Chen, X.; Xu, L. Satellite data regarding the eutrophication response to human activities in the plateau lake Dianchi in China from 1974 to 2009. Sci. Total Environ. 2014, 485-486, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Shi, K.; Zhang, Y.; Song, K.; Liu, M.; Zhou, Y.; Zhang, Y.; Li, Y.; Zhu, G.; Qin, B. A semi-analytical approach for remote sensing of trophic state in inland waters: Bio-optical mechanism and application. Remote Sens. Environ. 2019, 232. [Google Scholar] [CrossRef]
- Smith, V.H.; Schindler, D.W. Eutrophication science: Where do we go from here? Trends Ecol. Evol. 2009, 24, 201–207. [Google Scholar] [CrossRef]
- Dodds, W.K. Trophic state, eutrophication and nutrient criteria in streams. Trends Ecol. Evol. 2007, 22, 669–676. [Google Scholar] [CrossRef]
- Chen, Q.; Huang, M.; Tang, X. Eutrophication assessment of seasonal urban lakes in China Yangtze River Basin using Landsat 8-derived Forel-Ule index: A six-year (2013–2018) observation. Sci. Total Environ. 2020, 745. [Google Scholar] [CrossRef] [PubMed]
- Wezernak, C.T.; Tanis, F.J.; Bajza, C.A. Trophic state analysis of inland lakes. Remote Sens. Environ. 1976, 5, 147–164. [Google Scholar] [CrossRef]
- Olmanson, L.G.; Bauer, M.E.; Brezonik, P.L. A 20-year Landsat water clarity census of Minnesota’s 10,000 lakes. Remote Sens. Environ. 2008, 112, 4086–4097. [Google Scholar] [CrossRef]
- Song, K.; Li, L.; Li, S.; Tedesco, L.; Hall, B.; Li, L. Hyperspectral Remote Sensing of Total Phosphorus (TP) in Three Central Indiana Water Supply Reservoirs. Water Air Soil Pollut. 2011, 223, 1481–1502. [Google Scholar] [CrossRef]
- Palmer, S.C.J.; Kutser, T.; Hunter, P.D. Remote sensing of inland waters: Challenges, progress and future directions. Remote Sens. Environ. 2015, 157, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Wen, Z.; Song, K.; Liu, G.; Shang, Y.; Fang, C.; Du, J.; Lyu, L. Quantifying the trophic status of lakes using total light absorption of optically active components. Environ. Pollut. 2019, 245, 684–693. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhou, Y.; Shi, K.; Qin, B.; Yao, X.; Zhang, Y. Optical properties and composition changes in chromophoric dissolved organic matter along trophic gradients: Implications for monitoring and assessing lake eutrophication. Water Res. 2018, 131, 255–263. [Google Scholar] [CrossRef]
- Shi, L.; Mao, Z.; Wu, J.; Liu, M.; Zhang, Y.; Wang, Z. Variations in Spectral Absorption Properties of Phytoplankton, Non-algal Particles and Chromophoric Dissolved Organic Matter in Lake Qiandaohu. Water 2017, 9, 352. [Google Scholar] [CrossRef] [Green Version]
- She, Q.; Peng, X.; Xu, Q.; Long, L.; Wei, N.; Liu, M.; Jia, W.; Zhou, T.; Han, J.; Xiang, W. Air quality and its response to satellite-derived urban form in the Yangtze River Delta, China. Ecol. Indic. 2017, 75, 297–306. [Google Scholar] [CrossRef]
- Duan, H.; Loiselle, S.A.; Zhu, L.; Feng, L.; Zhang, Y.; Ma, R. Distribution and incidence of algal blooms in Lake Taihu. Aquat. Sci. 2015, 77, 9–16. [Google Scholar] [CrossRef]
- Duan, H.; Ma, R.; Hu, C. Evaluation of remote sensing algorithms for cyanobacterial pigment retrievals during spring bloom formation in several lakes of East China. Remote Sens. Environ. 2012, 126, 126–135. [Google Scholar] [CrossRef]
- Cao, Z.; Duan, H.; Feng, L.; Ma, R.; Xue, K. Climate- and human-induced changes in suspended particulate matter over Lake Hongze on short and long timescales. Remote Sens. Environ. 2017, 192, 98–113. [Google Scholar] [CrossRef]
- Mobley, C.D. Estimation of the remote-sensing reflectance from above-surface measurements. Appl. Opt. 1999, 38. [Google Scholar] [CrossRef] [PubMed]
- Andersen, J. An ignition method for determination of total phosphorus in lake sediments. Water Res. 1976, 10, 329–331. [Google Scholar] [CrossRef]
- Tassan, S.; Ferrari, G.M. Proposal for the measurement of backward and total scattering by mineral particles suspended in water. Appl. Opt. 1995, 34. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Li, J.; Zhang, B.; Lee, Z.; Spyrakos, E.; Feng, L.; Liu, C.; Zhao, H.; Wu, Y.; Zhu, L.; et al. Changes of water clarity in large lakes and reservoirs across China observed from long-term MODIS. Remote Sens. Environ. 2020, 247. [Google Scholar] [CrossRef]
- Huang, C.; Zhang, Y.; Huang, T.; Yang, H.; Li, Y.; Zhang, Z.; He, M.; Hu, Z.; Song, T.; Zhu, A.x. Long-term variation of phytoplankton biomass and physiology in Taihu lake as observed via MODIS satellite. Water Res. 2019, 153, 187–199. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Son, S.; Shi, W. Evaluation of MODIS SWIR and NIR-SWIR atmospheric correction algorithms using SeaBASS data. Remote Sens. Environ. 2009, 113, 635–644. [Google Scholar] [CrossRef]
- Shenglei, W.; Junsheng, L.; Bing, Z.; Qian, S.; Fangfang, Z.; Zhaoyi, L. A simple correction method for the MODIS surface reflectance product over typical inland waters in China. Int. J. Remote Sens. 2016, 37, 6076–6096. [Google Scholar] [CrossRef]
- Wang, M. Estimation of ocean contribution at the MODIS near-infrared wavelengths along the east coast of the U.S.: Two case studies. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef] [Green Version]
- Ruddick, K.G.; Ovidio, F.; Rijkeboer, M. Atmospheric correction of SeaWiFS imagery for turbid coastal and inland waters. Appl. Opt. 2000, 39. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, C. A novel ocean color index to detect floating algae in the global oceans. Remote Sens. Environ. 2009, 113, 2118–2129. [Google Scholar] [CrossRef]
- Carlson, R.E. A trophic state index for lakes1. Limnol. Oceanogr. 1977, 22, 361–369. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.; Huang, N.E. Ensemble Empirical Mode Decomposition: A Noise-Assisted Data Analysis Method. Adv. Adapt. Data Anal. 2011, 1, 1–41. [Google Scholar] [CrossRef]
- Carpenter, S.R.; Caraco, N.F.; Correll, D.L.; Howarth, R.W.; Sharpley, A.N.; Smith, V.H. Nonpoint Pollution of Surface Waters with Phosphorus and Nitrogen. Ecol. Appl. 1998, 8, 559–568. [Google Scholar] [CrossRef]
- Le, C.; Zha, Y.; Li, Y.; Sun, D.; Lu, H.; Yin, B. Eutrophication of Lake Waters in China: Cost, Causes, and Control. Environ. Manag. 2010, 45, 662–668. [Google Scholar] [CrossRef]
- Timoshkin, O.A.; Moore, M.V.; Kulikova, N.N.; Tomberg, I.V.; Malnik, V.V.; Shimaraev, M.N.; Troitskaya, E.S.; Shirokaya, A.A.; Sinyukovich, V.N.; Zaitseva, E.P.; et al. Groundwater contamination by sewage causes benthic algal outbreaks in the littoral zone of Lake Baikal (East Siberia). J. Great Lakes Res. 2018, 44, 230–244. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Arnone, R.A. Deriving inherent optical properties from water color: A multiband quasi-analytical algorithm for optically deep waters. Appl. Opt. 2002, 41. [Google Scholar] [CrossRef]
- Lyu, H.; Yang, Z.; Shi, L.; Li, Y.; Guo, H.; Zhong, S.; Miao, S.; Bi, S.; Li, Y. A Novel Algorithm to Estimate Phytoplankton Carbon Concentration in Inland Lakes Using Sentinel-3 OLCI Images. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6512–6523. [Google Scholar] [CrossRef]
- Deng, R.; He, Y.; Qin, Y.; Chen, Q.; Chen, L. Pure water absorption coefficient measurement after eliminating the impact of suspended substance in spectrum from 400 nm to 900 nm. Yaogan Xuebao-J. Remote Sens. 2012, 16, 174–191. [Google Scholar]
- Ruddick, K.G.; De Cauwer, V.; Park, Y.-J.; Moore, G. Seaborne measurements of near infrared water-leaving reflectance: The similarity spectrum for turbid waters. Limnol. Oceanogr. 2006, 51, 1167–1179. [Google Scholar] [CrossRef] [Green Version]
- Sydor, M.; Gould, R.W.; Arnone, R.A.; Haltrin, V.I.; Goode, W. Uniqueness in remote sensing of the inherent optical properties of ocean water. Appl. Opt. 2004, 43. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gitelson, A.A.; Dall’Olmo, G.; Moses, W.; Rundquist, D.C.; Barrow, T.; Fisher, T.R.; Gurlin, D.; Holz, J. A simple semi-analytical model for remote estimation of chlorophyll-a in turbid waters: Validation. Remote Sens. Environ. 2008, 112, 3582–3593. [Google Scholar] [CrossRef]
- Simis, S.G.H.; Ruiz-Verdú, A.; Domínguez-Gómez, J.A.; Peña-Martinez, R.; Peters, S.W.M.; Gons, H.J. Influence of phytoplankton pigment composition on remote sensing of cyanobacterial biomass. Remote Sens. Environ. 2007, 106, 414–427. [Google Scholar] [CrossRef]
- Shi, K.; Zhang, Y.; Zhu, G.; Liu, X.; Zhou, Y.; Xu, H.; Qin, B.; Liu, G.; Li, Y. Long-term remote monitoring of total suspended matter concentration in Lake Taihu using 250m MODIS-Aqua data. Remote Sens. Environ. 2015, 164, 43–56. [Google Scholar] [CrossRef]
- Carrick, H.J.; Aldridge, F.J.; Schelske, C.L. Wind Influences phytoplankton biomass and composition in a shallow, productive lake. Limnol. Oceanogr. 1993, 38, 1179–1192. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, Y.; Zhou, Y.; Liu, M.; Shi, K.; Yu, Z. Seasonal-Spatial Distribution and Long-Term Variation of Transparency in Xin’anjiang Reservoir: Implications for Reservoir Management. Int. J. Environ. Res. Public Health 2015, 12, 9492–9507. [Google Scholar] [CrossRef] [PubMed]
- Nazari-Sharabian, M.; Ahmad, S.; Karakouzian, M. Climate Change and Eutrophication: A Short Review. Eng. Technol. Appl. Sci. 2018, 8, 3668–3672. [Google Scholar] [CrossRef]
- Jeppesen, E.; Kronvang, B.; Meerhoff, M.; Søndergaard, M.; Hansen, K.M.; Andersen, H.E.; Lauridsen, T.L.; Liboriussen, L.; Beklioglu, M.; Özen, A.; et al. Climate Change Effects on Runoff, Catchment Phosphorus Loading and Lake Ecological State, and Potential Adaptations. J. Environ. Qual. 2009, 38, 1930–1941. [Google Scholar] [CrossRef] [PubMed]
- Lindeman, R.L. The Trophic-Dynamic Aspect of Ecology. Ecology 1942, 23, 399–417. [Google Scholar] [CrossRef]
- Bennett, E.M.; Carpenter, S.R.; Caraco, N.F. Human Impact on Erodable Phosphorus and Eutrophication: A Global Perspective. BioScience 2001, 51. [Google Scholar] [CrossRef]
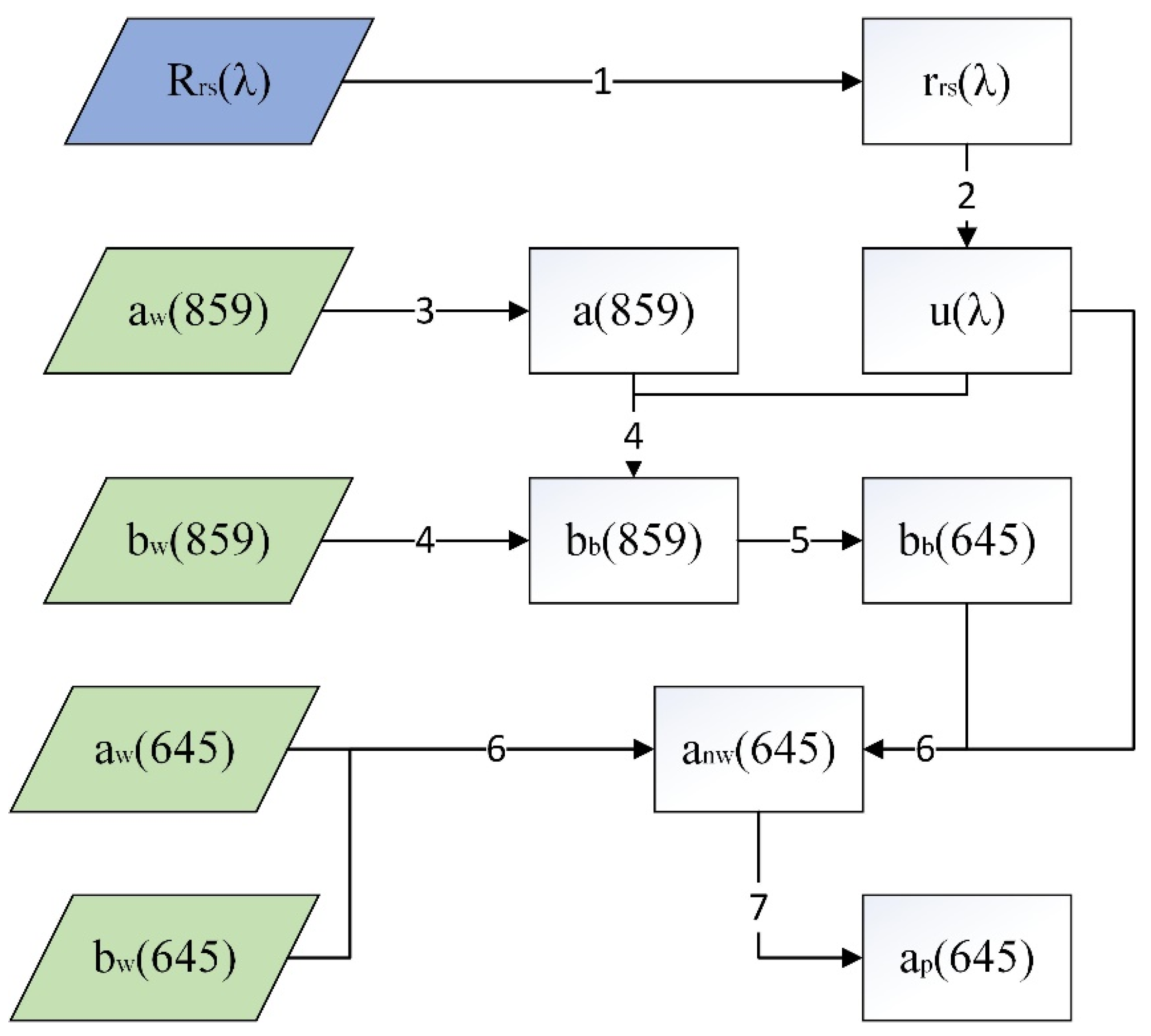
| Step | Property | Expression | Source |
|---|---|---|---|
| 1 | rrs(λ) | QAA_v5 | |
| 2 | u(λ) | QAA_v5 | |
| 3 | a(λ0) | - | |
| 4 | bb(λ0) | - | |
| 5 | bb(645) | - | |
| 6 | anw(645) | - | |
| 7 | ap(645) | - |
| Regions | IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | IMF6 | Residue | |
|---|---|---|---|---|---|---|---|---|
| YRD | Period | 2.2 | 12 | 12.5 | 37 | 80 | 227.3 | |
| Contribution | 31.2% | 26.5% | 14.5% | 11.4% | 4.9% | 9.5% | 2.2% | |
| LYR | Period | 3.7 | 12.3 | 27.8 | 37.3 | 73.69 | 185.18 | |
| Contribution | 29.6% | 20.2% | 16.7% | 4.9% | 33.2% | 25.3% | 0.04% | |
| LHR | Period | 4 | 12.2 | 22.2 | 44.1 | 227.3 | 295.9 | |
| Contribution | 27.8% | 37.4% | 11.2% | 10.3% | 10.9% | 2.4% | 0.01% |
| Atmospheric Correction Methods | Bands | N | R2 | RMSE (sr−1) | MAPE (%) |
|---|---|---|---|---|---|
| W16 | 645 nm | 134 | 0.66 | 0.004967 | 15.46 |
| 859 nm | 0.58 | 0.004974 | 93.17 | ||
| SWIR | 645 nm | 116 | 0.72 | 0.009135 | 29.18 |
| 859 nm | 0.52 | 0.002762 | 45.02 | ||
| MUMM | 645 nm | 104 | 0.75 | 0.006309 | 22.92 |
| 859 nm | 0.56 | 0.001741 | 47.17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bian, Y.; Zhao, Y.; Lyu, H.; Guo, F.; Li, Y.; Xu, J.; Liu, H.; Ni, S. Nineteen Years of Trophic State Variation in Large Lakes of the Yangtze River Delta Region Derived from MODIS Images. Remote Sens. 2021, 13, 4322. https://doi.org/10.3390/rs13214322
Bian Y, Zhao Y, Lyu H, Guo F, Li Y, Xu J, Liu H, Ni S. Nineteen Years of Trophic State Variation in Large Lakes of the Yangtze River Delta Region Derived from MODIS Images. Remote Sensing. 2021; 13(21):4322. https://doi.org/10.3390/rs13214322
Chicago/Turabian StyleBian, Yingchun, Ying Zhao, Heng Lyu, Fei Guo, Yunmei Li, Jiafeng Xu, Huaiqing Liu, and Shang Ni. 2021. "Nineteen Years of Trophic State Variation in Large Lakes of the Yangtze River Delta Region Derived from MODIS Images" Remote Sensing 13, no. 21: 4322. https://doi.org/10.3390/rs13214322
APA StyleBian, Y., Zhao, Y., Lyu, H., Guo, F., Li, Y., Xu, J., Liu, H., & Ni, S. (2021). Nineteen Years of Trophic State Variation in Large Lakes of the Yangtze River Delta Region Derived from MODIS Images. Remote Sensing, 13(21), 4322. https://doi.org/10.3390/rs13214322






