Abstract
Satellite-based observations of sea wind are useful for forecasting marine weather and performing marine disaster management. Meteorological Operational Satellite-B (MetOp-B) is one of the satellites that provide wind products through a scatterometer named the Advanced Scatterometer (ASCAT). Since the linear regression method has been conventionally employed for calibrating remotely-sensed wind data, deviations and biases remain un-resolved to some degree. For coastal applications, these remotely-sensed wind data need to be calibrated again using local in-situ measurements in order to provide more accurate and realistic information. Thus, this study proposed a new method to calibrate ASCAT-based wind speed estimates using artificial neural networks. Herein, a deep neural network (DNN) model was applied. Wind databases collected during a period from 2012 to 2019 by the MetOp-B ASCAT and ten buoy stations in Korean seas were considered for deep learning-based calibration. ASCAT-based wind data and in-situ measurements were collocated in space and time. They were then separated into training and validation sets. A DNN model was designed and trained using multiple input variables such as observation location, sensing date and time, wind speed, and wind direction of the training set. The DNN-based best fit calibration model was evaluated using the validation set. The mean of biases between ASCAT-based and in-situ wind speeds was found to be decreased from 0.41 to 0.05 m/s on average for all buoy locations. The root mean squared error (RMSE) of wind speed was reduced from 1.38 m/s to 0.93 m/s. Moreover, the DNN-based calibration considerably improved the quality of wind speeds of less than 4 m/s, and of high wind speeds of 11–25 m/s. These results suggest that ASCAT-based observations can accurately represent real wind fields if a DNN-based calibration approach is applied.
1. Introduction
Sea wind is a key parameter for studying ocean physical phenomena and processes such as ocean surface waves, ocean currents, ocean circulation, storm surges, sea-fog formation, marine meteorology, and so on [1,2,3,4,5,6,7]. For instance, measurements of sea winds with a wide coverage and high accuracy are now keenly used as inputs for marine weather forecasting, wave modeling, and predicting natural disasters in the ocean [8,9,10,11,12,13]. Conventionally, sea winds have been measured using offshore buoys or automatic weather stations (AWS) located on the coast or islands [14,15]. However, point-measurement systems are inefficient in covering wide oceans due to the expense of installation, the difficulty of maintenance, unexpected loss, defects, and failures. In-situ measurements cannot efficiently cover large oceanic expanses, either.
In order to overcome these limitations of in-situ measurements, satellite-borne instruments capable of observing sea surface winds over global oceans continuously for a long time at a low cost have been developed [8,16,17,18,19,20,21,22]. Typically, a scatterometer sensor is adopted on satellites to measure both sea wind speed and direction. Examples of space-based scatterometers are Seasat-A [23], Quick Scatterometer (QuikSCAT) [8,16,18,19,20,21], OceanSat-2 [24], and Meteorological Operational satellite-A/B/C (MetOp-A/B/C) [2,25,26,27]. Altimeters can also be used to measure wind speed at the ocean surface, such as Geodetic Satellite (GEOSAT) [28], European Remote-Sensing Satellite-1/2 (ERS-1/2) [29], Topography Experiment/Poseidon (TOPEX/Poseidon) [17,22], Jason-1/2/3 [2,30,31,32], and Environmental Satellite (EnviSat) [25,33]. Among satellite-mounted scatterometers, The Advanced Scatterometers (ASCAT) carried on the MetOp satellite are used for marine research in three marginal seas around the Korean peninsula (i.e., the East Sea, the Korean Strait, and the Yellow Sea) because these scatterometers collect both wind speed and direction over these seas with a long time-span from 2006 to present, in which in-situ measurement systems have been also operated. These two wind observation databases collected concurrently from space and the sea surface are now available to accurately evaluate the remote-sensing performance for local sea areas around Korea [2,34].
ASCAT beams measure the ratio of transmitted and received radar energy over the radar cross-section along a nadir track below the satellite. Measured backscatter coefficients are related to wind speeds at the surface [35]. To date, retrieved wind speeds from ASCAT have been calibrated and validated in many global and regional oceans by comparison with in-situ wind measurements from buoys [2,35,36,37,38]. The Ocean and Sea Ice Satellite Application Facility (OSI SAF) of the European Organization for the Exploitation of Meteorological Satellites (EMSAT) requires that ASCAT performance for wind products should be consistent over the globe. In addition, the standard deviation and the bias of the ASCAT-based wind speeds should be less than 2 m/s and 0.5 m/s, respectively [35]. For instance, comparisons with winds measured on offshore buoys located in a tropical zone between Europe and North America and coastal buoys near North America have found that the standard deviation of wind speed is about 1.5 m/s and the bias is about -0.25 m/s [35]. Similarly, for three seas around Korea, ASCAT-based wind speeds have been found to display a root mean squared error (RMSE) of about 1.6 m/s compared to buoy-based wind data [2]. Nevertheless, it has been reported globally that ASCAT-based wind observations tend to show larger deviations for wind speeds below 5 m/s and above 15 m/s in general [36,37].
Calibration and validation of ASCAT data have been performed mostly based on linear regression equations using in-situ measurements to improve their performance [2,35,36,37]. The linear regression approach itself typically causes deviations and biases of ASCAT-based wind estimates to remain unsolved to some extent. When ASCAT-based wind observations are used for coastal applications such as coastal weather prediction and disaster assessments, they need to be calibrated again using local in-situ measurements which better represent local climatology. In particular, near land or islands where various human activities occur, wind estimation performance by remote-sensing needs to be improved to the level of in-situ measurements. However, ASCAT-based wind results might be different from the reality, and there were features that are difficult to calibrate using linear regression equations [2,35,36,37]. In previous studies that evaluated the accuracy of ASCAT-based wind speeds in the Korean peninsula, it was reported that the tendency of RMSE was related to wind speed and direction. In the case of wind speed, it was also reported that the RMSE was increased when the wind speed was larger than 10 m/s [34]. A study using QSCAT analyzed that, when the wind speed was larger than 15 m/s, the error was increased [19,39]. Since the wind strength in winter is about 40% stronger than that in summer in Korea, this may show a seasonal pattern in which the error in winter increases [40]. In addition, these ASCAT wind errors were different for each in-situ point used in the evaluation [2]. That is, the complicatedly intertwined errors suggest that there is a limit to re-calibration using the linear regression equations.
For the reasons described above, it is necessary to improve the accuracy of ASCAT-based wind estimates by considering localized characteristics of the target area such as observation location, wind speed and direction, sensing time, and so on. Recently, a deep neural network (DNN) model has been applied as a method for regression analysis considering multiple input variables [41,42,43,44]. This deep learning model can retrieve the relationship between training (or input) and reference (or output target) datasets. A DNN model consists of multiple layers and nodes to iteratively calculate coefficients of the two datasets and produce the best fit function for them.
In this study, the deep learning approach was applied to improve the ASCAT performance for local marginal seas around Korea considering various localized factors that might affect sea wind fields. The ASCAT-based database, including ground coordinates (or observation location), sensing time (or date and time), wind speed, and wind direction, was used as the training data and the buoy-based database was used as the reference data to produce a deep-learning based best-fit model.
2. Study Area and Dataset
Research areas for this study were three marginal seas: the East Sea, the Korean Strait, and the Yellow Sea around the Korean peninsula (Figure 1). Since the study area is located between 33 and 39 degrees North, it is mainly influenced by westerlies. It also shows characteristics of a monsoonal climate, which includes seasonal change of wind patterns induced by effects of the Siberian air mass, the Okhotsk Sea air mass, the Yangtze River air mass, the Equatorial air mass, and the Northwest Pacific air mass encountered in the vicinity of these research areas [45]. In summer, the Northwest Pacific high air pressure is strongly developed to suppress sea winds around Korea. Tropical typhoons pass occasionally, with high wind speeds from the south. In winter, storm events caused by northwesters from the Siberian continent occur frequently.
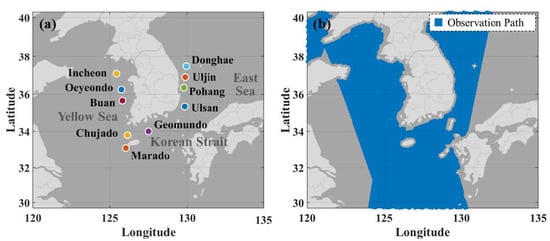
Figure 1.
Study areas with (a) ten buoy locations and (b) an example of the ASCAT observation path on 2 January 2013.
The ASCAT-based wind database considered in this study was collected by the MetOp-B satellite operated by the European Space Agency (ESA) and the European Organization for the Exploitation of Meteorological Satellite (EUMETSAT). The MetOp-B satellite was launched in September 2012. The satellite orbits the earth at an altitude of about 817 km. It has a repeat cycle of 29 days [24,40]. The ASCAT sensor relies on real-aperture radars using vertically polarized antennas. A long pulse of 5.255 GHz (C band) with Linear Frequency Modulation (chirp) is emitted from these antennas. Backscattered signals from the sea surface are acquired after a de-chirping process. Two sets of antennas are used to generate side-looking radar beams at 45° and 135° relative to nadir, each under the flight direction of the MetOp-B satellite. The swath of each beam is about 550 km wide. As the received backscatter signals are dependent on the sea surface roughness as a function of wind speed and direction, sea surface wind speed and direction are retrieved from these backscatter signals by specifying a geophysical model function (GMF) [25,26,27,35,36,37,46]. Wind speed and direction of the ASCAT-based data are provided as 10 m-Equivalent Neutral Winds (U10) with two spatial resolutions (25 and 12.5 km) over the global ocean.
In this study, the ASCAT 25 km-wind data remotely sensed during a period from October 2012 to December 2019 were used for a DNN-based investigation of data quality and data calibration. This period is defined by the coincident set of observations of the MetOp-B satellite and the in-situ buoys. Figure 1b shows an example of the coverage of ASCAT on MetOp-B off the coast of South Korea on 2 January 2013. Level 2b ASCAT wind products are used here. These products provide the latitude, longitude, sensing date and time of each cell, in addition to wind speed and direction. These data were provided at each wind vector cell of 25 km by 25 km. Given that the swath width is about 550 km, there were 42 wind vector cells collected across the two swaths. Thus, a total of about 3,518,000 data-points were collected in the study area.
The in-situ database used as the output target data during the period of interest for training and testing of the DNN model was collected from ten moored buoy stations maintained around Korea by the Korea Meteorological Administration (KMA). The accuracy of the winds obtained from these buoys is <0.5 m/s for wind speeds <10 m/s and <5 m/s for wind speeds >10 m/s according to the Guidelines for Ocean Meteorological Observation. Figure 1a shows locations of the ten buoys, including three located in the Yellow Sea, three in the Korean Strait, and four in the East Sea. This combination of buoy locations reflects environmental characteristics of these three seas of South Korea properly. Table 1 presents location, observation period, observation height, and the number of observed data-points for these buoy stations. Data collected during a period from 2012 to 2019 were selected. The total number of these collected in-situ data-points was about 494,000.

Table 1.
List of in-situ measurements from ten buoy stations around Korea.
3. Methodology
A flow chart of data processing for calibration of the ASCAT wind data is presented in Figure 2. The data processing procedure was divided into two parts. The first part was the pre-processing of the input and target databases used for the deep learning approach. It included the conversion of wind speed at the buoy-measurement level to that at the elevation level of 10 m above the mean sea level (i.e., U10), the quality control (QC) process of the ASCAT and buoy data, and the collocation of the two databases as a data table comprising match-up pairs with regard to observation location and sensing time. The second part was the training and validation of the deep learning model. This part consisted of the following procedures: (1) collocated (or matched-up) data were separated into training and validation sets; (2) a DNN-based calibration model with model structures and hyper-parameters was designed and trained using the training set, and (3) the DNN-based calibration model (or best fit function) was evaluated using the validation set.
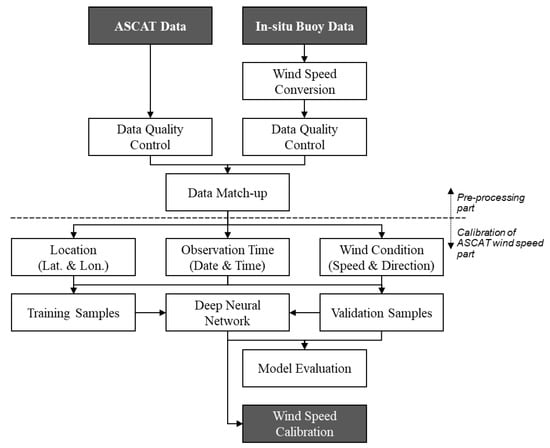
Figure 2.
Flowchart of deep learning approach to calibrate ASCAT-based wind speed estimates.
3.1. Pre-Processing
The data pre-processing procedure was performed to prepare collected data to be used as training and validation sets for the deep learning model. In this step, as in other studies, in-situ winds were converted to U10, which was provided in the same format as the ASCAT wind data [2,35,36,37]. The Liu–Katsaros–Businger (LKB) formula was applied to convert the buoy-level wind speed to U10 as follows [2,47,48]:
where was the equivalent neutral wind speed at the height of 10 m above the mean sea level, was the friction velocity (m/s), (= 0.4) was the von Karman constant, was the roughness length in neutral stratification (m), and was the reference height of 10 m [2,47,48,49].
In the QC process of the ASCAT and the buoy data, a standard deviation-based threshold was used to remove outliers. Unrealistic negative values were also removed. In addition, ASCAT wind speeds larger than 25 m/s were removed because that speed range of the ASCAT wind data could considerably decrease accuracy [35].
Prior to investigation and calibration of the ASCAT wind data using the deep learning approach, the ASCAT wind data were collocated with the buoy data in space and time. When ASCAT data-points were within 10 km of a buoy location and the time difference between the two observations was less than 15 min, the ASCAT and buoy data pairs were collocated. At this time, the biases were minimized by performing bilinear interpolation on the distance of the buoys position and the wind vector grid of the selected ASCAT. The buoy and the ASCAT data pairs were arranged in chronological order in a table of observation location (latitude and longitude), sensing time (date and time), and the buoy-based and ASCAT-based wind properties (wind speed and direction).
3.2. Calibration of ASCAT wind Speed Using DNN
The deep learning model used in this study is the Deep Neural Network (DNN) that performs training and predicts the results in the same way as multi-layer perceptron artificial neural networks (MLP-ANN). DNN composes one architecture by adding multiple hidden layers between the input layer and the output layer. The network becomes more complex and requires much more computation as the number of layers increases, but it is known to better explain the relationship between the input layer and the output layer. This approach has been successfully used to estimate and predict wind speed [41,42,43,44].
In addition to wind speed and direction, the location (latitude and longitude) and time (i.e., date and time in a day) were also used as inputs to the neural network. This is different from conventional linear regression methods, which have been applied for global open seas. They used only the satellite-based and the buoy-based wind speeds to obtain a linear fit between the two data sources.
In this study, it is assumed that the wind estimation error may vary depending on the observation location. In this context, errors are also possibly influenced by wind direction. The sensing date and time are assumed to represent seasonal or daily patterns of wind fields, which may contribute to the tendency of the error. Thus, observation location, wind direction, and sensing date and time are also used as input variables to find the best fit function between wind speeds of input and output targets.
All input and target data were normalized to a range of 0 to 1. The latitudinal range, 30~45 degrees North, and the longitudinal range, 115~140 degrees East, were linearly converted to a range of 0 to 1. Dates of observation were converted into days counted from 1 January the yearly first day (i.e., Day of Year) and divided by the maximum number of days per year (365 or 366). Time of observation was rounded to the nearest hour and divided by 24. Wind speeds were divided by 25 m/s, the upper bound of the ASCAT wind speed [35]. Wind directions were also transformed to a range from 0 to 1 by applying both cosine and sine functions.
The neural network was designed to encompass five hidden layers, in which 256, 128, 64, 32, and 16 nodes were selected from the first to the last hidden layer, respectively. The input layer comprised one to seven nodes (normalized ASCAT wind speed, two normalized wind directions using cosine and sine function, normalized date of observation, normalized time of observation, normalized latitude, and normalized longitude) according to test models. The output layer comprised one node, the calibrated wind speed. Rectified Linear Unit (ReLU) was selected as the activation function to improve the nonlinear properties of the network in input and hidden layers. Mean Squared Error (MSE) was used as the loss function. Through backpropagation, the gradient of the loss function was calculated by means of Stochastic Gradient Descent (SGD). Weights connecting nodes were updated in an iterative manner. As for hyper-parameters used in the model, the maximum epoch was set to be 300 with a batch size of 50 and a learning rate of 0.001.
The match-up database was divided into two sets: a training set and a validation set. The training set (80% of total data) was randomly sampled from the total data. It was used to generate the best fit function between wind speeds of inputs and those of output targets given in the training set. The trained model was tested and evaluated with the remaining validation set.
In order to evaluate the performance of the DNN, the two linear regression models and the Support Vector Regression (SVR) model suggested by Mohandes et al. [50] were adopted to compute their best fit functions between wind inputs and output targets. The best fit functions derived using the all test models were applied to the validation set. Performances of these approaches were compared with regard to wind speed and direction.
4. Results
4.1. Pre-Processing Results
Results of collocation of ASCAT and buoy data pairs in space and time are summarized in Table 2, showing numbers of selected data-points and the ratio of the matched to the initial buoy data at each buoy station. About 14,000 of the total 494,000 buoy observations were matched with ASCAT ones. These matched observations could explain the full data statistically, showing a margin of error of about 1.1% with a confidence level of 99% [51]. At locations of Buan, Ulsan, Uljin, and Incheon buoys, less than a thousand match-ups were identified because observation periods were slightly shorter than those of the other buoys as shown in Table 1. The overall matched ratio was 2.86%, ranging from 2.57% to 3.13% over all buoy locations. It shows that the data for any one particular buoy is not overly contained.

Table 2.
Collocation results of the buoy data.
4.2. Comparison of Results by the DNN-Based Model and Other Calibration Methods
The two linear regressions, SVM, and four DNN models were trained using the training set to obtain the best fit function, which was evaluated using the validation set. Buoy wind speeds () minus calibrated wind speeds () were used to prepare a histogram as shown in Figure 3d and summarized in Table 3. For comparison, results of the linear regression and the SVR method are also shown in Figure 3 and Table 3. Mean () and median () values of differences were closer to zero, meaning that ASCAT wind speed estimates were better calibrated. In addition, as the shape of the histogram distribution was more zero-centered with thinner width, the RMSE was smaller because the RMSE was computed as:
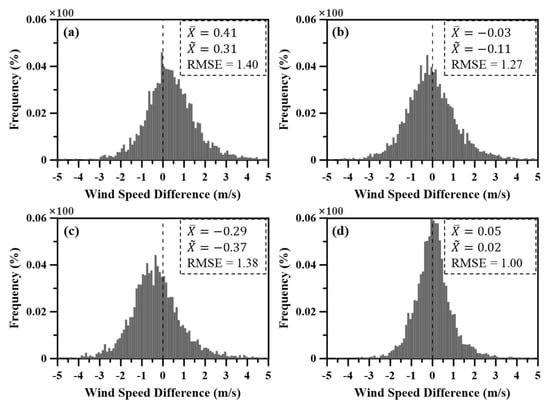
Figure 3.
Histogram of the wind speed difference between the ASCAT-based and the in-situ wind speeds computed from the validation set: (a) Before calibration, (b) by linear regression-2 model, (c) by SVR approach, and (d) by DNN-4 model approach.

Table 3.
Statistical analysis results of the outputs by the calibration method adopted in this study.
Figure 3a is a histogram of uncalibrated wind speed differences. The mean and the median values were positive at 0.41 and 0.31 m/s, respectively, and the RMSE was 1.40 m/s (Table 3). This meant that the uncalibrated level 2B ASCAT wind speeds were lower than the in-situ measurements. ASCAT wind speeds calibrated with DNN model-4 resulted in an approximately 10-fold reduction in the bias, a 40% reduction in the RMSE and an 80% increase in kurtosis (Figure 3 and Table 3).
The two linear regression methods improved the mean and median values. This considerably reduced the bias. However, the RMSEs were only marginally reduced compared with uncalibrated wind speeds (Figure 3a,b). The SVR approach showed virtually no improvement when compared with uncalibrated winds.
Table 3 shows the results of the four DNN methods tested to investigate the effects of input variable conditions on results. In all DNN models, the biases of the mean and median were reduced. Among them, the model in which both statistical values were close to 0 was the DNN-4 model. Their RMSEs were also closer to zero than those of the linear models and the SVR method.
Overall, the results of these comparisons revealed that the condition with all input variables combined in the DNN training produced the best outputs. The DNN-4 model, which considered all input factors, showed the best performance among all approaches.
4.3. Consistency of DNN-Based Calibration Results
A scatter plot of data pairs of calibrated ASCAT wind speeds and buoy wind speeds is shown in Figure 4a. Post-calibration ASCAT wind speeds via linear regression-2 and DNN-4 models were also compared (Figure 4b,c). The results of comparison between these two datasets for evaluating the quality of ASCAT wind speed estimates before and after calibration revealed a linear function as shown below:
where and were ASCAT and buoy wind speeds, respectively, and a and b were underdetermined coefficients of the linear function used to represent the relationship between them. Coefficients of determination of the linear function and statistical indicators from these comparisons are also given in Figure 4.
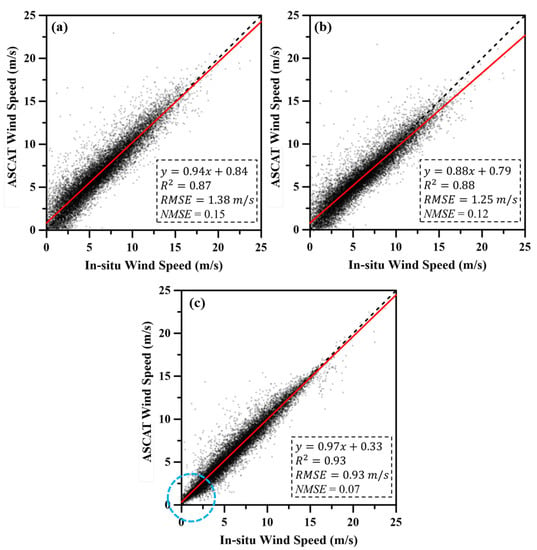
Figure 4.
Scatter plot for comparison between ASCAT-based and in-situ measured wind speeds: (a) before calibration, (b) after linear regression-2 model-based calibration, and (c) after DNN-4 model-based calibration.
Before calibration, the linear function showed a = 0.94, b = 0.84, RMSE = 1.38 m/s and Normalized Mean Square Error (NMSE) = 0.15, which contributed to a bias of prior-calibration ASCAT wind speeds as shown in Figure 4a. The linear regression-2 model slightly improved R-square, RMSE and NMSE, but the effect was not significant (Figure 4b). After calibration using the DNN-4 model, the slope (i.e., a) of the linear function was improved from 0.94 to 0.97 along with the y-intercept, b changed from 0.84 to 0.33 and the R-square increased from 0.87 to 0.93. In particular the RMSE and NMSE were significantly improved from 1.38 to 0.93 m/s and from 0.15 to 0.07, respectively. Much of the improvement was made when the wind speed was low (<5 m/s). These results indicated that ASCAT wind speeds were calibrated to agree more closely with buoy wind speeds (Figure 4c).
To investigate the consistency of DNN-4 model-based calibration results over study areas, outputs from the training set and the validation set were statistically analyzed all together with regard to observation location, wind direction, and wind speed, with results presented in Figure 5, Figure 6 and Figure 7, respectively.
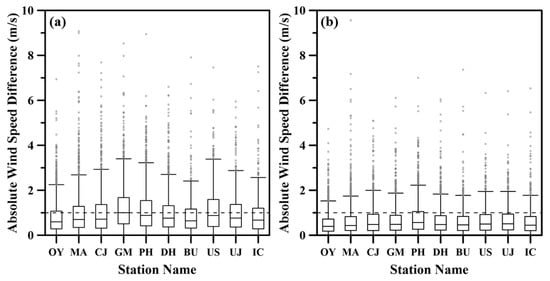
Figure 5.
Statistical indications (i.e., the median, the first and third quartiles, the minimum and maximum bounds excluding outliers) of the absolute wind speed differences between the ASCAT and the buoy wind speeds at each buoy location (a) before calibration and (b) after DNN-4 model-based calibration.
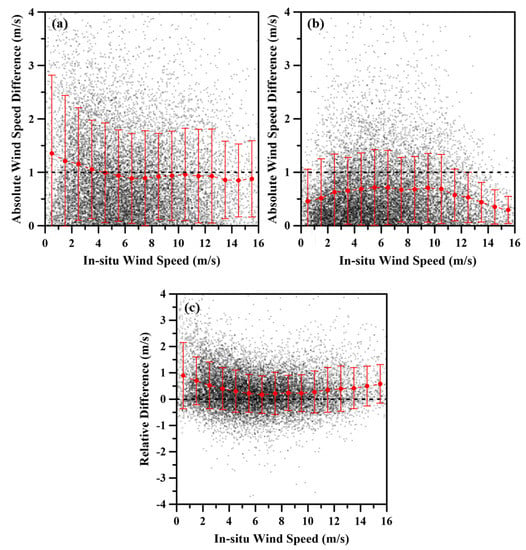
Figure 6.
Statistical indications (i.e., the mean and the standard deviation) of absolute wind speed differences between the ASCAT and buoy wind speeds over the wind speed range of interest (a) before calibration, (b) after DNN-4 model-based calibration and (c) relative difference between before and after calibration.
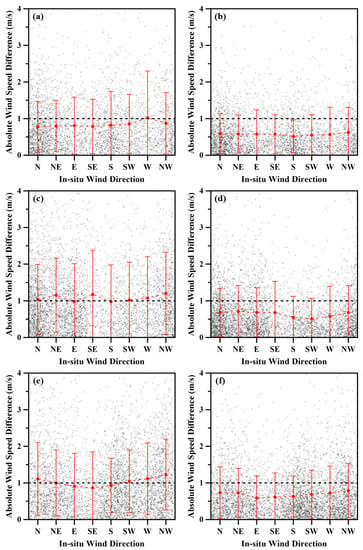
Figure 7.
Statistical indications (i.e., the mean and the standard deviation) of absolute wind speed differences between ASCAT and the buoy wind speeds over all wind directions (a,b) before and after calibration in Yellow sea (c,d) before and after calibration in Korean Strait (e,f) before and after calibration in East sea.
Deviations of absolute wind speed differences (i.e., absolute biases) at observation locations were evaluated. Results are presented in Figure 5 using a type of box plot with indications of the median, the first and third quartiles, and the minimum and maximum bounds excluding outliers. Before calibration, deviations of the speed difference were not consistent. They largely varied depending on the observation location (Figure 5a). Qualitatively, the median and the upper quartile values of the speed difference ranged from about 0.5 to 1.0 m/s and from about 1.1 to 1.7 m/s, respectively. In cases of Geomundo (GM), Pohang (PH), and Ulsan (US), located in the southeast part of South Korea, it was notable that statistical indicators were more deviated compared to those of other locations. After calibration, deviations of speed differences were reduced to be consistent over all observation locations (Figure 5b). The median and the upper quartile values of the speed difference were improved to encompass ranges of about 0.4~0.6 m/s and about 0.7~1.1 m/s, respectively. The results of such comparative analysis between observation locations revealed that the DNN method could calibrate ASCAT wind speeds more evenly and more accurately by reflecting local characteristics well.
Next, to look into distribution of absolute wind speed differences over the wind speed range of interest, speed differences were calculated in bins of wind speeds of 1 m/s. Results are presented in Figure 6 and Table 4. Red dots and error bars in the graph denote mean and standard deviation of speed differences in each bin. At this time, wind speeds higher than 16 m/s were excluded from the analysis because the number of samples was less than 50. Before calibration, the mean of speed differences was evenly distributed at around 1 m/s, tending to increase at low wind speeds (less than 4 m/s) (Figure 6a). After calibration, these speed differences were largely reduced over the full speed range of interest (less than about 0.7 m/s). In particular, bins of low wind speed (less than 4 m/s) and high wind speed (11 m/s) were greatly improved with much lower mean and standard deviation values, as shown in Figure 6b. It is known that ASCAT wind speeds tend to have larger errors in lower and higher wind speeds [36,37]. However, this problem was solved using the DNN method in this study. Nevertheless, the calibration was insufficient for the wind speed of 4–11 m/s, which is thought to be due to some overestimated results during the calibration process (Figure 6c).

Table 4.
The mean and standard deviation of wind speed differences (△WS) at each 1 m/s bin.
To analyze absolute wind speed differences from the aspect of wind direction, speed differences were calculated in bins of wind directions of 45 degrees (Figure 7 and Table 5). The results were analyzed by dividing each of the ten buoys into three marginal seas. The three buoys located in the Yellow Sea (Incheon, Oeyeondo, and Buan) displayed a small difference and standard deviation compared to other sea areas even before the calibration, except for the W direction. In the buoys in the Korean Strait (Chujado, Marado, and Geomundo), both difference and standard deviation were found to be larger than those in the other two seas. As a result of the buoy located in the East Sea (Donghae, Uljin, Pohang, and Ulsan), the E direction wind from the sea showed the smallest difference. All three marginal seas showed a large difference when the wind was westerly. The large difference in the other directions in the Korean Strait Sea and East Sea is probably due to the influence of typhoons or strong northeasterly winds in winter. After calibration, the mean and standard deviation of speed differences were remarkably reduced to between 0.6 and 0.8 m/s in all wind directions.

Table 5.
The mean and standard deviation of wind speed differences (△WS) at each wind direction bin.
To analyze the performance of the DNN model on seasonal variability, the time series bias was expressed over all observation periods. Figure 8 shows the data analyzed in Figure 4 as a time series, and Figure 9 is a monthly boxplot to quantitatively analyze seasonal variability. As can be seen from Figure 8a and Figure 9a, the difference carries seasonal characteristics. The ASCAT-based wind speed tends to overestimate the buoy wind speed in winter, repeating every year. This seasonal variability still remains, even when the linear regression model with date factor as input variables was applied (Figure 8b and Figure 9b). However, the seasonal dependence was eliminated using the DNN method in this study, because the DNN network succeeded in inferring the complex relationship between the input variables and the buoy wind speeds (Figure 8c and Figure 9c). The median value of wind speed differences in all months converges to zero.
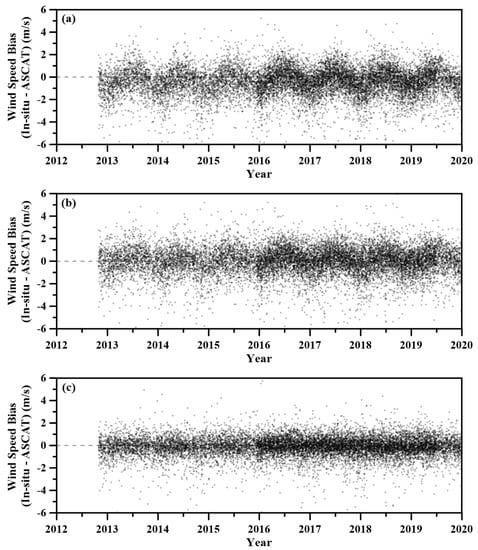
Figure 8.
Seasonal variability of wind speed differences between ASCAT and the buoy wind speeds over observation period (a) before calibration (b) after linear regression-2 model-based calibration (c) after DNN-4 model-based calibration.
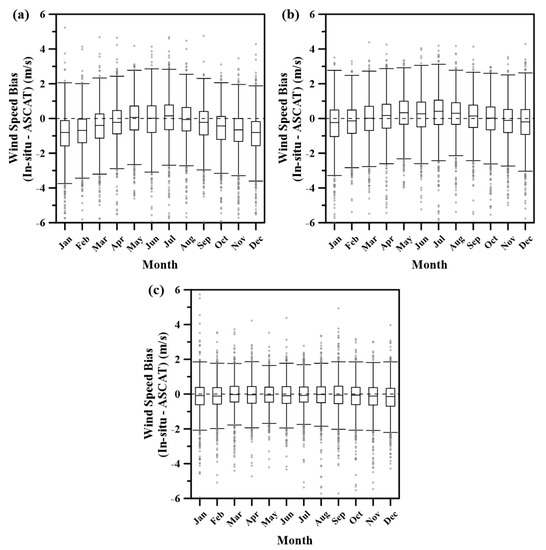
Figure 9.
Monthly box-plot to quantitatively represent seasonal variability of wind speed differences between ASCAT and the buoy wind speeds over observation period (a) before calibration (b) after linear regression-2 model-based calibration (c) after DNN-4 model-based calibration.
5. Discussion
In this study, ASCAT-based wind data of the provider level were compared to in-situ measurements around Korea. It was found that the average RMSE was 1.38 m/s (Figure 4). It was also found that the quality of the ASCAT wind speed estimates showed large fluctuations in three marginal seas around the Korean peninsula depending on the observation location (Figure 5), wind speed (Figure 6), and wind direction (Figure 7). To better calibrate ASCAT wind speeds (so that the accuracy of ASCAT wind speeds could be improved) known to be influenced by local geographic and climatologic factors, this study proposed a DNN-based calibration method using multiple input factors, unlike traditional linear regression methods [2,35,36,37,38,39,40]. The ASCAT wind data were calibrated using the DNN method by considering wind direction, observation location, and sensing date and time as input variables to agree well with in-situ measurements (Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9).
This was more effective than the previously performed method using linear regression [2,35,36,37,38,39,40]. As a result of analyzing the bias trend before calibration through Figure 5, Figure 6, Figure 7 and Figure 8, it is expected that it will be difficult to design a multiple regression analysis that reflects this trend well. In particular, ASCAT-based wind speed was confirmed to show seasonal variability, and multicollinearity between variables was also expected. In this situation, the DNN model that constructs complex networks of each variable-hidden layer-true value and learns weights repeatedly was effective.
The most significant improvement after applying the proposed method was observed for ranges of low wind speed (<5 m/s) and high wind speed (>11 m/s). Accurate monitoring is required for both wind ranges in terms of coastal disaster management. The low wind speed is related to the occurrence of sea fog in South Korea [52]. In addition, high wind speeds can cause high waves that can cause severe damage to coastal areas [53,54]. Accurate observation can promote prediction of threats by sea fog and high waves. Thus, the results of this study are meaningful from this perspective, as mentioned in the introduction.
The DNN-based best fit calibration model proposed in this study can be applied to the whole swath of ASCAT observations. Figure 10 shows an example of application of the proposed approach for calibrating ASCAT wind speeds over two side swaths of a path. Wind data were captured at 12:00 PM (local Korean time) on 19 January 2016 when a large wave event occurred in winter. The maximum wave height was 6.5 m. As shown in Figure 10a,b, wind speeds larger than 15 m/s were developed across South Korea in the NW–SE direction.
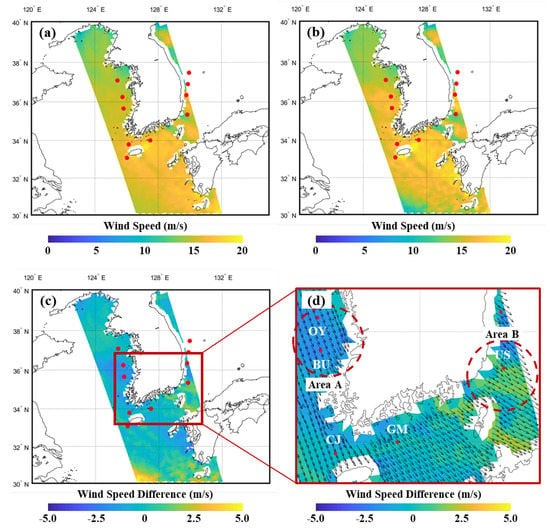
Figure 10.
DNN model application result for ASCAT swath at 12:00 on 19 January 2016 (UTC): (a) Before application, (b) After application, (c) Difference between before and after application, and (d) Zoomed area of the red box in (c).
After the calibration model was applied, winds around Oeyendo (OY) and Buan (BU) in the Yellow Sea became stronger. The negative value meant that the wind speed after calibration was larger (area A denoted in Figure 10d). There was not much difference found between the locations of Chujado (CJ) and Geomundo (GM), located in the Korean Strait of Korea. In contrast, winds around Ulsan (US) located in the East Sea of Korea were adjusted to be weaker (area B denoted in Figure 10d). These results indicate that the proposed method can incorporate these regional characteristics in the best fit model and consequently adjust this wind to be weaker. The positive value means that the wind speed after calibration is smaller. The RMSE calculated by comparison of the ASCAT wind data and the in-situ measurements was improved from 2.66 m/s to 1.74 m/s on average after calibration. As for the area around Oyeondo and Buan, the wind speed difference was improved from 1.60 to 1.00 m/s. As for Ulsan, the speed difference was remarkably reduced from 2.08 to 0.44 m/s. These results confirmed that the DNN-based calibration model could improve the quality of ASCAT wind estimates evenly over the study area by compensating for regionally signified atmospheric characteristics.
The study results effectively proved that a DNN model using the observation position of ASCAT, sensing time, wind speed and direction as input variables is useful for improving its wind speed estimation performance. The scatterometer measures the backscatter coefficient, and the surface wind vector can be determined using a geophysical model function (GMF) and measured backscatter coefficient. In this process, if any external factors other than wind affect the surface roughness of the sea surface, the wind may be incorrectly estimated from the disturbed backscattering coefficient. The surfactants in the water due to near shore biological processes, the relationship between sea state and surface friction, neutral stability of the atmosphere, air temperature, and depth of shallow water may affect surface roughness. In future, it is necessary to study comparative analysis with numerical wind model results, such as the European Centre for Medium-Range Weather Forecasts re-analysis v5 (ERA5), and a fundamental consideration of the causes of wind estimation errors.
6. Conclusions
Sea wind is one of key forces that cause coastal disasters by inducing large waves, storm surges, coastal currents, heavy sea-fog events, and so on. Observation of sea winds with a wide coverage and high accuracy by using wind data for numerical predictions or statistical analysis of a long-term database is becoming essential to prevent coastal disasters. Satellite-based observation has been developed to observe global sea surface winds continuously for a long time at a low cost. Typically, satellite-mounted scatterometer is used to measure both sea wind speed and direction.
The results of this study suggested that ASCAT-based wind estimates could be used for coastal disaster management purposes, such as predictions of coastal waves and sea-fog events. These ASCAT-based wind data were calibrated using in-situ measurements in global open seas. The linear regression method conventionally adopted for calibrating the remotely-sensed wind data caused deviations and biases to remain unresolved to some extent. Besides, earlier studies have reported that ASCAT-based wind observations tend to display larger deviations for lower (i.e., <5 m/s) and higher (i.e., >11 m/s) wind speeds. In order to use ASCAT-based wind observation more usefully, it is necessary to improve the observation reliability to the level of in-situ measurements.
For these reasons, a deep neural network (DNN) model was applied in this study to better calibrate ASCAT-based wind speeds in marginal seas around Korea by considering multiple coastal factors that might affect sea wind fields. The wind database collected during a period from 2012 to 2019 by the MetOp-B ASCAT and in-situ sensors at 10 buoy stations in Korean seas were collocated and separated into a training set (80%) and a validation set (20%) for the deep learning-based approach. ASCAT wind data were used as inputs for training the DNN model while in-situ measured data were used as output targets. As for input variables, observation locations, sensing time, wind speed, and wind direction were used to reflect local climate characteristics.
As a result, the bias between ASCAT-based and in-situ wind speeds was decreased from 0.41 to 0.05 m/s on average for all buoy locations. In addition, the RMSE of wind speed was reduced from 1.38 m/s (before calibration) to 0.93 m/s. Moreover, the speed difference between the two datasets was considerably improved for low wind speeds (below 4 m/s) and high wind speeds (above 11 m/s). It was also found that the DNN-based calibration model improved the quality of ASCAT wind estimates evenly over study areas by properly compensating for those coastal atmospheric characteristics causing the errors to be larger.
In conclusion, the proposed method was effective in calibrating ASCAT-based wind speeds in marginal seas by considering local impact factors. It improved the accuracy for low and high wind speeds. In addition, the proposed approach can be more reliable through training with more evenly-spaced and long-term in-situ measurements. This study also indicates that improved ASCAT wind speeds can be used for more accurate prediction and assessment of coastal disasters such as wind impact on waves, coastal storm surge, sea-fog hazard, and maritime management of marginal seas around Korea.
Author Contributions
Conceptualization, S.-H.P. and J.Y.; Methodology, S.-H.P. and J.Y.; Validation, D.S. and J.K.; Formal analysis, S.-H.P. and J.Y.; Investigation, S.-H.P.; Writing—original draft preparation; S.-H.P. and H.-S.J.; Writing—review and editing, J.Y. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by KIOST(PE99942) and the project “Establishment of the ocean research station in the jurisdiction zone and convergence research” funded by the Ministry of Oceans and Fisheries, Korea.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: https://podaac-opendap.jpl.nasa.gov/opendap/allData/ascat/preview/L2/metop_b/25km/.
Acknowledgments
We would like to thank Won-Kyung Baek.
Conflicts of Interest
The authors have no conflict of interest relevant to this study to disclose.
References
- Jang, J.C.; Park, K.A.; Yang, D. Validation of Sea Surface Wind Estimated from KOMPSAT-5 Backscattering Coefficient Data. Korean J. Remote Sens. 2018, 34, 1383–1398. [Google Scholar]
- Son, D.; Jun, K.; Shim, J.S.; Kown, J.I.; Yoo, J. Validation of MetOp-B and Jason-2 Sea Surface Wind Data around the Korean Peninsula. Korea Soc. Coast. Disaster Prev. 2020, 7, 233–241. [Google Scholar] [CrossRef]
- Janssen, P.A.E.M. Quasi-Linear Theory of Wind-Wave Generation Applied to Wave Forecasting. J. Phys. Oceanogr. 1991, 21, 1631–1642. [Google Scholar] [CrossRef]
- Kara, A.B.; Metzger, E.J.; Bourassa, M.A. Ocean current and wave effects on wind stress drag coefficient over the global ocean. Geophys. Res. Lett. 2007, 34, 1–4. [Google Scholar] [CrossRef]
- Brostrom, G. On the influence of large wind farms on the upper ocean circulation. J. Mar. Syst. 2008, 74, 585–591. [Google Scholar] [CrossRef]
- Debernard, J.B.; Roed, L.P. Future wind, wave and storm surge climate in the Northern Seas: A revisit. Tellus A Dyn. Meteorol. Oceanogr. 2008, 60, 427–438. [Google Scholar] [CrossRef]
- Lee, C.M.; Orlic, M.; Poulain, P.M.; Cushman-Roisin, B. Introduction to special section: Recent advances in oceanography and marine meteorology of the Adriatic Sea. J. Geophys. Res. Ocean 2007, 112, 1–3. [Google Scholar] [CrossRef]
- Chelton, D.B.; Freilich, M.H.; Sienkiewicz, J.M.; Von Ahn, J.M. On the use of QuikSCAT scatterometer measurements of surface winds for marine weather prediction. Mon. Weather Rev. 2006, 134, 2055–2071. [Google Scholar] [CrossRef]
- Atlas, R.; Hoffman, R.N.; Leidner, S.M.; Sienkiewicz, J.; Yu, T.W.; Bloom, S.C.; Brin, E.; Ardizzone, J.; Terry, J.; Bungato, D.; et al. The effects of marine winds from scatterometer data on weather analysis and forecasting. Bull. Am. Meteorol. Soc. 2001, 82, 1965–1990. [Google Scholar] [CrossRef]
- Cavaleri, L.; Barbariol, F.; Benetazzo, A. Wind-Wave Modeling: Where We Are, Where to Go. J. Mar. Sci. Eng. 2020, 8, 260. [Google Scholar] [CrossRef]
- Ruiz-Salcines, P.; Salles, P.; Robles-Diaz, L.; Diaz-Hernandez, G.; Torres-Freyermuth, A.; Appendini, C.M. On the Use of Parametric Wind Models for Wind Wave Modeling under Tropical Cyclones. Water 2019, 11, 2044. [Google Scholar] [CrossRef]
- Choo, T.H.; Kim, Y.S.; Sim, S.B.; Son, J.K. Development of the Wind Wave Damage Predicting Functions in southern sea based on Annual Disaster Reports. J. Korea Acad. Ind. Coop. Soc. 2018, 19, 668–675. [Google Scholar]
- Zheng, C.W.; Li, C.Y.; Pan, J.; Liu, M.Y.; Xia, L.L. An overview of global ocean wind energy resource evaluations. Renew. Sustain. Energy Rev. 2016, 53, 1240–1251. [Google Scholar] [CrossRef]
- Li, J.; Wang, D.X.; Chen, J.; Yang, L. Comparison of remote sensing data with in-situ wind observation during the development of the South China Sea monsoon. Chin. J. Oceanol. Limnol. 2012, 30, 933–943. [Google Scholar] [CrossRef]
- Rashmi, R.; Aboobacker, V.M.; Vethamony, P.; John, M.P. Co-existence of wind seas and swells along the west coast of India during non-monsoon season. Ocean Sci. 2013, 9, 281–292. [Google Scholar] [CrossRef]
- Pickett, M.H.; Tang, W.Q.; Rosenfeld, L.K.; Wash, C.H. QuikSCAT satellite comparisons with nearshore buoy wind data off the US West Coast. J. Atmos. Ocean. Technol. 2003, 20, 1869–1879. [Google Scholar] [CrossRef]
- Hwang, P.A.; Teague, W.J.; Jacobs, G.A.; Wang, D.W. A statistical comparison of wind speed, wave height, and wave period derived from satellite altimeters and ocean buoys in the Gulf of Mexico region. J. Geophys. Res. Ocean 1998, 103, 10451–10468. [Google Scholar] [CrossRef]
- Kumar, S.V.V.A.; Nagababu, G.; Kumar, R. Comparative study of offshore winds and wind energy production derived from multiple scatterometers and met buoys. Energy 2019, 185, 599–611. [Google Scholar] [CrossRef]
- Ebuchi, N.; Graber, H.C.; Caruso, M.J. Evaluation of wind vectors observed by QuikSCAT/SeaWinds using ocean buoy data. J. Atmos. Ocean. Technol. 2002, 19, 2049–2062. [Google Scholar] [CrossRef]
- Satheesan, K.; Sarkar, A.; Parekh, A.; Kumar, M.R.R.; Kuroda, Y. Comparison of wind data from QuikSCAT and buoys in the Indian Ocean. Int. J. Remote Sens. 2007, 28, 2375–2382. [Google Scholar] [CrossRef]
- Carvalho, D.; Rocha, A.; Gomez-Gesteira, M.; Santos, C.S. Comparison of reanalyzed, analyzed, satellite-retrieved and NWP modelled winds with buoy data along the Iberian Peninsula coast. Remote Sens. Environ. 2014, 152, 480–492. [Google Scholar] [CrossRef]
- Gower, J.F.R. Intercalibration of wave and wind data from TOPEX POSEIDON and moored buoys off the west coast of Canada. J. Geophys. Res. Ocean 1996, 101, 3817–3829. [Google Scholar] [CrossRef]
- Jones, W.L.; Schroeder, L.C.; Boggs, D.H.; Bracalente, E.M.; Brown, R.A.; Dome, G.J.; Pierson, W.J.; Wentz, F.J. The SEASAT-A satellite scatterometer: The geophysical evaluation of remotely sensed wind vectors over the ocean. J. Geophys. Res. 1982, 87, 3297–3317. [Google Scholar] [CrossRef]
- Yang, J.G.; Zhang, J. Comparison of Oceansat-2 Scatterometer Wind Data with Global Moored Buoys and ASCAT Observation. Adv. Meteorol. 2019, 2019, 1651267. [Google Scholar] [CrossRef]
- Yang, X.F.; Li, X.F.; Pichel, W.G.; Li, Z.W. Comparison of Ocean Surface Winds From ENVISAT ASAR, MetOp ASCAT Scatterometer, Buoy Measurements, and NOGAPS Model. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4743–4750. [Google Scholar] [CrossRef]
- Sharoni, S.M.H.; Reba, M.N.M.; Hossain, M.S. Tropical Cyclone Wind Speed Estimation From Satellite Altimeter-Derived Ocean Parameters. J. Geophys. Res. Ocean 2021, 126, e2020JC016988. [Google Scholar] [CrossRef]
- Wang, Z.X.; Stoffelen, A.; Zou, J.H.; Lin, W.M.; Verhoef, A.; Zhang, Y.; He, Y.J.; Lin, M.S. Validation of New Sea Surface Wind Products From Scatterometers Onboard the HY-2B and MetOp-C Satellites. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4387–4394. [Google Scholar] [CrossRef]
- Witter, D.L.; Chelton, D.B. A Geosat Altimeter Wind-Speed Algorithm and a Method for Altimeter Wind-Speed Algorithm Development. J. Geophys. Res. Ocean 1991, 96, 8853–8860. [Google Scholar] [CrossRef]
- Horstmann, J.; Schiller, H.; Schulz-Stellenfleth, J.; Lehner, S. Global wind speed retrieval from SAR. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2277–2286. [Google Scholar] [CrossRef]
- Ménard, Y.; Fu, L.-L.; Escudier, P.; Parisot, F.; Perbos, J.; Vincent, P.; Desai, S.; Haines, B.; Kunstmann, G. The Jason-1 Mission Special Issue: Jason-1 Calibration/Validation. Mar. Geod. 2003, 26, 131–146. [Google Scholar] [CrossRef]
- Abdalla, S.; Janssen, P.A.E.M.; Bidlot, J.R. Jason-2 OGDR Wind and Wave Products: Monitoring, Validation and Assimilation. Mar. Geod. 2010, 33, 239–255. [Google Scholar] [CrossRef]
- Yang, J.G.; Zhang, J.; Jia, Y.J.; Fan, C.Q.; Cui, W. Validation of Sentinel-3A/3B and Jason-3 Altimeter Wind Speeds and Significant Wave Heights Using Buoy and ASCAT Data. Remote Sens. 2020, 12, 2079. [Google Scholar] [CrossRef]
- Horstmann, J.; Koch, W.; Lehner, S. Ocean wind fields retrieved from the advanced synthetic aperture radar aboard ENVISAT. Ocean. Dyn. 2004, 54, 570–576. [Google Scholar] [CrossRef]
- Park, J.; Kim, D.W.; Jo, Y.H.; Kim, D. Accuracy Evaluation of Daily-gridded ASCAT Satellite Data Around the Korean Peninsula. Korean J. Remote Sens. 2018, 34, 213–225. [Google Scholar]
- Verhoef, A.; Portabella, M.; Stoffelen, A. High-Resolution ASCAT Scatterometer Winds Near the Coast. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2481–2487. [Google Scholar] [CrossRef]
- Bentamy, A.; Croize-Fillon, D.; Perigaud, C. Characterization of ASCAT measurements based on buoy and QuikSCAT wind vector observations. Ocean Sci. 2008, 4, 265–274. [Google Scholar] [CrossRef]
- Ribal, A.; Young, I.R. Calibration and Cross Validation of Global Ocean Wind Speed Based on Scatterometer Observations. J. Atmos. Ocean. Technol. 2020, 37, 279–297. [Google Scholar] [CrossRef]
- Bentamy, A.; Fillon, D.C. Gridded surface wind fields from Metop/ASCAT measurements. Int. J. Remote Sens. 2012, 33, 1729–1754. [Google Scholar] [CrossRef]
- Jeong, J.Y.; Shim, J.S.; Lee, D.K.; Min, I.K.; Kwon, J.I. Validation of QuikSCAT Wind with Resolution of 12.5 km in the Vicinity of Korean Peninsula. Ocean Polar Res. 2008, 30, 47–58. [Google Scholar] [CrossRef][Green Version]
- Kim, D.W.; Byun, H.R. Spatial and temporal distribution of wind resources over Korea. Atmosphere 2008, 18, 171–182. [Google Scholar]
- Kalra, R.; Deo, M.C. Derivation of coastal wind and wave parameters from offshore measurements of TOPEX satellite using ANN. Coast. Eng. 2007, 54, 187–196. [Google Scholar] [CrossRef]
- Huang, C.J.; Kuo, P.H. A Short-Term Wind Speed Forecasting Model by Using Artificial Neural Networks with Stochastic Optimization for Renewable Energy Systems. Energies 2018, 11, 2777. [Google Scholar] [CrossRef]
- Liu, Y.X.; Collett, I.; Morton, Y.J. Application of Neural Network to GNSS-R Wind Speed Retrieval. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9756–9766. [Google Scholar] [CrossRef]
- Duan, J.K.; Zuo, H.C.; Bai, Y.L.; Duan, J.Z.; Chang, M.H.; Chen, B.L. Short-term wind speed forecasting using recurrent neural networks with error correction. Energy 2021, 217, 119397. [Google Scholar] [CrossRef]
- Kim, M.K.; Kim, Y.H.; Lee, W.S. Seasonal prediction of Korean regional climate from preceding large-scale climate indices. Int. J. Climatol. 2007, 27, 925–934. [Google Scholar] [CrossRef]
- Figa-Saldana, J.; Wilson, J.J.W.; Attema, E.; Gelsthorpe, R.; Drinkwater, M.R.; Stoffelen, A. The advanced scatterometer (ASCAT) on the meteorological operational (MetOp) platform: A follow on for European wind scatterometers. Can. J. Remote Sens. 2002, 28, 404–412. [Google Scholar] [CrossRef]
- Fairall, C.W.; Bradley, E.F.; Hare, J.E.; Grachev, A.A.; Edson, J.B. Bulk parameterization of air-sea fluxes: Updates and verification for the COARE algorithm. J. Clim. 2003, 16, 571–591. [Google Scholar] [CrossRef]
- Smith, S.D. Coefficients for Sea-Surface Wind Stress, Heat-Flux, and Wind Profiles as a Function of Wind-Speed and Temperature. J. Geophys. Res. Ocean 1988, 93, 15467–15472. [Google Scholar] [CrossRef]
- Byun, D.S.; Kim, H.; Lee, J.; Lee, E.; Park, K.A.; Woo, H.J. Converting Ieodo ocean research station wind speed observations to reference height data for real-time operational use. J. Koream Soc. Ocean. 2018, 23, 153–178. [Google Scholar]
- Mohandes, M.A.; Halawani, T.O.; Rehman, S.; Hussain, A.A. Support vector machines for wind speed prediction. Energy 2004, 29, 939–947. [Google Scholar] [CrossRef]
- Serdar, C.C.; Cihan, M.; Yücel, D.; Serdar, M.A. Sample size, power and effect size revisited: Simplified and practical approaches in pre-clinical, clinical and laboratory studies. Biochem. Med. 2021, 31, 010502. [Google Scholar] [CrossRef] [PubMed]
- Choo, T.H.; Kwak, K.S.; Ahn, S.H.; Yamg, D.U.; Son, J.K. Development for the function of Wind wave Damage Estimation at the Western Coastal Zone based on Disaster Statistics. J. Korea Acad. Ind. Coop. Soc. 2017, 18, 14–22. [Google Scholar]
- Choo, Y.M.; Chun, K.H.; Jeon, H.S.; Sim, S.B. A Predictive Model for Estimating Damage from Wind Waves during Coastal Storms. Water 2021, 13, 1322. [Google Scholar] [CrossRef]
- Kim, C.K.; Yum, S.S. Local meteorological and synoptic characteristics of fogs formed over Incheon international airport in the west coast of Korea. Adv. Atmos. Sci. 2010, 27, 761–776. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).