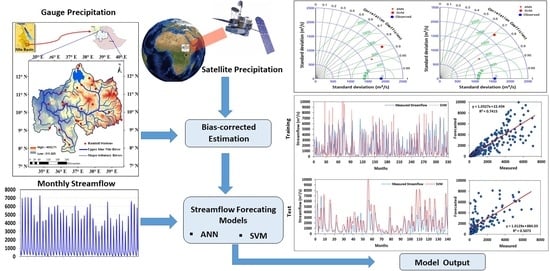
Remote-Sensing-Based Streamflow Forecasting Using Artificial Neural Network and Support Vector Machine Models
Abstract
:1. Introduction
2. Materials and Methods
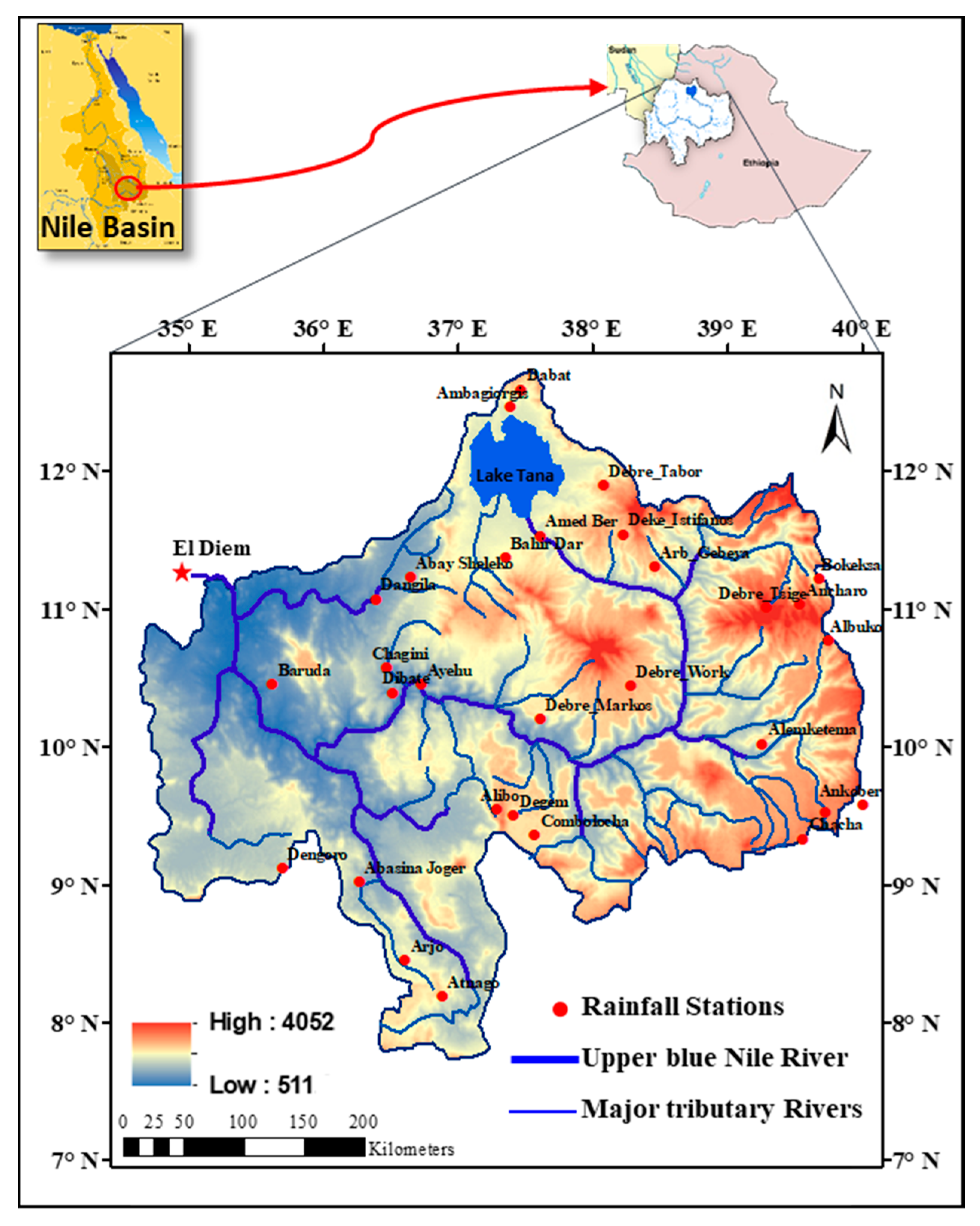
2.1. Case Study
2.2. Data Collection
2.2.1. Ground Data
2.2.2. Gridded Precipitation Datasets
CHIRPS Dataset
TRMM-3B42V7 Dataset
RFE 2.0 Dataset
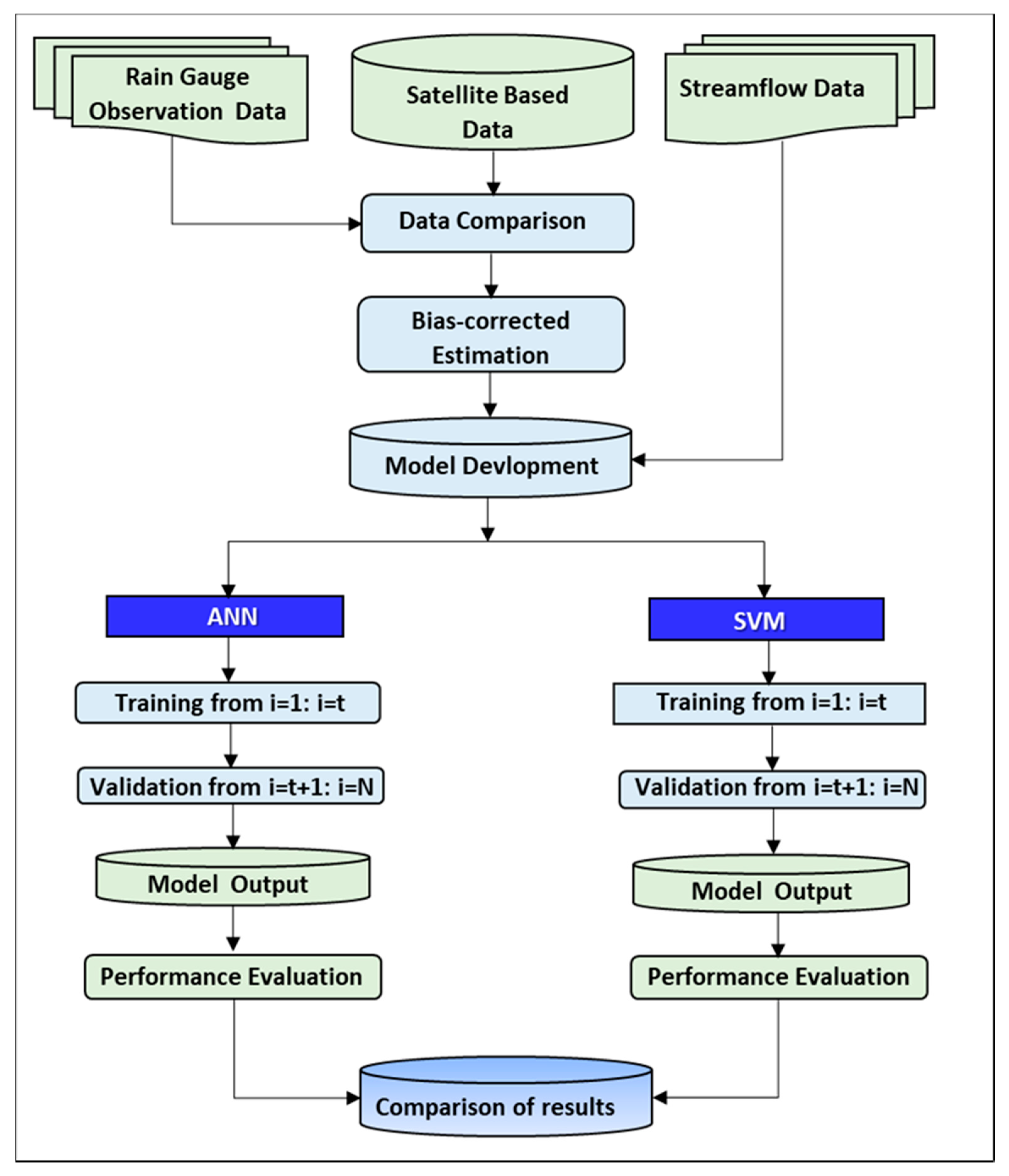
2.3. Methodology
2.3.1. Performance Evaluation of Precipitation Datasets
2.3.2. Forecasting Models
Support Vector Machine (SVM) Model
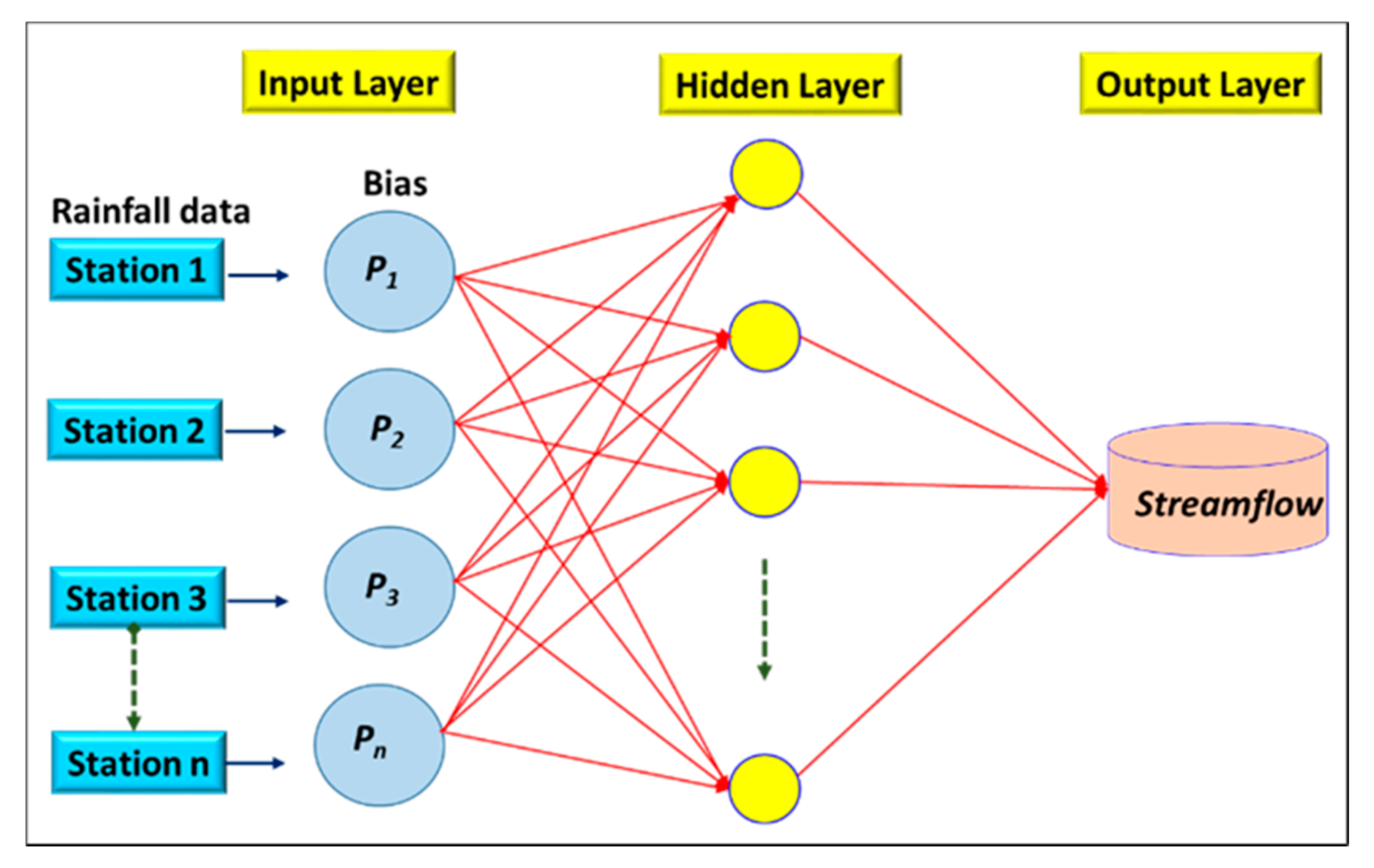
Artificial Neural Network (ANN)
2.3.3. Model Performance Measures
- Nash–Sutcliffe efficiency coefficient (NSE) [47], expressed as:
- Mean absolute error (MAE), expressed as:
- Root mean square error (RMSE), expressed as:
- The absolute variance fraction, R2, is calculated as follows:where Qo is the observed streamflow, Qf is the predicted streamflow, is the average of the observed streamflow, and n is the total amount of data.
2.4. Design of Experiments for Streamflow Simulation
- ▪
- First of all, the analysis evaluated the quality of the investigated precipitation products against the observed rain gauge dataset at a monthly scale using visual inspection and statistical methods (Equations (1)–(10)).
- ▪
- A linear scaling method was then applied for the purpose of bias correction. The goal of this method was to precisely match the monthly mean of corrected estimations with that of observed estimations, assuming that the rain gauge records were the true observations and the satellite estimations (TRMM-3B42 V7, RFE 2.0 and CHIRPS) were the biased estimation.
- ▪
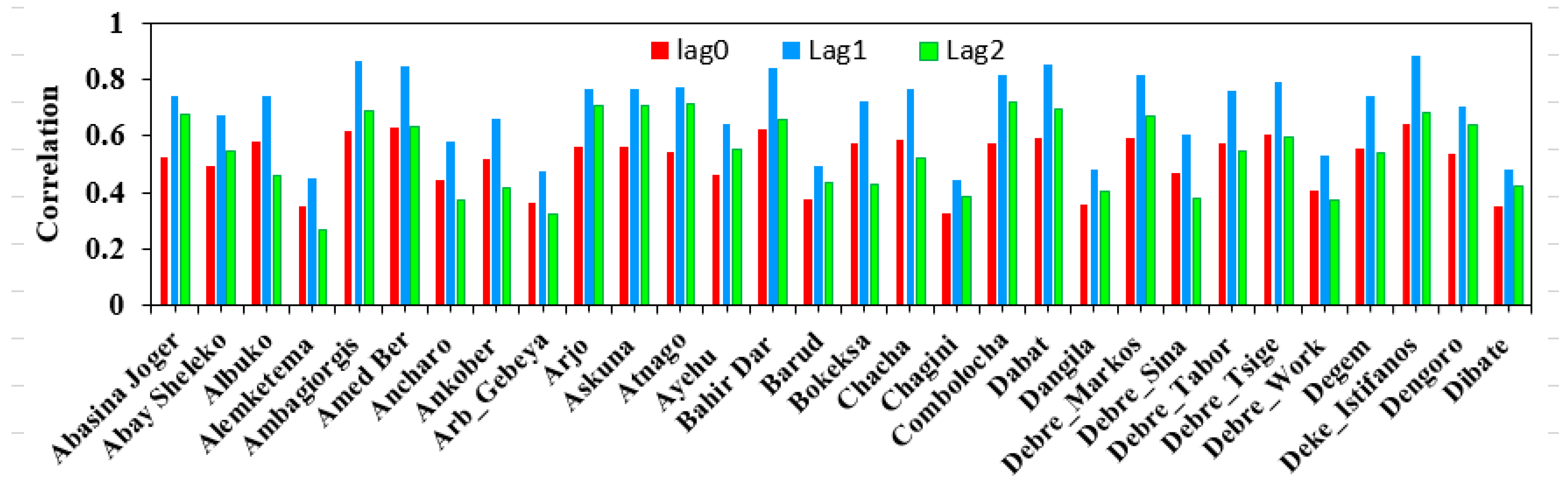
- To check for the presence of correlation between monthly precipitation products and the monthly streamflow, the Pearson’s coefficient was calculated to ascertain the existence of statistically significant correlations.
- ▪
- The forecasting model (either SVM or ANN) and, consequently, the required precipitation and streamflow input data were then selected.
- ▪
- The input datasets were split into two sets, namely training (70% of the data) and testing datasets (30% of the data).
- ▪
- The process of model training was then performed to obtain the best evaluation parameters of each model.
- ▪
- The selected forecasting model was then tested, and the model performance was evaluated using the evaluation criteria (Equations (16)–(19)).
- ▪
- Finally, the historical observed monthly streamflow data were compared with the forecasted values obtained from the SVM and ANN models.
3. Results
3.1. Evaluation of Raw Satellite Estimates
3.2. Correlation Analysis of Rainfall and Streamflow Data
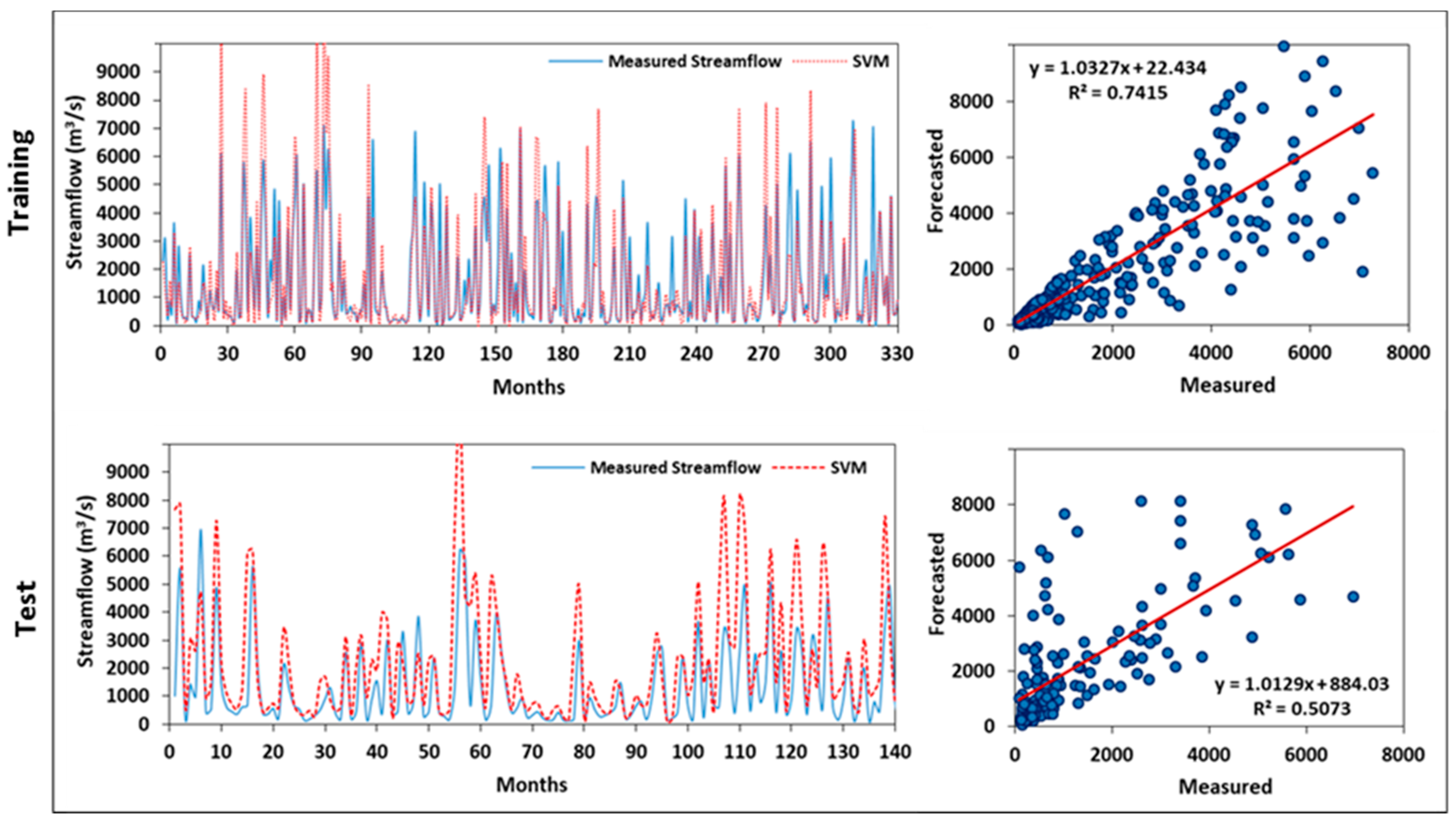
3.3. SVM Model Development Using CHIRPS
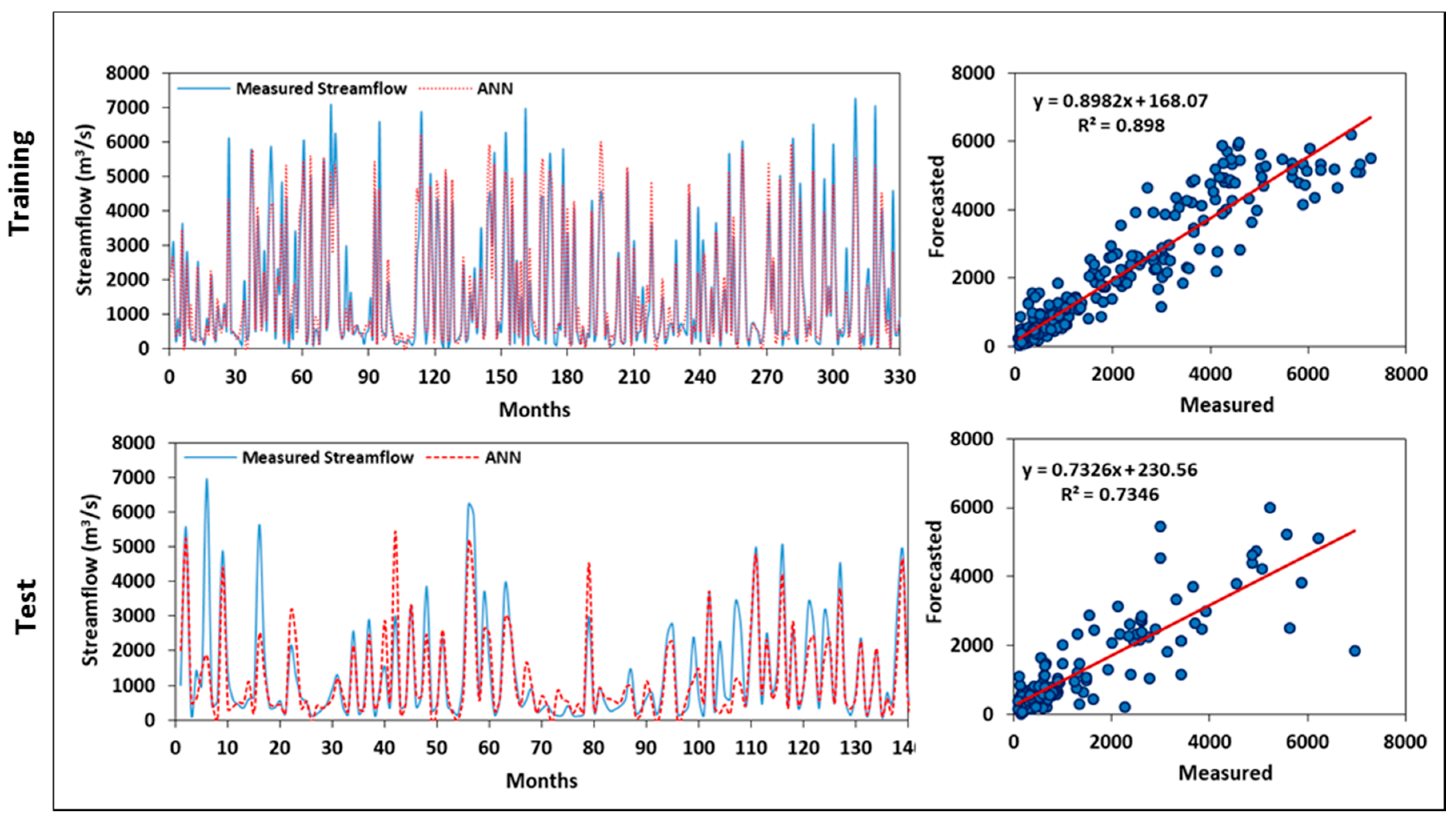
3.4. ANN Model Development Using CHIRPS
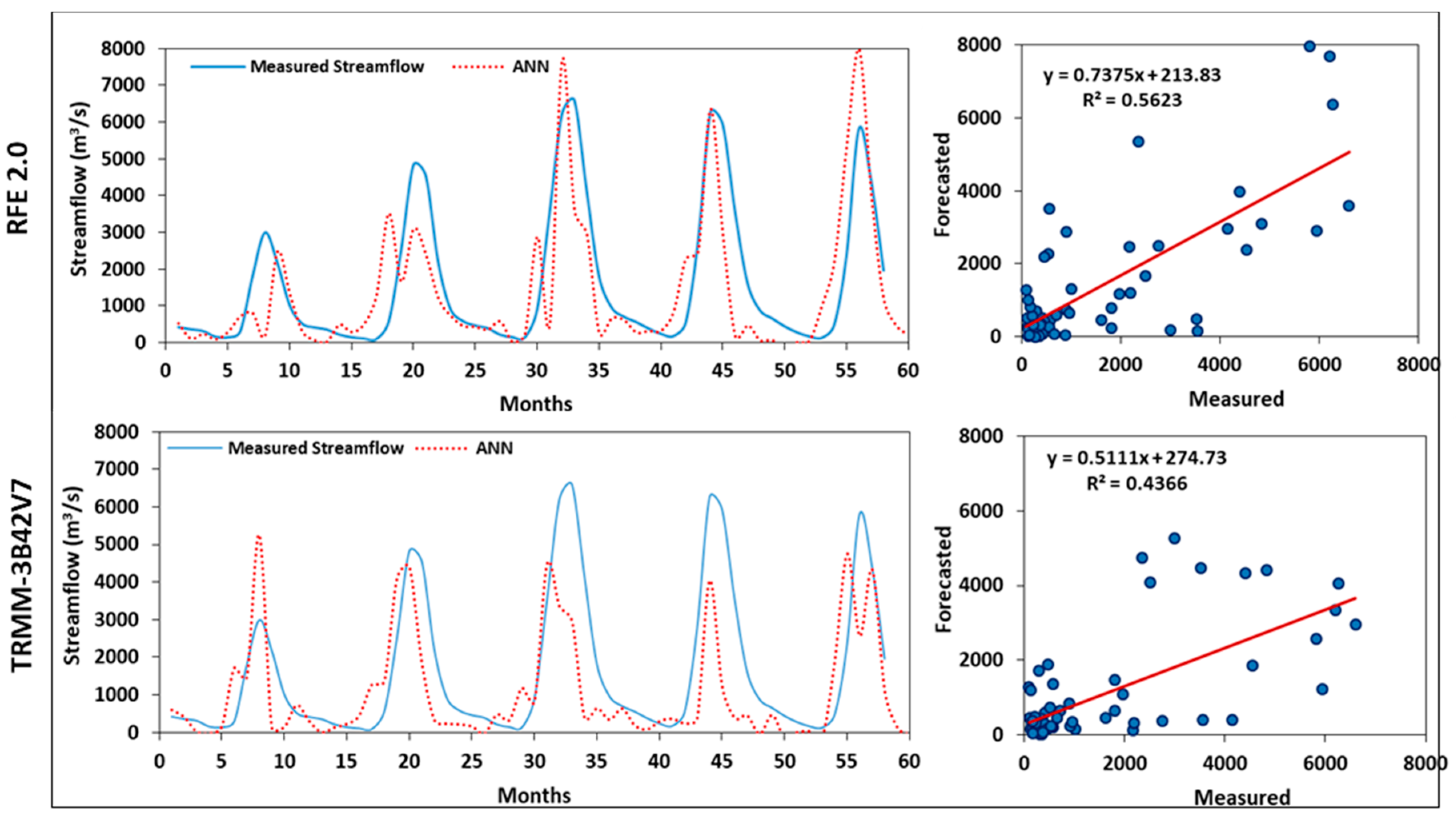
3.5. Performance Evaluation of TRMM-3B42V7 and RFE 2.0 Data in Streamflow Forecasting
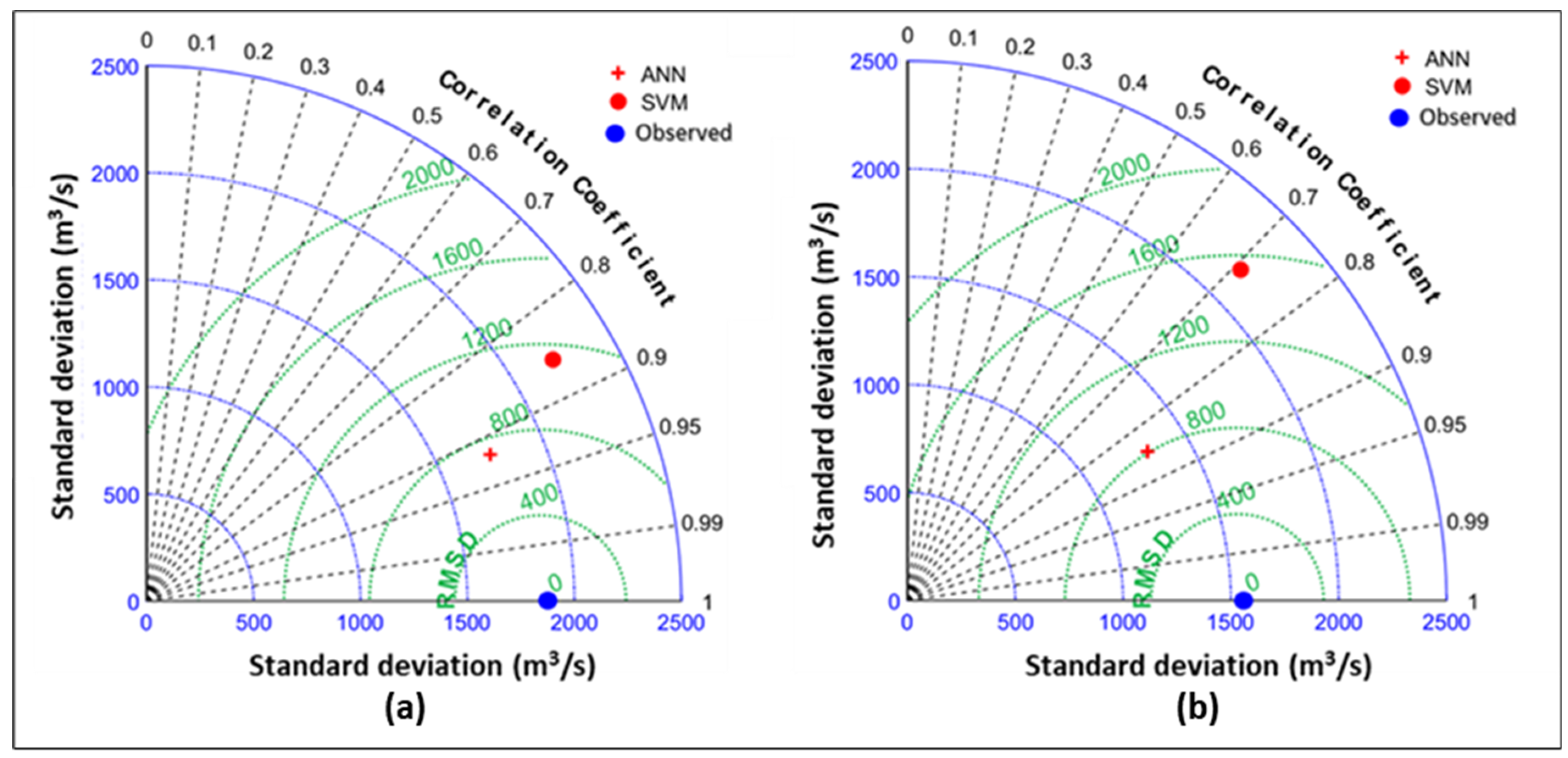
3.6. Comparison of ANN and SVM Models for Monthly Streamflow Forecasting
4. Discussion
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Abrahart, R.J.; See, L. Comparing neural network and autoregressive moving average techniques for the provision of continuous river flow forecasts in two contrasting catchments. Hydrol. Process. 2000, 14, 2157–2172. [Google Scholar] [CrossRef]
- Wu, C.; Chau, K.; Li, Y. Predicting monthly streamflow using data-driven models coupled with data-preprocessing techniques. Water Resour. Res. 2009, 45, 1–23. [Google Scholar] [CrossRef] [Green Version]
- Valipour, M. Long-term runoff study using SARIMA and ARIMA models in the United States. Meteorol. Appl. 2015, 22, 592–598. [Google Scholar] [CrossRef]
- Srivastava, P.K.; Han, D.; Ramirez, M.R.; Islam, T. Machine Learning Techniques for Downscaling SMOS Satellite Soil Moisture Using MODIS Land Surface Temperature for Hydrological Application. Water Resour. Manag. 2013, 27, 3127–3144. [Google Scholar] [CrossRef]
- Adams, T.E., III; Chen, S.; Dymond, R. Results from operational hydrologic forecasts using the NOAA/NWS OHRFC Ohio river community HEC-RAS model. J. Hydrol. Eng. 2018, 23, 04018028. [Google Scholar] [CrossRef]
- Bagatur, T.; Onen, F. Development of predictive model for flood routing using genetic expression programming. J. Flood Risk Manag. 2018, 11, S444–S454. [Google Scholar] [CrossRef] [Green Version]
- Yaseen, Z.M.; Jaafar, O.; Deo, R.C.; Kisi, O.; Adamowski, J.; Quilty, J.; El-Shafie, A. Stream-flow forecasting using extreme learning machines: A case study in a semi-arid region in Iraq. J. Hydrol. 2016, 542, 603–614. [Google Scholar] [CrossRef]
- Kasiviswanathan, K.; He, J.; Sudheer, K.; Tay, J.-H. Potential application of wavelet neural network ensemble to forecast streamflow for flood management. J. Hydrol. 2016, 536, 161–173. [Google Scholar] [CrossRef]
- Muhammad, S.; Asaad, Y.; Shamseldin, B.; Melville, W.; Mudasser, M.K. Hybrid Wavelet Neural Network Approach. In Artificial Neural Network Modelling; Springer: Berlin, Germany, 2016; pp. 127–143. [Google Scholar]
- Bertone, E.; O’Halloran, K.; Stewart, R.A.; de Oliveira, G.F. Medium-term storage volume prediction for optimum reservoir management: A hybrid data-driven approach. J. Clean. Prod. 2017, 154, 353–365. [Google Scholar] [CrossRef] [Green Version]
- Dariane, A.; Farhani, M.; Azimi, S. Long term streamflow forecasting using a hybrid entropy model. Water Resour. Manag. 2018, 32, 1439–1451. [Google Scholar] [CrossRef]
- Allawi, M.F.; Jaafar, O.; Hamzah, F.M.; Abdullah, S.M.S.; El-Shafie, A. Review on applications of artificial intelligence methods for dam and reservoir-hydro-environment models. Environ. Sci. Pollut. Res. 2018, 25, 13446–13469. [Google Scholar] [CrossRef] [PubMed]
- Modini, G.C. Long-lead precipitation outlook augmentation of multi-variate linear regression streamflow forecasts. In Proceedings of the 68th Annual Western Snow Conference, Port Angeles, WA, USA, 17–20 April 2000. [Google Scholar]
- Khan, M.Y.A.; Hasan, F.; Panwar, S.; Chakrapani, G.J. Neural network model for discharge and water-level prediction for Ramganga River catchment of Ganga Basin, India. Hydrol. Sci. J. 2016, 61, 2084–2095. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.Y.A.; Hasan, F.; Panwar, S.; Chakrapani, G.J. Typhoon event-based evolutionary fuzzy inference model for flood stage forecasting. J. Hydrol. 2013, 490, 134–143. [Google Scholar]
- Ch, S.; Anand, N.; Panigrahi, B.K.; Mathur, S. Streamflow forecasting by SVM with quantum behaved particle swarm optimization. Neurocomputing 2013, 101, 18–23. [Google Scholar] [CrossRef]
- Feng, C.; Cui, M.; Hodge, B.-M.; Zhang, J. A data-driven multi-model methodology with deep feature selection for short-term wind forecasting. Appl. Energy 2017, 190, 1245–1257. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Zhou, P.; Chen, G.; Guo, L. Evaluating a coupled discrete wavelet transform and support vector regression for daily and monthly streamflow forecasting. J. Hydrol. 2014, 519, 2822–2831. [Google Scholar] [CrossRef]
- Mohammadpour, R.; Shaharuddin, S.; Chang, C.K.; Zakaria, N.A.; Ab Ghani, A.; Chan, N.W. Prediction of water quality index in constructed wetlands using support vector machine. Environ. Sci. Pollut. Res. 2014, 22, 6208–6219. [Google Scholar] [CrossRef]
- Poul, A.K.; Shourian, M.; Ebrahimi, H. A comparative study of MLR, KNN, ANN and ANFIS models with wavelet transform in monthly stream flow prediction. Water Resour. Manag. 2019, 33, 2907–2923. [Google Scholar] [CrossRef]
- Gong, Y.; Zhang, Y.; Lan, S.; Wang, H. A Comparative Study of Artificial Neural Networks, Support Vector Machines and Adaptive Neuro Fuzzy Inference System for Forecasting Groundwater Levels near Lake Okeechobee, Florida. Water Resour. Manag. 2016, 30, 375–391. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Mahjouri, N. Integrating support vector regression and a geomorphologic artificial neural network for daily rainfall-runoff modeling. Appl. Soft Comput. 2016, 38, 329–345. [Google Scholar] [CrossRef]
- Dehghani, N.; Vafakhah, M.; Bahremand, A. Rainfall-runoff modeling using artificial neural network and neuro-fuzzy inference system in kasilian watershed. J. Watershed Manag. Res. 2016, 7, 128–137. [Google Scholar]
- Zare, M.; Koch, M. Using ANN and ANFIS Models for simulating and predicting groundwater level fluctuations in the Miandarband Plain, Iran. In Proceedings of the 4th IAHR Europe Congress. Sustainable Hydraulics in the Era of Global Change, Liege, Belgium, 27 July 2016; p. 416. [Google Scholar]
- Vetrivel, N.; Elangovan, K. Application of ANN and ANFIS model on monthly groundwater level fluctuation in lower Bhavani River Basin. Indian J. Geo. Mar. Sci. 2017, 46, 2114–2121. [Google Scholar]
- Tabbussum, R.; Dar, A.Q. Performance evaluation of artificial intelligence paradigms—Artificial neural networks, fuzzy logic, and adaptive neuro-fuzzy inference system for flood prediction. Environ. Sci. Pollut. Res. 2021, 28, 1–18. [Google Scholar] [CrossRef]
- Javanmard, S.; Yatagai, A.; Nodzu, M.I.; BodaghJamali, J.; Kawamoto, H. Comparing high-resolution gridded precipitation data with satellite rainfall estimates of TRMM_3B42 over Iran. Adv. Geosci. 2010, 25, 119–125. [Google Scholar] [CrossRef] [Green Version]
- Musie, M.; Sen, S.; Srivastava, P. Comparison and evaluation of gridded precipitation datasets for streamflow simulation in data scarce watersheds of Ethiopia. J. Hydrol. 2019, 579, 124168. [Google Scholar] [CrossRef]
- Beven, K.; Westerberg, I. On red herrings and real herrings: Disinformation and information in hydrological inference. Hydrol. Process. 2011, 25, 1676–1680. [Google Scholar] [CrossRef]
- Nguyen-Xuan, T.; Ngo-Duc, T.; Kamimera, H.; Trinh-Tuan, L.; Matsumoto, J.; Inoue, T.; Phan-Van, T. The Vietnam Gridded Precipitation (VnGP) Dataset: Construction and Validation. SOLA 2016, 12, 291–296. [Google Scholar] [CrossRef] [Green Version]
- Tapiador, F.J.; Turk, F.J.; Petersen, W.; Hou, A.Y.; García-Ortega, E.; Machado, L.A.; Carlos, F.; Angelis, P.S.; Chris, K.; George, J.; et al. Global precipitation measurement: Methods, datasets and applications. Atmos. Res. 2012, 104, 70–97. [Google Scholar] [CrossRef]
- Nijssen, B.; Lettenmaier, D.P. Effect of precipitation sampling error on simulated hydrological fluxes and states: Anticipating the Global Precipitation Measurement satellites. J. Geophys. Res. Atmos. 2004, 109, 1–15. [Google Scholar] [CrossRef]
- Abd Elhamid, A.M.; Eltahan, A.M.; Mohamed, L.M.; Hamouda, I.A. Assessment of the two satellite-based precipitation products TRMM and RFE rainfall records using ground based measurements. Alex. Eng. J. 2020, 59, 1049–1058. [Google Scholar] [CrossRef]
- Sulugodu, B.; Deka, P.C. Evaluating the performance of CHIRPS satellite rainfall data for streamflow forecasting. Water Resour. Manag. 2019, 33, 3913–3927. [Google Scholar] [CrossRef]
- Nguyen, P.; Ombadi, M.; Sorooshian, S.; Hsu, K.; AghaKouchak, A.; Braithwaite, D.; Ashouri, H.; Thorstensen, A.R. The PERSIANN family of global satellite precipitation data: A review and evaluation of products. Hydrol. Earth Syst. Sci. 2018, 22, 5801–5816. [Google Scholar] [CrossRef] [Green Version]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J. Integrated Multi-satellitE Retrievals for GPM (IMERG) technical documentation. NASA/GSFC Code 2015, 612, 2019. [Google Scholar]
- Maidment, R.I.; Grimes, D.; Allan, R.P.; Tarnavsky, E.; Stringer, M.; Hewison, T.; Roebeling, R.; Black, E. The 30 year TAMSAT African Rainfall Climatology And Time series (TARCAT) data set. J. Geophys. Res. Atmos. 2014, 119, 10619–10644. [Google Scholar] [CrossRef] [Green Version]
- Tarnavsky, E.; Grimes, D.; Maidment, R.; Black, E.; Allan, R.; Stringer, M.; Chadwick, R.; Kayitakire, F. Extension of the TAMSAT Satellite-Based Rainfall Monitoring over Africa and from 1983 to Present. J. Appl. Meteorol. Clim. 2014, 53, 2805–2822. [Google Scholar] [CrossRef] [Green Version]
- Conway, D. The climate and hydrology of the Upper Blue Nile River. Geogr. J. 2000, 166, 49–62. [Google Scholar] [CrossRef] [Green Version]
- Nour-El-Din, M.M. Climate Change Risk Management in Egyp: Proposed Climate Change Adaptation Strategy for the Ministry of Water Resources & Irrigation in Egypt. 2013. Available online: https://research.fit.edu/media/site-specific/researchfitedu/coast-climate-adaptation-library/africa/egypt-amp-libya/EL-Din.--2013.--Ministry-of-Water-Resource--Irrigation.pdf (accessed on 11 October 2021).
- Funk, C.C.; Peterson, P.J.; Landsfeld, M.F.; Pedreros, D.H.; Verdin, J.P.; Rowland, J.D.; Romero, B.E.; Husak, G.J.; Michaelsen, J.C.; Verdin, A.P. A quasi-global precipitation time series for drought monitoring. US Geol. Surv. Data Ser. 2014, 832, 1–12. [Google Scholar]
- Chen, C.; Chen, Q.; Duan, Z.; Zhang, J.; Mo, K.; Li, Z.; Tang, G. Multiscale Comparative Evaluation of the GPM IMERG v5 and TRMM 3B42 v7 Precipitation Products from 2015 to 2017 over a Climate Transition Area of China. Remote Sens. 2018, 10, 944. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.; Park, J.; Baik, J.; Choi, M. Evaluation of topographical and seasonal feature using GPM IMERG and TRMM 3B42 over Far-East Asia. Atmos. Res. 2017, 187, 95–105. [Google Scholar] [CrossRef]
- Kecman, V. Learning and Soft Computing: Support Vector Machines, Neural Networks, and Fuzzy Logic Models; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Lafdani, E.K.; Nia, A.M.; Ahmadi, A. Daily suspended sediment load prediction using artificial neural networks and support vector machines. J. Hydrol. 2013, 478, 50–62. [Google Scholar] [CrossRef]
- Bafitlhile, T.M.; Li, Z. Applicability of ε-support vector machine and artificial neural network for flood forecasting in humid, Semi-Humid and Semi-Arid Basins in China. Water 2019, 11, 85. [Google Scholar] [CrossRef] [Green Version]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Santos, C.A.G.; Neto, R.M.B.; Nascimento, T.V.M.D.; da Silva, R.M.; Mishra, M.; Frade, T.G. Geospatial drought severity analysis based on PERSIANN-CDR-estimated rainfall data for Odisha state in India (1983–2018). Sci. Total. Environ. 2021, 750, 141258. [Google Scholar] [CrossRef] [PubMed]
- Arvor, D.; Funatsu, B.M.; Michot, V.; Dubreuil, V. Monitoring Rainfall Patterns in the Southern Amazon with PERSIANN-CDR Data: Long-Term Characteristics and Trends. Remote Sens. 2017, 9, 889. [Google Scholar] [CrossRef] [Green Version]
- Bâ, K.M.; Balcázar, L.; Diaz, V.; Ortiz, F.; Gómez-Albores, M.A.; Díaz-Delgado, C. Hydrological Evaluation of PERSIANN-CDR Rainfall over Upper Senegal River and Bani River Basins. Remote Sens. 2018, 10, 1884. [Google Scholar] [CrossRef] [Green Version]
- Mosaffa, H.; Sadeghi, M.; Hayatbini, N.; Afzali Gorooh, V.; Akbari Asanjan, A.; Nguyen, P.; Sorooshian, S. Spatiotemporal variations of precipitation over Iran using the high-resolution and nearly four decades satellite-based PERSIANN-CDR dataset. Remote Sens. 2020, 12, 1584. [Google Scholar] [CrossRef]
- Ombadi, M.; Nguyen, P.; Sorooshian, S.; Hsu, K. Developing Intensity-Duration-Frequency (IDF) Curves From Satellite-Based Precipitation: Methodology and Evaluation. Water Resour. Res. 2018, 54, 7752–7766. [Google Scholar] [CrossRef]
- Ombadi, M.; Nguyen, P.; Sorooshian, S.; Hsu, K.-L. Retrospective Analysis and Bayesian Model Averaging of CMIP6 Precipitation in the Nile River Basin. J. Hydrometeorol. 2021, 22, 217–229. [Google Scholar] [CrossRef]
- Ashouri, H.; Nguyen, P.; Thorstensen, A.; Hsu, K.-L.; Sorooshian, S.; Braithwaite, D. Assessing the Efficacy of High-Resolution Satellite-Based PERSIANN-CDR Precipitation Product in Simulating Streamflow. J. Hydrometeorol. 2016, 17, 2061–2076. [Google Scholar] [CrossRef]
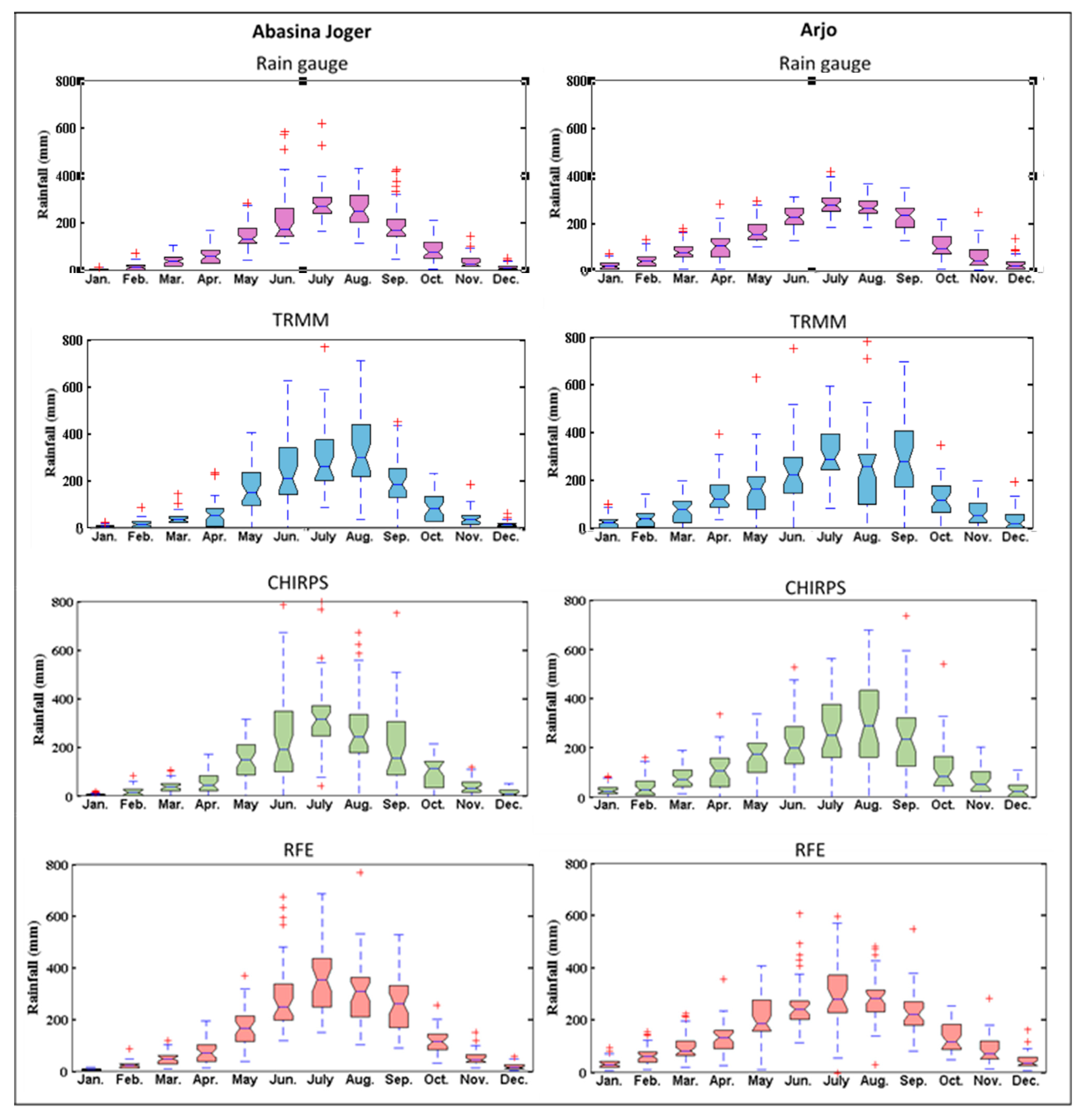
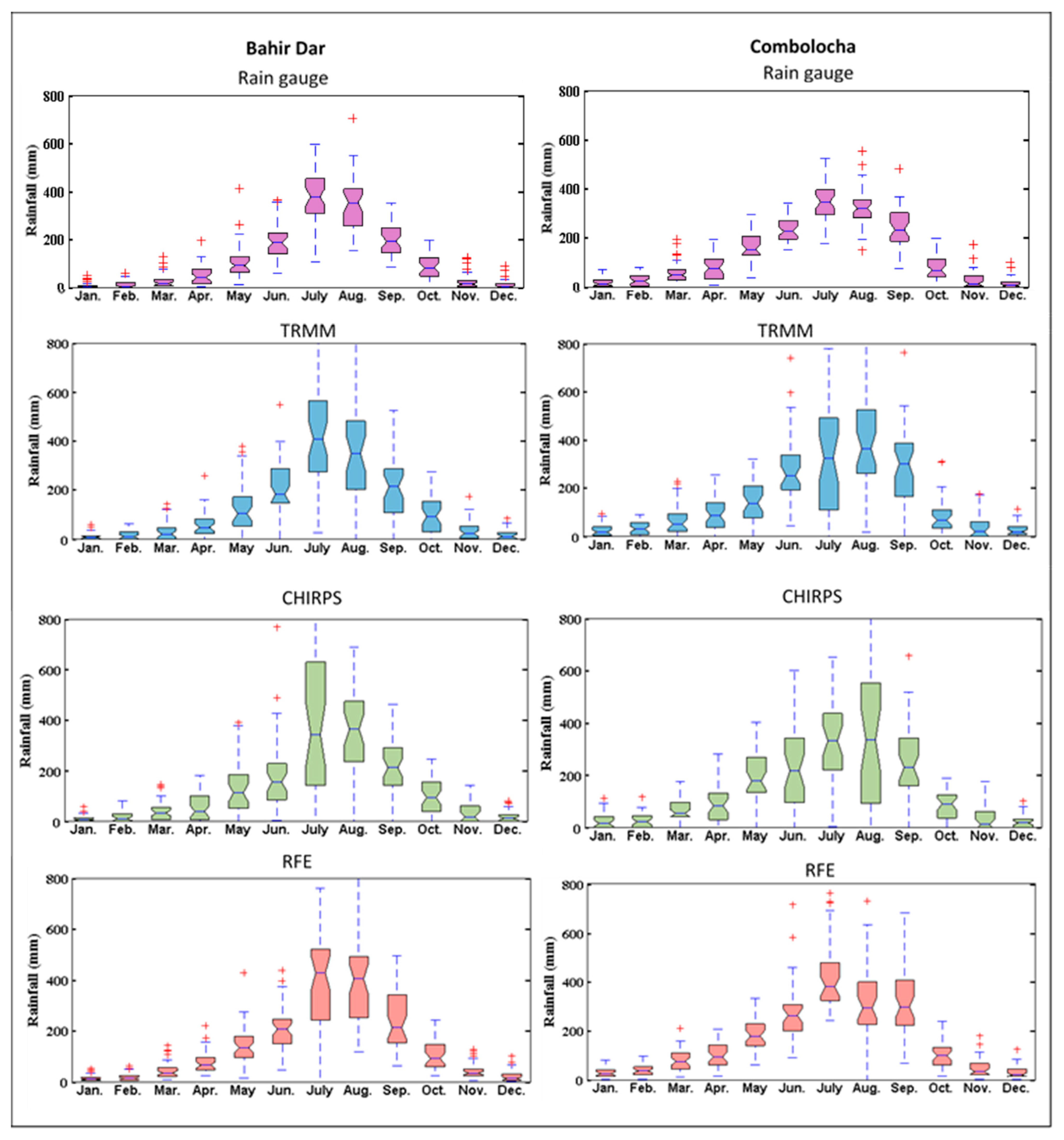
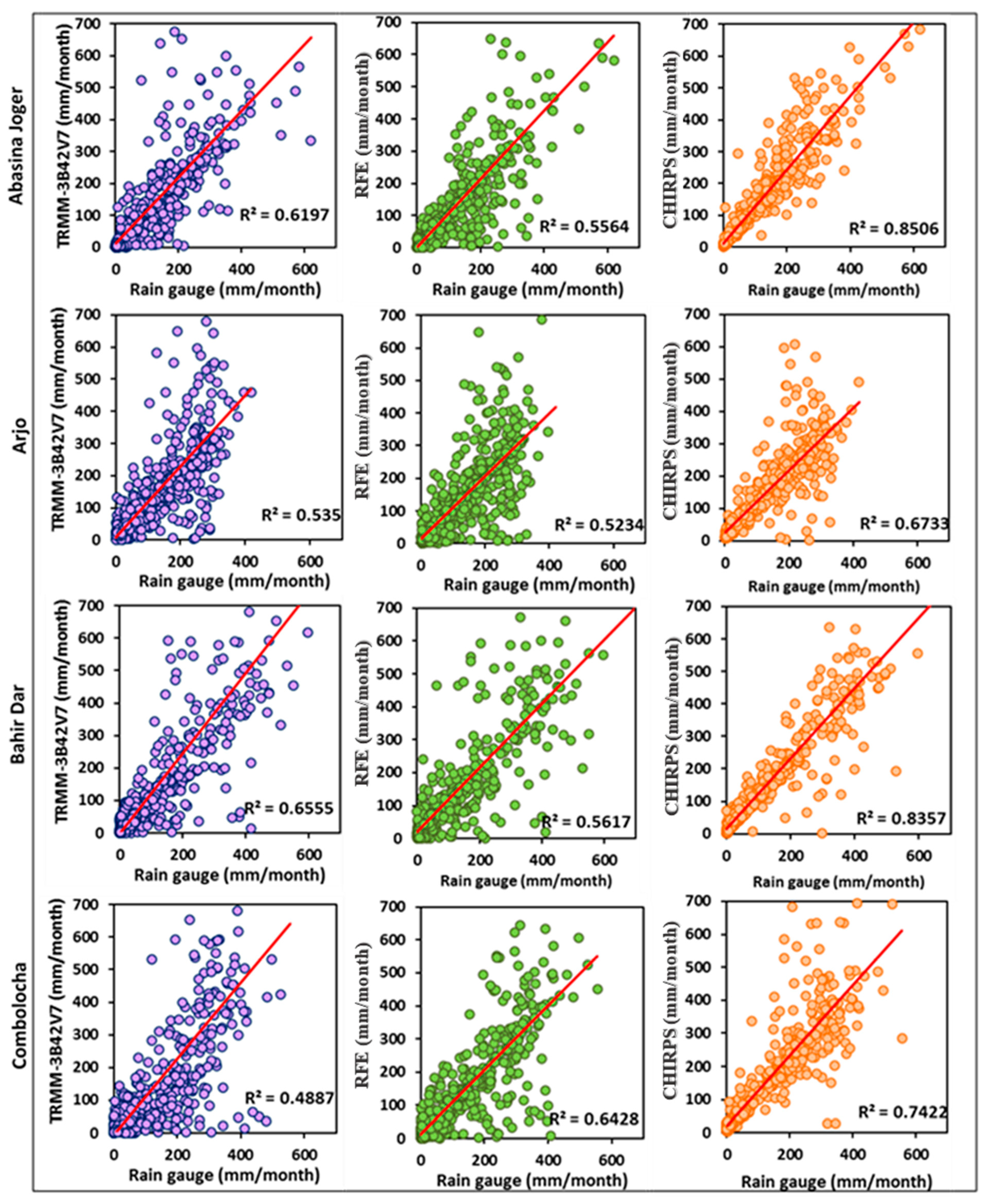


| Product | Start | End | Resolution | Coverage | |
|---|---|---|---|---|---|
| Spatial | Temporal | ||||
| CHIRPS | 1981 | Present | 0.25° | Daily | 50°N to 50°S |
| REF 2.0 | 1998 | Present | 0.10° | Daily | 40″S to 40″N |
| TRMM-3B42V7 | 1998 | Present | 0.25° | Daily | 50°N to 50°S |
| Station | Rainfall Sources | Cr | RMSE (mm) | ME | BIAS (%) | CSI | POD | FAR |
|---|---|---|---|---|---|---|---|---|
| Abasina Joger | TRMM-3B42V7 | 0.79 | 110.39 | 16.92 | 14.72 | 0.70 | 0.70 | 0.18 |
| CHIRPS | 0.92 | 66.31 | 19.86 | 8.17 | 0.66 | 0.66 | 0.23 | |
| RFE | 0.75 | 96.54 | 29.80 | 25.93 | 0.68 | 0.68 | 0.21 | |
| Arjo | TRMM-3B42V7 | 0.72 | 93.01 | 10.77 | 14.53 | 0.62 | 0.62 | 0.28 |
| CHIRPS | 0.82 | 70.02 | 10.77 | 7.88 | 0.60 | 0.60 | 0.30 | |
| RFE | 0.73 | 105.20 | 22.45 | 16.43 | 0.64 | 0.64 | 0.25 | |
| Bahir Dar | TRMM-3B42V7 | 0.81 | 121.62 | 24.88 | 23.14 | 0.58 | 0.58 | 0.32 |
| CHIRPS | 0.91 | 72.63 | 17.32 | 20.22 | 0.54 | 0.54 | 0.37 | |
| RFE | 0.75 | 132.10 | 28.47 | 14.07 | 0.56 | 0.56 | 0.35 | |
| Combolocha | TRMM-3B42V7 | 0.80 | 92.43 | 14.83 | 10.85 | 0.49 | 0.50 | 0.43 |
| CHIRPS | 0.70 | 154.24 | 29.50 | 21.58 | 0.51 | 0.52 | 0.41 | |
| RFE | 0.80 | 92.43 | 14.83 | 10.85 | 0.49 | 0.50 | 0.48 |
| Model | Product | Training | Test | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | E | R2 | RMSE | MAE | E | ||
| ANN | CHIRPS | 0.898 | 587.289 | 385.732 | 0.913 | 0.735 | 535.322 | 208.193 | 0.809 |
| TRMM | - | - | - | - | 0.562 | 1336.465 | 913.897 | 0.495 | |
| RFE | - | - | - | - | 0.437 | 1517.094 | 1018.638 | 0.350 | |
| SVM | CHIRPS | 0.742 | 1125.687 | 638.661 | 0.625 | 0.507 | 1188.968 | 487.442 | 0.060 |
| TRMM | - | - | - | - | 0.307 | 2431.665 | 1486.513 | −0.67 | |
| RFE0 | - | - | - | - | 0.204 | 2705.930 | 1641.719 | −1.06 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alquraish, M.M.; Khadr, M. Remote-Sensing-Based Streamflow Forecasting Using Artificial Neural Network and Support Vector Machine Models. Remote Sens. 2021, 13, 4147. https://doi.org/10.3390/rs13204147
Alquraish MM, Khadr M. Remote-Sensing-Based Streamflow Forecasting Using Artificial Neural Network and Support Vector Machine Models. Remote Sensing. 2021; 13(20):4147. https://doi.org/10.3390/rs13204147
Chicago/Turabian StyleAlquraish, Mohammed M., and Mosaad Khadr. 2021. "Remote-Sensing-Based Streamflow Forecasting Using Artificial Neural Network and Support Vector Machine Models" Remote Sensing 13, no. 20: 4147. https://doi.org/10.3390/rs13204147
APA StyleAlquraish, M. M., & Khadr, M. (2021). Remote-Sensing-Based Streamflow Forecasting Using Artificial Neural Network and Support Vector Machine Models. Remote Sensing, 13(20), 4147. https://doi.org/10.3390/rs13204147