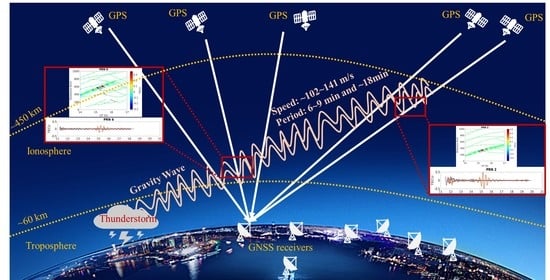
Observation of Ionospheric Gravity Waves Introduced by Thunderstorms in Low Latitudes China by GNSS

Abstract

The disturbances of the ionosphere caused by thunderstorms or lightning events in the troposphere have an impact on global navigation satellite system (GNSS) signals. Gravity waves (GWs) triggered by thunderstorms are one of the main factors that drive short-period Travelling Ionospheric Disturbances (TIDs). At mid-latitudes, ionospheric GWs can be detected by GNSS signals. However, at low latitudes, the multi-variability of the ionosphere leads to difficulties in identifying GWs induced by thunderstorms through GNSS data. Though disturbances of the ionosphere during low-latitude thunderstorms have been investigated, the explicit GW observation by GNSS and its propagation pattern are still unclear. In this paper, GWs with periods from 6 to 20 min are extracted from band-pass filtered GNSS carrier phase observations without cycle-slips, and 0.2–0.8 Total Electron Content Unit (TECU) magnitude perturbations are observed when the trajectories of ionospheric pierce points fall into the perturbed region. The propagation speed of 102.6–141.3 m/s and the direction of the propagation indicate that the GWs are propagating upward from a certain thunderstorm at lower atmosphere. The composite results of disturbance magnitude, period, and propagation velocity indicate that GWs initiated by thunderstorms and propagated from the troposphere to the ionosphere are observed by GNSS for the first time in the low-latitude region.

1. Introduction

The solar activities have effects on the ionospheric electron content from the top, which can be retrieved by the global navigation satellite system (GNSS) [1,2]. In recent years, perturbations from the underlying atmosphere have been found to be another important factor in ionospheric variability [3]. In addition to earthquakes [4] and typhoons [5], which have been explored extensively, lightning or thunderstorms can drive significant ionospheric perturbations. Ionospheric perturbations induced by thunderstorms can be propagated by gravity waves (GWs) as carriers, which have been reported both in mid-latitudes and low-latitudes [6,7].

In mid-latitudes, the ionospheric Total Electron Contents (TECs) obtained by GNSS measurements with and without thunderstorms were compared [7]. Large ionospheric disturbances induced by thunderstorms were reported, and the maximum variation was about 1.4 Total Electron Content Units (TECUs) (1 TECU = 10¹⁶ e/m²). During the periods without thunderstorms, no detectable GW was found. When the Ionospheric Pierce Points (IPPs) of the GNSS signal path were above the thunderstorms, high-frequency (period about 4 min) perturbations were present [8]. It was deemed that the source of the disturbance could be located from the infrasound observations from different GNSS stations. The positioning results showed that the disturbance sources were in the regions of thunderstorm monoliths or strong convection, suggesting that the infrasound disturbances were triggered by thunderstorms. The statistical study from North America further elucidated the correlation between thunderstorms and ionospheric GWs at mid-latitudes [6].

Compared with the obvious observation of the ionospheric GWs induced by thunderstorms at mid-latitudes, GW observation through GNSS data is difficult in low latitudes, likely due to the low-latitudes complex ionospheric dynamical processes. The statistical correlation study [9] suggested that thunderstorms could drive the unstable post-sunset ionosphere to a state with significant spatial irregularities. Moreover, when the ionospheric spatial irregularities do not dominate, thunderstorm-induced acoustic and GWs could be observable in the low-latitude ionosphere. The band-pass filters could be used to extract ionospheric GWs at specific periods. A positive correlation between the amplitudes of band-pass filtered GW and thunderstorm activities was found [10]. Besides the wave-like ionospheric disturbances during thunderstorms, a TEC variations analysis [11] showed that ionospheric anomalies could reach up to 70 TECU/min. This magnitude was significantly larger than the disturbances in Brazil [9] and West Africa [12]. Further, wavelet analysis was used to analyze the possible causes of ionospheric disturbances under lightning. It was shown that a combination of plasma bubbles and GWs could be responsible for the 10–100 min disturbance periodicity [11]. The ionospheric disturbances brought about by thunderstorms during the daytime were analyzed in West Africa [12]. It was pointed out that visible GWs by GNSS were correlated with thunderstorms and propagated in a specific direction. However, in comparison with the clearly observable GWs caused by typhoons [13,14,15], the direct observations of GWs introduced by thunderstorms are unclear through GNSS in low latitudes. The ionospheric GWs in the low-latitude/equatorial region induced by thunderstorms need to be further investigated.

Considering that GWs propagate in the atmosphere before reaching the ionosphere, the properties of GWs should be explored from the perspective of atmospheric medium propagation theory [16]. This study mainly focuses on 1, determining the observability and magnitude of GWs induced by lightning at low latitudes; 2, investigating the period, propagation direction, distance, and speed of GWs in the ionosphere; and 3, the relationship between the period characteristics of GWs and the propagation distance considering the atmospheric conditions.

The structure of the article is organized as follows: in Section 2, the data used in this paper are introduced; in Section 3, the methods of data processing are described; in Section 4, the observation results and characteristics of GWs under thunderstorms/lightning are analyzed; in Section 5, the results are discussed in comparison with existing studies; and Section 6 contains the Summary.

2. Data

2.1. GNSS Raw Data

GPS dual-frequency carrier phase in Receiver Independent Exchange (RINEX) format for 2–5 April 2019 for stations at low latitudes (105–120°E 15–30°N) in China from National Earthquake Data Center (https://data.earthquake.cn/ (accessed on 12 October 2020)) and all stations in the Hong Kong Geodetic Network (https://www.geodetic.gov.hk/ (accessed on 5 April 2021)) were used. The sampling rate of the data was 30 s.

2.2. Lightning Data

The data included the lightning occurrences number, magnitude, and location, which were obtained from the lightning meter 1-min event product of the lighting mapping imager (LMI) of FY-4 satellite (http://data.cma.cn/data/cdcdetail/dataCode/SK.0983.001.html (accessed on 16 July 2021)) and the ground-based observations from the Institute of Electrical Engineering Chinese Academy of Sciences (http://www.iee.ac.cn/ (accessed on 13 April 2021)).

2.3. Kp and Dst Index

The Kp-index is an index used by individual geomagnetic stations to describe the intensity of geomagnetic disturbances every 3 h of the day. The Dst index was measured every hour, mainly to measure the variation in the horizontal component of the geomagnetic field. The Kp and Dst indexes are available from: http://wdc.kugi.kyoto-u.ac.jp/index.html (accessed on 1 June 2021).

3. Methods

3.1. Extraction of Ionospheric Disturbances

First, the L1 and L2 carrier phase data are used to do geometry-free combinations. For low latitudes, especially in areas where thunderstorms are frequent, the handling of cycle slips is tricky. The presence of undetected cycle slips may lead to great TECU errors in the results. For ionospheric disturbances extraction, the calculation of the absolute TECU values is not necessary. The cycle slips can be treated as biases using the time difference method [17,18]. The ambiguity is similarly eliminated during the time differencing process. By the method of using only the carrier phase to obtain the ionospheric perturbation, the accuracy of the total electron content on the signal path can reach 0.03 TECU [13]. The detailed derivation of formulas can be found in studies of Savastano et al. [17] and Jian et al. [13].

3.2. Extraction of Ionospheric Gravity Waves

GWs associated with thunderstorms typically have a short period of 6–20 min [9,10]. For the extraction of such disturbances with known periods, a band-pass filter can be used [6,9]. The passband of the filter is 0.8–2.8 mHz. Due to the presence of apparent dispersive shifts in the unidirectional bandpass filter, a bidirectional bandpass filter needs to be utilized. The bandpass filter used in this study is a bidirectional Butterworth filter [19].

3.3. GW Period with Propagation Distance

The periodic term of GWs is integrated into the atmospheric dynamical equations. In the case of a normal wind field (wind speed below a first-order typhoon) and without considering the Coriolis force, the dispersion equation of high-frequency waves is [16,20,21]:

$${\widehat{\omega }}^2=\frac{N^2{k}_{\mathrm{h}}^2}{k_{\mathrm{h}}^2+m^2}=N^2{\cos }^2\alpha$$

(1)

where $\widehat{\omega }$ denotes the GW intrinsic frequency and N denotes the Brunt–Vaisala frequency. Horizontal wave number k_h = 2π/λ_h, λ_h is the horizontal wavelength; vertical wave number m = 2π/λ_z, α is the angle between the horizontal propagation direction of the GW and the vertical direction. Denoting the GW period by τ, from $\widehat{\omega }$ = 2π/τ [16]:

$$\tau =\frac{2\mathsf{\pi }}{N}\sec \alpha =\frac{2\mathsf{\pi }}{N}\sqrt{1+\frac{R^2}{\mathsf{\Delta }{z}^2}}$$

(2)

Δz denotes the vertical distance from the height of the GW source to the thin ionospheric shell. The default ionospheric thin shell height of 300 km is set in the calculation. R denotes the horizontal distance from the observed GW to the wave source. Equation (2) expresses the period of the GW as a function of the horizontal propagation distance. In the equation, the Brunt–Vaisala frequency is taken as N = 2π/5 min⁻¹ [16]. Therefore, when the period of the GW is observed, the horizontal propagation distance can be determined when the ionospheric height is known.

4. Results

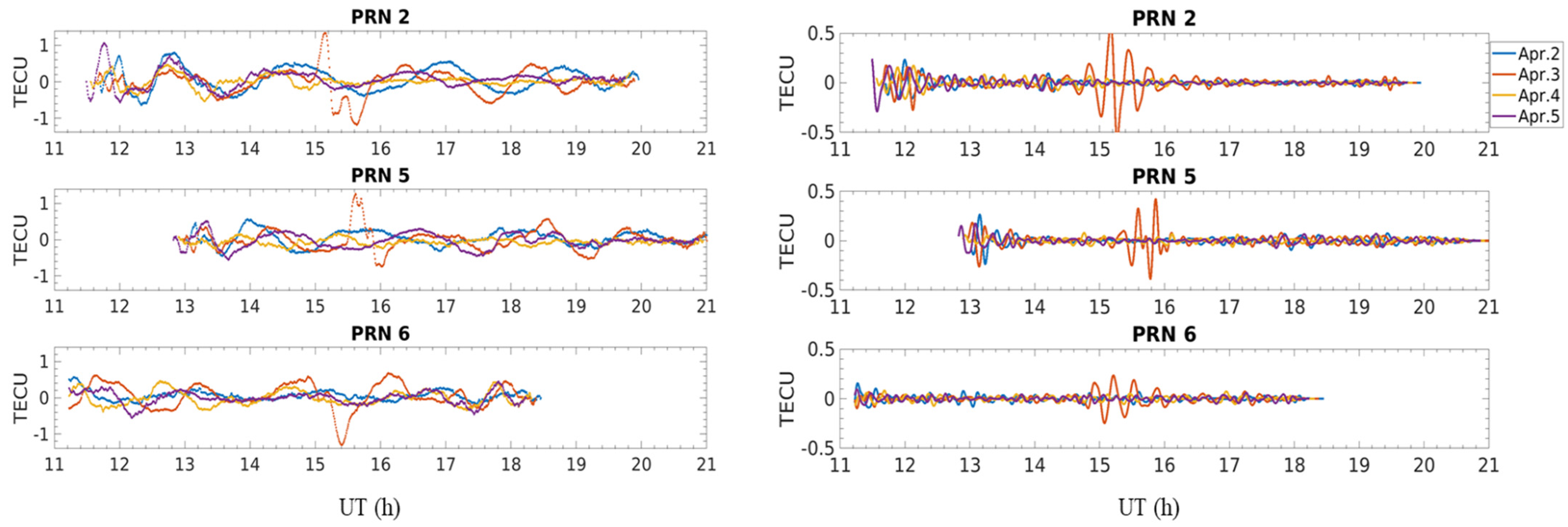
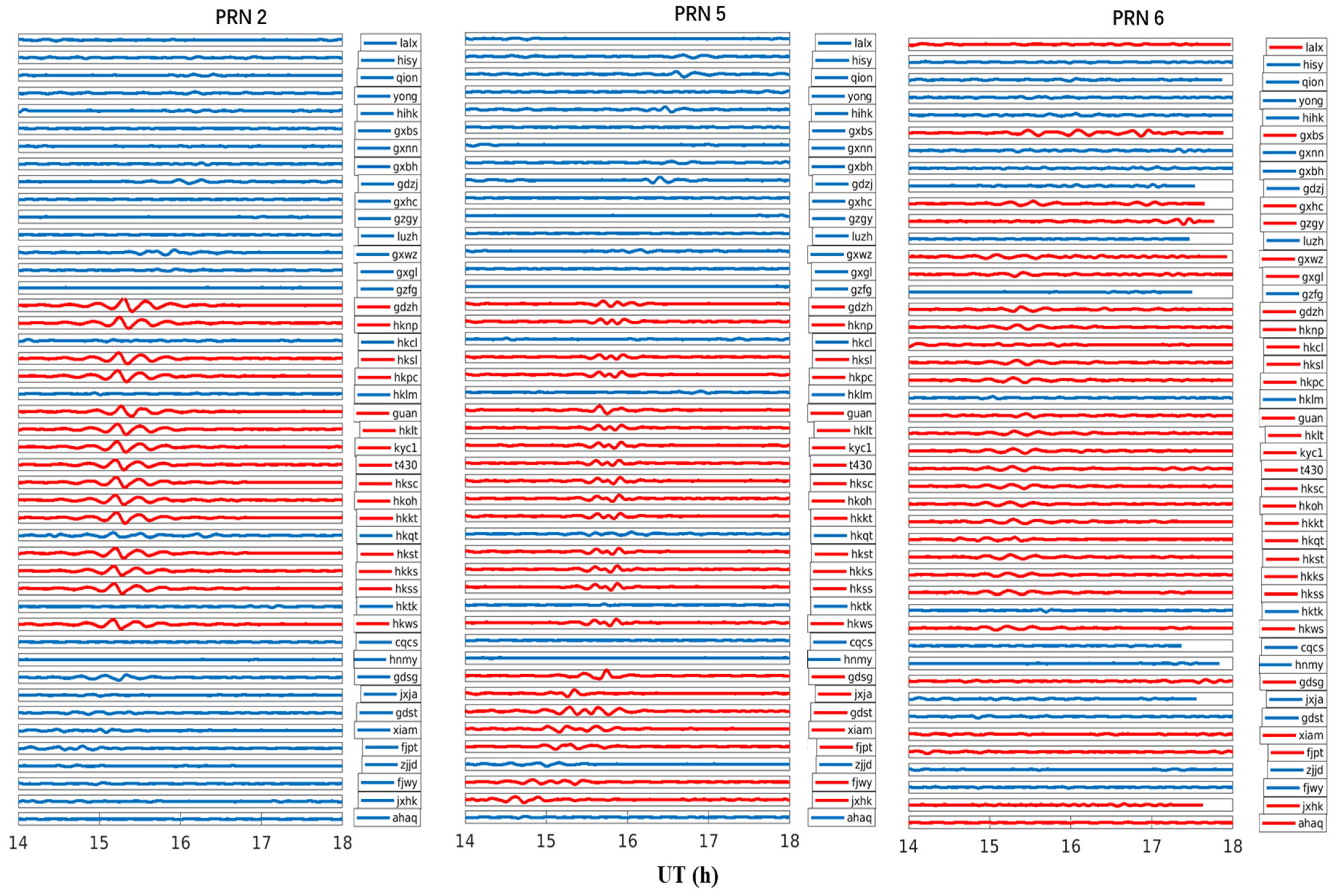
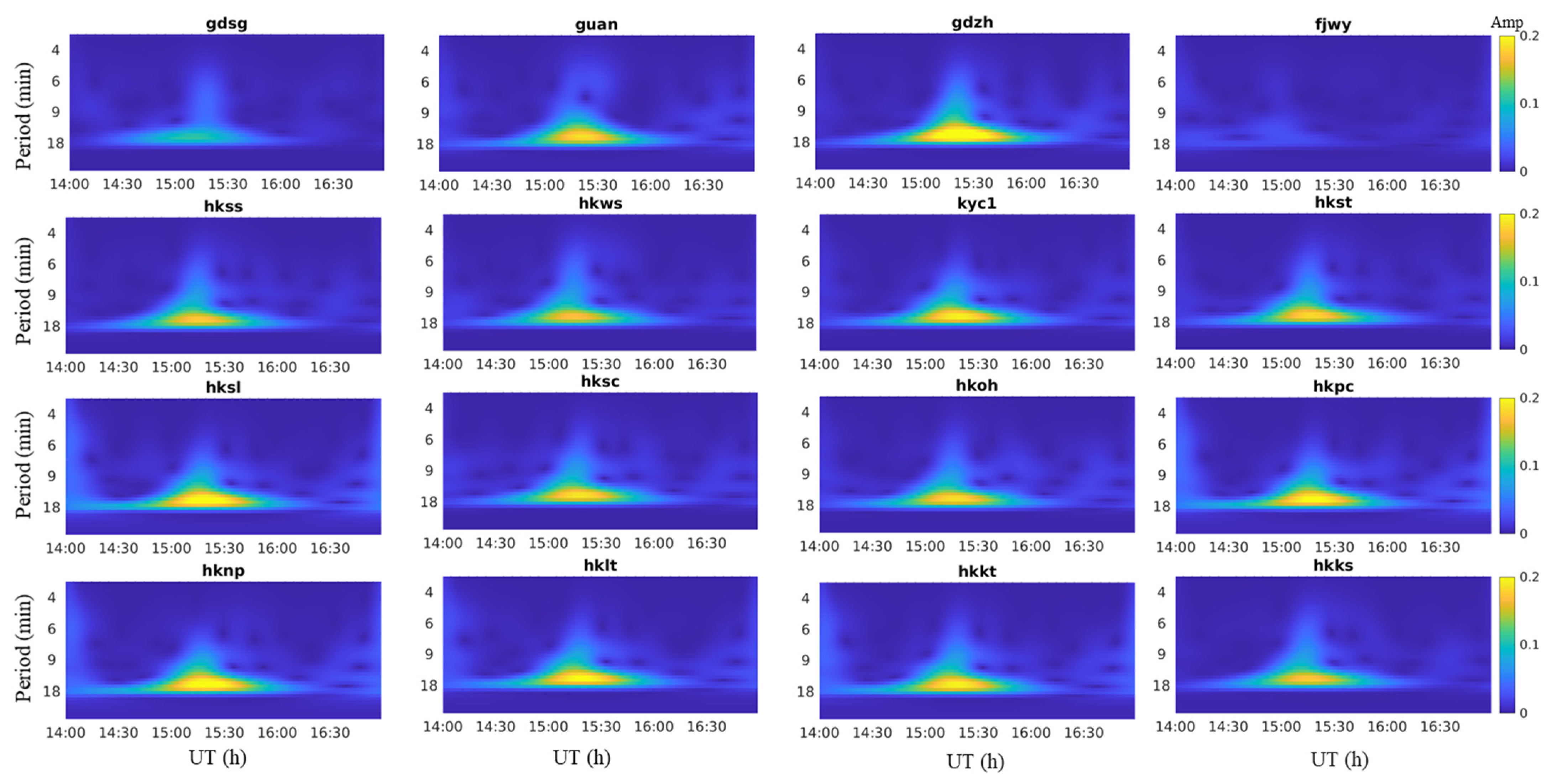
4.1. Extraction of GWs from Time Series

First, the consistency of thunderstorm occurrence and GW observations is analyzed in terms of time.

The satellites over the low latitudes of China at 12–20 h are pseudo random noise code (PRN) 2, 3, 5, 6, 9, 17, 19, 28, and 30. Using a polynomial fit, after removing the trend of daily variation, all satellites still have cyclical disturbances in hourly units. The results of the perturbation before removing the trend term with long periods are shown in the left panel of Figure 1.

After processing with band-pass filters, only PRN 2, 5, and 6 have distinct disturbances with a period of 6–20 min at around 15–16 h, which are in the range of the period of lightning-induced GWs [6,9,10], as the right panel shows. Figure 1 only shows the results of the HKWS station; the results of most stations in Hong Kong, China are consistent with HKWS.

To explore whether the observations are triggered by a thunderstorm, the number of lightning events at 12–16 h from 2–5 April are used as a reference, as shown in Figure 2.

The GW observed at 15–16 h, considering the 1–2 h delay [10,11,22], is probably generated at 13–14 h and coincides with the lightning peak time of 3 April 2019. The lighting event from LMI is also recorded on April 2 and April 4; however, no satellites show observable GWs. No lightning is recorded on April 5. The results in Figure 1 and Figure 2 tentatively show that, although there is no inevitable causal relationship between GW generation by thunderstorms and its GNSS observation, but some TECU variations can be associated with the thunderstorms.

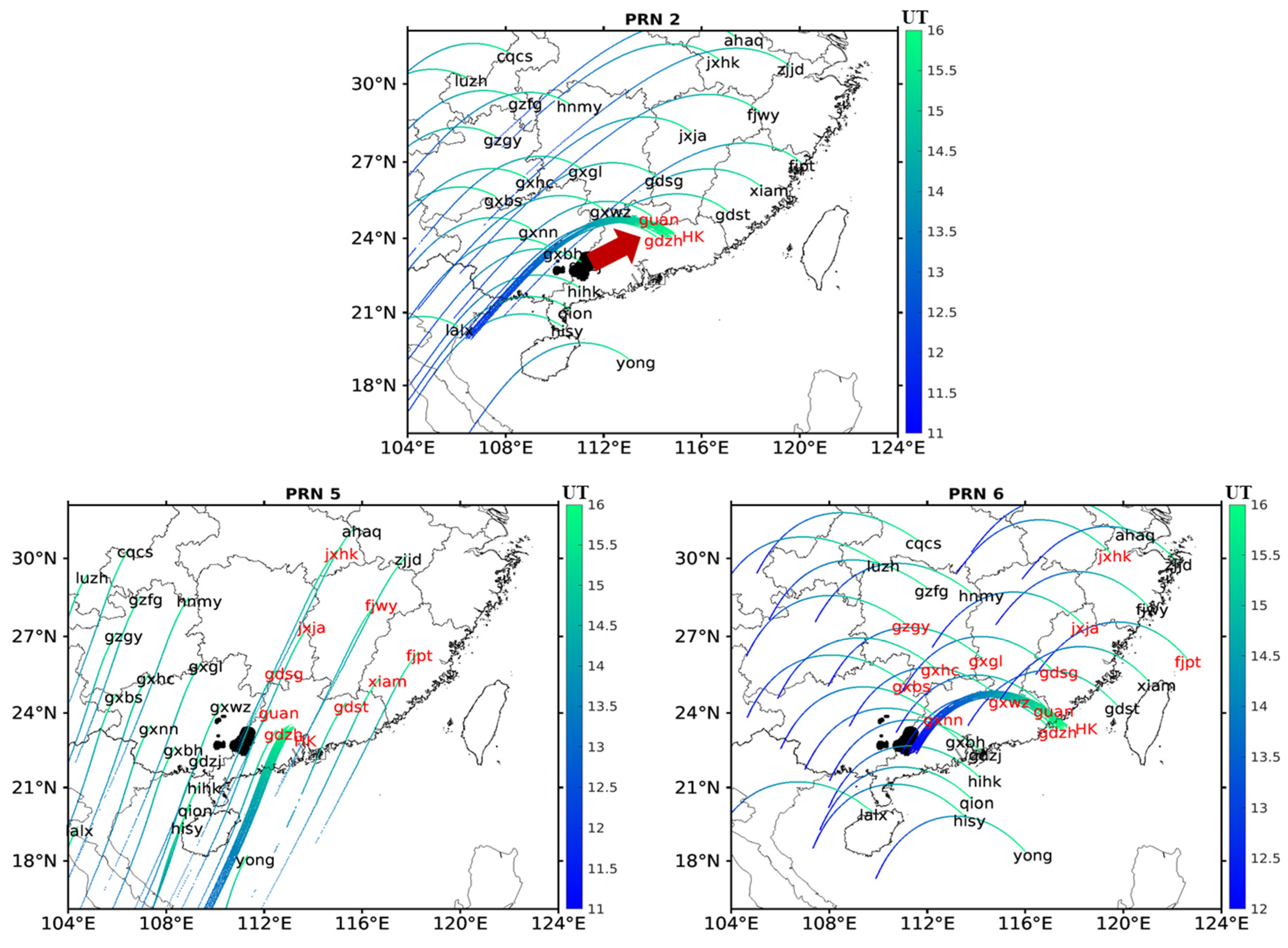
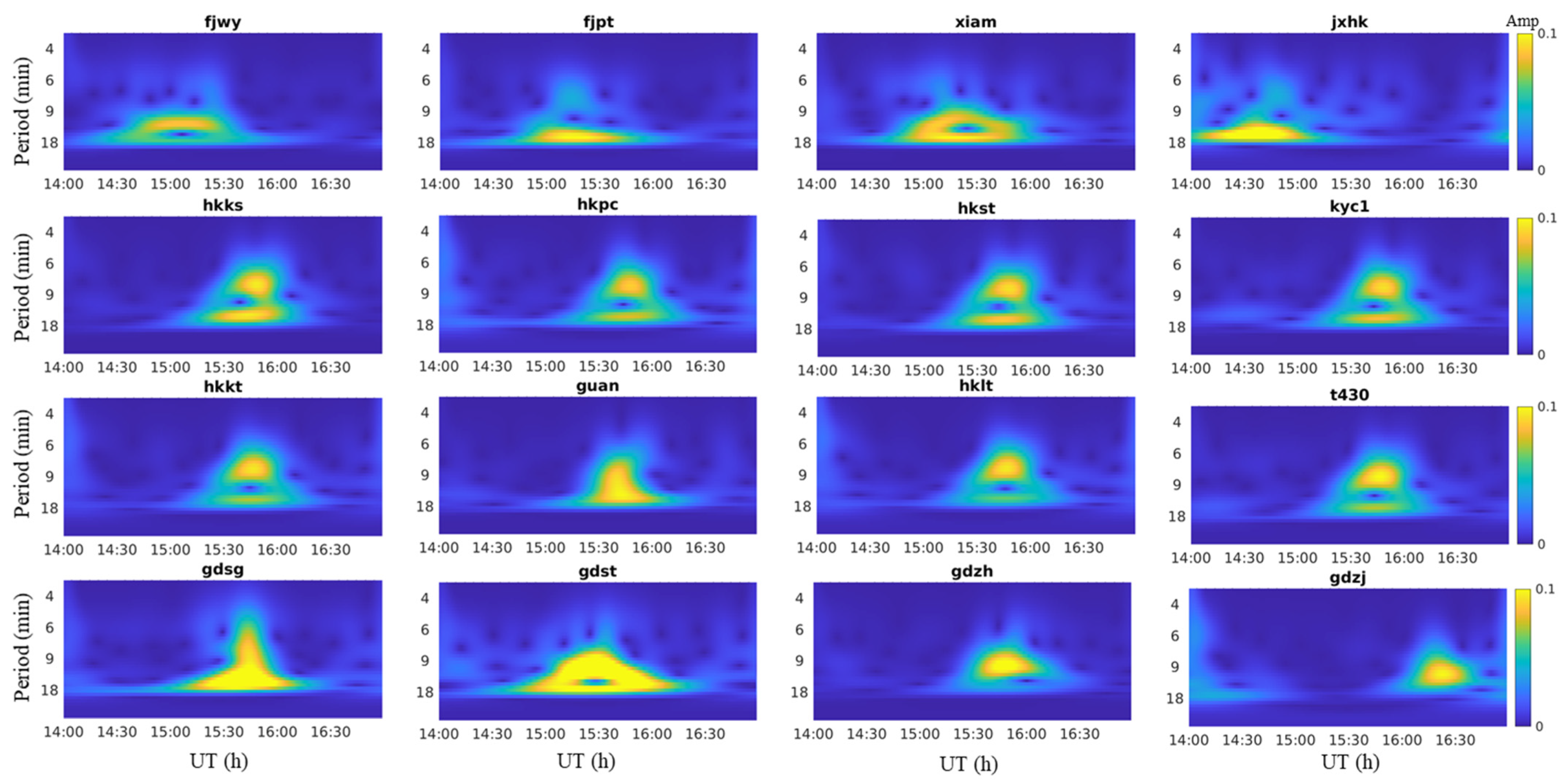
4.2. Location of Thunderstorms and GWs

To further investigate the spatial location relationship between ionospheric GWs and lightning, the map of lightning position using LMI data is shown in Figure 3. The GWs observed on April 3 are located directly north of Hong Kong and Shenzhen, as shown in the upper right subplot of Figure 3. GWs are not observed in the same area on other days. Around Vietnam and Laos (about 105°E, 18°N), located on the southwest of China, there are longer period waves in days with and without thunderstorms.

As shown in Figure 3, the April 3 thunderstorm is located near the location of the GWs: the thunderstorm location is the western part of Guangdong Province (about 113°E, 23°N), and the ionospheric GW location is about 114°E, 24°N. There are no thunderstorms in other areas during that period. This suggests that the GWs observation on April 3 are most likely caused by nearby thunderstorms.

Even if thunderstorms existed on April 2 and 4, GWs similar to those on April 3 are not detected. This suggests that although the observed GWs may be triggered by thunderstorms, not all thunderstorms can trigger GWs and then be captured by GNSS observations. It is possible that GWs would propagate in a specific direction and not necessarily intersect with the IPP trajectory. The perturbation would only be captured if the GWs could cross the GNSS signal path.

On April 2 and April 4, the disturbances observed by PRN 2 are located on the southwest of China (~105°E, 18°N), but there are no local thunderstorms. The only thunderstorm area is located north of Guangdong (~112°E, 26°N). The thunderstorm region is far from the disturbance region, which suggests that there should be no correlation between the two.

In addition, comparing the results of April 2, 4, and 5, it can be found that there are slight GWs on the southwest of China (~105°E, 18°N) regardless of the presence of thunderstorms. This further verifies that the presence of waves in the region is not caused by thunderstorms in and around Guangdong.

4.3. GW Propagation Direction

The thunderstorm area is located at 111°E, 23°N and the GW observation area is located at 114°E, 24°N. If the GW is triggered by a thunderstorm, then the direction of propagation of the GW is north of east. On the condition that the stations are in columns, the GW direction of propagation can be observed visibly from the time-series perturbation maps of multiple stations simultaneously or in sequence [23]. However, the stations in our study are dispersed. Thus, the relative position of all the stations needs to be ordered. As shown in Figure 4, in general, these three satellites PRN 2, 5, and 6 move from southwest to northeast. Therefore, all stations are ordered according to the southwest-northeast direction of their positions, as shown in Figure 5.

In the first subplot of Figure 4, The Hong Kong and Guangdong stations (GUAN and GDZH) of PRN 2 crossed the GW region at around 16 h, while the IPPs of other stations did not cross the region. Therefore, as shown in the left panel of Figure 5, only the stations in and around Hong Kong are disturbed. The direction of the IPP motion of PRN 2 is similar to the direction of GW propagation, pointing from the black area to the area marked by the red station name but at different speeds. Therefore, theoretically, the two motions cross only once, i.e., the fluctuations can be observed only at a particular time.

In the second subplot of Figure 4, during the motion of the PRN 5 satellite, the IPP in the northeast is more likely to fall into the range of the GW first. Therefore, before 15:30, the stations in Jiangxi, Fujian, and Zhejiang (JXHK, FJWY, and JXJA) observe the disturbances first. With time, the stations in and around Hong Kong fall into the GW region only; finally, the IPPs of GDZJ in Guangdong and HIHK, QION in Hainan enter the GW range.

In the last subplot of Figure 4, during the motion of PRN 6, the IPP trajectories of the stations located in Guangdong and Guangxi first move northeastward and crossed over the thunderstorm; after that, they move southeastward and fell into the GW region. This results in the GWs of PRN 6 from different stations being observed at different times, especially the stations in Guangxi, where the thunderstorms originate.

The perturbation magnitude of PRN 2 is the largest (±0.8 TECU) among the observations from the three satellites. Observations from most of the dense stations in Hong Kong show the consistency of this magnitude. Figure 5 shows that the GW observation of PRN 2 is just after 15:00. At this time, the station of PRN 5 leaning to the east is also in the GW range and has a large disturbance. When the Hong Kong stations of PRN 5 fall into the GW region at 15:30, the amplitude has decayed (±0.5 TECU). This indicates that the time when PRN 2 crosses the disturbance region is closer to the time when the GW is largest.

The initial disturbance times of the Hong Kong and additional stations of PRN 2 and PRN 6 are more consistent. However, spatially, the IPPs of PRN 6 are located at 117°E, 24°N, further away from the thunderstorm region than the 113°E, 24°N of PRN 2. The farther position of PRN 6 leads to an attenuation of the magnitude (±0.4 TECU).

4.4. Properties of the Gravity Wave Period

The propagation period is a primary property of GWs. Figure 6 and Figure 7 show the period characteristics obtained using the S transform [14,24]. The occasion of perturbation observed by PRN 2 is around 15:00 for most stations, which is consistent with the left panel of Figure 5. The frequency of the disturbances is 1–2 mHz, corresponding to a period of 8.3–16.7 min, which is exactly the range of GWs induced by thunderstorms [6].

The majority of stations with large magnitudes of disturbances are those in Hong Kong. The stations named GDZH and GUAN are located in south Guangdong, adjacent to Hong Kong, so their disturbances are similar. The GDSG station is located in northern Guangdong. GDSG station observes small-magnitude GWs with similar periods to the Hong Kong station at about the same time.

The disturbance can be obtained from the GNSS signal only when the IPP trajectory intersects with the GW propagation trajectory. Geometrically, there is only one possible encounter between two objects moving in the same direction with different speeds. The eastward direction of the IPP motion of PRN 2 and PRN 6 is similar to the direction of GW propagation but at different speeds. Therefore, theoretically, these two motions only intersect once, i.e., the disturbance can be observed only at one particular time.

The multiple IPP trajectories of PRN 5 intersects the GW propagation direction at multiple locations; thus, the disturbance is more likely to be observed multiple times. The observation of PRN 5 is shown in Figure 7. The IPPs of five stations (JXHK, FJPT, FJWY, XIAM, and JXJA) located in Jiangxi and Fujian, which are at the easternmost side, first sense the GW before 15:30. After that, the IPPs deviate from the GW-induced disturbance area as the satellite moved. Then, between 15:30 and 16:30, the IPPs of stations around Guangdong and Hong Kong fall into the GW region. Although these stations observe GWs at different times, the observed frequencies are all in the range of about 1–3 mHz (5.6–16.7 min).

As shown in Figure 7, two perturbation periods of about 6–9 min and 18 min exist for most of the stations. This is due to the fact that the obtained observations are the total number of electrons on the line between the GNSS station and the satellite. The signal passes through the top and bottom of the ionosphere successively. It is possible that the GW periods of 6–9 min are at the bottom of the ionosphere and GW periods of around 18 min at the top. The continuous excited GWs lead to the simultaneous presence of perturbations of different periods in the ionosphere.

The GWs with periods of 6–9 min are only significantly observed by PRN 5 but not PRN2. One possible reason is that the main propagation direction of the GW with a period of 6–9 min is east–south, intersecting only the trajectory of PRN 5.

4.5. The Relationship between GW Propagation Distance and Period

To further determine the periodic characteristics, the theory that the period of GWs in the atmosphere varies with the propagation distance is introduced. Equation (2) indicates that different ionospheric heights produce inconsistencies in the theoretical values of the wave period. As shown in Figure 8, the four colored solid lines indicate the theoretical periods of GWs versus horizontal propagation distance for different ionospheric thin-shell assumptions. In the legend, 60 km and 90 km represent the bottom and top of the ionospheric layer D, and 150 km and 450 km represent the bottom and top of layer F. Layer E is between layers D and F. The wave source location is set to 111°E, 23°N, which is the central region of the thunderstorm during 13:00–15:00 on April 3. The distance marked on the horizontal axis is the Euclidean distance between the location of the IPP and the center of the thunderstorm in the WGS-84 coordinate system.

The three subplots in Figure 8 represent the observations of PRN 2, 5, and 6, respectively. From the observations at the Hong Kong station indicated by the black scattered points in Figure 8, it can be seen that the disturbance observed at PRN 5 is closest to the center of the thunderstorm, PRN 2 is the next closest, and PRN 6 is the farthest. This is consistent with that shown in Figure 4.

In the left panel, most of the measured horizontal propagation distances of GWs lie between 250 and 500 km, between the blue and yellow lines. This reveals that the observed GWs are mainly present at the D, E, and bottom of the F layers.

In comparison with PRN 2 and PRN 6, PRN 5 observes this disturbance from a wider length range. In the range of horizontal propagation distance less than 500 km, the disturbances have periods of 6–20 min. When the distance is greater than 500 km, only disturbances with a period of 10 min or more are observed. The disturbances are present in almost the entire region from the D to F layers. The purple line of the PRN5 subplot of Figure 8, enveloping the measured values, indicates the variation of the shortest period with horizontal distance. The envelope line is located between 150 km and 450 km of ionospheric altitude. By the black and green scatters and the four solid lines, it can be inferred that the higher the region where the ionospheric GWs exist, the longer the period. The GNSS measurements show that there are longer periods of GWs with the increase of propagation distance, which is consistent with the propagation theory of GW.

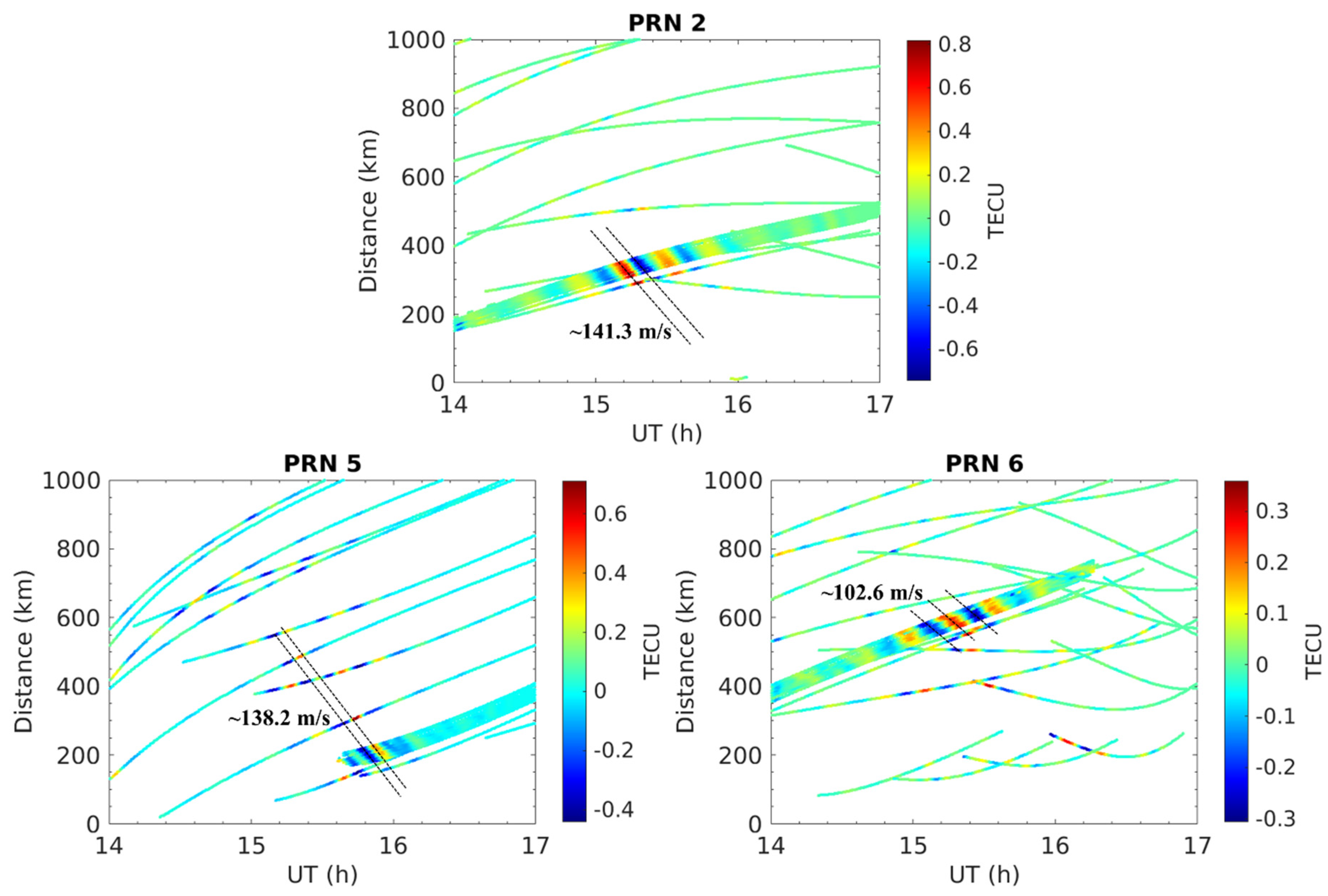
4.6. Properties of the Propagation Velocity of Perturbation

When GWs propagate into the ionosphere, the measured TECU exhibits clear wave-like structures, as shown in Figure 9. The peaks and troughs of the disturbed region are imaged on the IPP trajectory at different moments and different propagation distances, making it possible to estimate the propagation speeds of the GWs.

In Figure 9, the wave peaks or troughs on the IPP at different stations are fitted linearly. The slope of the fitted line is the propagation speed of the GWs [15,17]. For instance, 141.3 m/s is measured by PRN 2, 138.2 m/s by PRN 5, and 102.6 m/s by PRN 6, as shown in Figure 9. The disturbance observed by PRN 2 is during 15:00–16:00 and propagates at a distance of 200–400 km. During the same period, the disturbances observed by PRN 6 are located at a propagation distance of 600 km, which means that the IPP of PRN 6 is further from the source of the thunderstorms at this time slot. This indicates more than one type of GWs generated by the thunderstorms and the different IPP distances observing the waves with different wave propagation speeds.

The observation of PRN 5 is located close to 16:00, around 200 km. Although the measured wave speeds of PRN 2 and 5 are close, they are observed at different times and places. PRN 2 firstly observes a disturbance with a speed of ~140 m/s at a further location before PRN 5 captures a disturbance with a slower speed at a closer location. This implies that the satellites are not observing the same GWs but successively excited GWs. In conjunction with Figure 2, it can be shown that both the thunderstorm and its generated GWs possess temporal continuity.

5. Discussion

5.1. Extraction Methods of Gravity Waves and the Observability at Low Latitudes

The GWs perturbations triggered by thunderstorms in the GNSS signals at low-latitude regions are difficult to be extracted separately. However, the present study successfully demonstrates that GWs perturbations at low latitudes can be retrieved and analyzed by using appropriate methods.

Firstly, for the accurate calculation of ionospheric perturbations, the accuracy of using only code observations is insufficient. If only carrier smoothing pseudorange is used, the hidden cycle slips or gross errors of the carrier phase may be difficult to detect, leading to an abrupt change in the TEC calculation. This abrupt change could bring in otherwise non-existent periodic terms through Hatch filtering. To avoid this issue, the detection of cycle slips using only the time difference of the carrier can be utilized to calculate the ionospheric perturbations with relatively high accuracy [17,18].

Secondly, polynomial fitting can remove the long-period trend, and it is a necessary step to extract short-period ionospheric perturbations [25]. At mid-latitudes, this approach is effective [6,7]. However, at low latitudes, due to the complex ionospheric variations, the disturbances of TEC obtained after detrending only by polynomial fitting still contain multiple periods. Therefore, the employment of band-pass filters is necessary to extract the perturbations for a known range of periods [8,10,15]. Studies [6,26] have shown that GWs can be observed at night with the aid of bandpass filters, both at mid and low latitudes. Statistical studies have proved the validity of such methods [9,10].

If the geomagnetic field is active on that day, the mixed perturbations may be introduced into the TEC, causing inaccurate GWs extraction. The Dst index shows that the range of the geomagnetic is −33 to 5 nT and the Kp index is lower than 5 from March 29 to April 5, 2019, both indicating that the geomagnetic is quiet. Therefore, the TEC results of this study can exclude the effects of large-scale geomagnetic disturbances.

A detailed analysis that GWs at ~114°E, 24°N are indeed triggered by thunderstorms is given in this paper. Besides, in Figure 3, disturbances with a period of 20 min are present over Vietnam and Laos (~105°E, 18°N). There is no evidence that the disturbances are associated with thunderstorms. Similar disturbances propagating in the southwest–northeast direction are also observed at low latitudes in China [27]; meanwhile, the southwest-oriented Traveling Ionospheric Disturbances (TIDs) are observed in India [28]. There are possible causes for this kind of TID: (1) the electric field excites the Electrical Medium-Scale TID (EMSTID) propagating southwestward in the northern hemisphere [29]; and (2), these disturbances are caused by the perturbation of the neutral winds [30].

5.2. Periodic Characteristics and Perturbation Magnitudes

Some studies have shown that the GWs driven by thunderstorms are less than 20 min, and the periods of GWs triggered from the troposphere are about 20 min [31]. High frequency (period 4 min) shocks exhibits when a thunderstorm passes [7]. The disturbances with infrasound periods of 1–5 min could be found during thunderstorms [8]. Besides, some studies suggested that the period should be 15 min to 1 h [32]. At 150 km high, there are GWs of 0.2–1 mHz (16.7–83.3 min) with 0.4–1.5TECU. At 250 and 375 km, there are secondary GWs of 0.2–0.5 mHz (33.3–83.3 min) with 0.2–0.6 TECU [33]. GWs of 30–100 min have been shown for low-latitude thunderstorms in China [11], while the perturbation period is longer than one hour in West Africa [12].

In our study, the right panel of Figure 2 and Figure 3 show that waves with periods of 6–20 min exist in the presence of thunderstorms. Further, the propagation theory of GWs in the atmosphere is introduced to confirm that the waves are very likely triggered by those thunderstorms within a certain distance.

Notably, the left panel of Figure 2 and Figure 3 shows that longer period disturbances are present both on thunderstorm days and non-thunderstorm days. This suggests that some long-period disturbances are not dependent on thunderstorms.

For the magnitude of GWs, Erin et al. [6,9] and Rahmani et al. [34] use 0.08 TECU as the threshold, which is also used in this paper for the 6–16 min perturbation. In Figure 5 and Figure 9, PRN 6 has the smallest perturbation magnitude; however, it reaches 0.3 TECU, which exceeds the threshold of 0.08 TECU [9] and can therefore be judged as a GW perturbation.

For the periods of the perturbations longer than 20 min, the magnitudes of perturbation are 0.5–1.5 TECU during the day in West Africa [12] and even up to 10 TECU or 100 TECU in low latitude China [11] during the night. The presence of inherent long-period perturbations at low latitudes may be caused by the PRE during sunset [35] or a nighttime plasma bubble due to upward currents [36]. Numerous studies have shown that the magnitude of perturbations propagating from the atmosphere to the ionosphere is quite low [13,14,15,17,37,38]. Therefore, in our study, the extreme perturbations of TECUs are treated as anomalies.

Large magnitudes of perturbations found during the thunderstorms are highly likely caused by the cycle slips in GNSS receivers when the ionosphere is disturbed. The measured TEC in this scenario may have large biases due to lightning [11]. However, the ionosphere at low latitudes is unstable, and the presence of thunderstorms or strong convective weather may exacerbate this instability, resulting in larger magnitudes of long-period perturbations [9,10,39]. Both of these scenarios can produce larger GNSS signal perturbations, which are not directly caused by GWs from thunderstorms.

5.3. Properties of the Propagation Speed

The theory and results of Vadas and Liu [22] show that most of the GWs that originated from the bottom atmosphere have propagation speeds of less than 250–300 m/s. Studies of the typhoon-induced TID show the wave propagation velocity from 118–186 m/s [15] and around 240 m/s [13]. Song et al. [38] give wave velocities that are 143 m/s and 268 m/s for two types of TID during a typhoon. In our cases, we show that the wave propagation speeds during thunderstorms are from 102 m/s to 141 m/s. Extreme weathers like typhoons and thunderstorms have in common that the characteristics of the dynamics time scales are comparable. Therefore, the wave triggered by the extreme weathers may have similar propagation velocities, i.e., both less than 250–300 m/s. However, propagation velocities larger than 150 m/s were not found in this study. This is most likely because the waves with propagation velocities larger than 150 m/s may exist but are not captured due to the sparse deployment stations. BeiDou’s geostationary orbit (GEO) satellite may provide a solution to this problem [40,41].

6. Conclusions

This study shows an effective method to exact small ionospheric perturbations from GNSS signals and presents clear cases that the GWs induced by thunderstorms can be observed from low latitudes by GNSS. The characteristics of the GWs triggered by low-latitude thunderstorms in terms of wave magnitudes, periods, and proparation speed are provided. The main conclusions are as follows:

(1) Ionospheric GW structures in low latitudes China are detectable by GNSS by proper methods, and the characteristics of the ionospheric GWs can be extracted from the complex variations of the low-latitude ionosphere.

(2) Tropospheric thunderstorms can drive ionospheric perturbations with magnitudes of 0.2–0.8 TECU and periods of 6–20 min. The disturbance is temporally located 1–2 h after the peak of the thunderstorm and spatially located 200–800 km from the center of the thunderstorm. The propagation velocity is less than 250–300 m/s, indicating that the observed GWs are propagated from the bottom atmosphere to the ionosphere.

(3) The theory of GW period variation with propagation distance in the atmosphere is introduced. The variation of the theoretical period with propagation distance of the model is consistent with the observed period, indicating that GWs triggered by the thunderstorms have impacts on the distant ionosphere from the thunderstorms, not directly above the thunderstorms.

This analytical framework can be equally applied to the analysis of GWs triggered by thunderstorms or strong convection in other regions. In addition, this study illustrates that GWs can be observed both during the day and at night. For sustained thunderstorms, GWs can be continuously activated, leading to different periodic perturbations of the ionosphere at different altitudes. The presence of GWs both with and without thunderstorms should be caused by other physical processes.

In this paper, ionospheric acoustic waves (disturbances of less than 6 min period) and disturbances larger than 20 min are not included. At low latitudes, the correlation between such disturbances and thunderstorms and the validation of physical models are still to be further investigated.