An Optimized Deep Neural Network for Overhead Contact System Recognition from LiDAR Point Clouds
Abstract
:1. Introduction
- High efficiency: The measurement of LiDAR accelerates OCS recognition compared with manual measurement. LiDAR point clouds do not require as much processing time as high-resolution images produced by cameras;
- High reliability: Irrelevant interferents are easily filtered by LiDAR, such as the SICK LMS511-20100 PRO LiDAR employed in this article. For example, the measurement error of the LMS511-20100 PRO LiDAR reaches the millimeter level. High measurement accuracy enables high reliability for OCS recognition;
- Low requirements: LiDAR has almost no requirements on the measurement environment, such as lighting conditions, while computer vision methods have strict requirements for light conditions.
- High computational complexity: The above methods usually use complex model structures to improve the accuracy of OCS recognition. The complex algorithm structures increase the computational complexity;
- High latency: As the above methods have more computational operations, their latency is higher than simple models. They are also rarely accelerated to achieve low inference latency on embedded systems;
- High model complexity: Due to the intensive computation, the above methods have a high model complexity, which is a burden for embedded devices.
- (1)
- We designed a lightweight neural network, EffNet, to segment point clouds for OCS recognition. EffNet was integrated with ExtractA, AttenA, and AttenB. The three modules have different functions and handle different tasks separately; that is, when features need to be extracted, we employed the ExtractA module. We adopted the AttenA module when it was necessary to make information flow in neural networks and extract features, simultaneously. We used the AttenB module when needing to focus on attention mechanism efficiency. Benefiting from these three modules, EffNet increased the mean recognition accuracy of point clouds by 0.57% for OCS recognition with lower model/computational complexity and a higher speed than others;
- (2)
- We optimized EffNet with a generation framework of tensor programs (Auto-scheduler) to further accelerate it and adapted to different device architectures. The Auto-scheduler can generate corresponding tensor programs for each subgraph, according to defined tasks. Then, the tensor programs were auto-tuned with RPC, which uses the computing power of a high-performance host for fast calculation. The host conducted the reproduction, crossover, and mutation of the configuration parameters relying on a learnable cost and an evolutionary search model. The host generated possibly higher-quality tensor programs. The tensor programs were adapted to different hardware architectures on devices through different technologies such as LLVM and CUDA. Then, with iterative tuning on the host, we could obtain the best-performing tensor program, which had the least latency when running on the embedded devices;
- (3)
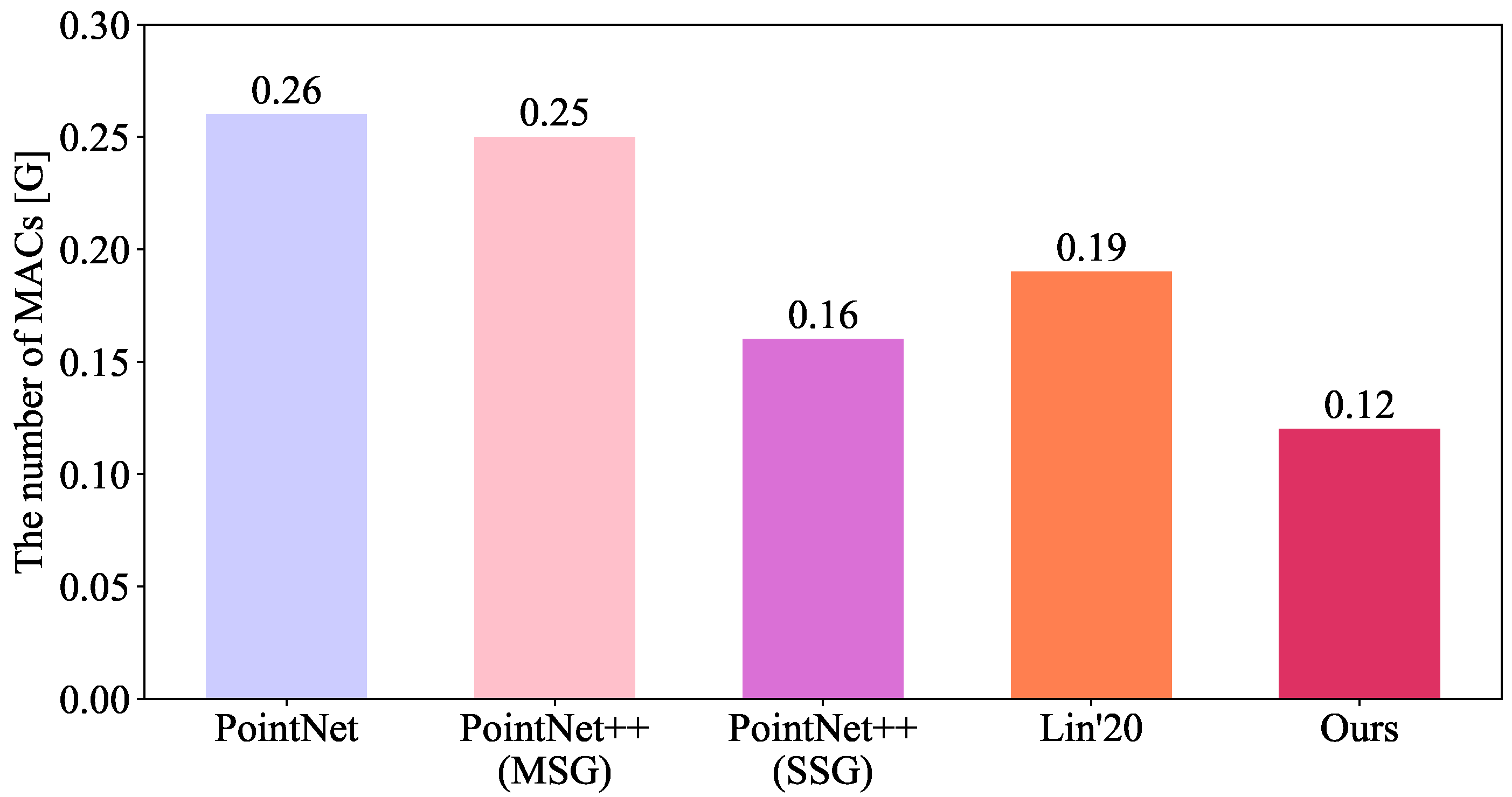
- We performed extensive experiments to validate EffNet on different architectures in complex high-speed railway scenarios. The experiments confirmed that EffNet is effective at recognizing point clouds for OCS recognition. EffNet also matches different architectures. The mean accuracy of EffNet was at least 1.13% higher in the intersection over union (IoU) than that of similar methods. The optimized EffNet had the same accuracy and computational/model complexity as before. Compared with other methods, the optimized EffNet obtained the same accuracy range, but its model and computational complexities were at least 9.30% and 25.00% lower. In addition, the optimized EffNet reduced the inference latency by 91.97%, 51.97%, 82.58%, 56.47%, 63.63%, and 85.85% on the RTX 2,080 Ti GPU, Nano CPU, Nano GPU, TX2 CPU, UP Board CPU, and TX2 GPU, respectively.
2. Related Work
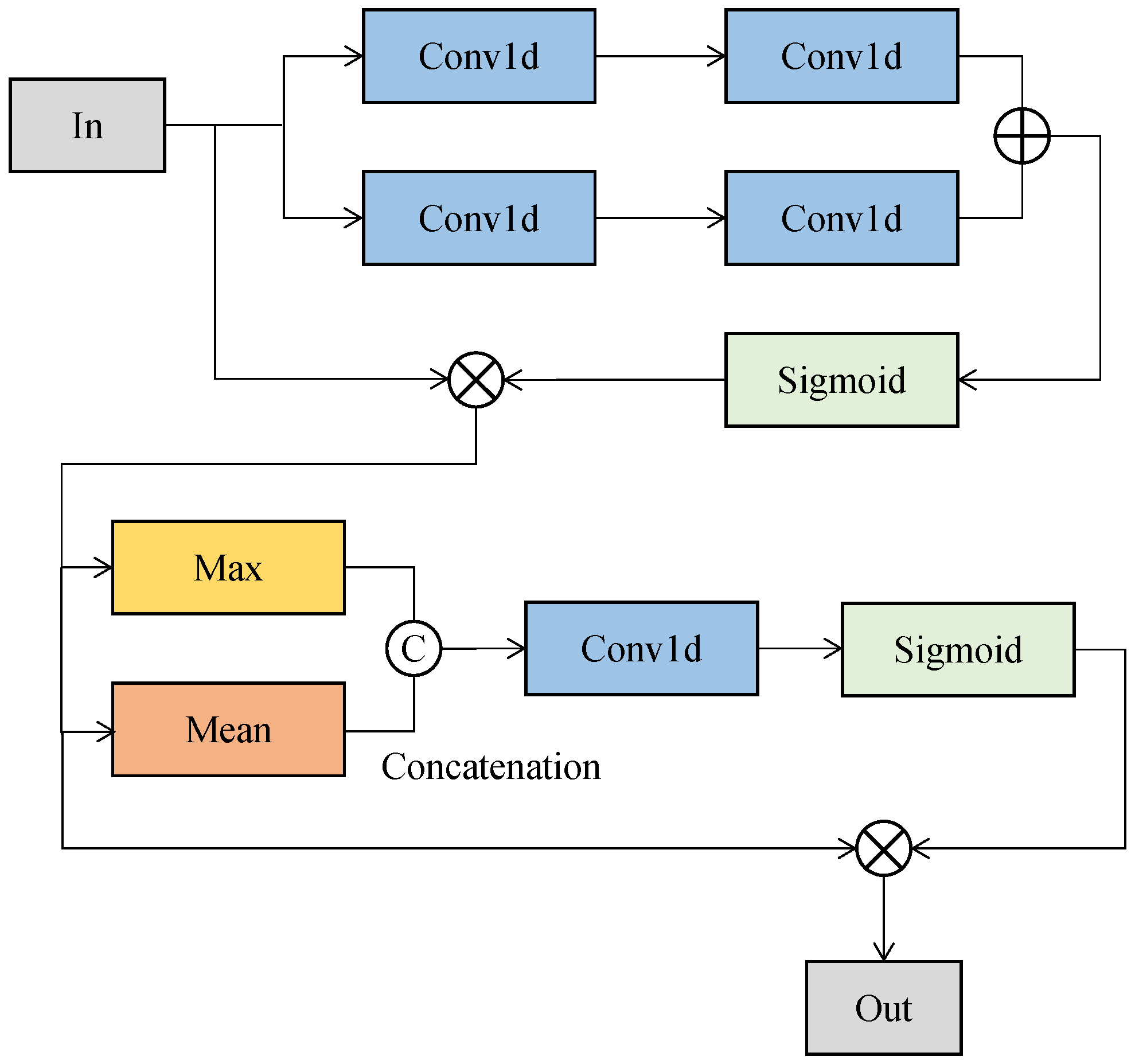
3. Proposed Methods
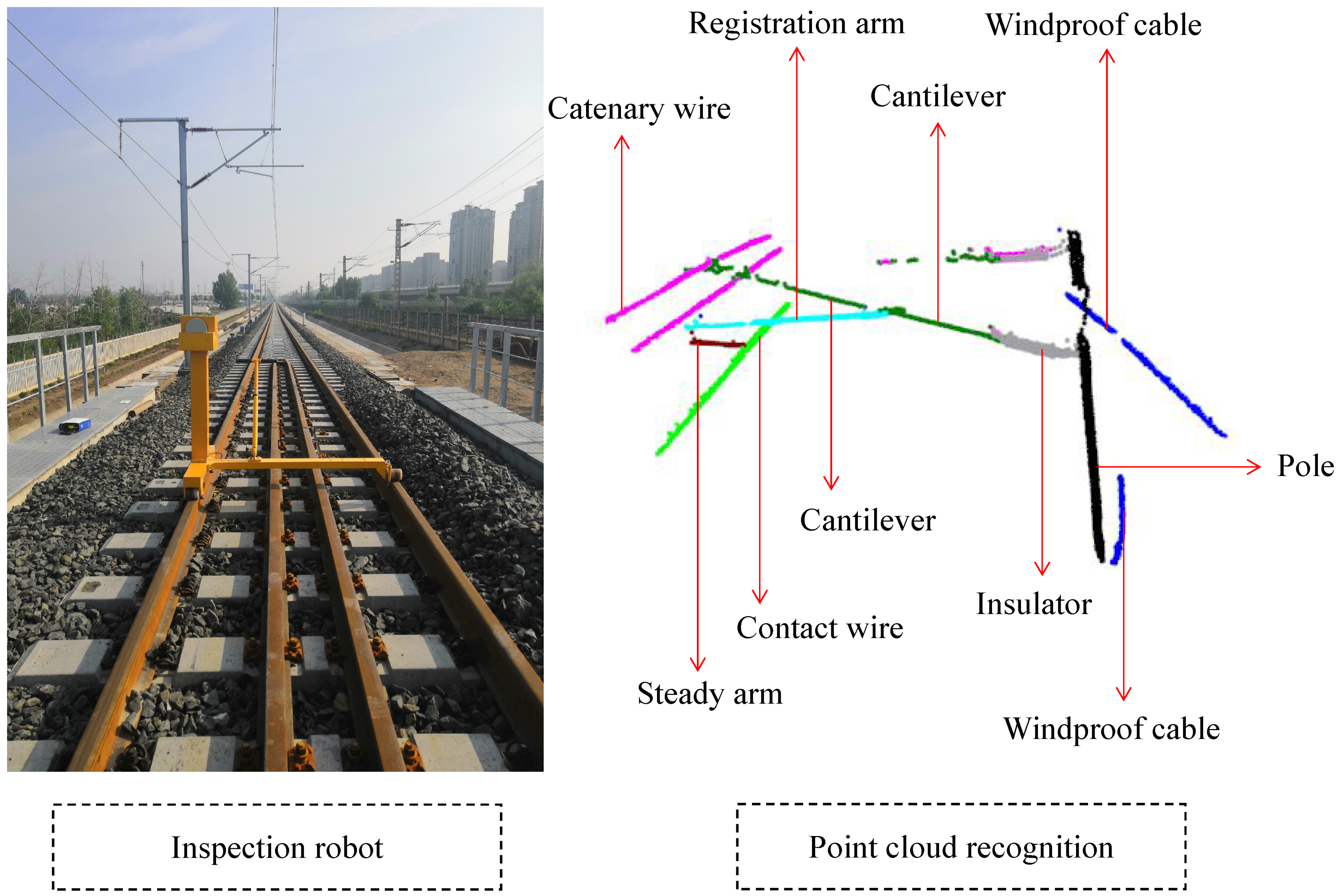
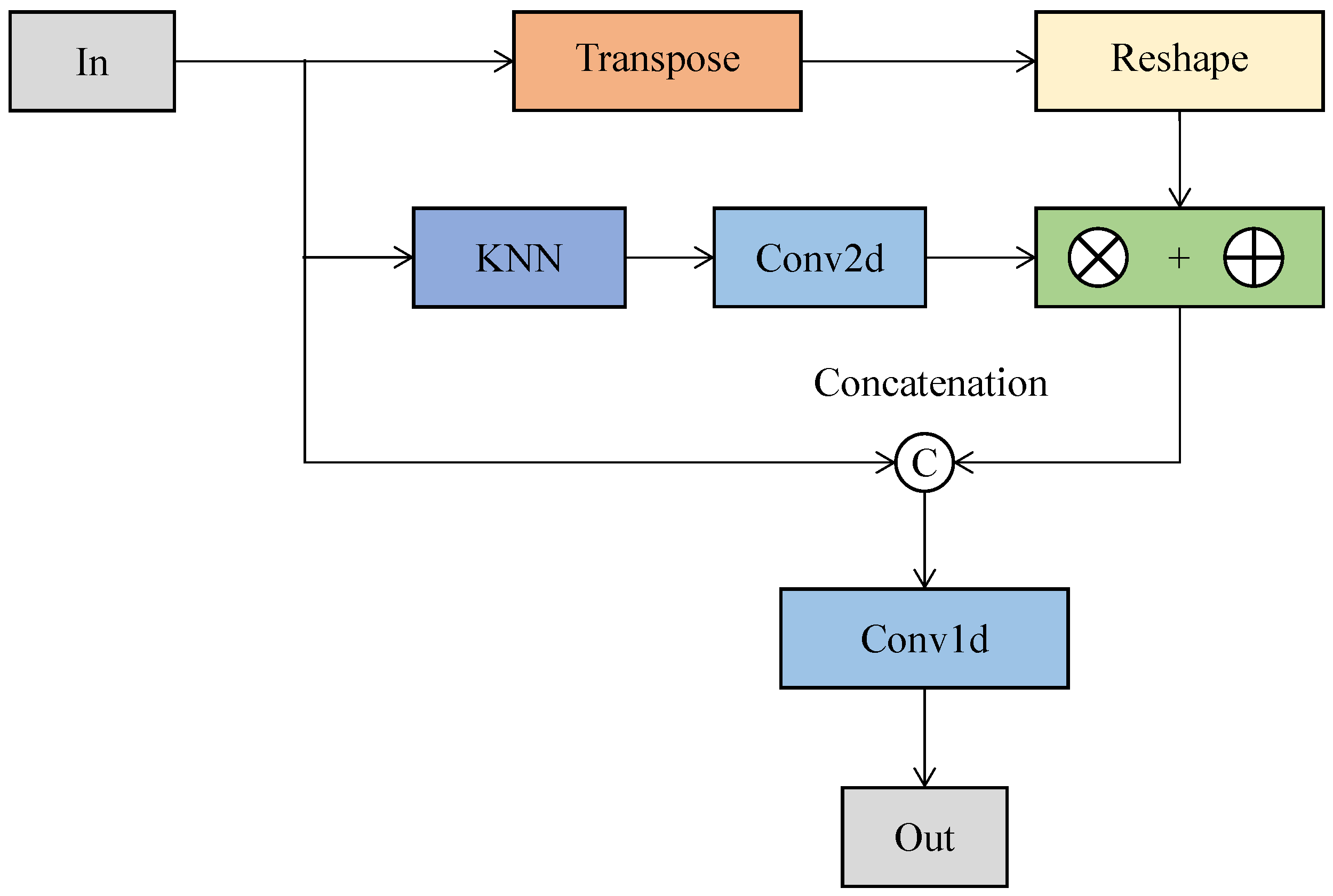
3.1. Recognizing Point Clouds
- Assume that each point is a center point;
- Calculate the distance value between the center point and neighboring points in a 3D coordinate system;
- Sort these distance values in the order of smallest to largest;
- Select the top M points (, where k = ) according to the sorted results;
- Construct a local region containing the center point and first M points near it.
3.2. Accelerating Recognition of Point Clouds
4. Experiments
4.1. Real Experimental Scenarios
4.2. Evaluating the Accuracy Results
4.3. Evaluating the Number of Parameters and MACs
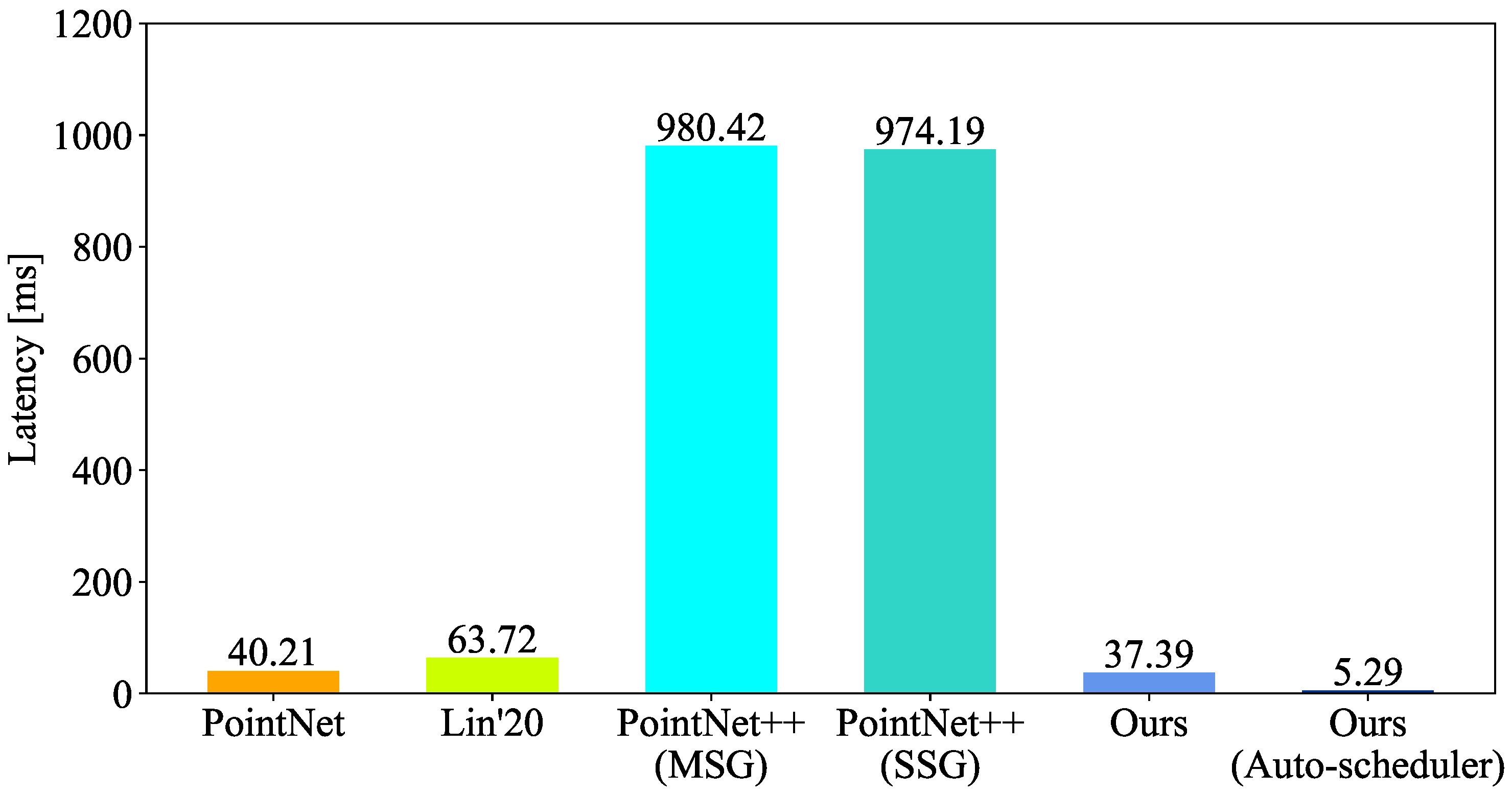
4.4. Evaluating the Latency on Different Platforms
4.5. Evaluating the Visualized Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tian, Y.; Chen, L.; Song, W.; Sung, Y.; Woo, S. DGCB-Net: Dynamic Graph Convolutional Broad Network for 3D Object Recognition in Point Cloud. Remote Sens. 2021, 13, 66. [Google Scholar] [CrossRef]
- Pierdicca, R.; Paolanti, M.; Matrone, F.; Martini, M.; Morbidoni, C.; Malinverni, E.S.; Frontoni, E.; Lingua, A.M. Point Cloud Semantic Segmentation Using a Deep Learning Framework for Cultural Heritage. Remote Sens. 2020, 12, 1005. [Google Scholar] [CrossRef] [Green Version]
- Arastounia, M. Automated Recognition of Railroad Infrastructure in Rural Areas from LIDAR Data. Remote Sens. 2015, 7, 14916–14938. [Google Scholar] [CrossRef] [Green Version]
- Tang, Y.C.; Li, L.J.; Feng, W.X.; Liu, F.; Zou, X.J.; Chen, M.Y. Binocular vision measurement and its application in full-field convex deformation of concrete-filled steel tubular columns. Measurement 2018, 130, 372–383. [Google Scholar] [CrossRef]
- Kang, G.; Gao, S.; Yu, L.; Zhang, D. Deep Architecture for High-Speed Railway Insulator Surface Defect Detection: Denoising Autoencoder With Multitask Learning. IEEE Trans. Instrum. Meas. 2019, 68, 2679–2690. [Google Scholar] [CrossRef]
- Tu, X.; Xu, C.; Liu, S.; Xie, G.; Li, R. Real-Time Depth Estimation with an Optimized Encoder-Decoder Architecture on Embedded Devices. In Proceedings of the IEEE 21st International Conference on High Performance Computing and Communications, Zhangjiajie, China, 10–12 August 2019; pp. 2141–2149. [Google Scholar] [CrossRef]
- Wei, X.; Jiang, S.; Li, Y.; Li, C.; Jia, L.; Li, Y. Defect Detection of Pantograph Slide Based on Deep Learning and Image Processing Technology. IEEE Trans. Intell. Transp. Syst. 2020, 21, 947–958. [Google Scholar] [CrossRef]
- Han, Z.; Yang, C.; Liu, Z. Cantilever Structure Segmentation and Parameters Detection Based on Concavity and Convexity of 3-D Point Clouds. IEEE Trans. Instrum. Meas. 2020, 69, 3026–3036. [Google Scholar] [CrossRef]
- Pastucha, E. Catenary System Detection, Localization and Classification Using Mobile Scanning Data. Remote Sens. 2016, 8, 801. [Google Scholar] [CrossRef] [Green Version]
- Tu, X.; Xu, C.; Liu, S.; Li, R.; Xie, G.; Huang, J.; Yang, L.T. Efficient Monocular Depth Estimation for Edge Devices in Internet of Things. IEEE Trans. Ind. Inform. 2021, 17, 2821–2832. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 77–85. [Google Scholar] [CrossRef] [Green Version]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5099–5108. [Google Scholar]
- Chen, Y.; Liu, G.; Xu, Y.; Pan, P.; Xing, Y. PointNet++ Network Architecture with Individual Point Level and Global Features on Centroid for ALS Point Cloud Classification. Remote Sens. 2021, 13, 472. [Google Scholar] [CrossRef]
- Lin, S.; Xu, C.; Chen, L.; Li, S.; Tu, X. LiDAR Point Cloud Recognition of Overhead Catenary System with Deep Learning. Sensors 2020, 20, 2212. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Altman, N.S. An Introduction to Kernel and Nearest-Neighbor Nonparametric Regression. Am. Stat. 1992, 46, 175–185. [Google Scholar] [CrossRef] [Green Version]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.L.; Yang, Y.B. SA-Net: Shuffle Attention for Deep Convolutional Neural Networks. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Toronto, ON, Canada, 6–11 June 2021; pp. 2235–2239. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is All you Need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Curran Associates, Inc.: Nice, France, 2017; Volume 30, pp. 6000–6010. [Google Scholar]
- Zheng, L.; Jia, C.; Sun, M.; Wu, Z.; Yu, C.H.; Haj-Ali, A.; Wang, Y.; Yang, J.; Zhuo, D.; Sen, K.; et al. Ansor: Generating High-Performance Tensor Programs for Deep Learning. In Proceedings of the 14th USENIX Symposium on Operating Systems Design and Implementation, Banff, AB, Canada, 4–6 November 2020; pp. 863–879. [Google Scholar]
- Lattner, C.; Adve, V. LLVM: A compilation framework for lifelong program analysis & transformation. In Proceedings of the International Symposium on Code Generation and Optimization, Palo Alto, CA, USA, 20–24 March 2004; pp. 75–86. [Google Scholar] [CrossRef]
- Garland, M.; Le Grand, S.; Nickolls, J.; Anderson, J.; Hardwick, J.; Morton, S.; Phillips, E.; Zhang, Y.; Volkov, V. Parallel Computing Experiences with CUDA. IEEE Micro 2008, 28, 13–27. [Google Scholar] [CrossRef]
- Vikhar, P.A. Evolutionary algorithms: A critical review and its future prospects. In Proceedings of the International Conference on Global Trends in Signal Processing, Information Computing and Communication, Jalgaon, India, 22–24 December 2016; pp. 261–265. [Google Scholar] [CrossRef]
- Chen, T.; Zheng, L.; Yan, E.; Jiang, Z.; Moreau, T.; Ceze, L.; Guestrin, C.; Krishnamurthy, A. Learning to Optimize Tensor Programs. In Proceedings of the Advances in Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018; Volume 31, pp. 3393–3404. [Google Scholar]
- Chen, L.; Jung, J.; Sohn, G. Multi-Scale Hierarchical CRF for Railway Electrification Asset Classification From Mobile Laser Scanning Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3131–3148. [Google Scholar] [CrossRef]
- Tu, X.; Xu, C.; Liu, S.; Lin, S.; Chen, L.; Xie, G.; Li, R. LiDAR Point Cloud Recognition and Visualization with Deep Learning for Overhead Contact Inspection. Sensors 2020, 20, 6387. [Google Scholar] [CrossRef] [PubMed]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, Y.; He, K. Group Normalization. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar] [CrossRef]
- Chen, M.; Tang, Y.; Zou, X.; Huang, K.; Li, L.; He, Y. High-accuracy multi-camera reconstruction enhanced by adaptive point cloud correction algorithm. Opt. Lasers Eng. 2019, 122, 170–183. [Google Scholar] [CrossRef]







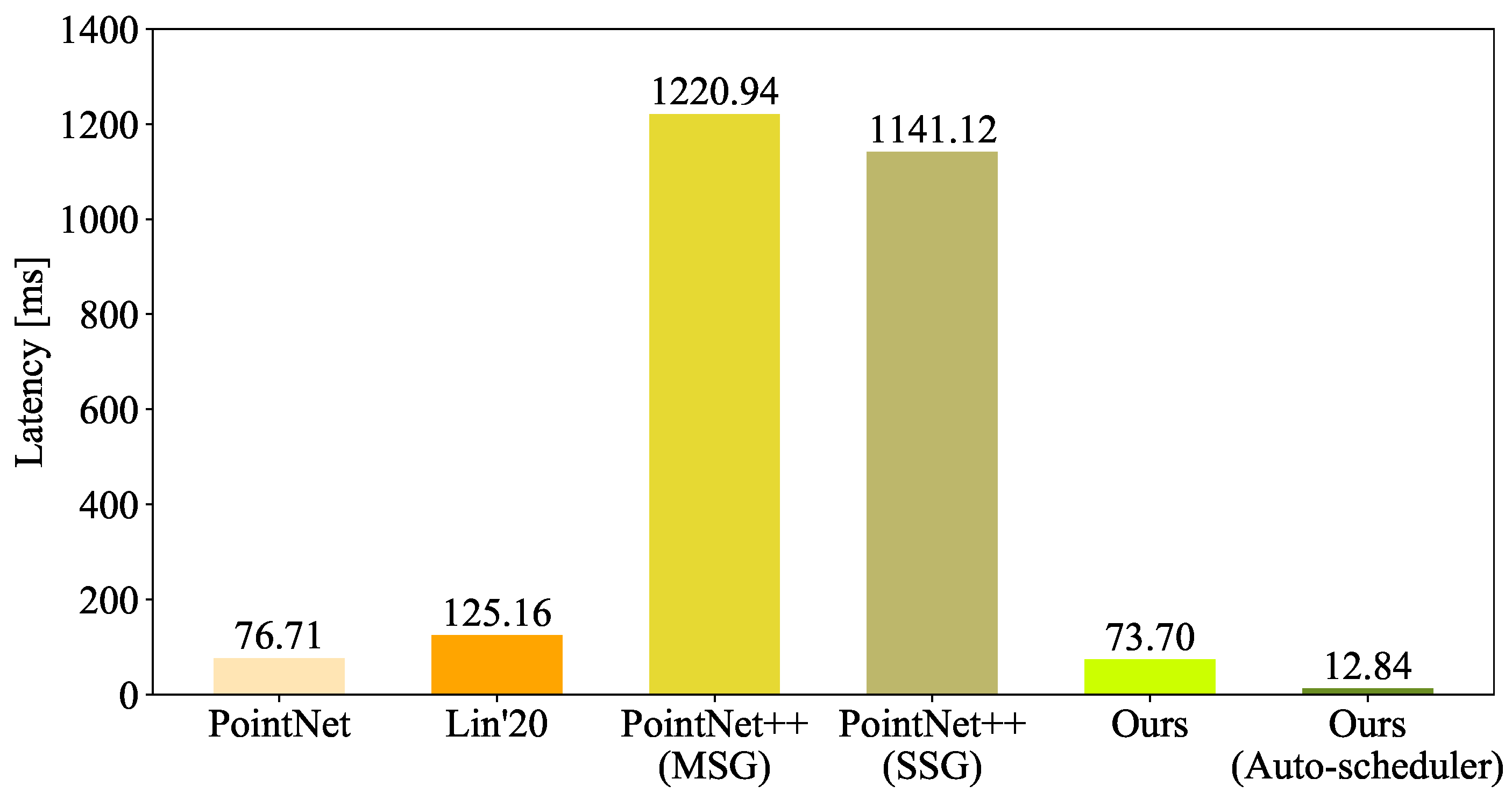
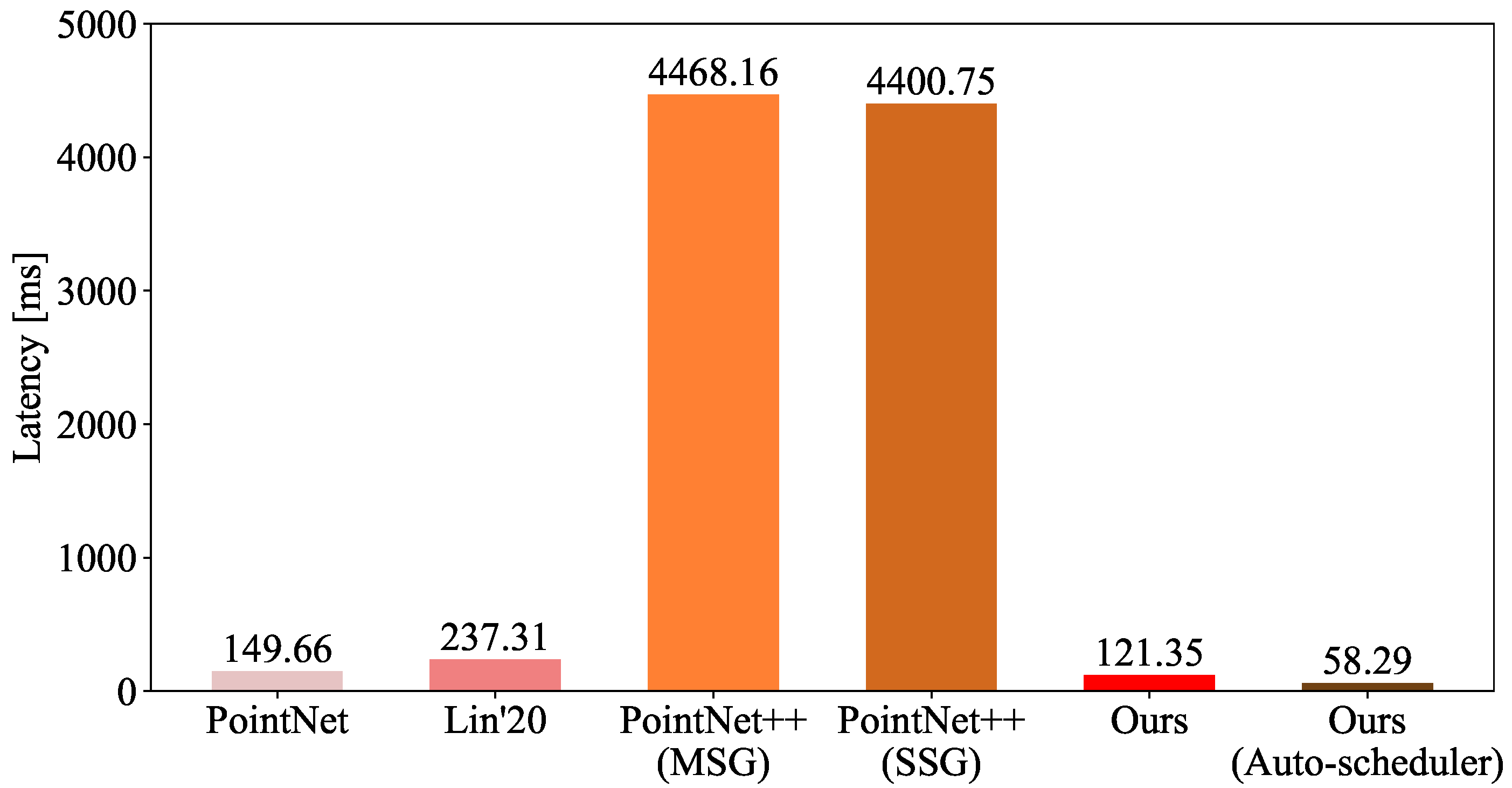



| Method | Accuracy | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | Mean |
|---|---|---|---|---|---|---|---|---|---|---|
| PointNet | Precision | 99.73 | 98.99 | 99.14 | 96.03 | 89.67 | 92.02 | 93.59 | 87.03 | 94.52 |
| IoU | 99.34 | 98.12 | 98.74 | 91.68 | 76.84 | 82.23 | 88.64 | 77.87 | 89.18 | |
| PointNet++(SSG) | Precision | 99.85 | 98.57 | 99.37 | 97.26 | 97.22 | 91.12 | 95.42 | 92.60 | 96.42 |
| IoU | 99.65 | 97.93 | 98.28 | 94.45 | 93.15 | 83.33 | 89.83 | 87.88 | 93.06 | |
| PointNet++(MSG) | Precision | 99.86 | 98.61 | 99.51 | 97.10 | 96.96 | 90.80 | 95.39 | 93.38 | 96.45 |
| IoU | 99.64 | 98.06 | 98.47 | 94.21 | 93.72 | 84.51 | 90.61 | 87.75 | 93.37 | |
| Lin et al. [14] | Precision | 99.80 | 99.45 | 99.79 | 97.36 | 96.39 | 95.27 | 95.23 | 92.81 | 97.01 |
| IoU | 99.64 | 99.16 | 99.60 | 93.59 | 91.91 | 86.44 | 92.11 | 87.23 | 93.71 | |
| Tu et al. [25] | Precision | 99.91 | 99.65 | 99.89 | 97.18 | 97.16 | 95.97 | 94.70 | 93.87 | 97.17 |
| IoU | 99.76 | 99.51 | 99.75 | 94.12 | 93.68 | 85.68 | 91.38 | 88.68 | 94.07 | |
| Ours | Precision | 99.91 | 99.87 | 99.87 | 98.96 | 97.13 | 95.90 | 95.54 | 94.78 | 97.72 |
| IoU | 99.81 | 99.74 | 99.74 | 96.01 | 93.01 | 88.44 | 93.11 | 91.43 | 95.13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Tu, X.; Xu, C.; Chen, L.; Lin, S.; Li, R. An Optimized Deep Neural Network for Overhead Contact System Recognition from LiDAR Point Clouds. Remote Sens. 2021, 13, 4110. https://doi.org/10.3390/rs13204110
Liu S, Tu X, Xu C, Chen L, Lin S, Li R. An Optimized Deep Neural Network for Overhead Contact System Recognition from LiDAR Point Clouds. Remote Sensing. 2021; 13(20):4110. https://doi.org/10.3390/rs13204110
Chicago/Turabian StyleLiu, Siping, Xiaohan Tu, Cheng Xu, Lipei Chen, Shuai Lin, and Renfa Li. 2021. "An Optimized Deep Neural Network for Overhead Contact System Recognition from LiDAR Point Clouds" Remote Sensing 13, no. 20: 4110. https://doi.org/10.3390/rs13204110
APA StyleLiu, S., Tu, X., Xu, C., Chen, L., Lin, S., & Li, R. (2021). An Optimized Deep Neural Network for Overhead Contact System Recognition from LiDAR Point Clouds. Remote Sensing, 13(20), 4110. https://doi.org/10.3390/rs13204110






