1. Introduction
It is generally considered that clouds play one of the primary roles in climate by mediating short wave and long wave radiative fluxes [
1,
2,
3]. Clouds are also crucial for the hydrological cycle on both a global and regional scale [
4]. Cloud cover plays a vital role in regulating climatic feedback and thus cloud cover may be exploited as a diagnostic in sensitivity studies of climate models in different scenarios. Cloud cover variability over the ocean is a key variable for understanding global and regional circulation phenomena and modes of variability, such as monsoons, ENSO (El Niño Southern Oscillation), Intertropical Convergence Zone (ITCZ) shift, North Atlantic Oscillation (NAO), and Pacific Decadal Oscillation (PDO). Clouds also strongly impact sea-air interactions in boundary currents zones and upwelling zones [
5,
6].
Clouds also play a major role in various processes, like solar power production and air traffic dispatching. In scientific observations, clouds may be unavoidable obstacles. In satellite observations, clouds mask land and ocean surface, thus significantly decreasing the rate of useful satellite information about the surface in cloud-rich regions. In optical observations in land-based astronomy, clouds are unavoidable obstacles as well [
7,
8]. Thus, accurate estimating and forecasting of cloud characteristics is crucial for observational time planning [
9,
10].
There are a number of data sources available for studies of clouds in the ocean. Among the most frequently used are remote sensing archives, data from reanalyses, and observations made at sea from research vessels and voluntary observing ships. Each of these data sources have their own advantages and flaws. Satellite observations may be considered accurate, and they are uniformly scattered spatially and temporally, though their time series are limited as they started only in the early 1980s [
11,
12,
13,
14,
15,
16]. Satellite measurements are also characterized by different flaws, e.g., underestimating cloudiness over sea ice in nighttime conditions [
17] which may be significant in the Arctic. Data from reanalyses is uniformly sampled as well. However, although the models applied in reanalyses for diagnostic cloud cover estimation continuously improve, they need further development and validation [
17,
18]. Reanalyses were shown to underestimate total cloud cover compared to measurements provided by land-based weather stations, and observations over the ocean [
17,
19]. A possible cause of this underestimation may be the overestimated downward short-wave radiation that is taken into account within the computations for cloud coverage [
20]. It is worth mentioning, however, that in some particular cases reanalyses may be consistent with meteorological stations data in terms of the low-frequency temporal variability of cloud characteristics [
21].
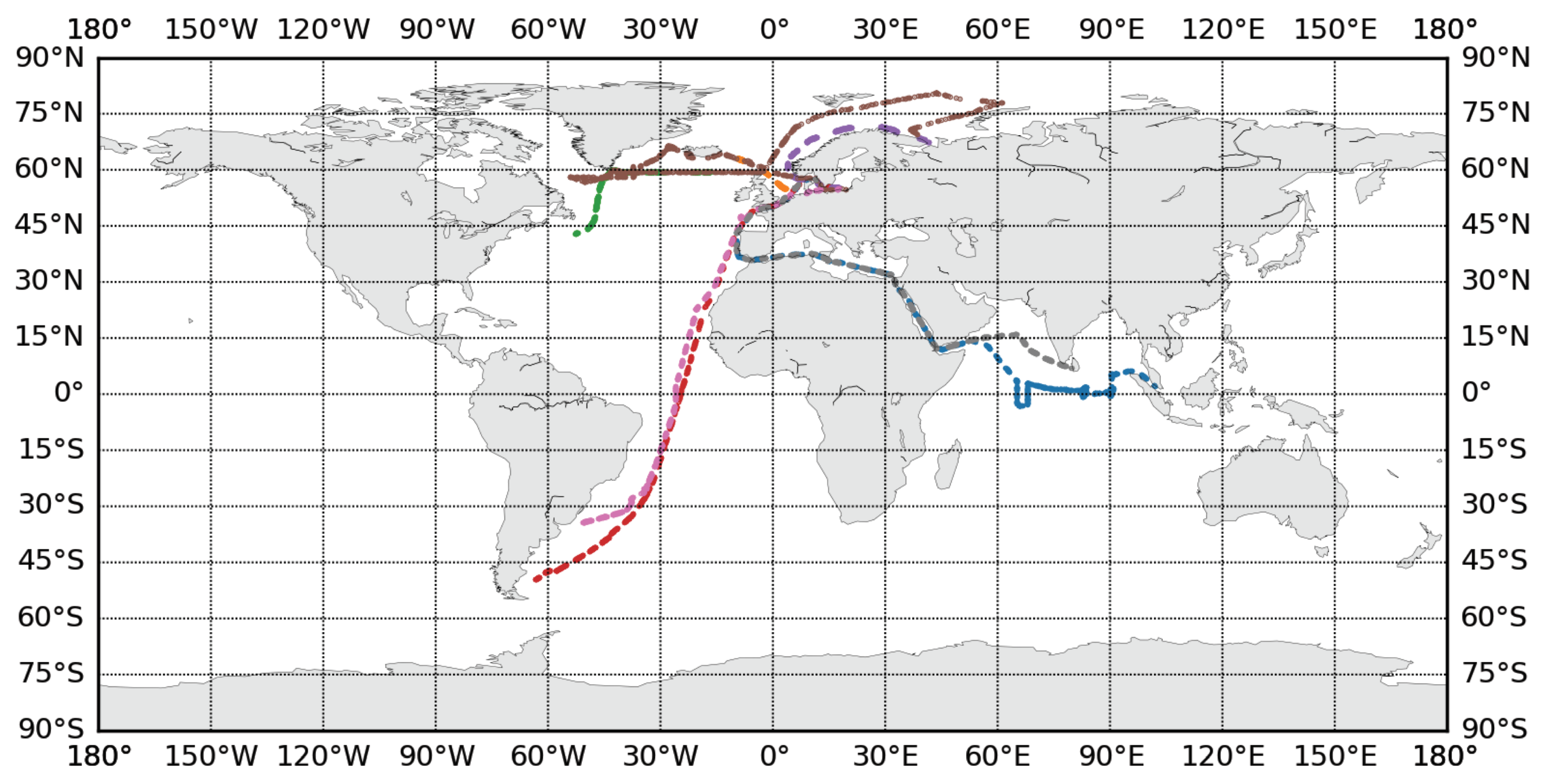
The best data source for climatological studies of clouds is the archive of observations made from Voluntary Observing Ships (VOS) which are organized into the International Comprehensive Ocean-Atmosphere Data Set (ICOADS) [
22,
23]. The very first visual observations at sea were made in the middle of the nineteenth century, though there were not many before the twentieth century. Most studies use the ICOADS observations dated from the early 1950s [
24,
25,
26]. The change of cloudiness codes in the late 1940s [
27] reduces the validity of climatic studies relying on long-term homogeneity of the time series of cloudiness characteristics over the ocean in the twentieth century. The key disadvantage of the ICOADS records is their temporal and spatial inhomogeneity. Most observations are made along the major sea traffic routes in the North Atlantic and North Pacific. In contrast, the central regions of the Atlantic and Pacific are not covered by measurements tightly enough. The Southern ocean coverage is poor as well [
28].
Visual observations of clouds are considered the most reliable at the moment [
29,
30]. The observations over the ocean are conducted every three or every six hours at UTC time divisible by 3 h. This procedure provides four or eight measurements a day per observing ship. Observed parameters include Total Cloud Cover (TCC) and low cloud cover, the morphological characteristics of clouds, and an estimate of cloud-base height. The total cloud coverage is estimated by a meteorology expert based on the visible hemisphere of the sky. To estimate the total cloud cover, the expert considers the temporal characteristics of the clouds being observed along with their additional parameters, e.g., precipitation, preceding types of clouds, light scattering phenomena, etc. For TCC retrieval, the observer visually estimates the fraction of the sky dome occupied by clouds. This procedure is described in detail in the WMO manual on codes [
29], the WMO guide on meteorological observations [
31], and in the International Cloud Atlas [
30]. The procedure for estimating TCC involves making a decision on whether to consider the gaps in the clouds through which the sky is visible as “sky” or as “cloud”. The decision is based on the cloud type. For example, the gaps are countered as “clear sky” in the case of low clouds or convective clouds, e.g., cumulus and stratocumulus clouds. In contrast, the sky gaps are not countered as “sky” in the case of cirrus, cirrocumulus, and almost all sub-types of altocumulus clouds. This feature of the TCC estimation procedure introduces uncertainty into the results of automated TCC retrieval schemes.
Cloud characteristics remain one of the few meteorological parameter subsets still observed by experts visually whereas most of the other indices are measured automatically today. The procedure is hard to automate due to the high amount of non-formalized rules of thumb and heuristics that are learned by an expert as a result of long-term practice. This way an expert estimating cloud characteristics adjusts their understanding of cloud formation processes, relates them to the state of clouds theory, and learns how the observed visuals correspond to the underlying physics dictated by the theory. The whole expert experience results in a somewhat consistent measurement of quantitative characteristics that are recommended by WMO as the most reliable source of information about clouds. The flaws of the approach of visual estimation are: It suffers from subjectivity; the learning curve mentioned above may result in biased estimates; and the approach itself is highly time-consuming and requires massive human resources even today, in the era of Artificial Intelligence and advanced computer vision.
In this study, we discuss mostly the problem of data-driven TCC retrieval, although the classification of observed clouds is also an intriguing problem addressed in a number of studies employing data-driven methods along with expert-designed and fused approaches [
32,
33,
34,
35,
36,
37].
1.1. On the Optimization Nature of the Known Schemes for TCC Retrieval from All-Sky Optical Imagery
A number of automated schemes were proposed in last 20 years, beginning with the pioneering work of Long et al. presented along with the optical package for the all-sky imagery retrieval in 1998 [
38] and described in detail in 2006 [
39]. Since the first scheme of Long et al., numerous variations of algorithms were described for estimating some quantitative characteristics based on different in situ measurements such as all-sky imagery [
38,
40,
41,
42,
43,
44,
45] or downward short-wave radiation [
46]. Most of these algorithms are designed by experts integrating their own understanding of the physical processes that result in all-sky imagery similar to the ones presented in
Figure 1a,b.
Given all-sky imagery acquired, in most simple cases, an index is calculated pixel-wise, e.g., red-to-blue ratio (RBR) in a series of papers by Long et al. [
38,
39,
47] or in the following studies [
48,
49,
50], or the ratio
in [
42,
43,
51], or even a set of indices [
52]. Then, an empirical threshold is applied for the classification of pixels into two classes: “cloud” and “clear sky”. A few schemes with a more complex algorithm structure were presented recently [
41,
45,
47,
53,
54]. These schemes were introduced mostly for tackling the flaw of simple yet computationally efficient schemes: Taking the sun disk and the circumsolar region of an all-sky image as “cloud”.
In contrast with the expert-designed algorithms for TCC retrieval, only a few data-driven schemes have been presented lately for estimating TCC [
55,
56,
57] or for clouds segmentation in optical all-sky imagery [
58]. Researchers may consider the problem of TCC retrieval to be solved or to be too simple to address with complex machine learning algorithms. However, none of the presented approaches demonstrated any significant improvement in the quality of TCC estimation.
The only exception here is the method presented by Krinitskiy [
57] which claimed to achieve an almost human-like accuracy in TCC estimation. There is, however, an error at the validation stage resulting in incorrect quality assessment. This study may be considered a corrigendum to the conference paper of Krinitskiy [
57].
At this point we need to note, that the so-called data-driven methods for the approximation of some variable (say, TCC) do not differ considerably from the ones that are designed by an expert. An expert-designed method implies an understanding of the underlying processes that form the source data (say, optical ground-based imagery) and its features (say, relations between red, green, and blue channels of a pixel registering clear sky or a part of a cloud). Then, these human-engineered features are used in some sort of an algorithm for the computation of an index or multiple indices, which then are aggregated over the image to a quantitative measure. The algorithm may be considered simple [
38,
39,
42,
44,
54], adaptive [
45,
53], it may be designed to be complex to some extent in an attempt to take some advanced spatial features into account [
40,
41,
47,
49,
50], or in an attempt to correct the distortion of imagery or other features of imagery that are not consistent with the initial researcher’s assumptions [
42,
49,
50,
52]. However, all these methods rely on the aggregation step at some point that is commonly implemented as a variation of thresholding. The threshold value(s) is empirical and should be adjusted to minimize the error of TCC estimates or maximize the quality of the method that is proposed in the corresponding study. This adjustment stage is commonly described vaguely [
49] or briefly [
39], though in this sense, the above mentioned expert-designed algorithms are essentially data-driven and inherently have an optimization nature, thus the optimization is a key part of the development of these schemes.
In case of the schemes employing Machine Learning (ML) methods [
55,
56,
57], the algorithms are inherently of an optimization nature since the essence of almost any supervised ML algorithm is the optimization of empirical costs based on a training data set.
In the context of this study, the mentioned training dataset consists of ground-based all-sky imagery with corresponding TCC estimates ("labels" hereafter). These estimates were made by an expert in the field at the same time as the image was taken. It is worth mentioning that this labeling procedure is subject to noise. There are multiple sources of noise and uncertainties in labels and the imagery itself:
Subjectivity of an observer. As mentioned above, the whole prior expert experience may impact the quality of TCC estimates. The uncertainty introduced by a human observer has not been assessed thoroughly yet. We can only hope that this uncertainty is less than 1 okta (one eighth of the whole sky dome, the unit of TCC dictated by WMO [
29,
30]), though from the subjective experience of the authors, the uncertainty may exceed 1 okta when one scene is observed by multiple experts;
Violation of the observations procedure. Ideally, an expert needs to observe the sky dome in an environment clear from obstacles, which may not always be the case not only in strong storm conditions at sea, but even in the case of land-based meteorological stations. In our study, every record made in hard-to-observe conditions was flagged accordingly, thus no such record is used in the filtered training, validation, and test datasets;
Temporal discrepancy between the time of an observation and the time of acquisition of corresponding imagery. This time gap can never be zero, thus a decision always needs to be made on whether is small enough to be considered negligible, and the expert records to be considered correct for the corresponding all-sky image;
Reduced quality of imagery. There is always room for improvement in the resolution of optical cameras, their light sensitivity, and corresponding signal-to-noise ratio in low-light cases (e.g., for registering in nighttime conditions). The conditions of imagery acquisition may play a role as well, since raindrops, dust, and dirt may distort the picture significantly and may be considered strong noise in source data;
Reduced relevance of the acquired imagery to the TCC estimation problem. It should be mentioned that in storm and high waves conditions in the ocean, an optical package tightly mounted to the ship may partly register the sea surface instead of the sky dome. In our experience, the inclination may reach 15°, and even 25° in storm conditions. This issue, along with the uncertain heading of the ship, also prevents the computation of the exact sun disk position in an all-sky image;
Reduced relevance of the acquired imagery to the labeling records. Ideally, the TCC labeling site should be collocated with the optical package performing the imagery acquisition. This is not exactly the case in some studies [
41].
All these factors may be considered as introducing noise to the labels or imagery of the datasets that are essentially the basis of all the data-driven algorithms mentioned above. The impact of these factors may be reduced by modifying the observation and imagery acquisition procedures, or by data filtering. Some factors may be addressed by the releases of more strictly standardized procedures for cloud observations, though the WMO guide seems strict and straightforward enough [
29,
30].
However, there are factors that are unavoidable, that were not mentioned above. Typical types of clouds and their amounts differ in various regions of the ocean. Typical states of the atmosphere and its optical depth differ significantly as well, strongly influencing the quality of imagery and its features. Statistically speaking, for the development of a perfect unbiased TCC estimator within the optimization approach, one needs to acquire a training dataset perfectly and exhaustively representing all the cases and conditions that are expected to be met at the inference phase. This requirement seems unattainable in practice. Alternatively, a data-driven algorithm is expected to have some level of generalization ability, thus being capable of inferring TCC for new images acquired in previously unmet conditions. The effect of significant changes in the source data is well known in machine learning and in the theory of statistical inference as covariate shift. The capability of an algorithm to generalize is called generalization ability. This ability may be expressed in terms of discrepancy between the quality of the algorithm assessed on different datasets within one downstream task.
1.2. On the Climatology of Clouds
Climatology of clouds shows a big difference between characteristics of clouds in various regions of the world ocean not only in terms of total cloud cover, but in terms of typical cloud types and their seasonal variability. In Aleksandrova et al. 2018 [
28], the climatology of total cloud coverage for the period of 1950–2011 is presented.
The climatology is based on ICOADS [
22,
23] data and limited to periods from January to March, and from July to September. In the tropics, the average TCC varies from 1.5 to 3 okta, whereas the average TCC in the middle latitudes and sub-polar regions ranges from 6.5 to 7.5 okta. In the middle latitudes and sub-polar regions of the ocean, seasonal variability results in an increase in TCC in summer compared to winter. In contrast, in the tropics and subtropics, the average TCC in summer is lower than in winter, which is especially noticeable in the Atlantic ocean. The most striking seasonal variations are registered in the Indian ocean, which is characterized by strong monsoon circulation. That is, in the northern regions of the Indian ocean, in winter dry seasons, the mean seasonal TCC varies from 1 to 3 okta, whereas in wet summer seasons the average seasonal TCC is from 5 to 6.5 okta. A time series of the total cloud coverage for distinct regions of the world ocean demonstrate significant differences in characteristics of the inter-annual variability of TCC. Cloud coverage in the southern Atlantic rarely drops below 80–90%, whereas the inter-annual seasonally averaged TCC variability may exceed 50%. In the central Pacific, some years may be considered outliers with TCC significantly exceeding the mean values due to ENSO [
26].
At the same time, averaged TCC values are not representative enough within the scope of our study. One needs to consider the regimes of cloudiness over the regions of the ocean. In the middle latitudes, both the regime of long-lasting broken clouds (4–6 okta), and the regime of interchanging short periods of overcast and clear-sky conditions may result in the same seasonal mean TCC. The diversity of the regimes of cloudiness may be shown by the empirical histograms of the fractional TCC for various regions of the world ocean (see [
28], Figure 5).
Types of clouds are not distributed evenly over the ocean as well. This feature strongly impacts the average TCC as well as the characteristics of the acquired imagery. The frequency of different types of clouds varies between the tropics, mid-latitudes, and sub-polar regions. The difference between the western and eastern regions of oceans is significant as well, especially when one considers low clouds [
59].
Cumulonimbus, denoted by two codes in the WMO manual on codes (
for
cumulonimbus calvus and
for
cumulonimbus capillatus) [
29] are observed frequently in the tropics, are rare in the mid-latitudes, and can almost never be registered in sub-polar regions of the world ocean. At the same time, there is a considerable difference even between the distributions of the two sub-types of cumulonimbus over the ocean: Records of
cumulonimbus calvus over the ocean are twice as frequent as those of
cumulonimbus capillatus. There is also a significant difference in spatial distributions of these two sub-types:
Cumulonimbus capillatus are registered sometimes in the North Atlantic and northern regions of the Pacific ocean, whereas
cumulonimbus calvus are observed almost only in the tropics and the equatorial zone.
Cumulonimbus calvus has a maximum frequency in the central regions of the oceans, whereas
cumulonimbus capillatus are more frequent in coastal zones.
Cumulus clouds include two WMO codes: for cumulus humilis and for cumulus mediocris or cumulus congestus. The frequency of cumulus clouds is high in the western and central regions of the subtropics and tropics of the oceans. In the mid-latitudes, cumulus clouds are not that frequent in general, and even less frequent in summer. There are however exceptions, which are the eastern part of the North Atlantic and the northern regions of the Pacific ocean, where cold-air outbreaks are more frequent, thus the conditions for cumulus clouds are more favorable. Generally, cumulus humilis are less frequent over the ocean compared to cumulus mediocris and cumulus congestus.
In contrast with
cumulus clouds,
stratus clouds are much more frequent in mid-latitudes (WMO codes
for
stratocumulus other than
stratocumulus cumulogenitus, and
for
stratus nebulosus or
stratus fractus other then
stratus of bad weather). They are also frequent in eastern regions of the subtropics over the ocean. In some studies, these two codes are considered as one type [
60,
61], however, their spatial distributions differ considerably.
Stratocumulus clouds (
) are registered most frequently in eastern regions of the oceans’ subtropical zones, whereas
stratus clouds (
) are mostly found in the mid-latitudes, especially in summer.
Stratus clouds (
) are rare in eastern regions of the subtropics (excluding some of the upwelling zones). There are also
stratus fractus or
cumulus fractus of bad weather (WMO code
), which are frequently observed in the mid-latitudes in winter, when the synoptic activity is strong. Sometimes, clouds of
are registered in the low latitudes, in the stratiform precipitation regions [
62].
Sometimes there are even no low clouds (WMO code ). This code is frequently registered in the coastal region of the ocean, in the Arctic, and the Mediterranean sea.
As one may notice from the brief and incomplete climatology of clouds above, different types of clouds are distributed very unevenly over the world ocean. If one collects a dataset in a limited number of the regions of the ocean for the optimization of a data-driven algorithm, the resulting scheme may lack quality in the regions that were not represented in the training set.
1.3. On Data-Driven Algorithms for TCC Retrieval from All-Sky Optical Imagery
A few data-driven methods were presented recently for estimating TCC from all-sky optical imagery [
55,
56,
58]. In [
56], the only improvement compared to simple schemes [
39] is the application of a clustering algorithm in the form of a superpixel segmentation step. This step allows the authors to transform the scheme to an adaptive one. However, one still needs to compute the threshold value for each superpixel. In [
58], a probabilistic approach for cloud segmentation is proposed employing Principal Components Analysis (PCA) approach along with the Partial Least Squares (PLS) model. The whole approach may be expressed as PLS-based supervised feature engineering resulting in the pixel-wise linearly computed index claimed to be characterizing the probabilistic indication of the “belongingness” of a pixel to a specific class (i.e., cloud or sky). For this index to be technically interpreted as a measure of probability, it is normalized to the
range linearly. The model described in this study is similar to logistic regression with the only reservation being that the log-regression model has strong probabilistic foundations resulting in both the logistic function and binary cross-entropy loss function. The logistic function naturally transforms the covariates to the probability estimates within the
range without any normalization. Thus, the model proposed in [
58] has questionable probabilistic foundations compared to well-known logistic regression. However, the study [
58] is remarkable, as it is the first (to the best of our knowledge) to formulate the problem of cloud cover retrieval as a pixel-wise semantic segmentation employing a simple ML method. In [
55], the authors employ the stat- of-the-art (at the time of the study) neural architecture namely U-net [
63] for semantic segmentation of clouds in optical all-sky imagery. The two latter approaches are very promising if one has a segmentation mask as supervision. It is worth mentioning that labeling all-sky images in order to create a cloud mask is very time-consuming. In our experience, this kind of labeling of one image may take an expert 15 to 30 min depending on the amount of clouds and their spatial distribution. To the best of our knowledge, no ML-based algorithms were presented that are capable of estimating TCC directly without preceding costly segmentation labeling.
One more issue with most of the presented schemes for TCC estimation is the lack of universal quality measure. In some studies, the quality measure is not even introduced [
52]. Other studies with the problem formulated as a semantic segmentation of clouds, employ typical pixel-wise quality measures adopted from computer vision segmentation tasks, such as Precision, Recall, F1-score, and misclassification rate [
56,
58]. This decision may be motivated by the models applied and by the state of the computer vision. However, the definition of a quality measure should never depend on the way the problem is solved. In some studies, the quality measures that are used are common for regression problems, e.g., correlation coefficient [
55], MSE (Root Mean Squared Error), or RMSE (Root Mean Squared Error) [
49]. In probability theory, these measures usually imply specific assumptions about the distribution of the target value (TCC), and also assumptions about the set of all possible outcomes and their type (real values). In the case of TCC, these assumptions are obviously not met. It is also obvious that the assessment of the quality of TCC retrieval by any valid algorithm (that does not produce invalid TCC) is biased for the events labeled as 8 okta or 0 okta. Since the set of possible outcomes of TCC is limited, any non-perfect algorithm underestimates TCC for the 8-okta events and overestimates TCC for the 0-okta events. Thus, any quality metric is biased by design as it is calculated using the deviation of the result of an algorithm from the expert label. We are confident that one should never use a biased-by-design quality measure. Thus, if one were to employ the quality measures of regression problems (MSE, RMSE, correlation coefficient, determination coefficient, etc.), it would be consistent with solving the problem as regression, which is not always the case for the studies mentioned above.
In our understanding, the problem of TCC retrieval should be formulated as a classification since the set of possible outcomes is finite and discreet. Alternatively, one may formulate the problem as ordinal regression [
64]. In these cases, accuracy (event-wise, rather than pixel-wise) or other quality measures for the classification problem may be the right choice. In our study, we balance the datasets prior to the training and quality assessment, thus accuracy may be considered a suitable metric. In the case of ordinal regression, the categorical scale of classes is implied, which shows an order between the classes. This is exactly the case in the problem of TCC retrieval, since the classes of TCC are ordered in such a way that the label “1 okta” denotes more clouds compared to the label “0 okta”; “2 okta” is more than “1 okta”, and so on. In this case, the conditional distribution of the target variable
is still not defined, which would be necessary for the formulation of a loss function and quality measures (MSE, RMSE, etc.) within the approaches of Maximum Likelihood Estimator or Maximum a Posteriori Probability Estimator, similar to regression statistical models. However, the “less or equal than one-okta error accuracy” (“Leq1A” hereafter) is frequently considered as an additional quality measure in the problem of TCC retrieval [
49,
55]. In our understanding, this metric is still not valid and may be biased due to the reasons given above, though we include its estimates for our results in order to be comparable to other studies.
In the context of the introduction given above, the contributions of our study are the following:
We present the framework for the assessment of the algorithms for TCC retrieval from all-sky optical imagery along with the results of our models;
We present a novel scheme for estimating TCC over the ocean from all-sky imagery employing the model of convolutional neural networks within two problem formulations: Classification and ordinal regression;
We demonstrate the degradation of the quality of data-driven models in the case of a strong covariate shift.
The rest of the paper is organized as follows: In
Section 2, we describe our Dataset of All-Sky Imagery Over the Ocean (DASIO); in
Section 3.1, we describe the neural models we propose in this study and the design of the experiment for the assessment of their generalization ability; and in
Section 4, we present the results of the experiment.
Section 5 summarizes the paper and presents an outlook for further study.
4. Results and Discussion
In this section, we present the results of the numerical experiments described in
Section 3. For each of the data-driven models proposed in this study, we performed the training and quality assessment several times (typically five to nine times) to estimate the uncertainty of the quality measures. The results in this section are presented in the following manner: First, in
Table 4, we present the results of the PyramidNet-based models PNetPC and PNetOR in the region-agnostic scenario for assessing the influence of the problem formulation. Then, in
Table 5, we present the results of the PNetOR model in both the region-agnostic and region-aware scenarios to assess the generalization ability in the case of a strong covariate shift.
In our study, we also performed the optimization and quality assessment of some of the known schemes mentioned in
Section 1.1 of the Introduction for a comparison with ours. This analysis was performed within the same framework as PNetPC and PNetOR. As mentioned in
Section 1.1, each of the schemes is essentially data-driven and has its own parameters (at least one) subjected to optimization based on a training subset. The schemes used for comparison are the ones that may be considered a baseline. In particular, we assessed the following algorithms:
The algorithm proposed by Long et al. in [
38,
39], which we name "RBR" hereafter after the main index proposed in these studies (red-to-blue ratio);
The algorithm proposed by Yamashita et al. in [
42,
43,
51], which we name "SkyIndex" hereafter after the index proposed in these studies.
As with the models proposed in this study (see
Section 3.3), we assessed the uncertainty of the schemes RBR and SkyIndex by training them and estimating their quality multiple times. The schemes RBR and SkyIndex are not as highly demanding computationally as PNetPC and PNetOR. Thus, we were able to repeat the procedure 31 times. The results of this quality assessment are presented in the
Table 5.
From the results presented in
Table 4, we can see that PNetOR is slightly superior. However, we need to mention that this superiority is not statistically significant, at least for such a small number of runs. In addition, in terms of
, PNetPC is slightly better than PNetOR. It is worth mentioning that state-of-the-art expert-designed schemes for TCC retrieval demonstrate a considerably lower quality level: In no fair conditions,
for them exceeds 30% [
49,
57]. In the scenarios employed in this study, the estimated accuracy did not exceed 27%. In
Table 5, we present more detailed quality characteristics of the RBR and SkyIndex’s schemes estimated within the proposed framework.
According to the considerations set out in
Section 1.3, RMSE may be a biased quality metric in the case of an ordered finite set of outcome values (e.g., TCC). In
Table 5, these metrics are provided for a comparative purpose only.
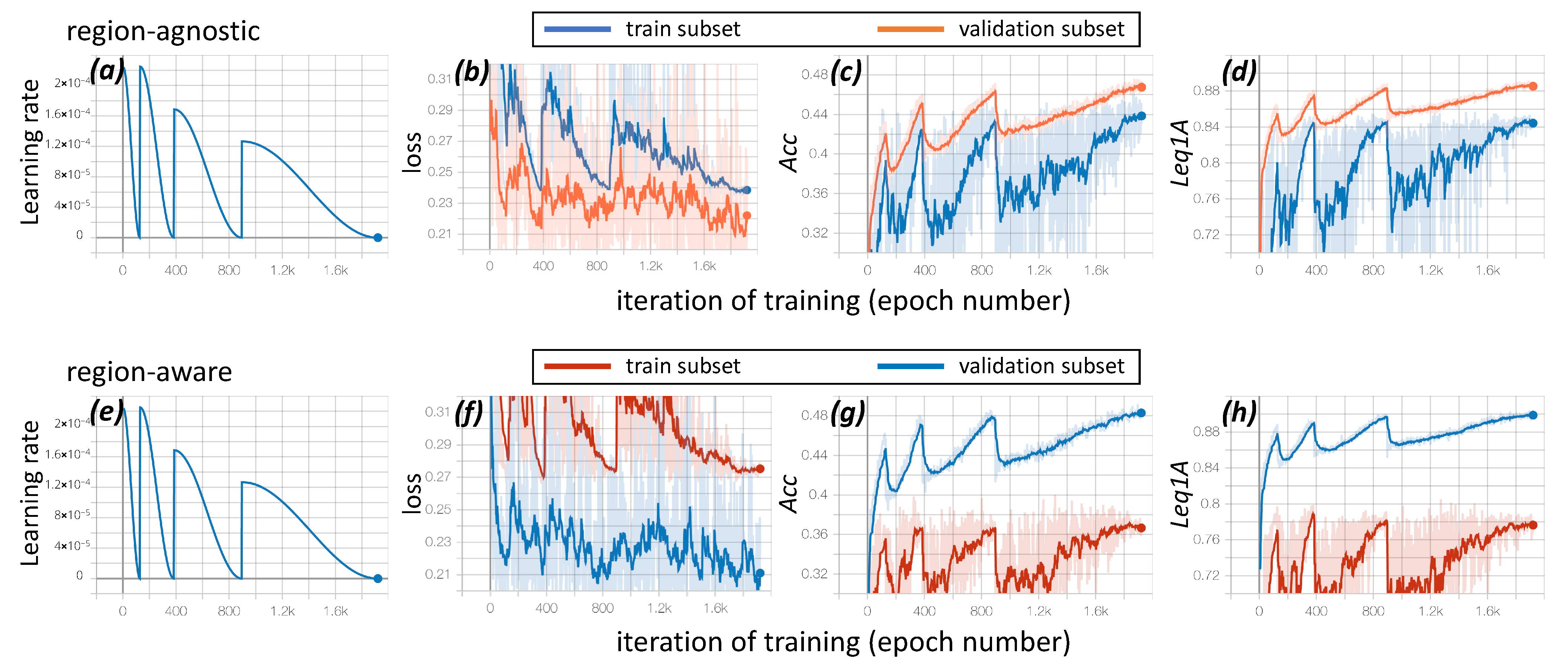
From the results presented in
Table 5, one can see a considerable difference in the gaps between training accuracy and its test estimate in different sampling scenarios. In the region-agnostic scenario, the gap is
, while in the region-aware scenario, the gap is
. We need to remind the reader that this gap is inevitable, and only a perfect model would deliver the same quality on the test set as on the training set (sometimes even better in some particular cases). However, as mentioned in
Section 3.3 (Experiment design), we assess a data-driven model’s capability to generalize in terms of these gaps. This means if the gap increases significantly, then the typical covariate shift between regions is too strong, and the combination of model flexibility and data variability guides a researcher to collect more data for the model to be applicable in a new region with an acceptable level of confidence. In the presented cases, a significant difference is noticeable.
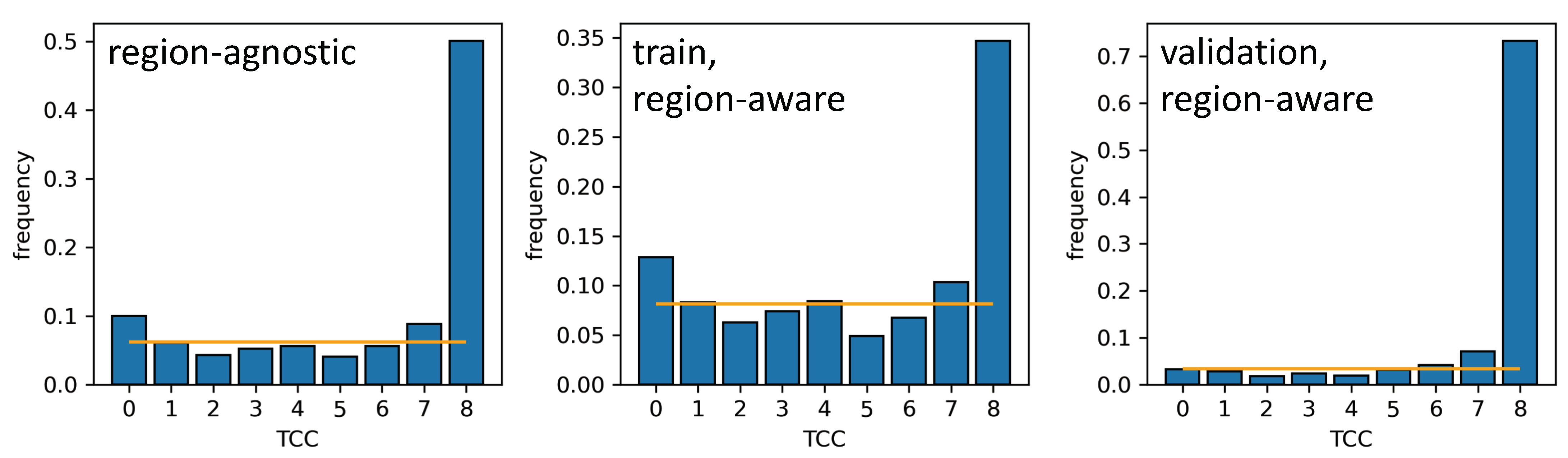
One possible reason for that may be a substantial disproportion of TCC classes in the region-aware test subset. One may conduct a hypothetical experiment of assessing the quality of a scheme that predicts 8 oktas disregarding the real skydome scene characteristics. The accuracy score of such an algorithm in high latitudes would be outstanding. However, this quality measure would be definitely unreliable. It is worth mentioning that our CNN-based approach is still superior to the previously published results even in this worst-case scenario of a strongly unbalanced test subset.
One may propose another possible reason for the significant increase in the quality gap between the region-agnostic and region-aware scenarios. In a routine study involving machine learning, the common reason for such a considerable quality gap would be overfitting. Indeed, convolutional neural networks may be engineered to have such high expressive power that they would be able to "memorize" training examples, demonstrating low quality on the test set. However, the concept of overfitting relies on the relations between the quality estimates on training and test samples that are drawn from the same distribution or at least on the samples demonstrating weak signs of covariate shift. This is the case in the region-agnostic scenario, where the sampling and subsetting procedures described in
Section 3.4.1 ensure that the data of training and test sets was at least acquired in similar conditions. In the region-aware scenario, training and test sets should be treated as having a substantial covariate shift, as discussed in
Section 1.2. Thus, the concept of overfitting per se cannot be applied in this case. On the contrary, such a significant increase in the quality gap between the region-agnostic and region-aware scenarios suggests a strong covariate shift in the latter case.
One may also notice that the thresholding-based schemes like RBR or SkyIndex demonstrate an outstanding generalization ability: The quality drops from training to test subsets do not differ much between region-agnostic and region-aware scenarios. However, the expressive power of these models is weak, and even in the worst-case scenario the PNetOR model demonstrates significantly higher quality in terms of all the presented measures.
5. Conclusions and Outlook for Future Study
In this study, we presented the DASIO collected in various regions of the world ocean. Some of the imagery is accompanied by cloud characteristics observed in situ by experts. We demonstrated that there was a strong covariate shift in this data due to the natural climatological features of the regions represented in DASIO. We proposed a framework for the systematic study of automatic schemes for total cloud cover retrieval from all-sky imagery. We also proposed quality measures for the assessment and comparison of the algorithms within this framework. We also presented a novel data-driven model based on convolutional neural networks of state-of-the-art architecture capable of performing the task of TCC retrieval from all-sky optical imagery. We demonstrated alternatives for the formulation of the TCC estimation problem: Classification and ordinal regression. The results demonstrated a slight superiority of the version based on ordinal regression. We assessed the quality measures of the proposed models guided by the framework we introduced. These data-driven models based on convolutional neural networks demonstrated a considerable improvement in TCC estimation quality compared to the schemes known from the previous studies.
Most importantly, in this study we proposed an approach for testing the generalization ability of data-driven models in TCC retrieval from the imagery of the DASIO collection. We demonstrated a considerable drop in the generalization ability expressed in terms of the gap between the train and test quality measures in the scenario implying close distributions of objects’ features compared to the scenario characterized by a strong covariate shift (∼4 and ∼12 percentage points accordingly). The considerable quality gap in the former scenario (namely “region-aware”) may indicate that specialized algorithms with high expressive power applied in regionally limited conditions may practically be of higher demand than the ones characterized by high generalization ability along with low accuracy. There is also an indication of a strong need for additional field observations in a greater variety of regions of the world ocean with the concurrent acquisition of all-sky imagery. This would help enrich the part of the DASIO collection with low TCC values.
In addition, although convolutional neural networks demonstrate impressive results in the problems of low-noise images recognition with strongly curated labeling information, in the TCC retrieval problem, a CNN model based on state-of-the-art architecture does not deliver that high quality being trained with the most-used tricks aimed for the improvement of generalization ability and training stabilization. The quality drop may also be due to noisy source data or uncertain labels. The issue of the labels’ uncertainty will be addressed in our future studies.
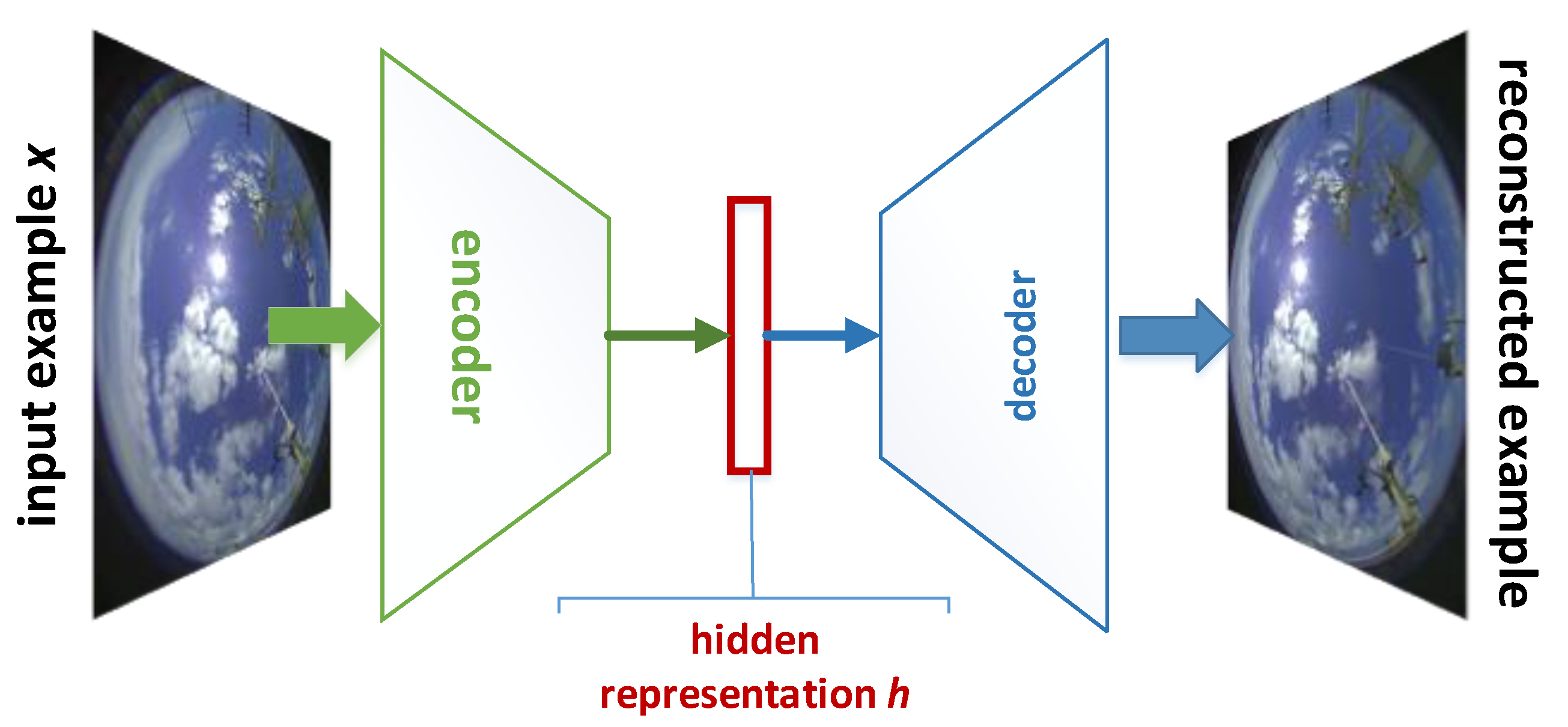
Several unanswered questions remain that may be addressed regarding data-driven models in the problems of retrieving cloud characteristics from the DAISO data. We will tackle the problems of estimating the cloud base height since the SAILCOP optical package allows us to acquire paired imagery. We also will assess the uncertainty of expert labels for TCC and other characteristics. This may be possible due to the presented CVAE model’s capability to preserve the proximity relations between examples of the dataset. One may assess the uncertainty of expert labels for similar examples identified with the use of CVAE. We will also continue the neural architecture search to find a CNN-based model that is balanced in quality and generalization. We will reproduce the results of all the previously published schemes for automatic TCC retrieval and assess their ability to generalize within the framework proposed in this study. We will also formulate a similar approach for the assessment of automated algorithms for cloud type identification.