Regional Modeling of Forest Fuels and Structural Attributes Using Airborne Laser Scanning Data in Oregon
Abstract
1. Introduction
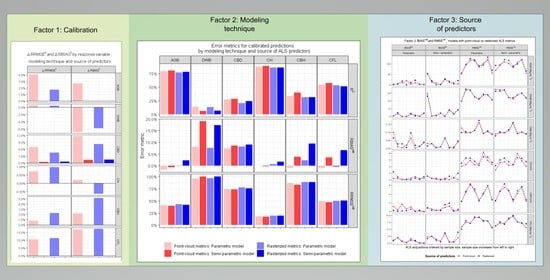
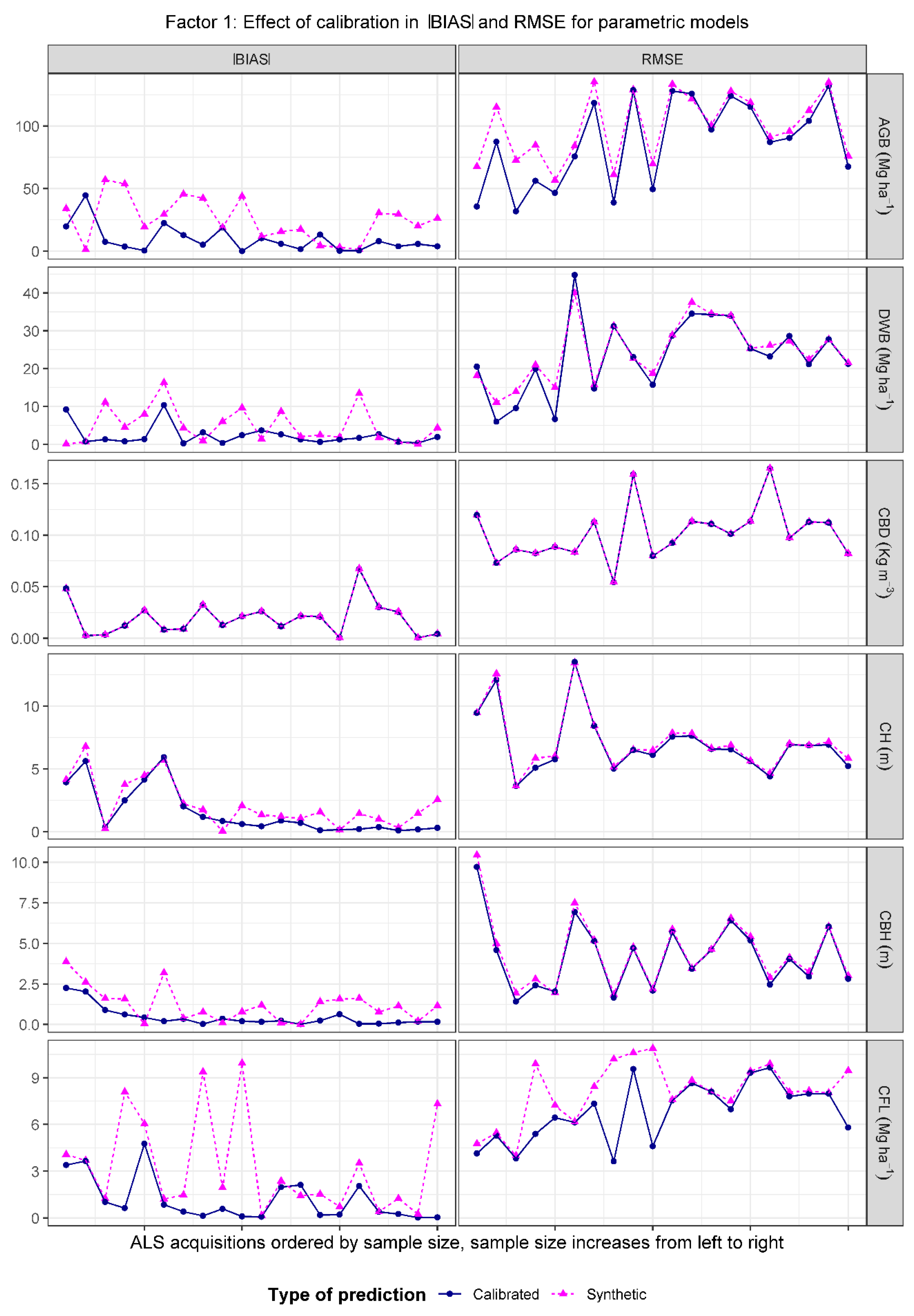
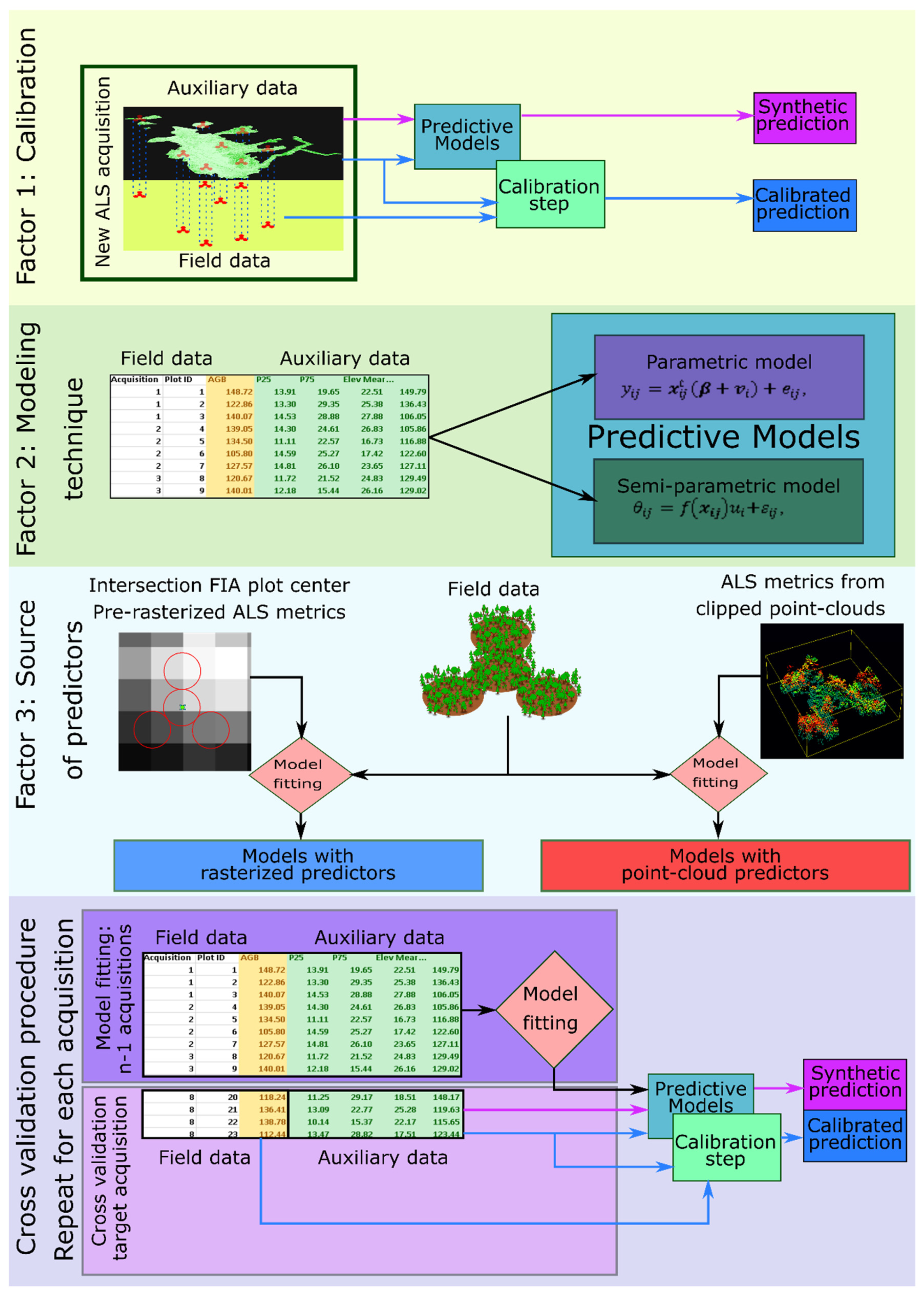
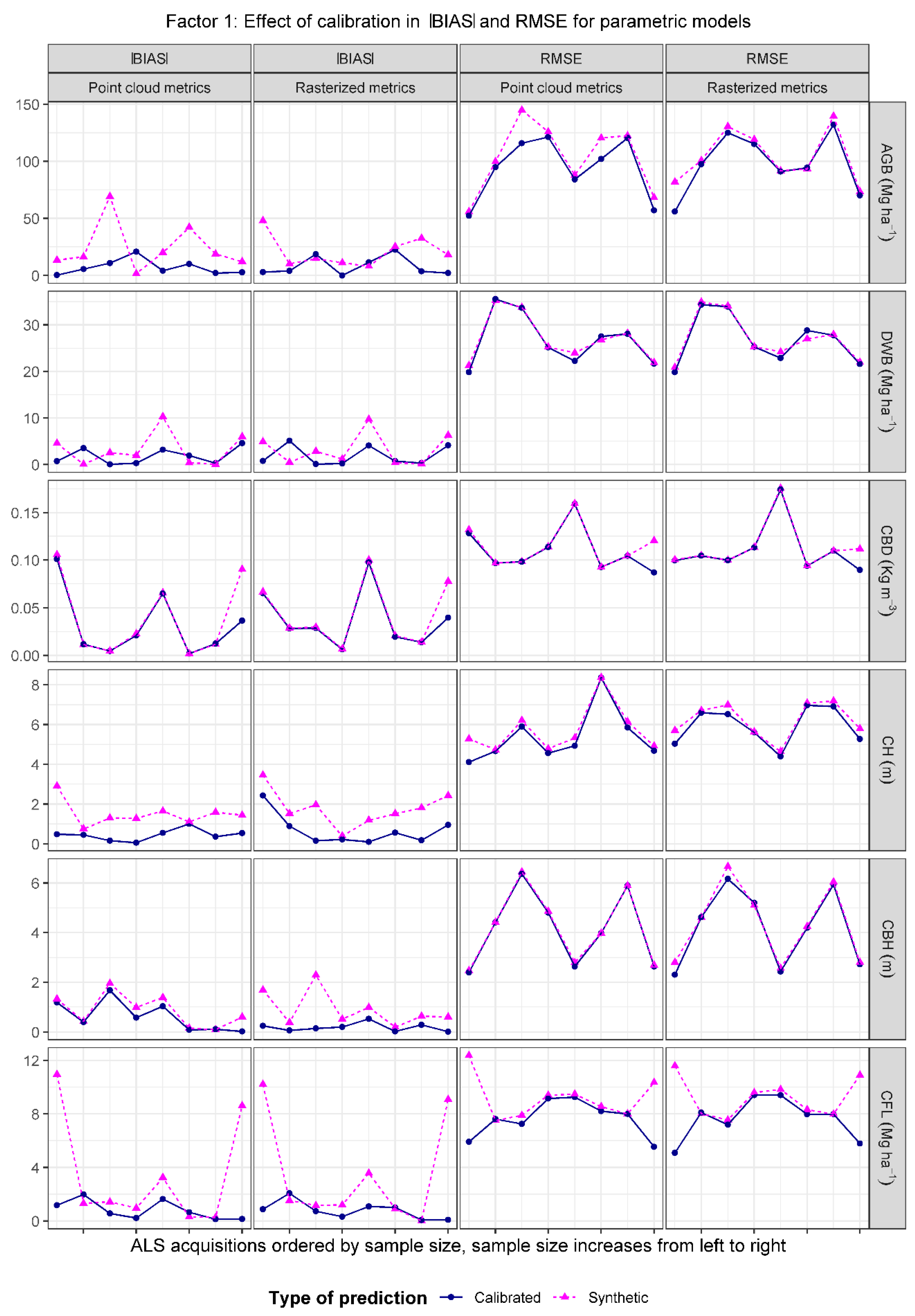
- Transferability and effect of calibration. Comparisons focused on analyzing differences in accuracy and precisions between synthetic predictions and predictions obtained using the same models but performing an additional calibration step with available ground and ALS data. We will refer to this factor in the following sections as “calibration”.
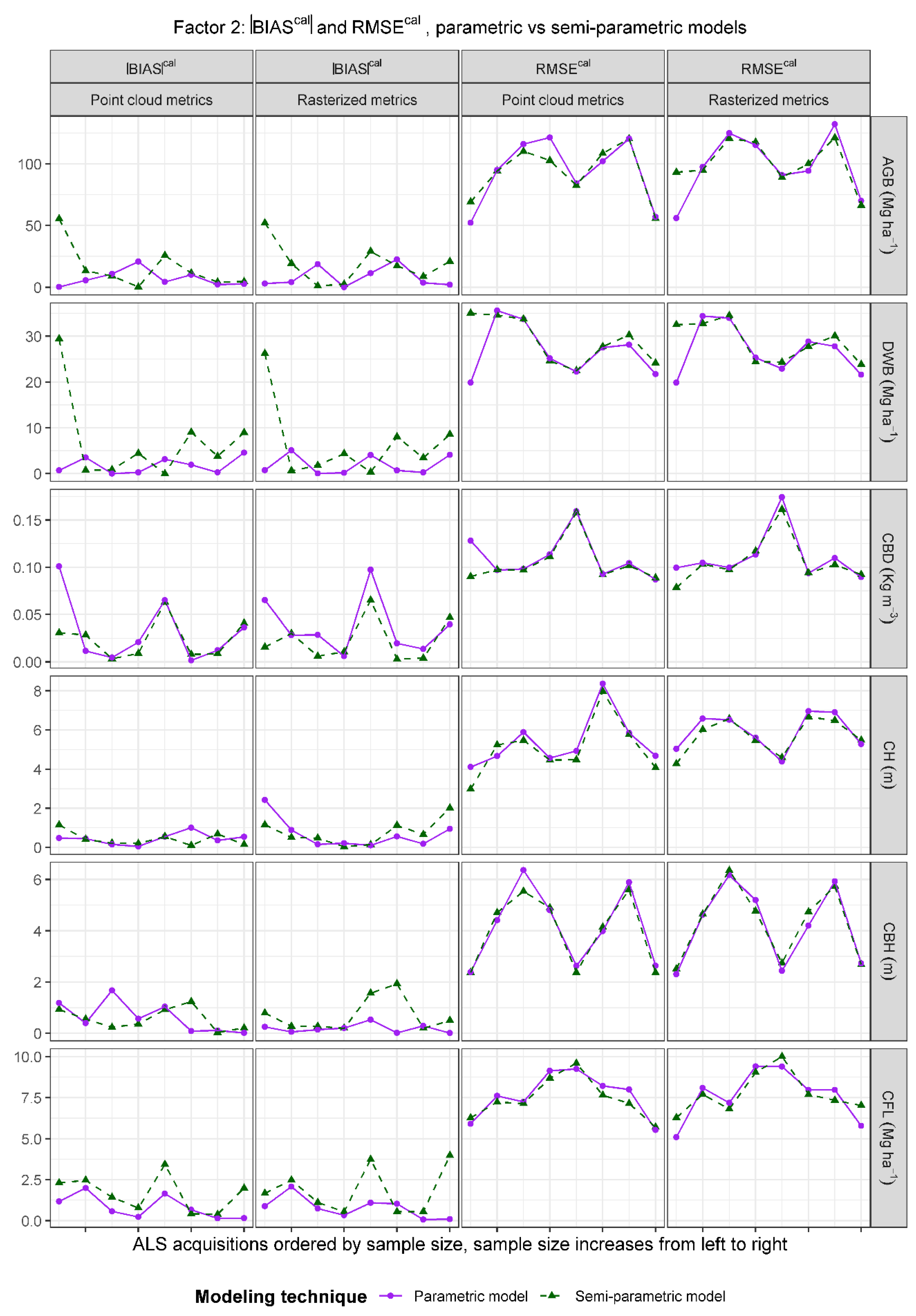
- Differences between modeling techniques. Comparisons focused on analyzing differences between parametric linear mixed-effects models and semiparametric models. We will refer to this factor in the following sections as “modeling technique”.
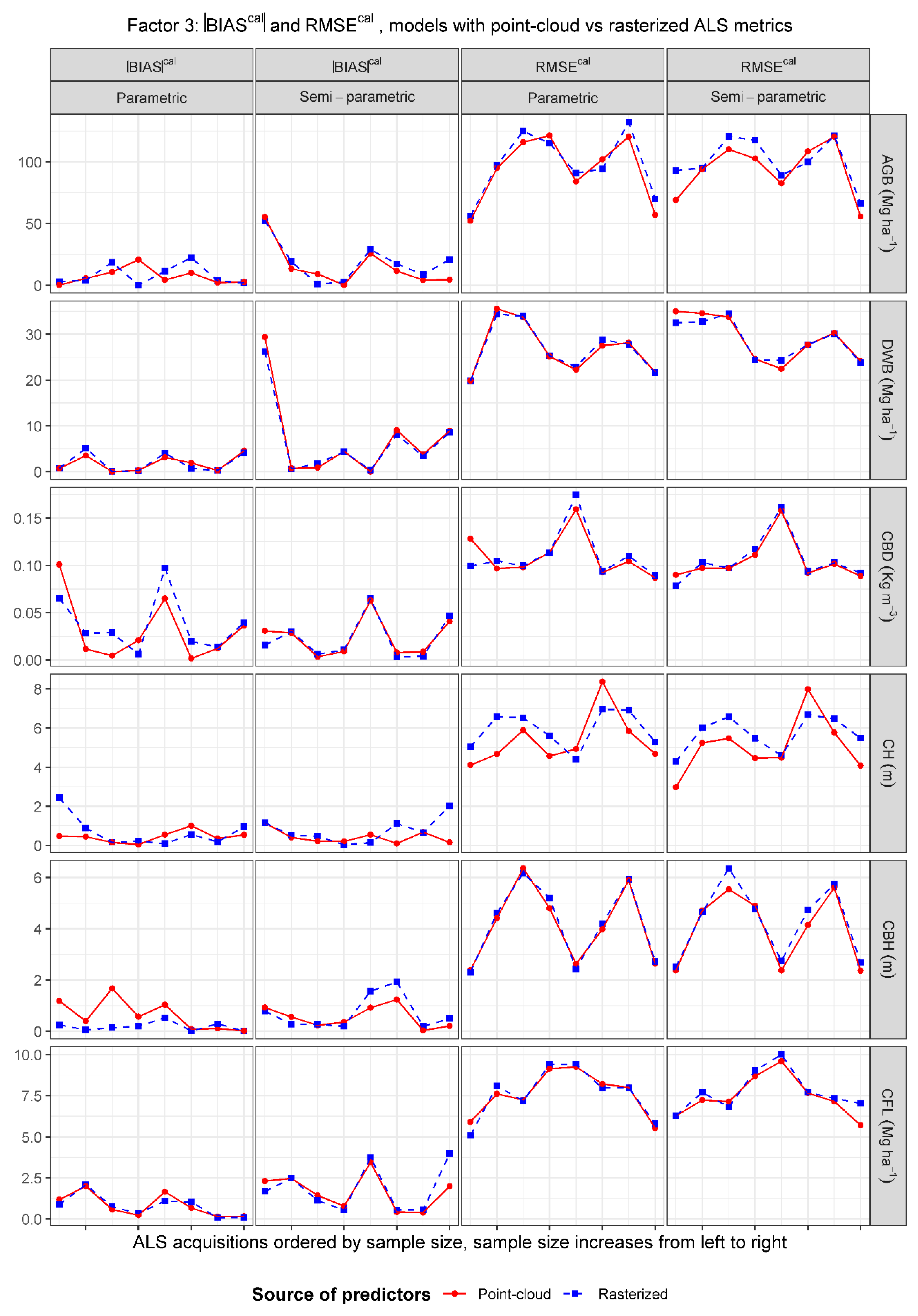
- Differences between models using a different source of ALS metrics. Comparisons focused on analyzing differences between models using ALS predictors computed from point-clouds clipped around the training plot footprints, i.e., point-cloud predictors, and models using predictors extracted from raster layers, i.e., rasterized predictors. We will refer to this factor in the following sections as “source of predictors”.
2. Materials and Methods
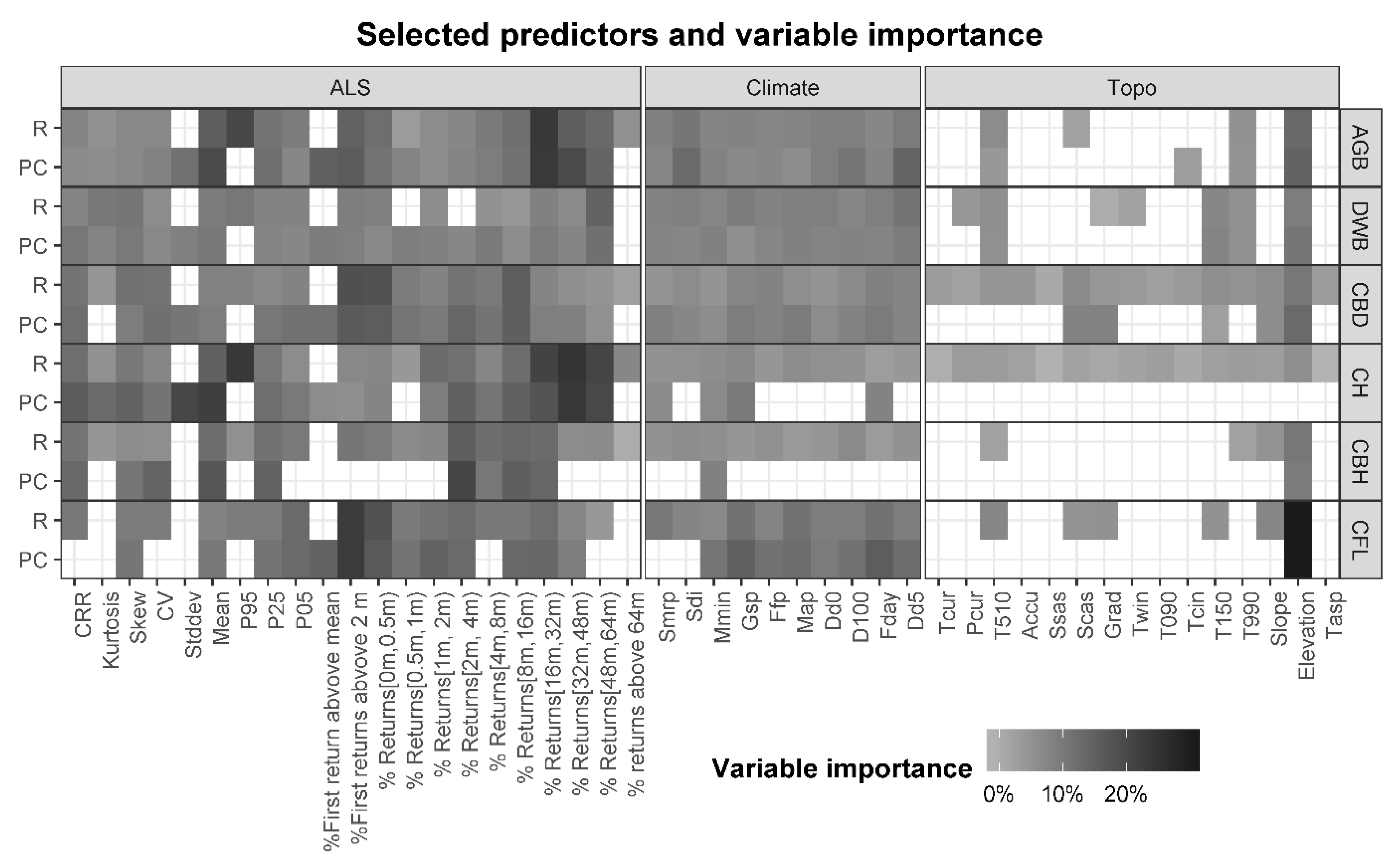
2.1. ALS Data Acquisitions and ALS, Climate, and Topographic Metrics
2.2. Ground Data and Response Variables
2.3. Parametric Models
2.3.1. Model Selection
2.3.2. Prediction and Calibration with Parametric Models
2.4. Semiparametric Models
2.4.1. Model Selection
2.4.2. Prediction and Calibration with Semiparametric Models
2.5. Accuracy Assessment and Comparisons
2.5.1. Cross-Validation and Performance Metrics
2.5.2. Differences between Calibrated and Synthetic Predictions, Modeling Techniques, and Sources of ALS Metrics
3. Results
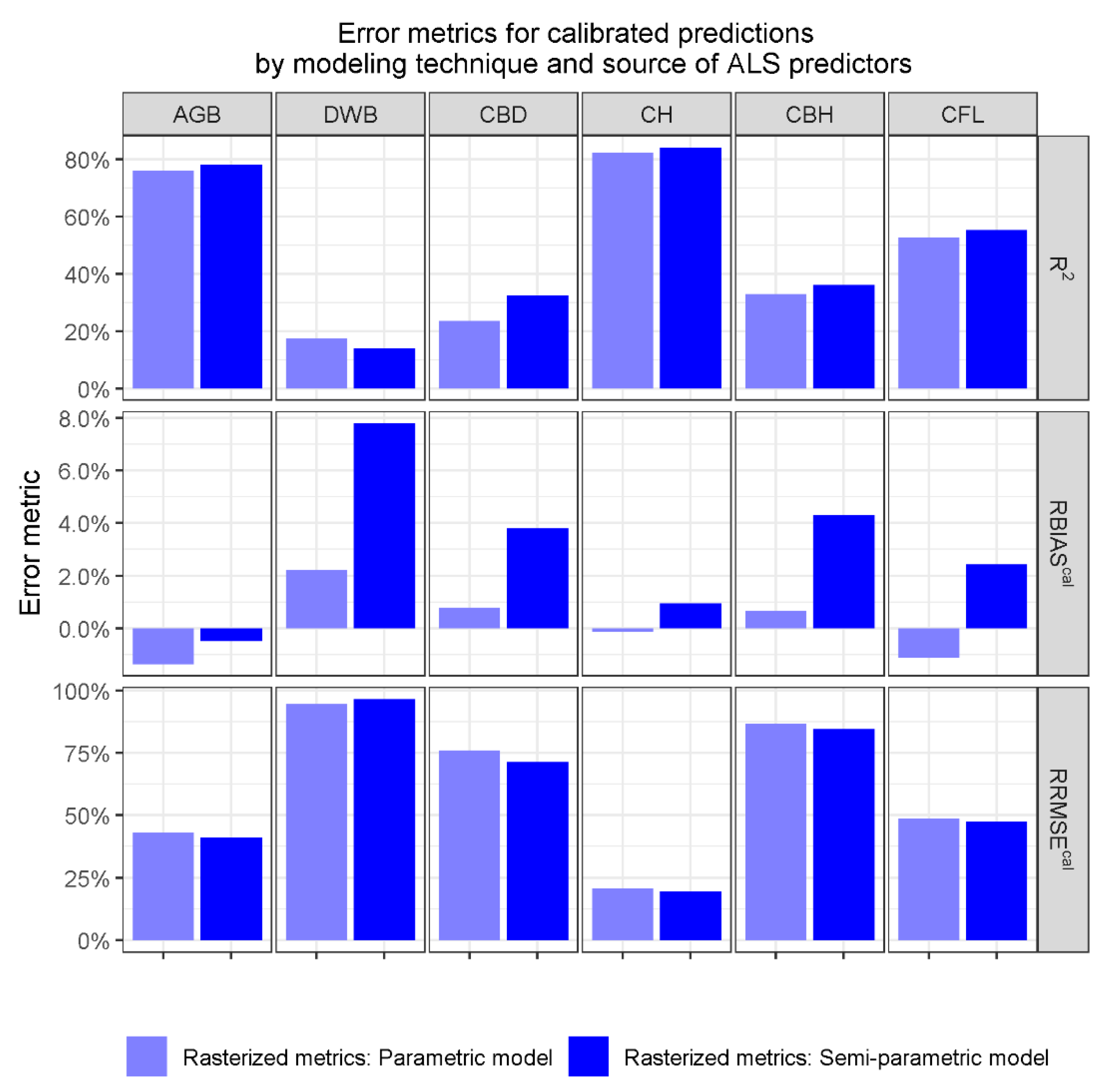
3.1. Parametric and Semiparametric Models
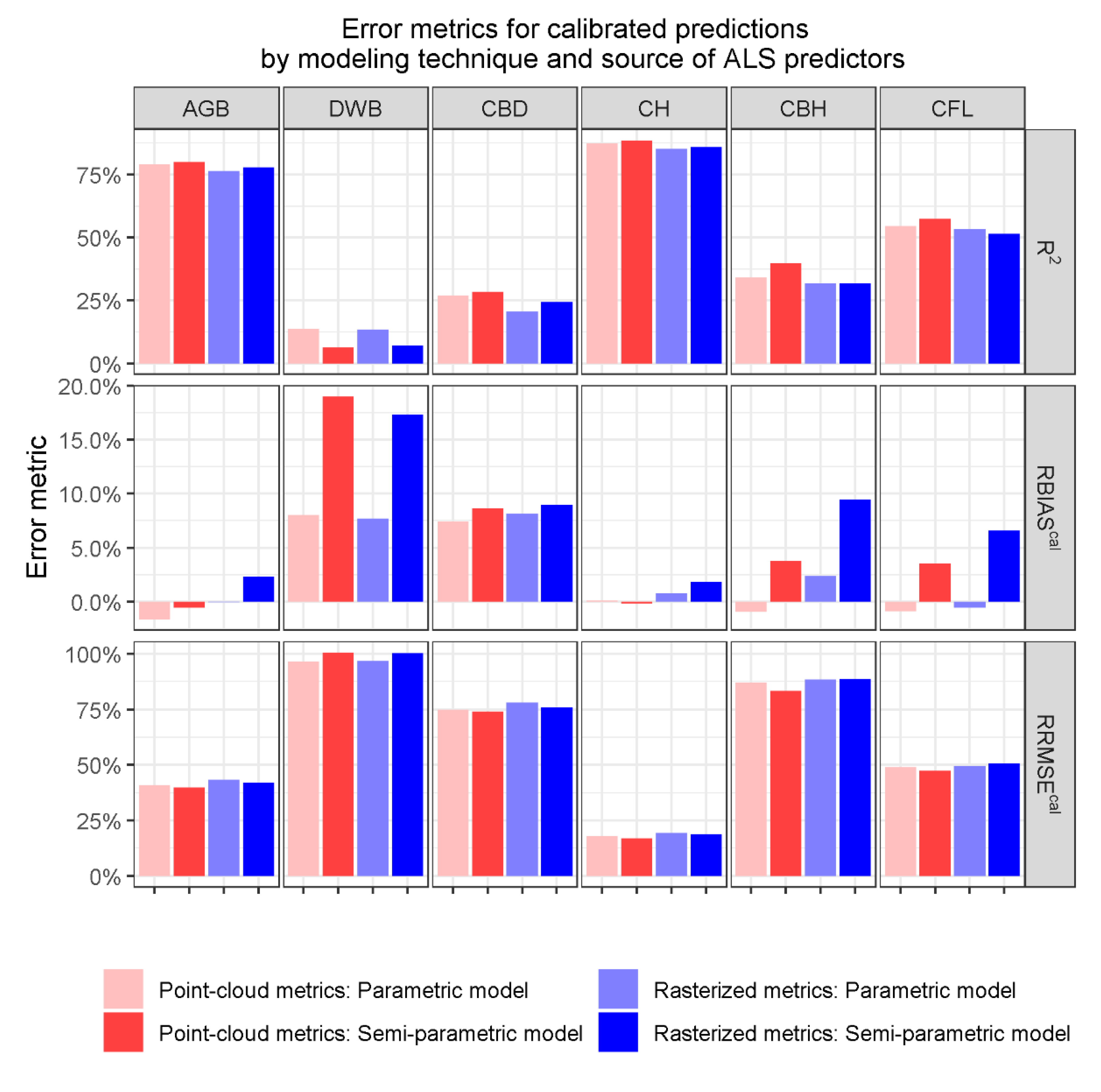
3.2. Differences between Synthetic and Calibrated Predictions
3.3. Differences between Parametric and Semiparametric Models
3.4. Differences between Sources of ALS Metrics
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Effect of Calibration and Modeling Technique using Rasterized Predictors and an Extended Set of ALS Acquisitions
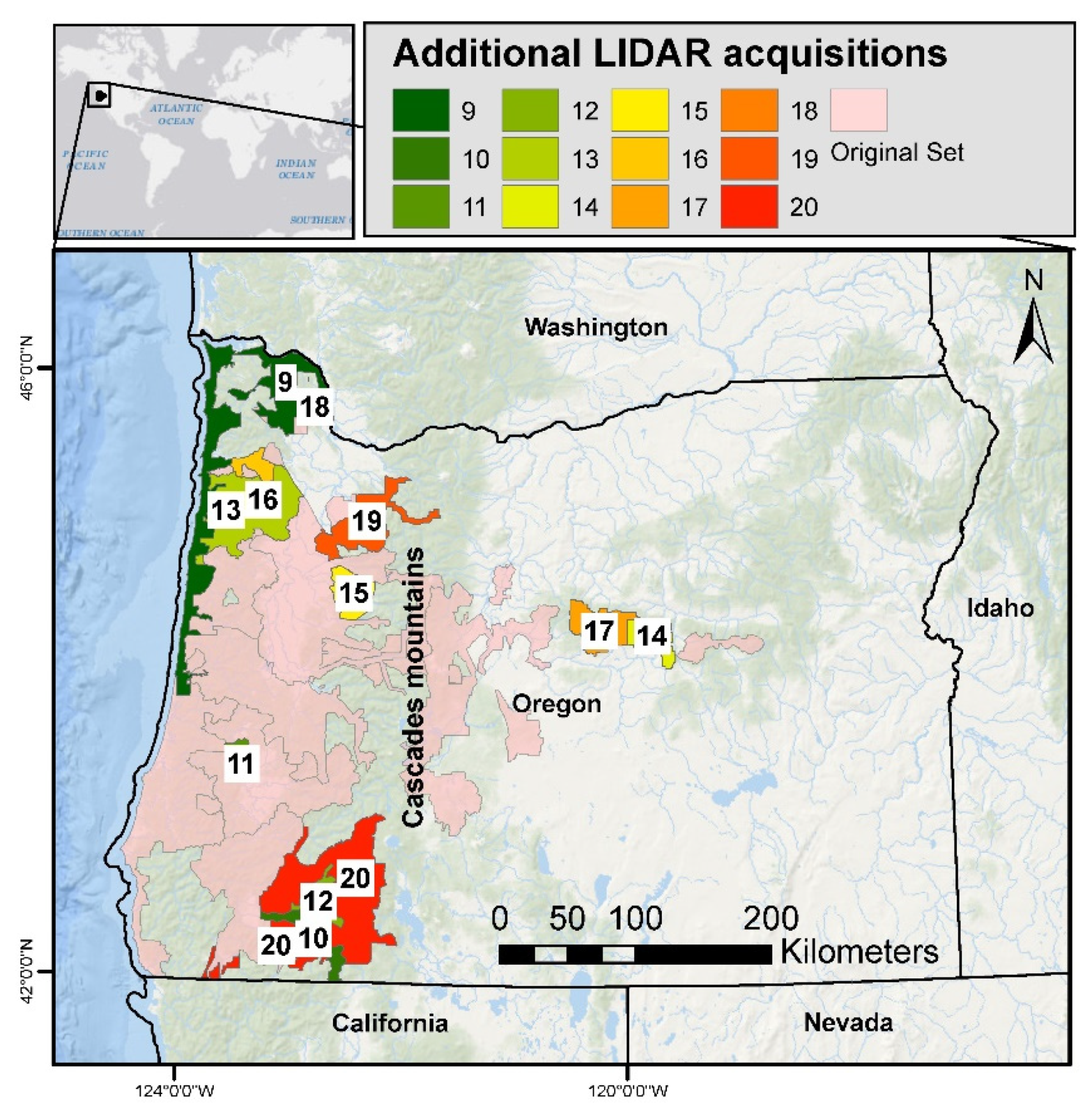
| ALS Data Acquisition | End Year | Flying Altitude (m) | Sensor | Average Pulse Density (Pulses/m2) | Area (Km2) | FIA PLOTS |
|---|---|---|---|---|---|---|
| 9. North Coast | 2009 | 900 * | Leica ALS50 PII* | 8.00 | 4506.55 | 77 |
| 10. Medford | 2009 | 900 * | Leica ALS50 PII* | 7.80 | 984.5 | 14 |
| 11. Umpqua | 2008 | 900 | Leica ALS50 PII | 8.80 | 272.92 | 6 |
| 12. Eagle Point | 2010 | 900 | Leica ALS60 | 8.08 | 546.58 | 7 |
| 13. Yambo | 2010 | 900–1300 | Leica ALS50 and ALS60 | 9.17 | 2803.88 | 69 |
| 14. Ochoco A | 2011 | 1300 | Leica ALS50 | 9.74 | 795 | 57 |
| 15. Green Peter | 2012 | 900 | Leica ALS60 | 9.81 | 897.71 | 25 |
| 16. Tillamook Yamhill | 2012 | 900 | Leica ALS50 and ALS60 | 9.72 | 808.72 | 16 |
| 17. Ochoco B | 2013 | 900 | Leica ALS60 | 9.07 | 1228.71 | 39 |
| 18. Scapoose | 2013 | 900 | Leica ALS60 | 7.60 | 150.64 | 3 |
| 19. Clackamol | 2013 | 900 | Leica ALS60 | 9.19 | 1835.42 | 40 |
| 20. Upper Rogue | 2015 | 1200–1500 | Optech Orion H, LeicaALS 70 and ALS80 | 12.24 | 5654.01 | 166 |
| Additional plots | 20,548.66 | 519 | ||||
| Total dataset (Including acquisitions 1–8) | 66,695.17 | 1652 | ||||
| FIA PLOTS | Mean (Standard Deviation) of Response Variables | ||||||
|---|---|---|---|---|---|---|---|
| AGB (Mg/ha) | DWB (Mg/ha) | CBD (Kg/m3) | CH (m) | CBH (m) | CFL (Mg/ha) | ||
| All acquisitions | 1652 | 236.26 | 27.7 | 0.14 | 31.11 | 4.97 | 15.51 |
| (206.52) | (28.82) | (0.12) | (15.31) | (5.26) | (10.99) | ||
| Variable | Set of Acquisitions & Source of ALS Metrics | t-Test Accuracy | t-Test Magnitude | ∆RBIASm | ∆RRMSEm | ||
|---|---|---|---|---|---|---|---|
| Mean Difference | p-Value | Mean Difference | p-Value | ||||
| AGB (Mg/ha) | Extended set raster | −2.05 | 6.41 × 10−2 | 4.25 | 1.36 × 10−5 | 0.87% | 1.94% |
| DWB (Mg/ha) | Extended set-raster | −1.54 | 7.90 × 10−9 | −3.84 × 10−1 | 1.12 × 10−1 | −5.57% | −1.96% |
| CBD (Kg/m3) | Extended set-raster | −4.27 × 10−3 | 3.49 × 10−5 | 2.40 × 10−3 | 1.24 × 10−2 | −3.01% | 4.56% |
| CH (m) | Extended set-raster | −3.40 × 10−1 | 3.29 × 10−6 | 7.87 × 10−2 | 2.42 × 10−1 | −0.80% | 1.03% |
| CBH(m) | Extended set-raster | −1.81 × 10−1 | 7.55 × 10−5 | 7.14 × 10−2 | 9.20 × 10−2 | −3.63% | 2.15% |
| CFL (Mg/ha) | Extended set-raster | −5.50 × 10−1 | 5.25 × 10−13 | 9.35 × 10−2 | 1.48 × 10−1 | −1.30% | 1.39% |

Appendix B. Selected Parametric and Semiparametric Models
| Variable | Fixed-Effect Parameters | Error Variance | Random Effects | RMSEcal | Biascal | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Coefficient | Value | p-Value | σe | α | Var(v)0.5 | Correlation Matrix of v | ||||||
| AGB (Mg/ha) | (Intercept) | 3.20 × 101 | 9.60 × 10−6 | 2.02 × 102 | 2.62 × 10−1 | 1.58 × 101 | 1.00 | −0.94 | 0.59 | −0.75 | 9.59 × 101 | −3.88 |
| % Returns [16 m, 32 m) | 3.80 × 102 | 4.90 × 10−16 | 1.19 × 102 | −0.94 | 1.00 | −0.39 | 0.85 | |||||
| % Returns [32 m, 48 m) * | 7.30 × 102 | 1.20 × 10−31 | 1.12 × 102 | 0.59 | −0.39 | 1.00 | −0.54 | |||||
| % Returns [48 m, 64 m) | 1.80 × 103 | 3.30 × 10−10 | 6.94 × 102 | −0.75 | 0.85 | −0.54 | 1.00 | |||||
| DWB (Mg/ha) | (Intercept) | 2.40 × 101 | 6.80 × 10−17 | 1.12 × 101 | 1.89 × 10−1 | 1.83 | 1.00 | 0.11 | 0.05 | 2.65 × 101 | 2.20 | |
| sdi | −2.60 | 1.60 × 10−7 | 8.00 × 10−1 | 0.11 | 1.00 | −0.99 | ||||||
| P95 * | 1.80 × 10−1 | 2.60 × 10−15 | 3.20 × 10−2 | 0.05 | −0.99 | 1.00 | ||||||
| CBD (Kg/m3) | (Intercept) | −1.30 × 10−2 | 4.60 × 10−1 | 8.10 × 10−2 | 5.00 × 10−2 | 3.15 × 10−2 | 1.00 | −0.98 | −0.49 | −0.08 | 1.06 × 10−1 | 1.05 × 10−2 |
| %First returns above 2 m * | 2.50 × 10−3 | 2.40 × 10−34 | 3.53 × 10−4 | −0.98 | 1.00 | 0.63 | −0.09 | |||||
| StdDev | −2.70 × 10−3 | 3.90 × 10−25 | 1.99 × 10−4 | −0.49 | 0.63 | 1.00 | −0.83 | |||||
| ×10lev | 8.90 × 10−5 | 3.00 × 10−5 | 5.22 × 10−5 | −0.08 | −0.09 | −0.83 | 1.00 | |||||
| CH (m) | (Intercept) | 2.00 | 2.10 × 10−6 | 3.50 | 1.04 × 10−1 | 2.58 × 10−1 | 1.00 | −1.00 | 5.58 | 3.97 × 10−2 | ||
| P95 * | 3.00 × 10−1 | 4.50 × 10−252 | 1.46 × 10−2 | −1.00 | 1.00 | |||||||
| CBH (m) | (Intercept) | 6.60 × 10−1 | 1.10 × 10−1 | 4.67 × 10−1 | 5.32 × 10−1 | 4.31 × 10−1 | 1.00 | 0.90 | −0.20 | −0.83 | 4.36 | −4.78 × 10−2 |
| CRR | 7.30 | 5.80 × 10−8 | 1.24 | 0.90 | 1.00 | −0.60 | −0.99 | |||||
| P50 * | 5.20 × 10−2 | 1.70 × 10−13 | 9.06 × 10−3 | −0.20 | −0.60 | 1.00 | 0.72 | |||||
| ×10lev | −1.60 × 10−3 | 3.90 × 10−6 | 5.75 × 10−4 | −0.83 | −0.99 | 0.72 | 1.00 | |||||
| CFL (Mg/ha) | (Intercept) | −1.10 × 101 | 3.40 × 10−11 | 7.43 | 3.44 | 1.00 | 0.30 | −0.99 | 0.80 | 7.53 | −1.40 × 10−1 | |
| P05 | 1.80 × 10−1 | 1.10 × 10−9 | 3.40 × 10−2 | 0.30 | 1.00 | −0.40 | 0.81 | |||||
| %First returns above 2 m | 2.60 × 10−1 | 1.20 × 10−24 | 6.04 × 10−2 | −0.99 | −0.40 | 1.00 | −0.86 | |||||
| ×10lev | 9.70 × 10−3 | 1.80 × 10−9 | 3.98 × 10−3 | 0.80 | 0.81 | −0.86 | 1.00 | |||||
| Variable | Fixed-Effect Parameters | Error Variance | Random Effects | RMSEcal | Biascal | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Coefficient | Value | p-Value | σe | α | Var(v)0.5 | Correlation Matrix of v | |||||||
| AGB (Mg/ha) | (Intercept) | 3.10 × 101 | 2.50 × 10−1 | 3.78 × 101 | 3.30 × 10−1 | 6.80 × 101 | 1.00 | −0.99 | 0.76 | −0.63 | 1.02 × 102 | −9.64 × 10−2 | |
| CRR | −3.30 × 102 | 2.40 × 10−6 | 1.66 × 102 | −0.99 | 1.00 | −0.80 | 0.66 | ||||||
| Mean * | 1.80 × 101 | 4.00 × 10−34 | 3.63 | 0.76 | −0.80 | 1.00 | −0.96 | ||||||
| %First returns above 2 m | 5.90 × 10−1 | 2.50 × 10−2 | 6.44 × 10−1 | −0.63 | 0.66 | −0.96 | 1.00 | ||||||
| DWB (Mg/ha) | (Intercept) | 2.50 × 101 | 3.90 × 10−16 | 1.52 × 101 | 1.68 × 10−1 | 3.77 | 1.00 | 0.58 | −0.69 | 2.66 × 101 | 2.11 | ||
| sdi | −2.60 | 4.50 × 10−8 | 7.32 × 10−1 | 0.58 | 1.00 | −0.99 | |||||||
| P95 * | 5.60 × 10−1 | 2.80 × 10−10 | 1.72 × 10−1 | −0.69 | −0.99 | 1.00 | |||||||
| CBD (Kg/m3) | (Intercept) | 1.30 × 10−1 | 9.80 × 10−2 | 6.46 × 10−2 | 1.06 × 10−1 | 1.67 × 10−1 | 1.00 | −0.95 | −0.52 | −0.08 | 0.15 | 1.10 × 10−1 | 1.15 × 10−2 |
| mmax | −8.50 × 10−3 | 2.00 × 10−3 | 5.87 × 10−3 | −0.95 | 1.00 | 0.24 | −0.14 | 0.15 | |||||
| sday | 1.00 × 10−3 | 2.10 × 10−4 | 5.78 × 10−4 | −0.52 | 0.24 | 1.00 | 0.50 | −0.91 | |||||
| %First returns above 2 m * | 2.20 × 10−3 | 1.80 × 10−24 | 4.29 × 10−4 | −0.08 | −0.14 | 0.50 | 1.00 | −0.43 | |||||
| StdDev | −8.70 × 10−3 | 3.10 × 10−17 | 1.43 × 10−3 | 0.15 | 0.15 | −0.91 | −0.43 | 1.00 | |||||
| CH (m) | (Intercept) | 5.00 | 2.30 × 10−30 | 5.98 | 3.37 × 10−2 | 1.00 | 0.99 | 6.01 | 2.36 × 10−1 | ||||
| P95 | 9.50 × 10−1 | 4.10 × 10−215 | 5.25 × 10−2 | 0.99 | 1.00 | ||||||||
| CBH (m) | (Intercept) | 2.30 | 9.50 × 10−3 | 5.63 | 3.18 × 10−1 | 1.66 | 1.00 | −0.52 | −0.98 | −0.32 | 4.44 | 1.19 × 10−1 | |
| CRR * | 1.30 × 101 | 1.60 × 10−15 | 3.29 | −0.52 | 1.00 | 0.31 | −0.65 | ||||||
| % Returns [8 m,16 m) | −7.30 | 5.40 × 10−11 | 1.58 | −0.98 | 0.31 | 1.00 | 0.52 | ||||||
| Elev | −2.60 × 10−3 | 1.70 × 10−5 | 1.39 × 10−3 | −0.32 | −0.65 | 0.52 | 1.00 | ||||||
| CFL (Mg/ha) | (Intercept) | −8.50 | 2.10 × 10−8 | 7.52 | 3.06 | 1.00 | 0.42 | −0.99 | 0.77 | 7.63 | −8.23 × 10−2 | ||
| P05 | 4.10 × 10−1 | 4.90 × 10−9 | 1.21 × 10−1 | 0.42 | 1.00 | −0.52 | 0.88 | ||||||
| %First returns above 2 m | 2.20 × 10−1 | 6.60 × 10−22 | 5.41 × 10−2 | −0.99 | −0.52 | 1.00 | −0.84 | ||||||
| Elev | 9.70 × 10−3 | 3.10 × 10−10 | 3.75 × 10−3 | 0.77 | 0.88 | −0.84 | 1.00 | ||||||
| Variable | Fixed-Effect Parameters | Error Variance | Random Effects | RMSEcal | Biascal | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Coefficient | Value | p-Value | σe | α | Var(v)0.5 | Correlation Matrix of v | ||||||
| AGB (Mg/ha) | (Intercept) | 4.80 × 101 | 3.70 × 10−2 | 3.83 × 101 | 3.33 × 10−1 | 8.69 × 101 | 1.00 | −0.99 | 0.73 | −0.73 | 1.01 × 102 | −3.23 |
| CRR | −3.50 × 102 | 8.30 × 10−11 | 1.81 × 102 | −0.99 | 1.00 | −0.79 | 0.77 | |||||
| Mean * | 1.80 × 101 | 9.70 × 10−45 | 4.67 | 0.73 | −0.79 | 1.00 | −0.96 | |||||
| %First returns above Mean | 1.10 | 1.60 × 10−2 | 1.64 | −0.73 | 0.77 | −0.96 | 1.00 | |||||
| DWB (Mg/ha) | (Intercept) | 2.40 × 101 | 1.70 × 10−11 | 1.28 × 101 | 2.13 × 10−1 | 1.11 × 101 | 1.00 | −0.84 | 0.33 | 2.62 × 101 | 6.15 × 10−1 | |
| sdi | −3.10 | 1.50 × 10−5 | 2.61 | −0.84 | 1.00 | −0.79 | ||||||
| P95 * | 6.50 × 10−1 | 1.00 × 10−19 | 2.03 × 10−1 | 0.33 | −0.79 | 1.00 | ||||||
| CBD (Kg/m3) | (Intercept) | 5.90 × 10−2 | 1.30 × 10−6 | 5.49 × 10−2 | 1.54 × 10−1 | 3.84 × 10−2 | 1.00 | −0.94 | 0.22 | 1.08 × 10−1 | 1.11 × 10−3 | |
| %First returns above Mean * | 2.10 × 10−3 | 1.60 × 10−28 | 5.91 × 10−4 | −0.94 | 1.00 | 0.12 | ||||||
| StdDev | −8.80 × 10−3 | 1.30 × 10−27 | 8.55 × 10−4 | 0.22 | 0.12 | 1.00 | ||||||
| CH (m) | (Intercept) | 5.60 | 2.30 × 10−20 | 6.39 | 1.70 | 1.00 | −0.60 | 6.42 | −4.61 × 10−2 | |||
| P95 | 9.40 × 10−1 | 2.80 × 10−265 | 6.44 × 10−2 | −0.60 | 1.00 | |||||||
| CBH (m) | (Intercept) | 3.70 | 7.30 × 10−15 | 2.32 | 2.45 × 10−1 | 1.40 | 1.00 | −0.14 | −0.91 | 4.30 | 3.33 × 10−2 | |
| P25* | 2.60 × 10−1 | 2.90 × 10−40 | 4.27 × 10−2 | −0.14 | 1.00 | −0.03 | ||||||
| ELEV | −2.20 × 10−3 | 5.20 × 10−10 | 9.25 × 10−4 | −0.91 | −0.03 | 1.00 | ||||||
| CFL (Mg/ha) | (Intercept) | −6.20 | 7.00 × 10−8 | 7.49 | 3.15 | 1.00 | 0.33 | −0.93 | 0.25 | 7.55 | −1.74 × 10−1 | |
| P05 | 4.40 × 10−1 | 3.10 × 10−16 | 9.89 × 10−2 | 0.33 | 1.00 | −0.30 | 0.24 | |||||
| %First returns above 2 m | 2.00 × 10−1 | 1.60 × 10−34 | 5.20 × 10−2 | −0.93 | −0.30 | 1.00 | −0.57 | |||||
| Elev | 8.10 × 10−3 | 5.80 × 10−10 | 4.51 × 10−3 | 0.25 | 0.24 | −0.57 | 1.00 | |||||
| Variable | Source of ALS Predictors | κ | RMSEcal | Biascal | ||
|---|---|---|---|---|---|---|
| AGB (Mg/ha) | Point-cloud | 6.84 | 9.54 × 10−10 | 4.63 × 10−1 | 9.36 × 101 | 1.33 |
| Rasterized | 7.59 | 7.14 × 10−11 | 4.54 × 10−1 | 9.84 × 101 | −5.41 | |
| DWB (Mg/ha) | Point-cloud | 2.33 | 7.04 × 10−6 | 7.15 × 10−1 | 2.76 × 101 | −5.23 |
| Rasterized | 2.20 | 6.33 × 10−6 | 7.27 × 10−1 | 2.76 × 101 | −4.77 | |
| CBD (Kg/m3) | Point-cloud | 3.73 × 10−1 | 4.98 × 10−2 | 7.06 × 10−1 | 1.05 × 10−1 | −1.22 × 10−2 |
| Rasterized | 3.47 × 10−1 | 6.21 × 10−2 | 6.52 × 10−1 | 1.08 × 10−1 | −1.27 × 10−2 | |
| CH (m) | Point-cloud | 2.01 | 9.20 × 10−10 | 2.84 × 10−1 | 5.29 | 6.15 × 10−2 |
| Rasterized | 4.07 | 5.21 × 10−10 | 9.85 × 10−2 | 5.89 | −5.61 × 10−1 | |
| CH (m) | Point-cloud | 9.52 × 10−1 | 2.60 × 10−7 | 8.24 × 10−1 | 4.17 | −1.90 × 10−1 |
| Rasterized | 1.25 | 3.03 × 10−7 | 7.12 × 10−1 | 4.44 | −4.73 × 10−1 | |
| CFL (Mg/ha) | Point-cloud | 1.89 | 1.69 × 10−13 | 4.75 × 10−1 | 7.29 | −5.40 × 10−1 |
| Rasterized | 1.91 | 3.22 × 10−13 | 4.86 × 10−1 | 7.78 | −1.01 |

| Variable | Set of ALS Acquisitions and Source of ALs Predictors | κ | RMSEcal | Biascal | ||
|---|---|---|---|---|---|---|
| AGB (Mg/ha) | Extended set Rasterized | 3.56 | 2.61 × 10−2 | 5.95 × 10−1 | 9.67 × 101 | 1.18 |
| DWB (Mg/ha) | Extended set Rasterized | 2.23 | 6.81 × 10−4 | 7.22 × 10−1 | 2.67 × 101 | −2.16 |
| CBD (Kg/m3) | Extended set Rasterized | 3.45 × 10−1 | 6.31 × 10−2 | 6.63 × 10−1 | 1.01 × 10−1 | −5.38 × 10−3 |
| CH (m) | Extended set Rasterized | 5.94 | 4.65 × 10−3 | 0.00 | 6.10 | −2.94 × 10−1 |
| CBH(m) | Extended set Rasterized | 1.30 | 4.91 × 10−7 | 6.76 × 10−1 | 4.20 | −2.14 × 10−1 |
| CFL (Mg/ha) | Extended set Rasterized | 1.80 | 3.06 × 10−6 | 5.04 × 10−1 | 7.34 | −3.76 × 10−1 |

References
- Sing, L.; Metzger, M.J.; Paterson, J.S.; Ray, D. A Review of the Effects of Forest Management Intensity on Ecosystem Services for Northern European Temperate Forests with a Focus on the UK. For. Int. J. For. Res. 2017, 91, 151–164. [Google Scholar] [CrossRef]
- Dunn, C.J.; Thompson, M.P.; Calkin, D.E. A Framework for Developing Safe and Effective Large-Fire Response in a New Fire Management Paradigm. For. Ecol. Manag. 2017, 404, 184–196. [Google Scholar] [CrossRef]
- Kangas, A. Value of Forest Information. Eur. J. For. Res. 2010, 129, 863–874. [Google Scholar] [CrossRef]
- Kangas, A.; Gobakken, T.; Puliti, S.; Hauglin, M.; Naesset, E. Value of Airborne Laser Scanning and Digital Aerial Photogrammetry Data in Forest Decision Making. Silva Fenn. 2018, 52. [Google Scholar] [CrossRef]
- McCarley, T.R.; Hudak, A.T.; Sparks, A.M.; Vaillant, N.M.; Meddens, A.J.H.; Trader, L.; Mauro, F.; Kreitler, J.; Boschetti, L. Estimating Wildfire Fuel Consumption with Multitemporal Airborne Laser Scanning Data and Demonstrating Linkage with MODIS-Derived Fire Radiative Energy. Remote Sens. Environ. 2020, 251, 112114. [Google Scholar] [CrossRef]
- Bechtold, W.A.; Patterson, P.L. The Enhanced Forest Inventory and Analysis Program: National Sampling Design and Estimation Procedures; US Department of Agriculture Forest Service, Southern Research Station Asheville, North Carolina: Asheville, NC, USA, 2005; p. 85.
- Palmer, M.; Christensen, G.; Kuegler, O.; Chase, J.; Fried, J.; Jovan, S.; Mercer, K.; Gray, D.; Loreno, S.; Morgan, T. Oregon’s Forest Resources, 2006–2015: Ten-Year Forest Inventory and Analysis Report; U.S. Department of Agriculture, Forest Service, Pacific Northwest Research Station: Portland, OR, USA, 2018.
- Næsset, E. Predicting Forest Stand Characteristics with Airborne Scanning Laser Using a Practical Two-Stage Procedure and Field Data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- Hudak, A.T.; Strand, E.K.; Vierling, L.A.; Byrne, J.C.; Eitel, J.U.; Martinuzzi, S.; Falkowski, M.J. Quantifying Aboveground Forest Carbon Pools and Flu × es from Repeat LiDAR Surveys. Remote Sens. Environ. 2012, 123, 25–40. [Google Scholar] [CrossRef]
- Valbuena, R.; Maltamo, M.; Martín-Fernández, S.; Packalen, P.; Pascual, C.; Nabuurs, G.-J. Patterns of Covariance between Airborne Laser Scanning Metrics and Lorenz Curve Descriptors of Tree Size Inequality. Can. J. Remote Sens. 2013, 39, S18–S31. [Google Scholar] [CrossRef]
- Huete, A.R.; Liu, H.Q.; Batchily, K.; van Leeuwen, W. A Comparison of Vegetation Indices over a Global Set of TM Images for EOS-MODIS. Remote Sens. Environ. 1997, 59, 440–451. [Google Scholar] [CrossRef]
- Steininger, M.K. Satellite Estimation of Tropical Secondary Forest Above-Ground Biomass: Data from Brazil and Bolivia. Int. J. Remote Sens. 2000, 21, 1139–1157. [Google Scholar] [CrossRef]
- Dong, J.; Kaufmann, R.K.; Myneni, R.B.; Tucker, C.J.; Kauppi, P.E.; Liski, J.; Buermann, W.; Ale × eyev, V.; Hughes, M.K. Remote Sensing Estimates of Boreal and Temperate Forest Woody Biomass: Carbon Pools, Sources, and Sinks. Remote Sens. Environ. 2003, 84, 393–410. [Google Scholar] [CrossRef]
- Avitabile, V.; Baccini, A.; Friedl, M.A.; Schmullius, C. Capabilities and Limitations of Landsat and Land Cover Data for Aboveground Woody Biomass Estimation of Uganda. Remote Sens. Environ. 2012, 117, 366–380. [Google Scholar] [CrossRef]
- Zhang, G.; Ganguly, S.; Nemani, R.R.; White, M.A.; Milesi, C.; Hashimoto, H.; Wang, W.; Saatchi, S.; Yu, Y.; Myneni, R.B. Estimation of Forest Aboveground Biomass in California Using Canopy Height and Leaf Area Index Estimated from Satellite Data. Remote Sens. Environ. 2014, 151, 44–56. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, D. Improving Forest Aboveground Biomass Estimation Using Seasonal Landsat NDVI Time-Series. ISPRS J. Photogramm. Remote Sens. 2015, 102, 222–231. [Google Scholar] [CrossRef]
- Durante, P.; Martín-Alcón, S.; Gil-Tena, A.; Algeet, N.; Tomé, J.L.; Recuero, L.; Palacios-Orueta, A.; Oyonarte, C. Improving Aboveground Forest Biomass Maps: From High-Resolution to National Scale. Remote Sens. 2019, 11, 795. [Google Scholar] [CrossRef]
- Rollins, M.G. LANDFIRE: A Nationally Consistent Vegetation, Wildland Fire, and Fuel Assessment. Int. J. Wildland Fire 2009, 18, 235–249. [Google Scholar] [CrossRef]
- Peterson, B.; Nelson, K.J.; Seielstad, C.; Stoker, J.; Jolly, W.M.; Parsons, R. Automated Integration of Lidar into the LANDFIRE Product Suite. Remote Sens. Lett. 2015, 6, 247–256. [Google Scholar] [CrossRef]
- Bright, C.B.; Hudak, T.A.; Meddens, J.A.; Hawbaker, J.T.; Briggs, S.J.; Kennedy, E.R. Prediction of Forest Canopy and Surface Fuels from Lidar and Satellite Time Series Data in a Bark Beetle-Affected Forest. Forests 2017, 8, 322. [Google Scholar] [CrossRef]
- Kraus, K.; Pfeifer, N. Determination of Terrain Models in Wooded Areas with Airborne Laser Scanner Data. ISPRS J. Photogramm. Remote Sens. 1998, 53, 193–203. [Google Scholar] [CrossRef]
- A × elsson, P. Processing of Laser Scanner Data—Algorithms and Applications. ISPRS J. Photogramm. Remote Sens. 1999, 54, 138–147. [Google Scholar] [CrossRef]
- Matei, B.C.; Sawhney, H.S.; Samarasekera, S.; Kim, J.; Kumar, R. Building Segmentation for Densely Built Urban Regions Using Aerial LIDAR Data. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- James, L.A.; Watson, D.G.; Hansen, W.F. Using LiDAR Data to Map Gullies and Headwater Streams under Forest Canopy: South Carolina, USA. Catena 2007, 71, 132–144. [Google Scholar] [CrossRef]
- Pirotti, F.; Tarolli, P. Suitability of LiDAR Point Density and Derived Landform Curvature Maps for Channel Network E × traction. Hydrol. Process. Int. J. 2010, 24, 1187–1197. [Google Scholar] [CrossRef]
- Hudak, A.T.; Fekety, P.A.; Kane, V.R.; Kennedy, R.E.; Filippelli, S.K.; Falkowski, M.J.; Tinkham, W.T.; Smith, A.M.S.; Crookston, N.L.; Domke, G.M.; et al. A Carbon Monitoring System for Mapping Regional, Annual Aboveground Biomass across the Northwestern USA. Environ. Res. Lett. 2020, 15, 095003. [Google Scholar] [CrossRef]
- Fekety, P.A.; Falkowski, M.J.; Hudak, A.T. Temporal Transferability of LiDAR-Based Imputation of Forest Inventory Attributes. Can. J. Res. 2014, 45, 422–435. [Google Scholar] [CrossRef]
- Fekety, P.A.; Falkowski, M.J.; Hudak, A.T.; Jain, T.B.; Evans, J.S. Transferability of Lidar-Derived Basal Area and Stem Density Models within a Northern Idaho Ecoregion. Can. J. Remote Sens. 2018, 44, 131–143. [Google Scholar] [CrossRef]
- Tompalski, P.; White, J.C.; Coops, N.C.; Wulder, M.A. Demonstrating the Transferability of Forest Inventory Attribute Models Derived Using Airborne Laser Scanning Data. Remote Sens. Environ. 2019, 227, 110–124. [Google Scholar] [CrossRef]
- Kotivuori, E.; Maltamo, M.; Korhonen, L.; Packalen, P. Calibration of Nationwide Airborne Laser Scanning Based Stem Volume Models. Remote Sens. Environ. 2018, 210, 179–192. [Google Scholar] [CrossRef]
- Kotivuori, E.; Korhonen, L.; Packalen, P. Nationwide Airborne Laser Scanning Based Models for Volume, Biomass and Dominant Height in Finland. Silva Fenn. 2016, 50. [Google Scholar] [CrossRef]
- Temesgen, B.H.; LeMay, V.M.; Froese, K.L.; Marshall, P.L. Imputing Tree-Lists from Aerial Attributes for Complex Stands of South-Eastern British Columbia. For. Ecol. Manag. 2003, 177, 277–285. [Google Scholar] [CrossRef]
- Gagliasso, D.; Hummel, S.; Temesgen, H. A Comparison of Selected Parametric and Non-Parametric Imputation Methods for Estimating Forest Biomass and Basal Area. Open J. For. 2014, 4, 42–48. [Google Scholar] [CrossRef]
- Chirici, G.; Mura, M.; McInerney, D.; Py, N.; Tomppo, E.O.; Waser, L.T.; Travaglini, D.; McRoberts, R.E. A Meta-Analysis and Review of the Literature on the k-Nearest Neighbors Technique for Forestry Applications That Use Remotely Sensed Data. Remote Sens. Environ. 2016, 176, 282–294. [Google Scholar] [CrossRef]
- Ohmann, J.L.; Gregory, M.J. Predictive Mapping of Forest Composition and Structure with Direct Gradient Analysis and Nearest- Neighbor Imputation in Coastal Oregon, U.S.A. Can. J. Res. 2002, 32, 725–741. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Frank, B.; Mauro, F.; Temesgen, H.; Ford, K.R. Analysis of Classification Methods for Identifying Stands for Commercial Thinning Using LiDAR. Can. J. Remote Sens. 2019, 1–18. [Google Scholar] [CrossRef]
- Esteban, J.; McRoberts, E.R.; Fernández-Landa, A.; Tomé, L.J.; Nӕsset, E. Estimating Forest Volume and Biomass and Their Changes Using Random Forests and Remotely Sensed Data. Remote Sens. 2019, 11, 1944. [Google Scholar] [CrossRef]
- Rice, J.A.; Wu, C.O. Nonparametric Mi × ed Effects Models for Unequally Sampled Noisy Curves. Biometrics 2001, 57, 253–259. [Google Scholar] [CrossRef]
- Nothdurft, A.; Saborowski, J.; Breidenbach, J. Spatial Prediction of Forest Stand Variables. Eur. J. For. Res. 2009, 128, 241–251. [Google Scholar] [CrossRef]
- Andersen, H.-E.; McGaughey, R.J.; Reutebuch, S.E. Estimating Forest Canopy Fuel Parameters Using LIDAR Data. Remote Sens. Environ. 2005, 94, 441–449. [Google Scholar] [CrossRef]
- González-Ferreiro, E.; Arellano-Pérez, S.; Castedo-Dorado, F.; Hevia, A.; Vega, J.A.; Vega-Nieva, D.; Álvarez-González, J.G.; Ruiz-González, A.D. Modelling the Vertical Distribution of Canopy Fuel Load Using National Forest Inventory and Low-Density Airbone Laser Scanning Data. PLoS ONE 2017, 12, e0176114. [Google Scholar] [CrossRef]
- Scott, J.; Reinhardt, E. Assessing Crown Fire Potential by Linking Models of Surface and Crown Fire Potential; U.S. Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2001. [CrossRef]
- Finney, M.A. An Overview of FlamMap Fire Modeling Capabilities. In Proceedings RMRS-P-41, Portland, OR, USA, 28–30 March 2006; U.S. Department of Agriculture, Forest Service, Rocky Mountain Research Station: Portland, OR, USA, 2006; pp. 213–220. [Google Scholar]
- Ager, A.A.; Vaillant, N.M.; Finney, M.A. Integrating Fire Behavior Models and Geospatial Analysis for Wildland Fire Risk Assessment and Fuel Management Planning. J. Combust. 2011, 2011. [Google Scholar] [CrossRef]
- Finney, M.A.; McHugh, C.W.; Grenfell, I.C.; Riley, K.L.; Short, K.C. A Simulation of Probabilistic Wildfire Risk Components for the Continental United States. Stoch. Environ. Res. Risk Assess. 2011, 25, 973–1000. [Google Scholar] [CrossRef]
- Roussel, J.-R.; Auty, D. LidR: Airborne LiDAR Data Manipulation and Visualization for Forestry Applications. 2017. Available online: https://cran.r-project.org/web/packages/lidR/index.html (accessed on 12 January 2021).
- Mc Gaughey, R.J. FUSION\LDV: Software for LIDAR Data Analysis and Visualization. 2019. Available online: http://forsys.cfr.washington.edu/FUSION/fusion_overview.html (accessed on 12 January 2021).
- Crookston, N.L. Climate Estimates and Plant-Climate Relationships’ Climate-FVS. 2016. Available online: https://www.fs.fed.us/fvs/whatis/climate-fvs.shtml (accessed on 12 January 2021).
- O’Connell, B.M.; Conkling, B.L.; Wilson, A.M.; Burrill, E.A.; Turner, J.; Pugh, S.A.; Christiansen, G.; Ridley, T.; Menlove, J. The Forest Inventory and Analysis Database: Database Description and User Guide Version 7.2 for Phase 2; U.S. Department of Agriculture, Forest Service: Portland, OR, USA, 2017; p. 830.
- Andersen, H.-E.; Clarkin, T.; Winterberger, K.; Strunk, J. An Accuracy Assessment of Positions Obtained Using Survey- and Recreational-Grade Global Positioning System Receivers across a Range of Forest Conditions within the Tanana Valley of Interior Alaska. West. J. Appl. For. 2009, 24, 128–136. [Google Scholar] [CrossRef]
- Valbuena, R.; Mauro, F.; Rodriguez-Solano, R.; Manzanera, J. Accuracy and Precision of GPS Receivers under Forest Canopies in a Mountainous Environment. Span. J. Agric. Res. 2010, 8. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Chen, Q.; Walters, B.F.; Kaisershot, D.J. The Effects of Global Positioning System Receiver Accuracy on Airborne Laser Scanning-Assisted Estimates of Aboveground Biomass. Remote Sens. Environ. 2018, 207, 42–49. [Google Scholar] [CrossRef]
- Reinhardt, E.; Lutes, D.; Scott, J. FuelCalc: A Method for Estimating Fuel Characteristics. In Proceedings RMRS-P-41, Portland, OR, USA, 28–30 March 2006; U.S. Department of Agriculture, Forest Service, Rocky Mountain Research Station: Portland, OR, USA, 2006; pp. 273–282. [Google Scholar]
- Lumley, T. Leaps: Regression Subset Selection. 2009. Available online: https://cran.r-project.org/web/packages/leaps/index.html (accessed on 12 January 2021).
- Pinheiro, J.; Bates, D.; DebRoy, S.; Sarkar, D.; R Core Team. Nlme: Linear and Nonlinear Mixed Effects Models; R Core Team: Vienna, Austria, 2017; Available online: https://cran.r-project.org/web/packages/nlme/index.html (accessed on 12 January 2021).
- McCulloch, C.E.; Searle, S.R.; Neuhaus, J.M. Generalized, Linear, and Mixed Models; Wiley Series in Probability and Statistics; Wiley: Hoboken, NJ, USA, 2008; ISBN 978-0-470-07371-1. [Google Scholar]
- Mauro, F.; Molina, I.; García-Abril, A.; Valbuena, R.; Ayuga-Téllez, E. Remote Sensing Estimates and Measures of Uncertainty for Forest Variables at Different Aggregation Levels. Environmetrics 2016, 27, 225–238. [Google Scholar] [CrossRef]
- Breidenbach, J.; Magnussen, S.; Rahlf, J.; Astrup, R. Unit-Level and Area-Level Small Area Estimation under Heteroscedasticity Using Digital Aerial Photogrammetry Data. Remote Sens. Environ. 2018, 212, 199–211. [Google Scholar] [CrossRef]
- Evans, J.S.; Cushman, S. Gradient Modeling of Conifer Species Using Random Forest. Landsc. Ecol. 2009, 24, 673–683. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by RandomForest. R News 2002, 2, 18–22. [Google Scholar]
- González-Ferreiro, E.; Diéguez-Aranda, U.; Miranda, D. Estimation of Stand Variables in Pinus Radiata D. Don Plantations Using Different LiDAR Pulse Densities. Forestry 2012, 85, 281–292. [Google Scholar] [CrossRef]
- Mauro, F.; Monleon, V.J.; Temesgen, H.; Ruíz Fernández, L.Á. Analysis of Spatial Correlation in Predictive Models of Forest Variables That Use LiDAR Au × iliary Information. Can. J. Res. 2017. [Google Scholar] [CrossRef]
- Navarro, J.A.; Tomé, J.L.; Marino, E.; Guillén-Climent, M.L.; Fernández-Landa, A. Assessing the Transferability of Airborne Laser Scanning and Digital Aerial Photogrammetry Derived Growing Stock Volume Models. Int. J. Appl. Earth Obs. Geoinf. 2020, 91, 102135. [Google Scholar] [CrossRef]
- Breidenbach, J.; Astrup, R. Small Area Estimation of Forest Attributes in the Norwegian National Forest Inventory. Eur. J. For. Res. 2012, 1–13. [Google Scholar] [CrossRef]
- Mentch, L.; Hooker, G. Quantifying Uncertainty in Random Forests via Confidence Intervals and Hypothesis Tests. J. Mach. Learn. Res. 2016, 17, 841–881. [Google Scholar]
- Gobakken, T.; Næsset, E. Assessing Effects of Positioning Errors and Sample Plot Size on Biophysical Stand Properties Derived from Airborne Laser Scanner Data. Can. J. For. Res. 2009, 39, 1036–1052. [Google Scholar] [CrossRef]
- Zald, H.S.J.; Ohmann, J.L.; Roberts, H.M.; Gregory, M.J.; Henderson, E.B.; McGaughey, R.J.; Braaten, J. Influence of Lidar, Landsat Imagery, Disturbance History, Plot Location Accuracy, and Plot Size on Accuracy of Imputation Maps of Forest Composition and Structure. Remote Sens. Environ. 2014, 143, 26–38. [Google Scholar] [CrossRef]
- Grafström, A.; Schnell, S.; Saarela, S.; Hubbell, S.P.; Condit, R. The Continuous Population Approach to Forest Inventories and Use of Information in the Design. Environmetrics 2017, 28, e2480. [Google Scholar] [CrossRef]
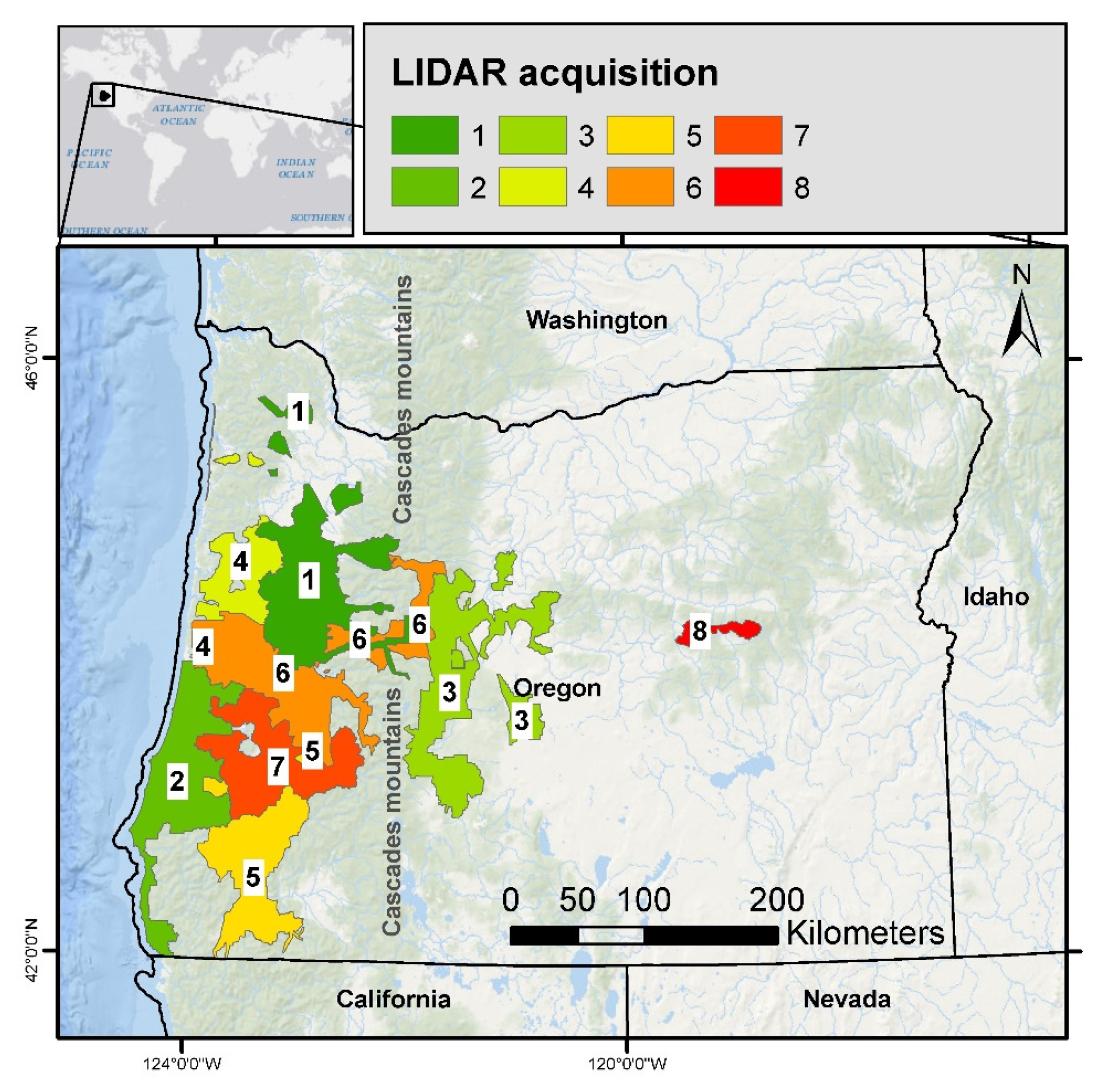

| ALS Data Acquisition | End Year | Flying Altitude (m) | Sensor | Average Pulse Density (Pulses/m2) | Area (Km2) | Number of FIA Plots |
|---|---|---|---|---|---|---|
| 1. Willamette | 2008 | 900 | Leica ALS50 PII | 8.00 | 8189.74 | 85 |
| 2. South Coast | 2009 | 900 | Leica ALS50 PII | 8.50 | 6541.11 | 132 |
| 3. Deschutes | 2010 | 900 | Leica ALS50 and ALS60 | 8.60 | 7891.78 | 347 |
| 4. Central Coast | 2012 | 900–1400 | Leica ALS50, ALS60 and ALS70 | 11.54 | 3263.96 | 102 |
| 5. Rogue Valley | 2012 | 900–1400 | Leica ALS50 and ALS60 | 10.70 | 5510.75 | 119 |
| 6. Lane County | 2015 | 1500 | Leica ALS 80 | 11.50 | 8354.98 | 221 |
| 7. Upper Umpqua | 2015 | 1200–1500 | Optech Orion H and LeicaALS 80 | 11.88 | 5722.48 | 117 |
| 8. Canyon Creek | 2016 | 1500 | Leica ALS 80 | 11.00 | 671.72 | 10 |
| Total area and number of FIA plots | 46,146.51 | 1133 | ||||
| Group | Description Auxiliary Variables | Acronym |
|---|---|---|
| ALS predictors (Derived from point clouds or extracted from raster files) | Mean, standard deviation, skewness coefficient, kurtosis coefficient, coefficient of variation of the distribution of heights of the point cloud. | Mean, Stddev, CV, Skew, Kurtosis |
| Percentiles of the distribution of heights of the point cloud. | P05, P25, P50, P75, P95 | |
| Canopy relief ratio | CRR | |
| Percentage of first (Fst) returns above 2 m and mean | % First returns above 2 m, % First returns above mean | |
| Proportion of points in the height intervals [0–0.5), [0.5, 1), [1, 2), [2, 4), [4, 8), [8, 16), [16, 32), [32, 48), [48, 64) and [64, ∞), meters. | % Returns above 64 m, % Returns [48 m, 64 m), % Returns [32 m, 48 m), % Returns [16 m, 32 m), % Returns [8 m, 16 m), % Returns [4 m, 8 m), % Returns [2 m, 4 m), % Returns [1 m, 2 m), % Returns [0.5 m,1 m), % Returns [0 m, 0.5 m) | |
| Climate variables | Mean annual precipitation (mm) and temperature | Map, Mat |
| Mean maximum temperature in the warmest month | Mmax | |
| Mean minimum temperature (°C) in the coldest month | Mmin | |
| Mean temperature (°C) in the coldest month | Mtcm | |
| Mean temperature (°C) in the warmest month | Mtwm | |
| Degree-days above 0 and 5 °C | Dd0, Dd5 | |
| Julian day when the sum of degree-days >5 °C reaches 100 | D100 | |
| Julian date of the first freezing date of autumn | Fday | |
| Julian date of the last freezing date of spring | Sday | |
| Length of the frost-free period (days) | Ffp | |
| Growing season precipitation, April to September | Gsp | |
| Summer dryness index | Sdi | |
| Topographic indexes | Elevation | Elev |
| Slope | Slop | |
| Transformed aspect | Tasp | |
| Slope × Sine of Aspect transformation | Ssas | |
| Slope × Cosine of Aspect transformation | Scas | |
| Global incoming radiation | Grad | |
| Accumulated number of pixels that flow through the plot center | Accu | |
| Profile curvature | Pcur | |
| Tangential curvature | Tcur | |
| Topographic wetness index | Twin | |
| Topographic convergence index | Tci | |
| Topographic position index calculated at 90 m (3 pixels) | T090 | |
| Topographic position index calculated at 150 m (5 pixels) | T150 | |
| Topographic position index calculated at 510 m (17 pixels) | T510 | |
| Topographic position index calculated at 990 m (33 pixels) | T990 |
| FIA PLOTS | Mean (Standard Deviation) of Response Variables | |||||
|---|---|---|---|---|---|---|
| AGB (Mg/ha) | DWB (Mg/ha) | CBD (Kg/m3) | CH (m) | CBH (m) | CFL (Mg/ha) | |
| 1133 | 234.27 | 27.52 | 0.14 | 31.11 | 5.01 | 15.36 |
| (209.49) | (28.59) | (0.12) | (15.67) | (5.37) | (11.18) | |
| Variable | Source of ALS Metrics | t-Test Accuracy: | t-Test Magnitude | ∆RBIASm | ∆RRMSEm | ||
|---|---|---|---|---|---|---|---|
| Mean Difference | p-Value | Mean Difference | p-Value | ||||
| AGB (Mg/ha) | Point-cloud | −2.56 | 1.21 × 10−1 | 3.69 | 7.28 × 10−3 | 1.09% | 1.02% |
| Rasterized | −5.51 | 2.70 × 10−5 | 2.39 | 3.94 × 10−2 | −2.27% | 1.35% | |
| DWB (Mg/ha) | Point-cloud | −3.03 | 6.59 × 10−22 | −1.44 | 3.07 × 10−7 | −10.99% | −4.04% |
| Rasterized | −2.66 | 6.88 × 10−15 | −1.37 | 6.61 × 10−6 | −9.65% | −3.58% | |
| CBD (Kg/m3) | Point-cloud | −1.67 × 10−3 | 1.44 × 10-1 | 1.61 × 10−3 | 1.22 × 10−1 | −1.18% | 0.74% |
| Rasterized | −1.16 × 10−3 | 3.19 × 10−1 | 1.86 × 10−3 | 9.07 × 10−2 | −0.82% | 1.96% | |
| CH (m) | Point-cloud | 1.01 × 10−1 | 2.25 × 10−1 | 9.39 × 10−3 | 9.01 × 10−1 | −0.07% | 0.94% |
| Rasterized | −3.25 × 10−1 | 3.86 × 10−5 | −1.25 × 10−1 | 7.75 × 10−2 | −1.04% | 0.37% | |
| CBH (m) | Point-cloud | −2.37 × 10−1 | 3.61 × 10−5 | 2.02 × 10−1 | 9.80 × 10−5 | −2.83% | 3.84% |
| Rasterized | −3.54 × 10−1 | 4.80 × 10−9 | −6.10 × 10−2 | 2.60 × 10−1 | −7.06% | −0.03% | |
| CFL (Mg/ha) | Point-cloud | −6.81 × 10−1 | 1.16 × 10−10 | 2.80 × 10−2 | 7.49 × 10−1 | −2.60% | 1.57% |
| Rasterized | −1.09 | 4.13 × 10−21 | −3.32 × 10−1 | 4.41 × 10−4 | −6.05% | −0.93% | |
| Model Type | Variable | t-Test Accuracy | t-Test Magnitude | ∆RRBIASS | ∆RRMSES | ||
|---|---|---|---|---|---|---|---|
| Mean Difference | p-Value | Mean Difference | p-Value | ||||
| Parametric models | AGB (Mg/ha) | 3.79 | 7.08 × 10−2 | 3.55 | 4.06 × 10−2 | −1.61% | 2.40% |
| DWB (Mg/ha) | −9.35 × 10−2 | 5.24 × 10−1 | 2.79 × 10−2 | 8.35 × 10−1 | −0.34% | 0.17% | |
| CBD (Kg/m3) | 1.03 × 10−3 | 2.75 × 10−1 | 3.23 × 10−3 | 1.42 × 10−4 | 0.73% | 3.28% | |
| CH (m) | 1.96 × 10−1 | 1.57 × 10−1 | 4.82 × 10−1 | 9.61 × 10−5 | 0.63% | 1.36% | |
| CBH (m) | 1.67 × 10−1 | 4.64 × 10−4 | 4.85 × 10−2 | 2.68 × 10−1 | 1.43% | 1.50% | |
| CFL (Mg /ha) | 5.82 × 10−2 | 4.02 × 10−1 | 1.45 × 10−1 | 1.72 × 10−2 | −0.38% | 0.68% | |
| Semiparametric models | AGB (Mg/ha) | 6.74 | 5.74 × 10−5 | 4.86 | 4.28 × 10−4 | 1.73% | 2.08% |
| DWB (Mg/ha) | −4.63 × 10−1 | 3.15 × 10−2 | −4.26 × 10−2 | 8.33 × 10−1 | −1.68% | −0.28% | |
| CBD (Kg/m3) | 5.20 × 10−4 | 5.75 × 10−1 | 2.98 × 10−3 | 5.41 × 10−4 | 0.37% | 2.06% | |
| CH (m) | 6.22 × 10−1 | 1.99 × 10−6 | 6.17 × 10−1 | 5.19 × 10−8 | 1.61% | 1.92% | |
| CBH (m) | 2.84 × 10−1 | 2.48 × 10−7 | 3.12 × 10−1 | 7.59 × 10−10 | 5.69% | 5.39% | |
| CFL (Mg /ha) | 4.72 × 10−1 | 5.81 × 10−8 | 5.05 × 10−1 | 2.58 × 10−10 | 3.05% | 3.17% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mauro, F.; Hudak, A.T.; Fekety, P.A.; Frank, B.; Temesgen, H.; Bell, D.M.; Gregory, M.J.; McCarley, T.R. Regional Modeling of Forest Fuels and Structural Attributes Using Airborne Laser Scanning Data in Oregon. Remote Sens. 2021, 13, 261. https://doi.org/10.3390/rs13020261
Mauro F, Hudak AT, Fekety PA, Frank B, Temesgen H, Bell DM, Gregory MJ, McCarley TR. Regional Modeling of Forest Fuels and Structural Attributes Using Airborne Laser Scanning Data in Oregon. Remote Sensing. 2021; 13(2):261. https://doi.org/10.3390/rs13020261
Chicago/Turabian StyleMauro, Francisco, Andrew T. Hudak, Patrick A. Fekety, Bryce Frank, Hailemariam Temesgen, David M. Bell, Matthew J. Gregory, and T. Ryan McCarley. 2021. "Regional Modeling of Forest Fuels and Structural Attributes Using Airborne Laser Scanning Data in Oregon" Remote Sensing 13, no. 2: 261. https://doi.org/10.3390/rs13020261
APA StyleMauro, F., Hudak, A. T., Fekety, P. A., Frank, B., Temesgen, H., Bell, D. M., Gregory, M. J., & McCarley, T. R. (2021). Regional Modeling of Forest Fuels and Structural Attributes Using Airborne Laser Scanning Data in Oregon. Remote Sensing, 13(2), 261. https://doi.org/10.3390/rs13020261