An Efficient Downscaling Scheme for High-Resolution Precipitation Estimates over a High Mountainous Watershed
Abstract
1. Introduction
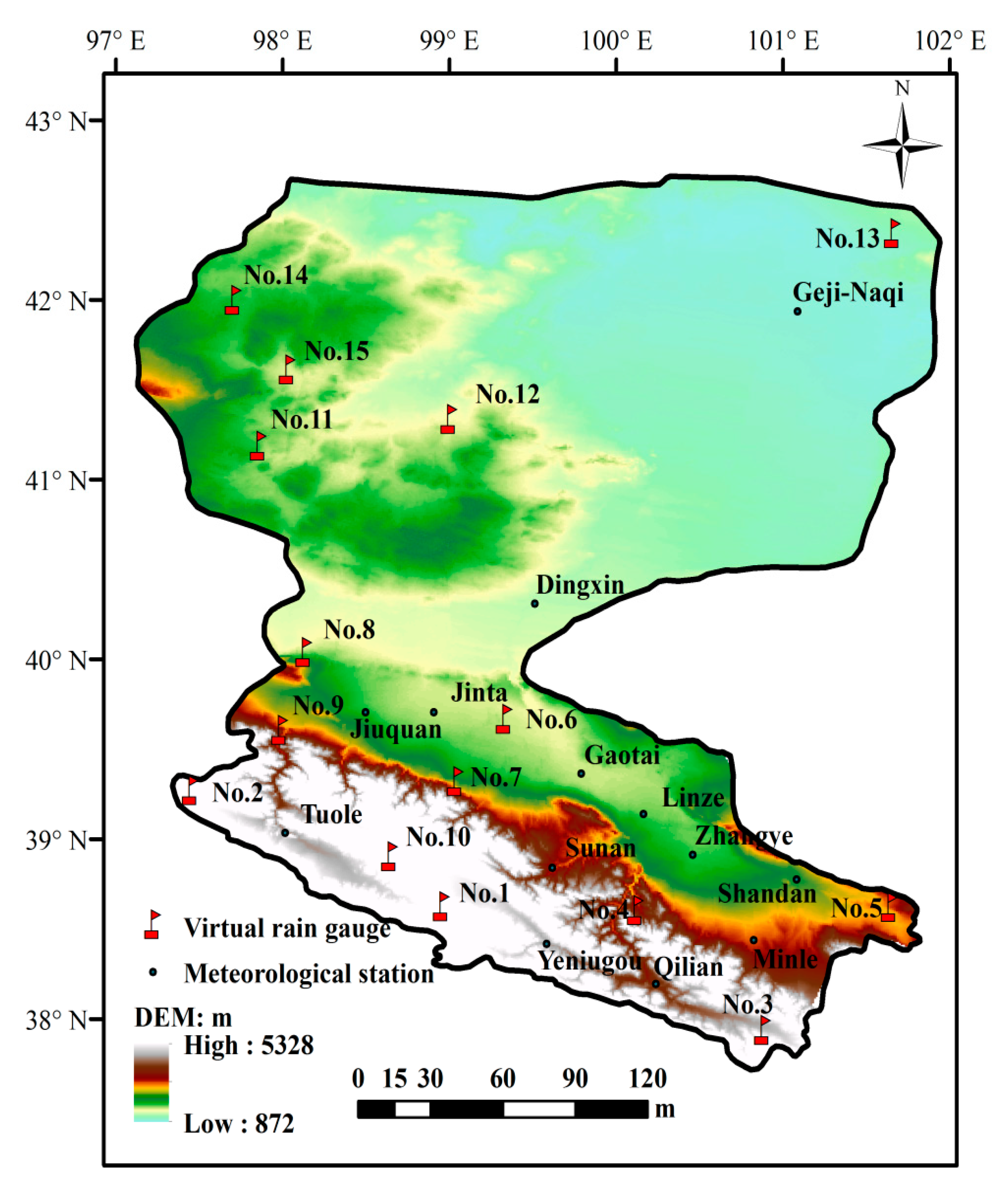
2. Study Area and Data
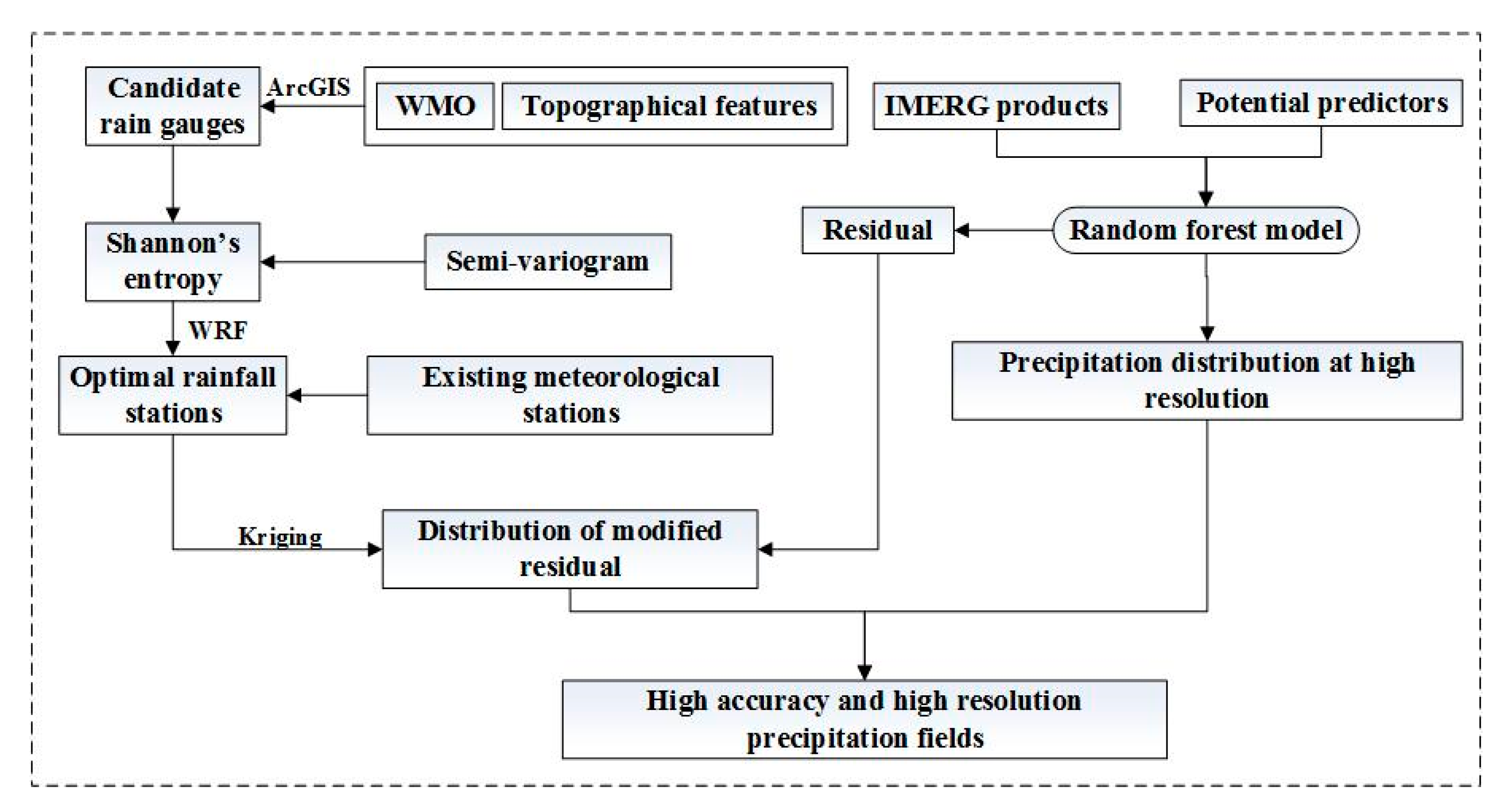
3. Methods
3.1. Designing a Rain Gauge Network Using Shannon’s Entropy
3.2. Random Forest
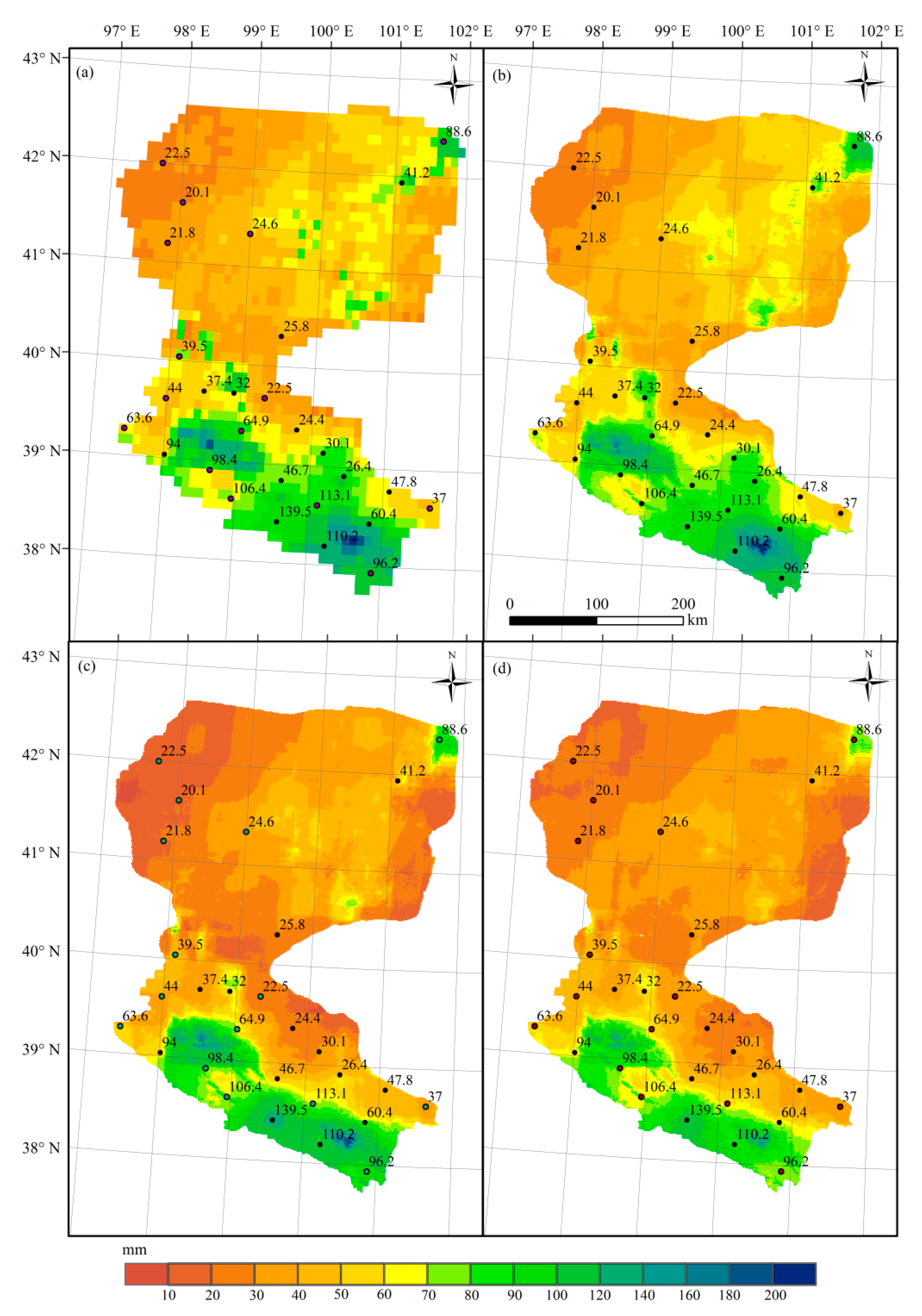
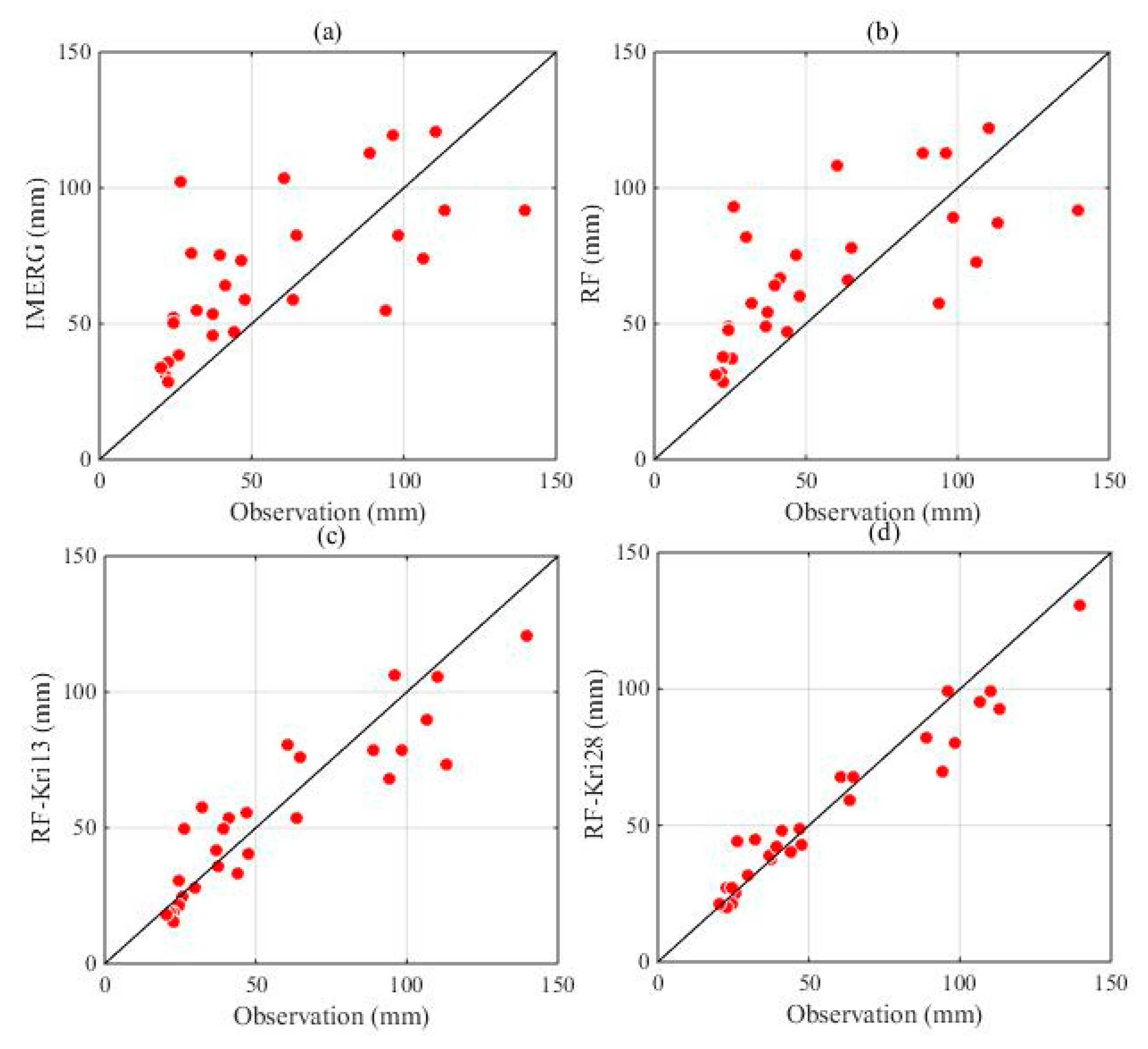
4. Results
5. Discussion
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Langella, G.; Basile, A.; Bonfante, A.; Terribile, F. High-resolution space–time rainfall analysis using integrated ANN inference systems. J. Hydrol. 2010, 387, 328–342. [Google Scholar] [CrossRef]
- Bruni, G.; Reinoso, R.; van de Giesen, N.C.; Clemens, F.H.L.R.; ten Veldhuis, J.A.E. On the sensitivity of urban hydrodynamic modeling to rainfall spatial and temporal resolution. Hydrol. Earth Syst. Sci. 2015, 19, 691–709. [Google Scholar] [CrossRef]
- Paul, P.K.; Kumari, N.; Panigrahi, N.; Mishra, A.; Singh, R. Implementation of cell-to-cell routing scheme in a large scale conceptual hydrological model. Environ. Modell Softw. 2018, 101, 23–33. [Google Scholar] [CrossRef]
- Piccolroaz, S.; Healey, N.C.; Lenters, J.D.; Schladow, S.G.; Hook, S.J.; Sahoo, G.B.; Toffolon, M. On the predictability of lake surface temperature using air temperature in a changing climate: A case study for Lake Tahoe (U.S.A.). Limnol. Oceanorg. 2018, 63, 243–261. [Google Scholar] [CrossRef]
- Rousta, I.; Olafsson, H.; Moniruaaaman, M.; Zhang, H.; Liou, Y.-A.; Mushore, T.; Mushore, T.D.; Gupta, A. Impacts of drought on Vegetation assessed by vegetation indices and meteorological factors in Afghanistan. Remote Sens. 2020, 12, 2344. [Google Scholar] [CrossRef]
- Singh, R.; Ranjan, K.; Verma, H. Satellite imaging and surveillance of infectious diseases. J. Trop. Dis. 2015, S1-004, 1–6. [Google Scholar] [CrossRef]
- He, X.Y.; Chaney, M.; Schleiss, M.; Sheffield, J. Spatial downscaling of precipitation using adaptable random forests. Water Resour. Res. 2016, 52, 8217–8237. [Google Scholar] [CrossRef]
- Solakian, J.; Maggioni, V.; Godrej, A. Investigating the error propagation from satellite-based input precipitation to output water quality indicators simulated by a hydrologic model. Remote Sens. 2020, 12, 3728. [Google Scholar] [CrossRef]
- Hijmans, R.J.; Cameron, S.E.; Parra, J.L.; Jones, P.G.; Jarvis, A. Very high resolution interpolated climate surfaces for global land areas. Int. J. Climatol. 2005, 25, 1965–1978. [Google Scholar] [CrossRef]
- Rasmussen, R.M.; Baker, B.; Kochendorfer, J.; Meyers, T.; Landolt, S.; Fischer, A.P.; Black, J.; Thériault, J.M.; Kucera, P.; Gochis, D.; et al. How well are we measuring snow: The NOAA/FAA/NCAR winter precipitation test bed. B. Am. Meteorol. Soc. 2012, 93, 811–829. [Google Scholar] [CrossRef]
- Martens, B.; Cabus, P.; Jongh, I.; Verhoest, N.E.C. Merging weather radar observations with ground-based measurements of rainfall using an adaptive multiquadric surface fitting algorithm. J. Hydrol. 2013, 500, 84–96. [Google Scholar] [CrossRef]
- Kidd, C.; Dawkins, E.; Huffman, G. Comparison of precipitation derived from the ECMWF operational forecast model and satellite precipitation datasets. J. Hydrol. 2013, 14, 1463–1482. [Google Scholar] [CrossRef]
- Zhang, X.; Anagnostou, E.N.; Vergara, H. Hydrologic evaluation of NWP-adjusted CMORPH estimates of hurricane-induced precipitation in the Southern Appalachians. J. Hydrol. 2016, 17, 1087–1099. [Google Scholar] [CrossRef]
- Zheng, D.; Bastiaanssen, W.G.M. First results from version 7 TRMM 3B43 precipitation product in combination with a new downscaling–calibration procedure. Remote Sens. Environ. 2013, 131, 1–13. [Google Scholar]
- Adhikary, S.K.; Yilmaz, A.G.; Muttil, N. Optimal design of rain gauge network in the Middle Yarra River catchment, Australia. Hydrol. Process 2015, 29, 2582–2599. [Google Scholar] [CrossRef]
- Oliveira, R.; Maggioni, V.; Vila, D.; Porcacchia, L. Using Satellite Error Modeling to Improve GPM-Level 3 Rainfall. Remote Sens. 2018, 10, 336. [Google Scholar] [CrossRef]
- Hu, Q.; Yang, D.; Li, Z.; Mishra, A.; Wang, Y.; Yang, H. Multi-scale evaluation of six high-resolution satellite monthly rainfall estimates over a humid region in China with dense rain gauges. Int. J. Remote Sens. 2014, 35, 1272–1294. [Google Scholar] [CrossRef]
- Sun, R.C.; Yuan, H.L.; Liu, X.L.; Jiang, X.M. Evaluation of the latest satellite-gauge precipitation products and their hydrologic applications over the Huaihe River basin. J. Hydrol. 2016, 536, 302–319. [Google Scholar] [CrossRef]
- Islam, M.D.; Yu, B.F.; Cartwright, N. Assessment and comparison of five satellite precipitation products in Australia. J. Hydrol. 2020, 590, 125474. [Google Scholar] [CrossRef]
- Retalis, A.; Katsanos, D.; Tymvios, F.; Michaelides, S. Comparison of GPM IMERG and TRMM 3B43 products over Cyprus. Remote Sens. 2020, 12, 3212. [Google Scholar] [CrossRef]
- Kirschbaum, D.B.; Huffman, G.J.; Adler, R.F.; Braun, S.; Garrett, K.; Jones, E.; McNally, A.; Skofronick-Jackson, G.; Stocker, E.; Wu, H.; et al. NASA’s remotely sensed precipitation: A reservoir for applications users. Bull. Am. Meteorol. Soc. 2017, 98, 1169–1184. [Google Scholar] [CrossRef]
- Dezfuli, A.K.; Ichoku, C.M.; Huffman, G.J.; Mohr, K.I.; Selker, J.S.; van de Giesen, N.; Hochreutener, R.; Annor, F.O. Validation of IMERG precipitation in Africa. J. Hydrol. 2017, 18, 2817–2825. [Google Scholar] [CrossRef]
- Wang, S.M.; Wang, D.K.; Huang, C. Evaluating the applicability of GPM satellite precipitation data in Heihe River Basin. J. Nat. Res. 2018, 33, 1847–1860. [Google Scholar]
- Tang, G.Q.; Clark, M.P.; Papalexiou, S.M.; Ma, Z.Q.; Hong, Y. Have satellite precipitation products improved over last two decades? A comprehensive comparison of GPM IMERG with nine satellite and reanalysis datasets. Remote Sens. Environ. 2020, 240, 111–697. [Google Scholar] [CrossRef]
- Sharifi, E.; Saghafian, B.; Steinacker, R. Downscaling satellite precipitation estimates with multiple linear regression, artificial neural networks, and spline interpolation techniques. J. Geophys Res. 2019, 124, 789–805. [Google Scholar] [CrossRef]
- Ma, Z.Q.; He, K.; Tan, X.; Xu, J.T.; Fang, W.Z.; He, Y.; Hong, Y. Comparisons of spatially downscaling TMPA and IMERG over the Tibetan Plateau. Remote Sens. 2018, 10, 1883. [Google Scholar] [CrossRef]
- Lu, X.Y.; Tang, G.Q.; Wang, X.Q.; Liu, Y.; Wei, M.; Zhang, Y.X. The development of a two-step merging and downscaling method for satellite precipitation products. Remote Sens. 2020, 12, 398. [Google Scholar] [CrossRef]
- Nourani, V.; Razzaghzadeh, Z.; Baghanam, A.H.; Molajou, A. ANN-based statistical downscaling of climatic parameters using decision tree predictor screening method. Theor. Appl. Climatol. 2019, 137, 1729–1746. [Google Scholar] [CrossRef]
- Maggioni, V.; Massari, C. On the performance of satellite precipitation products in riverine flood modeling: A review. J. Hydrol. 2018, 558, 214–224. [Google Scholar] [CrossRef]
- Baez-Villanueva, O.M.; Zambrano-Bigiarini, M.; Beck, H.E.; McNamara, I.; Ribbe, L.; Nauditt, A.; Birkel, C.; Verbist, K.; Giraldo-Osorio, J.D.; Thinh, N.X. RF-MEP: A novel random forest method for merging gridded precipitation products and ground-based measurements. Remote Sens. Environ. 2020, 239, 111606. [Google Scholar] [CrossRef]
- Zhao, N.; Yue, T.X.; Chen, C.F.; Zhao, M.W.; Fan, Z.M. An improved statistical downscaling scheme of tropical rainfall measuring mission precipitation in the Heihe River basin, China. Int. J. Climatol. 2018, 38, 3309–3322. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistical approaches for incorporating elevation into the spatial interpolation of rainfall. J. Hydrol. 2000, 228, 113–129. [Google Scholar] [CrossRef]
- Pan, X.D.; Li, X.; Cheng, G.D.; Li, H.Y.; He, X.B. Development and evaluation of a river basin scale high spatio-temporal precipitation data set using the WRF model: A case study of the Heihe River basin. Remote Sens. 2015, 7, 9230–9252. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J. Integrated Multi-SatellitE Retrievals for GPM (IMERG) Technical Documentation; NASA/GSFC Code; NASA/GSFC: Greenbelt, MD, USA, 2015.
- Hosseini-Moghari, S.M.; Tang, Q. Validation of GPM IMERG V05 and V06 precipitation products over Iran. J. Hydrol. 2020, 21, 1011–1037. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.L.; Joyce, R.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Tan, J.; Xie, P. Algorithm Theoretical Basis Document (ATBD) Version 06 NASA Global Precipitation Measurement (GPM) Integrated Multi-SatellitE Retrievals for GPM (IMERG); National Aeronautics and Space Administration (NASA): Washington, DC, USA, 2019; pp. 1–34.
- Kang, L.J.; Di, L.P.; Deng, M.X.; Shao, Y.Z.; Yu, G.N.; Shrestha, R. Use of geographically weighted regression model for exploring spatial patterns and local factors behind NDVI–precipitation correlation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4530–4538. [Google Scholar] [CrossRef]
- Shi, Y.; Song, L. Spatial downscaling of monthly TRMM precipitation based on EVI and other geospatial variables over the Tibetan Plateau from 2001 to 2012. Mt. Res. Dev. 2015, 35, 180–194. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Rutten, M.M.; Droogers, P. Spatial downscaling of TRMM precipitation using vegetative response on the Iberian Peninsula. Remote Sens. Environ. 2009, 113, 362–370. [Google Scholar] [CrossRef]
- WMO. Guide to Hydrological Practices, Volume 1, Hydrology-From Measurement to Hydrological Information, 6th ed.; WMO-No. 168; WMO: Geneva, Switzerland, 2008. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 623–656. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning: With Applications in R; Springer: New York, NY, USA, 2013. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Schiemann, R.; Erdin, R.; Willi, M.; Frei, C.; Berenguer, M.; Sempere-Torres, D. Geostatistical radar-rain gauge combination with nonparametric correlograms: Methodological considerations and application in Switzerland. Hydrol. Earth Syst. Sci. 2011, 15, 1515–1536. [Google Scholar] [CrossRef]
- Gao, F.; Kustas, W.P.; Anderson, M.C. A data mining approach for sharpening thermal satellite imagery over land. Remote Sens. 2012, 4, 3287–3319. [Google Scholar] [CrossRef]
- Chen, X.H.; Li, W.T.; Chen, J.; Rao, Y.H.; Yamaguchi, Y. A combination of TsHARP and Thin Plate Spline interpolation for spatial sharpening of Thermal imagery. Remote Sens. 2014, 6, 2845–2863. [Google Scholar] [CrossRef]
- Hutengs, C.; Vohland, M. Downscaling land surface temperature at regional scales with random forest regression. Remote Sens. Environ. 2016, 178, 127–141. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Huang, J.F.; Sheng, S.X.; Mansaray, L.R.; Liu, Z.X.; Wu, H.Y.; Wang, X.Z. A new downscaling-intergation gramework for high-resolution monthly precipitation estimates: Combining rain gauge observations, satellite-derived precipitation data and geographical ancillary data. Remote Sens. Environ. 2018, 214, 154–172. [Google Scholar] [CrossRef]
- Hamza, A.; Anjum, M.N.; Cheema, M.J.M.; Chen, X.; Afzal, A.; Azam, M.; Shafi, M.K.; Gulakhmadov, A. Assessment of IMERG-V06, TRMM-3B42V7, SM2RAIN-ASCAT, and PERSIANN-CDR precipitation products over the Hindu Kush Mountains of Pakistan, South Asia. Remote Sens. 2020, 12, 3871. [Google Scholar] [CrossRef]
- Gao, Z.; Huang, B.S.; Ma, Z.Q.; Chen, X.H.; Qiu, J.; Liu, D. Comprehensive comparisons of state-of the art gridded precipitation estimated for hydrological applications over southern China. Remote Sens. 2020, 12, 3997. [Google Scholar] [CrossRef]
- Valipour, M. How much meteorological information is necessary to achieve reliable accuracy for rainfall estimations? Agriculture 2016, 6, 53. [Google Scholar] [CrossRef]
- Bhardwaj, A.; Ziegler, A.D.; Wasson, R.J.; Chow, T.L. Accuracy of rainfall estimates at high altitude in the Garhwal Himalaya (India): A comparison of secondary precipitation products and station rainfall measurements. Atmos. Res. 2017, 188, 30–38. [Google Scholar] [CrossRef]
- Liu, Z.F.; Xu, Z.X.; Charles, S.P.; Liu, L. Evaluation of two statistical downscaling models for daily precipitation over an arid basin in China. Int. J. Climatol. 2011, 31, 2006–2020. [Google Scholar] [CrossRef]
- Jing, W.L.; Yang, Y.P.; Yue, X.F.; Zhao, X.D. A spatial downscaling algorithm for satellite-based precipitation over the Tibetan Platetu based on NDVI, DEM and land surface temperature. Remote Sens. 2016, 8, 655. [Google Scholar] [CrossRef]
- Fu, Y.Z.; Xu, S.G.; Zhang, C.K.; Sun, Y. Spatial downscaling of MODIS Chlorophyll-a using Landsat 8 images for complex coastal water monitoring. Estuar. Coast. Shelf Sci. 2018, 209, 149–159. [Google Scholar] [CrossRef]

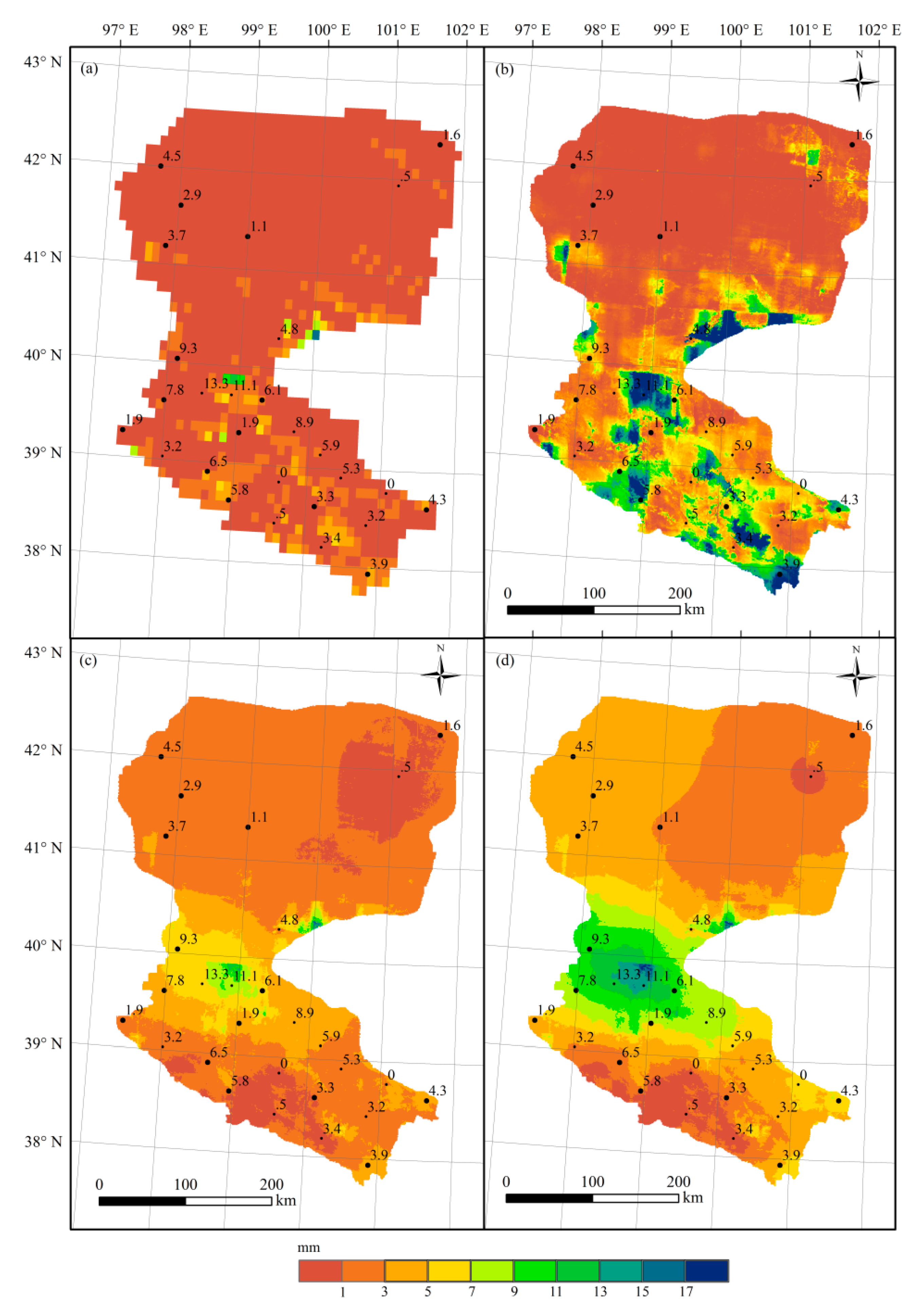
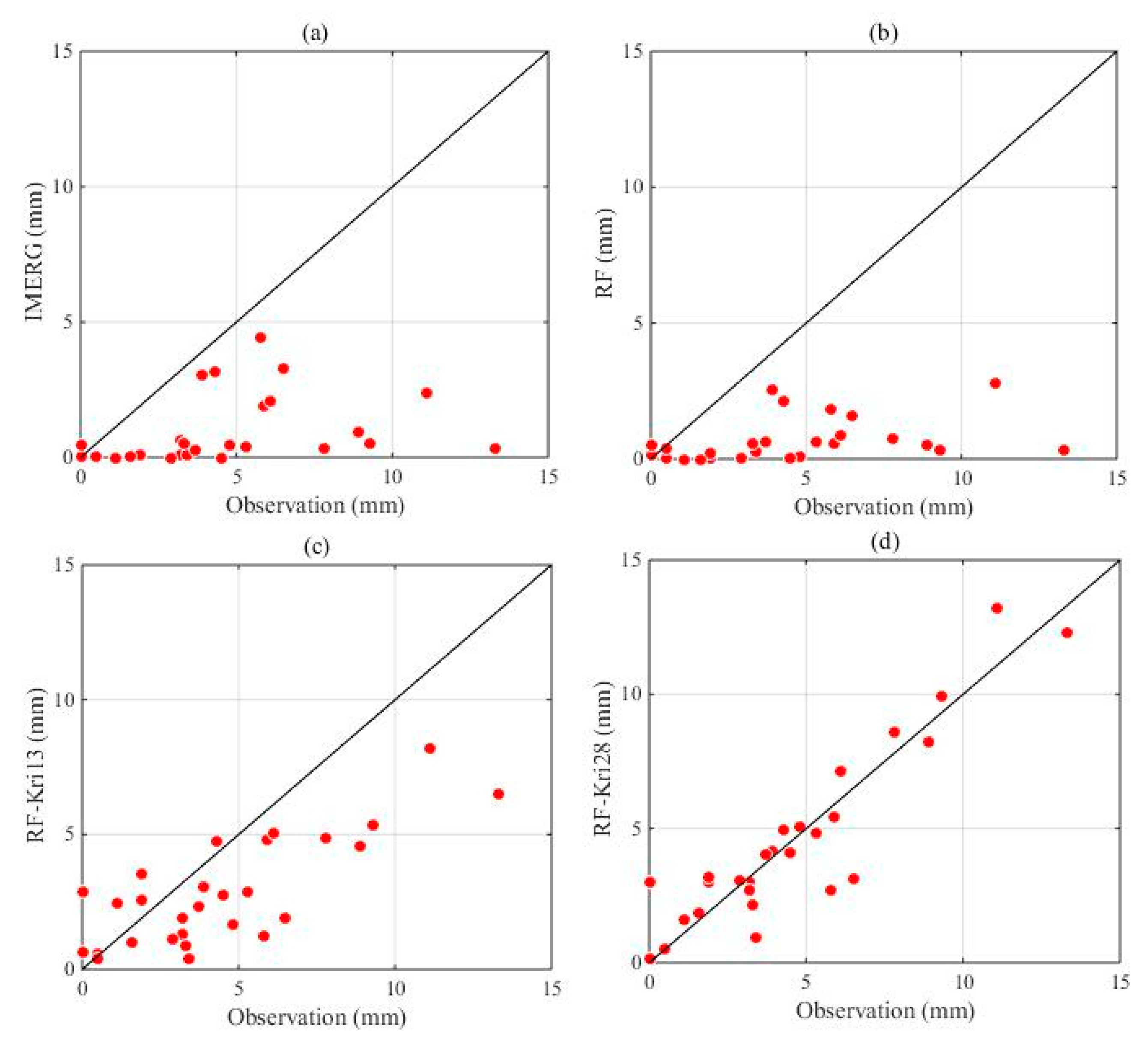
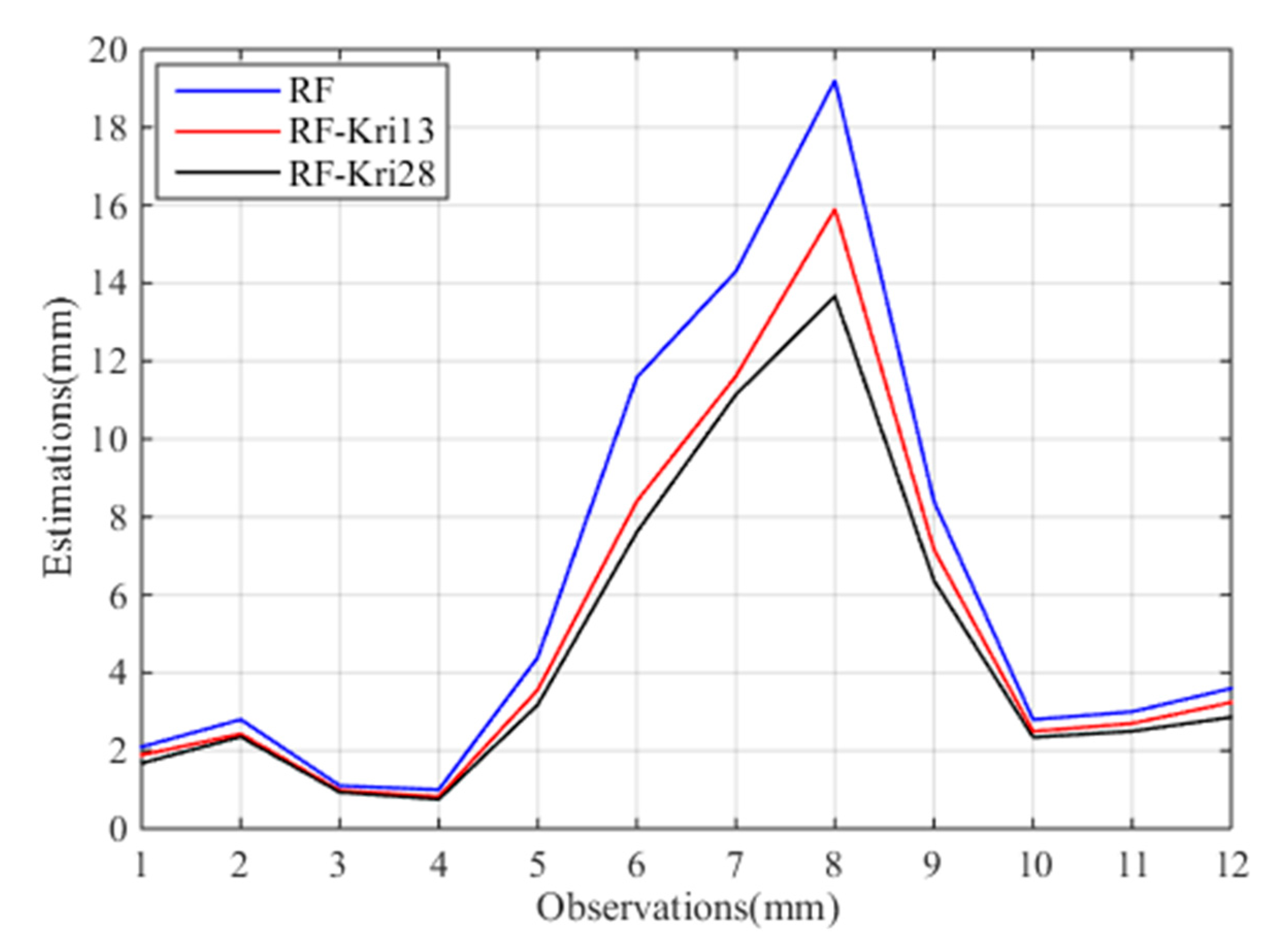
| Name | Latitude (°) | Longitude (°) | Elevation (m) | Max. 1 (mm) | Min. 1 (mm) | Mean 1 (mm) | Std. 1 (mm) |
|---|---|---|---|---|---|---|---|
| Geji-Naqi | 101.07 | 41.95 | 940.00 | 48.2 | 0 | 9.4 | 17.7 |
| Dingxin | 99.51 | 40.31 | 1176.00 | 61.4 | 0 | 9.5 | 18.7 |
| Jingta | 98.90 | 40.01 | 1266.20 | 42.8 | 0 | 10.5 | 14.8 |
| Gaotai | 99.83 | 39.39 | 1348.20 | 42.4 | 0 | 12.0 | 16.5 |
| Linze | 100.10 | 39.15 | 1450.00 | 42.9 | 0 | 13.5 | 15.7 |
| Jiuquan | 98.48 | 39.78 | 1473.60 | 37.4 | 0 | 10.0 | 13.5 |
| Zhangye | 100.44 | 38.81 | 1484.30 | 30.6 | 0 | 20.9 | 11.1 |
| Shandan | 101.07 | 38.81 | 1775.50 | 53.9 | 0.8 | 39.8 | 21.4 |
| Minle | 100.82 | 38.46 | 2264.60 | 60.4 | 0.2 | 41.6 | 22.1 |
| Sunan | 99.61 | 38.85 | 2307.50 | 46.9 | 0.7 | 32.0 | 18.8 |
| Qilian | 100.24 | 38.20 | 2720.00 | 110.2 | 0 | 24.1 | 39.3 |
| Yeniugou | 99.58 | 38.44 | 3240.00 | 139.5 | 1.1 | 18.3 | 45.5 |
| Tuole | 98.42 | 38.94 | 3370.90 | 94 | 0 | 10.5 | 35.7 |
| No. | Lat. (°) | Lon. (°) | Ele. (m) | Jan. (mm) | Fer. (mm) | Mar. (mm) | Apr. (mm) | May (mm) | June (mm) | July (mm) | Aug. (mm) | Sep. (mm) | Oct. (mm) | Nov. (mm) | Dec. (mm) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 38.6 | 99.0 | 4104 | 1.8 | 3.2 | 1.7 | 15.2 | 40.1 | 69.1 | 106.4 | 46.7 | 30.9 | 6.8 | 11.6 | 5.8 |
| 2 | 39.3 | 97.4 | 3933 | 1.9 | 2.1 | 0.2 | 5.0 | 16.6 | 33.1 | 63.6 | 41.3 | 17.7 | 2.7 | 2.4 | 1.9 |
| 3 | 37.9 | 101.0 | 3354 | 3.6 | 3.9 | 5.6 | 23.1 | 34.6 | 44.1 | 96.2 | 90.6 | 66.9 | 31.9 | 14.9 | 3.9 |
| 4 | 38.6 | 100.0 | 2869 | 1.7 | 3.5 | 4.1 | 18.1 | 39.9 | 57.7 | 113.1 | 52.8 | 37.3 | 7.3 | 7.6 | 3.3 |
| 5 | 38.6 | 102.0 | 2279 | 1.9 | 4.3 | 1.7 | 19.4 | 13.9 | 22.7 | 37.0 | 72.6 | 58.4 | 6.3 | 5.3 | 4.3 |
| 6 | 39.7 | 99.3 | 1339 | 1.8 | 3.1 | 3.2 | 4.0 | 7.6 | 18.0 | 22.5 | 25.1 | 13.5 | 2.2 | 5.0 | 6.1 |
| 7 | 39.3 | 99.0 | 1809 | 1.9 | 4.6 | 18.5 | 19.5 | 35.9 | 57.6 | 64.9 | 58.9 | 26.1 | 3.9 | 6.9 | 1.9 |
| 8 | 40.0 | 98.1 | 1366 | 2.1 | 3.7 | 0.3 | 0.0 | 7.9 | 14.4 | 39.5 | 33.2 | 3.8 | 2.1 | 5.2 | 9.3 |
| 9 | 39.6 | 98.0 | 2535 | 2.0 | 3.7 | 1.6 | 0.1 | 11.0 | 38.7 | 44.0 | 28.8 | 7.2 | 2.0 | 4.3 | 7.8 |
| 10 | 38.9 | 98.6 | 4108 | 1.2 | 3.0 | 1.9 | 22.5 | 30.2 | 59.2 | 98.4 | 35.3 | 28.5 | 3.5 | 8.7 | 6.5 |
| 11 | 41.2 | 97.9 | 1490 | 1.7 | 2.4 | 2.6 | 5.0 | 4.9 | 9.5 | 21.8 | 35.1 | 12.8 | 3.7 | 2.2 | 3.7 |
| 12 | 41.3 | 99.0 | 1285 | 2.2 | 2.8 | 1.4 | 2.4 | 6.5 | 9.9 | 24.6 | 28.9 | 16.8 | 6.1 | 2.7 | 1.1 |
| 13 | 42.4 | 102.0 | 1008 | 2.4 | 1.1 | 0.3 | 1.9 | 6.1 | 7.0 | 88.6 | 55.8 | 9.6 | 1.9 | 1.6 | 1.6 |
| 14 | 42.0 | 97.7 | 1497 | 2.2 | 1.8 | 0.9 | 4.6 | 2.0 | 7.0 | 22.5 | 25.0 | 5.4 | 4.9 | 2.5 | 4.5 |
| 15 | 41.6 | 98.0 | 1335 | 2.2 | 2.8 | 1.8 | 0.2 | 3.1 | 5.3 | 20.1 | 33.1 | 2.7 | 1.7 | 3.5 | 2.9 |
| Method | Error (mm) | Jan. | Fer. | Mar. | Apr. | May | June | July | Aug. | Sep. | Oct. | Nov. | Dec. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IMERG | MAE | 2.0 | 3.8 | 2.7 | 6.3 | 19.3 | 25.1 | 33.3 | 28.5 | 9.0 | 3.9 | 3.0 | 4.1 |
| RMSE | 2.5 | 4.6 | 3.6 | 6.8 | 22.4 | 28.3 | 37.8 | 34.0 | 11.2 | 5.3 | 3.9 | 5.7 | |
| RF | MAE | 2.0 | 3.8 | 2.7 | 6.1 | 19.5 | 24.8 | 33.5 | 29.1 | 9.5 | 3.7 | 3.0 | 4.0 |
| RMSE | 2.4 | 4.6 | 3.5 | 6.5 | 22.5 | 28.1 | 37.8 | 35.7 | 11.4 | 4.8 | 3.8 | 5.6 | |
| RF_Kri13 | MAE | 1.8 | 3.3 | 2.4 | 5.0 | 15.8 | 18 | 27.2 | 24.1 | 8.1 | 3.3 | 2.7 | 3.6 |
| RMSE | 2.1 | 4.1 | 3.1 | 5.4 | 18 | 20.9 | 30.4 | 26.7 | 9.3 | 4.3 | 3.3 | 5.2 | |
| RF_Kri28 | MAE | 1.6 | 3.2 | 2.3 | 4.6 | 14.1 | 16.3 | 26.1 | 20.7 | 7.2 | 3.1 | 2.5 | 3.1 |
| RMSE | 1.9 | 3.8 | 2.9 | 5.0 | 16.2 | 18.9 | 28.5 | 23.5 | 8.0 | 4.0 | 3.0 | 4.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, N. An Efficient Downscaling Scheme for High-Resolution Precipitation Estimates over a High Mountainous Watershed. Remote Sens. 2021, 13, 234. https://doi.org/10.3390/rs13020234
Zhao N. An Efficient Downscaling Scheme for High-Resolution Precipitation Estimates over a High Mountainous Watershed. Remote Sensing. 2021; 13(2):234. https://doi.org/10.3390/rs13020234
Chicago/Turabian StyleZhao, Na. 2021. "An Efficient Downscaling Scheme for High-Resolution Precipitation Estimates over a High Mountainous Watershed" Remote Sensing 13, no. 2: 234. https://doi.org/10.3390/rs13020234
APA StyleZhao, N. (2021). An Efficient Downscaling Scheme for High-Resolution Precipitation Estimates over a High Mountainous Watershed. Remote Sensing, 13(2), 234. https://doi.org/10.3390/rs13020234




