1. Introduction
Soil is an important natural resource that is vital to the survival of life on Earth. The salt level is an important attribute of soil [
1]. A proper salt content can provide the ions needed for the growth and development of plants, while a higher salt content will cause “salt damage” to the growth of plants, such as salt stress, salt-alkali stress and alkali stress. Therefore, the salt information obtained quickly and accurately is the key to the improvement of saline soil, for example, Metternicht et al. [
2] introduced the potentials and constraints of remote sensing of soil salinity. The soil salinity caused by natural or human-induced processes is considered a major environmental hazard, and the paper reviewed various sensors and approaches used for remote identification and mapping of salt-affected areas, in order to curb degradation trends and secure sustainable land use. Farifteh et al. [
3] predicted the salt concentrations in soils using partial least squares regression (PLSR) and an artificial neural network (ANN). Their results showed that either of the two methods was satisfactory for establishing the relationship between soil electrical conductivity (EC) and soil reflectance, which indicates that the relation between soil salinity and soil reflectance could be approximated by a linear function. Peng et al. [
4] estimated soil salinity in Xinjiang using a PLSR model and a cubist model, and the results indicated that cubist model could predict EC values with better accuracy and stability under variable environmental conditions than PLSR, and the cubist model was recommended for mapping soil salinity under environmental conditions with a large spatial variation of vegetation, soil moisture and salinization.
Most of the saline soils in Xinjiang mainly contain water-soluble chlorides and sulfates, and the soluble salts in saline soils often exist in the form of base ions (which refers to the CO
32−, Cl
−, SO
42−, Na
+, Ca
2+, Mg
2+ ions generated after the dissociation of sodium salts, magnesium salts and calcium salts). The characteristics of water-soluble base ions can show the migration trend of total salt to a certain extent. They are an important factor in the response of soil hyperspectral reflectivity and can be used as a characteristic factor of soil salinization. As one of the water-soluble base ions, Na+ ion is the main indicator of the degree of soil salinization [
5], and the accurate estimation of its content can provide important technical support for the treatment of saline soils.
The traditional method of obtaining salt content information content is to collect a limited number of soil samples in the field, and then bring the samples back to the laboratory for chemical analysis. Although the salt information content information provided by this method has high accuracy, it has the disadvantages of expensive labor costs, long test cycles, low real-time efficiency and being time-consuming and laborious, which cannot meet the demands of dynamic, rapid, accurate monitoring and evaluation of saline soils from a large-scale perspective. However, hyperspectral remote sensing technology has the advantages of being dynamic, fast, accurate, pollution-free, non-destructive, with wide coverage, high resolution, and multiple bands [
6], and it has become a convenient and efficient method to monitor soil salinization. For example, Wang et al. [
7] collected soil samples from the Hetao area in Inner Mongolia. Three methods of gray correlation, stepwise regression and variable importance projection (VIP) were used to screen the characteristic bands of the eight major ions. The paper studied the inversion performance of PLSR and support vector machine (SVM) models for ions. It is found that the model established by the spectra data pretreated by VIP has the best accuracy, the prediction effect of PLSR is better than that of SVM, and the model can better predict Na
+, Mg
2+, Ca
2+, SO
42− and Cl
- ions, while the prediction performance of K
+, CO
32− and HCO
3− ions is poor. Srivastava et al. [
8] collected soil samples from farmers’ fields in three villages in the Ganges Plain, India, and used the PLSR model to predict soil salinity information. Their simulation showed that the 1390–2400 nm band can successfully predict the saline soil information. It has strong predictive ability for electrical conductivity, Na
+, and Cl
−, as well as good predictive ability for Ca
2+, good predictive ability for SO
42−, and poor predictive ability for CO
32−, PH, and HCO
3−.
The pretreatment of VNIR-SWIR spectroscopy data is the key to establishing a high-precision inversion model. Integer-order derivatives (1.0-order, 2.0-order) are often used to preprocess soil VNIR-SWIR data because it can enhance the hyperspectral signals [
9,
10]. However, the original hyperspectral curve is quite different from the hyperspectral curve pretreated by a 1.0-order or 2.0-order derivative. Ignoring the gradual information of the three at different fractional-order derivative (FOD) levels [
11] will lead to the loss of important hyperspectral information and affect the estimation accuracy of the inversion model. FOD expands the concept of integer-order derivative, which extends the order to any order. In recent years, a small number of scholars have used FOD to preprocess the indoor hyperspectral data of soils and extract more useful spectral information hidden in the fractional-order results, which can improve the accuracy of subsequent inversion models. For instance, Hong et al. [
12] collected soil samples from a typical peri-urban agricultural area in Wuhan City (Hubei Province, China) and proposed a new FOD algorithm. An, ASD FieldSpec
®3 portable spectrometer was used to measured spectra, which was done in a dark room. The lead (Pb) and zinc (Zn) concentrations of the samples were obtained in the laboratory and PLSR and random forest (RF) were used as calibration methods. This study demonstrated that the model accuracy of RF was better than PLSR, and the RF model for predict the concentration of Pb and Zn at 0.25- and 0.5-order had the optimal prediction accuracies. Zhang et al. [
13] collected soil samples in northwestern China, and soil organic matter content (SOMC) and reflectance spectra were measured in the laboratory, FOD were used to pretreat soil spectra and a partial least squares-support vector machine (PLS-SVM) model was used to estimate SOMC. The conclusions showed that the 1.05- to 1.45-order range had the highest “signal-to-noise ratio”, and it was most suitable for SOMC analysis. Wang et al. [
14] used soil located at the Ebinur Lake Wetland National Nature Reserve (ELWNNR) in northwest China as research object. Three new FOD methods, the optimal remote sensing index and the subsection of spectral band method were selected to predict SOMC. Results showed that the optimal model appeared at 1.2-order, and its lowest root mean square error (RMSE) was 1.70 g/kg. Wang et al. [
15] applied FOD was to the pretreatment of soil hyperspectral signals of samples collected from the Ebinur Lake basin in the Xinjiang Uighur Autonomous Region of China, and the PLSR model was used to estimate the clay content of the desert soils. Spectral reflectance and clay content were measured in the laboratory. Simulations showed that the 1.8-order FOD was effective.
At present, although some scholars use FOD to preprocess soil indoor hyperspectral signals, the indoor hyperspectral test environment is too ideal, and it can weaken the influence of the surrounding environment and weather on the hyperspectral data. In addition, the collected soil needs to be naturally air-dried, impurities must be-removed, the soil ground, sieved, leveled and other man-made operations applied before recording the indoor hyperspectral signals [
16,
17,
18], which destroys the original porosity and water content of the soil, resulting in changes in the characteristics of the hyperspectral signals. The field hyperspectral are a true reflection of the soil growth environment, and their research value is greater. However, it is more difficult to collect field hyperspectra than indoor hyperspectra, and there are more external interference factors during the collection process, resulting in a lower “signal-to-noise ratio”. At the same time, the collected field VNIR-SWIR is limited, and the amount of soil samples is small. However, although there are few reports on the processing of field spectroscopy data, there are still some scholars who provide good solutions to the problems existing in field spectroscopy measurements. For example, Ben-Dor et al. [
19] developed a new assembly named Soil field PRObe (SoilPRO) for measuring the surface reflectance in the field, which was capable of measuring soil spectra in the field in a very precise and optimal manner that avoided most of the current soil-measurement problems experienced by users in the field, and the SP assembly was unique in that it eliminated the need for advanced planning and a reliance on independent environmental conditions. Francos et al. [
20] developed a transfer function (TF) to predict the field spectral measurements from laboratory spectra and concluded that soil surface reflectance values could be estimated based on laboratory spectra using a TF, which could assist in the processing of remote-sensing data and proximal sensing of surface properties.
In addition, stress caused by human activities such as farming, grazing, irrigation, development of wasteland, deforestation, etc. is a widespread interference phenomenon in Nature [
21]. Unreasonable human activities lead to an increase in the groundwater level, which is strongly affected by surface evaporation, which will bring the bottom soil salt to the surface to accumulate, causing secondary salinization of the soil. At the same time, different human activity modes, degrees, and durations will affect the physical and chemical properties of the soil, and different degrees of human activity disturbances have different responses to soil water-soluble base ions. However, there are few reports on related studies in those areas.
Most of the research objects are soil samples collected in the same environment, and there are few published comparative analyses of the pretreatment effects for soil water-soluble base ions under different human interference environments. Therefore, this study collects VNIR-SWIR spectroscopy of soil samples from different human interference regions, preprocesses the soil VNIR-SWIR using FOD, observes the details of changes in the hyperspectral reflectance curve in different derivative, and verifies the feasibility of the application for FOD in the field hyperspectral under different degrees of human activity stress. The VNIR-SWIR spectroscopy of soil is measured by a ASDFieldSpec®3Hi-Res spectrometer in the field environment. This study provides a new method for the hyperspectral pretreatment of saline soils in different human interference areas, which has important practical significance for promoting the sustainable development of Xinjiang land resources, improving the saline soil in oases, and preventing further soil degradation.
3. Simulation Results
3.1. Statistical Characteristics of Soil Salinity Information under Different Disturbance Degrees
We calculate the correlation of the three areas between the total salt content and water-soluble base ions (Na
+, K
+, Ca
2+, Mg
2+, Cl
−, SO
42−, CO
32−, HCO
3−) (
Table 1,
Table 2 and
Table 3), and give the values of the correlation coefficients in absolute values.
It can be seen from
Table 1 that the correlation between total salt and Na
+ in Area A is better (0.738) and the correlation between total salt and SO
42− is better (0.527), while the correlation between total salt and Ca
2+ is lower (0.309) and total salt and the remaining five ions (K
+,Mg
2+,Cl
−,CO
32−,HCO
3−) have very low correlations. In addition, the correlation between SO
42− and Ca
2+ is better (0.653), and the correlation between SO
42− and Mg
2+ is good at 0.559, which indicates that there is more CaSO
4 and MgSO
4 in the soil of Area A. The correlation between CO
32− and Ca
2+,CO
32− and Mg
2+,CO
32− and Na
+,HCO
3− and Ca
2+ is general, and its value is about 0.3, which shows that there is also a certain amount of CaCO
3, MgCO
3, NaCO
3 and CaHCO
3 in the soil of Area A.
It can be seen from
Table 2 that the correlation between total salt and Na
+ in Area B is better (0.859), the correlation between total salt and Cl
− is good at 0.717, the correlation between total salt and Ca
2+ is general at 0.433, and the correlation between total salt and Mg
2+ is less at 0.336, and the correlation between total salt and SO
42− is small at 0.319, and the correlation between total salt and the remaining three ions (K
+, CO
32−, HCO
3−) is very low. At the same time, the correlation between CO
32− and Ca
2+ is better (0.629), the correlation between HCO
3− and Ca
2+ is better (0.579), the correlation between Cl
− and Mg
2+ is better (0.598), and the correlation between Cl
− and Ca
2+ is better at 0.523, which shows that there is a lot of CaCO
3, CaHCO
3, MgCl and CaCl in the soil of Area B. The correlation between CO
32− and Mg
2+ is general (0.376), the correlation between HCO
3− and Mg
2+ is general (0.393), the correlation between Cl
− and Na
+ is general at 0.390, and the correlation between SO
42− and Ca
2+ is general at 0.330. It shows that there is also a certain amount of MgCO
3, MgHCO
3, NaCl and CaSO
4 in the soil of Area B.
It can be seen from
Table 3 that the correlation between total salt and Cl
− and Na
+ in Area C is very good, reaching 0.979 and 0.971, respectively. The correlation between total salt and SO
42− is as good as 0.697, and the correlation between total salt and Ca
2+ is also as good as 0.685, the correlation between the total salt and the remaining four ions (K
+, Mg
2+, CO
32−, HCO
3−) is very low. At the same time, the correlation between Cl
− and Na
+ is 0.990, and the correlation between SO
42− and Ca
2+ is 0.801, which indicates that there are a lot of NaCl and CaSO
4 in the soil of Area C. The correlation between Cl
− and Ca
2+ is 0.574, and the correlation between SO
42− and Na
+ is 0.580, which shows that there is more CaCl and NaSO
4 in the soil of Area C. The correlation between HCO
3− and Mg
2+ is 0.477, the correlation between HCO
3− and Ca
2+ is 0.474, the correlation between CO
32− and Ca
2+ is 0.361, and the correlation between SO
42− and Mg
2+ is 0.335, so we can conclude there is a certain amount of MgHCO
3, CaHCO
3, CaCO
3 and MgSO
4.
The correlation analysis results of
Table 1,
Table 2 and
Table 3 show that the total salt in Area B and C has a good correlation with Na
+ and Cl
− (the correlation is greater than 0.7), while the total salt in Area A only has a good correlation with Na
+.
3.2. Curve Characteristics of Soil Original Hyperspectral Reflectance Pretreated by FOD
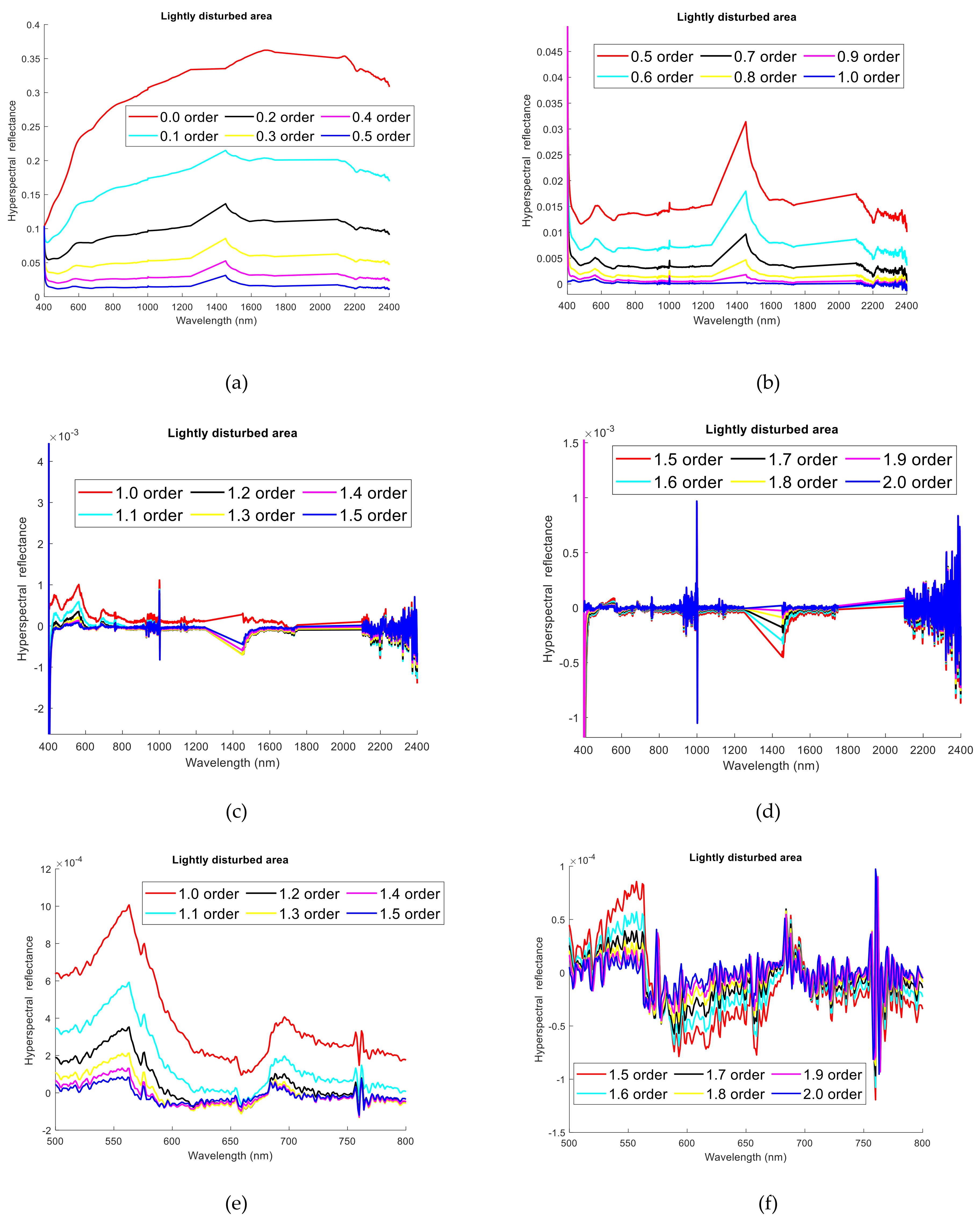
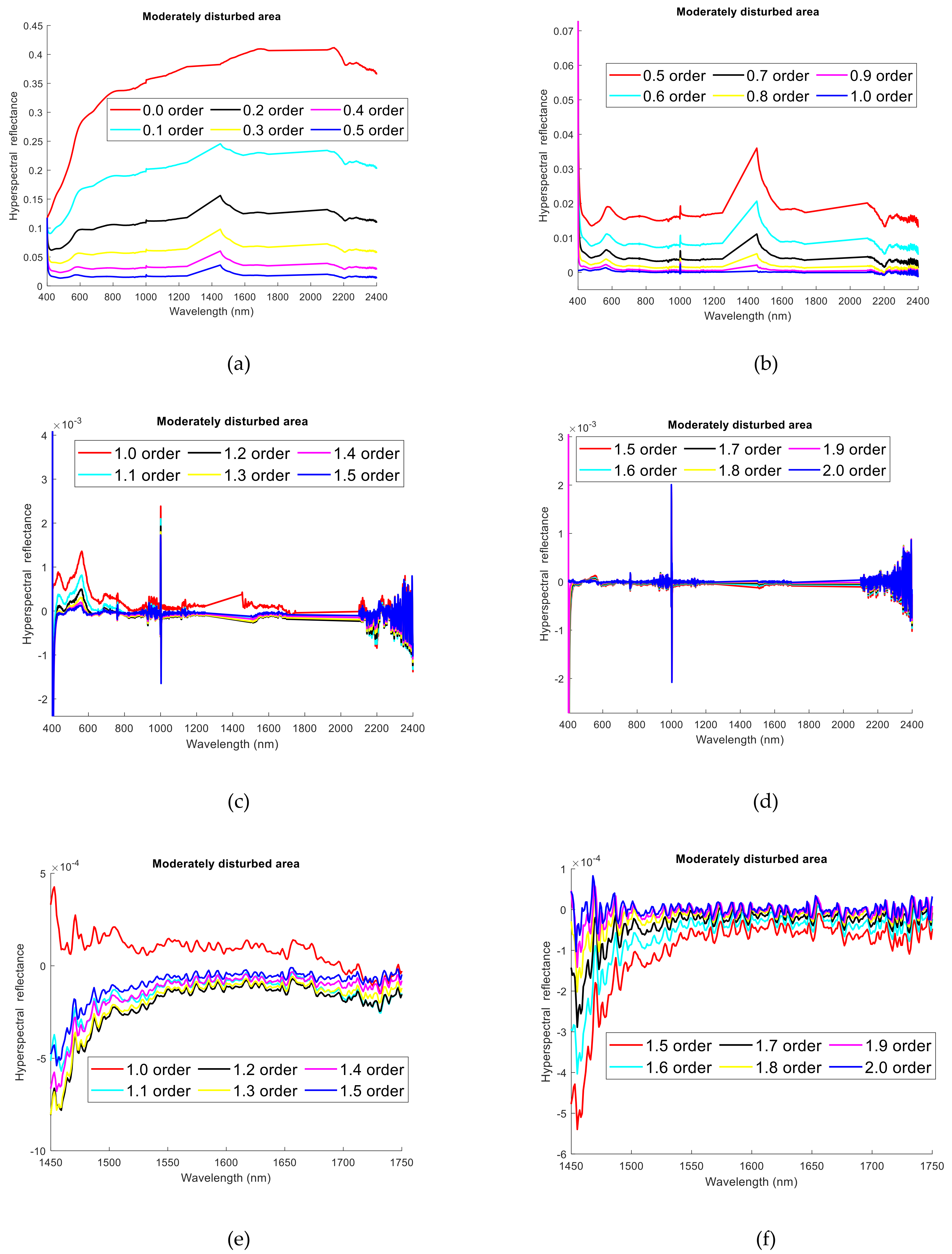
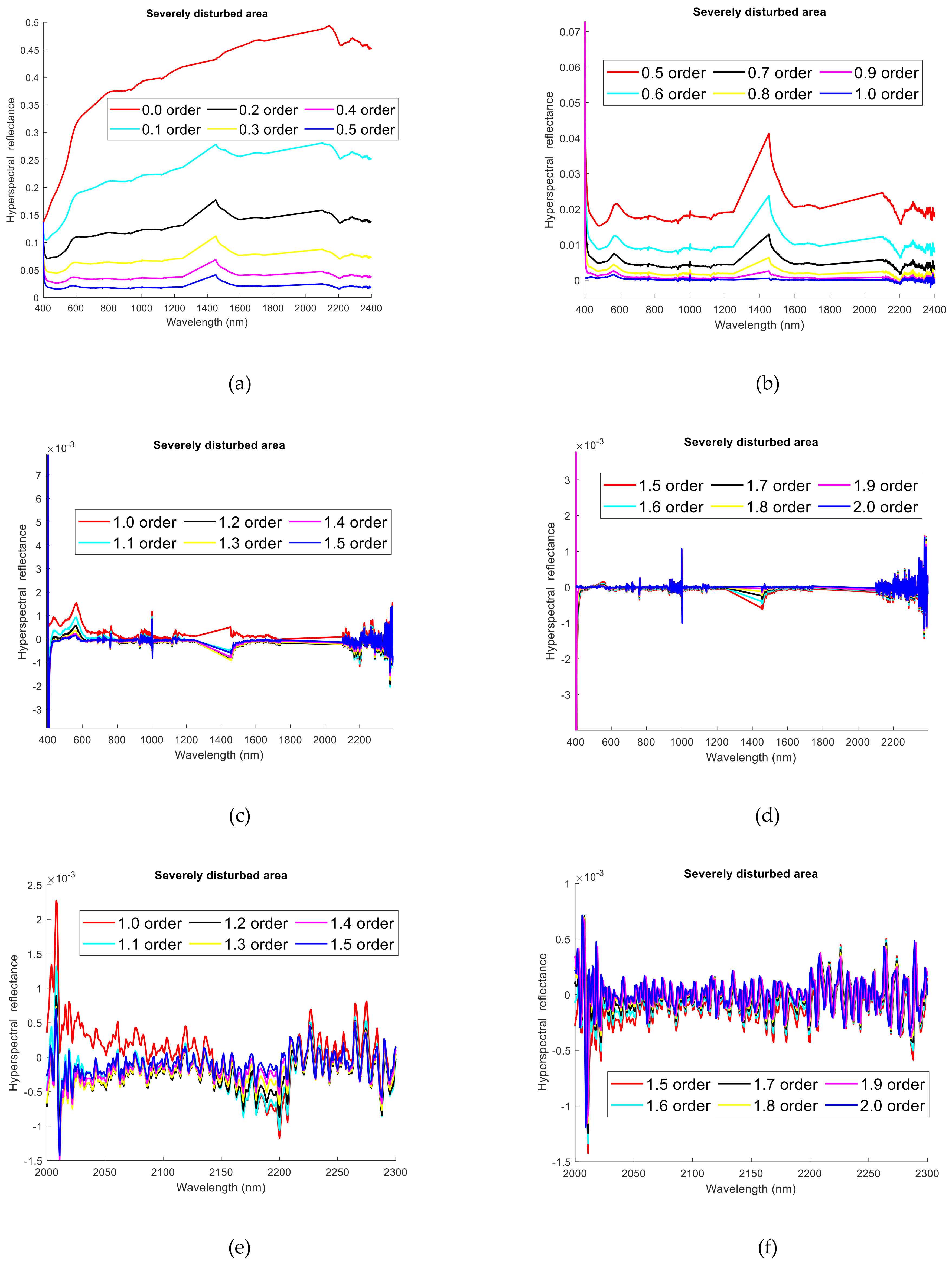
In the MatLab software, the original hyperspectral reflectance curve (R) of the soil is subjected to FOD pretreatment, and the calculation process of the Grünwald-Letnikov FOD in Equation (6) is realized through MatLab language programming. Among them, 0.1 is selected as the order interval of the FOD, 0.0-order is the starting order, and 2.0-order is the ending order. The characteristics of the original hyperspectral average reflectance curve of the soil in each interference area are shown in
Figure 2,
Figure 3 and
Figure 4. The abscissa represents the band range, and the ordinate represents the reflectance of the hyperspectral calculated by FOD. Because the number of all the bands of the hyperspectral is too large, and the difference of hyperspectral reflectance values processed by FOD within different orders is too large (
Figure 2c,d,
Figure 3c,d and
Figure 4c,d), it is not easy to see the FOD characteristics of the hyperspectral reflectance curve. This article enlarges the local bands of 1.0-order to 1.5-order and 1.5-order to 2.0-order. In the front, middle, and back of the entire waveband range (350–2500 nm), 500–800 nm, 1450–1750 nm, and 2000–2300 nm are selected to discuss the hyperspectral reflectance of the soil in the lightly, moderately, and severe interference regions (
Figure 2e,f,
Figure 3e,f and
Figure 4e,f).
In the three different interference regions, with the gradual increase of the orders, the reflectance derivative value of the ordinate gradually decreases, and it finally swings up and down at the derivative value of 0 (
Figure 2,
Figure 3 and
Figure 4). For example, the derivative value of the original hyperspectral reflectance of Area A ranges from 0.02 to 0.38 between 0.0-order and 0.5-order, and between 0.5-order and 1.0-order is 0.001 to 0.035, between 1.0-order and 1.5-order (
Figure 1e) is −0.5 × 10
−4~10 × 10
−4, and the range between 1.5-order and 2.0-order (
Figure 1f) is −1.25 × 10
−4~0.96 × 10
−4. The derivative value of the original hyperspectral reflectance of Area B ranges from 0.03 to 0.43 between 0.0-order and 0.5-order, and between 0.5-order and 1.0-order is 0.001 to 0.036, and between 1.0-order and 1.5-order (
Figure 2e) is −8 × 10
−4~5 × 10
−4, and the range between 1.5- order and 2.0-order (
Figure 2f) is −5.2 × 10
−4~0.9 × 10
−4. The derivative value of the original hyperspectral reflectance of Area C ranges from 0.03 to 0.49 between 0.0-order and 0.5-order, and from 0.5-order to 1.0-order is 0.001 to 0.043, and between 1.0-order and 1.5-order (
Figure 3e) is −1.5 × 10
−3~2.23 × 10
−3, and the range between 1.5-order and 2.0-order (
Figure 3f) is −1.4 × 10
−3~0.8 × 10
−3. The reason is that as the order of the fractional-order derivative gradually increases, the peak profile of the hyperspectral reflectance curve is gradually changed, and the peak removal operation is continuously completed, which causes the reflectance derivative value of the ordinate to gradually decrease.
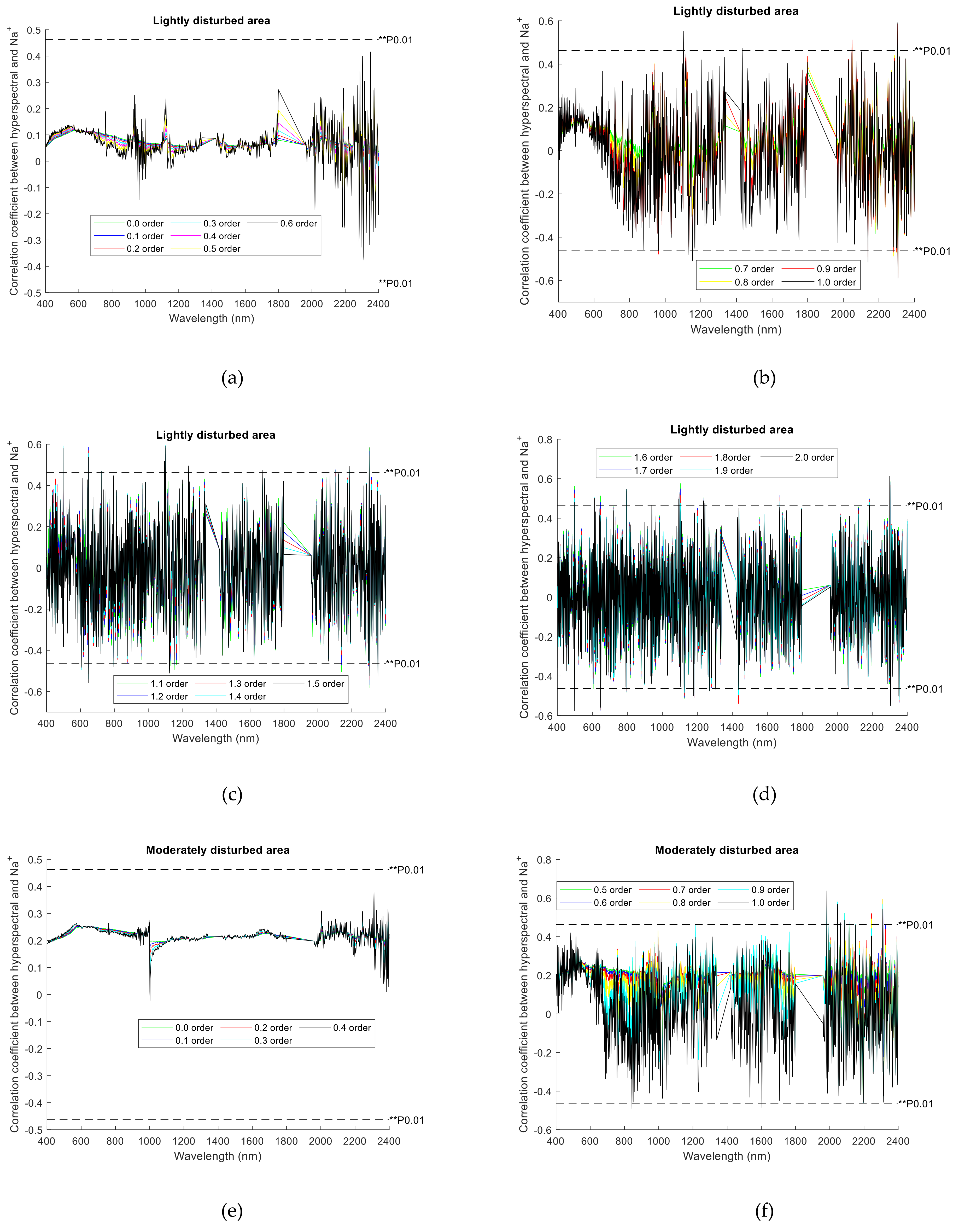
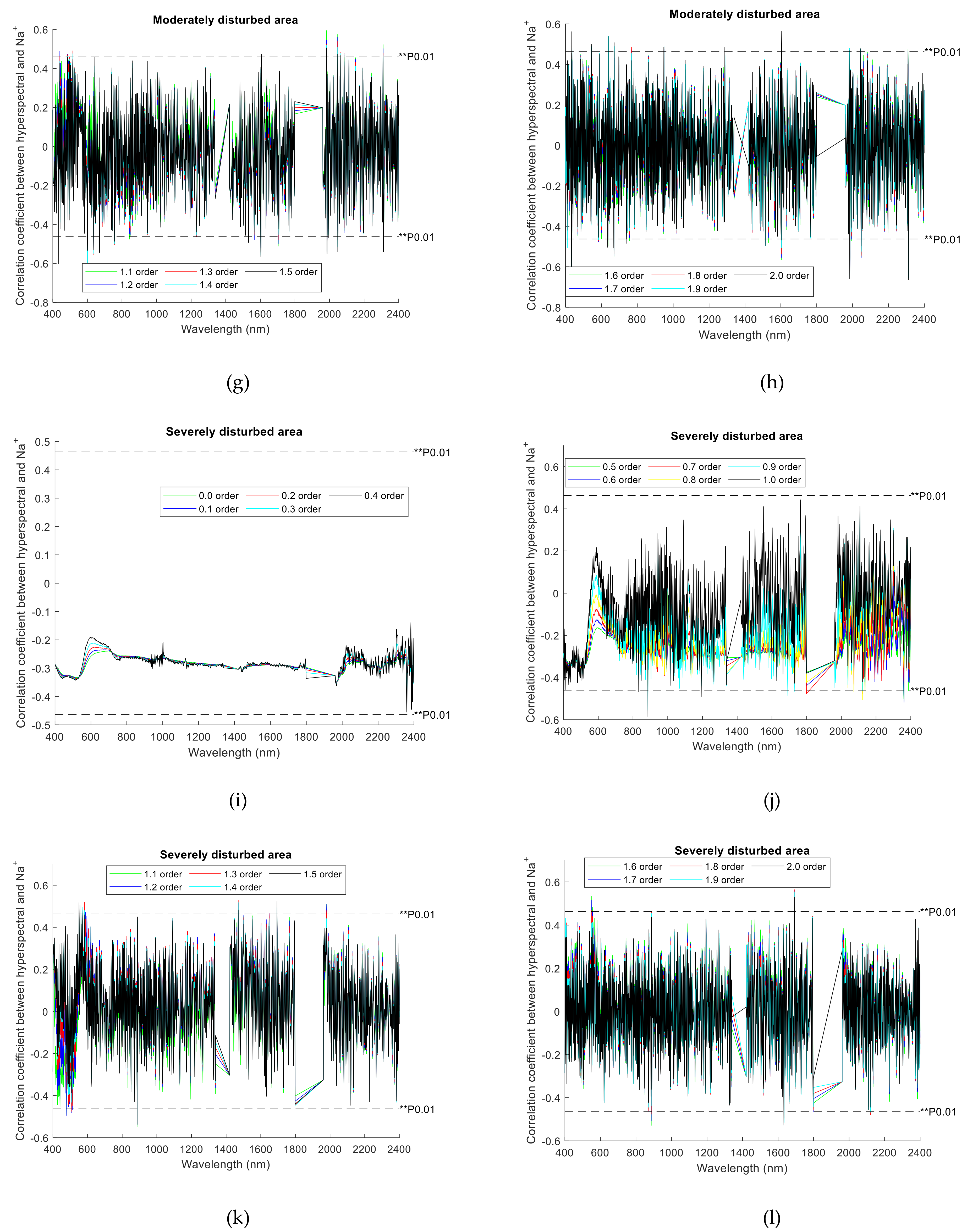
3.3. The Correlation Coefficient between the Original Hyperspectral and Na+ Is Affected by FOD
For soils with different degrees of human interference, the effect of FOD on the correlation coefficient between the original hyperspectral and Na
+ is shown in
Figure 5. The simulation shows that when the correlation coefficients were in the light 0.0-order to 0.6-order, moderate 0.0-order to 0.4-order and severe 0.0-order to 0.4-order, none of the correlation coefficients in any band passed the 0.01 significance level test. When the order of the FOD is increased from 0.0-order to 1.0-order, the change trend of the correlation coefficient curve shows a certain gradual form. For example, the more obvious band range of the gradual change trend of the correlation coefficient curve is: 400–700 nm, 790–900 nm and 1200–1300 nm in the Area A; 400–950 nm, 1000–1300 nm and 1450–1750 nm in the Area B; and 400–900 nm, 1120–1330 nm and 1500–1780 nm in the Area C. However, when the order increases from 1.0-order to 2.0-order, the variation of the correlation coefficient curve fluctuates greatly, which is less obvious than the gradual change from 0.0-order to 1.0-order.
There are certain differences in the shape of the correlation coefficient curve in different FOD. Regardless of the area of human interference, the correlation coefficient curve is shown that the outline is clearer in the low-order derivative (order 0.0–0.4), and the trend of change is relatively gentle. In addition, for the hyperspectral data without FOD pretreatment (it is 0.0-order), the correlation coefficient ranges are very small, and show different positive and negative correlations in each area, such as 0.0330~0.1175 in Area A, 0.1843~0.2512 in Area B, and −0.3514~−0.2395 in Area C.
In addition,
Figure 5 also shows that the FOD pretreatment can improve the correlation coefficient between the original hyperspectral and Na
+. For example, in the Area A, the 0.2-order is −0.0101~0.1255, the 0.5-order is −0.2350~0.3557, the 0.7-order is −0.5105~0.4855, the 0.9-order is −0.5861~0.5848, the 1.2-order is −0.5678~0.5853, the 1.5-order is −0.5580~0.5921, and the 1.9-order is −0.5692~0.5940. In Area B, the order of 0.3 is 0.0685~0.3147, the order of 0.5 is −0.1196~0.4758, the order of 0.8 is −0.4290~0.5942, the order of 1.1 is −0.5183~0.5933, the order of 1.4 is −0.5961~0.5170, and the order of 1.7 is −0.6589~0.5262. In Area C, the order of 0.3 is −0.3966~−0.2111, the order of 0.5 is −0.5094~−0.0205, the order of 0.8 is −0.5058~0.2962, the order of 1.1 is −0.5494~0.5102, the order of 1.4 is −0.5406~0.5178, and the order of 1.7 is- 0.5075~0.5612. Therefore, with the increase of the FOD, the overall variation range of the correlation coefficient between the original hyperspectral and Na
+ is gradually increased.
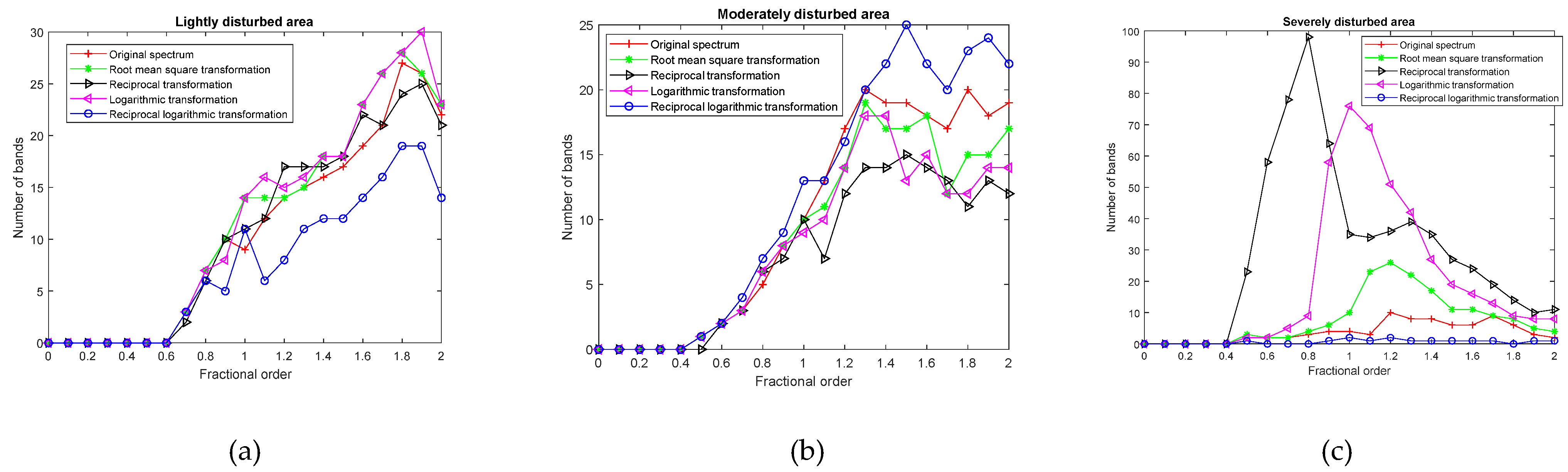
3.4. The Correlation Coefficient between Each Spectra and Na+ Passed the 0.01 Test under Different Derivative
In the original spectrum and its transformation spectrum, many of the bands that passed the 0.01 test appear in the fractional order, but the FOD and the band numbers have certain differences in each spectrum (R, , 1/R, lgR, 1/lgR). For example, the sequence of the band numbers in Area A under the different FOD from large to small is: 30 band numbers in lgR of 1.9-order > 28 band numbers in of 1.8-order > 27 band numbers in R of 1.8-order > 25 band numbers in 1/R of 1.9-order> 19 band numbers in 1/lgR of 1.8- and 1.9-order. In Area B that is 25 band number in 1/lgR of 1.5-order > 20 band numbers in R of 1.3- and 1.8-order > 19 band numbers in of 1.3-order > 18 band numbers in lgR of 1.3- and 1.4-order > 15 band numbers in 1/R of 1.5-order. In Area C that is 98 band numbers in 1/R of 0.8-order > 76 band numbers in lgR of 1-order > 26 band numbers in of 1.2-order > 10 band numbers in R of 1.2-order > 2 band numbers in 1/lgR of 1.2-order.
We count the number of bands where the correlation coefficient between different spectral transformations and Na+ passed the 0.01 test pretreated by FOD. In each spectrum, there are many FOD band numbers that exceed the integer-order, and they are concentrated in higher-order FOD derivative (1.2- to 1.6-ordder). For example, the band numbers of FOD are more than integer 1.0-order, it mainly appears in the 1.4- to1.9-order of each spectrum in the Area A, it mainly appears in the 1.2- to1.9-order of each spectrum in the Area B, while in the Area C it mainly appears in the R and from 1.2- to 1.6-order, in the 1/R from 0.6- to 0.9-order or 1.2- to 1.3-order.
Whereas it can been seen that the band numbers of FOD are more than integer 2.0-order from
Figure 6, it mainly appears in the 1.7- to 1.9-order of each spectrum in the Area A, it mainly appears in the 1.3- to 1.9-order of each spectrum in the Area B, and in the Area C it mainly appears in R,
, 1/R of 0.9- to 1.1-order, as well as 1.2-order of 1/lgR.
3.5. The Maximum Correlation Coefficient between Each Spectrum and Na+ Pretreated by FOD
We analyze the absolute value of the maximum correlation coefficient between each spectrum and Na
+, as well as its corresponding fractional-order and band (
Table 4,
Table 5 and
Table 6). Overall, with the increase of the FOD, the absolute value of the maximum correlation coefficient of each spectrum at different orders shows a trend of first increasing and then decreasing, and the improvement of the correlation coefficient by the low-order derivative is small. While the improvement of the correlation coefficient by the higher-order derivative is great, for example, 1.4- and 1.5-order in Area A, 1.8- and 1.9-order in Area B, and 1.0- to 1.8-order in Area C.
In addition, the maximum correlation coefficient of each spectrum appears in the fractional order under different FOD, such as, the absolute value of the maximum correlation coefficient for five spectrum (R, , 1/R, lgR, 1/lgR) and its corresponding fractional-order and band in Area A are 0.5948 and 1.4-order of 1103 nm, 0.6081 and 1.4-order of 1103 nm, 0.6335 and 1.5-order of 1103 nm, 0.6193 and 1.5-order of 1103 nm, 0.5770 and 1.9-order of 2301 nm, respectively. They are 0.6820 and 1.9-order of 434 nm, 0.6699 and 1.9-order of 434 nm, 0.6155 and 1.7-order of 434 nm, 0.6538 and 1.8-order of 434 nm, 0.6800 and 1.9-order of 434 nm, respectively in the Area B. While they are 0.5644 and 1.8-order of 1694 nm, 0.6204 and 1.3-order of 556 nm, 0.6265 and 1.7-order of 1694 nm, 0.6680 and 1.4-order of 555 nm, 0.5189 and 1.1-order of 886 nm, respectively in the Area C.
Therefore, whether it is the original hyperspectral or the transformed hyperspectral under different human interference areas, the absolute value of the maximum correlation coefficient between the hyperspectral reflectance of each spectrum and the cation Na+ appears in the FOD, and its corresponding bands in Area A are 1103 nm (R,
, 1/R, lgR) and 2301 nm (1/lgR), and they appear in 1.4-, 1.5-, 1.9-orders. In Area B they are 434 nm (R,
, 1/R, lgR, 1/lgR), and they appear in 1.7-, 1.8-, and 1.9-orders. While in the Area C they are 555 nm (lgR), 556 nm (
), 886 nm (1/lgR) and 1694 nm (R, 1/R), and they appear in 1.1-, 1.3-, 1.4-, 1.7-, 1.8-orders (
Table 4,
Table 5 and
Table 6).
4. Discussion
4.1. Fractional-Order Derivative Improves the Resolution between Hyperspectral Peaks
In the derivation calculation process of the FOD, the derivation calculation itself is a method to increase the resolution of the spectral signal, and the selection of the order has the characteristics of continuity, so the detailed change process of the derivative value of the hyperspectral reflectance can be accurately displayed, and the resolution between the peaks of the spectrum can be improved. For example, as the order increases, the peaks and valleys in the hyperspectral reflectance curve become more and more obvious (
Figure 1,
Figure 2 and
Figure 3).
FOD is a derivative that extends the integer-order to any order. Because of its advantages of “memory” and “globality”, it can more clearly describe the physical characteristics of the system, and reveal the non-linear characteristics and variation laws of the field hyperspectra of saline soil. That is, when the order of FOD increases from 0.0-order to 1.0-order, the hyperspectral reflectance curve of each order slowly approaches the 1.0-order hyperspectral reflectance curve, and the result of the derivate value reflects the increased sensitivity to the slope of the hyperspectral reflectance curve. While the order of the FOD is increased from 1.0-order to 2.0-order, the hyperspectral reflectance curve of each order slowly approaches the 2.0-order hyperspectral reflectance curve, and the result of the differential value reflects the increased sensitivity to the curvature of the hyperspectral reflectance curve. Therefore, the former describes various changes from 0.0-order derivation to 1.0-order derivation, and the latter describes in more detail the subtle difference between the slope and curvature of the hyperspectral reflectance curve. This further illustrates that FOD calculation can enhance the pretreatment effect of soil field hyperspectral data, improve the resolution between hyperspectral peaks, and highlight the “sensitivity” characteristics of FOD.
In addition, as far as this research is concerned, we compare and analyze the change law of the correlation coefficient of each derivative for each transformation and the influence of the derivative processing on the correlation coefficient, which can explore the application value of fractional-order derivatives in hyperspectral data preprocessing.
4.2. Comparison of the Fractional-order derivative and Integer-order derivative
According to the theory of integer-order derivatives, the first derivative of the differentiable function
is defined as:
The second derivative of the function is defined as:
The third derivative of the function is defined as:
If the derivative order of the function is increased to a higher-order n, then the n-order derivative of the function can be written as follows:
If the gamma function is used to replace the binomial coefficients of Formula (11), and the derivative order is extended to a non-integer order, then the Grünwald-Letnikov fractional derivative (Equation (5)) can be obtained.
It can be seen from the derivation of the above formula that the FOD extends the order to a non-integer order, generalizing the definition of the derivative, and when the derivative order is a positive integer, the integer-order derivative becomes a special case of the FOD. In the numerical calculation process, the integer-order derivative is only related to the information of the points in the derivative window, and has nothing to do with the points far away. While the FOD is not only related to the value of this point, but also related to the value of all points before this point.
For the fractional-order derivative, it can be seen from Equation (6) that the value of the v-order FOD of the function
f(X) in a certain waveband is not only related to the hyperspectral reflectance
f(X) of this waveband, but also related to the previous wavebands, namely, it is related to
f(X−1), f(X−2),
f(X−3), …,
f(X-n). This phenomenon shows that the closer the point is, the greater the weight and the impact is. On the contrary, the farther the point is, the smaller the weight, and the influence also decreases. These are the well-known “memory” and “non-locality” of the FOD. It is also the biggest difference between the fractional-order derivative and the integer-order derivative [
29,
30,
31,
32].
In addition, the order choice of FOD is not limited to integers, and the order of operations is expanded [
33,
34,
35,
36], which has a wider selection range and higher degree of freedom than integer-order derivatives. Meanwhile, many systems belong to the fractional-order, and the integer-order derivative model is used to describe it, which will lead to a large deviation between the model and the actual result, and the system simulation and prediction cannot be performed well, it also ignores the authenticity of the system to a certain extent.
4.3. The Percentage Improvement of the Fractional-Order Maximum Correlation Coefficient Compared with the Integer-Order
Compared with the absolute value of the maximum correlation coefficient of integer-order, the percentage increase of the absolute value of the maximum correlation coefficient of fractional-order in each spectrum is studied (
Table 7). From
Table 4,
Table 5 and
Table 6, it can be seen that the fractional-order where the maximum correlation coefficient between the five transform spectra and the cation Na
+ is located is 1.4-, 1.5-, 1.9-orders in Area A, and 1.7-, 1.8-orders in Area B, and 1.1-, 1.3-, 1.4-, 1.7-, 1.8-orders in Area C.
Compared with the integer-order 1.0-order, the fractional improvement percentages of the five spectra are all greater than 0.22% in the Area A, greater than 7% in the Area B, and greater than 1.7% in the Area C. Among them, the 1.9-order of 1/lgR transformation has the largest increase percentage in Area A, which is 2.85%; the 1.9-order of 1/lgR transformation has the largest increase percentage in Area B, which is 14.79%; the 1.4-order of lgR transformation has the largest increase percentage in Area C, which is 4.97%.
Compared with the integer-order 2.0-order, the fractional improvement percentages of the five spectra are all greater than 0.6% in the Area A, greater than 0.05% in the Area B, and greater than 5.5% in the Area C. Among them, the 1.5-order of 1/R conversion in the Area A has a maximum increase of 5.30%; the 1.7-order of 1/R conversion in Area B has a maximum increase of 4.11%; the 1.4-order of lgR conversion in the Area C has a maximum increase of 17.23%.
Regardless of whether it is compared with the 1.0-order or the 2.0-order integer-order, the percentage of increase in the absolute value of the maximum correlation coefficient between the FOD and the cation Na+ in the three regions is mostly more than 3%, and the highest is more than 17%. It can be seen that the effect of the fractional-order on the correlation between hyperspectral and cation Na+ is significantly better than that of the integer-order.
4.4. The Advantages of Different Transform Spectra
The advantages of different transform spectra are as follows:
We perform non-linear mathematical transformation on the original spectral reflectance (R). Non-linear mathematical transformations that are often used mainly include: root mean square transformation (), reciprocal transformation (1/R), logarithmic transformation (lgR), logarithm reciprocal transformation (1/lgR). The main purpose of this implementation is as follows:
On the one hand, the purpose of introducing these spectral transformation forms is to enrich spectral data, increase the sensitivity of spectral data to the properties of the soil to be tested, and improve the correlation between the spectral data and soil property, so that the relationship between the data can be found more conveniently.
On the other hand, the implementation of nonlinear transformation can enhance the spectral difference to a certain extent and reduce the influence of multiplicative factors caused by changes in lighting conditions, also can distinguish the influence on the spectrum caused by the difference of the surface parameters.